Exploring Students’ Metacognitive Knowledge: The Case of Integral Calculus

Abstract

Previous studies of integral calculus have mainly explored students’ conceptual and procedural knowledge; only a few have focused on students’ metacognition in relation to integral calculus. The study reported here explored students’ metacognitive knowledge of integral calculus by interviewing nine first-year university and eight Year 13 students. The design of the interview questions was based on the structure of metacognitive knowledge in Revised Bloom’s Taxonomy. The findings suggest there are differences between students’ metacognitive knowledge at Year 13 and the first year of university. In particular, the importance of knowing the rationale behind the theorems and formulas was not obvious for Year 13 students. Moreover, students’ metacognitive knowledge could be developed further at both levels, particularly in terms of developing strategies to identify how integral calculus questions could be solved and to check the outcome of problem-solving.

1. Introduction

Metacognitive knowledge is “knowledge of cognition in general as well as awareness and knowledge of one’s own cognition” [1] (p. 46). Metacognitive activities are necessary for becoming a successful mathematical problem solver [2,3,4]. So far, however, there has been little discussion in the literature about metacognitive knowledge in relation to the teaching and learning of mathematics at upper secondary and tertiary levels. Integral calculus is one of the topics involved in mathematical courses at these levels, one that has several applications in different disciplines (see, [5]) and is a key subject in transitioning from secondary to tertiary education [6]. It is part of gateway mathematics courses at universities for many majors and is important for the development of the sciences [7]. Several studies have explored students’ learning of integral calculus. These studies provided some useful information regarding students’ understanding of integral calculus in terms of their conceptual and procedural knowledge (e.g., [8,9,10,11]). However, no study was found that explored metacognitive knowledge in relation to students’ learning of integral calculus. This study seeks to address this gap in the literature by answering the following questions: what metacognitive knowledge do students hold about integral calculus in Year 13, the last year of secondary school in New Zealand, and the first year of university? What differences exist between students’ metacognitive knowledge at these two levels? These two groups were chosen as Year 13 students have less experiences of studying integral calculus compared to first-year university students. Given the different academic experiences, it would be interesting to know if there are any corresponding differences in the metacognitive knowledge each group developed. Moreover, several studies highlighted the issues students face during the transition from secondary to tertiary level (e.g., [12,13]). For instance, many students may face difficulties in university since mathematical concepts are presented in more depth and problems require more technical and conceptual understanding in comparison to secondary level teaching [14]. Exploring students’ metacognitive knowledge between these two levels could shed light on which aspect of Year 13 students’ metacognitive knowledge needs further development to be able to fit with the academic rigor of studying mathematics at the tertiary level. These research questions will be explored in relation to the Revised Bloom’s Taxonomy (RBT) [1] structure of metacognitive knowledge, as it is a useful tool for exploring the teaching, learning, and assessment of mathematics [15].

2. Literature Review

In this section, metacognition, metacognitive knowledge, and previous studies in relation to integral calculus are described to frame the study.

2.1. Metacognition and Metacognitive Knowledge

Since the introduction of the term ‘metacognition’ by Flavell in 1976, different operational definitions of metacognition have been introduced (see, [16]). A group of scholars believed cognition and metacognition are separate entities and hierarchical in nature (e.g., [17]), while another group believed cognition and metacognition are integrated (e.g., [18]). For instance, Shoenfeld [17] believed metacognition works as an executive control, helping to solve mathematical problems by self-regulating, monitoring, and controlling the allocation of resources. On the other hand, Kramarski et al. [18] highlighted to teach metacognition effectively, its teaching should be embedded in the teaching of the content.

Despite these differences, many scholars agree that metacognition is a model of cognition that works at a meta-level to cognition by monitoring and controlling cognitive tasks [19,20]. It is a reflection on thinking that successful learners have, which enables them to monitor, assess, and modify their thinking processes while engaged in a learning task [21,22]. “It can help students develop their knowledge for teaching themselves and improve positive learning transfer to new settings and events” [21] (p. 377).

The development of metacognition happens gradually by constructing or identifying efficient cognitive strategies to replace inefficient ones [23,24]. Many scholars agree that metacognitive abilities improve with age; however, monitoring and evaluating cognition was found to develop slowly and might not be complete in many adults (see, [24]). Through adolescence and young adulthood, strategic knowledge continues to develop when learners understand the interactions between variables of memory such as task features, effort, and strategies [24]. Many studies have reported that metacognition is teachable, and several specific instructions have been suggested in this regard (e.g., [24,25,26]). For instance, Schraw [25] recommended, during teaching and problem-solving in classrooms, a checklist with sections for planning, monitoring, and evaluation, with sub-questions included under each section, could be used to help students to be more systematic and efficient during problem-solving.

Metacognition has three facets, including metacognitive knowledge or knowledge of cognition, metacognitive skills or regulation of cognition, and metacognitive experiences or concurrent metacognition [19,21,26,27,28,29].

Metacognitive knowledge, the focus of this study, is a declarative knowledge about cognition which derives from a person’s long-term memory about him/herself or others [19]. It refers to individuals’ explicit or implicit knowledge (e.g., ideas and beliefs) about different factors, including persons, tasks, goals, and strategies [19,27,30,31]. The person factor addresses how individuals perform and feel about different tasks; the task factor refers to task categories, features, relationships, and the way they work; the goal factor is about the goals individuals pursue when engaged with a task; and finally, the strategy factor refers to different strategies that should be used to complete a task and when, why, and how these strategies should be used [19,27]. Metacognitive knowledge also encompasses knowledge about the different cognitive functions (e.g., thinking and memory) in terms of what they are and how they work [19,27]. Self-monitoring, monitoring others’ cognitive activities, communicating with others, and awareness about personal metacognitive experiences could help to constantly develop, update, and revise metacognitive knowledge [21,27,28].

Metacognitive knowledge is different from metacognitive skills and experiences. Metacognitive knowledge is a declarative knowledge about cognition while metacognitive skills consist of procedural knowledge [19], helping individuals to control their cognitive activities (e.g., mathematical problem solving) [25] by deliberate activities such as task orientating, planning, monitoring, regulating, and evaluating [19,27]. Unlike metacognitive knowledge and skills, metacognitive experience is present in working memory [19] and includes awareness and feeling when dealing with a task and processing information [27] (p. 279). As a consequence of these differences, two different methods are suggested to explore these facets: offline and online methods [15,26]. Offline methods are those that assess metacognitive knowledge without concurrent problem-solving assessment, whereas online methods assess metacognitive skills and experiences during problem-solving activity [26].

Recently, Radmehr & Drake [10,11] have explored the metacognitive experiences and skills of students in relation to integral calculus. The findings show that during mathematical problem solving, many students do not check their responses, and their judgments of their ability to solve a mathematical problem are not accurate and need further improvement. However, previous studies have not explored what metacognitive knowledge students hold in relation to integral calculus. For example, are students aware of the importance of monitoring strategies for improving their ability to solve mathematical problems successfully? Are they aware of such monitoring strategies? Or there are other reasons for not using these strategies during mathematical problem-solving.

2.2. Integral Calculus

Integral calculus is important for understanding a wide range of real-world problems, including a range of contexts in physics and engineering (e.g., [32]), and is also significant when studying mathematics (e.g., real and complex analysis) [33]. However, it has been less frequently explored than other fundamental calculus topics [34]. Previous studies (e.g., [34,35,36,37,38,39]) have reported that students can have difficulties with concepts within integral calculus such as the integral–area relationship, the relationship between integrals as a function and the algebraic sum of areas, and the Fundamental Theorem of Calculus (FTC). In particular, while the majority of students can successfully apply basic procedures for finding antiderivatives, their conceptual understanding is limited. For instance, Thomas and Hong [38] highlighted that some students consider integral calculus “as a series of processes with associated algorithms and do not develop the grasp of concepts which would give them the necessary versatility of thought” (p. 577). Previous studies have also reported that students can have difficulties with understanding the definite integral as an area under the curve for piecewise-defined functions and improper integrals [40]. Furthermore, Kiat [36] found that if the graph of the integrand is not given to students, some students fail to set up integrals correctly for finding the area, which Kiat suggested is due to their understanding of definite integrals being procedural and that they cannot make the connection between a definite integral and area.

Several important concepts are involved in Riemann sums and the definite integral $\underset{n\to \infty }{\lim }{{\displaystyle \sum }}_{k=1}^{n}f\left(c_i\right)\Delta x$, including series, functions, limits, rate of change, and multiplication [41]. Students’ difficulties with understanding the definite integral as the limit of a sum have also been highlighted in the literature [42,43]. For example, Sealey [43] found that the product of $f\left(x\right)$ and $\Delta x$ in the definition of the definite integral is the most complex part of problem-solving for students. “Difficulties in this layer are not necessarily related to the operation of multiplication and performing calculations, but are typically related to understanding how the product is formed and understanding how to use each factor within the product” ([43], p. 238).

The FTC is another important part of integral calculus, because it connects the definite and indefinite integral and offers an efficient method for evaluating definite integrals that uses anti-derivatives [5]. The FTC describes the relationship between the accumulation of a quantity and the rate-of-change of the accumulation [39] and is recognized as one of the intellectual hallmarks in the development of calculus [44]. To understand the FTC, encapsulating both differentiation and integration seems to be required [38]. The literature shows that many students who could apply the FTC to find a definite integral did not know why the FTC provides the results [10]. Student difficulties with the FTC were found to be related to their understanding of function (e.g., [39]), limits (e.g., [32]), rate of change [39], and the notational aspect of the accumulation function [32]. Several studies have also highlighted that both undergraduate and high school students have several difficulties with understanding limits (e.g., [45]), which might prevent them from understanding the FTC [32]. From the notational aspect, the role of $t$ in ${{\displaystyle \int }}_a^{x}f\left(t\right)dt$ is confusing for several students [32]. The concept of accumulation function in the FTC, represented by $F\left(x\right)={{\displaystyle \int }}_a^{x}f\left(t\right)dt$, involves several parts that make it hard for some students to understand it [32]. First, students should understand that $f\left(t\right)$ is a number depending on the value of $t$. Second, they need to have a covariational understanding [44,46] of the relationship between $t$ and $f$, which means understanding that as the value of $t$ changes from $\left[a,x\right]$, the value of $f\left(t\right)$ varies accordingly. Third, students need to understand the bounded area accumulating as $t$ and $f\left(t\right)$ vary, and that these values are changing in tandem [32].

As shown, the literature provides some useful information regarding students’ understanding of integrals in terms of conceptual and procedural knowledge (e.g., [37]). So far, however, no study was found that explores students’ metacognitive knowledge in relation to integral calculus, the focus of this study. In the following section, the method of the study is described.

3. Method

The study being reported is a multiple case study [47]. In the study, a case was considered to be an educational institution in New Zealand (i.e., a university or a college (also called secondary school or high school in New Zealand)) in which integral calculus was taught in the 2014–2015 academic year. Data from the cases were collected through student interviews. The goal of the case study was to understand students’ metacognitive knowledge in relation to integral calculus questions. The rationale for such a design was that university and Year 13 students might have different metacognitive knowledge about integral calculus because of the different contexts in which they were learning. The data collected were analysed using an abbreviated version of grounded theory [48]. In this approach, researchers only collected data in one phase, and “theoretical sensitivity, theoretical saturation and negative case analysis can only be implemented within the texts that are being analysed” [48] (pp. 221–222) because of time or resource constraints. However, the principles of grounded theory were followed (i.e., the processes of open, axial, and selective coding and conducting constant comparative analysis) in this abbreviated version [48].

3.1. Study Participants

Case 1 was one of the major universities in New Zealand and Case 2 was one of the colleges in the Wellington region. These two cases were selected as they offer calculus courses regularly to students and also were accessible to the researchers for data collection purposes. Theoretical sampling [49] was used to choose Case 2 students for interviews. To obtain this sample, students with different calculus backgrounds were selected from a scholarship and a regular class to develop a rich understanding of students’ metacognitive knowledge. Scholarship students were high-achieving students who had an hour weekly additional class to learn more advanced mathematics. Two students from each of the four identified achievement groups (i.e., low, medium, high, and scholarship students) were chosen. Students’ calculus backgrounds can be identified by their student code (

Table 1. College students who participated in the interviews.

Identifying Code	Gender	Calculus Background
Y1	Male	Low
Y2	Male	Low
Y3	Male	Medium
Y4	Male	Medium
Y5	Male	High
Y6	Male	High
Y7	Male	Scholarship student
Y8	Male	Scholarship student

); therefore, any connections between students’ metacognitive knowledge and their calculus background can be identified. All of the participants from the college were male. Two teachers of the college identified the suitable participants and invited them to participate in the research. The teachers told them the participation in the research was voluntary.

Convenience sampling was used to choose the university students, as the lecturers did not know their students’ calculus background. All students enrolled in the course were invited via email to participate, and nine students (seven males and two females) volunteered. During interviews, different levels of mathematical performance were observed.

This paper was part of a larger study that explored six aspects of students’ knowledge, abilities and skills in relation to mathematical problem solving using a recent framework designed by Radmehr & Drake [15]. These six aspects were (1) factual, (2) conceptual, (3) procedural, and (4) metacognitive knowledge, (5) metacognitive experiences, and (6) metacognitive skills. In this paper, parts of the results in relation to the metacognitive knowledge are reported. Nine integral questions were used to explore the students’ factual, conceptual, and procedural knowledge in relation to integral calculus. The think-aloud protocol was used to explore students’ metacognitive experiences and skills while solving the integral questions. For exploring students’ metacognitive knowledge, 13 questions were designed based on RBT’s metacognitive knowledge. Only seven of these questions are reported in this paper because of the words limit of a research paper. All students, except one, answered the nine integral questions first and then answered the metacognitive knowledge questions. Overall, students were able to score a total of 36 marks. The analysis of responses showed that the students had a mean score of 23.4 with standard deviation 8.0, which indicates that students achieved a range of different scores, suggesting that, similar to the college students, they had different levels of achievement (

Table 2. University students’ performances in the integral test.

	U1	U2	U3	U4	U5	U6	U7	U8	U9
Score on the integral questions	13	8	27	29	30	26	20	30	28

).

3.2. Instrument

As mentioned earlier, metacognition has three facets (i.e., metacognitive knowledge, metacognitive experiences, and metacognitive skills). To explore students’ metacognition in relation to each facet, different approaches have been suggested [15]. In particular, to explore students’ metacognitive experiences and skills verbalizing thought, using a think-aloud protocol during solving a mathematical task was found to be a useful method [10,11,50]. However, to explore students’ metacognitive knowledge, which is declarative knowledge, using such a method is not appropriate. Instead, students could be asked a set of questions about what they do when they face specific mathematics-related situations [15].

To explore students’ metacognitive knowledge, the design of the interview questions (

Table 3. Questions that probe metacognitive knowledge in relation to integral calculus.

Item	Interview Questions Used
M1	Do you take notes in class? Why/Why not?
M2	Do you do any pre-reading before attending sessions in relation to integral calculus? Why/Why not?
M3	Do you look at your previous lecture notes, or textbook, etc before coming to the classes? Why/Why not?
M4	Have you made a summary of the concepts, formulas, or procedures presented in integral calculus for yourself? Why?
M5	When you are studying integral calculus do you think about the justification or rationale behind the formulas or do you just try to apply the formulas? Why?
M6	How do you check your answers when solving problems involving finding the area enclosed between curves? How about the Fundamental Theorem of Calculus?
M7	Do you have a plan for solving problems related to enclosed area between curves? Why/why not? How about a plan for solving problems related to the Fundamental Theorem of Calculus? If not, can you create one now?

) was based on the Revised Bloom’s Taxonomy (RBT) [1] structure of metacognitive knowledge. RBT is a powerful framework to explore the teaching, learning, and assessment of a topic. Of the three facets of metacognition highlighted in the literature, metacognitive knowledge is explicitly highlighted in RBT’s knowledge dimension [1]. RBT’s metacognitive knowledge is designed based on Flavell’s conceptualization of metacognition [28]:

In Flavell’s [28] classical article on metacognition, he suggested that metacognition included knowledge of strategy, task, and person variables. We have represented this general framework in our categories by including … strategic knowledge, …, knowledge about cognitive tasks, [and] self-knowledge [1].

(p. 56)

Metacognitive skills and experiences are not explicitly mentioned in the RBT, but these two facets are implicitly addressed in the RBT table (see, [51]). As part of its knowledge dimension, RBT identifies that metacognitive knowledge has three different subtypes: (1) strategic knowledge; (2) knowledge about cognitive tasks, including appropriate contextual and conditional knowledge; and (3) self-knowledge [1]. The questions reported in this study relate to the first subtype, strategic knowledge—“knowledge of general strategies for learning, thinking, and problem solving” [1] (p. 56). Learning strategies are grouped into three categories: rehearsal, elaboration, and organizational [1]. The first four questions (M1 to M4) relate to the elaboration and organizational aspects of learning strategies. M1 explores to what extent students take notes during teaching. Note-taking has been found to be useful for encoding information and also works as an external storage of information, helping students to improve their learning and retention of information [52]. M2 investigates whether students undertake pre-reading before attending teaching sessions. Here, the literature highlights that pre-reading reinforces students’ prior knowledge and helps relate new topics to their prior knowledge [53]. M3 explores to what extent students review previous teaching materials before attending class. Reviewing previous materials before class is a study technique suggested in the literature (e.g., [54,55]). M4 explores to what extent students use summarising strategies to assist them in learning mathematics. The literature identifies summarising as a tool that helps students learn [56,57,58]; it helps students comprehend knowledge and more easily transfer knowledge to long-term memory as it motivates them to read for understanding, identify important ideas, and express them using their own words [57]. Summarising can also help students to make connections between the new concepts and their prior knowledge [56]. However, there is little research about how useful summarising strategies are for learning mathematics and how much they are being used by students.

Another aspect of strategic knowledge is “general strategies for deductive and inductive thinking, including evaluating the validity of different logical statements, avoiding circularity in arguments, making appropriate inferences from different sources of data, and drawing on appropriate samples to make inferences” [1] (p. 57). To address this aspect of strategic knowledge, M5 was designed to explore whether students are aware of the importance of the proofs and rationales behind mathematical formulas and theorems. Mathematical proofs are a mechanism to connect different parts of mathematical knowledge [59]. They are an intersection between students and experts [60] and one of the main parts of professional mathematical practice [61].

In addition to these general learning strategies, strategic knowledge also includes the knowledge that planning, monitoring, and regulating cognition are useful for learning a topic and being a successful problem-solver [1,62]. Consequently, M6 was designed to explore what monitoring strategies students are aware of for checking the answers of integral calculus questions. However, as monitoring strategies are often topic-specific, students were asked a more directed question about the topics of integral-area relationships and the FTC. As the literature notes, these are two core aspects of learning about integral calculus that students can struggle with [34,35,36,37,38], and addressing these two topics should provide a good indication of the use of monitoring strategies in integral calculus as a whole. Finally, M7 investigates the complexity of students’ plans for solving integral questions, but again addresses the specific topics of integral-area relationships and the FTC, for similar reasons. Making a solution plan is part of metacognition in the domain of mathematics [17], while asking students to make a plan also identifies whether verifying answers is part of their plan or not.

The interviews were conducted by the first author. He was one of the tutors of the calculus course at the university, but he has no relationship with the college students. The interviews with university students took place in the university in the free time of the students. The interviews with the college students took place in the college during the study time of the students.

4. Results

In this section, the students’ responses are presented question by question.

4.1. M1: Taking Notes in Lectures, Tutorials, and Classes

Most students in the sample took notes while attending classes and were aware of the importance of taking notes. In detail, thirteen students (U1234567; Y124568, the notation means U1, U2, U3, U4, U5, U6, U7, Y1, Y2, Y4, Y5, 6, and Y8) took notes when attending lectures, tutorials, and classes. The remaining four students (U89; Y37) did not take notes. The reasons for taking notes are summarised in

Table 4. Reasons for taking notes.

	Case 1	Case 2	Total
Useful for studying later, including reviewing and revising the materials	1 (U4)	5 (Y23568)	6
Useful for learning the steps of problem solving and understanding the topic	1 (U2)	2 (Y16)	3
Helpful for remembering the topic	1 (U6)	1 (Y4)	2
Good for “engaging brain”	2 (U25)	0	2
Useful to “supplement textbook and online notes”	2 (U37)	0	2
Easier to follow than online notes	2 (U46)	0	2
Good for keeping students focused	1 (U4)	0	1

.

The four students who did not take notes gave a variety of reasons for this. Y3 believed it a waste of time as he could use the textbook to understand the topic. Y7 said he did not take notes this year because he was repeating the course. U8 did not take notes because he only used online notes and said, “…because we have online notes and I find it easier if I have got full attention to the material. But if it is an example, I try to follow along and compare them”. U9 said because calculus is computational and the material is not new; he did not need to write notes for this course; however, he took notes for other courses (e.g., discrete mathematics).

Comparing the responses of students of Case 1 and 2 shows that students from both cases were almost all aware of the importance of note-taking; however, in both cases, the instructors did not encourage or discourage students to take note. It should be noted the first author observed and video recorded the teaching of integral calculus in both Cases. The reasons provided for taking notes by Case 1 students were more diverse, while reasons provided by students from Case 2 were categorized into only three groups.

4.2. M2: Pre-Reading before Attending Lectures, Tutorials, and Classes

Most of the students in the sample did not pre-read before attending classes; only four students (U358; Y2) did. Most of these four students had similar reasons for their pre-reading. U8 did this to be introduced to the ideas so the lectures were easier to understand—the content was being seen for a second time. U5 believed that if she did not pre-read, she would not understand the topic in the lecture, while Y2 said: “It is easy to understand when you have taken a look ahead”. By comparison, U3 preferred self-learning, therefore, “read around the topic” before attending sessions. He added, “I go to lectures to pick up odd things, information, stuff, that might not come up naturally”.

Those who did not pre-read had different reasons for not doing so. Three students (U6; Y14) believed this was a good idea, but had never thought of doing so: “I did not think about it. Thinking about it, it would be a good idea, probably” (Y1). Y1 also said he did have time to pre-read. Two students (U2; Y6) believed they did not have time to pre-read. Two university students (U47) believed that they were not organized enough to pre-read before attending lectures. Four students (U9; Y758) believed the teaching of the instructor was enough for learning the topic, indicating a reliance on the instructor: “the teacher does everything” (Y5), and U9 said, “I think it is not necessary. I expect the lecturers to stand by themselves”. Y3 did not do any pre-reading because he preferred self-reading; therefore, he only attended classes because it was compulsory. Y8 said doing pre-reading may cause misunderstanding about the topic:

We cover all of the workings in class. We do not require to do pre-reading. I think it would be quite difficult because a lot of things that we are learning is complicated, so if we go and try to understand it ourselves, we might get the wrong idea, or we might not able to understand it. But if the teacher teaching it to us we might get a better idea and starting off from the right places rather than us starting off from a wrong place and have to do re-work to understand it.

[sic]

Comparing Case 1 and 2 responses shows that the usefulness of pre-reading is ignored by most of the students from both cases. However, the number of students who are aware of its usefulness was more in Case 1 (N = 3) compared to Case 2 (N = 1). In both Cases, the instructors did not encourage or discourage students from doing pre-reading. This might be the reason why no difference was found between cases.

4.3. M3: Reviewing Previous Materials before Attending the Next Session

This section is different from the previous section as it relates to studying topics that have already been taught in class, rather than new topics. Twelve students (U13457; Y1245678) had regularly studied previous material before attending the next session. These students found it:

• reinforced learning (U1345; Y678);
• helpful for doing homework/assignments (U7; Y1246); and
• helpful for remembering the material (Y25).

Two sample responses were: “it allows me to filter to unique lecture note. I can filter information that is not trivial, but, can be easily adapted [sic]” (U3); and, “help me understand it and makes it easier to understand new content which is based on it” (U4).

Students who did not regularly study previous material had different reasons for not doing so. U6 believed it is a good idea, but was not something she had thought of doing. U2 said he only looked at them if it helped him with assignments. Two students (U89) said they looked at these materials if they were confused or the topic was hard: “If I was confused, I would, but if I have got it, I am not looking at it again” (U9). U8 also looked at them if he had a problem with assignments. Y3 said that as he preferred to read the textbook at home instead of engaging in class discussion, he did not regularly review previous material before attending the classroom.

Comparing students of Case 1 and Case 2 shows that students from Case 2 reviewed previous materials before attending the next session more often compared to Case 1 students. However, similar to the previous strategies, there were no differences between the instructors in the sense that none of them encourage doing this learning strategy.

4.4. M4: Summarising Strategies

Eleven students (U12358; Y235678) said that they did not use any summarising strategies for learning these topics. The rest said they had done some sort of summarising or intended to do so later (

Table 5. Summarising strategies given by students for learning these topics.

Summarising Strategies for Learning These Topics	Case 1	Case 2	Total
Make a summary close to exams	3 (U469)	0	3
Add a summary to class-notes	0	1 (Y4)	1
Make a summary of the course materials in a page	1 (U9)	0	1
Make flip cards of steps	0	1 (Y1)	1
Summarise mathematical statements and make a list of possible ways to deal with similar statements	1 (U7)	0	1
None	5 (U12358)	6 (Y235678)	11

). Three students from Case 1 (U469) said they would make a summary of the materials close to their exams: “I write down everything in pages, then I make it smaller and smaller to a page. It is a process of writing and copying help me. It is how I study previously. Writing helps” [sic] (U9). U6 supported the idea that writing helped and added another reason why making summaries is useful: “writing it down helps you remember it. Also, for last minute study before going to the test, you can look at it [your summary].” Y1 used flip cards to remember the steps of problem-solving, which can also be considered a summarising strategy: “it kind of make it easier, rather than having a whole lot of information. You can break it down to particular things you need to remember. Make it easier to remember the procedures”. Y4 said he added a summary to his class-notes to know what he needed to focus on. U1 and Y8 said having a summary is useful, but they had not made one so far.

Students who had not done any summarising, or did not intend to, had different reasons for this (

Table 6. Reasons for not using summarising strategies for these topics.

Themes	Sub-Themes/Example	Case 1	Case 2	Total
Use other resources	Formula sheet	1 (U8)	3 (Y278)	4
Use other learning strategies	Summarising not necessary if you practice questions	0	3 (Y236)	3
	Read lecturer/class notes rather than summarising	1 (U8)	2 (Y68)	3
	Not for these topics because it is not complicated	1 (U5)	0	1
	“Never felt the need”	1 (U4)	0	1
Negative attitude toward summarising strategies	Dislike rote learning	1 (U3)	0	1
	Mathematics is not about memorizing stuff	0	1 (Y5)	1

). Four students (U8; Y278) said that because they had the formula sheet, they did not feel it necessary to make a summary:

No, I just use the formula sheet. I found that you need to practice how to use each formula, and then you can just see the formula there. You get faster at doing them. I think it is more effective than trying to memorize formulas.

(Y2)

U5 said she had done that before, but because these topics are not complicated, she did not feel it necessary to make a summary of them:

I do that for the trig, inverse trig, hyperbolic trig, and inverse hyperbolic trig. But for the FTC I did not do that because it is not that complicated…when you have lots of materials that look similar, you need to read it and compare.

U3 was against using summarising strategies because he felt it is related to rote learning: “No, I just make sure I am comfortable going through everything without it…I dislike rote learning…with understanding the relationships are obvious. The reason I like math is there is no real rote learning”. Y5 made a similar claim, saying “Mathematics is not a memorizing stuff [sic]”.

Similar to previous questions, summarising strategies were not suggested by the instructors of the Cases. Comparing Case 1 and Case 2 students reveals that while the majority of students did not summarise the materials they studied in these two topics, there were more students who were familiar with the usefulness of such strategy among Case 1 students. In contrast, Case 2 students seem to rely on formula sheets and practicing questions more than students of Case 1. Furthermore, one student from each case had a negative attitude toward summarising strategies.

4.5. M5: Thinking about Justifications behind the Formulas

In response to M5, eight students (U345689; Y57) said they had thought about the justification/rationale behind the formulas rather than just applying them. The remaining students said they had only applied the formulas. Students who just applied the formulas had different reasons for doing so (

Table 7. Reasons for not thinking about justifications.

Themes	Sub-Themes	Case 1	Case 2	Total
Negative attitude towards justifications	Do not need to know it/not in the examinations or questions	0	4 (Y1368)	4
	Do not have time to think about them	2 (U27)	0	2
	Sometimes justifications are more complicated than memorising them	1 (U1)	0	1
	Justifications confuse me	0	1 (Y1)	1
No access to justification	Have not seen a thorough justification for the topic	0	3 (Y248)	3
	Does not mention it in the textbook	0	1 (Y3)	1

). The main reason was that the exams did not have justification questions, so they did not need to learn them:

I think it can be quite interesting, but I guess it probably might not be necessary at this level if it is not asking questions about it in the exam… I think it is an extra; I think for most people, including myself, want to do well in exams...rather spending time making sure I am better at things which gonna be in the exam.

[sic] (Y6)

The second reason was not seeing a thorough justification for the materials in class. Y8 thought the integral calculus topic did not have thorough justifications behind it: “Not in the integration probably because they do not have a thorough understanding. I do in differentiation”. Y4 said that he would have liked to see justifications, but the teacher did not provide them because of time constraints:

I do wonder about the justification behind it… It allows to have a deep understanding of what you are actually doing with the formulas. I do not ask specifically, but I noticed people asking about it, but the teacher said we do not have time to explain it.

Two students from Case 1 (U27) said they did not have time to go over the justifications: “I wish I had time to think more about the rationale, but I am too busy applying trig identities in every conceivable combination” (U7). Y3, who said the justifications are not stated in the textbook, said: “when I do [questions from] the textbook, I am using the formulas, and I do not care about anything behind or around the question. I just do the question and get the answer”. Those students who had thoughts about the justifications behind the formulas had different reasons for doing so (

Table 8. Reasons of thinking about the justifications behind the formulas.

Themes	Sub-Themes	Case 1	Case 2	Total
Helpful for remembering, applying, or reproducing formula	Help to reproduce the formula when necessary	4 (U3458)	0	4
	Help to remember the formula	2 (U69)	0	2
	So, you do not need to remember the formula	1 (U4)	0	1
	It is easier to apply formula when you understand it	1 (U8)	0	1
Have a better understanding	To have a better understanding about the topic	2 (U89)	1 (Y7)	3
	Remembering the formula is not sufficient	1 (U5)	0	1
Have a better performance in exams, and when answering questions	It is easier not to make a mistake	1 (U8)	0	1
	Helpful for checking workings	1 (U5)	0	1
	To answer some questions, knowing the justification is necessary	0	1 (Y5)	1
	Maybe a question about the justification being asked in the scholarship exam	N/A	1 (Y7)	1

). Three main themes were found, including that they are helpful for remembering, applying, or reproducing formulas, to have a better understanding of the topic, and for better performance in exams and when answering questions.

A sample response from the first theme is, “I do not have to remember the formula. If I understand the concept I can come up with the formulas for different questions” (U4). In terms of the second theme, U8 said:

It just makes sense a lot better when I understand what is going on. That is what I like about the math. It is theorems and proofs, not just the tools. If I understand it, it is easier to apply it correctly and not make a mistake. If I do forget it and if I understood it, it is easier to reproduce it.

In relation to the last theme, U5 believed that by knowing the justification you could check your workings: “…otherwise, how can you double-check it is legit?”.

Comparing the responses of students from Case 1 and 2 shows that Case 1 students were more aware of the importance of knowing the justification behind the formulas. In detail, most of the students from Case 2 had a negative attitude towards exploring the justifications behind the formulas or had no access to these justifications. One possible reason for such findings might be related to the teaching of integral calculus in the Cases. In Case 1, the teaching was more conceptual, and Riemann sums were the focus of teaching definite integrals, and examples were solved in this regard. In addition, during the teaching of other topics, such as finding volume by slicing and cylindrical shells, the proofs for volume formulas were taught to students. The ideas used in those proofs are related to Riemann sums, and therefore can help students to have a better understanding of the Riemann sums and Riemann integral. However, in Case 2, the teacher did not introduce Riemann sums until end of the teaching of integral calculus and no example was solved in the classroom. This teacher had a procedural approach toward teaching definite integrals, i.e., “I am going to take the expedient route...I am going to give you the application…saying without proving…”. Such approaches toward teaching mathematics are related to instrumental learning which can have negative consequences for students’ learning (e.g., they influence their attitude toward mathematics and their understanding of the structure of mathematics).

4.6. M6: Strategic Knowledge: Monitoring Strategies

When responding to M6, students from Cases 1 and 2 mentioned different strategies for checking their answers in integral-area (

Table 9. Monitoring strategies for integral-area problems.

Themes	Sub-Themes	Case 1	Case 2	Total
Monitoring strategies related to integral-area relationship	Approximating the area using geometric shapes	6 (U134689)	2 (Y78)	8
	Check the area is positive	2 (U39)	3 (Y156)	5
	Check the antiderivative by differentiating it	2 (U27)	3 (Y458)	5
General monitoring strategies	Double-check/redo working	6 (U134568)	4 (Y2457)	10
	Use the Wolfram alpha website to check answers	5 (U34567)	0	5
	Check answers with classmates	2 (U46)	2 (Y67)	4
	Use the answers at the end of the textbook	0	4 (Y2346)	4
	Use assignment solutions	2 (U23)	N/A	2
	Use calculator to check answers/graph of curves	0	2 (Y36)	2
	Use the Maple software for checking answers	1 (U8)	0	1
	Long answer-simple equation: You probably do it wrong	1 (U6)	0	1
	Express the final answer as an English statement to see whether it makes sense	1(U7)	0	1
	Think about the answer before solving the problem and compare the answer with your thoughts	1(U6)	0	1

) and FTC (

Table 10. Monitoring strategies for the FTC problems.

Themes	Sub-Themes	Case 1	Case 2	Total
Monitoring strategies related to the FTC	Check the antiderivative using differentiation	4 (U45677)	2 (Y58)	6
General monitoring strategies	Double-check /redo working	4 (U3458)	1 (Y8)	5
	Check whether the final answer makes sense	1 (U6)	2 (Y28)	3
	Use the Wolfram alpha website	1 (U7)	0	1
	Check with classmates	1 (U4)	0	1
	Express the final answer as an English statement to see whether it makes sense	1 (U7)	0	1
None	N/A	3 (U129)	5 (Y13467)	8

) problems. However, three students from Case 1 (U137) highlighted that they did not have time to use monitoring strategies in their exams.

For integral-area problems, the most frequent strategy for checking answers was going over the calculation (U134568; Y2457). The second was approximating using geometric shapes to find out whether the answer makes sense (U134689; Y78). Using the fact that the area should be positive was a strategy mentioned by five students (U39; Y156); these students were aware that if the final answer is negative, then some part of their working is incorrect. As finding the area enclosed by curves using integration requires the antiderivative of the curves to be found, five students (U27; Y458) said they check whether they found the correct antiderivative by differentiating it. All of these strategies could be used equally successfully during exams and when working on problems outside exams.

For non-exam situations, five students from Case 1 (U34567) used the Wolfram alpha (Wolfram alpha has the capability to solve indefinite and definite integrals and if a person subscribes to the website, he/she can access step-by-step solution methods); U8 used Maple software, and two )U23) used the assignment solutions to check answers. However, students from Case 2 did not use these resources, and only two (Y36) said that they had used a calculator to check answers; rather, checking the answers at the end of their textbook was more common (used by four students, Y2346). Four students (U46; Y67) mentioned comparing their answers to those of their classmates. Several other strategies were only mentioned by one student. U6 from Case 1 noted that if you are dealing with a simple equation and your answer is long, you had probably done the question incorrectly. U7 writes the final answer as an English statement to find out whether it makes sense for him. Finally, U4, before solving the problem, thought about the possible answer, and then after finding the answer, he compared his answer with his initial thoughts.

The most frequent strategy for checking answers for the FTC problems was checking the antiderivative using differentiation (Table 10). This strategy is useful for questions that relate to the definite integral, the first part of the FTC. Students mentioned no specific strategies for checking questions related to the second part of the FTC. U3 highlighted that “I feel there is little I can do. Ensure understanding if you can. It is more abstract. Harder to check”. Double-checking/redoing working, checking whether the final answer makes sense, using the Wolfram Alpha site, checking with classmates, and expressing the final answer as an English statement are strategies mentioned by students that are not FTC specific, so were also mentioned in relation to integral-area problems. Eight students (U129; Y13467) said they were not sure how to check answers to FTC problems, suggesting they may not have had a good understanding of this theorem.

In both Cases, the instructors did not highlight the importance of monitoring strategies in relation to integral-area and FTC questions; however, comparing the monitoring strategies of Case 1 and Case 2 students for integral-area problems shows that students from Case 1 were more aware that the answer of integral-area problems could be checked by approximating the area using geometric shapes. Also, Case 1 students tended more often to use online websites to check their answers in non-exam situations. In contrast, calculators were used by Case 2 students more often compared to Case 1 students. Finally, Case 1 students had more diverse ways to check their answers compared to Case 2 students. In relation to the FTC questions, there were more Case 2 students who had no monitoring strategies for this type of questions compared to Case 1 students. Furthermore, similarly to the integral-area questions, Case 1 students had more diverse ways to check their answers to the FTC questions compared to Case 2 students.

4.7. M7: Strategic Knowledge: Problem-Solving Strategies

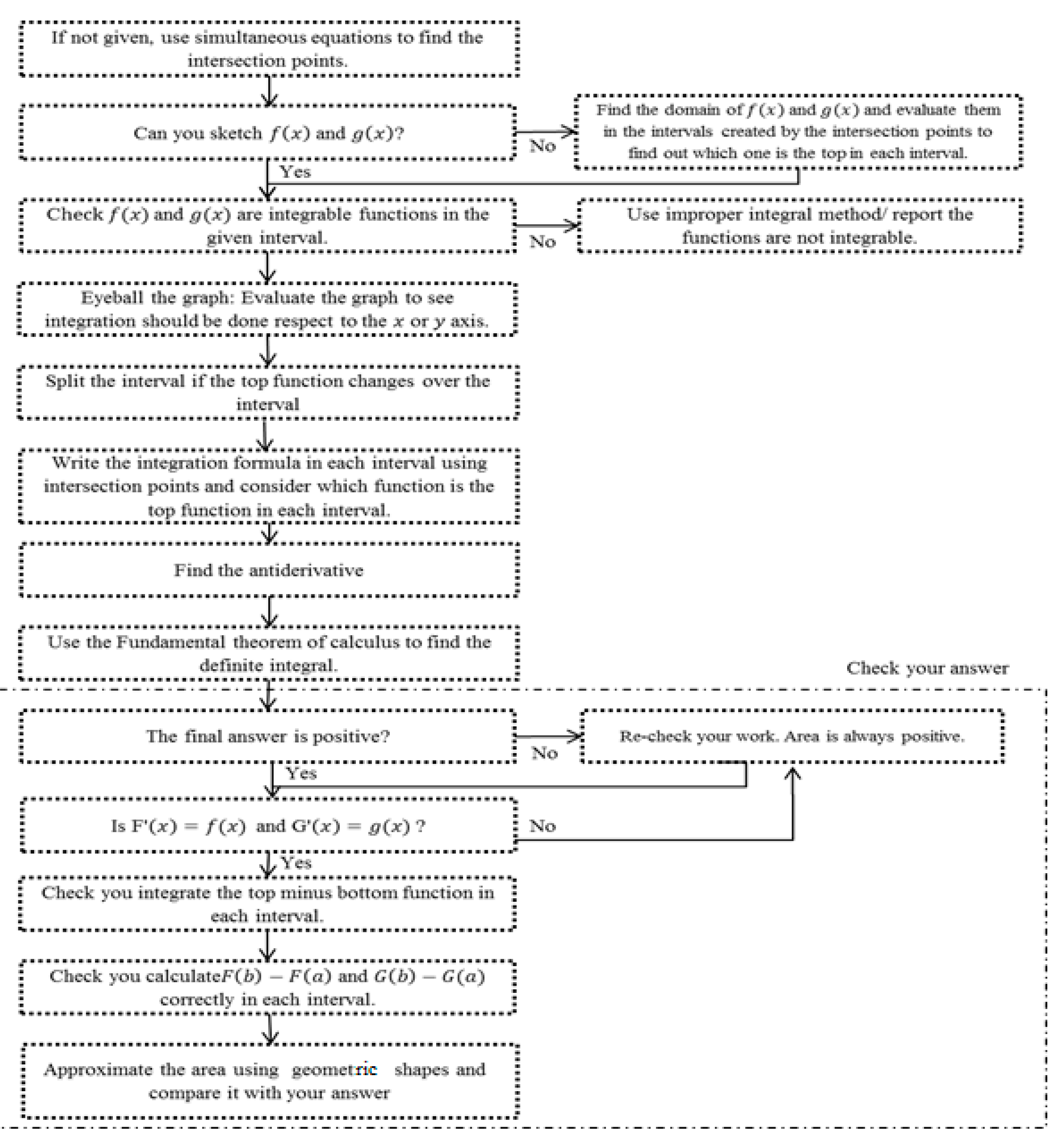
In response to M7, students were asked to pose two plans, one for how they would solve the enclosed area between curves problems, and one for the FTC problems. All students were able to provide a plan for the area between curves problems. Six plans (U23; Y1247) were general, and the remaining 11 plans were detailed (U1456789; Y3568). Those plans that had three, or less than three, steps were considered to be ‘general plans’, and those with more than three steps were considered to be ‘detailed plans’. A sample of a general plan was: “1. Look for the bounds. 2. Integrate the function. 3. Use appropriate formula to find the area” (Y4). An example of a detailed plan was “1. Visualise/sketch. 2. Find the top and bottom function. 3. Calculate $f\left(x\right)-g\left(x\right)$. 4. Integrate $f\left(x\right)-g\left(x\right)$ 5. Put the bounds in [the anti-derivative]” (Y6).

Students’ use of metacognitive knowledge when creating a plan to solve an integral-area problem was identified by looking for two features. First, checking that the integrand is continuous on the interval of integration (a specific strategy necessary for this type of problem), and second, checking/evaluating the processes and answers (which can include both specific and general strategies). Only U1 mentioned the process of checking the integrand is continuous as part of his plan. The first step in his plan is to “check that both curves are continuous on the closed interval - where you are trying to find the area”. In terms of checking the processes and answer, three students from Case 1 (U489) mentioned checking as part of their plans. U8, at the end of his plan wrote, “make sure the answer makes sense”. In U9′s plan, the final step was checking that the answer is positive. U4 had more checking processes in his plan. After he set up the integral for the enclosed area between curves, he checked that he had not made a mistake in writing $f\left(x\right)$ and $g\left(x\right)$ because he said I “usually write them wrong”. Then, after finding the area by solving the integral, he asked himself, “whether it [the answer] is reasonable.” He also said that before solving the problem, he tried to guess the answer to compare it with his final answer. If the final answer makes sense for him, he took “a quick look at the working”; if not, he took “a quite thorough look at the working”.

It is worth noting that ‘FTC problems’ is a broad category in integral calculus, and several types of question questions can be considered as FTC problems. Thirteen students (U134569; Y123467) had no plan for solving such problems. For example, U9 said, “no [I do not have any strategy, just] cry”, and U3 said, “if obvious, then solve, if not try something with no confidence”. Of the four students who created a plan, one related to the first part of the FTC (Y5), two related to the second part (U8; Y8), and one was a general plan (U7). Y5′s plan for the FTC was: “1. [consider the] power of the variable. 2. Raise or reduce depends on the question. 3. Change the shape of the graph. 4. Add/derive the power. 5. Check the answer, maybe”. Y8′s plan for the FTC was: “Try to get my head around stationary points and points of inflection”. His plan was suitable for contextual FTC questions similar to one proposed in Carlson et al. [44]. U8′s plan was related to FTC questions where students are asked to differentiate an integral (e.g., $\frac{d}{dx}\left[{{\displaystyle \int }}_{2x-5}^{4x+4}{t}^{3}dt\right]$), “If necessary, split up, use the chain rule to find resulting function”. The general plan mentioned by U7 was “1. Express the problem as a function. 2. Do all the maths stuff”.

At the end of the interview, all students were shown a plan similar to that in Appendix A, and this plan was discussed with them. Students were then asked if they would have liked to see such a plan while the topic was being taught. All the students thought this would be a good idea. For instance, U5 said, “It is super,” and U4 said, “It could be quite helpful to see something like this”. Some of the students provided more comments about the plan. For example, Y5 said, “It can show you step by step what you should do to get the correct answer”. Two students from Case 1 (U25) and all students from Case 2 said they would like to see a plan after some questions were solved in class, and U1 said he would like to see it at the start of the topic. Others did not provide any comment about when they wanted to see the plan. For instance, Y8 said, “…probably after you have been taught because if I did not know what I was doing and I got this, probably overwhelming. Probably have a few practical demonstrations of it”. U1, who would have liked to see a plan at the start, said:

Right at the start, to be honest, and when you go along at the end of each lecture you can come back and say this part is checked off and move on. Because we have a lecture on calculating the intersection points, one session finding the limits between two parts, you could refer back to the lecture, and at the end you have got your list and you can track through it. So, you feel equipped.

In both cases, the instructors did not pose a plan for questions in relation to integral-area and FTC; however, comparing the plans posed by students from Case 1 and Case 2 in relation to enclosed area between curves problems shows that no students from Case 2 considered checking as part of their plans, while four students from Case 1 considered some sort of checking as part of their plans. Furthermore, the number of students who posed detailed plans in Case 1 (seven out of nine students) was more than Case 2 (four out of eight students). However, such differences were not found between Cases in relation to the plans posed for the FTC problems.

5. Discussion

This study has added to the existing literature of mathematics education in at least three ways. First, for the first time, it explores students’ metacognitive knowledge in relation to integral calculus. Second, this is the first study that used RBT’s metacognitive knowledge as a framework to explore metacognitive knowledge in relation to a mathematical topic. This approach can be used by other researchers who are interested to explore metacognitive knowledge in relation to mathematics. Third, this study compared Year 13 and first-year university students’ metacognitive knowledge in relation to a mathematical topic. Such a comparison has not been conducted in the past. This study shows which aspects of students’ metacognitive knowledge in relation to the integral calculus need further development. The findings highlight that some aspects of Year 13 students’ metacognitive knowledge are less developed compared to first-year university students, mainly in relation to the importance of knowing the justification behind the formulas and monitoring strategies that can be used in integral problems. In the following, the obtained results for the questions are discussed in detail.

In relation to M1, Anderson and Armbruster [63], gave two main reasons for taking notes during classes, encoding and external storage. Encoding is important because it helps students learn and remember topics. Taking notes is considered as external storage because it preserves information for later use (e.g., for studying before examinations) [52,63]. These two reasons were identified by students as reasons for taking notes, indicating that students from both cases were aware of the usefulness of this practice. Therefore, the results indicate the presence of this aspect of metacognitive knowledge for a majority of students.

Regarding M2, the literature highlights that there is a direct relationship between pre-reading and academic achievement (e.g., [53,64]). Pre-reading reinforces students’ prior knowledge and relates new topics to students’ existing knowledge [53]. Pre-reading also relates to the idea of a flipped-classroom approach to teaching, “students prepare for class by engaging with resources that have been pre-prepared by their teachers” ([65], pp. 149-150), an approach that has gained more attention in the past few years (see, [65]). As most of the students in the sample had not used pre-reading and did not seem aware of its value, the results indicate that students may benefit from using this learning strategy, which could be suggested to them by lecturers and teachers.

Concerning M3, reviewing previous materials before attending class is one of the study techniques suggested in the literature (e.g., [54,55]). Most of the students in the sample did this and were aware of its effectiveness. Therefore, the results indicate the presence of this aspect of metacognitive knowledge for a majority of students.

In relation to M4, the literature suggests summarising as a tool that helps students to comprehend knowledge, facilitate transferring knowledge to long-term memory, and make connections between new concepts and students’ prior knowledge [56,57]. However, it was not used by most of the students in the sample. Two students also had negative attitudes toward summarising strategies, linking it to rote memorization. Overall, the value of summarising strategies was not well understood, which suggests that time could be well spent on both showing students how summaries can facilitate learning and teaching students strategies for making effective summaries. For example, if websites such as https://bubbl.us/ were used in class by lecturers and teachers as an example to show how different mathematical concepts and theorems in a topic are related to each other, students might also realize its usefulness and use summarising strategies for other topics as well.

Regarding M5, half the students from Case 2 thought they did not need to know the justifications behind the formulas they learned to use, while two more believed they did not have access to them. The comments of these six students indicate that their teachers felt that time pressures and the nature of the exam meant that thoroughly developing the mathematics the students were learning to use was a luxury rather than an essential part of their learning. This may have affected these students’ ability to develop a relational understanding [66] about integral calculus and how it should be learned. By way of comparison, most students from Case 1 were aware of the importance and usefulness of justifications. Given the importance of knowing the rationale behind theorems and formulas is addressed in the literature (e.g., [59]), this suggests that there is a good case for changing what is examined at secondary school, so that a conceptual understanding is developed.

In relation to M6, approximating area using geometric shapes, differentiating antiderivatives, and the fact that area should be positive are all useful monitoring strategies that can be promoted to students as useful ways to check answers of certain types of integral question. However, more than half of the students in the sample did not mention these strategies for checking answers. Perhaps if lecturers/teachers were to routinely ask, “how can we check this answer?” then discuss and model the use of appropriate strategies, more students might learn to use them.

Approximately half the students (8 out of 17) had no idea how they could check the answers of FTC problems. In particular, there was no specific strategy mentioned by students for checking questions related to the second part of the FTC. Strategies that can be used for checking answers in questions related to the second part of the FTC are not fixed, unlike questions related to the first part of the FTC or integral-area relationships. However, using the geometric interpretation of the second part of the FTC might be useful for checking whether the answer makes sense and could be discussed with students.

Five students from Case 1 had used Wolfram Alpha and one used Maple software to check answers on this topic, while none from Case 2 did so, possibly because their mathematics texts had the answers at the back of the book. Several websites can be used to check answers, some of which provide step-by-step solutions free of charge (e.g., http://www.integral-calculator.com/). Promoting such websites to college students could be beneficial as they would not only be able to independently verify if they are wrong, but also identify where they have gone wrong, which is especially useful when working through problems out of class time. Alternatively, if teachers were to use a site to compare solutions to questions that have been solved on the board, this might encourage college students to adopt the practice. Differences between the two sets of working would also encourage discussion about what is important to show as working, and the amount of working used, both of which would foster the development of relational understanding [66].

Finally, for M7, since for most students, checking whether the integrand was continuous or not, and monitoring problem-solving were not part of students’ plans for solving integral problems, working metacognitively could be emphasized more with students from both cases. The need for the first check could be established by asking students to find the area under curves that are not continuous over the interval such as ${{\displaystyle \int }}_{-3}^3\frac{1}{x}dx$ or ${{\displaystyle \int }}_{-\pi }^{\pi }\tan xdx$, encouraging students to sketch the curves to figure out whether the functions change during the interval of integration, and getting them to check solutions with something like Wolfram alpha. The use of monitoring strategies could be addressed when solving questions on the board by regularly asking students, “how could we check if this bit is right?” and if no strategy is forthcoming, introducing appropriate strategies, such as approximating the area using geometric shapes. The fact that more than half the students (13 out of 17, including five university students) had no plan for solving FTC problems is additional evidence that students have difficulty with this topic.

6. Conclusions

The number of studies focusing on metacognition in relation to the teaching and learning of mathematics at upper secondary and tertiary levels is limited. In detail, while a few studies in relation to metacognitive experiences and skills in relation to integral calculus have been conducted [10,11], no study was found that explored students’ metacognitive knowledge in relation to integral calculus. This study used questions based on the structure of RBT’s metacognitive knowledge to explore 17 students’ metacognitive knowledge in relation to integral calculus. The findings suggest that several aspects of these students’ metacognitive knowledge could be further developed, both at Year 13 and the first year of university. Improvements could occur both in terms of general (e.g., the importance of the rationale behind formulas and checking the outcome of problem-solving) and domain-specific aspects of metacognitive knowledge (e.g., how to check the outcome of a problem in a specific topic such as the integral-area relationship). More broadly, as discussing aspects of metacognitive knowledge in class has the potential to improve achievement outcomes for students, they are valuable elements of teaching to keep in mind, as this study shows that some of the students may not have had the skills to work on a metacognitive level on their own.

As this study is based on a small sample, replication studies would be valuable to assess whether or not the problem identified is specific to this group of students or more widespread. Further research is also necessary to explore students’ metacognitive knowledge of integral calculus in relation to other facets of metacognitive knowledge—the self-assessment of capabilities and limitations in relation to particular topics, and personal beliefs regarding the nature of mathematical ability. Finally, it would be of value to explore students’ metacognitive knowledge in relation to other topics at this level.