Measuring Characteristics of Explanations with Element Maps
Abstract
1. Introduction
2. Theory
- (a)
- The size, s, of a network is the number of its vertices.
- (b)
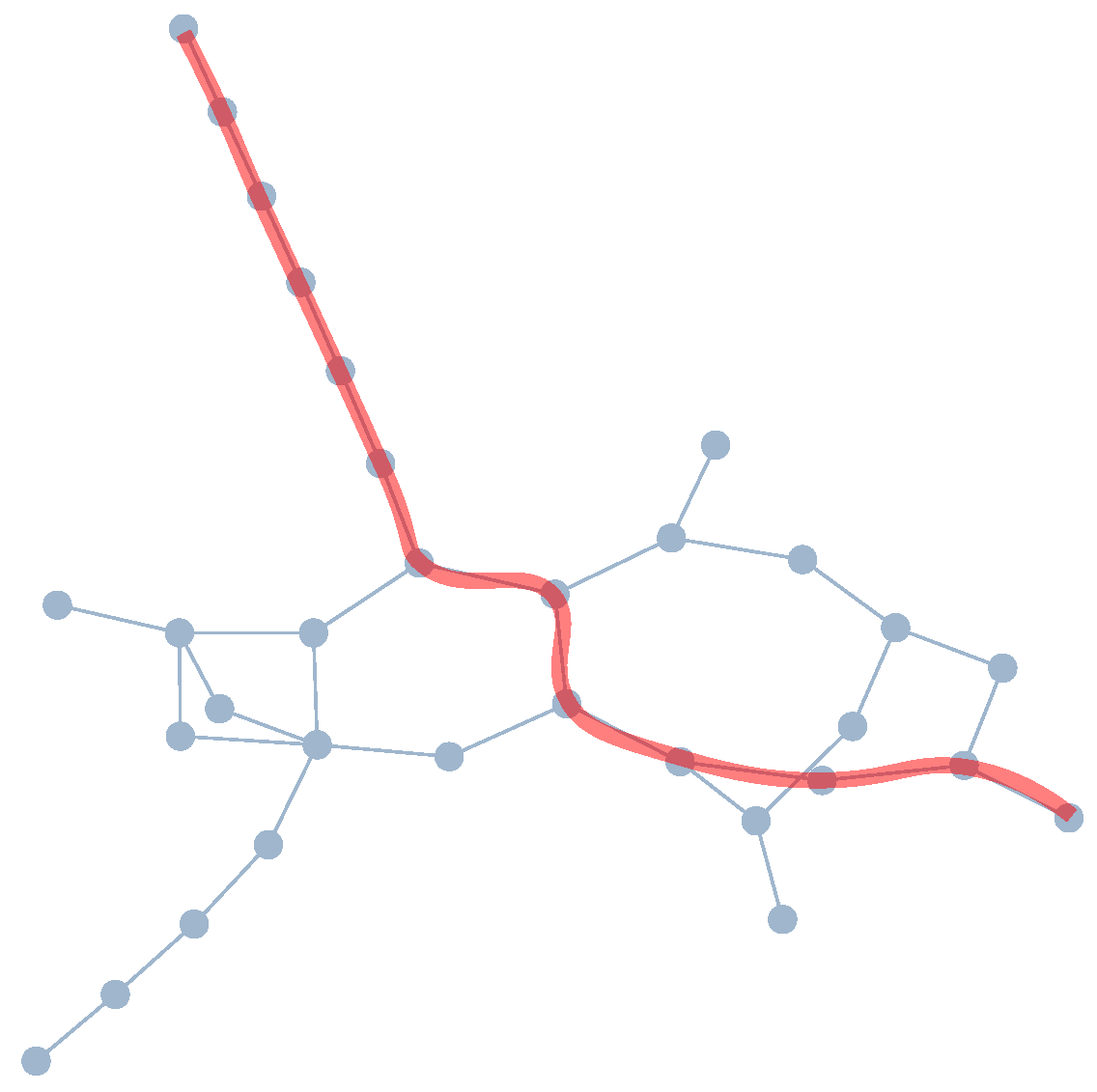
- The distance between two vertices in a network is the smallest number of edges that connect these vertices. The diameter, d, is the largest distance in a network.
- (c)
- There are different measures for the level of intertwinement (e.g., density and average path length) for different purposes. By intertwinement, we mean the level of complexity, or how interwoven the network is. We use the ratio of the diameter and the size, , as our measure for intertwinement.
- (d)
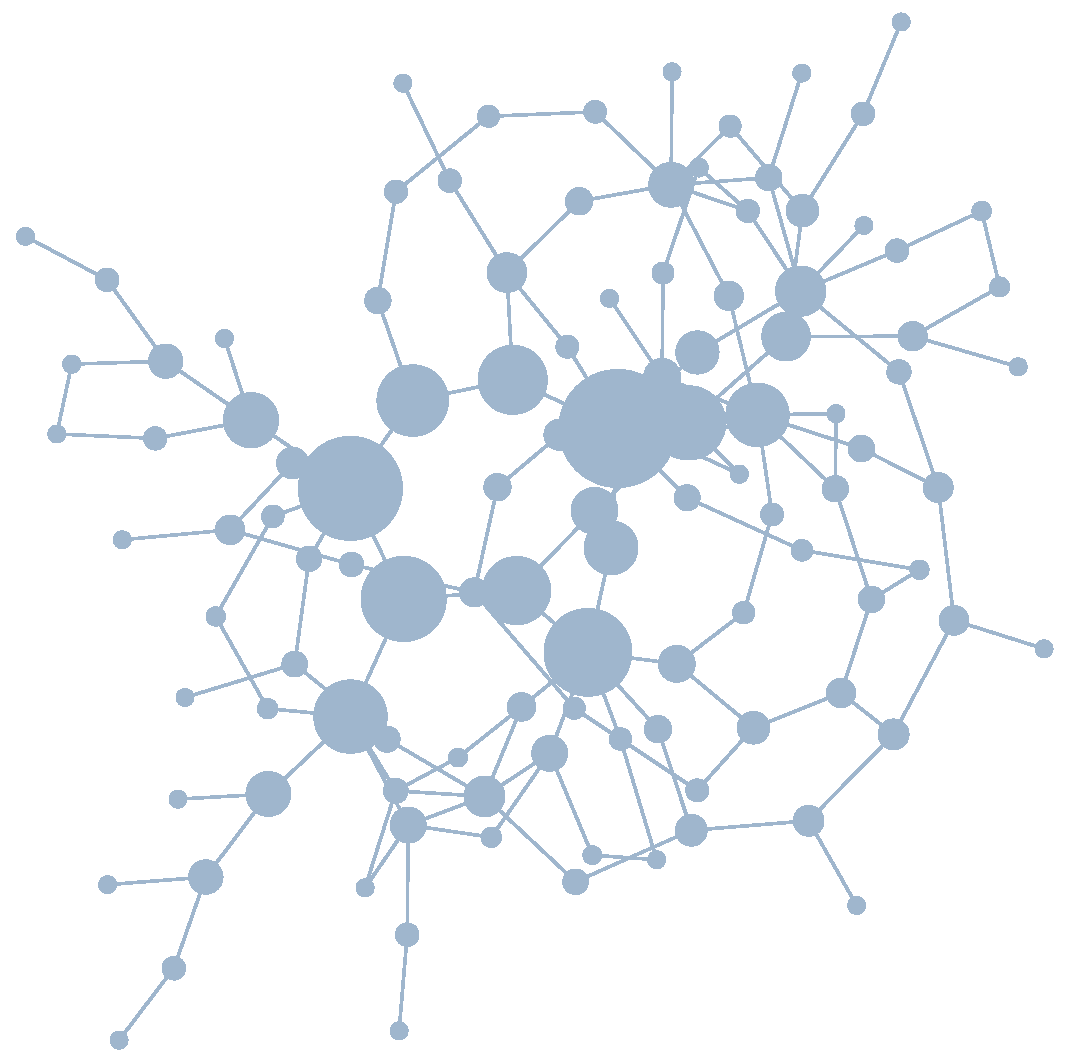
- A variety of established centrality measures for vertices quantify how important a vertex is for a network from different perspectives. We use the betweenness centrality, which indicates how many distances a vertex is placed [40]. Vertices with a high betweenness centrality act as mediators that tie together different parts (e.g., those representing theory and the phenomenon) of the network and form central elements around which the network is formed.
Research Question
- Which structural characteristics do explanations of a phenomenon given by experts and students have from the perspective of the network approach in element maps?
- What differences emerge in the networks between experts and students?
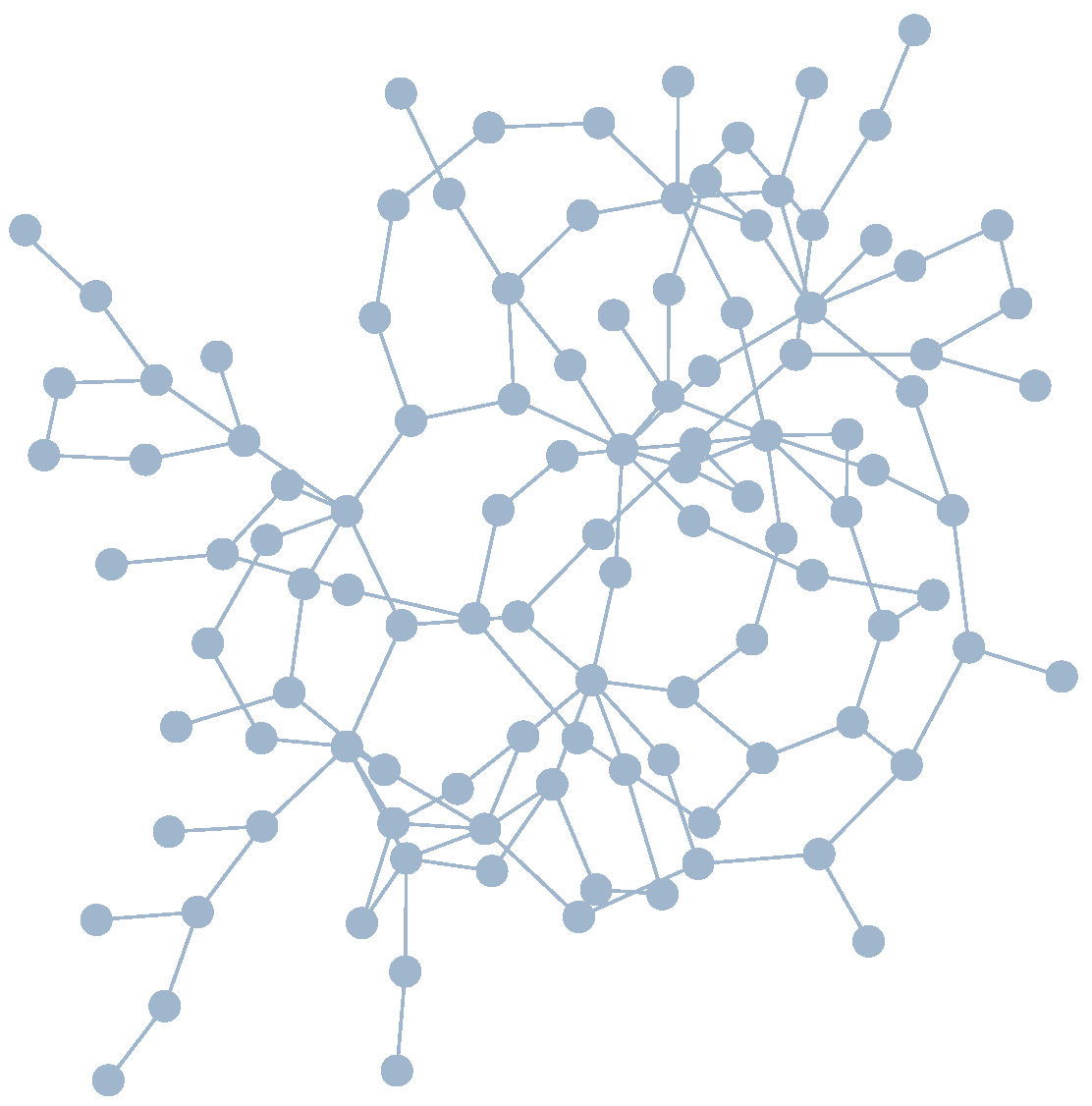
3. Materials and Methods
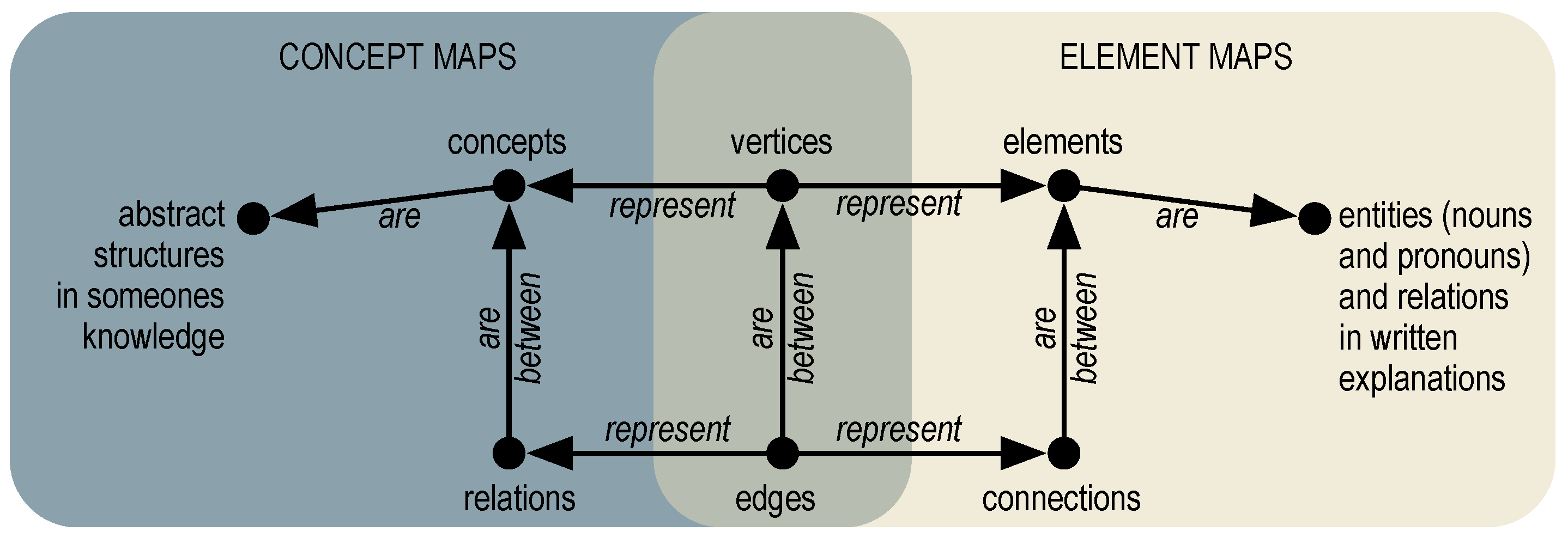
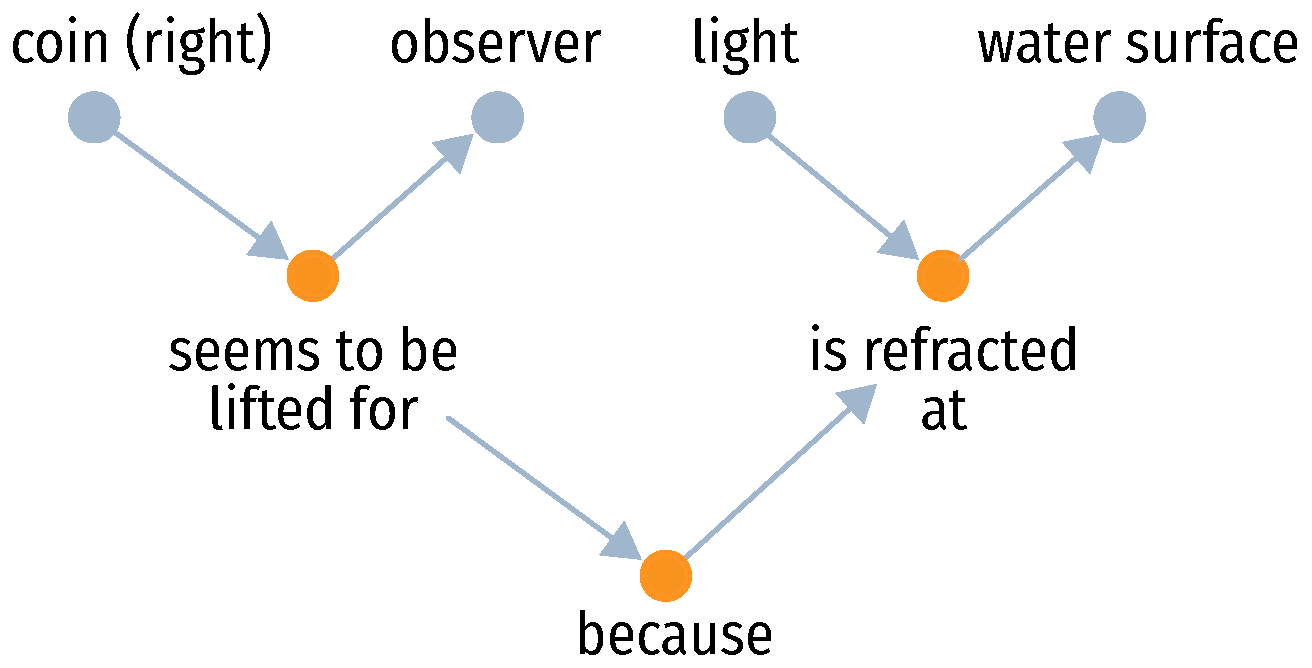
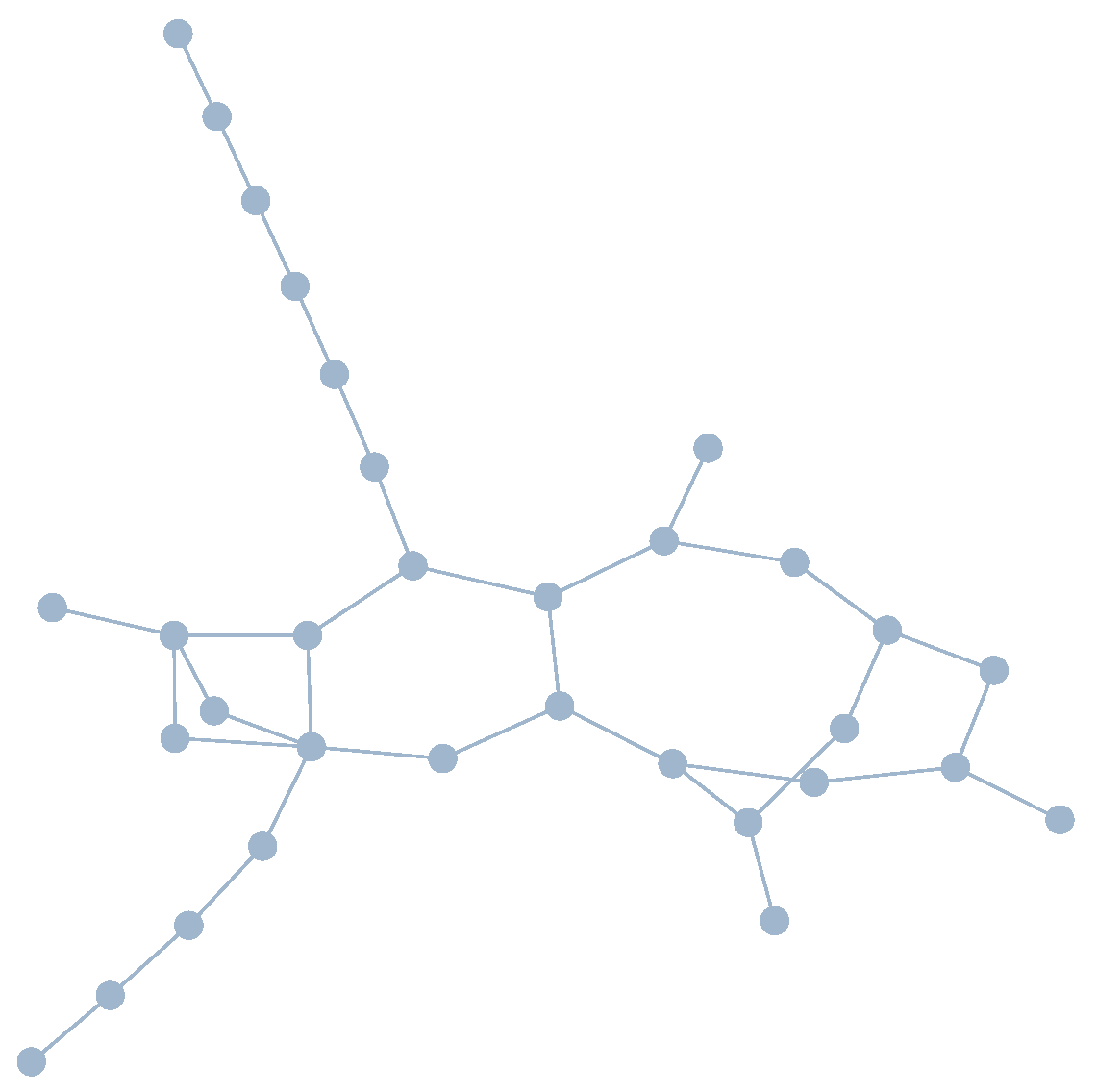
Generating Element Maps
“The coin on the right seems to be lifted for the observer because the light is refracted at the water surface.”
4. Results
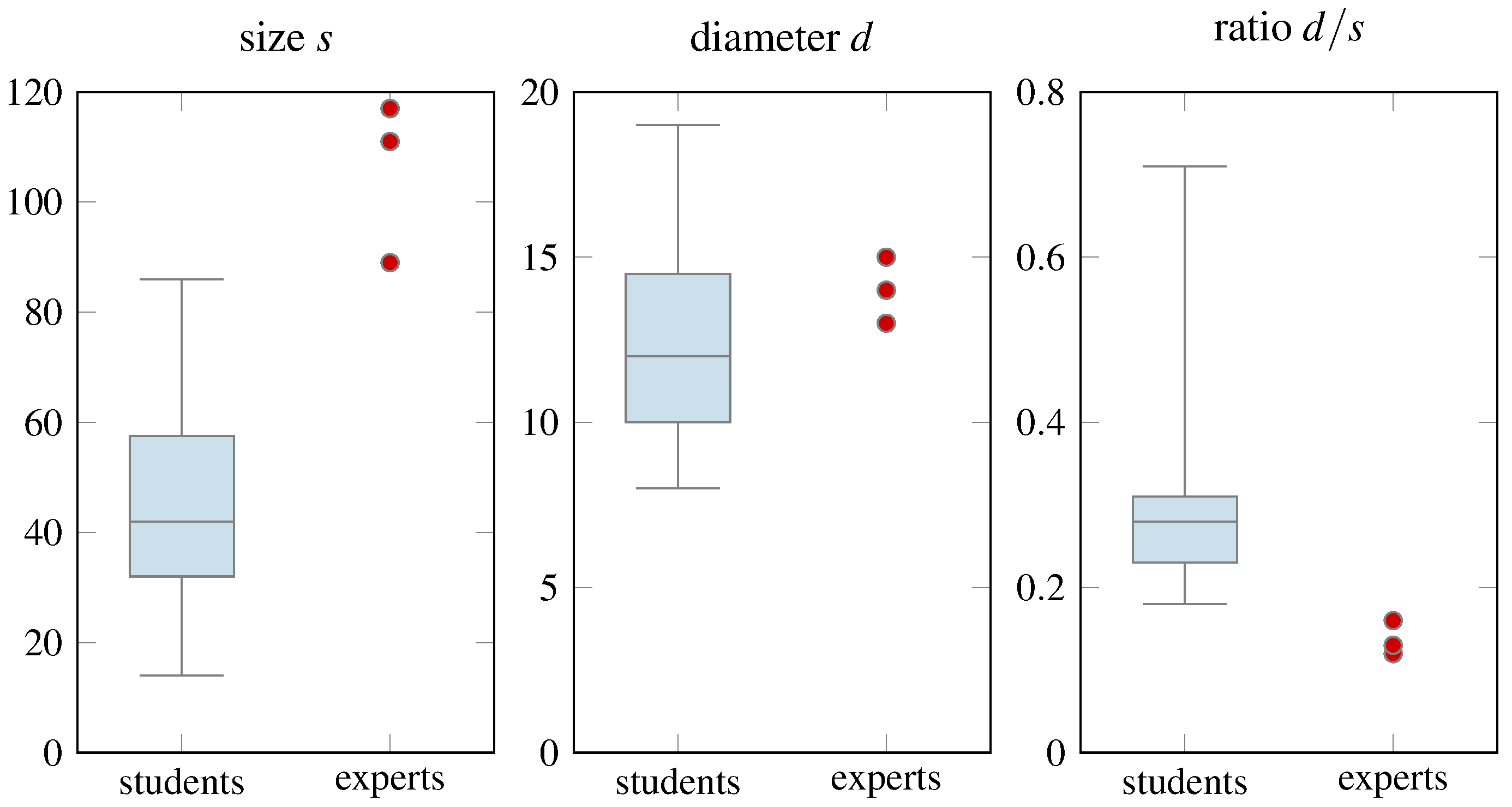
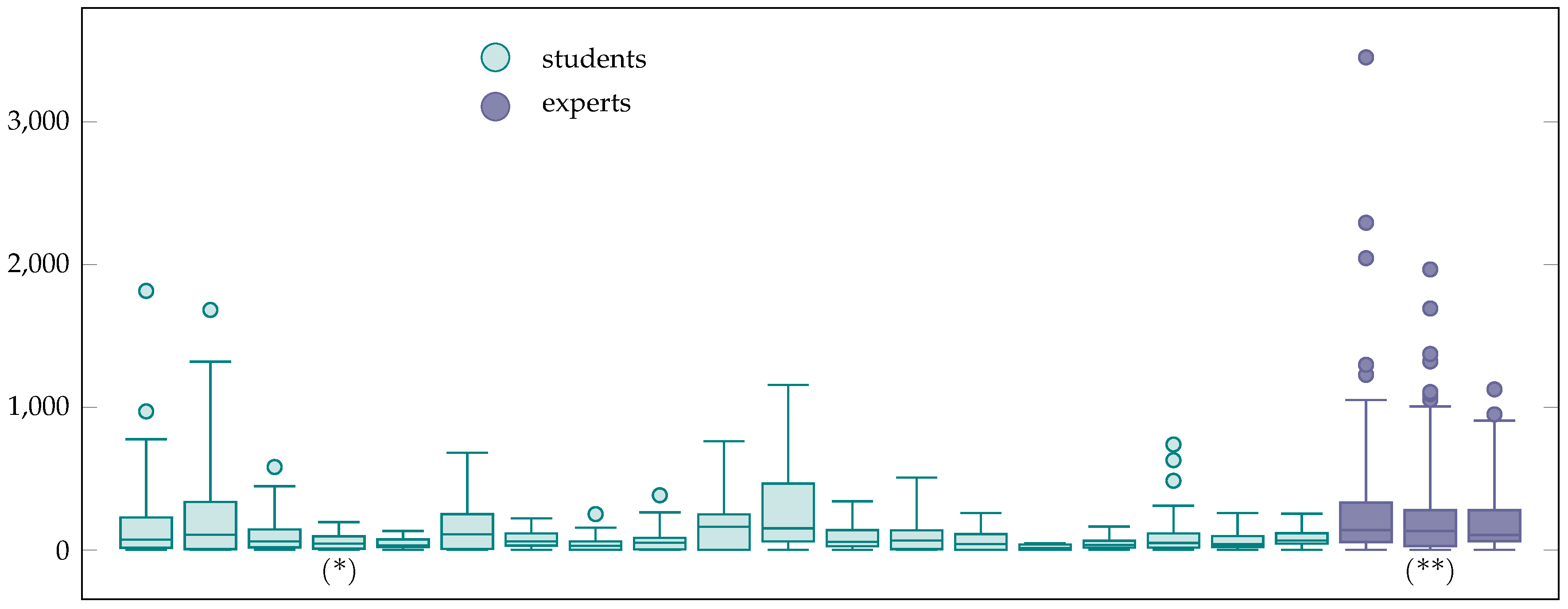
4.1. Size
4.2. Diameter
4.3. Ratio Diameter/Size
4.4. Betweenness Centrality
5. Discussion and Conclusions
5.1. Size
5.2. Ratio Diameter/Size
5.3. Betweenness Centrality
6. Limitations and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Morgan, M.S.; Morrison, M. (Eds.) Models as Mediators: Perspectives on Natural and Social Sciences; Cambridge University Press: New York, NY, USA, 1999. [Google Scholar]
- Hempel, C.G. Aspects of Scientific Explanation and Other Essays in the Philosophy of Science; Free Press: New York, NY, USA, 1965. [Google Scholar]
- Friedman, M. Explanation and scientific understanding. J. Philos. 1974, 71, 5–19. [Google Scholar] [CrossRef]
- Salmon, W.C. Four Decades of Scientific Explanation; University of Pittsburgh Press: Pittsburgh, PA, USA, 2006. [Google Scholar]
- Bevins, S.; Price, G. Reconceptualising Inquiry in Science Education. Int. J. Sci. Educ. 2016, 38, 17–29. [Google Scholar] [CrossRef]
- Forman, E.A. The Practice Turn in Learning Theory and Science Education. In Constructivist Education in an Age of Accountability; Kritt, D.W., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 97–111. [Google Scholar]
- NGSS Lead States. Next Generation Science Standards: For States, by States; The National Academic Press: Washington, DC, USA, 2013. [Google Scholar]
- Nationaal Expertisecentrum Leerplanontwikkeling. Kennisbasis Natuurwetenschappen En Technologie Voor de Onderbouw Vo: Een Richtinggevend Leerplankader; Technical Report 4.6691.552; Nationaal Expertisecentrum Leerplanontwikkeling: Enschede, The Netherlands, 2014. [Google Scholar]
- National Research Council; Division of Behavioral and Social Sciences and Education; Board on Science Education; Committee on a Conceptual Framework for New K-12 Science Education Standards. A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas; National Academies Press: Washington, DC, USA, 2012. [Google Scholar]
- Kultusministerkonferenz (Ed.) Bildungsstandards im Fach Physik für den Mittleren Schulabschluss; Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, Wolters Kluwer: München, Neuwied, 2005. [Google Scholar]
- Kuhn, T.S. The Road Since Structure: Philosophical Essays, 1970–1993, with an Autobiographical Interview; University of Chicago Press: Chicago, IL, USA, 2000. [Google Scholar]
- Gilbert, J.K.; Boulter, C.; Rutherford, M. Models in Explanations, Part 1: Horses for Courses? Int. J. Sci. Educ. 1998, 20, 83–97. [Google Scholar] [CrossRef]
- Abrahams, I.; Millar, R. Does Practical Work Really Work? A study of the effectiveness of practical work as a teaching and learning method in school science. Int. J. Sci. Educ. 2008, 30, 1945–1969. [Google Scholar] [CrossRef]
- Berland, L.K.; Schwarz, C.V.; Krist, C.; Kenyon, L.; Lo, A.S.; Reiser, B.J. Epistemologies in Practice: Making Scientific Practices Meaningful for Students. J. Res. Sci. Teach. 2016, 53, 1082–1112. [Google Scholar] [CrossRef]
- Chinn, C.A.; Malhotra, B.A. Epistemologically Authentic Inquiry in Schools: A Theoretical Framework for Evaluating Inquiry Tasks. Sci. Educ. 2002, 86, 175–218. [Google Scholar] [CrossRef]
- Galili, I.; Hazan, A. Learners’ Knowledge in Optics: Interpretation, Structure and Analysis. Int. J. Sci. Educ. 2000, 22, 57–88. [Google Scholar] [CrossRef]
- Andersson, B.; Kärrqvist, C. How Swedish Pupils, Aged 12–15 Years, Understand Light and its Properties. Eur. J. Sci. Educ. 1983, 5, 387–402. [Google Scholar] [CrossRef]
- Peel, A.; Zangori, L.; Friedrichsen, P.; Hayes, E.; Sadler, T. Students’ Model-Based Explanations about Natural Selection and Antibiotic Resistance through Socio-Scientific Issues-Based Learning. Int. J. Sci. Educ. 2019, 41, 510–532. [Google Scholar] [CrossRef]
- Peker, D.; Wallace, C.S. Characterizing High School Students’ Written Explanations in Biology Laboratories. Res. Sci. Educ. 2011, 41, 169–191. [Google Scholar] [CrossRef]
- Redfors, A.; Ryder, J. University Physics Students’ Use of Models in Explanations of Phenomena Involving Interaction between Metals and Electromagnetic Radiation. Int. J. Sci. Educ. 2001, 23, 1283–1301. [Google Scholar] [CrossRef]
- Rocksén, M. The Many Roles of “Explanation” in Science Education: A Case Study. Cult. Stud. Sci. Educ. 2016, 11, 837–868. [Google Scholar] [CrossRef]
- Yun, E.; Park, Y. Extraction of Scientific Semantic Networks from Science Textbooks and Comparison with Science Teachers’ Spoken Language by Text Network Analysis. Int. J. Sci. Educ. 2018, 40, 2118–2136. [Google Scholar] [CrossRef]
- Geelan, D. Teacher Explanation of Physics Concepts: A Video Study. Res. Sci. Educ. 2013, 43, 1751–1762. [Google Scholar] [CrossRef]
- Kulgemeyer, C. Towards a Framework for Effective Instructional Explanations in Science Teaching. Stud. Sci. Educ. 2018, 54, 109–139. [Google Scholar] [CrossRef]
- McNeill, K.L.; Lizotte, D.J.; Krajcik, J.; Marx, R.W. Supporting Students’ Construction of Scientific Explanations by Fading Scaffolds in Instructional Materials. J. Learn. Sci. 2006, 15, 153–191. [Google Scholar] [CrossRef]
- Passmore, C.; Gouvea, J.S.; Giere, R. Models in Science and in Learning Science: Focusing Scientific Practice on Sense-making. In International Handbook of Research in History, Philosophy and Science Teaching; Matthews, M.R., Ed.; Springer: Dordrecht, The Netherlands, 2014; pp. 1171–1202. [Google Scholar] [CrossRef]
- Sandoval, W.A. Conceptual and Epistemic Aspects of Students’ Scientific Explanations. J. Learn. Sci. 2003, 12, 5–51. [Google Scholar] [CrossRef]
- Kokkonen, T.; Mäntylä, T. Changes in University Students’ Explanation Models of DC Circuits. Res. Sci. Educ. 2018, 48, 753–775. [Google Scholar] [CrossRef]
- Yeo, J.; Gilbert, J.K. Constructing a Scientific Explanation—A Narrative Account. Int. J. Sci. Educ. 2014, 36, 1902–1935. [Google Scholar] [CrossRef]
- Sandoval, W.A.; Millwood, K.A. The Quality of Students’ Use of Evidence in Written Scientific Explanations. Cogn. Instr. 2005, 23, 23–55. [Google Scholar] [CrossRef]
- Lachner, A.; Nückles, M. Bothered by Abstractness or Engaged by Cohesion? Experts’ Explanations Enhance Novices’ Deep-Learning. J. Exp. Psychol. Appl. 2014, 21, 101–115. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Lachner, A.; Gurlitt, J.; Nückles, M. A Graph-Oriented Approach to Measuring Expertise—Detecting Structural Differences between Experts and Intermediates. In Proceedings of the 34th Annual Conference of the Cognitive Science Society, Austin, TX, USA, 24–27 July 2012; pp. 653–658. [Google Scholar]
- Novak, J.D. Concept Mapping: A Useful Tool for Science Education. J. Res. Sci. Teach. 1990, 27, 937–949. [Google Scholar] [CrossRef]
- Slater, S.; Joksimović, S.; Kovanovic, V.; Baker, R.S.; Gasevic, D. Tools for Educational Data Mining: A Review. J. Educ. Behav. Stat. 2017, 42, 85–106. [Google Scholar] [CrossRef]
- Cañas, A.J.; Novak, J.D.; Reiska, P. How Good Is My Concept Map? Am I a Good Cmapper? Knowl. Manag. E-Learn. 2015, 7, 6–19. [Google Scholar]
- Clark, D.B. Longitudinal Conceptual Change in Students’ Understanding of Thermal Equilibrium: An Examination of the Process of Conceptual Restructuring. Cogn. Instr. 2006, 24, 467–563. [Google Scholar] [CrossRef]
- Airey, J.; Linder, C. A Disciplinary Discourse Perspective on University Science Learning: Achieving Fluency in a Critical Constellation of Modes. J. Res. Sci. Teach. 2009, 46, 27–49. [Google Scholar] [CrossRef]
- Ogden, C.K.; Richards, I.A. The Meaning of Meaning: A Study of the Influence of Language upon Thought and of the Science of Symbolism; Harcourt Brace Jovanovich: San Diego, CA, USA, 1989. [Google Scholar]
- Freeman, L.C. A Set of Measures of Centrality Based on Betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Strautmane, M. Concept Map-Based Knowledge Assessment Tasks and Their Scoring Criteria: An Overview. In Proceedings of the Fifth International Conference on Concept Mapping, Valetta, Malta, 17–20 September 2012. [Google Scholar]
- Koponen, I.T.; Nousiainen, M. Concept Networks of Students’ Knowledge of Relationships between Physics Concepts: Finding Key Concepts and Their Epistemic Support. Appl. Netw. Sci. 2018, 3, 14. [Google Scholar] [CrossRef]
- Sanders, K.; Boustedt, J.; Eckerdal, A.; McCartney, R.; Moström, J.E.; Thomas, L.; Zander, C. Student understanding of object-oriented programming as expressed in concept maps. ACM SIGCSE Bull. ACM 2008, 40, 332–336. [Google Scholar] [CrossRef]
- Williams, C.G. Using Concept Maps to Assess Conceptual Knowledge of Function. J. Res. Math. Educ. 1998, 29, 414. [Google Scholar] [CrossRef]
- Schaal, S. Concept Mapping in Science Education Assessment: An Approach to Computer-Supported Achievement Tests in an Interdisciplinary Hypermedia Learning Environment. In Proceedings of the 3rd International Conference on Concept Mapping, Talllinn, Estonia, 22 September 2008. [Google Scholar]
- Ruiz-Primo, M.A.; Shavelson, R.J. Problems and Issues in the Use of Concept Maps in Science Assessment. J. Res. Sci. Teach. 1996, 33, 569–600. [Google Scholar] [CrossRef]
- Nassar, A.B. Apparent depth. Phys. Teach. 1994, 32, 526–529. [Google Scholar] [CrossRef]
- Wagner, S. Erklärung physikalischer Phänomene mit Modellen. Ph.D. Thesis, Humboldt-Universität zu Berlin, Berlin, Germany, 2018. [Google Scholar]
- Glaser, R. Expert Knowledge and the Processes of Thinking. In Subject Learning in the Primary Curriculum; Bourne, J., Briggs, M., Murphy, P., Selinger, M., Eds.; Routledge: London, UK, 2005; pp. 261–275. [Google Scholar]
- Lintern, G.; Moon, B.; Klein, G.; Hoffman, R.R. Eliciting and Representing the Knowledge of Experts. In The Cambridge Handbook of Expertise and Expert Performance; Ericsson, K.A., Hoffman, R.R., Kozbelt, A., Williams, A.M., Eds.; Cambridge University Press: Cambridge, UK, 2018; pp. 458–522. [Google Scholar]
- Jonassen, D.H.; Beissner, K.; Yacci, M. Structural Knowledge: Techniques for Representing, Conveying, and Acquiring Structural Knowledge; Routledge: New York, NY, USA, 2013. [Google Scholar]
- Tang, K.S. Constructing Scientific Explanations through Premise–Reasoning–Outcome (PRO): An Exploratory Study to Scaffold Students in Structuring Written Explanations. Int. J. Sci. Educ. 2016, 38, 1415–1440. [Google Scholar] [CrossRef]
- Wheatley, G.H. Constructivist Perspectives on Science and Mathematics Learning. Sci. Educ. 1991, 75, 9–21. [Google Scholar] [CrossRef]
- Gilbert, J.K.; Bulte, A.M.W.; Pilot, A. Concept Development and Transfer in Context-Based Science Education. Int. J. Sci. Educ. 2011, 33, 817–837. [Google Scholar] [CrossRef]
- Caballero, D.; Araya, R.; Kronholm, H.; Viiri, J.; Mansikkaniemi, A.; Lehesvuori, S.; Virtanen, T.; Kurimo, M. ASR in classroom today: Automatic visualization of conceptual network in science classrooms. In Proceedings of the European Conference on Technology Enhanced Learning, Leeds, UK, 3–6 September 2017; Springer: Cham, Switzerland, 2017; pp. 541–544. [Google Scholar]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wagner, S.; Kok, K.; Priemer, B. Measuring Characteristics of Explanations with Element Maps. Educ. Sci. 2020, 10, 36. https://doi.org/10.3390/educsci10020036
Wagner S, Kok K, Priemer B. Measuring Characteristics of Explanations with Element Maps. Education Sciences. 2020; 10(2):36. https://doi.org/10.3390/educsci10020036
Chicago/Turabian StyleWagner, Steffen, Karel Kok, and Burkhard Priemer. 2020. "Measuring Characteristics of Explanations with Element Maps" Education Sciences 10, no. 2: 36. https://doi.org/10.3390/educsci10020036
APA StyleWagner, S., Kok, K., & Priemer, B. (2020). Measuring Characteristics of Explanations with Element Maps. Education Sciences, 10(2), 36. https://doi.org/10.3390/educsci10020036




