Abstract
Classrooms are complex in their real sets. To understand such sets and their emergent patterns, network approach provides useful theoretical and methodological tools. In this work, we used network approach to explore two domains of complexity in a classroom: the interpersonal domain, via social networks; and the representational domain, through collective semantic networks. This work is grounded in both Social Network Analyses and Social Representation Theory for gathering information from interpersonal and representational domains. We investigated a physics high school classroom by proceeding sociometric tests and by using words freely evoked by students to explore relations between students’ dyad’s weights, in social networks, and emerging consensus in semantic networks. Our findings showed closer relations between social ties’ weight and consensus formed on intra-school representational objects, while consensus on extra-school representational objects is less dependent on the classroom interpersonal ties’ strength.
1. Introduction
Entanglements in which independent and elementary unities constantly interact can be viewed as complex systems. In such systems, structural organization can emerge from interaction between its elementary entities (or unities). These emerging organizations enable stabilities. Once some stability arises, patterns can be noticed in the system. In order to investigate emergent patterns, it is required to have (i) suitable methods that allow one to make inferences from data that capture objective features of the world and (ii) ways to formally represent those patterns [1].
Complexity is inherent to real systems, such as classrooms. Although there is no unanimous definition of what a complex system would be, they are often informally defined as being a network of interacting elements, exhibiting complex behavior and without central control [2]. Complex networks provide methods for referring to complex systems and tools for explicitly representing complex structures. Networks, in general, can be conceived as a set of elements and the connections between them. Such element/connections sets can refer to basically any group of unities and its relations, or actors and its interactions, as long as there is an objective way to recognize nodes (i.e., vertexes, elements, actors, or other) and its links (i.e., edges, connections, interactions, or other). Networks can be formally represented as mathematical sets, a matrix, or images, operating under norms from the graph theory [3,4].
In borrowing those notions to think as a classroom, its complex structures can be seen as networks in numerous ways. In the interpersonal domain, network approach can be used, considering each student as a vertex and each student/student link as an edge, from a social network perspective [5]. The social network approach has been adopted as a way to understand aspects of classrooms, such as partnership formation [6] and student leadership [7]. Although networks used in a strict social domain can be a rich source of information on interpersonal realm, it does not account for the thought domain. Social networks can clarify structural positions of each student, how their position operates in the group, what are the sub-communities formed, or even show who are the closest pairs in the classroom. On the other hand, they are not about tracing students ideas.
In this work, we are interested in investigating not only interpersonal networks but also which ideas students share. That calls for approaching another dimension: Networks can also be used for exploring and understanding domain of thought. In this sense, applying the network approach to students’ thinking in science education has been used in various ways, from an individual’s propositional networks in concept maps [8] to structural analyses of semantic networks built from an individual’s words associations [9] or even for analyzing oral discourse [10].
Notwithstanding, each of those domains can work alone as a fruitful informative tool to investigate classrooms; our interest in using networks is to expand the research landscape on teaching and learning processes. In doing so, networks serve as a way to lump together different features from both social and thought domains. Even though one may say those domains would be ontologically disjointed, because each of them has its own intrinsic complexity, the more we amplify our view on a certain complex scenario, such as classrooms, the more we see that boundaries are not clear and interdependencies between levels and domains always play a role. This is essentially what the complex system approach accounts for. Thus, networks can be used as a way to think and investigate a classroom in its complexity. It can merge in the same analysis domains that are supposedly separate.
Efforts to relate structural traces from different domains via a network has been posed as a cutting edge approach for deepening the understanding of classroom complexity. One example of this effort can be seen in the so-called epistemic network analysis [11], in which networks from different domains are plotted in the same topological space to be analyzed together. Another example is the analysis of a correlation network to study the multiple influences of problem-solving, concept discussion, and classroom communication in students’ grades performance, by binding different network’s dimensions [12]. Although not in a learning context, another approach can be pointed to, which uses a socio-semantic perspective for studying the interplay between social structures and commonalities in group discourse [13]. The diversity of networks as a research approach for mixing dimensions of analysis indicates an existing field to be explored in classroom-grounded educational research.
In this work, our aim was to use the network approach to investigate both social and semantic structures in a classroom in order to explore relations between the strength of interpersonal ties and shared ideas.
2. Theoretical Background
Our approach for looking at both social and semantic networks is located in one of the edges of the so-called didactic triangle [14]. A classroom didactic system was proposed by Chevallard for problematizing the process of transposition that must be done in order to bring knowledge produced in professional contexts to a kind of knowledge to be taught in classrooms. In the didactic system, a triangle schematically represents three main elements involved in the process of teaching and learning: teacher, knowledge, and students.
In the didactic system, knowledge refers to which content-specific knowledge should be brought from its production context to classes, said transposed. Transposition refers to a series of transformations made onto professional scientific knowledge, so-called wise knowledge, in order to be teachable. In Chevallard’s sense, transposition is not a process of making easier a complex and distant knowledge. Instead, transposition refers to creating a new kind of knowledge, deeply related to the “wise” one but occupying a different epistemic niche [15].
In its new epistemic niche, knowledge to be taught unfolds in a learned knowledge. The unfolding process includes how students would share meanings on the themes they interact with in classrooms. Those shared meanings help to build a consensual universe in classrooms. In this case, while one way of using networks is to analyze individuals’ cognitive structures [16], another focal point can be to understand what are the shared meanings circulating in the group [17]. In a second sense, networks can be used in a socio-representational perspective for exploring the domain of thought in the consensual universe.
The consensual universe can be captured in social representations built by a social group, as proposed by Moscovici [18]. Social representations are phenomena of emerging consensual ideas that help a group to deal with social life demands. It is a process of sharing symbolic referents in order to make an object familiar to a group, helping to built the group’s social reality. The consensual universe is in opposition to the reified universe. In a consensual universe, any member of a group has the same authority over truth because what would be the truth is defined by the meanings those same members can share. On the other hand, in a reified universe, norms and rules determine what is valid as truth. Professional knowledges are produced and validated in the reified universe.
In a reified universe, society consists of a set of solid entities and science has authority over individual experience. In contrast, a consensual universe has truths created by individuals’ experiences. Individuals can share their experiences and produce representations that give identity and carry historicity to the collective. Coupling Moscovici’s and Chevallard’s frameworks (Figure 1), reified and consensual universes distinguish two kinds of knowledge. The first one is the “knowledge to be taught” from the didactic triangle, which takes place in the scholar institutional sphere; therefore, it is related to reified universe. The other one is the “learned knowledge” crystallized in meanings that students share in classrooms, which builds students consensual realities; ergo, it is related to the consensual universe. We are interested in the latter and how it is related to interpersonal complex structuring.
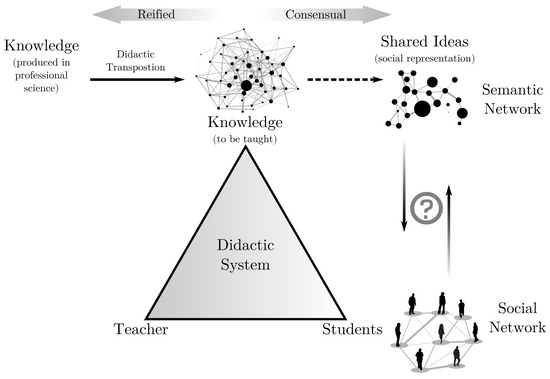
Figure 1.
Schematic representation of our network perspective for the classroom and its location in Chevallard’s didactic system.
Although the consensual universe is less organized then the reified one, it is feasible to investigate social representations despite its intricacy. Social representation are very dynamic; however, at the same time, they are stable enough to be perceived. This seems to be contradictory; but, instead, stability and dynamics are actually coexisting features of the same complex structure of a social representation.
This supposed contradiction is solved by a structural approach of a social representation [19]. A social representation holds a central core and a periphery. The central core stands for the collective memory and values, giving continuity to the group and having prominent elements. The peripheral region of a social representation would be more influenced by immediate material and social contexts, being more fuzzy and more dynamic. Periphery would work under an evolutionary dynamic and would accommodate contradictions and heterogeneity.
This structural approach to social representations proposes that the central core has a functional role in generating meanings and organizing the representation. It would emerge more stable than periphery and would help to organize the representational field. The core could reveal its semantic identification from similarities existing between lexemes (structuring words) freely evoked by individuals in a group [20]. Hence, semantic networks in the present research refer to structures of social representations produced by students and to their shared meanings in the learning process.
Considering the didactic system and its vertexes (teacher, students, and knowledge), it can be said that social representations stands for the thought domain. Not in an individual sense of thought but in the collectively shared thought. In order to bridge the edge knowledge ↔ students from a didactic system (Figure 1), we might also draw our attention to interpersonal social structures formed in the classroom.
Group structures study has roots in Moreno’s sociometry [21], in which sociograms were used as explicit representations of an individual’s social position and its relation with peers. Sociograms have evolved, shifting from its original “gravitational” form to a complex relation structure [22]. Since sociograms have met graph theory, it gained a new configuration: the complex social networks. That allows one to change the observations from the social attractor perspective to a more elaborate analysis of the structural features, such as the relations actor/actor (network edges).
Today, social networks are still metaphorically associated with physical systems, in which any dyadic relation can be seen as a network, or to chemical structures, in which social binding works as an analog to covalent bonding [23]. In classrooms, dyadic relations could be any kind of student/student transfer, like direct interactions or server logs in discussion forums [24]. It can also be explicit nomination of preferred peers for collaborating in problem-solving [6].
Despite objections one can make to readily import natural sciences logic to analysis of social contexts, parallels to natural sciences can be helpful allegories for minding that the network’s approach is a way to make sense of classroom complex sets. As classrooms interpersonal relations and social representation both emerge as complex organizations, networks can be used first as a metaphor to think about classroom complexity and, secondly, as a method to explore it.
By articulating social networks and semantic networks, we can work on the students ↔ knowledge edge of the didactic triangle. That makes it possible to explore relations between interpersonal and consensual thought domains. There is where our research question lies, as schematically represented in Figure 1.
Both wise knowledge and specific knowledge brought to school are reified knowledges, in a reified universe. In classrooms, the construction of social representations regarding the taught knowledge occurs when elements from reified universe permeate students’ consensual universe, allowing the emergence of shared meanings.
In Figure 1, the solid line between professional knowledge and knowledge to be taught indicates that didactic transposition is first made by the teacher at an institutional level. Therefore, its process is guaranteed by institutional norms. Regarding the teacher’s role, she/he operates this first transposition, playing a central role in the teaching and learning process. The teacher’s role is so relevant that she/he her/himself became one of the vertexes of Chevallard’s system. Thus, proceeding an analysis, including the teacher in the network means that both her/his social and epistemic authority would be included. Although that could be worthy because it would inform the teacher’s influence in bridging institutional and pedagogical instances, in this work, we are interested in a later step, when the knowledge spreads among students and shared ideas are formed. Thus, in this second order process, the dashed line between knowledge to be taught and shared knowledge (Figure 1) indicates that another transformation in knowledge occurs, not institutionally but consensually among members of the group. Once social representations cannot be imposed, the emergence of shared ideas takes place in a consensual universe. This implies uncertainties as to whether or not socially shared representations, said learned knowledge, would include elements of the reified universe.
The remaining question regards what role interpersonal ties would play on that process of sharing ideas. In this matter, we borrowed from Saxe and collaborators [25] the idea of analyzing social ties weight. They take a vygotskyan developmental approach [26] and use a sociocultural perspective for relating interpersonal affiliation and the process of traveling ideas in classroom communities. Sociograms built from table mates choices in classroom were used as social structuring explicit representations. For those authors (ibid), social and thought realms would be coupled in a genetic perspective: while ontogenesis refers to shifting in patterns of thinking over time, microgenesis involves ongoing production of meaningful representations, and sociogenesis deals with reproductions and transformations of representations, in order to promote communication among group members.
Although in the present work we are not taking the genetic perspective, and we are using a different approach specially regarding thought domain, their proposal of investigating the interpersonal affiliation strength (or intensity or weight) in the social networks has shed some light on the necessity to account for student/student ties. That has been a particularly important informative source in our findings, as we will show in the following.
3. Materials and Methods
3.1. Research Context
We conducted the present investigation by following an 11th grade high school physics classroom in a comprehensive public institution in São Paulo, Brazil, between March and May 2018. The school had between 800 and 850 students enrolled that year (the precise number was omitted in order to keep school anonymity). São Paulo is the biggest city in the country of Brazil. As a huge metropolis, the city is a multitude of contrasts.
Socioeconomic contrast can be addressed to studied school reality. The school facility is located in an upper middle class neighborhood, but most of its students come from surrounding “low income” neighborhoods. As they walk uphills to get to school, they experience a spectrum of changing in the landscape. In this adverse reality, our research subjects struggled to obtain their basic education.
The class we followed had 36 students enrolled, 23 male and 13 female. During the period of observation, students were having classes on heating exchange. The teacher was a young licensed physics teacher and had an apparently good relation to students, demonstrated by their shared friendliness.
Regarding the research design, we are proceeding an exploratory and explanatory case study [27]: we are using multiple sources of evidence (semantic networks and social networks), and we are exploring an area where context and phenomenon cannot be clearly detached.
As an exploratory and explanatory case study, the present research design works as an informative process that must be addressed to a specific environment and context. Dealing with complex sets, our networks are not in service of deterministic assumptions nor generalizations. On the contrary, investigating a classroom through its emerging semantic and social networks and exploring relations between those domains must be used as a form of making sense to subtle complex structuring process.
3.2. Research Instruments and Procedures
During the first week, having previously obtained permission from the teacher, the researcher presented himself to the class, presented a brief of the kind of research would be conducted, and asked students permission to proceed. Each student received an authorization form they had to bring back signed by their responsible parent or guardian. After the forms had been returned, data started to be collected. The data for the present work were collected between the third and the fourth week.
3.2.1. Semantic Networks
The process of gathering data for the semantic network followed the free word evoking technique [28]. The technique consists of asking a research subject to say the first words that come to their mind when we say some inductor term. Then, a network made by words and word links is built. The uses of word networks in semantic contexts can vary, although the main idea is to use associations between words for inferring similarities, meanings, or structural features. Proximity can be either phonological or semantic [29]. It can also be obtained by free association between words, considering its valency [30]. In the present research, as we are investigating shared ideas in a group, proximity between words was obtained by a similarity index, considering the co-occurrence of evoked terms. Although big data surveys using free word evocation technique have standardized the use of three evocations for each inductor term [31], in this work, we opted for more evocations, providing students with more opportunities to express their related words and enhancing nuances of Social Representations studied. In order to survey representations on objects varying from inner classroom content to students extra-school world, we asked students to freely evoke the five first words that would come to their mind on the following five inductor terms:
- (i)
- Heat: it was the specific content they were studying during the research, and it would be a vivid theme to them;
- (ii)
- Physics: as a scholar discipline, it could still being an inner school theme to them;
- (iii)
- Science: its meanings could bridge inner school ideas and the outer school world. As science is present as an object in media but also in the classes they were taking, related words could reveal the overlapping of both;
- (iv)
- School: words evoked on this inductor bring thoughts on students daily life but, at the same time, could accommodate both their expressed feelings about the school reality and the contrast they experience on their way;
- (v)
- Future: it should be the more distant one, both in space and time. The prospective features of ideas regarding future was considered and related words can show social representations of possible life-paths on which they imagine themselves.
All present students, by the day we collect the evoking data (22/36 students), answered the evoking sheet. Evoked words were lemmatized, reducing gender and plurals to a single form, and the data was converted to a .CSV file. Then, it was imported to IRaMuTeQ software [32] for a proceeding similarity analysis between words.
The co-occurrence similarity index was computed using Russel’s algorithm [33], which provides a proximity value used for an undirected network. Directional dependence between the cue and the response were not considered. For all pairs of words, the details are shown in the following figure (Figure 2). All five similarity matrices computed were converted into another .CSV file and exported to be post-processed in R software [34] using the Igraph package [35].

Figure 2.
Steps for the process of converting evoked words into a co-occurrence network.
In Figure 2 is shown a proxy as an hypothetical example of four students evoking five words that came to their mind on the inductor term “pet”. The process of building semantic networks takes as raw data all evoked words (Figure 2A). Then, all lexemes are sorted by frequency, and an occurrence matrix is built (Figure 2B). A contingency matrix (Figure 2C) is used for computing the co-occurrence similarity index for each pair of words.
In this matrix, position a is the total number of co-occurrences for both words; position b is the total number of occurrence of only word 2 but not word one; position c is for total number of occurrence of only word 1 but not word 2, and position d is the number of absences for both words. With the similarity index computed for all possible pairs, it gives a similarity matrix which is taken as an adjacency matrix. In the network, the similarity index was used as the edge weight value. The vertexes’ (words’) diameters are plotted proportional to its degree.
3.2.2. Social Networks
For the social network, we proceed with a sociometric test by free choices [36], which consists of asking students to declare who are their preferred peers or who do they feel more connected with in different situations. Although classic sociometry includes the possibility of asking who are the peers they feel in opposition with or disconnected to, we did not use disruptive criteria of choice in order to avoid that research instrument itself becoming a disruptive factor in the classroom.
After validating different criteria of choice (i.e., sociometric questions) in our research group, we end up with eight criteria. They would vary from direct interpersonal affiliation, such as (i) who are the classmates you usually have lunch with?, to a cultural commonalities, such as (ii) who are the class mates that like the same kind of music as you?.
The other six criteria concerned pairs who (iii) practice same sport as you, (iv) you use to meet outside school, (v) you would invite for a party, (vi) you like to do school work with, (vii) support same soccer team as you (in Brazil, soccer as a strong cultural element and can bind friend together), and (viii) overall you feel more connected with.
Students were presented with a class list, and each one was asked to dash her/his own name. That was used for identifying her/himself as the respondent. Each criteria generated a directed unweighted social network. Then, all eight networks were concatenated for building an undirected and weighted social network. In this network, edges were plotted with their thickness proportional to total weight, as shown in Figure 3.
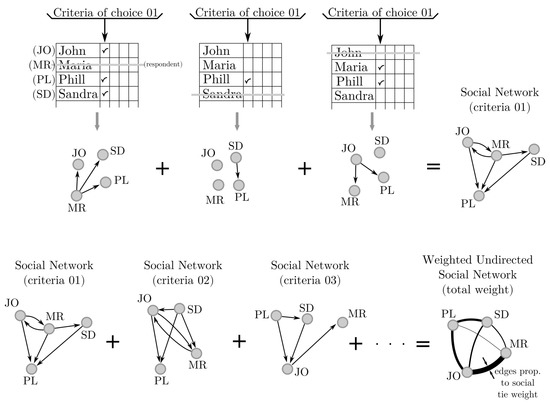
Figure 3.
Steps for the process of building directed unweighted social networks for each criteria and one undirected weighted social network for all eight criteria.
Even though the sociometric test was not answered by all present students (28/36 students) by the day we collected that data, the social network was built using all 36 enrolled students, due the fact that even an absent mate could be chosen by her/his peers and would, therefore, be part of that social network.
The data were analyzed in R software [34] with the Igraph package [35]. For each respondent, an outward edge list was taken from the respondent perspective to be imported to R. For each criteria, a symmetric adjacency matrix was built. Then, all eight criteria networks were concatenated summing the total number of edges between each pair and a weighted undirected social network was built. A heatmap from the adjacency matrix was plotted in order to visually check possible randomness. The vertex’s degree distribution and the edge weight distribution were plotted.
3.2.3. Dimensional Reduction
Having both a social and semantic network, we sorted six numerical variables (Table 1) to process a dimensional reduction. They were (i) weight of edges for each dyad connected in the social network and the number of coincident words evoked for (ii) heat; (iii) physics; (iv) science; (v) school; and (vi) future.

Table 1.
Summary of numerical variables for all pairs of students (dyad) and steps for data processing.
All complete cases, i.e., pairs formed in the social network and having both students answered the word evoking sheet, were selected. Internal consistency index [37] was computed using R’s cocron package [38]. Then, a Scree Test [39] was proceeded using R’s nFactors package [40] in order to determine the number of components to be retained. Finally, a Principal Components Analysis (PCA) [41] for the variables was computed using R’s FactorMineR package [42]. All data and the R script used for the analysis are available online [43].
4. Results
4.1. Social Representations and Similarities Networks Description
The words’ co-occurrence networks are shown in Figure 4, along with all evoked terms as vertexes and with the edge thickness proportional to computed similarity index. The network for Heat has 48 words with 290 co-occurrence relations. Sun, fire, and beach had highest degrees, and the pairs Sun–beach, Sun–fire, and beach–fire were the most similar ones (Figure 4A).
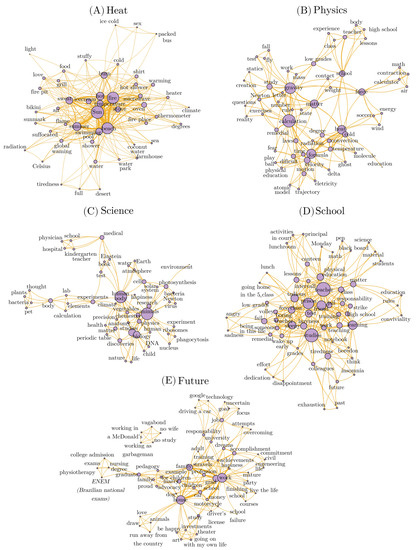
Figure 4.
Words’ co-occurrence network for (A) Heat; (B) Physics; (C) Science; (D) School, and (E) Future. Vertexes with diameter proportional to degree and edges with thickness proportional to similarity index computed with Russel’s algorithm.
For Physics, the network showed 60 words and 188 co-occurrence relations. Calculation, gravity, and formula were the highest degrees, and the most similar pairs were heat–cold, calculation–studies, and school–teacher (Figure 4B).
For Science, a network with 52 words having human body, animals, and studies as highest degrees and 151 pairs (physics–biology, physics–chemistry, and chemistry–biology were the most similar pairs) are shown in Figure 4C.
Evocations for School (Figure 4D) showed a 60 words network with teacher, studies, and prison as more connected words and 303 relations with teacher– physical education, teacher–test, and teacher–friend as the closest ones.
The last network, Future, showed 63 words with 214 relations. The elements work, house, and grad school were the highest degree, and the pairs work–grad school, work–money, and car–house were the closest pairs (Figure 4E).
4.2. Interpersonal Ties and the Social Network Description
The weighted social network with all pairs of student is shown in Figure 5. Regarding the ego perspective, the degree distribution (shown in Figure 5, bottom right) highest total degrees, considering the sum of in and out degrees, were from PS (), AA () and PF ().
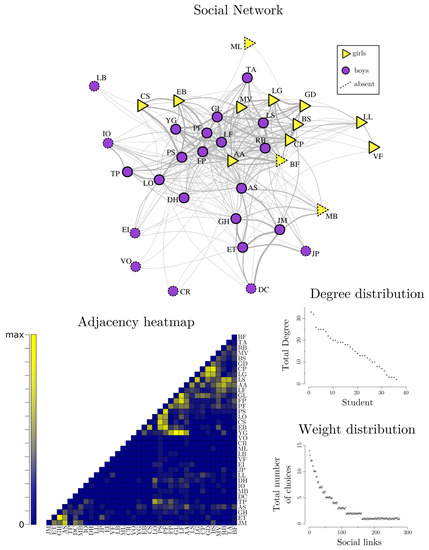
Figure 5.
(top) Weighted social network for all the eight criteria of choice concatenated. In the social network, edges thickness is proportional to social tie weight, computed by the total of choices between two students. (bottom left) The adjacency matrix heatmap for the group; (bottom right) The vertex degree distribution for all students and the edge weight distribution for all pairs.
Considering an ego–alteri perspective, social network showed 277 pairs with social tie weight varying from 1 to 14. The heatmap ( Figure 5, bottom left) is a graphical representation of the social network in a N × N matrix with values of social strengths represented in different colors: stronger social ties are in yellow, and weaker are in blue. Edge distribution (shown in Figure 5, bottom right) presents largest weights for two pairs with (GH–ET and YG–GL), followed by two other pairs with (BS–CP and YG–LF). The strongest social ties were all intra-gender, of which only BS–CP were girl/girl. The following six pairs had , and among them, the network shows its first inter-gender social tie.
4.3. Dimensionality Reduction via PCA
The total of complete cases were 128 observations, and the internal consistency index was . Although there is no cutoff point for internal consistence, a recent survey [44] suggests this is largely accepted as satisfactory. The Scree test suggests that the hypothesis of two principal components would be sufficient to explain most of the data variance. This is reinforced by a parallel analysis, which suggests retention of a single component (Figure 6, left).
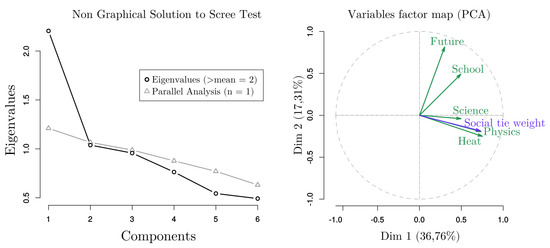
Figure 6.
Scree test suggesting two principal components to retain (left) and Principal Components Analysis (PCA) map with the numerical variables (right).
The first principal component (Figure 6, on the right, horizontal axis) takes loads mainly from the following variables: social tie weight (); number of coincident words in evocations for Heat (); and number of coincident words in evocations for Physics (). They are followed by number of coincident words in evocations for Science (), for School (), and Future () on the first component.
The second component (Figure 6, on the right, vertical axis) had variable loading 0.81 for consensus emerging in evocations for Future and 0.49 for consensus in evoked words for School. All other variables have had loads less than 0.3 in the second principal component.
5. Discussion
Both social and semantic networks showed non-hierarchical structures, and despite having core elements, they did not show a clear central control. These are traces of a complex structuring both in interpersonal and in thought domains.
Structures emerged in social representations, seen in semantic networks, accommodated both common sense and reified terms regarding school objects (Heat, Physics, and Science). As proposed by Chevallard [14], school systems bridge the general sphere of thinking, so-called “noosphere”, and students reality in the the didactic system. That kind of open system overlaps reified and consensual universes. It is expected that fuzzy borders would combine different sources of representation in students’ evocations.
Main words and main relations in the Heat network (Figure 4A) were related to common sense ideas about heat, while Elements from scientific discourse were sparse on that network. Words from scientific discourse appear more frequently in the “Physics” network (Figure 4B) but often related by a supposed opposition, e.g., heat–cold. This kind of contrast is recognized by reified scientific discourse as an alternative conception but circulates as consensus among students.
Co-occurrence networks patterns seem to be consistent to social representation theory [18] in its structural approach [19]: fewer elements aggregate representation’s central core having strong connectivity power. Although not exerting a central control in the system, it helps to organize the representational field. They are emerging cores consensually formed by the group. Core elements carry historicity and give identity to the group and would not, therefore, depend on immediate material context.
The fact that students evoke Sun when we say “Heat”, for instance, is how they—using Moscovici’s words—transform the unfamiliar, which would be how physicists define heat and how concepts of heat are presented in physics classes, into the familiar, which by its turn, would be objects that would make sense in students’ daily lives. Social representations are built for helping a social group to deal with social life, social realities, and social demands.
Professionals in science could take heat as some “amount of transfered energy” as a first snapshot idea. When students start to deal with new school knowledge, the idea of heat, for example, would not be thought in the same way as physicists would think about it. Once there could be no representational object for a group if members of the group do not deal with such object in their life demands, a reified lexicon on heat could not circulate among students if they do not deal with life demands in which such lexicon is consensually shared.
Professional and scientific discourses use reified definitions in a reified lexicon because they are produced and used in a reified world. Considering this, the science teaching challenge would not be to convert students’ common sense representations on science matters into reified representations. Instead, it would be to promote situations in which real demands start to be part of students’ social lives. Then, in order to deal with such demands, new social representations must be produced by them and then would become consensual notions and would circulate among members of the collective.
In representation for “Physics”, the network brought the issue of thinking about physics as being a discipline focused in formulas and calculations. That is consistent with recent findings reported in Reference [45], where another kind of word network showed a similar relation. Besides that, pragmatic elements of physics can be seen but not related to heat. Again, heat appears to be an unfamiliar object for the group. Negative feelings, such as low grades, fear, and remedial lessons, suggests that disciplinary physics is seen as an epistemic obstacle for those students.
In the network for “Science” (Figure 4C), the emergent structure has its core anchored in biology elements (animal, human body), even though data gathering was conducted during physics classes. This representation may be influenced by a stereotypical view of what science would be like. Another feature is that the closest words in this network are all disciplinary relations between school classes regarding biology, physics, or chemistry. It shows an image of school science in its typical curricular discipline separation.
Considering the “School” network, it goes back to didactic triangle. The didactic system has a remarkable asymmetry: the teacher occupies alone one of the three vertexes (Figure 1). Thus, her/his importance is undeniable. Even in the most democratic teaching sets is to be expected a relevant role for the teacher in terms of being recognized as social and epistemic authority in classroom.
That can be confirmed in the representation for “School” (Figure 4D), which emerges centered in the image of the teacher and relates her/his figure in first most similar pairs. The “School” network would not be the case of a tension between scientific and common sense discourses. However, an image of school teacher-centered would be a consensual idea circulating among students that has been built since they began their school lives. Contemporary teaching sets tend to be focused in scaffold students’ autonomy. However, the teacher-centered representation for school in students’ evocations does not necessarily oppose that view. This can be seen in one of highest pair similarities, which was teacher–friend, confirming a positive image of the teacher in relation to students. The central role of the teacher in the classroom can actually be a key factor for promoting students’ autonomy.
Another feature for “School” network is the emergence of negative images, such as “prison” and “boring”. That can be addressed with traditional school sets which can be seen by students as an imposing structure over them. Those negative evocations for school call a reflection: one can only be jailed if she or he would be put inside a place. So, social representation of school as a place that jails the student suggests another teaching challenge: the necessity to foment ways to empower students and enacting their agency in order to build representations of school in which students could see themselves more as being part of school instead of being at this place called school.
Despite some negative representation on “School”, the group appears to keep valuing studies as an exit door for socioeconomic issues. While core elements in the network for “Future” were anchored in what we could call by middle class desires, such as having a job, building a house, or getting married, the closest pairs attached “grad school” to “work” and “work” to “money”. It shows that students share values on the following studies in order to achieve their life goals.
Since, in all real representation, contrasts are an inherent feature, in the“Future” network, a disconnected subgraph (Figure 4F) shows an evident negative self image. Contrasts aside, even in this detached sub-network, the negative view of future is related to not having finished school. That confirms the strong relation between schooling and work opportunities as a shared representation in the group.
Going beyond representational content analysis, we are exploring networks brought from two domains, social and representational, particularly interested in how an interpersonal emerging structure, formed by several sociometric tests, would or would not be related to consensus described above. In this case, the dimensionality reduction supports the notion of a social tie being influential in the consensus formation.
PCA results in having its first principal component mainly loaded by the social tie weights and coincident words evoked by students for intra-school themes (Physics, Heat, and Science). That is consistent with Saxe and his colleagues’ proposal [25], in which traveling ideas in the classroom depend on the strength of student–student affiliation. However, the first principal component showed that this is not for any consensus. The PCA variables map (Figure 6, on the right) shows that the more themes are getting “outer school“ (School and Future), the more they become independent from the classroom’s social tie weight. As a classroom’s social structure is an open system, it would be always interacting with a broader noosphere, and social representations formation on outer school objects would be less driven by inner classroom social relations.
6. Conclusions
The aim of this work was to use the network approach to investigate both social and semantic structures in a classroom in order to explore relations between the strength of interpersonal ties and shared ideas. Representations shared by members of a social group cannot be thought apart from the group itself. Findings reported in the present work indicate that interdependence between interpersonal tie strength and shared ideas on objects closer to students’ school is stronger than the interdependence between interpersonal relation strength and consensus regarding objects more distant from school daily life.
Network approach for both students social relations and shared representations was a fruitful way for building interpretative landscapes on both domains. We could show evidence that interpersonal structures are indeed related to consensus formation in the classroom. Because each student’s life is an overlapping of a multitude of different social groups, each of them sharing its own values and building its own identities, it is likely that themes related to non-scholar life contents produce representation which are shared by a broader community. Therefore, classroom social ties is less related to them.
In this work, we analyzed classroom emerging structures synchronously. The advantage of doing so is that networks can be addressed for a particular moment in the classroom and to a specific teaching content and context. It is challenging to proceed with an analysis when operating two domains of such a complex set, as a real classroom, but the dimensional reduction was helpful to dig relations inter-domain. Further research on this perspective points out the importance exploring beyond synchronic networks. That means accounting for network dynamics in order to understand how the classroom’s emerging structures evolve through time. In addition, this goes beyond single-layer networks, including new advances in the so-called multilayer networks perspective [29,46], to bridge semantic and social networks dimensions as layers of the same system.
Author Contributions
Both authors have contributed equally to the work reported. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code 001.
Acknowledgments
The authors would like to thank the members from the NUPIC research group from University of São Paulo for the feedback given in previous version of this work. We are also in debt to G. Saxe and A. DiSessa, from U.C. Berkeley, for comments and constructive critiques given to rough versions of this work. In addition, three anonymous reviewers made valuable comments and suggestions that improved the quality of this work.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Ladyman, J.; Lambert, J.; Wiesner, K. What is a complex system? Eur. J. Philos. Sci. 2013, 3, 33–67. [Google Scholar] [CrossRef]
- Mitchell, M. Complex systems: Network thinking. Artif. Intell. 2006, 170, 1194–1212. [Google Scholar] [CrossRef]
- Barabási, A.L. Linked: How Everything is Connected to Everything Else and What It Means; Plume: New York, NY, USA, 2003. [Google Scholar]
- Christakis, N.A.; Fowler, J.H. Connected: The Surprising Power of Our Social Networks and How They Shape Our Lives; Back Bay Books: New York, NY, USA, 2009. [Google Scholar]
- Scott, J. Social network analysis. Sociology 2014, 22, 109–127. [Google Scholar] [CrossRef]
- Sengupta-Irvin, T. Affinity through mathematical activity: Cultivating democratic learning communities. J. Urban Math. Educ. 2014, 7, 31–54. [Google Scholar]
- Farmer, T.W.; Rodkin, P.C. Antisocial and prosocial correlates of classroom social positions: The social network centrality perspective. Soc. Dev. 1996, 5, 174–188. [Google Scholar] [CrossRef]
- Cicuto, C.A.T.; Correia, P.R.M. Análise de vizinhança: Uma nova abordagem para avaliar a rede proposicional de mapas conceituais. Revista Brasileira de Ensino de Física 2012, 34, 1401-1–1401-10. [Google Scholar] [CrossRef]
- Rodrigues, E.V.; Camiletti, G.G. Análise estrutural de redes semânticas: Um estudo exploratório das relações entre representações proposicionais e evolução conceitual em um tópico da física. Investigações em Ensino de Ciências 2018, 23, 211–227. [Google Scholar] [CrossRef]
- Teixeira, G.M.; Aguiar, S.F.; Carvalho, C.F.; Dantas, D.R.; Cunha, M.V.; Morais, J.H.M.; Pereira, H.B.B.; Miranda, J.G.V. Complex semantic networks. Int. J. Modern Phys. 2010, 21, 333–347. [Google Scholar] [CrossRef]
- Shaffer, D.W.; Collier, W.; Ruis, A.R. A tutorial on epistemic network analysis: Analyzing the structure of connections in cognitive, social, and interaction data. J. Learn. Anal. 2016, 3, 9–45. [Google Scholar] [CrossRef]
- Bruun, J.; Brewe, E. Talking and learning physics: Predicting future grades from network measures and Force Concept Inventory pretest scores. Phys. Rev. Spec. Top. Phys. Educ. Res. 2013, 9, 020109-1–020109-13. [Google Scholar] [CrossRef]
- Saint-Charles, J.; Mongeau, P. Social influence and discourse similarity networks in workgroups. Soc. Netw. 2018, 52, 228–237. [Google Scholar] [CrossRef]
- Chevallard, Y. La Transposición Didáctica: Del Saber Sabio al Saber Enseñado; Aique: Buenos Aires, Argentina, 1991. [Google Scholar]
- Brockington, G.; Pietrocola, M. Serão as regras da transposição didática aplicáveis aos conceitos de física moderna? Investigações em Ensino de Ciências 2016, 10, 387–404. [Google Scholar]
- Koponen, I.T.; Nousiainen, M. Concept networks in learning and the epistemic support of their key concepts. In International Conference on Complex Networks and their Applications; Springer: Berlin, Germany, 2017. [Google Scholar]
- Rodrigues, E.V.; Borges, A.; Pietrocola, M. The use of history of science on physics teaching as a social representation from pre-service teachers. J. Phys. Conf. Ser. 2019, 1287, 012044. [Google Scholar] [CrossRef]
- Moscovici, S. Notes towards a description of social representations. Eur. J. Soc. Psychol. 1988, 18, 211–250. [Google Scholar] [CrossRef]
- Abric, J.C.; Moscovici, S. Central system, peripheral system: Their functions and roles in the dynamics of social representations. Pap. Soc. Represent. 1993, 2, 75–78. [Google Scholar]
- Guimelli, C. Locating the central core of social representations: Towards a method. Eur. J. Soc. Psychol. 1993, 23, 555–559. [Google Scholar] [CrossRef]
- Moreno, J.L. Who Shall Survive?: A New Approach to the Problem of Human Interrelations; Nervous and Mental Disease Publishing Co: Washington, DC, USA, 1934. [Google Scholar]
- Freeman, L. The Development of Social Network Analysis; Empirical press: Vancouver, BC, Canada, 2004. [Google Scholar]
- Borgatti, S.P.; Mehra, A.; Brass, D.J.; Labianca, G. Network analysis in the social sciences. Science 2009, 323, 892–895. [Google Scholar] [CrossRef]
- Martınez, A.; Dimitriadis, Y.; Rubia, B.; Gomez, E.; de la Fuente, P. Combining qualitative evaluation and social network analysis for the study of classroom social interactions. Comput. Educ. 2003, 41, 353–368. [Google Scholar] [CrossRef]
- Saxe, G.B.; Gearhart, M.; Shaughnessy, M.; Earnest, D.; Cremer, S.; Sitabkhan, Y.; Platas, L.; Young, A. A methodological framework and empirical techniques for studying the travel of ideas in classroom communities. In Transformation of Knowledge trough Classroom Interaction; Schwartz, B., Dreyfus, T., Hershkowitz, R., Eds.; Routledge: New York, NY, USA, 2009; pp. 203–222. [Google Scholar]
- Kozulin, A.; Vygotskii, L.S. Thought and Language; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Yin, R.K. The case study as a serious research strategy. Knowledge 1981, 3, 97–114. [Google Scholar] [CrossRef]
- Di Giacomo, J.P. Intergroup alliances and rejections within a protest movement (analysis of the social representations). Eur. J. Soc. Psychol. 1980, 10, 329–344. [Google Scholar] [CrossRef]
- Stella, M.; Kenett, Y. Viability in multiplex lexical networks and machine learning characterizes human creativity. Big Data Cogn. Comput. 2019, 3, 45. [Google Scholar] [CrossRef]
- Stella, M. Forma mentis networks reconstruct how Italian high schoolers and international STEM experts perceive teachers, students, scientists, and school. Educ. Sci. 2020, 10, 17. [Google Scholar] [CrossRef]
- De Deyne, S.; Navarro, D.J.; Storms, G. Better explanations of lexical and semantic cognition using networks derived from continued rather than single-word associations. Behav. Res. Method 2013, 45, 480–498. [Google Scholar] [CrossRef] [PubMed]
- Ratinaud, P. Interface de R pour les Analyses Multidimensionnelles de Textes et de Questionnaires. Available online: http://www.iramuteq.org/ (accessed on 30 January 2020).
- Russell, P.F.; Rao, T.R. On habitat and association of species of anopheline larvae in south-eastern Madras. J. Malaria Inst. India 1940, 3, 153–178. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Development Core Team: Vienna, Austria, 2008. [Google Scholar]
- Csardi, G.; Nepusz, T. The igraph software package for complex network research. Int. J. Complex Syst. 2006, 1695, 1–9. [Google Scholar]
- Lira, A.; Cerquera, E.C.; Gomes, C.A. As relações interpessoais entre adolescentes: O teste sociométrico como recurso para superar conflitos e violências escolares. Revista Brasileira de Psicodrama 2016, 24, 24–33. [Google Scholar]
- Cronbach, L.J. Coefficient alpha and the internal structure of tests. Psychometrika 1951, 16, 297–334. [Google Scholar] [CrossRef]
- Diedenhofen, B.; Musch, J. Cocron: A web interface and R package for the statistical comparison of Cronbach’s Alpha coefficients. Int. J. Int. Sci. 2016, 11, 51–60. [Google Scholar]
- Cattell, R.B. The scree test for the number of factors. Multivar. Behav. Res. 1966, 1, 245–276. [Google Scholar] [CrossRef]
- Raiche, G.; Magis, D. nFactors. An R Package for Parallel Analysis and non Graphical Solutions to the Cattell Scree Test. Available online: https://cran.r-project.org/web/packages/nFactors/ (accessed on 31 January 2020).
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Lê, S.; Josse, J.; Husson, F. FactoMineR: A package for multivariate analysis. J. Stat. Softw. 2008, 25, 1–18. [Google Scholar] [CrossRef]
- Rodrigues, E. NetScript and Data. Available online: https://bit.ly/2MFeaG8 (accessed on 30 January 2020).
- Taber, K.S. The use of Cronbach’s alpha when developing and reporting research instruments in science education. Res. Sci. Educ. 2018, 48, 1273–1296. [Google Scholar] [CrossRef]
- Stella, M.; De Nigris, S.; Aloric, A.; Siew, C.S.Q. Forma mentis networks quantify crucial differences in STEM perception between students and experts. PLoS ONE 2019, 14, e0222870. [Google Scholar] [CrossRef] [PubMed]
- Kivelä, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer networks. J. Complex Netw. 2014, 2, 203–271. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).