Digital Escape Room, Using Genial.Ly and A Breakout to Learn Algebra at Secondary Education Level in Spain

Abstract

One of the main objectives in mathematics education is to motivate students due to the fact that their interest in this area is often very low. The use of different technologies, as well as gamification in the classroom, can help us to meet this goal. In this case, it is presented the use of two techniques, which are a digital escape room, using Genial.ly and a breakout, for learning algebra in the third course of secondary education. To carry out the experience, a comparison of the course 2018/2019 and the course 2019/2020 is made. Students of both courses completed an exam of algebraic fractions and then an equations exam; the exams were done in the course 2019/2020 taken after having used the techniques. The results show that there are low significant differences between both courses in the algebraic fractions exam qualifications, but those of the equations exam were significant, with a difference of almost two points, which led us to conclude that the use of this techniques improved the qualifications of students. Finally, the perception that students had of the experience was very positive, as shown by the data obtained and allowed them to improve their knowledge as well as their motivation and teamwork.

1. Introduction

Certain school contents are abstract and far from the student motivations. To address these situations, there are teachers who are concerned with improving their students’ motivation by incorporating strategies and methodologies into the classroom that are linked to daily life and that are meaningful and related to the interests of the students.

The use of escape rooms has risen in popularity over the last few years. The application of this type of activity in the classroom has led to an improvement in the motivation of students, and this playful approach facilitates learning. All this acquires special importance in the learning of algebra.

Escape rooms are action games that take place in a real environment, in which groups or teams are required to pass tests, find clues and follow a series of challenges in order to solve a mystery or to find a way to leave a certain space—all this with the condition of a certain available time [1]. The game begins outside the room, in which a character describes a situation as an introduction while instructions are offered, as well as the details of the story and the possible challenges to the team.

Once the escape room starts, the participants must explore, discover clues, take tests and perform other activities that allow them to solve the puzzles that guide them towards the achievement of the final objective.

Reviewing the scientific literature, the first reference to this type of activity carried out under the name of “escape room” was done by the company SCRAP, located in Kyoto, Japan [2]. This activity was very well-received; this led to its expansion throughout the world [2,3,4]. In Europe, Budapest was the first city to implement them. In Spain, the first was run around 2012 in Barcelona.

The objective of introducing the escape room into the school context is not to contribute to the teacher’s leisure, but to motivate learning [2]. The playful perspective ensures that motivation and learning occurs through the game, its dynamics, rules and components. The application of escape rooms improves the learning process and promotes meaningful learning, as well as enhances the development of cognitive abilities with high motivation for a fun and playful activity.

There is evidence of educational escape rooms being carried out in elementary-education-level classrooms, with good results. Additionally, the application of escape rooms at University level has shown an improvement in motivation and performance of students [2,3,4,5].

Among escape rooms, there is the “breakout”, which consists of an adventure with the aim of finding the way out of a room through the solution of puzzles and tests. These are very appropriate in education as they are dynamic and easily adapted to the classrooms. With the playful approach and through the resolution of puzzles, challenges and tests linked to curricular content and skills, the students manage to open doors, locks or boxes in order to find the exit. This has the attraction of having the elements of a fun activity that motivates participation, which facilitates the creation of more interesting classroom dynamics for students.

We found different possibilities for creating these games by companies that sell kits to make an escape room in the classroom. There is also the possibility of creating one with digital tools such as Google Forms or Pygmy. This allow the design of the box itself with a padlock and the tracks in relation to the contents of each subject.

It should be considered that the success of the escape room in the educational field is related to the different benefits it produces in students [1], which are:

• Intellectual benefits: It promotes logic, memory, concentration, attention, deductive thinking, creativity, imagination, mental agility, conflict resolution, time management and management of available resources;
• Social benefits: It favors teamwork, cooperation, the sum of skills, coordination and leadership;
• Emotional benefits: It promotes the expression of emotions and the feeling of accomplishment;
• Psychological benefits: It causes avoidance of routine and self-knowledge.

Regarding the elaboration of an escape room, a series of essential components should be considered [6,7]:

• Context: Contextualization is required to place the action. The context should be described to facilitate the experience to motivate the students. The game is intended to be of the interest to the player. Some of the most used themes are escape from somewhere, solve a murder and escape from prison;
• General information: It is important to detail the logic of the game rules, the operation of certain objects, the purpose, the objective, etc.;
• Game director or game master: They are responsible for exposing the participants to the context, the rules and general information. They will also verify the development of the action. In the case that participants are stuck in any part of the challenges, they can contact the game master to get some guidance or clue;
• Participants: These types of activities are designed to be developed in groups. It is through the cooperation of a group of people that challenges are overcome. With the contribution of the whole group and with the complementarity of the capacities of each one, it is possible to achieve success. The capacities are observation, memorization, pattern recognition, logic, etc. To guarantee the participation and the greatest potential for learning of the whole group, the number of participants must be of four to six members.
• Puzzles: These must be in relation to the context of the game and can be related to logic, precision, joining pieces, manipulating objects, etc. When solving these puzzles, a certain pattern must be followed, such as: opening a box closed with a padlock, finding a solution or having a reward.
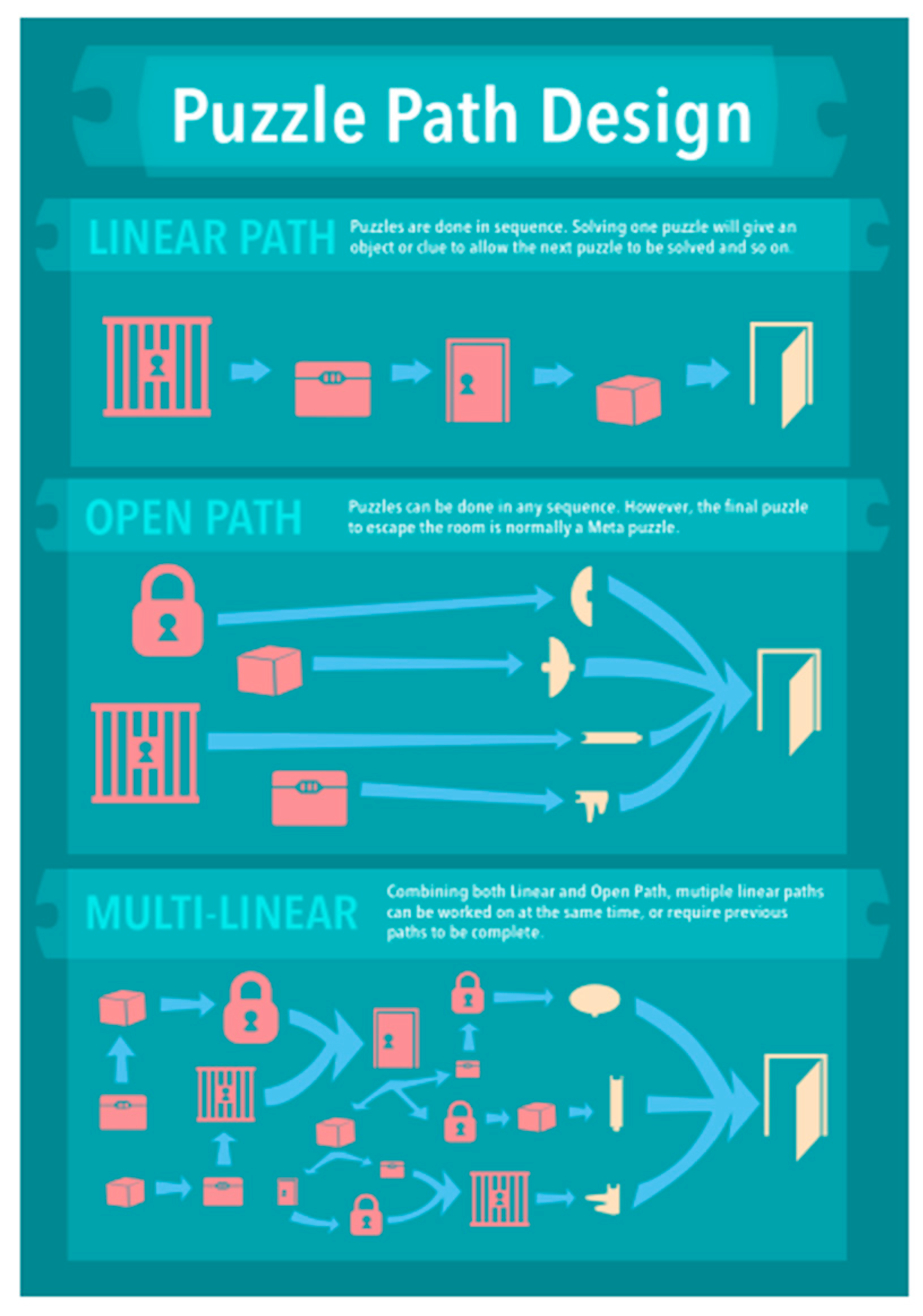
• Sequence of the game: The main objective can be achieved in different ways:
  • Linear path. This involves following a linear or sequential pattern. That is, one challenge must be achieved to access the next one.
  • Open path. This implies an open pattern where it is not necessary to follow a certain sequence.
  • Multilinear: This is a multi-sequential pattern where there is a high level of optionality and different options to complete the game.

Figure 1 defines the different options.

The main problems in algebra learning, many of them related to students are shown in [8], are due to its abstract reasoning and generalization, called as psychologic difficulties [9], as well as others known as cognitive-type difficulties, which are related to the use of symbols and the relations between them, as it can be seen in [10]. According to teacher’s point of view, some experiences related to the way they teach algebra are shown in [11]. Moreover, teachers also need to dominate four different skills as it appears in [12]: the need to know that variables are symbols, the symbols for generalizations, the use of functions in the association between sets and the use of patterns. Moreover, in [13] it is commented that there are several algebraic levels related to the tasks associated with a problem.

In order to help new teachers in the algebra teaching and learning process, there are several guides related to the study of how different methodologies can be used such as described in [14,15,16,17] in which authors show several strategies to teach algebra in the classroom, which includes manipulative materials with non-manipulative ones. On the other hand, other studies such as [18] show the relation between theoretical thinking and technique in a combined paper-and-pencil environment and computer algebra.

As it has been previously commented, one of the main problems in algebra learning—and more concretely in equations and polynomials learning—is the combination of symbols or letters, numbers and mathematical signs and also the different meanings that a symbol can get in different situations, as can be seen in [19], in which there are interesting results about this fact and which offers solutions in order to beat this problem. In this topic, there also are studies related to the role of future teachers and their problems with this field, as it appears in [20,21].

In the last years, game-based learning for algebra has really growth and several authors have studied its benefits. As authors in [22] prove, the used of the app “DragonBox 12+” can help Student’s to reach greater performance in algebraic thinking and attitudes toward algebra. Moreover, in [23] the application of the game-based learning approach for teaching and learning algebraic expressions in undergraduate level is shown with really good results. Furthermore, in [24] it is shown how the use of games with avatar customization in a mobile can help students in algebra learning and in [25] it is demonstrated the goodness of using gamification and serious games in algebra. Other serious games for the learning of algebra in other levels can be seen in [26,27,28].

Changes in the students of primary education way of thinking should be encouraged in order to enable them to advance in algebraic thinking. For this reason, this study promotes the overcoming of challenges in the context of an ecape room as a tool. Authors in [29] refer to aspects such as diagrams, graphs or the technology itself, which allow Student’s to take on increasingly complex challenges. To carry out these types of activities implies a change in the student’s motivation, who in a playful way and with greater significance, can access the representation and resolution of problems.

In this study, it is presented an application experience in the classroom, where the data collected confirms that there is an increase in motivation and the improvement in learning and performance in final tests.

2. Methodology

2.1. Sample

For the development of this study, a sample of 101 students from two different courses of the subjects related to Mathematics was taken. Fifty-one students were from the course 2018/2019, taken as control group and 50 students from the course 2019/2020, taken as experimental group from the secondary education level in a school placed in the city of Madrid, Spain. Students distributed in third course of secondary education level (14–15 years old).

2.2. Procedure

This activity is designed with the purpose of reviewing all the algebra contents of the third-year curriculum in secondary education. It is a dynamic and motivating activity that requires a broad involvement on the part of the student.

The didactic proposal presented was carried out in 2 sessions. In the first a digital escape room is performed, with the aim of consolidating and reviewing the factorization of polynomials and their roots, using Genial.ly tool; in the second a breakout is introduced. The escape room consists of a mansion which is full of zombies and students must escape from it by means of solving algebraic questions, such us factorizing a polynomial, finding the solutions of an equation or answering some theoretical questions related to polynomials or roots.

The escape room begins with a screen in which students should press a button in order to enter the mansion. Once they have entered, each student must solve, individually and on their device, the different challenges that appear in the mansion in which they are digitally locked up. Considering that the objective is to review the factorization of polynomials, most of the enigmas that will be found will address the different contents of the curriculum, such us finding the roots of a polynomial or using factorization. In addition, students can use pen and paper to perform the calculations needed. Moreover, along the game student need to find clues in order to continue solving enigmas, since several of the problems need that previous enigmas had been solved. An example of an enigma is the following:

• In order to open a new clue, you must play a song with the piano—but which melody should you play?
• The keys you must press are the solutions of the polynomial:

  $$p\left(x\right)=\left(x-5\right)\left(x-1\right)\left(x-3\right)$$
• Once the correct keys were pressed a note appears with another clue to continue with the following enigma, which is hidden, so they first need to find the location of that new clue.

The tool allows the Student’s to learn from their own mistakes, since each time an answer fails, they can start over, so it is an activity that allows retractions and it is repeatable, which enables the student to learn the concepts in case of error. In addition, once the students have correctly solved the escape room, the teacher can review the processes and calculations performed to verify that they have done them correctly and without errors.

In the second session, polynomials and equations are reviewed through a breakout. Two boxes locked with a padlock are presented to the students and these boxes can be opened with a combination of three numbers. The objective of this activity is to open the two boxes by means of solving problems related to polynomials and equations correctly.

The students are organized into groups of four members each; in this case the groups were the same cooperative groups in which they usually work in math class. After placing the two boxes in a visible place in the classroom, the mission is presented to the students, which consists of opening them before the end of the time stipulated by the teacher.

In order to open the first box, the teacher must give a sheet to the students in which a three-letter code appears; each of these letters is equivalent to a number which is the combination that will open the lock. The only way to know those three numbers is by solving the three mathematical exercises that appear below. An example of a mission is:

• You need to find the combination that open the padlock, the solution is written as RKX, where those values are:

  ○

  R is the rest of the quotient:

  $$\frac{x^4-3x^3+x^2-3x+5}{x^2+1}$$

  ○

  K is the value that makes the rest of the quotient equal to −4:

  $$\frac{x^5-k{x}^2-3}{x-1}$$

  ○

  X is the positive solution of:

  $$x^4-8x-9=0$$

The original text that students receive in order to solve this mission can be seen in Figure 2, in which the padlock is also shown.

Each time a group manages to open a box, the teacher will verify that the students have carried out the necessary processes to solve the proposed activities correctly. Once the session ends, if a group has not managed to open any of the boxes, the teacher will explain to the group how the activity is solved, in such a way that all students finish the class with the knowledge acquired.

2.3. Variables and Data Collection Tools

The variables of the study are the marks obtained by the students each year in the exam of the second term. The first exam concerning algebraic fractions was used to verify that the differences between the groups where depreciable before carrying out the experiment. On the other hand, the results obtained in a satisfaction survey carried out with 2019/2020 course students were studied.

In order to obtain the information required for the students’ satisfaction about the use of this tool in the teaching–learning process, a questionnaire performed in Google Forms was used.

This questionnaire used is an adaptation of the Driscoll questionnaire designed in 2012, which was used by authors such as Sacristán et al. in [30] for the development of their research in the field of didactics of mathematics. It was chosen in this study due to the fact that it is based on the selection of the most representative and appropriate items to address the objective of this work and it was used in other studies in the area such as the one in [31].

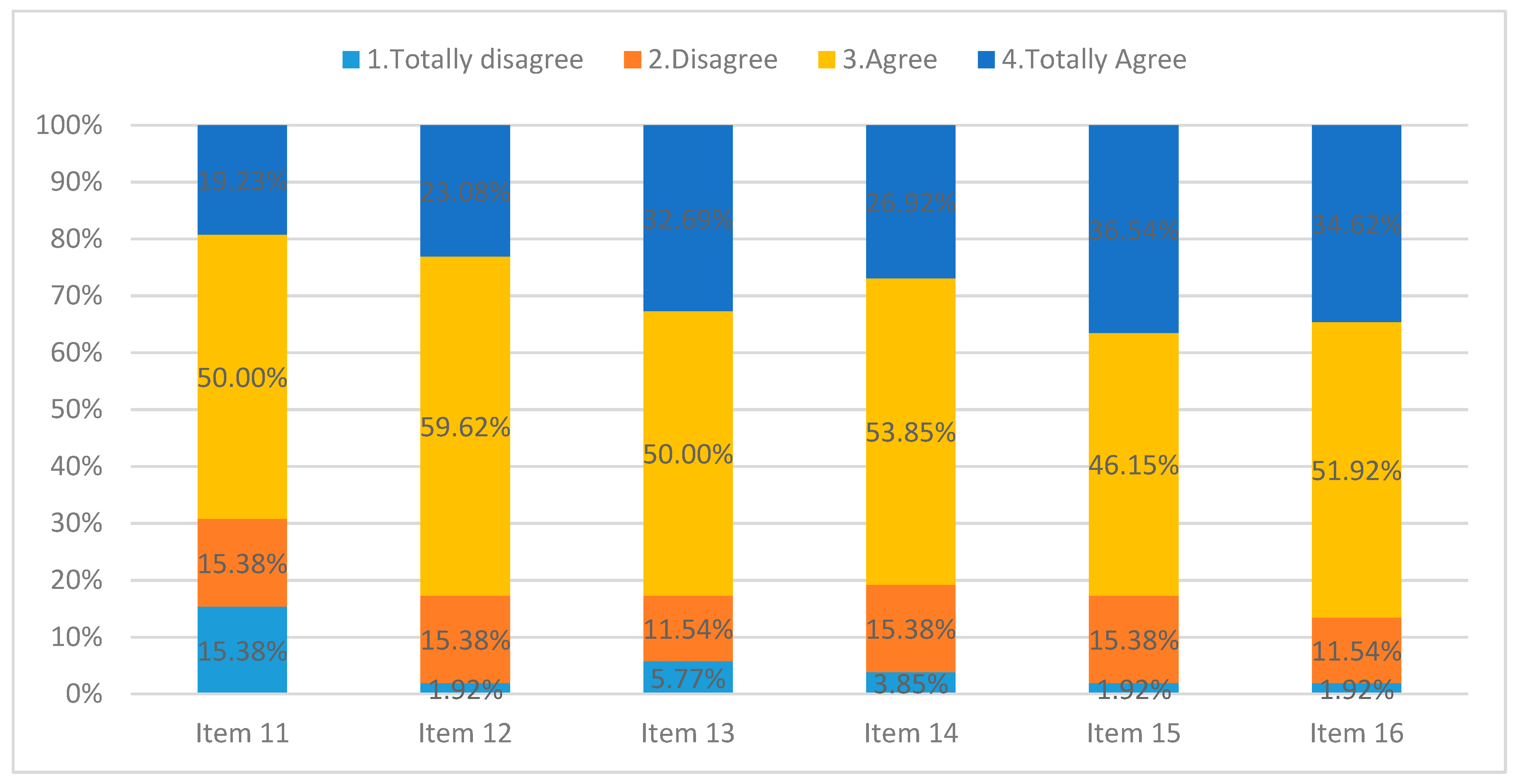
The modified questionnaire consists of 16 items rated on a Likert scale (4 totally in agreement and 1 totally in disagreement). The items in the questionnaire are the following and the descriptive and the correlations, using Kendall’s tau B, were analyzed to correlate ordinal variables, between the different responses:

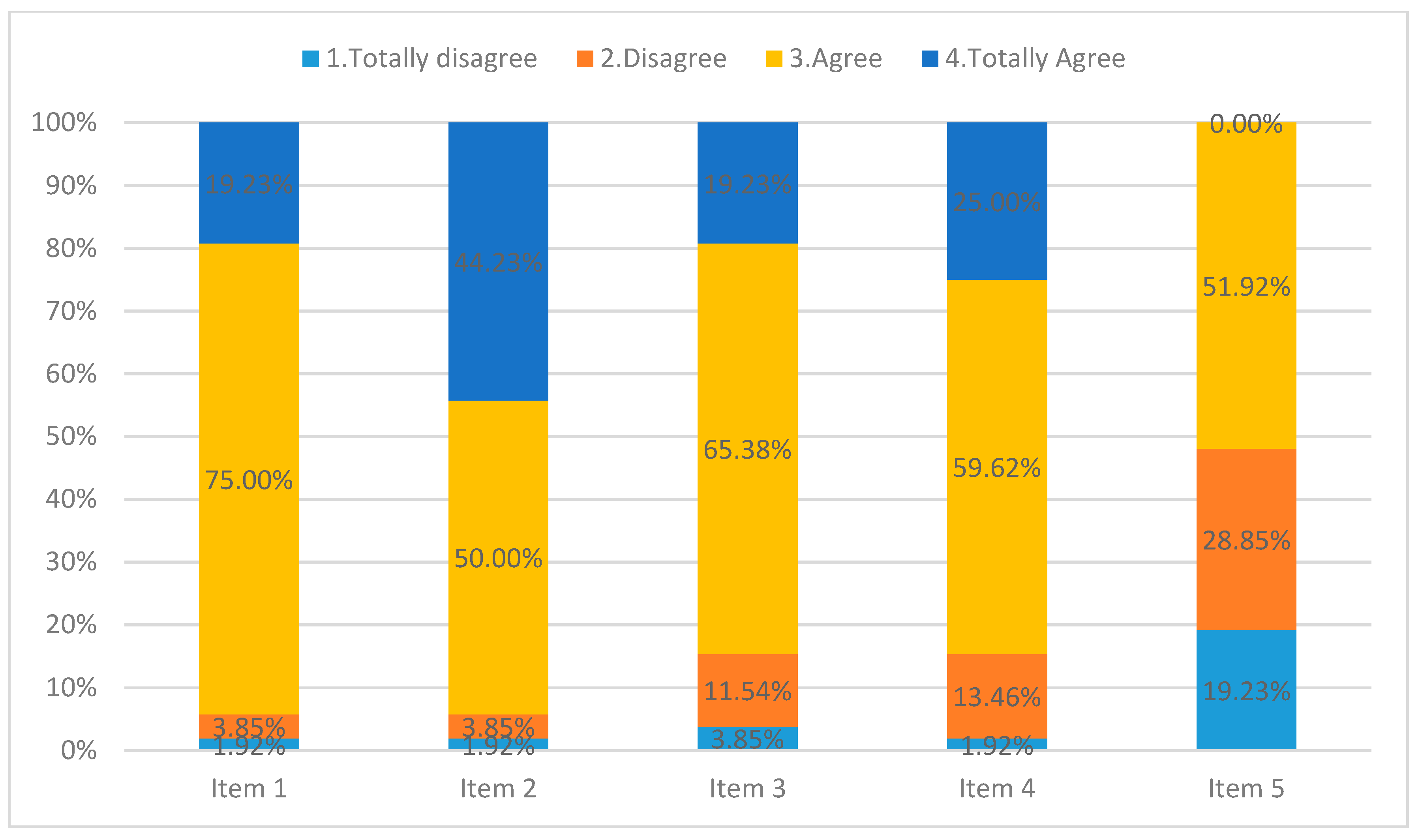
• Item 1—My learning results have increased;
• Item 2—I have fun while learning;
• Item 3—I have greater autonomy in my learning;
• Item 4—I have improved my learning process;
• Item 5—I have worked more on my oral expression;
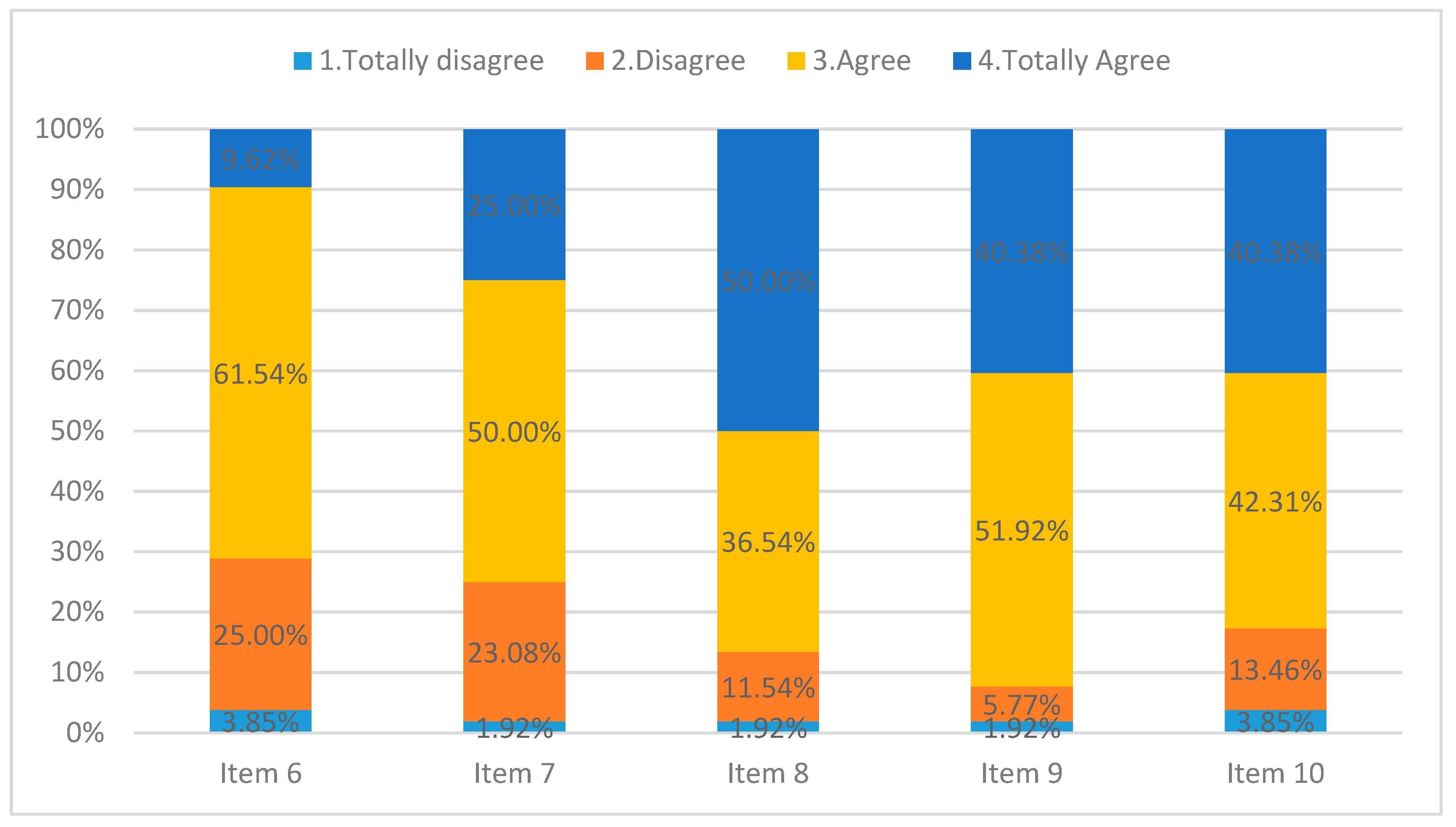
• Item 6—I have worked more on my written expression;
• Item 7—I have increased my creativity;
• Item 8—I have increased my motivation;
• Item 9—I believe that learning is more active and experiential;
• Item 10—I see more possibilities to show, to the teacher or to my classmates, what I have learned;
• Item 11—I have more possibilities to work at my own pace;
• Item 12—I have facility to access the materials and contents;
• Item 13—I have been able to self-evaluate my learning process;
• Item 14—I have increased my learning working as a team;
• Item 15—I have increased my learning by helping my classmates;
• Item 16—I have increased my learning by the help of my classmates.

2.4. Data Analysis

First, the average marks obtained using all the qualifications were calculated and then these averages, in each of the years, were used in order to compare these marks. Once corroborated that there are considerable differences between the notes, in order to see if these differences are due to random or if, on the contrary, they are significant, a comparison of means test was used. For this aim the Student’s t-test for independent groups is used, since due to the data, it is a parametric case, as the variables are measuring continuous quantities (qualifications obtained) and in both groups there are more than 30 measurements.

Regarding the questionnaire for the evaluation of the activity by the students, the descriptive analysis of the information given by the answers to the items was done, as well as a study of correlations between the responses.

2.5. Research Questions

As part of this research, the following research questions were considered:

• Can a digital escape room and a breakout help students in algebra learning process?
• Is it possible to develop a digital escape which increases the motivation of students?

3. Results and Discussion

In this section, the results obtained from the analysis of the qualifications in the variables of both years are presented.

3.1. Results Obtained in the Algebraic Fractions Exam

The comparison of the qualifications of the algebraic fractions exam for both groups (2018/2019 and 2019/2020) was used as a pretest in order verify both groups were homogeneous.

As can be seen in

Table 1. Marks obtained by students in the different exams.

Year	Variable	Number of Responses	Mean
2019	algebraic fractions	51	5.1171
2020	algebraic fractions	48	5.2347

, the difference between the means of the qualifications of the groups is 0.1176, which is quite low. In order to see if this difference is significant, first, we used a study of the equality of variances with Levene’s test. As can be seen in

Table 2. Levene’s test in both exams.

Exam	Value of F	Associated Significance
Algebraic fractions	0.022	0.882

, the significance was greater than 0.05, so equality of variances can be assumed.

After assuming equal variances, the Student’s t-statistic shown in

Table 3. Student’s t-test.

Exam	Value of t	gl	Sig; (bil)	Mean Differences
Algebraic fractions	−0.208	98	0.836	−0.11764

was used to study whether the difference of means is significant. The value of the statistic is 0.836, which shows that the differences were not significant, so both groups are homogeneous in terms of knowledge of algebra.

3.2. General Descriptive Statistics in the Equations Exam

Table 4. Qualifications obtained by students in the final exam.

Year	Variable	Number of Responses	Mean
2019	Equations	48	5.1510
2020	Equations	48	7.0469

shows the grades obtained in the two courses by the students and it is observed that in both there is a clear difference in the means of almost two points. The marks obtained in course 2019/2020 were higher with respect to the previous one in which the escape room and the breakout were not used.

In Figure 3, there is a diagram of the qualifications obtained each year as well as the difference between them. As can be seen, the difference in the qualifications for the equations exam was greater than that of the algebraic fractions.

3.3. Means Comparison in the Equations Exam

Once the differences that exist between the grades in both academic years in each of the variables considered were studied, to see if the differences were significant, the means comparison test is used. For this aim, the Student’s t-test is computed, as commented above, but first the Levene’s test for equality of variances must be done. As commented above, Levene’s test tells us whether equal variances can be assumed. When the probability associated with the Levene’s statistic is greater than 0.05, as it happens in both cases, equality of variances is assumed. Therefore, from the data shown in

Table 5. Levene’s test in both exams.

Exam	Value of F	Associated Significance
Equations	1.381	0.243

, it can be concluded that there is equality of variances in both exams.

After assuming equal variances, the T statistic with its bilateral significance level is shown. The value of the statistic will confirm the compatibility between the hypothesis of equality of means and the difference between means obtained. In

Table 6. Student’s t-test.

Exam	Value of t	gl	Sig. (bil)	Mean Differences
Equations	−3.131	94	0.002	−1.89583

the information provided by the t-test is shown.

We see how, in the case of the marks obtained in the equations exams, the significance is less than 0.05. As a consequence, the difference between the marks obtained in the equations exams is significant with a value of 1.89583.

3.4. Satisfaction Questionnaire of the Escape Room

As can be seen in Figure 4, Figure 5 and Figure 6, the students’ assessment of the experience carried out with an escape room for learning equations was very satisfactory for them, especially in the items: 1—“My learning results are have increased” and 2—“I have fun while learning” with almost 95% positive responses and Item 3—“I think learning is more active and experiential” with more than 92% positive responses.

On the other hand, the items: 3—“I have greater autonomy in my learning”, 4—“I have improved my learning process”, 8—“I have increased my motivation”, 10—“I see more possibilities to show, to the teacher or to my classmates, what I have learned”, 12—“I have had facility to access the materials and contents”, 13—“I have been able to self-evaluate my learning process”, 14—“I have increased my learning by working as a team”, 15—“I have increased my learning by helping my classmates” and 16—“I have increased my learning by the help of my classmates” are positively valued by more than 80% of the students who participated.

In addition, Items 6—“I have increased my written expression”, 7—“I have increased my creativity” and 11—“I have more possibilities to work at my own pace” stand out for having a percentage of positive responses greater than 69%, which is very positive, since it proves that the perception that creativity is increased and also the pace they require are well evaluated. Finally, the worst valued item was Item 5—“I have worked more on my oral expression” with just over 50% of the positive responses, but this is assumable since students does not interpret the exercises as oral ones.

Finally, the analysis of the correlations, using Kendall’s tau B, as the variables considered are ordinal, was done between the different responses. It was found that several of them are positive correlations among which stand out those that appear in

Table 7. Main correlations obtained.

Items	Tau b de Kendall	Sig.
15–16	0.681	0.000
8–13	0.655	0.000
3–4	0.537	0.000
14–15	0.511	0.000
1–8	0.456	0.000
2–10	0.455	0.000
8–9	0.417	0.001

.

From data in Table 7, can be seen that the responses obtained by the students in the item about the motivation of the escape room are correlated to the responses given to the items related to the perception of the increase in the learning outcomes, to the active and experiential nature of learning and to the self-evaluation of their learning process. On the other hand, it is shown how the responses related to teamwork seem to be linked to each other. Finally, the responses of the items related to the improvement of the learning process are related to the students’ own learning autonomy, as well as the responses related to fun while learning are correlated to those given to the answers about the possibilities of showing the knowledge to both the teacher and the rest of the students.

4. Conclusions and Limitations

This experience shows that the application of the educational escape room and breakout for learning algebra and more specifically for learning equations and algebraic fractions in the third year of the secondary education level was highly motivating for the students and has allowed them to enjoy learning and work together with their peers, as well as to show the progress made. For all this and given that the students valued the escape room very positively, it was shown that the activity was motivating enough for all of them to overcome possible difficulties and to escape from each challenge of the game.

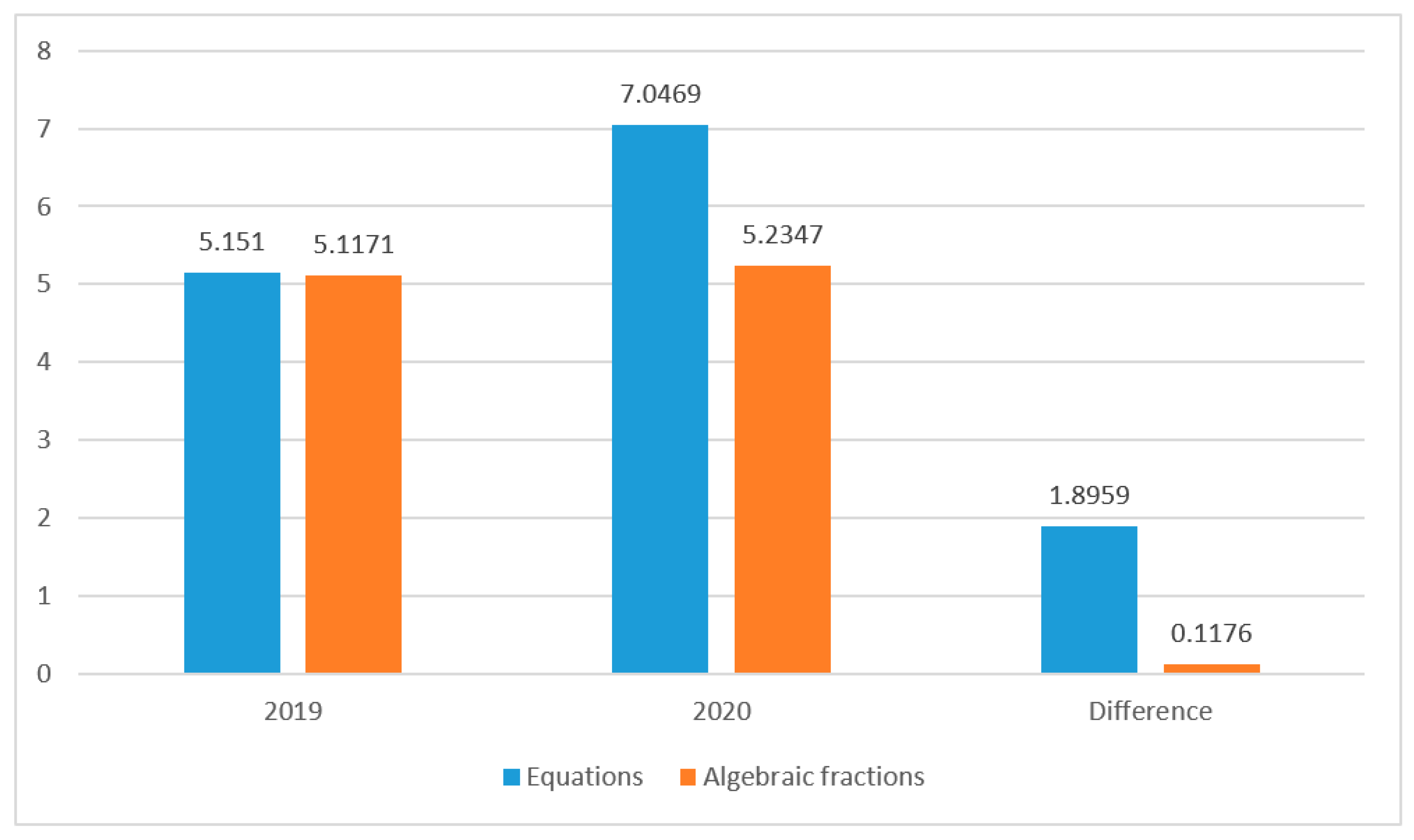
In addition to the good impressions shown by the students in the use of the escape room, the academic results obtained in the equations exam were considerably higher compared to those obtained in the previous year, with a difference of almost 2 points. This fact represents an increase in the learning process, so the use of escape room and breakout has encouraged meaningful learning in this case. Moreover, in order to see if the groups are homogenous, a comparison about the results obtained in the algebraic fractions exam done immediately before the experience, was carried out and it was demonstrated that the knowledge that both groups had in algebra is similar.

It is evident that with the realization of the escape room and breakout, cooperative learning is encouraged, since all the members of the group participate in solving the enigmas, and so, in generating mutual help.

It is found that the preparation and execution of these techniques requires more time of dedication on the part of the teacher, although the final results obtained encourage that its application may be very interesting.

In addition, after consulting the scientific bibliography available in this field, it was shown that this methodology can be applied in both primary and secondary education levels and in training cycles. Moreover, it can be also appropriate for University level and, as future work, the possibility to carry it out the experience in this level as well as with other contents related to Mathematics and other subjects will be considered.

Finally, related to the limitations of this study, it is clear that the sample considered is small so the conclusions of this study can just be taken into account in the sample studied. In a near future, a new experience with a bigger group will be done and related to other technique such as the flipped classroom used in [32]. Moreover, related to the satisfaction questionnaire, in a near future, also a bigger group can answer it in order to obtain deeper conclusions or even including other questions such as the ones appearing in [33] in order to obtain study similar conclusions.