Does FDI Really Matter to Economic Growth in India?
Abstract
:1. Introduction
2. The Model
2.1. The Link between Total Factor Productivity and FDI
2.2. The Cointegrated Vector Autoregression (CVAR) Approach
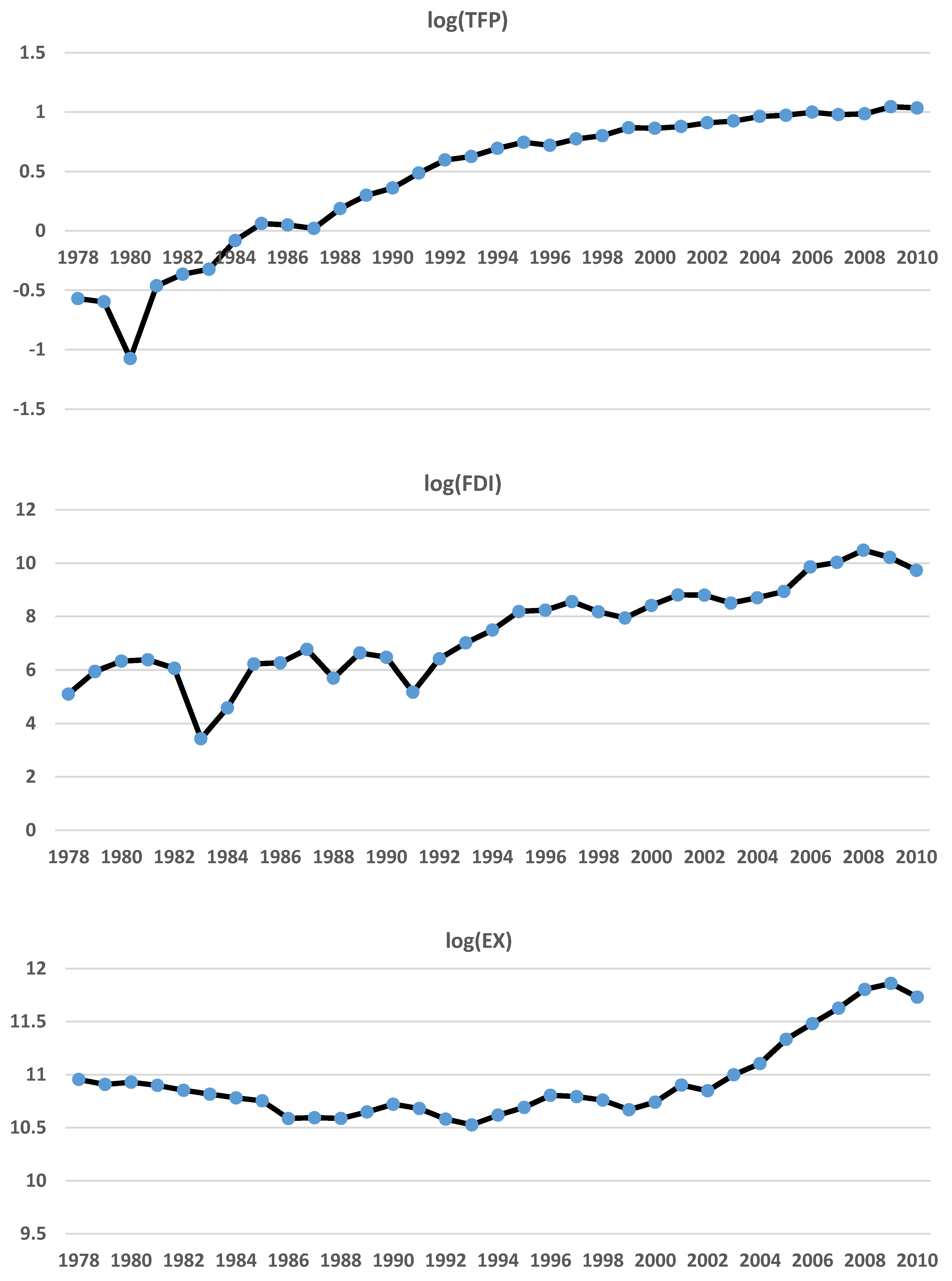
3. Data
4. Empirical Results
4.1. Measuring the Total Factor Productivity
4.2. The CVAR Approach: Does FDI Matter to the Total Factor Productivity?
5. Concluding Remarks
Author Contributions
Conflicts of Interest
References
- Aghion, Phillippe, and Peter Howitt. 1998. Endogenous Growth Theory. Cambridge: MIT Press. [Google Scholar]
- Agrawal, Gaurav, and Mohd A. Khan. 2011. Impact of FDI on GDP: A comparative study of China and India. International Journal of Business and Management 6: 71–79. [Google Scholar] [CrossRef]
- Agrawal, Pradeep. 2005. Foreign direct investment in South Asia: Impact on economic growth and local investment. In Multinationals and Foreign Investment in Economic Development. Edited by Edward M. Graham. Basingstoke: Palgrave Macmillan, pp. 94–118. [Google Scholar]
- Alfaro, Laura. 2003. Foreign Direct Investment and Growth: Does the Sector Matter? Cambridge: Harvard Business School, Harvard University. [Google Scholar]
- Alfaro, Laura, Sabnem Kalemli-Ozcan, and Selin Sayek. 2009. FDI, Productivity and Financial Development. World Economy 32: 111–35. [Google Scholar] [CrossRef]
- Ashraf Ayesha, Dierk Herzer, and Peter Nunnenkamp. 2016. The effects of greenfield FDI and cross-border M&As on total factor productivity. World Economy 39: 1728–55. [Google Scholar]
- Baltabaev, Botirjan. 2014. FDI and total factor productivity growth: New macro evidence. World Economy 37: 311–34. [Google Scholar] [CrossRef]
- Bende-Nabende, Anthony, Jim Ford, and Jim Slater. 2001. FDI, regional economic integration and endogenous growth, some evidence from Southeast Asia. Pacific Economic Review 6: 383–99. [Google Scholar] [CrossRef]
- Borensztein Eduardo, José De Gregorio, and Jong-Wha Lee. 1998. How does foreign direct investment affect economic growth? Journal of International Economics 45: 115–35. [Google Scholar] [CrossRef]
- Chakraborty, Chandana, and Parantapu Basu. 2002. Foreign direct investment and growth in India: A cointegration approach. Applied Economics 34: 1061–73. [Google Scholar] [CrossRef]
- Chakraborty, Chandana, and Peter Nunnenkamp. 2008. Economic reforms, FDI, and economic growth in India: A sector level analysis. World Development 36: 1192–12. [Google Scholar] [CrossRef]
- Chang, Shu Chen. 2007. The interactions among foreign direct investment, economic growth, degree of openness and unemployment in Taiwan. Applied Economics 39: 1647–61. [Google Scholar] [CrossRef]
- Coe, David T., and Elhanan Helpman. 1995. International R&D spillovers. In NBER Working Papers 4444. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Dash, Ranjan Kumar, and Purna Chandra Parida. 2013. FDI, services trade and economic growth in India: Empirical evidence on causal links. Empirical Economics 45: 217–38. [Google Scholar] [CrossRef]
- De Mello, Luiz R., Jr. 1997. Foreign direct investment in developing countries and growth: A selective survey. Journal of Development Studies 34: 1–34. [Google Scholar] [CrossRef]
- Doornik, Jurgen, and David Hendry. 1994. Interactive Econometric Modeling of Dynamic System (PcFiml 8.0). London: International Thomson Publishing. [Google Scholar]
- Findlay, Ronald. 1978. Relative backwardness, direct foreign investment and the transfer of technology: A simple dynamic model. Quarterly Journal of Economics 92: 1–16. [Google Scholar] [CrossRef]
- Gorg, Holger, and David Greenway. 2004. Much ado about nothing? Do domestic firms really benefit from foreign direct investment? World Bank Research Observer 19: 171–97. [Google Scholar] [CrossRef]
- Grossman, Gene M., and Elhanan Helpman. 1992. Innovation and Growth in the Global Economy. Cambridge: MIT Press. [Google Scholar]
- Grossman, Gene M., and Elhanan Helpman. 2002. Outsourcing in a global economy. In NBER Working Papers 8728; Cambridge: National Bureau of Economic Research. [Google Scholar]
- Hansen, Henrik, and John Rand. 2005. On the Causal Links between FDI and Growth in Developing Countries. Discussion Papers 04-30. Demark: Institute of Economics, University of Copenhagen. [Google Scholar] [CrossRef]
- Johansen, Søren. 1988. Statistical analysis of co-integrating vectors. Journal of Economic Dynamics and Control 12: 231–54. [Google Scholar] [CrossRef]
- Johansen, Søren, and Katarina Juselius. 1990. Maximum likelihood estimation and inference on cointegration—With applications to the demand for money. Oxford Bulletin of Economics and Statistics 52: 169–210. [Google Scholar] [CrossRef]
- Kannen, Peter, Julian Donaubauer, and Dierk Herzer. 2017. How do South-South and North-South FDI affect total factor productivity growth in developing countries? Economics Bulletin 37: 429–43. [Google Scholar]
- Lipsey, Robert E. 2002. Home and host country effects of FDI. In Paper for ISIT Conference on Challenges to Globalization. Sweden: Lidingö. [Google Scholar]
- Liu, Xiaming, Haiyan Song, and Peter Romilly. 1997. An empirical investigation of the causal relationship between openness and economic growth in China. Applied Economics 29: 1679–87. [Google Scholar] [CrossRef]
- Liu, Xiaming, Peter Burridge, and Peter Sinclair. 2002. Relationships between economic growth, foreign direct investment and trade: Evidence from China. Applied Economics 34: 1433–40. [Google Scholar] [CrossRef]
- Lütkepohl, Helmut. 2005. New Introduction to Multiple Time-Series Analysis. New York: Springer. [Google Scholar]
- Park, S. R., and X. Lee. 2003. International Technology Spillovers and Its Effect on China’s Economic Growth. KERI Major Research Paper 2003-11. Seoul: Korea Economic Research Institute. [Google Scholar]
- Pradhan, Jaya P. 2002. Foreign direct investment and economic growth in India: A production function analysis. Indian Journal of Economics 82: 582–86. [Google Scholar]
- Sahoo, Dukhabandhu, and Maathai K. Mathiyazhagan. 2003. Economic growth in India: Does foreign direct investment inflow matter? Singapore Economic Review 48: 151–71. [Google Scholar] [CrossRef]
- Shan, Jordan. 2002. A VAR approach to the economics of FDI in China. Applied Economics 34: 885–93. [Google Scholar] [CrossRef]
- Sun, Haishun, and Ashok Parikh. 2001. Exports, inward foreign direct investment (FDI) and regional economic growth in China. Regional Studies 35: 187–96. [Google Scholar] [CrossRef]
- Tsai, Pan-Long. 1991. Determinants of foreign direct investment in Taiwan: An alternative approach with time-series data. World Development 19: 275–85. [Google Scholar] [CrossRef]
- Urata, Shujiro. 2001. Emergence of an FDI-trade nexus and economic growth in East Asia. In Rethinking the East Asian Miracle. Edited by Joseph E. Stiglitz and Shahid Yusuf. New York: Oxford University Press, pp. 409–59. [Google Scholar]
- Wang, Zhen Quan, and Nigel Swain. 1997. Determinants of inflow of foreign direct investment in Hungary and China: Time-series approach. Journal of International Development 9: 695–726. [Google Scholar] [CrossRef]
- Woo, Jaejoon. 2009. Productivity growth and technological diffusion through foreign direct investment. Economic Inquiry 47: 226–48. [Google Scholar] [CrossRef]
- Yao, Shujie. 2006. On economic growth, FDI and exports in China. Applied Economics 38: 339–51. [Google Scholar] [CrossRef]
- Zhang, Kee H. 2001. Does foreign direct investment promote economic growth? Evidence from East Asia and Latin America. Contemporary Economic Policy 19: 175–85. [Google Scholar] [CrossRef]
| 1 | However, it should be admitted at the onset that the difference between analyzing the FDI-GDP nexus or FDI-TFP nexus is more technical than conceptual; that is, the spillover effects are implicit in the former and explicit in the latter. When estimating the effect of FDI on GDP, for example, the effects of the inputs such as labor and capital on outputs could change in response to FDI. On the other hand, concentrating on TFP in a two-step procedure adopted here may give rise to different results by removing those input effects and then looking at the effect of FDI on TFP, holding the contribution from inputs being fixed. For completeness, therefore, we also analyze the FDI-GDP nexus in India using the same data set. The results show that FDI plays little role in boosting economic growth. Interested readers can contact the authors for more details of the analysis. The authors thank a referee for raising the issue discussed here. |
| 2 | It should be noted that the presence of unit roots in the variables in Equation (2) is tested using the augmented Dickey–Fuller (ADF) test. The results show that all the variables appear to be stationary and integrated of order one; hence, OLS can be safely used to estimate Equation (2) without worrying about spurious regression problem. |
| 3 | It is worth mentioning that interpreting the coefficients in Equation (5) as long-run elasticities may ignore the dynamics of the system (Lütkepohl 2005). For example, a 1% increase in FDI may not cause a long-run change of India’s TFP by 0.364%, since a change in FDI is likely to have an impact on exports as well that may interact in the long-run. |
| Variable | (Gross Domestic Product) | |
|---|---|---|
| Coefficient | t-Statistic | |
| (Labor) | 5.382 | 2.206 ** |
| (Capital) | 1.094 | 1.111 |
| [ (Labor)]2 | 1.306 | 3.576 ** |
| [ (Capital)]2 | 0.249 | 2.213 ** |
| (Labor) * (Capital) | 0.506 | 2.634 ** |
| Constant | 18.663 | 2.467 ** |
| Variable | Level | First Difference | Decision |
|---|---|---|---|
| ADF test with no trend | |||
| Total Factor Productivity | −1.765 | −3.676 * | I(1) |
| (0) | (0) | ||
| FDI | −1.076 | −5.686 ** | I(1) |
| (0) | (0) | ||
| Exports | 0.978 | −8.992 ** | I(1) |
| (0) | (0) | ||
| ADF test with trend | |||
| Total Factor Productivity | −1.257 | −5.868 ** | I(1) |
| (0) | (0) | ||
| FDI | −3.251 | −5.838 ** | I(1) |
| (0) | (0) | ||
| Exports | −2.234 | −5.458 ** | I(1) |
| (0) | (0) | ||
| Null Hypothesis | Eigenvalue | Trace Statistics | 5% Critical Value |
|---|---|---|---|
| H0: r = 0 | 0.731 | 53.822 * | 35.193 |
| H0: r ≤ 1 | 0.239 | 14.430 | 20.262 |
| H0: r ≤ 2 | 0.187 | 6.208 | 9.165 |
| Variable | Exclusion H0: βi = 0 (LR Test Statistic) | Weak Exogeneity H0: αi = 0 (LR Test Statistic) |
|---|---|---|
| Total Factor Productivity | 7.777 [0.000] ** | 27.461 [0.000] ** |
| FDI | 31.096 [0.000] ** | 1.396 [0.238] |
| Exports | 4.815 [0.028] * | 0.001 [0.977] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, Y.J.; Baek, J. Does FDI Really Matter to Economic Growth in India? Economies 2017, 5, 20. https://doi.org/10.3390/economies5020020
Choi YJ, Baek J. Does FDI Really Matter to Economic Growth in India? Economies. 2017; 5(2):20. https://doi.org/10.3390/economies5020020
Chicago/Turabian StyleChoi, Yoon Jung, and Jungho Baek. 2017. "Does FDI Really Matter to Economic Growth in India?" Economies 5, no. 2: 20. https://doi.org/10.3390/economies5020020
APA StyleChoi, Y. J., & Baek, J. (2017). Does FDI Really Matter to Economic Growth in India? Economies, 5(2), 20. https://doi.org/10.3390/economies5020020







