The EU Public Debt Synchronization: A Complex Networks Approach

Abstract

This study examines the evolution of public debt among the 27 EU member states using Graph Theory tools; the Threshold Weighted–Minimum Dominating Set (TW–MDS) and the k-core decomposition method, alongside a standard network quantitative metric, the density. By separating the data into three distinct periods, pre-crisis (2000–2007), European sovereign debt crisis (2008–2015), and post-crisis (2016–2023), we examine the potential synchronization of the debt ratios among EU countries through cross-correlations of the public debts. The findings reveal that public debt correlation was at its highest level during the 2008–2015 period, reflecting the universal impact of the crisis and the subsequent synchronized fiscal and monetary policy measures taken within EU. A significantly lower network density is observed in both the pre- and post-crisis periods. These results contribute to the overall debate on fiscal stability and policy coordination by showing how EU countries tend to align their fiscal behaviors during periods of crisis while behaving more independently during stable times. In addition, we yield a deeper insight into how economic shocks reorganize public debt interconnections within the crisis period. Finally, this analysis highlights to what extent European economic integration strengthens connections between the fiscal positions (through public debt) of the European Union member countries.

1. Introduction

The formation of the Euro Area in 1999 was a significant milestone for the economic integration of the participating European Union nations. The introduction of the common currency was intended to promote stability and stimulate economic growth. It was a necessary—but not sufficient—condition to move from the theoretical towards a real Optimal Currency Area (OCA) by Robert Mundell standards (Mundell, 1961). However, the European sovereign debt crisis that manifested in the 2010s exposed fundamental weaknesses in real economic integration, governance, and policy coordination among the member states. This crisis underscored the need for improved mechanisms to monitor and manage macroeconomic imbalances that could threaten the overall stability of the region (Alves et al., 2020).

The evolution of the EU has been shaped by both economic and policy-driven challenges. The Maastricht Treaty, approved in 1992, laid the foundation for a monetary union by setting convergence criteria that countries must meet to adopt the euro. These criteria include limits on budget deficits, public debt levels, inflation, long-term interest rates, and exchange rate stability.

The introduction of the euro in 1999 marked the beginning of a new monetary era, with the European Central Bank (ECB) assuming responsibility for the unified monetary policy. Following the establishment of the Eurozone, the Stability and Growth Pact (SGP) became the fiscal rule for countries belonging to the monetary union. The pact seeks to balance fiscal discipline with government flexibility. The fact that these fiscal rules have been reformed several times highlights that public debt remains a persistent challenge, especially under heightened scrutiny from financial markets. The latest reform, adopted in 2024, reaffirms the 3% GDP deficit limit and the 60% GDP debt threshold and introduces flexible adjustment pathways. Due to the geopolitical context, including the war in Ukraine, which started in 2022, and political instability in the United States since early 2025, this new rule has already been relaxed. This measure allows countries to exclude defense spending from the criteria assessed under the excessive deficit procedures for a period of four years. Nevertheless, uncertainty in the markets regarding the sustainability of public debt remains, influencing credit ratings and economic stability within the region.

The financial crisis of 2008 and the following European sovereign debt crisis (which occurred in 2010) further exposed the weaknesses of a monetary union without a common fiscal policy. The crisis, triggered in part by the revelation of underreported budget deficits in certain Eurozone countries, led to a loss of market confidence and a sharp rise in borrowing costs. In response, emergency measures such as the European Stability Mechanism (ESM) were implemented to provide financial assistance to struggling economies. In addition to these temporary measures, permanent reforms were taken to address the drawbacks associated with the lack of a centralized fiscal authority. One of the most significant was the European Semester, established in 2010, which serves as a key instrument for ensuring economic policy alignment and coordination within the Euro Area. It integrates the Stability and Growth Pact (SGP), the Broad Economic Policy Guidelines (BEPGs), the European Employment Strategy (EES), the Lisbon Strategy, and the Social Open Method of Coordination (OMC), critical frameworks designed to maintain fiscal discipline and economic stability (Verdun & Zeitlin, 2017). Under this system, the European Commission assesses national economic policies, issues country-specific recommendations, and monitors macroeconomic imbalances, including labor market and credit developments. These measures aim to synchronize economic cycles across member states and mitigate the risks of future financial crises (Papadopoulos & Piattoni, 2019).

In addition, the implementation and the second reform of the Stability and Growth Pact (through the Six Pack (2011) and the Two Pack (2013)) strengthened the coordination of fiscal policies and improved the monitoring of member states’ fiscal positions.

Similar measures were taken following the 2020 pandemic crisis for the whole EU with the Next Generation EU, the European recovery plan (a 30-year bond launched to enable European countries to address both short-term emergencies and long-term challenges), and the third reform of the Stability and Growth Pact adopted in 2024 for EMU countries.

Thus, since the advent of the Eurozone in 1999, numerous measures, both temporary (implemented only during economic crises) and permanent (reforms of fiscal rules), have been taken to ensure a greater convergence of the fiscal positions, thus strengthening European economic integration.

This study examines the economic network of the 27 EU countries, focusing on public debt levels over three distinct periods: 2000–2007 (Period 1), 2008–2015 (Period 2), and 2016–2023 (Period 3). By analyzing cross-correlations among member states, it seeks to identify the patterns of synchronization in public debt dynamics. The findings will contribute to a deeper understanding of the EU’s fiscal landscape and inform future policy decisions that promote economic resilience and integration (Mundell, 1961; McKinnon, 1963; Kenen, 1969). This study also contributes to the assessment of fiscal integration in the EU by examining the synchronization and interconnections of public debt trajectories among member states.

The originality of this research lies in its application of complex network analysis to measure both the network’s intensity as well as the number of interconnected countries within the European Union, as already employed by Papadimitriou et al. (2022). The member states constitute a union in which they adhere to shared rules regarding debt ratios. If the ratios move in different directions, implementing a unified policy across all countries becomes quite challenging.

In light of this, the study aims to examine the following: (a) how the debt ratios of the European economies have evolved over time and whether their trajectories have followed the same direction; (b) the extent to which countries are interconnected in terms of debt evolution (specifically, whether they form groups exhibiting similar behavior); and (c) how the debt ratio synchronization was affected by events that had a global effect—principally the 2007–2008 financial crisis, followed by the COVID-19 pandemic in 2020 and the outbreak of the Russo-Ukrainian war in 2022. Understanding whether public debt trajectories are intertemporally linked across countries is essential for assessing the degree to which EU member states are moving in a common fiscal direction.

The rest of the paper is structured as follows: In Section 2, we present the related literature, in Section 3 and Section 4, we present the dataset and the methodology, respectively, and in Section 5, we analyze the results, while Section 6 concludes the paper.

2. Literature Review

As the EU continues to navigate the challenges of fiscal sustainability, particularly in the aftermath of recent crises, it has become increasingly important to understand how its fiscal rules influence public debt. Recent research sheds light on the effectiveness of EU-level mechanisms and national fiscal frameworks, raising important questions about what works, what does not, and where reforms are needed.

The study of Kraemer and Lehtimäki (2023) examines how EU-level fiscal institutions and national fiscal rules have influenced public debt dynamics across EU member states from 1990 to 2019. Using a panel data approach with fixed effects, the authors find that the Stability and Growth Pact (SGP) significantly reduced government debt, especially after its establishment. However, later reforms to the SGP showed mixed effectiveness. National fiscal rules had varying impacts depending on the rule type and sector, with general government balance and debt rules showing more consistent debt-reducing effects. Interestingly, some rules at the central government level were linked to rising debt. The results highlight that EU and national rules are largely complementary, but their design and coordination are critical for effective fiscal governance.

In a follow-up study Kraemer and Lehtimäki (2024), assess the impact of European integration and the EU’s fiscal framework on public debt levels across the member states. Using the Synthetic Control Method, the authors construct counterfactual scenarios to estimate what debt trajectories might have looked like without EU membership or the SGP. Their findings reveal that, for most EU countries, actual government debt levels were significantly lower than those in the synthetic alternatives, suggesting a clear debt-restraining effect. This effect persists even in cases of limited rule compliance, highlighting the anchoring influence of EU fiscal structures. However, important heterogeneities are also underscored, particularly after the global financial crisis.

In a complementary perspective, Arnold et al. (2022) argue that the European Union’s current fiscal rules have fallen short in ensuring debt sustainability and macroeconomic stabilization. The authors propose a risk-based framework linking fiscal targets to debt sustainability analysis, while maintaining the 3% deficit and 60% debt-to-GDP thresholds. A strengthened role for national fiscal institutions and medium-term frameworks is emphasized, alongside the creation of a central EU fiscal capacity to support public goods and counteract asymmetric shocks. The paper calls for institutional reforms, including an independent European Fiscal Council and more robust national fiscal councils. The goal is to design rules that are both effective and realistically implementable, especially in a high-debt, post-crisis context.

Beyond fiscal rules, the broader questions of economic integration and convergence remain central to the viability of the Eurozone. From a theoretical standpoint, the concept of economic synchronization has been widely discussed in the literature, particularly in relation to the Optimum Currency Area (OCA) theory (Mundell, 1961; McKinnon, 1963; Kenen, 1969). The OCA framework posits that regions adopting a common currency should exhibit synchronized business cycles and economic homogeneity to ensure effective monetary policy transmission. However, empirical studies suggest that persistent structural disparities among Eurozone economies pose challenges to achieving full convergence (Frankel & Rose, 1998; Rogoff, 1985).

Recent empirical studies have continued to uncover persistent structural disparities among the Eurozone economies. For instance, Coutinho and Turrini (2020) analyzed how economies in the Euro Area have been converging compared to other EU and non-EU countries. They found that, overall, the patterns are similar across groups. However, the countries that initially adopted the euro have shown weaker convergence—a trend that seems to have started even before the financial crisis, likely due to the persistent differences in productivity levels.

Similarly, Franks et al. (2018) examined the economic convergence among Euro Area countries and concluded that while nominal convergence occurred in areas such as inflation and interest rates, the real convergence of per capita income levels has not been achieved among original Euro Area members following the introduction of the common currency.

Methodologically, network analysis has gained significant traction in recent years, as it provides a robust framework for evaluating economic linkages and offering valuable insights into economic synchronization. Previous studies have applied this approach to evaluate financial contagion, trade dependencies, and sovereign debt risks (Dellas & Tavlas, 2009). One such study is that of Papadimitriou et al. (2014), which focuses on analyzing financial stability and economic convergence. The authors present two empirical examples: one based on a banking network of 200 US banks and another based on GDP growth rates among 22 European countries. Their findings emphasize the effectiveness of the T-MDS methodology in analyzing complex economic systems. By leveraging techniques from complex networks, researchers can identify synchronization patterns that significantly contribute to stability. Within the framework of our research, policy coordination is most effective when synchronization is widespread and encompasses the maximum possible number of member states.

In another study, Papadimitriou et al. (2016) highlight the utility of network-based approaches in assessing economic cohesion within the Eurozone. The research examines the synchronization of economic cycles through complex network metrics, demonstrating how central and peripheral countries interact within the Euro Area’s financial framework. The findings suggest that while certain core economies exhibit strong interconnections, peripheral nations often display greater volatility and weaker ties to the network center, impacting overall economic stability.

Further, Dias (2012) examines the sovereign debt crisis in the European Union, employing minimum spanning trees within a rolling window framework. The study uses data from 19 EU countries concerning daily 10-year government bond yield rates, spanning from April 2007 to October 2010. The results highlight a lack of synchronization between the four most impacted countries—Greece, Ireland, Portugal, and Spain—and the more resilient nations in the Euro Area, such as Germany and the Netherlands.

Kantar et al. (2014) examine the relationships between European countries by constructing networks based on debt-to-GDP ratios. To analyze the topological properties over the period of 2000–2011, they develop hierarchical and minimum spanning trees. Their study covers both the entire period (2000–2011) and two specific sub-periods (2000–2004 and 2005–2011). The analysis reveals distinct clusters of countries grouped by their debt levels.

Matesanz and Ortega (2015) examine the evolving network dynamics of quarterly public debt-to-GDP ratios across 29 European countries from 2000 to 2014. Utilizing a rolling window approach, they construct hierarchical trees and minimum spanning trees while evaluating various standard metrics associated with complex networks. Their findings reveal that the period of the financial crisis exhibits the highest level of connectivity among countries within the network.

Papadimitriou et al. (2022) explore the synchronization levels of a range of macroeconomic variables in Europe, including the general government debt-to-GDP ratio. Using correlation-based networks and Graph Theory metrics, their analysis spans three distinct periods: 1999–2004, 2005–2010, and 2011–2019. Their findings reveal significant synchronization of the debt-to-GDP ratio during the 2005–2010 period, a trend that is disrupted in the subsequent interval.

The present study builds on this literature by examining public debt dynamics in the EU over three distinct periods. By analyzing the evolving structure of the network, this research aims to contribute to the ongoing discourse on fiscal stability and policy coordination within the European monetary union. Furthermore, from a methodological standpoint, the potential of k-core analysis remains largely unexplored in this context.

3. The Dataset

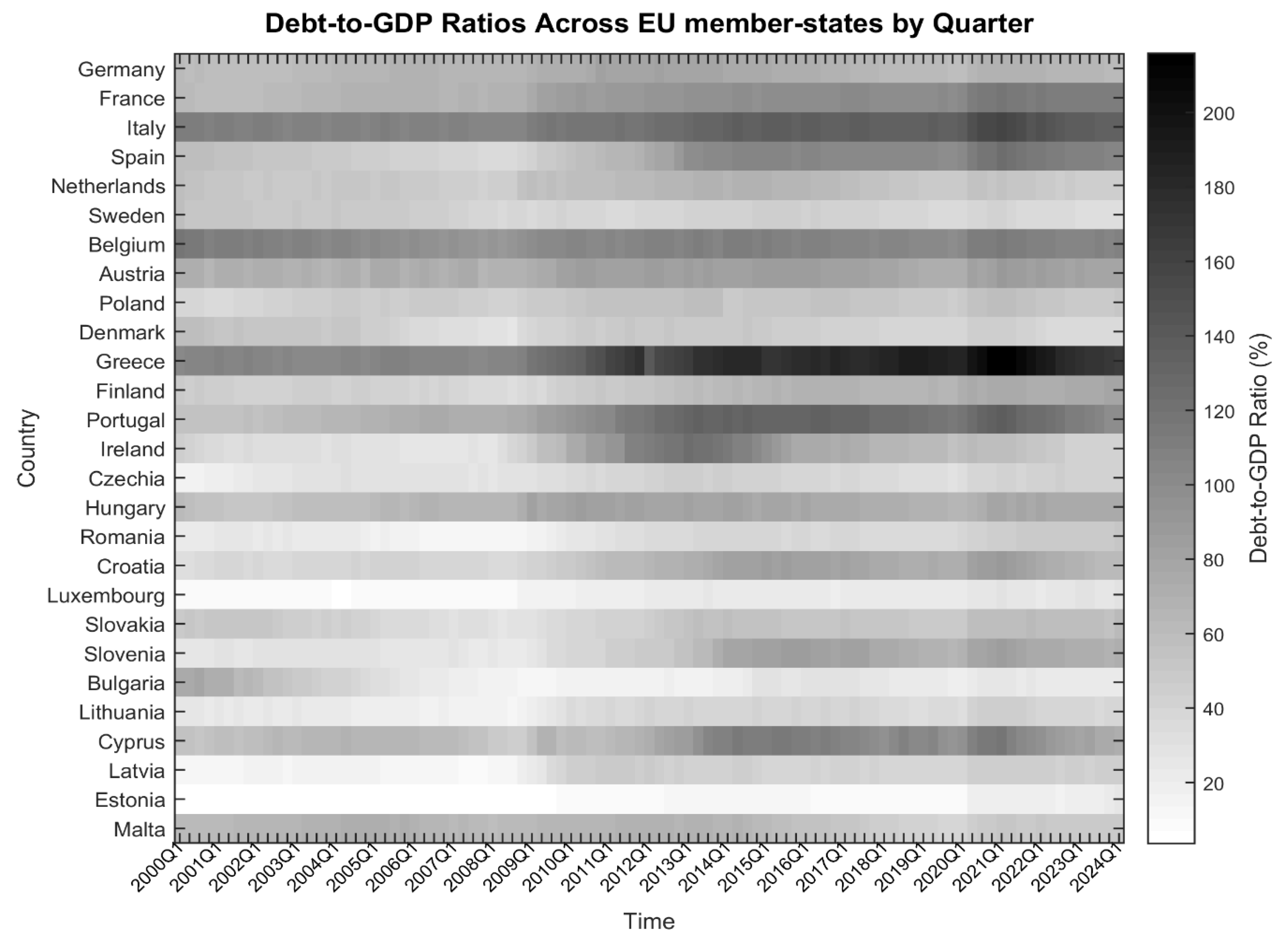
The dataset consists of government consolidated gross debt for the general government sector, expressed as a percentage of GDP1, in quarterly frequency (Figure 1), spanning from 2000Q1 to 2023Q42. It concerns the 27 countries (

Table 1. The 27 member states of the European Union in the dataset (alphabetical order).

1	Austria	15	Italy
2	Belgium	16	Latvia
3	Bulgaria	17	Lithuania
4	Croatia	18	Luxembourg
5	Cyprus	19	Malta
6	Czechia	20	Netherlands
7	Denmark	21	Poland
8	Estonia	22	Portugal
9	Finland	23	Romania
10	France	24	Slovakia
11	Germany	25	Slovenia
12	Greece	26	Spain
13	Hungary	27	Sweden
14	Ireland

) that are currently EU member states, of which 18 also belong to the Euro Area and use the common currency. Figure 1 illustrates the progression of debt-to-GDP ratios for the 27 EU member states from the first quarter of 2000 to the first quarter of 2024. The figure highlights substantial variation among countries, with ratios spanning a wide range from low to high levels. Descriptive statistics for each country and each period are presented in

Table A1. Descriptive statistics (mean, standard deviation, minimum, and maximum) by country and period.

	Mean			Std			Min			Max
Country	2000–2007	2008–2015	2016–2023	2000–2007	2008–2015	2016–2023	2000–2007	2008–2015	2016–2023	2000–2007	2008–2015	2016–2023
Germany	62.86	74.38	65.06	3.36	5.10	3.39	57.60	64.00	58.70	67.30	81.00	70.90
France	64.14	87.95	105.92	3.40	9.48	7.14	58.80	67.00	98.10	68.20	98.30	117.60
Italy	108.40	123.29	140.11	2.14	10.41	7.07	103.50	104.40	133.70	112.70	138.10	157.60
Spain	47.91	74.30	107.28	7.06	25.09	7.41	35.70	34.90	97.70	59.70	104.50	124.20
Netherlands	50.00	60.71	52.31	3.40	6.95	5.14	42.80	43.60	44.40	59.60	68.20	63.40
Sweden	47.94	39.47	37.75	3.98	3.11	3.65	39.20	35.00	30.30	57.40	45.70	43.50
Belgium	103.35	103.84	106.32	7.93	5.92	4.02	87.30	89.70	97.70	117.40	111.00	116.00
Austria	70.51	80.38	79.58	2.90	5.87	4.47	65.40	66.70	70.70	76.10	86.10	86.90
Poland	43.72	51.93	51.60	4.18	4.15	3.32	35.70	42.70	45.70	49.10	57.90	58.60
Denmark	46.37	45.08	39.77	8.59	6.60	3.83	29.50	26.40	33.60	58.20	52.60	46.40
Greece	104.31	151.74	187.98	1.89	26.03	12.62	99.90	103.70	167.50	107.80	182.30	215.90
Finland	42.25	52.14	70.33	3.27	11.14	4.13	34.80	30.70	64.80	48.60	68.80	77.10
Portugal	63.97	110.53	123.52	7.00	22.82	9.26	54.00	71.40	97.90	73.80	134.70	137.50
Ireland	30.61	87.54	59.25	5.19	29.28	10.41	23.60	26.40	42.40	45.20	123.10	75.90
Czechia	25.27	37.81	37.72	4.56	5.78	4.24	15.20	26.00	29.60	30.60	44.90	43.50
Hungary	59.53	77.77	73.27	4.74	4.75	3.91	52.20	64.40	65.00	66.80	83.80	79.70
Romania	19.57	29.33	41.01	4.76	9.61	6.27	11.60	10.50	33.50	25.90	39.10	49.70
Croatia	38.00	62.80	75.75	2.53	16.33	6.45	31.40	35.60	61.80	41.70	85.20	88.50
Luxembourg	7.58	18.85	23.26	0.40	4.37	2.47	6.80	8.30	19.60	8.30	26.80	28.30
Slovakia	42.15	44.58	54.47	7.58	10.19	4.10	29.60	26.60	48.00	51.70	57.50	60.20
Slovenia	26.58	51.32	75.52	1.32	20.89	5.36	22.90	21.90	66.00	28.60	84.70	85.50
Bulgaria	44.25	17.21	23.67	19.89	4.83	2.86	16.30	12.70	20.00	77.40	28.70	29.30
Lithuania	20.41	33.30	38.68	3.21	9.41	3.62	14.60	13.30	32.60	24.50	42.40	45.90
Cyprus	61.16	79.32	98.83	4.14	24.25	11.97	53.10	46.00	73.60	68.10	114.70	117.50
Latvia	12.94	38.10	41.77	1.84	11.50	2.86	8.60	10.40	37.70	15.30	48.80	46.50
Estonia	4.97	8.76	13.82	0.62	2.52	4.82	3.60	4.10	8.30	5.80	11.70	20.20
Malta	65.78	64.60	47.74	3.35	3.60	4.73	60.80	55.00	39.20	71.20	69.70	56.20

in Appendix A.

The GDP of each country, expressed in current prices (millions of euros), is utilized to assign a corresponding weight to that country (the specific details are thoroughly explained in Section 4). The data source for government debt and GDP is Eurostat, ensuring consistency and comparability across all EU member states.

The objective of this research, as previously stated, is to examine the temporal evolution of the debt-to-GDP ratio among the member states of the European Union and to evaluate the extent to which their movements align over time, suggesting possible synchronization. To achieve this and uncover possible structural shifts in public debt dynamics, we divide the initial 2000–2023 dataset into three consecutive intervals: 2000–2007, 2008–2015, and 2016–2023. The partitioning is based on significant macroeconomic events that shaped fiscal policy and debt dynamics in the EU. More specifically, the intervals are the following:

• 2000–2007 (Period 1): A pre-crisis period characterized by relative economic stability, with no major economic shocks. Moreover, the largest expansion occurred during this period, with ten countries joining the EU in 2004 (Czech Republic, Estonia, Cyprus, Latvia, Lithuania, Hungary, Malta, Poland, Slovakia, and Slovenia), followed by two more in 2007 (Bulgaria and Romania). This brought the total number of member states to 27 (EU27).
• 2008–2015 (Period 2): The period encompassing the global financial crisis and the subsequent European sovereign debt crisis, along with the fiscal measures and policy responses implemented to stabilize EU economies for both crises.
• 2016–2023 (Period 3): A post-crisis period marked by two major external shocks: the COVID-19 pandemic and the war in Ukraine, both of which had significant macroeconomic repercussions, including energy price fluctuations and inflationary pressures.

The temporal partitioning of time periods enables the network analysis techniques to assess the evolving interconnections, in terms of government debt levels. By segmenting the data, we aim to capture shifts in the fiscal relationships across EU member states, identifying key structural changes in debt dynamics before, during, and after economic crises.

4. Methodology

The analysis is conducted separately for each defined time period, yielding three successive networks that reflect the temporal evolution of inter-country relationships. Each node represents an EU country for a total of 27 nodes. The edges that connect the nodes denote the relationship between each pair of countries in terms of the selected variable. In our empirical analysis, the variable selected is the Pearson correlation of the debt-to-GDP ratio for each pair of countries. The Pearson correlation coefficient $r_{i,j}$ is defined as

$$r_{i,j} \triangleq {\displaystyle \frac{COV\left(Z_i,Z_j\right)}{\sqrt{VAR \left(Z_i\right) VAR\left(Z_j\right)}}}$$

(1)

where $Z_i, Z_j$ are pairs of observations for the variable under examination for member states i and j. The correlation coefficient value, in the range of [−1, 1], quantifies the strength and direction of the linear relationship between the two countries. Values close to the upper and lower bounds indicate a strong relationship; when near +1, it signifies a strong positive relationship, while values close to −1 indicate a strong negative relationship. Values near zero suggest no linear association between countries i and j.

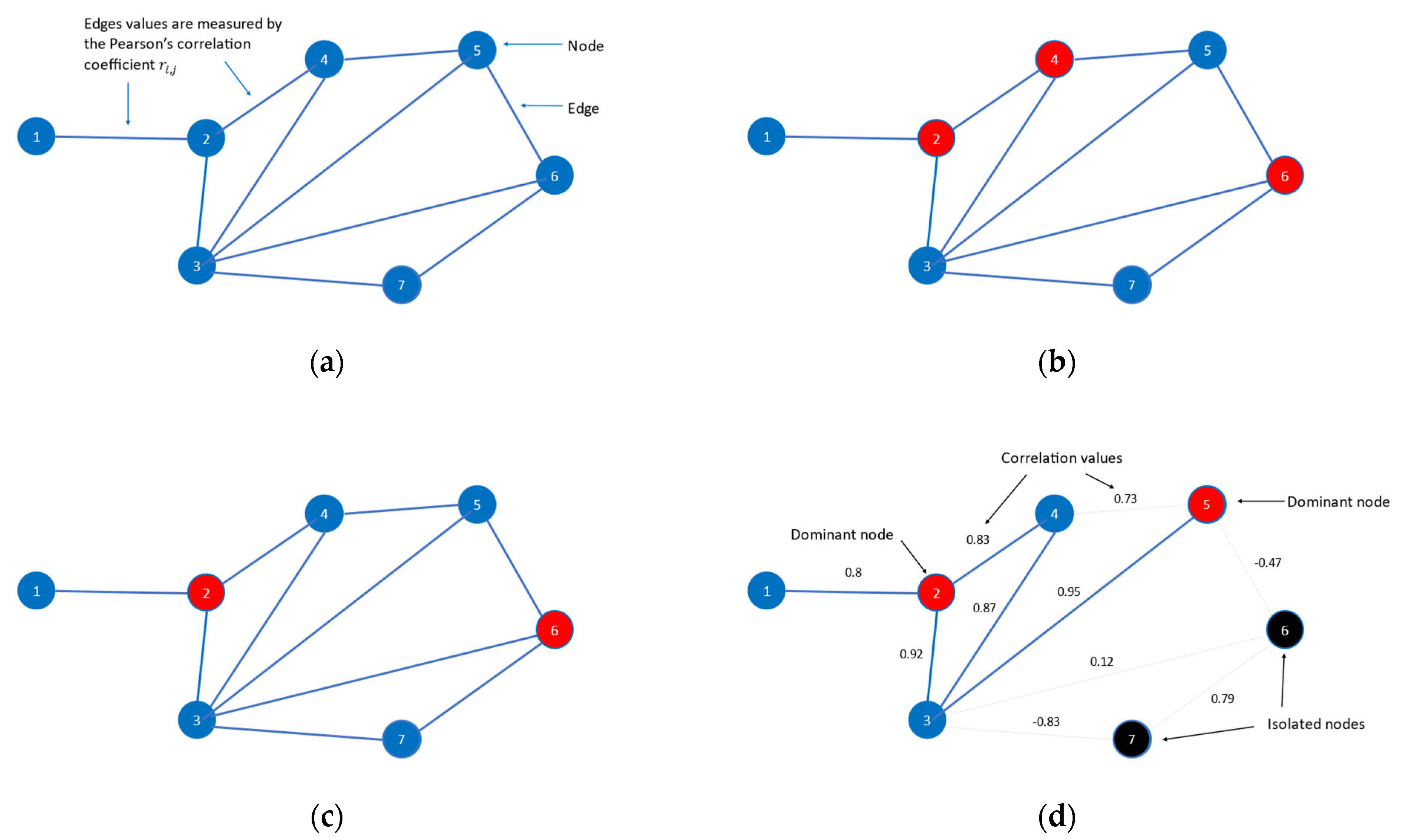
The following part introduces some key concepts of network analysis used in the empirical part of this paper, aiming to provide a clearer understanding of the concept.

Graph/network: A graph G = (V, E) consists of a set of nodes V and a set of edges E through which the nodes are connected (i.e., an edge e_i,j $\in$ E links the nodes i and j $\in$ V). Each edge e_i,j $\in$ E connecting the nodes i and j carries a value which is calculated by the Pearson’s correlation coefficient $r_{i,j}$ (Figure 2a). This parameter measures the temporal similarity between the nodes i and j. In addition, the set of nodes associated with node i is defined as the neighborhood B_i of node i, i.e., ${{\rm B}}_i=\left\{j\in V:\exists e_{ij}\in E\right\}$.

Isolated node: A node i $\in$ V is considered isolated when there are no edges connecting it to any of the rest nodes of the network.

Interconnected node: A node i $\in$ V is termed interconnected when it is connected to at least one other node in the network via an edge. In its initial arrangement, the network of the present research is complete, meaning that there is an edge connecting every single pair of nodes, and hence no isolated nodes exist.

Dominating Set: A Dominating Set DS ⊆ V is a subset of the interconnected nodes in the network, characterized by the following property: every node i that is not part of the DS is connected to at least one DS node j through an edge e_i,j i.e., $\left\{\forall i \notin DS, \exists j \in DS :e_{ij }\in E\right\}$ (Figure 2b).

For each of the n nodes of the network, a binary parameter x_i, i = 1, 2, … n is considered to symbolize its DS membership status, such that

$$x_i=\left\{\begin{array}{c} 0, if i \notin DS\\ 1, if i \in DS\end{array}\right.$$

(2)

Formula (3) mathematically displays the DS concept:

$$x_i+\sum _{j\in B_i}{x}_j\ge 1, \hspace{1em}i=1, 2, \dots n$$

(3)

An interconnected node i has to be either a node of the DS or adjacent (i.e., connected) to at least one such node. However, this is not a mutually exclusive relationship; there may be nodes that meet both conditions (Figure 2b). When the edges in a network reflect high similarity, as is the case here, the dominance attribute produces an intriguing effect: the behavior of the entire network can be effectively represented by the behavior of the DS.

Minimum Dominating Set: The Minimum Dominating Set (MDS) is the DS with the smallest cardinality.

$$\mathit{min}\left(\sum _{i=1}^n{x}_i\right)$$

(4)

The Minimum Dominating Set (MDS) is identified by applying condition (4) while complying with the constraints outlined in condition (3) (Figure 2c).

Since the core focus of the current research is the temporal similarity between nodes, the standard Minimum Dominating Set (MDS) algorithm is not well-suited for this purpose due to an inherent limitation. In a correlation-based network, such as the one examined here, edges do not necessarily indicate similarity. Given that correlation values range from −1 to 1, edges may represent strong positive similarity, strong negative similarity, or no similarity at all between nodes.

To overcome this issue, the MDS algorithm is modified following the approach of Papadimitriou et al. (2014). Specifically, edges with low correlation values should be excluded from the MDS calculation. The modification involves filtering out edges with low correlation values before computing the MDS. This is achieved by applying a threshold on the correlation values, so that edges falling below this threshold are removed. This adjustment leads to two key structural changes in the network: (a) it is no longer complete, as weaker connections (in terms of correlation values) are removed; (b) isolated nodes emerge, as certain nodes may lose all their connections due to edge elimination.

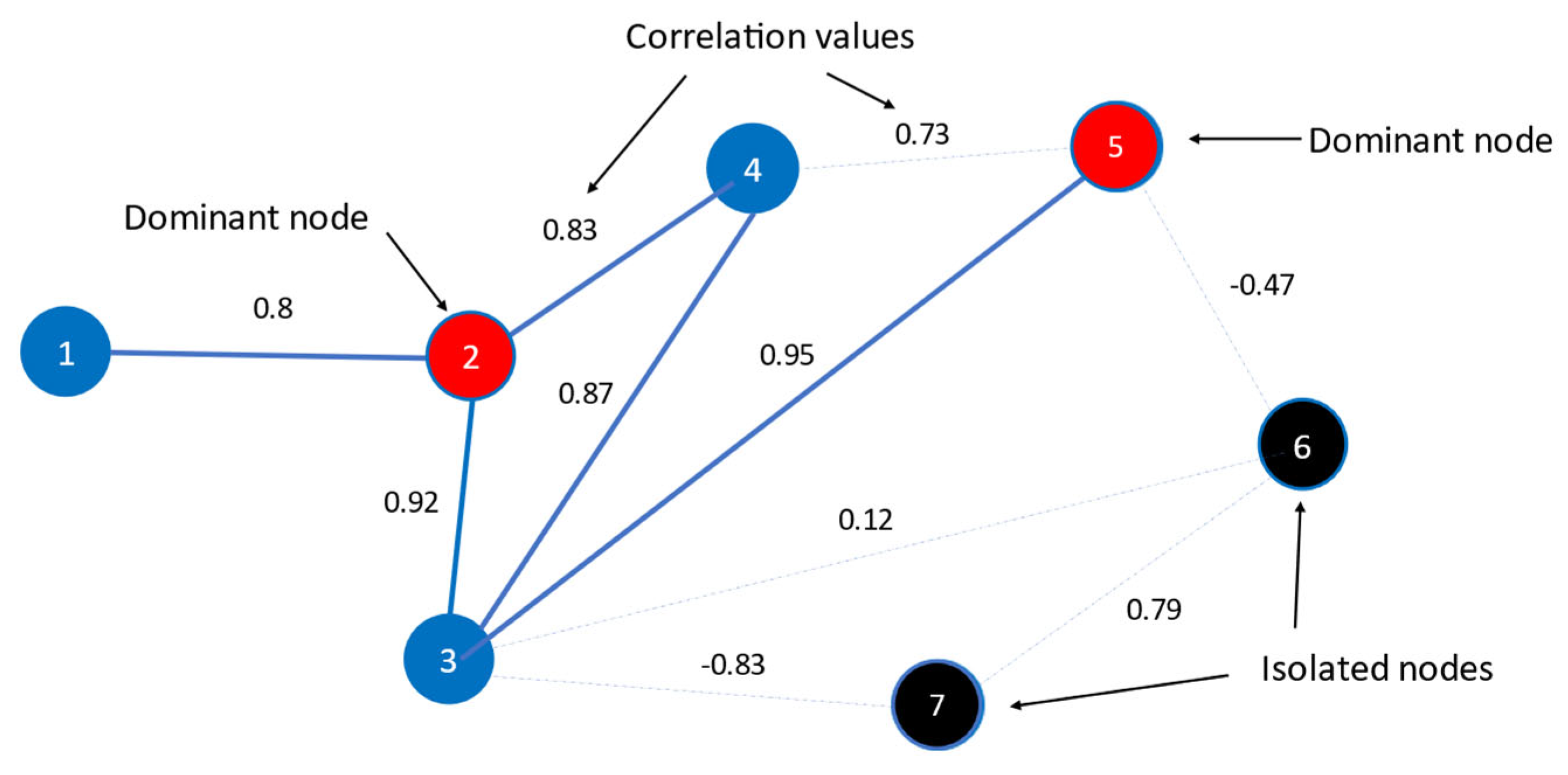
Threshold–Minimum Dominating Set: The Threshold–Minimum Dominating Set (T–MDS) algorithm consists of two main steps:

Threshold Application: A threshold is imposed on the correlation values of the edges, eliminating those with correlations below the specified level.

MDS Identification: The MDS nodes are determined within the filtered network (Figure 2d).

The T–MDS consists of both dominant and isolated nodes. Each dominant node defines a neighborhood, which includes all the nodes connected to it. While the nodes within a neighborhood are linked to the dominant node, they may also be interconnected with one another and can simultaneously belong to multiple neighborhoods. Since these nodes exhibit a high correlation with the dominant node, they share similar behaviors. In contrast, isolated nodes have no connections to any other nodes. Each isolated node represents a distinct, independent behavior, as it does not correlate with any other part of the network.

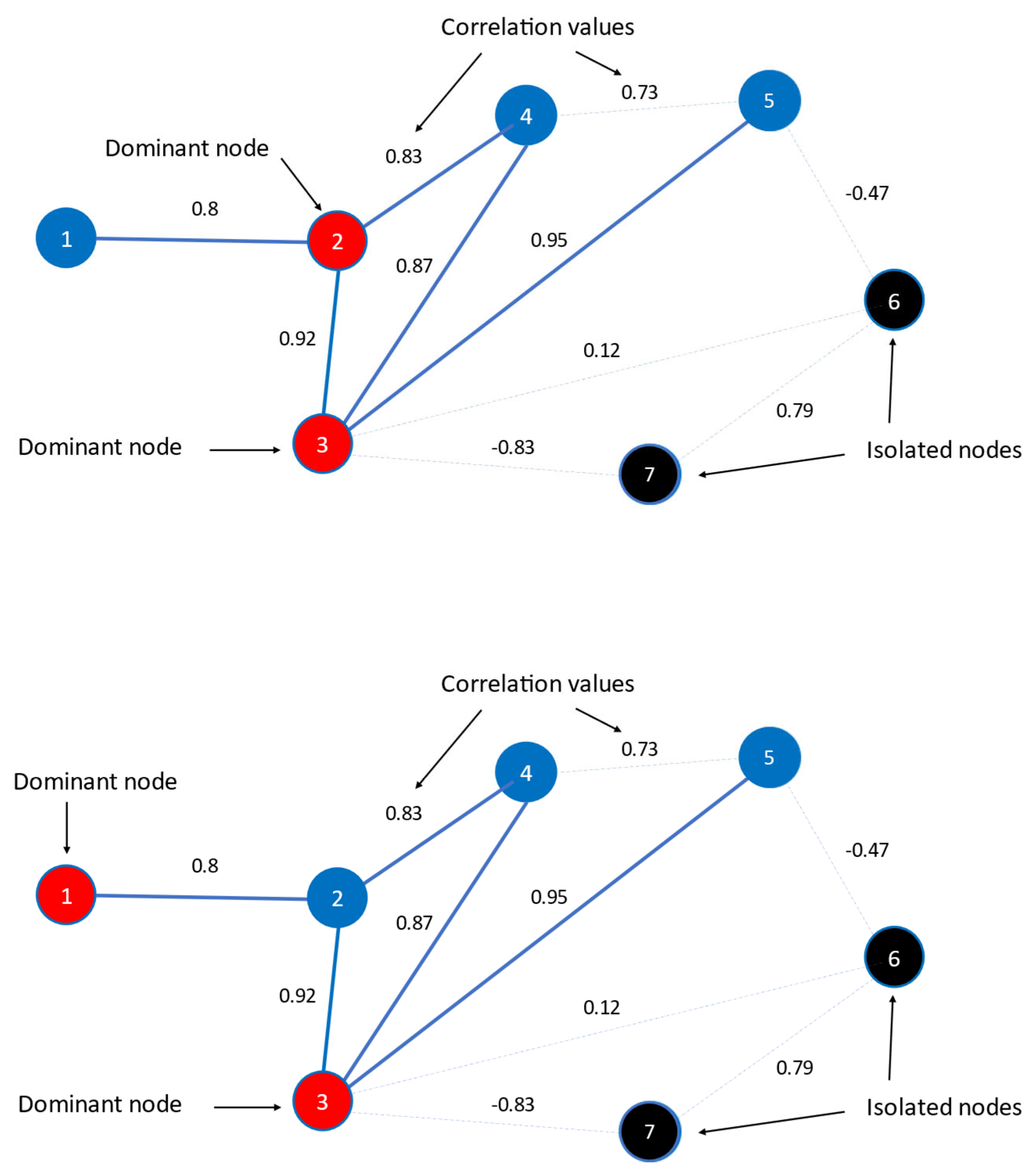
A key limitation of the optimization algorithm described above is that it may yield multiple solutions, with no control over which specific outcome will be produced (Figure 3). This inconsistency makes the T-MDS method unsuitable for temporal analysis.

To deal with this limitation, a new parameter was introduced into the T–MDS algorithm, resulting in a modified version called the Threshold Weighted–Minimum Dominating Set (TW–MDS) (Papadimitriou et al., 2020; Papadimitriou et al., 2022; Gkatzoglou et al., 2024). In this approach, a weight w_i is attributed to every node according to (5)

$$\mathit{min}\left(\sum _{i=1}^n{w}_i{x}_i\right)$$

(5)

The TW–MDS is determined by applying condition (5) while satisfying the constraints of condition (3). By introducing node weights, this modification significantly reduces the likelihood of multiple solutions arising from the optimization process. As a result, MDS generation remains consistent across different time periods, ensuring the method’s suitability for temporal network analysis. In this study, each country’s assigned weight is inversely proportional to its GDP. This means that member states with a higher GDP are more likely to be identified as dominant nodes, as a greater GDP results in a lower weight within the minimization process.

Tracking changes in the TW-MDS over time can reveal critical insights. When the sum of all dominant nodes increases, this provides evidence of desynchronization in the network’s entities. The network becomes progressively less connected, resulting in the identification of additional dominant nodes. On the other hand, when the number of dominant nodes decreases, it indicates an increased synchronization. The network becomes denser, and thus, fewer dominant nodes are required to describe it. This pattern also holds for the isolated nodes, whose variations reflect similar network trends: fewer isolated nodes mean more synchronization, while more isolated nodes imply less synchronization.

In addition to the TW-MDS algorithm, the present analysis also utilizes the density d_G, a graph-level metric. This measure quantifies the extent of interconnectivity within a network and is defined by the following formula:

$$d_G= {\displaystyle \frac{2 │E_t│}{v\left(v-1\right)}}$$

(6)

E_t measures the number of edges remaining after the thresholding step3, while v denotes the total number of nodes in the network. A density value of 1 signifies a complete (fully connected) network, where every possible edge is present. In contrast, a density of 0 indicates a disconnected network, where all nodes are isolated.

Aside from the TW-MDS and density d_G, the k-core decomposition method—also rooted in network science—is the third tool utilized in this study. Applied in various fields, including economics and finance, it is a widely studied concept for understanding the structure of complex networks (Kong et al., 2019; Malliaros et al., 2020). This method examines network structural properties by identifying subgraphs in which each node maintains at least k connections to other nodes within the same subgraph. In this manner, the identification of highly interconnected entities is accomplished. It operates through an iterative pruning process, removing nodes that do not meet the specified degree threshold k: a k-core of a graph G is the maximal subgraph $G_k=\left(V_k,E_k\right)$, where $V_k=\left\{v\in V│{deg}_{G_k}\left(v\right)\ge k\right\}$, $E_k=\left\{e_{ij}\in E│i,j\in V_k\right\}$ and ${deg}_{G_k}\left(v\right)$ is the degree of node $v$ in the subgraph $G_k$. The k-core decomposition uncovers a hierarchy of nested k-cores, with each successive core forming a more cohesive and densely connected subgraph, since each higher k-core is derived from a lower one by removing nodes that do not meet the degree requirement: $G_0\supseteq G_1\supseteq G_2\supseteq \cdots \supseteq G_{max}$, where $G_0$ is the original graph before any node removal takes place (since every node in G has at least 0 connections), $G_1$ is the 1-core subgraph consisting of all nodes with at least one connection, $G_2$ is the 2-core subgraph, which includes only nodes with at least two connections and their associated edges, and finally, $G_{max}$ is the core with the highest k in the network, representing the most interconnected substructure within the network.

The k-core decomposition contributes to our research in two key ways. The first is its role in analyzing synchronization within the network. A k-core subgraph that exhibits an increasing maximum k value and growing cardinality over time indicates stronger synchronization among entities. Conversely, a shrinking core and a decrease in the maximum k-core value as time progresses signal that the network is losing its synchronized structure, with nodes exhibiting dissimilar behaviors. The second contribution to this study is the identification of the nodes that constitute the k-core of the network, along with the corresponding subnetwork structure4.

The density, TW-MDS, and k-core decomposition metrics offer distinct yet complementary perspectives on network structure. Density provides a macroscopic snapshot, capturing the overall level of interconnectivity by measuring the proportion of actual connections relative to the total possible ones. While a higher/lower density suggests a more/less interconnected network, this metric alone does not capture network complexity, as other factors (e.g., clustering) also play a crucial role in shaping network behavior. In other words, density does not expose the underlying structural patterns, nor does it disclose whether the network is connected or fragmented. Networks with identical density values may exhibit significantly different topological structures, making density an informative yet limited descriptor. The TW-MDS, on the other hand, delves deeper into the network’s internal architecture. It uncovers the formation of local neighborhoods, identifies dominant and isolated nodes, and determines whether the network remains cohesive or breaks into disconnected components. That being said, the TW-MDS goes beyond simple connectivity by capturing synchronization patterns and shedding light on the way nodes cluster and interact. Still, one aspect of the network is not sufficiently illuminated. This refers to the potential formation of a node cluster with the highest level of connectivity. The analysis and similarity examined through the TW-MDS relate to the formation of neighborhoods and the emergence of dominant nodes. While all nodes within a neighborhood are connected to its dominant node, they are not necessarily interconnected with each other. Additionally, a node linked to the dominant node does not necessarily maintain multiple connections with other nodes in the same neighborhood5, although it may hold link(s) to other neighborhoods. Furthermore, a node may simultaneously belong to multiple neighborhoods and have more connections in one than in another. Considering all the above, the neighborhoods may overlap, remain distinct yet connected, or even be entirely disconnected, as observed in fragmented networks. Regardless of the specific structure, clearly identifying the core of the network proves to be a challenging task. Since the focus of this research is to identify member states exhibiting similar behavior, determining the core of the network is of significance. It provides valuable insight into the internal structure, complementing the information gained from neighborhood formation and dominant node emergence and uncovering the connections that constitute the most compact part of the network. Especially, identifying the network’s maximal k-core substructure reveals the entities that are most tightly connected, irrespective of the neighborhoods they belong to. The subgraph that refers to the maximal k-core substructure may display an exceptionally high density, even when the overall network density is quite low. Combining insights from the TW-MDS and k-core decomposition enables researchers, policymakers, and financial institutions to identify clusters of countries exhibiting similar behavior. Recognizing these communities enhances policy coordination, leading to a more effective approach to ensuring overall economic stability.

We consider that the line of action followed concerning the network analysis not only enriches the research but also provides a more nuanced understanding of structural development. By integrating density with the TW-MDS and k-core decomposition, we bridge the gap between global overview, localized details, and the core of the network, crafting a more holistic approach to network interpretation.

5. Empirical Results and Discussion

The imposed correlation threshold critically influences the network’s architecture. Altering the threshold, one can control the count of remaining edges. This, in turn, has a direct effect on the number of dominant and isolated nodes, and finally on the sizes of both the TW-MDS and the k-core structure. A lower threshold permits more edges to survive, potentially diluting the intended similarity by allowing weaker correlations to persist. This may result in a densely interconnected network. Conversely, a higher threshold imposes stricter similarity requirements, which leads to the elimination of a larger number of edges. In this case, the network may fragment into isolated components, thus having smaller overall structural coherence and interpretability.

Considering the above, the selection of the appropriate correlation threshold is significant. For this reason, we employed and tested multiple thresholds ranging from 0.6 to 0.9 with a step of 0.05. Next, we present the results for threshold levels 0.7 and 0.8. This threshold selection was guided by the following key consideration: the inclusion of meaningful relationships while filtering out weaker, potentially economically insignificant relationships between countries. Given the study’s focus, we believe that the selected thresholds preserve meaningful connections while providing a clear representation of the network’s evolution and structural changes over time. Moreover, presenting the results of two alternative thresholds offers a broader perspective of the network’s evolution through time.

These alternative thresholds are used in all three sub-period networks constructed using the TW-MDS and the k-core decomposition algorithms, alongside the calculation of the density metric. For reference, the network topology corresponding to a threshold of 0.7 is presented in Figure A1, Figure A2 and Figure A3 in Appendix C.

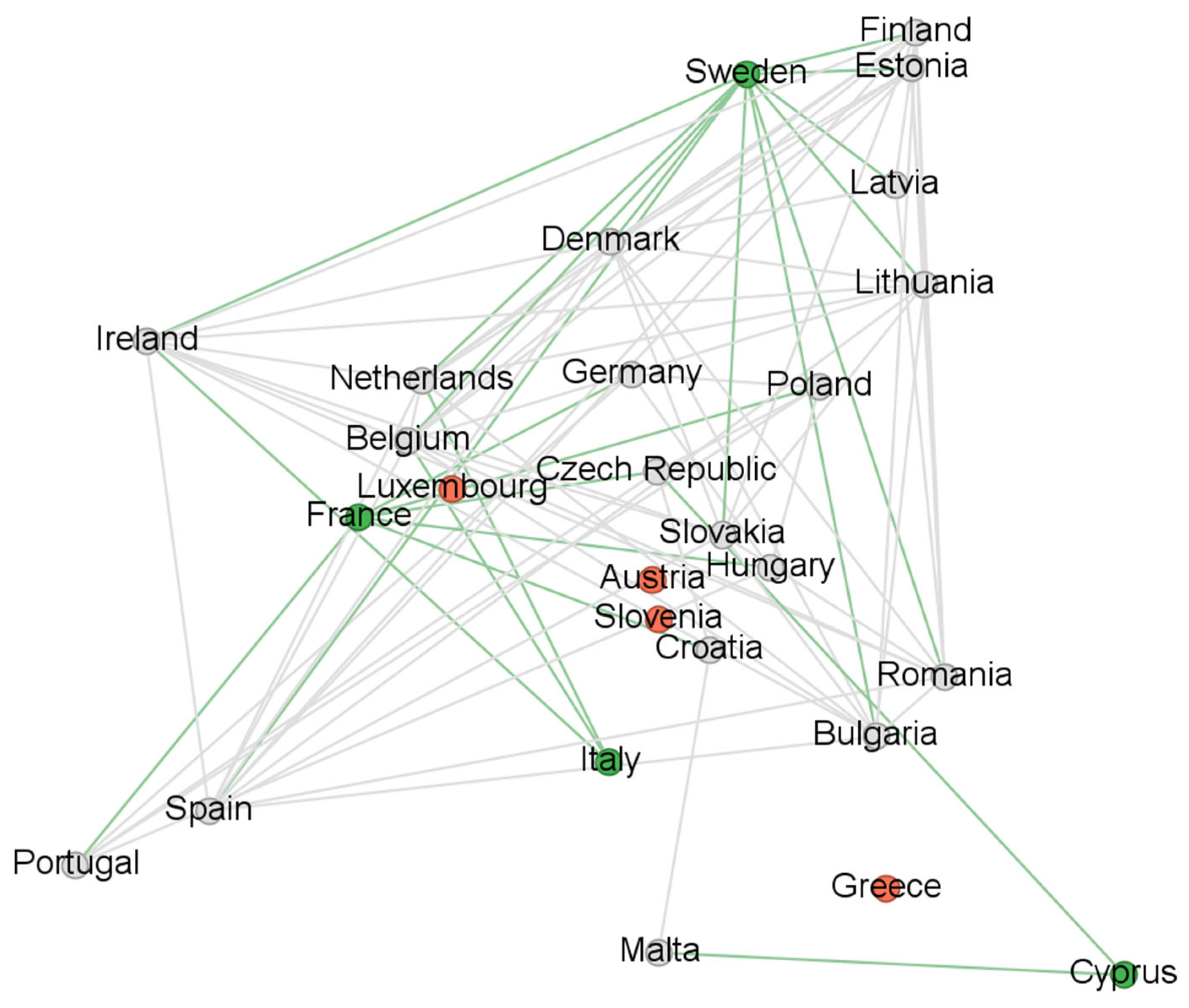
5.1. Threshold Level 0.7

Table 2. Network metrics for 0.7 and 0.8 threshold levels.

			Metrics	2000–2007	2008–2015	2016–2023
threshold	0.7	TW-MDS	Density	0.25	0.68	0.3
			Dominant nodes	4	2	4
			Isolated nodes	4	1	0
			Interconnected nodes	23	26	27
		k-core decomposition	Max k-core	9	16	7
			Max k-core cardinality	10	19	9
			Max k-core density	1	0.98	0.97
	0.8	TW-MDS	Density	0.17	0.55	0.19
			Dominant nodes	5	2	5
			Isolated nodes	6	1	0
			Interconnected nodes	21	26	27
		k-core decomposition	Max k-core	7	14	6
			Max k-core cardinality	9	16	7
			Max k-core density	0.97	0.99	1

presents the findings of this study. Based on the density and TW-MDS metrics, Period 2 exhibits the highest level of synchronization. Specifically, at the 0.7 threshold level, the density from Period 1 to Period 2 increases by more than 2.5 times, from 0.25 to 0.68. However, in Period 3, the density declines to 0.3, slightly higher than in Period 1. Regarding the TW-MDS metrics, both the number of dominant and isolated nodes decrease from Period 1 to Period 2, from four and four to two and one, respectively. This indicates that in Period 2, two dominant nodes are sufficient to describe the overall network behavior (each representing its neighborhood). Compared to Period 1, the number of neighborhoods is smaller, yet they are densely populated; the first consists of 21 countries and the second of 23 (

Table A2. Identity of the dominant nodes (with the corresponding cardinality of the neighborhood they represent), the isolated nodes, and the entities that compose the max k-core subgraph in periods 2000–2007, 2008–2015, and 2016–2023 for the 0.7 threshold level.

	2000–2007		2008–2015		2016–2023
TW-MDS	Dominant nodes	Neighborhood cardinality	Dominant nodes	Neighborhood cardinality	Dominant nodes	Neighborhood cardinality
	France	6	Italy	21	Germany	8
	Italy	3	Netherlands	23	France	10
	Sweden	12			Italy	7
	Cyprus	2			Sweden	7
	Isolated nodes		Isolated nodes		Isolated nodes
	Austria		Malta		No isolated
	Greece
	Luxembourg
	Slovenia
k-core decomposition (max k-core)	Spain Sweden Belgium Denmark Finland Ireland Romania Slovakia Bulgaria Lithuania		France Italy Spain Netherlands Belgium Austria Denmark Greece Finland Portugal Ireland Czechia Romania Croatia Luxembourg Slovakia Slovenia Lithuania Estonia		France Spain Finland Czechia Romania Luxembourg Slovakia Latvia Estonia

in Appendix B). The overlap between these neighborhoods, as reflected in their sizes, highlights a significant number of shared connections among countries, signaling a move toward more unified behavior. In Period 3, the number of dominant nodes returns to 4, but now there are no isolated nodes. This indicates that in Periods 1 and 3, network connectivity is significantly lower than in Period 2, impacting the density and TW-MDS size. However, compared to Period 1, Period 3 shows a slight improvement. The network retains more connections, leading to a marginally higher density, and unlike the first period, all nodes remain interconnected without isolated ones. Four counties that in Period 1 exhibited distinct idiosyncratic behavior and thus were isolated are now integrated into the network. This is evidence of mitigated idiosyncratic behavior; extreme deviations of individual countries are eliminated.

As expected, the k-core decomposition results shown in Table 2 follow a similar pattern. The metrics pertain to the most interconnected substructure within the network, $G_{max}$. The maximum k-core value reflects the highest value found across the sequence of subgraphs generated through the k-core decomposition process. The maximum k-core cardinality indicates the number of nodes present in the maximum k-core. The maximum k-core density is the density that refers to the $G_{max}$.

The most interconnected segment of the network is observed during Period 2. This subgraph consists of 19 nodes (70% of the total), each maintaining at least 16 connections, resulting in a density of 0.98. In contrast, during both Period 1 and Period 3, the maximum k-core contains about half the nodes compared to Period 2, with each node also holding roughly half as many connections. Yet, the k-core decomposition metrics reveal an interesting insight. Even in periods of low overall network connectivity, such as Periods 1 and 3, a tightly connected subnetwork persists. This subnetwork exhibits a density of 1 in Period 1 and 0.97 in Period 3, consisting of 10 and 9 nodes, respectively. Another key observation is that, although network density and TW-MDS metrics suggest a slightly better-connected structure in Period 3 compared to Period 1, according to the k-core decomposition results, the story unfolds a bit differently. Period 1 actually features a greater k-core subgraph with more nodes, even if only marginally. This suggests that the network of Period 1 contains a more cohesive core, which actually forms a complete subnetwork.

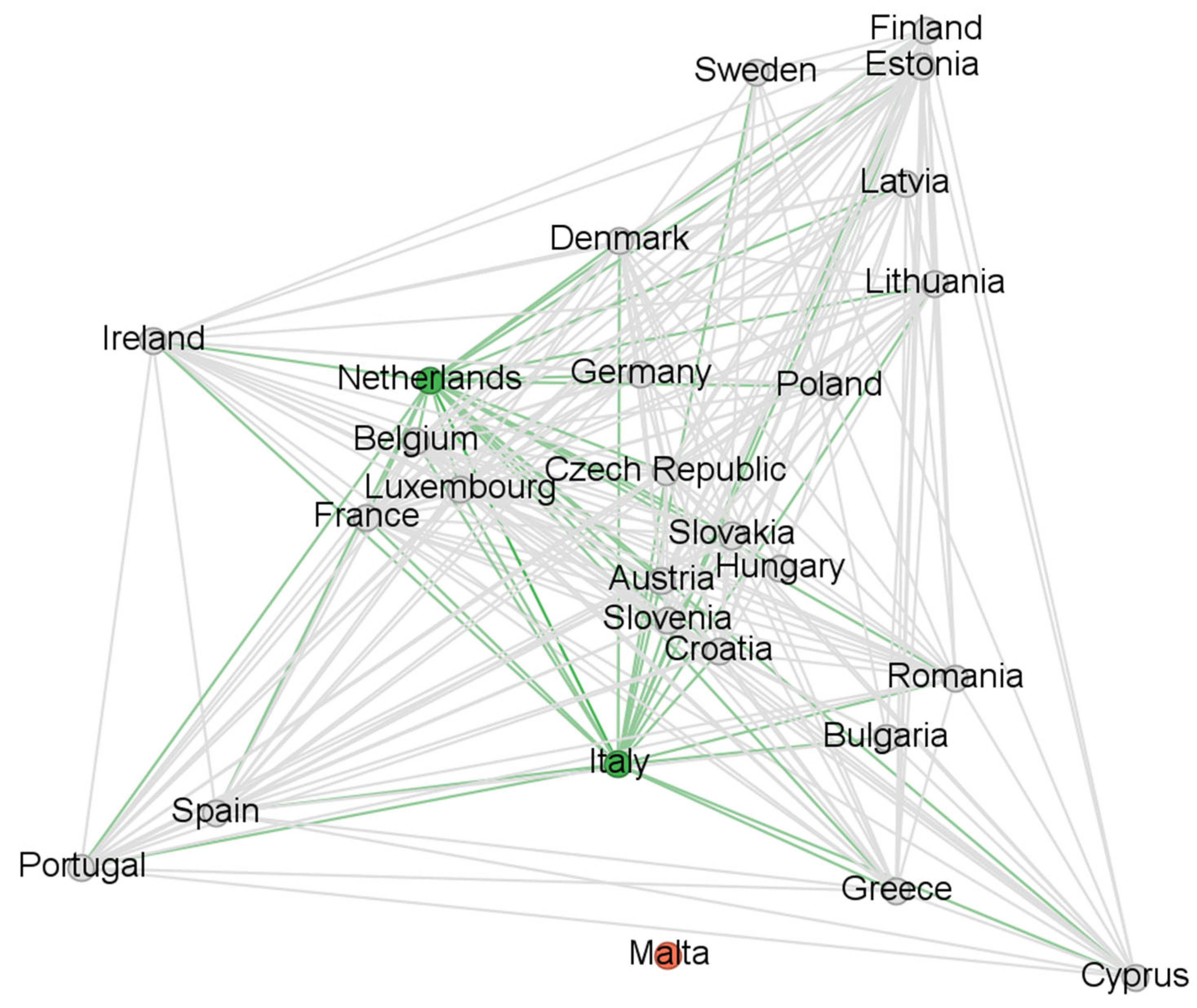
5.2. Threshold Level 0.8

At the 0.8 threshold level, fewer edges remain in place. Consequently, both the density and the k-core decomposition metrics decline, while the TW-MDS size increases (Table 2). Nonetheless, the general pattern noted and described for the 0.7 threshold level also applies to the 0.8 threshold.

According to the density and TW-MDS metrics, Period 2 demonstrates the highest degree of synchronization. At the 0.8 threshold, the density more than triples, increasing from 0.17 in Period 1 to 0.55. In contrast, Period 3 sees a decline in density to 0.19, which remains slightly above the level observed in Period 1. The TW-MDS results show a drop in both dominant and isolated nodes during Period 2, falling from five and six, respectively, in Period 1, to two and one. Similarly to the case of the 0.7 threshold, the network’s behavior at the 0.8 threshold level can still be effectively captured by two dominant nodes. However, the stricter threshold leads to a reduction in the size of their respective neighborhoods, with one encompassing 14 countries and the other 15 (

Table A3. Identity of the dominant nodes (with the corresponding cardinality of the neighborhood they represent), the isolated nodes, and the entities that compose the max k-core subgraph in periods 2000–2007, 2008–2015, and 2016–2023 for the 0.8 threshold level.

	2000–2007		2008–2015		2016–2023
TW-MDS	Dominant nodes	Neighborhood cardinality	Dominant nodes	Neighborhood cardinality	Dominant nodes	Neighborhood cardinality
	Germany	4	Denmark	14	Germany	6
	Spain	10	Slovenia	15	Italy	3
	Poland	4			Netherlands	4
	Cyprus	1			Denmark	3
	Latvia	1			Finland	8
	Isolated nodes		Isolated nodes		Isolated nodes
	Italy		Malta		No isolated
	Austria
	Greece
	Croatia
	Luxembourg
	Slovenia
k-core decomposition (max k-core)	Spain Sweden Belgium Denmark Ireland Romania Slovakia Bulgaria Lithuania		France Italy Spain Netherlands Belgium Austria Greece Finland Portugal Czechia Romania Croatia Luxembourg Slovakia Lithuania Estonia		France Finland Romania Luxembourg Slovakia Latvia Estonia

in Appendix B). In Period 3, the number of dominant nodes rises again to five, while no isolated nodes are identified. This pattern indicates that the overall network connectivity was considerably stronger during Period 2, with reduced cohesion in both the earlier and later periods. Nonetheless, Period 3 reflects a modest improvement over Period 1, as more connections are retained and all nodes remain integrated. Notably, six countries that were isolated in Period 1 are now part of the network, suggesting that even under the stricter 0.8 threshold, extreme divergence in behavior diminished.

These results illustrate the impact of the measures implemented to support EU countries during economic crises on the intensity of connections, considering the number of countries isolated from networks and the trajectory of public debt. By absorbing part of the cyclical shocks linked to the financial crisis (2008–2015) and then the pandemic crisis (2016–2023), the European mechanisms implemented have improved the synchronization of public debts (with a strong increase in density between 2008 and 2015, and a much lower intensity between 2016 and 2023, though still higher than between 2000 and 2007), intensifying the connections between national public debts and eliminating the number of isolated countries between Periods 1 and 3.

In terms of k-core decomposition, the most interconnected part of the network emerges in Period 2. This subgraph includes 16 nodes—nearly 60% of the total—with each node sustaining at least 14 connections, yielding a density of 0.99. In contrast, during Period 1 and Period 3, the maximum k-core is considerably smaller, containing about half as many nodes and connections as in 2008–2015. Similarly to the findings at the 0.7 threshold, the k-core metrics provide a notable insight: even when overall network connectivity is low, as in Periods 1 and 3, a tightly connected substructure still exists. This core displays a density of 0.97 in Period 1 and reaches full connectivity—a density of 1—in Period 3. While the subnetwork of Period 1 includes more nodes compared to that of Period 3 (nine versus seven, respectively), it is the latter that forms a fully connected core.

5.3. Discussion

Period 2 exhibits maximum synchronization, as evidenced by the steep rise in density and the decline in dominant and isolated nodes. This suggests that the sovereign debt crisis, along with the associated relative policy responses, contributed to strengthening the synchronization of the debt-to-GDP ratios of the EU countries. This empirical finding is probably the result of the heightened debt of almost all EU countries and coordinated policy measures such as the ESM. The presence of a large, densely connected core confirms that public debt dynamics were closely interrelated across member states.

In contrast, the initial (2000–2007) and last (2016–2023) periods display significantly lower levels of connectivity and, thus, synchronization. Period 1 features a network of weaker interconnections between EU member states. However, despite lower overall density, the presence of a highly connected core during this period (a 9-core with a density of 1 and a 7-core with a density of 0.97 for 0.7 and 0.8, respectively) indicates the existence of a subnetwork of countries exhibiting highly similar behavior. The network in Period 3, even with slightly greater density than in Period 1, is composed differently. The absence of isolated nodes suggests higher synchronization across the network, and it is likely to be a sign of the influence of the EU-level coordination of policies due to external pressures such as the COVID-19 pandemic, the war in Ukraine, and the proactive policy of the 2008 crisis.

Several factors can contribute to post-crisis divergence. The drivers of divergence stem from structural heterogeneities linked to structural differences in an economic, demographic, institutional, and political nature that exist in Europe. Such structural heterogeneities help explain why European economies respond differently to economic shocks (see Guerini et al., 2018; Campos et al., 2020). Differences in productive specialization remain significant within the EU and contribute to varying reactions to economic shocks, as each economy relies to different extents on certain sectors, sectors that themselves respond differently to changes in demand, price fluctuations, supply shocks, etc. The socio-demographic characteristics of countries (e.g., the proportion of over-65s in the population and exposure to the risk of poverty or social exclusion) and institutional diversity (e.g., parliamentary vs. semi-presidential systems), as highlighted by Lopez-Gomez (2024), also play an important role.

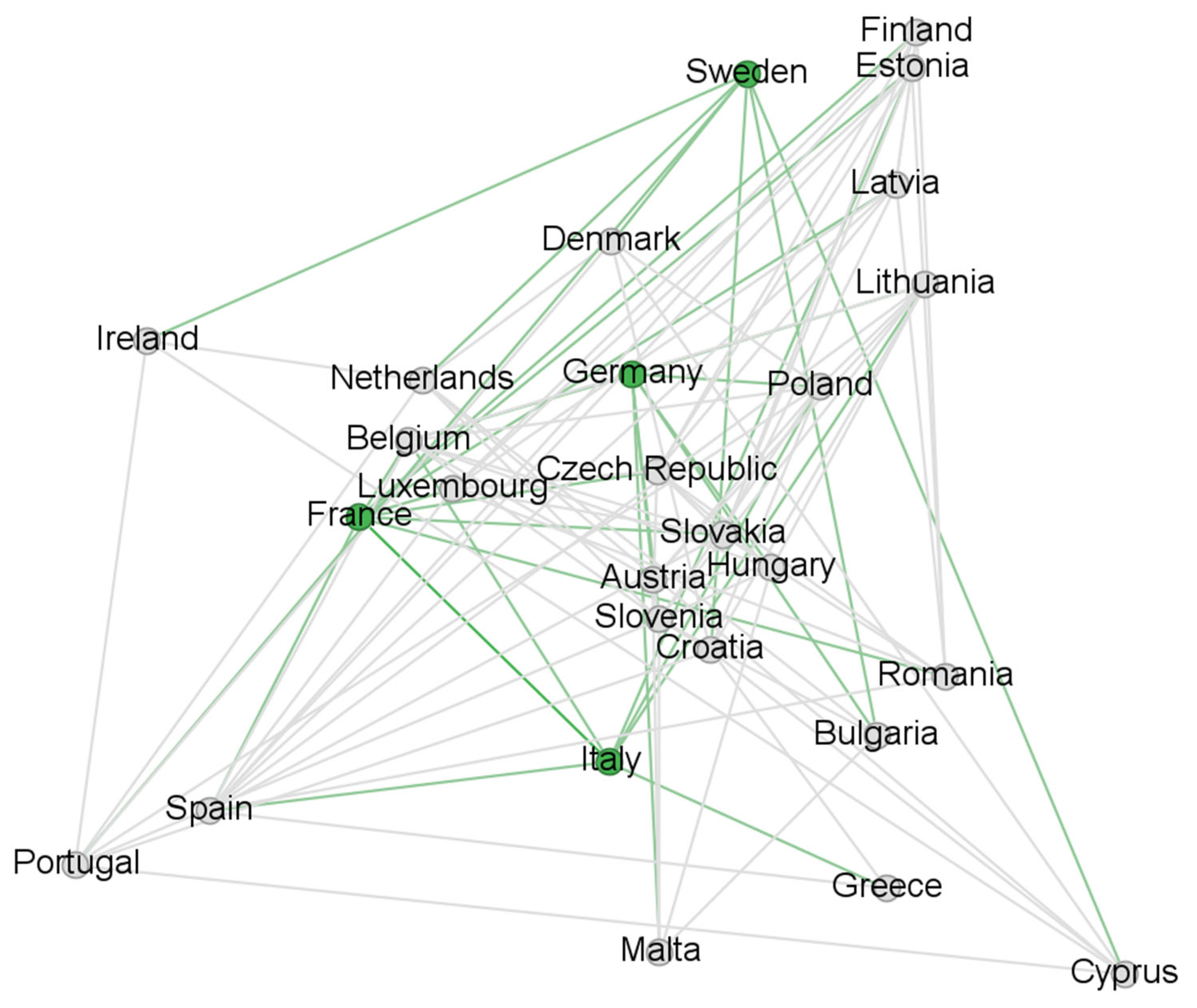
A qualitative examination of the networks (Table A2 and Table A3 in Appendix B) uncovers several noteworthy findings. While the TW-MDS algorithm tends to favor countries with higher GDPs when identifying dominant nodes, this is not consistently the case. For instance, in the case of the 0.7 threshold, Germany—despite having the highest GDP in the EU—is not identified as a dominant node in any period except for Period 3. Interestingly, even during Period 2, when network connectivity is high, Germany does not emerge as dominant. Additionally, Germany is absent from the maximum k-core in all three periods. Summarizing the behavior of the EU’s three largest economies, France appears as a dominant node in Periods 1 and 3, while Italy consistently holds a dominant status across all periods. Under the stricter 0.8 threshold, Germany is identified as dominant in Periods 1 and 3, France does not appear as dominant in any period, and Italy is identified as dominant only in Period 3. Notably, Germany remains excluded from the maximum k-core throughout all periods, regardless of the threshold.

It is worth noting that Germany not only remains outside the maximum k-core but also maintains significantly fewer connections than the countries included in that core across all periods. This discrepancy is especially evident under the 0.8 threshold: in Period 1, Germany is part of the 3-core while the maximum one is the 7-core; in Period 2, it belongs to the 6-core, whereas the maximum is the 14-core and includes around 60% of the countries; and in Period 3, Germany is again in the 3-core, compared to the maximum of the 6-core (

Table A4. The highest k-core to which each EU member state belongs across all three time periods, under both the 0.7 and 0.8 threshold levels.

		2000–2007		2008–2015		2016–2023
country		0.7	0.8	0.7	0.8	0.7	0.8
	threshold
		highest k-core
Germany		4	3	12	6	6	3
France		4	3	16	14	7	6
Italy		3	0	16	14	6	2
Spain		9	7	16	14	7	5
Netherlands		8	6	16	14	5	2
Sweden		9	7	7	3	5	2
Belgium		9	7	16	14	6	3
Austria		0	0	16	14	6	3
Poland		4	3	12	7	6	3
Denmark		9	7	16	10	5	3
Greece		0	0	16	14	3	1
Finland		9	6	16	14	7	6
Portugal		4	3	16	14	5	3
Ireland		9	7	16	12	4	2
Czechia		3	1	16	14	7	3
Hungary		4	3	6	2	6	3
Romania		9	7	16	14	7	6
Croatia		2	0	16	14	5	3
Luxembourg		0	0	16	14	7	6
Slovakia		9	7	16	14	7	6
Slovenia		0	0	16	13	6	3
Bulgaria		9	7	7	3	5	1
Lithuania		9	7	16	14	6	3
Cyprus		2	1	15	13	5	3
Latvia		4	1	12	7	7	6
Estonia		8	3	16	14	7	6
Malta		2	1	0	0	5	3

in Appendix B). These findings suggest that Germany, despite being the EU’s largest economy, occupies a peripheral position within the network in terms of its debt ratio evolution. This has important implications, potentially complicating the policy coordination efforts related to fiscal stability.

Another finding is that the behavior of the countries appears to be independent of their Euro Area membership status. No clear patterns emerge in terms of clustering into neighborhoods or cores or the identification of isolated status based on whether a country is part of the common currency area. Furthermore, the synchronization observed during the 2008–2015 period does not seem to be limited to Euro Area members. Finally, there is no indication of geographical divisions, such as a north–south split. Table A2 and Table A3 in Appendix B provide relative information for the 0.7 and 0.8 thresholds, respectively.

The findings presented suggest that big crises have a considerable impact on fiscal interrelations between the EU member states. During relatively tranquil periods, countries tend to behave more independently, reflecting a rather dissimilar behavior in their actions. In contrast, events that trigger global financial uncertainty—along with the resulting policy interventions (such as the ESM)—force countries to act in a more coordinated manner, following a similar trajectory.

This article highlights the impact of progress made since 2008 in terms of fiscal integration on the synchronization of national public debt. Indeed, the ad hoc intervention mechanisms implemented since the 2008 financial crisis (European Stability Mechanism, European Semester, Six Pack, Two Pack, Next Generation EU, etc.) appear to have borne fruit by preventing excessive national divergence in public finance.

These results confirm that when stabilization mechanisms for economic shocks that affect countries differently (i.e., asymmetric shocks, or symmetric shocks with asymmetric effects) are implemented at the EU level, the ultimate impact on national public debt is reduced, and synchronization is strengthened. In such cases, an EU-level stabilization mechanism steps in to cushion economic shocks, relieving pressure on national budgets.

This suggests that the optimality of the Eurozone may be an endogenous process, driven by the gradual implementation of tools for stabilizing economic shocks within the Eurozone, but it will also have an impact on non-Eurozone countries.

Looking ahead, the key challenge is to ensure the sustainability of these alternative economic stabilization mechanisms, which have so far been implemented only temporarily, to ease the constraints on national budgets. The creation of a European fiscal capacity could fulfill this role of absorbing symmetric shocks (with asymmetric effects due to structural heterogeneities) on national economies (see Burriel et al., 2020), ultimately stabilizing public debt trajectories, as already occurs in the United States, Canada, and Australia.

This would allow national budgets to focus primarily on delivering public goods and services (such as education, health, social protection, security, and transport) while being subject to rigorous oversight under the reformed Stability and Growth Pact (2024), excluding national defense expenditure. Meanwhile, cyclical stabilization would be handled through a European fiscal capacity.

6. Conclusions

In this paper, we explore how fiscal behavior and interconnections among EU countries evolved over time, especially in response to major economic shocks, based on public debt.

By using Graph Theory tools, we examined public debt dynamics across three distinct periods: Period 1, the years before the global financial crisis (2000–2007), Period 2, the turbulent years of crisis and response (2008–2015), and Period 3, the post-crisis period shaped by new global disruptions (2016–2023). It is important to note that this study is limited to the period following the year 2000 due to data constraints. While analyzing the network of countries prior to 2000 could potentially yield valuable insights into the early stages of the union, such an analysis is unfortunately not feasible given the lack of available data.

The findings show a clear pattern: when external pressures rise, so does the fiscal synchronization across member states. Period 2 presents the highest level of connectivity among countries, with fewer isolated nodes and a large, dense core. This suggests that the financial and sovereign debt crises, combined with policy responses like the ESM, brought EU countries closer together in terms of fiscal behavior.

In contrast, in more stable periods, such as the years preceding the crisis and the most recent interval, the overall network density tends to decrease. Still, there is nuance here. Even in those less turbulent periods, we discovered tightly connected subnetworks, pointing to smaller groups of countries with similar debt dynamics. Interestingly, the network in Period 3, while not as synchronized as in the crisis years, shows some improvement over the pre-crisis era. The absence of isolated countries and a slightly greater density suggest that past experiences and EU-wide coordination mechanisms might have laid the groundwork for closer fiscal alignment, even in the face of new shocks like the pandemic or the war in Ukraine.

Thus, our results highlight the impact that the various measures implemented to support EU countries during the various economic crises have had on the intensity of connections in terms of the trajectories of public debt. By taking charge of part of the cushioning of the cyclical shocks linked first to the financial crisis (Period 2) and then to the pandemic crisis (Period 3), the European mechanisms implemented have favored the better synchronization of public debts, an intensification of the connections between national public debts, and also the disappearance of the isolated countries.

To conclude, the results highlight the importance of shared challenges in shaping how EU member states manage their public finances. During periods of stability, national strategies tend to diverge, reflecting local priorities and political contexts. However, in times of crisis, there is a clear shift toward convergence, likely driven by the need for coordinated responses and shared tools. This has implications not only for interpreting past behavior but also for how EU policymakers may approach the design of future fiscal frameworks.

Thus, a better synchronization of national public debts in the EU represents a real opportunity to ensure the lasting monetary and financial stability of the monetary union and could appear as the solution to the challenge posed by the surveillance of national public finances. More synchronized national public debts would make it possible to establish effective common European tools to support the cushioning of economic shocks.

Looking ahead, maintaining debt synchronization may require formalizing some of the stabilization tools introduced since 2008. A permanent European fiscal capacity could help absorb economic shocks more evenly, reducing the pressure on national budgets and allowing them to focus on providing public goods and services to citizens. Over time, this could support stronger fiscal alignment across the EU and reinforce the goals of the reformed Stability and Growth Pact.