Abstract
Using time-varying Granger causality, Neural Networks Nonlinear VAR, and Wavelet Coherence analysis, we evidence the unstable effect of the money market rate on industrial production and consumer price index in Tunisia. The effect is asymmetric and depends on geopolitical risk (low versus high). We show that global geopolitical risk has both detriments and benefits sides—it is a threat and an opportunity for monetary policy transmission mechanisms. Interacted local projections (LPs) reveal short–medium-term volatility or dampening effects, suggesting that geopolitical uncertainty might weaken the immediate impact of monetary policy on output and prices. In uncertain environments (e.g., high geopolitical risk), economic agents—households and businesses—may adopt a wait-and-see approach. They delay consumption and investment decisions, which could initially mute the impact of monetary policy. Agents may delay their responses until they gain more information about geopolitical developments. Once clarity emerges, they may adjust their behavior, aligning with the long-run effects observed in the Vector Error Correction Model (VECM). Furthermore, we identify an exacerbating investor sentiment following tightening monetary policy, during global and local geopolitical episodes. The impact is even more pronounced under conditions of high domestic weakness. Evidence is extracted through a novel composite index that we construct using Principal Component Analysis (PCA). Our results have implications for the Central Bank’s monetary policy conduct and communication practices.
1. Introduction
Since the early 2000s, the global economy has become increasingly interconnected, making it more vulnerable to the ripple effects of geopolitical and economic events. Major incidents such as the 9/11 attacks, the initial conflict in Ukraine, the ongoing US–China trade tensions, the COVID-19 pandemic, and the more recent war in Ukraine have highlighted the interconnected nature of economies worldwide. These events have not only disrupted regional stability, but have also triggered significant shifts in the global business and financial cycles. Kose et al. (2003), Monfort et al. (2003), Ciccarelli and Mojon (2010), Miranda-Agrippino and Rey (2020), and Ginn (2023a, 2023b, 2023c) emphasized the synchronized nature of global economic activities and financial markets, revealing how shocks in one part of the world can propagate rapidly across borders. Policymakers play a crucial role in mitigating the adverse effects of global shocks. They often resort to accommodative monetary policies—such as lowering interest rates or increasing liquidity—to stabilize their economies and counteract negative impacts on growth and employment. These measures help buffer domestic markets against external disruptions, but require careful calibration to avoid long-term consequences, such as inflationary pressures or financial instability. As globalization deepens, the need for coordinated international policy responses becomes increasingly evident in effectively addressing challenges that transcend national boundaries (Dang et al., 2025).
Tunisia’s monetary policy faces increasing challenges amid climbing geopolitical tensions and domestic instability. The country’s central bank must navigate a complex environment characterized by external shocks, including regional conflicts and global economic uncertainty, which exacerbate volatility in foreign exchange markets and capital flows (Mbarek et al., 2019; Moussa & Talbi, 2019; Jallouli & Yalouli, 2022; Belhoula, 2024; Trabelsi, 2024a). In such a context, the central bank is often forced to adopt restrictive measures, such as raising interest rates, to stabilize prices and the currency. However, these measures can inadvertently slow economic growth and deepen social discontent, creating a delicate balancing act between ensuring macroeconomic stability and fostering economic resilience.
Since the late 1980s, Tunisia’s monetary policy has undergone substantial changes to facilitate structural reforms and address emerging economic challenges (Ghali & Mohnen, 2004). In 1987, the Central Bank of Tunisia (CBT) implemented a strategy centered on regulating money supply growth to achieve price stability, specifically targeting a growth rate of the money supply (M2) that was 2% lower than the anticipated nominal GDP growth, under the assumption of a stable money multiplier. This framework was designed to synchronize the base money supply with the growth objectives for M2. A significant transformation occurred in 2006 with the revision of Organic Law No. 58–90, which explicitly defined the CBT’s primary objective as maintaining price stability (see Murphy, 1999; S. J. Friedman & Sharkey, 2010; Wahyuningsih & Fatmawati, 2024). This reform was executed in two phases: initially, by managing the monetary base to target broad money (M3) in alignment with nominal GDP growth, and subsequently, by adopting an inflation-targeting framework that employed interest rates as the principal policy tool. To improve market regulation, the CBT introduced deposit and lending facilities in 2009, enhancing the flexibility of monetary policy implementation. However, the economic upheaval following the 2011 revolution led to considerable disruptions, including increased cross-border smuggling and illicit trade with Libya and Algeria, which intensified inflationary pressures and necessitated a greater reliance on inflation-targeting mechanisms (Arieff & Humud, 2011, 2014; End et al., 2020).
The progression of monetary policy in Tunisia illustrates the CBT’s adaptive responses to economic and financial challenges over the past decade. The introduction of new legislation (Law No. 2016-35, enacted on 25 April 2016) reaffirmed price stability as the central objective, while also elevating the importance of financial stability relative to the 2006 framework (see Tayssir & Feryel, 2018). In the aftermath of the Arab Spring, the CBT transitioned towards greater exchange rate flexibility, coinciding with the emergence of a structural liquidity deficit within the banking sector. The terrorist attacks of 2015 further complicated monetary policy, leading to a substantial increase in central bank refinancing, which compromised control over monetary aggregates and undermined initial efforts to mitigate inflation through policy rate increases (Arieff, 2018; Salem & Bouaziz, 2024). In light of these challenges, the CBT has adopted more stringent tightening measures since 2018 to address rising inflation. To achieve its price stability mandate, the central bank has established both an intermediate objective—focused on inflation forecasting—and an operational objective, which involves guiding the interbank rate as the primary instrument of monetary policy.
In the absence of these interventions, the repercussions of inaction would have been dire: inflation could have escalated to double-digit levels, and real interest rates would have remained significantly negative, thereby promoting excessive credit expansion and consumption. Additionally, heightened demand for imported goods would have exacerbated the current account deficit, depleting foreign exchange reserves and intensifying inflationary pressures. Furthermore, escalating inflation would have reduced deposit returns, undermining bank resources and increasing dependence on central bank refinancing, thereby heightening liquidity risks. The evolving policy framework of the CBT highlights the essential role of monetary policy in sustaining economic stability amidst persistent domestic and external shocks (Ben Youssef, 2024).
This research focuses on Tunisia, an emerging economy that has been notably underexplored in scholarly literature. As a result, the findings of this study may have important implications for central bankers and macroeconomists.
The selection of Tunisia as a case study is based on three primary considerations. First, Tunisia exemplifies a small, open, emerging economy that is undergoing institutional transition within the Middle East North Africa (MENA) region. Over the past decade, the country has shifted its exchange rate and monetary policy framework from a currency basket system to a managed floating regime, which theoretically enhances the effectiveness of monetary policy. Additionally, Tunisia has recently granted legal independence to its central bank. If this independence translates into practical effectiveness, it is expected to strengthen monetary policy by providing the central bank with greater autonomy in decision-making and improving the signaling capacity for market participants. Furthermore, central bank independence is anticipated to enhance the efficiency of monetary policy by limiting direct government financing, thereby increasing financial autonomy and reinforcing accountability through more transparent policy communication.
Second, the CBT has consistently raised interest rates to alleviate inflationary pressures, reflecting trends seen in many other countries. However, the effectiveness of this strategy remains debatable, as inflation continues to remain high despite the tightening of monetary policy. Furthermore, the persistent depreciation of the exchange rate and the widening trade deficit cast doubt on the efficacy of interest rate hikes. The discretionary nature of Tunisia’s monetary policy, which has not yet adopted a clear targeting framework, further complicates this situation.
Third, research is scarce regarding aggregate production and inflationary responses to monetary policy shocks in Tunisia, with a lack of consensus on both the magnitude and direction of these effects. Furthermore, existing studies predominantly focus on overall GDP, leaving the responses of sectoral components largely unexamined. Previous analyses have often treated monetary policy as a “black box”, in the words of Mimoun et al. (2024), failing to investigate how various transmission mechanisms influence the economy.
We study the effectiveness of monetary policy transmission in Tunisia. We use advanced econometric techniques to compare the money market rate behavior under high and low geopolitical risks. Frequently, the production–money market rate–risk relationship is puzzling. First, we solve the enigma by distinguishing between global and local geopolitical risk. Second, we consider production at the aggregate and the sectoral levels. Third, we delve into a deeper analysis of monetary policy’s (in)effectiveness by establishing a novel composite index of investor sentiment in the stock markets. As such, our contribution is distinctive and comprehensive in terms of the research question, the context, and the econometric methods used, and it offers a wide range of practical implications for the practices of central banks that can be applied to similar emerging small open economies.
2. Literature Review
2.1. Theoretical Deliberations
2.1.1. Irreversibility Theory
In unstable environments, a crucial question of whether monetary policy is effective arises. Earlier theories suggest that monetary policy becomes less effective when uncertainty is high. Investors’ sentiment plays a key role in channeling uncertainty into monetary policy. This was outlined by the irreversibility theory (B. S. Bernanke, 1983; Bloom, 2009; Bloom, 2014). Uncertainty affects firms and economies in two primary ways; first, through the “real options” mechanism, where the irreversibility of investment decisions encourages firms to delay or remain flexible amid uncertainty. This hesitancy, as described by Henry (1974), extends beyond investment to consumer behavior, particularly for durable goods such as homes and cars, which are often deferred during uncertain times. This delay in consumption is less pronounced for nondurable goods but still impacts overall economic activity. Bloom (2014) expanded on this by linking uncertainty with reduced responsiveness to economic stimuli, like tax cuts or interest rate adjustments, necessitating stronger stabilization policies during volatile periods. Furthermore, high uncertainty disrupts productivity growth by stalling resource reallocation, a key driver of economic efficiency. Second, uncertainty influences financial dynamics by raising risk premiums. Investors demand higher compensation for increased risks, escalating financing costs and default probabilities. This, in turn, elevates bankruptcy expenses and contributes to a slowdown in economic activity. Arellano et al. (2010) and Christiano et al. (2014) highlighted how uncertainty amplifies the likelihood of extreme adverse outcomes, further discouraging borrowing and investment. Moreover, uncertainty fuels “ambiguity aversion”, where economic agents focus on worst-case scenarios, reducing confidence and promoting precautionary savings over consumption.
2.1.2. Credit Transmission Channel Theory
According to the credit transmission channel theory, the nonlinear effects of interest rates during financial crises are less substantial than monetary policy shocks. Because of the greater external financing premiums, businesses are facing liquidity limitations (as noted by Romer & Romer, 1993; Morgan, 1998; B. Bernanke, 1999; He & Krishnamurthy, 2013; Brunnermeier & Sannikov, 2014). According to the idea, changes in the external finance premium—which represents the cost differential between money raised internally (via retained earnings) and externally (through stock or debt)—amplify the immediate impact of monetary policy on interest rates. The external finance premium highlights flaws in the credit markets that lead to a discrepancy between the expenses and the profits that lenders anticipate. The “credit view” holds that monetary policy tends to affect the external finance premium in the same way as it affects open-market interest rates. The overall effect of monetary policy on borrowing rates is strengthened by this additional policy effect on the external finance premium, which in turn influences real spending and economic activity (see B. S. Bernanke & Gertler, 1995).
2.1.3. Central Bank Communication and Credibility
Economic agents’ expectations depend on how they—economic agents—digest the central bank’s messages. The content, clarity, timing, and credibility of monetary policy announcements have long been surveyed in the literature (Woodford, 2005; Blinder et al., 2008; Blinder, 2009; De Haan & Sturm, 2019). Central banks are often perceived as having superior insights into the economic outlook due to their extensive forecasting resources and ability to analyze unobservable economic factors. Research, such as that by Andersson et al. (2006), showed that financial markets respond significantly to the information central banks share, with investors adjusting their views based on these announcements. Kohn and Sack (2003) emphasized that private agents tend to trust central banks’ forecasts, particularly when the institution has built a strong reputation for accurate economic assessments. Economic agents vary in their levels of sophistication—some favor straightforward, concise information, while others seek in-depth, detailed analyses to inform their decisions (Filardo, 2004). Some recent research has looked into splitting monetary policy shocks into surprise policy shocks and central bank information shocks through high-frequency identification strategies (e.g., Jarociński & Karadi, 2017, 2020; Laséen, 2020; Ostapenko, 2020; Laumer & Santos, 2024). Others, like Hansen et al. (2019), employed a different strategy to show that future expectations are sensitive to communicating about uncertainty.
2.2. Empirical Literature
There is a growing body of literature on the effects of monetary policy under uncertainty focusing on the US market (e.g., Tenreyro & Thwaites, 2016; Barnichon & Matthes, 2018; Alpanda et al., 2021; Bruns & Piffer, 2023; etc.). Those papers show that tightening monetary policy under heightened uncertainty generally slows the monetary transmission mechanism. Evidence is retrieved from nonlinear modeling such as Vector Autoregressive (VAR) and local projections (LPs).
Papers that present research questions similar to ours are very novel. The influential work by Caldara and Iacoviello (2022) introduced a news-based geopolitical risk indicator, demonstrating that a geopolitical risk shock has contractionary effects on the economy, with investment in industries more exposed to geopolitical risks being particularly affected. Caldara et al. (2024) expanded this analysis to a comprehensive panel of countries, revealing that during geopolitical events, supply-side disruptions typically outweigh reduced aggregate demand, resulting in increased inflation and varied effects on economic activity. Notably, while geopolitical risk shocks stimulate economic activity in the US—largely due to heightened defense spending—they lead to recessions in other nations. Building on this, Bondarenko et al. (2024) refined the geopolitical risk index by utilizing country-specific news sources, offering a perspective that better reflects local geopolitical dynamics instead of a predominantly Western viewpoint. Pinchetti (2024) categorized geopolitical risk shocks into those arising from energy market disruptions and those linked to weak aggregate demand. Brignone et al. (2024) highlighted that those large geopolitical shocks primarily affect the economy by increasing uncertainty. Kilian et al. (2024) proposed a dynamic stochastic general equilibrium (DSGE) global economy model, examining the relationship between geopolitical oil price risks and economic fluctuations. Their findings indicate that while geopolitical tension plays a critical role in driving oil price volatility, it has a limited impact on broader macroeconomic fluctuations. In episodes of high geopolitical tensions, it is important to account for monetary–fiscal coordination (Franconi, 2024). How geopolitical risk affects business cycles and economic conditions is a matter of research. Geopolitical risk shocks influence the economy through various channels, with some exerting inflationary pressures, while others have deflationary effects. Inflationary channels include the impact on commodity prices, particularly oil, as highlighted by Mignon and Saadaoui (2024), and the currency channel, as discussed by Gopinath (2015), Kisswani and Elian (2021), and Yilmazkuday (2025). Conversely, deflationary effects arise from channels such as consumer sentiment, where heightened uncertainty dampens spending, and financial conditions, which tighten during periods of geopolitical instability (Forbes & Warnock, 2012; Forbes et al., 2017; Choi & Hadad, 2025).
Our contribution. We distinguish our work from the existing literature by focusing on Tunisia. Since the late 1980s, Tunisia has implemented market-oriented reforms, though the state continues to play a substantial role. It influences consumer prices, employs a significant portion of the labor force, and actively participates in wage negotiations. State-owned banks dominate the financial sector, which remains underdeveloped despite a notable level of lending relative to economic output. The sector faces challenges, including a lack of an efficient securities market, reliance on collateral-based lending, and a considerable burden of non-performing loans. The informal economy is significant, contributing substantially to employment in the private sector. Before 2011, state capture was prevalent; businesses connected to the presidential family outperformed competitors, and dominated specific sectors that were heavily regulated and restricted for foreign investment (Przystupa & Wróbel, 2015). After an unsuccessful mix of exchange rate and monetary aggregate targeting, the CBT now uses interest rates as the primary monetary tool. The 2011 revolution marked a major shift in the country’s economic landscape. In 2016, the CBT became independent. Tunisia presents the key characteristics of small, trade-open, emerging market economies, and serves as a valuable case for analysis.
In our work, we argue that the Tunisian monetary policy’s reaction to geopolitical risk is subject to both inflationary and deflationary channels. There are instances in which the central bank cares about curbing inflation, while in others, dealing with investors’ sentiments becomes a priority (Ginn & Saadaoui, 2024).
3. Research Methodology
3.1. Data Collection
3.1.1. The Geopolitical Risk Index
A key aspect of economic policy planning involves addressing risks associated with geopolitical events. These include wars, political unrest, elections, natural disasters, shifts in political regimes, and escalating tensions between nations. Such geopolitical uncertainties influence economic conditions and financial markets (Kisswani & Elian, 2021).
Caldara and Iacoviello (2022) developed a novel indicator to quantify adverse geopolitical events by analyzing the frequency of related articles in prominent newspapers. Their measure, known as the Geopolitical Risk (GPR) index, captures the dynamics of geopolitical tensions and their economic implications from 1900 onwards.
The GPR index is derived using automated text analysis from the digital archives of ten major newspapers—Chicago Tribune, The Daily Telegraph, Financial Times, The Globe and Mail, The Guardian, Los Angeles Times, The New York Times, USA Today, The Wall Street Journal, and The Washington Post. The index calculation involves identifying articles discussing adverse geopolitical events each month and expressing them as a proportion of the total number of articles. The dataset consists of approximately 25 million news articles from leading English-language newspapers, covering publications from 1900 to the present. In recent years, the sample has included around 30,000 articles per month, while the historical dataset contains about 10,000.
The methodology employs a dictionary-based approach, selecting words that closely align with the concept of geopolitical risk. This selection process is informed by geopolitical textbooks, historical linguistic databases, and the analysis of high-frequency words appearing in news reports during periods of heightened geopolitical tension. Key terms include “war”, “threat”, “terror”, “blockade”, “invasion”, and “troops”, which are significantly more prevalent in media coverage during geopolitical crises.
The analysis categorizes articles into eight thematic groups: threats of war, threats to peace, military buildups, nuclear threats, terror threats, war initiations, war escalations, and acts of terror. Two subindices are constructed from these categories: the Geopolitical Threats index, encompassing the first five categories, and the Geopolitical Acts index, covering the last three.
As Caldara and Iacoviello (2022, p. 5) have put it, the dictionary used for constructing the index is developed based on a structured approach. First, it is designed to align with the definition of geopolitical risk established in this study, ensuring that selected terms accurately reflect relevant events. Second, references from geopolitical textbooks and the Corpus of Historical American English help identify key themes associated with geopolitical events, such as “war on terror” or “nuclear weapon”, as well as words commonly linked to conflict, like “declare”. Third, the selection process prioritizes high-frequency words and their synonyms that tend to appear more frequently in news reports during periods of heightened geopolitical tension. For example, terms such as “crisis”, “terror”, “blockade”, “invasion”, “troops”, and “war” are significantly more prevalent in media coverage during geopolitical crises.
Then, an audit was conducted to ensure reliability, involving a human review of 16,000 newspaper articles and comparisons with external indicators, and confirming that the index effectively tracks geopolitical risk fluctuations.
The primary GPR index, based on all ten newspapers, began in 1985. The country-specific GPR indices are derived from automated text searches of newspaper archives. For 44 advanced and emerging economies, Caldara and Iacoviello (2022) constructed these indices by identifying, for the Recent Index, the monthly proportion of articles from 1985 onward that (1) qualify for inclusion in the general GPR index and (2) reference the specific country or its major cities. These indices are expressed as a percentage of total articles published each month, and provide insights into geopolitical risks as perceived from a US perspective for each country. We have gathered the global GPR and the local GPR related to Tunisia. However, we selected data from 1993 onwards, as data coverage of other variables is available starting from that year.1
Notable spikes in the index are observed during significant historical events, such as the aftermath of 9/11, the US–Iraq war, the Russia–Ukraine war, and the banking instability of Silicon Valley Bank (see Figure 1). Elevated geopolitical risk is linked to declines in investment (S. Wang et al., 2019), stock market performance (Agoraki et al., 2022), and employment levels (Ji et al., 2025). Others established a link with energy transition and environmental sustainability (Q. Wang et al., 2024; Cutcu et al., 2025). The GPR also correlates with an increased likelihood of economic crises and heightened downside risks for the global economy. Importantly, the GPR is associated with high inflation and uncertainty levels (Caldara et al., 2024).
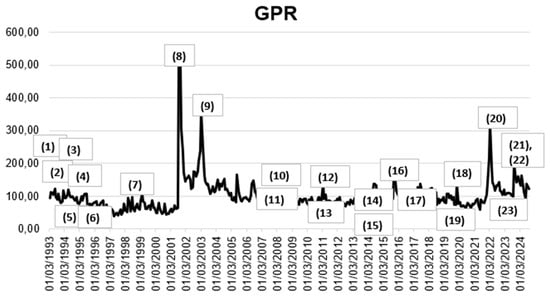
Figure 1.
The evolution of the global geopolitical risk (GPR). (1) 01/1993: START II Treaty signed between the United States and Russia to reduce nuclear weapons. (2) 09/1993: The Oslo Accords are signed, marking a step toward peace between Israel and Palestine. (3) 04–07/1994: The Rwandan Genocide claims the lives of approximately 800,000 people. (4) 12/1994: Russia launches its first war in Chechnya. (5) 07/1995: Srebrenica massacre during the Bosnian War; over 8000 Bosniaks are killed. (6) 11/1995: End of the Bosnian War. (7) 03/1999: NATO intervenes in the Kosovo War through airstrikes against Yugoslavia. (8) 09/2001: Terrorist attacks in the US. (9) 03/2003: The US and allies invade Iraq, alleging weapons of mass destruction. (10) 08/2008: Russia–Georgia War over South Ossetia and Abkhazia. (11) 09/2008: Global Financial crisis with the collapse of Lehman Brothers. (12) 01/2011: The Arab Spring begins in Tunisia, spreading across the Arab world. (13) 03/2011: Syrian Civil War begins, becoming a prolonged and devastating conflict. (14) 02/2014: Russia annexes Crimea following unrest in Ukraine. (15) 06/2014: ISIS declares the establishment of a caliphate in Iraq and Syria. (16) 11/2015: Paris terrorist attack. (17) 06/2016: The UK votes to leave the European Union (Brexit). (18) 12/2019: COVID-19 is first detected in Wuhan, China, leading to a global pandemic, (19) 03/2020: COVID-19 lockdowns begin worldwide, leading to economic and social upheaval. (20) 02/2022: Russia invades Ukraine, triggering the largest European conflict since WWII. (21) 03/2023: Banking instability emerges following the collapse of Silicon Valley Bank. (22) 07/2023: Record-breaking global heatwaves intensify calls for climate action. (23) 10/2023: Hamas’s attack and Israel’s invasion of Gaza. Sources: Washington Watch, US Institute of Peace, Human Rights Watch, Carnegie Endowment.
The local GPR was more pronounced during the Arab Spring, known as the 2011 revolution in Tunisia, and the multiple elections and parliaments following the fallout of the Ben Ali regime (see Figure 2). During these periods, Tunisia underwent a complicated political and economic transition, resulting in a prolonged economic decline over the last decade. Additionally, the country has been impacted by regional instability and conflict.
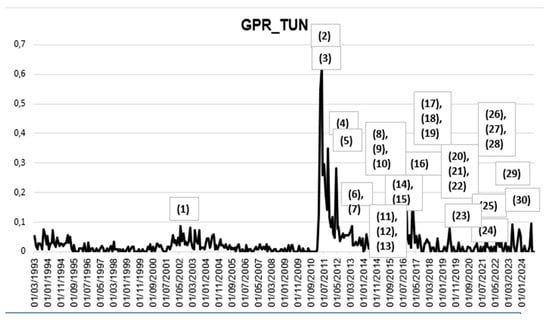
Figure 2.
The evolution of the local geopolitical risk (GPR_TUN). (1) 04/2002: A terrorist bombing at the Ghriba synagogue in Djerba kills 21 people, including foreign tourists. (2) 01/2011: The Arab Spring begins in Tunisia. (3) 10/2011: Tunisia holds its first free elections. The Islamist Ennahdha party wins a majority in the Constituent Assembly. (4) 04/2012: Heightened political debate and economic instability in Tunisia. (5) 02/2013: Opposition leader Chokri Belaid is assassinated, leading to political turmoil. (6) 07/2013: Opposition leader Mohamed Brahmi is assassinated, triggering mass protests. (7) 10/2013: Political crisis due to (5) and (6). (8) 01/2014: Tunisia adopts a new democratic constitution. (9) 10/2014: Parliamentary elections are held, with Nidaa Tounes emerging as the largest party. (10) 12/2014: Beji Caid Essebsi is elected as Tunisia’s first democratically chosen president. (11) 03/2015: The Bardo Museum attack in Tunis kills 22 people, mostly foreign tourists. (12) 06/2015: A terrorist attack in Sousse targets tourists, killing 38 people. (13) 11/2015: A suicide bombing on a presidential guard bus in Tunis kills 12 people. (14) 03/2016: Terrorist attack in Ben Guerdane. (15) 09/2016: Internal political tensions. (16) 02/2017: Transiotional justice mechanisms, (17) 05/2018: Tunisia holds its first municipal elections under the new constitution. (18) 01/2018: Protests erupt against austerity measures tied to IMF reforms. (19) 09/2018: Socio-economic pressures. (20) 04/2019: Slight economic improvements despite fiscal challenges. (21) 07/2019: President Beji Caid Essebsi dies, triggering early presidential elections. (22) 10/2019: Kais Saied, an independent candidate, wins the presidential runoff election. (23) 03/2020: Tunisia implements strict lockdowns to combat COVID-19, highlighting economic vulnerabilities. (24) 07/2021: President Kais Saied suspends parliament, dismisses the prime minister, and assumes executive authority, citing a national emergency. Critics call this a coup. (25) 09/2021: Saied issues a decree consolidating his control over legislative and executive powers. (26) 02/2022: Saied dissolves the Supreme Judicial Council, further centralizing power. (27) 07/2022: A new constitution is approved in a controversial referendum, significantly expanding presidential powers. (28) 12/2022: Parliamentary elections are held with low voter turnout, indicating public discontent. (29) 03/2023: Protests erupt over worsening economic conditions, including inflation and unemployment. (30) 11/2023: Debates on governance reforms and managing public debt. Sources: Washington Watch, US Institute of Peace, Human Rights Watch, Carnegie Endowment.
3.1.2. The Dependent Variables and Controls
We gather macroeconomic variables from various databases (see Table 1). The dependent variable is either real activity measured by the industrial production (LNIPIT) or the consumer price index (LNIPIT), used to portray inflationary pressures. The system includes money supply (LNM2TND), money market rate (TMM), and the real effective exchange rate (LNTCER). The sample covers the period from 01/1993 to 08/2024, with missing data. All variables are transformed using the natural logarithm, except TMM, which is expressed in rate.

Table 1.
Summary of the variables.
3.2. Data Properties
Table 2 presents descriptive statistics for all variables. The variables exhibit different levels of dispersion and skewness, with the money market rate (TMM) showing the highest variability (standard deviation of 1.66), while the log-transformed industrial production index (LNIPIT) has relatively low variability (0.15). The mean values of the variables are close to their respective medians, except for LNIPIT, which shows a slight negative skew, indicating a longer left tail. Geopolitical risk indices (LNGPR and LNGPR_TUN) have extreme values, as indicated by their high kurtosis and positive skewness, especially LNGPR_TUN, which has a remarkably high skew of 5.26. All variables fail the Jarque–Bera test for normality, suggesting that the distributions are non-normal, with some variables exhibiting heavy tails or outliers. These findings indicate that methods robust to non-normal distributions may be more suitable for further analysis.

Table 2.
Descriptive statistics.
The Pearson correlation results in Table 3 indicate several strong relationships. For instance, there is a strong positive correlation between the industrial production index (LNIPIT) and the money supply (LNM2TND) (0.834), and a similarly strong positive correlation between the consumer price index (LNCPI) and LNM2TND (0.983). The money market rate (TMM) is negatively correlated with LNIPIT (−0.829), LNCPI (−0.610), and LNM2TND (−0.717), suggesting that higher money market rates are associated with lower values of industrial production and consumer prices. The geopolitical risk indices (LNGPR and LNGPR_TUN) exhibit weak positive correlations with the economic variables, with the latter showing significant negative correlations with TMM, LNTCER, and LNCPI, indicating potential inverse relationships. The statistical significance of all correlations is confirmed by the low p-values, with most correlations being highly significant (p < 0.05), except for the correlations involving LNGPR, which are more modest but still statistically relevant.

Table 3.
Pearson correlation matrix.
3.3. Econometric Modeling
3.3.1. Time-Varying Granger Causality
The validity and robustness of VAR results often depend on the specific period under consideration, emphasizing the importance of adopting a comprehensive approach to structural stability assessment. Granger causality between two variables may hold during a one-time frame but appear fragile when examined over alternative periods. Recent advancements in the literature, particularly by Phillips et al. (2011, 2014, 2015a, 2015b), have introduced methods to detect and date financial bubbles using right-tailed unit root tests combined with date-stamping techniques. Building on these developments, Shi et al. (2018, 2020) extended the concept of Granger causality by integrating these methods, enabling a more robust evaluation of causal relationships. Granger causality has been subject to critique for its inability to establish authentic causal relationships; instead, it identifies predictive associations derived from the historical values of variables. Mariusz Maziarz (2015) argues that Granger causality is epistemically insufficient when utilized by researchers who do not possess a foundational theoretical comprehension of the mechanisms that underlie the relationships between variables. This approach is limited as it relies solely on statistical correlations within time series data, neglecting to account for underlying causal structures, omitted variables, or potential feedback loops.
In light of these limitations, the concept of time-varying Granger causality has been introduced to mitigate one of the primary shortcomings of traditional Granger causality, namely, the presumption of a stable causal relationship over time. In practice, economic and financial relationships frequently undergo evolution due to structural changes, policy adjustments, or external shocks. Conventional Granger causality tests may overlook such variations, resulting in potentially erroneous conclusions. By permitting causal relationships to fluctuate over time, time-varying Granger causality provides a more adaptable and dynamic framework for understanding the evolution of relationships between variables, thereby proving particularly beneficial in contexts marked by uncertainty and regime shifts (e.g., Cepni et al., 2023; Ren et al., 2023).
Shi et al. (2018, 2020) propose the lag-augmented VAR (LA VAR) in the spirit of Toda and Yamamoto (1995). We consider a multivariate series, and is a vector of variables
where is a time trend, is the optimal lag of VAR, is the maximum order of integration of the variables, and is the error term. Equation (1) can be rewritten as
where
, and .
The null hypothesis of Granger non-causality is given by the restrictions
where is a matrix of dimension with is the number of restrictions. A more compact expression of Equation (2) can be modeled as follows:
where
Let and .
The Ordinary Least Squares (OLS) estimator is
The Wald statistic to test the null hypothesis is
where with “vec” being the column stacking operator, , is the Kronecker product, and is the number of restrictions.
To investigate time-varying Granger causality, recursive estimation techniques are employed. These involve calculating a series of test statistics across successive periods, which are then used for inference. Common algorithms for generating these test statistic sequences include the forward expanding window (FE) method (Thoma, 1994), the rolling window (RO) approach (Arora & Shi, 2016; Swanson, 1998), and the recursive evolving (RE) technique (Phillips et al., 2015a; Shi et al., 2020).
The recursive Granger causality tests utilize Wald statistics calculated from data subsamples. Let f1 and f2 represent the fractional starting and ending points of the regression sample, with fw = f2 − f1 denoting the fraction of the sample used. The Wald statistic derived from this subsample, based on the LA VAR model, is denoted as . Defining s1 = ⌊f1T⌋, s2 = ⌊f2T⌋, and sw = ⌊fwT⌋, where T is the total number of observations, s0 = ⌊f0T⌋ represents the minimum number of observations required to estimate the VAR system.
In the forward expanding window procedure, the starting point s1 is fixed at the first observation (s1 = 1), while the regression window expands from s0 to T. This corresponds to s2 gradually increasing from s0 to T.
For the rolling window procedure, the regression window size is fixed at s0. The starting point s1 moves from the first observation to T − s0 + 1, and the endpoint s2 is defined as s2 = s1 + s0 − 1. Alternatively, s1 and s2 can be expressed as s2 = {s0, …, T} and s1 = s2 − s0 + 1. In this procedure, the endpoint of the regression moves from s0 to the final observation T.
For the recursive window, the endpoint is s2 = {s0, …, T}, while the starting point is s1. For each observation f, one obtains a sequence of . The test statistic is defined to be the supremum of the Wald statistic sequence for observation ⌊fT⌋
Both rolling and recursive methods provide more reliable results than the forward method. Thus, our interpretation will be more oriented towards the former techniques (Ante & Saggu, 2024).
3.3.2. (Non)linear Local Projections
Local projections (LPs) provide estimates of both linear and non-linear Impulse Response Functions (IRFs), which were initially introduced by Jordà (2005) and extended by Jordà and Taylor (2025). This method facilitates the straightforward application of various options found in the expanding body of literature on LPs. The LP is written as follows:
Explicitly,
The associated IRF is given by
where denotes the size of the shock, with , pertaining to a one standard deviation in a variable. The subscript indicates the causal link between the intervention and the result. The specific value is not particularly relevant if a linear model is used. However, if a non-linear relationship is proposed, it may influence the shock variable. From Equation (5), we can easily deduce that . We assume that is exogenous, leading to . Equation (4) is then estimated using Ordinary Least Squares (OLS) for each subsequent horizon , which relates to a semi-parametric estimation of . Although may exhibit serial correlation up to certain lags, this does not impact the consistency of . In contrast to Vector Autoregressive (VAR) models, Equation (4) is a single equation rather than a system of equations.
We extend Equation (4) to allow the interaction of the shock variable () with another specific variable ():
In our case, the shock variable TMM interacted with LNGPR and (LNGPR_TUN), respectively.
4. Results and Discussion
4.1. Unit Root Test
A crucial part of estimating LA VAR is to assess the stationarity characteristics of the time series in question. There are primarily two well-known tests for this purpose. The first is the Augmented Dickey–Fuller (ADF) test, introduced by Dickey and Fuller (1979). The authors examine the following random walk.
Dickey and Fuller (1979) utilized the maximum likelihood approach to develop an estimator for . Additionally, the Phillips–Perron (PP) test introduced by Perron and Phillips (1987) proposes a minor adjustment to Equation (7), and uses a semi-parametric approach to estimate ;
The hypothesis test is given by
There is also the Dickey–Fuller test for a unit root, in which the series has been transformed by a generalized least-squares regression (DF-GLS) introduced by Elliott et al. (1996). There are two possible alternative hypotheses, as follows: is stationary around a linear trend, or yt is stationary with no linear time trend. Under the first alternative hypothesis, the DF-GLS test is performed by first estimating the intercept and trend via GLS. The GLS estimation is performed by generating the new variables, , where
An OLS regression is performed on the Equation above. Then, we generate the following:
Finally, we perform ADF on the transformed model,
Table A1 in Appendix A.1 presents the unit root findings from ADF and PP for various assumptions about the intercept and trend. If Prob is lower than the significance level, then we reject the null hypothesis of a unit root in the series. All variables are stationary after taking the first difference. They are integrated into order 1 (I(1)), except LNIPIT, LNGPR, and LNGPR_TUN, which are I(0) and I(1) at the same time. We ensure the credibility of those results in three ways. First, we conduct the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test for the same set of variables. The results in Table A2 of Appendix A.1 reveal that all variables are integrated in the order of 1(I(1)), except LNCPI. Second, we conduct the DF-GLS for each variable in level and first difference by considering continuous samples. The results are available in Table 4, and reveal that all variables are I(1), except LNGPR and LNGPR_TUN, which are I(0) and I(1) at the same time.

Table 4.
DF-GLS of ERS unit root test results.
Taking all the findings together, we consider that all variables are I(1).
Next, we conduct a unit root test that accounts for structural breaks. We utilize the Zivot–Andrews method for this analysis. The Zivot and Andrews (2002) test permits the identification of breakpoints that occur endogenously, and evaluates the null hypothesis of a unit root in contrast to the alternative hypothesis. The variable is stationary with a structural break in intercept, in trend, or in both trend and intercept. Equation (9) is identical to Equation (7), but includes two dummies ;
The results are available in the Supplementary File (see Table S1) and confirm again the order of integration of the variables.
4.2. Connection/Disconnection Episodes of the Interest Rate: Time-Varying Granger Causality Results
We follow Ivanov and Kilian (2005) and use the Akaike Information Criterion (AIC) to select the optimal lag (see Tables S2–S5), as this gives more accurate estimations for monthly data. There are four VAR systems that we consider. Model 1 includes the industrial production (LNIPIT), the money supply (LNM2TND), the money market rate (TMM), the real effective exchange rate (LNTCER), and the global geopolitical risk index (LNGPR) as endogenous variables. Model 2 is similar to Model 1, but we consider the consumer price index (LNCPI) instead of LNIPIT. Model 3 replicates Model 1 with the local geopolitical risk index (LNGPR_TUN). Model 4 substitutes LNIPIT with LNCPI in Model 3. Table 5 presents the results of the Max–Wald statistic using three methods: forward, rolling, and recursive. We reject the null hypothesis of no causality from all variables to LNIPIT. In particular, TMM does Granger cause LNIPIT at a 1% level of significance according to rolling and recursive expanding methods, while the null hypothesis is not rejected under the forward expanding method.

Table 5.
Time-varying Granger causality results. Dependent variable—LNIPIT, globalg geopolitical risk—LNGPR.
Now focusing on the plots of Figure 3, the null hypothesis of no causality is rejected whenever the test statistic portrayed by the solid line exceeds the critical values (dotted lines).
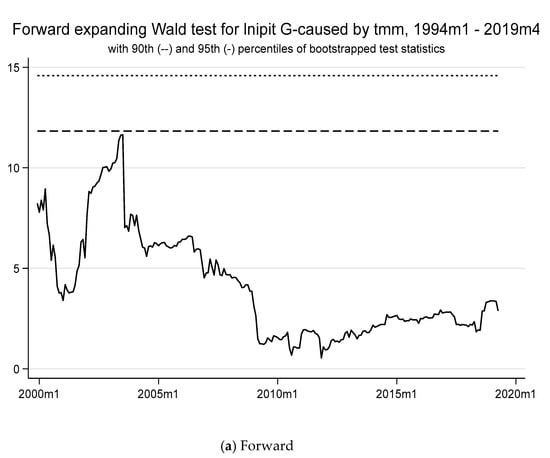
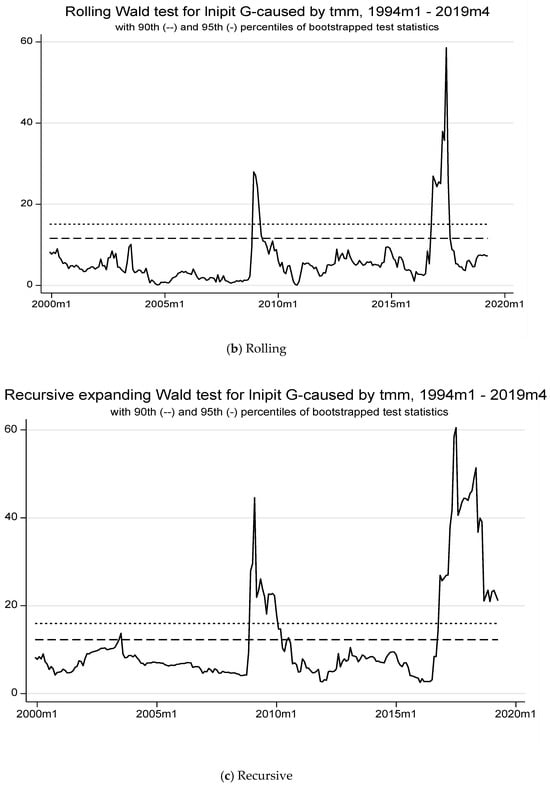
Figure 3.
The forward, rolling, and recursive evolving test results with lag augmentation d = 1 are displayed in panels (a–c) with a minimum window size = 72. The regression model 1 is (LNIPIT LNM2TND TMM LNTCER LNGPR)’, allowing for heteroscedastic errors. The empirical size is 5%, controlled over a 1-year period and obtained from bootstrapping. Lag orders are assumed to be constant and selected using AIC(=3) with a maximum length of 8 for the whole sample period. LNIPIT: Industrial production (in log). LNCPI: Consumer price index (in log). LNM2TND: Monetary Aggregates 2 in TND (in log). TMM: Money market rate. LNTCER: Real effective exchange rate (in log). LNGPR: Global geopolitical risk (in log).
According to the forward-expanding Wald test, the test statistic gradually declines and remains below the critical values (90th and 95th percentiles) for most of the period, suggesting a weaker or non-existent causal relationship between TMM and industrial production during these times. The declining trend could signify a gradual disconnection effect, potentially related to geopolitical risks disrupting the transmission mechanism. The rolling Wald test shows a fluctuating causal relationship, with the test statistic frequently exceeding the critical thresholds in certain periods (e.g., around 2009 and briefly after 2015). These periods of connection suggest that TMM might have influenced output during times of lower geopolitical risks or relative economic stability. The intermittent disconnections (test statistics falling below critical values) align with heightened geopolitical risks, potentially dampening the effectiveness of monetary policy on industrial production.
The recursive method highlights persistent peaks (e.g., around 2009 and after 2015), with the test statistic exceeding the critical values during these periods. These sustained connections might indicate moments when geopolitical risks were less disruptive, allowing monetary policy to impact industrial production. However, the sharp declines in other periods (e.g., 2009–2015) suggest significant disconnections, possibly due to heightened geopolitical risk.
Overall, the results indicate alternating periods of connection and disconnection between TMM and industrial production in Tunisia. Global geopolitical risks likely played a role in weakening the causal relationship by disrupting financial markets and economic stability. Periods of disconnection correspond to heightened risk, reducing the effectiveness of monetary policy transmission mechanisms. Conversely, connections emerge during more stable periods, allowing monetary policy to influence production.
The empirical findings indicate that geopolitical risks significantly influence the effectiveness of monetary policy in Tunisia. This relationship is mediated through several critical transmission channels, which ultimately affect the connection between the Tunisian money market (TMM) and industrial production.
One primary mechanism involves disruptions in financial markets, where heightened geopolitical risks increase uncertainty, leading to capital flight, exchange rate volatility, and liquidity shortages within domestic financial markets (see Zhao, 2024). These factors undermine the transmission of monetary policy by reducing banks’ willingness to extend credit and altering investors’ risk perceptions. Consequently, adjustments to the policy rate by CBT may not effectively translate into changes in credit conditions or decisions regarding industrial investment.
Another significant channel relates to inflationary pressures and risk premiums, as geopolitical shocks often lead to supply chain disruptions, increase import costs, and trigger inflationary surges. In response to rising inflationary expectations, the CBT may adopt contractionary measures, such as raising interest rates, to stabilize prices. However, during periods marked by geopolitical turbulence, such measures may inadvertently worsen economic slowdowns rather than promote growth, thereby reducing the expected impact of monetary policy on industrial production.
Furthermore, the credibility of policy and the interventions of the central bank are crucial in determining the strength of the relationship between monetary policy and industrial production. In times of heightened geopolitical risk, the central bank may resort to unconventional measures, such as liquidity injections or foreign exchange interventions, to stabilize financial conditions (Ben Youssef, 2024). While these interventions can alleviate short-term instability, they may also lead to episodes of policy disconnection, during which traditional transmission mechanisms become less effective due to shifts in investor behavior and economic uncertainty. Conversely, during more stable periods, when financial markets operate efficiently, the transmission of monetary policy is reinforced, enabling the transmission mechanism to exert a more predictable influence on industrial production.
The cyclical effectiveness of monetary policy in Tunisia reflects the interplay of external shocks, policy responses, and economic conditions, strengthening when geopolitical risks subside and weakening amid heightened uncertainty.
When considering Model 2, we observe the same causality pattern for all variables related to LNCPI. Particularly, TMM does Granger LNCPI over the sample period for rolling and recursive expanding methods at the 1% significance level (see Table 6). Nevertheless, we identify episodes of connection and disconnection when examining the graphs of Figure 4. Except for the forward method, both rolling and recursive expanding methods show a fluctuating pattern, with high statistical significance depicted for the period (2005–2009) and then around 2012–2013, before showing up again with a fair impact during 2017–2018. These periods coincide with the low values of global GPR (LNGPR).

Table 6.
Time-varying Granger causality results. Dependent variable—LNCPI; global geopolitical risk—LNGPR.
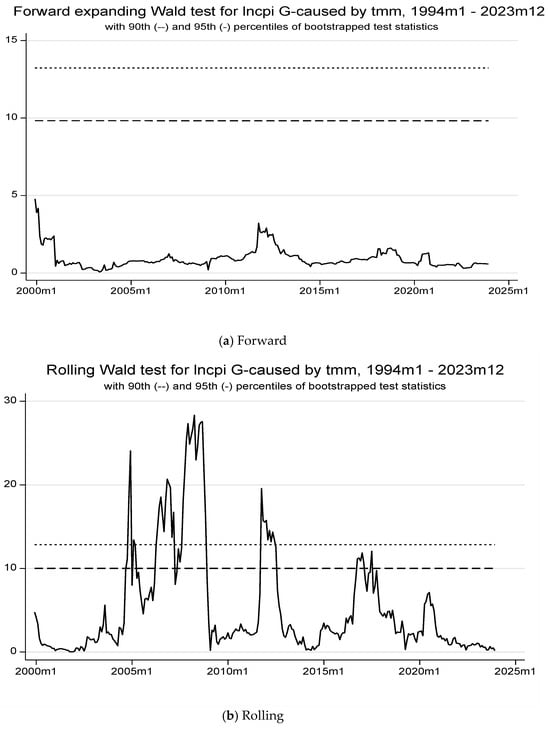
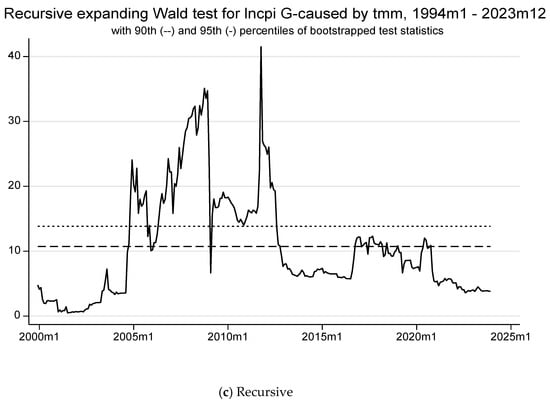
Figure 4.
The forward, rolling, and recursive evolving test results with lag augmentation d = 1 are displayed in panels (a–c) with a minimum window size = 72. The regression model 2 is (LNCPI LNM2TND TMM LNTCER LNGPR)’, allowing for heteroscedastic errors. The empirical size is 5%, controlled over 1 year and obtained from bootstrapping. Lag orders are assumed to be constant and selected using AIC(=2), with a maximum length of 8 for the whole sample period. LNCPI: Consumer price index (in log). LNM2TND: Monetary Aggregates 2 in TND (in log). TMM: Money market rate. LNTCER: Real effective exchange rate (in log). LNGPR: Global geopolitical risk (in log).
We replace the global GPR with the local GPR (LNGPR_TUN). All macroeconomic variables significantly impact production (LNIPIT) throughout the period, as shown by expanding the Wald methods (Table 7). Figure 5 illustrates a fluctuating relationship between TMM and LNIPIT, especially in rolling and recursive methods, with notable spikes around 2009 and 2017–2018, linked to low local geopolitical risk. High geopolitical risk correlates with ineffective monetary transmission.

Table 7.
Time-varying Granger causality results. Dependent variable—LNIPIT; local geopolitical risk—LNGPR_TUN.
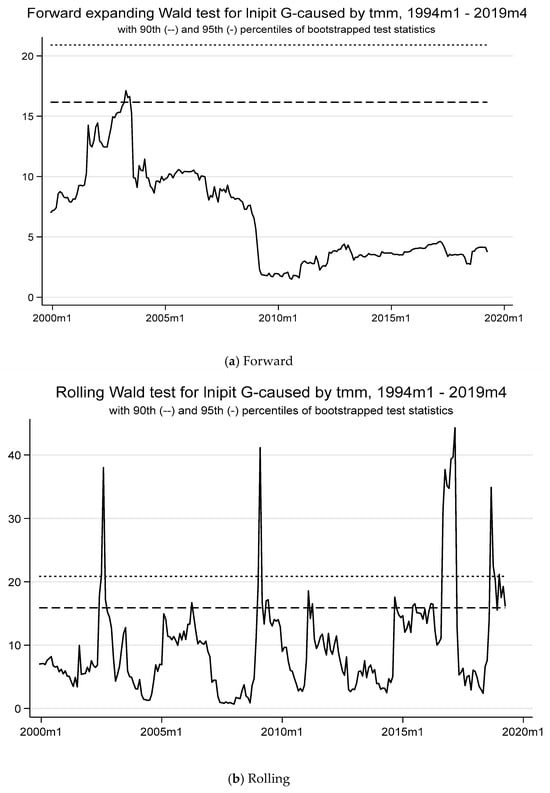
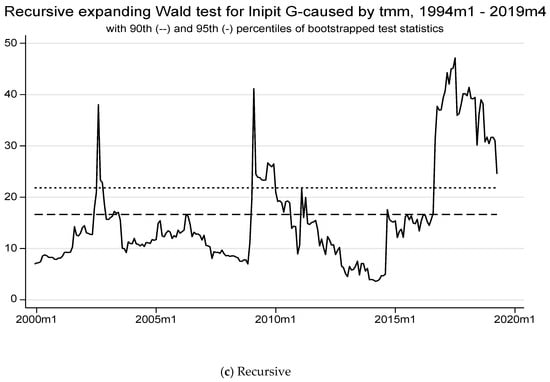
Figure 5.
The forward, rolling, and recursive evolving test results with lag augmentation d = 1 are displayed in panels (a–c) with a minimum window size = 72. The regression model 3 is (LNIPIT LNM2TND TMM LNTCER LNGPR_TUN)’, allowing for heteroscedastic errors. The empirical size is 5%, controlled over 1 year and obtained from bootstrapping. Lag orders are assumed to be constant and selected using AIC(=4) with a maximum length of 8 for the whole sample period. LNIPIT: Industrial production (in log). LNM2TND: Monetary Aggregates 2 in TND (in log). TMM: Money market rate. LNTCER: Real effective exchange rate (in log). LNGPR_TUN: Local geopolitical risk (in log).
Macroeconomic variables significantly affect consumer prices at the 5% level (see Table 8). The forward expanding method does not reject the null hypothesis of no causality to LNCPI, indicating its lower reliability. In contrast, rolling and recursive expanding methods show brief connections between TMM and LNCPI, revealing the money market rate’s ineffectiveness during other periods (see Figure 6). These periods align with notable political unrest in Tunisia, including the 2011 revolution, parliamentary elections, COVID-19 lockdowns, and governance reform discussions. These observations join those found in Table 5 and Table 6, and align with concrete facts. After the 2011 revolution, CBT initially responded to the depreciation of the dinar by intervening in the foreign exchange market while sterilizing these interventions through liquidity injections. Although these actions aimed to stabilize the currency, they inadvertently disrupted the transmission of monetary policy by altering domestic liquidity conditions and diminishing the effectiveness of interest rate adjustments. Following the terrorist attacks in 2015, the authorities shifted their focus toward maintaining credit growth, injecting additional liquidity to support lending activities. However, this response undermined inflation-targeting efforts, resulting in a period of disconnection in monetary policy, during which interest rate adjustments had a limited impact on inflation and industrial production. It was not until 2018, with a shift toward tighter monetary policies (including increases in policy rates and macroprudential tightening), that the central bank restored its ability to influence inflation and economic activity more effectively, marking a renewed period of connection in monetary policy (see Ben Youssef, 2024). Furthermore, the surge in international prices accompanied by a depreciation of the dinar explains inflationary pressures in the aftermath of COVID-19.

Table 8.
Time-varying Granger causality results. Dependent variable—LNCPI; local geopolitical risk—LNGPR_TUN.
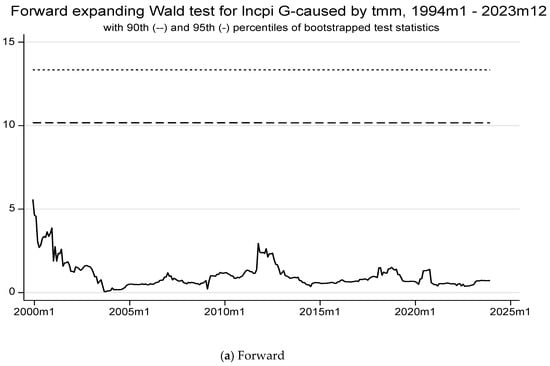
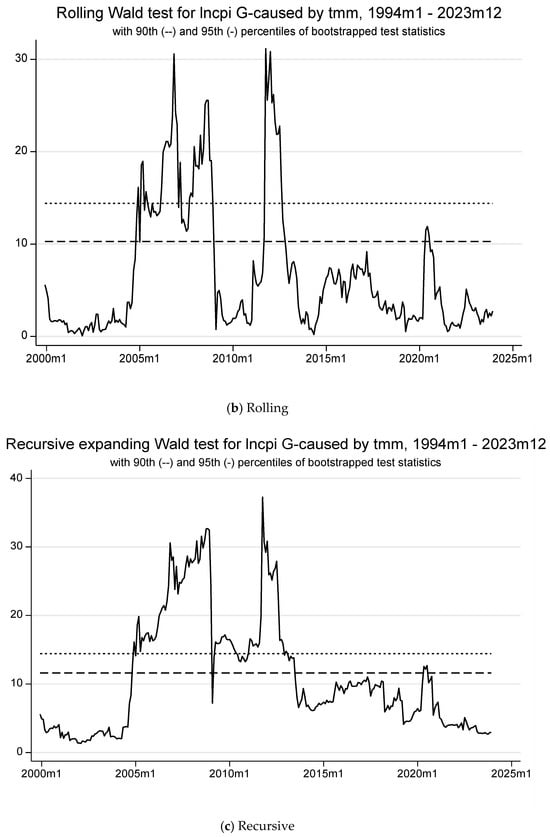
Figure 6.
The forward, rolling, and recursive evolving test results with lag augmentation d = 1 are displayed in panels (a–c) with a minimum window size = 72. The regression model 4 is (LNCPI LNM2TND TMM LNTCER LNGPR_TUN)’, allowing for heteroscedastic errors. The empirical size is 5%, controlled over 1 year and obtained from bootstrapping. Lag orders are assumed to be constant and selected using AIC(=2) with a maximum length of 8 for the whole sample period. LNCPI: Consumer price index (in log). LNM2TND: Monetary Aggregates 2 in TND (in log). TMM: Money market rate. LNTCER: Real effective exchange rate (in log). LNGPR_TUN: Local geopolitical risk (in log).
4.3. Neural Network VAR Nonlinear Causality
Hmamouche (2020) extends Granger testing to account for nonlinear dependencies and implements transfer entropy via the Kraskov approximation. NlinTS provides VARNN models, discrete and continuous entropy measures, and mutual information. It uses two multilayer perceptron networks to assess causality strength through the Granger causality index and F-test, exploring causal relationships in nonlinear systems. A common heuristic is to set two lags for the embedding dimension in the case of simple systems (Hmamouche, 2020). The results in Table 9 indicate that the nonlinear money market rate causes industrial production to be at a 5% level of significance, while we cannot reject the null hypothesis for the relationship that runs from the money market rate to the consumer price index. Overall, the analysis gives a robust and conclusive result of the nonlinear relationship between TMM and LNIPIT, even when there are one, three, four, five, and six hidden layers of the embedding dimension.2

Table 9.
Neural network nonlinear VAR causality.
4.4. Bivariate Wavelet Coherence Analysis
An alternative to nonlinear causality is to focus on the time and frequency domains through the bivariate Wavelet coherence analysis, as developed by Torrence and Compo (1998). This technique is an effective means of investigating the time–frequency relationship between two time series (see Tissaoui et al., 2021; Trabelsi, 2024a). In contrast to conventional time–domain approaches, wavelet coherence enables us to analyze how the connection between the money market rate and industrial production (respectively, the consumer price index) changes over time and frequency. This method relies on the continuous wavelet transform, which breaks down a time series into time–frequency space. The wavelet transform of a time series x1 to a “Wavelet” is defined as
where is the translation parameter related to time, is the scale parameter related to frequency, and denotes the complex conjugate of the wavelet function. The integral in wavelet coherence reflects its continuous nature, ensuring a smooth measure of correlation over time and frequency.
The wavelet coherence is the squared partial correlation coefficient between two time series x1(t) and x2(t), given by this expression
where is a smoothing operator for both time and scale. ranges between 0 and 1. The closer the wavelet coherence coefficient is to 1, the more correlated x1(t) and x2(t) are.
We utilize wavelet coherence analysis to investigate the time–frequency relationship between the money market rate (TMM) and industrial production (LNIPIT). This technique helps us pinpoint periods of strong connection between the two series, indicating that the money market rate may serve as a time-varying predictor. In Figure 7, the wavelet coherence plot shows significant coherence between TMM and LNIPIT, especially at lower frequencies (short- and medium-term cycles) during the periods of 05/2004–05/2011 and 2017–2018. These findings imply that the relationship between TMM and LNIPIT was not only robust, but also stable during these times. However, the coherence is not consistent throughout the entire sample period, suggesting that the strength and nature of the relationship fluctuate over time. Notably, low coherence is seen during times of political turmoil, such as the revolution, the COVID-19 pandemic, and the Russia–Ukraine conflict. This observation aligns with the rolling–recursive window analysis, supporting the notion that TMM has a more pronounced effect on industrial production during periods of reduced geopolitical risk. The wavelet coherence analysis reinforces the results from the rolling and recursive window analyses, providing additional evidence that the relationship between TMM and LNIPIT is both time-dependent and frequency-sensitive. The identified patterns indicate that market participants may respond differently to TMM based on the broader geopolitical landscape and current market sentiment, often becoming more cautious and adopting a “wait and see” strategy until they receive more information. According to the scale, Figure 7 shows that the relationship between money market rates and industrial production is most pronounced at medium- to long-term scales (8–64 months). The phase arrows consistently indicate that changes in the money market rate lead industrial production, reflecting a lagged effect of monetary policy. However, this influence is not evident at short-term scales, where the coherence remains weak. This suggests that monetary policy adjustments require time to affect real economic activity.
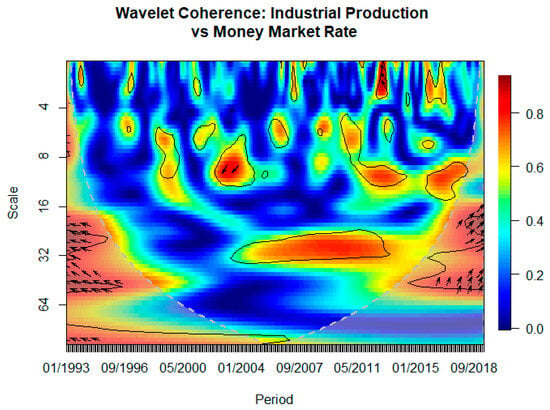
Figure 7.
Wavelet Transform Coherence: money market rate (TMM) versus industrial production (LNIPIT). Notes: The regions where the spectrum is significant against red noise at the 5% level are indicated by the black outline. The cone of influence restricts the autocorrelation of wavelet power at each scale, and is distinguished by the lighter shading that marks regions of high power. Time (from 011993 to 04/2019) and scale ranges (monthly frequency) are represented by the horizontal and vertical axes, respectively. A positive (negative) relationship between the variables is indicated by arrows pointing left (right), which also show that the variables are out of phase. The first variable x1 (TMM) is the driver (or follower), when arrows move to the right and up (or down). Conversely, the variable x2 (LNIPIT) is leading (or lagging) if the arrows move left and up (down).
Similarly, we examine the wavelet analysis of TMM and the consumer price index (LNCPI). A significant relationship between the two series is evident in the early 1990s, mid-2000s, and around 2010. These periods indicate that the connection between the money market rate and the consumer price index was not only robust, but also stable over medium to long durations. Additionally, a strong correlation is noted during times of low geopolitical risk, both globally and locally, further reinforcing the ineffectiveness of the money market rate as a monetary transmission mechanism during periods of increased geopolitical risk (see Figure 8). Examining Figure 8 according to the scale reveals the presence of lagged effects of money market rates on the consumer price index in Tunisia, particularly over medium- to long-term horizons. The high-coherence regions (represented in red and orange) indicate a strong relationship between the two variables, with the most significant connection occurring at time scales ranging from 16 to 32 months. The direction of the phase arrows within these regions provides further insights into the dynamics of this relationship. Specifically, the arrows pointing upwards and slightly to the right suggest that changes in money market rates tend to lead to changes in the consumer price index, implying a lagged influence. This finding aligns with economic theory, as adjustments in monetary policy often take time to affect inflation dynamics and price levels. Overall, the analysis highlights that the impact of money market rates on the consumer price index is not immediate, but unfolds gradually over extended periods.
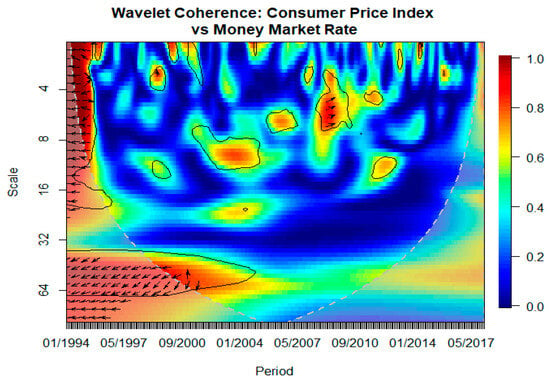
Figure 8.
Wavelet Transform Coherence: money market rate (TMM) versus consumer price index (LNCPI). Notes: The regions where the spectrum is significant against red noise at the 5% level are indicated by the black outline. The cone of influence restricts the autocorrelation of wavelet power at each scale, and is distinguished by the lighter shading that marks regions of high power. Time (from 01/1994 to 05/2017) and scale ranges (monthly frequency) are represented by the horizontal and vertical axes, respectively. A positive (negative) relationship between the variables is indicated by arrows pointing left (right), which also show that the variables are out of phase. The first variable x1 (TMM) is the driver (or follower) when arrows move to the right and up (or down). Conversely, the variable x2 (LNCPI) is leading (or lagging) if the arrows move left and up (down).
4.5. Connection/Disconnection and Effectiveness of Monetary Policy: Results of Interacted LPs
We examine the response of macroeconomic variables to a shock in monetary policy while interacting with global (then local) geopolitical risk. We use the new command “locproj” available in Stata 18. It calculates both linear and non-linear IRFs using the local projections approach initially introduced by Jordà (2005). This method facilitates the straightforward application of various options found in the expanding body of research on local projections. The optimal lag order selection of VAR models used in interacted LPs is available in the Supplementary File (see Tables S6–S9).
Initially, the response hovers around zero, showing no clear trend after the shock, with broad confidence intervals indicating high uncertainty (see Figure 9). From months 2 to 18, responses fluctuate significantly between positive and negative values, suggesting instability in industrial production due to puzzling interactions between monetary policy and global geopolitical risk. By month 20, the response sharply rises, but wide confidence intervals may signal increased risk or substantial impacts. Overall, the erratic response implies that the money market rate may influence industrial production inconsistently, depending on geopolitical risk levels. Preliminary evidence suggests that interest rates may not effectively transmit monetary policy. To draw a conclusive view, we need to compare and quantify the impact of the money market rate on production during low- and high-geopolitical-risk periods.
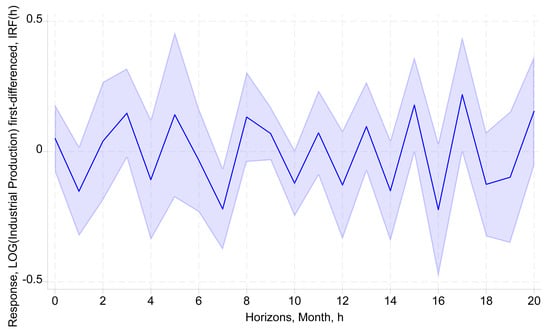
Figure 9.
Response of industrial production (IPITLOGDIFF) to a shock in money market rate (TMMDIFF) and allowing for interaction with the global geopolitical risk (GPRLOGDIFF) based on interacting local projections. Sample: 01/1993–08/2024. Control variables include money supply (M2TNDLOGDIFF) and real effective exchange rate (TCERLOGDIFF). 95% confidence bands are shown.
Figure 10 shows that the response starts with a small, positive deviation that quickly turns slightly negative, indicating minor, short-lived inflationary effects resulting from an initial shock in the money market rate. Between months 10 and 11, the response fluctuates around zero with small amplitudes and wide confidence intervals, suggesting limited effects on consumer prices. After month 18, the response stabilizes near zero, indicating that the effects of monetary shocks on consumer prices are transitory and dissipate over time.
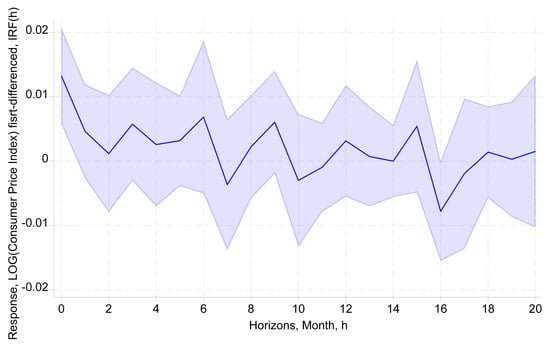
Figure 10.
Response of the consumer price index (CPILOGDIFF) to a shock in money market rate (TMMDIFF) and allowing for the interaction with the global geopolitical risk (GPRLOGDIFF) based on interacted local projections. Sample: 01/1993–08/2024. Control variables include money supply (M2TNDLOGDIFF) and real effective exchange rate (TCERLOGDIFF). The 95% confidence bands are shown.
The brief responses of consumer prices indicate that the interaction between money market rates and geopolitical risk has a minimal, temporary effect on inflation dynamics.
Figure 11 shows that the response starts with a small but positive deviation that quickly turns slightly negative, indicating small effects of the money market rate. The response of industrial production still fluctuates between positive and negative values in the remaining periods (months). The effect converges towards zero in longer horizons. The money market rate seems to exert short and brief effects on production, and does not act effectively as a monetary transmitter mechanism, especially in times of high local geopolitical risk.
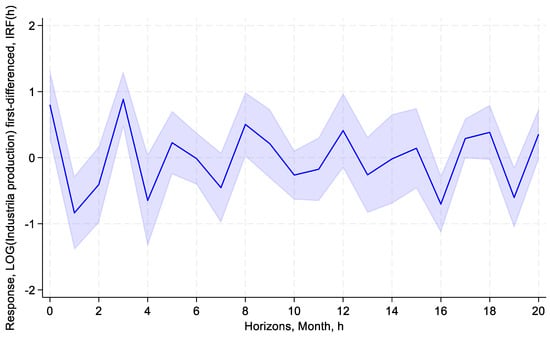
Figure 11.
Response of industrial production (IPITLOGDIFF) to a shock in money market rate (TMMDIFF) and allowing for interaction with the local geopolitical risk (GPR_TUNLOGDIFF) based on interacted local projections. Sample: 01/1993–08/2024. Control variables include money supply (M2TNDLOGDIFF) and real effective exchange rate (TCERLOGDIFF). The 95% confidence bands are shown.
We can infer from Figure 12 that the impact of the money market rate on consumer prices is frequently positive in many periods (months). A shock in the money market rate decreases consumer prices around months 6–8 and in month 17, before restoring its positive effect in longer horizons, underlining the ineffectiveness of the interest rate to counter inflationary prices.
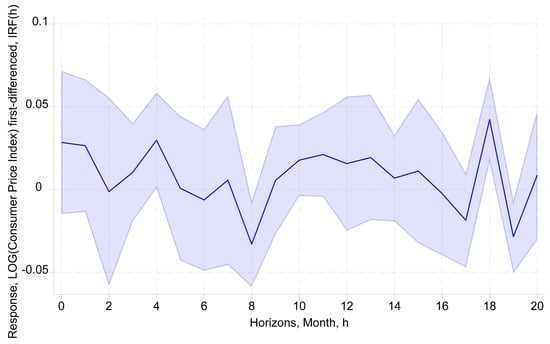
Figure 12.
Response of the consumer price index (CPILOGDIFF) to a shock in money market rate (TMMDIFF) and allowing for interaction with the local geopolitical risk (GPR_TUNLOGDIFF) based on interacting local projections. Sample: 01/1993–08/2024. Control variables include money supply (M2TNDLOGDIFF) and real effective exchange rate (TCERLOGDIFF). The 95% confidence bands are shown.
Overall, the interacted LPs display volatile IRFs, and can be explained by the dynamic and heterogeneous responses of macroeconomic variables to global and local geopolitical risk shocks over time.
In the short term, the responses of industrial production and inflation are relatively muted in Figure 9 and Figure 10. This reflects the economy’s initial rigidity or the lagged effects of global shocks, as it takes time for economic agents to adjust their behaviors or for policy measures to take effect. The stability may also indicate a limited immediate transmission of global and spillover shocks, as domestic factors (e.g., contracts, price stickiness, or existing inventories) buffer the economy against rapid changes.
Over the medium and long term, the responses become more pronounced and variable. This can be attributed to the economy’s gradual adjustment to the shock as expectations, prices, and policies adapt. Volatility could arise as businesses adjust their production levels to shifts in global demand or supply chain disruptions caused by the shock. Changes in global commodity prices, exchange rate pass-through, or heightened uncertainty can lead to volatile inflationary pressures. Central banks might alter interest rates dynamically in response to economic conditions, creating volatility in monetary policy variables. These fluctuations reflect economic uncertainty and the varying effectiveness of policy responses over time. The IRFs of LPs in Figure 11 and Figure 12 suggest that the central bank reacts with a tightening monetary policy that has a temporary desirable impact on production in the short term (around horizon 1) and on inflation over the long term only (around horizon 19). These findings suggest the limited efficiency or ineffectiveness of monetary policy as a transmitting mechanism.
4.6. Effectiveness of Monetary Policy Under Test: Results of the Long-Run Dynamics of VECM
The previous developments emphasize the nonlinear effects of monetary shocks on industrial production and consumer prices. The sensitivity of these results can be assessed to quantify the significance and the magnitude of monetary policy during episodes of low and high geopolitical risk. This is possible via the Vector Error Correction Model (VECM), which accommodates I(1) variables that are cointegrated. VAR lag order selection for VECM is performed, and the related results are available in the Supplementary File (see Tables S10–S19). The Johansen cointegration test results, including trace statistic and maximum eigenvalue, are readable from Tables S20–S29, confirming the use of VECM.
The general form of VECM (p − 1) is given by
We augment Equation (12) to let the money market rate (TMM) interact with global geopolitical risk (LNGPR) and local geopolitical risk (LNGPR-TUN), respectively.
where y is the dependent variable and X is a vector of control variables, encompassing LNM2TND and LNTCER, in addition to the variable of interest TMM and the geopolitical risk measures (LNGPR, LNGPR_TUN); is the coefficient associated to , are the intercept and the long-run coefficients, is the short-run coefficients of the lagged , is a vector of the short-run coefficients of the lagged , is the optimal lag in the VAR model according to AIC, and is a white noise process.
The normalized long-run equation is written as follows:
Thus, the coefficients in the cointegrating equation of the VECM results should be sign-reversed (Johansen, 1995).
4.6.1. VECM with an Interaction Term of the Money Market Rate and Global Geopolitical Risk
Specifications differ according to assumptions about the intercept and data trend. Choices based on the log-likelihood, Akaike, and Schwarz are unreliable because the estimations differ in the numbers of parameters. Our focal point is the sign and the statistical significance of CointEq1 (ECT). Banerjee et al. (1998) said it should be negative and statistically significant. Thus, only models that satisfy this condition are selected. The speed of adjustment of the industrial production (LNIPIT) to its equilibrium is about 11.9% (see Table 10). Taking the first model, we can write the cointegrating equation as follows:

Table 10.
VECM long-run and short-run dynamics. Dependent variable: D(LNIPIT), model 1.
We can arrange it as:
LNIPIT_{t−1} = 0.139080 × LNM2TND_{t−1} − 0.687007 × TMM_{t−1} + 0.166795 × LNTCER_{t−1} −
0.775811 × LNGPR_{t−1} + 0.147131 × TMM_GPR_{t−1} + 5.917379 + CointEq1
0.775811 × LNGPR_{t−1} + 0.147131 × TMM_GPR_{t−1} + 5.917379 + CointEq1
The full VECM equation is given by:
The remaining columns of Table 10 can be inferred in a similar way.
Both the money market rate (D(TMM)) and the real effective exchange rate (D(LNTCER)) have insignificant effects on short-term production. The money supply D(LNM2TND) has an unstable coefficient on D(LNIPT), confirming ineffective monetary targeting through the money supply (End et al., 2020). Turning to the long-run coefficients, we observe further interesting results. Importantly, the coefficient of the interaction term (TMM_GPR) is positive and statistically significant. Under a low global GPR regime (10th percentile), the marginal effect of monetary policy is about a 0.07% decrease in industrial production, while it pertains to a 0.04% increase under a high global GPR regime (90th percentile). The magnitude is small under both regimes, and this suggests that there are some benefits over global geopolitical tensions. This result may be explained by the green energy transition plan of Tunisia in the following years. Tightening monetary policy encourages some firms to invest in renewable energy as an alternative to fossil fuels. However, we should note that this result applies to industrial production at the aggregate level. By establishing a sectoral analysis, we consider manufacturing, mines, and energy sectors. We re-estimate the VECM for the LNIPIT of each sector. We find that production improves in the case of tightening interest rates under a high global GPR regime in the manufacturing sector, while the effect is insignificant for the mines sector, and dampened in the case of the energy sector, consistent with the irreversibility theory. Investors’ confidence diminishes and then delays investment until getting additional information. For the manufacturing sector, tight monetary policy can curb exchange rate volatility by attracting foreign investment or preventing capital flight, reducing the cost of imports for manufacturers, and supporting production. Long-term benefits are rendered with strategies leveraged toward sustainable economic growth (Udeaja et al., 2024). Nevertheless, the impact of TMM is asymmetric, and this suggests that central bank information might be fragmented between economic agents (Trabelsi, 2024b). While some prefer basic information, others prefer detailed information. Some understand the message, while others get confused (Filardo, 2004).
Results related to consumer prices are available in Table 11. Two specifications among the five assumptions about the intercept and data trend meet the condition related to CointEq1. The coefficient is negative and statistically significant at least at the 10% level.

Table 11.
VECM long-run and short-run dynamics. Dependent variable: D(LNCPI), model 2.
Money supply D(LNM2TND) and the real effective exchange rate have no significant impact on D(LNCPI) in the short run. There is a temporary inflationary improvement under high global geopolitical risk when tightening monetary policy, as testified by the negative coefficient of the interaction term and a positive coefficient of D(TMM). Tightening monetary policy (e.g., raising interest rates or reducing money supply) reduces aggregate demand by increasing borrowing costs and discouraging consumption. In the short run, this lower demand helps reduce inflationary pressures. In the long run, higher money supply (LNM2TND) decreases consumer prices (LNCPI). The result contradicts the quantity theory of money (M. Friedman, 1961, 1968, 1970) and suggests the ineffectiveness of monetary targeting (End et al., 2020). The statistical significance of LNTCER is not stable across specifications, highlighting an ambiguous role of the real effective exchange rate (Agénor & Montiel, 2007). For the interaction term (TMM_GPR), the coefficient is negative and statistically significant, in addition to a negative coefficient associated with TMM. Under low global geopolitical risk, increasing the money market rate leads to a decrease by 0.59% in consumer prices against an increase of 0.53% under high global geopolitical risk. High global geopolitical risk tends to increase the volatility of international commodity prices (e.g., energy and food) and disrupt global supply chains. Over time, these fluctuations can negate the initial benefits of monetary tightening, particularly if Tunisia’s monetary policy cannot address supply-side shocks. If fiscal imbalances persist, the inflationary pressures of tightening monetary policy could outweigh its intended stabilizing effects. Meanwhile, higher interest rates might push firms to adopt more efficient production methods or invest in technologies that improve productivity, leading to long-term industrial growth. The paradoxical monetary transmission mechanism signals differences in how economic agents digest messages from the central bank (Filardo, 2004), or even raises doubts about its credibility (Blinder, 2000; Montes & Nicolay, 2017; Reid & Siklos, 2020).
4.6.2. VECM with an Interaction Term of Money Market Rate and Local Geopolitical Risk
We consider the impact of local geopolitical tensions on industrial production (see Table 12). We have selected specifications that satisfy a negative and statistically significant coefficient of CointEq1 (Banerjee et al., 1998). In the short run, aggregate industrial production persists, mirrored by the significant D(LNIPIT) at lags 1 and 2. Money supply (D(LNM2TND)) has a negative and statistically significant impact on aggregate industrial production. Still, it is unstable in terms of sign and statistical significance if we focus on sectoral production. This highlights the ineffectiveness of monetary targeting (End et al., 2020). An increase in money supply can raise inflation expectations, especially in an economy prone to supply-side constraints or external price shocks. Businesses may respond by raising prices rather than increasing production, as higher input costs (e.g., raw materials and wages) limit their ability to scale output. As seen later, the short-term impact of money supply on consumer prices is positive but insignificant (see Table 13). This stems from price stickiness and muted aggregate demand. TMM and the interaction term (TMM_LNGPR_TUN) also have muted impacts on short-run aggregate production. High geopolitical risk may lead to precautionary savings by households and delayed investment decisions by firms. In the long run, the real effective exchange rate (LNTCER) is negatively related to the manufacturing sector only. A depreciation of the Tunisian dinar by 1% leads to an increase in manufacturing production by 0.59%. The same impact is muted at the aggregate level and for the Mines and Energy sectors. Tightening interest rates is detrimental to aggregate production under high local geopolitical risk. There is a weak transmission mechanism of monetary policy. The finding is consistent with the irreversibility theory. However, when disentangling the impact of specific sectors, only investors in the energy sector seem to be inclined to delay investment. Manufacturing and mining firms develop a risk appetite for investing during local turbulences. Tightening interest rates harm the energy sector due to its high reliance on debt, long investment horizons, and vulnerability to financing costs. In contrast, manufacturing and mining benefit in the long run from cost stabilization, improved export competitiveness, and potentially increased efficiency. Differences in firm behavior might signal disparities in how different sectors digest the central bank’s information. Issues related to clarity and credibility are of the utmost importance in the conduct of monetary policy.

Table 12.
VECM long-run and short-run dynamics. Dependent variable: D(LNIPIT), model 3.

Table 13.
VECM long-run and short-run dynamics. Dependent variable: D(LNCPI).
Turning to consumer prices, we have selected the specification with “linear intercept and trend” since it meets the condition of CointEQ1. In the short run, the consumer prices are persistent, as seen from the statistically significant coefficients on D(LNCPI(−1)), D(LNCPI(−2)), D(LNCPI(−3)), and D(LNCPI(−4)), respectively. Money supply and the real effective exchange rate have muted impacts, suggesting their inefficiency as monetary instruments. The interaction of TMM with the local geopolitical risk suggests mixed impacts in terms of sign, magnitude, and statistical significance. Therefore, we move to the long-run estimations to gain more insights. The coefficient of the interaction term (TMM_GPR_TUN) is high and statistically significant at a 1% level. Under a low local GPR regime (10th percentile), the marginal effect of TMM on consumer prices is −0.37% if TMM increases by 1%. This effect is, however, insignificant. Under the high local GPR regime (90th percentile), the marginal effect pertains to 2.889% after tightening the money market rate by 1%. Heightened local geopolitical risk severely weakens the monetary transmission mechanism. Risk-averse businesses and firms delay investment, seeking more detailed information. Geopolitical risks often disrupt production and supply chains, leading to higher production costs (e.g., through rising import costs, energy prices, or security concerns). This cost–push inflation can overshadow the demand-side impact of higher interest rates, causing consumer prices to increase. This aligns with the findings of Table 12.
In conclusion, we have examined the serial correlation of the residuals and found no reason to reject the null hypothesis of no autocorrelation at a 5% level of significance, indicating that the VECM is applicable in all models, except Model 1.4.1 in Table 10 (colored in yellow) (see Tables S30–S39 in the Supplementary File).
4.7. Discussion
The VECM findings suggest a mixture of theories that interacted to contribute to the transmission mechanism of the money market rate. We provide key takeaways below.
4.7.1. Irreversibility Theory
The irreversibility theory suggests that firms delay investment decisions when faced with uncertainty because of the high cost of reversing such investments. However, in the case of tightening interest rates in Tunisia, the following occurs:
- Improvement in aggregate production—Higher interest rates may create a more stable macroeconomic environment by reducing speculative activity and inflationary pressures in the long run. This stability could encourage firms to invest in productive activities despite higher borrowing costs, especially if uncertainty is reduced;
- Increased consumer prices—If firms pass on higher borrowing costs to consumers via higher prices, it reflects rigidity in pricing decisions. This aligns with the irreversibility theory, where firms, once committed to production and pricing strategies, find it difficult to reverse course quickly in response to changing monetary policy.
4.7.2. Credit Channel Theory
The credit channel theory highlights how monetary policy affects the economy through its impact on credit availability and cost. It has two key mechanisms (Mateut, 2005):
- Bank lending channel—Tightening interest rates reduce bank reserves and loanable funds, increasing the cost of borrowing. This might initially constrain investment and production, but over time, firms that survive the credit squeeze become more efficient, leading to long-term improvements in aggregate production;
- Balance sheet channel: Higher interest rates increase the cost of servicing debt, worsening the financial health of borrowers. This could lead firms to pass on these costs to consumers, contributing to higher consumer prices. Additionally, households might reduce consumption due to higher debt burdens, yet this impact seems overshadowed by inflationary dynamics.
4.8. Robustness Check: Investor Sentiment Sensitivity to Monetary Policy Changes
Monetary policy aims to achieve two primary goals: maintaining price stability and fostering sustainable economic growth (Marschner & Ceretta, 2021). These goals can be realized through the influence of monetary policy on financial markets, including stock markets (Kurov, 2010). Furthermore, uncertainty and risk shocks can adversely affect businesses by deterring investment and production, and impact households by decreasing their consumption tendencies. The findings suggest that tracking investor sentiment regarding the market can provide insights into their financial decisions, making it a valuable indicator for predicting the trajectory of the Tunisian economy. For this purpose, we have collected monthly data on investor sentiment (IS1) using different sources. We construct a composite index using Principal Component Analysis (PCA) and the Softmax normalization technique. Data include the volatility of TUNINDEX stock prices derived from an ARMA(1,1)-GARCH(1,1) conditional variance modeling (downloadable from: https://fr.investing.com/indices/tunindex-historical-data (accessed on 24 January 2025)), price–earning ratio (extracted from: https://www.ceicdata.com/en/tunisia/tunis-stock-exchange-price-earnings-ratio/pe-ratio-tse), dividend yield (extracted from: https://www.ceicdata.com/en/tunisia/tunis-stock-exchange-dividend-yield (accessed on 24 January 2025)), market capitalization (extracted from: https://www.ceicdata.com/en/tunisia/tunis-stock-exchange-market-capitalization/market-capitalization-tse), and the variation of the exchange rate (USD/TND) (downloadable from: https://www.bct.gov.tn/bct/siteprod/tableau_statistique.jsp?params=PL213010 (accessed on 24 January 2025)). Due to missing values, our sample boils down to 09/2007–08/2024.
Softmax normalization, or the normalized exponential function, mitigates the influence of outliers while retaining them in the dataset. It preserves important data within one standard deviation of the mean through a nonlinear transformation using a sigmoidal function. The Softmax function normalizes a variable () using exponential function, mean (), and standard deviation (), as follows:
are the variables used to calculate the composite index and observed at time from the set {Volatility of TUNINDEX, Price Earning Ratio, Dividend Yield, Market Capitalization, Exchange Rate}.
The composite index is calculated as follows:
where are the first principal component loadings (from PCA). The Softmax normalization ensures that all variables are transformed into a comparable scale while preserving relative differences. PCA captures the most important common variation in these five variables, and the first three components are used as the composite index because they explain the highest proportion of variance.
Furthermore, the validity of PCA is checked through Kaiser–Meyer–Olkin (KMO = 0.564 > 0.5) and Bartlett’s test of sphericity (Chi-Square = 261.411, p-value = 0.000).
The resulting investor sentiment index IS1 is a time series reflecting the aggregated investor sentiment in Tunisia (see Figure 13). The evolution of IS1 in Tunisia reflects the impact of global and domestic events on market confidence. Sentiment plummeted during the 2007–2009 financial crisis, and showed a gradual recovery from 2010 to 2013, albeit with volatility linked to Tunisia’s political transition. From 2014 to 2018, IS1 displayed moderate stability with intermittent fluctuations, followed by a sharp decline in 2019–2020 due to the COVID-19 pandemic and domestic economic challenges. Sentiment remained historically low from 2021 to 2023, reflecting prolonged pessimism driven by political instability and economic stagnation. However, a notable recovery in 2024 suggests renewed optimism, potentially driven by improving economic conditions and policy interventions.
Figure 13.
Evolution of the composite index of IS1 using PCA and the Softmax normalization technique.
We have checked the unit root tests through PP and ADF, and find that IS1 is integrated in the order of 1 (I(1)) (see Table A3 in Appendix A.2). VAR lag order selection using AIC and the results of the Johansen cointegration test are readable from Tables S40 and S41 in the Supplementary File, justifying the use of VECM again. The validity of VECM passes through the Portmanteau test of serial correlation in residuals (see Table S42 in the Supplementary File).
The results in Table 14 indicate that the coefficient of the error correction term (CointEq1) is negative and statistically significant at 5%, confirming a long-run equilibrium relationship between the variables. The short-run findings indicate a persistence of investor sentiment, captured by the significant one-period lagged D(IS1), while other coefficients are statistically insignificant. In the long run, the impact of the money market rate on investor sentiment is asymmetric according to the geopolitical risk regime. When considering the global geopolitical risk (LNGPR) (model (1)), we find that a 1% increase in TMM increases IS1 by 0.05% (low regime), while it decreases IS1 by 1.18%. The magnitude of the marginal effect under high global geopolitical tensions is ultimately more important, emphasizing that monetary policy shifts investor sentiment during intense geopolitical episodes. Now focusing on model (2) in Table 14, we find that the marginal impact of TMM is about 0.22 units in the low-local-geopolitical-risk regime, compared to −3.85 units in the high regime. Again, changes in investor sentiment are more pronounced during periods of turbulent local weakness. The magnitudes of the marginal effect of TMM (in the absolute value) are higher when we incorporate local geopolitical risk (LNGPR_TUN) into the model. The finding strengthens our previous results about delayed investment following pessimism, and that investment decisions are more sensitive to local weaknesses.

Table 14.
VECM long- and short-run dynamics. Dependent variable: D(IS1).
The findings suggest several policy recommendations. To improve investor sentiment in Tunisia, policymakers should focus on stabilizing financial markets by reducing stock market volatility, enhancing market capitalization, and promoting transparency and corporate governance. Measures to mitigate exchange rate volatility, such as maintaining adequate reserves and offering hedging instruments, are crucial. Strengthening earnings reliability, fostering consistent dividend policies, and supporting diversified investment portfolios can boost market confidence. Monetary policy should align with market dynamics, using interest rate adjustments and forward guidance to reduce uncertainty. Meanwhile, addressing geopolitical risks and enhancing investor protections will further attract local and foreign investment, fostering sustainable economic growth.
5. Concluding Notes
Central banks face risk and uncertainties in formulating monetary policy, particularly regarding its effectiveness during high-uncertainty periods. It is vital to examine the effects of interest rates on other variables under varying economic conditions, especially when geopolitical risk is high or low (Balcilar et al., 2022). Understanding the relationship between interest rates and macroeconomic variables is crucial for assessing the effectiveness of monetary policy. The literature is divided on whether risk diminishes this effectiveness; the irreversible theory suggests it does, while the credit transmission channel theory argues otherwise. In this paper, we provide meaningful insights into Tunisia’s transmission mechanism of the money market rate by applying a battery of advanced econometric techniques. The time-varying Granger causality reveals significant phases of connection and disconnection, highlighting the improper functioning of the interest rate, which is used as a primary tool of monetary policy by CBT. The Wavelet coherence analysis further proves the lagged effects of the money market rate. Both global and local geopolitical risks perturbed the effectiveness of monetary policy. The results reveal significant implications for the effectiveness of the money market rate as an economic policy instrument, particularly in the context of irreversibility theory and precautionary behavior. The observed oscillating and delayed responses for industrial production in LPs highlight a volatile and state-dependent relationship. This suggests that under heightened uncertainty, such as geopolitical risk, firms are hesitant to adjust production or make new investments. This aligns with irreversibility theory, which argues that firms adopt a cautious approach when faced with uncertainty, limiting the responsiveness of industrial production to monetary policy changes. The precautionary behavior is evident here, as firms delay decisions in a “wait-and-see” manner, further reducing the effectiveness of the money market rate as a tool to influence production dynamics. Consequently, monetary policy alone may not be sufficient to stimulate or constrain industrial activity during uncertain periods, necessitating complementary measures such as targeted fiscal interventions or risk-reduction strategies.
For consumer prices, the response to monetary shocks is weak and short-lived, indicating a limited pass-through effect of the money market rate on inflation. This could be attributed to price stickiness, weak demand-side pressures, or supply-side dominance under conditions of geopolitical uncertainty. The precautionary behavior of firms and consumers may also contribute to this muted response, as pricing adjustments are likely conservative during uncertain times. These findings suggest that monetary policy relying on the money market rate may struggle to anchor inflation expectations effectively, particularly during periods of heightened risk. Alternative tools, such as exchange rate policies or direct market interventions, may be required to achieve desired inflation outcomes.
The findings of VECM highlight the nonlinear nature of monetary policy effectiveness. The interaction with both global and local geopolitical risk emphasizes the asymmetric impact of monetary shocks, with the money market rate appearing less effective in stimulating production or controlling inflation during high-local risk periods. This limitation reinforces the need for policymakers to adopt adaptive and flexible frameworks that account for the broader macroeconomic environment. To strengthen these results, we have constructed a novel composite index of Tunisian investor sentiment through PCA. We find that tightening interest rates deteriorates investor sentiment sharply during heightened periods of risk, with a more pronounced impact under high levels of local geopolitical risk. Contractionary monetary policy increases pessimism and fear among firms, discouraging them from investing.
We have evidence, however, of an effective monetary policy transmission on aggregate industrial production during periods of high global geopolitical risk. Examining industrial production at the sectoral level yields further insights into the puzzling relationship with the money market rate. We find that global geopolitical risk benefits the manufacturing and energy sectors, while local geopolitical risk is an opportunity for the manufacturing and mining sectors. Global geopolitical risk creates opportunities for Tunisia’s manufacturing and energy sectors by encouraging diversification and investments in resilience. Conversely, local geopolitical risk poses a dual challenge; while it can drive growth in the manufacturing and mining sectors over the long term, it threatens the energy sector due to its direct dependence on political stability and foreign investment. To address these challenges, policymakers should prioritize reducing geopolitical and macroeconomic uncertainty, which could enhance the responsiveness of industrial production and consumer prices to monetary policy. Diversifying policy tools is also essential, as relying solely on the money market rate may not suffice under uncertain conditions. Combining interest rate adjustments with fiscal policies, exchange rate interventions, or sector-specific support could improve policy outcomes. Moreover, incorporating models that explicitly account for nonlinearities and state dependencies in the transmission of monetary policy can aid in more effective decision-making. In sum, while the money market rate remains an important tool, its effectiveness is constrained in uncertain environments, necessitating a broader, more flexible approach to economic policy. Taken together, the findings indicate that the long-run positive effects of tighter monetary policy on productivity outweigh the short-term costs of credit tightening. This aligns with the credit channel theory, but highlights a potentially unique aspect whereby long-term investment benefits emerge despite the short-term credit constraints. However, the irreversibility theory suggests that higher consumer prices may persist because firms adjust prices slowly due to high switching costs or other rigidities.
We want to emphasize that our results should be interpreted carefully due to the sample size and the statistical methods employed. VECM focuses on capturing long-run relationships and adjustments in systems where cointegration exists, making them ideal for analyzing structural and equilibrium dynamics. In contrast, LPs are more flexible, modeling short- to medium-term dynamics, including nonlinear and state-dependent effects, without requiring cointegration. While VECM explicitly targets long-run equilibrium and involves a more complex setup, LPs are simpler to implement and better suited for transient, state-dependent shocks (see Table 15). However, they open up numerous research opportunities concerning the short- and long-term impacts of monetary policy on output and inflation during various phases of risk and uncertainty. Our goal is to unravel the dynamics of monetary policy transmission by distinguishing between inflationary and deflationary channels, offering a more profound and insightful understanding of the underlying mechanisms at play. In the meantime, there is a need to go deeply into the drivers of investor sentiment. Changes in monetary policy exhibit excess optimism or pessimism for firms. It is of the utmost importance to see how the CBT contemplates conventional and unconventional monetary policy, such as quantitative easing (Lutz, 2015). When central banks adopt unconventional monetary policy tools or forward guidance, clear communication about their expected mechanisms, implementation, and reaction functions is crucial. Due to the innovative nature of these tools, their outcomes and interactions with traditional instruments remain somewhat uncertain. As such, transparency is essential to foster a shared understanding among observers, align expectations, and enhance predictability. The central bank’s reaction functions link policy actions to economic conditions, making communication inherently state-dependent. State-contingent forward guidance allows economic agents to adjust expectations dynamically in response to new developments, reducing the need for frequent policy updates (Coenen et al., 2017).

Table 15.
VECM versus LPs.
Our paper suggests several policy recommendations for execution. To effectively address inflationary pressures, sustain economic growth, and enhance the efficacy of monetary policy in Tunisia, authorities must implement a comprehensive strategy. Strengthening forward guidance through more transparent communication regarding interest rates and inflation targets can help stabilize market expectations. Proactive liquidity management, which includes the careful adjustment of open market operations and reserve requirements, is crucial to prevent excess liquidity from exacerbating inflation. Furthermore, closer coordination between monetary and fiscal policies is essential to avoid contradictory measures, ensuring that fiscal policies do not undermine monetary tightening while still supporting targeted social expenditures. Additionally, bolstering financial stability through more stringent credit controls and risk-based capital requirements will ensure that credit expansion is directed toward productive investments. A more flexible exchange rate framework would facilitate the absorption of external shocks and reduce the necessity for frequent foreign exchange interventions. Lastly, advancing structural reforms aimed at enhancing market efficiency, formalizing economic activities, and encouraging investment in high-productivity sectors will improve monetary policy transmission and bolster long-term economic resilience. By adopting these measures, Tunisia can stabilize inflation expectations and promote sustainable economic growth. To tackle these challenges, policymakers must prevent inflationary pressures driven by a price–wage spiral. Achieving this goal requires complementary macroeconomic stabilization policies and structural reforms that support long-term growth. Ensuring the central bank’s independence will be crucial for maintaining price and economic stability. Future research should delve deeper into this area to uncover valuable insights and expand our understanding.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/economies13070185/s1, Table S1: Zivot Andrews unit root test; Table S2: VAR lag order selection criteria for Model 1 (Dependent variable: LNIPIT); Table S3: VAR lag order selection criteria for Model 2 (Dependent variable: LNCPI); Table S4: VAR lag order selection criteria for Model 3 (Dependent variable: LNIPIT); Table S5: VAR lag order selection criteria for Model 4 (Dependent variable: LNCPI); Table S6: VAR lag order selection criteria for Model 1 (Dependent variable; LNIPIT); Table S7: VAR lag order selection criteria for Model 2 (Dependent variable; LNCPI); Table S8: VAR lag order selection criteria for Model 3 (Dependent variable; LNIPIT); Table S9: VAR lag order selection criteria for Model 4 (Dependent variable; LNCPI); Table S10: VAR lag order selection criteria for Model 1.1 (Dependent variable: LNIPIT); Table S11: VAR lag order selection criteria for Model 1.2 (Dependent variable: LNIPIT_MAN); Table S12: VAR lag order selection criteria for Model 1.3 (Dependent variable: LNIPIT_MINES); Table S13: VAR lag order selection criteria for Model 1.4 (Dependent variable: LNIPIT_ENERGY); Table S14: VAR lag order selection criteria for Model 2 (Dependent variable: LNCPI); Table S15: VAR lag order selection for Model 3.1 (Dependent variable: LNIPIT); Table S16: VAR lag order selection for Model 3.2 (Dependent variable: LNIPIT_MAN); Table S17: VAR lag order selection for Model 3.3 (Dependent variable: LNIPIT_MINES); Table S18: VAR lag order selection for Model 3.4 (Dependent variable: LNIPIT_ENERGY); Table S19: VAR lag order selection for Model 4 (Dependent variable: LNCPI); Table S20: Trace and Maximum Eigenvalue tests for Model 1.1 (Dependent variable: LNIPIT); Table S21: Trace and Maximum Eigenvalue tests for Model 1.2 (Dependent variable: LNIPIT_MAN); Table S22: Trace and Maximum Eigenvalue tests for Model 1.3 (Dependent variable: LNIPIT_MINES); Table S23: Trace and Maximum Eigenvalue tests for Model 1.4 (Dependent variable: LNIPIT_ENERGY); Table S24: Trace and Maximum Eigenvalue tests for Model 2 (Dependent variable: LNCPI); Table S25: Trace and Maximum Eigenvalue tests for Model 3.1 (Dependent variable: LNIPIT); Table S26: Trace and Maximum Eigenvalue tests for Model 3.2 (Dependent variable: LNIPIT_MAN); Table S27: Trace and Maximum Eigenvalue tests for Model 3.3 (Dependent variable: LNIPIT_MINES); Table S28: Trace and Maximum Eigenvalue tests for Model 3.4 (Dependent variable: LNIPIT_ENERGY); Table S29: Trace and Maximum Eigenvalue tests for Model 4 (Dependent variable: LNCPI): Table S30: Serial correlation of residuals in Model 1.1 (Dependent variable: LNIPIT); Table S31: Serial correlation of residuals in Model 1.2 (Dependent variable: LNIPIT_MAN); Table S32: Serial correlation of residuals in Model 1.3 (Dependent variable: LNIPIT_MINES); Table S33: Serial correlation of residuals in Model 1.4 (Dependent variable: LNIPIT_ENERGY); Table S34: Serial correlation of residuals in Model 2 (Dependent variable: LNCPI); Table S35: Serial correlation of residuals in Model 3.1 (Dependent variable: LNIPIT); Table S36: Serial correlation of residuals in Model 3.2 (Dependent variable: LNIPIT_MAN); Table S37: Serial correlation of residuals in Model 3.3 (Dependent variable: LNIPIT_MINES); Table S38: Serial correlation of residuals in in Model 3.4 (Dependent variable: LNIPIT_ENERGY); Table S39: Serial correlation of residuals in Model 4 (Dependent variable: LNCPI); Table S40: VAR lag order selection criteria for investor sentiment models; Table S41: Johansen cointegration test for investor sentiment models; Table S42: Serial correlation test of residuals for investor sentiment models.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available upon request from the author.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ADF | Augmented Dickey–Fuller |
| AIC | Akaike Information Criterion |
| CBT | Central Bank of Tunisia |
| CE | Cointegrating Equation |
| COVID | Coronavirus Infectious Disease |
| CPILOGDIFF | Consumer Price Index in First-Difference Logarithm |
| DSGE | Dynamic Stochastic General Equilibrium |
| ECT | Error Correction Term |
| FE | Forward Expanding Window |
| GPR_TUNLOGDIFF | Local Geopolitical Risk in first-difference Logarithm |
| GPRLOGDIFF | Global Geopolitical Risk in first-difference Logarithm |
| IFS | International Financial Statistics |
| IPILOGDIFF | Industrial Production in first-difference logarithm |
| IRFs | Impulse Response Functions |
| IS1 | Investor Sentiment |
| LA VAR | Lag Augmented Vector Autoregressive |
| LNCPI | Consumer Price Index in Logarithm |
| LNGPR | Global Geopolitical Risk in Logarithm |
| LNGPR_TUN | Local Geopolitical Risk in Logarithm |
| LNIPIT | Industrial Production in Logarithm |
| LNM2TND | Monetary Aggregate 2 in Logarithm |
| LNTCER | Real Effective Exchange Rate in Logarithm |
| LPs | Local Projections |
| M2TNDLOGDIFF | Monetary Aggregate 2 in First-Difference Logarithm |
| MAN | Manufacturing |
| NIS | National Institute of Statistics |
| PCA | Principal Component Analysis |
| PP | Phillips–Perron |
| RE | Recursive Evolving Window |
| RO | Rolling Window |
| SC | Schwarz Criterion |
| TCERLOGDIFF | Real Effective Exchange Rate in first-difference Logarithm |
| TMM | Money Market Rate |
| TMMDIFF | Money Market Rate in first difference |
| TND | Tunisian Dinar |
| US | United States |
| USD | United States Dollar |
| VAR | Vector Autoregressive |
| VECM | Vector Error Correction Model |
Appendix A
Appendix A.1
We present the results of PP and ADF tests for all variables by taking into account non-missing values. The sample boils down to 1994/01–2019/04.

Table A1.
PP and ADF unit root test results with a non-missing values subsample.
Table A1.
PP and ADF unit root test results with a non-missing values subsample.
| UNIT ROOT TEST TABLE (PP) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Null Hypothesis: the variable is nonstationary | ||||||||
| At Level | ||||||||
| LNIPIT | LNCPI | LNM2TND | TMM | LNTCER | LNGPR | LNGPR_TUN | ||
| With Constant | t-Statistic | −3.9169 | 3.0317 | −1.2611 | −1.7358 | 1.5059 | −5.6212 | −7.8735 |
| Prob. | 0.0022 | 1.0000 | 0.6483 | 0.4122 | 0.9993 | 0.0000 | 0.0000 | |
| *** | no | no | no | no | *** | *** | ||
| With Constant and Trend | t-Statistic | −6.7627 | 1.6769 | −0.9652 | 0.4786 | −1.9803 | −5.7019 | −8.1825 |
| Prob. | 0.0000 | 1.0000 | 0.9458 | 0.9992 | 0.6093 | 0.0000 | 0.0000 | |
| *** | no | no | no | no | *** | *** | ||
| Without Constant and Trend | t-Statistic | 1.0094 | 16.8441 | 13.2768 | −0.6814 | −2.7989 | −0.1701 | −6.4268 |
| Prob. | 0.9177 | 1.0000 | 1.0000 | 0.4213 | 0.0052 | 0.6241 | 0.0000 | |
| no | no | no | no | *** | no | *** | ||
| At First Difference | ||||||||
| d(LNIPIT) | d(LNCPI) | d(LNM2TND) | d(TMM) | d(LNTCER) | d(LNGPR) | d(LNGPR_TUN) | ||
| With Constant | t-Statistic | −56.1953 | −13.4437 | −21.1482 | −13.8814 | −15.5335 | −31.7360 | −41.4198 |
| Prob. | 0.0001 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0001 | |
| *** | *** | *** | *** | *** | *** | *** | ||
| With Constant and Trend | t-Statistic | −83.9170 | −13.6979 | −20.8271 | −14.1820 | −15.6408 | −31.6253 | −41.2756 |
| Prob. | 0.0001 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0001 | |
| *** | *** | *** | *** | *** | *** | *** | ||
| Without Constant and Trend | t-Statistic | −49.3566 | −8.2853 | −18.0517 | −13.9004 | −15.1685 | −31.8156 | −41.5243 |
| Prob. | 0.0001 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0001 | |
| *** | *** | *** | *** | *** | *** | *** | ||
| UNITROOTTESTTABLE (ADF) | ||||||||
| Null Hypothesis: the variable is stationary | ||||||||
| At Level | ||||||||
| LNIPIT | LNCPI | LNM2TND | TMM | LNTCER | LNGPR | LNGPR_TUN | ||
| With Constant | t-Statistic | −2.8165 | 2.6154 | −1.4502 | −1.3709 | 1.4832 | −5.9467 | −4.4626 |
| Prob. | 0.0571 | 1.0000 | 0.5575 | 0.5967 | 0.9993 | 0.0000 | 0.0003 | |
| * | no | no | no | no | *** | *** | ||
| With Constant and Trend | t-Statistic | −0.4333 | 1.3959 | −1.6424 | 0.5761 | −1.8407 | −6.0146 | −7.8762 |
| Prob. | 0.9860 | 1.0000 | 0.7738 | 0.9995 | 0.6825 | 0.0000 | 0.0000 | |
| no | no | no | no | no | *** | *** | ||
| Without Constant and Trend | t-Statistic | 2.0226 | 10.1470 | 2.4372 | −0.4301 | −3.0322 | −0.2960 | −3.1723 |
| Prob. | 0.9900 | 1.0000 | 0.9966 | 0.5273 | 0.0025 | 0.5786 | 0.0016 | |
| no | no | no | no | *** | no | *** | ||
| At First Difference | ||||||||
| d(LNIPIT) | d(LNCPI) | d(LNM2TND) | d(TMM) | d(LNTCER) | d(LNGPR) | d(LNGPR_TUN) | ||
| With Constant | t-Statistic | −7.1762 | −13.3547 | −2.9650 | −10.7848 | −15.5572 | −17.0047 | −13.3922 |
| Prob. | 0.0000 | 0.0000 | 0.0395 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| *** | *** | ** | *** | *** | *** | *** | ||
| With Constant and Trend | t-Statistic | −7.8624 | −13.6912 | −3.2194 | −11.1417 | −15.7319 | −16.9768 | −13.3699 |
| Prob. | 0.0000 | 0.0000 | 0.0827 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| *** | *** | * | *** | *** | *** | *** | ||
| Without Constant and Trend | t-Statistic | −6.8185 | −0.6343 | −1.0028 | −10.8174 | −15.1615 | −17.0330 | −13.4153 |
| Prob. | 0.0000 | 0.4420 | 0.2833 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| *** | no | no | *** | *** | *** | *** | ||
Notes: (*) significant at 10%; (**) significant at 5%; (***) significant at 1% and (no) not significant.

Table A2.
KPSS unit root test results with non-missing values subsample.
Table A2.
KPSS unit root test results with non-missing values subsample.
| UNIT ROOT TEST RESULTS TABLE (KPSS) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Null Hypothesis: the variable is stationary | ||||||||
| At Level | ||||||||
| LNIPIT | LNCPI | LNM2TND | TMM | LNTCER | LNGPR | LNGPR_TUN | ||
| With Constant | t-Statistic | 1.6823 | 2.1075 | 2.1255 | 1.2531 | 2.0436 | 0.2273 | 0.4129 |
| Prob. | *** | *** | *** | *** | *** | no | * | |
| With Constant and Trend | t-Statistic | 0.4601 | 0.4614 | 0.3400 | 0.3817 | 0.1816 | 0.1393 | 0.0729 |
| Prob. | *** | *** | *** | *** | ** | * | no | |
| Without Constant and Trend | t-Statistic | ======= | ======= | ======= | ======= | ======= | ======= | ======= |
| Prob. | ||||||||
| At First Difference | ||||||||
| d(LNIPIT) | d(LNCPI) | d(LNM2TND) | d(TMM) | d(LNTCER) | d(LNGPR) | d(LNGPR_TUN) | ||
| With Constant | t-Statistic | 0.3219 | 0.9203 | 0.2445 | 0.6290 | 0.3615 | 0.0751 | 0.1042 |
| Prob. | no | *** | no | ** | * | no | no | |
| With Constant and Trend | t-Statistic | 0.0654 | 0.4173 | 0.0944 | 0.0859 | 0.0741 | 0.0638 | 0.1006 |
| Prob. | no | *** | no | no | no | no | no | |
| Without Constant and Trend | t-Statistic | ======= | ======= | ======= | ======= | ======= | ======= | ======= |
| Prob. | ||||||||
Notes: a: (*) significant at 10%; (**) significant at 5%; (***) significant at 1% and (no) not significant. b: Lag Length based on SIC. c: Probability based on Kwiatkowski et al. (1992).
Appendix A.2
We present the results of PP and ADF tests for IS1 in level and first difference.

Table A3.
Unit root test results of IS1.
Table A3.
Unit root test results of IS1.
| UNIT ROOT TEST TABLE (PP) | ||
|---|---|---|
| At Level | ||
| IS1 | ||
| With Constant | t-Statistic | −1.4953 |
| Prob. | 0.5342 | |
| no | ||
| With Constant and Trend | t-Statistic | −3.3420 |
| Prob. | 0.0625 | |
| * | ||
| Without Constant and Trend | t-Statistic | −1.5060 |
| Prob. | 0.1235 | |
| no | ||
| At First Difference | ||
| d(IS1) | ||
| With Constant | t-Statistic | −16.1866 |
| Prob. | 0.0000 | |
| *** | ||
| With Constant and Trend | t-Statistic | −16.2158 |
| Prob. | 0.0000 | |
| *** | ||
| Without Constant and Trend | t-Statistic | −16.2182 |
| Prob. | 0.0000 | |
| *** | ||
| UNIT ROOT TEST TABLE (ADF) | ||
| At Level | ||
| IS1 | ||
| With Constant | t-Statistic | −1.6809 |
| Prob. | 0.4394 | |
| no | ||
| With Constant and Trend | t-Statistic | −3.4282 |
| Prob. | 0.0505 | |
| * | ||
| Without Constant and Trend | t-Statistic | −1.6896 |
| Prob. | 0.0862 | |
| * | ||
| At First Difference | ||
| d(IS1) | ||
| With Constant | t-Statistic | −16.1804 |
| Prob. | 0.0000 | |
| *** | ||
| With Constant and Trend | t-Statistic | −16.2158 |
| Prob. | 0.0000 | |
| *** | ||
| Without Constant and Trend | t-Statistic | −16.2123 |
| Prob. | 0.0000 | |
| *** | ||
Notes: (*) significant at 10%; (**) significant at 5%; (***) significant at 1% and (no) not significant.
Notes
| 1 | For further details on how GPR is derived, we refer readers to Caldara and Iacoviello (2022). |
| 2 | Trying an optimizer like the False Nearest Neighbor is not appropriate because the series are not sufficiently long. |
References
- Agénor, P. R., & Montiel, P. (2007). Credit market imperfections and the monetary transmission mechanism part II: Flexible exchange rates. Centre for Growth and Business Cycle Research, Economic Studies, University of Manchester. [Google Scholar]
- Agoraki, M. E. K., Kouretas, G. P., & Laopodis, N. T. (2022). Geopolitical risks, uncertainty, and stock market performance. Economic and Political Studies, 10(3), 253–265. [Google Scholar] [CrossRef]
- Alpanda, S., Granziera, E., & Zubairy, S. (2021). State dependence of monetary policy across business, credit and interest rate cycles. European Economic Review, 140, 103936. [Google Scholar] [CrossRef]
- Andersson, M., Dillén, H., & Sellin, P. (2006). Monetary policy signaling and movements in the term structure of interest rates. Journal of Monetary Economics, 53(8), 1815–1855. [Google Scholar] [CrossRef]
- Ante, L., & Saggu, A. (2024). Time-varying bidirectional causal relationships between transaction fees and economic activity of subsystems utilizing the ethereum blockchain network. Journal of Risk and Financial Management, 17(1), 19. [Google Scholar] [CrossRef]
- Arellano, C., Bai, Y., & Kehoe, P. (2010). Financial markets and fluctuations in uncertainty. Working Paper, No. 896. Federal Reserve Bank of Minneapolis. [Google Scholar]
- Arieff, A. (2018). Tunisia: In brief. Current Politics & Economics of Africa, 11(4), 287. [Google Scholar]
- Arieff, A., & Humud, C. E. (2011). Political transition in Tunisia (Vol. 15). Congressional Research Service. [Google Scholar]
- Arieff, A., & Humud, C. E. (2014). Political transition in Tunisia. CRS Report, RS21666. CRS. [Google Scholar]
- Arora, V., & Shi, S. (2016). Energy consumption and economic growth in the United States. Applied Economics, 48(39), 3763–3773. [Google Scholar] [CrossRef]
- Balcilar, M., Ozdemir, Z. A., Ozdemir, H., Aygun, G., & Wohar, M. E. (2022). Effectiveness of monetary policy under the high and low economic uncertainty states: Evidence from the major Asian economies. Empirical Economics, 63(4), 1741–1769. [Google Scholar] [CrossRef]
- Banerjee, A., Dolado, J., & Mestre, R. (1998). Error-correction mechanism tests for cointegration in a single-equation framework. Journal of Time Series Analysis, 19(3), 267–283. [Google Scholar] [CrossRef]
- Barnichon, R., & Matthes, C. (2018). Functional approximation of impulse responses. Journal of Monetary Economics, 99, 41–55. [Google Scholar] [CrossRef]
- Belhoula, M. M. (2024). Economic Policy Uncertainty (EPU) in emerging countries: The case of Tunisia. Journal of Accounting and Finance in Emerging Economies, 10(2), 127–138. [Google Scholar] [CrossRef]
- Ben Youssef, A. (2024). Accelerating the progress of Tunisia towards the sustainable development goals. Working Paper, PRR 53. ERF. [Google Scholar]
- Bernanke, B. (1999). The financial accelerator in a quantitative business cycle framework. In Handbook of macroeconomics. Elsevier. [Google Scholar]
- Bernanke, B. S. (1983). Irreversibility, uncertainty, and cyclical investment. The Quarterly Journal Of Economics, 98(1), 85–106. [Google Scholar] [CrossRef]
- Bernanke, B. S., & Gertler, M. (1995). Inside the black box: The credit channel of monetary policy transmission. Journal of Economic Perspectives, 9(4), 27–48. [Google Scholar] [CrossRef]
- Blinder, A. S. (2000). Central-bank credibility: Why do we care? how do we build it? American Economic Review, 90(5), 1421–1431. [Google Scholar] [CrossRef]
- Blinder, A. S. (2009). Talking about monetary policy: The virtues (and vice?) of central bank communication. BIS Working Paper, No. 274. Bank for International Settlements. [Google Scholar]
- Blinder, A. S., Ehrmann, M., Fratzscher, M., De Haan, J., & Jansen, D. J. (2008). Central bank communication and monetary policy: A survey of theory and evidence. Journal of Economic Literature, 46(4), 910–945. [Google Scholar] [CrossRef]
- Bloom, N. (2009). The impact of uncertainty shocks. Econometrica, 77(3), 623–685. [Google Scholar]
- Bloom, N. (2014). Fluctuations in uncertainty. Journal of economic Perspectives, 28(2), 153–176. [Google Scholar] [CrossRef]
- Bondarenko, Y., Lewis, V., Rottner, M., & Schüler, Y. (2024). Geopolitical risk perceptions. Journal of International Economics, 152, 104005. [Google Scholar] [CrossRef]
- Brignone, D., Gambetti, L., & Ricci, M. (2024). Geopolitical risk shocks: When the size matters. Working Paper n°2024/2972. ECB. [Google Scholar]
- Brunnermeier, M. K., & Sannikov, Y. (2014). Monetary analysis: Price and financial stability. Navigating Monetary Policy in the New Normal, 8, 61. [Google Scholar]
- Bruns, M., & Piffer, M. (2023). A new posterior sampler for Bayesian structural vector autoregressive models. Quantitative Economics, 14(4), 1221–1250. [Google Scholar] [CrossRef]
- Caldara, D., Ferrante, F., Iacoviello, M., Prestipino, A., & Queralto, A. (2024). The international spillovers of synchronous monetary tightening. Journal of Monetary Economics, 141, 127–152. [Google Scholar] [CrossRef]
- Caldara, D., & Iacoviello, M. (2022). Measuring geopolitical risk. American Economic Review, 112(4), 1194–1225. [Google Scholar] [CrossRef]
- Cepni, O., Dogru, T., & Ozdemir, O. (2023). The contagion effect of COVID-19-induced uncertainty on US tourism sector: Evidence from time-varying granger causality test. Tourism Economics, 29(4), 906–928. [Google Scholar] [CrossRef]
- Choi, S. Y., & Hadad, E. (2025). The dynamic relationship among economic and monetary policy, geopolitical risk, sentiment, and risk aversion: A TVP-VAR approach. Finance Research Letters, 72, 106532. [Google Scholar] [CrossRef]
- Christiano, L. J., Motto, R., & Rostagno, M. (2014). Risk shocks. American Economic Review, 104(1), 27–65. [Google Scholar] [CrossRef]
- Ciccarelli, M., & Mojon, B. (2010). Global inflation. The Review of Economics and Statistics, 92(3), 524–535. [Google Scholar] [CrossRef]
- Coenen, G., Ehrmann, M., Gaballo, G., Hoffmann, P., Nakov, A., Nardelli, S., Persson, E., & Strasser, G. (2017). Communication of monetary policy in unconventional times. Working Paper, WP No. 578. CFS. [Google Scholar]
- Cutcu, I., Altiner, A., & Bozkurt, E. (2025). The impact of economic policy uncertainty and geopolitical risk on environmental quality: An analysis of the environmental kuznets curve hypothesis with the novel QRPD approach. Sustainability, 17(1), 269. [Google Scholar] [CrossRef]
- Dang, B. K., Anh, H. N., & Pham, T. V. T. (2025). The Impact of policy uncertainty and economic freedom on bank stability: Global evidence. Journal of International Commerce, Economics and Policy, 2025, 2550005. [Google Scholar] [CrossRef]
- De Haan, J., & Sturm, J. E. (2019). Central bank communication. In The Oxford handbook of the economics of central banking (p. 231). Oxford University Press. [Google Scholar]
- Dickey, D. A., & Fuller, W. A. (1979). Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association, 74(366a), 427–431. [Google Scholar]
- Elliott, G., Rothenberg, T. J., & Stock, J. H. (1996). Efficient tests for an autoregressive unit root. Econometrica, 64, 813–836. [Google Scholar] [CrossRef]
- End, N., El Hamiani Khatat, M., & Kolsi, R. (2020). Tunisia monetary policy since the arab spring: The fall of the exchange rate anchor and rise of inflation targeting. Working Paper, No. 2020/167. IMF. [Google Scholar]
- Filardo, A. J. (2004). Monetary policy and asset price bubbles: Calibrating the monetary policy trade-offs. BIS Working Paper, No. 155. BIS. [Google Scholar]
- Forbes, K. J., Hjortsoe, I., & Nenova, T. (2017). Current account deficits during heightened risk: Menacing or mitigating? The Economic Journal, 127(601), 571–623. [Google Scholar] [CrossRef]
- Forbes, K. J., & Warnock, F. E. (2012). Capital flow waves: Surges, stops, flight, and retrenchment. Journal of International Economics, 88(2), 235–251. [Google Scholar] [CrossRef]
- Franconi, A. (2024). Central banking in times of high geopolitical risk. SSRN, 4728914. DNB.
- Friedman, M. (1961). The lag in effect of monetary policy. Journal of Political Economy, 69(5), 447–466. [Google Scholar] [CrossRef]
- Friedman, M. (1968). Money: Quantity theory. In D. L. Sills (Ed.), International encyclopedia of the social sciences. Macmillan Free Press. [Google Scholar]
- Friedman, M. (1970). A theoretical framework for monetary analysis. Journal of Political Economy, 78(2), 193–238. [Google Scholar] [CrossRef]
- Friedman, S. J., & Sharkey, H. (2010). A tale of two economic developments: Tunisia and Morocco. College Undergraduate Research Electronic Journal, 2010, 1–69. [Google Scholar]
- Ghali, S., & Mohnen, P. (2004, May 25–27). The Tunisian path to development: 1961–2001. World bank global conference on reducing poverty, sustaining growth: What works, what doesn’t, and why, Shanghai, China. [Google Scholar]
- Ginn, W. (2023a). Global dimensions of economic uncertainty: Evidence via global VECM. Preprint (Version 1). Available online: https://www.researchsquare.com/article/rs-3203983/v1 (accessed on 24 January 2025).
- Ginn, W. (2023b). The impact of economic policy uncertainty on stock prices. Economics Letters, 233, 111432. [Google Scholar] [CrossRef]
- Ginn, W. (2023c). World output and commodity price cycles. International Economic Journal, 37(4), 530–554. [Google Scholar] [CrossRef]
- Ginn, W., & Saadaoui, J. (2024). Monetary policy reaction to geopolitical risks: Some nonlinear evidence. Working Papers 2024.03. International Network for Economic Research—INFER. [Google Scholar]
- Gopinath, G. (2015). The international price system. No. w21646. National Bureau of Economic Research. [Google Scholar]
- Hansen, S., McMahon, M., & Tong, M. (2019). The long-run information effect of central bank communication. Journal of Monetary Economics, 108, 185–202. [Google Scholar] [CrossRef]
- He, Z., & Krishnamurthy, A. (2013). Intermediary asset pricing. American Economic Review, 103(2), 732–770. [Google Scholar] [CrossRef]
- Henry, C. (1974). Investment decisions under uncertainty: The “irreversibility effect”. The American Economic Review, 64(6), 1006–1012. [Google Scholar]
- Hmamouche, Y. (2020). NlinTS: An R package for causality detection in time series. The R Journal, 12(1), 21. [Google Scholar] [CrossRef]
- Ivanov, V., & Kilian, L. (2005). A practitioner’s guide to lag order selection for VAR impulse response analysis. Studies in Nonlinear Dynamics & Econometrics, 9(1), 1–36. [Google Scholar]
- Jallouli, F., & Yalouli, T. (2022). Monetary policy in Tunisia during the COVID-19 pandemic: A BVAR model. Journal of Financial, Accounting & Managerial Studies, 9(2), 76–92. [Google Scholar]
- Jarociński, M., & Karadi, P. (2017). Central bank information shocks. In 2017 meeting papers. No. 1193. Society for Economic Dynamics. [Google Scholar]
- Jarociński, M., & Karadi, P. (2020). Deconstructing monetary policy surprises—The role of information shocks. American Economic Journal: Macroeconomics, 12(2), 1–43. [Google Scholar] [CrossRef]
- Ji, J., Cao, Z., Zhang, C. Y., & Zheng, X. (2025). Dissecting the influence of geopolitical risks on employment decisions: The role of employment protection across countries. SSRN Working Paper, 4995635. [Google Scholar]
- Johansen, S. (1995). Identifying restrictions of linear equations with applications to simultaneous equations and cointegration. Journal of Econometrics, 69(1), 111–132. [Google Scholar] [CrossRef]
- Jordà, Ò. (2005). Estimation and inference of impulse responses by local projections. American Economic Review, 95(1), 161–182. [Google Scholar] [CrossRef]
- Jordà, Ò., & Taylor, A. M. (2025). Local projections. Journal of Economic Literature, 63(1), 59–110. [Google Scholar] [CrossRef]
- Kilian, L., Plante, M., & Richter, A. W. (2024). Geopolitical oil price risk and economic fluctuations. FRB of Dallas Working Paper, No. 2403. FRB. [Google Scholar]
- Kisswani, K. M., & Elian, M. I. (2021). Analyzing the (a) symmetric impacts of oil price, economic policy uncertainty, and global geopolitical risk on exchange rate. The Journal of Economic Asymmetries, 24, e00204. [Google Scholar] [CrossRef]
- Kohn, D. L., & Sack, B. P. (2003). Central bank talk: Does it matter and why? Finance and Economics Discussion Series (FEDS). [Google Scholar]
- Kose, M. A., Prasad, E. S., & Terrones, M. E. (2003). Financial integration and macroeconomic volatility. IMF Staff Papers, 50(Suppl. 1), 119–142. [Google Scholar] [CrossRef]
- Kurov, A. (2010). Investor sentiment and the stock market’s reaction to monetary policy. Journal of Banking & Finance, 34(1), 139–149. [Google Scholar]
- Kwiatkowski, D., Phillips, P. C., Schmidt, P., & Shin, Y. (1992). Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? Journal of econometrics, 54(1–3), 159–178. [Google Scholar] [CrossRef]
- Laséen, S. (2020). Monetary policy surprises, central bank information shocks, and economic activity in a small open economy. Working Paper Series, No. 396. Sveriges Riksbank. [Google Scholar]
- Laumer, S., & Santos, I. M. (2024). The impact of monetary policy shocks—Do not rule out central bank information effects or economic news. Economics Letters, 237, 111634. [Google Scholar] [CrossRef]
- Lutz, C. (2015). The impact of conventional and unconventional monetary policy on investor sentiment. Journal of Banking & Finance, 61, 89–105. [Google Scholar]
- Marschner, P. F., & Ceretta, P. S. (2021). Investor sentiment, economic uncertainty, and monetary policy in Brazil. Revista Contabilidade & Finanças, 32(87), 528–540. [Google Scholar]
- Mateut, S. (2005). Trade credit and monetary policy transmission. Journal of Economic Surveys, 19(4), 655–670. [Google Scholar] [CrossRef]
- Maziarz, M. (2015). A review of the Granger-causality fallacy. The Journal of Philosophical Economics: Reflections on Economic and Social Issues, 8(2), 86–105. [Google Scholar] [CrossRef]
- Mbarek, L., Marfatia, H. A., & Juko, S. (2019). Time-varying response of treasury yields to monetary policy shocks: Evidence from the Tunisian bond market. Journal of Financial Regulation and Compliance, 27(4), 422–442. [Google Scholar] [CrossRef]
- Mignon, V., & Saadaoui, J. (2024). How do political tensions and geopolitical risks impact oil prices? Energy Economics, 129, 107219. [Google Scholar] [CrossRef]
- Mimoun, M. B., Boukhatem, J., & Raies, A. (2024). Aggregate demand and inflation response to monetary policy shocks in Tunisia. Journal of Policy Modeling, 46(3), 592–612. [Google Scholar] [CrossRef]
- Miranda-Agrippino, S., & Rey, H. (2020). US monetary policy and the global financial cycle. The Review of Economic Studies, 87(6), 2754–2776. [Google Scholar] [CrossRef]
- Monfort, A., Renne, J. P., Rüffer, R., & Vitale, G. (2003, November). Is economic activity in the G7 synchronized? Common shocks versus spillover effects. Common Shocks Versus Spillover Effects. CEPR. [Google Scholar]
- Montes, G. C., & Nicolay, R. T. F. (2017). Does clarity of central bank communication affect credibility? Evidences considering governor-specific effects. Applied Economics, 49(32), 3163–3180. [Google Scholar] [CrossRef]
- Morgan, D. P. (1998). The credit effects of monetary policy: Evidence using loan commitments. Journal of Money, Credit and Banking, 102–118. [Google Scholar] [CrossRef]
- Moussa, F. B., & Talbi, M. (2019). Stock market reaction to terrorist attacks and political uncertainty: Empirical evidence from the Tunisian stock exchange. International Journal of Economics and Financial Issues, 9(3), 48–64. [Google Scholar] [CrossRef][Green Version]
- Murphy, E. (1999). Economic and political change in Tunisia. Palgrave Macmillan UK. [Google Scholar]
- Ostapenko, N. (2020). Central bank communication: Information and policy shocks. SSRN, 3607817. University Library of Munich. [Google Scholar]
- Perron, P., & Phillips, P. C. (1987). Does GNP have a unit root?: A re-evaluation. Economics Letters, 23(2), 139–145. [Google Scholar] [CrossRef]
- Phillips, P. C., Shi, S., & Yu, J. (2014). Specification sensitivity in right-tailed unit root testing for explosive behaviour. Oxford Bulletin of Economics and Statistics, 76(3), 315–333. [Google Scholar] [CrossRef]
- Phillips, P. C., Shi, S., & Yu, J. (2015a). Testing for multiple bubbles: Historical episodes of exuberance and collapse in the S&P 500. International Economic Review, 56(4), 1043–1078. [Google Scholar]
- Phillips, P. C., Shi, S., & Yu, J. (2015b). Testing for multiple bubbles: Limit theory of real-time detectors. International Economic Review, 56(4), 1079–1134. [Google Scholar] [CrossRef]
- Phillips, P. C., Wu, Y., & Yu, J. (2011). Explosive behavior in the 1990s Nasdaq: When did exuberance escalate asset values? International Economic Review, 52(1), 201–226. [Google Scholar] [CrossRef]
- Pinchetti, M. (2024). Geopolitical risk and inflation: The role of energy markets. No. 2431. London School of Economics and Political Science. [Google Scholar]
- Przystupa, J., & Wróbel, E. (2015). Modelling less developed emerging markets: The case of monetary transmission in Tunisia. Working Paper, 211. National Bank of Poland. [Google Scholar]
- Reid, M., & Siklos, P. L. (2020). Building credibility and influencing expectations: The evolution of central bank communication. Economic Research and Statistics Department, South African Reserve Bank. [Google Scholar]
- Ren, X., Li, J., He, F., & Lucey, B. (2023). Impact of climate policy uncertainty on traditional energy and green markets: Evidence from time-varying granger tests. Renewable and Sustainable Energy Reviews, 173, 113058. [Google Scholar] [CrossRef]
- Romer, C. D., & Romer, D. H. (1993). Credit channel or credit actions? An interpretation of the postwar transmission mechanism. Working Paper, no 4485. NBER. [Google Scholar]
- Salem, R., & Bouaziz, R. (2024). Natural Rate of Interest, Monetary Policy and Shocks in Tunisia. Monetary Policy and Shocks in Tunisia. SSRN Working Paper, 4990836. [Google Scholar]
- Shi, S., Hurn, S., & Phillips, P. C. (2020). Causal change detection in possibly integrated systems: Revisiting the money–income relationship. Journal of Financial Econometrics, 18(1), 158–180. [Google Scholar] [CrossRef]
- Shi, S., Phillips, P. C., & Hurn, S. (2018). Change detection and the causal impact of the yield curve. Journal of Time Series Analysis, 39(6), 966–987. [Google Scholar] [CrossRef]
- Swanson, N. R. (1998). Money and output viewed through a rolling window. Journal of monetary Economics, 41(3), 455–474. [Google Scholar] [CrossRef]
- Tayssir, O., & Feryel, O. (2018). Does central banking promote financial development? Borsa Istanbul Review, 18(1), 52–75. [Google Scholar] [CrossRef]
- Tenreyro, S., & Thwaites, G. (2016). Pushing on a string: US monetary policy is less powerful in recessions. American Economic Journal: Macroeconomics, 8(4), 43–74. [Google Scholar] [CrossRef]
- Thoma, M. A. (1994). Subsample instability and asymmetries in money-income causality. Journal of Econometrics, 64(1–2), 279–306. [Google Scholar] [CrossRef]
- Tissaoui, K., Hkiri, B., Talbi, M., Alghassab, W., & Alfreahat, K. I. (2021). Market volatility and illiquidity during the COVID-19 outbreak: Evidence from the Saudi stock exchange through the wavelet coherence approaches. The North American Journal of Economics and Finance, 58, 101521. [Google Scholar] [CrossRef]
- Toda, H. Y., & Yamamoto, T. (1995). Statistical inference in vector autoregressions with possibly integrated processes. Journal of econometrics, 66(1–2), 225–250. [Google Scholar] [CrossRef]
- Torrence, C., & Compo, G. P. (1998). A practical guide to wavelet analysis. Bulletin of the American Meteorological Society, 79(1), 61–78. [Google Scholar] [CrossRef]
- Trabelsi, E. (2024a). COVID-19 and uncertainty effects on Tunisian stock market volatility: Insights from GJR-GARCH, wavelet coherence, and ARDL. Journal of Risk and Financial Management, 17(9), 403. [Google Scholar] [CrossRef]
- Trabelsi, E. (2024b). Welfare fragmented information effects: The cost-benefit analysis and Trade-offs. Journal of Information Economics, 2(1), 1–32. [Google Scholar] [CrossRef]
- Udeaja, E. A., Tule, J. M., Akadiri, S. S., Akanni, E. O., & Offum, P. F. (2024). Do economic policy uncertainty and geopolitical risk impede economic transformation? Evidence from resource rich country. Journal of Economics and Finance, 48, 1145–1165. [Google Scholar] [CrossRef]
- Wahyuningsih, N., & Fatmawati, P. N. (2024). Analysis of monetary policy in Muslim Majority Countries: Tunisia. Peradaban Journal of Economic and Business, 3(2), 104–117. [Google Scholar] [CrossRef]
- Wang, Q., Zhang, C., & Li, R. (2024). Impact of different geopolitical factors on the energy transition: The role of geopolitical threats, geopolitical acts, and geopolitical risks. Journal of Environmental Management, 352, 119962. [Google Scholar] [CrossRef]
- Wang, S., Chen, L., & Xiong, X. (2019). Asset bubbles, banking stability and economic growth. Economic Modelling, 78, 108–117. [Google Scholar] [CrossRef]
- Woodford, M. (2005). Central bank communication and policy effectiveness. Working Paper, No 11898. NBER. [Google Scholar]
- Yilmazkuday, H. (2025). Geopolitical Risks and Exchange Rates. Finance Research Letters, 74, 106769. [Google Scholar] [CrossRef]
- Zhao, Y. (2024). International economic policies for cross-border payments in digital money in the context of geopolitical risks. SSRN Working Paper, 4815891. [Google Scholar] [CrossRef]
- Zivot, E., & Andrews, D. W. K. (2002). Further evidence on the great crash, the oil-price shock, and the unit-root hypothesis. Journal of Business & Economic Statistics, 20(1), 25–44. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).