Female Wage Employment and Fertility in Kenya

Abstract

The paper examines the association between fertility and female wage employment in Kenya using nationally representative cross-sectional data collected by the Kenya’s National Bureau of Statistics, a government-owned statistical organization. Two findings emerge from our analysis. The first finding is that female wage employment is negatively correlated with the number of births. Incompatibility of childrearing with wage employment is one of the main explanations for this evidence. The other finding is a much larger magnitude of the negative association between wage employment and male births relative to female newborns, but the difference in the estimated gender-specific coefficients is statistically insignificant. However, there is need for further significance tests on the difference between the gendered coefficients because the larger drop in the number of male births relative to female, as female wage employment expands, has strong support in the biomedical literature. The relevance of the second finding in the context of the biomedical literature on the link between a child’s gender at birth and the environment in which the mother works and lives provides a justification for further research on this issue. The tentative findings of the paper point to labor market policies that could be explored in Kenya and elsewhere in Africa to address the problem of excess fertility, and thus enhance women’s health, agency, and socioeconomic empowerment.

1. Introduction

We analyze the association between fertility and female labor force participation in Kenya, restricting participation to female wage employment. We focus on the nexus between women’s employment and four indicators of fertility, derived from the information available in the Kenya Integrated Household Budget Survey (KIHBS), conducted by the Kenya National Bureau of Statitics in 2015–6. The key fertility indicators that are empirically analyzed in depth—in relation to female wage employment are:

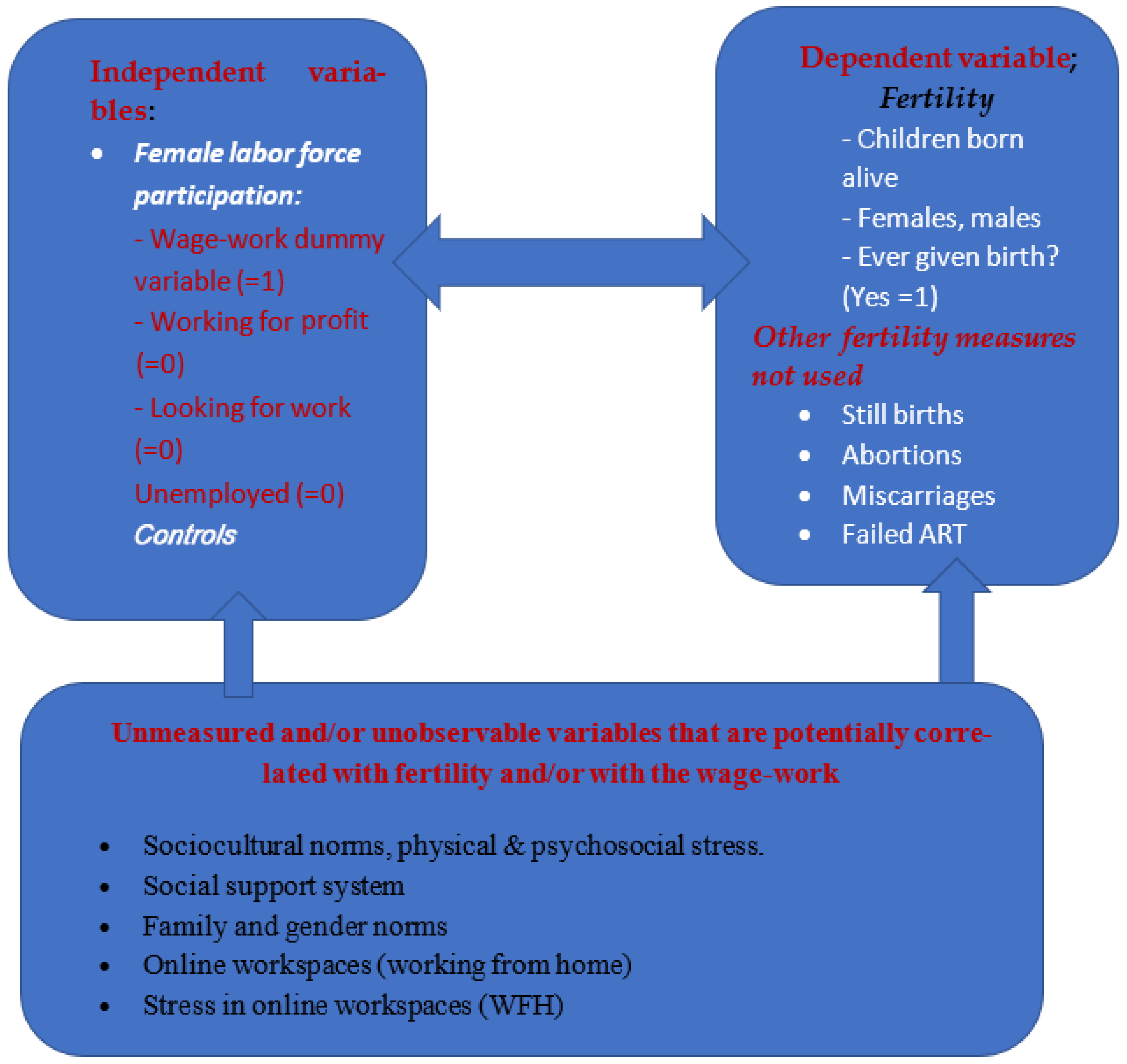
• Whether a woman has ever given a live birth, irrespective of the baby’s gender.
• Total number of children ever born alive.
• Number of males.
• Number of females.

All of the above fertility indicators have been used in previous studies in analyses of the relationship between female labor force participation and fertility. Additional fertility measures in the literature, none of which is used for lack of data include unrealized fertility, such as abortions, fetal losses, concealed fertility (e.g., non-marital births, births associated with rape or incest, and failed assisted reproductive technology). Ideally, information on fertility should include births resulting from all conception decisions, i.e., decisions that give rise to “live births as well as in abortions, miscarriages and stillbirths” (Hald & Ozcan, 2021, p. 2). In the present study, focus is on the relationship between fertility (live births) and female wage employment.

The paper’s main finding is that female wage employment has a strong negative association with fertility. Incompatibility of childrearing with wage employment is the socioeconomic explanation for this evidence (Brewster & Rindfuss, 2000). However, the first birth is positively associated with women’s wage employment. An overwhelming positive income effect appears to be the reason for this evidence. A wage job increases a woman’s opportunity cost of child-rearing while giving her the ability to have and raise a child. The conflicting associations (i) between wage employment with the first birth plus (ii) between wage employment with subsequent births–together–suggest that in the case of first-time mothers, the negative fertility effect of the wage forgone in order to raise children, is more than offset by the positive effect of wage income.

We further find a negative association between wage employment with male births that is larger than that for female births, but the difference is statistically insignificant. Nonetheless, the gap is numerically large and is observed in all the fertility models we estimate, with its plausibility being supported by biomedical literature (Orzack et al., 2015; McCarthy, 2019).

Our paper simplifies estimation of an econometric model characterized by a sample selection feature (Heckman, 1979), which is appropriate for empirically modelling a mother’s fertility decisions at the extensive margin (whether to have a child or not) and at the insensitive margin (how many children to have). We leverage this well-known model with the Poisson distribution, to analyze the determinants of fertility (number of births), accounting for the endogeneity of the main regressor, i.e., female wage employment (see, Appendix A and Appendix B). We formulate a multidisciplinary (hybrid) model of fertility that can account for observed fertility outcomes at birth (e.g., differences in the number of births at birth by gender), that are implausibly hard to attribute to women’s fertility decisions (Appendix F).

The remainder of the paper is organized as follows. Section 2 presents an overview of related literature. Section 3 reviews multidisciplinary fertility studies and synthesizes them into a hybrid model of fertility. Section 4 outlines empirical fertility models, and briefly discusses identification issues. In Section 5, we provide a snapshot of the data used for estimations. Section 6 presents estimation results whereas Section 7 highlights the main findings. In Section 8 and Section 9 we discuss the policy value of the preferred estimates and conclude the paper. The accompanying appendixes contain details on data, estimation methods, results, and the hybrid model.

2. Overview of Related Literature

We start by reviewing studies that look at effects of fertility on labor force participation, before examining the reverse relationship. Fertility matters for women because it affects their human capital directly and the type of socioeconomic activities they can pursue. Many studies have investigated the nexus between fertility and female labor force participation. A recent study in India shows that an increase in the number of children born reduces labor force participation and earnings (Tiwari et al., 2022). This evidence is in accordance with labor market theory because childrearing reduces the time available for market activities. Tiwari et al. (2022) show that women with more than three children had a 3.5% higher probability of exiting the labor market relative to their counterparts with two children or less. The reduction in female labor force participation associated with fertility is often referred to as the motherhood penalty (see, e.g., Correll et al., 2007; Francavilla & Giannelli, 2011; D. E. Bloom et al., 2009; Cáceres-Delpiano, 2012; Chun & Oh, 2002; He & Zhu, 2016; Heath, 2017; Adair et al., 2002).

On the other hand, some studies have found little to no effect of fertility on female labor force participation. For example, labor force participation by young women in poorer countries is only marginally reduced by having children (Chun & Oh, 2002). Other studies find very small negative effects (He & Zhu, 2016), while evidence from Germany and Denmark shows no effect (Giannelli, 1996). A study in Australia found no relationship between motherhood and labor force participation or the number of hours worked (Rammohan & Whelan, 2005).

Regarding the reverse relationship, the effect of the female labor force participation on fertility–seems to be dependent on economic contexts, and the prevailing sociocultural norms. A stream of literature from diverse settings has explored the effect of the expansion in women’s work opportunities on fertility. Empirical evidence from South Asia (Heath & Mobarak, 2015) shows that an expansion of women’s work opportunities, coupled with an increase in the relative return to women’s labor, reduces fertility. Using data from the Demographic and Health Surveys, Zipfel (2022) shows that desired fertility in Africa is reduced by higher levels of wealth and by female wage employment. Low fertility is further associated with higher levels of development and schooling (Ajayi et al., 2024). In particular, as economies develop, there is better healthcare, greater schooling opportunities, and better information on the causes of diseases, especially among women, leading to reduced child mortality and to the decline in fertility because women do not need to have as many children to achieve their desired family sizes. Socioeconomic development, which is associated with increased use of modern family planning methods, is cited as further reason for fertility decline, especially in Africa (Younger, 2006). Other strands of the literature show that fertility is jointly determined with female wage employment. This issue is well studied in experimental and non-experimental settings in low- and high-income countries (see, e.g., Schultz, 2005; Angrist & Evans, 1998; Kornstad & Rønsen, 2018).

Kornstad and Rønsen’s study is the closest to ours because it identifies the effect of wage employment on fertility using aggregate and predicted wage rates that are exogenous to women’s hazards of experiencing a first, a second, and a third birth, respectively. They also examine the wage effect on the hazard of the first birth, and further measure the effect of implicit female wage on the number of children born alive, disaggregated by gender. Kornstad and Rønsen show that depending on model structure and context, the estimated fertility wage effects can be zero, negative or positive. If, for example, the wage rate represents the opportunity cost that women incur in order to have a child, the wage employment coefficient should be negative. If, instead, the wage rate is a proxy for ability to afford childcare or to afford both child quality and quantity, a positive coefficient should be expected. Culture, social norms, work environments, and unobservable biological processes in utero also affect the sign and size of the coefficient on the wage, wage-employment variable, or its proxies in models of fertility demand (Barrett et al., 2020; Zipfel, 2022).

Beguy (2009) investigates fertility effects of female employment in Dakar (Senegal) and in Lome (Togo) using urban datasets. The main finding is that in Lome, female wage work reduces fertility, whereas in Senegal, wage has no effect. Differences in social norms and gender-specific roles in the two countries are posited as the reason for this finding, which is credible, given that the fertility models were estimated taking into account regional fixed effects and religious affiliations of mothers.

Evidence from East Asia suggests that despite marriage rates being high, total fertility rate in the region is low. In particular, married women on average have one child and single women generally have no children (Myong et al., 2020). The authors attribute this evidence to two social norms that shape marriage and fertility in East Asia, namely, the unequal gendered distribution of childcare, where the care burden is on women, and the huge stigma attached to out-of-wedlock births. Myong et al. (2020) find that the social norm of unequal gender-based division of childcare in favor of men can explain the fertility outcomes by marital status in East Asia, and by extension in African regions where similar norms exist.

Recent work in China shows that a woman’s fertility intentions are influenced by neighborhood and group norms (Yu & Liang, 2022). The authors observe that the role of social norms in shaping individual fertility intentions vary by gender and that rural residents are more significantly influenced by them. This evidence resonates with Kiiru (2021), who found that the effect of social norms (e.g., the stigma of non-payment of group loans) was more binding in rural than in urban areas. There is also evidence that norms that are recognized and widespread in a specific region are observed by the region’s residents without enforcement (see, e.g., Barrett et al., 2020). Similarly, Yu and Liang (2022) conclude that, in addition to macro and individual-specific factors, social norms strongly influence fertility intentions and realizations.

It is clear from the empirical literature that social norms play a key role in affecting demand for fertility and in controlling it. It is therefore reasonable to hypothesize that social norms that emphasize the importance of male children (as is the case in Kenya) are likely to put pressure on individual women to increase demand for male children. However, what is not clear is why, despite this pressure, the women engaged in wage employment could have fewer predicted number of male children than the unemployed women or their counterparts in nonwage employment.

There is influential biomedical literature on how stress affects fertility, and on how adverse biological processes in utero and adverse work environments in which mothers operate differentially afflict male and female fetuses—with males generally being negatively affected at a higher level. At conception, there are 50–50 chances of conceiving a boy or girl (Schulman & Karabinus, 2005). However, in the first few weeks of pregnancy, there are more male losses compared to girls due to a higher rate of genetic abnormalities in male embryos, while in later stages of the first trimester there is increased loss of female fetuses. Overall, more girl fetuses die in the womb compared to boy fetuses (Orzack et al., 2015). Thus, more boys than girls are born in the total population with a standard sex ratio at birth of 104–106 boys to every 100 girls (see, e.g., UNFPA, 2012, p. 9).

However, in cases of prenatal stress arising from a mother’s environment, more girl fetuses are likely to be carried to term compared to boy embryos (Di Renzo et al., 2007). Further evidence suggests that early childhood developmental outcomes of male fetuses exposed to a combination of prenatal and perinatal adversities are more highly impaired than those of female fetuses (DiPietro & Voegtline, 2017; Navara, 2010). Additionally, although Chuard (2020) finds no adverse effect of prenatal employment on newborns using observable health outcomes such as birthweight or Apgar score, its effects in utero were not investigated.

Acute stress resulting from natural disasters can alter the sex ratio at birth. Fukuda et al. (1998) show that the Kobe earthquake in Japan in 1995 led to the birth of more girls compared to boys, 9 months later. Schacht et al. (2019) also find that boys were less likely to be born in stressful periods, like the Spanish Flu and the Great Depression. Livingston (2013) attributes this situation to an increased likelihood of a miscarriage of the male fetus due to the stressors to which boys are less resilient relative to girls. An emerging literature on the “fragile male” attributes the relatively lower resilience of male fetuses to shocks arising from environmental and gestational processes to male genetic fragility, which currently is not well understood (Kraemer, 2000). However, taking greater genetic fragility in male fetuses as given, healthcare decisions of pregnant individuals (Manca, 2025)—that women are culturally expected to make as good mothers—can lead to working women having fewer boys than girls. For example, if working women have greater access to misinformation about effects of vaccination on fetal health, their rejection of vaccine uptake during pregnancy can expose them to diseases or viruses to which a male fetus might be less resilient.

In the same vein, social conflicts during pregnancy can lead to a lower probability of a male birth. Using data from the National Longitudinal Survey of Youth (NLSY79) in the U.S., Hamoudi and Nobles (2014) find that conflicts in relationships predict a high probability of a girl being born. More generally, factors that adversely affect fetal health, such as unfavorable temperatures (see, e.g., Hajdu & Hajdu, 2023), can be expected to induce greater mortality among embryos that have high levels of chromosomal abnormalities (Hajdu, 2024). However, fetal losses due to climate change have not so far been analyzed by gender. Briefly, even though there is a dearth of socioeconomic studies linking a mother’s engagement in stressful work to a higher probability of a female birth, there is no shortage of biomedical evidence that stressful environments are likely to lead to the birth of more girls compared to boys.

We hypothesize that social norms that emphasize the importance of male children are likely to put pressure on women and thus to increase the demand for male children. Pressure from social norms, coupled with a stressful work environment, is likely to disadvantage the survival of the male fetus more. To better understand this issue, future research work in this area should include analyses of samples for working-age women in nonwage employment, unpaid care work plus samples of females seeking work or not in any employment.

In the present paper, we focus only on the female wage employment part of the FLFP because we use the wage women forgo to care for children as the price of fertility. FLFP is not a good proxy for the opportunity cost of rearing children because it also captures the resources required to establish a business or to sustain a job search. Moreover, FLFP is linked to social norms that prevent women from engaging in wage labor, and to factors that deprive women of the skills they need to compete in wage-labor markets.

Although the FLFP can be disaggregated into its various components (e.g., wage work, business enterprise, livestock herding, unpaid care-work, job-seeking) this refinement unnecessarily complicates a model whose main purpose is to understand the association between fertility and the wage rate, i.e., the income forgone per unit of time spent rearing children. It is also worth clarifying that the wage employment dummy is used in this study as a proxy for the wage rate. However, in the next section, we also discuss women’s nonwage work to place our study into a broader context of FLFP.

3. Modelling Women’s Work and Fertility

3.1. Feminism Model

As explanations of observed women’s work, feminist theories focus on variables such as gender inequality and gendered barriers of access to power, resources, and employment. The feminist perspectives on reproductive choices, as held by both sexes, focus on women’s rights over reproduction and related matters (Petchesky, 1995).

The inequality experienced by women in workspaces stems from discriminatory factors that can be addressed by public policy changes. The literature on this issue argues for equitable treatment in workplaces; see, e.g., Crenshaw (1989), and Davis (1981).

Another stream of literature stresses the high burden that excess fertility, as promoted by social norms, exerts on working women, forcing them in some cases to reduce or terminate market work or even delay or forgo childbearing (Goldin, 2021; Donald et al., 2024). There is thus a need for policies to address women’s labor-market disempowerment (Blau & Kahn, 2000) taking into account the intersection of the many factors involved.

3.2. Economic Model

3.2.1. Background

Time is the natural measure of labor-effort quantities that people allocate to livelihood and leisure activities (Becker, 1965). Schultz (1973) argues that a working-age household member allocates their own labor (measured, for example, by hours per day) to wage work, childcare, and to the tasks needed to produce a composite consumption commodity. The composite commodity typically consists of home and market goods. The time allocations across all activities cannot exceed the total units of the time available to each person, i.e., 24 h per day. Moreover, due to sociocultural norms, women allocate the bulk of their time to childcare and to the production of non-market goods. Thus, women’s opportunity cost of engaging in wage work should be quite high relative to men’s, because of the large variety and quantities of the market and non-market goods that they must give up. Since childcare is the primary input into childrearing, women’s engagement in wage employment decreases the amount of time available for childcare and should be negatively correlated with fertility. The amount of time spent on childrearing determines the opportunity cost of fertility because it reflects the wage income forgone to raise children. Thus, other things being equal, an increase in wage rate should reduce fertility.

Becker and Lewis (1973, p. 85) observe that, at the family level, a child is a public good. Accordingly, the existence of strong social norms that encourage high fertility within and across families should be expected. Such norms can increase fertility even as a higher wage rate decreases it, making both the sign and the magnitude of the estimated coefficient on female wage employment ambiguous.

Moreover, social norms can push fertility far beyond the level that a mother considers optimal. Data on sociocultural norms are needed to properly estimate fertility demand functions. Becker and Lewis (1973) and Becker (1981) present analytical concepts for understanding the causal link between female wage employment and fertility.

3.2.2. Child Quantity, Child Quality, and Full Income

Becker and Lewis (1973) show that wage income alone is not enough for a full understanding of the effect of female wage employment on fertility (first birth and higher-order births). Information is also needed on full income, which can be approximated by a life-time wage that includes current wage, wage savings and the associated assets, such as durable goods, land, and machinery. Employing the full income concept, differing effects of income type on fertility have been analyzed. Becker and Lewis demonstrate that the concept of the interaction between child quantity and child quality provides a convenient way to introduce these quantities into a mother’s utility function, alongside a consumption commodity, y, without having to make the strong assumption that child quantity (n) and quality (q) are more closely related than any other two goods chosen at random (Becker, 1960). The ‘quantity–quality’ interaction variable in Becker and Lewis’s (1973) utility function rests on the idea that child quality is inseparable from child quantity, and vice versa. That is, there exists some minimum quality in every child so that a quality increase at the margin necessarily raises the minimum quality for all subsequent children. Thus over time, and holding income constant, a family can increase child quality only by scaling down the desired number of children. According to Becker and Lewis’s framework, the following scenarios are also feasible even in a static context: a family can use (i) a fraction of its consumption commodity to improve child quality; and (ii) an increase in full-income to improve both child quality and quantity. Additionally, according to Becker and Lewis, improvement in child quality can happen “mechanically” because it is linked to the wellbeing of parents (see James Duesenberry’s comment on Becker, 1960, p. 234; and similarly, Bernard Okun’s comment, p. 236). The above scenarios indicate that identification of the effect of female wage work on fertility is complicated because it is intertwined with the family’s full income.

3.2.3. Formal Model

We follow Becker and Lewis (1973) and specify a mother’s or a family’s utility function, U, as follows:

U = U (n, q, y)

(1)

where

n is the number of children, q is their quality, and y is consumption of all other commodities.

Although child quantity, n, and child quality, q, enter the utility function separately, they do not generate utility independently of each other. In the budget constraint (Equation (2)), quality and quantity are interacted to emphasize the fact that full income can be spent to increase either child quality or quantity, as shown below. The full income in the budget constraint reflects the fact that utility is derived from wage goods, child quantity, and child quality, all of which require time expenditure to acquire. The family full income (I) is easily augmentable with wealth, but this is not done here (see Schultz, 2005).

I = nqπ + yπ_y

(2)

where π is the shadow value of the interaction between child quantity and quality, i.e., π is the unobserved true monetary value of the quality imbedded in one child, so that if quality is low, a large number of children can be had, and vice versa. Alternatively, π can be viewed as the monetary value of one unit of child quality, when the number of children is fixed, so that if quality increases, the cost of having children rises, and their number is reduced. Finally, π_y is the shadow monetary value of a unit of y, proxied by the marginal cost of its production. The shadow price of child quantity depends primarily on the mother’s time intensity in childrearing, whereas the shadow price of child quality is determined mainly by the marginal cost of producing a child’s human capital—using purchasable education and health inputs—such as school uniforms and medical care, respectively.

Forming a Lagrangean function (from Equations (1) and (2)) to determine the quantities of n, q, and y (given I) that maximize a mother’s utility function, we obtain the following first-order conditions for optimum levels of n, q and y (see Becker & Lewis, 1973, pp. 82–83).

MU_n, = λqπ = λp_n

(3a)

MU_q, = λnπ = λp_q

(3b)

MU_y, = λπ_y = λp_y

(3c)

MU_λ = I = nqπ + yπ_y

(3d)

Equation (3a) states that the marginal utility of child quantity, n, is the shadow monetary value of child quality (qπ) weighted by the marginal utility of money income (λ), which in turn is equal to the price of child quantity times the marginal utility of income, i.e., the marginal utility associated with p_n is λp_n (Equation (3a)). This is similar for Equation (3b,c). Equation (3d) asserts that a unit increase in the marginal utility of income raises a mother’s utility by I utils, which is equal to the sum of utility the mother derives from the quantity and the quality of children, plus the utility from the consumption of other commodities. Equation (3d) states that given her income (Equation (2)), the marginal costs of children (p_n and p_q), and the marginal costs of the other commodities (p_y), a mother has no incentive to change her consumption pattern, including her fertility level. To change her consumption pattern, policies that alter income and/or observed prices of nq and y are needed. If, in addition to the first-order conditions (3a–3d), the second-order conditions hold, and focusing on Equation (3a, b), the demand for fertility can be expressed in general form as:

n = f(p_n, p_q, p_y, I, d, x, s, w, b) + ε

(4)

where d = demographics, x = work environment and related shocks, s = sociocultural factors, w = wealth, b = biomedical processes in utero, ε = disturbance term, and p denotes price. The previous discussion has shown that an increase in p_n, holding everything else constant, reduces fertility. Equation (4) is estimated using the full sample of n, and by sub-samples of male and female children. Moreover, the price of child quantity, p_n, is proxied by the female wage employment dummy because it is closely linked to the wage income that mothers give up in order to care for children at home, in line with social norms. It has already been noted that p_q and p_y are determined, respectively, by the marginal cost of child quality formation and that of producing the composite commodity, y, proxied by costs of schooling, medical care, and the outlay on inputs into the production of y. The higher the opportunity cost of childcare, the greater the mother’s incentive to reduce fertility in order to participate in wage work. Estimations of Equation (4) should be performed accounting for the potential endogeneity of p_n (proxied by female wage employment) and considering the potential sample selection bias that could arise from the fact that the fertility-demand model is estimated using a sub-sample of mothers that excludes women who have never had a live birth.

3.2.4. Predictions and Limitations of the Model

An increase in female wage participation should be negatively correlated with fertility for the total number of children born alive, and for boys and girls. An income increase enhances a mother’s ability to invest in the quality of all children. Thus wage income can be assumed to be positively correlated with child quality. However, the higher the child quality, the lower the child quantity, because it is more expensive to invest in all children.

As previously noted, an increase in child quality raises the shadow price of child quantity—thus reducing the demand for fertility through the goods-substitution channel, i.e., the demand for the alternative good falls, which in this case is n, whose price has risen. It is worthwhile to clarify that the demand for children falls because the cost of the marginal utility for a given unit of n increases relative to the shadow cost of a marginal utility obtainable from a unit of the rival good, q (see Equations (3b) and (3b)).

Moreover, an increase in female wage employment, or in the number of hours that a mother spends working, raises the opportunity cost of childrearing and also reduces fertility. In contrast, an increase in wealth improves a mother’s ability to afford non-self-childcare, thus reducing her opportunity cost of childrearing (because direct time input into child raising declines). Hence, ceteris paribus, demand for children increases. In the same vein, wealth can increase child quality through the ability-to-pay channel.

Intuitively, an increase in child quality raises the opportunity cost of having children, thereby reducing fertility. Thus the effect of wealth on fertility is ambiguous. Generally, the literature reports strong positive correlations between fertility and wealth or exogenous income (see, e.g., Schultz, 2005; Donald et al., 2024).

The quantity-quality model can explain the negative association between fertility and female wage employment but cannot account for why female wage work reduces the number of male live births more than it reduces that of females. The opportunity cost of raising children, expressed in terms of the wage income forgone, provides the reason why fertility falls as female wage employment increases. Similarly, the opportunity cost that a mother or a family incurs by giving up a smaller number of children, with a high-quality human capital, for a larger number of children, with a lower endowment, provides the incentive for fertility reduction.

The higher the child quality, the greater the incentive to reduce child quantity. However, as just noted, the model cannot explain why the reduction is larger for male births. In this connection, there is evidence in the biomedical literature that male embryos are less likely to survive a mother’s work-related shocks or stress relative to their female counterparts (McCarthy, 2019).

3.2.5. The Emerging Research Hypothesis

Thus, expectant mothers who work in adverse environments are predicted to deliver fewer boys than the mothers operating in supportive or non-hazardous work environments. The hypothesis that expectant women who work or live in hazardous environments will, other things being equal, deliver fewer boys than girls requires detailed quantitative and qualitative datasets to test, which is typically unavailable in household surveys conducted by national statistical bureaus.

In addition to data requirements, a rigorous testing of the above hypothesis in an enhanced study requires a thorough review and synthesis of the literature on biomedical, sociocultural, and psychological contexts surrounding women’s physical and online workspaces.

3.3. Hybrid Model

Figure A1 (Appendix F) integrates ideas from diverse streams of the literature to specify an eclectic, mixed model of the relationship between fertility and female labor force participation that guides the empirical analysis, taking into account different interdisciplinary perspectives on this relationship. Examples of similar economic hybrid models in different contexts include Brown et al. (2018), Alatas et al. (2012) and Follett and Henderson (2023). Even though only a subset of the model shown in Figure A1 is estimated, the full model is presented in Appendix F as it has the potential to serve as a guide for future work in this area.

4. Empirical Models and Estimation Methods

The OLS and Heckit fertility demand models are estimated in turn, first without accounting for endogeneity and sample selection biases, and then accounting for these biases. The endogenous regressor in both models is a female wage employment dummy. In the structural part of the Heckit (the intensive-margin model), identification is achieved by using generalized residual as a regressor, constructed by exploiting the binary nature of the endogenous explanatory variable—the wage employment dummy (see Gourieroux et al., 1987, p. 14; Wooldridge, 2015, p. 428). In the reduced-form Heckit (the extensive-margin model), we follow the literature and include instruments for the female wage employment dummy in the Probit model for the first birth, while omitting them from the intensive-margin model. We avoid writing down the Heckman equations because the model is well known and firmly established in the econometric literature in which our empirical analysis is situated (see, e.g., Heckman, 1979). An important limitation of the Heckman two-step model is addressed in (Nawata, 1994; Wolfolds & Siegel, 2019), but as it turns out, the main concerns expressed in the literature about the two-step Heckit are side-stepped by the sequential estimation approach we use. Specifically, the two parts of the Heckit model can be properly estimated separately, in a sequence, provided that the inverses of the Mills ratios computed from each of the two probits (wage employment and the first-birth dummies) are used as controls in the intensive part of the model.

We compute the sample values for generalized residuals using the generalized residual equations in Gourieroux et al. (1987, Section 2.4.20, last equation, p. 14), and in Wooldridge (2015, pp. 427–428). Despite their differences in appearance, the two equations yield the same, manually generated solution, which is identical to the inverse of the Mills ratio for the wage employment probit, computed using STATA version 17, but is also computable using other packaged algorithms.

Since the generalized-residual procedure is essentially an instrumental variables method in non-linear contexts, it is imperative that the validity of the instruments for the female wage employment dummy be tested, as in other IV estimation contexts. The tests conducted reveal that the instruments (log of household landholding) and household rental income (proxied by a dummy variable), are relevant but weak because, although they pass exogeneity tests in the reduced-form regression, they fail the over-identification restriction in our two structural models (i.e., the wage equation for all births, and the equation for male births; see Appendix D). The over-identification test shows that one or both of the excluded instruments could be correlated with the structural error term, undermining the IV assertion that the instruments affect fertility only through wage employment. The generalized residual procedure addresses this issue by ensuring that, by design, the wage employment dummy is independent of the structural error term (Wooldridge, 2015, p. 428). The drawback of this procedure is that the error term of the reduced-form probit for the wage employment dummy might not be normally distributed, as assumed, in which case, its expected mean could be different from zero, thus allowing a correlation between the reduced-form and the structural error. Thus, we treat the estimated coefficient on female wage employment as a correlation rather than as a causal effect.

Despite its strong assumption, the probit-based generalized residual procedure is recommended (when available) because it estimates an unbiased causal effect if the reduced-form probit model is a true characterization of how unobservable fertility is distributed. The Olsen procedure (Olsen, 1980) achieves the same result, since in our dataset, this procedure approximates the IMR for the employment probit quite well (see

Table A1. The Effect of Female Wage Employment on Fertility (OLS Estimates derived using manually computed GR and IMR.

Variables	Male Births (1)	Female Births (2)	Total Births (3)	First Birth? (Yes = 1) Reduced-Form Probit Estimates (Average Marginal Effects), (4)
Wage Employment (=1)	−0.141 (3.87)	−0.057 † (1.47) *	−0.197 3.92	0.026 † (3.70) **
Generalized Residual (GR), obtained from Employment Probit (controls for endogeneity)	0.414 (3.96)	0.377 (3.41)	0.791 (5.46)	…
Shocks (=1)	0.192 (6.11)	0.196 (5.88)	0.388 (8.89)	0.019 (3.69)
Religion (1 = Christians)	−0.061 (1.79)	−0.052 (1.42)	−0.113 (2.38)	0.0005 (0.09)
Married	0.351 (7.50)	0.269 (5.43)	0.621 (9.55)	0.173 (34.6)
Education (=1)	−0.704 (11.14)	−0.0715 (10.71)	−1.420 (16.03)	−0.034 (2.67)
Rural	0.038 (0.99)	−0.715 (10.75)	0.173 (3.26)	0.012 (1.88)
Age	0.276 (11.7)	0.135 (3.33)	0.553 (16.82)	0.059 (37.1)
Age Squared × (10−2)	−0.268 (8.54)	−0.266 (8.01)	−0.534 (12.3)	−0.075 (28.1)
Food-Budget Share	0.953 (9.95)	0.821 8.10	1.77 (13.4)	0.128 (8.94)
IMR for the First Birth Probit (Controls for sample Selection)	0.401 (4.54)	0.368 3.94	0.769 (6.29)	…
Log (Household Total Landholding, Acres)	-	-	-	−0.016 * (3.90)
Household Rent, Dummy	-	-	-	−0.008 * (0.81)
Constant	−5.23 (9.42)	−5.18 (8.81)	−10.4 (13.5)	-
R2/Pseudo R2	0.240	0.229	0.404	0.66
N	8135	8135	8135	12,715 ξ

* p < 0.05; ** p < 0.000. ^† Note: Joint tests of significance: (i) First test: correlation of female births with female wage employment equals zero plus the correlation of employment with ever given birth equals zero; χ²(2) = 15.77 (p = 0.000). Thus, the χ² test rejects the hypothesis that the two associations are jointly equal to zero. Second test: (ii) the correlation of ever-given-birth with log of land acreage equals zero, and further that the association of first birth with household rent is zero; χ²(2) = 15.74 (p = 0.000). This joint hypothesis is equally rejected. ^ξ: Censored observations = 12,715 − 8135 = 4580.

and

Table A5. Effect of Female Wage Employment on Fertility (GR/LPM Estimates), t-statistics in parentheses (see Appendix A, Table A1 which reports nearly identical estimates).

Variables	Male Births (1)	Female Births (2)	Total Births (3)	First Birth? (Yes = 1) Reduced−Form Probit (Marginal Effects) (4)	Wage Employment? (Yes = 1) Reduced−Form (LPM Estimates), (5)
Wage Employment (=1)	−0.14089 (3.92) **	−0.0558 (1.43) *	−0.1967 (3.88) **	0.026 (3.70) **	0.0335 (4.72) **
Generalized Residual for Wage Employment (controls endogeneity)	−1.16 (3.61)	−1.16 (3.41)	−2.32 (5.14)	…	…
Shocks (=1)	0.185 (5.99)	0.188 (5.79)	0.373 (8.83)	0.019 (3.69)	0.018 (3.49)
Religion (1 = Christians)	−0.058 (1.75)	−0.048 (1.35)	−0.107 (2.32)	0.0005 (0.09)	−0.0012 (0.34)
Married (=1)	−0.326 (6.22)	−0.239 (4.23)	0.565 (7.48)	0.173 (34.6)	0.259 (36.3)
Education (=1)	−0.695 (9.07)	−0.696 (8.68)	−1.39 (13.88)	−0.034 (2.67)	−0.066 (6.12)
Rural (=1)	0.057 (1.59)	0.148 (3.91)	0.206 (4.13)	0.012 (1.88)	0.011 (1.63)
Age	0.250 (12.3)	0.254 (12.0)	0.504 (18.4)	0.059 (37.1)	0.150 (52.9)
Age Squared × (10−2)	−0.236 (8.40)	−0.240 (8.12)	−0.476 (12.4)	−0.075 (28.1)	−0.143 (43.0)
Food-Budget Share	0.928 (9.50)	0.793 (7.80)	1.72 (12.7)	0.128 (8.94)	0.209 (12.9)
IMR for the First Birth, Derived From Heckit Probit (addresses selectity bias)	0.405 (4.54)	0.368 (4.95)	0.773 (8.24)	…	…
Log (Household Total Landholding)	−	−	−	−0.016 (3.90) **	−0.021 (−4.69)
Household Rent, Dummy	−	−	−	−0.008 (−0.81)	−0.002 (−0.20)
Constant	−5.02 (9.49)	−5.09 (9.36)	−10.1 (14.1)	−	−1.54
R2/Pseudo R2	0.241	0.230	0.404	0.66	0.68
N	8135	8135	8135	12,715	12,715 ξ

* p < 0.05; ** p < 0.000. Notes: ^ξ: Censored observations: 12,715 minus 8135 = 4580; column (4) computes probit IMR and column (5) computes LPM GR (P^hat − 1) that turns out to be a good approximation to the IMR for the wage employment probit. In order to use the Olsen method, estimations are required of the LPM for selection of mothers into wage employment sample (column 5) and the probit model for the selection of women into the motherhood sample, column (4). Notice that in the rare and unlikely case where the selections are random, the two estimations are not needed.

). However, the Olsen linear probability specification for the first-birth, yields very different results as seen in the estimates obtained using the Wooldridge (2015) and Gourieroux et al. (1987) generalized residuals procedure. Still, when the probit specification is used to characterize the first birth in both the Olsen and the Heckman setups, the parameter estimates on wage employment in either case are nearly the same because the probit design for the wage employment dummy rules out the correlation between the structural error term and the inverse of Mills ratio that serves as a crucial exogenous regressor in the fertility models. In a further analysis, we find that the Poisson model yields better estimates than those obtained using the Heckman approach because the Poisson takes into account the count nature of the fertility variable (in the linear part of the Heckit model), when the parameter of interest (the coefficient on wage employment dummy) is being estimated (see Appendix C). It is worth emphasizing that the two-step Heckit procedure, as currently implemented using STATA and other algorithms, cannot handle the count data nature of the dependent variable of interest here, i.e., the number of live births recorded in a household over a given time period. To address this issue, the Poisson model (Favero et al., 2020), leveraged on control functions (Gourieroux et al., 1987; Wooldridge, 2015), is chosen as the preferred estimation method.

5. A Snapshot of Sample Data

The estimation dataset is derived from a nationally representative household survey conducted by the Kenya National Bureau of Statistics (KNBS) in 2015-16. A snapshot of the summary statistics for the main variables–derived from the analytic sample (see Appendix E), shows the following:

• About 17.4% of women had wage employment.
• Close to 65% of women had given birth by the time of the survey.
• The household size was 5.5.
• The total number of children born (per woman) was 3.5.
• The number of male children born alive was 1.79 per woman.
• The number of female children born alive was 1.75.
• About 65% of households had experienced severe drought or floods.
• The average age of women in the labor force (age 15–64) was 32.2 years, but for those in the estimation sample it was below 30.
• Approximately, 63% of the households lived in rural areas.
• Nearly 85% of women had attended school.
• The food-budget share was 60% of household total expenditure, suggesting that the majority of the households were food poor.
• About 1.4 children lived away from home.
• Around 47% of women were in monogamous marriages.

6. Key Findings

6.1. OLS Estimates

Table 1. The association between fertility and female wage employment, controlling for sociodemographic covariates, OLS Estimates (t-statistics in parentheses).

Variables	Number of Males Born Alive	Number of Females Born Alive	Total Number of Children Born Alive	Ever Given Birth? (Yes = 1)
Wage Employment (=1)	−0.174 (4.88) **	−0.087 (2.25) **	−0.261 (5.18) **	0.037 (5.01) **
Shocks
(1 = Severe Droughts/Floods)	0.185 (5.98) **	0.189 (5.82) **	0.373 (8.80) **	0.017 (3.21) **
Religion
(1 = Christians)	−0.068 (1.81) *	−0.051 (1.41) *	−0.111 (2.40)	−0.003 (0.57)
Married (1 = Yes)
	0.252 (8.02) **	0.178 (5.31) **	0.430 (9.5) **	0.260 (36.4) **
Educated (1 = Yes)
	−0.776 (11.3) **	−0.780 (10.9) **	−1.56 (16.3) **	−0.064 (1.90) *
Rural (=1)
	0.102 (3.02) **	0.193 (5.53) **	0.294 (6.43) **	0.010 (1.69) *
Age, Years
	0.152 (11.82) **	0.163 (12.0) **	0.314 (17.6) **	0.118 (63.0) **
Age Squared × 10−2
	−0.111 (5.71) **	−0.123 (5.93) **	−0.234 (8.56) **	0.151 (53.3) **
Food-Budget Share
	0.740 (9.36) **	0.762 (9.52) **	1.61 (12.4) **	0.222 (13.9) **
Constant
	−2.07 (9.56) **	−2.29 (10.1) **	−4.36 (14.3) **	−1.57 (54.7) **
R-Squared	0.237	0.227	0.398	0.683
N	8135	8135	12,715	8135

** p < 0.000; * p < 0.05. Note: The coefficients on the wage employment dummy in the intensive margin models (births) are all negative and statistically significant at p > 0.000 but the counterpart estimate for the extensive margin (ever given birth?) is positive and equally statistically significant.

presents baseline results that serve as benchmarks for demonstrating improvements made by estimation methods that depart from the OLS assumptions.

6.2. Heckit/CF Estimates

Table 2. Wage Employment and Fertility: Summary of Regression Results.

	Heckit/CF Estimates (t-Statistics in Parentheses)
	Dependent Variables (Intensive Margin, Structural Models			Ever Given Birth? (Yes), Extensive Margin, Reduced-Form Models
	Total Babies Born Alive (CF/Heckit)	Babies Born Alive, Males (CF/Heckit)	Babies Born Alive, Females (CF/Heckit)	LPM Reduced Form-Estimates a	Probit Marginal Effects: Reduced- Form Estimates a
Female Wage Employment (=1) t-tests	−0.197 (3.87) **	−0.141 (3.85) **	−0.057 (1.47) *	0.034 (4.72) **	0.026 (3.70) **
χ2/F tests	χ2(2) = 28.61 * (p < 0.05)	χ2(2) = 28.4 ** (p < 0.000)	χ2(2) = 15.77 (p < 0.000)	F (1) = 20.5 (p < 0.000)	χ2(2) = 11.87 (p < 0.000)
Estimates of births for a cohort of 1000 women, given prob. of first-birth = 0.026.	(−0.197 × 0.026) = −5.122	(−0.140 × 0.026) = −3.640	(−0.057 × 0.026) = −1.482
	N = 8135	N = 8135	N = 8135	N = 12,715 ξ

** p > 0.000; * p < 0.05. Notes: ^ξ: Censored observations: N = 12,715 minus 8135 = 4580 (women with missing dependent variables in the intensive margin models, i.e., women without a first birth and therefore have zero. higher-order births: All the controls in the OLS models in Table 1 are included in the Heckit/CF and Poisson/CF models in Table 2 and Table 3 (see also Appendix A and Appendix B). ^a: Includes instruments for wage employment dummy.

contains estimation results that are free of endogeneity and sample selectivity biases but may still contain a bias due to the disrete nature of births.

6.3. Poisson/Negative-Binomial Results (Preferred Estimates)

Table 3 shows regression estimates derived taking into account the discrete nature of births. The results show that the Heckit estimates understate the number of male, female, and total births, by 11.4%, 24.6%, and 15.7%, respectively.

Table 3. Wage Employment and Fertility: Summary of Regression Results (Poisson/Negative Binomial Regression Estimates, Average Marginal Effects (AME), t-statistics in parentheses.

Variables	Male Live Births (1)	Female Live Births (2)	Total Live Births (3)	First Birth? (Yes = 1) Reduced-Form Probit: AME (4)
Wage Employment (=1)	Coef = −0.085 AME = −0.157 t = (4.44) **	−0.039 −0.071 (1.82) *	−0.062 −0.228 (4.44) **	0.026 (3.70) **
Estimation Method	Generalized Negative Binomial	Poisson	Negative Binomial	MLE
Over-Dispersion Test; Ho: Equidispersion	Ln pr (Male Births) −0.066 (8.97) **	Ln pr (Female Births) 0.0099 (1.22)	Ln pr (Total Births) −0.040 (10.72) **	…
All Covariates Included in the Baseline, OLS Model Included here?	Yes	Yes	Yes	Yes
N	8135	8135	8135	12,715

** p > 0.000; * p < 0.05. Notes: (i) Equidispersion hypothesis is rejected for male and total births; (ii) The AME coefficients show the changes in logs of births associated with the wage employment dummy in the intensive margin models (columns 1–3) plus changes in probability of first birth (column 4).

Table 3. Wage Employment and Fertility: Summary of Regression Results (Poisson/Negative Binomial Regression Estimates, Average Marginal Effects (AME), t-statistics in parentheses.

Variables	Male Live Births (1)	Female Live Births (2)	Total Live Births (3)	First Birth? (Yes = 1) Reduced-Form Probit: AME (4)
Wage Employment (=1)	Coef = −0.085 AME = −0.157 t = (4.44) **	−0.039 −0.071 (1.82) *	−0.062 −0.228 (4.44) **	0.026 (3.70) **
Estimation Method	Generalized Negative Binomial	Poisson	Negative Binomial	MLE
Over-Dispersion Test; Ho: Equidispersion	Ln pr (Male Births) −0.066 (8.97) **	Ln pr (Female Births) 0.0099 (1.22)	Ln pr (Total Births) −0.040 (10.72) **	…
All Covariates Included in the Baseline, OLS Model Included here?	Yes	Yes	Yes	Yes
N	8135	8135	8135	12,715

** p > 0.000; * p < 0.05. Notes: (i) Equidispersion hypothesis is rejected for male and total births; (ii) The AME coefficients show the changes in logs of births associated with the wage employment dummy in the intensive margin models (columns 1–3) plus changes in probability of first birth (column 4).

7. Observations on Parameter Estimates

The Poisson/Negbin/control function estimates are the preferred results because they are free of sample selection and endogeneity biases, and are further consistent with the count data nature of the dependent variable—the number of children born per woman over a given time period. The Poisson coefficient on wage employment (−0.228) for total births is 15.7% larger than that for the Heckit coefficient (−0.197) because the latter procedure does not take into address the count nature of births. However, the qualitative conclusion of the paper remains the same, irrespective of the estimation method—i.e., female wage employment is negatively associated with higher order births and positively with the probability of the first birth.

• The decline in the number of male live births associated with female wage employment is 2.0–2.5 times larger than that for female babies in all models, including the OLS estimates.
• Female wage employment is associated with a 0.197 and a 0.228 reduction in the total number of babies born alive in the Heckit and Poisson models, respectively, with the Poisson estimate being 15.7% higher.
• Additionally, female wage employment is associated with a 2.6% increase in the probability of the first birth.
• The number of subsequent live births associated with female wage employment status naturally depends on the first birth; thus, the two should be modeled together, as performed in this paper.
• If fertility at the intensive margin is zero, it is also zero at the extensive margin, i.e., in a given survey period, women who report a zero for the first birth also report a zero for a higher-order birth. It is worth clarifying that women who report a zero for the first birth are taken into account in the estimation of the association between fertility and female wage employment at both margins using the Heckit (Heckman, 1979) and the Poisson (Favero et al., 2020) procedures.
• In the Heckit formulation of the fertility model, women reporting a zero for the first birth are included in the selection equation (estimated with a sample for all women) but are excluded from the structural equation (estimated using only the motherhood sample). In the Poisson model, only women with non-zero counts for the number of children born alive are included in the motherhood sample, by design of the Heclit, even though the Poisson counts zeros (Favero et al., 2020). However, as in the usual Heckman setup, a variable that captures the unobservable covariates in the selection equation, i.e., the inverse of the Mills ratio, is included as an explanatory in the fertility models to ensure that the estimates are generalizable outside of the motherhood sample (see Appendix A). Thus, data from both sample margins are taken into account during estimations.
• Changes in fertility at both margins determine the population-level fertility associated with an exogenous variation in the female labor force participation.
• A 1% exogenous increase in the probability of female wage employment in the Poisson model is associated with a 0.05 reduction in fertility, i.e., (−0.228)*(0.026) = −0.051; see the first row of Table 3 and columns 3 and 4.
• The evidence generated in this paper can be used to design female wage employment policies that encourage population-level fertility decisions in socially desired ways while also: (i) enhancing women’s reproductive health; (ii) empowering women economically and socially; (iii) improving child health in utero; (iv) addressing disparities in sex ratios; (v) improving work environments for expectant mothers; (vi) making childcare broadly available; and (vi) improving women’s overall human capital.
• The Heckit two-step estimates are consistent across specifications when the correlation between the structural equation error term and the error term of the selection equation is not close to + −1 (see Nawata, 1994, Tables 1–6). The rho values for our Heckit two-step models are generally less than 0.45. Multi-collinearity is absent from the data because the VIF value is below two. Additional robustness tests show that the two-step Heckit coefficient estimates are close to the estimates obtainable with the MLE estimator using publicly available data in STATA software, version 14).
• The OLS estimate (−0.261) of the association between fertility and female wage employment (Table 2) is 32.5% larger than the CF’s estimate. The OLS upward bias in the structural models is 23–56% of the Heckit/Poisson estimates. However, even though when expressed in ratio form, these coefficients are about the same across gender (2.0–2.5), the OLS ratios are misleading because they fail to reveal that the underlying absolute OLS coefficient estimates exaggerate the reduction in fertility associated with an increase in female wage employment.
• It is worth noting that the models generating the preferred parameter estimates presented in Table 2 and Table 3 are short-form versions of complex Heckit/Control function models (see Appendix E). The coefficient estimates for the long-form models are the same as for the short-form models, designed to shorten lengthy results tables, printed out by estimation algorithms currently in use (see e.g., appendix results printouts from STATA versions 14 or 17). The results for the long-form models (STATA results printouts) are included in the Appendix tables to highlight the enormous economy of presentation made possible by the short-form models presented in the main text. The exact correspondence of parameter estimates in the two forms is worth noting, especially since they are derived differently. Lastly, in some results tables in the main text, and in the Appendixes, the term effects and correlations are used synonymously, but the estimated coefficients should be interpreted as associations, not as causal effects.

8. Contextualization and Synthesis

Between the 1980s and 2022, Kenyan fertility declined from around 7 to 3.4 children per woman. However, since our paper relies on cross-sectional data, we cannot tell the extent to which this decline is associated with female wage employment, as low wage participation rate (a proxy for FLFP) can coexist with low fertility; see, e.g., Stuart et al. (2021) for data from South Asia. Although our paper documents a strong negative association between wage employment and fertility in Kenya, this correlation may not hold over time or even across other African countries because contextual factors can confound it. Still, as shown in the biomedical literature, it is possible to attribute differences in the numbers of boys and girls born to unfavorable work environments of mothers, to which male embryos are more vulnerable. We treat this as a mere hypothesis. Adverse cultural and social factors can also generate evidence consistent with the above hypothesis. An example of an adverse cultural factor in this respect is the social pressure for women to have a male child. Such pressure, combined with demands of wage work can elevate an expectant mother’s stress and affect the health of unborn children. DiPietro and Voegtline (2017, p. 1) cite evidence showing that “male fetuses exposed to prenatal and perinatal adversities are more highly impaired than those of female fetuses” due to ‘selective male affliction.

Moreover, there are male-specific biological adversities in utero. Orzack (2016, p. 26) observes that “in the week or so after conception, more male than female embryos may die, since the former have a higher tendency to contain chromosomal abnormalities that are incompatible with normal development.” Elaborating further, Orzack notes “… unbiased sex ratio at conception and the male bias at birth imply necessarily that total female mortality during pregnancy exceeds total male mortality…” Orzack (2016, p. 27).

These points are worth emphasizing. Since the biomedical evidence reveals that the sex ratio at conception is unbiased and national demographic statistics show that there are more males than females at birth, it follows that mortality in utero must be higher for girls. It seems, therefore, that boys are more resilient to adversities in utero than girls, contrary to the biomedical evidence. Everything else held constant—except for the unobservable determinants of fetal health during the gestation period—more male embryos would survive shocks in utero, with the overall outcome being a pro-male sex ratio at birth. However, the interaction between the two kinds of adversities that afflict fetal health during the gestation period, i.e., (i) the mother’s work-related external shocks and (ii) the shocks in utero that are due to unobservable biological and genetic processes, can have unpredictable net effects on the numbers of boys and girls born alive.

Additional biomedical evidence shows that male embryos are characterized by excess abnormalities and are more vulnerable to adversities in utero, as well as to shocks arising from the mother’s work context. However, lacking in this literature is the role played by cultural and socioeconomic factors in the survival of embryos. As already noted, the effects of external adversities are transmitted to the embryo through the mother during pregnancy. Thus, the survival probability of an embryo depends on its resilience to external stress. Subsequently, a mother’s adverse work conditions should reduce the number of boys and girls she delivers. However, if everything else were to be held constant except for selective male afflictions in utero (McCarthy, 2019), the number of boys born would be smaller than the number of girls, due to afflictions. The econometric estimates are consistent with this view. Notably, an increase in female wage employment, holding other factors constant, yields the same outcome. The difference in the number of female and male births at birth cannot be determined by simple predictions.

The finding of a negative correlation between fertility and female wage employment may not be generalizable to other African contexts or even to population sub-samples across Kenyan counties. See, e.g., Donald et al. (2024), who report a positive correlation between fertility and wage employment in a number of African countries. This positive association is consistent with the idea that wage income can increase mothers’ ability to pay for childcare, a scenario that is pro-natal, while also offering an opportunity to invest in greater child quality, a situation that could reduce fertility. Our hybrid model suggests that fertility–employment association can be zero, positive, or negative.

9. Conclusions

Female wage employment in Kenya is negatively associated with the number of live births and positively with the probability of the first birth. The latter association is noteworthy because, as women in Kenya and other African countries delay marriage and first births to invest in education and careers (see, e.g., Schultz, 2002), policies to increase fertility at older ages would become necessary. The literature suggests that although assisted reproductive health technologies (Yi et al., 2022) can be used to achieve this objective, they also carry major risks (Yu & Liang, 2022). An inverted U-shaped relationship between fertility and the mother’s age (Table A1 and Table A5) suggests existence of an optimal child-bearing age, with lower and upper bounds. Teenage pregnancy occurs below the lower bound, and is strongly discouraged by widespread social norms in many societies (Stuart et al., 2021). However, even when such norms are in force, policies and support systems can be designed to enable teenage mothers to continue learning (see, e.g., Morgan et al., 2025). Such policies could also avoid severe side effects and financial risks associated with the use of assisted reproductive technologies beyond the optimal age.

The estimation results from all the four methods employed (Poisson, Heckit/CF, Olsen/CF, and the OLS) consistently show that: (i) female education is negatively and significantly correlated with fertility (number of live births); (ii) more births occur in rural than in urban areas; (iii) adverse shocks correlate positively with fertility; (iv) poverty (proxied by the food-budget share) is positively associated with fertility (see Aassve et al., 2006); (v) marriage is an important predictor of fertility. Although these results capture associations between fertility indicators and female wage employment, they also point to factors outside the measured correlations that could be explored in the design of policies to accelerate the development of women’s human capital in Kenya and beyond.

Finally, there is need to search for policies to improve fetal and maternal health and other forms of women’s human capital, over and above what is currently being achieved, by the existing antenatal interventions in low-income countries, especially in Africa. An example of such an intervention—based on the literature, is the establishment of social support groups for expectant mothers, especially the unemployed, as these are the ones at greatest risk of suffering physical and/or psychological distress (McCarthy, 2019). The groups should be community-based, but entrenched within the public health system via a separate budgetary allocation.