On the Asymmetric Relation between Inflation and Growth in Mexico: A NARDL Approach
Abstract
1. Introduction
2. A Brief Literature Review
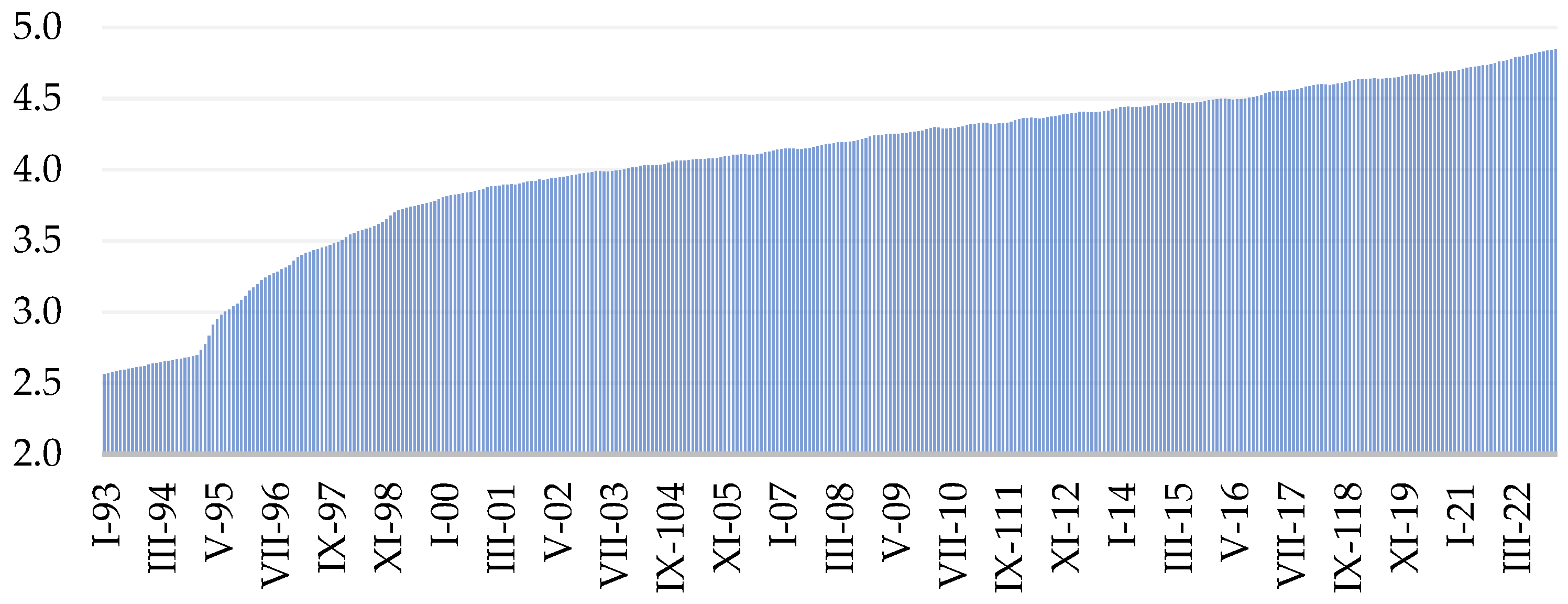
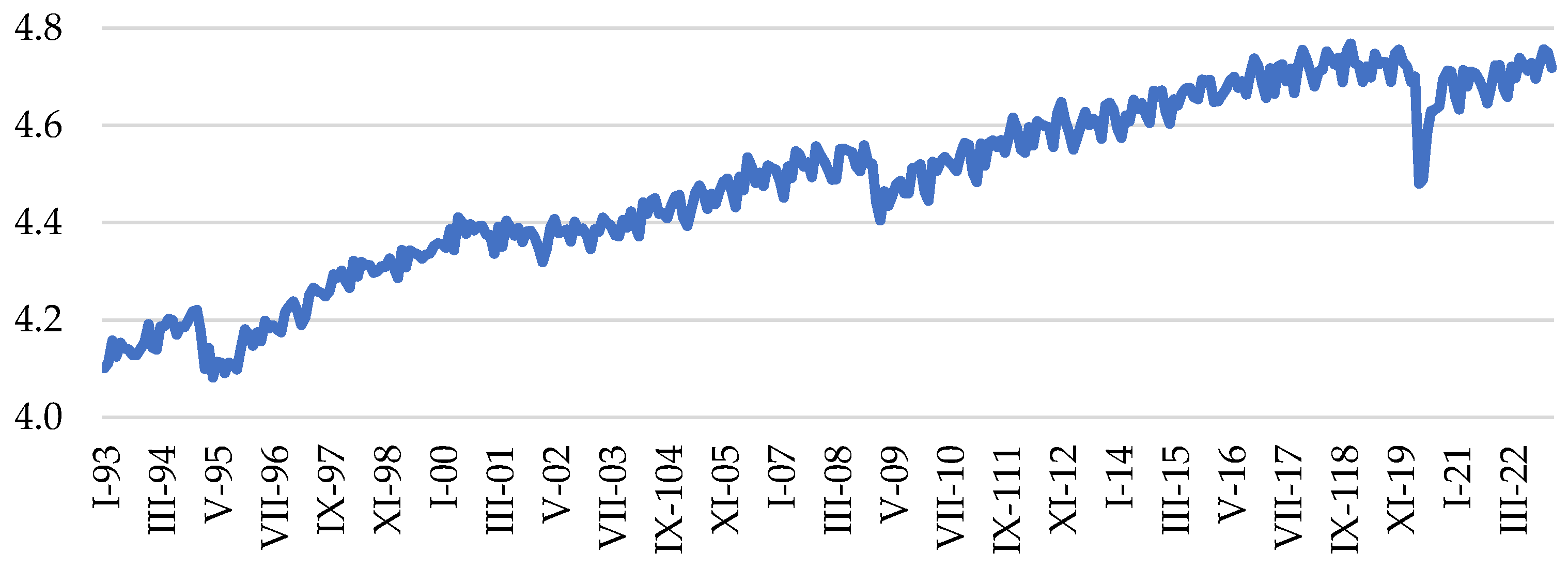
3. Price Level and Economic Activity in Mexico from 1993 to 2023
- -
- US Fed’s balance sheet (WALCL) as a proxy for the US unconventional monetary policy and its spillovers (Cortes et al. 2022), which considers changes in the size of the Federal Reserve’s balance sheet and liquidity provided can have significant implications for global financial markets, including Mexico (liquidity, interest rates, exchange rates, and investment flows);
- -
- Shadow rates (SR) (Wu and Xia 2016), as indicative of the monetary policy stance in economies practicing near-zero or negative interest rates. In this case, possible impacts are (1) monetary policy transmission (unconventional monetary policies of central banks), (2) risk appetite (lower shadow rates in major economies, increased risk appetite of investors flowing capitals into emerging markets), and (3) currency valuation (weakened currency in a major economy can make exports more competitive in emerging markets).
- -
- Global Policy Uncertainty Index (GPUI) (Davis 2016; Coronado et al. 2020) that measures the uncertainty related to economic policy globally, which can affect economic decision-making and outcomes, such as investment decisions (uncertain about future policies, more risk, and investment reduction), consumer behavior (economic growth reduction, inflation, job losses), trade flows (global economic conditions impact on exports and imports), and inflation expectations (adjustment of monetary policy in response to).
4. Methodology and Justification of the Nonlinear Autoregressive Distributed Lag (NARDL) Model
4.1. Limitations of Other Specifications
4.2. Setting Up the NARDL
5. Empirical Results: Identification of Unit Root Test and the ARDL Model as First Step
5.1. Unit Root Test
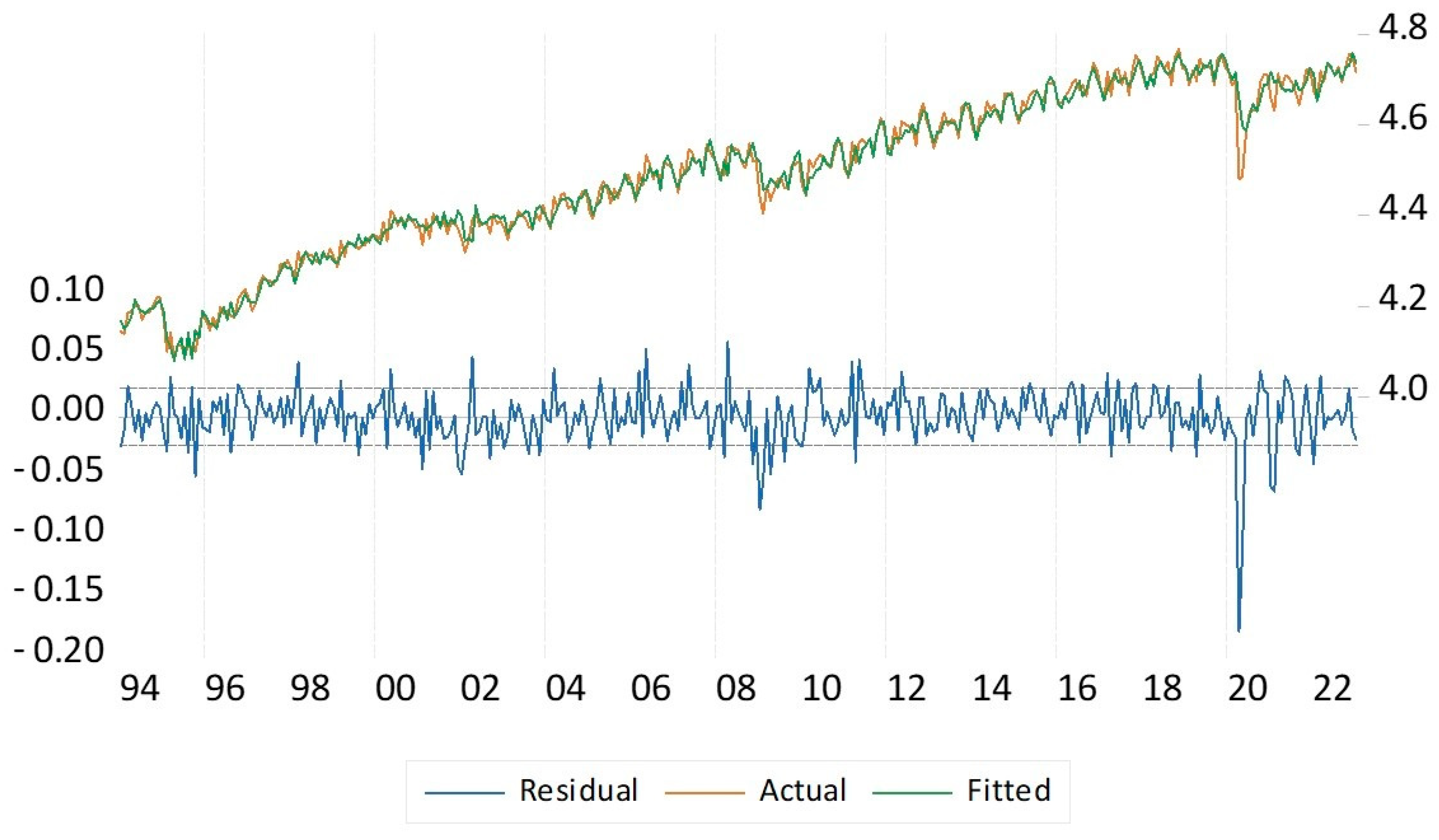
5.2. Validation and Application of the ARDL Model
6. Empirical Results of the Asymmetric Relationship and Identification of the Optimal NARDL Model
6.1. Optimal Lags for NARDL
6.2. Estimation and Optimization of Asymmetry
6.3. Long-Run Form (LRF) Asymmetric Test and Wald Test Validation
6.4. Asymmetric Dynamic Multipliers
7. Discussion of the Empirical Results
7.1. Short-Term Implications
7.2. Long-Term Implications
8. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adeleye, Bosede Ngozi, Sodiq Arogundade, and Biyase Mduduzi. 2023. Empirical Analysis of Inclusive Growth, Information and Communication Technology Adoption, and Institutional Quality. Economies 11: 124. [Google Scholar] [CrossRef]
- Al Khatib, Abdullah Mohammad Ghazi. 2023. The complexity of financial development and economic growth nexus in Syria: A nonlinear modelling approach with artificial neural networks and NARDL model. Heliyon 9: e20265. [Google Scholar] [CrossRef] [PubMed]
- Alharbi, Farea Mohammed. 2022. How Do the Remittance Outflows React to Economic Development in Saudi Arabia? Evidence from NARDL. Economies 10: 105. [Google Scholar] [CrossRef]
- Allen, David, and Michael McAleer. 2021. A Nonlinear Autoregressive Distributed Lag (NARDL) Analysis of the FTSE and S&P500 Indexes. Risks 9: 195. [Google Scholar] [CrossRef]
- Anda, Milin Ioana, Bușan Gabriela, Ecobici Nicolae, and Abdul Rehman. 2023. Economic Growth Drivers in Romania: Evidence from a NARDL Analysis. Sustainability 15: 5916. [Google Scholar] [CrossRef]
- Arize, Augustine C., John Malindretos, and Emmanuel U. Igwe. 2017. Do Exchange Rate Changes Improve the Trade Balance: An Asymmetric Nonlinear Cointegration Approach. International Review of Economics & Finance 49: 313–26. [Google Scholar] [CrossRef]
- Atil, Ahmed, Amine Lahiani, and Duc Khuong Nguyen. 2014. Asymmetric and Nonlinear Pass-through of Crude Oil Prices to Gasoline and Natural Gas Prices. Energy Policy 65: 567–73. [Google Scholar] [CrossRef]
- Atkeson, Andrew, and Patrick J. Kehoe. 2004. Deflation and Depression: Is There an Empirical Link? American Economic Review 94: 99–103. [Google Scholar] [CrossRef]
- Azariadis, Costas, and Bruce D. Smith. 1996. Private Information, Money, and Growth: Indeterminacy, Fluctuations, and the Mundell-Tobin Effect. Journal of Economic Growth 1: 309–32. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, Mohsen, Dan Xi, and Sahar Bahmani. 2019. More Evidence on the Asymmetric Effects of Exchange Rate Changes on the Demand for Money: Evidence from Asian. Applied Economics Letters 26: 485–95. [Google Scholar] [CrossRef]
- Bailey, Warren, Kalok Chan, and Y. Peter Chung. 2000. Depositary receipts, country funds, and the peso crash: The intraday evidence. The Journal of Finance 55: 2693–717. [Google Scholar] [CrossRef]
- Bailey, Warren, and Peter Chung. 1995. Exchange rate fluctuations, political risk, and stock returns: Some evidence from an emerging market. Journal of Financial and Quantitative Analysis 30: 541–61. [Google Scholar] [CrossRef]
- Banerjee, Jyotirmoy. 1998. United Germany: Quo Vadis? Jadavpur Journal of International Relations 4: 1–12. [Google Scholar] [CrossRef]
- Banxico. 2009. Inflation Report January—March 2009 Resume. Banco de México. CDMX, Mexico. April 28. Available online: https://www.banxico.org.mx/publicaciones-y-prensa/informes-trimestrales/%7BE5FA3814-DF51-6A97-1B9E-AEF929F93A5E%7D.pdf (accessed on 1 September 2023).
- Banxico. 2017. Executive Summary, Quarterly Report October—December 2017. Banco de México. CDMX, Mexico. December 31. Available online: https://www.banxico.org.mx/publicaciones-y-prensa/informes-trimestrales/%7B263682EB-EEC3-BCD1-BF5E-A595871E8EB8%7D.pdf (accessed on 31 December 2023).
- Banxico. 2022. Press Release. Monetary Policy Announcement. Banco de México. CDMX, Mexico. September 29. Available online: https://www.banxico.org.mx/publicaciones-y-prensa/anuncios-de-las-decisiones-de-politica-monetaria/%7BE6A0E26E-D9C0-97D7-64B7-7F2BF274178E%7D.pdf (accessed on 1 December 2023).
- Barro, Robert. 1995. Inflation and Economic Growth. Cambridge: National Bureau of Economic Research. [Google Scholar] [CrossRef]
- Bayer, Christian, and Christoph Hanck. 2013. Combining Non-Cointegration Tests. Journal of Time Series Analysis 34: 83–95. [Google Scholar] [CrossRef]
- Bloom, Nicholas. 2009. The Impact of Uncertainty Shocks. Econometrica 77: 623–85. [Google Scholar] [CrossRef]
- Bordo, Michael D., and Angela Redish. 2004. Is Deflation Depressing? Evidence From the Classical Gold Standard. In Deflation. Edited by Burdekin Richard and Siklos Pierre. Cambridge: Cambridge University Press, pp. 191–217. [Google Scholar] [CrossRef]
- Borio, Claudio, and Andrew Filardo. 2004. Back to the Future? Assessing the Deflation Record. No. 152. Basel: Bank for International Settlements. [Google Scholar] [CrossRef]
- Boswijk, H. Peter. 1995. Efficient Inference on Cointegration Parameters in Structural Error Correction Models. Journal of Econometrics 69: 133–58. [Google Scholar] [CrossRef]
- Brock, William, Davis Dechert, and José Sheinkman. 1996. A Test of Independence Based on the Correlation Dimension. Econometric Reviews 15: 197–235. Available online: https://scholar.google.com/scholar_lookup?journal=Econom.+Rev.&title=A+test+for+independence+based+on+the+correlation+dimension&author=W.A.+Brock&author=J.A.+Scheinkman&author=W.D.+Dechert&author=B.+LeBaron&volume=15&publication_year=1996&pages=197-235&doi=10.1080/07474939608800353& (accessed on 1 September 2023). [CrossRef]
- Brooks, Chris. 2019. Introductory Econometrics for Finance. Cambridge: Cambridge University Press. [Google Scholar] [CrossRef]
- Campello, Murillo, Gustavo Cortes, Fabrício d’Almeida, and Guarav Kankanhalli. 2022. Exporting Uncertainty: The Impact of Brexit on Corporate America. Journal of Financial and Quantitative Analysis 57: 3178–222. [Google Scholar] [CrossRef]
- Cerezo-García, Verónica, Teresa S. López-González, and Francisco López-Herrera. 2019. Crecimiento Económico e Inflación En México, 1993–2018: ¿Una Relación Lineal o No Lineal? Investigación Económica 79: 83. [Google Scholar] [CrossRef]
- Chang, Chiu-Lan, and Ming Fang. 2023. Impact of a Sharing Economy and Green Energy on Achieving Sustainable Economic Development: Evidence from a Novel NARDL Model. Journal of Innovation & Knowledge 8: 100297. [Google Scholar] [CrossRef]
- Chen, Hao, Duncan O. Hongo, Max William Ssali, Maurice Simiyu Nyaranga, and Consolata Wairimu Nderitu. 2020. The Asymmetric Influence of Financial Development on Economic Growth in Kenya: Evidence From NARDL. SAGE Open 10: 2158244019894071. [Google Scholar] [CrossRef]
- Chen, Tinggui, Lijuan Peng, Jianjun Yang, and Guodong Cong. 2021. Analysis of User Needs on Downloading Behavior of English Vocabulary APPs Based on Data Mining for Online Comments. Mathematics 9: 1341. [Google Scholar] [CrossRef]
- Cho, Jin Seo, Tae-hwan Kim, and Yongcheol Shin. 2015. Quantile Cointegration in the Autoregressive Distributed-Lag Modeling Framework. Journal of Econometrics 188: 281–300. [Google Scholar] [CrossRef]
- Coronado, Semei, José N. Martínez, and Francisco Venegas-Martínez. 2020. Spillover Effects of the US Economic Policy Uncertainty in Latin America. Estudios de Economía 47: 273–93. Available online: https://estudiosdeeconomia.uchile.cl/index.php/EDE/article/view/59173 (accessed on 1 September 2023). [CrossRef]
- Cortes, Gustavo S., George P. Gao, Felipe B. G. Silva, and Zhaogang Song. 2022. Unconventional Monetary Policy and Disaster Risk: Evidence from the Subprime and COVID-19 Crises. Journal of International Money and Finance 122: 102543. [Google Scholar] [CrossRef]
- Das, Anupam, Leanora Brown, and Adian McFarlane. 2023. Asymmetric Effects of Financial Development on CO2 Emissions in Bangladesh. Journal of Risk and Financial Management 16: 269. [Google Scholar] [CrossRef]
- Davis, Steven J. 2016. An Index of Global Economic Policy Uncertainty. Macroeconomic Review. Cambridge: National Bureau of Economic Research. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1981. Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root. Econometrica 49: 1057. [Google Scholar] [CrossRef]
- Ekpeyong, Paul. 2023. Econometric Analysis of the Impact of Inflation, Unemployment, and Economic Growth on Poverty Reduction: A Novel Application of Asymmetric Technique. Munich Personal RePEc Archive. Available online: https://mpra.ub.uni-muenchen.de/117762/1/INFLATION%2C%20UNEMPLOYMENT%2C%20ECONOMIC%20GROWTH%20ON%20POVERTY.pdf (accessed on 31 December 2023).
- Elizondo, Rocio. 2012. Estimaciones Del PIB Mensual Basadas En El IGAE. 2012–11. CDMX, Mexico. Available online: https://www.banxico.org.mx/publicaciones-y-prensa/documentos-de-investigacion-del-banco-de-mexico/%7BB583DA23-0F6A-2F56-3B50-F575F405EEB1%7D.pdf (accessed on 1 September 2023).
- Engle, Robert F., and C. W. J. Granger. 1987. Co-Integration and Error Correction: Representation, Estimation, and Testing. Econometrica 55: 251. [Google Scholar] [CrossRef]
- Fischer, Stanley. 1993. The Role of Macroeconomic Factors in Growth. Cambridge: National Bureau of Economic Research. [Google Scholar] [CrossRef]
- Friedman, Milton. 1977. Nobel Lecture: Inflation and Unemployment. Journal of Political Economy 85: 451–72. [Google Scholar] [CrossRef]
- Gao, Cuixia, Ying Zhong, Isaac Adjei Mensah, Simin Tao, and Yuyang He. 2022. Spatio-Temporal Impact of Global Migration on Carbon Transfers Based on Complex Network and Stepwise Regression Analysis. Sustainability 14: 844. [Google Scholar] [CrossRef]
- Granger, Clive. W. J. 1969. Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econometrica 37: 424. [Google Scholar] [CrossRef]
- Gulen, Huseyin, and Mihai Ion. 2016. Policy Uncertainty and Corporate Investment. The Review of Financial Studies 29: 523–64. [Google Scholar] [CrossRef]
- Hattori, Masazumi, Andreas Schrimpf, and Vladyslav Sushko. 2016. The Response of Tail Risk Perceptions to Unconventional Monetary Policy. American Economic Journal: Macroeconomics 8: 111–36. [Google Scholar] [CrossRef]
- Hazell, Jonathon, Juan Herreño, Emi Nakamura, and Jón Steinsson. 2022. The slope of the phillips curve: Evidence from us states. The Quarterly Journal of Economics 137: 1299–344. [Google Scholar] [CrossRef]
- Hossain, Mohammed Akter, Hakan Acet, Zobayer Ahmed, and Alauddin Majumder. 2021. Revisiting Inflation and Growth Nexus: An Asymmetric Cointegration Based on Non-Linear ARDL Approach in Case of Bangladesh. Revista Finanzas y Política Económica 13: 371–402. [Google Scholar] [CrossRef]
- Hsu, Ching-Chi, and Fengsheng Chien. 2023. The Impact of High Economic Growth and Technology Advancement on Extensive Energy Production in China: Evidence Using NARDL Model. Environmental Science and Pollution Research 30: 1656–71. [Google Scholar] [CrossRef]
- INEGI. 2013. Sistema de Cuentas Nacionales de México, Fuentes y Metodologías, Indicador Global de Actividad Económica. INEGI. CDMX, Mexico. Available online: https://www.inegi.org.mx/contenidos/programas/igae/2013/metodologias/SCNM_Metodo_IGAE_B2013.pdf (accessed on 1 September 2023).
- Ismail, Yusra, and Mansur Masih. 2019. Is the Relationship between Inflation and Financial Development Symmetric or Asymmetric? New Evidence from Sudan Based on NARDL. Munich Personal RePEc Archive. Available online: https://mpra.ub.uni-muenchen.de/94694/1/MPRA_paper_94694.pdf (accessed on 1 December 2023).
- Johansen, Soren. 1991. Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models. Econometrica 59: 1551. [Google Scholar] [CrossRef]
- Kahneman, Daniel, and Amos Tversky. 1979. Prospect Theory: An Analysis of Decision under Risk. Econometrica 47: 263. [Google Scholar] [CrossRef]
- Kapetanios, George, Yongcheol Shin, and Andy Snell. 2003. Testing for a Unit Root in the Nonlinear STAR Framework. Journal of Econometrics 112: 359–79. [Google Scholar] [CrossRef]
- Karahan, Özcan, and Olcay Çolak. 2020. Inflation and Economic Growth in Turkey: Evidence from a Nonlinear ARDL Approach. In Economic and Financial Challenges for Balkan and Eastern European Countries. Edited by Marietta Janowicz-Lomott, Krzysztof Łyskawa, Persefoni Polychronidou and Anastasios Karasavvoglou. Cham: Springer, pp. 33–45. [Google Scholar] [CrossRef]
- Kassi, Diby François, Dilesha Nawadali Rathnayake, Akadje Jean Roland Edjoukou, Yobouet Thierry Gnangoin, Pierre Axel Louembe, Ning Ding, and Gang Sun. 2019. Asymmetry in Exchange Rate Pass-Through to Consumer Prices: New Perspective from Sub-Saharan African Countries. Economies 7: 5. [Google Scholar] [CrossRef]
- Khalili, Rahele, Kambiz Peykarjo, Kambiz Hojabr Kiani, and Abbas Memarnejad. 2023. Nonlinear effects of inflation on Iran’s economic growth: The NARDL approach. International Journal of Nonlinear Analysis and Applications 14: 1215–25. [Google Scholar] [CrossRef]
- Majeed, Muhammad Tariq, Isma Samreen, Aisha Tauqir, and Maria Mazhar. 2020. The Asymmetric Relationship between Financial Development and CO2 Emissions: The Case of Pakistan. SN Applied Sciences 2: 827. [Google Scholar] [CrossRef]
- Narayan, Paresh Kumar. 2004. Fiji’s Tourism Demand: The ARDL Approach to Cointegration. Tourism Economics 10: 193–206. [Google Scholar] [CrossRef]
- Nene, Shelter Thelile, Kehinde Damilola Ilesanmi, and Mashapa Sekome. 2022. The Effect of Inflation Targeting (IT) Policy on the Inflation Uncertainty and Economic Growth in Selected African and European Countries. Economies 10: 37. [Google Scholar] [CrossRef]
- Okun, Arthur M. 1971. The Mirage of Steady Inflation. Brookings Papers on Economic Activity 1971: 485. [Google Scholar] [CrossRef]
- Olamide, Ebenezer, Kanayo Ogujiuba, and Andrew Maredza. 2022. Exchange Rate Volatility, Inflation and Economic Growth in Developing Countries: Panel Data Approach for SADC. Economies 10: 67. [Google Scholar] [CrossRef]
- Olugbenga, Adaramola Anthony, and Oluwabunmi Dada. 2020. Impact of Inflation on Economic Growth: Evidence from Nigeria. Investment Management and Financial Innovations 17: 1–13. [Google Scholar] [CrossRef]
- Pan, Liurong, Asad Amin, Nian Zhu, Abbas Ali Chandio, Eric Yaw Naminse, and Aadil Hameed Shah. 2022. Exploring the Asymmetrical Influence of Economic Growth, Oil Price, Consumer Price Index and Industrial Production on the Trade Deficit in China. Sustainability 14: 15534. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, and Yongcheol Shin. 1995. An Autoregressive Distributed-Lag Modelling Approach to Cointegration Analysis. In Econometrics and Economic Theory in the 20th Century. Edited by Steinar Strom. Cambridge: Cambridge University Press, pp. 371–413. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, Yongcheol Shin, and Richard J. Smith. 2001. Bounds Testing Approaches to the Analysis of Level Relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Phelps, Edmund S. 1969. The New Microeconomics in Inflation and Employment Theory. The American Economic Review 59: 147–60. Available online: https://www.jstor.org/stable/1823664 (accessed on 1 September 2023).
- Phillips, Peter C. B., and Pierre Perron. 1988. Testing for a Unit Root in Time Series Regression. Biometrika 75: 335. [Google Scholar] [CrossRef]
- Pollin, Robert, and Zhu Andong. 2006. Inflation and Economic Growth: A Cross-Country Nonlinear Analysis. Journal of Post Keynesian Economics. Available online: https://www.jstor.org/stable/4538993 (accessed on 1 September 2023). [CrossRef]
- Rehman, Abdul, Laura Mariana Cismas, and Ioana Anda Milin. 2022. The Three Evils: Inflation, Poverty and Unemployment’s Shadow on Economic Progress—A Novel Exploration from the Asymmetric Technique. Sustainability 14: 8642. [Google Scholar] [CrossRef]
- Rodnyansky, Alexander, and Olivier M. Darmouni. 2017. The Effects of Quantitative Easing on Bank Lending Behavior. The Review of Financial Studies 30: 3858–87. [Google Scholar] [CrossRef]
- Sánchez-Vargas, Armando, and Francisco López-Herrera. 2020. Tasa de política monetaria en México ante los efectos de Covid-19. Revista Mexicana de Economía y Finanzas Nueva Época 15: 295–311. [Google Scholar] [CrossRef]
- Sargan, John. 1964. Wages and Prices in the United Kingdom: A Study in Econometric Methodology. Edited by E. Hart Peter, Mills Gordon and K. Whitaker John. Butterworth and London: Butterworth & Co Publishers Ltd. Available online: https://link.springer.com/referenceworkentry/10.1057/978-1-349-95121-5_2528-1#citeas (accessed on 1 September 2023).
- Saucedo, Eduardo, and Jorge Gonzalez. 2021. Exchange Rate Pass-Through to Prices in Mexico: A Study of the Main Border and Non-Border Cities. Revista Mexicana de Economía y Finanzas Nueva Época 16: e468. [Google Scholar] [CrossRef]
- Seker, Fahri, Hasan Murat Ertugrul, and Murat Cetin. 2015. The Impact of Foreign Direct Investment on Environmental Quality: A Bounds Testing and Causality Analysis for Turkey. Renewable and Sustainable Energy Reviews 52: 347–56. [Google Scholar] [CrossRef]
- Shiller, Robert J. 1998. Macro Markets. Oxford: Oxford University Press. [Google Scholar] [CrossRef]
- Shin, Yongcheol, Byungchul Yu, and Matthew Greenwood-Nimmo. 2014. Modelling Asymmetric Cointegration and Dynamic Multipliers in a Nonlinear ARDL Framework, 1st ed. Edited by Robin C. Sickles and William C. Horrace. New York: Springer. [Google Scholar] [CrossRef]
- Siaens, Alain. 1969. M. Friedman the Optimum Quantity of Money and Other Essays. Chicago, Aldine Publishing Company, 1969, VII p. 296 p., $ 9.95. Recherches Économiques de Louvain 35: 423–24. [Google Scholar] [CrossRef]
- Sowah, James Karmoh, Sema Yilmaz Genc, Rui Alexandre Castanho, Gualter Couto, Mehmet Altuntas, and Dervis Kirikkaleli. 2023. The Asymmetric and Symmetric Effect of Energy Productivity on Environmental Quality in the Era of Industry 4.0: Empirical Evidence from Portugal. Sustainability 15: 4096. [Google Scholar] [CrossRef]
- Temple, Jonathan. 2000. Inflation and Growth: Stories Short and Tall. Journal of Economic Surveys 14: 395–426. [Google Scholar] [CrossRef]
- Thanh, Su Dinh. 2015. Threshold Effects of Inflation on Growth in the ASEAN-5 Countries: A Panel Smooth Transition Regression Approach. Journal of Economics, Finance and Administrative Science 20: 41–48. [Google Scholar] [CrossRef]
- Tinoco-Zermeño, Miguel Ángel, Francisco Venegas-Martínez, and Víctor Hugo Torres-Preciado. 2014. Growth, Bank Credit, and Inflation in Mexico: Evidence from an ARDL-Bounds Testing Approach. Latin American Economic Review 23: 8. [Google Scholar] [CrossRef]
- Toda, Hiro Y., and Taku Yamamoto. 1995. Statistical Inference in Vector Autoregressions with Possibly Integrated Processes. Journal of Econometrics 66: 225–50. [Google Scholar] [CrossRef]
- Torun, Melike. 2023. Using the NARDL Model to Examine the Relationship between Oil Prices and Economic Growth: The Case of Turkey. Journal of Emerging Economies and Policy 8: 1–9. [Google Scholar]
- Wang, Xu, Jinrong Wang, and Michal Fečkan. 2020. BP Neural Network Calculus in Economic Growth Modelling of the Group of Seven. Mathematics 8: 37. [Google Scholar] [CrossRef]
- Wen, Jun, Samia Khalid, Hamid Mahmood, and Xiuyun Yang. 2022. Economic Policy Uncertainty and Growth Nexus in Pakistan: A New Evidence Using NARDL Model. Economic Change and Restructuring 55: 1701–15. [Google Scholar] [CrossRef]
- Wu, Jing Cynthia, and Fan Dora Xia. 2016. Measuring the macroeconomic impact of monetary policy at the zero lower bound. Journal of Money, Credit and Banking 48: 253–91. [Google Scholar] [CrossRef]
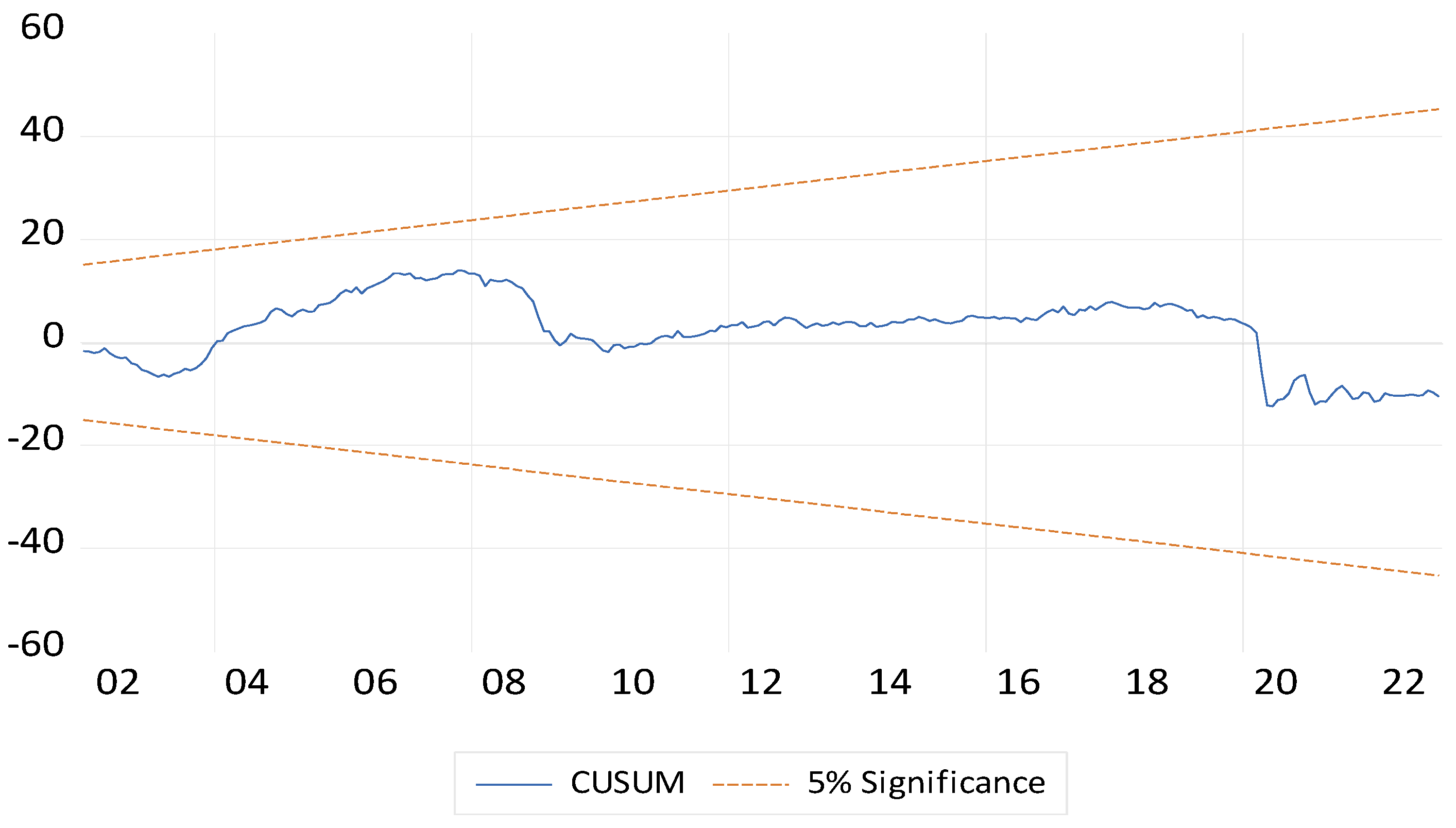
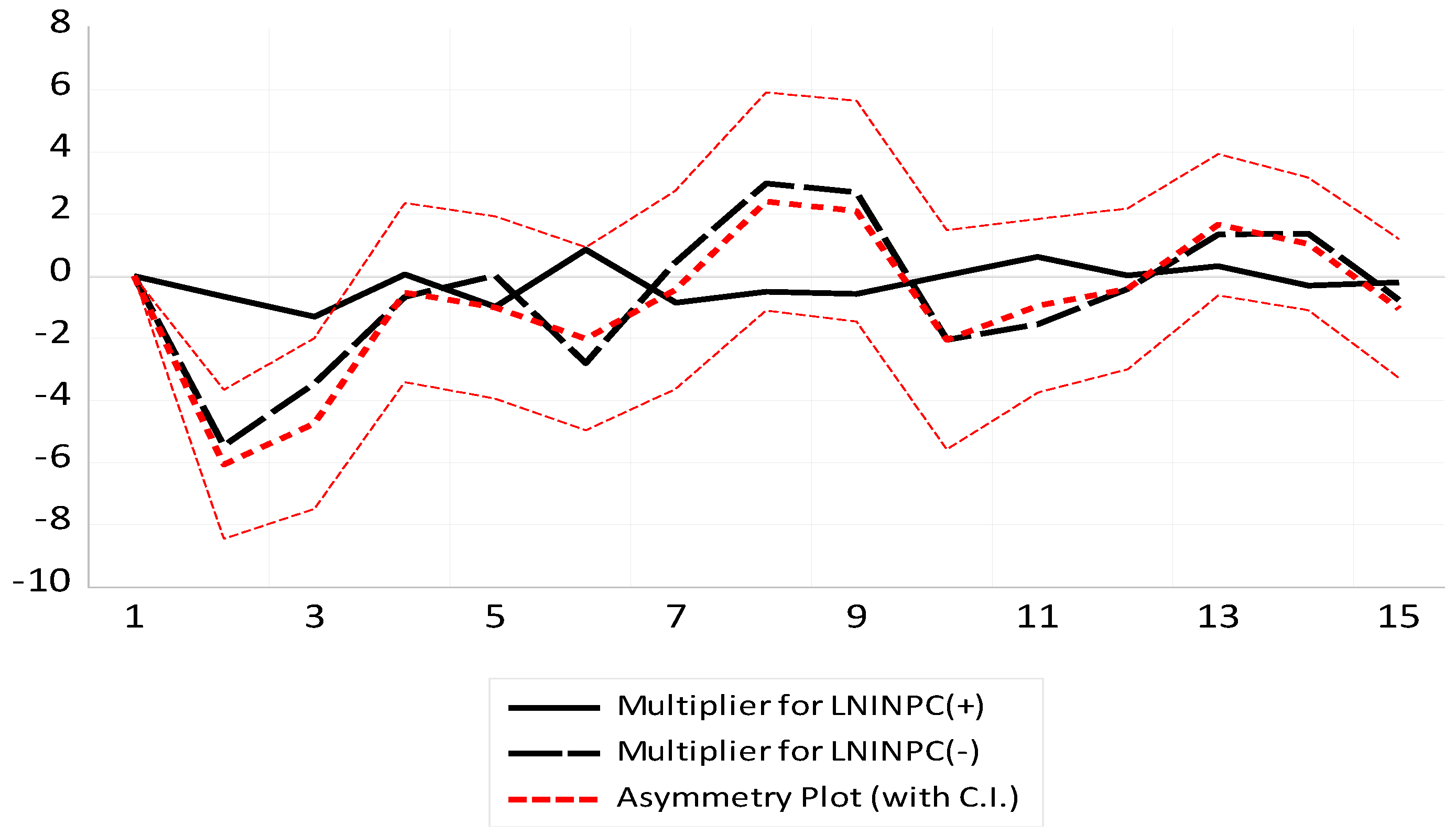
| Coefficients | Macrofactors | ||
|---|---|---|---|
| WALCL | Shadow Rates | GPUI | |
| 2.087563 * | 3.323633 * | 2.791119 * | |
| 0.726056 * | 0.287285 * | 0.413641 * | |
| −0.010568 * | −0.001492 * | −2.68 × 10−5 * | |
| lnINPCt | lnIGAEt | |||||
|---|---|---|---|---|---|---|
| Hypothesis Null: Unit Root (Prob > 0.05) | t-Stat. | Prob. | Level (0,1) | t-Stat. | Prob. | Level (0,1) |
| Augmented Dickey–Fuller (ADF test statistic) * (Intercept) Phillips–Perron (PP test statistic) ** (Intercept) | −3.6701 −4.7711 | 0.0049 0.0001 | (0) | −5.9783 −5.3803 | 0.0000 0.0000 | (1) |
| 1% | −3.4484 | −3.4490 | ||||
| 5% | −2.8693 | −2.8697 | ||||
| 10% | −2.5710 | −2.5711 | ||||
| KSS test (Intercept) *** | 6.1700 | 2.4884 | ||||
| 1% | 0.2160 | 0.2160 | ||||
| 5% | 0.1460 | 0.1460 | ||||
| 10% | 0.1190 | 0.1190 | ||||
| BDS test **** | ||||||
| Significance (alpha) | 0.0500 | 0.0500 | ||||
| p-value | 0.0000 | 0.0000 | ||||
| Variable | Coefficient | Prob. |
|---|---|---|
| Δ() | −0.367488 | 0.0000 |
| Δ() | −0.347604 | 0.0000 |
| Δ() | −0.266695 | 0.0000 |
| Δ() | −0.316163 | 0.0000 |
| Δ() * | 0.014178 | 0.8032 |
| Δ() | −0.122633 | 0.0309 |
| Δ() * | −0.044106 | 0.4396 |
| Δ() | −0.180673 | 0.0011 |
| Δ() | −0.172622 | 0.0016 |
| Δ() | −0.289257 | 0.0000 |
| Δ() | −0.277666 | 0.0000 |
| Δ() * | −0.355367 | 0.2788 |
| Δ() * | −0.685871 | 0.1114 |
| Δ() * | 0.436611 | 0.3101 |
| Δ() | −0.842715 | 0.0490 |
| Δ() | 1.690112 | 0.0001 |
| Δ() | −1.232793 | 0.0046 |
| Δ() * | −0.071487 | 0.8696 |
| Δ() * | −0.459121 | 0.2931 |
| Δ() | 1.228597 | 0.0003 |
| CointEq(−1) | −0.046964 | 0.0006 |
| R-squared | 0.456934 | |
| Adjusted R-squared | 0.423719 | |
| Durbin–Watson stat | 1.779343 |
| Value | df | Probability | |
|---|---|---|---|
| t-statistic | 2.196770 | 324 | 0.0287 |
| F-statistic | 4.825797 | (1, 324) | 0.0287 |
| Likelihood ratio | 4.145042 | 1 | 0.0233 |
| Dependent Variable (NARDL): | Restricted Constant and No Trend, Dependent Variables with Long-Run Form: ) | Dependent Variable in Error Correction Model and Bound Test: ) | ||||
|---|---|---|---|---|---|---|
| R-squared | 0.9836 | Asymmetric long-run coefficients: | F-Bound test: | |||
| Adjusted R-squared | 0.9819 | 0.1382 | F-static value * | 4.4224 | ||
| F-statistic | 570.3971 | (0.0063) | Significance 10% I(1) | Upper bound: 3.35 | ||
| (0.0000) | −2.1238 | Significance 5% I(1) | Upper bound: 3.87 | |||
| Granger test. causes : F-Statistic | 9.9282 (0.00006) | (0.00012) | Significance 2.5% I(1) | Upper bound: 4.38 | ||
| C.F.T.&Y test (****). causes : Wald-Statistic | 40.2252 (0.0001) | C | 4.30 | Serial correlation Lagrange multiplier, LM test ** (prob): | (0.0002) | |
| (0.0000) | Heteroskedasticity test (prob.): | (0.0000) | ||||
| Variable | Coefficients NARDL (12,9,10) | Variable | Coef. Long-Run Form | Variable | Coef. Error Correction Model | |
| 0.5338 | −0.1138 | CointEq(−1) | −0.1138 | |||
| (0.0000) | (0.0091) | (0.0000) | ||||
| 0.1172 | 0.0157 | Δ() | −0.3534 | |||
| (0.0580) | (0.0903) | (0.0000) | ||||
| 0.0196 | −0.2417 | Δ() | −0.2352 | |||
| (0.7555) | (0.0347) | (0.0000) | ||||
| −0.1232 | Δ() | −0.3524 | Δ() | −0.2156 | ||
| (0.0507) | (0.0000) | (0.0001) | ||||
| 0.3799 | Δ() | −0.2352 | Δ() | −0.3369 | ||
| (0.0000) | (0.0001) | (0.0000) | ||||
| −0.0396 | Δ() | −0.2156 | Δ() | 0.0430 | ||
| (0.5421) | (0.0004) | (0.4528) | ||||
| −0.0005 | Δ() | −0.3369 | Δ() | 0.0034 | ||
| (0.9994) | (0.0000) | (0.9535) | ||||
| −0.1706 | Δ() | 0.0430 | Δ() | −0.0034 | ||
| (0.0058) | (0.4900) | (0.9535) | ||||
| 0.0536 | Δ() | 0.0034 | Δ() | −0.1672 | ||
| (0.3898) | (0.9565) | (0.0024) | ||||
| −0.0941 | Δ() | −0.0034 | Δ() | −0.1136 | ||
| (0.1275) | (0.9556) | (0.0375) | ||||
| −0.0506 | Δ() | −0.1672 | Δ() | −0.2078 | ||
| (0.4094) | (0.0044) | (0.0001) | ||||
| 0.2584 | Δ() | −0.1136 | Δ() | −0.2584 | ||
| (0.0000) | (0.0494) | (0.0000) | ||||
| −0.6648 | Δ() | −0.2078 | Δ() | −0.6648 | ||
| (0.0543) | (0.0002) | (0.0457) | ||||
| −0.2182 | Δ() | −0.2584 | Δ() | −0.8988 | ||
| (0.7587) | (0.0000) | (0.0414) | ||||
| 1.6302 | Δ() | −0.6648 | Δ() | 0.7315 | ||
| (0.0346) | (0.0543) | (0.0986) | ||||
| −1.5519 | Δ() | −0.8988 | Δ() | −0.8204 | ||
| (0.0441) | (0.0424) | (0.0614) | ||||
| 2.0586 | Δ() | 0.7315 | Δ() | 1.2382 | ||
| (0.0069) | (0.1002) | (0.0045) | ||||
| −2.3017 | Δ() | −0.8204 | Δ() | −1.0634 | ||
| (0.0025) | (0.0629) | (0.0147) | ||||
| 1.3860 | Δ() | 1.2382 | Δ() | 0.3226 | ||
| (0.0692) | (0.0047) | (0.4602) | ||||
| −0.6907 | Δ() | −1.0634 | Δ() | −0.3681 | ||
| (0.3658) | (0.0152) | (0.3996) | ||||
| 1.0615 | Δ() | 0.3223 | Δ() | 0.6934 | ||
| (0.1350) | (0.4625) | (0.0446) | ||||
| −0.6934 | Δ() | −0.3681 | Δ() | 5.4293 | ||
| (0.0462) | (0.4020) | (0.0001) | ||||
| 5.4293 | Δ() | 0.6936 | Δ() | 1.1119 | ||
| (0.0001) | (0.0462) | (0.4267) | ||||
| −4.5591 | Δ() | 5.4293 | Δ() | −1.3701 | ||
| (0.0285) | (0.0001) | (0.3224) | ||||
| −2.4820 | Δ() | 1.11196 | Δ() | −0.5182 | ||
| (0.2333) | (0.4405) | (0.7081) | ||||
| 1.8519 | Δ() | −1.3701 | Δ() | 3.7905 | ||
| (0.6813) | (0.3329) | (0.0065) | ||||
| 4.3087 | Δ() | −0.5182 | Δ() | −3.0522 | ||
| (0.0383) | (0.7137) | (0.0304) | ||||
| −6.4827 | Δ() | 3.7905 | Δ() | −3.6844 | ||
| (0.0012) | (0.0084) | (0.0087) | ||||
| −0.6322 | Δ() | −3.0522 | Δ() | −0.8176 | ||
| (0.7666) | (0.0363) | (0.5633) | ||||
| 2.8668 | Δ() | −3.6844 | Δ() | 5.2600 | ||
| (0.1776) | (0.0107) | (0.0002) | ||||
| 6.0776 | Δ() | −0.8176 | Δ() | 1.9680 | ||
| (0.0041) | (0.5746) | (0.1551) | ||||
| −3.2920 | Δ() | 5.2600 | ||||
| (0.1241) | (0.0003) | |||||
| −1.9680 | Δ() | 1.9680 | ||||
| (0.1720) | (0.1720) | |||||
| C | 0.4900 | C | 0.4900 | |||
| (0.0071) | (0.0071) | |||||
| Model Specification | Fisher-Type Test statistics (B-H Coint. test) *** | Coint. Decision | ||||
| EG-J | 5% critical value | EG-J-BG-Bo | 5% critical value | |||
| lnigae = f (lninpc) | 23.835781 | 11.229 | 55.131965 | 21.931 | Cointegrated | |
| Variable | Coefficient | Prob. |
|---|---|---|
| C | 0.5422 = c(1) | 0.0008 |
| −0.1273 = c(2) | 0.0011 | |
| 0.0184 = c(3) | 0.0411 | |
| −0.2661 = c(4) | 0.0109 | |
| Δ() | 0.1135 = c(5) | 0.0220 |
| Δ() | 0.0950 = c(6) | 0.0423 |
| Δ() | −4.7372 = c(7) | 0.0005 |
| Δ() | −1.1511 = c(8) | 0.0000 |
| Δ() | 2.6416 = c(9) | 0.0560 |
| Δ() | 3.4768 = c(10) | 0.0113 |
| Δ() | −0.2466 = c(11) | 0.0000 |
| Δ() | −0.3624 = c(12) | 0.0000 |
| Δ() | −0.1821 = c(13) | 0.0001 |
| Δ() | −0.2539 = c(14) | 0.0000 |
| Δ() | −0.2810 = c(15) | 0.0000 |
| Δ() | −3.7702 = c(16) | 0.0051 |
| Δ() | −0.2264 = c(17) | 0.0001 |
| Δ() | 4.3162 = c(12) | 0.0018 |
| Δ() | 0.4792 = c(13) | 0.0339 |
| Equation: STEP_UNIDI | Long Run: c(3) and c(4) | Short Run: c(5) to c(13) | ||||
|---|---|---|---|---|---|---|
| Test Statistic | Value | df | Probab. | Value | df | Probab. |
| t-statistic | 4.0728 | 329 | 0.0001 | 3.8472 | 329 | 0.0001 |
| F-statistic | 16.5881 | (1, 329) | 0.0001 | 14.8008 | (1, 329) | 0.0001 |
| Chi-square | 16.5881 | 1 | 0.0001 | 14.8008 | 1 | 0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trejo-García, J.C.; Valencia-Romero, R.; Soto-Rosales, M.D.L.; Venegas-Martínez, F. On the Asymmetric Relation between Inflation and Growth in Mexico: A NARDL Approach. Economies 2024, 12, 21. https://doi.org/10.3390/economies12010021
Trejo-García JC, Valencia-Romero R, Soto-Rosales MDL, Venegas-Martínez F. On the Asymmetric Relation between Inflation and Growth in Mexico: A NARDL Approach. Economies. 2024; 12(1):21. https://doi.org/10.3390/economies12010021
Chicago/Turabian StyleTrejo-García, José Carlos, Ramón Valencia-Romero, María De Lourdes Soto-Rosales, and Francisco Venegas-Martínez. 2024. "On the Asymmetric Relation between Inflation and Growth in Mexico: A NARDL Approach" Economies 12, no. 1: 21. https://doi.org/10.3390/economies12010021
APA StyleTrejo-García, J. C., Valencia-Romero, R., Soto-Rosales, M. D. L., & Venegas-Martínez, F. (2024). On the Asymmetric Relation between Inflation and Growth in Mexico: A NARDL Approach. Economies, 12(1), 21. https://doi.org/10.3390/economies12010021







