The Market Structure Simulation of Heterogenous Firms
Abstract
1. Introduction
2. Literature Review
2.1. The Models of the Industrial Organisation Theory
2.2. The Models of the New Trade Theory
3. The Experimental Modelling
3.1. The Structure of the Experimental Model
3.2. The Theoretical Model of the Simulation
3.3. The Simulation Process
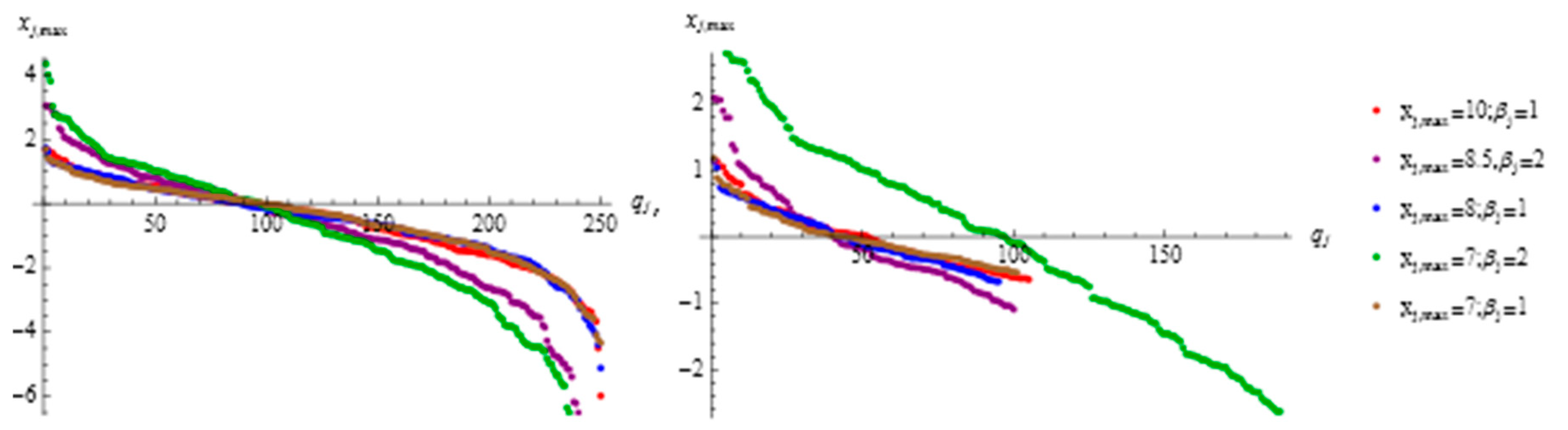
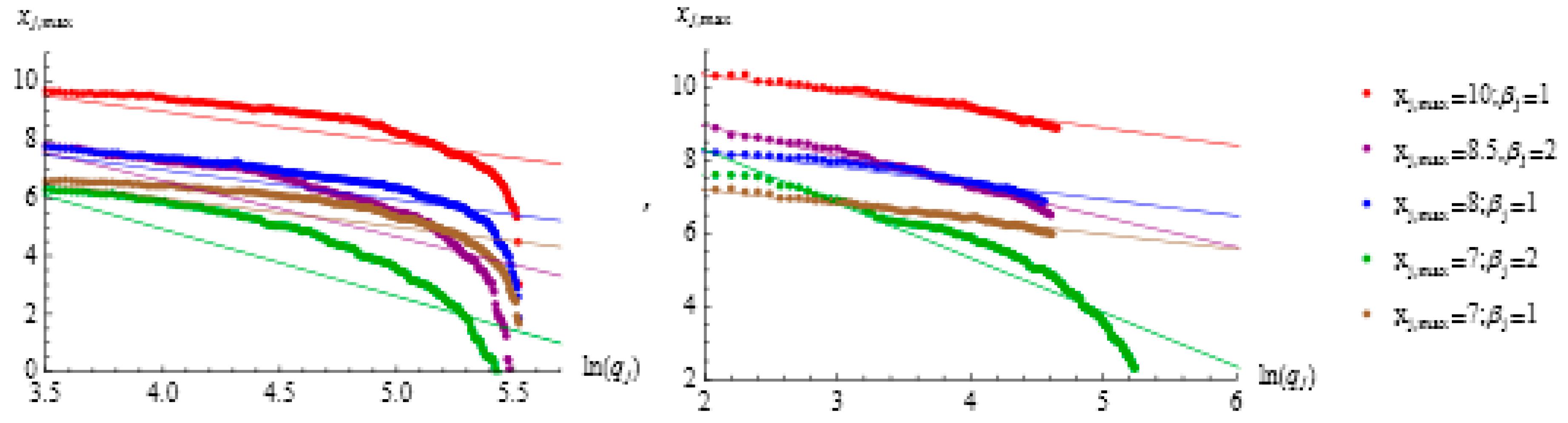
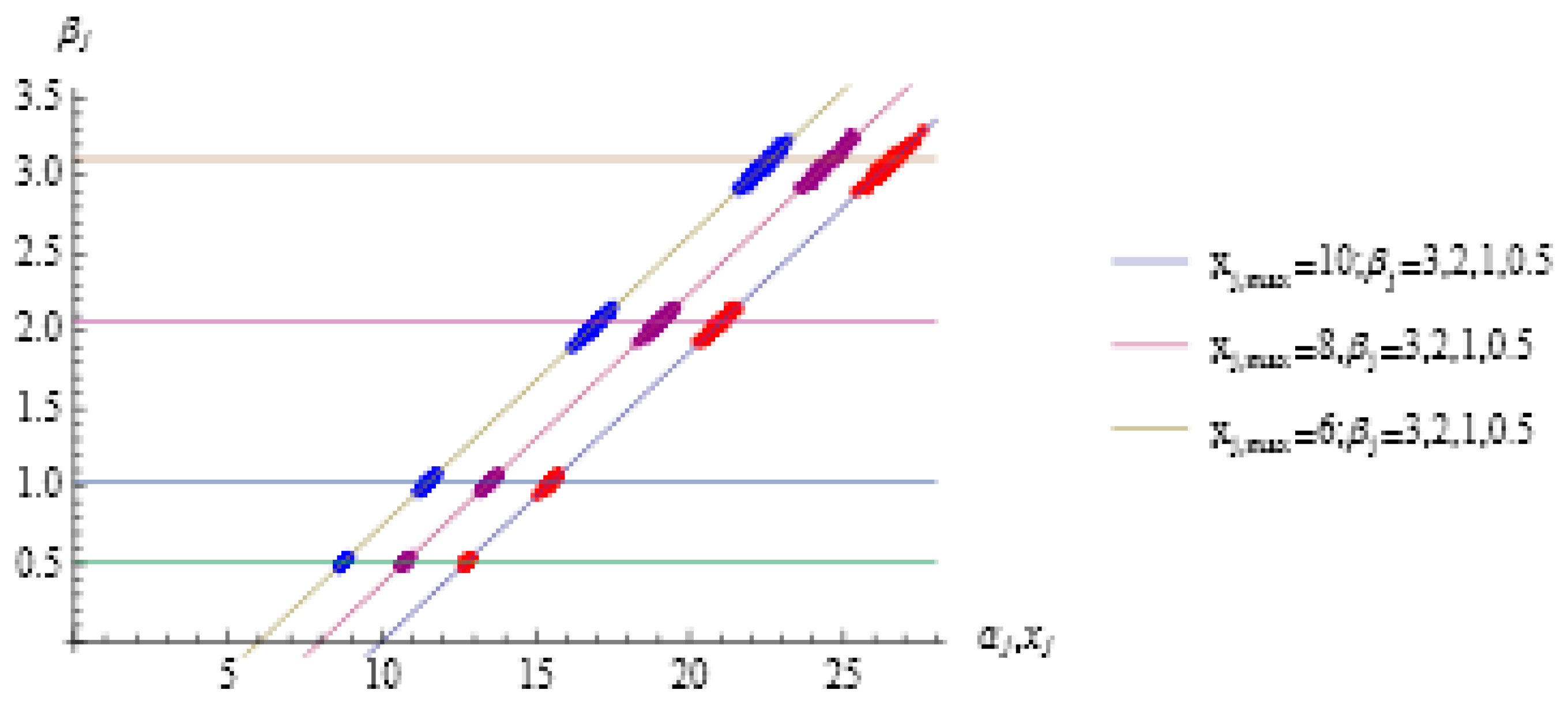
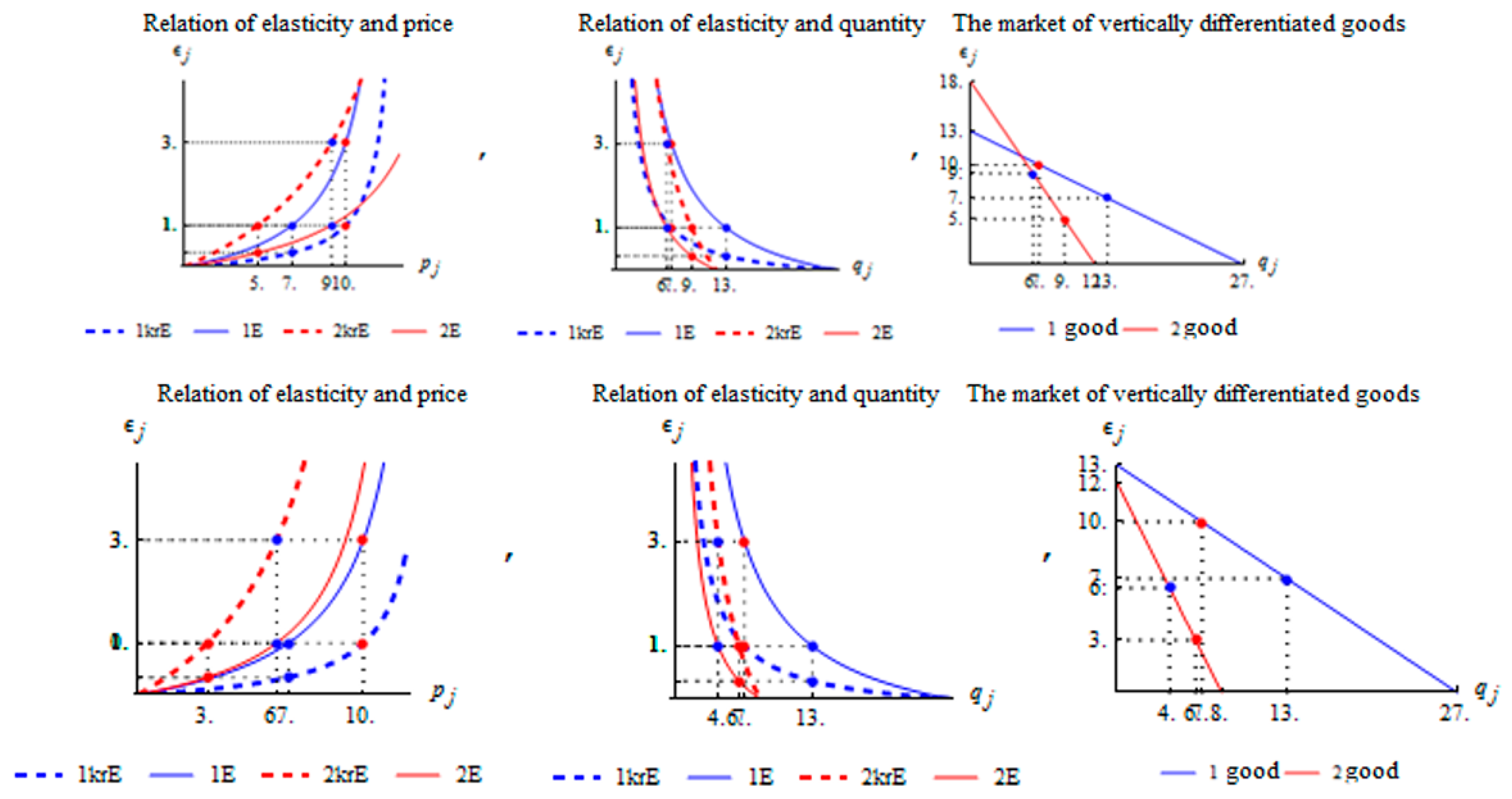
4. The Results of the Experimental Modelling
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adner, Ron, and Daniel Levinthal. 2001. Demand Heterogeneity and Technology Evolution: Implications for Product and Process Innovation. Management Science 47: 611–28. [Google Scholar] [CrossRef]
- Aghion, Philippe. 2006. A Primer on Innovation and Growth. in Bruegel Policy Brief, No. 06. Available online: https://www.bruegel.org/wp-content/uploads/imported/publications/pbf_061006_innovation.pdf (accessed on 19 December 2021).
- Aghion, Philippe, Nick Bloom, Richard Blundell, Rachel Griffith, and Peter Howitt. 2002. Competition and innovation: An inverted U relationship. National Bureau of Economic Research 120: 701–28. [Google Scholar]
- Amoroso, Sara. 2014. The Hidden Costs of R&D Collaboration. IPTS Working Papers on Corporate R&D and Innovation—No 02/2014. Brussels: European Commission. [Google Scholar]
- Arkolakis, Costas, Arnaud Costinot, and Andres Rodriguez-Clare. 2012. New Trade Models, Same Old Gains? American Economic Review 102: 94–130. [Google Scholar] [CrossRef]
- Bacchiega , Emanuele, Luca Lambertini, and Andrea Mantovaini. 2011. Process and product innovation in a vertically differentiated industry. International Game Theory Review 13: 209–21. [Google Scholar] [CrossRef]
- Bajari, Patrick, C. Lanier Benkard, and Jonathan Levin. 2007. Estimating Dynamic models of imperfect competition. Econometrica 75: 1331–370. [Google Scholar] [CrossRef]
- Baldwin, Richard, and James Harrigan. 2009. Zeros, quality and space: Trade theory and trade evidence. National Bureau of Economic Research 3: 60–88. [Google Scholar]
- Baldwin, Richard, and Takatoshi Ito. 2011. Quality competition versus price competition goods: An empirical classification. Journal of Economic Integration 26: 110–35. [Google Scholar] [CrossRef]
- Baldwin, Richard, and Toshihiro Okubo. 2014. International trade, offshoring and heterogeneous firms. Review of International Economics 22: 59–72. [Google Scholar] [CrossRef]
- Balistreri, Edward J., and David G. Tarr. 2018. Comparison of Welfare Gains in the Armington, Krugman and Melitz Models: Insights from a Structural Gravity Approach. Washington, DC: World Bank Policy Research Working Paper 8570. [Google Scholar]
- Bartelsman, Eric, and Mark Doms. 2000. Understanding productivity: Lessons from longitudinal microdata. Journal of Economic Literature 38: 569–94. [Google Scholar] [CrossRef]
- Benassi, Corrado, Alessandra Chirco, and Caterina Colombo. 2006. Vertical differentiation and the distribution of income. Bulletin of Economic Research 58: 345–67. [Google Scholar] [CrossRef]
- Bernard, Andrew, and Bradford Jensen. 1999. Exceptional exporter performance: Cause, effect, or both? Journal of International Economics 47: 1–25. [Google Scholar] [CrossRef]
- Bernard, Andrew, Bradford Jensen, Stephen Redding, and Peter Schott. 2006. Firms in international trade. National Bureau of Economic Research 21: 105–30. [Google Scholar]
- Berry, Steven, James Levinsohn, and Ariel Pakes. 1995. Automobile prices in market equilibrium. Econometrica: Journal of the Econometric Society 63: 841–90. [Google Scholar] [CrossRef]
- Boccard, Nicolas, and Xavier Y. Wauthy. 2010. Equilibrium vertical differentiation in a Bertrand model with capacity precommitment. International Journal of Industrial Organization 28: 288–97. [Google Scholar] [CrossRef]
- Brander, James, and Barbara Spencer. 2015. Intra-industry trade with Bertrand and Cournot oligopoly: The role of endogenous horizontal product differentiation. Research in Economics 69: 157–65. [Google Scholar] [CrossRef]
- Burinskas, Arunas, Rasmus Holmen, Manuela Tvaronavičienė, Agn4 Šimelytė, and Kristina Razminienė. 2021. FDI, technology & knowledge transfer from Nordic to Baltic countries. Insights into Regional Development 3: 31–55. [Google Scholar] [CrossRef]
- Church, Jeffrey R., and Roger Ware. 2000. Industrial organization: A strategic approach. Homewood, IL: Irwin McGraw Hill. [Google Scholar]
- Clerides, Sofronis K., Saul Lach, and James R. Tybout. 1998. Is learning by exporting important? Micro-dynamic evidence from Colombia, Mexico, and Morocco. The quarterly journal of economics 113: 903–47. [Google Scholar] [CrossRef]
- Costinot, Arnaud, and Andres Rodriguez-Clare. 2014. Trade Theory with Numbers: Quantifying the Consequences of Globalisation. In Handbook of International Economics. Edited by Elhanan Helpman, Kenneth Rogoff and Gita Gopinath. Amsterdam: Elsevier, vol. 4, pp. 197–262. [Google Scholar]
- Cremer, Helmuth, and Jacques-Francois Thisse. 1991. Location models of horizontal differentiation: A special case of vertical differentiation models. The Journal of Industrial Economics 39: 383–90. [Google Scholar] [CrossRef]
- Das, Sanghamitra, Mark J. Roberts, and James R. Tybout. 2007. Market entry costs, producer heterogeneity, and export dynamics. Econometrica 75: 837–73. [Google Scholar] [CrossRef]
- De Loecker, Jan. 2011. Product differentiation, multiproduct firms, and estimating the impact of trade liberalisation on productivity. Econometrica 79: 1407–51. [Google Scholar]
- De Loecker, Jan, and Pinelopi Koujianou Goldberg. 2014. Firm Performance in a Global Market. Annual Review of Economics 6: 201–27. [Google Scholar] [CrossRef]
- De Loecker, Jan, Pinelopi K. Goldberg, Amit K. Khandelwal, and Nina Pavcnik. 2016. Prices, Markups, and Trade Reform. Econometrica 84: 445–510. [Google Scholar] [CrossRef]
- Di Comite, Francesco. 2014. More Linear than You Would Think: Quadratic Utilities, Product Differentiation and Trade Patterns. Doctoral dissertation. Available online: http://dial.uclouvain.be/downloader/downloader.php?pid=boreal:151284&datastream=PDF_01 (accessed on 19 December 2021).
- Dixit, Avinash, and Victor Norman. 1980. The Theory of International Trade: A Dual, General Equilibrium Approach. Cambridge: Cambridge University Press. [Google Scholar]
- Doraszelski, Ulrich, and Jordi Jaumandreu. 2013. R&D and productivity: Estimating endogenous productivity. The Review of Economic Studies 3: 27–39. [Google Scholar]
- Dutta, Prajit K., Saul Lach, and Aldo Rustichini. 1995. Better Late than Early: Vertical Differentiation in the Adoption of a New Technology. Journal of Economics and Management Strategy 4: 563–89. [Google Scholar] [CrossRef]
- Duvaleix-Tréguer, Sabine, Charlotte Emlinger, Carl Gaigné, and Karine Latouche. 2015. Quality and Export Performance Evidence from Cheese Industry. Paper presented at 145th EAAE Seminar “Intellectual Property Rights for Geographical Indications: What Is at Stake in the TTIP?”, Parma, Italy, April 14–15; p. 11-p. [Google Scholar]
- Economides, Nicholas. 1989. Symmetric equilibrium existence and optimality in differentiated product markets. Journal of Economic Theory 47: 178–94. [Google Scholar] [CrossRef]
- Elhassnaoui, Ismail, Zineb Moumen, Manuela Tvaronavičienė, Mohamed Ouarani, Mohamed Ben-Daoud, Issam Serrari, Ikram Lahmidi, M.A.S. Wahba, Ahmed Bouziane, Driss Ouazar, and et al. 2021. Management of water scarcity in arid areas: A case study (Ziz Watershed). Insights into Regional Development 3: 80–103. [Google Scholar] [CrossRef]
- Eslava Marcela, John Haltiwanger, Adriana Kugler, and Maurice Kugler. 2008. Plant Survival, Market Fundamentals and Trade Liberalization. Paper presented at the Sixth Jacques Polak Annual Research Conference, Washington, DC, November 13–14. [Google Scholar]
- Filippini, Luigi, and Cecilia Vergari. 2012. Product Innovation in a Vertically Differentiated Model. Quaderni—Working Paper DSE, No. 833. Bologna: Alma Mater Studiorum—Università di Bologna, Dipartimento di Scienze Economiche (DSE). [Google Scholar]
- Foster, Lucia, John Haltiwanger, and Chad Syverson. 2008. Reallocation, Firm Turnover, and Efficiency: Selection on Productivity or Profitability? American Economic Review 98: 394–425. [Google Scholar] [CrossRef]
- Foster, Lucia, John Haltiwanger, and Chad Syverson. 2016. The slow growth of new plants: Learning about demand? Economica 83: 91–129. [Google Scholar] [CrossRef]
- Gabszewicz, J. Jaskold, and J.-F. Thisse. 1979. Price competition, quality and income disparities. Journal of Economic Theory 20: 340–59. [Google Scholar] [CrossRef]
- Geerolf, Francois. 2013. Reassessing Dynamic Efficiency. Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1111/caje.12171?casa_token=ZEon-afWQmoAAAAA:trmUISjxHJ0zHCrarSR2NNPsfbmrl667pSd0gfRacsWBpYKLm-jQ6wQK9fGU4KJ9CgGyzvSP5HV7wOg (accessed on 19 December 2021).
- Gervais, Antoine. 2013. Product Quality and Firm Heterogeneity in International Trade. Canadian Journal of Economics/Revue Canadienne D’économique 48: 1152–74. [Google Scholar] [CrossRef]
- Grenčíková, Adriana, Valentinas Navickas, Marcel Kordoš, and Matej Húževka. 2021. Slovak business environment development under the industry 4.0 and global pandemic outbreak issues. Entrepreneurship and Sustainability Issues 8: 164–79. [Google Scholar] [CrossRef]
- Hallak, Juan Carlos, and Jagadeesh Sivadasan. 2008. Productivity, Quality and Exporting Behavior under Minimum Quality Requirements. NBER working paper No. 14928. Cambridge: NBER. [Google Scholar]
- Helpman, Elhanan, and Pail R. Krugman. 1985. Market Structure and Foreign Trade: Increasing Returns, Imperfect Competition and the International Economy. Cambridge: MIT Press. [Google Scholar]
- Helpman, Elhanan, Marc J. Melitz, and Stephen R. Yeaple. 2003. Export versus FDI. American Economic Review 94: 300–16. [Google Scholar] [CrossRef]
- Hopenhayn, Hugo A. 1992. Entry, exit, and firm dynamics in long run equilibrium. Econometrica: Journal of the Econometric Society 60: 1127–50. [Google Scholar] [CrossRef]
- Johnson, Robert C. 2012. Trade and prices with heterogeneous firms. Journal of International Economics 86: 43–56. [Google Scholar] [CrossRef]
- Kancs, d’Artis, and Boriss Siliverstovs. 2012. R&D and Non-Linear Productivity Growth of Heterogeneous Firms. KOF Working Papers. Zurich: KOF Swiss Economic Institute. [Google Scholar]
- Kasperovica, Ludmila, and Natalja Lace. 2021. Factors influencing companies’ positive financial performance in digital age: A Meta-Analysis. Entrepreneurship and Sustainability Issues 8: 291–311. [Google Scholar] [CrossRef]
- Kathuria, Vikas. 2015. A conceptual framework to identify dynamic efficiency. European Competition Journal 11: 319–39. [Google Scholar] [CrossRef]
- Krugman, Paul R. 1979. Increasing returns, monopolistic competition and international trade. Journal of International Economics 9: 469–79. [Google Scholar] [CrossRef]
- Krugman, Paul R. 1980. Scale Economies, Product Differentiation, and the Pattern if Trade. American Economic Review 70: 950–59. [Google Scholar]
- Krugman, Paul R. 1981. Intra-industry specialisation and the gains from trade. Journal of Political Economy 89: 950–73. [Google Scholar] [CrossRef]
- Krugman, Paul R. 1991. Increasing returns and economic geography. Journal of Political Economy 99: 483–99. [Google Scholar] [CrossRef]
- Krugman, Paul R. 1995. Development, Geography and Economic Theory. Cambridge: MIT Press. [Google Scholar]
- Kugler, Maurice, and Eric Verhoogen. 2008. The quality-complementarity hypothesis: Theory and evidence from Colombia. National Bureau of Economic Research. No. w14418. Cambridge: National Bureau of Economic Research, Inc. [Google Scholar]
- Kurniawati, Elia, Idris Idris, Puji Handayati, and Osman Sharina. 2021. Digital transformation of MSMEs in Indonesia during the pandemic. Entrepreneurship and Sustainability Issues 9: 316–31. [Google Scholar] [CrossRef]
- Lambertini, Luca, and Piero Tedeschi. 2007. On the Social Desirability of Patents for Sequential Innovations in a Vertically Differentiated Market. Journal of Economics 90: 193–214. [Google Scholar] [CrossRef][Green Version]
- Lancaster, Kelvin. 1979. Variety, Equity, and Efficiency: Product Variety in an Industrial Society. New York: Columbia University Press. [Google Scholar]
- Lancaster, Kelvin. 1990. The economics of product variety: A survey. Marketing Science 9: 189–206. [Google Scholar] [CrossRef]
- Laužikas, Mindaugas, Aistė Miliūtė, Viltė Morozovaitė, and Danielius Karpičius. 2021. Effectiveness and efficiency criteria for strategic application of mechatronics in business processes. Insights into Regional Development 3: 79–105. [Google Scholar] [CrossRef]
- Makadok, Richard, and David Gaddis Ross. 2013. Taking Industry Structuring Seriously: A Strategic Perspective on Product Differentiation. Strategic Management Journal 34: 509–32. [Google Scholar] [CrossRef]
- Marino, Alfonso, and Paolo Pariso. 2021. Digital economy: Technological, organizational and cultural contexts for the development of cooperation in Europe. Entrepreneurship and Sustainability Issues 9: 363–83. [Google Scholar] [CrossRef]
- Marjit, Sugata, and Biswajit Mandal. 2021. Monopolistic Competition, Optimum Product Diversity, and International Trade-The Role of Factor Endowment and Factor Intensities. GLO Discussion Paper, No. 911. Essen: Global Labor Organization (GLO). [Google Scholar]
- Mayer, Thierry, Marc J. Melitz, and Gianmarco IP Ottaviano. 2011. Market Size, Competition, and the Product Mix of Exporters. American Economic Review 104: 495–536. [Google Scholar] [CrossRef]
- Melitz, Marc J. 2003. The impact of trade on intra-industry reallocations and aggregate industry productivity. Econometrica 71: 1695–725. [Google Scholar] [CrossRef]
- Melitz, Marc J. 2008. International trade and heterogeneous firms. In The New Palgrave Dictionary of Economics, 2nd ed. Edited by Steven N. Durlauf and Lawrence E. Blume. London: Palgrave Macmillan. [Google Scholar]
- Melitz, Marc J., and Gianmarco IP Ottaviano. 2008. Market Size, Trade, and Productivity. The Review of Economic Studies 75: 295–316. [Google Scholar] [CrossRef]
- Melitz, Marc J., and Stephen J. Redding. 2015. New Trade Models, New Welfare Implications. American Economic Review 105: 1105–46. [Google Scholar] [CrossRef]
- Meramveliotakis, Giorgos, and Manolis Manioudis. 2021. Sustainable Development, COVID-19 and Small Business in Greece: Small Is Not Beautiful. Administrative Sciences 11: 90. [Google Scholar] [CrossRef]
- Motta, Massimo. 1993. Endogenous quality choice: Price vs. quantity competition. The Journal of Industrial Economics 9: 113–31. [Google Scholar] [CrossRef]
- Mura, Ladislav, and Zuzana Hajduová. 2021. Small and medium enterprises in regions—Empirical and quantitative approach. Insights into Regional Development 3: 252–66. [Google Scholar] [CrossRef]
- Mussa, Michael, and Sherwin Rosen. 1978. Monopoly and product quality. Journal of Economic Theory 18: 301–17. [Google Scholar] [CrossRef]
- Neven, Damien, and Jacques-Francois Thisse. 1990. On Quality and Variety Competition. In Economic Decision Making: Games, Econometrics and Optimization. Edited by Jaskold Gabszewicz, Jean-Francois Richard and Laurence Wolsey. Amsterdam: Elsevier Science Publishers, pp. 112–54. [Google Scholar]
- Norman, George, and Darlene C. Chisholm. 2014. Dictionary of Industrial Organization. Cheltenham: Edward Elgar Publishing. [Google Scholar]
- Prakash, Ravi. 2021. Net energy and feasible economic growth: A developing country perspective from India. Insights into Regional Development 3: 106–13. [Google Scholar] [CrossRef]
- Qiu, Larry D. 1997. On the dynamic efficiency of Bertrand and Cournot equilibria. Journal of Economic Theory 75: 213–229. [Google Scholar] [CrossRef]
- Redding, Stephen J. 2010. Theories of heterogeneous firms and trade. National Bureau of Economic Research. Available online: https://www.nber.org/system/files/working_papers/w16562/w16562.pdf (accessed on 19 December 2021).
- Roberts, Mark J., Daniel Y. Xu, Xiaoyan Fan, and Shengxing Zhang. 2012. A structural model of demand, cost, and export market selection for Chinese footwear producers. National Bureau of Economic Research. Available online: https://economics.yale.edu/sites/default/files/xu-130325.pdf (accessed on 19 December 2021).
- Santos, Carlos Daniel. 2015. Sunk costs of R&D, trade and productivity: The molds industry case. The Economic Journal 3: 152–67. [Google Scholar]
- Schott, Peter K. 2004. Across-product versus within-product specialisation in international trade. The Quarterly Journal of Economics 2: 647–78. [Google Scholar] [CrossRef]
- Shaked, Avner, and John Sutton. 1982. Relaxing price competition through product differentiation. The Review of Economic Studies 5: 3–13. [Google Scholar] [CrossRef]
- Shaked, Avner, and John Sutton. 1983. Natural oligopolies. Econometrica: Journal of the Econometric Society 9: 1469–83. [Google Scholar] [CrossRef]
- Shy, Oz. 1995. Industrial Organisation: Theory and Applications. Cambridge: MIT Press. [Google Scholar]
- Singh, Nirvikar, and Xavier Vives. 1984. Price and quantity competition in a differentiated duopoly. The RAND Journal of Economics 12: 546–54. [Google Scholar] [CrossRef]
- Slogar, Helena. 2021. Longitudinal research—Entrepreneurial orientation impact, innovativeness, and business performance in Croatian companies. Entrepreneurship and Sustainability Issues 9: 152–68. [Google Scholar] [CrossRef]
- Spielkamp, Alfred, and Christian Rammer. 2009. Financing of innovation–thresholds and options. Management & Marketing 4: 3–18. [Google Scholar]
- Symeonidis, G. 2003. Comparing Cournot and Bertrand equilibria in a differentiated duopoly with product R&D. International Journal of Industrial Organization 21: 39–55. [Google Scholar]
- Syverson, Chad. 2011. What Determines Productivity? Journal of Economic Literature 49: 326–65. [Google Scholar] [CrossRef]
- Tremblay, Carol Horton, and Victor J. Tremblay. 2011. The Cournot–Bertrand model and the degree of product differentiation. Economics Letters 111: 233–35. [Google Scholar] [CrossRef]
- Uddin, Godwin. 2021. A Critique of Modern Theories of Trade. MPRA Paper No. 105194. Available online: https://mpra.ub.uni-muenchen.de/105194/1/MPRA_paper_105194.pdf (accessed on 19 December 2021).
- van Dijk, T. 1996. Patent Height and Competition in Product Improvements. Journal of Industrial Economics 44: 151–67. [Google Scholar] [CrossRef]
- Vandenbosch, Mark B., and Charles B. Weinberg. 1995. Product and price competition in a two-dimensional vertical differentiation model. Marketing Science 14: 224–49. [Google Scholar] [CrossRef]
- Vives, Xavier. 1985. On the efficiency of Bertrand and Cournot equilibria with product differentiation. Journal of Economic Theory 36: 166–75. [Google Scholar] [CrossRef]
- Wildenbeest, Matthijs R. 2011. An empirical model of search with vertically differentiated products. The RAND Journal of Economics 42: 729–57. [Google Scholar] [CrossRef]
- Wyrwa, Joanna. 2020. A review of the European Union financial instruments supporting the innovative activity of enterprises in the context of Industry 4.0 in the years 2021–27. Entrepreneurship and Sustainability Issues 8: 1146–61. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burinskas, A.; Tvaronavičienė, M. The Market Structure Simulation of Heterogenous Firms. Economies 2022, 10, 9. https://doi.org/10.3390/economies10010009
Burinskas A, Tvaronavičienė M. The Market Structure Simulation of Heterogenous Firms. Economies. 2022; 10(1):9. https://doi.org/10.3390/economies10010009
Chicago/Turabian StyleBurinskas, Arūnas, and Manuela Tvaronavičienė. 2022. "The Market Structure Simulation of Heterogenous Firms" Economies 10, no. 1: 9. https://doi.org/10.3390/economies10010009
APA StyleBurinskas, A., & Tvaronavičienė, M. (2022). The Market Structure Simulation of Heterogenous Firms. Economies, 10(1), 9. https://doi.org/10.3390/economies10010009






