An Inverse Pheromone Approach in a Chaotic Mobile Robot’s Path Planning Based on a Modified Logistic Map
Abstract
1. Introduction
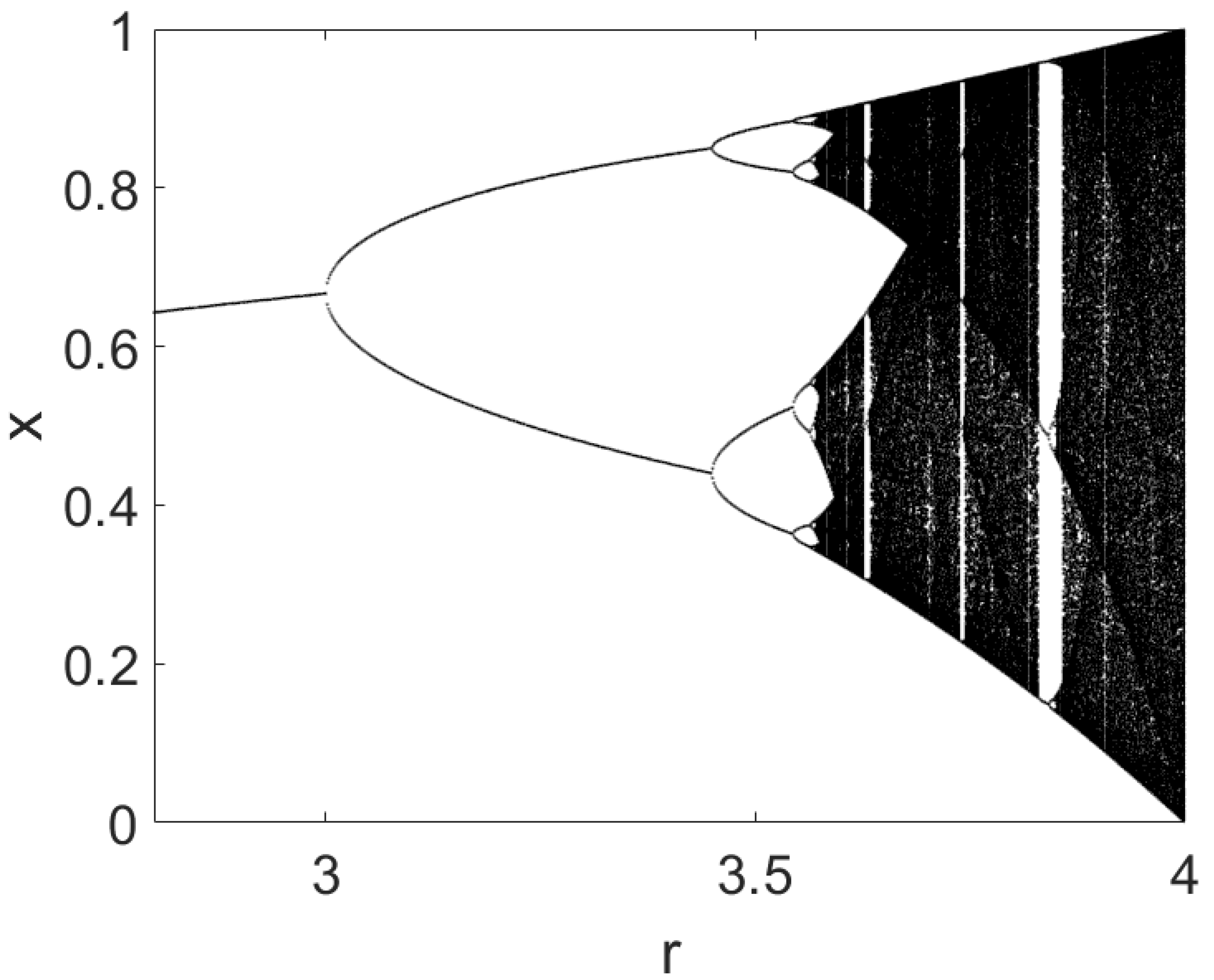
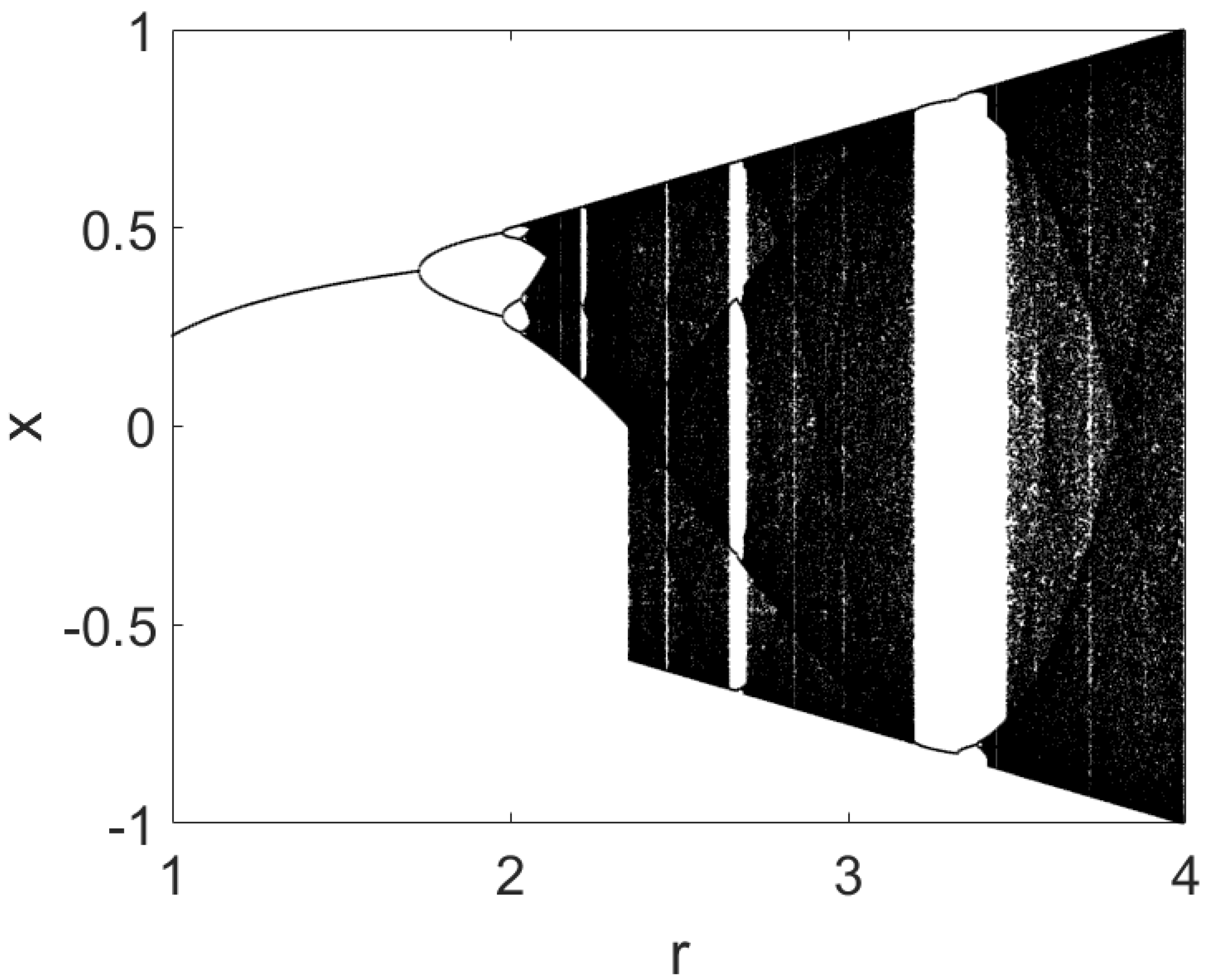
2. The Modified Logistic Map
- For , x decays to a fixed point (x→0).
- For , the previous point loses its stability and a new fixed point appears .
- For , the system goes from a periodic trajectory into chaos.
3. Pseudo Random Number Generator
4. Robot’s Motion Controller
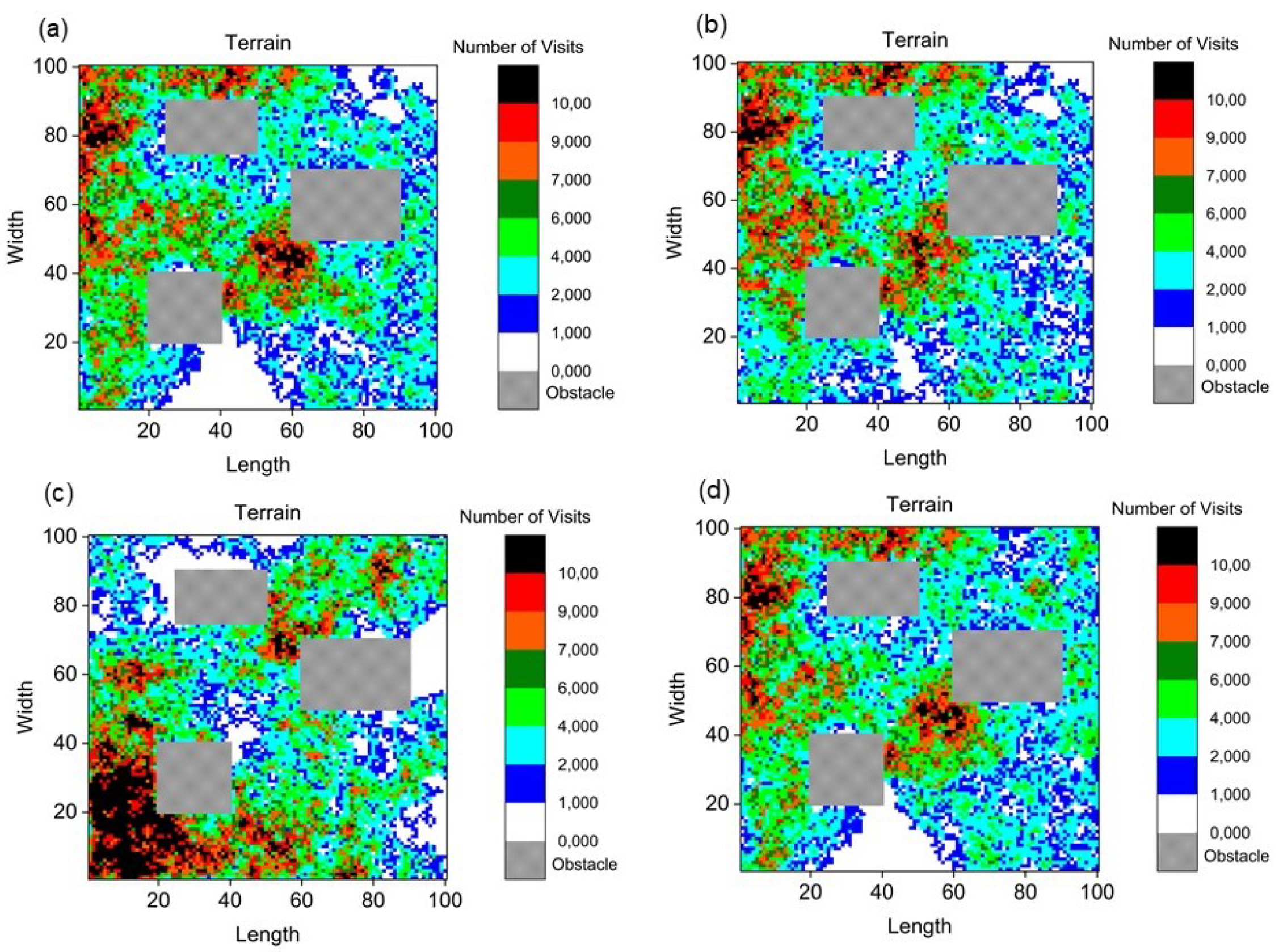
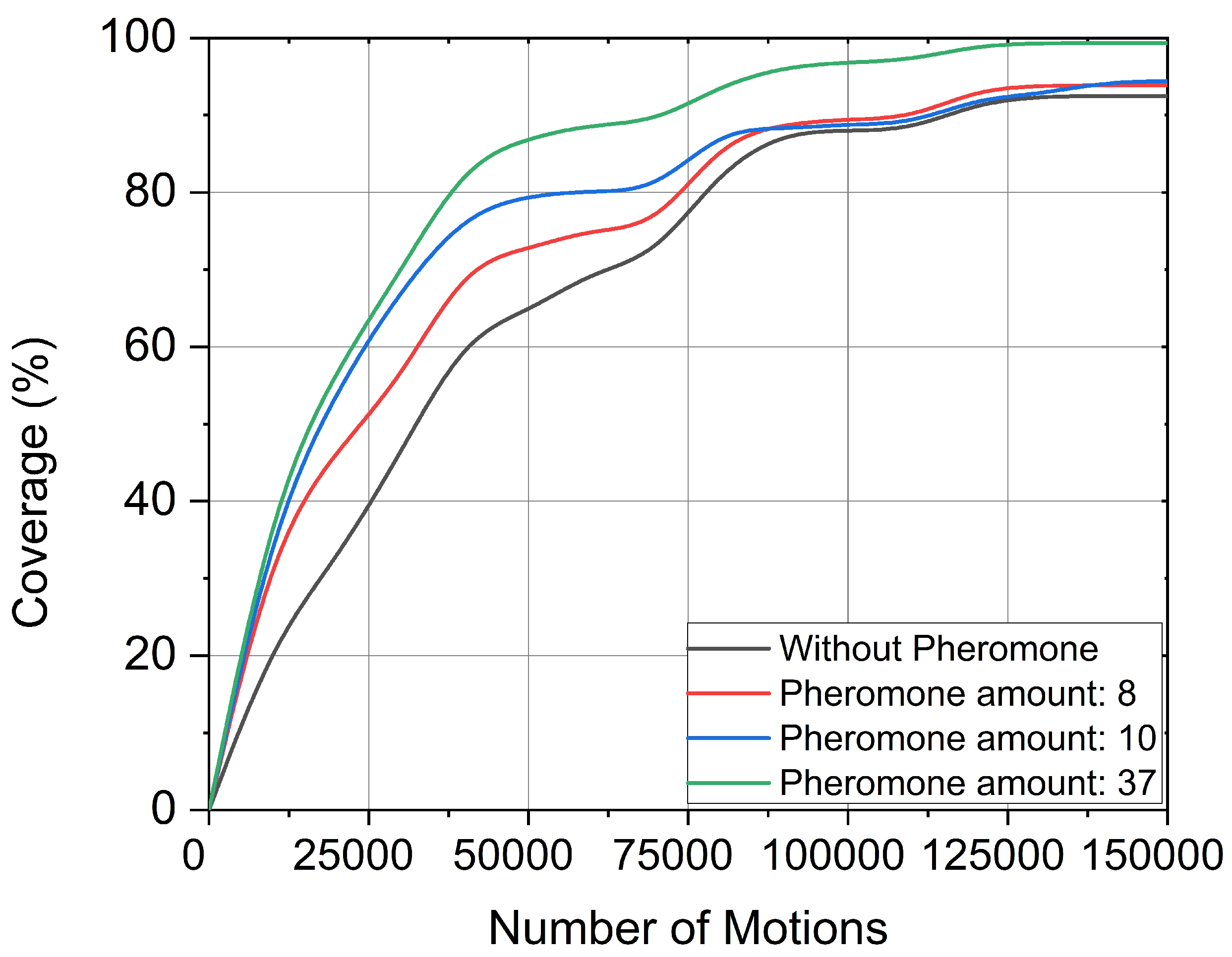
4.1. Inverse Pheromone Method
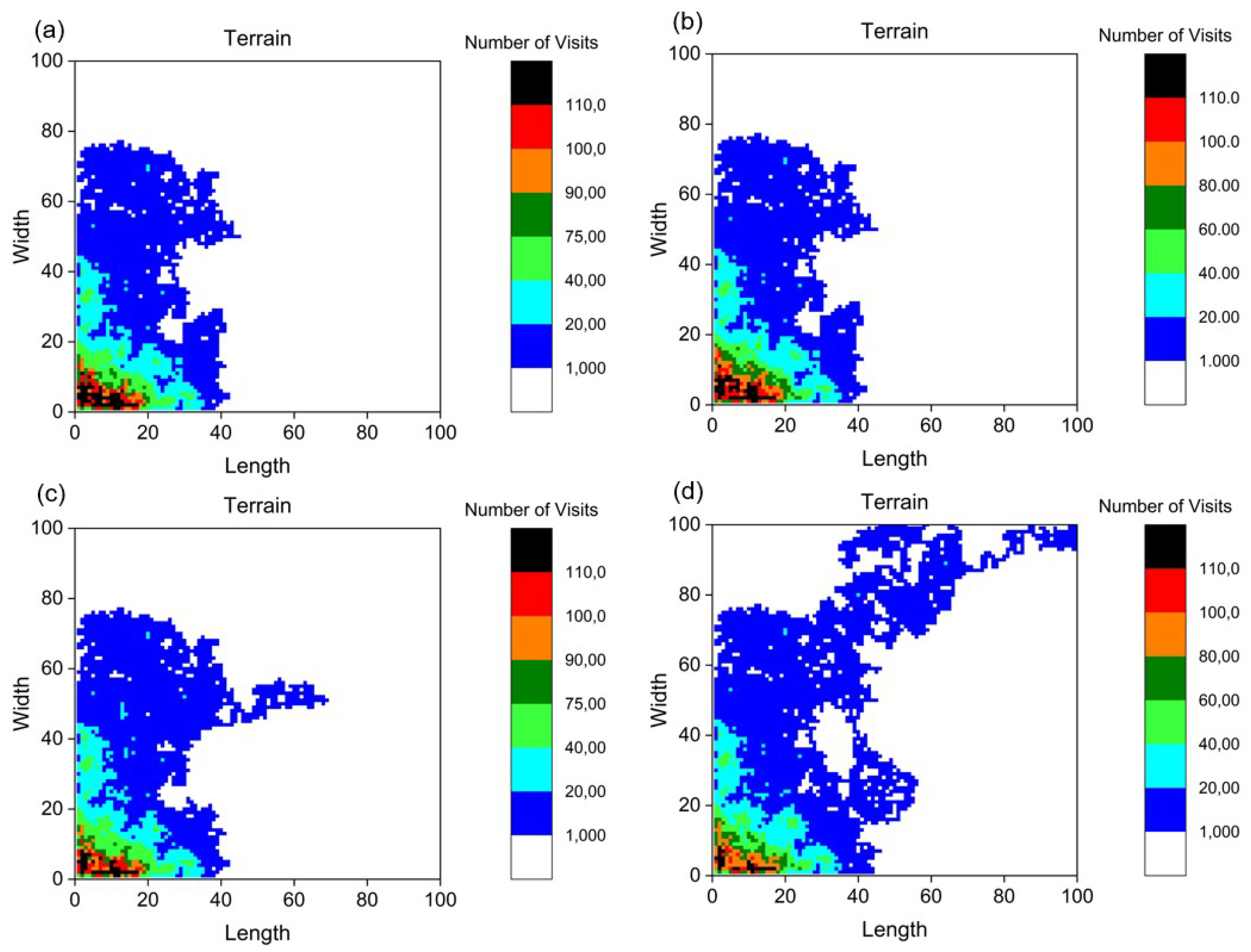
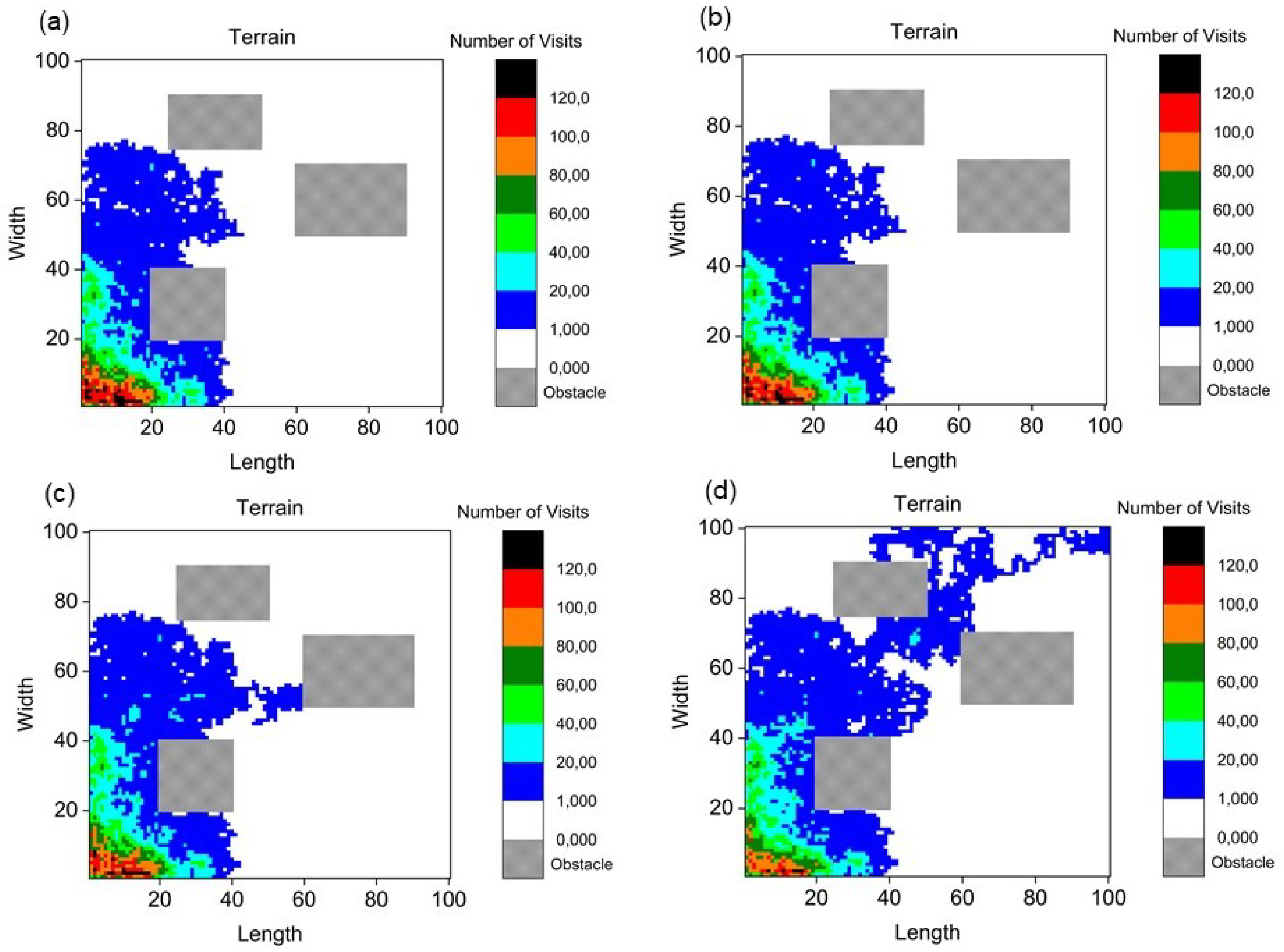
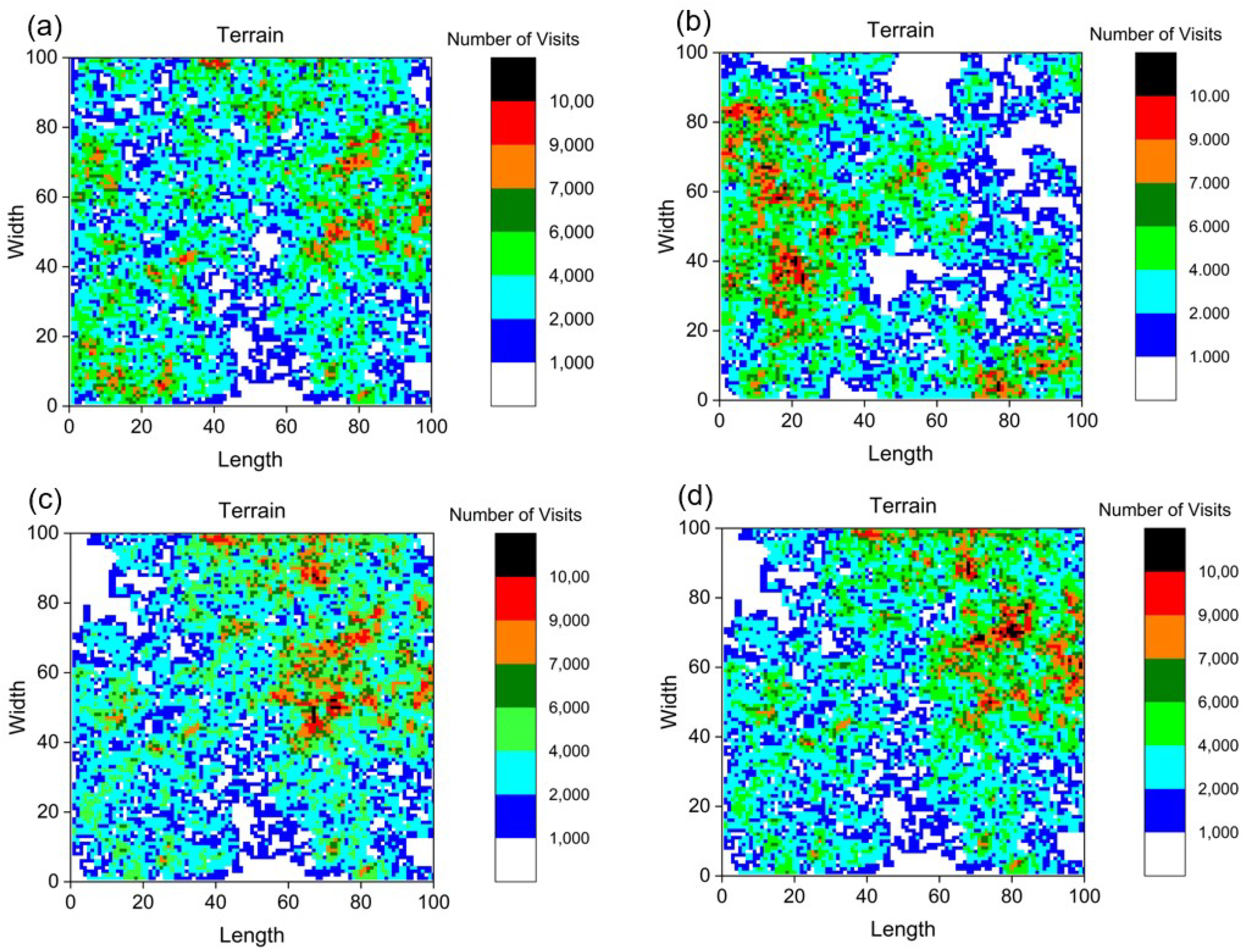
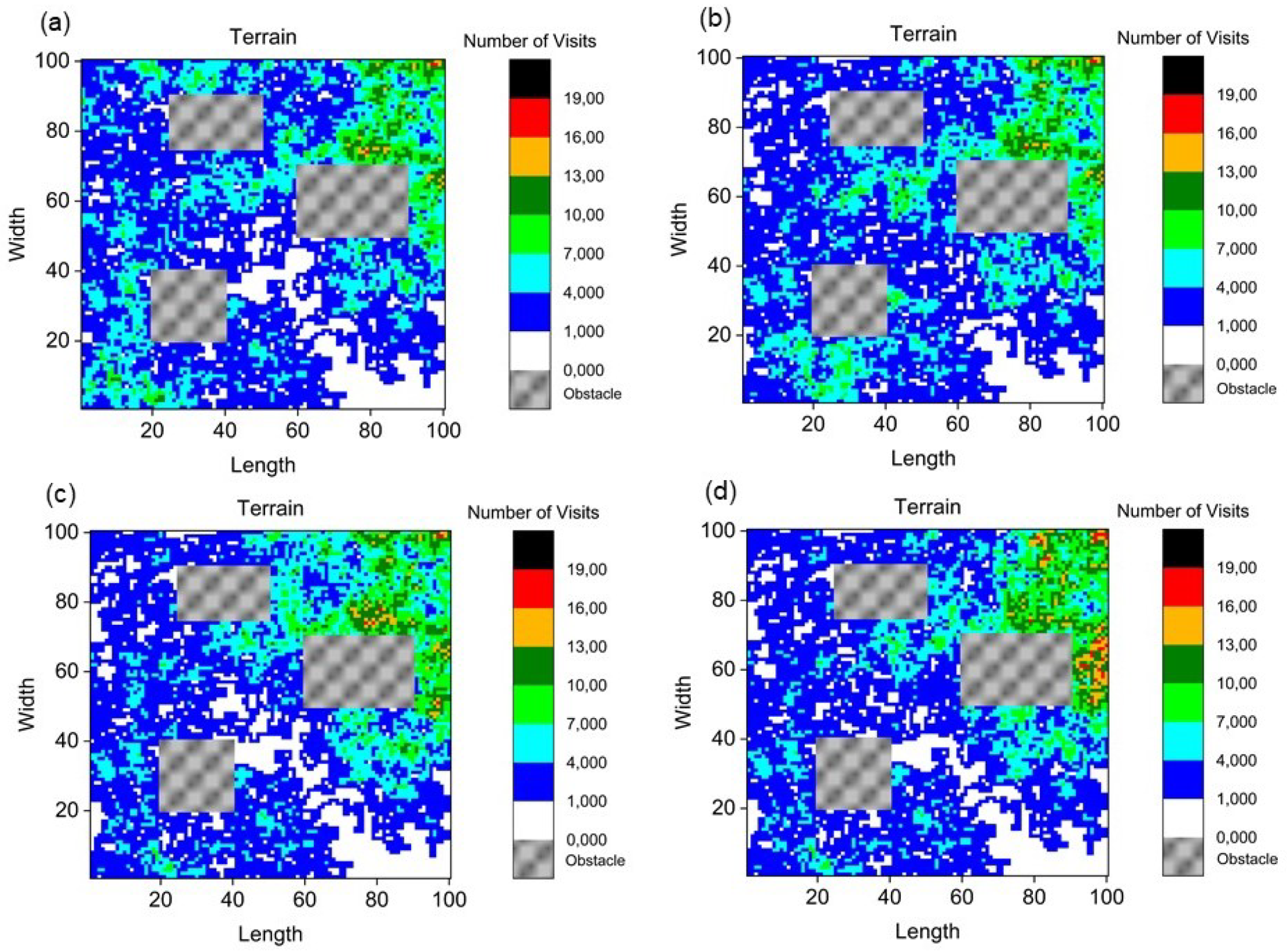
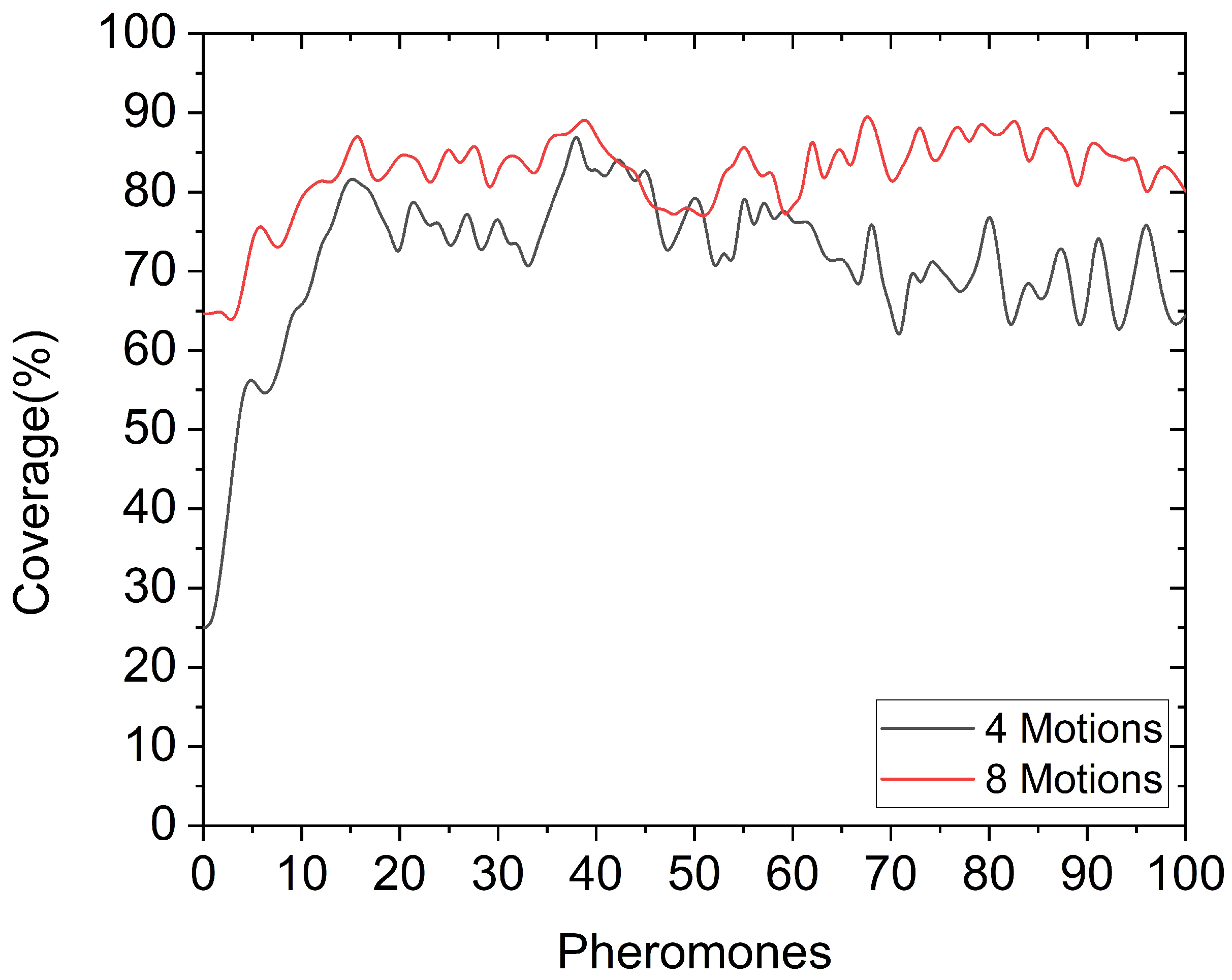
4.2. Motion in Four Directions
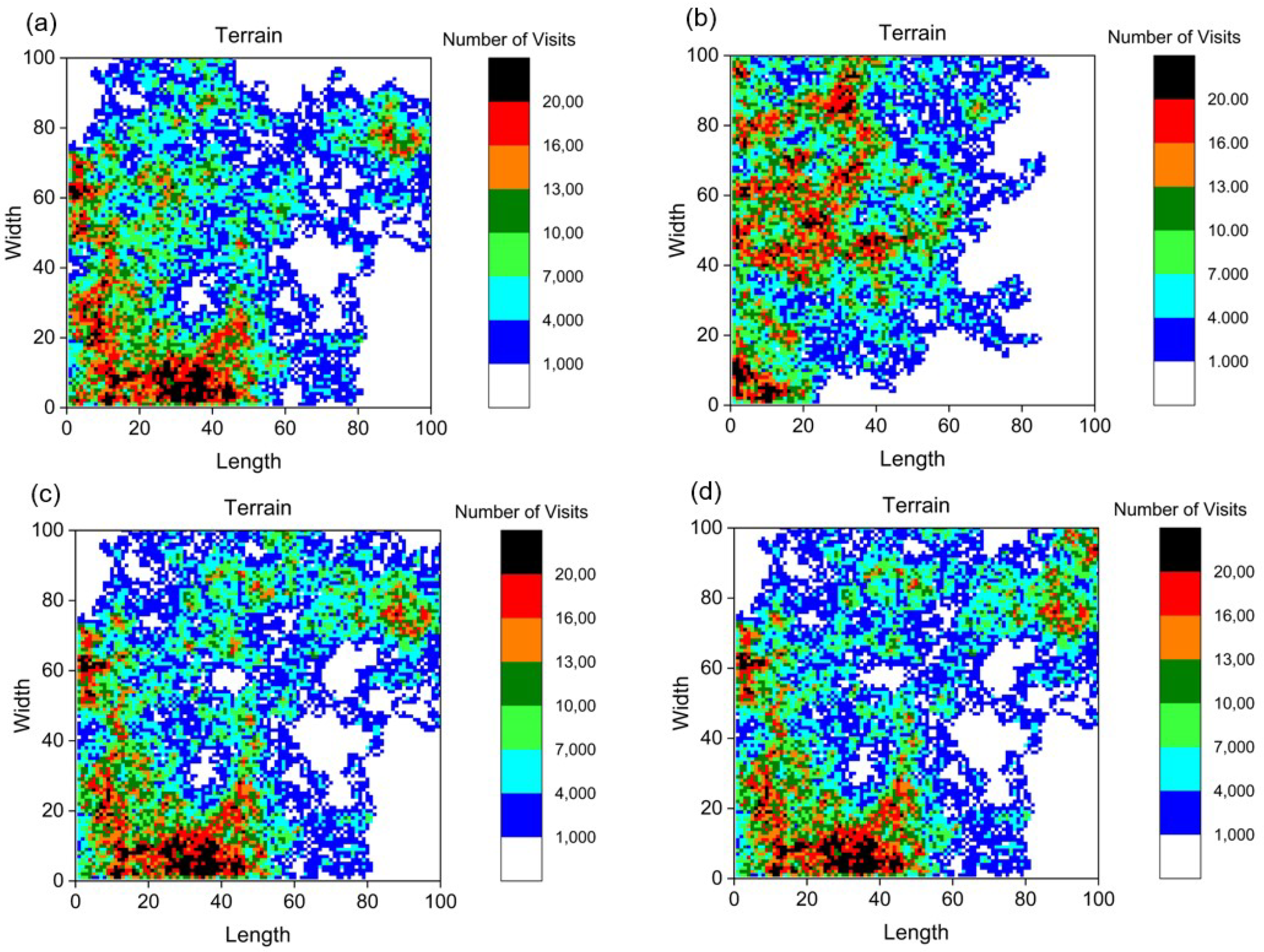
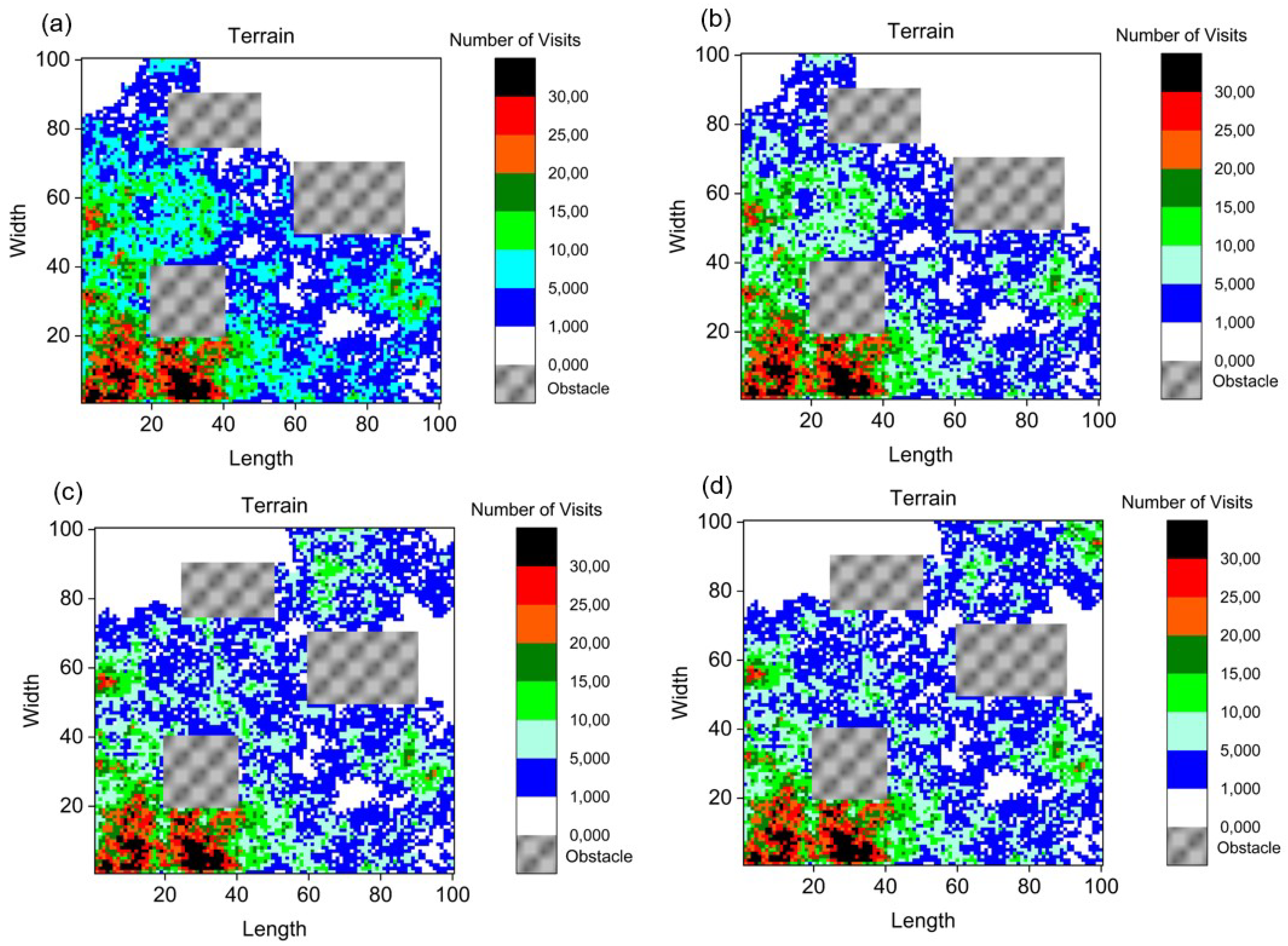
4.3. Motion in Eight Directions
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Siegwart, R.; Nourbakhsh, I.R.; Scaramuzza, D. Introduction to Autonomous Mobile Robots; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Palacin, J.; Salse, J.A.; Valgañón, I.; Clua, X. Building a mobile robot for a floor-cleaning operation in domestic environments. IEEE Trans. Instrum. Meas. 2004, 53, 1418–1424. [Google Scholar] [CrossRef]
- Tadokoro, S. (Ed.) Rescue Robotics: DDT Project on Robots and Systems for Urban Search and Rescue; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- Tavera, M.J.; Dutra, M.S.; Diaz, E.Y.V.; Lengerke, O. Implementation of Chaotic Behavior on a Fire Fighting Robot. In Mechatronics Series I—Intelligent Transportation Vehicles; Dutra, M.S., Lengerke, O., Eds.; Bentham Science Publishers: Sharjah, UAE, 2009. [Google Scholar]
- Murphy, R.R.; Kravitz, J.; Stover, S.L.; Shoureshi, R. Mobile robots in mine rescue and recovery. IEEE Robot. Autom. Mag. 2009, 16, 91–103. [Google Scholar] [CrossRef]
- Krotkov, E.; Blitch, J. The defense advanced research projects agency (DARPA) tactical mobile robotics program. Int. J. Robot. Res. 1999, 18, 769–776. [Google Scholar] [CrossRef]
- Martins-Filho, L.S.; Macau, E.E. Trajectory planning for surveillance missions of mobile robots. In Autonomous Robots and Agents; Springer: Berlin/Heidelberg, Germany, 2007; pp. 109–117. [Google Scholar]
- Martins-Filho, L.S.; Macau, E.E. Patrol mobile robots and chaotic trajectories. Math. Probl. Eng. 2007, 2007, 61543. [Google Scholar] [CrossRef]
- Gohari, P.S.; Mohammadi, H.; Taghvaei, S. Using chaotic maps for 3D boundary surveillance by quadrotor robot. Appl. Soft Comput. 2019, 76, 68–77. [Google Scholar] [CrossRef]
- Li, C.; Song, Y.; Wang, F.; Liang, Z.; Zhu, B. Chaotic path planner of autonomous mobile robots based on the standard map for surveillance missions. Math. Probl. Eng. 2015, 2015, 263964. [Google Scholar] [CrossRef]
- Portugal, D.; Rocha, R. Msp algorithm: Multi-robot patrolling based on territory allocation using balanced graph partitioning. In Proceedings of the 2010 ACM Symposium on Applied Computing, Sierre, Switzerland, 22–26 March 2010; pp. 1271–1276. [Google Scholar]
- Huang, Q.J.; Nonami, K. Humanitarian mine detecting six-legged walking robot and hybrid neuro walking control with position/force control. Mechatronics 2003, 13, 773–790. [Google Scholar] [CrossRef]
- Yim, M.; Roufas, K.; Duff, D.; Zhang, Y.; Eldershaw, C.; Homans, S. Modular reconfigurable robots in space applications. Auton. Robot. 2003, 14, 225–237. [Google Scholar] [CrossRef]
- Abdellilah, H.; Mohamed, B.; Abdellah, M.; Youcef, M.; Réda, A.M. Depth advanced control of an autonomous underwater robot. Int. J. Model. Identif. Control 2016, 26, 336–344. [Google Scholar] [CrossRef]
- Ośmiałowski, B. On path planning for mobile robots: Introducing the mereological potential field method in the framework of mereological spatial reasoning. J. Autom. Mob. Robot. Intell. Syst. 2009, 3, 24–33. [Google Scholar]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Choset, H. Coverage for robotics—A survey of recent results. Ann. Math. Artif. Intell. 2001, 31, 113–126. [Google Scholar] [CrossRef]
- Fahmy, A.A. Chaotic mobile robot workspace coverage enhancement. J. Autom. Mob. Robot. Intell. Syst. 2012, 6, 33–38. [Google Scholar]
- Fahmy, A.A. Implementation of the chaotic mobile robot for the complex missions. J. Autom. Mob. Robot. Intell. Syst. 2012, 6, 8–12. [Google Scholar]
- Low, K.H.; Dolan, J.M.; Khosla, P. Information-theoretic approach to efficient adaptive path planning for mobile robotic environmental sensing. In Proceedings of the Nineteenth International Conference on Automated Planning and Scheduling, Thessaloniki, Greece, 19–23 September 2009. [Google Scholar]
- Garrido, S.; Moreno, L.; Blanco, D.; Jurewicz, P. Path planning for mobile robot navigation using voronoi diagram and fast marching. Int. J. Robot. Autom. 2011, 2, 42–64. [Google Scholar]
- Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N.; Stavrinides, S.G.; Anagnostopoulos, A.N. An autonomous mobile robot guided by a chaotic true random bits generator. In Chaos and Complex Systems; Springer: Berlin/Heidelberg, Germany, 2013; pp. 337–343. [Google Scholar]
- Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N. A chaotic path planning generator for autonomous mobile robots. Robot. Auton. Syst. 2012, 60, 651–656. [Google Scholar] [CrossRef]
- Petavratzis, E.K.; Volos, C.K.; Stouboulos, I.N.; Nistazakis, H.E.; Kyritsi, K.G.; Valavanis, K.P. Coverage Performance of a Chaotic Mobile Robot Using an Inverse Pheromone Model. In Proceedings of the 2019 8th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 13–15 May 2019; pp. 1–4. [Google Scholar]
- Nasr, S.; Mekki, H.; Bouallegue, K. A multi-scroll chaotic system for a higher coverage path planning of a mobile robot using flatness controller. Chaos Solitons Fractals 2019, 118, 366–375. [Google Scholar] [CrossRef]
- Goyal, J.K.; Nagla, K.S. A new approach of path planning for mobile robots. In Proceedings of the 2014 International Conference on Advances in Computing, Communications and Informatics (ICACCI), New Delhi, India, 24–27 September 2014; pp. 863–867. [Google Scholar]
- Koziol, S.; Hasler, P.; Stilman, M. Robot path planning using field programmable analog arrays. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 1747–1752. [Google Scholar]
- Kanaya, M.; Cheng, G.X.; Watanabe, K.; Tanaka, M. Shortest path searching for robot walking using an analog resistive network. In Proceedings of the IEEE International Symposium on Circuits and Systems-ISCAS’94, London, UK, 30 May–2 June 1994; Volume 6, pp. 311–314. [Google Scholar]
- Cheng, G.X.; Ikegami, M.; Tanaka, M. A resistive mesh analysis method for parallel path searching. In Proceedings of the 34th Midwest Symposium on Circuits and Systems, Monterey, CA, USA, 14–17 May 1992; pp. 827–830. [Google Scholar]
- Li, C.H.; Song, Y.; Wang, F.Y.; Wang, Z.Q.; Li, Y.B. A chaotic coverage path planner for the mobile robot based on the Chebyshev map for special missions. Front. Inf. Technol. Electron. Eng. 2017, 18, 1305–1319. [Google Scholar] [CrossRef]
- Curiac, D.I.; Banias, O.; Volosencu, C.; Curiac, C.D. Novel Bioinspired Approach Based on Chaotic Dynamics for Robot Patrolling Missions with Adversaries. Entropy 2018, 20, 378. [Google Scholar] [CrossRef]
- Pippin, C.; Christensen, H.; Weiss, L. Performance based task assignment in multi-robot patrolling. In Proceedings of the 28th Annual ACM Symposium on Applied Computing, Coimbra, Portugal, 18–22 March 2013; pp. 70–76. [Google Scholar]
- Moysis, L.; Petavratzis, E.; Volos, C.; Nistazakis, H.; Stouboulos, I. A chaotic path planning generator based on logistic map and modulo tactics. Robot. Auton. Syst. 2019, 124, 103377. [Google Scholar] [CrossRef]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, R647. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, S.; Rondoni, L.; Mitra, M. Applications of Chaos and Nonlinear Dynamics in Science and Engineering; Springer: Berlin, Germany, 2015; Volume 4. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kocarev, L. Chaos-based cryptography: A brief overview. IEEE Circuits Syst. Mag. 2001, 1, 6–21. [Google Scholar] [CrossRef]
- He, H.; Wu, Y.; Zhang, B.; Zhang, D.; Tian, Y.; Wang, K.; Meng, H.; Hou, M. Discrete chaotic synchronization and secure communication design. In Proceedings of the 2009 Fifth International Conference on Natural Computation, Tianjin, China, 14–16 August 2009; Volume 5, pp. 473–476. [Google Scholar]
- Kabi, K.K.; Pradhan, C.; Saha, B.J.; Bisoi, A.K. Comparative study of image encryption using 2D chaotic map. In Proceedings of the 2014 International Conference on Information Systems and Computer Networks (ISCON), Mathura, India, 1–2 March 2014; pp. 105–108. [Google Scholar]
- Parida, R.R.; Singh, S.; Pradhan, C. Analysis of Color Image Encryption Using Multidimensional Bogdanov Map. In Histopathological Image Analysis in Medical Decision Making; IGI Global: Hershey, PA, USA, 2019; pp. 202–225. [Google Scholar]
- Rathore, D.; Suryavanshi, A. A proficient Image Encryption using chaotic map approach. Int. J. Comput. Appl. 2016, 134, 20–24. [Google Scholar] [CrossRef]
- Yang, T.; Wu, C.W.; Chua, L.O. Cryptography based on chaotic systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 469–472. [Google Scholar] [CrossRef]
- Cheng, C.T.; Fallahi, K.; Leung, H.; Chi, K.T. Cooperative path planner for UAVs using ACO algorithm with Gaussian distribution functions. In Proceedings of the 2009 IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009; pp. 173–176. [Google Scholar]
- Garcia, M.P.; Montiel, O.; Castillo, O.; Sepúlveda, R.; Melin, P. Path planning for autonomous mobile robot navigation with ant colony optimization and fuzzy cost function evaluation. Appl. Soft Comput. 2009, 9, 1102–1110. [Google Scholar] [CrossRef]
- Rosalie, M.; Danoy, G.; Chaumette, S.; Bouvry, P. Chaos-enhanced mobility models for multilevel swarms of UAVs. Swarm Evol. Comput. 2018, 41, 36–48. [Google Scholar] [CrossRef]
- Verhulst, P.F. La loi d’accroissement de la population. Nouv. Mem. Acad. Roy. Soc. Belle-lettr. Bruxelles 1845, 8, 1–58. [Google Scholar]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef]
- Ausloos, M.; Dirickx, M. (Eds.) The Logistic Map and the Route to Chaos: From the Beginnings to Modern Applications; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Patidar, V.; Sud, K.K.; Pareek, N.K. A pseudo random bit generator based on chaotic logistic map and its statistical testing. Informatica 2009, 33, 441–452. [Google Scholar]
- Lloyd, A.L. The coupled logistic map: A simple model for the effects of spatial heterogeneity on population dynamics. J. Theor. Biol. 1995, 173, 217–230. [Google Scholar] [CrossRef]
- Li, C.; Xie, T.; Liu, Q.; Cheng, G. Cryptanalyzing image encryption using chaotic logistic map. Nonlinear Dyn. 2014, 78, 1545–1551. [Google Scholar] [CrossRef]
- Tarasova, V.V.; Tarasov, V.E. Logistic map with memory from economic model. Chaos Solitons Fractals 2017, 95, 84–91. [Google Scholar] [CrossRef]
- McGonigal, G.; Elmasry, M. Generation of noise by electronic iteration of the logistic map. IEEE Trans. Circuits Syst. 1987, 34, 981–983. [Google Scholar] [CrossRef]
- Von Neumann, J. Various techniques used in connection with random digits. Appl. Math. Ser. 1951, 12, 5. [Google Scholar]
- NIST: Security Requirements for Cryptographic Modules, FIPS PUB 140–2. Available online: https://csrc.nist.gov/publications/detail/fips/140/2/final (accessed on 3 December 2019).
- Fraser, A.M. Information and entropy in strange attractors. IEEE Trans. Inf. Theory 1989, 35, 245–262. [Google Scholar] [CrossRef]

| Monobit Test | Poker Test | Runs Test | Long Run Test |
|---|---|---|---|
| 32.02% | No | ||
| (49.67%) | (for ) | ||
| Passed | Passed | Passed | Passed |
| Bits Pair | Motion Command |
|---|---|
| 00 | up |
| 01 | right |
| 10 | down |
| 11 | left |
| Bits Pair | Motion Command |
|---|---|
| 000 | up |
| 001 | up-right |
| 011 | right |
| 101 | down-right |
| 110 | down |
| 111 | down-left |
| 100 | left |
| 010 | up-left |
| Number of Pheromone Traces | Coverage (%) |
|---|---|
| without | 25.08 |
| 10 | 65.42 |
| 20 | 70.33 |
| 30 | 78.21 |
| 40 | 83.40 |
| 60 | 75.82 |
| 80 | 79.50 |
| 100 | 64.41 |
| Number of Pheromone Traces | Coverage (%) |
|---|---|
| without | 64.64 |
| 10 | 79.66 |
| 20 | 84.91 |
| 30 | 83.05 |
| 40 | 87.01 |
| 60 | 78.75 |
| 80 | 87.57 |
| 100 | 80.09 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petavratzis, E.K.; Volos, C.K.; Moysis, L.; Stouboulos, I.N.; Nistazakis, H.E.; Tombras, G.S.; Valavanis, K.P. An Inverse Pheromone Approach in a Chaotic Mobile Robot’s Path Planning Based on a Modified Logistic Map. Technologies 2019, 7, 84. https://doi.org/10.3390/technologies7040084
Petavratzis EK, Volos CK, Moysis L, Stouboulos IN, Nistazakis HE, Tombras GS, Valavanis KP. An Inverse Pheromone Approach in a Chaotic Mobile Robot’s Path Planning Based on a Modified Logistic Map. Technologies. 2019; 7(4):84. https://doi.org/10.3390/technologies7040084
Chicago/Turabian StylePetavratzis, Eleftherios K., Christos K. Volos, Lazaros Moysis, Ioannis N. Stouboulos, Hector E. Nistazakis, George S. Tombras, and Kimon P. Valavanis. 2019. "An Inverse Pheromone Approach in a Chaotic Mobile Robot’s Path Planning Based on a Modified Logistic Map" Technologies 7, no. 4: 84. https://doi.org/10.3390/technologies7040084
APA StylePetavratzis, E. K., Volos, C. K., Moysis, L., Stouboulos, I. N., Nistazakis, H. E., Tombras, G. S., & Valavanis, K. P. (2019). An Inverse Pheromone Approach in a Chaotic Mobile Robot’s Path Planning Based on a Modified Logistic Map. Technologies, 7(4), 84. https://doi.org/10.3390/technologies7040084









