Abstract
This article introduces a novel approach for generating low-sensitive Pareto fronts of analog circuit performances. The main idea consists of taking advantage from the social interaction between particles within a multi-objective particle swarm optimization algorithm by progressively guiding the global leading process towards low sensitive solutions inside the landscape. We show that the proposed approach significantly outperforms already proposed techniques dealing with the generation of sensitivity-aware Pareto fronts, not only in terms of computing time, but also with regards to the number of solutions forming the tradeoff surface. Performances of our approach are highlighted via the design of two analog circuits.
1. Introduction
Due to the unending technology evolution and the ever greedy need for higher performance, electronic circuit sizing has become very complex. Only skilled designers are able to propose a priori ‘optimal’ sizing for such circuits. Due to metaheuristics (in addition to the use of circuit simulators [1,2,3] for evaluating performances/constraints), designers and engineers (not only highly experienced specialists) have been able to handle complex circuit performances and, thus, they were capable of generating ‘optimal’ sizing that maximize/minimize such circuits/systems performances, while satisfying ‘complex’ intrinsic/extrinsic constraints [4,5,6,7,8]. Evolutionary algorithms and swarm intelligence techniques are examples of such nature inspired optimization techniques [6,7,8,9,10].
Most of the time, such circuits/systems performances are conflicting and non-commensurable ones [4,6,7]. Fortunately, multi-objective metaheuristics offer excellent solutions for handling such further complex optimization problems. They have already been used for optimally sizing analog, mixed signal and radio-frequency circuits; see for instance [1,2,4,10,11,12,13,14].
Due to the variability of CMOS technology parameters and tolerance of component values, sensitivity analysis has become unavoidable, as stressed in [15,16,17,18]. The available literature offers a plethora of published papers offering different approaches for sizing analog circuits, while taking into consideration sensitivity analysis. Most of them use the Richardson exploration technique within an in-loop sizing approach; see for instance [17,18,19,20]. However, the already published techniques generally proceed a posteriori for generating low sensitive solutions when handling multi-objective optimization problems. For instance, Pareto front, also known as the resulting archive, can be generated by applying multi-objective metaheuristics. Afterwards, sensitivity analysis of the feasible solutions can be evaluated. In this process, the solutions presenting sensitivity values higher than a certain acceptable threshold are discarded, while only interesting ones are maintained.
As stressed in [15], the resulting feasible set may be formed by a considerably reduced (or even null) number of solutions. The authors in [15] proposed a novel idea, allowing a full archive to be obtained that has been formed by low sensitive solutions. It consists of sensitivity within the inheritance process of an evolutionary algorithm, like the non-dominated sorting genetic algorithm NSGA-II, and the proposed approach considers sensitivity values, when ranking Pareto fronts during the algorithm execution. Different inheritance strategies have been considered and it has been shown that the most interesting one consists of starting with a high acceptable value of the sensitivity threshold, then linearly reducing it as iterations go on. The viability of that approach was showcased via two CMOS analog circuits, namely: Second-generation current conveyor (CCII) and a voltage follower. However, the significant drawback of that approach is its high computing time (around ten hours for optimizing analog circuits).
In this article we propose a new approach, based on the use of a swarm intelligence technique to alleviate the aforementioned burden. The proposed idea consists of taking benefits of the social interaction between particles, by altering the choice of the swarm’s leader, within a particle swarm optimization approach, and taking into account the sensitivity values for guiding the global move of the swarm. Our approach, as shown below, allows reducing the Pareto front generation time to the sixth, as compared to the one proposed in [15].
The rest of the article is structured as follows: Section 2 gives a brief overview of particle swarm optimization technique. Section 3 details the proposed multi-objective optimization approach. Section 4 presents the results obtained when applying the proposed approach for optimizing two CMOS analog circuits. Section 5 offers a brief discussion on the results obtained in Section 4. Finally, the conclusions are set out in Section 6.
2. Particle Swarm Optimization Technique
Metaheuristics are nature-inspired optimization techniques. A taxonomy of such stochastic optimization techniques is proposed in [21], where metaheuristics are classified into seven categories according to their intrinsic mechanisms: (i) Stochastic algorithms, such as tabu search [22]; (ii) Evolutionary algorithms, such as genetic algorithms [23]; (iii) physical algorithms, such as harmony search [24]; (iv) probabilistic algorithms, such as Bayesian algorithm [25]; (v) swarm algorithms (also known as swarm intelligence techniques (SI)), such as particle swarm optimization (PSO) [26]; (vi) immune algorithms, such as Dendritic cell algorithms [27]; and (vii) neural algorithms, such as Hopfield network [28]. All are known to be efficient and robust techniques.
PSO mimics swarming habits of animal species living in large colonies, namely fish and birds. It is known to be a very rapid algorithm. Besides, it is easy to be implemented within a computer program. Its convergence mechanism consists of moving the swarm’ particles, i.e., the problem variables in the fitness landscape via two simple equations, representing velocity and position of each particle, see Equations (1) and (2) that exploit psycho-social tradeoff between oneself trust and the particle’s social relationships.
where i is the particle index, w is the inertia coefficient (0.8 ≤ w ≤ 1.2), c1 and c2 are respectively the cognitive and the social acceleration coefficient (0 ≤ c1, c2 ≤ 2). r1, r2 are uniformly generated random values (0 ≤ r1, r2 ≤ 1) regenerated every velocity update. vi(t), and xi(t), are respectively, the particle’s velocity and position at time t. pb(t) and gb(t) are the particle’s individual and swarm’s best solution as of time t, respectively.
Figure 1 illustrates the basic concept of PSO algorithm that lies in using random weights to accelerate particles towards their individual and swarm’s best locations.
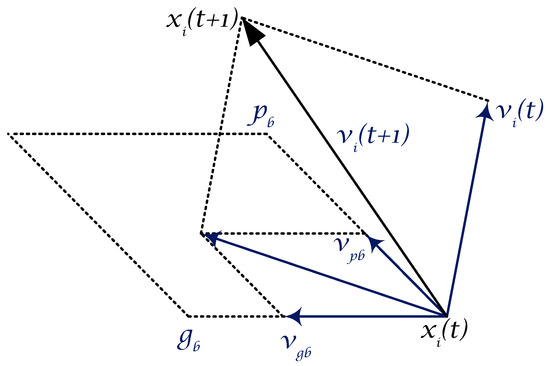
Figure 1.
Illustration of the concept of a particle’s move within the swarm.
MOPSO-CD is a variant of PSO that can handle multi-objective problems. It considers a crowding distance based routine to ensure good spread of the solutions along the Pareto front [29]. Its flowchart is depicted at Figure 2. In the following MOPSO-CD is used.
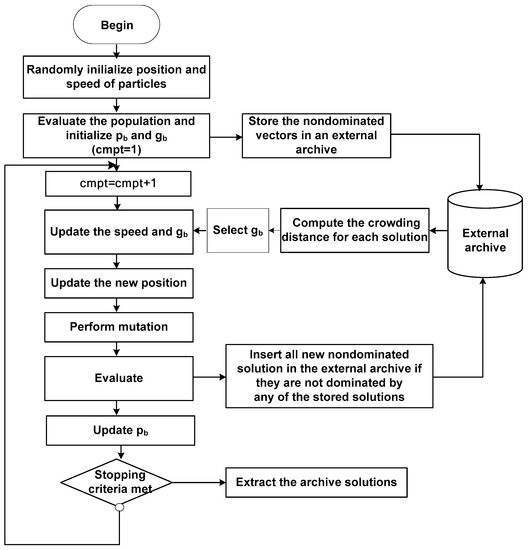
Figure 2.
Flowchart of MOPSO-CD.
3. Proposed Multi-Objective Optimization Approach
As introduced above, gb presents the current most promising location amongst the particle’s neighborhood. It is nothing but the first side of the balance “exploration/intensification” of the metaheuristic’s search mechanism. It represents the global search part (contrary to gp, which represents the second side, i.e., intensification or local search).
Each particle position change is influenced by the swarm’s best roost gb, i.e., by the experience of the whole swarm (or the experience of its neighborhood, depending on the chosen communication strategy). The proposed idea consists of altering the evolution process of PSO by including sensitivity within the choice of gb. Thus, at each iteration, the overall swarm searching process will be influenced by the most promising solution obtained so far, i.e. current less sensitive particle. pb is not subject to the same process, otherwise the program can easily converge prematurely. Richardson extrapolation technique [17,18,19,20] is applied herein within the in-loop algorithm to compute sensitivity values.
For fixing gb, different strategies have been considered (see Cases #0-4 below). For comparison, we present gb choice schemes, similar to those in [15]. Similarly, the same application examples were considered, and the same computing machines were used, i.e., Intel I7 3GHz 8Go 64 bits PCs. The number of iterations (100) is the stop criterion. The archive and the population sizes are both equal to 50. Regarding PSO, we considered the following parameters: c1 = c2 = 1, w = 0.4.
- Case #0: It is a direct generation of the Pareto front, using MOPSO-CD. This case serves as a reference for the computing time.
- Case #1: It consists of generating the Pareto front then eliminating solutions presenting sensitivity values higher than the predefined threshold. This case serves as a reference for the number of (remaining) valid solutions forming the Pareto front.
- Case #2: This case considers sensitivity as a constraint (penalty technique is applied).
- Case #3: It involves executing the algorithm ignoring sensitivity for the half of the total number of iterations, then, each iteration choosing gb as the lowest sensitive particle found so far.
- Case #4: Here we consider a linear decrease of the sensitivity threshold, starting from 1 down to the predefined acceptable one. At each iteration, the global first found particle offering a sensitivity value lower than the ‘dynamic’ threshold, is taken as gb. Figure 3 shows the flowchart of this case #4.
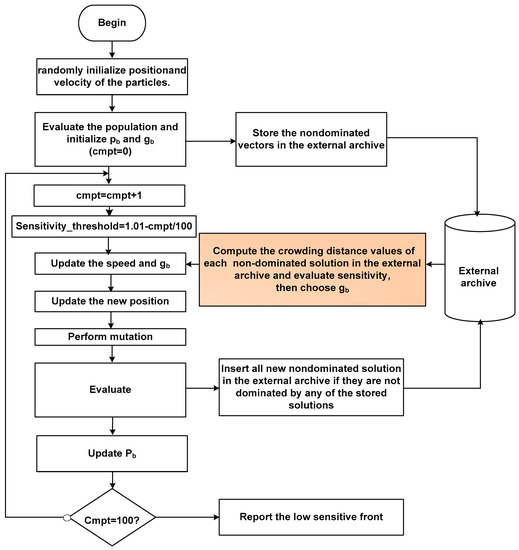 Figure 3. Flowchart of Case #4.
Figure 3. Flowchart of Case #4.
4. Application to Analog Circuit Optimization
As introduced above, both circuits of [15], namely a second-generation CMOS current conveyor (CCII shown in Figure 4) and a CMOS voltage follower (VF shown in Figure 5), are optimized herein to highlight performances of the proposed approach. The sizing of these circuits is performed as in [15], using AMS 0.35 µm technology, and with the following bias conditions: Vdd = –Vss = 1.5 V and Ibias = 50 µA, for the VF; and Vdd = –Vss = 2.5 V and Ibias = 100 µA, for the CCII.
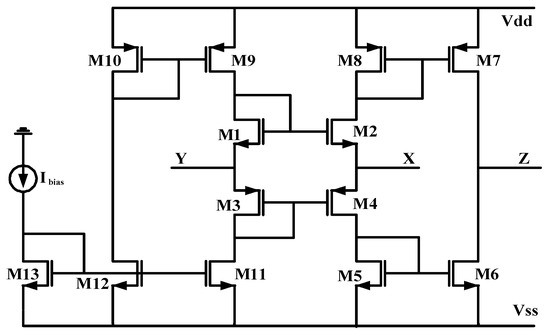
Figure 4.
A CMOS second-generation current conveyor (CCII) [30,31].
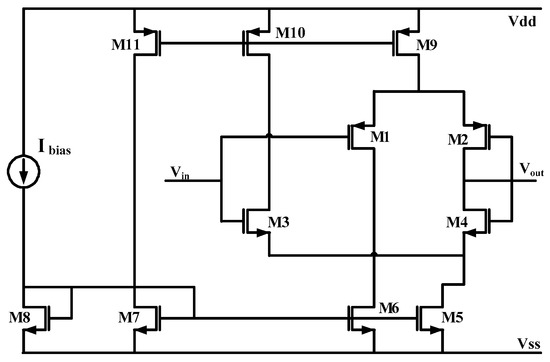
Figure 5.
A CMOS voltage follower (VF) [18].
The CCII is optimized to minimize the input parasitic impedance (Rx) and to maximize the current transfer bandpass (Fci). The optimization of the VF consists on minimizing the voltage offset (Offset) and maximizing the voltage transfer bandpass (Fcv). In both cases, the threshold sensitivity level is 1%. Table 1 summarizes the results obtained for the aforementioned cases, and shows a comparison between those results, by applying the approach provided in [15]. Compt-time and Nb-PF refer to the computing time and number of points forming the final archive, respectively.

Table 1.
Simulation results for the different cases.
Figure 6 and Figure 7 show Pareto fronts obtained for the different considered cases for both CCII and VF. Figure 8 and Figure 9 offer a comparison for both CCII and VF between fronts obtained by Case #4, and that in [15], respectively.
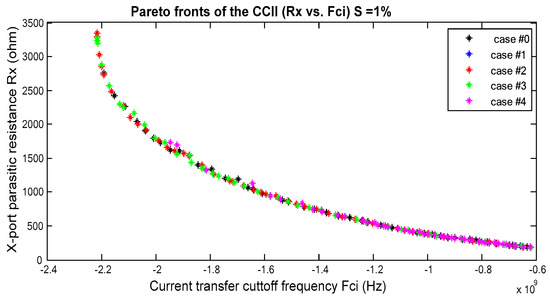
Figure 6.
CCII: Pareto fronts for Case #0-4.
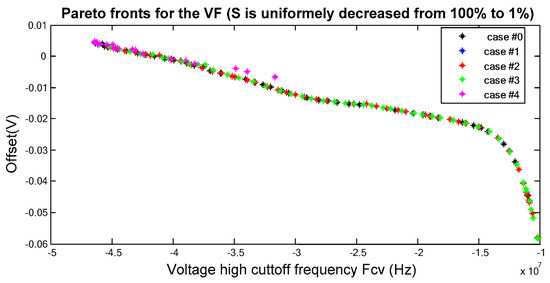
Figure 7.
VF: Pareto fronts for Case #0-4.
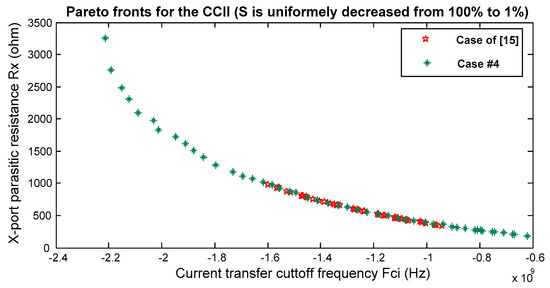
Figure 8.
CCII: Pareto fronts for cases #4 (the proposed approach vs. [15]).
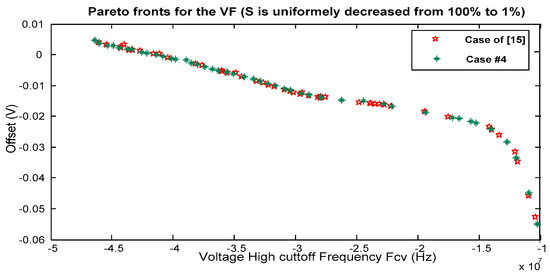
Figure 9.
VF: Pareto fronts for cases #4 (the proposed approach vs. [15]).
Figure 10 presents a boxplot for a 30-run robustness test for the computation time. Compt_time values presented in Table 1 correspond to the average ones executing 30 runs.
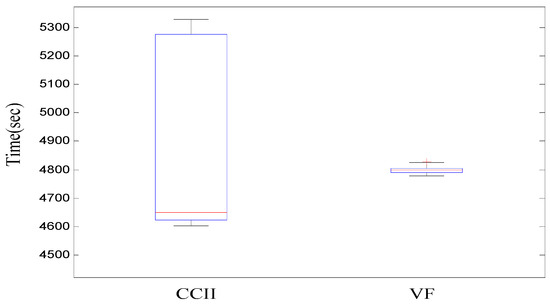
Figure 10.
Boxplot corresponding to the computation times for 30 runs for both CCII and VF.
5. Discussion
Table 1 clearly highlights that the proposed multi-objective optimization approach outperforms those proposed in published works dealing with the generation of sensitivity aware Pareto fronts, particularly in [15]; it allows getting a full archive (similarly to [15]) within around one sixth of the time. In [15], the approach consists of taking benefits from the inheritance process within genetic algorithms, in order to convey the considered features from one generation to the other. However, within NSGA-II, the ranking processes, as well as the evolutionary operators, are very time consuming. Here, we exploit the fact that the information sharing between particles within a PSO swarm is very rapid, hence the important time reduction. The computation time becomes reasonable; making our approach more suitable for a CAD program (the overall computation time is mainly limited by the Richardson exploration technique execution time, as it can be noticed when comparing Case #0 and Case #4 results in Table 1). Further, as shown in Figure 8 and Figure 9, the proposed approach allows more interesting Pareto fronts to be generated. It is thus proven that our approach is quite suitable for sizing analog circuits and ensures convergence to the optimal trade off surface without impairing the expected overall performances of the metaheuristic.
6. Conclusions
An MOPSO-CD sensitivity aware optimization approach has been proposed. It allows Pareto fronts linking conflicting performances of analog circuits to be generated. The basic idea consists of ‘positively’ altering the exploration process of the considered metaheuristic by introducing sensitivity analysis within the social influence of a swarm on a particle’s move decision. The proposed multi-objective optimization approach outperforms those proposed in the current literature. In addition, it is very suitable for being implemented within a sizing CAD tool. Similar philosophies can be applied to handle other complex objectives, such as yield optimization, as well as to other engineering problems.
The Richardson exploration technique remains a limitation regarding the computing time reduction, as stressed in Section 5. Our current work focusses on using metamodels for sensitivity evaluation.
Author Contributions
Investigation, A.G., M.K., O.B.K., M.F., O.G.-F., and E.T.-C.; writing, review, and editing, A.G., M.K., O.B.K., M.F., O.G.-F., and E.T.-C. All authors contributed equally to this work.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fakhfakh, M.; Tlelo-Cuautle, E.; Siarry, P. Computational Intelligence in Analog and Mixed-Signal (AMS) and Radio-Frequency (RF) Circuit Design; Springer: Basel, Switzerland, 2015. [Google Scholar]
- Fakhfakh, M.; Tlelo-Cuautle, E.; Siarry, P. Computational Intelligence in Digital and Network Designs and Applications; Springer: Basel, Switzerland, 2015. [Google Scholar]
- Barros, M.F.; Guilherme, J.; Horta, N. Analog Circuits and Systems Optimization Based on Evolutionary Computation Techniques; Springer: Berlin, Germany, 2010. [Google Scholar]
- Fakhfakh, M.; Tlelo-Cuautle, E.; Fino, M.H. Performance Optimization Techniques in Analog, Mixed-Signal, and Radio-Frequency Circuit Design; IGI-Global: Pennsylvania, PA, USA, 2014. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons: Chichester, UK, 2001. [Google Scholar]
- Roca, E.; Fakhfakh, M.; Castro-López, R.; Fernández, F.V. Applications of evolutionary computation techniques to analog, mixed-signal and RF circuit design–an overview. In Proceedings of the IEEE International Conference on Electronics, Circuits, and Systems, Hammamet, Tunisia, 13–16 December 2009; pp. 251–254. [Google Scholar]
- Liu, B.; Gielen, G.; Fernández, F.V. Fundamentals of optimization techniques in analog IC sizing. In Automated design of analog and high-frequency circuits; Liu, B., Gielen, G., Fernández, F.V., Eds.; Springer: Berlin, Germany, 2014; pp. 19–40. [Google Scholar]
- Padilla, F.; Torres, A.; Ponce, J.; Torres, M.D.; Ratté, S.; Ponce-de-León, E. Evolvable metaheuristics on circuit design. In Advances in Analog Circuits; Tlelo-Cuautle, E., Ed.; InTech: New Delhi, India, 2011; pp. 347–368. [Google Scholar]
- Sallem, A.; Benhala, B.; Kotti, M.; Fakhfakh, M. Application of swarm intelligence techniques to the design of analog circuits: Evaluation and comparison. Analog Integr. Circuits Signal Process. 2013, 75, 499–516. [Google Scholar] [CrossRef]
- Fatima, A.; Javaid, N.; Anjum Butt, A.; Sultana, T.; Hussain, W.; Bilal, M.; ur Rehman Hashmi, M.A.; Akbar, M.; Ilahi, M. An enhanced multi-objective gray wolf optimization for virtual machine placement in cloud data centers. Electronics 2019, 8, 218. [Google Scholar] [CrossRef]
- Kotti, M.; Sallem, A.; Bougharriou, M.; Fakhfakh, M.; Loulou, M. Optimizing CMOS LNA circuits through multiobjective meta heuristics. In Proceedings of the International Workshop on Symbolic and Numerical Methods, Modeling and Applications to Circuit Design, Gammarth, Tunisia, 4–6 October 2010. [Google Scholar]
- Sallem, A.; Pereira, P.; Fakhfakh, M.; Fino, H. A multi-objective simulation based tool: Application to the design of high performance LC-VCOs. In Technological Innovation for the Internet of Things; Camarinha-Matos, L.M., Tomic, S., Graça, P., Eds.; Springer: Berlin, Germany, 2013; pp. 453–462. [Google Scholar]
- Fakhfakh, M.; Cooren, Y.; Sallem, A.; Loulou, M.; Siarry, P. Analog circuit design optimization through the particle swarm optimization technique. Analog Integr. Circuits Signal Process. 2009, 63, 71–82. [Google Scholar] [CrossRef]
- Kotti, M.; González-Echevarría, R.; Fernandez, F.V.; Roca, E.; Sieiro, J.; Castro-López, R.; Fakhfakh, M.; Lopez Villegas, J.M. Generation of surrogate models of pareto-optimal performance trade-offs of planar inductors. Analog Integr. Circuits Signal Process. 2014, 78, 87–97. [Google Scholar] [CrossRef]
- Bellaaj Kchaou, O.; Garbaya, A.; Kotti, M.; Pereira, P.; Fakhfakh, M.; Fino, M.H. Sensitivity aware NSGA-II based pareto front generation for the optimal sizing of analog circuits. Integr. VLSI J. 2016, 55, 220–226. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Chavez, S. Graph-based symbolic technique for improving sensitivity analysis in analog integrated circuits. IEEE Lat. Am. T. 2014, 12, 871–876. [Google Scholar] [CrossRef]
- Sallem, A.; Pereira, P.; Helena Fino, M.; Fakhfakh, M. A hybrid approach for the sensitivity analysis of integrated inductors. Integr. VLSI J. 2016, 52, 237–242. [Google Scholar] [CrossRef]
- Guerra-Gomez, I.; Tlelo-Cuautle, E.; de la Fraga, L.G. Sensitivity analysis in the optimal sizing of analog circuits by evolutionary algorithms. In Proceedings of the International Conference on Electrical Engineering Computing Science and Automatic Control, Tuxtla Gutierrez, Mexico, 8–10 September 2010; pp. 381–385. [Google Scholar]
- Guerra-Gómez, I.; Tlelo-Cuautle, E.; de la Fraga, L.G. Richardson extrapolation-based sensitivity analysis in the multi-objective optimization of analog circuits. Appl. Math. Comput. 2013, 222, 167–176. [Google Scholar] [CrossRef]
- Bellaaj Kchaou, O.; Sallem, A.; Pereira, P.; Fakhfakh, M.; Fino, M.H. Multi-objective sensitivity-based optimization of analog circuits exploiting NSGA-II front ranking. In Proceedings of the International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design, Istanbul, Turkey, 7–9 September 2015. [Google Scholar]
- Brownlee, J. Clever Algorithms: Nature-Inspired Programming Recipes; LuLu: Raleigh, NC, USA, 2011. [Google Scholar]
- Glover, F. Tabu search-part 1. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Richardson, J. Genetic algorithms with sharing for multimodal function optimization, Genetic algorithms and their applications. In Proceedings of the International Conference on Genetic Algorithms; Lawrence Erlbaum Associates Inc.: Hillsdale, NJ, USA, 1987. [Google Scholar]
- Geem, Z.W. Harmony Search Algorithms for Structural Design Optimization; Springer: Berlin, Germany, 2009. [Google Scholar]
- Cooper, G.F.; Herskovits, E. A Bayesian method for the induction of probabilistic networks from data. Mach. Learn. 1992, 9, 309–347. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neuronal networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Greensmith, J. The Dendritic Cell Algorithm. Ph.D. Thesis, School of Computer Science, University of Nottingham, Nottingham, UK, 2007. [Google Scholar]
- Popovici, N.; Boncut, M. On the hopfield algorithm. foundations and examples. G. Math. 2005, 2, 35–50. [Google Scholar]
- Raquel, C.R.; Naval, P.C., Jr. An effective use of crowding distance in multiobjective particle swarm optimization. In Proceedings of the Genetic and Evolutionary Computation Conference, Washington, DC, USA, 25–29 June 2005; pp. 257–264. [Google Scholar]
- Ben Salem, S.; Fakhfakh, M.; Sellami Masmoudi, D.; Loulou, M.; Loumeau, P.; Masmoudi, N. A high performances CMOS CCII and high frequency applications. Analog Integr. Circuits Signal Process. 2006, 49, 71–78. [Google Scholar] [CrossRef]
- Sequin, F.; Fabre, A. New second generation current conveyor with reduced parasitic resistance and bandpass filter application. IEEE Trans. Circuits Syst. I: Fundam. Theory Appl. 2001, 48, 781–785. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).