Improved Parallel Legalization Schemes for Standard Cell Placement with Obstacles †
Abstract
:1. Introduction
2. Related Work
3. Obstacle-Aware Parallel Legalization Algorithms
| Pseudocode 1: Abacus algorithm | |
| input: circuit cells C, circuit rows R | |
| output: C cells aligned in R rows without overlaps | |
| 1 | sort C based on x-coordinate |
| 2 | foreach cell do |
| 3 | |
| 4 | |
| 5 | foreach row do |
| 6 | |
| 7 | if then |
| 8 | |
| 9 | |
| 10 | end if |
| 11 | end for |
| 12 | |
| 13 | end for |
| Pseudocode 2: Function insertCell() | |
| input: cell , row , mode | |
| output: Manhattan distance of ’s displacement | |
| 1 | oldPlacement: = existing placement before is inserted |
| 2 | ifthen |
| 3 | cost: = INF |
| 4 | end if |
| 5 | vertically align into //x-coordinate does not change |
| 6 | if does not overlap with any cluster then |
| 7 | create new cluster containing |
| 8 | cost: = displacement of |
| 9 | else |
| 10 | add into with which it overlaps |
| 12 | cost: = collapseClusters() |
| 12 | end if |
| 13 | if mode = TRIAL then |
| 14 | restore oldPlacement |
| 15 | end if |
| 16 | return cost |
| Pseudocode 3: poAbacus algorithm | |
| input: circuit cells C, circuit rows R, number of horizontal partitions N, number of vertical partitions M | |
| output: C cells aligned in R rows without overlaps | |
| 1 | //stores the leftover cells |
| 2 | |
| 3 | split chip area into N-1 horizontal partitions of b rows each //the Nth partition will have the |
| //remaining rows: | |
| 4 | foreach horizontal partition h do |
| 5 | avgFreeSpace: = (area(h) − obstacleArea(h))/M |
| 6 | xoffset: = chipAreaWidth/s //s is a tunable parameter |
| 7 | for v: = 1 to M-1 do |
| 8 | setTileBoundary(Thv, getTileBoundary(Th(v−1))+xoffset) // getTileBoundary(Th0) = 0 |
| 9 | while freeArea(Thv) < avgFreeSpace do |
| 10 | setTileBoundary(Thv, getTileBoundary(Thv)+xoffset) |
| 11 | end while |
| 12 | end for |
| 13 | setTileBoundary(ThM, chipAreaWidth) |
| 14 | end for |
| 15 | par-foreachThvdo //each tile is assigned to a different thread |
| 16 | : = {all cells contained in Thv} |
| 17 | : = {all sub-rows contained in Thv} |
| 18 | Abacus ( |
| 19 | foreach do |
| 20 | if exceeds then |
| 21 | down(mutex) |
| 22 | |
| 23 | up(mutex) |
| 24 | end if |
| 25 | end for |
| 26 | end par-for |
| 27 | barrier |
| 28 | ifthen |
| 29 | Abacus(, ) // is the set of subrows existing in the whole chip area |
| 30 | end if |
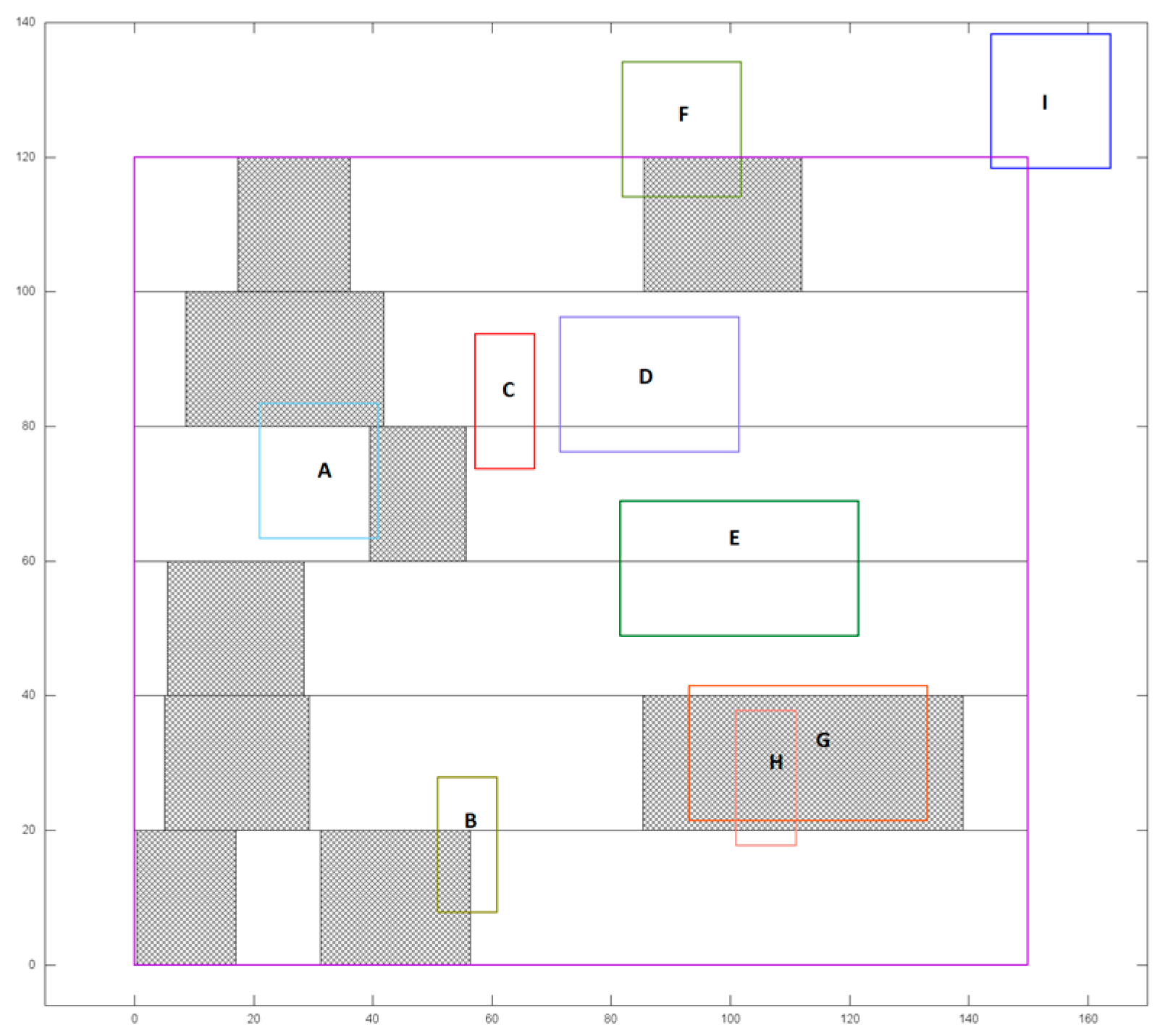
4. Experiments
4.1. Experimental Setup
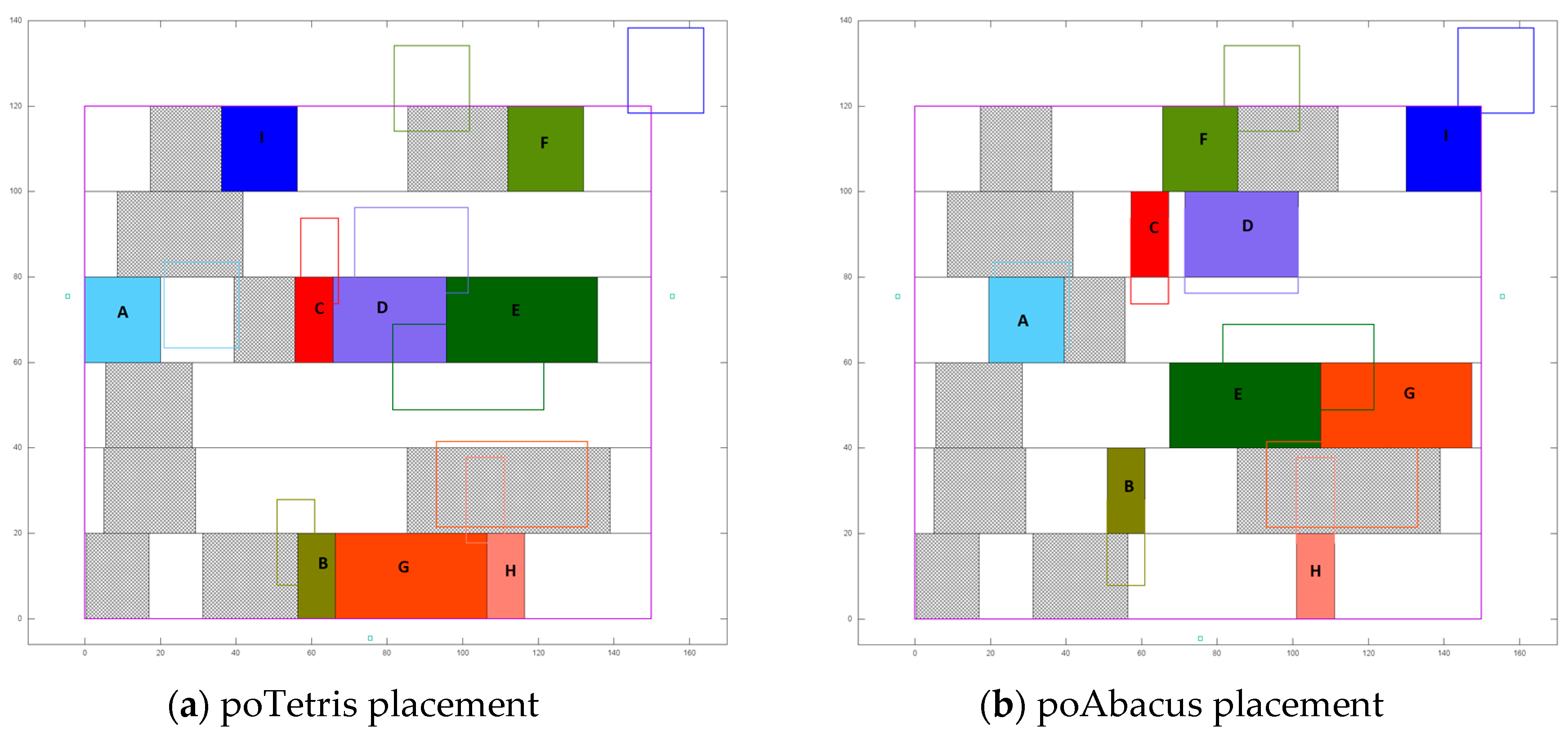
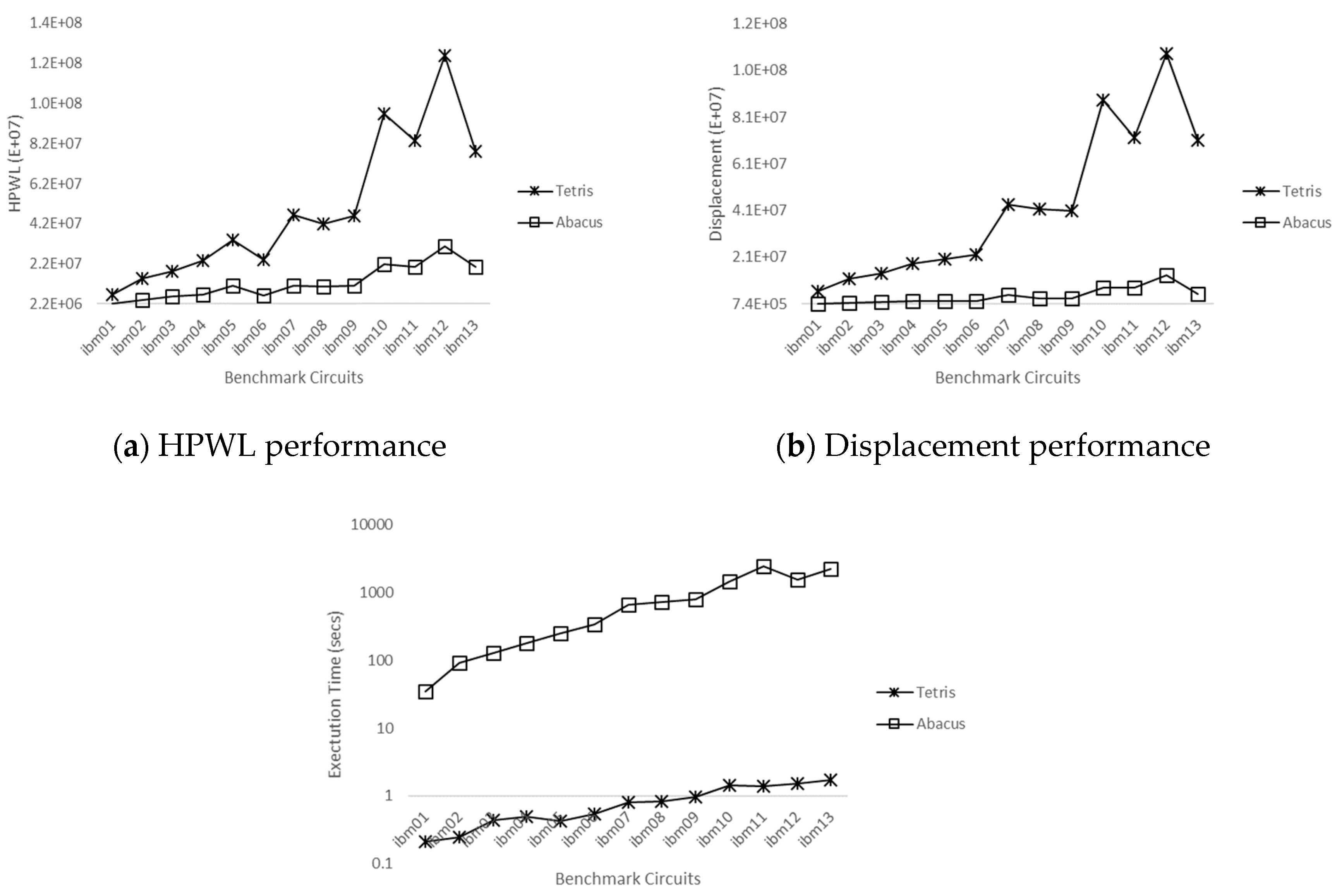
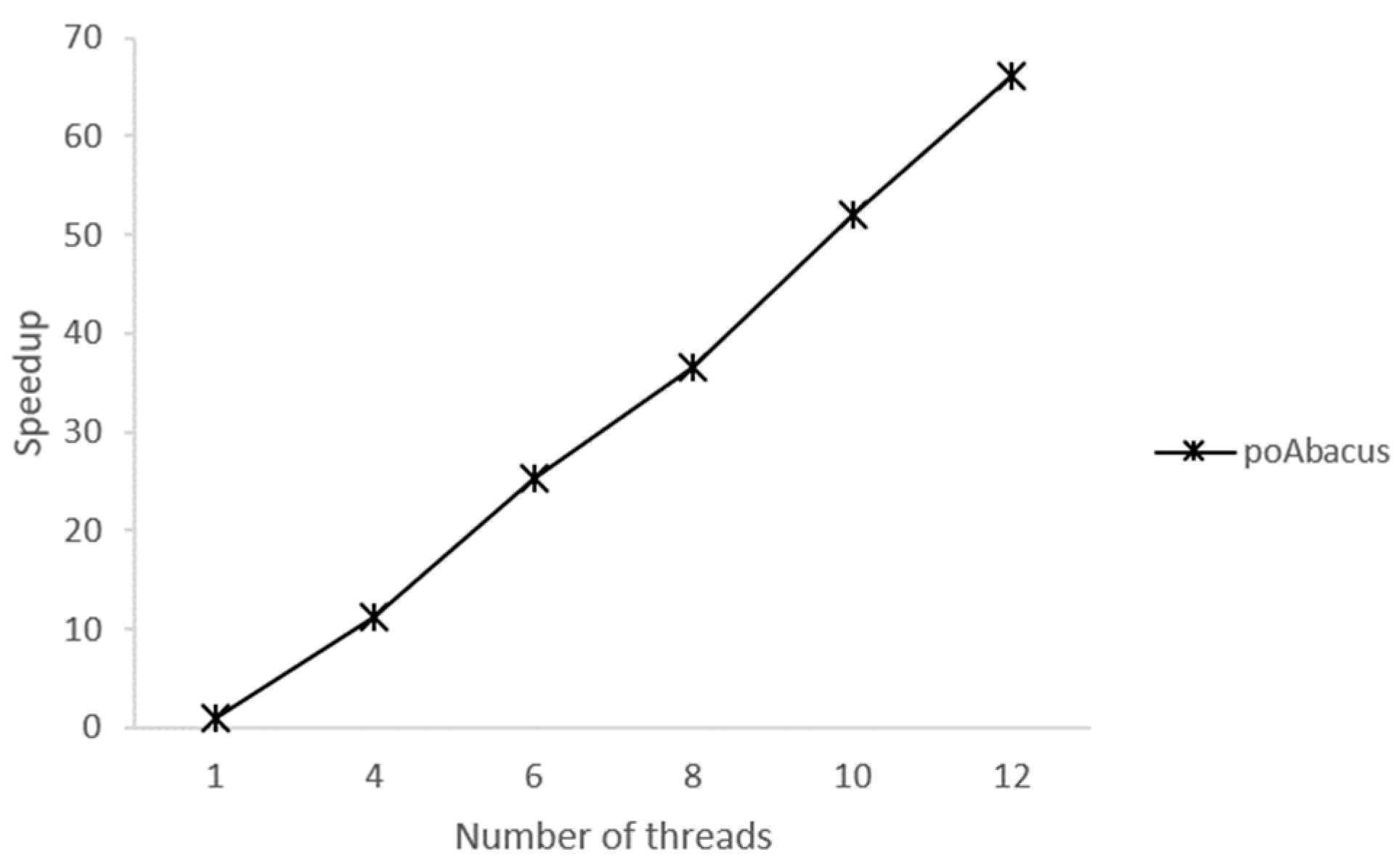
4.2. Standalone Tetris and Abacus Evaluation
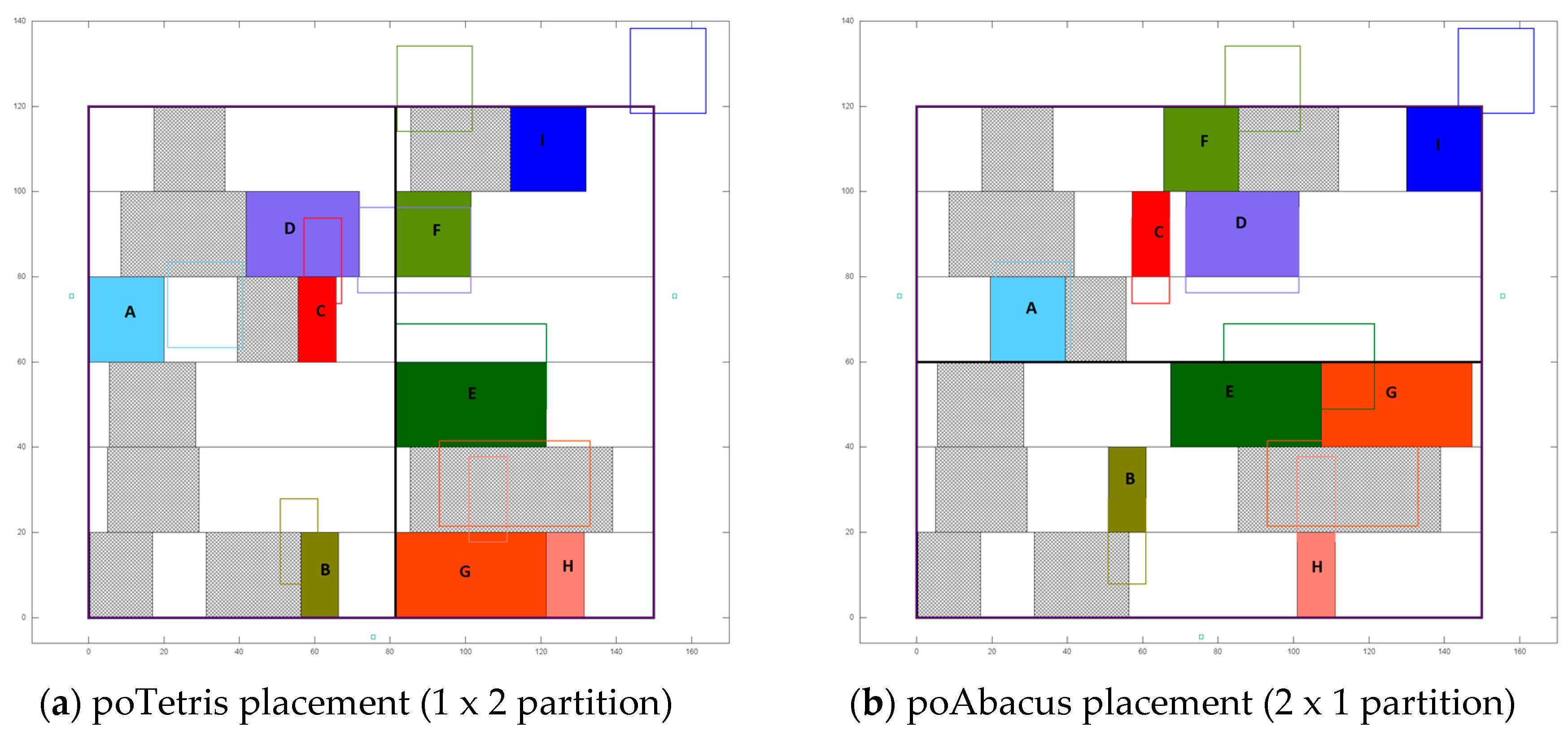
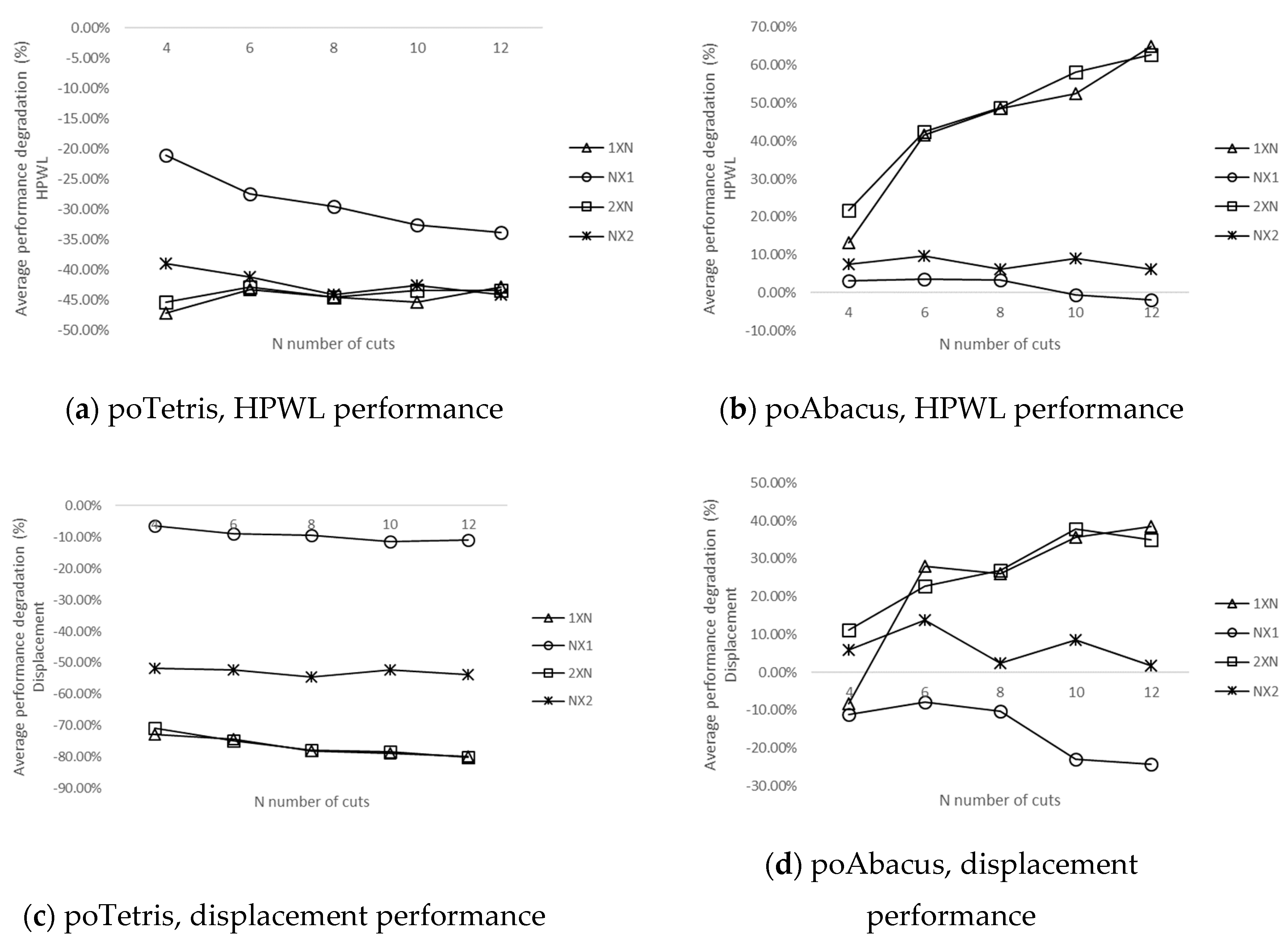
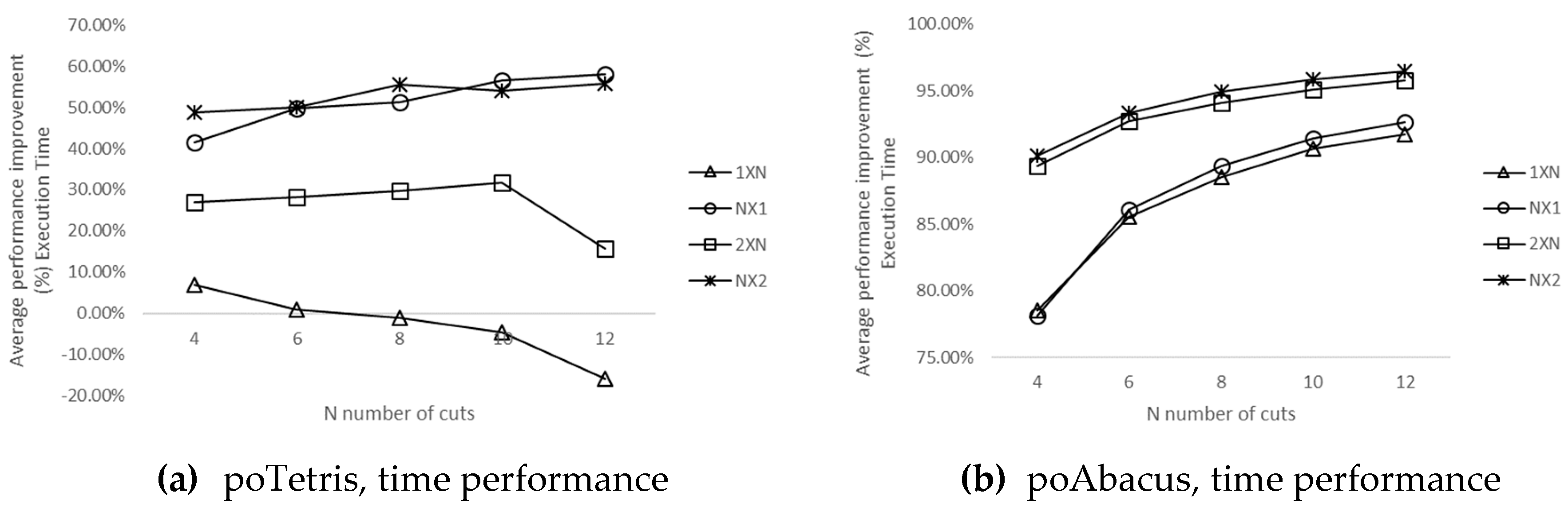
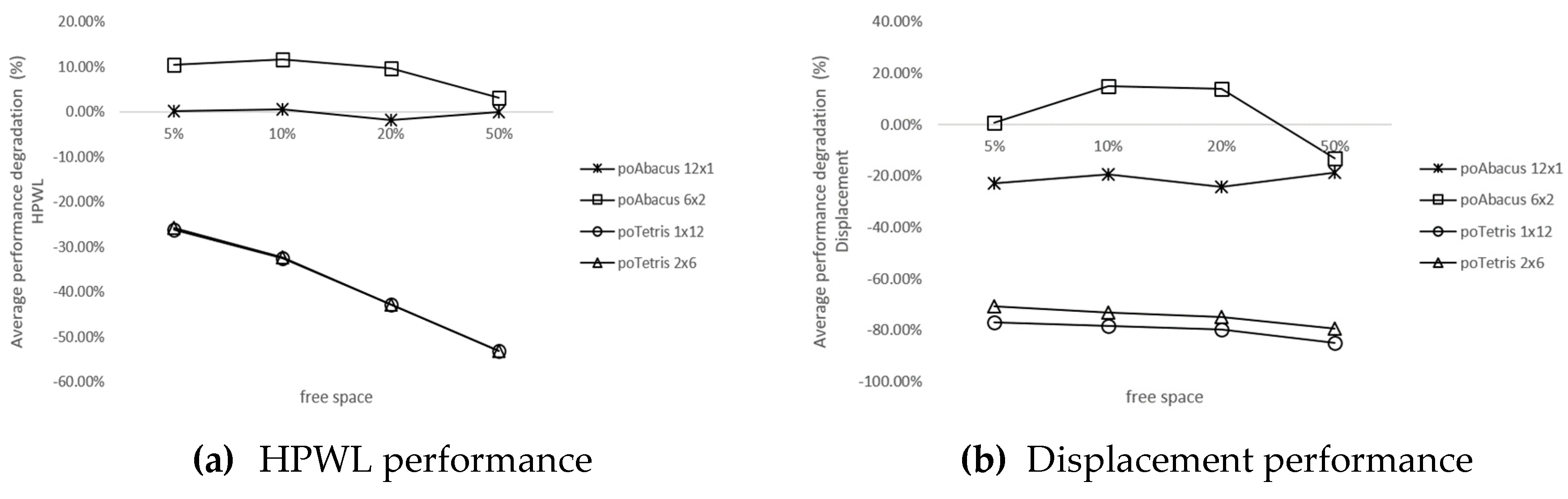
4.3. Evaluation of poTetris and poAbacus
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hill, D. Method and System for High Speed Detailed Placement of Cells within an Integrated Circuit Design. U.S. Patent 6370673 B1, 9 April 2002. [Google Scholar]
- Spindler, P.; Schlichtmann, U.; Johannes, F.M. Abacus: Fast Legalization of Standard Cell Circuits with Minimal Movement. In Proceedings of the 2008 International Symposium on Physical Design (ISPD ’08), Portland, OR, USA, 13–16 April 2008; ACM Press: New York, NY, USA, 2008. [Google Scholar]
- Oikonomou, P.; Dadaliaris, A.N.; Loukopoulos, T.; Kakarountas, A.; Stamoulis, G.I. A Tetris-based Legalization Heuristic for Standard Cell Placement with Obstacles. In Proceedings of the 7th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Cardoso, M.S.; Smaniotto, G.H.; Bubolz, A.A.O.; Moreira, M.T.; da Rosa, L.S.; de Souza Marques, F. Libra: An automatic design methodology for CMOS complex gates. IEEE Trans. Circuits Syst. II Express Br. 2018, 65, 1345–1349. [Google Scholar] [CrossRef]
- Guo, J.; Zhu, L.; Sun, Y.; Cao, H.; Huang, H.; Wang, T.; Qi, C.; Zhang, R.; Cao, X.; Xiao, L.; et al. Design of area-efficient and highly reliable RHBD 10T memory cell for aerospace applications. IEEE Trans. Very Larg. Scale Integr. Syst. 2018, 26, 991–994. [Google Scholar] [CrossRef]
- Mishra, V.K.; Chauhan, R.K. Area efficient layout design of CMOS circuit for high-density ICs. Int. J. Electron. 2018, 105, 73–87. [Google Scholar] [CrossRef]
- Dadaliaris, A.; Oikonomou, P.; Koziri, M.; Nerantzaki, E.; Hatzaras, Y.; Garyfallou, D.; Loukopoulos, T.; Stamoulis, G. Heuristics to augment the performance of tetris legalization: Making a fast but inferior method competitive. J. Low Power Electron. 2017, 13, 220–230. [Google Scholar] [CrossRef]
- Chou, S.; Ho, T.-Y. OAL: An obstacle-aware legalization in standard cell placement with displacement minimization. In Proceedings of the 2009 IEEE International SOC Conference (SOCC), Belfast, UK, 9–11 September 2009. [Google Scholar]
- Spindler, P.; Schlichtmann, U.; Johannes, F.M. Kraftwerk2—A fast force-directed quadratic placement approach using an accurate net model. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2008, 27, 1398–1411. [Google Scholar] [CrossRef]
- Chen, T.-C.; Jiang, Z.-W.; Hsu, T.-C.; Chen, H.-C.; Chang, Y.-W. NTUplace3: An analytical placer for large-scale mixed-size designs with preplaced blocks and density constraints. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2008, 27, 1228–1240. [Google Scholar] [CrossRef]
- Popovych, S.; Lai, H.-H.; Wang, C.-M.; Li, Y.-L.; Liu, W.-H.; Wang, T.-C. Density-Aware Detailed Placement with Instant Legalization. In Proceedings of the 51st Annual Design Automation Conference on Design Automation Conference (DAC ’14), San Francisco, CA, USA,, 1–5 June 2014; ACM Press: New York, NY, USA, 2014. [Google Scholar]
- Netto, R.; Guth, C.; Livramento, V.; Castro, M.; Pilla, L.L.; Guntzel, J.L. Exploiting parallelism to speed up circuit legalization. In Proceedings of the 2016 IEEE International Conference on Electronics, Circuits and Systems (ICECS), Monte Carlo, Monaco, 11–14 December 2016. [Google Scholar]
- Oikonomou, P.; Koziri, M.G.; Dadaliaris, A.N.; Loukopoulos, T.; Stamoulis, G.I. Domocus: Lock free parallel legalization in standard cell placement. In Proceedings of the 6th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 4–6 May 2017. [Google Scholar]
- Wang, C.-H.; Wu, Y.-Y.; Chen, J.; Chang, Y.-W.; Kuo, S.-Y.; Zhu, W.; Fan, G. An effective legalization algorithm for mixed-cell-height standard cells. In Proceedings of the 22nd Asia and South Pacific Design Automation Conference (ASP-DAC), Chiba, Japan, 16–19 January 2017. [Google Scholar]
- Kennings, A.; Darav, N.K.; Behjat, L. Detailed placement accounting for technology constraints. In Proceedings of the 2014 22nd International Conference on Very Large Scale Integration (VLSI-SoC), Playa del Carmen, Mexico, 6–8 October 2014. [Google Scholar]
- Sketopoulos, N.; Sotiriou, C.; Simoglou, S. Abax: 2D/3D legaliser supporting look-ahead legalisation and blockage strategies. In Proceedings of the 2018 Design, Automation and Test in Europe Conference and Exhibition (DATE), Dresden, Germany, 19–23 March 2018. [Google Scholar]
- Viswanathan, N.; Pan, M.; Chu, C. FastPlace 3.0: A fast multilevel quadratic placement algorithm with placement congestion control. In Proceedings of the 2007 Asia and South Pacific Design Automation Conference, Yokohama, Japan, 23–26 January 2007. [Google Scholar]
- Lu, J.; Chen, P.; Chang, C.-C.; Sha, L.; Huang, D.J.-H.; Teng, C.-C.; Cheng, C.-K. ePlace: Electrostatics-based placement using fast fourier transform and Nesterov’s method. ACM Trans. Des. Autom. Electron. Syst. 2015, 20, 1–34. [Google Scholar] [CrossRef]
- Lu, J.; Zhuang, H.; Chen, P.; Chang, H.; Chang, C.-C.; Wong, Y.-C.; Sha, L.; Huang, D.; Luo, Y.; Teng, C.-C.; et al. ePlace-MS: Electrostatics-based placement for mixed-size circuits. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2015, 34, 685–698. [Google Scholar] [CrossRef]
- Wu, G.; Chu, C. Detailed Placement Algorithm for VLSI Design with Double-Row Height Standard Cells. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2016, 35, 1569–1573. [Google Scholar] [CrossRef]
- Taghavi, T.; Yang, X.; Choi, B.-K. Dragon2005: Large-Scale Mixed-Size Placement Tool. In Proceedings of the 2005 International Symposium on Physical Design (ISPD ’05), San Francisco, CA, USA, 3–6 April 2005; ACM Press: New York, NY, USA, 2005. [Google Scholar]
- Ababei, C.; Navaratnasothie, S.; Bazargan, K.; Karypis, G. Multi-objective circuit partitioning for cutsize and path-based delay minimization. In Proceedings of the IEEE/ACM International Conference on Computer Aided Design (ICCAD 2002), San Jose, CA, USA, 10–14 November 2002. [Google Scholar]
- Kim, M.-C.; Lee, D.-J.; Markov, I.L. SimPL: An effective placement algorithm. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2012, 31, 50–60. [Google Scholar] [CrossRef]
- Brenner, U. VLSI legalization with minimum perturbation by iterative augmentation. In Proceedings of the 2012 Design, Automation and Test in Europe Conference and Exhibition (DATE), Dresden, Germany, 12–16 March 2012. [Google Scholar]
- Brenner, U. BonnPlace legalization: Minimizing movement by iterative augmentation. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2013, 32, 1215–1227. [Google Scholar] [CrossRef]
- Hu, J.; Zhou, Q.; Gao, W.; Qian, X.; Zhou, Q. An effective legalization approach based on multiple ordering. In Proceedings of the 2013 International Conference on Communications, Circuits and Systems (ICCCAS), Chengdu, China, 15–17 November 2013. [Google Scholar]
- Zhou, Q.; Hu, J.; Zhou, Q. An effective iterative density aware detailed placement algorithm. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems (ISCAS), Melbourne, VIC, Australia, 1–5 June 2014. [Google Scholar]
- Li, H.; Chow, W.-K.; Chen, G.; Young, E.F.Y.; Yu, B. Routability-driven and fence-aware legalization for mixed-cell-height circuits. In Proceedings of the 55th Annual Design Automation Conference on (DAC ’18), San Francisco, CA, USA, 24–29 June 2018; ACM Press: New York, NY, USA, 2018. [Google Scholar]
- Darav, N.K.; Bustany, I.S.; Kennings, A.; Westwick, D.; Behjat, L. Eh?Legalizer: A high performance standard-cell legalizer observing technology constraints. ACM Trans. Des. Autom. Electron. Syst. 2018, 23, 1–25. [Google Scholar] [CrossRef]
- Cho, M.; Ren, H.; Xiang, H.; Puri, R. History-Based VLSI Legalization Using Network Flow. In Proceedings of the 47th Design Automation Conference (DAC ’10), Anaheim, CA, USA, 13–18 June 2010; ACM Press: New York, NY, USA, 2010. [Google Scholar]
- Fabre, S.; Guntzel, J.L.; Pilla, L.; Netto, R.; Fontana, T.; Livramento, V. Enhancing Multi-threaded legalization through $k$-d tree circuit partitioning. In Proceedings of the 2018 31st Symposium on Integrated Circuits and Systems Design (SBCCI), Bento Goncalves, Brazil, 27–31 August 2018; pp. 1–6. [Google Scholar]
- Yan, C.; Salman, E. Mono3D: Open source cell library for monolithic 3-D integrated circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 1075–1085. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, S.; Xu, X.; Yu, B. Clustered fault tolerance TSV planning for 3-D integrated circuits. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2017, 36, 1287–1300. [Google Scholar] [CrossRef]
- Lepercq, É.; Blaquière, Y.; Savaria, Y. A pattern-based routing algorithm for a novel electronic system prototyping platform. Integration 2018, 62, 224–237. [Google Scholar] [CrossRef]
- Carbajal-Gomez, V.; Tlelo-Cuautle, E.; Sanchez-Lopez, C.; Fernandez-Fernandez, F. PVT-robust CMOS programmable chaotic oscillator: Synchronization of two 7-scroll attractors. Electronics 2018, 7, 252. [Google Scholar] [CrossRef]
- Abbas, Z.; Olivieri, M.; Ripp, A. Yield-driven power-delay-optimal CMOS full-adder design complying with automotive product specifications of PVT variations and NBTI degradations. J. Comput. Electron. 2016, 15, 1424–1439. [Google Scholar] [CrossRef]
- ISPD04 Benchmark Circuits. Available online: http://vlsicad.eecs.umich.edu/BK/Slots/cache/www.public. iastate.edu/~nataraj/ISPD04_Bench.html (accessed on 21 December 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oikonomou, P.; Dadaliaris, A.N.; Kolomvatsos, K.; Loukopoulos, T.; Kakarountas, A.; Stamoulis, G.I. Improved Parallel Legalization Schemes for Standard Cell Placement with Obstacles. Technologies 2019, 7, 3. https://doi.org/10.3390/technologies7010003
Oikonomou P, Dadaliaris AN, Kolomvatsos K, Loukopoulos T, Kakarountas A, Stamoulis GI. Improved Parallel Legalization Schemes for Standard Cell Placement with Obstacles. Technologies. 2019; 7(1):3. https://doi.org/10.3390/technologies7010003
Chicago/Turabian StyleOikonomou, Panagiotis, Antonios N. Dadaliaris, Kostas Kolomvatsos, Thanasis Loukopoulos, Athanasios Kakarountas, and Georgios I. Stamoulis. 2019. "Improved Parallel Legalization Schemes for Standard Cell Placement with Obstacles" Technologies 7, no. 1: 3. https://doi.org/10.3390/technologies7010003
APA StyleOikonomou, P., Dadaliaris, A. N., Kolomvatsos, K., Loukopoulos, T., Kakarountas, A., & Stamoulis, G. I. (2019). Improved Parallel Legalization Schemes for Standard Cell Placement with Obstacles. Technologies, 7(1), 3. https://doi.org/10.3390/technologies7010003






