An Energy Efficient Modulation Scheme for Body-Centric Terahertz (THz) Nanonetworks †
Abstract
1. Introduction
1.1. Motivation
1.2. Contribution
1.3. Structure
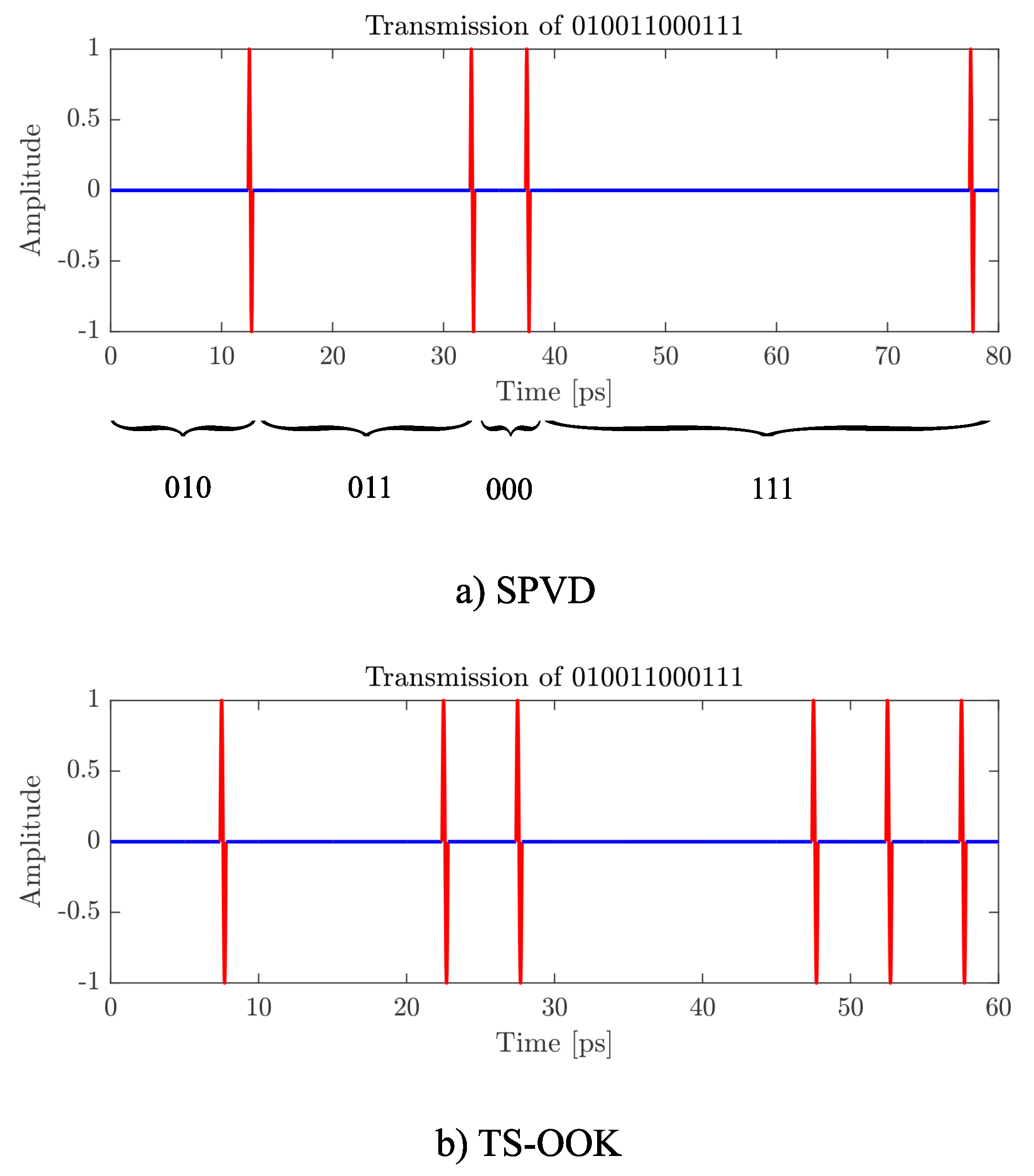
2. Single-Pulse Variable Duration (SPVD) Modulation
2.1. Basic Principle
2.2. Example for
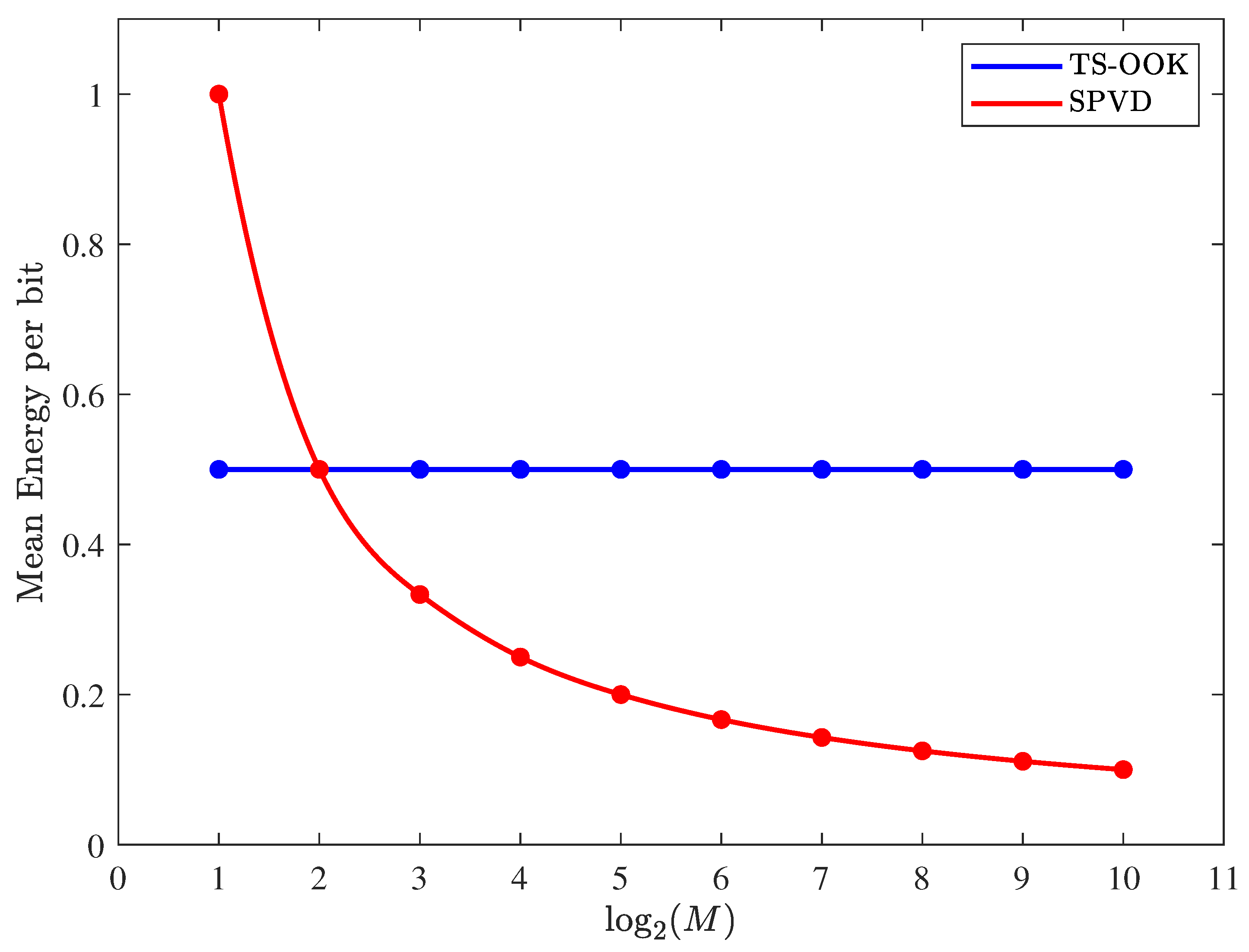
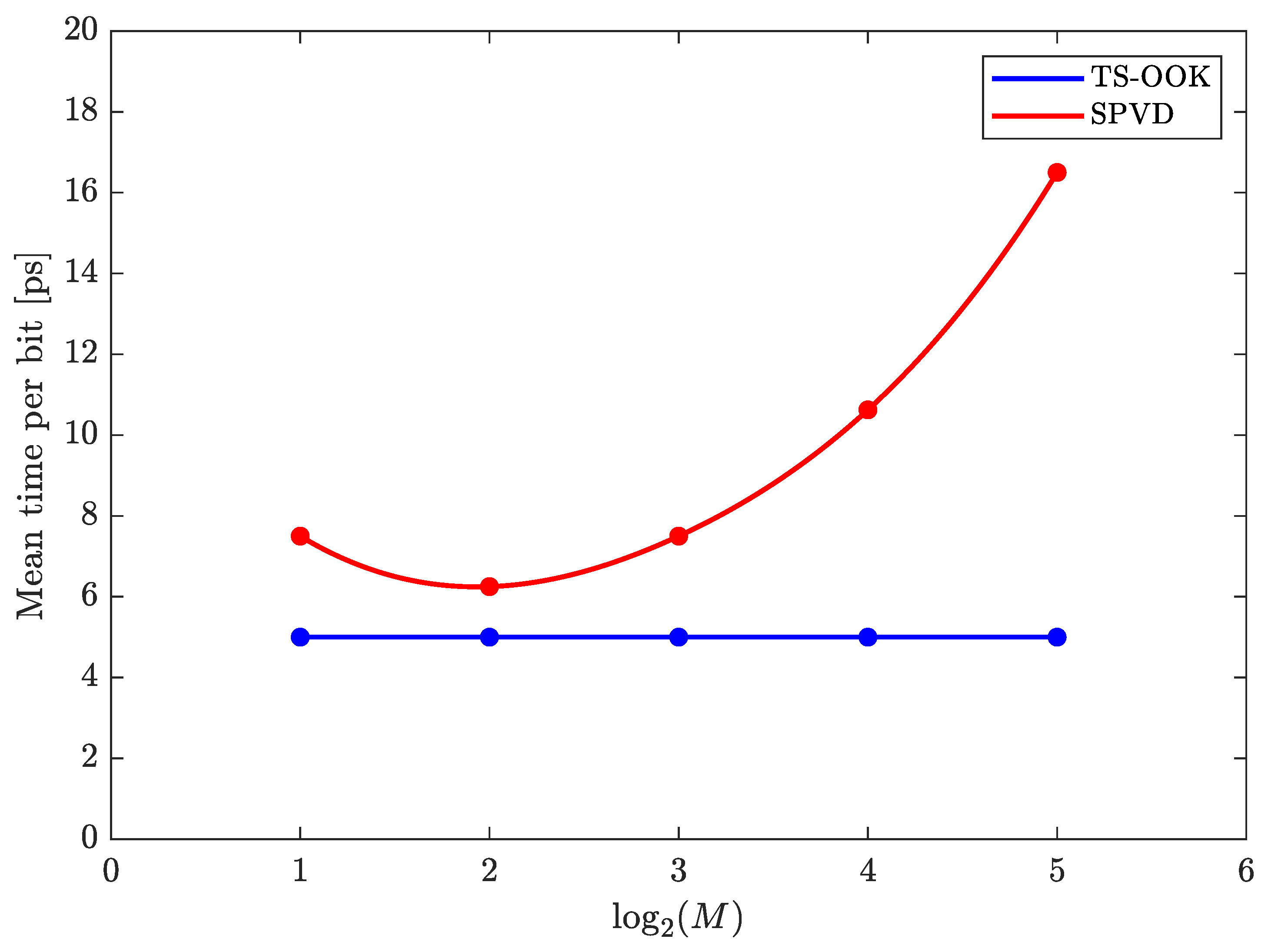
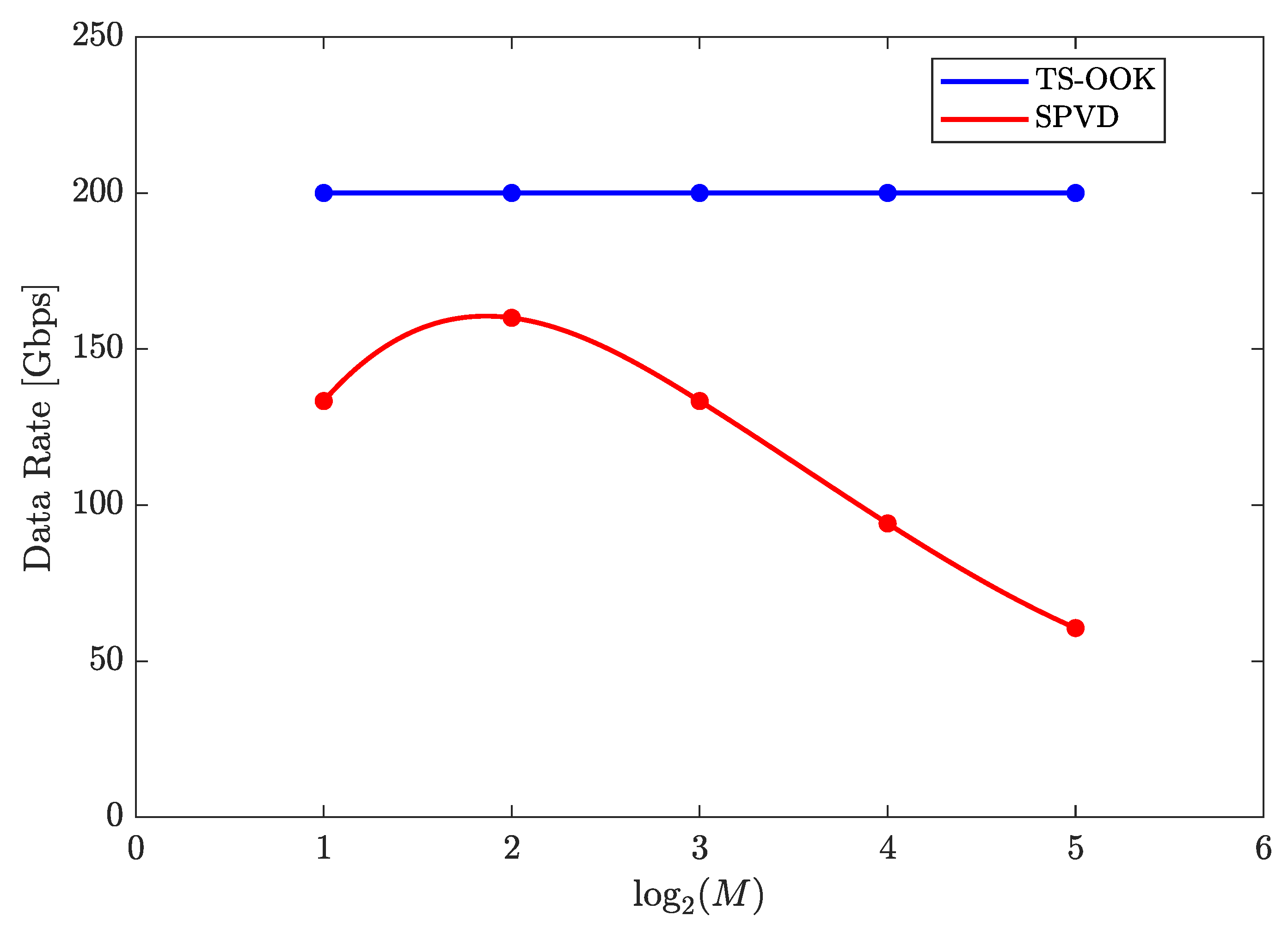
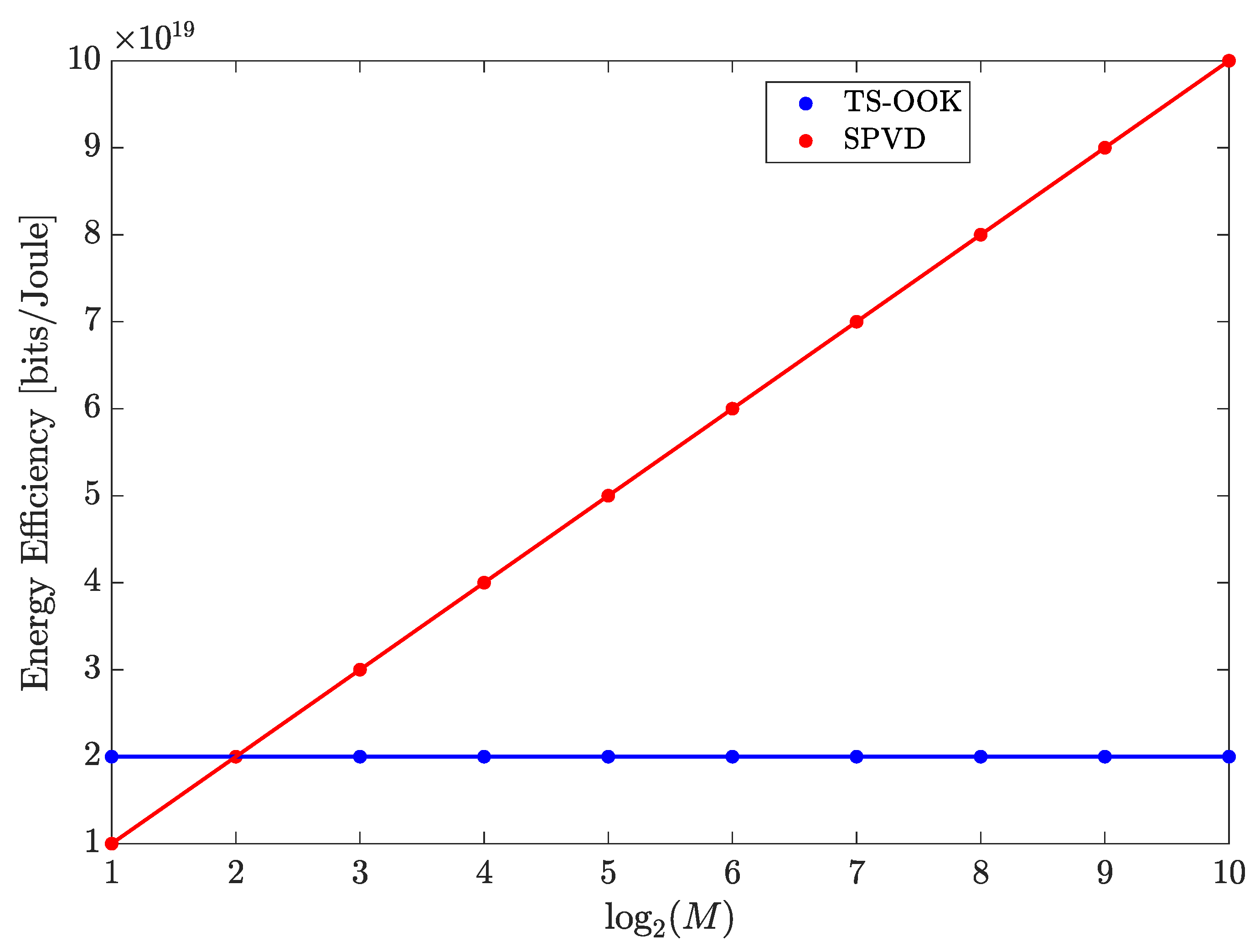
3. Trade-Off between Energy Consumption and Data Rate
3.1. Energy Consumption
3.2. Data Rate
3.3. Energy Efficiency
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Papanikolaou, V.K.; Karagiannidis, G.K. ChannelModeling of In-Vivo THz Nanonetworks: State-of-the-Art and Research Challenges. In Wireless Mobile Communication and Healthcare; Perego, P., Rahmani, A.M., TaheriNejad, N., Eds.; Springer: Cham, Switzerland, 2018; pp. 50–57. [Google Scholar]
- Abbasi, Q.H.; Nasir, A.A.; Yang, K.; Qaraqe, K.; Alomainy, A. Cooperative In-Vivo Nano-Network Communication at Terahertz Frequencies. IEEE Access 2017, 5, 8642–8647. [Google Scholar] [CrossRef]
- Safari, J.; Zarnegar, Z. Advanced drug delivery systems: Nanotechnology of health design A review. J. Saudi Chem. Soc. 2014, 18, 85–99. [Google Scholar] [CrossRef]
- Suri, S.S.; Fenniri, H.; Singh, B. Nanotechnology-based drug delivery systems. J. Occup. Med. Toxicol. 2007, 2, 16. [Google Scholar] [CrossRef] [PubMed]
- Jornet, J.M.; Akyildiz, I.F. Channel capacity of electromagnetic nanonetworks in the terahertz band. In Proceedings of the 2010 IEEE International Conference on Communications (ICC), Cape Town, South Africa, 23–27 May 2010; pp. 1–6. [Google Scholar]
- Jornet, J.M.; Akyildiz, I.F. Channel modeling and capacity analysis for electromagnetic wireless nanonetworks in the terahertz band. IEEE Trans. Wirel. Commun. 2011, 10, 3211–3221. [Google Scholar] [CrossRef]
- Jornet, J.M.; Akyildiz, I.F. Information capacity of pulse-based wireless nanosensor networks. In Proceedings of the 2011 8th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON), Salt Lake, UT, USA, 27–30 June 2011; pp. 80–88. [Google Scholar]
- Elayan, H.; Shubair, R.; Jornet, J.M.; Johari, P. Terahertz channel model and link budget analysis for intrabody nanoscale communication. IEEE Trans. Nanobiosci. 2017, 16, 491–503. [Google Scholar] [CrossRef] [PubMed]
- Kokkoniemi, J.; Lehtomäki, J.; Juntti, M. A discussion on molecular absorption noise in the terahertz band. Nano Commun. Netw. 2016, 8, 35–45. [Google Scholar] [CrossRef]
- Yang, K.; Pellegrini, A.; Munoz, M.O.; Brizzi, A.; Alomainy, A.; Hao, Y. Numerical analysis and characterization of THz propagation channel for body-centric nano-communications. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 419–426. [Google Scholar] [CrossRef]
- Piro, G.; Yang, K.; Boggia, G.; Chopra, N.; Grieco, L.A.; Alomainy, A. Terahertz communications in human tissues at the nanoscale for healthcare applications. IEEE Trans. Nanotechnol. 2015, 14, 404–406. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, K.; Alomainy, A.; Abbasi, Q.H.; Qaraqe, K.; Shubair, R.M. Modelling of the terahertz communication channel for in-vivo nano-networks in the presence of noise. In Proceedings of the 2016 16th Mediterranean Microwave Symposium (MMS), Abu Dhabi, UAE, 14–16 November 2016; pp. 1–4. [Google Scholar]
- Jornet, J.M. Low-weight error-prevention codes for electromagnetic nanonetworks in the Terahertz Band. Nano Commun. Netw. 2014, 5, 35–44. [Google Scholar] [CrossRef]
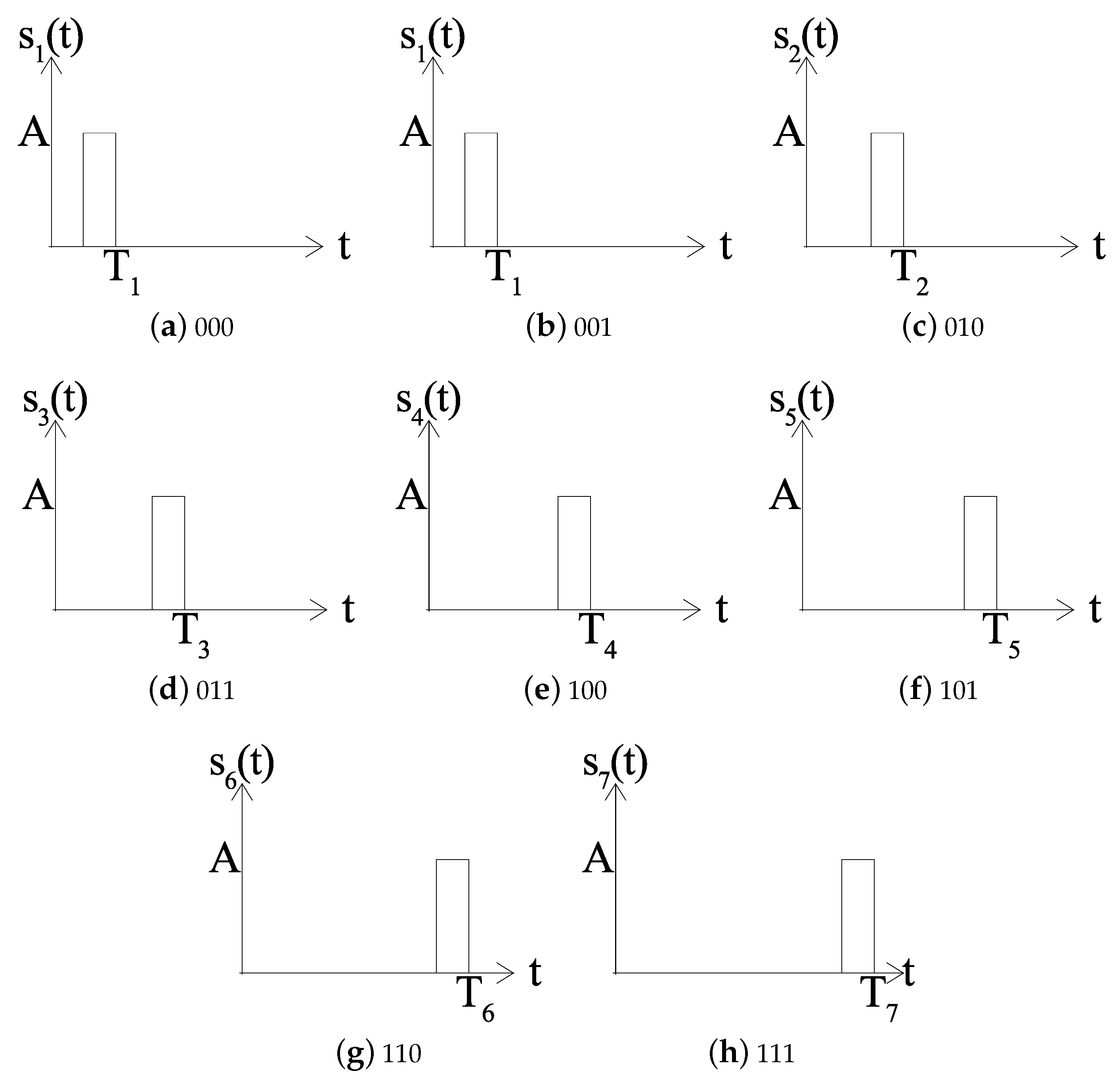
| Vector | Waveform | |
|---|---|---|
| 000 | ⟶ | |
| 001 | ⟶ | |
| 010 | ⟶ | |
| 011 | ⟶ | |
| 100 | ⟶ | |
| 101 | ⟶ | |
| 110 | ⟶ | |
| 111 | ⟶ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vavouris, A.K.; Dervisi, F.D.; Papanikolaou, V.K.; Diamantoulakis, P.D.; Karagiannidis, G.K.; Goudos, S.K. An Energy Efficient Modulation Scheme for Body-Centric Terahertz (THz) Nanonetworks. Technologies 2019, 7, 14. https://doi.org/10.3390/technologies7010014
Vavouris AK, Dervisi FD, Papanikolaou VK, Diamantoulakis PD, Karagiannidis GK, Goudos SK. An Energy Efficient Modulation Scheme for Body-Centric Terahertz (THz) Nanonetworks. Technologies. 2019; 7(1):14. https://doi.org/10.3390/technologies7010014
Chicago/Turabian StyleVavouris, Apostolos K., Foteini D. Dervisi, Vasilis K. Papanikolaou, Panagiotis D. Diamantoulakis, George K. Karagiannidis, and Sotirios K. Goudos. 2019. "An Energy Efficient Modulation Scheme for Body-Centric Terahertz (THz) Nanonetworks" Technologies 7, no. 1: 14. https://doi.org/10.3390/technologies7010014
APA StyleVavouris, A. K., Dervisi, F. D., Papanikolaou, V. K., Diamantoulakis, P. D., Karagiannidis, G. K., & Goudos, S. K. (2019). An Energy Efficient Modulation Scheme for Body-Centric Terahertz (THz) Nanonetworks. Technologies, 7(1), 14. https://doi.org/10.3390/technologies7010014








