Efficient Uncertainty Assessment in EM Problems via Dimensionality Reduction of Polynomial-Chaos Expansions †
Abstract
1. Introduction
2. Brief Literature Review of Related Works
3. Proposed Methodology
3.1. Polynomial Chaos Expansions
3.2. The Morris Method
- For all .
- Let g be the cells in the grid that satisfy .
- Calculate the mean , for the cells in g. Let this be .
- Compute the product , where is the number of values in g.
3.3. The Finite-Difference Time-Domain Technique
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tan, T.; Taflove, A.; Backman, V. Single Realization Stochastic FDTD for Weak Scattering Waves in Biological Random Media. IEEE Trans. Antennas Propag. 2013, 61, 818–828. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wilke, R.; Slim, J.; Alshrafi, W.; Heberling, D. Polynomial Chaos Expansion as a Tool to Quantify the Performance of the GeReLEO-SMART Satellite Antenna under Uncertainty. In Proceedings of the 2017 International Symposium on Antennas and Propagation (ISAP), Phuket, Thailand, 30 October–2 November 2017; pp. 1–2. [Google Scholar] [CrossRef]
- Hastings, F.D.; Schneider, J.B.; Broschat, S.L. A Monte-Carlo FDTD Technique for Rough Surface Scattering. IEEE Trans. Antennas Propag. 1995, 43, 1183–1191. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener–Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Rong, A.; Cangellaris, A.C. Transient Analysis of Distributed Electromagnetic Systems Exhibiting Stochastic Variability in Material Parameters. In Proceedings of the 2011 XXXth URSI General Assembly and Scientific Symposium, Istanbul, Turkey, 13–20 August 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Austin, A.C.M.; Sarris, C.D. Efficient Analysis of Geometrical Uncertainty in the FDTD Method Using Polynomial Chaos with Application to Microwave Circuits. IEEE Trans. Microw. Theory Tech. 2013, 61, 4293–4301. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Salis, C.; Kantartzis, N.; Zygiridis, T. Efficient Stochastic EM Studies via Dimensionality Reduction of Polynomial-Chaos Expansions. In Proceedings of the 2018 7th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Smolyak, S. Quadrature and Interpolation Formulas for Tensor Products of Certain Classes of Functions. Dokl. Akad. Nauk SSSR 1963, 148, 1042–1045. [Google Scholar]
- Beddek, K.; Clenet, S.; Moreau, O.; Costan, V.; Menach, Y.L.; Benabou, A. Adaptive Method for Non-Intrusive Spectral Projection—Application on a Stochastic Eddy Current NDT Problem. IEEE Trans. Magn. 2012, 48, 759–762. [Google Scholar] [CrossRef]
- Ma, X.; Zabaras, N. An Adaptive Hierarchical Sparse Grid Collocation Algorithm for the Solution of Stochastic Differential Equations. J. Comput. Phys. 2009, 228, 3084–3113. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. Adaptive Sparse Polynomial Chaos Expansion Based on Least Angle Regression. J. Comput. Phys. 2011, 230, 2345–2367. [Google Scholar] [CrossRef]
- Peng, J.; Hampton, J.; Doostan, A. A Weighted L1-Minimization Approach for Sparse Polynomial Chaos Expansions. J. Comput. Phys. 2014, 267, 92–111. [Google Scholar] [CrossRef]
- Diaz, P.; Doostan, A.; Hampton, J. Sparse Polynomial Chaos Expansions via Compressed Sensing and D-Optimal Design. Comput. Methods Appl. Mech. Eng. 2018, 336, 640–666. [Google Scholar] [CrossRef]
- Zhang, Z.; Weng, T.W.; Daniel, L. Big-Data Tensor Recovery for High-Dimensional Uncertainty Quantification of Process Variations. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 7, 687–697. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, X.; Oseledets, I.V.; Karniadakis, G.E.; Daniel, L. Enabling High-Dimensional Hierarchical Uncertainty Quantification by ANOVA and Tensor-Train Decomposition. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2015, 34, 63–76. [Google Scholar] [CrossRef]
- Xiu, D. Numerical Methods for Stochastic Computations: A Spectral Method Approach; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Aiouaz, O.; Lautru, D.; Wong, M.F.; Conil, E.; Gati, A.; Wiart, J.; Hanna, V.F. Uncertainty Analysis of the Specific Absorption Rate Induced in a Phantom Using a Stochastic Spectral Collocation Method. Ann. Telecommun. Ann. Des Télécommun. 2011, 66, 409–418. [Google Scholar] [CrossRef]
- Clenshaw, C.W.; Curtis, A.R. A Method for Numerical Integration on an Automatic Computer. Numer. Math. 1960, 2, 197–205. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An Effective Screening Design for Sensitivity Analysis of Large Models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Mur, G. Absorbing Boundary Conditions for the Finite-Difference Approximation of the Time-Domain Electromagnetic-Field Equations. IEEE Trans. Electromagn. Compat. 1981, EMC-23, 377–382. [Google Scholar] [CrossRef]
- Bowick, C. RF Circuit Design Approach; Newness: Oxford, UK, 1997. [Google Scholar]
- Salis, C.; Zygiridis, T. Dimensionality Reduction of the Polynomial Chaos Technique Based on the Method of Moments. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 2349–2353. [Google Scholar] [CrossRef]
- Park, K., II. Fundamentals of Probability and Stochastic Processes with Applications to Communications; Springer: Holmdel, NJ, USA, 2018. [Google Scholar]
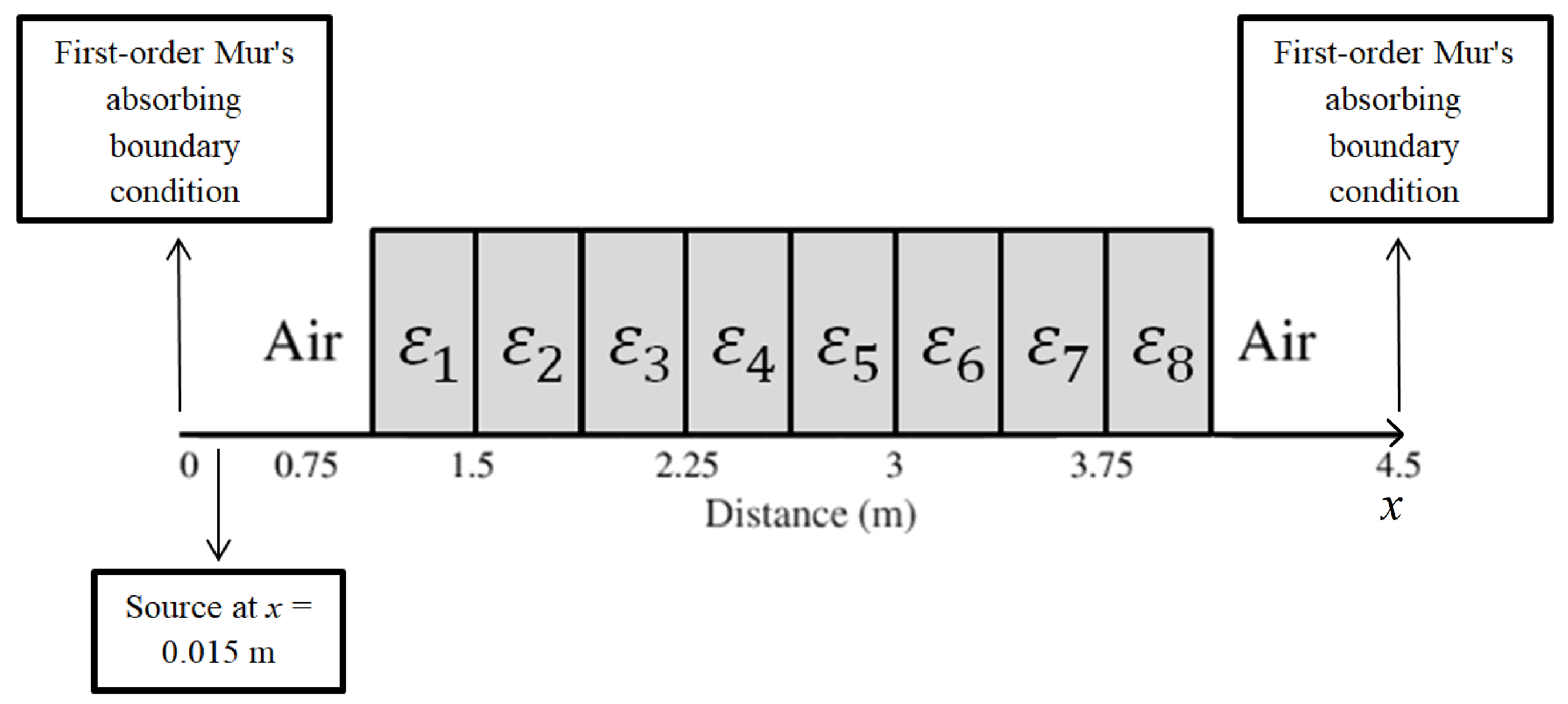
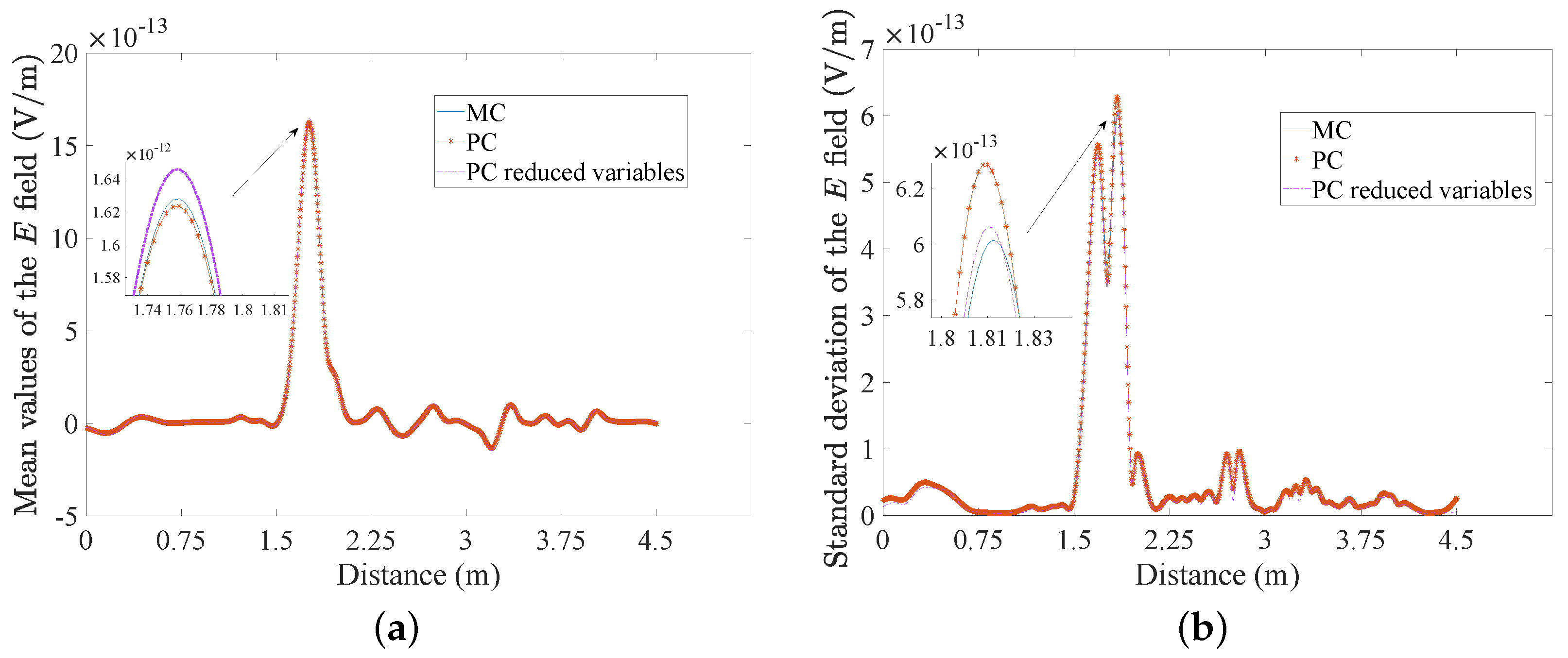
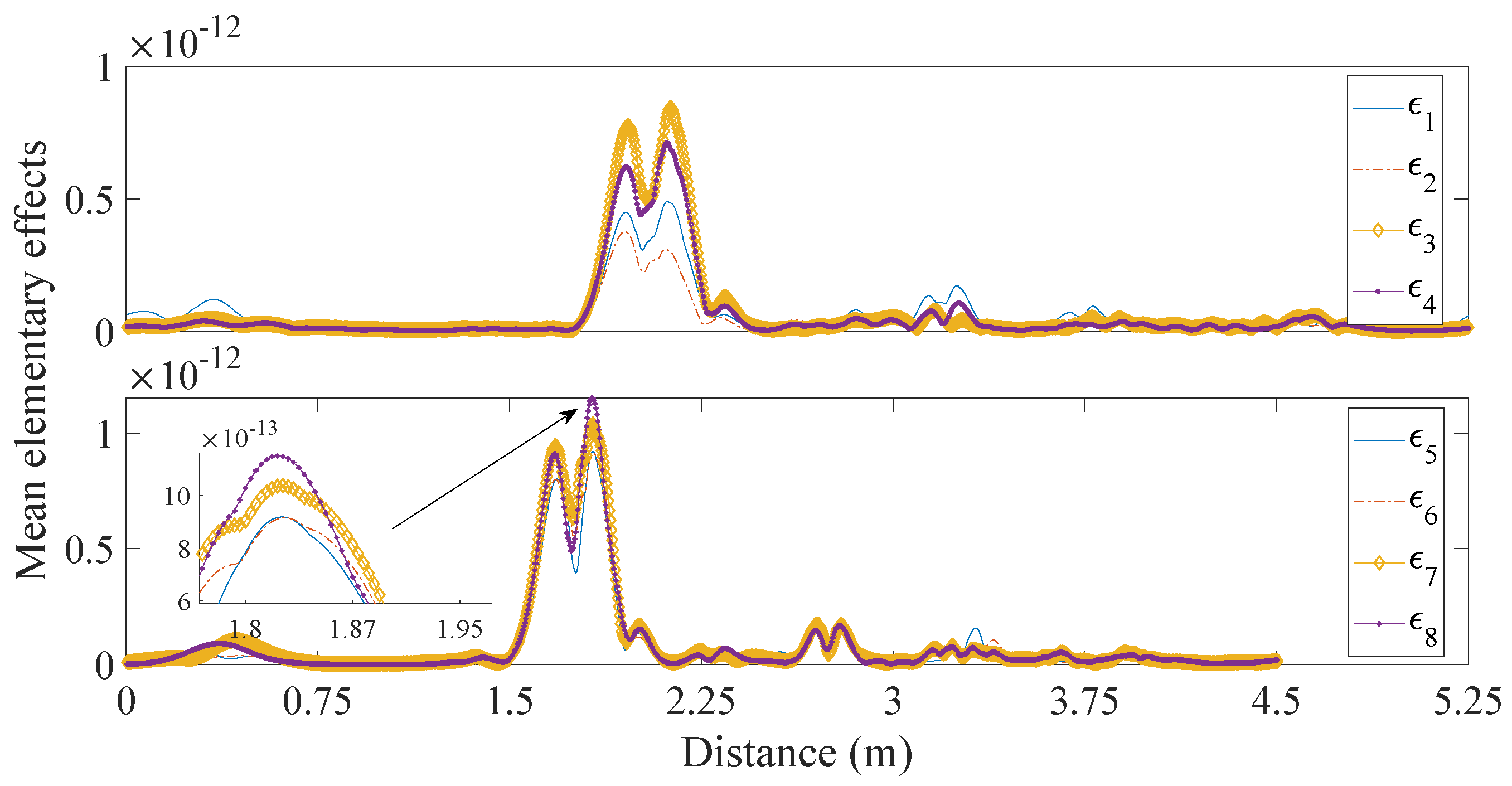
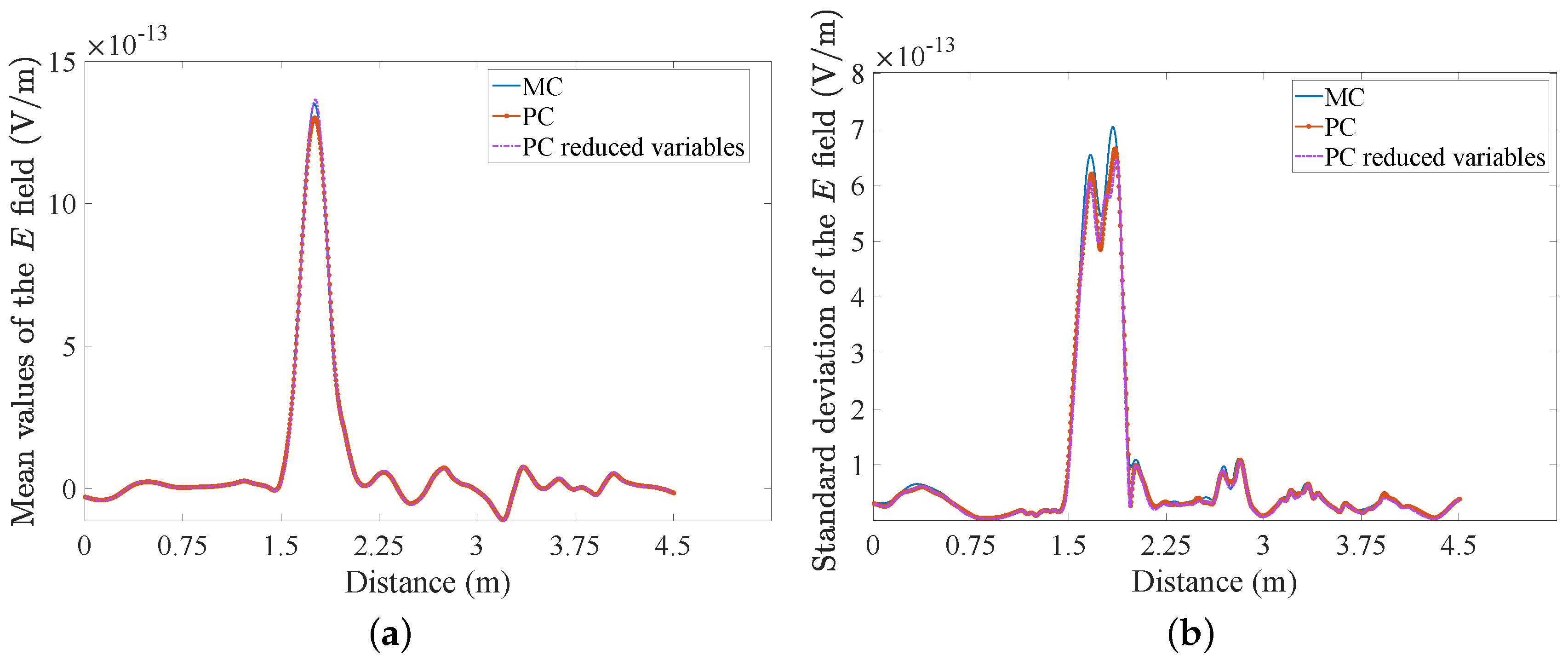
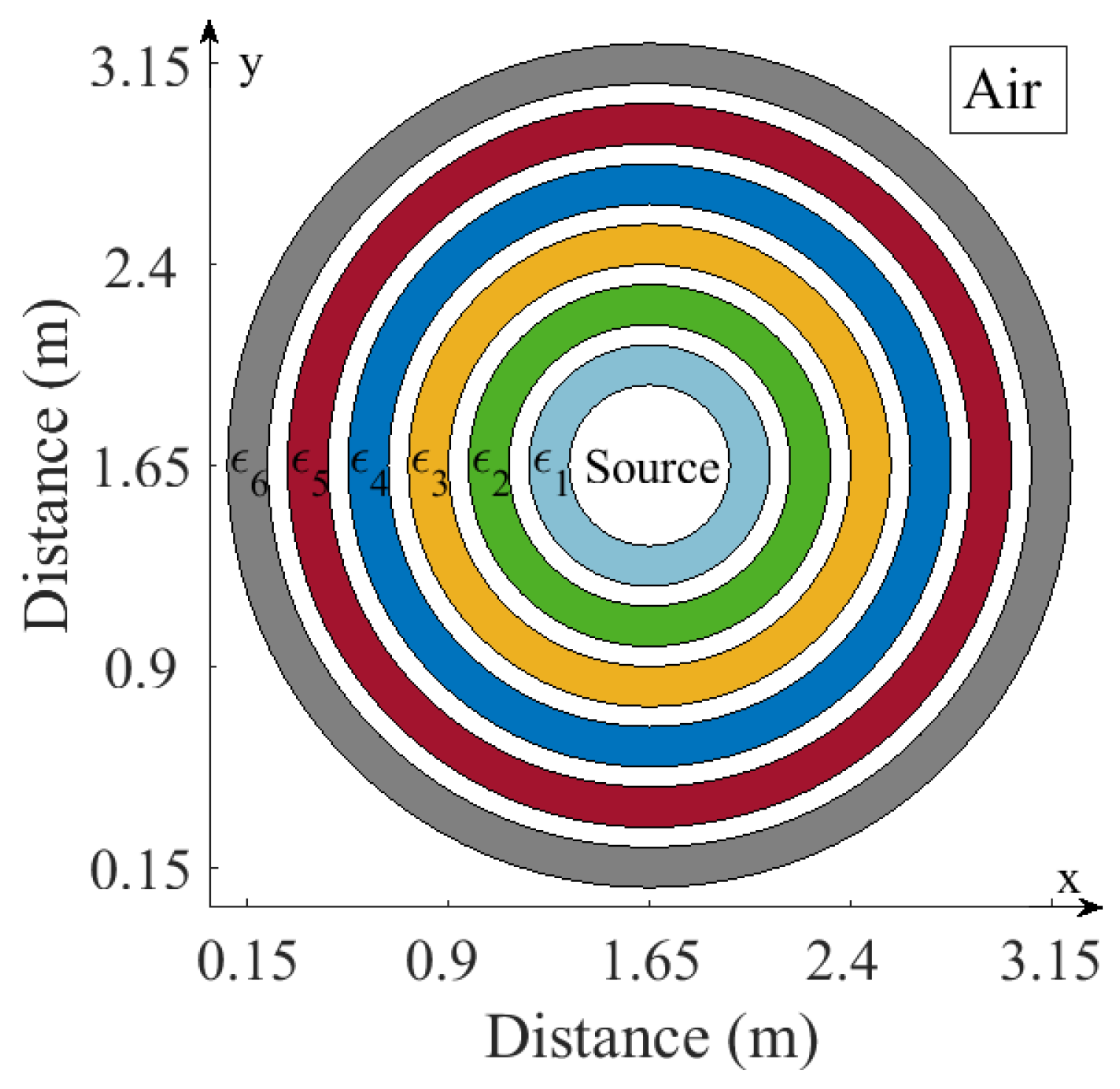
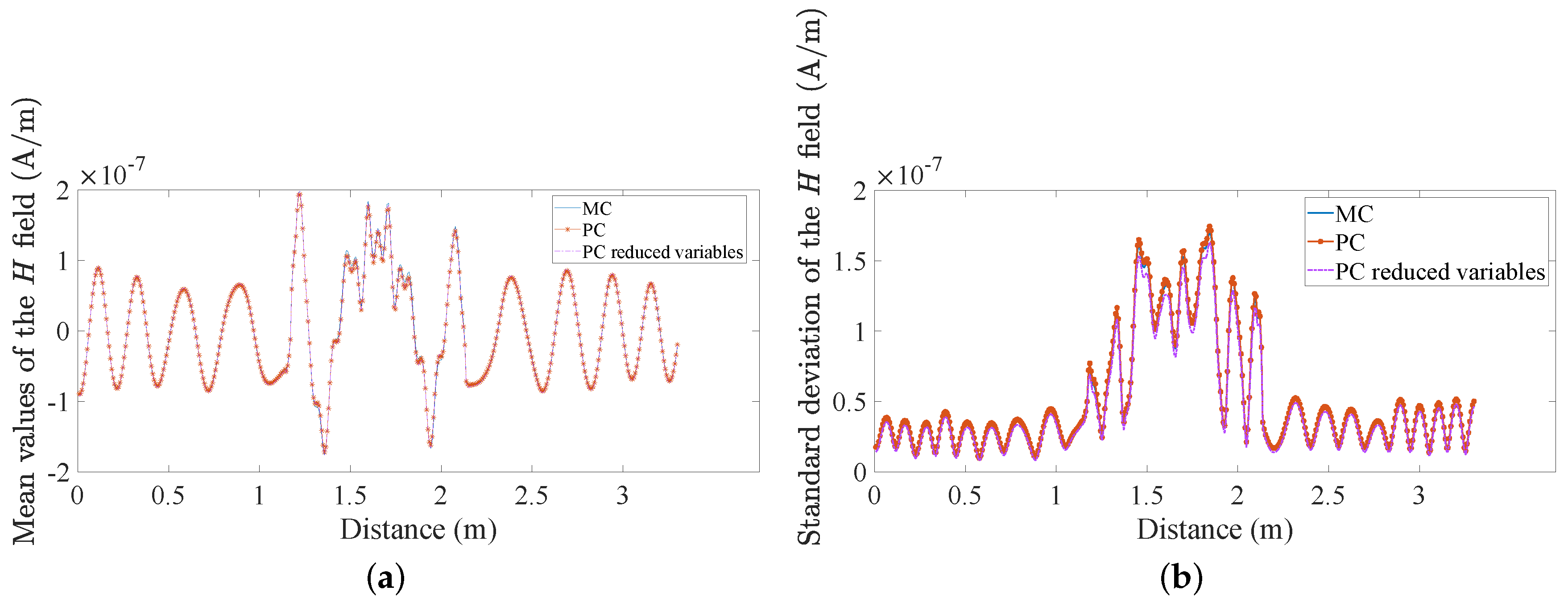
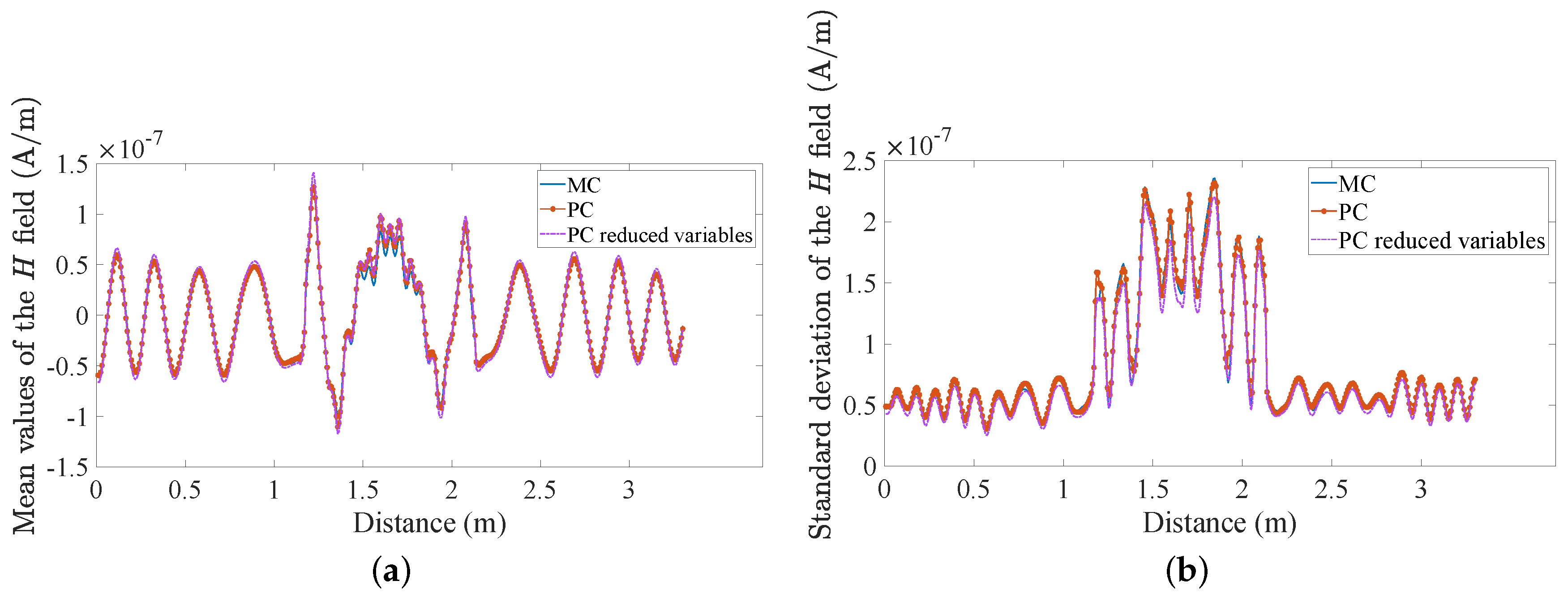
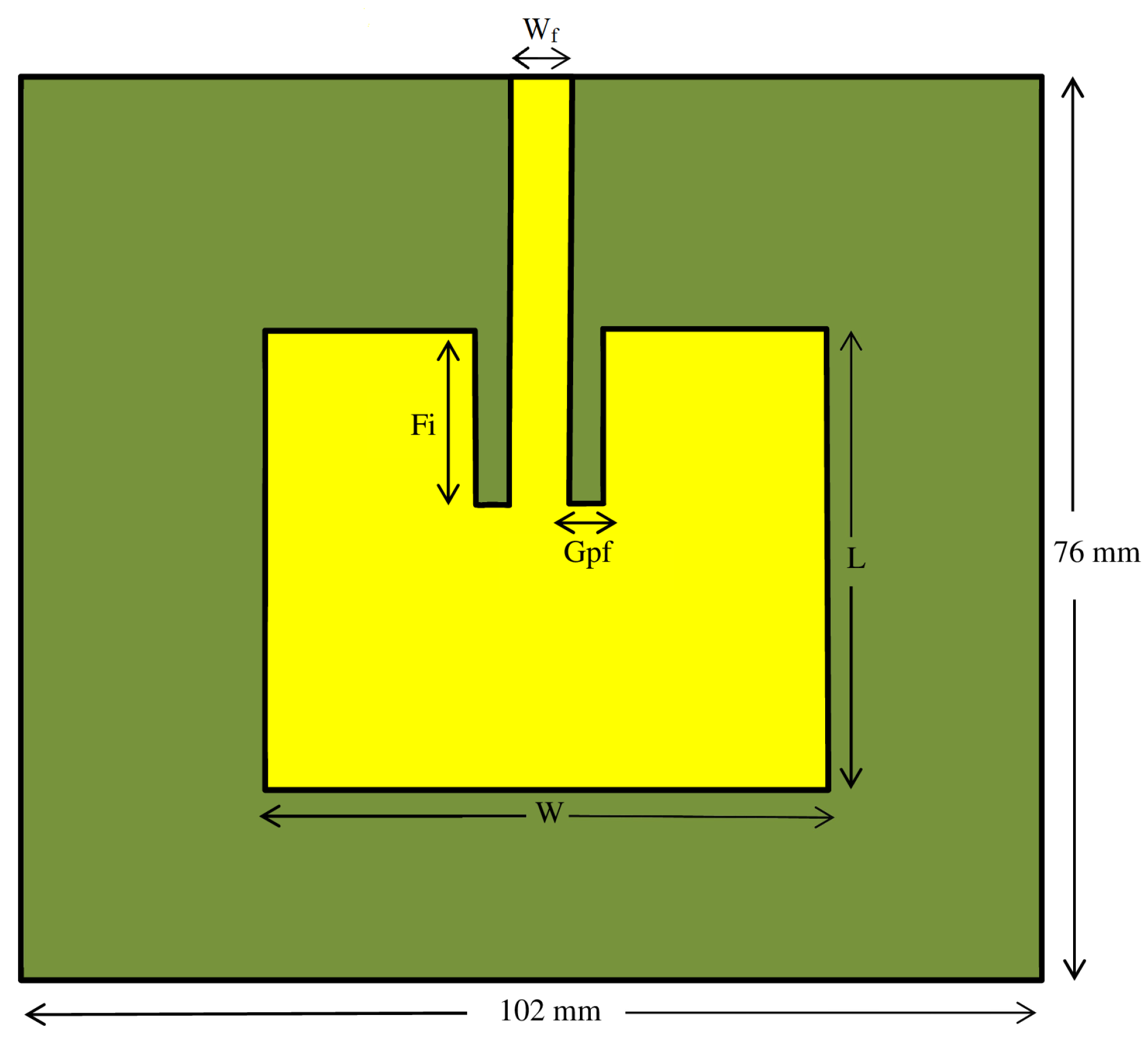
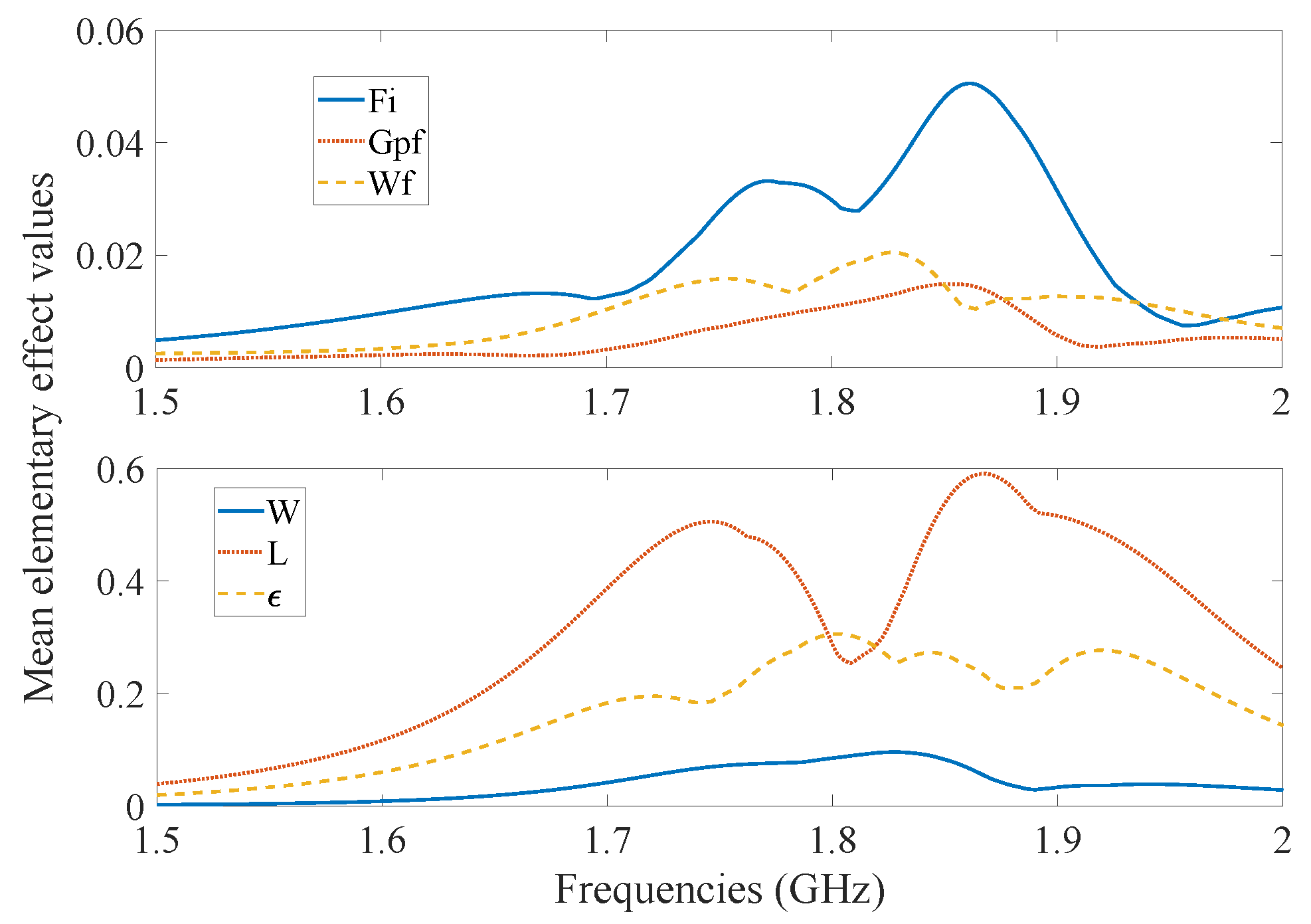
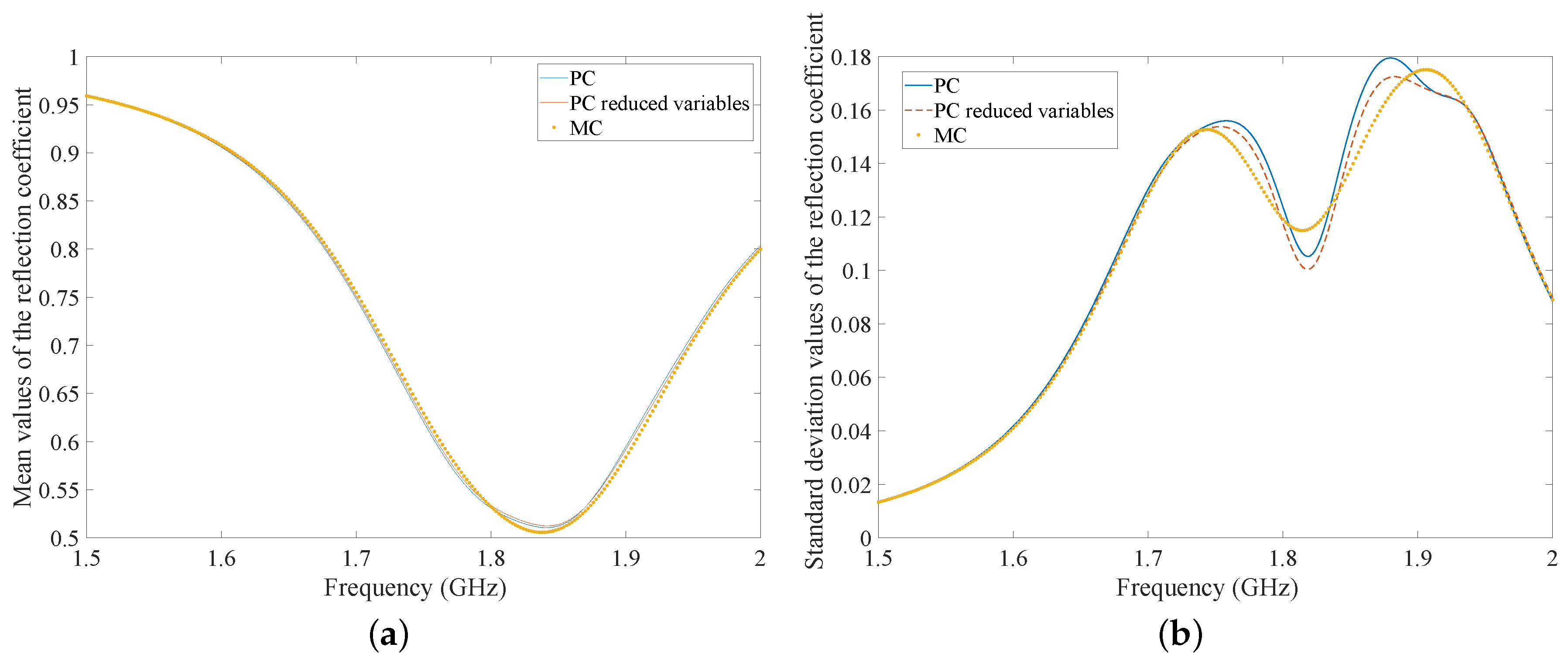
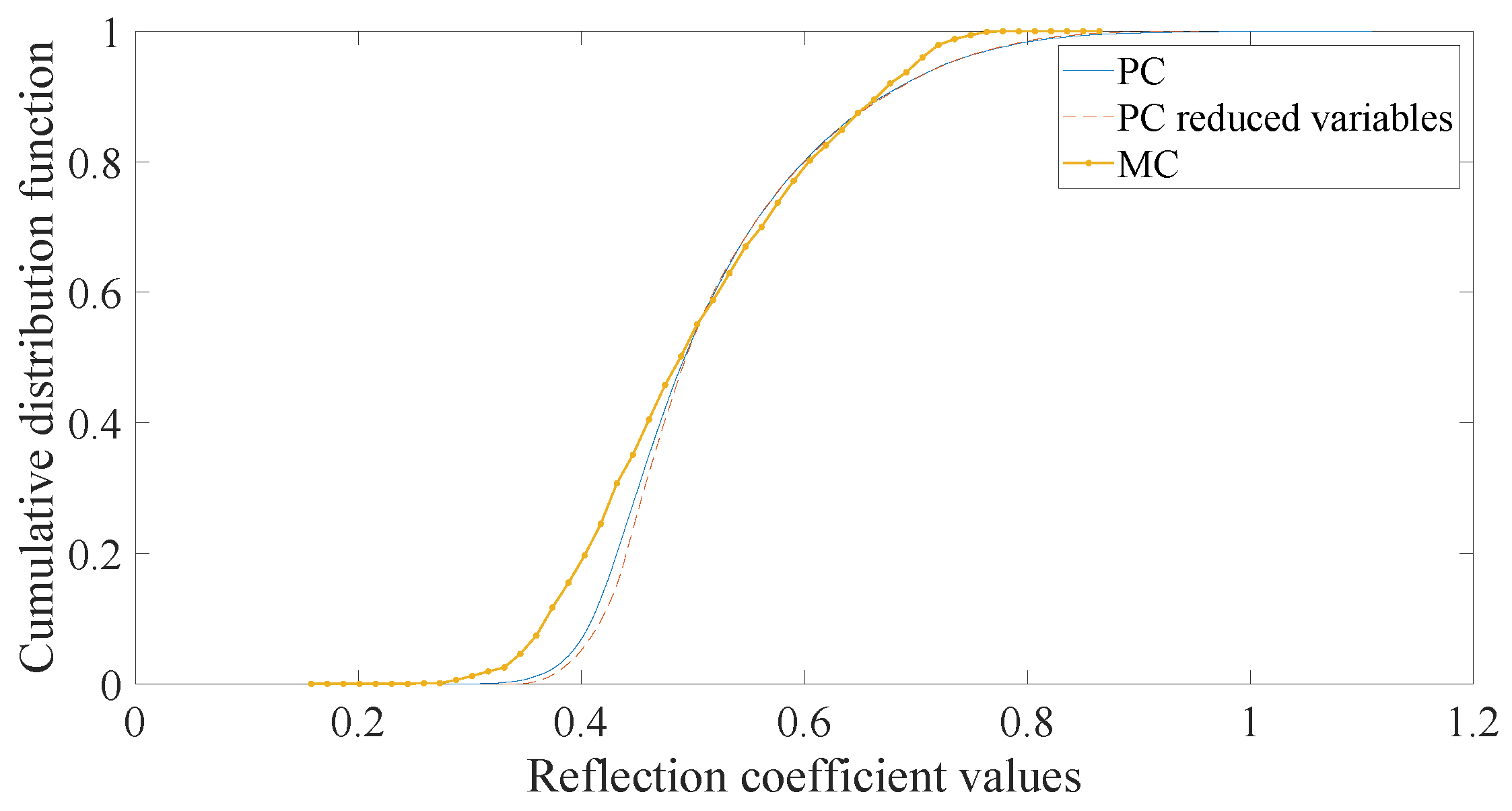
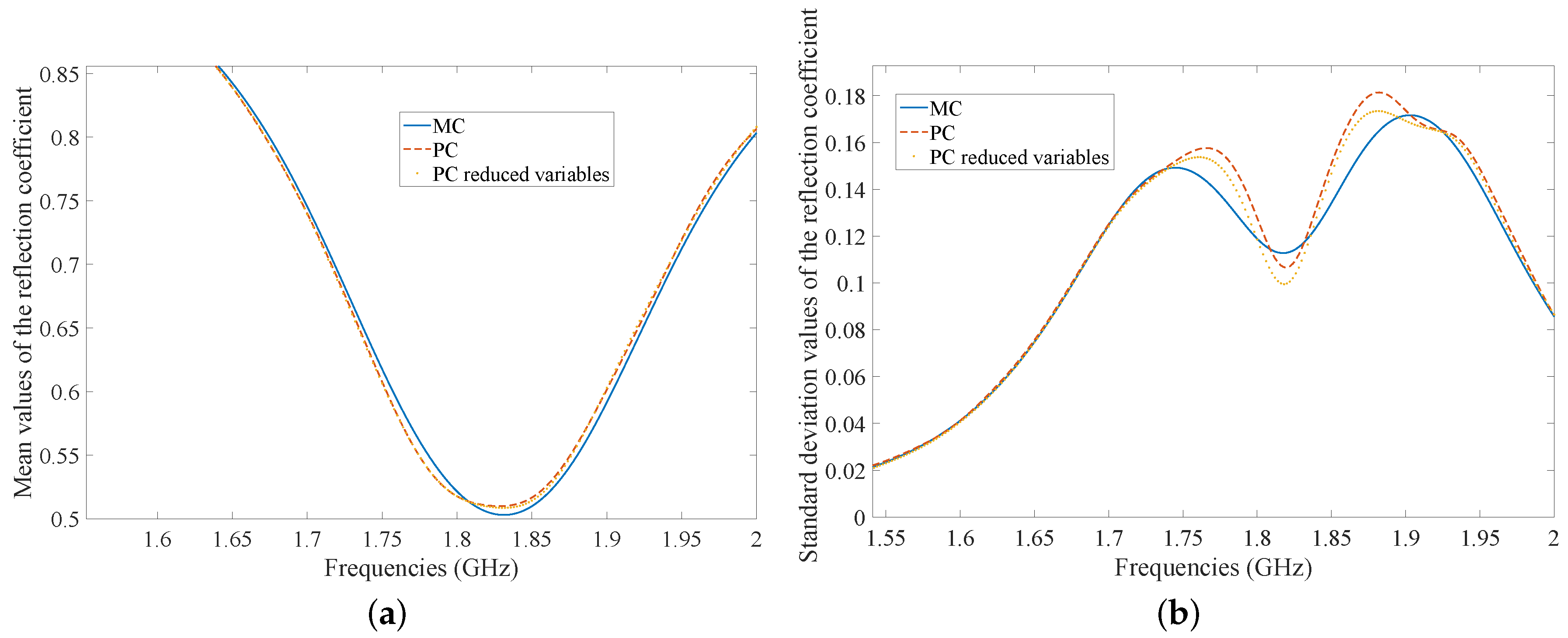
| Dielectric Materials | Mean Dielectric Permittivities |
|---|---|
| Dielectric Materials | Mean Dielectric Permittivities |
|---|---|
| Parameters | Mean Values | Standard Deviations |
|---|---|---|
| mm | mm | |
| mm | mm | |
| mm | mm | |
| W | mm | mm |
| L | mm | mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salis, C.; Kantartzis, N.; Zygiridis, T. Efficient Uncertainty Assessment in EM Problems via Dimensionality Reduction of Polynomial-Chaos Expansions. Technologies 2019, 7, 37. https://doi.org/10.3390/technologies7020037
Salis C, Kantartzis N, Zygiridis T. Efficient Uncertainty Assessment in EM Problems via Dimensionality Reduction of Polynomial-Chaos Expansions. Technologies. 2019; 7(2):37. https://doi.org/10.3390/technologies7020037
Chicago/Turabian StyleSalis, Christos, Nikolaos Kantartzis, and Theodoros Zygiridis. 2019. "Efficient Uncertainty Assessment in EM Problems via Dimensionality Reduction of Polynomial-Chaos Expansions" Technologies 7, no. 2: 37. https://doi.org/10.3390/technologies7020037
APA StyleSalis, C., Kantartzis, N., & Zygiridis, T. (2019). Efficient Uncertainty Assessment in EM Problems via Dimensionality Reduction of Polynomial-Chaos Expansions. Technologies, 7(2), 37. https://doi.org/10.3390/technologies7020037





