Memristors for the Curious Outsiders
Abstract
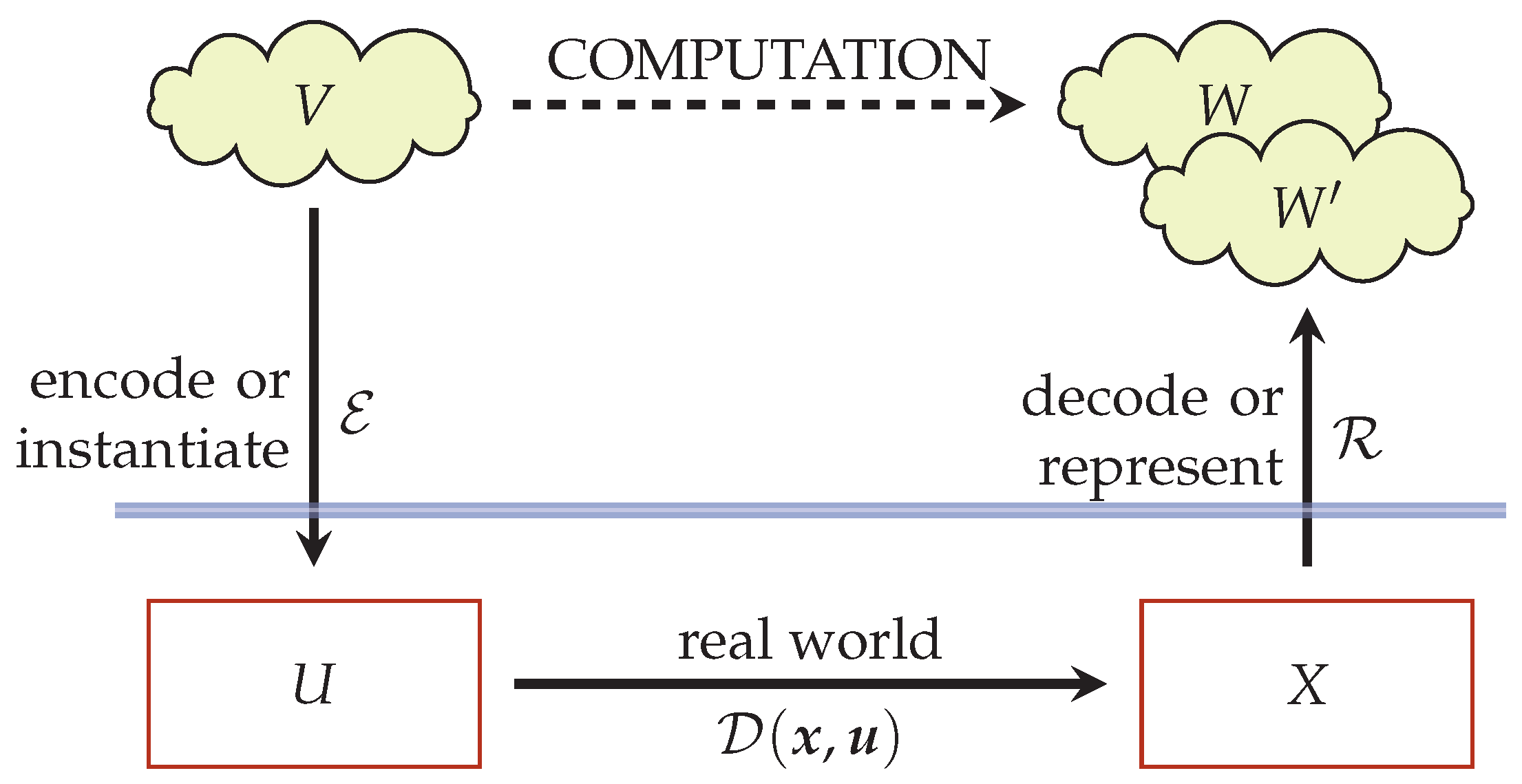
1. Introduction
- Structural changes in the material (PCM like): in these materials, the current or the applied voltage triggers a phase transition between two different resistive states;
- Resistance changes due to thermal or electric excitation of electrons in the conduction bands (anionic): in these devices, the resistive switching is due to either thermally or electrically induced hopping of the charge carriers in the conducting band. For instance, in Mott memristors, the resistive switching is due to the quantum phenomenon known as Mott insulating-conducting transition in metals, which changes the density of free electrons in the material.
- Electrochemical filament growth mechanism: in these materials, the applied voltage induces filament growth from the anode to the cathode of the device, thus reducing or increasing the resistance;
- Spin-torque: the quantum phenomenon of resistance change induced via the giant magnetoresistance switching due to a change in alignment of the spins at the interface between two differently polarized magnetic materials.
2. Brief History of Memristors
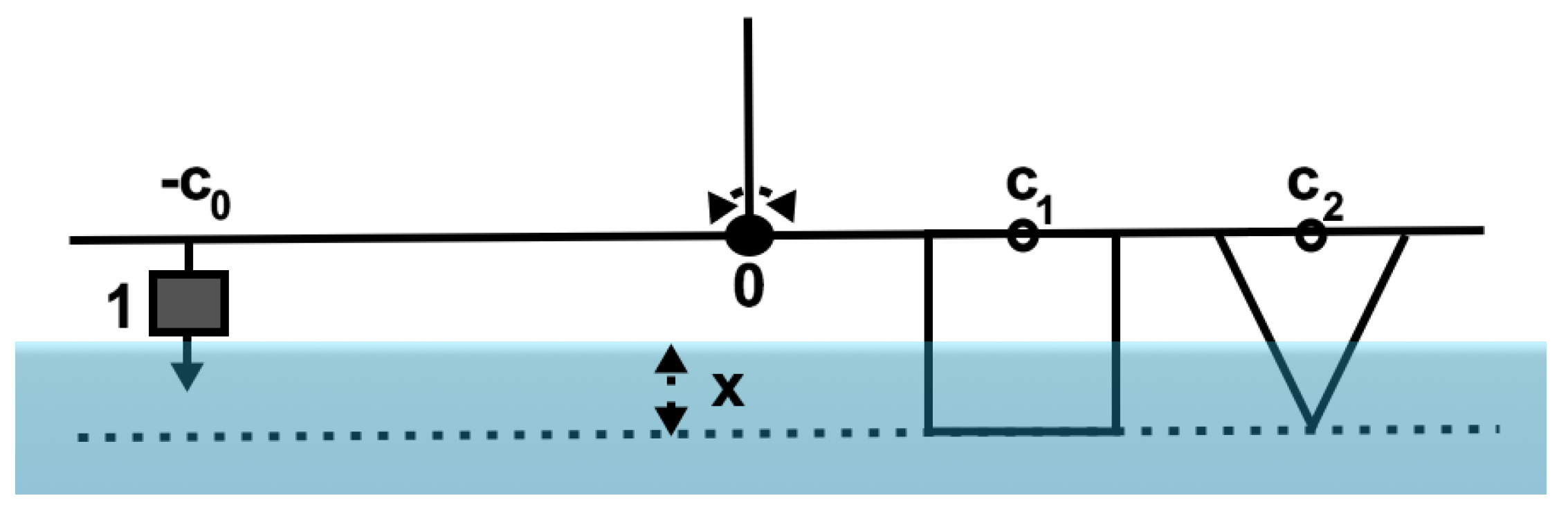
3. Mathematical Models of Memristors
4. Memristors for Storage
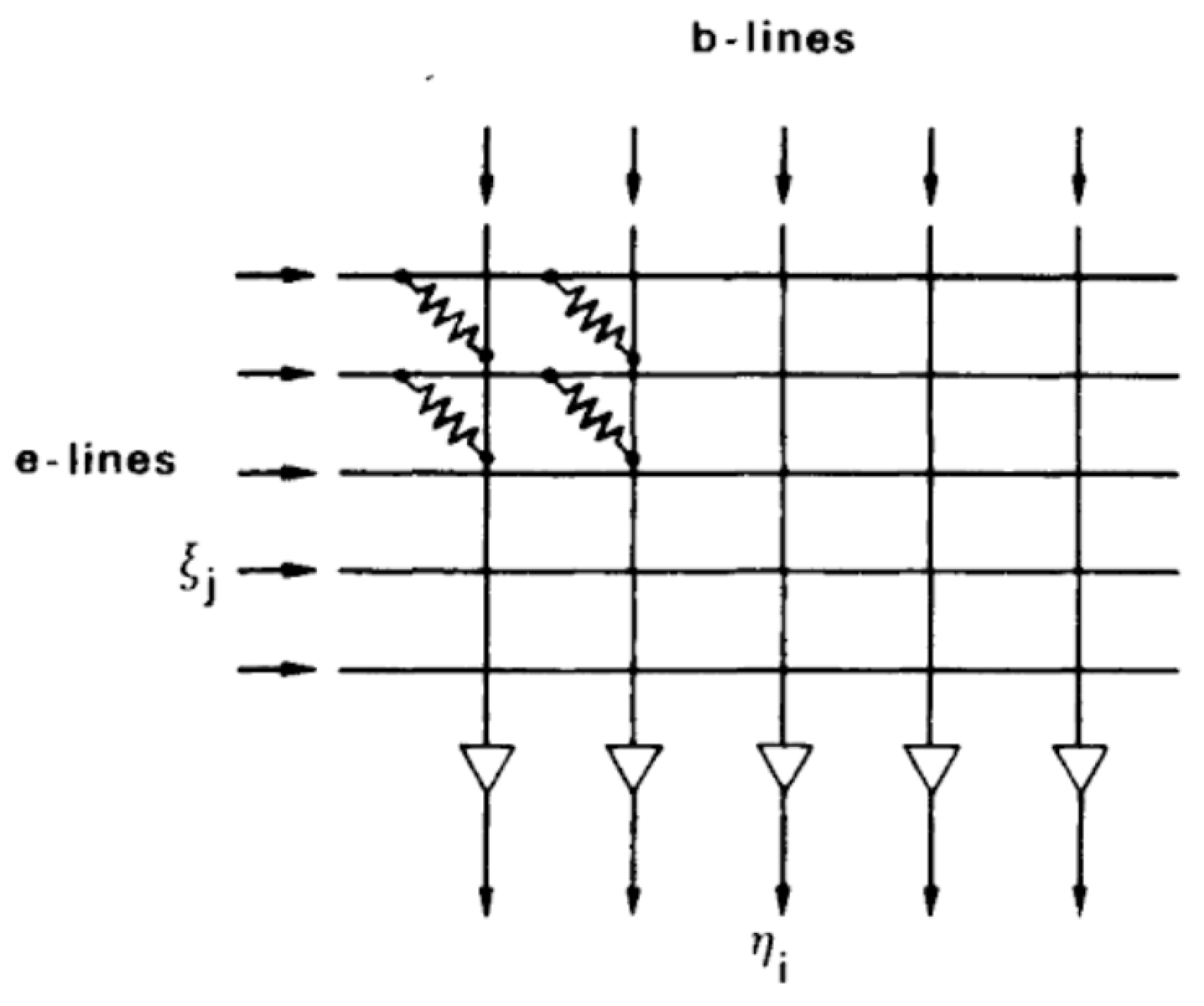
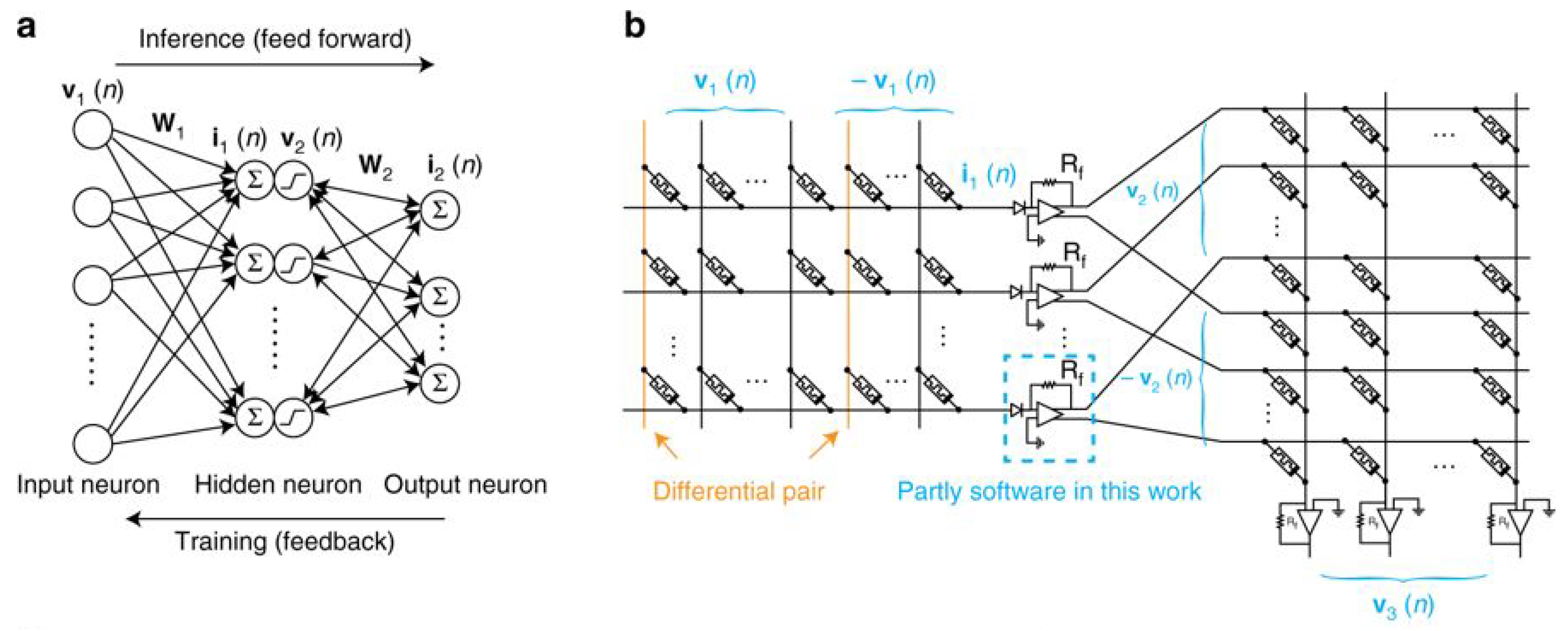
4.1. Crossbar Arrays
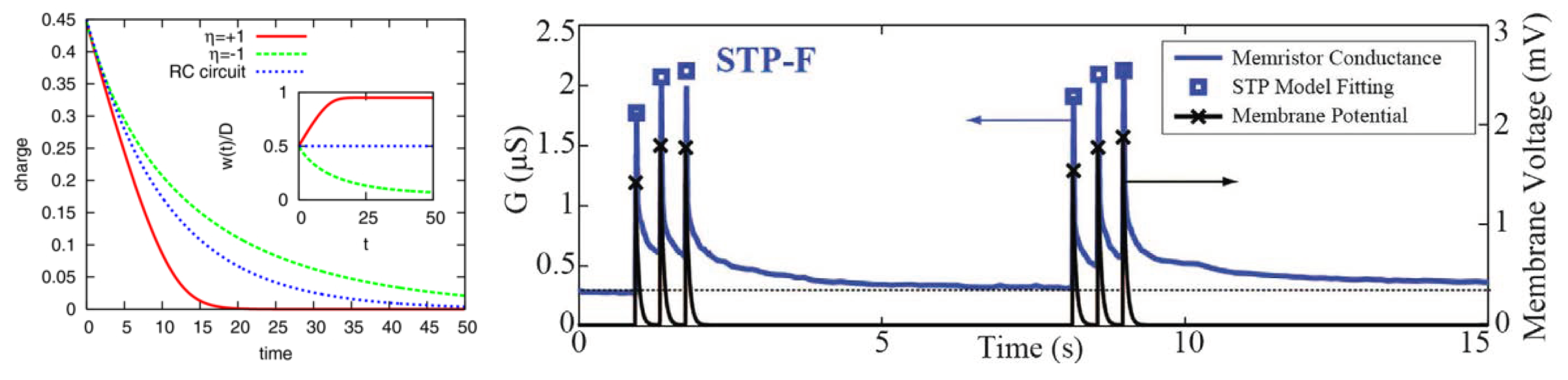
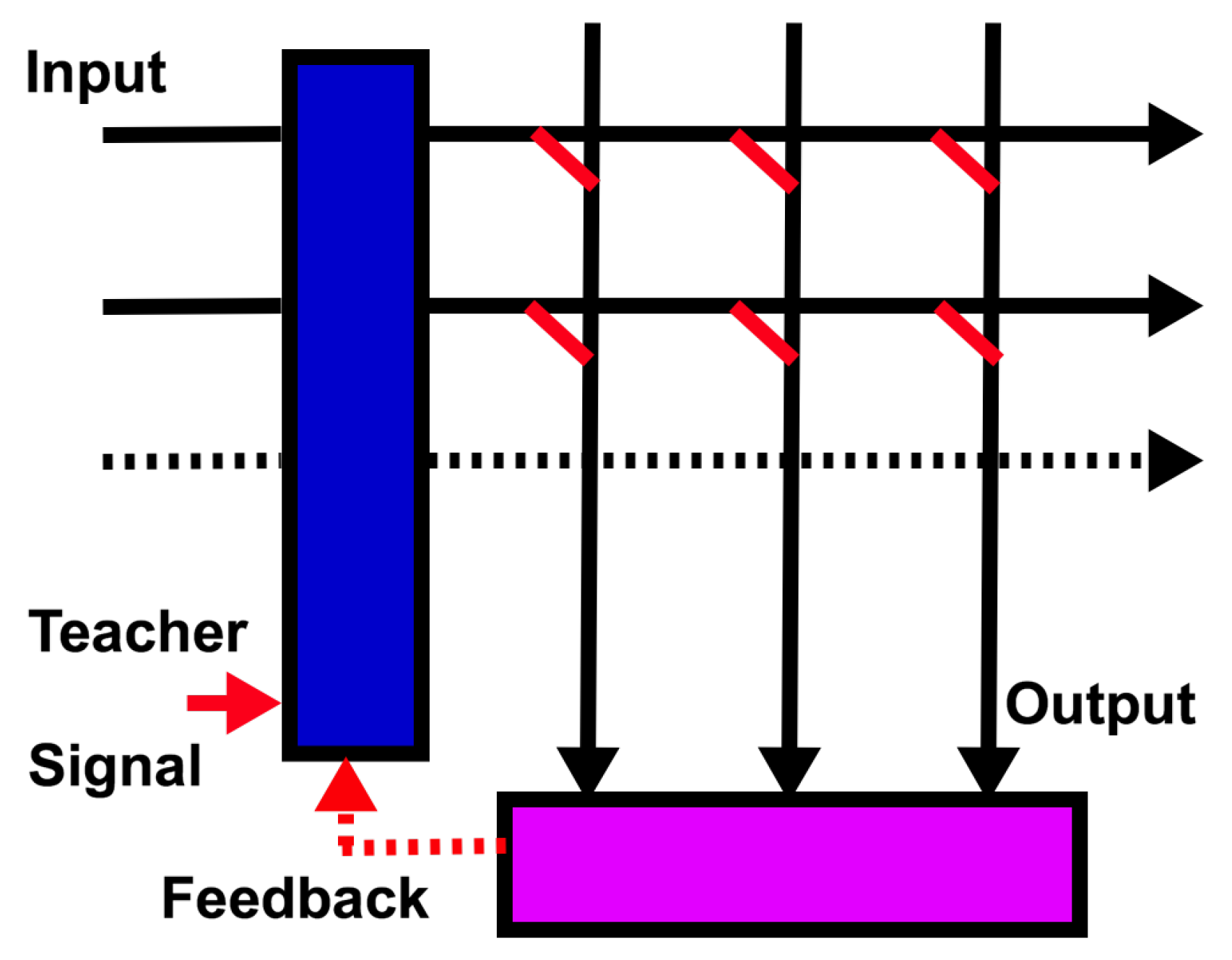
4.2. Synaptic Plasticity
5. Memristors for Data Processing
5.1. Analog Computation
5.2. Generalized Linear Regression, Extreme Learning Machines, and Reservoir Computing
5.3. Neural Engineering Framework
5.4. Volatility: Autonomous Plasticity
5.5. Basis of Computation
6. Memristive Galore!
6.1. Memristive Computing
6.2. Natural Memristive Information Processing Systems: Squids, Plants, and Amoebae
6.3. Self-Organized Critically in Networks of Memristors
6.4. Memristors and CMOS
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Physical Mechanisms for Resistive Change Materials
Appendix A.1. Phase Change Materials
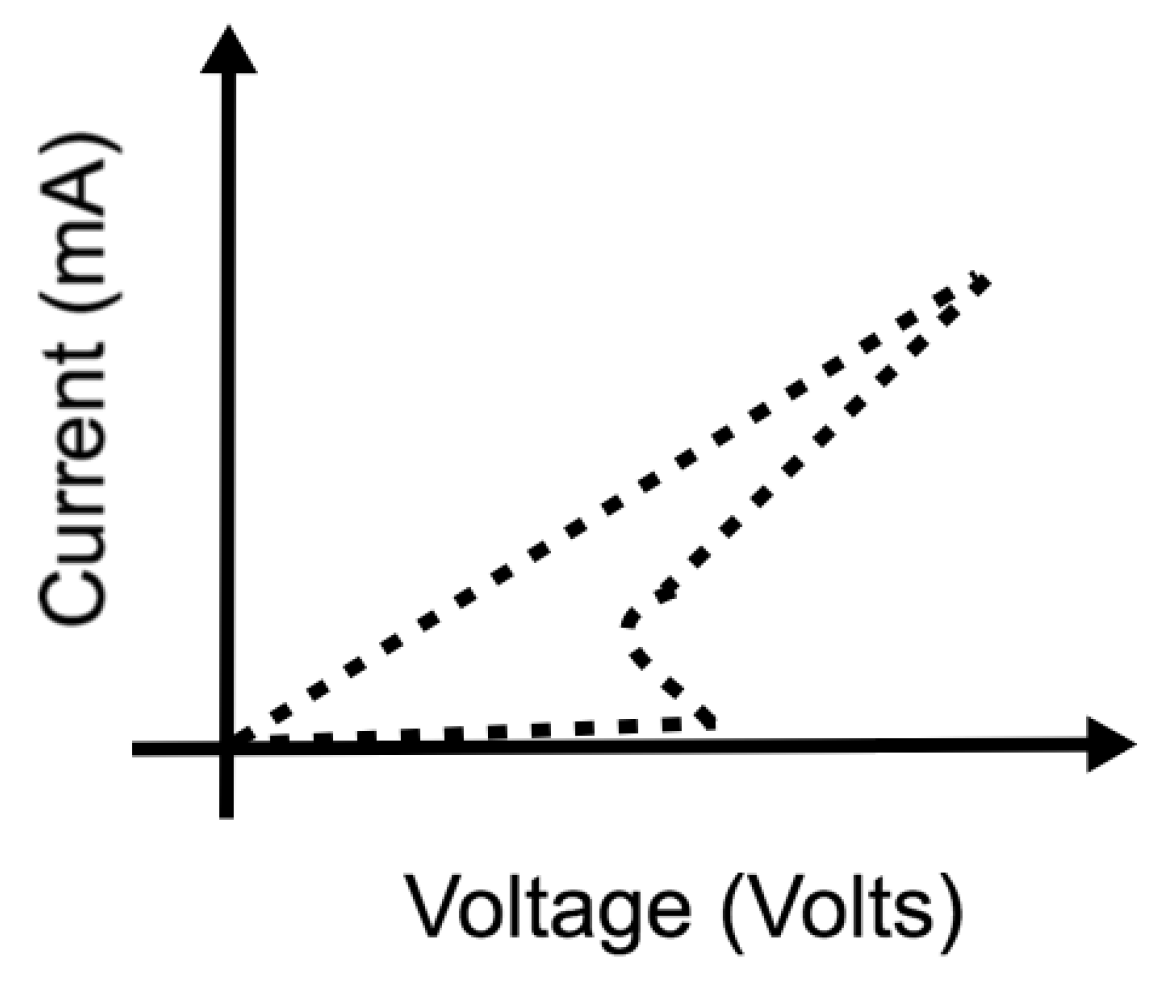
Appendix A.2. Oxide Based Materials
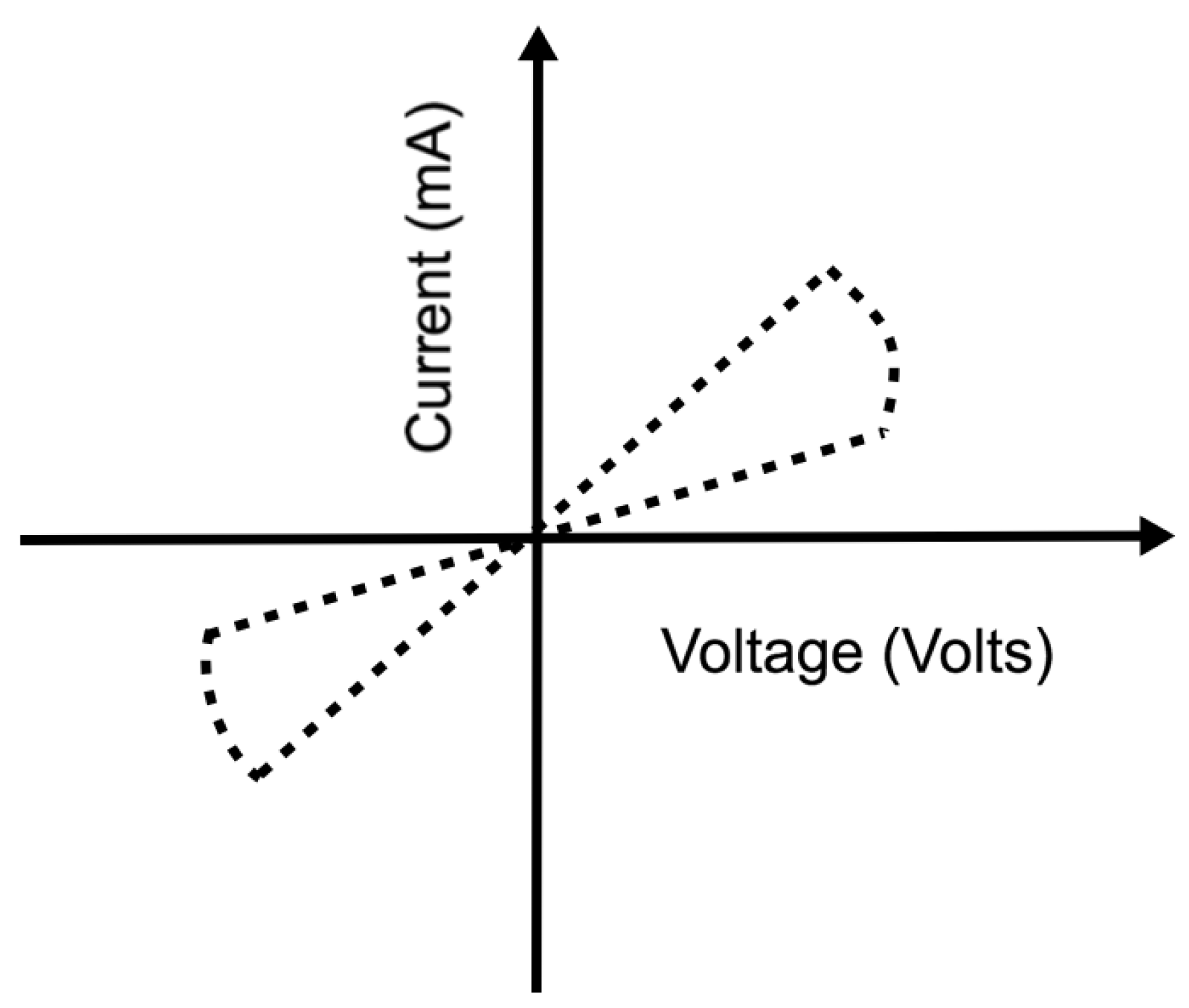
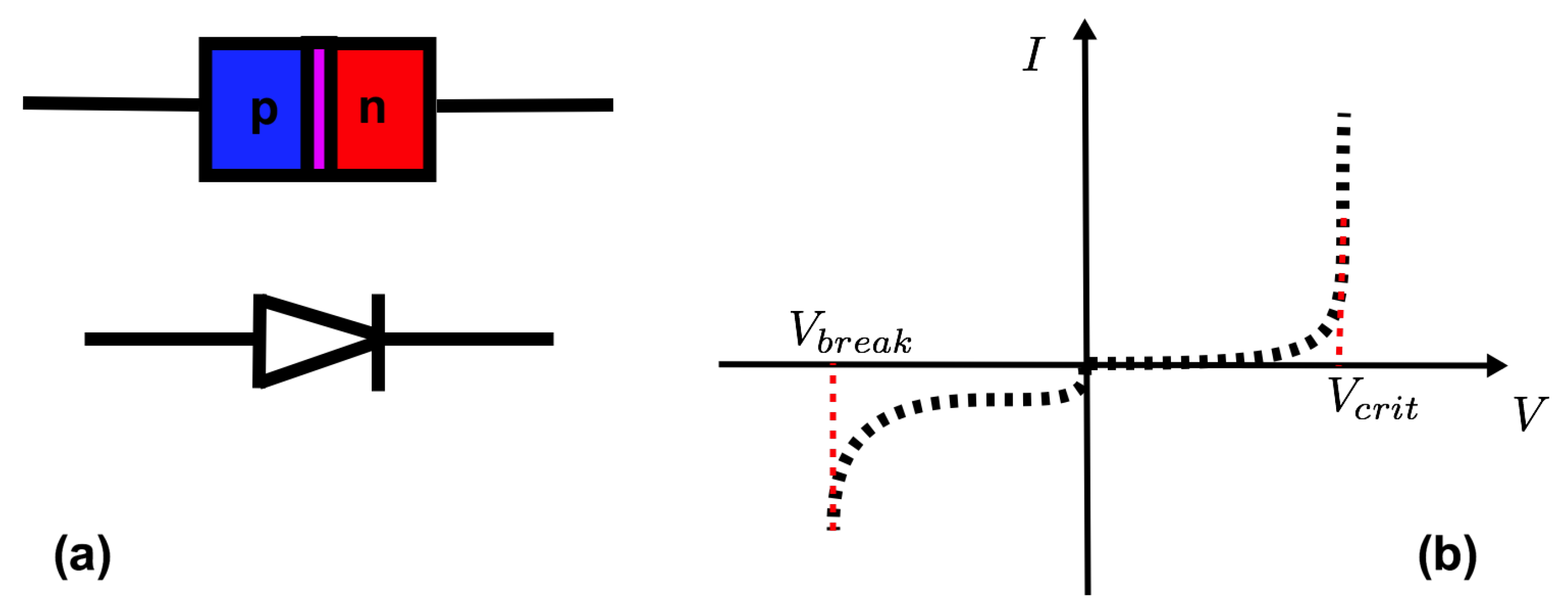
Appendix A.3. Atomic Switches

Appendix A.4. Spin Torque
Appendix A.5. Mott Memristors
Appendix B. Sparse Coding Example
References
- Chua, L. Memristor-The missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Chua, L. If it’s pinched it’s a memristor. Semicond. Sci. Technol. 2014, 29, 104001. [Google Scholar] [CrossRef]
- Chua, L.; Kang, S.M. Memristive devices and systems. Proc. IEEE 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Valov, I.; Linn, E.; Tappertzhofen, S.; Schmelzer, S.; van den Hurk, J.; Lentz, F.; Waser, R. Nanobatteries in redox-based resistive switches require extension of memristor theory. Nat. Commun. 2013, 4, 1771. [Google Scholar] [CrossRef]
- Béquin, P.; Tournat, V. Electrical conduction and Joule effect in one-dimensional chains of metallic beads: Hysteresis under cycling DC currents and influence of electromagnetic pulses. Granul. Matter 2010, 12, 375–385. [Google Scholar] [CrossRef]
- Di Ventra, M.; Pershin, Y.V. On the physical properties of memristive, memcapacitive and meminductive systems. Nanotechnology 2013, 24, 255201. [Google Scholar] [CrossRef]
- Mead, C. Neuromorphic electronic systems. Proc. IEEE 1990, 78, 1629–1636. [Google Scholar] [CrossRef]
- Freeth, T.; Bitsakis, Y.; Moussas, X.; Seiradakis, J.H.; Tselikas, A.; Mangou, H.; Zafeiropoulou, M.; Hadland, R.; Bate, D.; Ramsey, A.; et al. Decoding the ancient Greek astronomical calculator known as the Antikythera Mechanism. Nature 2006, 444, 587–591. [Google Scholar] [CrossRef]
- Adamatzky, A. (Ed.) Advances in Physarum Machines; Emergence, Complexity and Computation; Springer International Publishing: Cham, Switzerland, 2016; Volume 21. [Google Scholar] [CrossRef]
- Dalchau, N.; Szép, G.; Hernansaiz-Ballesteros, R.; Barnes, C.P.; Cardelli, L.; Phillips, A.; Csikász-Nagy, A. Computing with biological switches and clocks. Nat. Comput. 2018, 17, 761–779. [Google Scholar] [CrossRef]
- Di Ventra, M.; Pershin, Y.V. The parallel approach. Nat. Phys. 2013, 9, 200–202. [Google Scholar] [CrossRef]
- Davy, H. Additional experiments on Galvanic electricity. J. Nat. Philos. Chem. Arts 1801, 4, 326. [Google Scholar]
- Falcon, E.; Castaing, B.; Creyssels, M. Nonlinear electrical conductivity in a 1D granular medium. Eur. Phys. J. B 2004, 38, 475–483. [Google Scholar] [CrossRef]
- Falcon, E.; Castaing, B. Electrical conductivity in granular media and Branly’s coherer: A simple experiment. Am. J. Phys. 2005, 73, 302–307. [Google Scholar] [CrossRef]
- Branly, E. Variations de conductibilite sous diverse influences electriques. R. Acad. Sci 1890, 111, 785–787. [Google Scholar]
- Marconi, G. Wireless telegraphic communication: Nobel Lecture 11 December 1909, Nobel Lectures. In Physics; Elsevier Publishing Company: Amsterdam, The Netherlands, 1967; pp. 196–222, 198, 1901–1921. [Google Scholar]
- Abraham, I. The case for rejecting the memristor as a fundamental circuit element. Sci. Rep. 2018, 8, 10972. [Google Scholar] [CrossRef]
- Strogatz, S. Like Water for Money. Available online: https://opinionator.blogs.nytimes.com/2009/06/02/guest-column-like-water-for-money/ (accessed on 6 August 2018).
- Vongehr, S.; Meng, X. The missing memristor has not been found. Sci. Rep. 2015, 5, 11657. [Google Scholar] [CrossRef]
- Vongehr, S. Purely mechanical memristors: Perfect massless memory resistors, the missing perfect mass-involving memristor, and massive memristive systems. arXiv, 2015; arXiv:1504.00300. [Google Scholar]
- Volkov, A.G.; Tucket, C.; Reedus, J.; Volkova, M.I.; Markin, V.S.; Chua, L. Memristors in plants. Plant Signal Behav. 2014, 9, e28152. [Google Scholar] [CrossRef]
- Gale, E.; Adamatzky, A.; de Lacy Costello, B. Slime mould memristors. BioNanoScience 2015, 5, 1–8. [Google Scholar] [CrossRef]
- Gale, E.; Adamatzky, A.; de Lacy Costello, B. Erratum to: Slime mould memristors. BioNanoScience 2015, 5, 9. [Google Scholar] [CrossRef]
- Szot, K.; Dittmann, R.; Speier, W.; Waser, R. Nanoscale resistive switching in SrTiO3 thin films. Phys. Status Solidi 2007, 1, R86–R88. [Google Scholar] [CrossRef]
- Waser, R.; Aono, M. Nanoionics-based resistive switching memories. Nat. Mater. 2007, 6, 833–840. [Google Scholar] [CrossRef]
- Tsuruoka, T.; Terabe, K.; Hasegawa, T.; Aono, M. Forming and switching mechanisms of a cation-migration-based oxide resistive memory. Nanotechnology 2010, 21, 425205. [Google Scholar] [CrossRef]
- Chua, L. Everything you wish to know about memristors but are afraid to ask. Radioengineering 2015, 24, 319. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Gupta, I.; Serb, A.; Berdan, R.; Khiat, A.; Prodromakis, T. Volatility characterization for RRAM devices. IEEE Electron Device Lett. 2017, 38. [Google Scholar] [CrossRef]
- Abraham, I. Quasi-linear vacancy dynamics modeling and circuit analysis of the bipolar memristor. PLoS ONE 2014, 9, e111607. [Google Scholar] [CrossRef]
- Abraham, I. An advection-diffusion model for the vacancy migration memristor. IEEE Access 2016, 4, 7747–7757. [Google Scholar] [CrossRef]
- Tang, S.; Tesler, F.; Marlasca, F.G.; Levy, P.; Dobrosavljević, V.; Rozenberg, M. Shock waves and commutation speed of memristors. Phys. Rev. X 2016, 6, 011028. [Google Scholar] [CrossRef]
- Wang, F. Memristor for introductory physics. arXiv, 2008; arXiv:0808.0286. [Google Scholar]
- Ohno, T.; Hasegawa, T.; Nayak, A.; Tsuruoka, T.; Gimzewski, J.K.; Aono, M. Sensory and short-term memory formations observed in a Ag2S gap-type atomic switch. Appl. Phys. Lett. 2011, 203108, 1–3. [Google Scholar] [CrossRef]
- Pershin, Y.V.; Ventra, M.D. Spice model of memristive devices with threshold. Radioengineering 2013, 22, 485–489. [Google Scholar]
- Biolek, Z.; Biolek, D.; Biolková, V. Spice model of memristor with nonlinear dopant drift. Radioengineering 2009, 18, 210–214. [Google Scholar]
- Biolek, D.; Di Ventra, M.; Pershin, Y.V. Reliable SPICE simulations of memristors, memcapacitors and meminductors. Radioengineering 2013, 22, 945. [Google Scholar]
- Biolek, D.; Biolek, Z.; Biolkova, V.; Kolka, Z. Reliable modeling of ideal generic memristors via state-space transformation. Radioengineering 2015, 24, 393–407. [Google Scholar] [CrossRef]
- Nedaaee Oskoee, E.; Sahimi, M. Electric currents in networks of interconnected memristors. Phys. Rev. E 2011, 83, 031105. [Google Scholar] [CrossRef]
- Joglekar, Y.N.; Wolf, S.J. The elusive memristor: properties of basic electrical circuits. Eur. J. Phys. 2009, 30, 661–675. [Google Scholar] [CrossRef]
- Abdalla, A.; Pickett, M.D. SPICE modeling of memristors. In Proceedings of the IEEE International Symposium of Circuits and Systems (ISCAS), Rio de Janeirov, Brazil, 15–18 May 2011. [Google Scholar] [CrossRef]
- Li, Q.; Serb, A.; Prodromakis, T.; Xu, H. A memristor SPICE model accounting for synaptic activity dependence. PLoS ONE 2015, 10. [Google Scholar] [CrossRef]
- Corinto, F.; Forti, M. Memristor circuits: Flux—Charge analysis method. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1997–2009. [Google Scholar] [CrossRef]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. (TOMS) 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Caravelli, F.; Traversa, F.L.; Di Ventra, M. Complex dynamics of memristive circuits: Analytical results and universal slow relaxation. Phys. Rev. E 2017, 95, 022140. [Google Scholar] [CrossRef] [PubMed]
- Caravelli, F. Locality of interactions for planar memristive circuits. Phys. Rev. E 2017, 96. [Google Scholar] [CrossRef] [PubMed]
- Mostafa, H.; Khiat, A.; Serb, A.; Mayr, C.G.; Indiveri, G.; Prodromakis, T. Implementation of a spike-based perceptron learning rule using TiO2-x memristors. Front. Neurosci. 2015, 9. [Google Scholar] [CrossRef] [PubMed]
- Linn, E.; Di Ventra, M.; Pershin, Y.V. ReRAM cells in the framework of two-terminal devices. In Resistive Switching; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2016; pp. 31–48. [Google Scholar] [CrossRef]
- Pi, S.; Li, C.; Jiang, H.; Xia, W.; Xin, H.; Yang, J.J.; Xia, Q. Memristor crossbars with 4.5 terabits-per-inch-square density and two nanometer dimension. arXiv, arXiv:1804.09848.
- Meena, J.; Sze, S.; Chand, U.; Tseng, T.Y. Overview of emerging nonvolatile memory technologies. Nanoscale Res. Lett. 2014, 9, 526. [Google Scholar] [CrossRef] [PubMed]
- Steinbuch, K. Die Lernmatrix. Kybernetik 1961, 1, 36–45. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organization and associative memory. In Springer Series in Information Sciences; Springer: Berlin/Heidelberg, Germany, 1989; Volume 8. [Google Scholar] [CrossRef]
- Steinbuch, K. Adaptive networks using learning matrices. Kybernetik 1964, 2. [Google Scholar] [CrossRef]
- Xia, L.; Gu, P.; Li, B.; Tang, T.; Yin, X.; Huangfu, W.; Yu, S.; Cao, Y.; Wang, Y.; Yang, H. Technological exploration of RRAM crossbar array for matrix-vector multiplication. J. Comput. Sci. Technol. 2016, 31, 3–19. [Google Scholar] [CrossRef]
- Strukov, D.B.; Williams, R.S. Four-dimensional address topology for circuits with stacked multilayer crossbar arrays. Proc. Natl. Acad. Sci. USA 2009, 106, 20155–20158. [Google Scholar] [CrossRef]
- Li, C.; Han, L.; Jiang, H.; Jang, M.H.; Lin, P.; Wu, Q.; Barnell, M.; Yang, J.J.; Xin, H.L.; Xia, Q. Three-dimensional crossbar arrays of self-rectifying Si/SiO2/Si memristors. Nat. Commun. 2017, 8, 15666. [Google Scholar] [CrossRef]
- Li, C.; Belkin, D.; Li, Y.; Yan, P.; Hu, M.; Ge, N.; Jiang, H.; Montgomery, E.; Lin, P.; Wang, Z.; et al. Efficient and self-adaptive in-situ learning in multilayer memristor neural networks. Nat. Commun. 2018, 9, 2385. [Google Scholar] [CrossRef]
- Itoh, M.; Chua, L. Memristor cellular automata and memristor discrete-time cellular neural networks. In Memristor Networks; Springer International Publishing: Cham, Switzerland, 2014; pp. 649–713. [Google Scholar] [CrossRef]
- Nugent, M.A.; Molter, T.W. Thermodynamic-RAM technology stack. Int. J. Parall. Emerg. Distrib. Syst. 2018, 33, 430–444. [Google Scholar] [CrossRef]
- Hebb, D. The Organization of Behavior; Wiley & Sons: Hoboken, NJ, USA, 1949. [Google Scholar] [CrossRef]
- Koch, G.; Ponzo, V.; Di Lorenzo, F.; Caltagirone, C.; Veniero, D. Hebbian and anti-Hebbian spike-timing-dependent plasticity of human cortico-cortical connections. J. Neurosci. 2013, 33, 9725–9733. [Google Scholar] [CrossRef] [PubMed]
- La Barbera, S.; Alibart, F. Synaptic plasticity with memristive nanodevices. In Advances in Neuromorphic Hardware Exploiting Emerging Nanoscale Devices; Suri, M., Ed.; Springer: New Delhi, India, 2017. [Google Scholar] [CrossRef]
- Ielmini, D. Brain-inspired computing with resistive switching memory (RRAM): Devices, synapses and neural networks. Microelectron. Eng. 2018, 190, 44–53. [Google Scholar] [CrossRef]
- Payvand, M.; Nair, M.; Müller, L.; Indiveri, G. A neuromorphic systems approach to in-memory computing with non-ideal memristive devices: From mitigation to exploitation. Faraday Discuss. 2018. [Google Scholar] [CrossRef] [PubMed]
- Carbajal, J.P.; Dambre, J.; Hermans, M.; Schrauwen, B. Memristor models for machine learning. Neural Comput. 2015, 27. [Google Scholar] [CrossRef] [PubMed]
- Eliasmith, C.; Anderson, C.H. Neural Engineering: Computational, Representation, and Dynamics in Neurobiological Systems; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- MacLennan, B.J. Analog computation. In Computational Complexity: Theory, Techniques, and Applications; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2012; pp. 161–184. [Google Scholar] [CrossRef]
- MacLennan, B. The promise of analog computation. Int. J. Gener. Syst. 2014, 43, 682–696. [Google Scholar] [CrossRef]
- MacLennan, B.J. Physical and formal aspects of computation: Exploiting physics for computation and exploiting computation for physical purposes. In Advances in Unconventional Computing; Andrew, A., Ed.; Springer: Cham, Switzerland, 2017; pp. 117–140. [Google Scholar] [CrossRef]
- Horsman, C.; Stepney, S.; Wagner, R.C.; Kendon, V. When does a physical system compute? Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20140182. [Google Scholar] [CrossRef]
- Shannon, C.E. Mathematical theory of the differential analyzer. J. Math. Phys. 1941, 20, 337–354. [Google Scholar] [CrossRef]
- Borghetti, J.; Snider, G.S.; Kuekes, P.J.; Yang, J.J.; Stewart, D.R.; Williams, R.S. ‘Memristive’ switches enable ‘stateful’ logic operations via material implication. Nature 2010, 464, 873–876. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum theory, the Church–Turing principle and the universal quantum computer. Proc. R. Soc. 1985, 400. [Google Scholar] [CrossRef]
- Moreau, T.; San Miguel, J.; Wyse, M.; Bornholt, J.; Alaghi, A.; Ceze, L.; Enright Jerger, N.; Sampson, A. A taxonomy of general purpose approximate computing techniques. IEEE Embed. Syst. Lett. 2018, 10, 2–5. [Google Scholar] [CrossRef]
- Traversa, F.L.; Ramella, C.; Bonani, F.; Di Ventra, M. Memcomputing NP-complete problems in polynomial time using polynomial resources and collective states. Sci. Adv. 2015, 1, e1500031. [Google Scholar] [CrossRef] [PubMed]
- Levi, M. A Water-Based Solution of Polynomial Equations. Available online: https://sinews.siam.org/Details-Page/a-water-based-solution-of-polynomial-equations-2 (accessed on 20 June 2018).
- Axehill, D. Integer Quadratic Programming for Control and Communication. Ph.D. Thesis, Institute of Technology, Department of Electrical Engineering and Automatic Control, Linköping University, Linköping, Sweden, 2008. [Google Scholar]
- Venegas-Andraca, S.E.; Cruz-Santos, W.; McGeoch, C.; Lanzagorta, M. A cross-disciplinary introduction to quantum annealing-based algorithms. Contemp. Phys. 2018, 59, 174–197. [Google Scholar] [CrossRef]
- Rothemund, P.W.K.; Papadakis, N.; Winfree, E. Algorithmic self-assembly of DNA sierpinski triangles. PLoS Biol. 2004, 2, e424. [Google Scholar] [CrossRef]
- Qian, L.; Winfree, E.; Bruck, J. Neural network computation with DNA strand displacement cascades. Nature 2011, 475, 368–372. [Google Scholar] [CrossRef] [PubMed]
- Dorigo, M.; Gambardella, L.M. Ant colonies for the travelling salesman problem. Biosystems 1997, 43, 73–81. [Google Scholar] [CrossRef]
- Bonabeau, E. Editor’s introduction: Stigmergy. Artif. Life 1999, 5, 95–96. [Google Scholar] [CrossRef]
- Muller, K.R.; Mika, S.; Ratsch, G.; Tsuda, K.; Scholkopf, B. An introduction to kernel-based learning algorithms. IEEE Trans. Neural Netw. 2001, 12, 181–201. [Google Scholar] [CrossRef]
- Hofmann, T.; Schölkopf, B.; Smola, A.J. Kernel methods in machine learning. Ann. Stat. 2008, 36, 1171–1220. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedigns of the 2004 IEEE International Joint Conference on the Neural Networks; Budapest, Hungary, 25–29 July 2004, Volume 2, pp. 985–990.
- Patil, A.; Shen, S.; Yao, E.; Basu, A. Hardware architecture for large parallel array of Random Feature Extractors applied to image recognition. Neurocomputing 2017, 261, 193–203. [Google Scholar] [CrossRef]
- Parmar, V.; Suri, M. Exploiting variability in resistive memory devices for cognitive systems. In Advances in Neuromorphic Hardware Exploiting Emerging Nanoscale Devices; Manan, S., Ed.; Springer: New Delhi, India, 2017. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian model averaging: A tutorial. Stat. Sci. 1999, 14, 382–401. [Google Scholar]
- Jaeger, H. The “Echo State” Approach to Analysing and Training Recurrent Neural Networks—With an Erratum Note; Technical Report; German National Research Institute for Computer Science: Bonn, Germany, 2001. [Google Scholar]
- Maass, W.; Natschläger, T.; Markram, H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Comput. 2002, 14, 2531–2560. [Google Scholar] [CrossRef] [PubMed]
- Verstraeten, D. Reservoir Computing: Computation with Dynamical Systems. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2009. [Google Scholar]
- Dale, M.; Miller, J.F.; Stepney, S.; Trefzer, M.A. A substrate-independent framework to characterise reservoir computers. arXiv, 2018; arXiv:1810.07135. [Google Scholar]
- Fernando, C.; Sojakka, S. Pattern recognition in a bucket. In Advances in Artificial Life; Banzhaf, W., Ziegler, J., Christaller, T., Dittrich, P., Kim, J.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 588–597. [Google Scholar] [CrossRef]
- Du, C.; Cai, F.; Zidan, M.A.; Ma, W.; Lee, S.H.; Lu, W.D. Reservoir computing using dynamic memristors for temporal information processing. Nat. Commun. 2017, 8, 2204. [Google Scholar] [CrossRef] [PubMed]
- Sheriff, M.R.; Chatterjee, D. Optimal dictionary for least squares representation. J. Mach. Learn. Res. 2017, 18, 1–28. [Google Scholar]
- Corradi, F.; Eliasmith, C.; Indiveri, G. Mapping arbitrary mathematical functions and dynamical systems to neuromorphic VLSI circuits for spike-based neural computation. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems (ISCAS), Melbourne VIC, Australia, 1–5 June 2014; pp. 269–272. [Google Scholar] [CrossRef]
- Benna, M.K.; Fusi, S. Computational principles of synaptic memory consolidation. Nat. Neurosci. 2016, 19, 1697–1706. [Google Scholar] [CrossRef] [PubMed]
- Chialvo, D. Are our senses critical? Nat. Phys. 2006, 2, 301–302. [Google Scholar] [CrossRef]
- Hesse, J.; Gross, T. Self-organized criticality as a fundamental property of neural systems. Front. Syst. Neurosci. 2014, 23. [Google Scholar] [CrossRef]
- Avizienis, A.V.; Sillin, H.O.; Martin-Olmos, C.; Shieh, H.H.; Aono, M.; Stieg, A.Z.; Gimzewski, J.K. Neuromorphic atomic switch networks. PLoS ONE 2012, 7. [Google Scholar] [CrossRef]
- Caravelli, F.; Hamma, A.; Di Ventra, M. Scale-free networks as an epiphenomenon of memory. EPL (Europhys. Lett.) 2015, 109, 28006. [Google Scholar] [CrossRef]
- Caravelli, F. Trajectories entropy in dynamical graphs with memory. Front. Robot. AI 2016, 3. [Google Scholar] [CrossRef]
- Sheldon, F.C.; Di Ventra, M. Conducting-insulating transition in adiabatic memristive networks. Phys. Rev. E 2017, 95, 012305. [Google Scholar] [CrossRef] [PubMed]
- Veberic, D. Having fun with Lambert W(x) function. arXiv, 1003. [Google Scholar]
- Berdan, R.; Vasilaki, E.; Khiat, A.; Indiveri, G.; Serb, A.; Prodromakis, T. Emulating short-term synaptic dynamics with memristive devices. Sci. Rep. 2016, 6, 18639. [Google Scholar] [CrossRef] [PubMed]
- Krestinskaya, O.; Dolzhikova, I.; James, A.P. Hierarchical temporal memory using memristor networks: A survey. arXiv, 2018; arXiv:1805.02921. [Google Scholar] [CrossRef]
- Caravelli, F. The mise en scéne of memristive networks: effective memory, dynamics and learning. Int. J. Parall. Emerg. Distrib. Syst. 2018, 33, 350–366. [Google Scholar] [CrossRef]
- Caravelli, F.; Barucca, P. A mean-field model of memristive circuit interaction. EPL (Europhys. Lett.) 2018, 122, 40008. [Google Scholar] [CrossRef]
- Caravelli, F. Asymptotic behavior of memristive circuits and combinatorial optimization. arXiv, 2017; arXiv:1712.07046. [Google Scholar]
- Boros, E.; Hammer, P.L.; Tavares, G. Local search heuristics for Quadratic Unconstrained Binary Optimization (QUBO). J. Heuristics 2007, 13, 99–132. [Google Scholar] [CrossRef]
- Hu, S.G.; Liu, Y.; Liu, Z.; Chen, T.P.; Wang, J.J.; Yu, Q.; Deng, L.J.; Yin, Y.; Hosaka, S. Associative memory realized by a reconfigurable memristive Hopfield neural network. Nat. Commun. 2015, 6. [Google Scholar] [CrossRef]
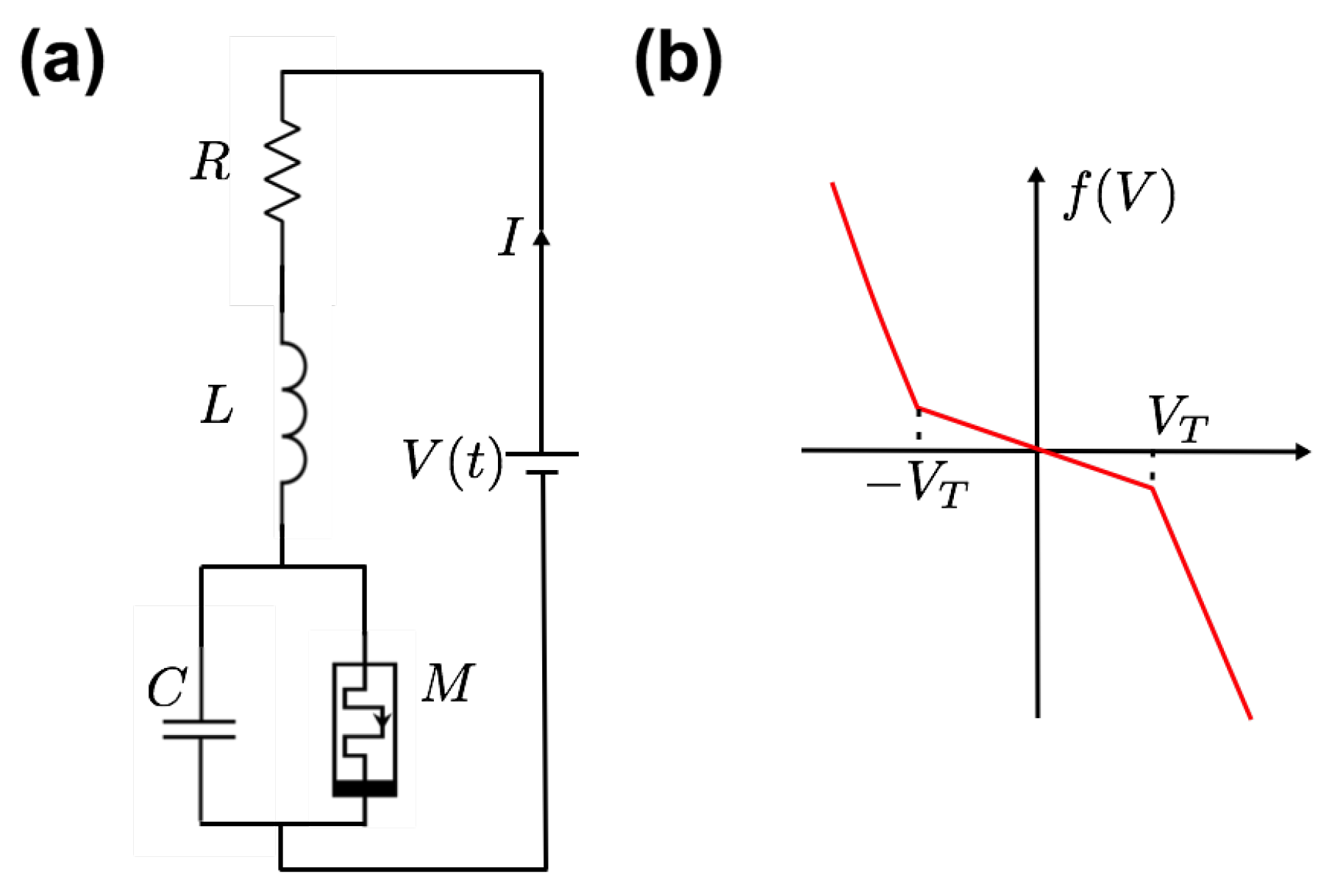
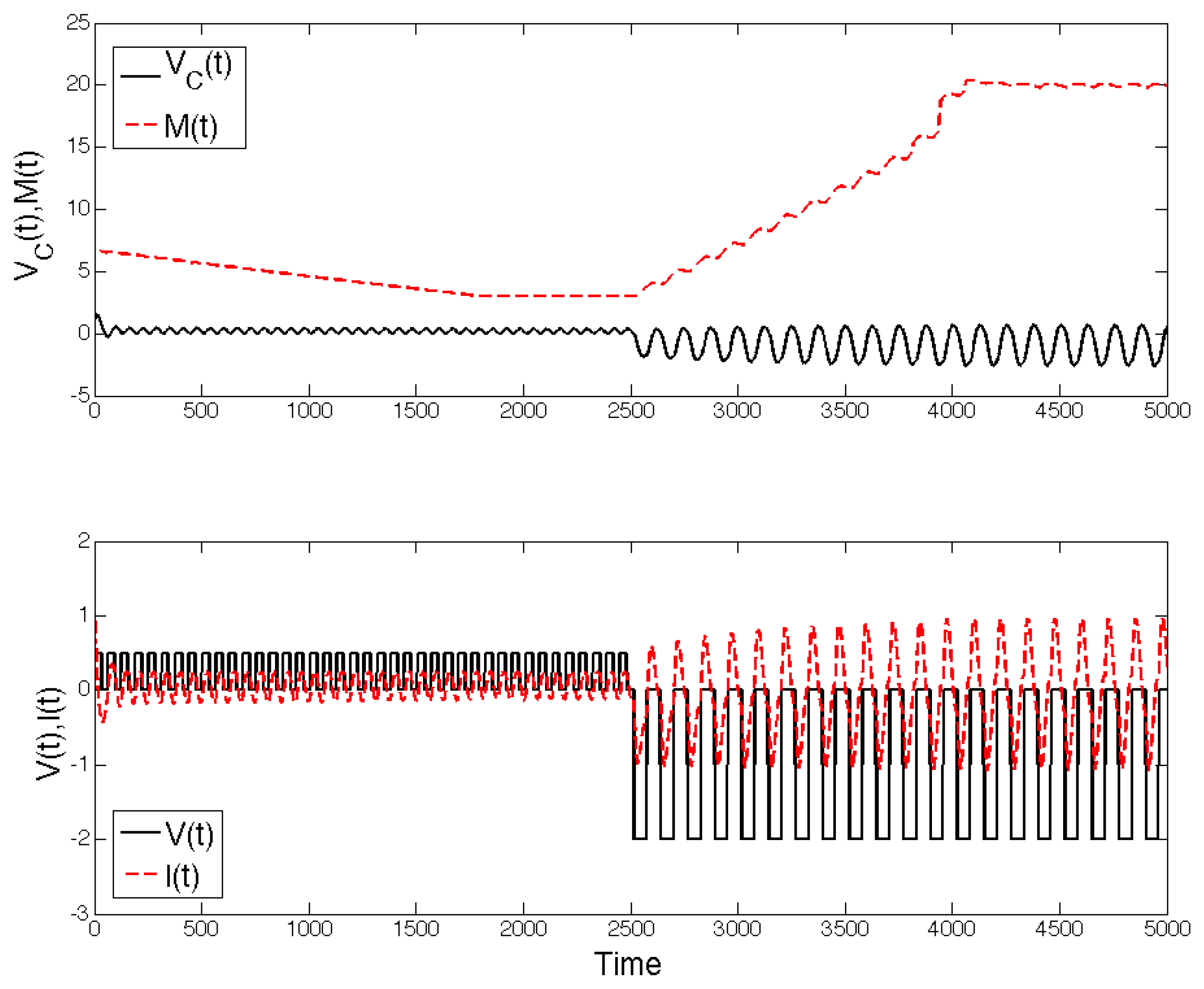
- Kumar, S.; Strachan, J.P.; Williams, R.S. Chaotic dynamics in nanoscale NbO2 Mott memristors for analogue computing. Nature 2017, 548, 318–321. [Google Scholar] [CrossRef]
- Tarkov, M. Hopfield network with interneuronal connections based on memristor bridges. Adv. Neural Netw. 2016, 196–203. [Google Scholar] [CrossRef]
- Sebastian, A.; Tuma, T.; Papandreou, N.; Le Gallo, M.; Kull, L.; Parnell, T.; Eleftheriou, E. Temporal correlation detection using computational phase-change memory. Nat. Commun. 2017, 8, 1115. [Google Scholar] [CrossRef] [PubMed]
- Parihar, A.; Shukla, N.; Jerry, M.; Datta, S.; Raychowdhury, A. Vertex coloring of graphs via phase dynamics of coupled oscillatory networks. Sci. Rep. 2017, 7, 911. [Google Scholar] [CrossRef] [PubMed]
- Ambrogio, S.; Narayanan, P.; Tsai, H.; Shelby, R.M.; Boybat, I.; di Nolfo, C.; Sidler, S.; Giordano, M.; Bodini, M.; Farinha, N.C.P.; et al. Equivalent-accuracy accelerated neural-network training using analogue memory. Nature 2018, 558, 60–67. [Google Scholar] [CrossRef]
- Hu, S.G.; Liu, Y.; Liu, Z.; Chen, T.P.; Wang, J.J.; Yu, Q.; Deng, L.J.; Yin, Y.; Hosaka, S. A memristive Hopfield network for associative memory. Nat. Commun. 2015, 6, 7522. [Google Scholar] [CrossRef]
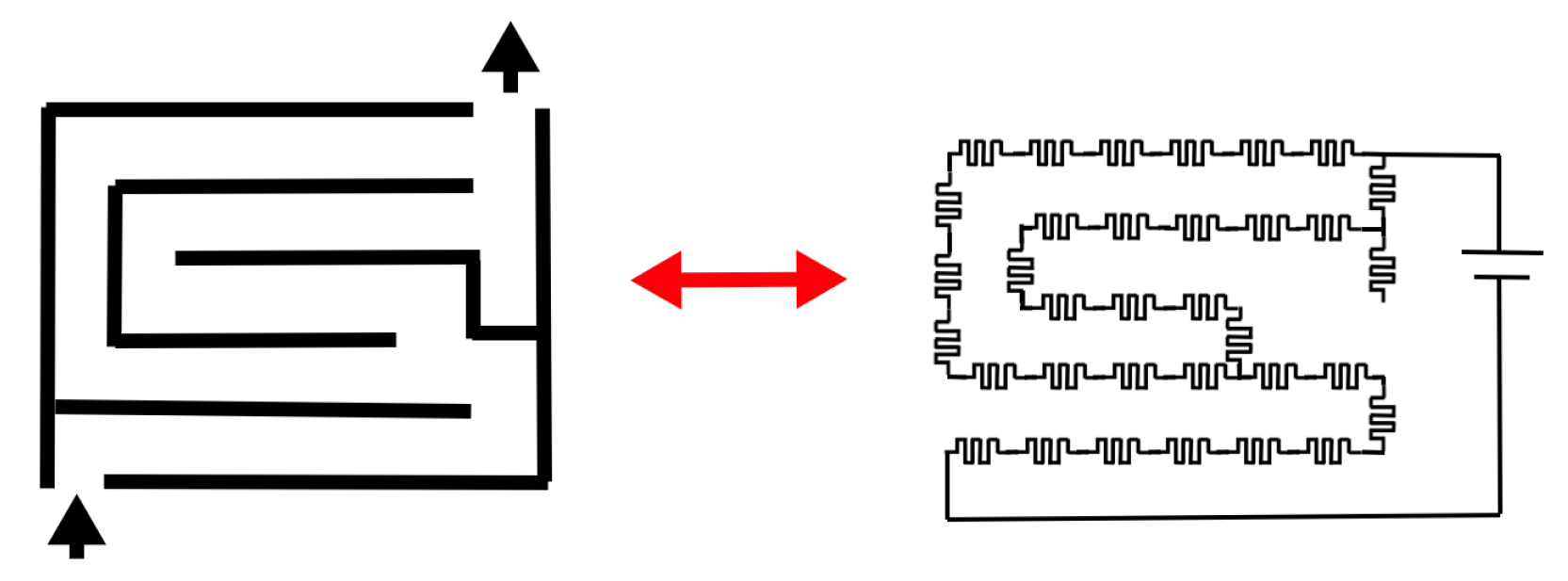
- Pershin, Y.V.; Di Ventra, M. Solving mazes with memristors: A massively parallel approach. Phys. Rev. E 2011, 84, 046703. [Google Scholar] [CrossRef] [PubMed]
- Pershin, Y.V.; Di Ventra, M. Self-organization and solution of shortest-path optimization problems with memristive networks. Phys. Rev. E 2013, 88, 013305. [Google Scholar] [CrossRef]
- Adlerman, L.M. Molecular computation of solutions to combinatorial problems. Science 1994, 266, 1021–1024. [Google Scholar] [CrossRef]
- Adamatzky, A. Computation of shortest path in cellular automata. Math. Comput. Model. 1996, 23, 105–113. [Google Scholar] [CrossRef]
- Prokopenko, M. Guided self-organization. HFSP J. 2009, 3, 287–289. [Google Scholar] [CrossRef]
- Borghetti, J.; Li, Z.; Straznicky, J.; Li, X.; Ohlberg, D.A.; Wu, W.; Stewart, D. R;. Williams, R.S. A hybrid nanomemristor/transistor logic circuit capable of self-programming. Proc. Nat. Acad. Sci. USA 2009, 106, 1699–1703. [Google Scholar] [CrossRef] [PubMed]
- Di Ventra, M.; Pershin, Y.V.; Chua, L.O. Circuit elements with memory: Memristors, memcapacitors, and meminductors. Proc. IEEE 2009, 97. [Google Scholar] [CrossRef]
- Traversa, F.L.; Ventra, M.D. Universal memcomputing machines. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2702–2715. [Google Scholar] [CrossRef] [PubMed]
- Nugent, M.A.; Molter, T.W. AHaH computing–from metastable switches to attractors to machine learning. PLoS ONE 2014, 9. [Google Scholar] [CrossRef] [PubMed]
- Hurley, P. A Concise Introduction to Logic, 12th ed.; Cengage Learning: Cambridge, UK, 2015. [Google Scholar]
- Gale, E.; de Lacy Costello, B.; Adamatzky, A. Boolean logic. In Unconventional Computation and Natural Computation; Mauri, G., Dennunzio, A., Manzoni, L., Porreca, A.E., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 79–89. [Google Scholar]
- Papandroulidakis, G.; Khiat, A.; Serb, A.; Stathopoulos, S.; Michalas, L.; Prodromakis, T. Metal oxide-enabled reconfigurable memristive threshold logic gates. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018. [Google Scholar] [CrossRef]
- Traversa, F.L.; Di Ventra, M. Polynomial-time solution of prime factorization and NP-complete problems with digital memcomputing machines. Chaos 2017, 27. [Google Scholar] [CrossRef] [PubMed]
- Traversa, F.L.; Cicotti, P.; Sheldon, F.; Di Ventra, M. Evidence of an exponential speed-up in the solution of hard optimization problems. Complexity 2018, 2018, 7982851. [Google Scholar] [CrossRef]
- Traversa, F.; Di Ventra, T. Memcomputing: Leveraging memory and physics to compute efficiently. J. Appl. Phys. 2018, 123. [Google Scholar] [CrossRef]
- Caravelli, F.; Nisoli, C. Computation via interacting magnetic memory bites: Integration of boolean gates. arXiv, 2018; arXiv:1810.09190. [Google Scholar]
- Sah, M.P.; Hyongsuk, K.; Chua, L.O. Brains are made of memristors. IEEE Circuits Syst. Mag. 2014, 14, 12–36. [Google Scholar] [CrossRef]
- Markin, V.S.; Volkov, A.G.; Chua, L. An analytical model of memristors in plants. Plant Signal. Behav. 2014, 9, e972887. [Google Scholar] [CrossRef]
- Saigusa, T.; Tero, A.; Nakagaki, T.; Kuramoto, Y. Amoebae anticipate periodic events. Phys. Rev. Lett. 2008, 100, 018101. [Google Scholar] [CrossRef] [PubMed]
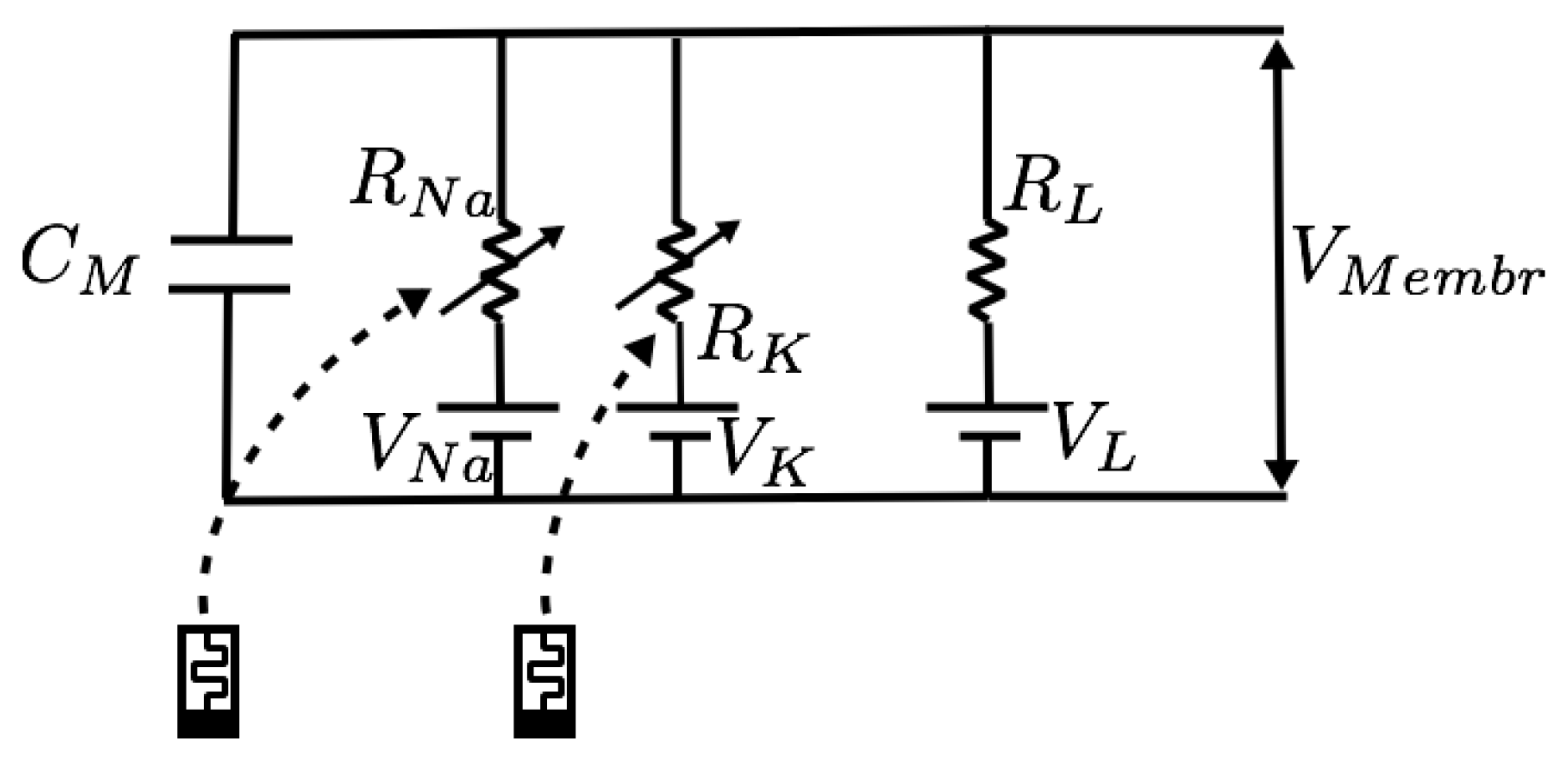
- Hodgkin, A.L.; Huxley, A.F. Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo. J. Physiol. 1952, 116, 449–472. [Google Scholar] [CrossRef] [PubMed]
- Pershin, Y.V.; La Fontaine, S.; Di Ventra, M. Memristive model of amoeba’s learning. Phys. Rev. E 2010, 80, 021926. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.J.; Pickett, M.D.; Li, X.; Ohlberg, D.A.; Stewart, D.R.; Williams, R.S. Memristive switching mechanism for metal/oxide/metal nanodevices. Nat. Nano 2008, 3, 429. [Google Scholar] [CrossRef] [PubMed]
- Pershin, Y.V.; Di Ventra, M. Experimental demonstration of associative memory with memristive neural networks. Neural Netw. 2010, 23, 881–886. [Google Scholar] [CrossRef] [PubMed]
- Tan, Z.H.; Yin, X.B.; Yang, R.; Mi, S.B.; Jia, C.L.; Guo, X. Pavlovian conditioning demonstrated with neuromorphic memristive devices. Sci. Rep. 2017, 7, 713. [Google Scholar] [CrossRef] [PubMed]
- Turcotte, D.L. Self-organized criticality. Rep. Prog. Phys. 1999, 62, 1377–1429. [Google Scholar] [CrossRef]
- Jensen, H.J. Self-Organized Criticality; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar] [CrossRef]
- Marković, D.; Gros, C. Power laws and self-organized criticality in theory and nature. Phys. Rep. 2014, 536, 41–74. [Google Scholar] [CrossRef]
- Alava, M.J.; Nukala, P.K.V.V.; Zapperi, S. Statistical models of fracture. Adv. Phys. 2006, 55, 349–476. [Google Scholar] [CrossRef]
- Widrow, B. An Adaptive ‘Adaline’ Neuron Using Chemical ‘Memistors’; Technical Report 1553-2; Stanford Electronics Laboratories: Stanford, CA, USA, 1960. [Google Scholar]
- Adhikari, S.P.; Kim, H. Why are memristor and memistor different devices. In Memristor Networks; Adamatzky, A., Chua, L., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 95–112. [Google Scholar] [CrossRef]
- Cai, W.; Tetzlaff, R. Why are memristor and memristor different devices. In Memristor Networks; Adamatzky, A., Chua, L., Eds.; Springer: Berlin, Germany, 2014; pp. 113–128. [Google Scholar]
- Johnsen, K.G. An introduction to the memristor—A valuable circuit element in bioelectricity and bioimpedance. J. Electr. Bioimpedance 2012, 3, 20–28. [Google Scholar] [CrossRef]
- DeBenedictis, E.P. Computational complexity and new computing approaches. Computer 2016, 49, 76–79. [Google Scholar] [CrossRef]
- Alibart, F.; Zamanidoost, E.; Strukov, D.B. Pattern classification by memristive crossbar circuits using ex situ and in situ training. Nat. Commun. 2013, 4, 2072. [Google Scholar] [CrossRef] [PubMed]
- Tissari, J.; Poikonen, J.H.; Lehtonen, E.; Laiho, M.; Koskinen, L. K-means clustering in a memristive logic array. In Proceedings of the IEEE 15th International Conference on Nanotechnology (IEEE-NANO), Rome, Italy, 27–30 July 2015. [Google Scholar]
- Merkel, C.; Kudithipudi, D. Unsupervised learning in neuromemristive systems. In Proceedings of the 2015 National Aerospace and Electronics Conference (NAECON), Dayton, OH, USA, 15–19 June 2015. [Google Scholar]
- Jeong, Y.; Lee, J.; Moon, J.; Shin, J.H.; Lu, W.D. K-means data clustering with memristor networks. Nano Lett. 2018, 18, 4447–4453. [Google Scholar] [CrossRef] [PubMed]
- Widrow, B.; Lehr, M. 30 years of adaptive neural networks: Perceptron, Madaline, and backpropagation. Proc. IEEE 1990, 78, 1415–1442. [Google Scholar] [CrossRef]
- Soudry, D.; Di Castro, D.; Gal, A.; Kolodny, A.; Kvatinsky, S. Memristor-based multilayer neural networks with online gradient descent training. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2408–2421. [Google Scholar] [CrossRef]
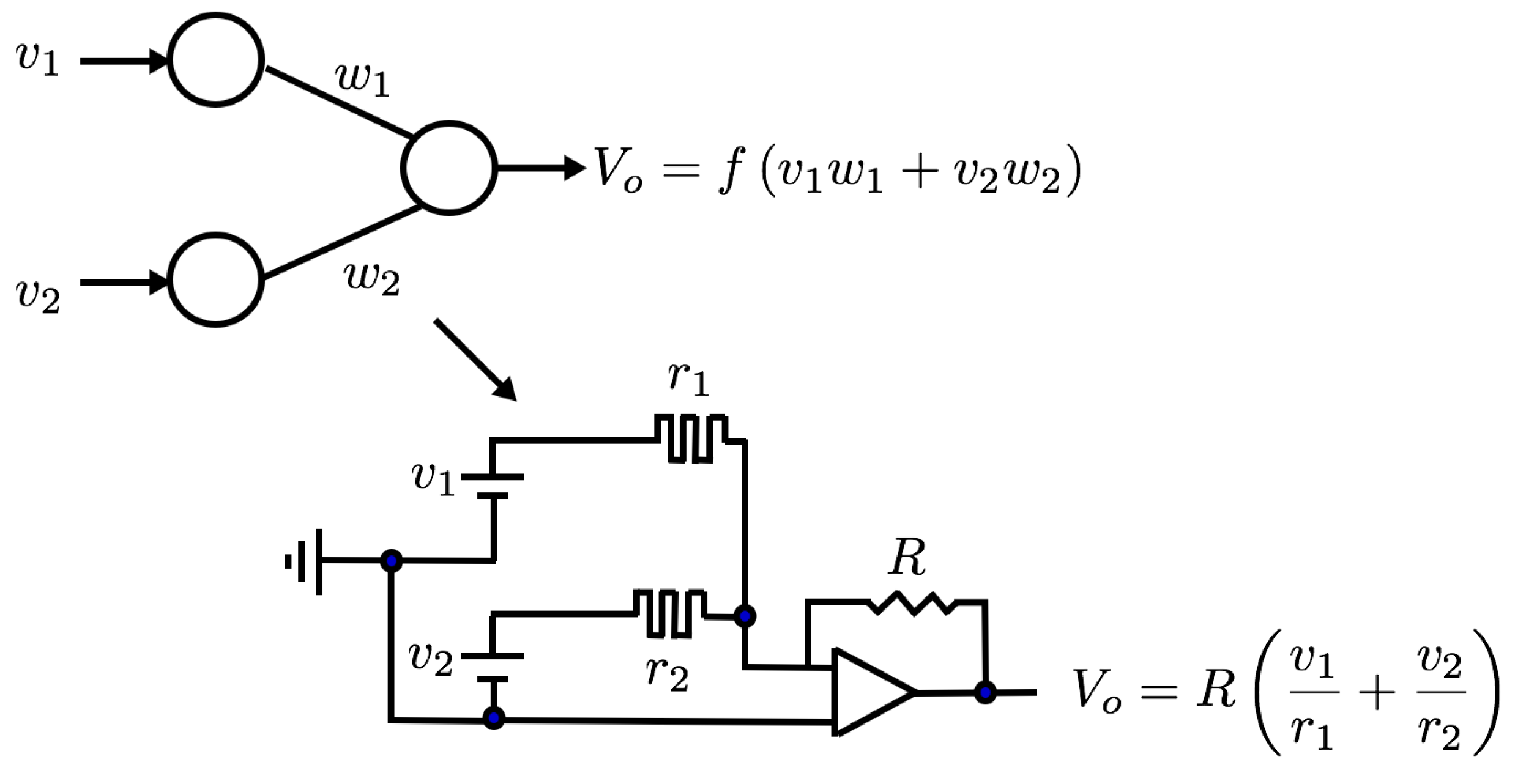
- Rozell, C.J.; Johnson, D.H.; Baraniuk, R.G.; Olshausen, B.A. Sparse coding via thresholding and local competition in neural circuits. Neural Comput. 2008, 20, 2526–2563. [Google Scholar] [CrossRef]
- Sheridan, P.M.; Cai, F.; Du, C.; Ma, W.; Zhang, Z.; Lu, W.D. Sparse coding with memristor networks. Nat. Nanotechnol. 2017, 12, 784–789. [Google Scholar] [CrossRef]
- Sanger, T.D. Optimal unsupervised learning in a single-layer linear feedforward neural network. Neural Netw. 1989, 2, 459–473. [Google Scholar] [CrossRef]
- Choi, S.; Sheridan, P.; Lu, W.D. Data clustering using memristor networks. Sci. Rep. 2015, 5, 10492. [Google Scholar] [CrossRef]
- Vergis, A.; Steiglitz, K.; Dickinson, B. The complexity of analog computation. Math. Comput. Simul. 1986, 28, 91–113. [Google Scholar] [CrossRef]
- Ercsey-Ravasz, M.; Toroczkai, Z. Optimization hardness as transient chaos in an analog approach to constraint satisfaction. Nat. Phys. 2011, 7, 966–970. [Google Scholar] [CrossRef]
- Wang, Z.; Joshi, S.; Savel’ev, S.E.; Jiang, H.; Midya, R.; Lin, P.; Hu, M.; Ge, N.; Strachan, J.P.; Li, Z.; et al. Memristors with diffusive dynamics as synaptic emulators for neuromorphic computing. Nat. Mater. 2017, 16, 101–108. [Google Scholar] [CrossRef] [PubMed]
- Moss, F. Stochastic resonance and sensory information processing: A tutorial and review of application. Clin. Neurophysiol. 2004, 115, 267–281. [Google Scholar] [CrossRef] [PubMed]
- McDonnell, M.D.; Abbott, D. What is stochastic resonance? Definitions, misconceptions, debates, and its relevance to biology. PLoS Comput. Boil. 2009, 5, e1000348. [Google Scholar] [CrossRef] [PubMed]
- McDonnell, M.D.; Ward, L.M. The benefits of noise in neural systems: Bridging theory and experiment. Nat. Rev. Neurosci. 2011, 12, 415–426. [Google Scholar] [CrossRef]
- Stotland, A.; Di Ventra, M. Stochastic memory: Memory enhancement due to noise. Phys. Rev. E 2012, 85, 011116. [Google Scholar] [CrossRef] [PubMed]
- Slipko, V.A.; Pershin, Y.V.; Di Ventra, M. Changing the state of a memristive system with white noise. Phys. Rev. E 2013, 87, 042103. [Google Scholar] [CrossRef]
- Patterson, G.A.; Fierens, P.I.; Grosz, D.F. Resistive switching assisted by noise. In Understanding Complex Systems; Springer: Berlin, Germany, 2014; pp. 305–311. [Google Scholar] [CrossRef]
- Fu, Y.X.; Kang, Y.M.; Xie, Y. Subcritical hopf bifurcation and stochastic resonance of electrical activities in neuron under electromagnetic induction. Front. Comput. Neurosci. 2018, 12. [Google Scholar] [CrossRef]
- Feali, M.S.; Ahmadi, A. Realistic Hodgkin–Huxley axons using stochastic behavior of memristors. Neural Process. Lett. 2017, 45, 1–14. [Google Scholar] [CrossRef]
- Peotta, S.; Di Ventra, M. Superconducting memristors. Phys. Rev. Appl. 2014, 2. [Google Scholar] [CrossRef]
- Di Ventra, M.; Pershin, Y.V. Memory materials: A unifying description. Mater. Today 2011, 14, 584–591. [Google Scholar] [CrossRef]
- Kuzum, D.; Yu, S.; Wong, H.S.P. Synaptic electronics: Materials, devices and applications. Nanotechnology 2013, 24, 382001. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.J.; Strukov, D.B.; Stewart, D.R. Memristive devices for computing. Nat. Nanotechnol. 2013, 8, 13–24. [Google Scholar] [CrossRef] [PubMed]
- Mikhaylov, A.N.; Gryaznov, E.G.; Belov, A.I.; Korolev, D.S.; Sharapov, A.N.; Guseinov, D.V.; Tetelbaum, D.I.; Tikhov, S.V.; Malekhonova, N.V.; et al. Field- and irradiation-induced phenomena in memristive nanomaterials. Phys. Status Solidi (c) 2016, 13, 870–881. [Google Scholar] [CrossRef]
- Ovshinsky, S.R. Reversible electrical switching phenomena in disordered structures. Phys. Rev. Lett. 1968, 21, 1450–1453. [Google Scholar] [CrossRef]
- Neale, R.G.; Nelson, D.L.; Moore, G.E. Nonvolatile and reprogrammable, the read-mostly memory is here. Electronic 1970, 43, 56–60. [Google Scholar]
- Buckley, W.; Holmberg, S. Electrical characteristics and threshold switching in amorphous semiconductors. Solid-State Electron. 1975, 18, 127–147. [Google Scholar] [CrossRef]
- Ielmini, D.; Lacaita, A.L. Phase change materials in non-volatile storage. Mater. Today 2011, 14, 600–607. [Google Scholar] [CrossRef]
- Campbell, K.A. Self-directed channel memristor for high temperature operation. Microelectron. J. 2017, 59, 10–14. [Google Scholar] [CrossRef]
- Hoskins, B.D.; Adam, G.C.; Strelcov, E.; Zhitenev, N.; Kolmakov, A.; Strukov, D.B.; McClelland, J.J. Stateful characterization of resistive switching TiO2 with electron beam induced currents. Nat. Commun. 2017, 8, 1972. [Google Scholar] [CrossRef]
- Chernov, A.A.; Islamov, D.R.; Pik’nik, A.A. Non-linear memristor switching model. J. Phys. Conf. Ser. 2016, 754, 102001. [Google Scholar] [CrossRef]
- Balatti, S.; Ambrogio, S.; Wang, Z.; Sills, S.; Calderoni, A.; Ramaswamy, N.; Ielmini, D. Voltage-controlled cycling endurance of HfOx-based resistive-switching memory. IEEE Trans. Electron Devices 2015, 62. [Google Scholar] [CrossRef]
- Hamed, E.M.; Fouda, M.E.; Radwan, A.G. Conditions and emulation of double pinch-off points in fractional-order memristor. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Stieg, A.Z.; Avizienis, A.V.; Sillin, H.O.; Aguilera, R.; Shieh, H.H.; Martin-Olmos, C.; Sandouk, E.J.; Aono, M.; Gimzewski, J.K. Self-organization and emergence of dynamical structures in neuromorphic atomic switch networks. In Memristor Networks; Adamatzky, A., Chua, L., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 173–209. [Google Scholar] [CrossRef]
- Sillin, H.O.; Aguilera, R.; Shieh, H.H.; Avizienis, A.V.; Aono, M.; Stieg, A.Z.; Gimzewski, J.K. A theoretical and experimental study of neuromorphic atomic switch networks for reservoir computing. Nanotechnology 2013, 24, 384004. [Google Scholar] [CrossRef] [PubMed]
- Stieg, A.Z.; Avizienis, A.V.; Sillin, H.O.; Martin-Olmos, C.; Aono, M.; Gimzewski, J.K. Emergent criticality in complex turing b-type atomic switch networks. Adv. Mater. 2012, 24, 286–293. [Google Scholar] [CrossRef] [PubMed]
- Scharnhorst, K.S.; Carbajal, J.P.; Aguilera, R.C.; Sandouk, E.J.; Aono, M.; Stieg, A.Z.; Gimzewski, J.K. Atomic switch networks as complex adaptive systems. Jpn. J. Appl. Phys. 2018, 57, 03ED02. [Google Scholar] [CrossRef]
- Wen, X.; Xie, Y.T.; Mak, M.W.C.; Cheung, K.Y.; Li, X.Y.; Renneberg, R.; Yang, S. Dendritic nanostructures of silver: Facile synthesis, structural characterizations, and sensing applications. Langmuir 2006, 22, 4836–4842. [Google Scholar] [CrossRef] [PubMed]
- Pickett, M.D.; Strukov, D.B.; Borghetti, J.L.; Yang, J.J.; Snider, G.S.; Stewart, D.R.; Williams, R.S. Switching dynamics in titanium dioxide memristive devices. J. Appl. Phys. 2009, 106, 074508. [Google Scholar] [CrossRef]
- Chang, T.; Jo, S.H.; Kim, K.H.; Sheridan, P.; Gaba, S.; Lu, W. Synaptic behaviors and modeling of a metal oxide memristive device. Appl. Phys. A 2011, 102, 857–863. [Google Scholar] [CrossRef]
- International Technology Roadmap for Semiconductors. Available online: http://www.itrs2.net/ (accessed on 8 December 2018).
- Ralph, D.C.; Stiles, M.D. Spin transfer torques. J. Magn. Magn. Mater. 2008, 320, 1190–1216. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Y.; Xi, H.; Li, H.; Dimitrov, D. Spintronic memristor through spin-torque-induced magnetization motion. IEEE Electron Device Lett. 2009, 30, 294–297. [Google Scholar] [CrossRef]
- Sun, J.Z. Spin-current interaction with a monodomain magnetic body: A model study. Phys. Rev. B 2000, 62, 570–578. [Google Scholar] [CrossRef]
- Pickett, D.M.; Medeiros-Riberi, G.; Williams, R.S. A scalable neuristor built with Mott memristors. Nat. Mater. 2013, 12. [Google Scholar] [CrossRef] [PubMed]
- Kagoshima, S. Peierls phase transition. Jpn. J. Appl. Phys. 1981, 20. [Google Scholar] [CrossRef]
- Evers, F.; Mirlin, A. Anderson transitions. Rev. Mod. Phys. 2008, 80. [Google Scholar] [CrossRef]
- Chopra, K.L. Current-controlled negative resistance in thin niobium oxide films. Proc. IEEE 1963, 51, 941–942. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Hopfield, J.J.; Tank, D.W. Computing with neural circuits: A model. Science 1986, 233, 625–633. [Google Scholar] [CrossRef]
| Memristor | PCM | STT-RAM | DRAM | Flash | HD | |
|---|---|---|---|---|---|---|
| Chip area per bit () | 4 | 10 | 14–64 | 6–8 | 4–8 | n/a |
| Energy per bit (pJ) | 0.1–3 | 0.1–1 | ||||
| Read time (ns) | <10 | 20–70 | 10–30 | 10–50 | ||
| Write time (ns) | 20–30 | 10 | ||||
| Retention (years) | 10 | 10 | 10 | 10 | ||
| Cycles endurance | ||||||
| 3D capability | yes | no | no | no | yes | n/a |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caravelli, F.; Carbajal, J.P. Memristors for the Curious Outsiders. Technologies 2018, 6, 118. https://doi.org/10.3390/technologies6040118
Caravelli F, Carbajal JP. Memristors for the Curious Outsiders. Technologies. 2018; 6(4):118. https://doi.org/10.3390/technologies6040118
Chicago/Turabian StyleCaravelli, Francesco, and Juan Pablo Carbajal. 2018. "Memristors for the Curious Outsiders" Technologies 6, no. 4: 118. https://doi.org/10.3390/technologies6040118
APA StyleCaravelli, F., & Carbajal, J. P. (2018). Memristors for the Curious Outsiders. Technologies, 6(4), 118. https://doi.org/10.3390/technologies6040118