Abstract
This paper presents a new approach for the analysis and characterization of the throughput region of wireless random access protocols enabled with multi-packet reception (MPR) capabilities. The derivation of a closed-form expression for the envelope of the throughput region under the assumption of an arbitrary number of terminals is an open issue in the literature. To partially fill this gap, a new method based on multi-objective optimization tools is herein presented. This innovative perspective allows us to identify the envelope of the throughput region as the Pareto frontier solution that results from maximizing simultaneously all individual terminal throughput functions. To simplify this problem, a modified MPR model is proposed that mimics the conditions of collision model protocols, but it also inserts new physical (PHY) layer features that allow concurrent transmission or MPR. The N-reception model is herein introduced, where collisions of up to N signals are assumed to be always correctly resolved from a population of J terminals, where N can be related to the number of antennas or degrees of freedom of the PHY-layer used at the receiver to resolve a collision. It is shown that by using this model and under the assumption of , the Pareto frontier expression can be obtained as a simple extension of the ALOHA solution. Unfortunately, for cases with , the structure of the resulting determinant matrix does not allow for a simple explicit solution. To overcome this issue, a symmetrical system is proposed, and the solution is obtained by the analysis of the roots of the resulting polynomial expression. Based on this result, an equivalent sub-optimal solution for the asymmetrical case is herein identified for systems where . An extension to more general reception models based on conditional reception probabilities is also presented using the proposed equivalence between the symmetric and asymmetric solutions. The results intend to shed light on the performance of MPR systems in general, and in particular to advance towards the solution of the conjecture of the equivalence between throughput and stability regions in random access.
1. Introduction
Random access protocols lie at the core of current and future wireless transmission technologies. Even in centralized radio access networks, such as 3G and 4G, random access technology is used whenever terminals request initial access to network resources. Random access technology is expected to receive renewed attention in the years to come. The huge demand for dense object connectivity, ultra-low latency, and higher data rates is not compatible with dedicated spectrum band allocation for each individual connection [1]. It is foreseen that 5G communications will combine the aspects of centralized/decentralized resource allocation, new low-cost multiple antenna technology (i.e., massive multiple-input multiple-output (MIMO), improved antenna design, and reconfigurable implementations [2]), and adaptive/cognitive radio sharing. This will open new fields for the evolution of random access tools. Other applications of random access can be found in [3,4].
Multi-packet reception (MPR) is one of the most attractive solutions to improve the performance of future wireless random access networks. Contrary to the conventional collision model used in ALOHA, in MPR systems, concurrent transmissions can be simultaneously decoded. This not only implies a boost of capacity, but also the opening of new interactions between the physical (PHY) and medium access control (MAC) layers. Cross-layer design is thus central to the study of MPR wireless random access protocols [5]. Pioneering works in this area were the studies of the effects of power capture on the stability and capacity of random access (see [6,7]). The first work that can be considered as a modern MPR random access protocol was presented in [8], where the authors proposed a stochastic MPR matrix that captures the reception capabilities of a symmetrical and infinite terminal network model with ALOHA operation. Multiple variations of protocols and retransmission strategies have been proposed based on this model (e.g., [9,10,11]). The extension to asymmetrical systems using a buffered and finite terminal population was presented in [12] using ALOHA operation with MPR capabilities. The stability region of the two-user case was obtained in closed-form. Approximate stability conditions were obtained for the case of more than two terminals.
The throughput and stability regions of wireless random access protocols with MPR was addressed in [13], emphasizing the conjecture known for ALOHA systems of equivalence between the two regions. The introduction of MPR PHY-layer metrics in random access design has opened many new fields for research. The work in [14] used game theory to derive transmission policies in random access with MPR. The work in [15,16] investigated the effects of channel state information in random access protocols with MPR. The work in [17] used multi-objective portfolio optimization tools to investigate trade-off regions of p-persistent carrier sense multiple access protocols with MPR. The work in [18] combined MPR based on multiple antenna with retransmission diversity and successive interference cancellation (SIC) to boost throughput beyond the limit of N packets per time slots, where N is the number of receiving antennas. Other works with interference cancellation in multiple access can be found in [19].
1.1. Open Issues and Paper Contributions
The optimization of random access protocols with MPR capabilities has not been addressed extensively in the literature. There are many gaps to be filled, particularly in terms of stability and throughput region analysis considering generalized MPR models. In addition, the open issue of the equivalence between stability and throughput regions needs to be addressed or verified (see [20]). This paper attempts to advance towards filling these gaps by adding more details in the study of the structure and properties of the throughput region of this type of protocol. The main objective is to attempt to derive closed-form expressions of the transmission policies that achieve the envelope of the throughput region. It is expected that in the future, this analytic framework could help in confirming the conjecture of equivalence between stability and throughput regions and also in the understanding of MPR protocols and how different channel conditions affect their performance.
1.2. Organization
The remainder of this paper is organized as follows. Section 2 presents the details of the system model and definitions. Section 3 addresses the multi-objective optimization to obtain the envelope of the throughput region under the N-reception model. Section 4 provides the extension to the generalized MPR reception model based on the findings of previous sections. Section 5 presents results that corroborate the validity of the expressions obtained in previous sections. Finally, Section 6 presents the conclusions of this paper.
Notation: Vectors and matrices are denoted, respectively, by bold lower-case (e.g., ) and upper-case letters (e.g., ); calligraphic letters denote set variables (e.g., , and ); is the statistical average operator; is the set cardinality operator when applied to a set variable, or the absolute value operator when applied to a scalar quantity, or the determinant operator when applied to a square matrix (e.g., ); is the Hermitian vector transpose operator; is the vector transpose operator; and is the combinatorial number of elements in positions.
2. System Model and Assumptions
2.1. Scenario Description and Epoch-Slot Definition
Consider the slotted wireless random access network depicted in Figure 1 with a set of J buffered terminals and one central node or base station (BS). The terminals are assumed to operate in full-buffer mode, which means they are considered to have always a packet ready to be transmitted at the head of the queue. The terminals have one antenna each, while the BS is provided with N receiving antennas. Whenever a terminal j is allowed to transmit in a given time slot, it will do so using a randomized transmission process controlled by a Bernoulli random experiment with parameter , which also denotes (under the full-queue assumption) the transmission probability of terminal j. It is assumed that the N antennas of the BS are used to enable multi-packet reception (MPR), which is the ability to decode simultaneously multiple concurrent transmissions from the uncoordinated terminals. The general MPR reception model to be used here is based on conditional reception probabilities. This model was originally proposed by the authors in [12]. The marginal correct reception probability of a set of terminals given a set of colliding terminals is defined here as follows:
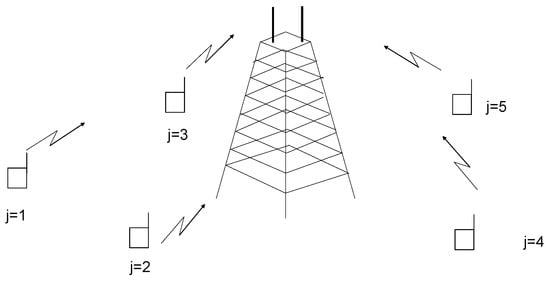
Figure 1.
Random access network with multi-packet reception capabilities (using a multiple-antenna receiver).
The conditional reception probability of a set of terminals is thus given by:
For convenience, a modified reception model called the N-reception model will be herein proposed. In this reception model, collisions of a size equal to or less than N will be assumed to be always correctly received by the BS. This means that:
where is the set cardinality operator when applied to a set variable. The list of main variables used in this paper is given in Table 1.

Table 1.
List of main variables.
2.2. Throughput and Throughput Region
Packet throughput of terminal j () is defined as the long-term ratio of correctly-received packets of terminal j to the time used in the measurement. Under the conditional reception model in (1), the throughput of terminal j can be written as the average over the probability space of cases with correct reception of terminal j:
By using the equality in (2), the previous expression becomes:
Consider the vectors of stacked variables and ; we can define the throughput region as the union of all realizable values of throughput of the terminals in the network [13]:
2.3. N-Reception Model
The throughput of terminal j under the assumption that collisions of a size equal to or less than N concurrent transmissions are always correctly decoded can be mathematically written as follows:
This expression represents the average over all possible realizations of collision sets of a size equal to or less than N () where terminal j is present in the collision set (). The throughput expression in (4) can be expanded in terms of the products of transmission probabilities as follows:
where is defined as a set of terminals of size l, and
See the Appendix A for details of the derivation of the coefficients .
3. Multi-Objective Optimization
This section addresses the simultaneous optimization of all the throughput functions of the terminals of the network. This can be expressed as the following multi-objective optimization problem:
A multi-objective optimization problem cannot always lead to a unique optimum solution as in conventional single objective optimization problems [21]. Instead, we use the concept of Pareto frontier and Pareto optimality. Pareto optimality refers to those solutions in the solution space where no individual or preference criterion can be better off without making at least one terminal throughput worse off. The Pareto frontier or surface is all the set of solutions (usually infinite) that achieve Pareto optimality. In engineering terms, Pareto optimality can be regarded as the best possible trade-off between competing metrics. In the context of the throughput region, the boundaries of such a region can be clearly linked to the best possible trade-off that can be achieved between all the individual terminal throughput functions. Therefore, we can claim that by deriving the Pareto frontier solution of the multi-objective optimization problem, we can also characterize the boundary of the throughput region of the multi-packet reception system. Using the method of scalarization [21], the multi-objective optimization problem in (7) can be rewritten as a single objective optimization problem:
where is the relative weight given to the j- throughput function . Differentiating the previous expression with respect to the different transmission probabilities yields the following system of equations set to zero:
Since the objective functions are polynomial (and therefore convex) with respect to the transmission probabilities, each one of the solutions to the derivative set to zero exists and is well behaved, and local optima can be identified by a simple boundary analysis. The Pareto frontier solution can be thus obtained by solving the set of equations for different values of the weighting factors . However, fine tuning of the relative values of these factors can be a difficult task. To overcome this issue, let us rewrite the system of linear equations in matrix form:
where is the square Jacobian matrix of size J with elements given by and the vector is the stacked array of weighting factors . The system of linear equations is homogeneous, and the condition to avoid the trivial solution is given by setting the determinant of the matrix to zero:
where:
This condition allows us to obtain an expression that is independent of particular values of the weighting factors . This means that there was no need to explicitly find the values of to obtain an expression for the Pareto frontier solution of the multi-objective optimization problem. Since all the objective functions are convex polynomial expressions, we expect that the determinant equation set to zero in (9) is well behaved in the range of interest of the transmission probabilities .
3.1. Case
To facilitate derivation, let us assume the case , for which the expression in (10) can be proven to become:
For details of the derivation, see the Appendix B. For this particular case, the determinant resembles a collision case protocol, for which the solution can be proven to yield:
See also Appendix C for the proof. The expression in (12) can be used as an approximation to the general case for . This expression can be regarded as the solution where the summation of all possible combinations of terminal sets of size equal to the MPR capacity of the PHY-layer N equals one. Note also that the solution in (12) for boils down to the ALOHA solution for the throughput region: .
3.2. Symmetrical Case N-Reception Model
Under the assumption of symmetrical network , , the throughput expression in (4) becomes:
Using the binomial expansion, the previous expression boils down to:
which can be rewritten as:
where:
or
Note that when , then the throughput expression in (13) becomes:
Differentiating this expression and setting it to zero leads to:
which can be further simplified to:
When comparing this last expression to the asymmetrical case in (12), it can be observed that they are equivalent under the symmetrical assumption, as expected.
This expression also turns out to be identical to the summation of all the elements of the Jacobian determinant matrix in (11) set to zero:
Note that by substituting explicitly (11) into the previous expression, we obtain exactly the transmission policy previously obtained in (12). This leads us to state the conjecture that will be explored in this paper. A sub-optimal transmission policy in the asymmetrical scenario can be obtained by adding all the elements of the determinant matrix and setting it to zero as in (16). This sub-optimum transmission policy has lower complexity as compared to the exact solution in the expression in (11). The next subsection confirms the validity of this conjecture for the general N-reception model case in the symmetrical scenario. This means that the proposed conjecture allows us to approximate the highly complex solution of the determinant equation in (11), by a simple sum of the elements of the Jacobian matrix as in (16). The analytic proof of this conjecture in the general asymmetrical is not addressed by this paper. This means that we will not prove that the solution to the exact determinant equation is given by the summation in (16). The section for the results show that the proposed sub-optimum solution has very good performance in most of the presented network scenarios.
3.3. General Case N-Reception Model
Using the conjecture formulated in the previous subsection, the sub-optimum solution for the determinant optimum equation in (9) is given by the summation of all the components of the determinant matrix as in (16). By substituting the explicit expression for the partial derivatives from (10) into (16), we obtain:
which can be rewritten as follows:
Note that:
which leads to:
where:
It is now possible to derive the symmetrical case from the previous equations. This leads to the following expression:
where
When compared to the expression in (15), equivalence can be confirmed term by term. This corroborates the conjecture previously stated of the equivalence between the symmetrical solution and the expression in (16). We recall here that this equivalence only applies in the symmetrical scenario. The proof of the validity for the asymmetrical scenario is not addressed analytically in this paper.
4. Generalized MPR Conditional Probabilistic Reception Model
This section addresses the optimization of the expressions for the generalized MPR reception model using the conjecture proposed in the previous section. The throughput under the generalized reception model is given in (3). The throughput expressions can be expanded in terms of the different products of the transmission probabilities, expanding all the product terms in (3) as follows:
where denotes any subset of terminals of size l (). Expanding the product term we obtain:
By substituting this last expression back in (19), we obtain:
This expression can be rewritten as follows:
where:
For convenience, let us normalize the throughput expressions and reception parameters as follows:
The elements of the resulting determinant matrix for the optimization problem can be written in this context as follows:
Symmetrical Case
Let us address the symmetrical use case to investigate the validity of the conjecture used to obtain the optimum transmission probabilities for the generalized MPR reception case. The overall throughput expression can be written as follows:
where , , and . Using binomial expansion, the expression in (23) becomes:
Normalizing the previous expression with respect to the single-user reception probability, we obtain:
Let us substitute the asymmetrical determinant elements in (22) into the proposed suboptimal solution in (16). This leads to:
Using the definition of the reception composite parameters in (21) and comparing term by term, we can confirm the equivalence of the asymmetrical and symmetrical solutions. The full details of this comparison have been omitted here because they are a straightforward extension of the proof of the N reception model presented in previous sections. The confirmation of equivalence of the optimum transmission probabilities of the symmetrical and asymmetrical cases corroborates the conjecture presented in previous subsections and allows us to present the expression in (16) as the sub-optimal solution of the boundary of the throughput region in both the N-reception, as well as for the general MPR models. We recall here that the confirmation of the conjecture has been obtained only in the symmetrical case; the full confirmation for any other point in the solution space different from the symmetrical case remains as an open problem.
5. Results
This section presents the sketches of the throughput region for different network settings that will corroborate the main derivations and conjectures stated in this paper. It is worth pointing out that the sketches in this section are bi-dimensional, and the system parameters have been set here to fit this restriction. The throughput region of J terminals is, in the strict sense, a J-dimensional figure, and therefore, many of these higher dimensional features cannot be represented graphically in a two-dimensional space. The first set of results was obtained for a network setting with terminals split into two subsets of three terminals each. All terminals in each set will experience the same queuing statistics. The results were obtained with the N-reception model with different values of . The Pareto frontier sketches of the boundary of the throughput region were obtained by setting one of the transmission probabilities as variable in the range and then solving the other transmission probability(ies) from the Pareto frontier optimum or sub-optimum expressions using well-known numerical methods for solving equations. The results of the throughput of the two sets of terminals were simply obtained by substituting the optimum or sub-optimum transmission probabilities in the expressions for packet throughput in (3). The results can be observed in Figure 2. The figure shows the exact solution obtained by exhaustive search computation, the optimum solution from the determinant equation set to zero in (9), the sub-optimal solution in the Expression (12), labeled as Subopt. 1, and the suboptimal solution in (16), labeled as Subopt. 2. It can be observed that in all cases, the suboptimal solution in (12) provided an almost exact approximation, even for cases where . By comparison, the suboptimal solution in (16) showed a better fit when the curves were near the point of statistical identity between the two subsets of terminals () and showed deviation at the edges of the main envelope curve where or .
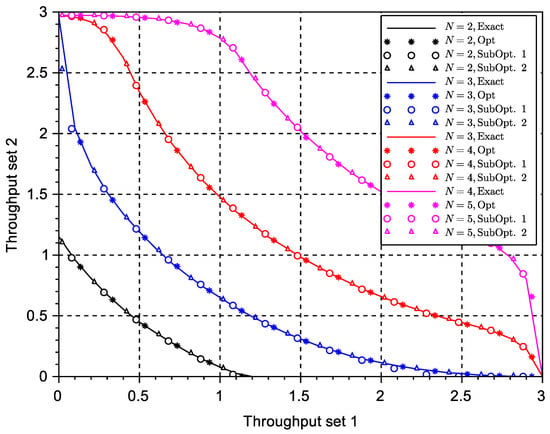
Figure 2.
Throughput region of a multi-packet reception (MPR) system with two subsets of terminals: using the N-reception model with different values of N.
A second case presented in Figure 3 was obtained also with the N-reception model, but this time with different sets of terminals: the first set had terminals, while the second set had terminal. A third case is presented in Figure 4 with a much higher number of terminals to illustrate the validity of the results in more realistic highly scalable settings. It can be shown that the solution Subopt. 1 is now more inaccurate due to the larger numbers of terminals. The results in Figure 5 and Figure 6 considered a general reception model based on the size of the collision: with different values of . This reception model is a straightforward extension of the N-reception model proposed in this paper. It simply indicates that collisions are correctly received with a probability that is inversely proportional to the size of the collision. Similar reception models in different contexts have been proposed in the literature using exponential functions, particularly in the power capture domain and successive interference cancellation systems (see [22]). The exact solution obtained by exhaustive search, the optimum solution from the determinant equation set to zero in (9), and the suboptimal solution in (16) are shown in the two figures. In this case, it can be observed that the suboptimal solution in (16) provides also a very good approximation to the exact envelope of the throughput region.
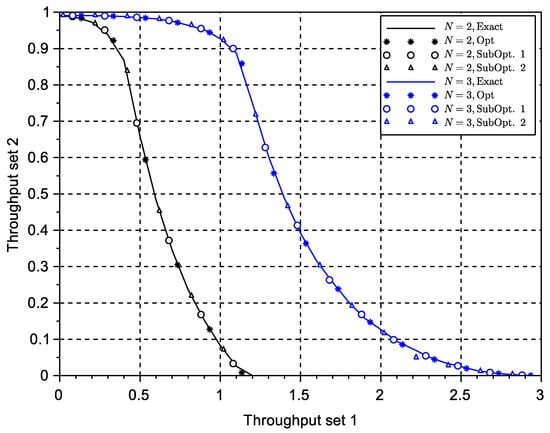
Figure 3.
Throughput region of a multi-packet reception (MPR) system with two subsets of terminals: and using the N-reception model with different values of N.
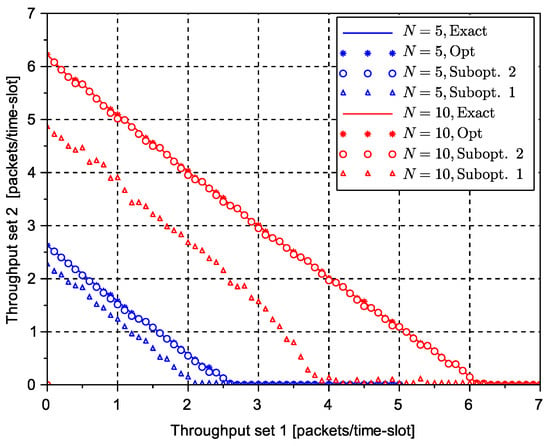
Figure 4.
Throughput region of a multi-packet reception (MPR) system with two subsets of terminals: and using the N-reception model with different values of N.
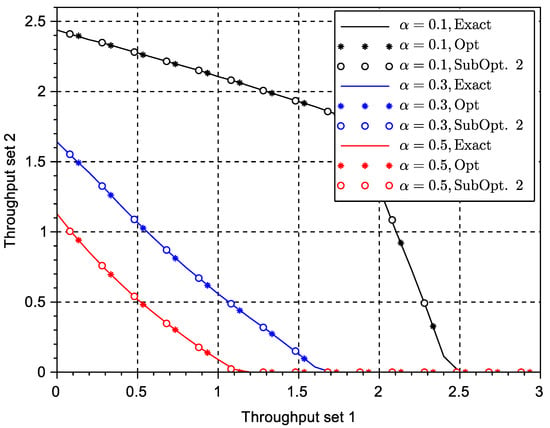
Figure 5.
Throughput region of a multi-packet reception (MPR) system with two subsets of terminals: using the general reception model with different values of the reception parameter .
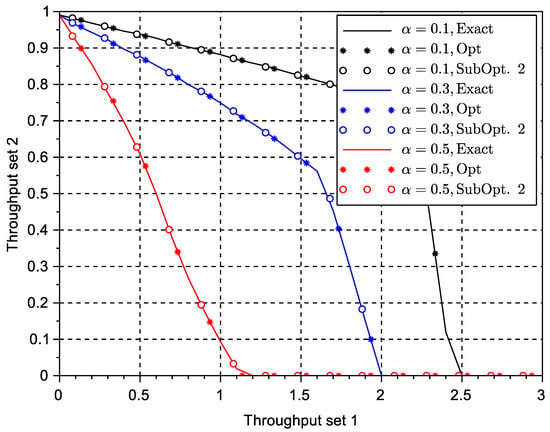
Figure 6.
Throughput region of a multi-packet reception (MPR) system with two subsets of terminals: and using the general reception model with different values of the reception parameter .
6. Conclusions
This paper presented a detailed analysis of the throughput region of random access protocols with multi-packet reception capabilities. Based on an observation obtained with a simplified reception model (called here the N-reception model), a conjecture has been established between the equivalence of the optimal transmission policy in symmetrical settings and the summation of the elements of a Jacobian determinant matrix of the asymmetrical formulation. This conjecture has allowed us to propose a sub-optimal solution for the transmission policy in the asymmetrical terminal scenario. The results showing sketches of the throughput region prove the validity of the observation for the given scenario. The exact solution for the case of using the N-reception model has also been derived and tested. The solution is shown to be a straightforward extension of the conventional ALOHA (non-MPR) optimum transmission policy. The results in this paper aim to advance the understanding of the properties of MPR for random access and eventually to clarify the conjecture of the equivalence between throughout and stability regions of multiple access protocols.
Funding
SCOTT (www.scottproject.eu) has received funding from the Electronic Component Systems for European Leadership Joint Undertaking under grant agreement No 737422. This Joint Undertaking receives support from the European Union’s Horizon 2020 research and innovation programme and Austria, Spain, Finland, Ireland, Sweden, Germany, Poland, Portugal, Netherlands, Belgium, Norway. Funded also by FCT/MEC (Fundacão para a Ciência e a Tecnologia) project 5GSDN (PTDC/EEI-TEL/32218/2017), ERDF (European Regional Development Fund) under PT2020, and by CISTER Research Unit (CEC/04234).
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Derivation of the Coefficients Cl in (6) of the Throughput Expansion Function in (5)
Consider the original throughput function for the N-reception model in (4). We are interested in expanding the function in terms of simple products of transmission probabilities for different sizes l of the set , where and is the cardinality set operator. Inspecting the throughput function in (4), some of the terms contribute with a positive or a negative element. For example, the term contains a positive term and a negative term . The generalization to an arbitrary number of elements is as follows. Each product term of size is present in all the terms where , and the sign depends on the difference where . This can be mathematically written as follows:
where the term accounts for all combinations of products of length l in the n position where one position is always occupied by terminal j of the throughput expression in (5). Note that when , the coefficients correspond to the binomial expansion of ; when , the coefficients mimic the full expansion for the binomial term , which is zero. For the case when , the summation is incomplete, and therefore, . For , the term is always one (), as terminal j is always present in the analysis. This concludes the derivation of the expression for in (6).
Appendix B. Derivation of the Expression in (11) of the Elements of the Jacobian Determinant Matrix for the N-Reception Model Considering
In the case of , the coefficients in (6) reduce to a single term for .
By using the change of variable , the previous expression can be modified as follows:
By noting that the binomial expansion of is given by:
it follows that:
Appendix C. Derivation of the Optimum Transmission Probabilities in (12) for the N-Reception Model Considering
Consider the Lemma 1 in [23] reproduced here for convenience. Consider any matrix with elements given by the following structure:
The determinant equation set to zero:
boils down to the following expression:
References
- Chen, Y.; Cheng, L.; Wang, L. Prioritized resource reservation for reducing random access delay in 5G URLLC. In Proceedings of the IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017; pp. 1–5. [Google Scholar]
- Hussain, S.; Khan, U.A.; Anjum, M.R.; Hayat, M.A. Reconfigurable antenna parameters with the change in the position of switches. Electron. Devices 2016, 5, 34–44. [Google Scholar]
- Meloni, A.; Murroni, M. Random access in DVB-RCS2: Design and dynamic control for congestion avoidance. IEEE Trans. Broadcast. 2014, 60, 16–28. [Google Scholar] [CrossRef]
- Casini, E.; de Gaudenzi, R.; Herrero, O.D. Contention resolution diversity slotted ALOHA (CRDSA): An enhanced random access schemefor satellite access packet networks. IEEE Trans. Wirel. Commun. 2007, 6, 1408–1419. [Google Scholar] [CrossRef]
- Tong, L.; Naware, V.; Venkitasubramaniam, P. Signal processing in random access. IEEE Signal Process. Mag. 2004, 21, 29–39. [Google Scholar] [CrossRef]
- Zorzi, M.; Rao, R. Capture and retransmission control in mobile radio. IEEE J. Sel. Areas Commun. 1994, 12, 1289–1298. [Google Scholar] [CrossRef]
- Yu, Y.; Cai, X.; Giannakis, G.B. On the stability of slotted ALOHA with capture. IEEE Trans. Wirel. Commun. 2006, 5, 257–261. [Google Scholar] [CrossRef]
- Ghez, S.; Verdu, S.; Schwartz, S. Stability properties of slotted Aloha with multipacket reception capability. IEEE Trans. Autom. Control 1988, 33, 640–649. [Google Scholar] [CrossRef]
- Ghez, S.; Verdu, S.; Schwartz, S. Optimal decentralized control in the random access multipacket channel. IEEE Trans. Autom. Control 1989, 34, 1153–1163. [Google Scholar] [CrossRef]
- Zhao, Q.; Tong, L. A dynamic queue protocol for multiaccess wireless networks with multipacket reception. IEEE Trans. Wirel. Commun. 2004, 3, 2221–2231. [Google Scholar] [CrossRef]
- Zhao, Q.; Tong, L. A multiqueue service room MAC protocol for wireless networks with multipacket reception. IEEE Trans. Netw. 2003, 11, 125–137. [Google Scholar] [CrossRef]
- Naware, V.; Mergen, G.; Tong, L. Stability and delay of finite-user slotted ALOHA with multipacket reception. IEEE Trans. Inf. Theory 2005, 51, 2636–2656. [Google Scholar] [CrossRef]
- Luo, J.; Ephremides, A. On the throughput, capacity, and stability regions of random multiple access. IEEE Trans. Inf. Theory 2006, 52, 2593–2607. [Google Scholar]
- Ngo, M.H.; Krishnamurty, V. Game theoretic cross-layer transmission policies in multipacket reception wireless networks. IEEE Trans. Signal Process. 2007, 55, 1911–1926. [Google Scholar] [CrossRef]
- Ngo, M.H.; Krishnamurthy, V.; Tong, L. Optimal channel-aware ALOHA protocol for random access in WLANs with multipacket reception and decentralized channel state information. IEEE Trans. Signal Process. 2008, 56, 2575–2588. [Google Scholar] [CrossRef]
- Adireddy, S.; Tong, L. Exploiting decentralized channel state information for random access. IEEE Trans. Inf. Theory 2005, 51, 537–561. [Google Scholar] [CrossRef]
- Samano-Robles, R.; Gameiro, A. Multi-Objective and Financial Portfolio Optimization of p-Persistent Carrier Sense Multiple Access Protocols with Multi-Packet Reception. Chapter Commun. Comput. Inf. Sci. Optim. Nat. Sci. 2015, 499, 68–94. [Google Scholar]
- Samano-Robles, R.; McLernon, D.C.; Ghogho, M. A random access protocol incorporating multi-packet reception, retransmission diversity and successive interference cancellation. In Proceedings of the 8th International Workshop on Multiple Access Communications (MACOM2015), Helsinki, Finland, 3–4 September 2015. [Google Scholar]
- Liva, G. Graph-based analysis and optimization of contention resolution diversity slotted ALOHA. IEEE Trans. Commun. 2011, 59, 477–487. [Google Scholar] [CrossRef]
- Rao, R.R.; Ephremides, A. On the stability of interacting queues in a multiple-access system. IEEE Trans. Inf. Theory 1988, 4, 918–930. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Tong, Y.; Dai, L. Maximum sum rate of slotted Aloha with successive interference cancellation. IEEE Trans. Commun. 2018, 16, 5385–5400. [Google Scholar] [CrossRef]
- Samano-Robles, R.; Ghogho, M.; McLernon, D.C. Wireless Networks with retransmission diversity and carrier sense multiple access. IEEE Trans. Signal Process. 2009, 57, 3722–3726. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).