Temperature Variability of Poisson’s Ratio and Its Influence on the Complex Modulus Determined by Dynamic Mechanical Analysis
Abstract
1. Introduction
2. Methodology
2.1. Materials
2.2. Tensile Testing
2.3. Dynamic Mechanical Analysis
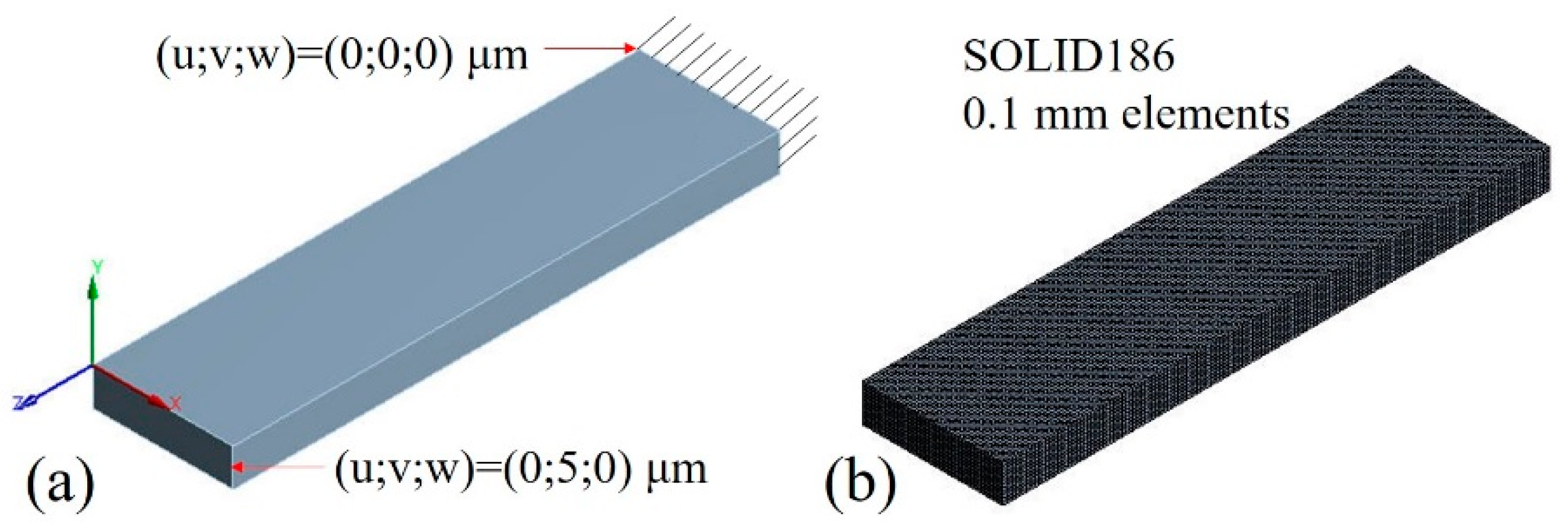
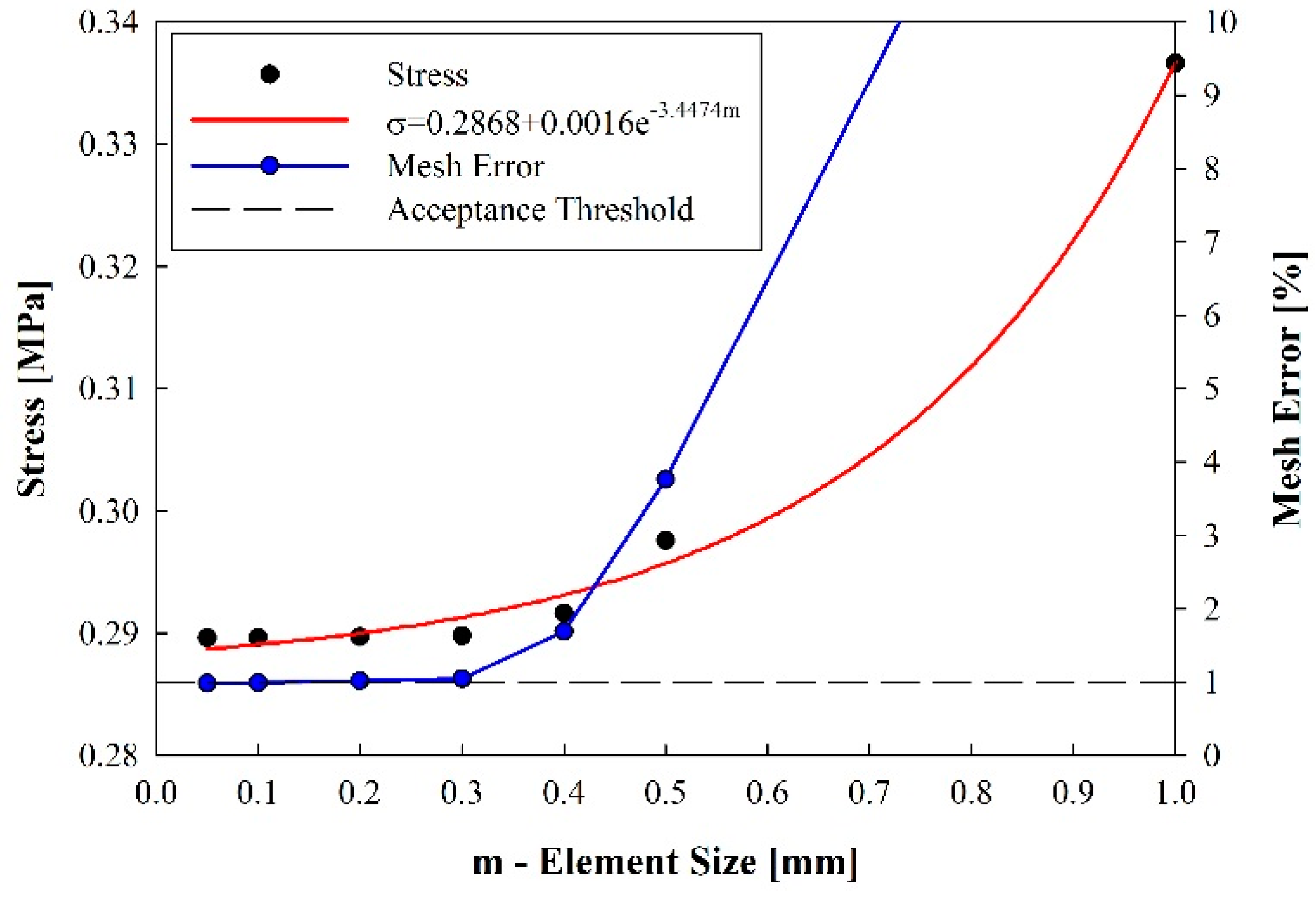
2.4. Finite Element Analysis
3. Results
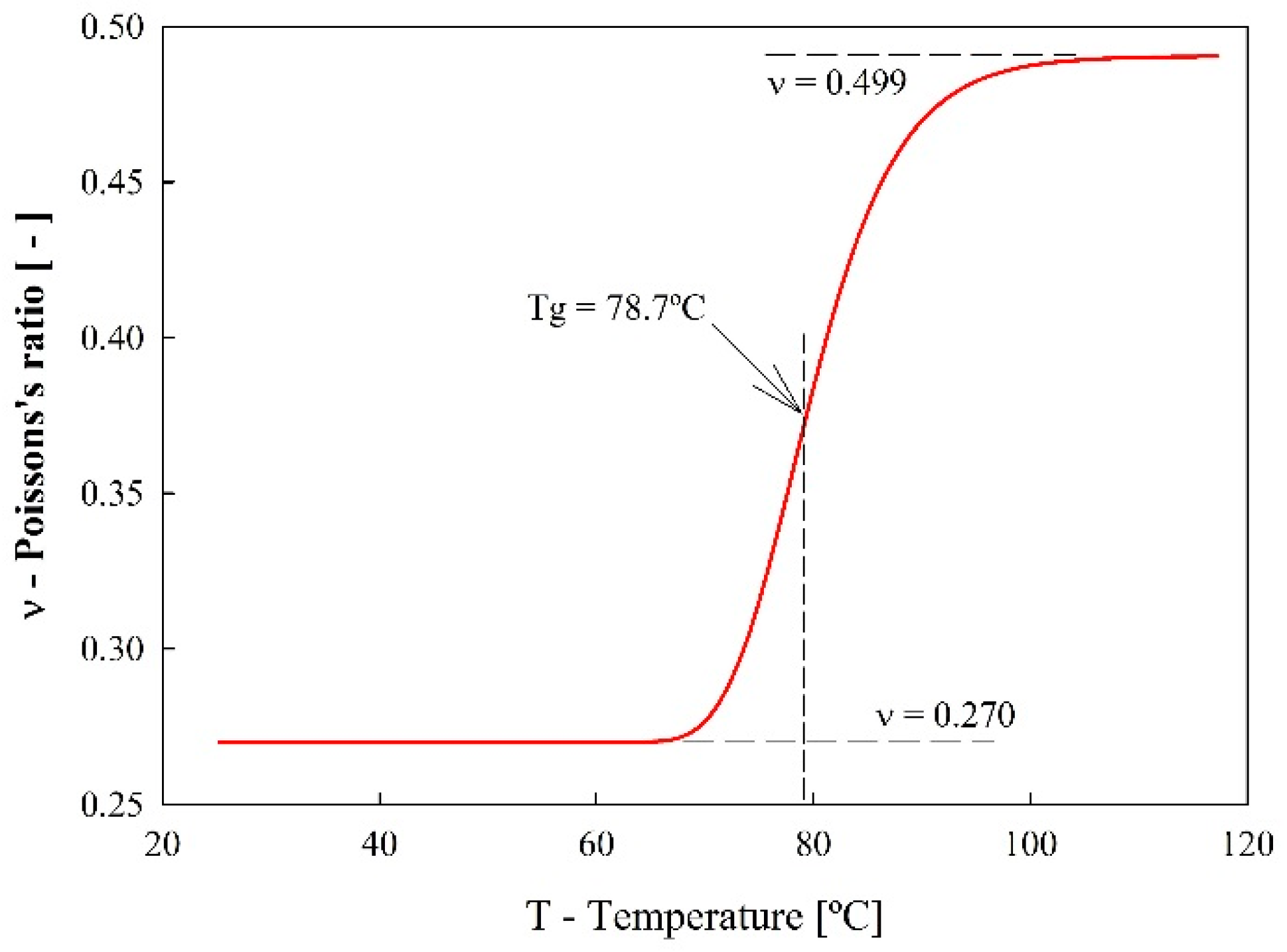
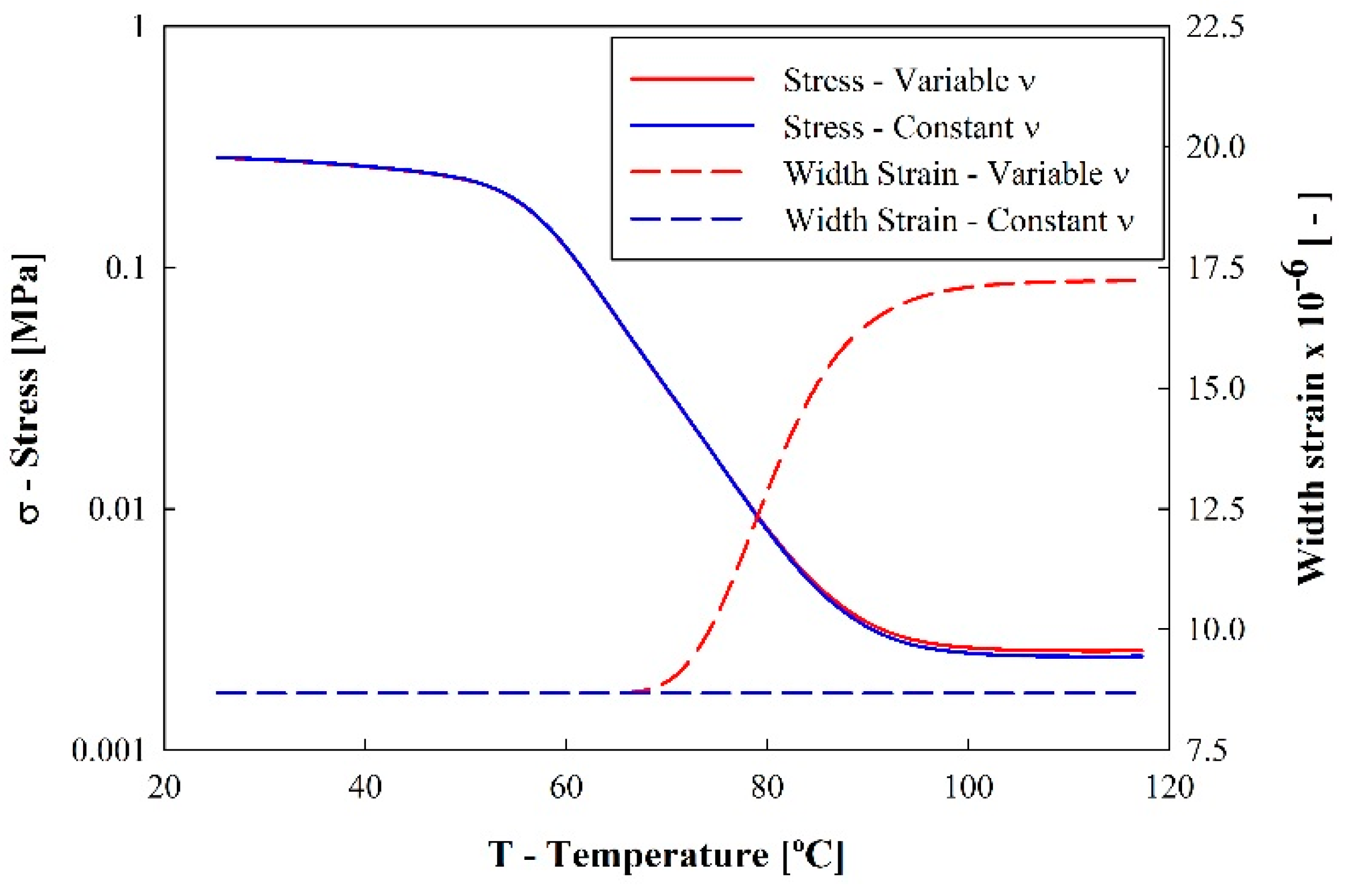
3.1. Theoretical Modeling
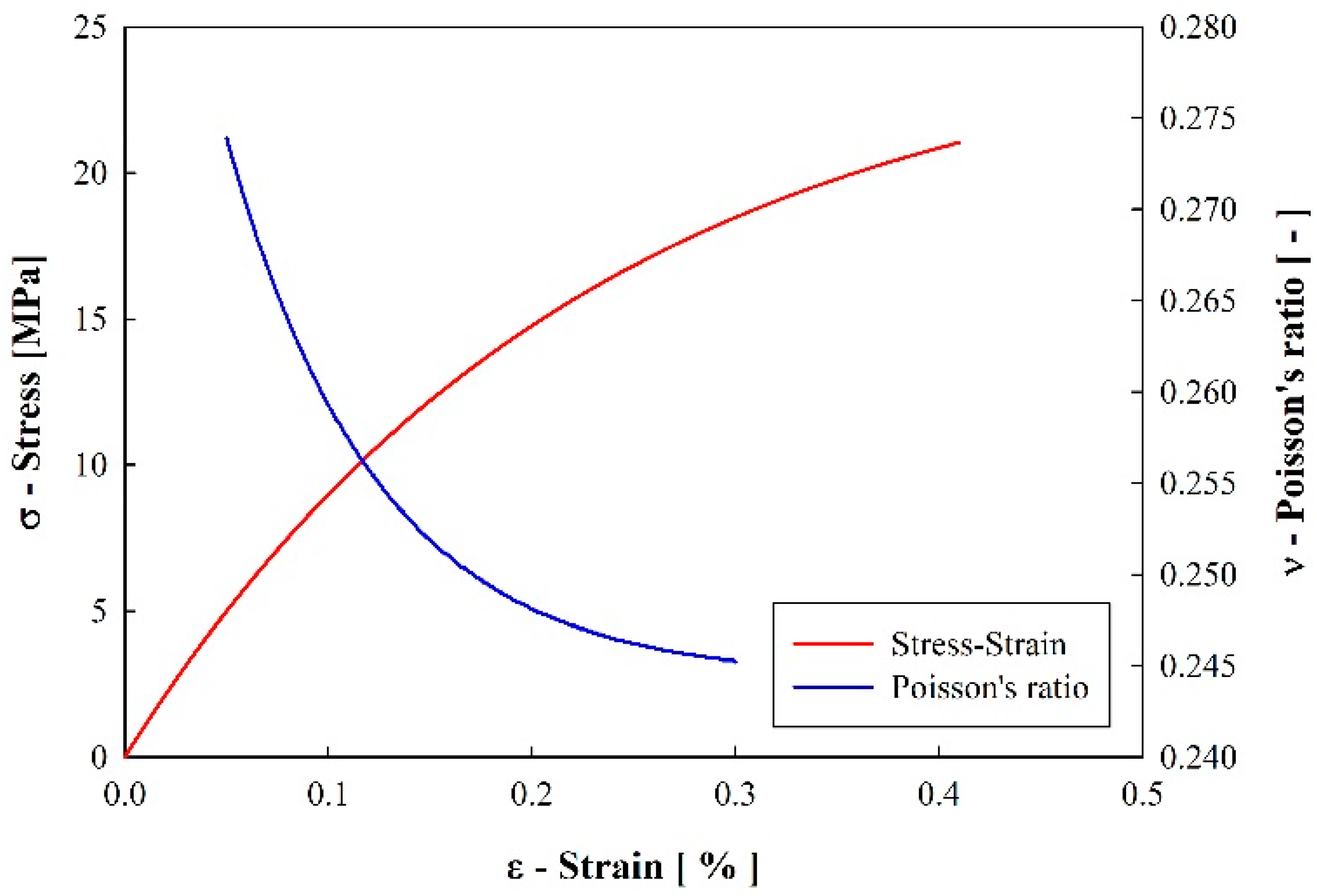
3.2. Experimental Tensile Testing
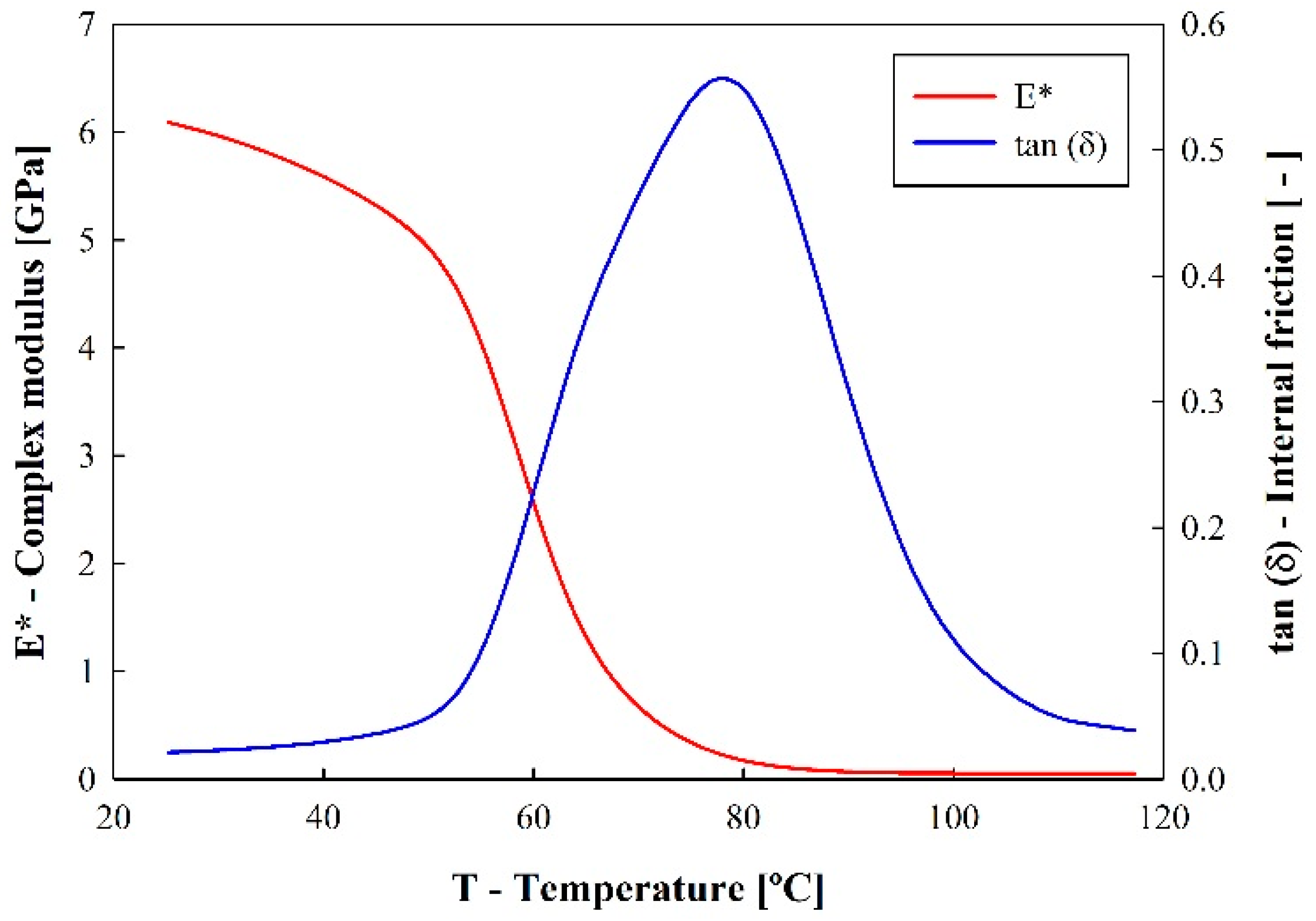
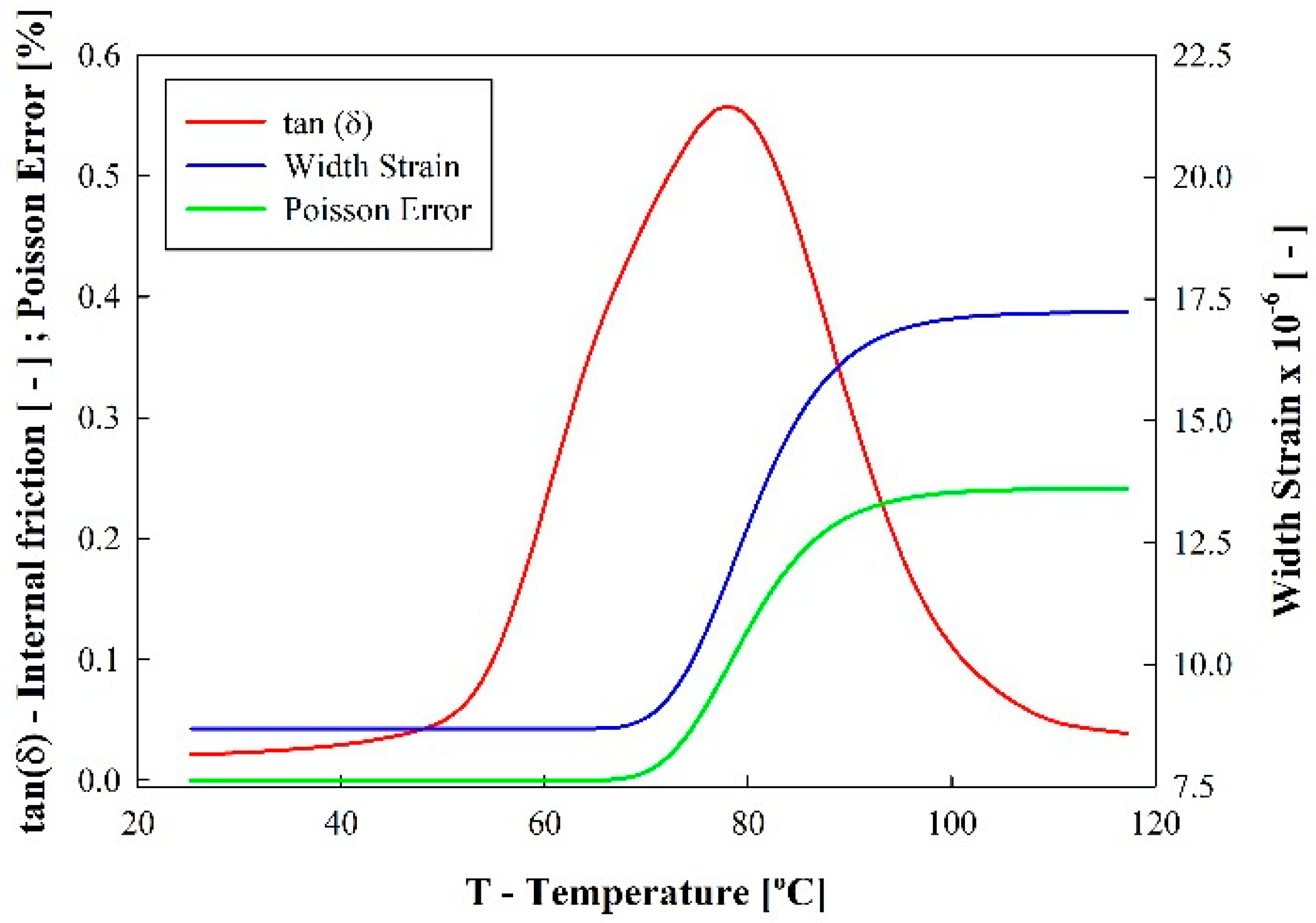
3.3. Dynamic Mechanical Analysis
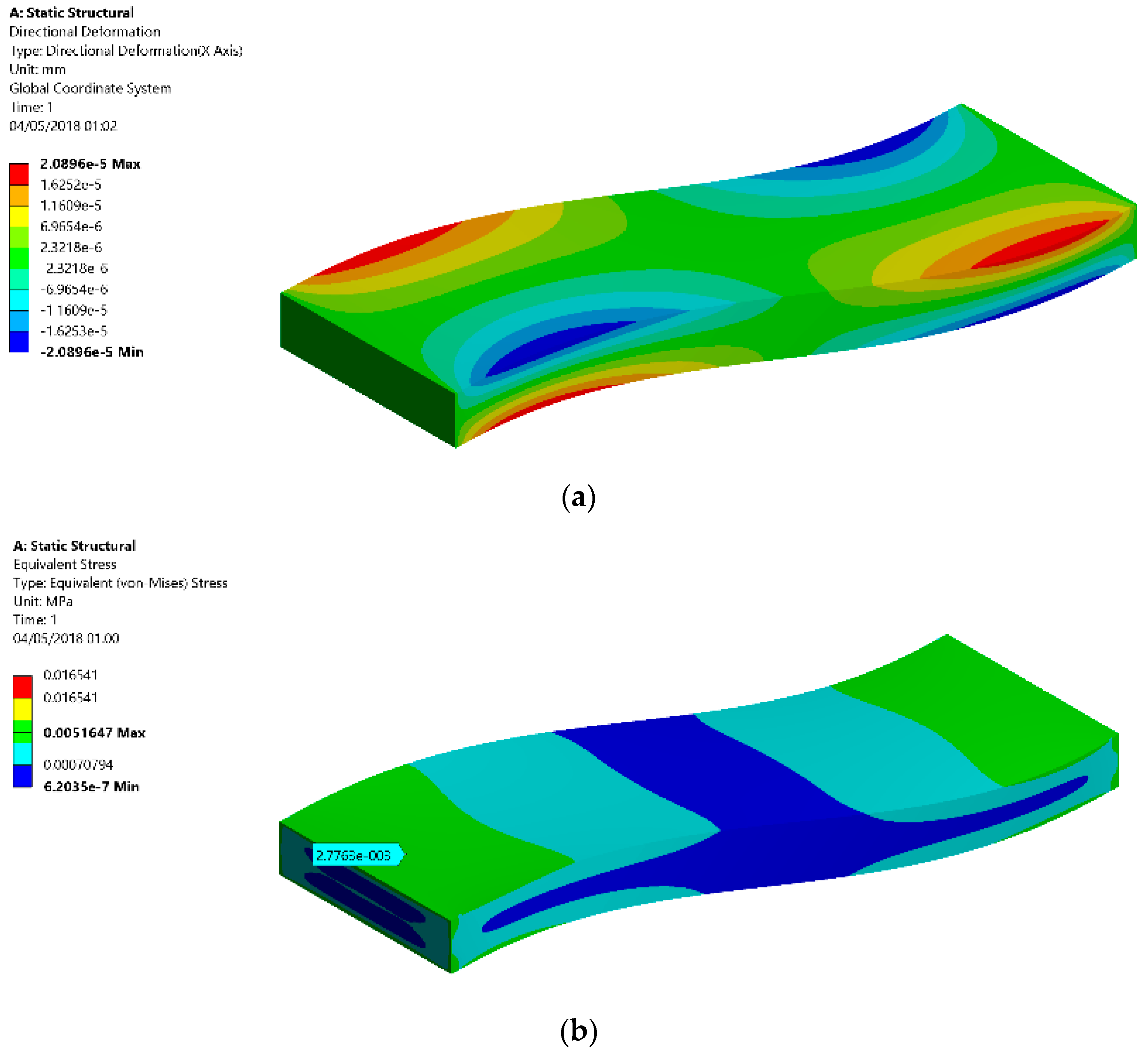
3.4. Finite Element Analysis
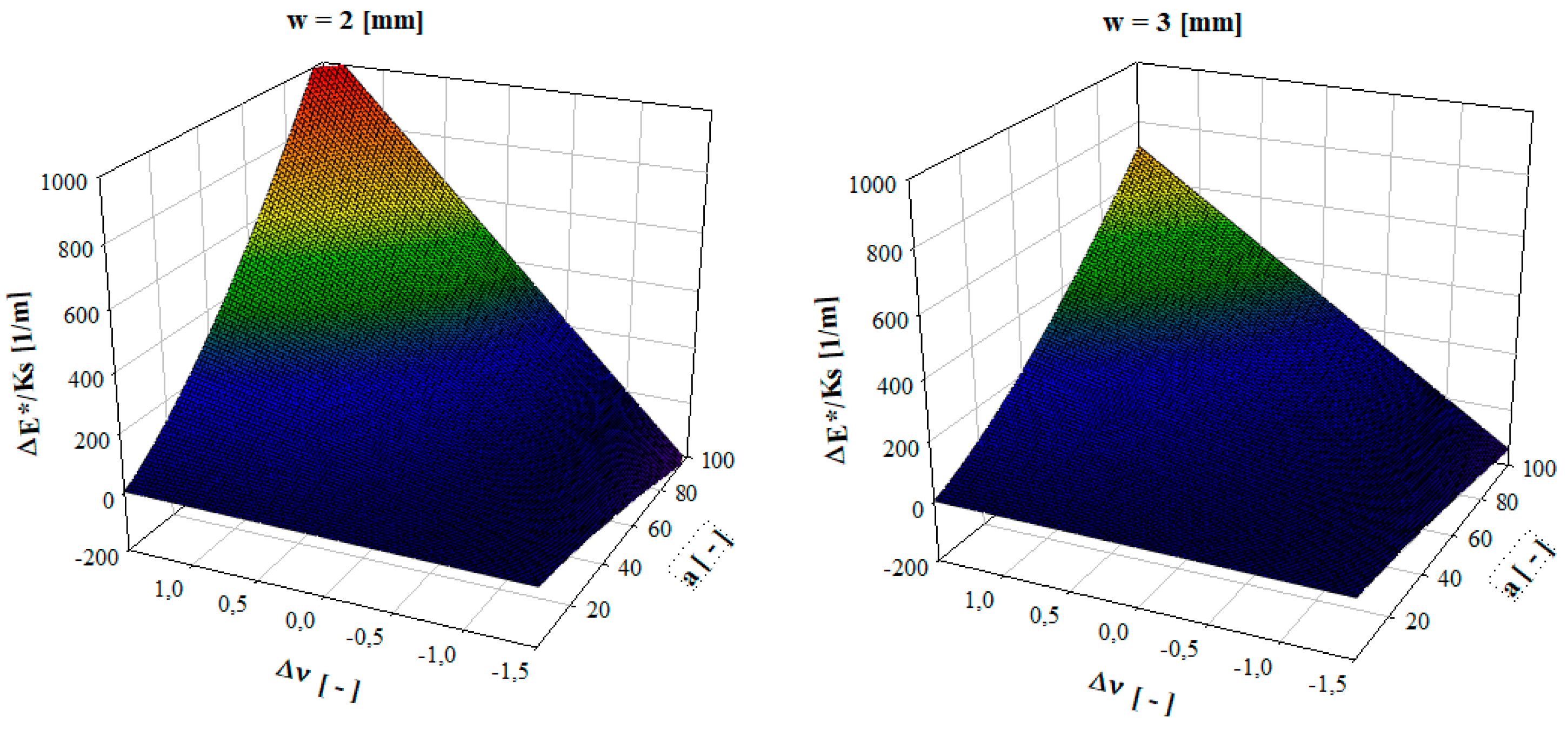
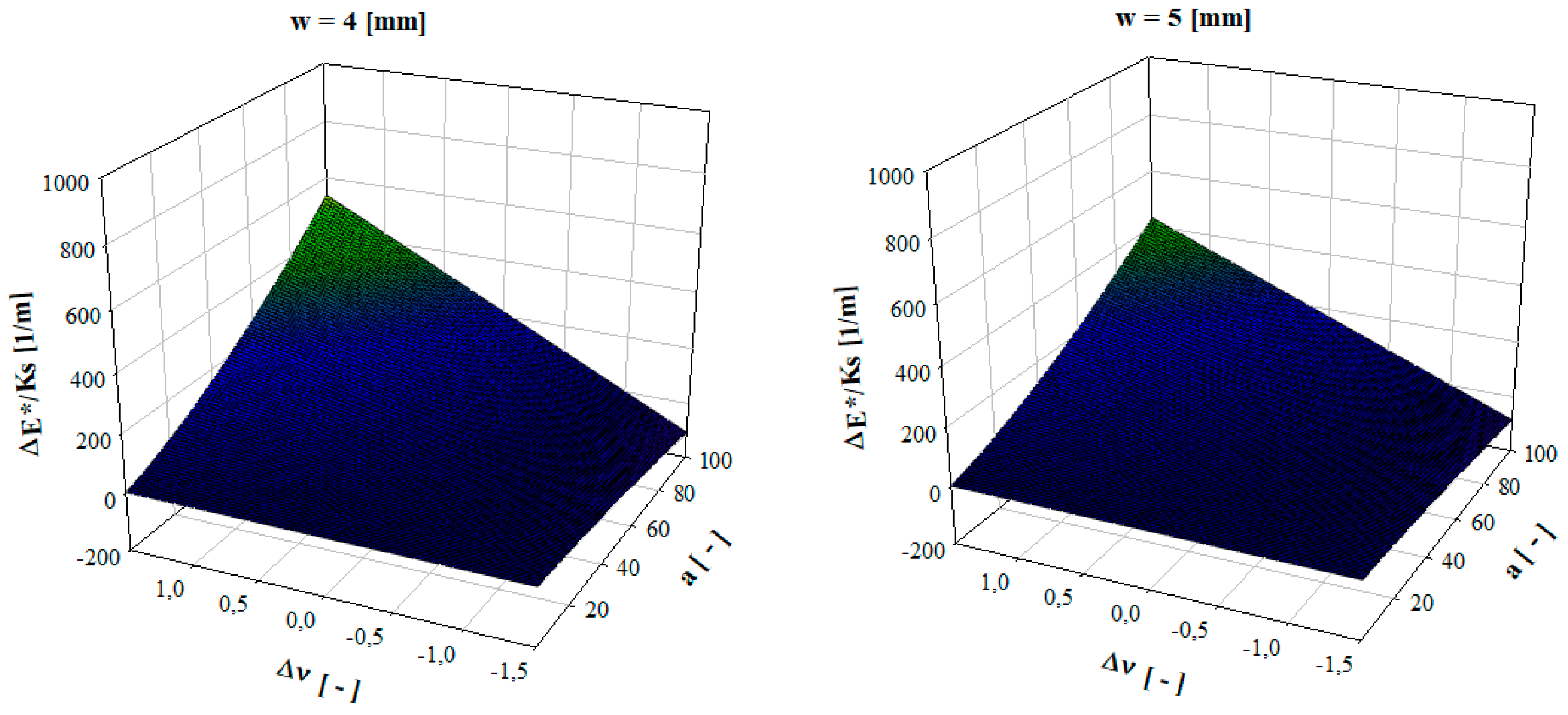
4. Discussion—Influence of Poisson’s Ratio
5. Conclusions
- -
- Given that the Poisson’s ratio may change due to external stimulation (e.g., temperature, loading, time, etc.) there is an error associated with the consideration of its value as constant during the DMA test;
- -
- The error is more prominent in situations where Poisson’s ratio increases significantly, and is attributed to shape variations in the specimen, especially in conditions where the final Poisson’s ratio approximates an isochoric (ν ~ 0.5) behavior;
- -
- It is suggested that the evolution of this technology should consider Poisson’s ratio as a variable to eliminate this error in future material characterization.
Author Contributions
Funding
Conflicts of Interest
References
- Tschoegl, N.W.; Knauss, W.G.; Emri, I. Poisson’s Ratio in Linear Viscoelasticity—A Critical Review. Mech. Time-Depend. Mater. 2002, 6, 3–51. [Google Scholar] [CrossRef]
- Lakes, R.S.; Wineman, A. On Poisson’s Ratio in Linearly Viscoelastic Solids. J. Elast. 2006, 85, 45–63. [Google Scholar] [CrossRef]
- Poynting, J.H. On Pressure Perpendicular to the Shear Planes in Finite Pure Shears, and on the Lengthening of Loaded Wires When Twisted. Proc. R. Soc. Lond. Ser. A 1909, 82, 546–559. [Google Scholar] [CrossRef]
- Murayama, T. Dynamic Mechanical Analysis of Polymeric Material; Elsevier Scientific Pub. Co.: Amsterdam, The Netherlands, 1978; ISBN 0-444-41684-6. [Google Scholar]
- Read, B.E.; Dean, G.D. The Determination of Dynamic Properties of Polymers and Composites; Halsted Press: Ultimo, Austrilia, 1978; ISBN 0-470-26543-4. [Google Scholar]
- Dealy, J.M. Rheometers for Molten Plastics: A Practical Guide to Testing and Property Measurement; Van Nostrand Reinhold Company: New York, NY, USA, 1982; ISBN 0-442-21874-5. [Google Scholar]
- Chen, D.-L.; Yang, P.-F.; Lai, Y.-S. A review of three-dimensional viscoelastic models with an application to viscoelasticity characterization using nanoindentation. Microelectron. Reliab. 2012, 52, 541–558. [Google Scholar] [CrossRef]
- Wineman, A. Nonlinear Viscoelastic Solids—A Review. Math. Mech. Solids 2009, 14, 300–366. [Google Scholar] [CrossRef]
- Chartoff, R.P.; Menczel, J.D.; Dillman, S.H. Dynamic Mechanical Analysis (DMA). In Thermal Analysis of Polymers; Wiley-Blackwell: New York, NY, USA, 2008; pp. 387–495. ISBN 978-0-470-42383-7. [Google Scholar]
- Menard, K.P. Dynamic Mechanical Analysis: A Practical Introduction; CRC Press: Boca Raton, FL, USA, 2008; ISBN 1-4200-5313-2. [Google Scholar]
- Madeira, S.; Carvalho, O.; Carneiro, V.H.; Soares, D.; Silva, F.S.; Miranda, G. Damping capacity and dynamic modulus of hot pressed AlSi composites reinforced with different SiC particle sized. Compos. Part B Eng. 2016, 90, 399–405. [Google Scholar] [CrossRef]
- McAninch, I.N.; Palmese, G.R.; Lenhart, J.L.; Scala, J.J.L. DMA testing of epoxy resins: The importance of dimensions. Polym. Eng. Sci. 2015, 55, 2761–2774. [Google Scholar] [CrossRef]
- Chen, C.P.; Lakes, R.S. Dynamic wave dispersion and loss properties of conventional and negative Poisson’s ratio polymeric cellular materials. Cell. Polym. 1989, 8, 343–359. [Google Scholar]
- Chen, C.P.; Lakes, R.S. Micromechanical analysis of dynamic behavior of conventional and negative Poisson’s ratio foams. J. Eng. Mater. Technol. 1996, 118, 285–288. [Google Scholar] [CrossRef]
- Ruzzene, M.; Scarpa, F.; Sorana, F. Wave beaming effects in two-dimensional cellular structures. Smart Mater. Struct. 2003, 12, 363–372. [Google Scholar] [CrossRef]
- Kolat, P.; Maruszewski, B.M.; Wojciechowski, K.W. Solitary waves in auxetic plates. J. Non-Cryst. Solids 2010, 356, 2001–2009. [Google Scholar] [CrossRef]
- Dinh, T.-B.; Long, V.C.; Wojciechowski, K.W. Solitary waves in auxetic rods with quadratic nonlinearity: Exact analytical solutions and numerical simulations. Phys. Status Solidi B 2015, 252, 1587–1594. [Google Scholar] [CrossRef]
- Sobieszczyk, P.; Majka, M.; Kuzma, D.; Lim, T.-C.; Zielinski, P. Effect of longitudinal stress on wave propagation in width-constrained elastic plates with arbitrary Poisson’s ratio. Phys. Status Solidi B 2015, 252, 1615–1619. [Google Scholar] [CrossRef]
- Carneiro, V.H.; Capela, P.; Teixeira, J.C.; Teixeira, S.; Cerqueira, F.; Macedo, F.; Ribas, L.; Soares, D. Influence of Copper Layer Content in the Elastic and Damping Behavior of Glass-Fiber/Epoxy-Resin Composites. Appl. Compos. Mater. 2016, 23, 1219–1228. [Google Scholar] [CrossRef]
- May, C. Epoxy Resins: Chemistry and Technology; CRC Press: Boca Raton, FL, USA, 1987; ISBN 0-8247-7690-9. [Google Scholar]
- TA Q800 Manual: DMA Modulus Equations. TA Instruments. Available online: http://www.tainstruments.com (accessed on 22 June 2018).
- Wojciechowski, K.W. Remarks on “Poisson Ratio beyond the Limits of the Elasticity Theory”. J. Phys. Soc. Jpn. 2003, 72, 1819–1820. [Google Scholar] [CrossRef]
- Michels, J.; Widmann, R.; Czaderski, C.; Allahvirdizadeh, R.; Motavalli, M. Glass transition evaluation of commercially available epoxy resins used for civil engineering applications. Comps. Part B Eng. 2015, 77, 484–493. [Google Scholar] [CrossRef]
- Carneiro, V.H.; Meireles, J.; Puga, H. Auxetic materials—A review. Mater. Sci.-Poland 2013, 31, 561–571. [Google Scholar] [CrossRef]
- Greaves, G.N.; Greer, A.L.; Lakes, R.S.; Rouxel, T. Poisson’s ratio and modern materials. Nat. Mater. 2011, 10, 823–837. [Google Scholar] [CrossRef] [PubMed]
- Tetriakov, K.V.; Wojciechowski, K.W. Monte Carlo simulation of two-dimensional hard body systems with extreme values of the Poisson’s ratio. Phys. Status Solidi B 2005, 242, 730–741. [Google Scholar] [CrossRef]
- Hirotsu, S. Softening of bulk modulus and negative Poisson’s ratio near the volume phase transition of polymer gels. J. Chem. Phys. 1991, 94, 3949–3957. [Google Scholar] [CrossRef]
| Chemical Composition | Specimens | |||
|---|---|---|---|---|
| Component A (Resin) |
| Dimension | Value (mm) | SD (mm) |
| Thickness | 1.23 | 0.08 | ||
| Component B (Hardener) |
| Width | 4.51 | 0.08 |
| Length | 30.20 | 0.11 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carneiro, V.H.; Puga, H. Temperature Variability of Poisson’s Ratio and Its Influence on the Complex Modulus Determined by Dynamic Mechanical Analysis. Technologies 2018, 6, 81. https://doi.org/10.3390/technologies6030081
Carneiro VH, Puga H. Temperature Variability of Poisson’s Ratio and Its Influence on the Complex Modulus Determined by Dynamic Mechanical Analysis. Technologies. 2018; 6(3):81. https://doi.org/10.3390/technologies6030081
Chicago/Turabian StyleCarneiro, Vitor H., and Helder Puga. 2018. "Temperature Variability of Poisson’s Ratio and Its Influence on the Complex Modulus Determined by Dynamic Mechanical Analysis" Technologies 6, no. 3: 81. https://doi.org/10.3390/technologies6030081
APA StyleCarneiro, V. H., & Puga, H. (2018). Temperature Variability of Poisson’s Ratio and Its Influence on the Complex Modulus Determined by Dynamic Mechanical Analysis. Technologies, 6(3), 81. https://doi.org/10.3390/technologies6030081






