Gathering and Analyzing Surface Parameters for Diet Identification Purposes

Abstract

Modern surface acquisition devices, such as interferometers and confocal microscopes, make it possible to have accurate three-dimensional (3D) numerical representations of real surfaces. The numerical dental surfaces hold details that are related to the microwear that is caused by food processing. As there are numerous surface parameters that describe surface properties and knowing that a lot more can be built, is it possible to identify the ones that can separate taxa based on their diets? Until now, the candidates were chosen from among those provided by metrology software, which often implements International Organization for Standardization (ISO) parameters. Moreover, the way that a parameter is declared as diet-discriminative differs from one researcher to another. The aim of the present work is to propose a framework to broaden the investigation of relevant parameters and subsequently a procedure that is based on statistical tests to highlight the best of them. Many parameters were tested in a previous study. Here, some were dropped and others added to the classical ones. The resulting set is doubled while considering two derived surfaces: the initial one minus a second order and an eighth order polynomial. The resulting surfaces are then sampled—256 samples per surface—making it possible to build new derived parameters that are based on statistics. The studied dental surfaces belong to seven sets of three or more groups with known differences in diet. In almost all cases, the statistical procedure succeeds in identifying the most relevant parameters to reflect the group differences. Surprisingly, the widely used Area-scale fractal complexity (Asfc) parameter—despite some improvements—cannot differentiate the groups as accurately. The present work can be used as a standalone procedure, but it can also be seen as a first step towards machine learning where a lot of training data is necessary, thus making the human intervention prohibitive.

1. Introduction

Fundamentally, dental microwear analysis involves gathering as many dental surface details that are related to wear as possible to aid in its characterization. It is a generic expression referring to the study of the patterns on teeth left by the processing of food.

Researchers have long acknowledged this technique as a means of providing information about the diet in the days or weeks prior to death. This way of inferring a diet is widespread and can be qualified as mature. Numerous works have been and are still published on the matter and champion the efficiency of the method in distinguishing some diets from others. In particular, depending on the mechanical properties of the foodstuff, scratches or pits are left on human or other animal teeth, thus making it possible to guess the predominant diet before death. The clearer the signal strength, the more certain the conclusions. For a less abbreviated history of dental microwear analysis, the reader is referred to Ungar et al. [1] (pp. 389–425), in which the authors describe dental microwear analysis from the early thirties up to the beginning of the 2000s. Ungar and DeSantis [2,3] provide more recent conclusions that were collected from works on mammals. As a novel approach to the method of analyzing the dental microwear data is presented here, only some recent works are cited to give a snapshot of the current uses.

Depending on the researcher’s habits, needs, equipment, etc., different ways of dealing with dental microwear analysis can be distinguished. Three kinds of devices are used today to analyze the tooth surfaces: three-dimensional (3D) optical profilers, two-dimensional (2D) Scanning Electron Microscopes (SEM), and 2D low-magnification light microscopes.

Light microscopes involved in stereomicroscopic microwear analysis are used to count the pits and scratches. The scratches are recognized as being characteristic of tough food, like mature grass and pits, are markers of brittle food, like fruit, seeds, some leaves, etc. The relative proportion of pits and scratches is then often used as an indicator of grazing or browsing habits. The efficacy of this method relies heavily on the observer experience, which explains the variability in the results: different operators count surface features differently and may tune the light orientation differently, highlighting more or fewer features on the surface [4,5]. However, this method is still in use and it proves to be efficient [6,7,8,9]. SEM is used less than before because it has been advantageously replaced by 3D optical profilers, such as confocal or interferometer microscopes. The latter are more affordable and easier to use. However, some recent works on dental microwear are based on SEM images, analyzed with the help of an image-processing software [10,11,12].

As for 3D digitized data treatment, Scale Sensitive Fractal Analysis (SSFA) has garnered a lot of interest because it uses a few parameters that correlate strongly to characteristic diets and has been successfully applied in numerous works, for which some of the more recent are references in this study [13,14,15,16,17,18]. Another approach, Surface Texture Analysis (STA), is sometimes used as a complement to SSFA, consists of computing ISO-25178 areal parameters, the extension of classic industrial profile parameters, see [19,20,21].

As pointed out by DeSantis [3], there are between 20 and 30 ISO-25178 parameters. However, SSFA parameters are more closely linked to the diet. STA parameters can prove to be more discriminant in some cases. As for selecting the relevant parameters, the question has been addressed in an industrial context by Najjar et al. [22,23], Bigerelle et al. [24], and Deltombe et al. [25], utilizing a methodology that is based on a bootstrap method. First, Najjar et al. [22] searched for the best correlation between a given surface property and roughness parameters. The correlation strength—the linear regression slope—was then quantified using a bootstrap approach. Then, Najjar et al., Bigerelle et al., and Deltombe et al. [23,24,25] used analysis of variance (ANOVA) to organize roughness parameters according their relevance (F statistics) in discriminating industrial process steps. The bootstrap was used to quantify the F probability density function. The authors proposed a methodology close to the one developed here that aims to address the following issue: among a given set of parameters, what are those which discriminate best between different surface types, without any preconceived opinion? Even if the question is the same, some differences lead to different approaches. Here, the surfaces are not presumed homogeneous, which broadens the parameter set. Hence, intensive calculations are avoided. As a given parameter is naturally supposed to behave as a normal variable among the individuals of the population, the use of a bootstrap approach is not justified. These two considerations, large parameter sets and no mandatory bootstrap, have lead the authors of this study to parametric tests. It is to be noted, though, that the cited works and the present one share similar methods to order the “best parameters” F statistics and p-values.

The first goal of 3D digitized surface analysis should be to determine whether it is better to build a set of parameters that can differentiate between different diet groups, provided that a parameter is not necessarily associated to a particular diet, or whether it is more desirable to work with a small set of parameters, perhaps less efficient, but more understandable. However, the present study does not aim to answer this question, but rather, to extend the existing parameters and test their ability in order to separate different groups. Some groups are easily distinguishable, others less so. The methodology here, based on surface sampling and automated statistical treatments, has previously been successfully tested and compared to Dental Microwear Texture Analysis (DMTA) results by Francisco et al. [26]. The surface sampling relies on a simple observation: some surfaces do not exhibit a given feature across their entire surface. For instance, a diet that is known to scar the enamel may fail to leave scratches on a part of the digitized surface. Regarding the surface feature analysis, the authors have proposed a sequence of statistical treatments to identify the meaningful parameters and leave aside the others. In the final discussion, it has been mentioned that the widely used Asfc parameter has surprisingly lead to moderate results and that it should be reworked. In addition to that point, it has also been concluded that the whole procedure should be applied to other species to confirm or refute its efficiency.

In the present work, the same methodology is followed, but with modifications. The set of discriminative parameters has been refined, as will be described in Section 2.2.

2. Materials and Methods

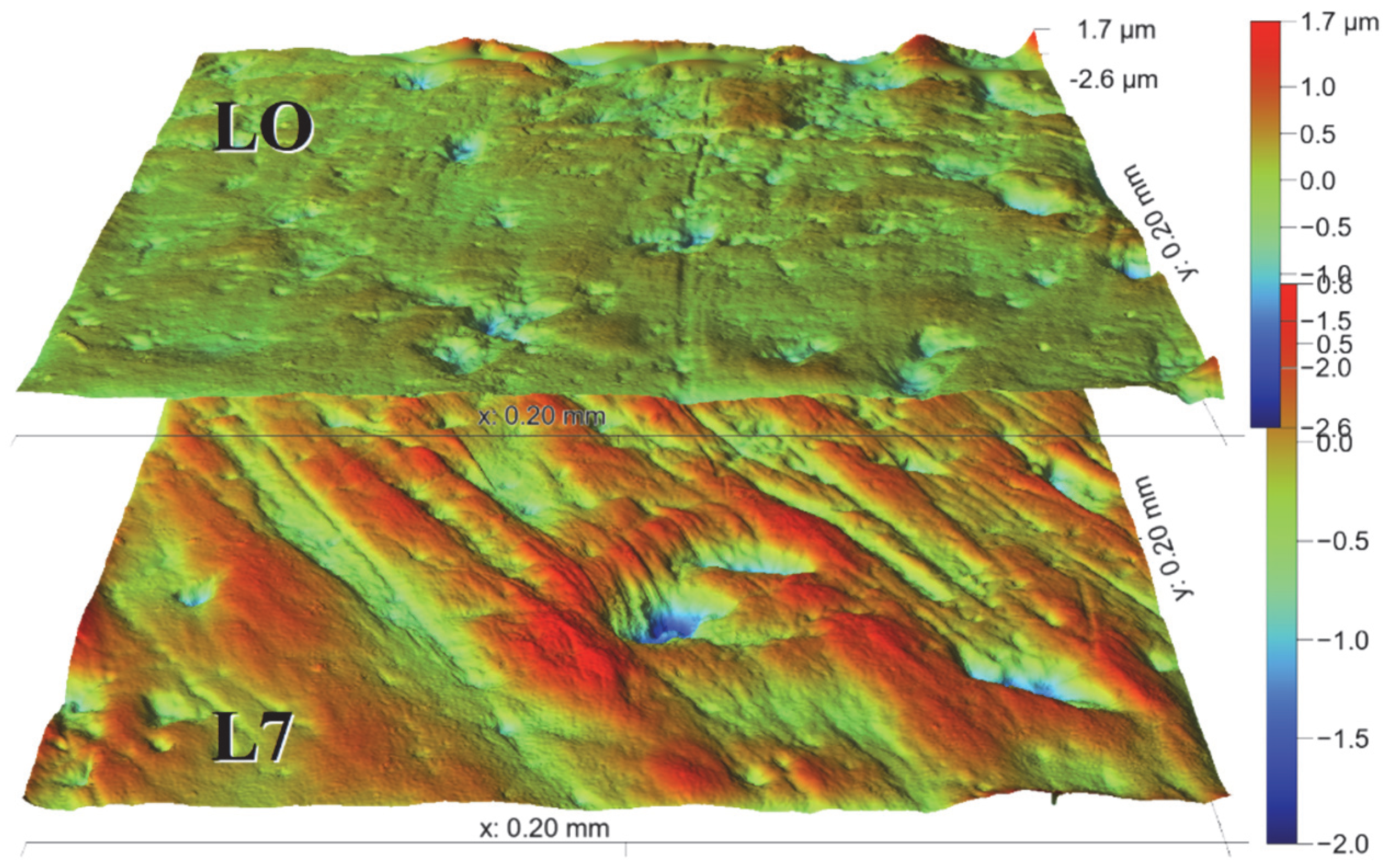
2.1. Material

Here, the reliability of new developments in describing dental microwear textures, as introduced in Francisco et al. [26], is tested. To do so, the choice was made to select six sets composed of modern wild species or samples of domesticated animals fed on different diets, issued by the ANR TRIDENT Project [27,28,29]. The reader will find in the Electronic Supplementary Material (ESM) some illustrations of the different species. It is important to note that we made the set assumptions before we started the simulations. The expectations related to the group separation are based on (from the strongest to the weakest):

• different tooth microwear textures,
• known diet habits of the studied species, and
• the confidence in the procedure reliability.

In the first case, it is a question a procedure validation. Even if it is not guaranteed that the results corroborates the tooth observations—some visual features may not be caught by the parameters—good results are expected. As for the two other cases, there is more uncertainty but the large number of parameters suggests that there should be interesting findings.

2.1.1. Triplet 1 (T1), “Old World Monkeys”

This triplet is composed of three African species of monkeys with divergent dietary habits and habitat preferences: 19 specimens of Cercocebus atys (CE), 19 of Papio hamadryas (PA), and 19 of Colobus polykomos (CO). The first species lives in Central African forest and feeds mostly on hard fruits and seeds [30,31]. The third species also occupies inter-tropical African forest, but differs from Cercocebus atys by being a leaf-eating monkey [32,33]. Papio hamadryas is more plastic in its dietary and habitat preferences. It mostly occupies wooded to open habitats and its diet varies from one season to another [34,35].

Testing hypothesis: leaf eating monkeys such as Colobus polykomos display significant differences in dental microwear textures when compared to seed- and fruit-eating monkeys, such as Cercocebus atys [36]. The wide spectrum of dietary habits for Papio hamadryas suggest a wide range of textures on tooth enamel surfaces overlapping the ecospaces of the two former taxa.

2.1.2. Triplet 2 (T2), “European Ruminants”

The triplet is composed of 20 specimens of Cervus elaphus (CE) from Białowieża, Poland, 20 specimens of Bos taurus (BO) from the Camargue, Rhône delta, France, and 20 specimens of chamois Rupicapra rupicapra (RU) from the Bauges National Park, Alps, France. The Polish cervids are forest dwellers and their microwear textures reflect browsing habits [37]. The semi-wild cattle from the Camargue displays dental microwear textures suggesting a high amount of herbaceous dicots. The chamois is a mountain species with a diet that is composed of dicots and monocots.

Testing hypothesis: to be able to discriminate the browsing red deer from the grazing wild cattle is only to be expected. Here, the question is how best to discriminate the chamois, a mixed feeding species, from the two other dietary categories.

2.1.3. Triplet 3 (T3), “African Ruminants”

The triplet is composed of African species represented by 15 specimens each: the grazing antelope Alcelaphus buselaphus (AB), the browsing Tragelaphus scriptus (TS), and the fruit-eating Cephalophus silvicultor (CS).

Testing hypothesis: simply put, to be able to discriminate between the three dietary categories here is expected.

2.1.4. Quadruplet (Q1), “Cervus”

The set is composed of four populations of red deer (Cervus elaphus) with contrasted habitats and diets. 15 specimens of red deer come from the Scottish highlands. They include high amounts of herbaceous monocots (GR) in their diet. A second 15-individual group comes from the Białowieża National Park, Poland. This group is composed of browsers (BR). Two 15-individual groups of red deer occupying woodland from Central France are representative of mixed feeding species (I1 and I2).

Testing hypothesis: the red deer is known to be plastic in its feeding preferences. The authors hypothesize that its diet and notably the amount of herbaceous monocots that is consumed correlates to the tree cover. The expectation here is that dietary differences can be detected and so too can preferences in habitat.

2.1.5. Triplet 4 (T4), “Three cervids”

This triplet is composed of 15 moose Alces alces (AA) from Bierzba, Poland, 15 roe deer Capreolus capreolus (CC) from the Dourdan forest in France, and 15 red deer Cervus elaphus (CE) from southern Spain. The sample of red deer is known to be one of the larger grazing populations of red deer in Europe. Alces alces mostly browse on leaves, buds, shoots and the bark of bushes, shrubs, and trees. The roe deer (Capreolus capreolus), however, is a selective browser, avoiding ligneous (woody) parts, but including in its diet a lot of forbs and leaves of variable toughness depending on the season.

Testing hypothesis: the challenge is multiple here.

• Although the red deer in southern Spain is highly engaged in grazing and the roe deer from Dourdan in France is a selective browser, many specimens share high anisotropy. The challenge here is to be able to distinguish between the two dietary habits, and thus, to find out which parameters are relevant for that purpose.
• Roe deer and moose are both browsers. However, they differ significantly in the widely used parameter epLsar (exact proportion length–scale anisotropy of relief, an anisotropy marker). The authors of this study hypothesize that it could be linked to the differences in the amount of ligneous material (woody parts), which is greater for the moose. So, the challenge is to be able to unite them and thus differentiate them from the grazing deer (Cervus elaphus).

2.1.6. Quintet (Q2), “Browse, Grass and Dust” (sheep experiment)

This set of five 10-ewe samples is issued from the ANR TRIDENT project (ANR-13-JSV7-0008-01). The first 10-ewe sample (L1) was fed with an assemblage dominated by ray grass. Sheep from samples L5 and L6 were fed with silage dominated by red clover. The ray grass and red clover were both sowed in September 2014 and were mowed in June 2015. Sheep from the samples L7 and L8 were fed with a grass-dominated silage. This multi-specific grass assemblage comes from a 15 year old pasture mowed and grazed by livestock every year. The silage given to samples L6 and L8 were laden daily with 13.2 g/ewe of fine quartz-dominated dust (under 100 µm). This simulates windblown deposits on vegetation in the West African Guinean savannah during the five-month long Harmattan wind season [27].

Testing hypothesis: herbaceous monocots, including grasses, are richer in biosilica phytoliths than herbaceous dicots, such as the red clover. These plants also differ in inner structure and thus on mechanical properties. Furthermore, fresh grasses are less likely to scar enamel than mature grasses from old pastures [38]. Exogenous particles are also responsible for the loss of dental tissue. The differences in dietary bolus will probably generate significant differences between these samples.

2.1.7. Triplet 5 (T5), “Seeds, Browse, and Grass” (Sheep Experiment)

This set of three 10-ewe samples is issued from the ANR TRIDENT project (ANR-13-JSV7-0008-01). The first 10-ewe sample, L5 was fed with a red clover-dominated silage. Sheep from sample L7 were fed with a grass-dominated silage. A final 10-ewe sample, LO, was fed with a red clover-dominated silage supplemented by 25% of barley kernels.

Testing hypothesis: herbaceous monocots including grasses are richer in biosilica phytoliths than herbaceous dicots, such as the red clover. Barley kernels are hard and brittle and their shells are rich in silica. The differences in dietary bolus, and notably the presence of seeds, should generate significant differences between these samples.

2.2. Methods

The primary extracted surfaces are obtained, as follows. First, the tooth surface is cleaned of any foreign items and a silicon polyvinylsiloxane elastomer is utilized to mold the surface (Regular Body President, ref. 6015—ISO 4823, medium consistency, polyvinylsiloxane addition type; Coltene Whaledent). Finally, the mold surface is digitized with a confocal, white light profilometer (Leica Microsystem DCM8; 100 × magnification lens, Numerical Aperture = 0.9; Working Distance = 0.9 mm, Lateral Resolution up to 140 nm, Vertical Resolution up to 2 nm).

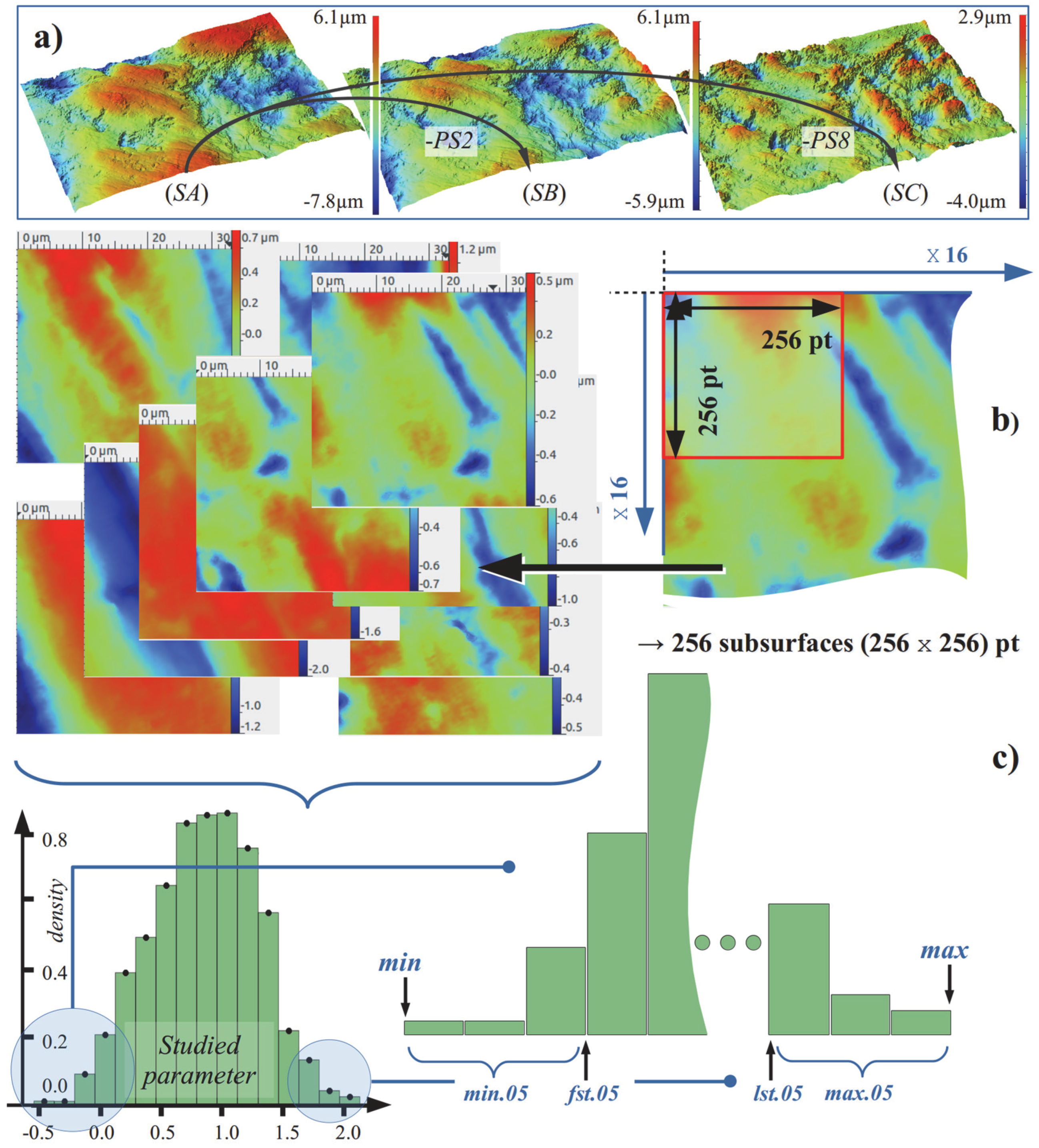
2.2.1. Surface Treatment and Sampling

Following the procedure that is defined by Francisco et al. [26], the primary extracted surface S1 is first numerically cleaned of any abnormal peaks. The resulting surface is called SA. Then, Figure 1a, considering the tooth surface geometry as a second order polynomial (PS2), the latter is subtracted via a least square approximation, yielding the surface SB. PS2 could be deemed sufficient due to the small area measured (0.2 mm), as dental facets are concave or convex with a single preferred axis. However, in order to enhance the finest scale roughness, the same operation is applied to SA with an eighth order polynomial (PS8), which creates SC. It must be noted that the order of the polynomial applies to each direction, and it must not be confused with the maximum polynomial order as proposed by some software.

The authors of this study have investigated all of the orders, from one to nine, for a wide range of surfaces and the analysis revealed no clear advantage in using a second order polynomial rather than a third order for SB. The same goes for SC, a ninth or seventh order polynomial is sometimes better. Therefore, the authors chose to keep the two orders, two and eight. Working on SC is possibly sufficient because it makes the roughness clearer, however an eighth order polynomial can erase wavy features from SA, which is a loss of information.

Following the SSFA parameters HAsfc(n²) (Asfc heterogeneity through n² cells), as proposed by Scott et al. [39], the heterogeneity of a surface is related to the spatial distribution of its features: a single hole implies more heterogeneity than several holes that are uniformly scattered across the surface. To be sure to center a particular feature (pit, peak, etc.) on a sample, the simplest way is to have enough samples uniformly distributed over the surface, Figure 1b. 1024 samples were used in the previous study [26], but further simulations have yielded similar results with just 256 samples. This makes the whole computational process much faster. Similarly, 256 × 256 px rather than 512 × 512 pt proved to be generally sufficient. The term “generally” is important here because the surface signals are sometimes enhanced and sometimes softened. For instance, with the previous surface set, the results are slightly less good in the configuration of 256 samples of 256 × 256 px than the configuration of 1024 samples of 512 × 512 px. But, while taking into account the computing time and the fact that the results are better for other surface sets, it seems reasonable to switch to 256 samples of 256 × 256 px.

Both minimum and maximum surface heterogeneity are determined (prefixes min_ and max_, Figure 1c). The standard deviation of the parameter distribution is also determined (std_ prefix). The “central” values, or mean and median, being an entire surface signature, are also determined (mean_ and med_ prefixes).

In order to be more robust when defining the extrema of the parameter distribution, the quantile 5% is used. fst.05_ refers to the 5% quantile and lst.05_ to the 95% quantile. However, the robustness must not hide extreme values that might not be outliers. That is why min.05_ and max.05_ are introduced. They are the mean of the values below (and respectively above) the quantile 5% (and 95%, respectively), Figure 1c. As a trade-off between 5% and 50%, the quantile 25% is also used: fst.25_ stands for the first quartile and lst.25_ stands for the last quartile. In the same way as before, min.25_ and max.25_ are also used. In the eventuality that the parameter distribution shape could be the signature of a particular diet, the skewness and kurtosis (skw_ and kurt_ respectively) are also calculated.

To conclude on the statistics that are deduced from the 256 samples of a given surface, each parameter generates 15 “sub-parameters”. It is obvious that some of them are strongly correlated, but it does not affect the process of finding those that are the most discriminative.

2.2.2. Height Parameters

As the height parameters are very common,

Table 1. Height parameters (* ISO 25178).

Parameter	Significance
Sa	Arithmetic mean of the absolute of the heights (*)
Sp	Absolute of the largest height (*)
Sq	Height standard deviation (*)
Sv	Absolute of the smallest height (*)
Ssk	Height skewness (*)
Sku	Height kurtosis (*)
Sdar	Relative area (developed area/projected area)
Sm	Mean height (0 for the whole surface, but non-zero for its samples)
Smd	Median height

simply recalls the standard parameters related to the surface heights.

2.2.3. Spatial Parameters

There are at least two ways to determine surface anisotropy.

The first one, which belongs to the SSFA toolbox is the so-called epLsar_1.8µm parameter [39]. In a given direction, uniformly discretized usually with a 1.8 µm step, the relative length of the profile is calculated. With 36 measurements, every 5°, a rosette diagram is formed and, after normalization, the eccentricity gives the resulting epLsar_1.8µm. The most interesting information provided by the rosette comes in the form of the multiple orientations that it can detect, when, for instance, there are scratches with different angles. For computational efficiency reasons, epLsar_1.8µm is not used to detect and quantify anisotropy.

Another approach is based on the autocorrelation function, f_ACF. f_ACF is the normalized product of the surface heights by the heights of the same surface shifted by the quantity (tx, ty). Therefore, at the origin (tx = 0, ty = 0), the function is maximal. It then decreases as the distance increases. The directions along which the surface heights resemble white noise exhibit low f_ACF values. Conversely, if a periodic pattern exists, f_ACF exhibits local maxima. Generally, when the roughness is oriented, the f_ACF decreases faster perpendicularly to the orientation. At a given height z, a horizontal plane intersects f_ACF (x,y) after a curve close to an ellipsis; the anisotropy is more pronounced for stretched ellipses. Three parameters are hence defined: Rmax the major ellipsis radius, Sal the minor ellipsis radius, and Str⁻¹ the ratio Rmax/Sal. An illustration is provided in ESM, Figure S1.

A complementary and original way of determining anisotropy is the f_ACF slope study. The f_ACF decrease in speed from (0,0) is related to its slope. The distance from the origin where the maximum slope is measured is recorded for each degree of angle. The minimum r_s of the recorded distances defines a circle on which the slopes are calculated for each degree. The minimum of the f_ACF slopes is named s.sl and the maximum of the f_ACF slopes b.sl. The anisotropy is characterized by the ratio r.sl = b.sl/s.sl. The reader is referred to ESM Figure S2 for an illustration on the f_ACF analysis and a recap of the spatial parameters is presented in

Table 2. Spatial parameters. (* ISO 25178).

Parameter	Significance
Rmax	Semi-major axis of the fACF ellipsis
Sal	Semi-minor axis of the fACF ellipsis (*)
Std	Texture direction (*)
Stri = Str−1	Rmax/Sal ratio (*)
b.sl	Highest slope of fACF at the distance rs from the origin
r.sl	b.sl/s.sl ratio
s.sl	Smallest slope of fACF at the distance rs from the origin

.

2.2.4. Topological Parameters

Parameters that have both spatial and height attributes are deemed to fall into this class. The main idea is to mask the heights that exceed a given value, then to count and measure the so-constituted cells.

The very first operation is to discard the smallest 15% of the heights, essentially pits. Sz, the height amplitude, becomes Sz’. Then, the heights that are above h₁ = 85% Sz’ or h₂ = 95% Sz’ are masked. h₁ and h₂ are defined based on experience. As tiny cells may appear, basic morphological operations are applied to the mask: first, five one-pixel-erosions, and then five one-pixel-dilatations. As a result, very small areas disappear while bigger areas are preserved. Three parameters are generated for each threshold h₁ and h2: Snb1 and Snb2, the number of cells, Smc1 and Smc2, the median relative size of the cells and Sk1 and Sk2, the relative area masked. The ESM Figure S3 provides additional information on the topological parameters and

Table 3. Topological parameters.

Parameter	Significance
Sk1, Sk2	Relative area of the surface above h1 and h2 respectively
Smc1, Smc2	Median relative area of the cells with heights exceeding h1 and h2 respectively
Snb1, Snb2	Number of cells with heights exceeding h1 and h2 respectively
Sh	Percentage of quasi-horizontal faces (normal within a 4° cone)

summarizes them.

2.2.5. Fractal Methods, Relative Area Analysis

In previous work [26], the authors of this study concluded that the Asfc parameter should be further investigated because of its ability to identify complex surfaces. Indeed, Asfc was no better than other parameters at separating the fruit-browsing group from the leaf-browsing or grazing group. From this, stems the hypothesis that the way that the steepest slope was determined could lack in robustness. In addition, using sampling approaches requires that the Asfc determination be faster. These points are addressed in the ESM in order to avoid too much technical detail in the paper itself. As a result of the study, an efficient procedure for the determination of Asfc is proposed along with the sampling characteristics: 256 samples of 512 × 512 px subsurfaces.

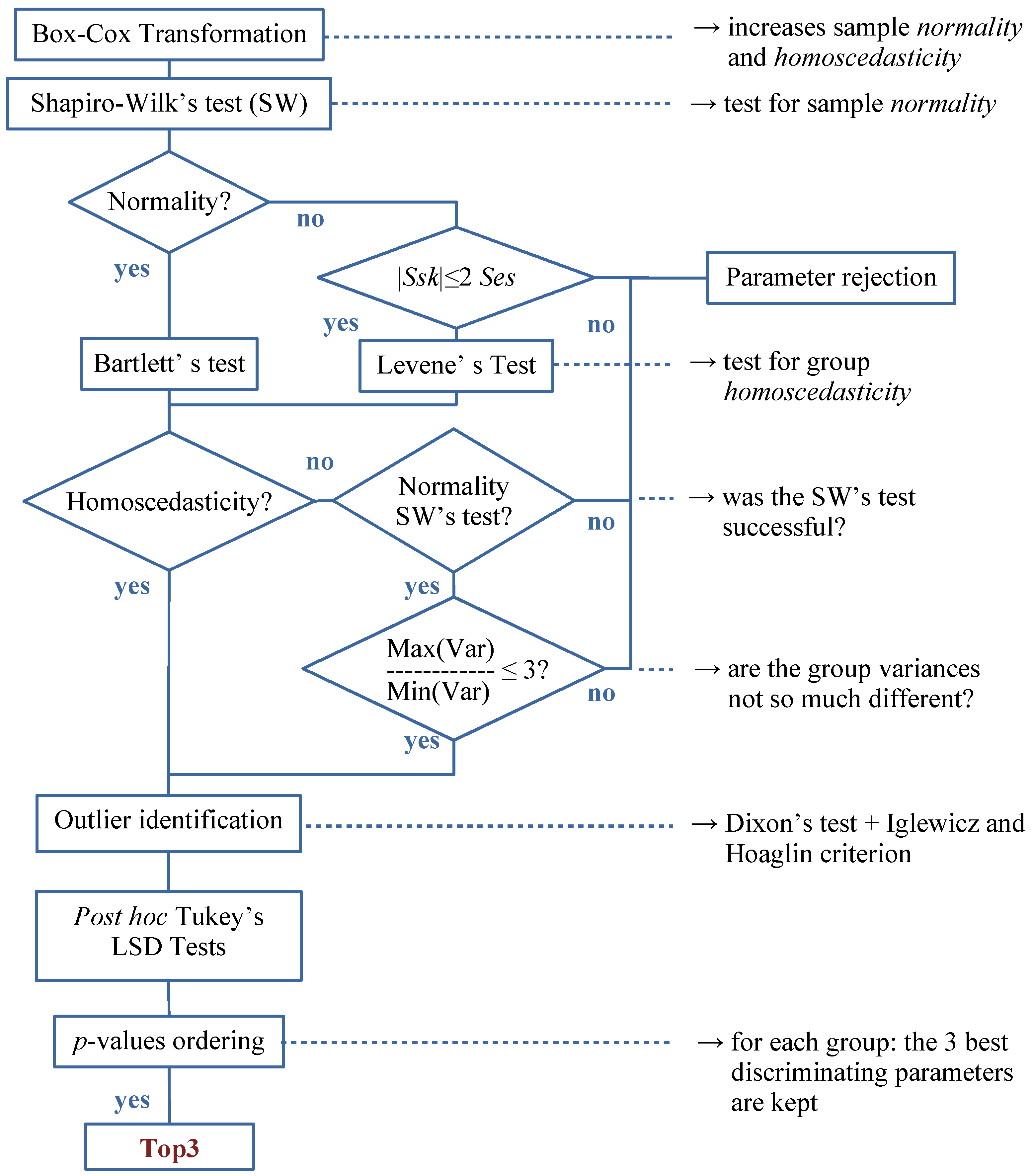
2.2.6. The Automatic Discriminative Procedure

The procedure proposed by Francisco et al. [26], in its simplified form, is recalled in Figure 2.

A Fortran program loads the surfaces and performs all of the treatments: cleaning, polynomial subtractions, sampling, and parameter calculations. The resulting files are brought together with a Python program and the statistics are calculated from the sampling results. A synthetic array is built in a .csv file that an R program analyzes, following the synopsis provided. Fortran is chosen for its execution speed, Python for its convenience in dealing with files and text processing, and R for its suitability for statistical analysis.

A short reminder of the different steps is as follows. As no human intervention is desired until the end of the process, the whole treatment is based on statistical tests. Almost all tests are built on assumptions that must be fulfilled to trust the results. In particular, parametric tests require normality and homoscedasticity properties. To maximize the chance of being eligible for the tests, the parameters are Box-Cox transformed instead of systematically log-transformed. What differs from the norm is the presence of retrieval steps: when tests reject a parameter, that parameter can be called into question regarding the tests that follow. Rules of thumb, based on expert experience, are introduced to soften test rigidity. Once the parameters are declared to be test-compliant, questions arise about post hoc analyses and the necessity of a preceding ANOVA test. However, based on the previous work by the authors of this study, a post hoc analysis is carried out directly. Because Fisher’s Least Significant Difference (LSD) test is less conservative than Tuckey’s Honest Significant Difference (HSD) version, the former is preferred.

The choice of parametric tests is justified in Francisco et al. [26], and is recapped hereafter. Based on experience, the parametric tests are quiet robust to non-normality. Moreover, non-parametric tests, such as Kruskal-Wallis’, sometimes reveal to be less robust against heteroscedasticity. It is nonetheless to be acknowledged that, for very small samples, non parametric tests are better suited. But where is the frontier between ‘small’ and ‘very small’? We suppose here that 10 individuals is indeed a small sample but still acceptable for parametric tests. To conclude on this point, the methodology that is proposed here ends with a graphical representation of the sets, which limits erroneous conclusions.

Another debate is about the p-value meaning and how best to draw conclusions about it. Once again, the choice is made from experience: until now, the lowest p-values have provided the most discriminating parameters. Therefore, the Top3 parameters will be selected based upon their p-value. In most cases treated below, three parameters appear to be enough to choose two low-correlated parameters for a biplot. The procedure aims to assist the researcher in finding the most discriminating parameters rather than be a substitute for him. Therefore, if the three proposed parameters are too greatly correlated, the next parameters in the p-value ordered list should be considered.

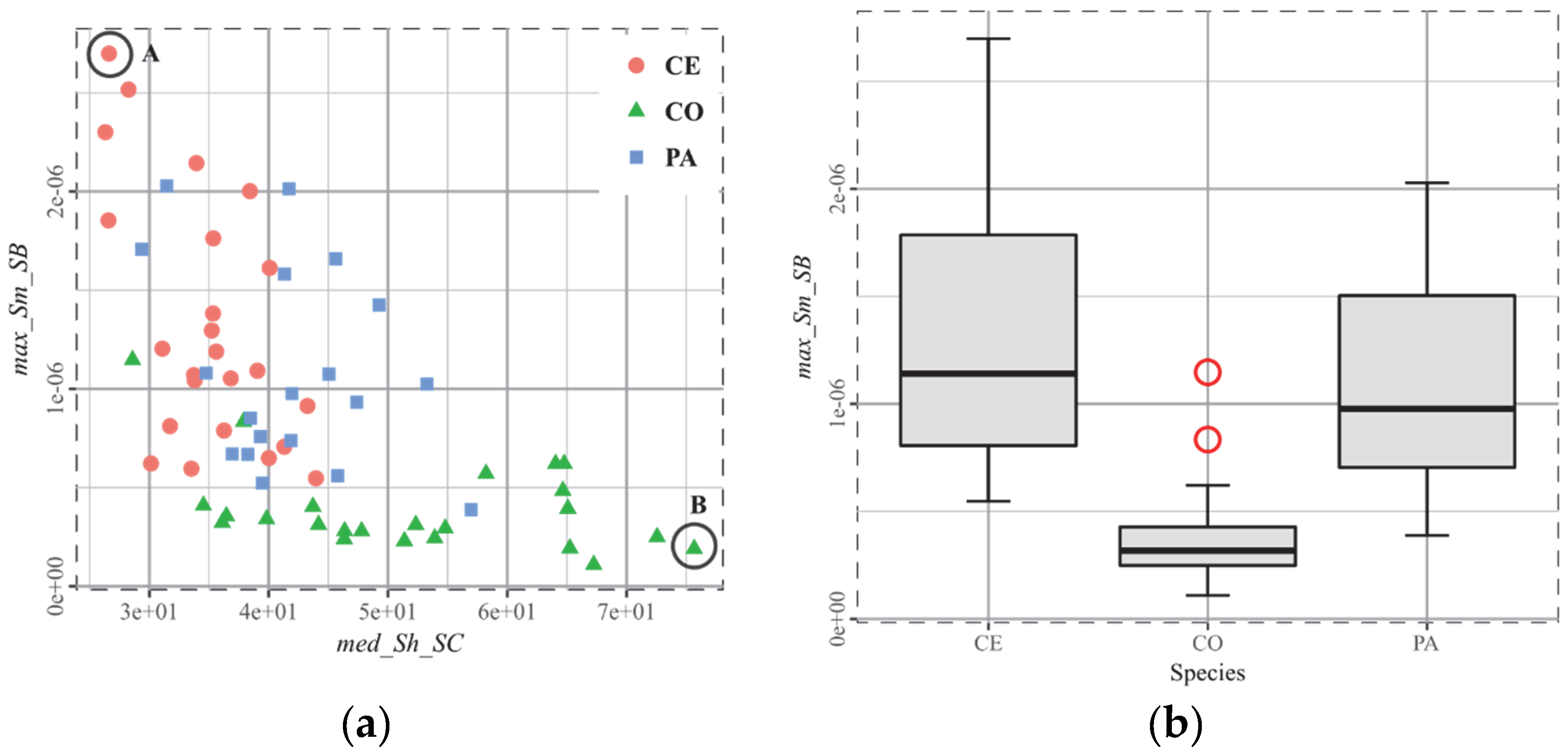
3. Results

The graphs present back-transformed data. Indeed, to increase the eligibility for F-tests, the parameters are all Box-Cox transformed. However, once the parameter selection has ended, there is no need to keep the transformation. When points are circled and labeled with a letter on the graphs, the reader is referred to the ESM to see the corresponding surface.

3.1. T1, Old World Monkeys

Sm is the mean height of a surface. max_Sm_SB is the maximum mean height value among all subsurfaces. The results of Figure 3 suggest that CO (Colobus polykomos) subsurfaces have less elevation than CE (Cercocebus atys) subsurfaces, which exhibit more relief. In addition, flatness (med_Sh_SC) occurs more often on CO subsurfaces. These results are quite consistent with the fact that leaf-eating is a smooth wear process that flattens the surfaces, whereas hard fruit-eating leads to greater wear.

As concerns PA (Papio hamadryas), it can be proposed on the basis of the preceding conclusions that the signal induced by hard item-eating is greater. This is because not enough is erased by smooth food wear, regardless of whether the species mostly feeds on it or it is a recent signal. It was expected that an anisotropy axis would leave CO on low value locations, which discriminates it from CE, but the anisotropy parameters are superseded by Sh, which is the flatness indicator.

3.2. T2, European Ruminants

As expected, an anisotropy parameter is the best choice to separate the grazing species BO (Bos taurus) and the browsing species CE (Cervus elaphus), Figure 4. The most discriminative parameter is fst.05_Stri_SB with p-value = 2.30 × 10⁻¹⁶. As a reminder, the greater Stri, the bigger the difference between the small and large axes of the f_ACF ellipsis and the higher the texture anisotropy. Low values of fst.05_Stri_SB (CE) mean that 5% of the 256 surface samples (almost 13) are very low (around 1). In other words, there is a significant area with no scratch (about 40 × 40 µm²).

The parameter that helps in separating the mixed habit species RU (Rupicapra rupicapra) from the others is Sk1, which measures the surface above 85% Sz’. It may suggest that significant wear has created relief on the tooth surface, and that softer wear has occurred, decreasing in this way the peak heights. Conversely, it could also be that little wear has occurred on the tooth.

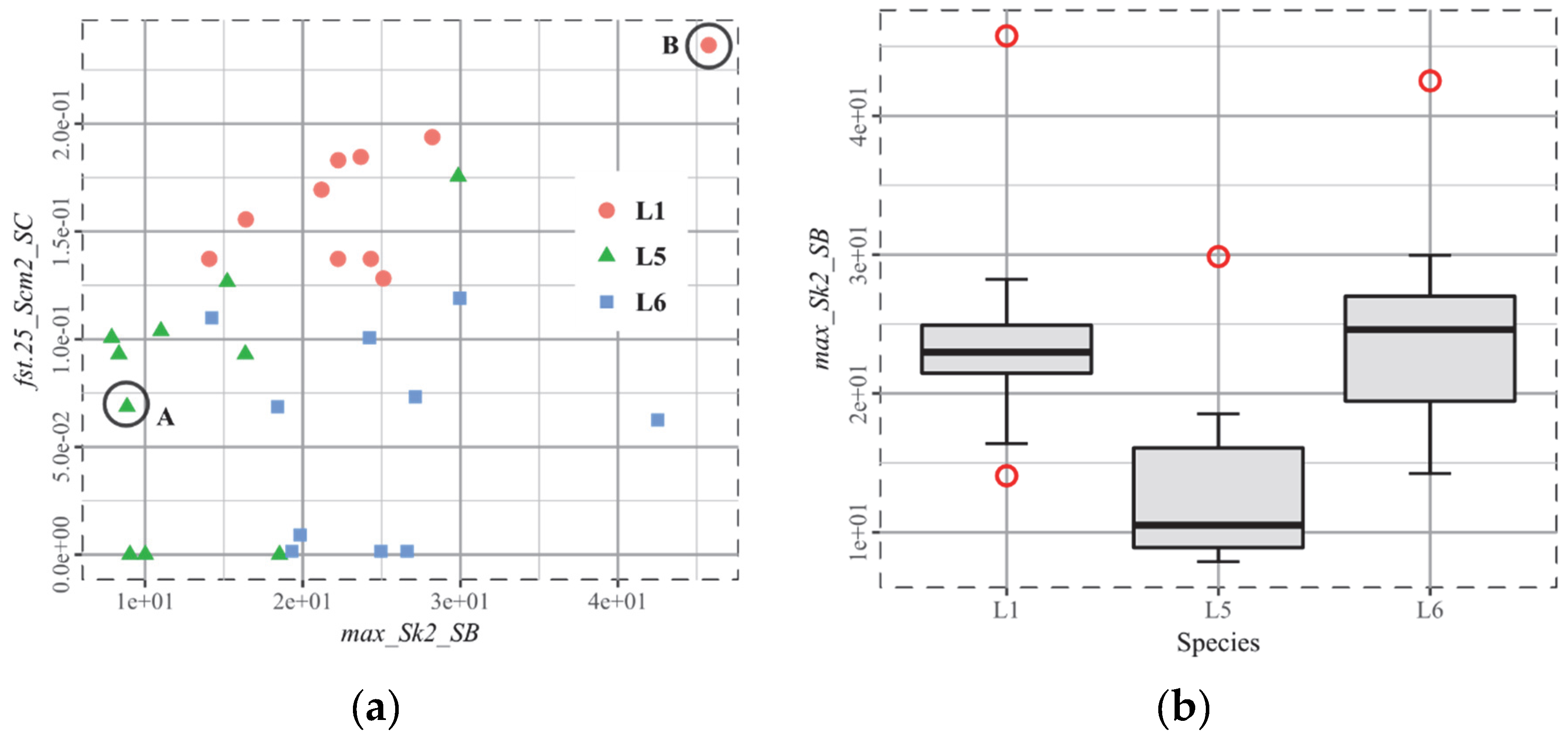
3.3. T3, African Ruminants

Once again, the anisotropy parameters are good candidates to separate the browsing TS (Tragelaphus scriptus) and the fruit-eating CS (Cephalophus silvicultor) from the grazing AB (Alcelaphus buselaphus) species, Figure 5. It is nonetheless important to note that another discriminative parameter is the kurtosis Sku, as also found by Francisco et al. [26], with an even better p-value (3.71 × 10⁻⁷). However, it separates less clearly AB and CS (p-value = 4.10 × 10⁻³ vs. 1.27 × 10⁻⁶ for r.sl, the f_acf slope ratio).

TS and CS are harder to discriminate: the related p-value is 3.83 × 10⁻⁴ for med_Ssk_SC. As there are 15 individuals per category, it can be assumed that the separation is statistically meaningful.

3.4. Q1, Cervus

Surprisingly, the best parameter for separating the browsing red deer from the grazing red deer species belongs to the topological class: Sk1, p-value = 5.13 × 10⁻⁶, Figure 6. However, a good compromise is r.sl, an anisotropy indicator, with the associated p-values BR-GR 3.74 × 10⁻⁴ and GR-I1 1.55 × 10⁻³. When both are used in a biplot graph, the separation is quite satisfactory. The results are to be read, as follows: when sampling a surface, the mean of the 25% highest values of r.sl is smaller for the browsing group (BR) than for the grazing group (GR). More concisely, GR surfaces have larger areas of marked scratches. As for min.25_Sk1_SC, it shows that the mean of the 25% lowest values of Sk1, the relative area above 85% of the threshold height amplitude is statistically greater for GR than for BR. GR surfaces exhibit fewer low areas.

When considering now the intermediate category I2 instead of I1 roughly leads to the same situation, Figure 7.

A question subsequently arises: is it possible to statistically distinguish I1 from I2? As shown in Figure 8, the pair of parameters (std_r.sl_SB, std_Snb1_SC) achieves this objective, with p-values 6.65 × 10⁻⁴ and 1.78 × 10⁻⁵, respectively. It seems that what best discriminates between the two categories is the surface heterogeneity. The statistic “std_” stands for the standard deviation of a given parameter computed on the 256 subsurfaces. Therefore, std_r.sl_SB quantifies variations of anisotropy on a surface and std_Snb1_SC quantifies variations of elevated cells, Figure 9.

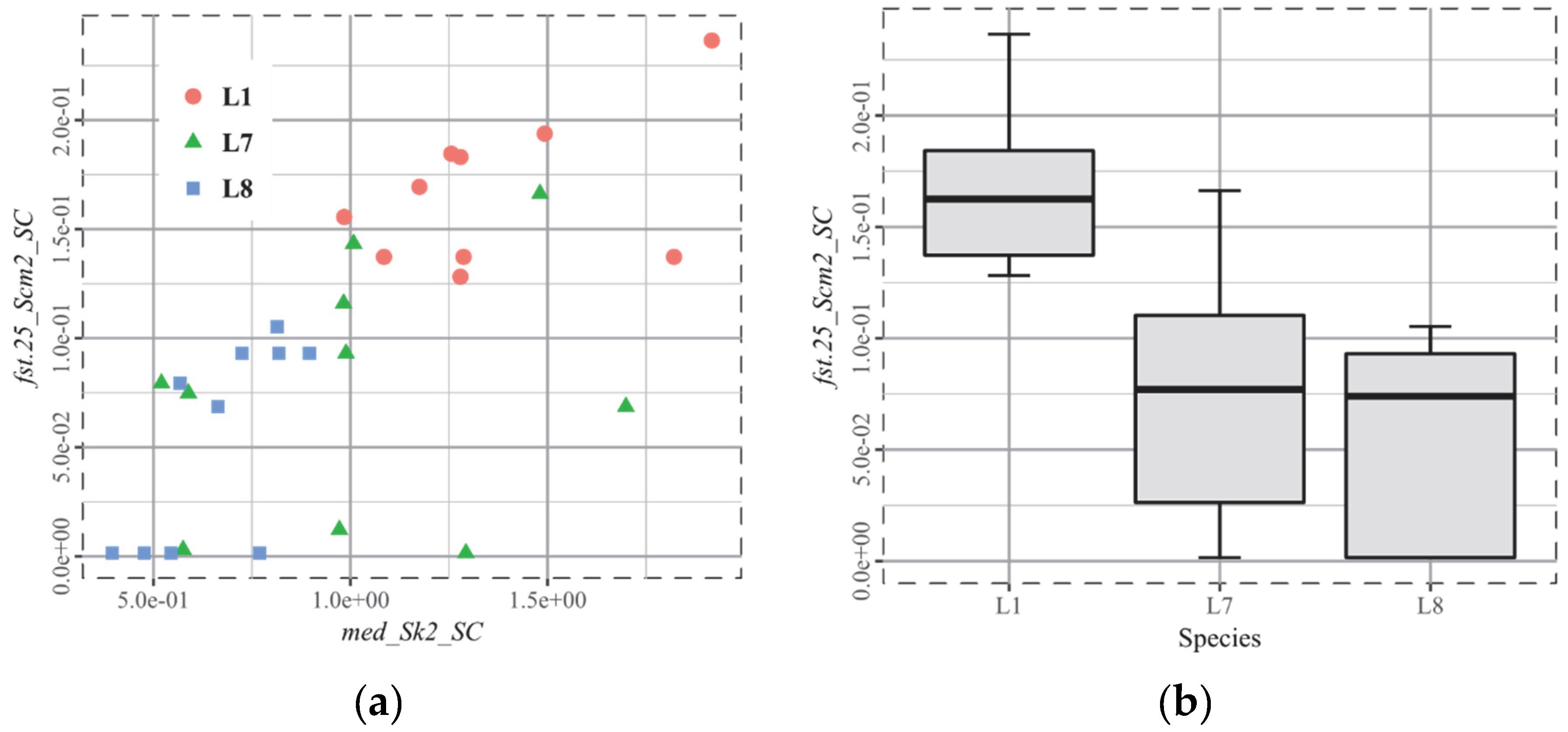
3.5. T4, Cervids

Capreolus capreolus CC and Cervus elaphus CE species are known to statistically share a high anisotropy, whereas Alces alces AA surfaces are expected to be more isotropic. It is clearly confirmed by the r.sl parameter med_r.sl_SC, Figure 10, for which the p-values of CC-AA and CE-AA are 4.56 × 10⁻⁸ and 1.52 × 10⁻⁸, respectively. The second challenge was to separate AA and CC from CE (the most prolific grazer). The separation is effective with max_Ssk_SB, for which the p-values of CE-AA and CE-CC are 7.86 × 10⁻⁵ and 2.68 × 10⁻³, respectively. In addition, CC and CE were not supposed to be statistically different from an anisotropy viewpoint. This is now confirmed.

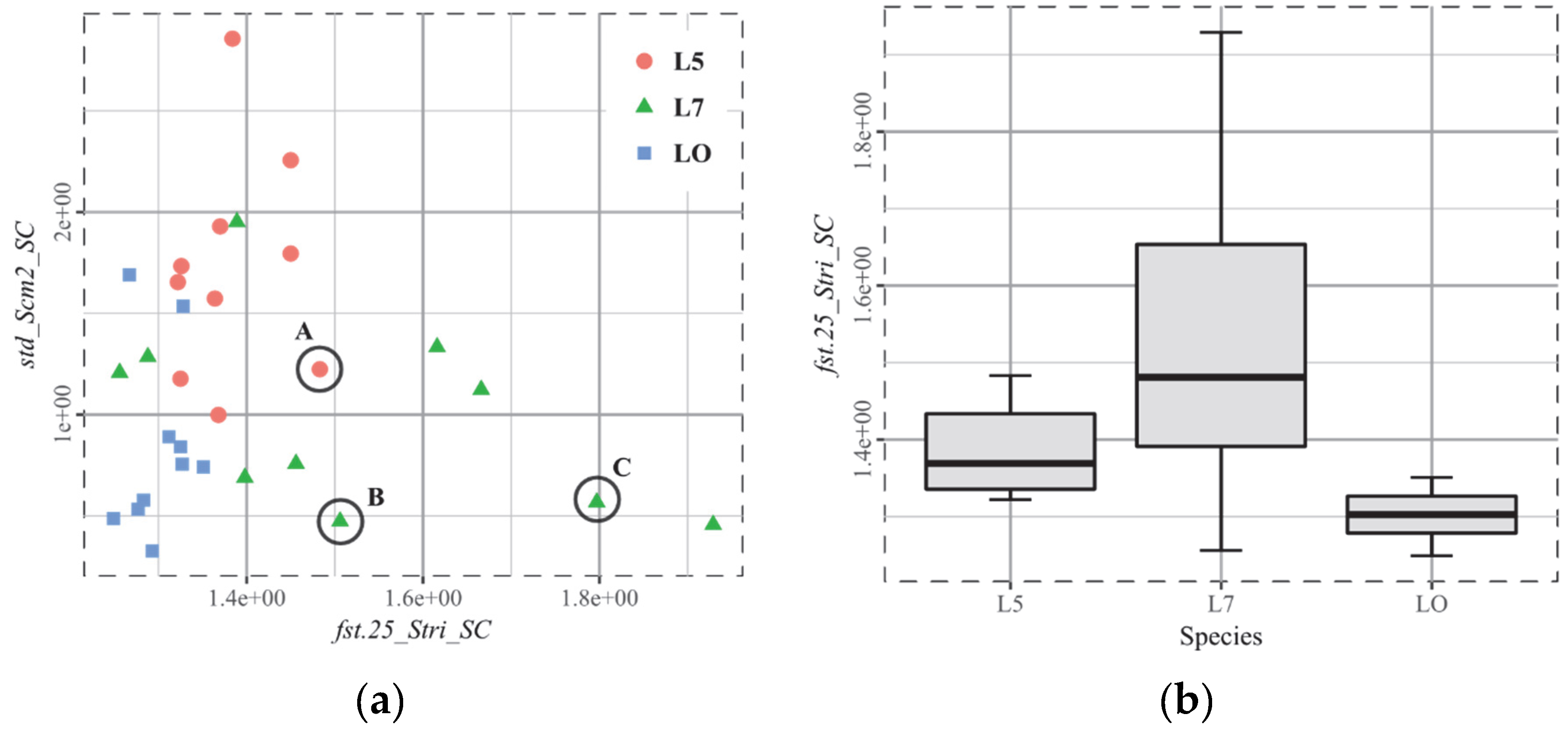
3.6. Q2, Browse, Grass and Dust (Sheep Experiment)

The tiny differences between groups and the small group sizes (10 individuals per group) undoubtedly pose the most challenging task. Contrary to expectations, no clear anisotropy difference is found between the categories L1, L5, and L7. Perhaps a weak signal can distinguish L5 from L7, but as will be seen, the conclusions have to remain moderate.

The set of parameters that seems to be discriminative is Sk, the relative area of the surface above a given height, Figure 11. However, the usual threshold 85% proved to be unsuitable in the present case (no distinction between groups). It explains the presence of the other set of Snb, Smc, and Sk (threshold 95%) numbered “2”, which better discriminates the groups. Despite a clear visual separation, the classification cannot be described as “robust” because of the low number of individuals per group. However, the results can still be trusted, as suggested by the p-values of max_Sk2_SB for L5-L6 (3.02 × 10⁻⁴) and fst.25_Scm2_SC for L1-L6 (1.07 × 10⁻⁵).

If there were more individuals in each group, it could be directly concluded that Scm2 is able to differentiate ray grass (L1) and red clover diets (L5, L6), and that Sk2 is able to identify the presence of dust (L6). Furthermore, higher values of fst.25_Scm2_SC for L1 reflect the fact that the cells marked (subsurface heights above 95% Sz’) are larger than L5 and L6 cells (p-value L1–L5: 1.61 × 10⁻⁴). Once again, with larger groups, it could be said that the ray grass (L1) induces homogeneous and greater wear than the red clover (L5, L6), for which the surfaces seem not to have been abraded, see ESM. With the same precautions, due to the size of the groups, there is a greater area above 95% Sz’ for L6 than for L5.The fact that max_Sk2_SB is greater for L6 may reflect more wear as induced by the dust (wider “polished” areas, see ESM).

However, given the small groups, this should remain a line of thought. The quantile plot seems to exhibit too many outliers, but it must be noted that there are few individuals per group, and the parameters are back-transformed. The Box-Cox transformation significantly reduces the sparsity of the data, which makes its distribution nearly normal and homoscedastic.

As it appears on Figure 12, fst.25_Scm2_SC remains a good discriminative parameter for L1 and (L7, L8) with p-values 1.27 × 10⁻⁴ and 7.46 × 10⁻⁶, respectively. Sk2 is still effective for separating groups, but it is used here with a different statistic “med”, which means that the median relative area above 95% Sz’ is higher for L1. No further explanation that is related to diet can be given about a hypothetical difference between L7 and L8 as the difference is visually too slight, which is confirmed by a p-value 1.10 × 10⁻². It is as if the mature grass is too abrasive to allow for the detection of dust scars on the tooth surface.

The lowest p-value when considering L5–L7 is obtained with max.05_r.sl_SC (6.14 × 10⁻³). If a true difference exists, it indicates that L7 statistically exhibits higher anisotropy than L5 and it would be correlated with the L5 and L7 diets: red clover and mature grass, respectively. However this cannot be stated with any degree of certainty.

3.7. T5, Seeds, Browse, and Grass (Sheep Experiment)

Figure 13 highlights why separating L5 (red clover) and L7 (mature grass) is so difficult: despite the ability of Stri to identify anisotropic surfaces, the signals overlap (p-value 1.92 × 10⁻¹). It means that the mature grass scars some individuals more than others within the L7 group, whereas the L5 surfaces exhibit approximately the same levels of anisotropy. Here, it can only be said for certain that the mature grass scatters the anisotropy values.

Adding barley kernels to red clover was expected to increase isotropy, which is confirmed by fst.25_Stri_SC p-values: 4.02 × 10⁻⁴ for LO-L7, L7 being the most anisotropic because of its richer silica grass. Figure 14 illustrates the surface aspects of LO and L7 individuals, which visually corroborates the presence of anisotropy on L7.

4. Discussion

4.1. Untangling the Jungle of Parameters

It is impossible to isolate a small set of universal parameters from within the 700+ derived parameter set. However, a given parameter can be evaluated if all of its derivatives are aggregated, then for each group set, seven in the present work, the minimum of its p-values is picked, and the mean is calculated. The results are presented in

Table 4. Mean p-value of the parameters for all group sets.

Sku	Sk1	Scm1	Sk2	Smd	Std
1.47 × 10−4	2.65 × 10−4	4.04 × 10−4	5.13 × 10−4	6.79 × 10−4	7.75 × 10−4
Ssk	r.sl	Scm2	Snb2	Sh	Rmax
1.06 × 10−3	1.07 × 10−3	1.17 × 10−3	1.21 × 10−3	1.35 × 10−3	2.06 × 10−3
Stri	Sv	Sdar	Asfc	Snb1	Sp
2.25 × 10−3	2.44 × 10−3	3.16 × 10−3	3.50 × 10−3	3.86 × 10−3	5.13 × 10−3
Sa	Sal	Sm	Sq	s.sl	b.sl
6.70 × 10−3	7.96 × 10−3	8.62 × 10−3	8.67 × 10−3	4.91 × 10−2	1.31 × 10−1

:

Given the above approximation about the efficiency of a parameter, some trends can be distinguished. In the “height class”, Sku, Ssk, and Smd are good candidates; in the “spatial class”, Std, r.sl and Stri should be kept; in the “topological class”, there should be just one threshold, maybe between 85% and 95%, to keep Sk(i), Scm(i), and Snb(i). The authors of the present study think that, despite the fact that Asfc has never been at the top of the best parameters, it potentially represents a relevant parameter: either the surface should be cleaned differently, or a different parameter, more related to curvature, should be investigated.

From experience, the expert eye sometimes succeeds in visually distinguishing groups where the above parameters cannot. Hence, as for SEM gray level pictures, parameters from image processing are worth adding. After numerical treatments, like gradient, smoothing, equalizing, and binarization, some parameters can be associated to features that allow for expert software to link them to a particular diet.

4.2. The Derived Parameters Outclass the Whole-Surface Parameters

SB, SC, and the sampling procedure are confirmed to be signal enhancers.

• Subtracting a second order polynomial does not alter the wear information: the geometry removed is not related to microwear. Things are different for an eighth order polynomial that can remove microwear patterns, but it also brings out details that are hidden in longer wavelength reliefs.
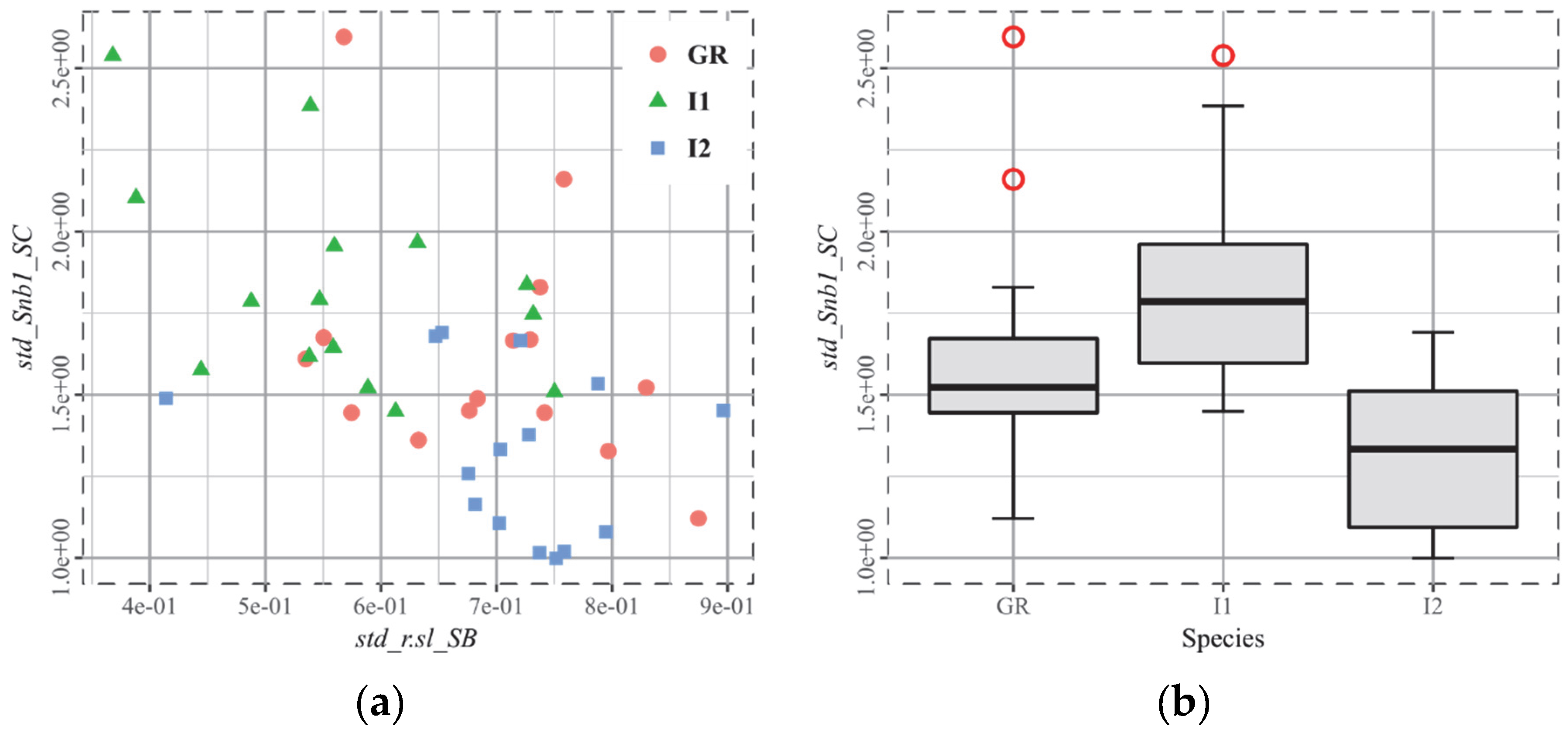
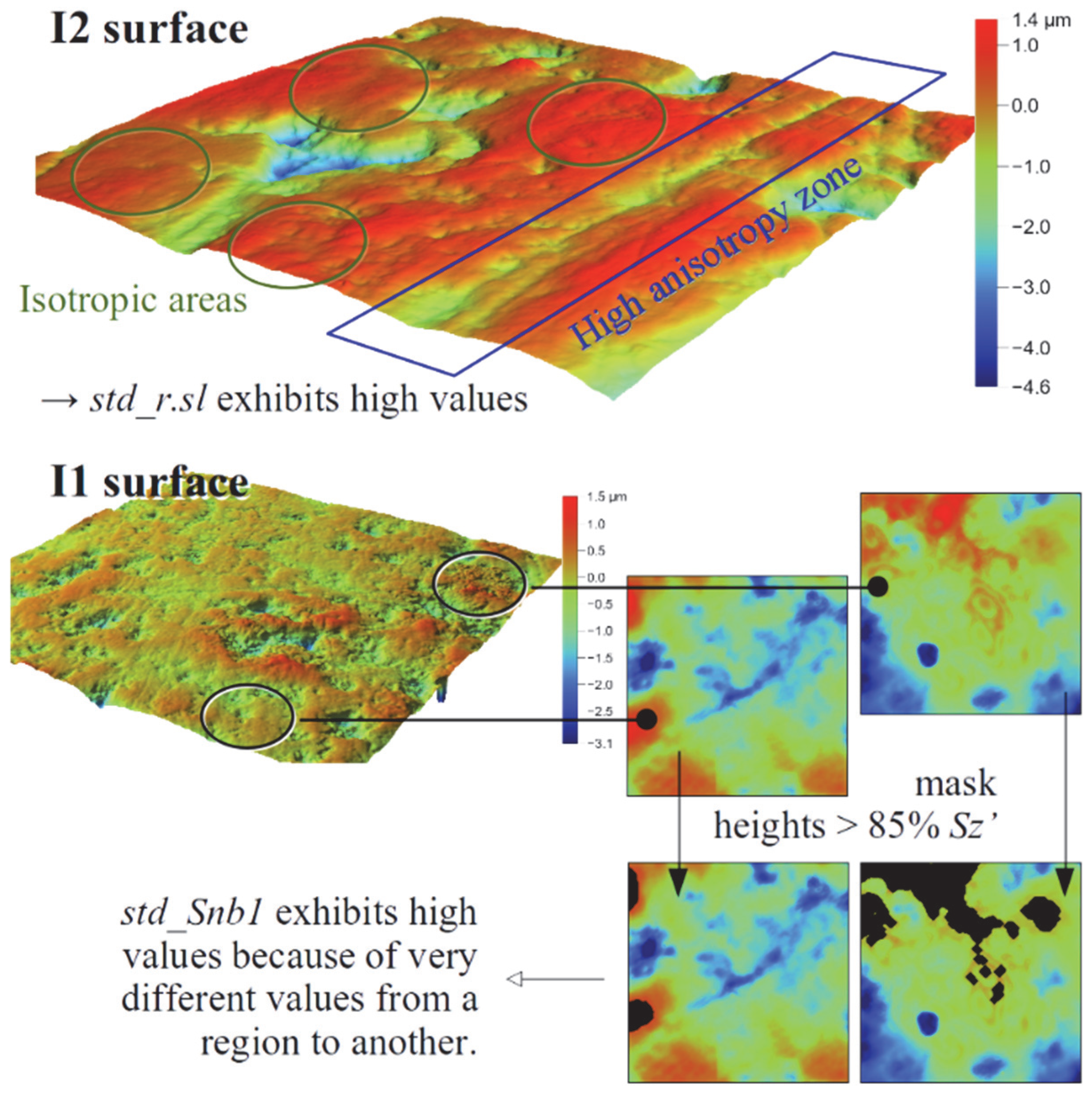
• When a given parameter, Stri, for instance, applied to the whole surface hardly separates two groups, its derived parameters, fst.25_Stri_SC for instance, are likely to perform a clearer separation. Besides this, the smallest p-values determined for the seven cases are all related to derived parameters. Thus, the quantiles 5%, 25%, 75%, and 95% are considered as “contrast mediums”. However, the standard deviation plays another role, especially when being applied to the texture direction Std. It then quantifies the different anisotropy orientations on a surface.

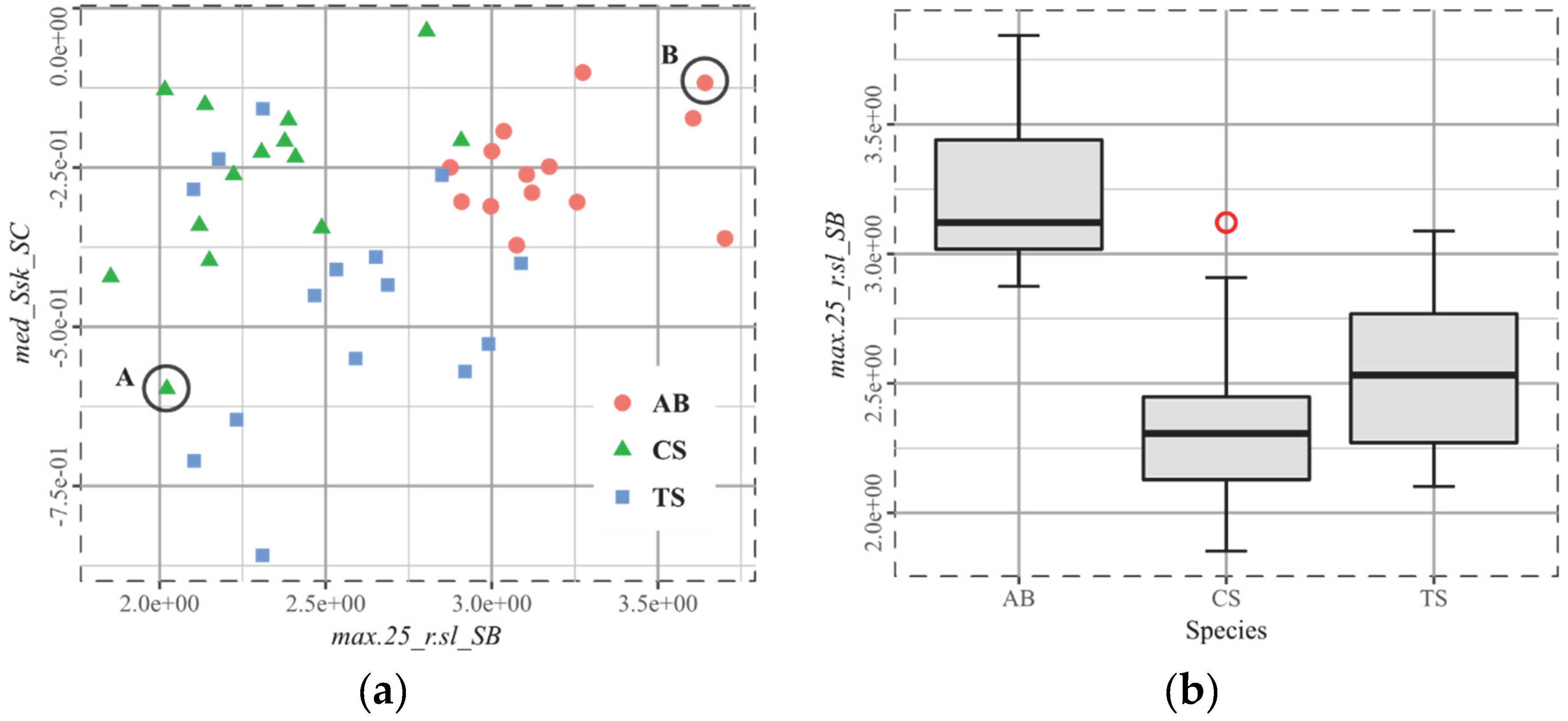
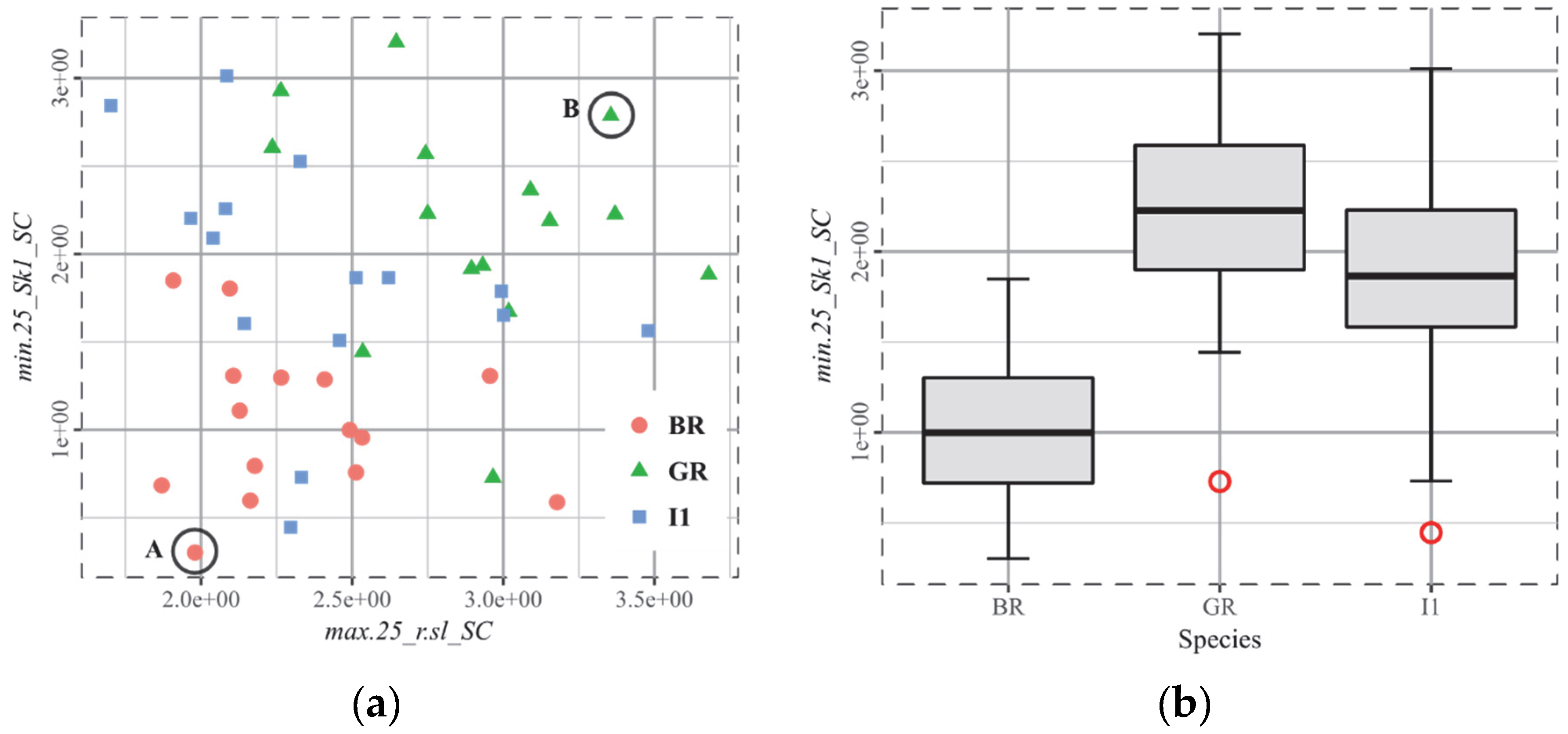
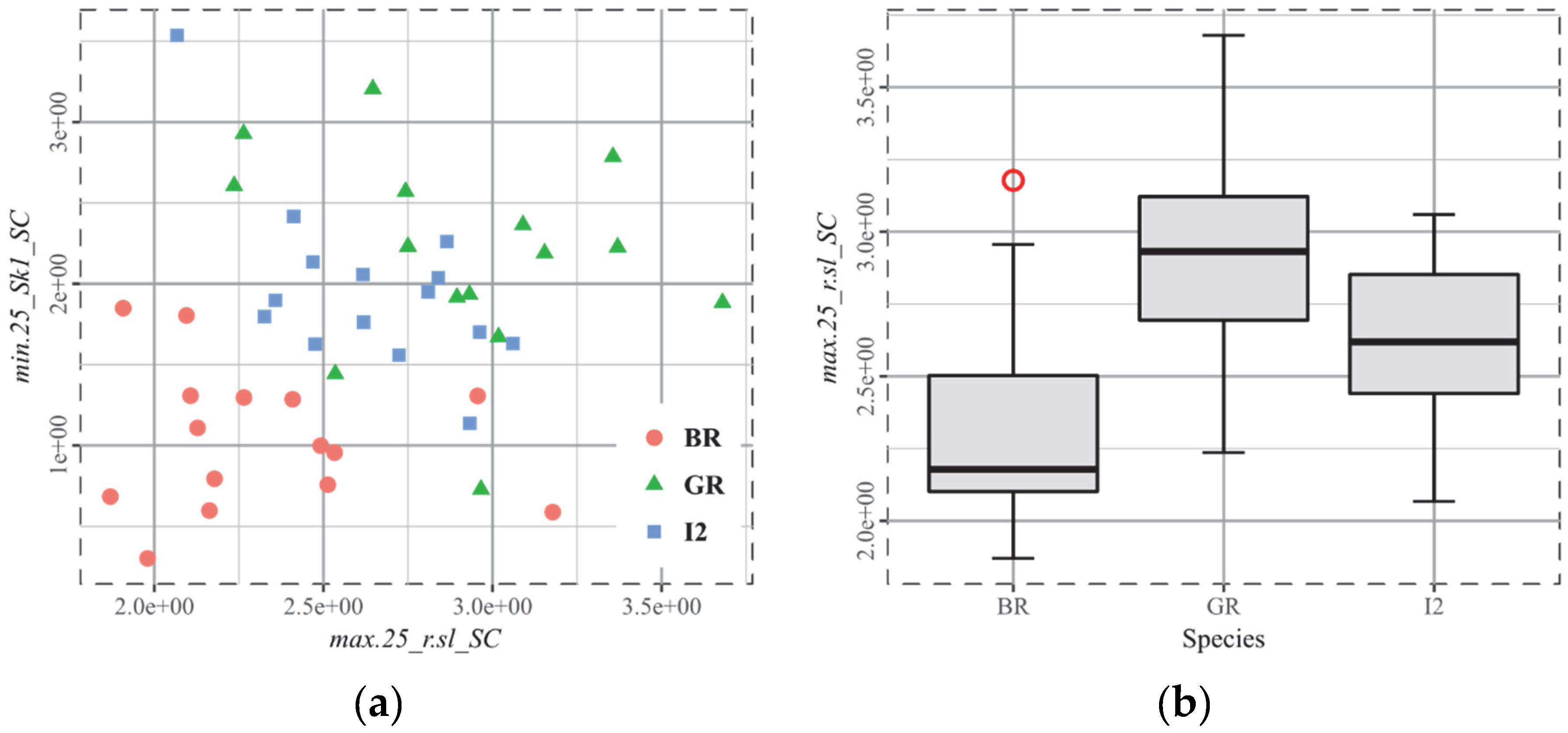
4.3. The Biplot as the Arbitor

The statistical procedure proves to be efficient: whenever it selects parameters with low p-values, the group separation is effective. However, parameters with high p-values, above 5%, can also be real markers. One group needs only to have a more limited range of values than another while both overlapping to guarantee a high p-value, and yet the signals are different. The first is homogeneous regarding its individuals, whereas the second is not. Except for this kind of exotic case, the biplot is the vital final step after the statistical procedure. Currently, it is hazardous for a program to act as a substitute for an expert appraisal: the authors here consider the procedure to be decision-making assistance. Indeed, it happens that one low p-valued parameter correlates too directly to another for a biplot representation, and that the user then advantageously switches to another parameter with a higher p-value, but a complementary potential for separation. It also happens that a low p-valued parameter is less meaningful than another parameter that has a higher, but still proximal, p-value. In that circumstance, the discrimination is slightly less accurate, but the results are easier to understand from a wear point of view.

4.4. Beware the Overfitting

Satisfying separations can be obtained by pure chance, an additional parameter is one more possibility to separate the group… by sheer luck! Signals are sometimes so weak that no real separation is possible using the actual parameters. Building an ad hoc additional parameter, combined with small size groups, can end in misleading conclusions. This could have happened with the Q2 set (i.e., the sheep experiment) where the parameters Sk2 and Scm2 are found to be the best for separating the groups, but rather than being artificially introduced, these parameters have been retained for their good mean performance.

4.5. Going Further

It is always possible, and even desirable, to refine and enhance the presented procedure, adding relevant parameters, or subtracting macro-geometries that are better suited than second or eighth order polynomials, or sampling in a different manner, etc. To go beyond this in the methodology, the authors believe that one question must first be asked: is the ethology more important than the classifying purposes?

• If the final goal is to be able to classify an unknown species based upon tooth surface characteristics, then machine learning will be the first step towards an appropriate answer. Supposing that an Artificial Neuron Network (ANN) is chosen for that task and provided a large training set of surfaces of several thousands, and a hundred parameters, the machine will succeed in classifying a given surface in the right diet group. Actually, the surface will be located across all of the diet groups together with a probability for each. It can be interpreted as a signal amount. For instance, if the classifying procedure results in 70% browser, 25% grazer, and 5% fruit or seed eater, if the training set is large and variate, it can be proposed that the individual fed on 70% smooth grass (or leaves), 25% tough grass, and 5% fruit (or seeds).
  Going even further, the deep learning is able to identify elementary surface features in its neuron deep layers. These are the elementary signatures of the different diets. Provided that it is possible to associate a given surface to the diet content, with in vivo experiments, for example, and that the training set is large enough, the ANN could propose a typical bolus content for an unknown surface. This second point is impractical for the moment because of the lack of precise information on diets, but the first is possible. It “only” needs the researchers to share a common surface database.
  The main drawback is that the whole process is a black box, the results are less prone to physical interpretation.
• If the final goal is to find the parameters that accurately separate already identified groups and to understand why this is, further developments are less ambitious and they have been mentioned in the first part of the discussion.