A Hybrid Feature Extractor using Fast Hessian Detector and SIFT

Abstract

This paper addresses a new hybrid feature extractor algorithm, which in essence integrates a Fast-Hessian detector into the SIFT (Scale Invariant Feature Transform) algorithm. Feature extractors mainly consist of two essential parts: feature detector and descriptor extractor. This study proposes to integrate (Speeded-Up Robust Features) SURF’s hessian detector into the SIFT algorithm so as to boost the total number of true matched pairs. This is a critical requirement in image processing and widely used in various corresponding fields from image stitching to object recognition. The proposed hybrid algorithm has been tested under different experimental conditions and results are quite encouraging in terms of obtaining higher matched pairs and precision score.

1. Introduction

Feature extractors have been widely used in different problems in image processing from recognition to reconstruction tasks [1]. SIFT (Scale Invariant Feature Transform) is a milestone in the fields of image processing and computer vision [2]. It is invariant to translation, scale, and rotation changes and partly invariant to changes in illumination and 3D camera viewpoint.

The first step of the SIFT algorithm is to calculate distinctive interest points (feature detector) which is carried out by applying an approximation to the scale-normalized Laplacian of Gaussian (LoG). The Difference-of-Gaussian (DoG) provides a good approximation for the LoG with a faster response time. Finally the local extreme points were extracted from DoG pyramid, followed by localization of keypoints and assignment of orientation to each keypoint. Once interest points are obtained, a 128 elements descriptor is generated for each point. In order to provide resistance to the linear illumination changes, the unit length of each descriptor is normalized. The details of the SIFT algorithm can be seen in the Lowe’s original paper [2]. SURF (Speeded-Up Robust Features) is other well-known rotation and scale invariant feature extractor algorithm and is partly inspired by the SIFT algorithm [3]. For interest point detection, the SURF algorithm employs integral images to approximate Hessian-matrix [4]. The detector used in SURF employs determinant of Hessian Matrix that the maximum determinant value of the matrix indicates the location candidate interest point. Besides, it employs a different scale space representation to provide scale invariance in which various size box filters are convolved with integral images. This results in computational efficiency and prevents aliasing.

Recently, another popular feature detector has been proposed, namely, BRISK [5] which in essence aims to find salient image regions in a shorter time and efficient manner. The BRISK algorithm incorporates FAST feature detector into a binary feature descriptor, BRIEF [6], so as to obtain similar robustness and reliability with SURF [2] algorithm in a shorter time. ORB (Oriented Fast and Rotated Brief) [7], on the other hand, proposes an alternative and free feature extractor algorithm. According to the results of the preliminary tests performed by the author reveal that it could be indicated that ORB achieves competitively performance with SURF algorithm in many cases except its sensitivity to illumination changes. For embedded applications, a novel feature descriptor inspired by the human visual system [8], Fast Retina Keypoint (FREAK), has been proposed. FREAK employs BRISK’s [5] multi-scale AGAST detector in order to detect features.

SIFER (Scale-Invariant Feature Detector with Error Resilience) is the most recent scale invariant feature detector, utilizing Cosine Modulated Gaussian (CM-Gaussian) filter and authors of the method claims that they have performed up to 20% improvement over the SIFT algorithm in terms of scale invariance [9].

2. Hybrid Architecture

Despite the recent developments, it is still a major challenge to extract features from images used in urban transformation and regeneration [10] that related tasks; including image stitching and silhouette extraction need as much as True Positive (TP) matches rather than computational performance. Accordingly, in order to boost TP matches, the SURF detector has been integrated into the SIFT algorithm that the all the interest points obtained from both detectors have been combined and employed as input to 128-elements SIFT descriptor, which surprisingly performs fairly well in off-line tasks as previously mentioned. The flowchart of the proposed hybrid algorithm is illustrated in Figure 1. According to which, first two different feature extraction method have been combined to obtain more key points. The Lowe’s method takes difference of Gaussians (DoG) of resampled images and selects the maxima and minima from the result in order to define key point locations. The mathematical formulization of the DoG operation is shown in the following expression [2].

$$DoG\left(x,y,\text{σ}\right)=L\left(x,y,k\text{σ}\right)-L\left(x,y,\text{σ})\right)$$

(1)

where $L\left(x,y,k\text{σ}\right)=G\left(x,y,k\text{σ}\right)\times I(x,y)$ and $L\left(x,y,k\text{σ}\right)=G\left(x,y,k\text{σ}\right)\times I(x,y)$.

The second detector is designed as an approximation to Hessian Detector which reduces overall computational time by employing integral images that is therefore called as “Fast Hessian detector” [3]. The Hessian matrix is shown as follows:

$$H=\left[\begin{array}{cc}{D}_{xx}& D_{xy}\\ D_{xy}& D_{yy}\end{array}\right]$$

(2)

Each members of the Hessian matrix includes second-order partial derivatives on corresponding coordinates where, for instance D_xy refers taking the derivate with respect to x first and then y direction. Essentially the derivatives are calculated by taking differences of neighboring sample pixels. Hessian matrix denotes the response of BLOB in the image to the corresponding location which are stored in the BLOB map of responses at different scales [3]. One of the most critical performance gains has been achieved performed by estimating the best features selected from the key-point space by ordering them according to the response values. This both removes outliners and put forwards the strongest key-points for the matching procedure. According to image size, an adaptive number is determined to select the number of best features, ordered in the list. An algorithm explains the complete combination process is given as follows:

Combination Algorithm:

Require:Input Image is a gray scale image

Ensure: Ordered List of Key-points

Main ProcedureCombine Features

Initial assignment of parameters

Scale Space Representation for SIFT

Estimate Difference of Gaussians (DoG)

Find extreme points and assign response to those SIFT features

Locate feature points employing interpolated location of the extremum

Poorly localized keypoints are eliminated and response values are calculated

Assign orientation to responsible key-points

Add keypoints to CommonList

End SubProcedure

Sub Procedure SURF_Detector (img1, img2)

Scale Space Representation for SURF

Applying box filter via integral image

Apply box Hessian to Locate extremes

Locate keypoints and eliminate poorly localized key-points

Assign orientation to responsible key-points

Add keypoints to CommonList

End SubProcedure

SortCommonList via response value

Select the best keywords according to the adaptive threshold

Return CommonList

End Procedure

Figure 1. Overview of the Hybrid Algorithm.

Figure 1. Overview of the Hybrid Algorithm.

3. Experimental Test and Discussion

This section presents the experimental results, including the hybrid algorithm performance to scale and illumination changes, rotation, affine transformation, and blurring effect. Number of total correct matches and precision parameters are employed as the main comparison criteria for the experiments. Experiments were conducted with an Intel Core 2 Quad machine running at 1.8 GHz, with 2 Gbytes of RAM memory, under Windows 7 operating system. An image database has been obtained from the previous study of the author [10], including street view images, for experimental section.

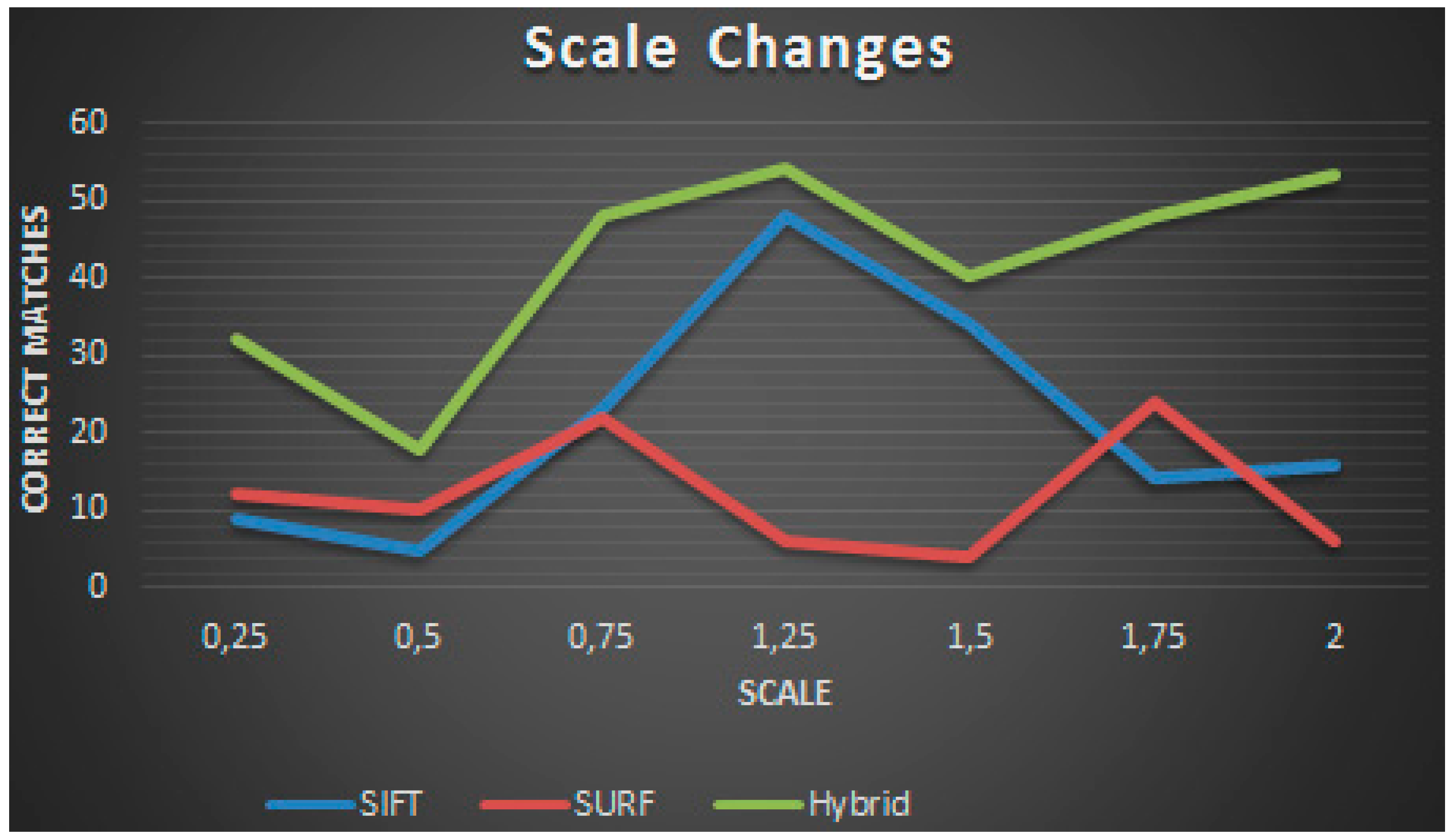
The first experiment has been conducted so as to evaluate the system performance against scale changes. The algorithms have been tested using different street view images that the scale changes lies in the range from 0.25 to 2.0 [2]. Average of these results have been illustrated in Figure 2. According to which, total number of correct matches obtained from the hybrid algorithm is far more than the SIFT and especially SURF algorithm in terms of resistance to the scale changes as seen in the corresponding figure. Besides, the enhancement in precision is better in the hybrid algorithm. Having robust scale invariance is a key factor for a feature detector that the hybrid algorithm resists scale changes far more than both the conventional SIFT and the SURF algorithms.

Figure 2. Scale changes.

Figure 2. Scale changes.

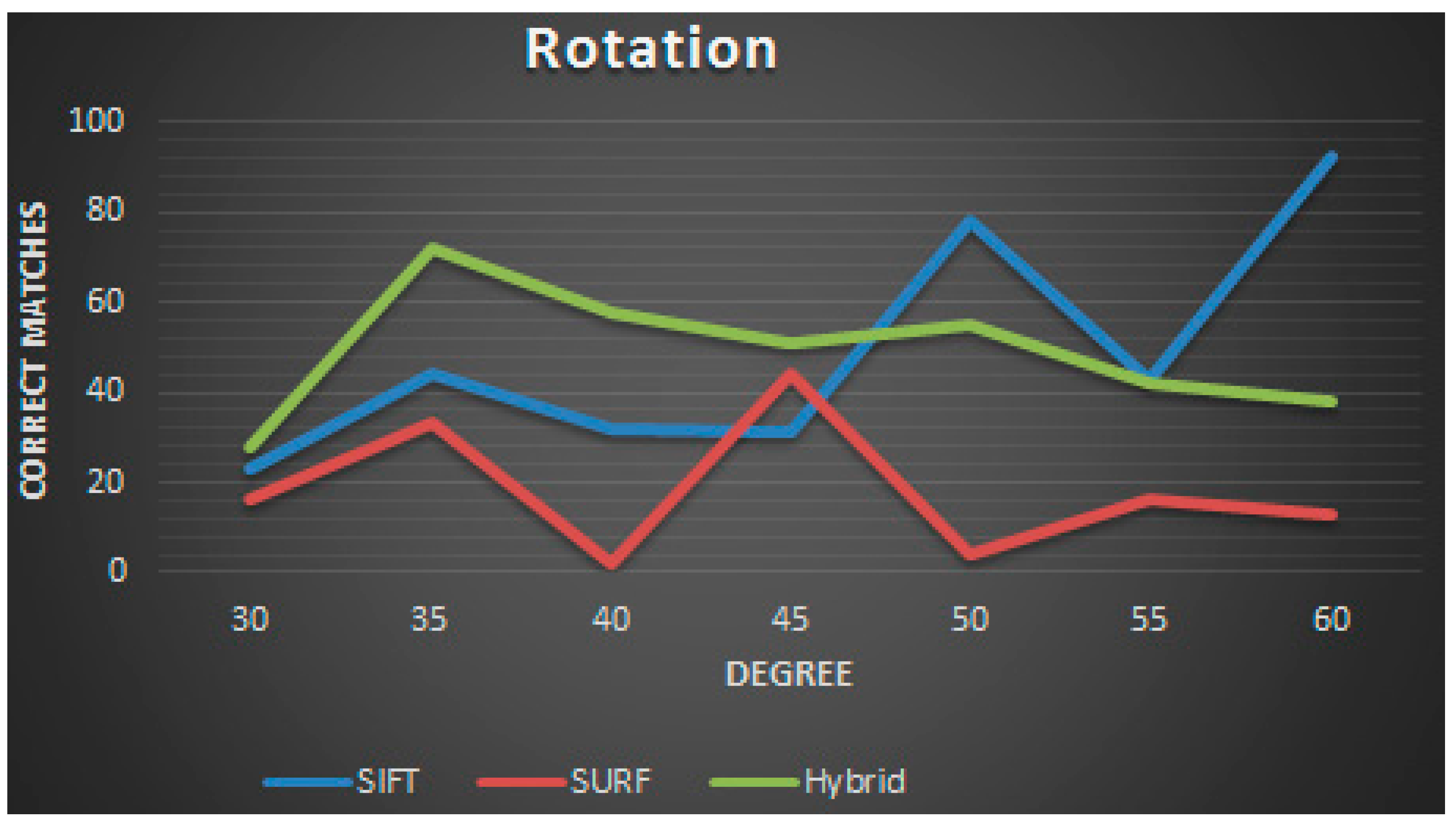
Rotation invariance is another critical feature used in the assessment and comparison of feature detectors. The same image corpus have been rotated and results reveal that the hybrid algorithm calculates more correct matches than the SURF between the angles 30 and 60 degrees, which, surprisingly generates less correct matches than the SIFT between 45 and 60 degrees (as seen in Figure 3). However, the overall precision score of the hybrid algorithm is better than the SIFT.

Figure 3. Rotation invariance.

Figure 3. Rotation invariance.

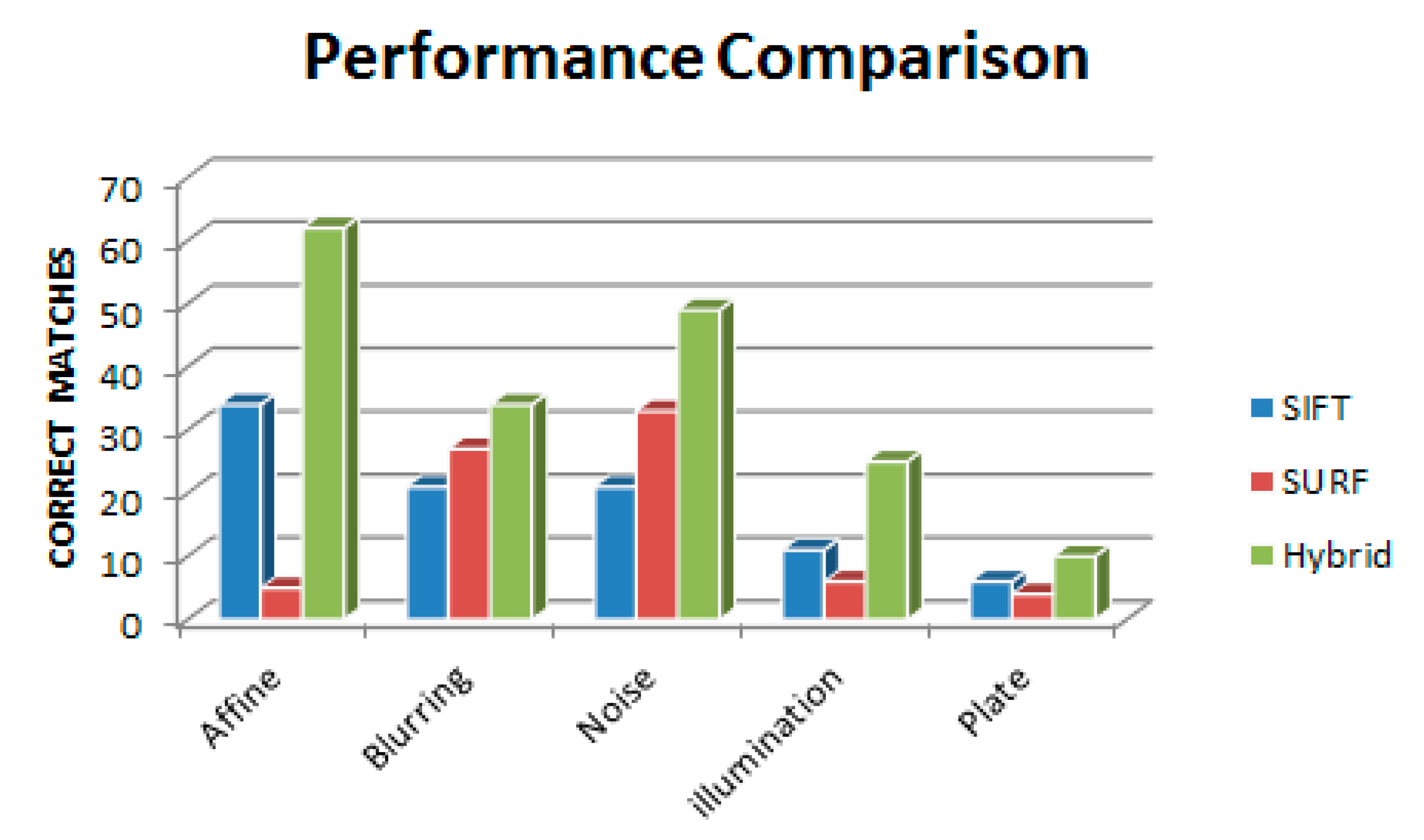
Figure 4 illustrates the results obtained from SIFT, SURF and the hybrid algorithms under different experimental conditions. The first experiment compares algorithms performance against 40 degrees viewpoint changes. The following three experiments test algorithms performance against Gaussian blurring, artificial noise, and illumination changes.

Figure 4. Affine, Blur Noise, Illumination and Plate test cases.

Figure 4. Affine, Blur Noise, Illumination and Plate test cases.

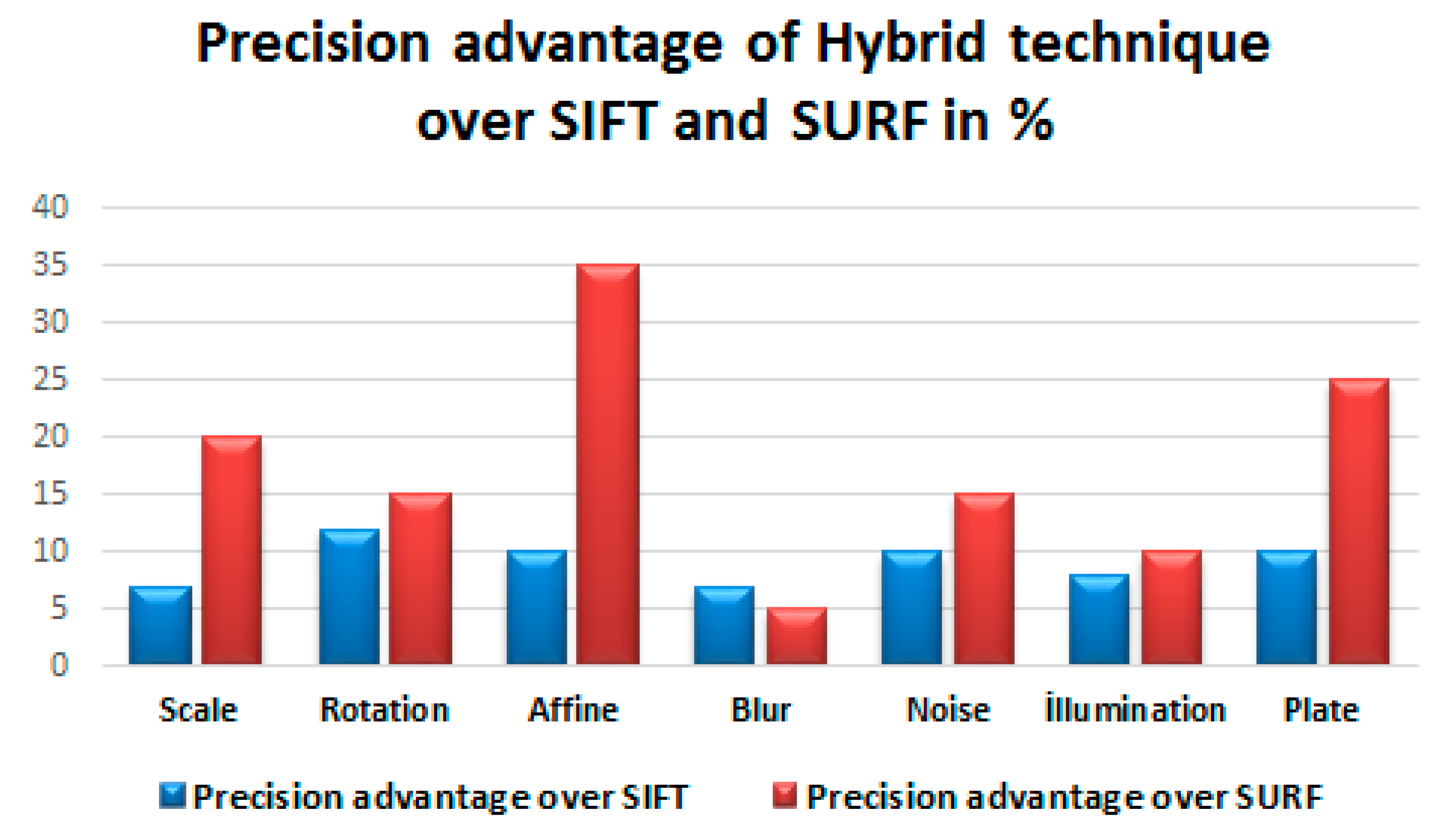
The final experiment compares hybrid algorithms performance and other algorithms in plate recognition problem. Results reveal that the hybrid algorithms generates higher number of correct matches than both algorithms, as well as it results in better precision under the given experimental conditions. Surprisingly, resistance to the Affine transformation within the hybrid algorithm is far more successful, especially than the SURF algorithm as illustrated in Figure 5.

Figure 5. Precision comparisons between algorithms.

Figure 5. Precision comparisons between algorithms.

Overall results reveal that the hybrid architecture generates higher numbers of True Positive (TP) matches almost in all experimental conditions than the conventional SIFT and SURF algorithm. The only exception has been encountered in rotation based experiments that SIFT generates more TP matches than the hybrid algorithm. However, overall precision score for all experimental conditions are being enhanced with the hybrid method when compared the other two algorithms as illustrated in the corresponding Figure.

The overall execution time of the proposed hybrid algorithm is far more than both the SIFT and SURF algorithm as expected. Nevertheless, the algorithm is designed for off-line tasks in image processing and computer vision that makes overall running time is not a critical evaluation aspect. Besides, if it is required to adapt the application for real time applications, parallel computing techniques can easily be integrated into the implementation.

4. Conclusions

This paper introduces a new hybrid algorithm for feature extraction problem, which is crucial in image processing and computer vision fields. The algorithm primarily integrates a hessian based detector used by SURF algorithm into the SIFT’s interest point detectors in order to boost the overall number of TP matches. Finally, SIFT’s descriptor algorithm, more robust and reliable than SURF’s algorithm, has been employed to generate descriptors for selected interest points.

Results reveal that this hybrid model increases the precision score and generates more TP matches than two leading feature extractor algorithms under different experimental conditions, including scale, rotation and view changes, as well as blurring, noise effect and plate recognition problem. In addition, the hybrid algorithm increases the precision score.

It should be noted that, as expected, having more TP matches provides better results in image recognition and corresponding fields. However, the hybrid algorithm consumes more time than those leading algorithms, making it a bad alternative for real time applications. Despite the computational cost due to the interest point detection step, having more TP matches within higher precision is a critical achievement in off-line tasks in image processing including fields from image stitching silhouette extraction to object recognition.