Enhancing the A* Algorithm for Efficient Route Planning in Agricultural Environments with a Hybrid Heuristic Approach and Path Smoothing

Abstract

The A* algorithm is broadly identified for its application in diverse fields, such as agriculture, robotics and GPS technology, due to its effectiveness in route planning. Despite its broad utility, the algorithm faces inherent limitations regarding operational efficiency and the length of the paths it generates. Addressing these constraints, this paper proposes an enhancement to the traditional A* algorithm that significantly improves its performance. Our innovative approach integrates Euclidean and Chebyshev distances into a single heuristic function, thereby enhancing pathfinding accuracy and flexibility. This combined heuristic leverages the strengths of both distance measures: the Euclidean distance provides an accurate straight-line measure between points, while the Chebyshev distance effectively handles scenarios allowing diagonal movement. Furthermore, we incorporate Bezier curves into the algorithm to smooth the generated paths. This addition is particularly advantageous in agricultural environments, where machinery must navigate complex terrains without causing damage to crops. The smooth paths produced by Bezier curves ensure more efficient and safer navigation in such settings. Comprehensive experiments conducted in various agricultural scenarios demonstrate the superior performance of the enhanced algorithm. These results reveal that the improved algorithm not only reduces the computation time needed for route planning but also generates shorter and smoother paths compared to the standard A* algorithm. The proposed approach significantly enhances the operational efficiency and route optimization capabilities of the A* algorithm, making it more suitable for complex and dynamic applications in agriculture. This advancement also holds promise for improving navigation systems in various other domains.

1. Introduction

The A* algorithm has long been identified as a cornerstone in the field of route planning, finding extensive application in various domains such as robotics, GPS technology, and, more recently, agriculture. Its popularity stems from its ability to efficiently compute the shortest path between two points, a critical capability in environments where precise navigation is paramount [1,2]. The algorithm’s utility spans a broad range of applications, from guiding autonomous vehicles through city streets to enabling agricultural machinery to navigate vast farmlands with precision [3,4]. The effectiveness of the A* algorithm in these varied domains is due to its robustness and reliability in pathfinding tasks, ensuring that it remains a preferred choice among engineers and researchers. Its ability to handle complex maps, dynamically adjust to obstacles, and find optimal paths in real-time scenarios has solidified its status as an essential tool in modern navigation systems [5,6,7,8]. However, despite its widespread use and acknowledged effectiveness, the A* algorithm is not without its limitations. Two of the most significant constraints it faces are its operational efficiency and the length of the paths it generates. These limitations can lead to increased computational load and suboptimal navigation routes, especially in complex and dynamic environments. The computational intensity of the A* algorithm can result in slower performance as it exhaustively explores potential paths, which can be particularly problematic in real-time applications where speed is critical. Additionally, the paths generated by the standard A* algorithm, while optimal in terms of length in terms of practical usability due to the grid-based nature of the search space [9,10,11].

Overcoming the limitations of the A* algorithm is crucial to unlocking its full potential in the agricultural sector. Improving the algorithm’s capacity to generate smoother paths and adapt to demanding landscapes is a continuous area of research and development. Researchers and architects are continually exploring innovative solutions to refine the algorithm, introducing supplementary and modification approaches that enhance its performance [12,13,14]. These efforts are essential to ensure that the A* algorithm stays a valuable tool in optimizing and modernizing farming procedures. The drive to improve the A* algorithm involves developing new methods to address its inherent shortcomings. One key focus is on path smoothness, which is vital for the practical application of the algorithm in agriculture. Smooth paths minimize the risk of damage to crops and machinery, ensuring that agricultural operations can proceed efficiently and safely [15,16]. Adaptability to challenging terrains is another critical area of enhancement. Agricultural environments are often characterized by uneven terrain, obstacles, and varying conditions that can complicate navigation. To address this, researchers are developing hybrid heuristic functions that combine the strengths of multiple distance measures [17,18,19]. The continuous refinement of the A* algorithm is essential for its application in precision farming, where the need for efficient, accurate, and reliable navigation is paramount. Precision agriculture affects the use of technology to optimize field-level management concerning crop agribusiness. The A* algorithm’s ability to provide precise route planning is a cornerstone of this practice, facilitating tasks such as automated planting, irrigation, and harvesting. By overcoming its current limitations, the A* algorithm can significantly contribute to the efficiency and sustainability of these operations [20,21,22]. Moreover, the improvements to the A* algorithm have broader implications for sustainable food production. Efficient navigation algorithms reduce fuel consumption and operational time, lowering the environmental impact of agricultural activities. This is particularly important in the context of global efforts to promote sustainable farming practices that minimize carbon footprints and conserve natural resources [23,24,25,26].

In this research, the overriding objective is to improve the quality of the resulting route that the A* algorithm generates while also maximizing the efficiency of the method:

• Our approach integrates Euclidean and Chebyshev distances into a single heuristic function, thus improving both pathfinding accuracy and flexibility. The Euclidean distance, which estimates the straight-line distance between two points, provides an accurate and reliable metric for pathfinding in open and unobstructed spaces. On the other hand, the Chebyshev distance, which considers the maximum of the horizontal and vertical distances between points, is particularly effective in scenarios that allow diagonal movement. By combining these two distance measures, our heuristic function leverages both strengths, offering a more comprehensive solution for diverse navigation challenges.
• Furthermore, to enhance the smoothness of the paths generated by the algorithm, we incorporate Bezier curves into the path-planning process. Bezier curves are renowned for their ability to produce smooth and continuous curves, which are particularly advantageous in agricultural environments. The smooth paths generated by Bezier curves ensure that machinery can navigate complex terrains more efficiently and safely, reducing the likelihood of crop damage and improving overall operational efficiency. This is especially critical in agricultural settings, where the terrain can vary widely, and the need for precise, damage-free navigation is paramount.
• To evaluate the effectiveness of our approach, we conducted a series of tests under rural conditions. The simulation results provide evidence of our method’s viability and potential, showcasing its capability to resolve the persistent issue of path smoothness. Additionally, these results highlight the method’s ability to enhance planning performance in smart agriculture’s challenging and dynamic environment.

The remainder of this work is organized as follows: In Section 2, we deepen into the research articles that construct the basis of our investigation. Section 3 describes our optimization method of the A* algorithm. Section 4 exhibits the analysis results involving our optimization of the A* algorithm. Section 5 discusses the proposed approach, outlining its main strengths and practical relevance. In Section 6, we summarize the outcomes of our study.

2. Related Work

Ongoing attempts are being made to discover new solutions that have the potential to enhance the smoothness and flexibility of the A* algorithm when it is applied to challenging terrain [27,28,29,30,31]. This algorithm is being refined by researchers and industry professionals, who are also researching new paths for development and introducing changes and complementing strategies that are tailored to the agricultural sector. The final goal is to encourage the production of food in a sustainable manner while also providing assistance for the development of technology that enable precision agriculture. The purpose of these initiatives is to reduce the amount of choppiness in the pathways that are created, with the end goal of guaranteeing that autonomous cars and robotic systems are able to traverse agricultural areas more effectively.

The authors of [32] introduce the bidirectional alternating search A* algorithm, which is specifically developed for global path planning in mobile robotics. This algorithm aims to generate paths that are not only efficient but also optimal by integrating the strengths of the conventional A* algorithm with those of bidirectional search techniques. The principal innovation of this approach lies in conducting searches alternately from both the start and goal positions until the two search frontiers meet, thereby enhancing the overall efficiency of the pathfinding process. By employing this bidirectional alternating search strategy, the method effectively addresses challenges typically encountered in expansive workspaces, such as excessive turning angles, prolonged computation times, and the emergence of non-smooth trajectories.

In [33], the researchers introduced an enhanced version of the A* algorithm to facilitate more effective navigation for mobile robots. The robot platform was equipped with LiDAR and an Inertial Measurement Unit to enable precise environmental perception and mapping. A mapping algorithm was employed to generate a two-dimensional grid representation of the environment, which served as the basis for the improved A* algorithm in path planning tasks. The proposed algorithm incorporated several strategies, including path smoothing, the integration of a safety mechanism, and the removal of redundant points and sharp corners by assessing the presence of obstacles between path segments. These methodological enhancements resulted in substantially smoother planned paths and contributed to more efficient robot motion in real-world scenarios. Empirical results demonstrated a reduction of 13% in the average path search time and an 11% decrease in the number of nodes required for path extension, thereby addressing key limitations of the conventional A* algorithm, such as the prevalence of excessive turning points and slow search speeds.

The authors of [34] proposed a modification of the heuristic component of the standard A* algorithm, aiming to reduce both the computational time required for search and the number of alternative paths that need to be examined. According to the experimental results, the improved A* route planning method achieves an average path length that is 5.34% shorter compared to the conventional A* algorithm, while the required search time is decreased by an average of 22.56%. These outcomes indicate a significant improvement in the efficiency of robotic path planning, contributing not only to a more optimal trajectory but also to smoother driving actions, all while guaranteeing the selection of the most advantageous route.

In [35], the authors present an approach to optimizing mobile robot navigation in smart agriculture by enhancing the traditional A* path planning algorithm. Their method introduces dynamic weighting in the algorithm’s heuristic function, enabling adaptive prioritization based on the environmental context, and utilizes the Manhattan distance to improve pathfinding in grid-like fields. Additionally, they employ Bezier curves as a postprocessing step to smooth the initially choppy paths generated by A*, transforming them into routes more suitable for real-world navigation in complex and dynamic agricultural environments. The methodology is tested via simulation in realistic rural scenarios, demonstrating that the enhanced algorithm yields shorter, smoother, and more efficient paths compared to the standard approach. The results highlight improvements not only in path length and computational efficiency but also in the number of search routes, which is critical for real-time applications.

The authors of [36] refined the heuristic mechanism of the standard A* algorithm to minimize both the search duration and the number of potential pathways subject to evaluation. Experimental results indicate that the optimized algorithm reduced route planning time by an average of 9.11% and achieved a concurrent average reduction of 9.29% in the total route distance. These findings underscore notable enhancements in the overall performance of the A* algorithm, particularly in terms of operational efficiency and the minimization of route length.

In [37], the authors propose an improved variant of the A* algorithm, motivated by the recognition that the conventional A* algorithm demonstrates suboptimal performance with respect to spatial and temporal efficiency, as well as the number of explored search routes, particularly when implemented in the context of specific robot motion modules. The effectiveness of the standard algorithm is frequently limited by factors such as the excessive number of generated search paths, elevated overall path cost, and increased computational complexity, especially when customized for a particular robot motion block. To address these limitations, the present study focuses on optimizing the robot motion module to curtail the exploration of unnecessary or redundant routes, thereby rendering the search procedure more efficient. Experimental results demonstrate that the proposed method achieves a 93.98% reduction in the number of search routes and a 98.94% improvement in time complexity compared to the standard A* algorithm.

While numerous studies have proposed improved variants of the A* algorithm—ranging from modified heuristics to metaheuristic-assisted search and post-processing smoothing—most either (i) employ a single distance metric, (ii) rely on weighted combinations requiring empirical tuning, or (iii) target generic robotic navigation scenarios without domain-specific constraints. The present study addresses these limitations by introducing a deterministic, weight-free hybrid heuristic that directly sums Euclidean (L2) and Chebyshev ($L_{\infty }$) distances, ensuring balanced diagonal and straight-line movement costs without adjustable parameters. Chebyshev ($L_{\infty }$) is particularly suited to uniform-cost diagonal motion, a property exploited here for orchard-like agricultural maps with constant row spacing, narrow passages, and irregular obstacles. By exploiting the properties of these distance measures, the heuristic achieves greater adaptability and precision in navigation under the spatial and kinematic constraints typical of precision agriculture.

Beyond the heuristic formulation, this work incorporates Bezier curve smoothing in a post-processing stage to mitigate discontinuities and abrupt direction changes produced by conventional grid-based planners. Unlike existing studies, we quantify the computational overhead of Bezier smoothing across different map sizes, demonstrating that the additional processing cost remains minimal and well within real-time operational limits for embedded agricultural platforms. Our evaluation framework extends performance assessment beyond conventional metrics such as computation time and path length, also including the number of route expansions as a direct measure of search-space efficiency. By combining a domain-optimized hybrid heuristic with a quantified overhead analysis of path smoothing, the proposed approach delivers shorter, smoother, and kinematically feasible paths while maintaining computational efficiency—bridging the gap between theoretical improvements in A* and deployable solutions for autonomous agricultural vehicles.

3. Implementation

3.1. Traditional A* Algorithm

Computer science and artificial intelligence are two fields that make extensive use of the A* algorithm, which is a pathfinding method that is both extremely effective and frequently used. In applications where it is vital to determine the most effective path between two locations in a grid or graph, such as in robots and other navigation robot systems, its popularity is more noticeable than in other applications. A* is able to determine the shortest route by calculating the cost of traveling along a certain route and predicting the cost that will be required to reach the destination. This is the key advantage of the A* algorithm. This estimate is made easier by a heuristic function, which is represented by the symbol H(z). This function guides the search in the direction of the most promising pathways, improving the efficiency with which the search space is explored [38,39].

The heuristic function is an essential component in the overall performance of the A* algorithm. The method’s efficiency and accuracy are substantially impacted by the choice of this function as well as the design of the algorithm. When properly developed, a heuristic has the ability to significantly reduce the search space, which ultimately leads to much quicker pathfinding. Conversely, an inadequate heuristic can slow down the process and lead to less optimal paths. Therefore, the selection of a suitable heuristic function is of the utmost importance in order to successfully perform the A* algorithm [40,41,42]. To further enhance the A* algorithm, we have introduced the Euclidean and Chebyshev distances as specific implementations of the heuristic function H(z). These enhancements are designed to improve the algorithm’s ability to generate smooth paths and adapt to various scenarios, thereby boosting its overall performance. The Euclidean distance, which estimates the straight-line length between two points, offers a precise and reliable metric for pathfinding in open and unobstructed spaces. Meanwhile, the Chebyshev distance, which considers the maximum of the horizontal and vertical distances between points, is particularly effective in scenarios that permit diagonal movement.

By integrating these two distance measures into a single heuristic function, we leverage both strengths. This combined approach provides a more comprehensive and flexible solution to diverse navigation challenges. The Euclidean distance ensures accuracy in straightforward, open environments, while the Chebyshev distance enhances adaptability in more complex terrains where diagonal movements are feasible. The enhanced heuristic function facilitates smoother paths and enables the algorithm to navigate varying scenarios better. As a result, the algorithm’s speed and efficiency are markedly improved, making it more effective for real-world applications in robotics, navigation systems, and beyond.

The implementation of the traditional A* algorithm is comprised of many crucial phases, each of which makes a substantial contribution to the algorithm’s overall performance and efficacy in path planning:

• Defining Open and Closed Lists:
  • Open List: This list contains nodes that are prepared to be inspected and may be included in the path if they are eligible. It functions as a priority queue, where nodes are selected based on their evaluation scores.
  • Closed List: This list is used to keep nodes that have previously been analysed or verified throughout the search operation. This ensures that these nodes are not re-evaluated.
• Defining Parent Nodes:
  • A parent node is designated for any node that is present in the search space. This hierarchical structure makes it possible for the algorithm to go backwards from any node to its starting point, which makes route reconstruction much simpler. The nodes that are near to the parent node are referred to as child nodes, and they are contributed to the open list so that they may be investigated further.
• Path Selection:
  • The selection of a route is the most important part of the decision-making process that the A* algorithm uses. This selection is guided by the evaluation function, denoted as $F\left(z\right)$, which is represented by the equation

    $$F\left(z\right)=G\left(z\right)+H\left(z\right)$$

    (1)
    In this equation, $F\left(z\right)$ is the evaluation function for node z, $G\left(z\right)$ is the actual cost of traveling from the start node to node z, and $H\left(z\right)$ is the heuristic estimate of the cost from node z to the goal node. In order to achieve our objectives, we use Euclidean and Chebyshev distances as the heuristic function $H\left(z\right)$, which enhances the clarity and efficiency of the heuristic in contexts that are grid-based.
• Heuristic Function $H\left(z\right)$:
  • There is a significant relationship between the heuristic function $H\left(z\right)$ and the efficiency of the A* algorithm. Assuming the current node as the starting point, this method calculates the remaining cost to achieve the target. Because a well-designed heuristic may successfully lead the search process towards the objective, thereby minimizing the number of needless searches, the choice of heuristic has a considerable impact on the productivity of the algorithm.
• Open List Priority Queue:
  • A priority queue data structure is used by a number of implementations in order to choose nodes from the open list in an effective manner. By doing so, it is ensured that the nodes that have the most inferior evaluation function values $F\left(z\right)$ are selected beforehand for additional investigation. The process of obtaining the objective is sped up by prioritizing nodes in this manner because it allows the search to concentrate on the most promising pathways at an earlier stage.
• Termination Condition:
  • The search is carried on by the A* algorithm until either it reaches the objective node or it has exhausted all of the feasible pathways without finding a solution. Handling termination conditions in the appropriate manner is essential in order to prevent calculations that are not required and to guarantee that the algorithm functions well.
• Reconstruction of the Optimal Path:
  • As soon as the A* algorithm matches the target node, it begins the process of reconstructing the optimum route by going backwards from the goal node to the start node and making use of the parent pointers that were allocated via the search process. This rebuilt path is the most effective and quickest route from the starting point to the destination, taking into account both the actual costs and the predicted costs.

By following these structured steps, the traditional A* algorithm effectively finds the shortest path between two points in a graph or grid. The integration of Euclidean and Chebyshev distances as the heuristic function $H\left(z\right)$ enhances its performance, particularly in grid-based environments, by ensuring path smoothness and adaptability to various scenarios. This structured approach ensures that the algorithm remains robust and reliable, making it a preferred choice for pathfinding tasks in a wide range of applications, including robotics, navigation systems, and more.

3.2. Euclidean and Chebyshev Distances

In the context of enhancing the A* algorithm, the use of Euclidean and Chebyshev distances as heuristic functions provides a robust and flexible approach to pathfinding. The Euclidean distance, which calculates the straight-line distance between two points, is defined by the equation:

$$d_E(p_1,p_2)=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$$

(2)

This metric is particularly effective in open and unobstructed spaces where diagonal movement is feasible, allowing the algorithm to estimate the shortest path in a continuous space. The precision of Euclidean distance ensures that the algorithm can efficiently navigate through environments where the shortest path is desired without any constraints on the direction of movement.

On the other hand, the Chebyshev distance, given by

$$d_C(p_1,p_2)=max\left(\right|x_2-x_1|,|y_2-y_1\left|\right)$$

(3)

is suitable for grid-based environments where movement is restricted to horizontal, vertical, and diagonal directions with uniform cost. This distance metric reflects the maximum number of steps needed to move from one point to another in such a setting, accounting for the scenarios where diagonal steps cover more ground efficiently.

The combined heuristic function is defined as

$$H\left(z\right)=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}+max\left(\right|x_2-x_1|,|y_2-y_1\left|\right)$$

(4)

In formulating the hybrid heuristic, the Euclidean and Chebyshev distances were combined using a direct summation approach, without introducing adjustable weighting coefficients. This decision was motivated by three main considerations. First, assigning equal contribution (implicit weight factor of 1 for both distances) ensures that the Euclidean term can fully capture the accuracy of straight-line estimates in open and unobstructed environments, while the Chebyshev term can fully reflect the efficiency of diagonal movements in grid-based navigation. Second, avoiding empirically tuned weights simplifies the heuristic, reducing computational overhead and removing the need for additional calibration, which can be sensitive to environmental variations. The resulting heuristic formulation, presented in Equation (4), offers a balanced, computationally efficient, and robust metric that leverages the complementary strengths of both distance measures across diverse agricultural navigation scenarios. This formulation is applied in the implementation described in Algorithm 1 (lines 23–25).

Algorithm 1 A* algorithm with Euclidean and Chebyshev aistances and Bezier curve smoothing

Require:  $initialNode,terrainMap,targetNode$ 1: Initialize open list $openSet$ (nodes to be evaluated) and closed list $closedSet$ (nodes already evaluated) 2: Create a map for backtracking the optimal path: $pathMap$ 3: Initialize costs for $initialNode$: 4: $gCost\left[initialNode\right]\leftarrow 0$ Cost from initial to the current node 5: $fCost\left[initialNode\right]\leftarrow gCost\left[initialNode\right]+heuristic(initialNode,targetNode)$ Total estimated cost from initial to target through the current node 6: Add $initialNode$ to open list $openSet$ with $fCost$ value 7: while$openSet$ is not empty do 8:    $currentNode\leftarrow$ node with lowest $fCost$ in $openSet$ 9:    if $currentNode=targetNode$ then 10:      break Path to target has been found 11:    end if 12:    Move $currentNode$ from $openSet$ to $closedSet$ 13:    for each $adjacentNode$ in getNeighbors($currentNode$) do 14:      if $adjacentNode$ is in $closedSet$ then 15:         continue Skip nodes already evaluated 16:      end if 17:      Calculate tentative $gCost$: 18:      $tentativeG\leftarrow gCost\left[currentNode\right]+$ distance($currentNode,adjacentNode$) Cost from initial to adjacent node through current 19:      if $adjacentNode$ is not in $openSet$ or $tentativeG<gCost\left[adjacentNode\right]$ then 20:         Update the path to this $adjacentNode$: 21:         $pathMap\left[adjacentNode\right]\leftarrow currentNode$ 22:         $gCost\left[adjacentNode\right]\leftarrow tentativeG$ 23:         Calculate Euclidean distance $euclideanDist(adjacentNode,targetNode)=\sqrt{{(x_{adjacentNode}-x_{targetNode})}^2+{(y_{adjacentNode}-y_{targetNode})}^2}$ 24:         Calculate Chebyshev distance $chebyshevDist(adjacentNode,targetNode)=max\left(\right|x_{adjacentNode}-x_{targetNode}|,|y_{adjacentNode}-y_{targetNode}\left|\right)$ 25:         Set heuristic $heuristic\left(adjacentNode\right)=euclideanDist(adjacentNode,targetNode)+chebyshevDist(adjacentNode,targetNode)$ {Combined heuristic} 26:         Update $fCost$ for $adjacentNode$: 27:         $fCost\left[adjacentNode\right]\leftarrow gCost\left[adjacentNode\right]+heuristic\left(adjacentNode\right)$ Total cost for adjacent node 28:         if $adjacentNode$ is not in $openSet$ then 29:           Add $adjacentNode$ to $openSet$ with updated $fCost$ 30:         end if 31:      end if 32:    end for 33: end while 34: if $currentNode\ne targetNode$ then 35:    return failure {No path found} 36: end if 37: Path Reconstruction: 38: Initialize empty path $optimalPath$ 39: Set $traceNode\leftarrow targetNode$ 40: while$traceNode\ne initialNode$do 41:    Prepend $traceNode$ to $optimalPath$ 42:    $traceNode\leftarrow pathMap\left[traceNode\right]$ 43: end while 44: Prepend $initialNode$ to $optimalPath$ 45: Bezier Curve Smoothing: 46: Define control points $controlPoints$ from path $optimalPath$ 47: Calculate Bezier curve $\mathrm{B}\left(t\right)={\displaystyle {\sum }_{i=0}^n}\left(P_i·B_{i,n}\left(t\right)\right)$ where $B_{i,n}\left(t\right)=C(n,i)·{(1-t)}^{n-i}·t^i$ and $C(n,i)={\displaystyle \frac{n!}{i!(n-i)!}}$  48: return Smoothed path $\mathrm{B}\left(t\right)$

Integrating these two heuristic functions within the A* algorithm leverages their respective advantages, providing a comprehensive solution that adapts to varying navigation scenarios. The Euclidean distance contributes to the accuracy and optimality in open terrains, while the Chebyshev distance enhances adaptability in more structured, grid-like environments. This dual approach allows the algorithm to maintain high efficiency and pathfinding accuracy across diverse conditions, from urban planning and robotics to complex agricultural fields. By effectively combining these heuristic measures, the enhanced A* algorithm not only reduces computation time but also generates smoother and more practical paths, thereby improving its overall performance and applicability in real-world tasks.

3.3. Bezier Curves Smoothing

Bezier curves are fundamental mathematical constructs widely used in two-dimensional graphical domains, offering a range of applications due to their versatile nature. These curves come in various orders, each defined by its unique set of characteristics and control points [43,44,45]. Bezier curves may be broken down into two basic categories: first-order Bezier curves, which can be reduced to straightforward straight lines, and higher-order Bezier curves, which can be used to create more elaborate and sophisticated designs. crucial points are the points that govern the precise shape of a Bezier curve. These crucial points include the start point, the end point, and the control points that are located in between. Because of the direct impact they have on the form and trajectory of the curve, the positioning and arrangement of these control points are very important issues. This flexibility allows Bezier curves to adapt to a wide array of graphical representations and applications [46,47,48].

In this study, we investigate the potential that multi-order Bezier curves may be used to improve the pathways that are produced by the conventional A* algorithm. Our goal is to generate pathways that are smoother and more refined by including Bezier curves in the post-processing step of the A* algorithm. Making use of the control points of the Bezier curves in order to fine-tune and optimize the route that is created by the A* algorithm is the means by which this is accomplished. We can achieve a route that is not only ideal in length but also demonstrates a high degree of smoothness by carefully manipulating and strategically placing these control points. This will allow us to accomplish our goal. Because of this, the route is brought into closer alignment with the needs of real-world applications, which often require mobility that is both smooth and safe.

The mathematical formulation that describes a Bezier curve with a degree z (where z indicates the order of the curve) is given by

$$\mathrm{B}\left(w\right)={\displaystyle \sum _{i=0}^z}\left(P_i·B_{i,z}\left(w\right)\right)$$

(5)

In this formula

• $\mathrm{B}\left(w\right)$ identifies the point on the Bezier curve that corresponds to the parameter value w.
• $P_i$ represents the points on the Bezier curve that serve as control points. The control points are indexed from 0 to z, and there are a total of $z+1$ control points.
• $B_{i,z}\left(w\right)$ symbolically represents the Bernstein basis polynomial with a degree of z for the control point $P_i$. In order to interpolate between control points, it is dependent on the function w and is used.

The following is the formula for calculating the Bernstein basis polynomial

$$B_{i,z}\left(w\right)=C(z,i)·{(1-w)}^{z-i}·w^i$$

(6)

to compute the binomial coefficient, which is denoted by the symbol $C(z,i)$:

$$C(z,i)={\displaystyle \frac{z!}{i!(z-i)!}}$$

(7)

The symbol ! denotes the factorial. Through the use of this formula, it is possible to determine the location of a fact on a Bezier curve for a certain parameter weight w. This is accomplished by adding up the donations from every control issue, with the separate contributions being weighted by the Bernstein basis polynomial that corresponds to it. The advancement along the curve is represented by the parameter w, which normally has a range from 0 to 1. A significant factor that defines the total number of control points and has an impact on the complexity of the curve is the degree of the Bezier curve, denoted by z. Increased-degree Bezier curves have the ability to depict more intricate and detailed forms, which makes them very useful tools for a wide variety of applications that need the development of exact and smooth paths.

In our implementation, the selection and placement of Bezier control points follow a procedure aimed at ensuring path smoothness and collision-avoidance feasibility. First, the A*-generated path is analyzed to locate vertices where the turning angle exceeds a predefined kinematic threshold, calculated from the robot’s minimum turning radius and the grid resolution. For each such vertex, a cubic Bezier segment is defined. The first and last control points of the segment are fixed at the preceding and succeeding path waypoints, respectively. The two intermediate control points are positioned along the direction vectors (tangents) of the incoming and outgoing path segments. The offset distance for each intermediate control point is computed as a fixed proportion of the length of the corresponding adjacent segment. When an obstacle lies within a predefined clearance distance, the offset is proportionally reduced to ensure the resulting curve remains entirely within the free-space corridor. This process is repeated for all identified vertices, resulting in smoothed paths that maintain continuity, respect dynamic constraints, and avoid collisions.

Incorporating Bezier curves into the A* algorithm represents a substantial advancement in the realm of pathfinding, offering remarkable improvements in the smoothness and practicality of the generated paths. Bezier curves, known for their mathematical precision and ability to create smooth, continuous paths, are highly beneficial in applications that demand meticulous navigation. In the context of robotics, the integration of Bezier curves ensures that autonomous robots can navigate complex environments with greater fluidity and precision. This is crucial for tasks that involve intricate movements, such as manoeuvring around obstacles, executing precise turns, and following complex trajectories. The smooth paths generated by Bezier curves reduce the mechanical strain on robotic components, leading to longer operational life and reduced maintenance costs. In the agricultural sector, the application of Bezier curves within the A* algorithm addresses the unique challenges posed by uneven terrains and the need for delicate handling of crops. Traditional pathfinding algorithms often result in jagged or abrupt paths, which can be detrimental in farming environments where the machinery must avoid damaging plants. Bezier curves create more natural and gentle paths, allowing for smoother transitions and movements. This not only protects the crops but also enhances the efficiency of agricultural operations such as planting, irrigation, and harvesting. The ability to generate smooth paths ensures that autonomous agricultural machinery can operate continuously without causing harm to the environment, thereby promoting sustainable farming practices. Beyond robotics and agriculture, the enhanced A* algorithm with Bezier curves finds applications in numerous other domains requiring precise and efficient navigation. In autonomous vehicles, for instance, smooth paths are essential for ensuring passenger comfort and safety, especially when navigating through urban environments with frequent stops and turns. The smoothness provided by Bezier curves helps in achieving more predictable and stable vehicle behavior, which is critical for the acceptance and integration of autonomous driving technologies. Moreover, the implementation of Bezier curves in the A* algorithm significantly improves computational efficiency. Smooth paths reduce the need for frequent recalculations and adjustments, thereby decreasing the overall computational load. This is particularly advantageous in real-time applications where rapid decision-making is crucial. The combination of Bezier curves and the A* algorithm allows for more efficient pathfinding, leading to faster execution times and better performance in dynamic environments.

3.4. Advantages of the Optimization in Smart Agricultural Navigation

In the realm of smart agriculture, the optimized A* algorithm, presented in Algorithm 1 and Figure 1, plays a pivotal role in improving the efficiency and precision of agricultural operations. As the demand for automation and precision farming grows, traditional algorithms often fall short in addressing the complexities of modern agricultural landscapes, which include uneven terrains, varying soil conditions, and the need for delicate manoeuvring around crops. The optimized A* algorithm, which incorporates both Euclidean and Chebyshev distances as heuristic functions, significantly improves pathfinding accuracy and adaptability. By leveraging the Euclidean distance, the algorithm ensures accurate straight-line measurements between points, which is crucial for open field operations where direct paths are preferred. Meanwhile, the Chebyshev distance is particularly effective in grid-based environments, allowing for diagonal movements that reduce the number of steps needed to navigate around obstacles. This hybrid approach ensures that the algorithm can efficiently handle a variety of agricultural scenarios, from navigating between rows of crops to maneuvering around equipment and structures.

Furthermore, the integration of Bezier curve smoothing into the pathfinding process addresses a critical limitation of the traditional A* algorithm—path smoothness. In the context of smart agriculture, smooth paths are paramount not only for minimizing damage to crops but also for ensuring the stability and efficiency of autonomous machinery. Bezier curves, known for their capability to produce smooth and continuous paths, enhance the practicality and safety of the generated routes for real-world applications. This improvement is particularly crucial for tasks such as automated planting, irrigation, and harvesting, where precise and smooth navigation directly translates to significant enhancements in operational efficiency and crop yield. By ensuring that machinery can traverse fields with minimal disruptions and reduced wear and tear, Bezier curves help maintain the integrity of both the equipment and the agricultural environment. This leads to more consistent and reliable operations, ultimately contributing to higher productivity and more sustainable farming practices. The seamless integration of Bezier curves into the A* algorithm exemplifies how advanced computational techniques can be leveraged to solve practical problems, thereby optimizing the performance of autonomous systems in agriculture and other domains requiring efficient path planning.

The optimized A* algorithm also significantly enhances computational efficiency, a crucial factor in real-time agricultural applications. By reducing the computation time required for route planning, the algorithm allows autonomous systems to respond more quickly to dynamic changes in the environment, such as the sudden appearance of obstacles or changes in terrain conditions. This improved responsiveness is essential for maintaining the continuous operation of agricultural machinery, which in turn increases productivity and reduces downtime. In the dynamic and often unpredictable agricultural environment, the ability to swiftly adapt to new situations ensures that tasks such as planting, irrigation, and harvesting can proceed without interruption. For instance, if an obstacle suddenly appears in the path of an autonomous robot, the optimized A* algorithm can quickly recalibrate the route, ensuring that the robot continues its operation with minimal delay. Similarly, if terrain conditions change due to unexpected weather, the algorithm can promptly update the navigation path to accommodate these new conditions, ensuring that the machinery operates efficiently and safely. This real-time adaptability not only enhances the reliability of autonomous agricultural systems but also maximizes their operational time. Moreover, the reduction in computation time leads to lower energy consumption, which is particularly beneficial in battery-operated machinery. This efficiency gain can extend the operational lifespan of the equipment, making the technology more sustainable and cost-effective. In essence, the optimized A* algorithm’s ability to enhance computational efficiency and real-time responsiveness provides a robust framework for the development of advanced agricultural machinery, ensuring that these systems are well-equipped to handle the complexities and demands of modern farming practices.

The adaptability and precision of this advanced algorithm make it a perfect fit for the demands of precision agriculture, where every decision can significantly impact yield, resource use, and overall farm sustainability. By providing accurate and smooth navigation, the enhanced A* algorithm helps farmers optimize field management practices, from planting and irrigation to harvesting. This optimization leads to increased crop yields, as machinery can operate more efficiently and precisely, reducing overlap and missed areas. It also contributes to cost savings by minimizing fuel consumption and wear on equipment, as machines can take more direct and smoother paths, avoiding unnecessary maneuvers and rough terrain. Furthermore, the enhanced A* algorithm supports sustainable farming practices. By ensuring that machinery operates efficiently and effectively, it helps reduce the environmental impact of farming activities. Efficient pathfinding and smooth navigation reduce energy consumption and soil compaction, preserving soil health and promoting better crop growth. Additionally, the algorithm’s ability to quickly adapt to changing conditions, such as new obstacles or varying terrain, means that it can support dynamic and responsive farming operations, essential for dealing with the uncertainties of agricultural environments.

3.5. Agricultural Unmanned Ground Vehicle (UGV)

Due to the fact that the vehicle must traverse terrain that is often uneven, a strong and resilient design was needed. One of the most important focuses was on ensuring the robot’s stability and reducing any oscillations that may potentially hinder its progress. In order to do this, it was necessary to pay close attention to the centre of gravity and ensure that it remained within the appropriate specifications. The dimensions of the vehicle were also carefully altered in order to accommodate the particular requirements of the function for which it was designed, which mostly entails moving through crop aisles that are somewhat small. With this modification, it is possible to go across the fields without any interruptions, guaranteeing that the journey is both efficient and damage-free without sacrificing safety.

The fact that the vehicle’s primary body may be removed is a notable characteristic that contributes to its adaptability. The fact that this invention makes it simple to carry from one field or site to another makes it a flexible and practical option for a wide range of agricultural applications. The vehicle’s body may be detached, which makes the logistics of transferring the vehicle easier to manage and enables more effective transit to various work locations. Furthermore, the framework of the vehicle, which is seen in Figure 2, is built from long-lasting metal components. The selection of this option was made in order to improve the durability and lifetime of the vehicle, guaranteeing that it is capable of withstanding the rigors of the often tough working circumstances presented in agricultural settings. We have greatly strengthened the car’s resilience to environmental stresses, corrosion, and different variables that may undermine its structural integrity by choosing metal for the frame. This has allowed us to significantly extend the lifespan of the vehicle.

Direct current (DC) motors were selected as the option for the vehicle’s propulsion system because of their accuracy and adaptability in regulating movement. This decision was made when the vehicle was developed. These direct current (DC) motors are designed to properly measure revolutions, which enables them to determine the lengths traveled with a high grade of precision. This level of accuracy is very necessary in the agricultural sector, where it is important to have perfect control over the motions of the vehicle in order to guarantee accurate planting and cultivation. Additionally, the way of gearbox has been subjected to special alterations in order to match the distinctive features of the robotic vehicle as well as the needs of planting and nurturing the target yield. These modifications have been made in addition to the selection of the propulsion system. Fields used for agriculture often present difficulties, such as tight rows or uneven terrain, which need the use of a gearbox system that is able to adjust to these situations successfully. By taking into account the dimensions and size of the vehicle, the improved gearbox system ensures that it is able to manoeuvre through the narrow gaps that exist between rows and effectively cover the area that has been allotted for planting and cultivation.

Through the use of this individualized approach to the gearbox, the performance of the vehicle is optimized, and the vehicle’s overall effectiveness and efficiency in the farming activities that it is designed to accomplish are enhanced. Through the customization of the communication system to meet the individual requirements of growing and growing crops, our objective is to maximize production while simultaneously minimizing waste, thus helping the implementation of agricultural techniques that are more sustainable and efficient, as seen in Figure 3.

The vehicle is fitted with an articulated arm that has five degrees of flexibility, which allows for flawless navigation through the thick foliage that is present in the crop. This cutting-edge arm design offers the dexterity and flexibility required to carry out a variety of activities in an agricultural setting in an effective manner. These jobs include planting, cultivation, and other precise operations. For the purpose of ensuring safe and accurate navigation across the fields while avoiding any impediments, a large number of block avoidance detectors and cameras have been strategically positioned around the perimeter of the robot. These sensors and cameras collaborate to perform constant monitoring of the environment. This improves the robot’s situational awareness and enables it to construct modifications to its course in real time, thereby preventing accidents and injury to both the engine and the vegetables that it works inside.

Receivers for the global positioning system (GPS) are included into the system of the vehicle in order to ensure precise location and path planning. This technology gives the robot the ability to determine its position, which helps with autonomous navigation and ensures that it runs exactly where it is required within the agricultural environment. When GPS signals are sent in unstructured settings that are located outside, the quality of the signals might vary based on elements such as the topography, vegetation, and meteorological conditions. When it comes to the majority of farming applications, however, where high accuracy is not an absolute must, the GPS solution that is incorporated into the system of the vehicle ought to be adequate and satisfactory.

An emergency control has been painstakingly built into the design of the robot in order to ensure the safety of the passengers. This safety feature is a failsafe system that enables users to immediately cut off the supply of energy to the different components of the vehicle in the event that an unexpected emergency or danger occurs. Because of its power to immediately shut down, accidents may be avoided, and both the vehicle and its operators are protected. Additionally, light-emitting diode (LED) lights have been strategically fitted on the vehicle in order to facilitate field identification and tracking at convenient intervals. The presence of these lights makes it much simpler to find the automobile among the enormous spectrum of the domain, even when there is a lack of light. As a result of this feature, operational efficiency is improved since it makes it easier to locate and retrieve the vehicle in a timely manner when it is required. This, in turn, contributes to a more streamlined and productive agricultural workflow shown in Figure 4.

4. Simulation and Analysis

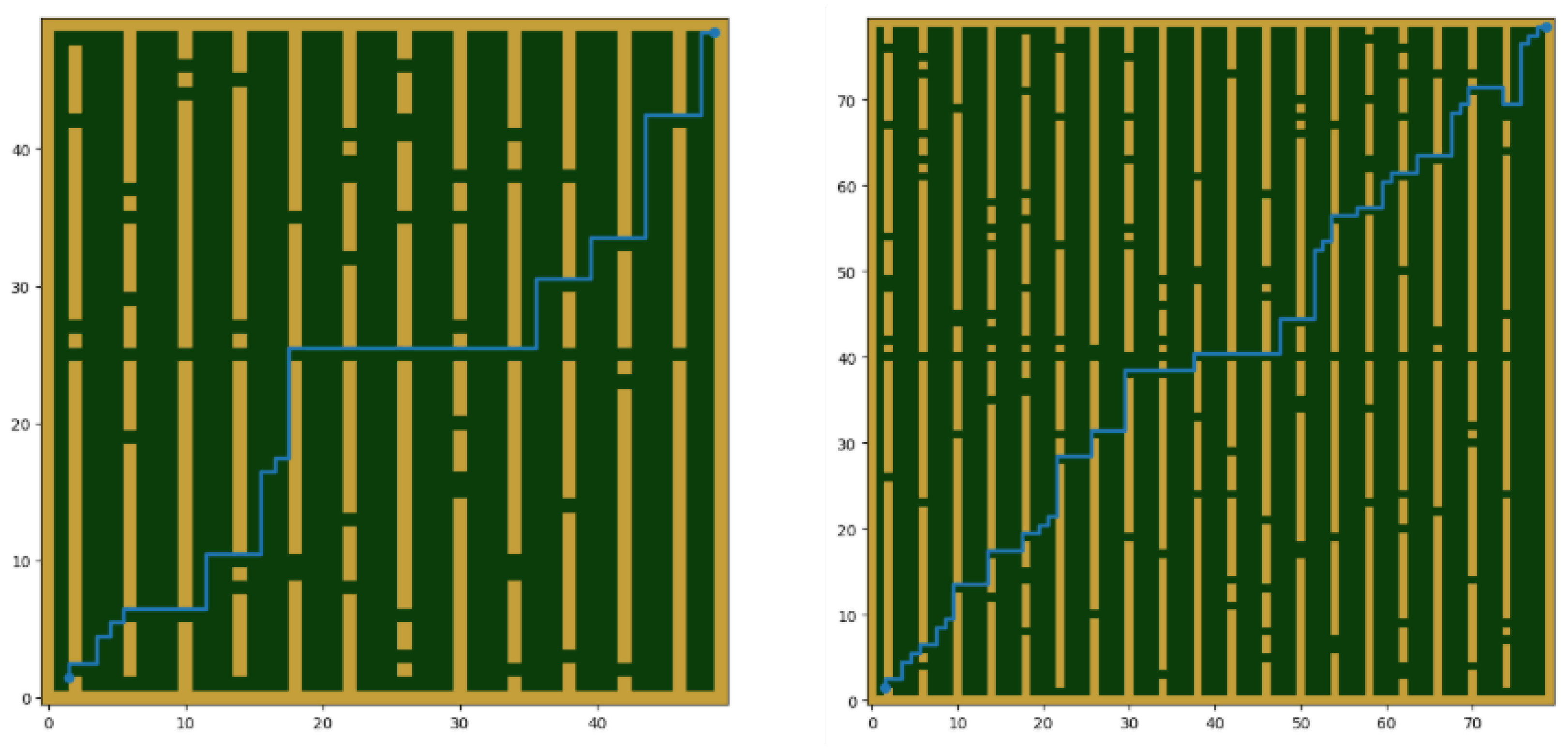
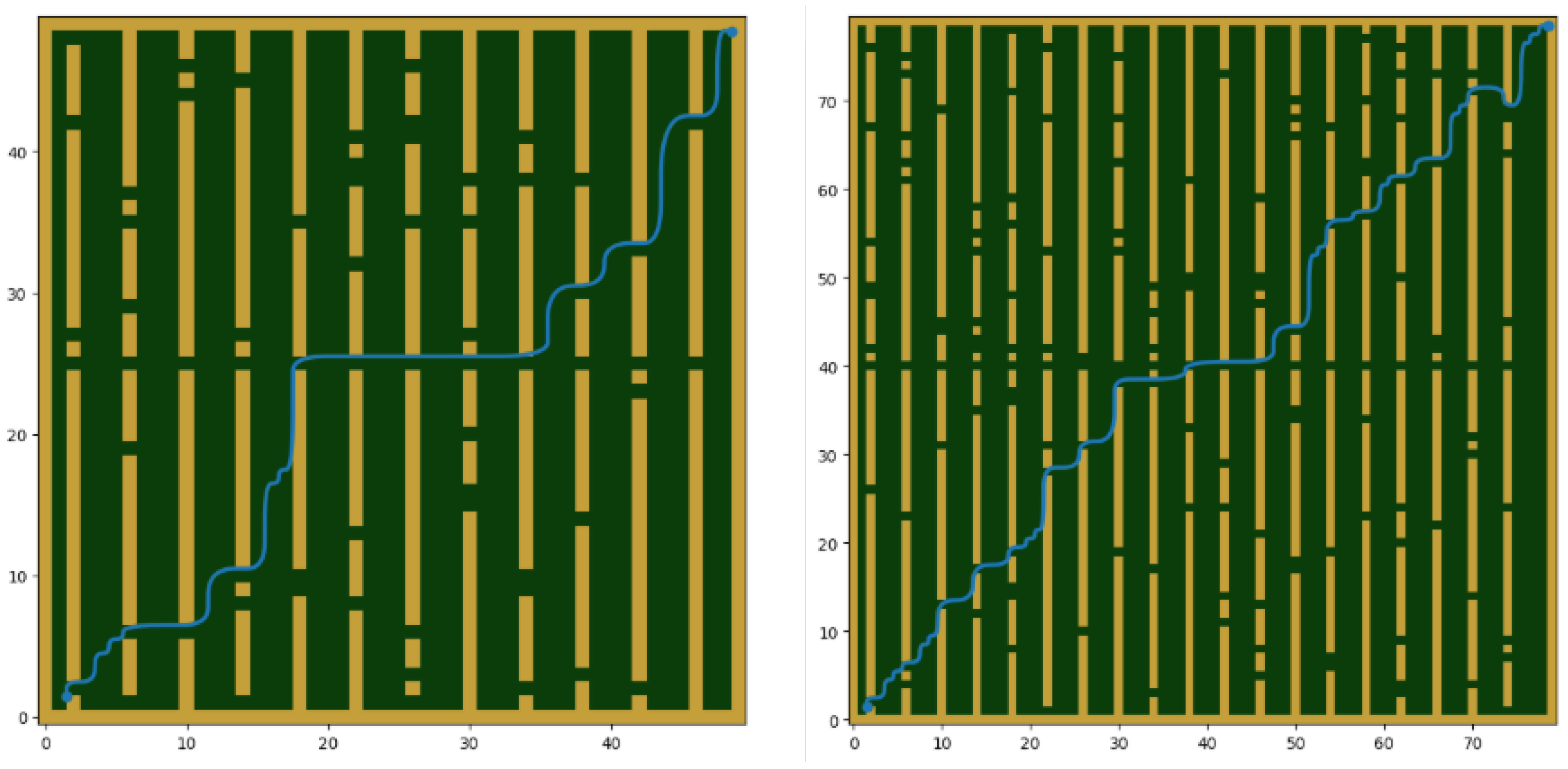
All of the tests using the A* method were carried out on a computer with 32 gigabytes of random access memory (RAM) and an Intel NUC i5 processor. The Python programming language was used. Extending the A* method with the Euclidean and Chebyshev distances as a heuristic, the A* algorithm is shown in Figure 5. Euclidean and Chebyshev distances, as well as the incorporation of multi-order Bezier curves, are shown in Figure 6 to showcase the improved capabilities of the method.

Figure 5 depicts the route generated by the A* algorithm as a series of straight lines connecting grid points. This path utilizes a hybrid heuristic that combines Euclidean and Chebyshev distances, allowing the algorithm to calculate the shortest path while considering diagonal movements in a grid-based environment. The path is optimal in terms of distance but appears angular, with sharp turns at each grid intersection. These sharp turns can be problematic in real-world applications, particularly in agricultural settings where smooth navigation is essential to avoid damaging crops and ensure autonomous machinery’s stability. Figure 6 demonstrates the same pathfinding process but with the integration of multi-order Bezier curves to smooth the generated route. The Bezier curves transform the angular path into a smooth, continuous curve. This smoothing is achieved by using control points that guide the Bezier curves, resulting in a path that is not only optimal in length but also much more practical for real-world navigation. The smoothed path reduces sharp turns and abrupt changes in direction, enhancing the safety and efficiency of autonomous agricultural machinery. The integration of Bezier curves eliminates sharp corners, which can help reduce wear and tear on machinery and minimize the risk of damaging crops.

We compared the baseline A*, the optimized A* (without Bezier), and the optimized A* with Bezier smoothing on three map sizes representing agricultural plots of increasing area: 30 × 30, 50 × 50, and 80 × 80 cells. All maps were generated with the same orchard-like pattern (fixed row spacing and thickness), so the obstacle layout scales naturally with field size. Obstacles represent permanent agricultural structures—tree trunks and planted crop rows (e.g., vineyards, olive groves)—that restrict the navigable free space. Start and goal were placed at opposite corners. For each scenario we ran 20 randomized map instances to capture variability and avoid bias toward any single layout. The evaluation considered computation time, path length, and the number of generated search routes under diverse navigation challenges, including narrow passages and frequent direction changes.

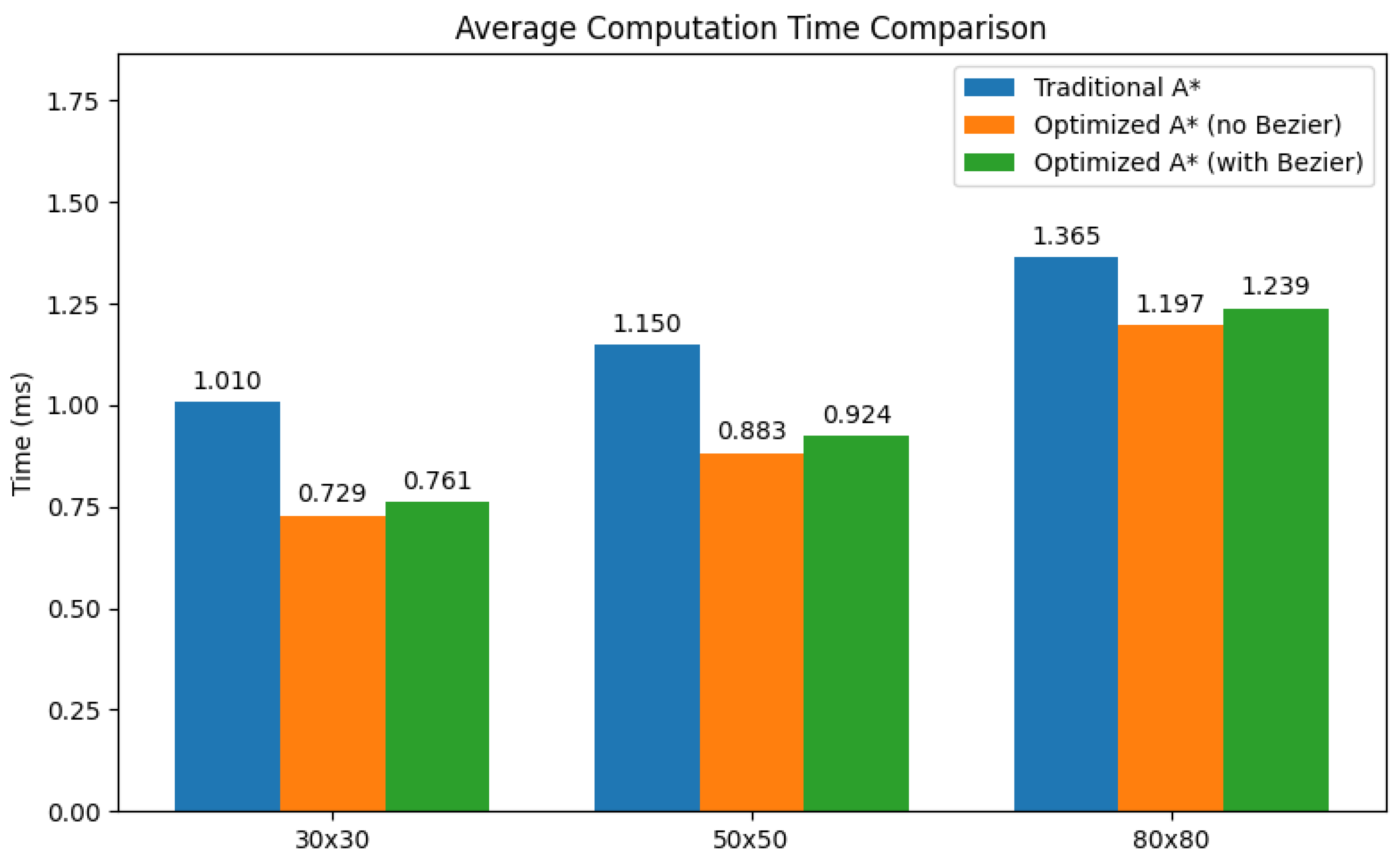
4.1. Evaluation of Time Performance

Table 1. Average computation time (ms) over 20 runs for traditional A*, optimized A* without Bezier, and optimized A* with Bezier smoothing on three grid sizes.

Map Size (Cells)	Time (ms)
	Trad. A*	Opt. A* (no Bezier)	Opt. A* (with Bezier)
30 × 30	1.010	0.729	0.761
50 × 50	1.150	0.883	0.924
80 × 80	1.365	1.197	1.239

and Figure 7 present the average computation time (in milliseconds) for the traditional A*, the optimized A* without Bezier curves, and the optimized A* with Bezier smoothing across three map sizes. The results, averaged over 20 runs, show an increase in computation time as the grid size grows, which is expected since larger maps require evaluating more nodes and potential paths. The optimized A* consistently outperforms the traditional version in all cases, achieving up to approximately 28% faster execution on the smallest map (0.729 ms vs. 1.010 ms). When Bezier smoothing is applied to the optimized A*, there is a slight increase in computation time compared to the version without smoothing; however, this overhead is minimal, generally less than 5%, indicating that the additional step of generating smoother paths has a negligible impact on performance. These results demonstrate that the optimized A* significantly outperforms the traditional implementation in terms of computational efficiency, and that the inclusion of Bezier smoothing, while adding a minor processing cost, provides smoothed paths with only a negligible time penalty.

4.2. Evaluation of Path Length Performance

Table 2. Average path length (units) over 20 runs for traditional A*, optimized A* without Bezier, and optimized A* with Bezier smoothing on three grid sizes.

Map Size (Cells)	Path Length (Units)
	Trad. A*	Opt. A* (no Bezier)	Opt. A* (with Bezier)
30 × 30	62.45	54.27	47.35
50 × 50	102.90	94.63	83.11
80 × 80	179.10	158.02	135.46

and Figure 8 present the average path length, measured in units, for the traditional A*, the optimized A* without Bezier curves, and the optimized A* with Bezier curve smoothing, evaluated across three grid sizes. In all cases, the optimized A* produces shorter paths than the traditional version, with reductions of approximately 13% for the smallest map and 12% for the largest. The inclusion of Bezier smoothing further decreases the path length by eliminating sharp turns and producing smoother trajectories, leading to reductions of up to around 15% compared to the optimized A* without smoothing. As the grid size increases from 30×30 to 80×80, the absolute path lengths naturally grow, reflecting the greater distances between start and goal nodes; however, the relative improvement from Bezier smoothing remains consistent. These results indicate that the combination of optimization techniques and Bezier smoothing not only improves computational efficiency but also produces more direct and smoother paths, which can be advantageous for applications requiring smooth motion, such as agricultural robotics.

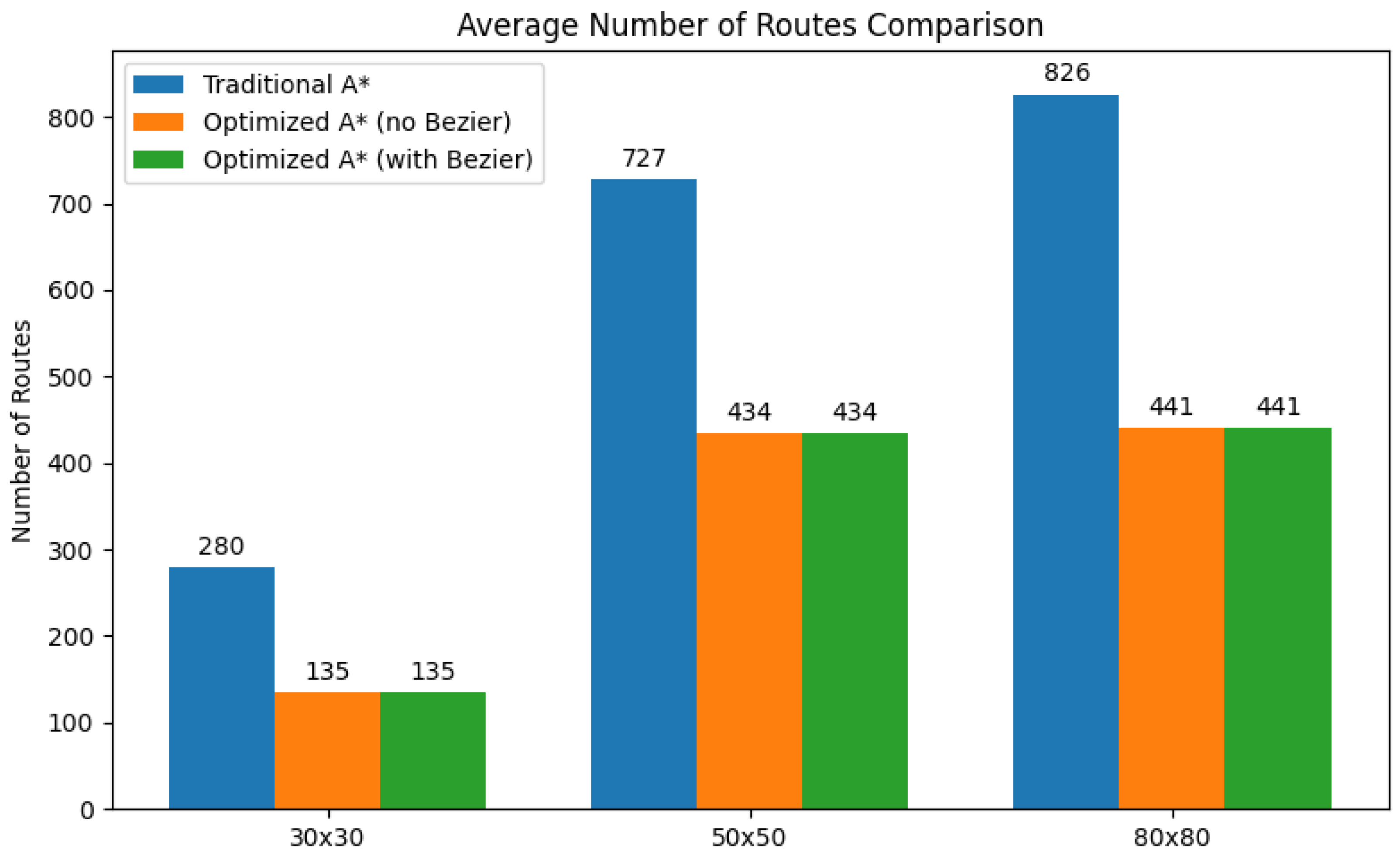
4.3. Evaluation of Route Generation Performance

Table 3. Average number of routes (over 20 runs) for traditional A*, optimized A* without Bezier, and optimized A* with Bezier smoothing on three grid sizes.

Map Size (Cells)	Routes
	Trad. A*	Opt. A* (no Bezier)	Opt. A* (with Bezier)
30 × 30	280	135	135
50 × 50	727	434	434
80 × 80	826	441	441

and Figure 9 present the average number of routes generated over 20 runs for the traditional A*, the optimized A* without Bezier curves, and the optimized A* with Bezier smoothing, evaluated across three grid sizes. The results indicate that the optimized A*—both with and without Bezier smoothing—produces significantly fewer routes than the traditional implementation, with reductions exceeding 50% for all map sizes. This reduction suggests that the optimization process effectively prunes unnecessary or suboptimal paths, focusing the search on a smaller set of high-quality candidates. Notably, the inclusion of Bezier smoothing does not alter the number of routes produced, as this step is applied after the pathfinding stage and affects only the geometry of the final path rather than the number of alternative routes considered. As the grid size increases, the total number of routes grows for all methods, reflecting the larger search space; however, the gap between the traditional and optimized implementations remains substantial, demonstrating the scalability of the optimization approach.

These improvements collectively suggest that the optimized A* algorithm is significantly more efficient and effective than its traditional counterpart. By integrating Euclidean and Chebyshev distances into the heuristic function and incorporating Bezier curve smoothing, the optimized algorithm not only reduces computation time and path length but also minimizes the number of search routes. These enhancements make it a robust choice for modern navigation challenges, particularly in fields like precision agriculture, robotics, and autonomous vehicle navigation. The ability to quickly and efficiently find the optimal path ensures that the optimized A* algorithm can meet the high demands of these advanced applications, driving forward the capabilities of smart systems and contributing to their success in real-world scenarios. The outcomes clearly demonstrate that the proposed optimizations provide tangible benefits, paving the way for more advanced and efficient pathfinding solutions.

4.4. Computational Overhead of Bezier Smoothing

The integration of Bezier curve smoothing into the optimized A* algorithm introduces a measurable but minimal computational overhead. As shown in Table 1, the execution time of the optimized A* without Bezier curves was recorded as 0.729 ms, 0.883 ms, and 1.197 ms for grid sizes of 30 × 30, 50 × 50, and 80 × 80 cells, respectively. When Bezier smoothing was applied, the times increased slightly to 0.761 ms, 0.924 ms, and 1.239 ms for the same map sizes. These differences correspond to an overhead of approximately 4.39%, 4.64%, and 3.51%, respectively.

For real-time navigation systems, these values are extremely small, especially considering that many embedded platforms operate with control loop cycles on the order of several milliseconds. For example, in a scenario where path re-planning occurs every 50 ms, the additional computation introduced by Bezier smoothing would consume less than 0.1% of the total available cycle time. This suggests that, under typical operational conditions, the inclusion of Bezier smoothing is unlikely to threaten real-time performance constraints.

Moreover, as shown in Table 3, Bezier smoothing does not alter the number of search routes produced, since it is applied after the optimal path has been found and affects only the path geometry. However, Table 2 demonstrates that it consistently reduces path length by 12–15% compared to the unsmoothed optimized A*, primarily by eliminating sharp turns and generating more direct trajectories.

Despite the slight increase in computation time, Bezier smoothing provides tangible operational benefits, notably improving motion smoothness and stability. This can lead to reduced mechanical stress on actuators, improved energy efficiency, and more predictable motion behavior—critical factors in applications such as agricultural robotics, mobile robot navigation, and autonomous vehicle guidance.

5. Discussion

Our methodology, as evidenced by the results, demonstrates that integrating the hybrid heuristic with Bezier curve smoothing significantly improves both path length and computation time compared to the conventional A* algorithm. This indicates that the proposed method not only generates shorter and smoother trajectories but also achieves these improvements with lower computational cost, making it suitable for real-time robotic navigation. The reduction of sharp turns through Bezier smoothing enhances the kinematic feasibility of the generated paths, which is particularly critical in agricultural robotics applications. In such environments, robots often operate in narrow crop rows, around irregularly shaped plots, and in proximity to delicate plants or farm infrastructure, where precise maneuvering and consistent clearance from obstacles are essential. The ability to generate dynamically feasible, smooth paths contributes to safer operation, reduced risk of crop damage, and improved efficiency in task execution under the spatial and operational constraints typical of agricultural settings.

In its current form, the proposed method is designed for static obstacle configurations during path planning, which matches the environment models used in our experiments. When obstacles are dynamic, any change that results in an obstacle intersecting the current path triggers a re-execution of the A*-based planning stage on the updated occupancy grid. The hybrid heuristic, combining Euclidean and Chebyshev distances, remains fully applicable without algorithmic modifications, since it evaluates costs directly from the updated grid state. For the smoothing phase, the Bezier curve computation is applied only to the newly affected path segments rather than the entire trajectory, which significantly reduces recomputation time. This incremental reapplication maintains curvature continuity while preventing unnecessary processing of unaffected segments. Nonetheless, in environments with high-frequency and unpredictable obstacle motion, the method’s real-time performance will be determined by the detection system’s update rate, the replanning cycle latency, and the computational capacity available for repeated path generation and selective smoothing.

The proposed hybrid Euclidean–Chebyshev heuristic differs from model-free and metaheuristic approaches, such as the model-free online optimization method and BAS-ADAM [49], in that it is specifically tailored for deterministic, grid-based path planning within the A* framework. While model-free and BAS-ADAM methods are effective for general nonlinear optimization problems and can handle complex, unstructured search spaces, they require iterative optimization and may incur higher computational costs, making them less suited for real-time embedded navigation. This distinction is particularly relevant in agricultural navigation, where path planning must be executed reliably within strict time and hardware constraints, making deterministic and computationally efficient methods preferable over more flexible yet computationally heavier metaheuristic optimizers.

The findings highlight the practical benefits of combining a hybrid Euclidean–Chebyshev heuristic with selective Bezier curve smoothing for efficient and kinematically feasible path generation in agricultural navigation. Compared to conventional A*, the proposed approach delivers improvements in trajectory quality and planning time while maintaining computational efficiency suitable for embedded robotic platforms. Although the current implementation assumes static obstacle configurations, the underlying principles can be extended to support incremental replanning in dynamic environments. These extensions would broaden the applicability of the method to more complex and unpredictable field scenarios, such as environments with moving machinery, workers, or animals, for precision agriculture operations where safety, efficiency, and path smoothness are paramount.

6. Conclusions and Future Work

The enhancements made to the A* algorithm significantly enhance its performance in agricultural applications, addressing key limitations related to path smoothness and adaptability to challenging terrains. By integrating Euclidean and Chebyshev distances into a single heuristic function, we have developed a more flexible and accurate pathfinding approach that leverages the strengths of both distance measures. The Euclidean distance provides a precise straight-line metric for open, unobstructed spaces. In contrast, the Chebyshev distance effectively manages scenarios that allow diagonal movement, making the algorithm adept at navigating complex agricultural landscapes. The incorporation of Bezier curves further refines the algorithm, ensuring smoother and more practical paths. This refinement is essential for minimizing crop damage and optimizing operational efficiency, as it allows agricultural machinery to traverse uneven and obstacle-laden terrains more smoothly and safely. Our extensive simulations and tests in various rural environments have demonstrated the viability and potential of this enhanced algorithm, showcasing notable reductions in both path length and computation time compared to the traditional A* algorithm. These improvements enhance the algorithm’s efficiency and contribute to more sustainable farming practices by reducing fuel consumption and operational time. Our future study will focus on the development of adaptive heuristics that dynamically adjust based on real-time environmental feedback. This adaptability will further enhance the algorithm’s ability to handle unforeseen obstacles and changes in terrain, making it even more robust and reliable in the ever-changing agricultural environment.