Abstract
This article provides an in-depth review of the concepts of interpretability and explainability in machine learning, which are two essential pillars for developing transparent, responsible, and trustworthy artificial intelligence (AI) systems. As algorithms become increasingly complex and are deployed in sensitive domains, the need for interpretability has grown. However, the ongoing confusion between interpretability and explainability has hindered the adoption of clear methodological frameworks. To address this conceptual ambiguity, we draw on the formal distinction introduced by Dib, which rigorously separates interpretability from explainability. Based on this foundation, we propose a revised classification of explanatory approaches structured around three complementary axes: intrinsic vs. extrinsic, specific vs. agnostic, and local vs. global. Unlike many existing typologies that are limited to a single dichotomy, our framework provides a unified perspective that facilitates the understanding, comparison, and selection of methods according to their application context. We illustrate these elements through an experiment on the Breast Cancer dataset, where several models are analyzed: some through their intrinsically interpretable characteristics (logistic regression, decision tree) and others using post hoc explainability techniques such as treeinterpreter for random forests. Additionally, the LIME method is applied even to interpretable models to assess the relevance and robustness of the locally generated explanations. This contribution aims to structure the field of explainable AI (XAI) more rigorously, supporting a reasoned, contextualized, and operational use of explanatory methods.
1. Introduction
The interpretability and explainability of artificial intelligence (AI) models have garnered increasing attention, particularly as a means of ensuring transparency, accountability, and trust in algorithmic decisions. This concern is especially critical in high-stakes domains such as education, finance, and healthcare, where a lack of understanding of model outputs can raise ethical concerns, hinder user trust, and challenge regulatory compliance. Despite growing demand, the field continues to suffer from conceptual ambiguity—most notably, the interchangeable use of the terms interpretability and explainability. This lack of clear distinction not only affects theoretical discussions but also hinders the design and assessment of reliable explanation methods.
Numerous studies have explored interpretability and explainability from different perspectives, including the explanation of deep learning models [1], interpretable approaches in heterogeneous catalysis [2], and technical challenges related to interpretable machine learning [3]. Several surveys have proposed taxonomies of explainability methods [4] or compared explanatory techniques in specific applications, such as offensive language detection [5].
However, as highlighted in recent surveys and position papers [3,4,6], the diversity of approaches and the lack of a unified framework complicate the adoption of standardized methodologies for understanding model behavior. These challenges are compounded by the conceptual overlap between interpretability and explainability, which hinders rigorous evaluation, reproducibility, and the comparison of methods across studies. Our work directly addresses these gaps by proposing a structured and multidimensional clarification of core concepts, thus contributing to the consolidation of the field and enabling more coherent methodological developments.
To address these issues, this work focuses on supervised machine learning models—the most commonly deployed models in real-world decision-making systems—and aims to clarify the conceptual foundations of interpretability and explainability.
This work builds upon a formal distinction recently proposed in the literature [7], which explicitly separates interpretability from explainability. In this formalization, local explainability refers to the ability to provide a clear and understandable justification for each individual prediction , meaning that for every input–output pair, there exists an explanation that makes the decision intelligible to users. In contrast, global interpretability relates to the overall comprehensibility of the model’s decision function such that users can grasp the model’s behavior as a whole without requiring per-instance explanations.
Based on this systematic foundation, we propose a unified classification of explanatory approaches, which are structured along three complementary dimensions: (1) intrinsic vs. extrinsic, (2) model-specific vs. model-agnostic, and (3) local vs. global. Unlike existing taxonomies, which are often limited to a single axis of classification, our framework provides a more systematic and multidimensional view of explanation methods. It is designed to enhance clarity and facilitate the comparison, selection, and evaluation of approaches across various application contexts.
This article is structured as follows. Section 2 introduces key definitions and conceptual clarifications related to interpretability and explainability, which are grounded in recent formal developments. Section 3 reviews classical approaches for understanding model decisions, distinguishing between inherently interpretable models and those relying on post hoc explanations. Section 4 presents our unified classification of explanatory methods, which is organized along the three aforementioned dimensions. Section 5 illustrates the application of these methods to standard machine learning models, analyzing the relevance and effectiveness of the generated explanations. Section 6 discusses the limitations of current approaches and highlights the main methodological challenges. Finally, Section 7 concludes by summarizing the key contributions of this work and outlining directions for future research in explainable AI.
While existing taxonomies (e.g., [4]) typically focus on one or two axes of classification, our contribution provides a multidimensional structure grounded in the latest formal advances [7], thus responding to calls for conceptual clarity and methodological rigor in the field of explainable AI [3,6].
2. Definitions and Concepts
The opacity of machine and deep learning algorithms has increased the need for techniques that enhance their transparency, making interpretability and explainability essential for data scientists. However, the lack of formal or mathematical definitions for these concepts [8] has led to semantic ambiguity. This ambiguity underscores the necessity for terminological clarification to support the development of robust algorithms and strengthen user trust. A recent contribution in the literature has proposed a more precise formal definition of model interpretability and explainability [7].
As interest in these notions has grown, so too has the diversity of terminology, which must be explored through the main definitions proposed in the literature.
To begin with, interpretability has been defined in various ways. It has been described as “the ease with which an analyst infers underlying data” [9], as a process of generating explanations for users [10], and as “the degree to which a human can understand the cause of a decision” [11]. This diversity of definitions has been criticized for its lack of precision, with some emphasizing that the concept varies across contexts [12].
Explainability is sometimes used interchangeably with interpretability and described as the ability to provide complete and accessible information to a user [13]. However, some works distinguish the two concepts. One distinction is based on the intended audience: explainability involves accessible, natural language suited for non-experts, while interpretability targets technical users with more specialized language [14]. Another distinction relies on the object of explanation: explainability focuses on a specific prediction, while interpretability seeks to understand the overall functioning of the model [11,15].
Adding to the confusion, some researchers acknowledge this distinction between understanding the model and understanding a prediction but adopt different terminology. They refer to local explainability for a prediction and global explainability for the model as a whole [16,17,18,19]. Others speak of interpretability at the learning stage versus at the prediction stage [20]. The term understanding is also sometimes used as a synonym for interpretability, further contributing to the ambiguity [21].
Certain key properties of learning algorithms, related to their explainability and interpretability, have been highlighted. These characteristics deserve particular attention due to their impact on user comprehension and trust in learning systems. Comprehensibility is defined as a property of machine learning algorithms that produce understandable models [22], or, according to others [23], as a characteristic of the model’s individual components, where each variable or parameter is clearly explained.
Transparency refers to a model whose decision-making logic is directly readable and understandable by the user [24]. Some authors explicitly distinguish transparent models from black-box models [6,25], noting that transparency can relate to either interpretability or explainability, depending on the type of understanding the user seeks.
Finally, interactivity is a property that allows users to visualize and correct the model’s predictions [26,27,28], thus stemming from the system’s explainability.
For illustration, a decision tree is often considered interpretable because a user can directly follow the decision path from root to leaf using feature thresholds, which allows for immediate understanding of how the output is generated. In contrast, black-box models such as neural networks require post hoc explanation methods—such as LIME [15] or SHAP [29]—to approximate the influence of individual features on a given prediction. These explanation techniques provide local insights that help users understand why a specific decision was made, even when the internal logic of the model is not directly accessible.
The various definitions and distinctions presented above illustrate the conceptual ambiguity surrounding interpretability and explainability. To address this confusion, we adopt a formal clarification in which interpretability refers to a model’s capacity to be understood by a user, while explainability involves providing understandable justifications for the decisions made by that model [7].
This formal distinction complements and clarifies earlier influential definitions. For example, Lipton (2016) [12] categorized interpretability into transparency and post hoc explanations but did not always separate them conceptually. Similarly, Doshi-Velez and Kim (2017) [10] proposed interpretability as the ability to explain or present a model in understandable terms, but their operational taxonomy left room for ambiguity. In contrast, the framework proposed by Dib (2024) [7] offers a more rigorous separation between interpretability—linked to intrinsic model understanding—and explainability—focused on external justification through additional methods. This distinction fosters conceptual clarity and supports the development of a unified classification of explanatory methods.
The next section surveys standard approaches used to interpret or explain the decisions made by machine learning models.
3. Common Approaches for Understanding the Decision Making of Machine Learning Models
Interpreting and explaining the decisions made by machine learning models has become a key challenge both for scientific validation and for building user trust and supporting informed decision making. This section provides an overview of the main current approaches used to make these models more transparent and understandable. We begin with so-called interpretable models, such as decision trees or rule lists, which provide direct access to the logic underlying predictions. We then present explainable artificial intelligence (XAI) techniques developed to explain the behavior of more complex models, such as deep neural networks, using methods like feature importance analysis, Shapley values, or dependency graphs.
3.1. Interpretable Models
Interpretable models are designed to be easily understood due to their simple and transparent structure. Examples include the following:
- Shallow Rule-Based Models: These models use simple logical rules for classification. For instance, a two-layer model was proposed in which each neuron represents a simple rule, and the output is a disjunction of these rules, thereby facilitating interpretation [30]. Classifiers based on association rules were also introduced to ensure efficiency with sparse data [3,31].
- Linear Models: These models detect interactions between features. A hybrid model combining rough sets and linear models was developed to enhance interaction detection and feature selection [32].
- Decision Trees: These models are highly interpretable due to their hierarchical structure, which explicitly displays decision rules and feature importance. Features closer to the root have a stronger influence on predictions.
3.2. XAI Approaches
XAI approaches are applied after the model has been trained with the goal of making complex models more understandable. They include result visualization, feature contribution analysis, and model simplification.
- Feature Contribution Analysis: This approach aims to understand and illustrate the impact of each feature on a model’s predictions. It relies on techniques such as SHAP (SHapley Additive exPlanations) values, which quantify and visualize the individual contribution of each variable to a given prediction using summary plots, dependency graphs, or heatmaps based on SHAP values [29]. Dependency plots, for instance, show how predictions change depending on the variation of one or more features, thus helping identify feature interactions [33]. Furthermore, permutation importance scores are used to evaluate the overall influence of features on the model by identifying the attributes with the most significant impact on predictions [34]. These tools are essential for interpreting and explaining model decisions by making the relationships between input data and outputs more transparent.
- Surrogate Models: The simplification of complex models, also known as surrogate modeling, involves replacing a complex and opaque model with a simpler one that mimics its behavior. The goal is to enhance explainability while maintaining satisfactory accuracy. For example, model distillation trains a simplified model from the predictions of a complex model, so that for any data input X, the simplified model approximates the behavior of the original model [35]. Surrogate models can be applied globally, replicating the predictions across the entire input space, or locally, focusing on explaining a specific prediction. A global surrogate offers interpretability across the full domain, while a local surrogate provides a targeted explanation for a specific decision. This approach reconciles the performance of advanced models with interpretability requirements, thereby enhancing user understanding and trust.
- Post hoc and Agnostic Explainability Methods: These methods are applied after training complex models, without requiring access to their internal structure, to interpret predictions and improve model transparency. Among the most common techniques, LIME (Local Interpretable Model-agnostic Explanations) builds a simple, interpretable local model around a specific prediction, highlighting the most influential features behind the decision [15]. SHAP, on the other hand, is based on Shapley values from cooperative game theory [36], which fairly distribute the total gain (i.e., prediction) among all features by considering all possible coalitions of features. Each feature’s contribution is computed as its average marginal effect across all possible subsets of features [37]. This ensures consistency and additivity, providing both local and global explanations of feature importance. These agnostic techniques can be applied to any machine learning model and are essential tools for fostering the trust, understanding, and validation of AI systems.
Several classifications of these methods have been proposed to structure the field according to various criteria. However, these typologies often show limitations, as they do not always provide clear or practical guidance for selecting the most appropriate method in real-world applications.
4. Classification of Methods in Explainable AI
A classification serves as a structured framework to organize and categorize the various methods used to understand the decision-making processes of machine learning models. It helps improve the understanding of existing methods, facilitates their comparison, and guides their selection according to the application context. By distinguishing methods based on fundamental criteria such as how they integrate with the model (intrinsic or extrinsic), their model dependency (specific or agnostic), and their scope of explanation (local or global), a structured classification enhances transparency and trust in AI systems. In this section, we first discuss classifications proposed in the literature and highlight their limitations. We then present in detail the classification we propose as a unifying framework.
4.1. Limitations of Existing Classifications
One of the most widespread classifications is based on the distinction between local and global explanations [15], where local methods explain a specific prediction, while global methods aim to provide an overall understanding of the model. Another important classification differentiates between post hoc and ad hoc approaches [10]: the former apply explanation techniques after the model is trained, while the latter embed interpretability mechanisms directly into the model design. A distinction is also made between intrinsically interpretable models and those requiring external explanations [38].
Other works have introduced classifications based on complementary criteria. One classification distinguishes methods according to their model specificity: on one hand, model-specific approaches, and on the other, agnostic approaches that use interpretable models as global approximations of complex models [39]. However, this classification does not fully capture methodological nuances or the limitations of agnostic techniques depending on the complexity of the underlying models.
Another classification focuses on model accessibility and the nature of the explanations provided, aligning with the distinction between explainability and interpretability [40]. This approach emphasizes the granularity of explanations (local or global) but does not address the suitability of explanatory methods to different types of data and application domains.
Despite their utility, these classifications present several limitations that reduce their applicability in real-world contexts. Notably, there is frequent confusion between interpretability and explainability in the literature. Some works emphasize post hoc approaches without clearly distinguishing interpretability (a human’s ability to directly understand a model) from explainability (the ability of a method to provide an a posteriori explanation) [10,15]. Others criticize this confusion, noting that some so-called explainable methods are actually post hoc interpretation techniques that do not guarantee genuine understanding of the underlying model [38]. While the local/global distinction is widely adopted, its relevance has been questioned by some researchers.
It has also been observed that global explanations do not necessarily lead to better understanding for end users, especially when models are complex [41]. Moreover, this distinction can create the illusion that a global explanation is sufficient to render a model understandable, even though interpretability also depends on the simplicity and structure of the underlying model.
Finally, most classifications focus on the technical characteristics of the methods without considering their relevance to specific domains such as medicine, education, or finance. Some categorizations, such as those based on model specificity, overlook how explanations are perceived and used in practice [39]. Others fail to address the alignment of explanatory methods with sector-specific requirements, thereby limiting their usefulness for end users with distinct needs [40].
To address these limitations, we propose a classification that explicitly integrates the concepts of explainability and interpretability. This classification is based on three fundamental axes and rests on a clear distinction between interpretability and explainability, as derived from dimensions outlined in the literature. It avoids conceptual confusion and enables a critical analysis of how these two concepts relate to each other, their interactions, and their limitations in the use of explanatory methods. Additionally, by taking into account the application context and the type of data, our classification helps evaluate the suitability of different methods in light of domain-specific requirements. It aims to go beyond the limitations of existing typologies by offering a more refined analysis of the various approaches. It thus facilitates the selection of the most appropriate methods according to the specific constraints of the problem under study, thereby strengthening the relevance and effectiveness of explanations provided by explainable AI models.
4.2. Toward a Formal Classification of Explainability and Interpretability Methods
To rigorously structure the various approaches to explainability and interpretability in artificial intelligence, we propose a classification grounded in a formal distinction that clearly separates the two concepts [7]. This classification is articulated around three key dimensions: (1) local versus global, (2) intrinsic versus extrinsic, and (3) model-specific versus agnostic. By organizing methods along these complementary dimensions, this framework provides a unified perspective that not only enables a systematic comparison of explanatory techniques but also supports their selection based on transparency requirements and model comprehension needs.
Recent methods such as TCAV [42] also illustrate how explanation techniques continue to evolve. TCAV provides concept-based, human-aligned global explanations, while attention weights in models like BERT or GPT [43] may serve as intrinsic explanations, highlighting input regions of interest.
Local vs. Global: The first axis of classification categorizes explanation methods according to the scope of their application, global or local. Local explanations aim to justify individual predictions without necessarily analyzing the model’s internal functioning. This sheds light on a specific decision by attributing contributions to input features, as seen with LIME [15], ANCHOR [44], and SHAP [29]. According to a formal definition [7], this corresponds to explaining the output for a given input .
Global explanations, on the other hand, provide an overall view of the model by analyzing how features influence predictions across the entire dataset [45]. Methods such as GIRP and DeepRED aim to generate coherent global explanations [39]. However, global explanations may overlook important local variations. A feature with low global importance can be decisive in certain instances, emphasizing the need to combine both perspectives. Although local explanations can sometimes be aggregated to form a global understanding, this transition is not always straightforward. Naively aggregating local explanations can lead to compensatory effects or biases, especially in nonlinear models with complex feature interactions. This is particularly true for methods such as LIME and SHAP, which, although effective for explaining individual predictions, may give a distorted view of the overall model behavior when improperly aggregated.
Interpretability, whether local or global, relies on the model’s intrinsic transparency, allowing for immediate understanding of its operation without the need for an external explanatory model. Local interpretability refers to the internal understanding of the model at the level of a single instance. It is provided by inherently understandable models, such as shallow decision trees or rule-based systems, which enable a direct explanation of each prediction [10,46]. At the global level, interpretability is supported by transparent models like shallow decision trees or linear models, which provide a clear view of the model’s general reasoning process [38,47].
This first dimension (local vs. global) will subsequently be combined with the two other complementary axes. This multidimensional structuring aims to go beyond traditional binary classifications and to propose a unified framework that enables a more systematic and context-sensitive analysis of explanatory methods.
Intrinsic vs. Extrinsic: This category focuses on model transparency, which is why the distinctions between interpretability and explainability may appear minimal in certain contexts. However, a possible nuance is that explainability places greater emphasis on understanding specific decisions made by the model, whereas interpretability emphasizes understanding the overall functioning of the model.
Intrinsic explainability refers specifically to the model’s ability to make its decisions understandable directly from its internal structure without the need for external techniques or post hoc methods. In other words, the decisions made by the model are naturally explicit due to how the model is designed. For instance, a decision tree provides a direct explanation for each decision made for a given instance without the need for additional interpretive tools. Conversely, extrinsic explainability concerns opaque models, such as neural networks or random forests, whose decisions require post hoc approaches. These methods use interpretable surrogate models or approximation techniques to make the predictions understandable. For example, LIME constructs a locally interpretable model to explain a prediction and aggregates these explanations to provide a global view of the model [15]. SHAP, on the other hand, assigns contributions to features using Shapley values, thereby offering insights into the impact of each feature [29].
Intrinsic interpretability refers to a model’s ability to be understood directly in its entirety due to its transparent structure, where the relationships between input variables and outputs are evident. Transparent models like decision trees and linear regressions exemplify this notion, as they allow users to comprehend the internal logic of the model without the need for external explanations [11]. In contrast, extrinsic interpretability applies to black-box models such as neural networks or SVMs, where post hoc approaches are used to infer interpretations. For instance, aggregating local explanations can help construct a global understanding of a model based on multiple local analyses.
This second dimension (intrinsic vs. extrinsic) complements the previous one (local vs. global) by shedding light on how the explanation is generated, whether directly by the model itself or through an external mechanism.
Specific vs. Agnostic: This distinction is based on the relationship between the explanatory method and the learning model being used. It differentiates approaches designed for specific model architectures from those that can be applied to any type of model regardless of its complexity or nature.
Model-specific explainability relies on methods tailored to particular architectures, leveraging their internal structure to explain the model’s decisions.
For example, decision trees use explicit conditional rules, and Gini importance scores—also known as Mean Decrease in Impurity (MDI)—quantify how much each feature contributes to reducing Gini impurity when used to split nodes in a random forest [34]. Additionally, techniques such as fuzzy logic can simplify complex models [48]. Agnostic explainability provides post hoc explanations without relying on the model’s internal structure, making it applicable across a broad range of models. For instance, SHAP generates both local and global explanations for any model [29,49]. Variants such as Kernel SHAP and AcME have been employed to interpret complex models, especially in contexts like ICU mortality risk prediction [50,51,52].
Model-specific interpretability seeks to understand how input data influence decisions by analyzing the model’s internal mechanisms. In neural networks, techniques like Grad-CAM highlight influential regions in images [53,54], while Layer-wise Relevance Propagation (LRP) identifies the neurons most responsible for a particular decision [54]. Agnostic interpretability aims to make black-box model decisions understandable without accessing internal mechanisms. LIME and anchors are methods that generate explanations independently of model architecture [15,44]. These methods are applied in various fields, such as healthcare and industry, to provide accessible explanations [37,55].
Whether specific or agnostic, these methods contribute to the explainability and interpretability of models by rendering their decisions understandable either by respecting or bypassing their internal structure.
To better illustrate the interaction and combination of the three fundamental dimensions—intrinsic/extrinsic, specific/agnostic, and local/global—we propose a three-dimensional representation (Figure 1). This 3D visualization positions various explainability methods according to their nature, their dependence on the model, and the level of granularity of the explanation. It highlights how these dimensions, while conceptually distinct, intertwine and jointly contribute to characterizing explainable AI methods.
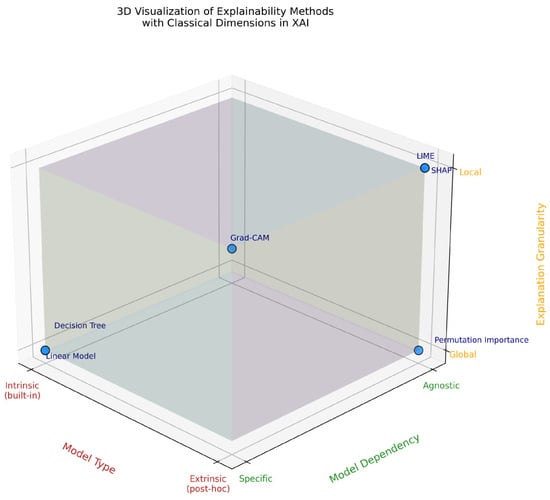
Figure 1.
Three-dimensional representation of explainability methods based on three key dimensions: model type (intrinsic vs. extrinsic), model dependence (agnostic vs. specific), and granularity (local vs. global).
To summarize our classification framework, we provide in Table 1 a synthetic view of the main interpretability and explainability paradigms along the three proposed dimensions.

Table 1.
Cross-typology of interpretability and explainability methods across three dimensions.
Subsequently, Table 2 illustrates how well-known explainability methods are positioned within this framework by mapping them according to their granularity, model dependence, and intrinsic/extrinsic nature.

Table 2.
Mapping of popular explainability methods across the three key dimensions.
This typology of interpretability and explainability approaches provides a structured framework for understanding the diversity of explanation strategies along with their respective assumptions, limitations, and trade-offs.
Beyond this classification, it is increasingly recognized that evaluating explanation methods requires dedicated metrics to assess their quality and reliability. Among the emerging evaluation criteria, faithfulness (how accurately the explanation reflects the model’s true reasoning), stability (how consistent the explanation is under small input perturbations), and comprehensiveness (how completely the explanation captures all the relevant features influencing the prediction) have gained prominence. These metrics provide quantitative means to compare explanation methods and reveal potential weaknesses in their behavior. Incorporating such evaluation strategies is crucial for ensuring that explanations are not only interpretable but also trustworthy and actionable in practice.
In the following section, we illustrate the application of our classification using various machine learning models in order to demonstrate its practical relevance and impact.
5. Application to Classical Machine Learning Models
We used the context of breast cancer diagnosis to illustrate different interpretability and explainability scenarios. We first applied intrinsically interpretable models, followed by the use of XAI techniques, with a particular focus on the LIME method. These methods were applied to the Breast Cancer dataset available in the scikit-learn library in order to analyze and interpret the predictions made by machine learning models. This dataset includes 569 data instances divided into two classes: malignant cancers (212 instances) and benign cancers (357 instances). The experiments were conducted using Python 3.9 with the scikit-learn library for model training, LIME for post hoc local explanations, and treeinterpreter for specific feature contributions in random forest models.
In all examples, a machine learning model is trained to predict a diagnosis (malignant or benign class), and our goal is to understand the rationale behind this prediction. For each experiment, we split the dataset using 80% for training and 20% for testing.
We considered three different models to highlight the key aspects of our classification: decision tree, logistic regression, and random forest.
5.1. Results with Decision Tree
A decision tree segments a population into homogeneous subgroups using recursive tests on input features. This process continues until the leaves are sufficiently homogeneous with respect to a target attribute. Once the tree is built, a new instance is classified by following the sequence of tests down to a corresponding leaf.
Using the Breast Cancer dataset, we obtained the tree shown in Figure 2, from which seven decision rules can be extracted. For example, we can derive the following rule:
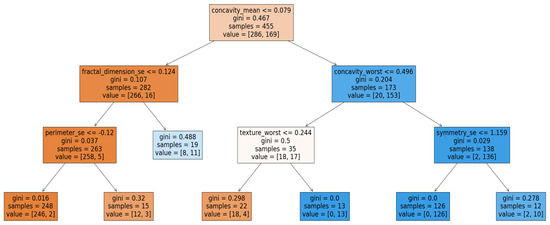
Figure 2.
Horizontal Decision tree trained on breast cancer data.
& & & .
The decision tree is a naturally interpretable model: it allows for a direct understanding of how a decision is made even though it may not always explain in depth the relationships between variables. Its tree-like structure, where each path can be expressed as a decision rule, makes it a particularly transparent model. Each node in the tree corresponds to a test on an attribute, and each path from the root to a leaf defines an explicit rule. Unlike so-called “black-box” models, the decision tree does not require additional methods to be understood.
At the global level, interpretability is reflected in the hierarchy of attributes, which depends on how frequently each attribute appears in the tree. This hierarchy is visible both in Table 3 and in the structure of the tree itself. For example, if the attribute concavity_mean is tested first, it indicates that it has the greatest influence. Conversely, attributes that are never selected in the tree have zero importance. From a local perspective, it is possible to interpret the prediction for a given individual (e.g., ) simply by tracing the path followed in the tree and applying the corresponding decision rules. This instance-specific interpretation does not require any post hoc method.

Table 3.
Coefficients of the LR model and feature importances of the AD and RF models.
Under its intrinsically interpretable structure, the decision tree allows for local analysis by retracing the path followed by a specific instance. Formalizing this path as a set of decision rules then constitutes a local explanation. This duality sometimes blurs the line between interpretation and explanation in the case of decision trees.
5.2. Results with Linear Regression
Linear regression estimates the output of an input by computing a weighted sum of its N attributes. Each coefficient reflects the global importance of attribute in the model. Thanks to its simple structure, linear regression is naturally interpretable: the coefficients are constant across all data and allow the identification, on average, of the attributes that most influence the model’s output.
To explain an individual prediction, one simply needs to examine the contribution of each coefficient multiplied by the value of the corresponding attribute for that instance. Thus, for a particular instance , the prediction is determined by the terms , which represent the specific contribution of each attribute to the prediction. For example, for , the attributes with the highest contributions (ID 21, 10, and 28, see Table 3) are the main drivers of the decision. The prediction analysis is therefore performed by decomposing these contributions, which makes it possible to identify the key factors that led to the classification of as benign ().
It is important to note that if an attribute has a high coefficient but a low value , its impact on the prediction of will be negligible. Conversely, an attribute with a moderate coefficient but a very high value can have a dominant influence on the local prediction.
This distinction between the global importance of coefficients and the local contribution of attributes is essential for the interpretability of the model. An attribute that is globally important may have little impact on a specific prediction. For example, if attribute has a high coefficient , but for , its value is low , the local contribution will be , which is a very weak influence. Thus, even a globally important attribute may not play a significant role in the decision for a particular instance.
This analysis allows us to distinguish two levels of interpretability in logistic regression: a global interpretation provided by the coefficients , common to the entire dataset, and a local interpretation obtained by applying these coefficients to a specific instance to analyze its individual prediction.
Although logistic regression allows for intrinsic interpretation at both global and local levels, it does not provide post hoc explanation in the sense that it does not rely on any external explanatory method such as LIME.
LIME, although originally designed to explain black-box models, is used here not to compensate for a lack of interpretability but rather to evaluate the quality of the explanations it generates.
In our case, LIME is used to analyze the prediction of the same instance , which is already interpreted intrinsically by the logistic regression model. This case study thus provides an opportunity to compare the local explanation produced by LIME with the one directly derived from the model’s structure, in a controlled setting where the internal mechanisms are fully known, providing a rigorous baseline to validate the fidelity of LIME’s explanations. This approach offers an ideal reference framework for assessing the coherence and accuracy of local explanations.
Application of LIME:
Unlike global approaches, LIME is a local, agnostic, and post hoc explanation method. It works by perturbing the data around a given instance and then fitting a simple model (e.g., linear regression) to identify the most influential features in the prediction.
To demonstrate how the LIME algorithm works and how it generates an explanation for a prediction of an input , we apply it to the logistic regression model to explain the same prediction of individual .
We configure LIME according to Ribeiro’s original settings and generate a surrogate model:
- K-Lasso linear regression with , selecting the five most influential features.
- Weights (with D being the Euclidean distance and ).
- samples adapted to the size of the Breast Cancer dataset.
- Functions and as defined by Ribeiro: preserves the original representation, and randomly selects subsets of attributes.
The resulting surrogate model is a linear regression over five attributes (see Table 4), two of which are among the most important globally (Table 3), two others are globally significant, and one, although less influential globally, plays a key local role for .

Table 4.
LIME explanation for .
LIME’s prediction () matches that of the LR model but differs from the true label . Both the local and global regression classify as benign, indicating a faithful local explanation. With LIME, four out of the five attributes strongly influence the prediction (Figure 3). In contrast, the global regression involves 21 attributes for the benign class and eight for the malignant class, making interpretation more complex despite the dominance of the benign class.
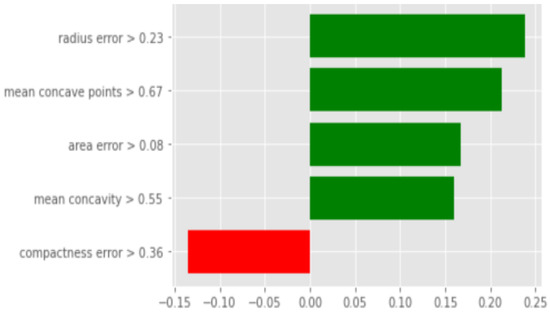
Figure 3.
Simulation 1: . Contribution of the k attributes of to the prediction (LIME).
5.3. Results with Random Forest
The random forest is an ensemble of decision trees trained on random subsets of the data. At each split, the test is chosen among a restricted subset of attributes, thus improving the robustness and generalization of the model.
However, the random forest is not intrinsically interpretable: it does not easily allow tracing the classification logic for a given instance due to the large number of trees involved. Therefore, it does not provide direct local explanations. Nonetheless, a global interpretation can be obtained by analyzing feature importance.
To analyze the prediction of a specific instance locally, post hoc methods such as treeinterpreter.predict or LIME must be used. For instance, the local explanation of the prediction for can be performed by analyzing the attribute contributions provided by treeinterpreter.predict. For example, the random forest classified as class M. To understand this decision, the treeinterpreter.predict method decomposes the prediction into two parts:
Table 3 presents these contributions for . For this example, the predicted probability is
5.4. Cross-Evaluation of Interpretability and Explainability of the Studied Models
The observed results show that logistic regression stands out with intrinsic interpretability, which is enabled by the readability of its coefficients. The decision tree allows the direct understanding of predictions through explicit rules, whereas the random forest, although more performant, has a complex structure that makes interpretation more challenging. In this context, explainability becomes essential to analyze the influence of variables both at the local and global levels.
Thus, to synthesize these characteristics, particularly intrinsic interpretability capabilities and the potential use of post hoc methods such as LIME, Table 5 provides a structured comparison between interpretability and explainability, according to their local, global, intrinsic, extrinsic, specific, and agnostic dimensions.

Table 5.
Mapping of models across interpretability and explainability dimensions. ✓ indicates applicability, ✗ indicates non-applicability.
Table 5 highlights the comparative capabilities of three models to provide an interpretation of their decisions whether intrinsic or extrinsic.
We observe that logistic regression and decision tree stand out for their intrinsic interpretability, which is accessible both at the global and local levels. Their explicit structure makes the use of external explainability methods unnecessary. In contrast, the random forest, due to its ensemble nature, presents a complexity that makes its internal mechanisms difficult to interpret directly. It therefore requires the use of post hoc methods such as LIME or SHAP to explain its predictions locally or globally. The table also highlights a key distinction between specific methods (model-dependent, such as treeinterpreter for RF) and agnostic methods (independent of the model structure, such as LIME or Kernel SHAP). This agnosticism constitutes an important advantage for explaining black-box models, providing interpretative consistency regardless of the underlying algorithm.
6. Limitations and Future Work
The rise of AI reinforces the need for explainability to ensure transparency and trust. The proposed classification structures these approaches by positioning them along three dimensions while also highlighting conceptual and practical limitations. This section discusses the contributions and limitations of the classification, explores the societal challenges of XAI, and outlines directions for developing systems that are both effective and responsible.
6.1. Summary of the Contributions of the Proposed Classification
The proposed classification is based on a three-dimensional structuring of explainability and interpretability methods. Conceptually grounded in the formal definition by Dib [7], this three-dimensional framework articulates the approaches according to their explanatory scope, transparency, and model dependency.
First, this typology clarifies the conceptual distinctions between interpretability and explainability, which are often used interchangeably in the literature. It makes their relationships explicit and positions them more precisely within the landscape of explanation methods.
Second, it unifies existing approaches into a coherent framework that allows methods to be positioned according to their fundamental characteristics. This avoids overly binary categorizations (e.g., “transparent” vs. “black box”) by introducing a fine-grained and nuanced grid that highlights possible complementarities between methods.
Third, the classification facilitates the comparison, selection, and evaluation of explanatory methods by researchers and practitioners. It allows users to quickly identify techniques suited to a specific use case, for example, the local explanation of an opaque model (LIME, SHAP), global analysis of an intrinsically interpretable model (linear regression), or methods specific to a particular architecture (Grad-CAM, dedicated to convolutional neural networks). This precise positioning guides users in choosing tools according to their needs for transparency, robustness, or understanding.
Finally, in a field where boundaries are sometimes blurred or redundant, this typology provides terminological and methodological clarification, which is essential for structuring the field, promoting the reproducibility of studies, and stimulating the development of new approaches that intelligently combine the identified dimensions.
To summarize these distinctions more systematically, Table 6 presents a cross-critical analysis of interpretability and explainability dimensions based on several key criteria.

Table 6.
Critical comparison table distinguishing interpretability and explainability according to various criteria.
6.2. Limitations of the Proposed Classification
Although this classification facilitates the positioning of methods within a structured and coherent framework, certain limitations remain concerning the boundaries between interpretability and explainability. For instance, techniques such as LIME produce interpretable outputs even though they fall under post hoc explainability. This ambiguity complicates their categorization and selection by practitioners, depending on the intended level of analysis.
Moreover, the categories are not always mutually exclusive. Emerging hybrid approaches challenge these boundaries by integrating intrinsic interpretability into structurally constrained opaque models, thereby complicating their placement within the proposed framework.
Furthermore, while the classification is useful for structuring the theoretical landscape, it does not account for essential practical criteria such as the stability of explanations, fidelity to the original model’s decisions, or computational cost. These aspects are critical in real-world application domains such as education, healthcare, or finance, and they should be integrated into a future extension of the framework.
Another important consideration is the inherent subjectivity involved in some classification axes. For example, the distinction between local and global explanations can depend on the granularity of analysis and the user’s perspective with what is considered a “local” explanation in one context potentially being seen as “global” in another. Similarly, the boundary between model-specific and model-agnostic methods can be blurred especially when certain explanation techniques adapt depending on the model architecture. This subjectivity calls for flexible interpretation and highlights the necessity for empirical validation and user-centered evaluation alongside theoretical classification.
Finally, the applicability of the classification to concrete use cases may be limited without additional guidance. The typology helps situate a method, but it does not provide explicit recommendations for the optimal choice in a given context particularly when trade-offs between interpretability, performance, and complexity must be considered.
In summary, while the proposed classification provides a useful foundation for structuring thought, it would benefit from being enriched with empirical dimensions (robustness, cost, stability), guided application examples, and a more refined consideration of hybrid methods in order to enhance its practical relevance.
6.3. Limitations of XAI in the Literature
Some explainability methods, such as SHAP, are computationally expensive because they rely on the exhaustive evaluation of all possible feature combinations to estimate their contribution [29]. In real-time or embedded systems, where speed is a key factor, integrating explainability methods is difficult without impacting performance [56].
Explainability methods do not always guarantee the robustness of their explanations [57]. For instance, a slight modification of an input can sometimes lead to significant variations in the explanations provided by LIME or SHAP, which undermines their reliability. This instability can be problematic in critical applications where decisions must be rigorously justified.
Post hoc techniques such as LIME and SHAP present several limitations in terms of robustness and consistency. Results may fluctuate depending on the sampling method and parameters used [15]. The choice of neighborhood or explanatory variables can influence the explanations, compromising their reliability. Finally, these approaches rely on simulations and approximations that are sometimes too heavy for real-time integration.
6.4. Current Challenges and Open Issues
Despite the progress made in the explainability and interpretability of machine learning models, several challenges and limitations persist, hindering the widespread adoption of XAI. These obstacles relate in particular to the reliability of explanations, the standardization of methods, and the compatibility between performance and transparency.
One of the main goals of XAI is to provide understandable explanations for diverse audiences (experts, decision-makers, end users). However, translating complex mathematical concepts into accessible explanations is a real challenge. An overly simplified explanation may lack precision, while one that is too technical becomes unusable for non-experts [11]. As previously mentioned, explanations can vary depending on the sampling method and parameters used with post hoc techniques. This instability reduces users’ trust in the explanations provided.
The lack of clear standards for evaluating explainability methods also represents a major barrier to adoption. Fidelity to predictions, the stability of explanations, and contextual relevance are all criteria that must be rigorously defined [10]. Without a normative framework, comparing different methods becomes complex, and the choice of an explainability technique often relies on subjective or empirical considerations.
Take, for example, deep learning models. Although effective, they are often seen as black boxes due to their complexity. Making these models explainable without compromising performance is a major challenge. Hybrid approaches, such as knowledge distillation, attempt to reconcile these two aspects, but they introduce issues of fidelity and the distortion of explanations [58].
6.5. Societal and Ethical Impacts
The adoption of explainable artificial intelligence models raises major ethical, legal, and societal challenges. It is essential to ensure that these systems respect principles of transparency, fairness, and accountability, which are central to fostering trust in AI [59]. Explainability helps better understand and justify automated decisions, thus facilitating the attribution of responsibility in the event of error or harm. However, the involvement of multiple stakeholders in the development and deployment of AI systems can lead to a responsibility gap, making it difficult to identify responsible parties in case of problems.
Explainability also raises challenges related to privacy. Some methods, such as counterfactual explanations, can inadvertently reveal sensitive information from the training data, compromising user privacy. This risk is particularly acute in sensitive areas such as healthcare or education where the protection of personal data is paramount.
Another critical issue concerns the reproduction and amplification of biases present in training data. Even explainability methods like LIME or SHAP can introduce their own biases especially depending on the selection of samples used to generate explanations. Moreover, the quality and relevance of explanations may vary across demographic groups, raising concerns about fairness and non-discrimination. The lack of transparency or tailored explanations can reinforce user mistrust and limit the social acceptability of AI systems.
It is necessary to develop context-aware explainability approaches, taking into account the needs of different users and regulatory requirements. Integrating robust mechanisms for data protection, regular audits to detect bias, and decision traceability protocols are essential levers for promoting responsible and trustworthy artificial intelligence.
6.6. Research Perspectives
To overcome these challenges, several research avenues in XAI deserve to be further explored. The development of hybrid methods that combine local and global explanations appears essential to provide a more coherent and comprehensive understanding of model behavior. At the same time, it is necessary to improve the stability of post hoc explanations, notably through regularization and optimization techniques, in order to ensure the reliability of the interpretations provided. Integrating XAI into clear regulatory frameworks is also a priority, as it would help ensure both system transparency and user protection. Finally, tailoring explanations to users’ specific needs is a key lever for fostering the acceptance and adoption of explainable artificial intelligence. Altogether, these advancements will contribute to a better understanding of models while promoting a more ethical and responsible use of AI.
7. Conclusions
Understanding the decisions made by AI models is a central issue for enhancing transparency and trust, especially in sensitive domains. This article aimed to clarify the distinction between interpretability and explainability by relying on a formal framework and to propose a structured classification of existing methods.
One of the main strengths of this classification lies in its three-dimensional structure, which is based on the following axes: local vs. global, intrinsic vs. extrinsic, and specific vs. agnostic. This organization moves beyond the usual binary typologies and better positions each method according to its explanatory properties. It provides a systematic conceptual framework that clarifies the local or global scope of a method, its level of transparency, and its more or less direct connection to the model architecture.
We illustrated the various concepts highlighted in our classification through concrete examples.
This typology helps identify the complementarities and gray areas between methods. It offers a useful analytical grid for guiding the selection of techniques based on objectives: explaining a specific prediction, understanding overall behavior, or assessing a model’s internal structure. It also serves as an educational tool to structure knowledge in a rapidly evolving field. However, some limitations must be acknowledged. The boundaries between explainability and interpretability remain sometimes blurred, and some hybrid methods escape strict categorization. In addition, important practical aspects, such as the fidelity of explanations, as well as their stability, robustness, or computational cost, are not covered by this classification, although they are crucial for practitioners. Lastly, the grid itself does not provide direct recommendations for selecting the most appropriate method in a given context; additional empirical criteria are still necessary to guide this choice.
This approach aims to facilitate the adoption of these methods in contexts where understanding algorithmic decisions is essential to ensure fairness and transparency.
Author Contributions
Conceptualization, L.D.; Methodology, L.D.; Software, L.D.; Formal analysis, L.D.; Writing—original draft, L.D. and L.C.; Supervision, L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available in the UCI Machine Learning Repository at https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Diagnostic) (accessed on 15 June 2024).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haar, L.V.; Elvira, T.; Ochoa, O. An analysis of explainability methods for convolutional neural networks. Eng. Appl. Artif. Intell. 2023, 117, 105606. [Google Scholar] [CrossRef]
- Esterhuizen, J.A.; Goldsmith, B.R.; Linic, S. Interpretable machine learning for knowledge generation in heterogeneous catalysis. Nat. Catal. 2022, 5, 175–184. [Google Scholar] [CrossRef]
- Rudin, C.; Chen, C.; Chen, Z.; Huang, H.; Semenova, L.; Zhong, C. Interpretable machine learning: Fundamental principles and 10 grand challenges. Stat. Surv. 2022, 16, 1–85. [Google Scholar] [CrossRef]
- Zhang, Y.; Tiňo, P.; Leonardis, A.; Tang, K. A survey on neural network interpretability. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 5, 726–742. [Google Scholar] [CrossRef]
- Risch, J.; Ruff, R.; Krestel, R. Explaining offensive language detection. J. Lang. Technol. Comput. Linguist. (JLCL) 2020, 34, 1–19. [Google Scholar] [CrossRef]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. 2018, 51, 639–662. [Google Scholar] [CrossRef]
- Dib, L. Formal Definition of Interpretability and Explainability in XAI. In Intelligent Systems And Applications: Proceedings of The 2024 Intelligent Systems Conference (IntelliSys); Springer: Cham, Switzerland, 2024; Volume 3, p. 133. [Google Scholar]
- Carvalho, D.V.; Pereira, E.M.; Cardoso, J.S. Machine learning interpretability: A survey on methods and metrics. Electronics 2019, 8, 832. [Google Scholar] [CrossRef]
- Chuang, J.; Ramage, D.; Manning, C.; Heer, J. Interpretation and trust: Designing model-driven visualizations for text analysis. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Austin, TX, USA, 5–10 May 2012; pp. 443–452. [Google Scholar]
- Doshi-Velez, F.; Kim, B. Towards a Rigorous Science of Interpretable Machine Learning. arXiv 2017, arXiv:1702.08608. [Google Scholar] [CrossRef]
- Miller, T. Explanation in Artificial Intelligence: Insights from the Social Sciences. Artif. Intell. 2019, 267, 1–38. [Google Scholar] [CrossRef]
- Lipton, Z.C. The mythos of model interpretability: In machine learning, the concept of interpretability is both important and slippery. Queue 2018, 16, 31–57. [Google Scholar] [CrossRef]
- Gilpin, L.; Bau, D.; Yuan, B.; Bajwa, A.; Specter, M.; Kagal, L. Explaining explanations: An overview of interpretability of machine learning. In Proceedings of the 2018 IEEE 5th International Conference on Data Science and Advanced Analytics (DSAA), Turin, Italy, 1–4 October 2018; pp. 80–89. [Google Scholar]
- Buhrmester, V.; Münch, D.; Arens, M. Analysis of explainers of black box deep neural networks for computer vision: A survey. Mach. Learn. Knowl. Extr. 2021, 3, 966–989. [Google Scholar] [CrossRef]
- Ribeiro, M.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Došilović, F.; Brčić, M.; Hlupić, N. Explainable artificial intelligence: A survey. In Proceedings of the 2018 41st International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 21–25 May 2018; pp. 0210–0215. [Google Scholar]
- Monroe, D. AI, explain yourself. Commun. ACM. 2018, 61, 11–13. [Google Scholar] [CrossRef]
- Montavon, G.; Lapuschkin, S.; Binder, A.; Samek, W.; Müller, K.R. Explaining nonlinear classification decisions with deep taylor decomposition. Pattern Recognit. 2017, 65, 211–222. [Google Scholar] [CrossRef]
- Mohseni, S.; Zarei, N.; Ragan, E. A survey of evaluation methods and measures for interpretable machine learning. arXiv 2018, arXiv:1811.11839. [Google Scholar]
- Murdoch, W.; Singh, C.; Kumbier, K.; Abbasi-Asl, R.; Yu, B. Interpretable machine learning: Definitions, methods, and applications. arXiv 2019, arXiv:1901.04592. [Google Scholar] [CrossRef]
- Piltaver, R.; Luštrek, M.; Gams, M.; Martinčić-Ipšić, S. What makes classification trees comprehensible? Expert Syst. Appl. 2016, 62, 333–346. [Google Scholar] [CrossRef]
- Zhou, Z. Comprehensibility of data mining algorithms. In Encyclopedia of Data Warehousing and Mining; IGI Global Scientific Publishing: Hershey, PA, USA, 2005; pp. 190–195. [Google Scholar][Green Version]
- Lou, Y.; Caruana, R.; Gehrke, J. Intelligible models for classification and regression. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 150–158. [Google Scholar]
- Chiticariu, L.; Li, Y.; Reiss, F. Transparent machine learning for information extraction: State-of-the-art and the future. EMNLP (tutorial). In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisboa, Portugal, 17–21 September 2015; pp. 4–6. [Google Scholar]
- Arrieta, A.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Fails, J.; Olsen, D., Jr. Interactive machine learning. In Proceedings of the 8th International Conference on Intelligent User Interfaces, Miami, FL, USA, 12–15 January 2003; pp. 39–45. [Google Scholar]
- Kulesza, T.; Burnett, M.; Wong, W.; Stumpf, S. Principles of explanatory debugging to personalize interactive machine learning. In Proceedings of the 20th International Conference on Intelligent User Interfaces, Atlanta, GA, USA, 29 March–1 April 2015; pp. 126–137. [Google Scholar]
- Holzinger, A.; Plass, M.; Holzinger, K.; Crişan, G.; Pintea, C.; Palade, V. Towards interactive Machine Learning (iML): Applying ant colony algorithms to solve the traveling salesman problem with the human-in-the-loop approach. In Proceedings of the International Conference on Availability, Reliability, and Security, Salzburg, Austria, 31 August–2 September 2016; pp. 81–95. [Google Scholar]
- Lundberg, S.; Lee, S. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4768–4777. [Google Scholar]
- Gacto, M.J.; Alcalá, R.; Herrera, F. Interpretability of linguistic fuzzy rule-based systems: An overview of interpretability measures. Inf. Sci. 2011, 181, 4340–4360. [Google Scholar] [CrossRef]
- Rudin, C.; Letham, B.; Madigan, D. Learning theory analysis for association rules and sequential event prediction. Mach. Learn. Res. 2013, 14, 3441–3492. [Google Scholar]
- Kega, I.; Nderu, L.; Mwangi, R.; Njagi, D. Model interpretability via interaction feature detection using roughset in a generalized linear model for weather prediction in Kenya. Authorea 2023. preprints. [Google Scholar] [CrossRef]
- Caruana, R.; Lou, Y.; Gehrke, J.; Koch, P.; Sturm, M.; Elhadad, N. Intelligible models for healthcare: Predicting pneumonia risk and hospital 30-day readmission. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, 10–13 August 2015; pp. 1721–1730. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Müller, R.; Kornblith, S.; Hinton, G. Subclass distillation. arXiv 2020, arXiv:2002.03936. [Google Scholar] [CrossRef]
- Shapley, L. A value for n-person games. Contrib. Theory Games 1953, 2, 307–317. [Google Scholar]
- Dave, D.; Naik, H.; Singhal, S.; Patel, P. Explainable ai meets healthcare: A study on heart disease dataset. arXiv 2020, arXiv:2011.03195. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Kale, D.C.; Elkan, C.; Wetzel, R. Learning to diagnose with LSTM recurrent neural networks. arXiv 2015, arXiv:1511.03677. [Google Scholar]
- Yang, G.; Ye, Q.; Xia, J. Unbox the black-box for the medical explainable AI via multi-modal and multi-centre data fusion: A mini-review, two showcases and beyond. Inf. Fusion 2022, 77, 29–52. [Google Scholar] [CrossRef]
- Jeyasothy, A. Génération D’Explications Post-Hoc Personnalisées; Sorbonne Université: Paris, France, 2024. [Google Scholar]
- Molnar, C.; Casalicchio, G.; Bischl, B. Interpretable machine learning–A brief history, state-of-the-art and challenges. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases; Springer International Publishing: Cham, Switzerland, 2020; pp. 417–431. [Google Scholar]
- Kim, B.; Wattenberg, M.; Gilmer, J.; Cai, C.; Wexler, J.; Viegas, F. Others Interpretability beyond feature attribution: Quantitative testing with concept activation vectors (tcav). In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 2668–2677. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.; Kaiser, Ł; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Ribeiro, M.; Singh, S.; Guestrin, C. Anchors: High-precision model-agnostic explanations. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Du, Y.; Rafferty, A.; McAuliffe, F.; Wei, L.; Mooney, C. An explainable machine learning-based clinical decision support system for prediction of gestational diabetes mellitus. Sci. Rep. 2022, 12, 1170. [Google Scholar] [CrossRef]
- Freitas, A. Comprehensible classification models: A position paper. ACM SIGKDD Explor. Newsl. 2014, 15, 1–10. [Google Scholar] [CrossRef]
- Rudin, C.; Radin, J. Why are we using black box models in AI when we don’t need to? A lesson from an explainable AI competition. Harv. Data Sci. Rev. 2019, 1, 1–9. [Google Scholar] [CrossRef]
- Craven, M.; Shavlik, J. Extracting tree-structured representations of trained networks. Adv. Neural Inf. Process. Syst. 1995, 8, 24–30. [Google Scholar]
- Giudici, P.; Raffinetti, E. Shapley-Lorenz eXplainable artificial intelligence. Expert Syst. Appl. 2021, 167, 114104. [Google Scholar] [CrossRef]
- Ho, L.V.; Aczon, M.; Ledbetter, D.; Wetzel, R. Interpreting a recurrent neural network’s predictions of ICU mortality risk. J. Biomed. Inform. 2021, 114, 103672. [Google Scholar] [CrossRef]
- Antwarg, L.; Miller, R.M.; Shapira, B.; Rokach, L. Explaining anomalies detected by autoencoders using Shapley Additive Explanations. Expert Syst. Appl. 2021, 186, 115736. [Google Scholar] [CrossRef]
- Dandolo, D.; Masiero, C.; Carletti, M.; Dalle Pezze, D.; Susto, G.A. AcME—Accelerated model-agnostic explanations: Fast whitening of the machine-learning black box. Expert Syst. Appl. 2023, 214, 119115. [Google Scholar] [CrossRef]
- Choi, E.; Bahadori, M.; Kulas, J.; Schuetz, A.; Stewart, W.; Sun, J. RETAIN: An interpretable predictive model for healthcare using reverse time attention mechanism. Adv. Neural Inf. Process. Syst. (NeurIPS) 2016, 29, 3504–3512. [Google Scholar] [CrossRef]
- Samek, W.; Wiegand, T.; Müller, K. Explainable artificial intelligence: Understanding, visualizing and interpreting deep learning models. arXiv 2017, arXiv:1708.08296. [Google Scholar] [CrossRef]
- Serradilla, O.; Zugasti, E.; Cernuda, C.; Aranburu, A.; Okariz, J.; Zurutuza, U. Interpreting remaining useful life estimations combining explainable artificial intelligence and domain knowledge in industrial machinery. In Proceedings of the 2020 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Chen, L.; Lou, S.; Zhang, K.; Huang, J.; Zhang, Q. Harsanyinet: Computing accurate shapley values in a single forward propagation. arXiv 2023, arXiv:2304.01811. [Google Scholar] [CrossRef]
- Alvarez-Melis, D.; Jaakkola, T. On the Robustness of Interpretability Methods. arXiv 2018, arXiv:1806.08049. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar] [CrossRef]
- Mehrabi, N.; Morstatter, F.; Saxena, N.; Lerman, K.; Galstyan, A. A survey on bias and fairness in machine learning. ACM Comput. Surv. (CSUR). 2021, 54, 1–35. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).