Grid-Search-Optimized, Gated Recurrent Unit-Based Prediction Model for Ionospheric Total Electron Content
Abstract
1. Introduction
2. Methodology
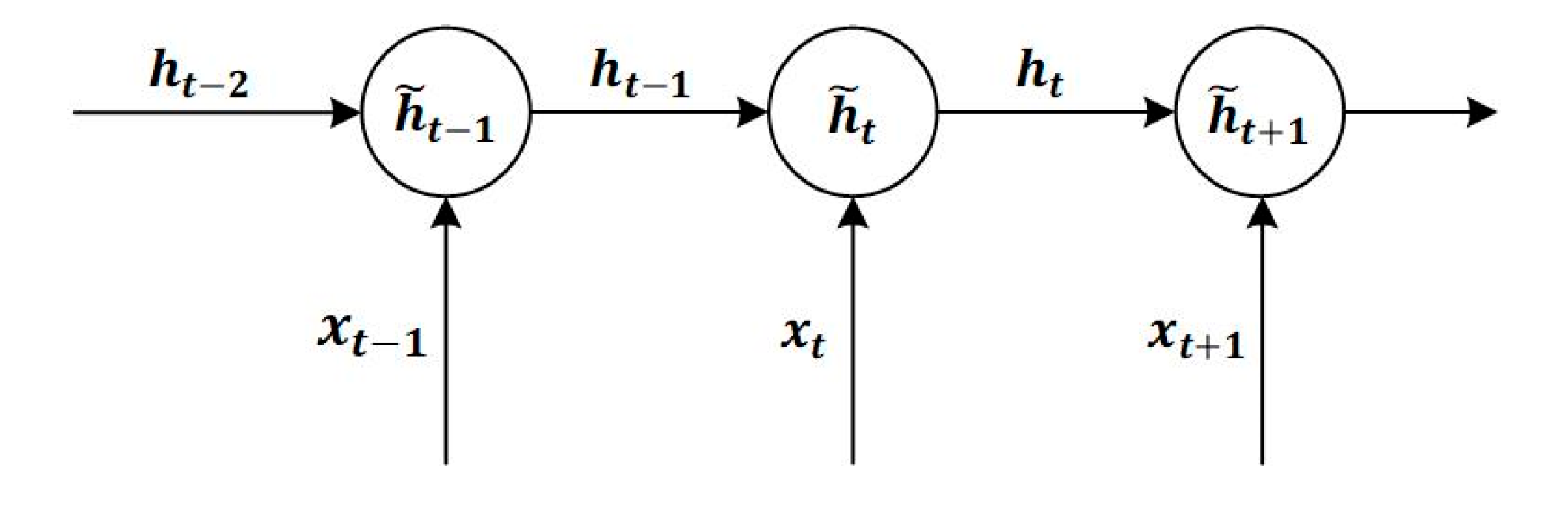
2.1. GRU Network
2.2. Grid Search Method
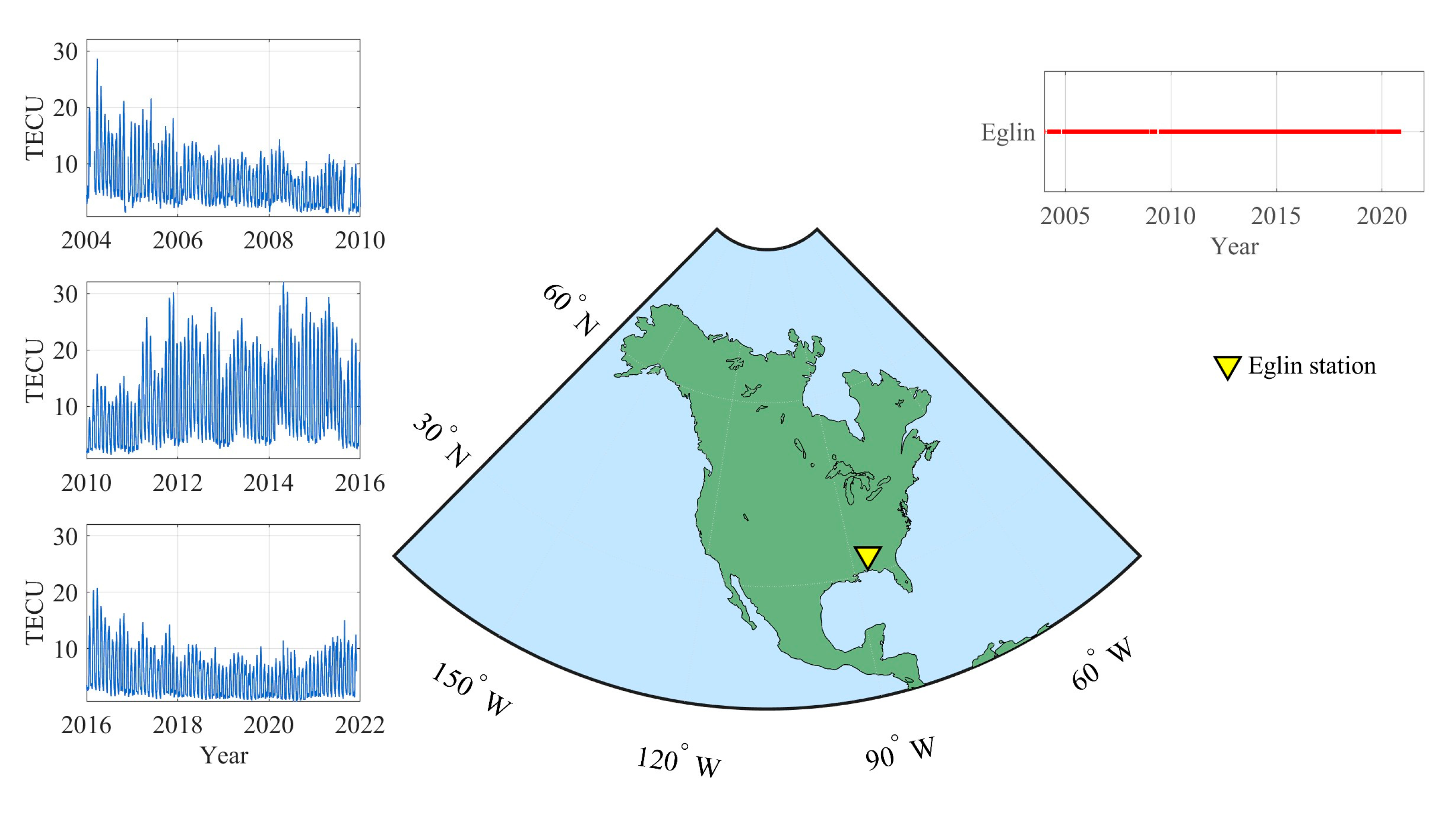
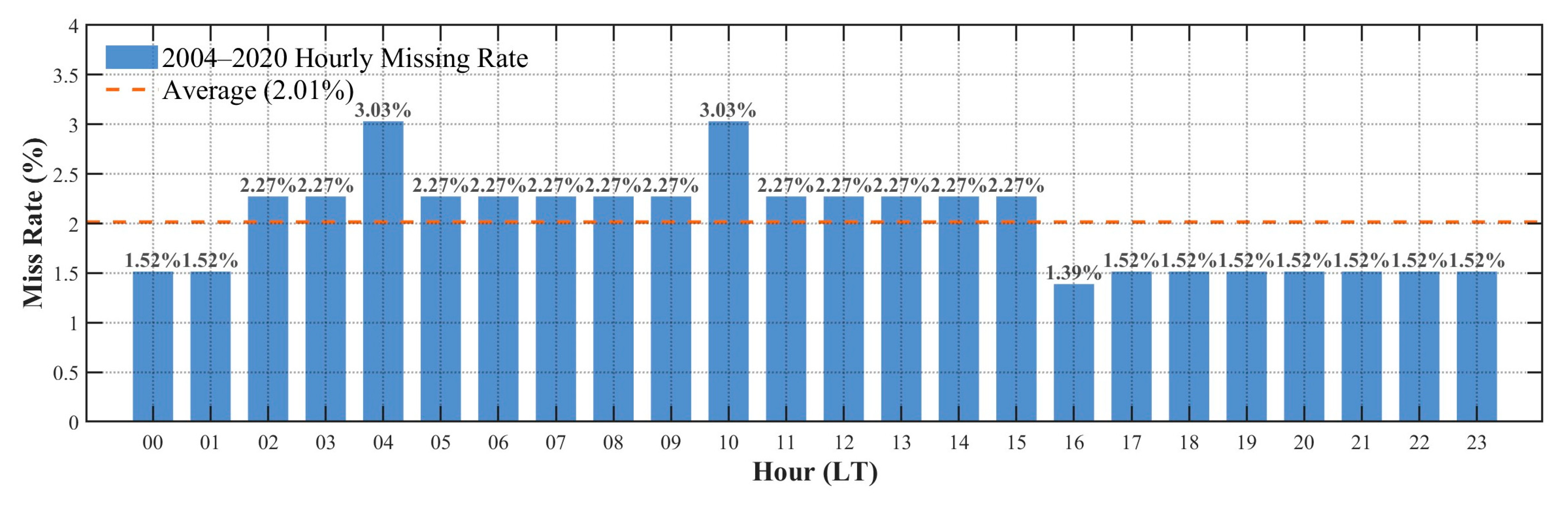
3. Data
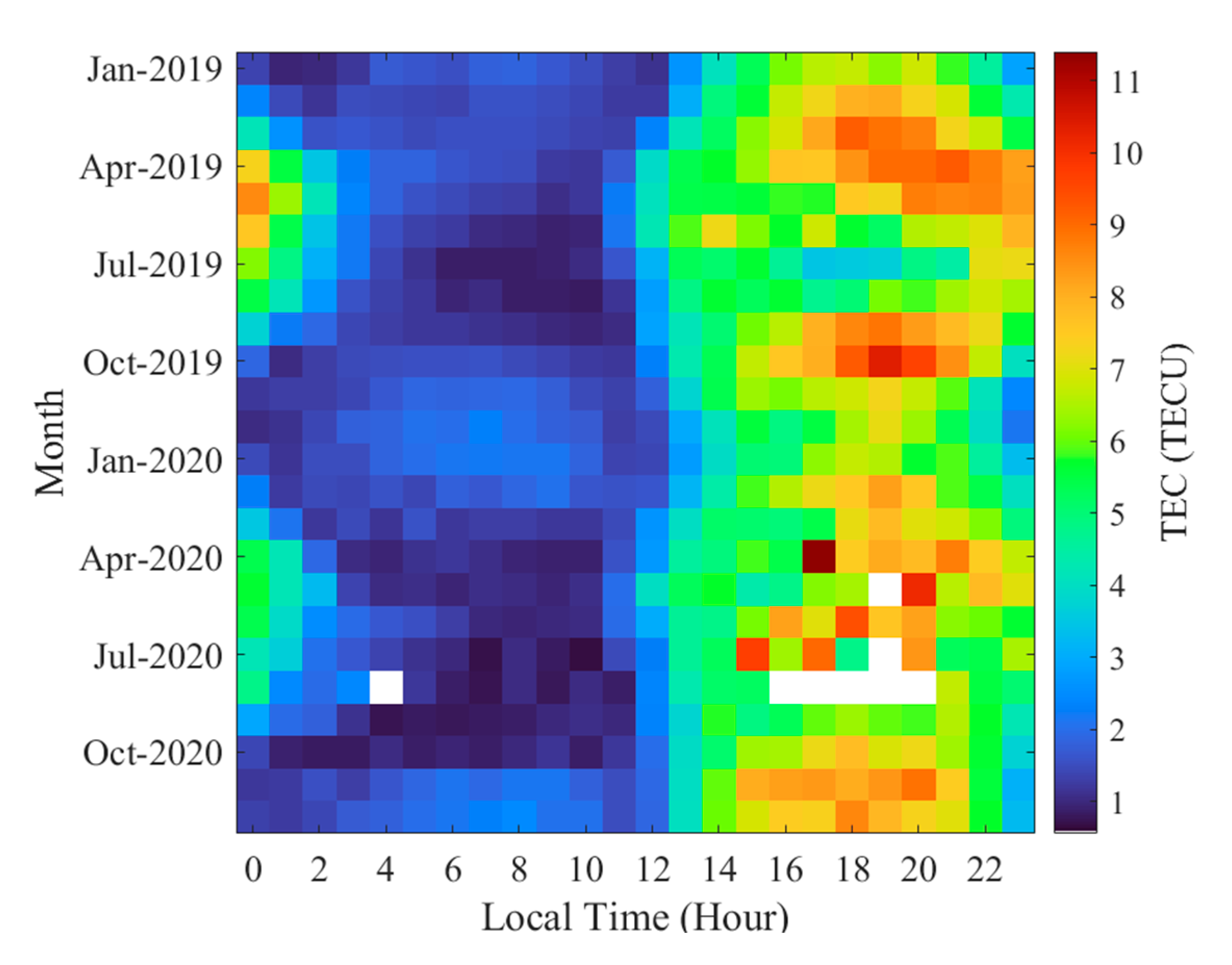
3.1. TEC
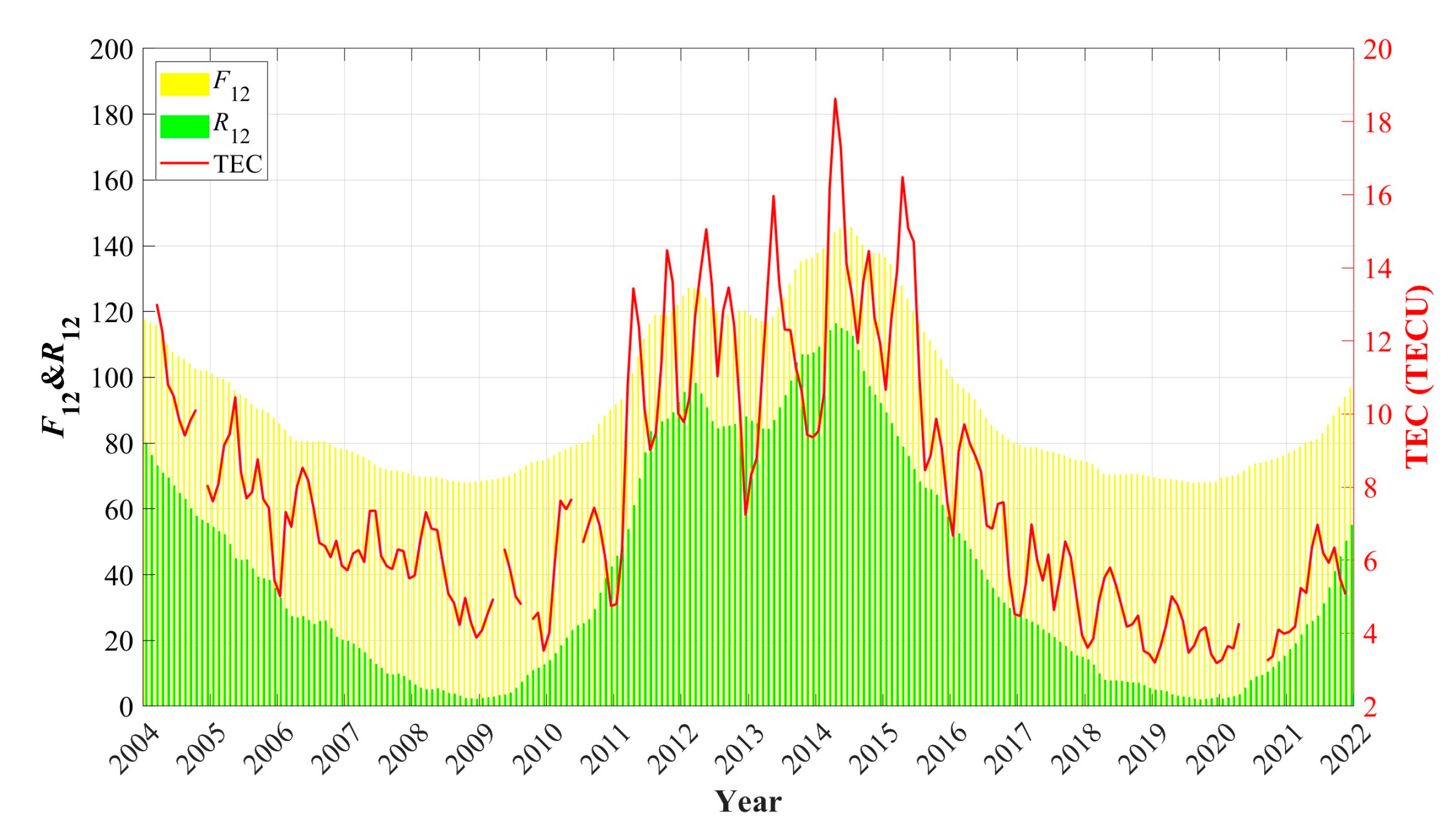
3.2. F10.7
3.3. Sunspot
4. Modeling
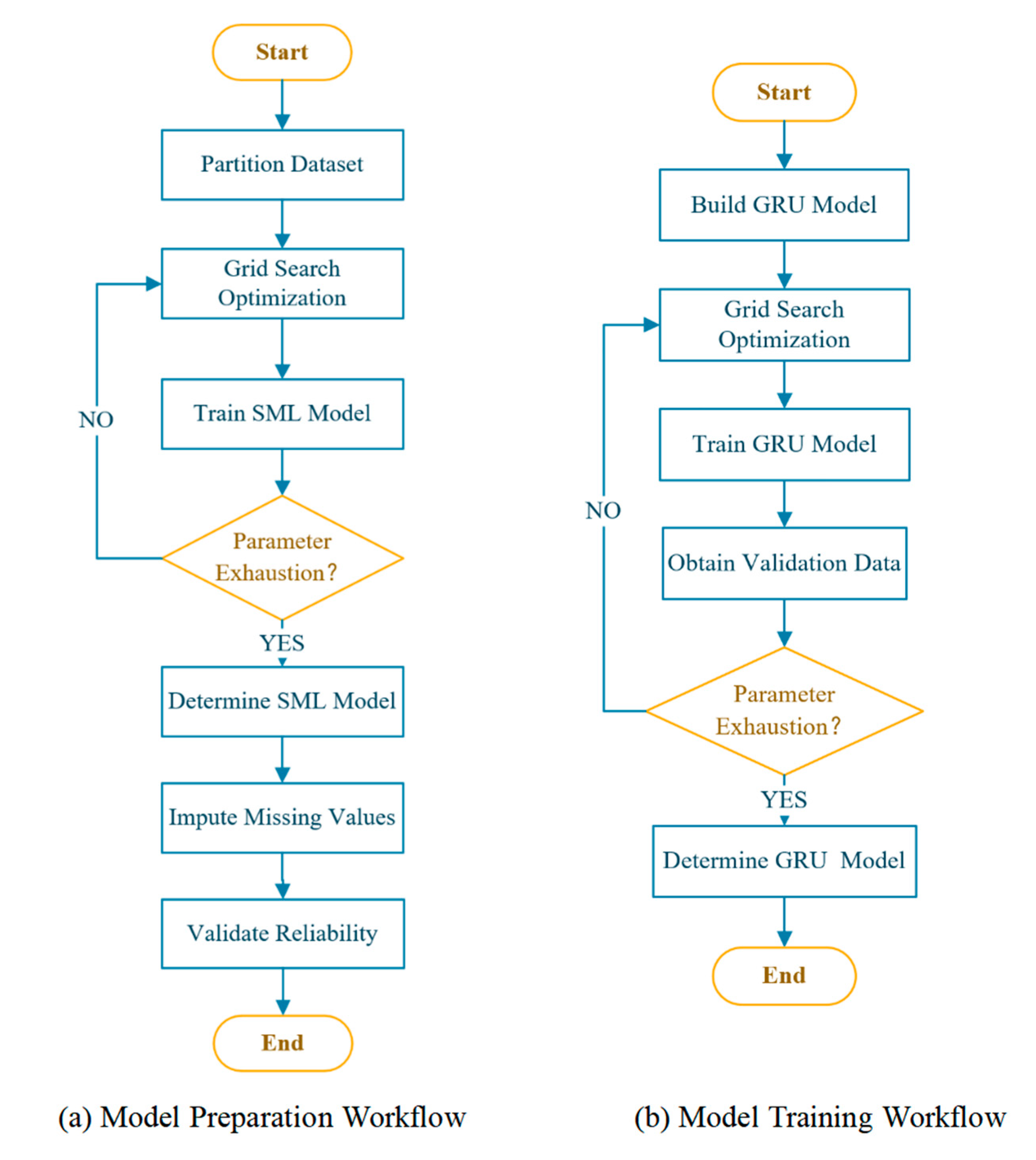
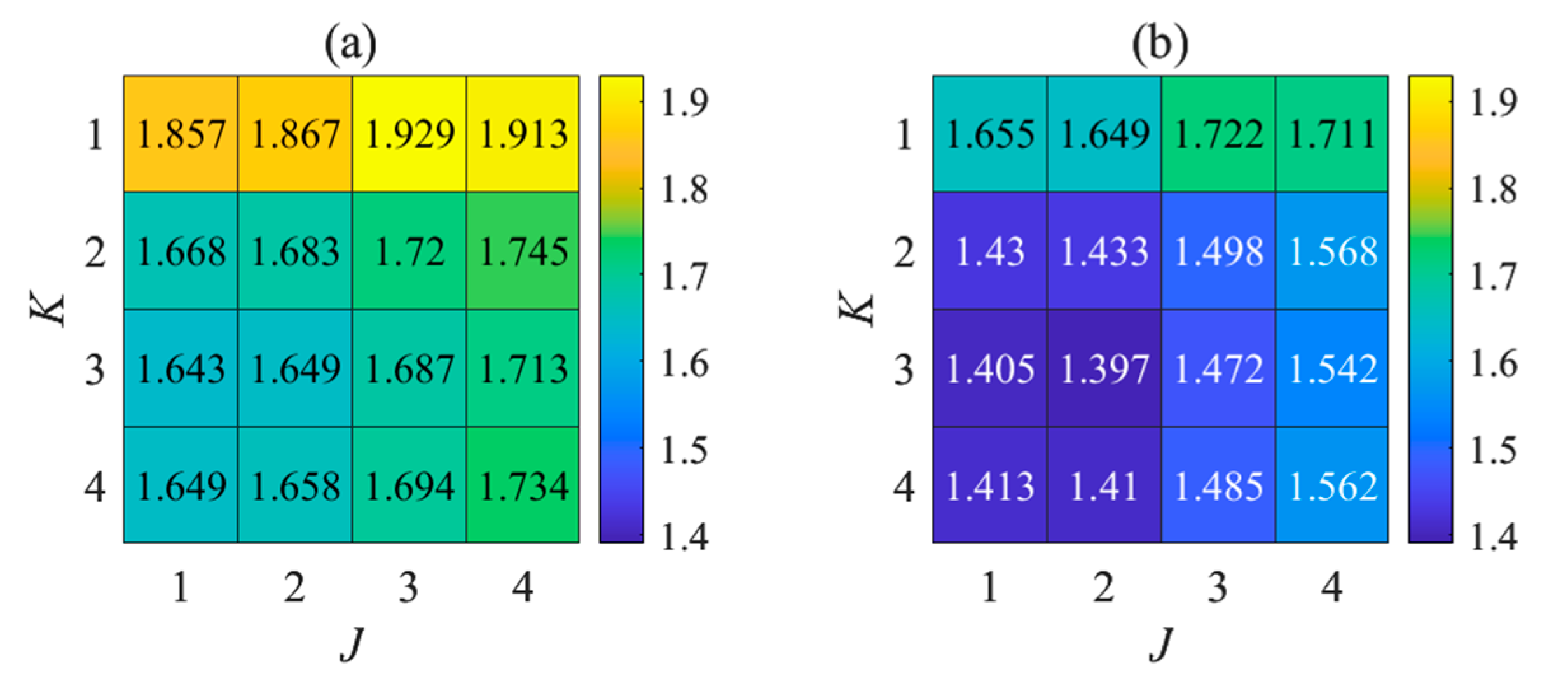
4.1. Modeling Preparation
4.2. Model Training
- Only the original TEC observation values (OBS);
- OBS combined with the R12 index;
- OBS combined with the F12 index;
- OBS combined with both the R12 and F12 dual indices.
- Number of training epochs: the search range is from 20 to 26;
- Learning rate: the search range is from 0.001 to 0.005, with a step size of 0.001;
- Number of hidden layer units: the search range is 120 to 136, with a step size of 4;
- Time step: The search range is 12 and 24;
- Number of GRU layers: the search range is 1 and 2.
- Number of training epochs = 25;
- Learning rate = 0.003;
- Number of hidden units = 120;
- Time step = 12;
- Number of GRU layers = 1.
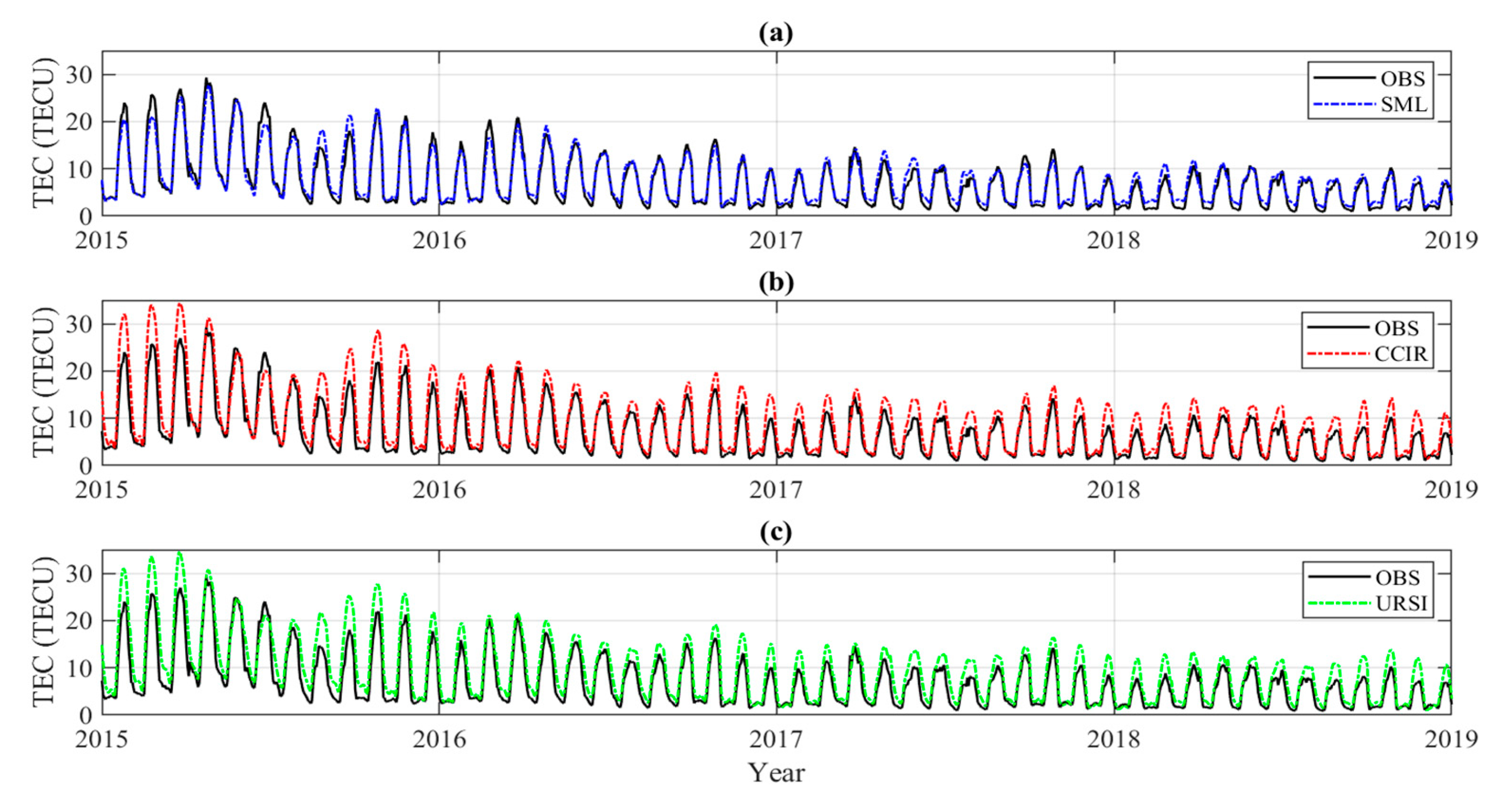
5. Discussion
- (1)
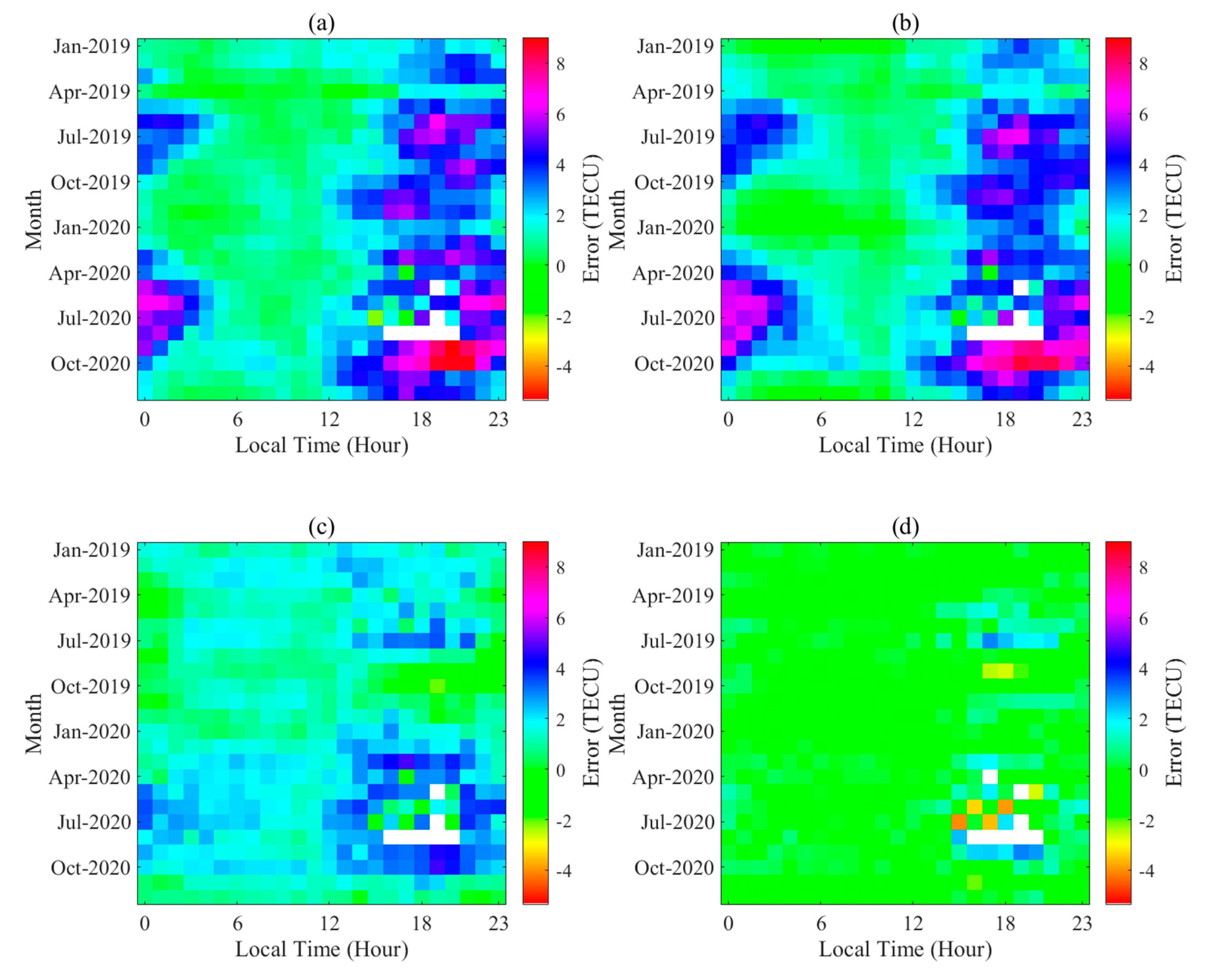
- All models demonstrate capability in tracking long-term TEC trends yet exhibit varying degrees of predictive accuracy across temporal segments.
- (2)
- Comparative analysis reveals distinct error patterns, as follows: The CCIR and URSI models systematically overestimate TEC measurements, particularly from LT = 20 to LT = 1 the next day. The SML approach shows elevated predictions between 22:00 and 10:00 LT. The proposed GRU model maintains prediction stability across all time segments without notable systematic bias.
- (3)
- In the predictions of different hours, the GRU model demonstrated the highest prediction accuracy, with a significant advantage.
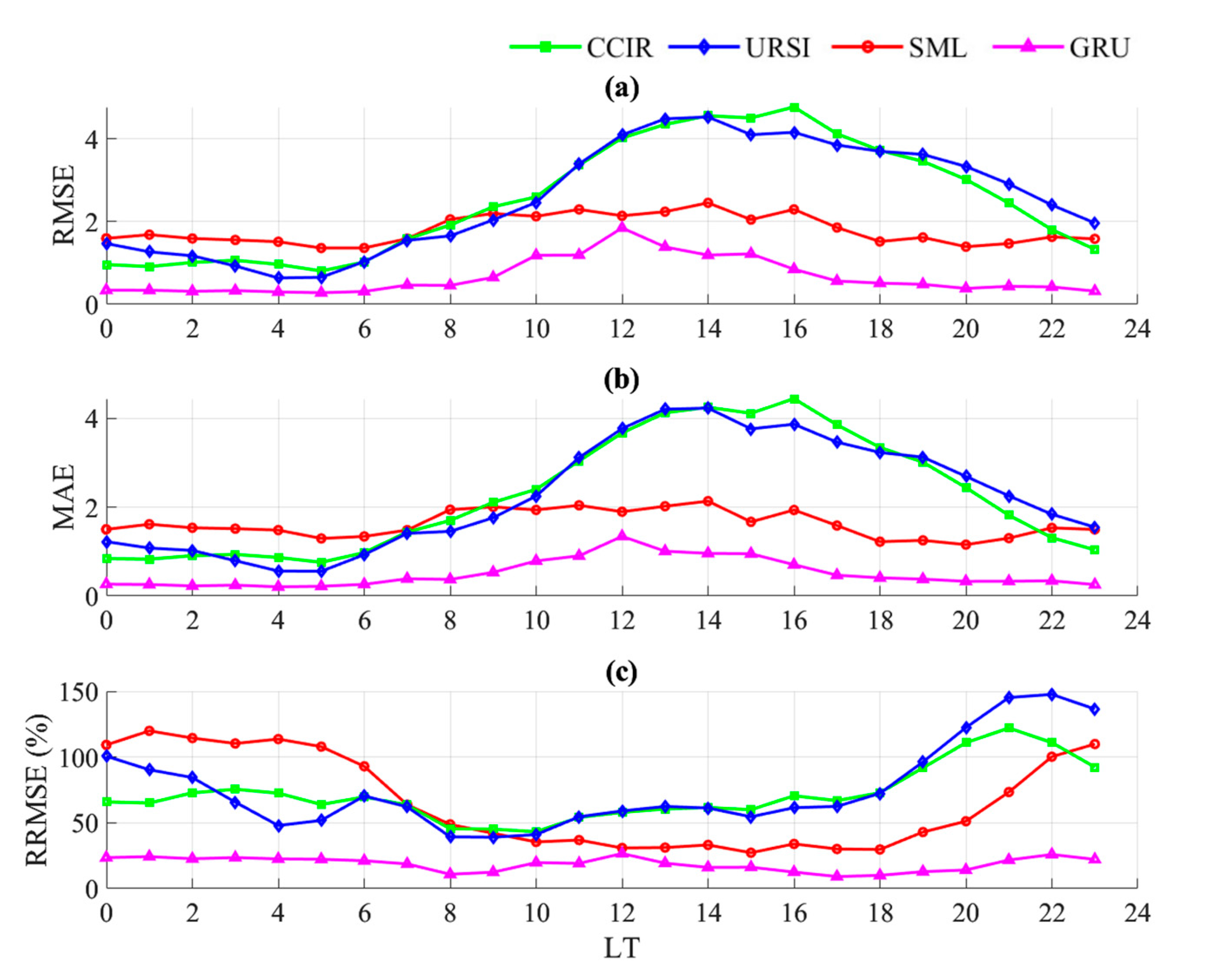
- (1)
- Throughout the entire testing period from 2019 to 2020, the relative magnitudes of the error indicators of the four models remained consistent. In other words, at the same point in time, regardless of the error indicator, the order of the error magni-tudes of the four models is consistent.
- (2)
- For the 24 h prediction, there are significant differences in error among the various models. From the perspectives of the RMSE and MAE, the errors of the CCIR and URSI models are relatively large, from LT = 11 to LT = 18. Analyzing the RRMSE, the SML-based model exhibited larger errors from LT = 23 to LT = 5 the next day, the CCIR from LT = 19 to LT = 23, and the URSI from LT = 19 to LT = 0 the next day.
- (3)
- Considering the overall performance of the 24 h prediction throughout the day, the GRU model’s RMSE, MAE, and RRMSE are significantly lower than those of the other models, indicating that the GRU model has higher prediction accuracy and better performance.
- (4)
- Further comparing the errors between the predicted values and the observed values of the GRU model showed the following: from LT = 17 to LT = 9 the next day, the RMSE and MAE are small, while from LT = 10 to LT = 16, the RMSE and MAE are large. This indicates that the absolute error of the GRU model predictions is significantly higher during LT = 10–16. However, the RRMSE performance is relatively consistent per hour because it reflects the relative differences, and the overall performance of the GRU model is relatively balanced.
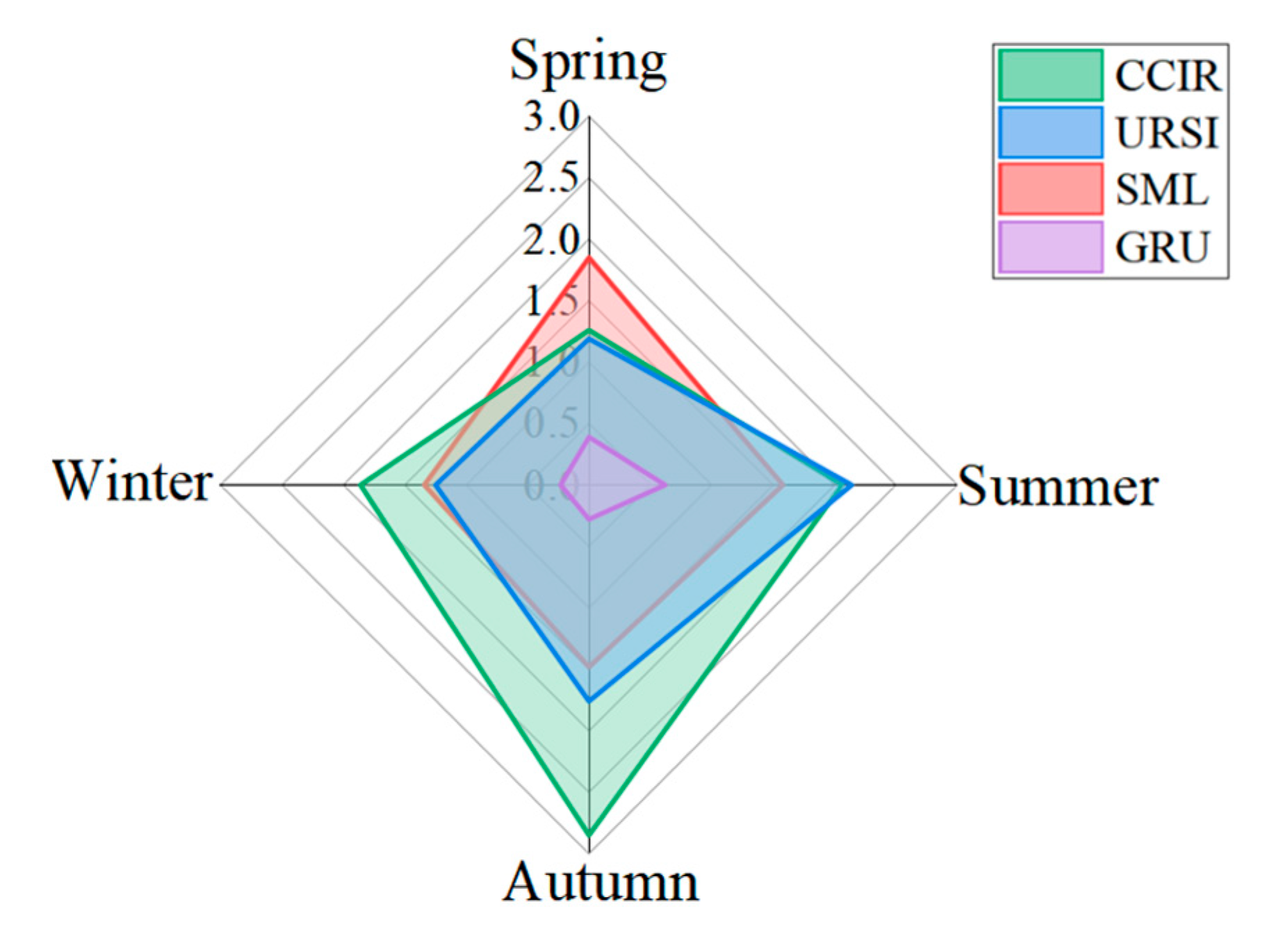
- (1)
- The SML-based model exhibits greater prediction errors in spring than other models due to inadequate representation of noontime ionospheric disturbances triggered by enhanced solar radiation [39].
- (2)
- CCIR shows large errors in autumn/winter because it ignores frequent magnetic storms in winter [40].
- (3)
- The GRU model achieves the smallest prediction errors across all seasonal metrics. However, its error is relatively higher in summer. This is because of physical processes not captured by the model (such as rapid electron loss at night via recombination), which represent a common challenge for purely data-driven methods like GRU to learn [41].
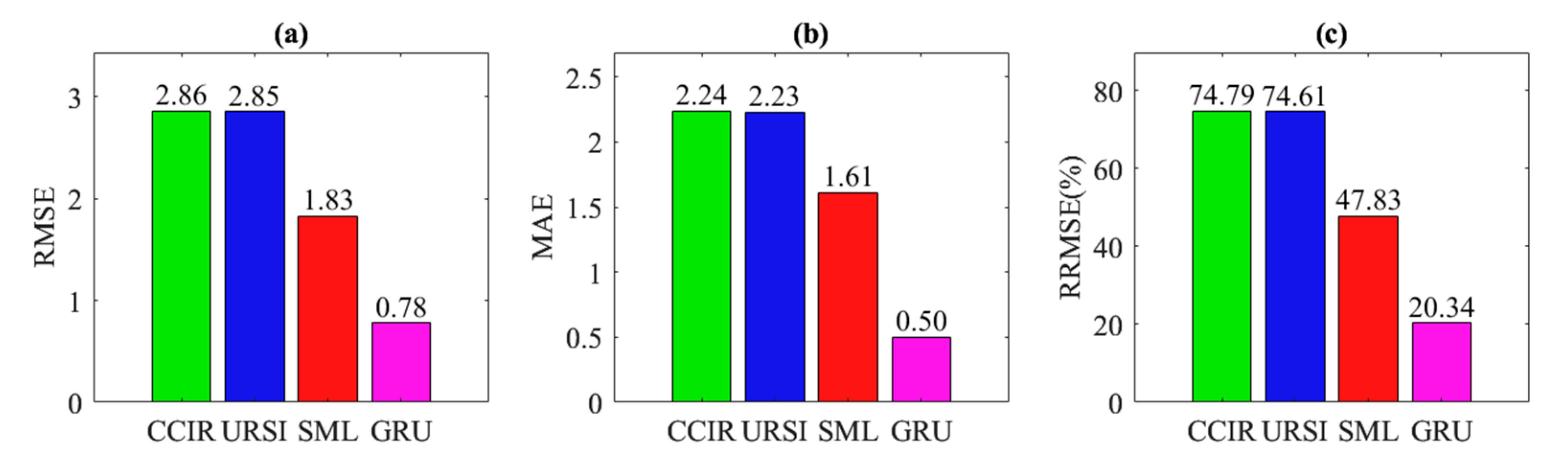
- (1)
- Regarding the RMSE, the GRU model has the smallest RMSE of 0.78 TECU. Compared with the SML-based model, CCIR model, and URSI model, it was reduced by 1.05 TECU, 2.08 TECU, and 2.07 TECU, respectively;
- (2)
- Regarding the MAE, the GRU model has the smallest MAE of 0.50 TECU. Compared with the SML-based model, CCIR model, and URSI model, it was reduced by 1.11 TECU, 1.74 TECU, and 1.73 TECU, respectively;
- (3)
- Regarding the RRMSE, the GRU model has the smallest RRMSE of 20.34%. Compared with the SML-based model, CCIR model, and URSI model, it was reduced by 27.49%, 54.45%, and 54.27%, respectively;
- (4)
- Overall, the GRU model significantly outperforms the RMSE, MAE, and RRMSE comparison models. The error reduction ranges from 1.05 to 2.08 TECU and 27.49% to 54.45%, demonstrating comprehensive performance advantages.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANNs | Artificial Neural Networks |
| CCIR | International Radio Consultative Committee |
| F10.7 | Solar 10.7 cm Radio Flux |
| foF2 | Ionospheric F2 layer |
| GRU | Gate Recurrent Unit |
| IRI | International Reference Ionosphere |
| LSTM | Long Short-Term Memory Network |
| MAE | Mean Absolute Error |
| OBS | Observations |
| R | Sunspot Relative Number |
| RNN | Recurrent Neural Network |
| RRMSE | Relative Root Mean Squared Error |
| SIDC | Solar Influences Data Analysis Center |
| SML | Statistical Machine Learning |
| sfu | Solar Flux Unit |
| TEC | Total Electron Content |
| URSI | International Union of Radio Science |
| LT | Local Time |
References
- Ming, F.X.; Ma, J.S. Study on Ionospheric Anomaly During Geomagnetic Storm by Beidou GEO Satellites. Geospat. Inf. 2023, 21, 100–103. [Google Scholar]
- Liu, L.B.; Wan, W.X.; Chen, Y.D.; Le, H.J. Solar activity effects of the ionosphere: A brief review. Chin. Sci. Bull. 2011, 56, 1202–1211. [Google Scholar] [CrossRef]
- Zhang, H.P. Research on China’s Regional Ionosphere Monitoring and Delay Correction Based on Ground-Based GPS. Ph.D. Thesis, Graduate University of Chinese Academy of Sciences, Shanghai Astronomical Observatory, Shanghai, China, 2006. [Google Scholar]
- Priyadarshi, S. A Review of Ionospheric Scintillation Models. Surv. Geophys. 2015, 36, 295–324. [Google Scholar] [CrossRef]
- Yuan, Y.B. Study on Theories and Methods of Correcting Ionospheric Delay and Monitoring Ionosphere Based on GPS. Ph.D. Thesis, Graduate University of Chinese Academy of Sciences, Institute of Geodesy and Geophysics, Wuhan, China, 2002. [Google Scholar]
- Yao, Y.B.; Chen, X.X.; Kong, J.; Zhou, C.; Liu, L.; Shan, L.L.; Guo, Z.H. An Updated Experimental Model of IG Indices Over the Antarctic Region via the Assimilation of IRI2016 With GNSS TEC. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1700–1717. [Google Scholar] [CrossRef]
- Zhang, W.; Huo, X.L.; Yuan, Y.B.; Li, Z.S.; Wang, N.B. Algorithm Research Using GNSS-TEC Data to Calibrate TEC Calculated by the IRI-2016 Model over China. Remote Sens. 2021, 13, 4002. [Google Scholar] [CrossRef]
- Bilitza, D. International Reference Ionosphere 2000. Radio Sci. 2001, 36, 261–275. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather-Int. J. Res. Appl. 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Liu, Y.R.; Wang, J.; Yang, C.; Zheng, Y.; Fu, H.P. A Machine Learning-Based Method for Modeling TEC Regional Temporal-Spatial Map. Remote Sens. 2022, 14, 5579. [Google Scholar] [CrossRef]
- Jia, W.K.; Zhao, D.A.; Ding, L. An optimized RBF neural network algorithm based on partial least squares and genetic algorithm for classification of small sample. Appl. Soft Comput. 2016, 48, 373–384. [Google Scholar] [CrossRef]
- Hu, X.; Zhou, C.; Zhao, J.; Liu, Y.; Liu, M.; Zhao, Z. The ionospheric foF2 prediction based on neural network optimization algorithm. Chin. J. Radio Sci. 2018, 33, 708–716. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, C.; Wang, C.; Zhao, J.; Liu, Y.; Xia, G.; Zhao, Z. Global ionospheric TEC prediction based on deep learning. Chin. J. Radio Sci. 2021, 36, 553–561. [Google Scholar]
- Li, W.; Zhao, D.S.; He, C.Y.; Hu, A.D.; Zhang, K.F. Advanced Machine Learning Optimized by The Genetic Algorithm in Ionospheric Models Using Long-Term Multi-Instrument Observations. Remote Sens. 2020, 12, 866. [Google Scholar] [CrossRef]
- Weng, J.X.; Liu, Y.R.; Wang, J. A Model-Assisted Combined Machine Learning Method for Ionospheric TEC Prediction. Remote Sens. 2023, 15, 2953. [Google Scholar] [CrossRef]
- Xia, G.Z.; Liu, Y.; Wei, T.F.; Wang, Z.K.; Huang, W.Q.; Du, Z.T.; Zhang, Z.B.A.; Wang, X.; Zhou, C. Ionospheric TEC forecast model based on support vector machine with GPU acceleration in the China region. Adv. Space Res. 2021, 68, 1377–1389. [Google Scholar] [CrossRef]
- Yu, Q.; Men, X.; Wang, J. A Prediction Model of Ionospheric Total Electron Content Based on Grid-Optimized Support Vector Regression. Remote Sens. 2024, 16, 2701. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014. [Google Scholar] [CrossRef]
- Injadat, M.; Moubayed, A.; Nassif, A.B.; Shami, A. Systematic ensemble model selection approach for educational data mining. Knowl.-Based Syst. 2020, 200, 105992. [Google Scholar] [CrossRef]
- Injadat, M.; Moubayed, A.; Nassif, A.B.; Shami, A. Multi-split optimized bagging ensemble model selection for multi-class educational data mining. Appl. Intell. 2020, 50, 4506–4528. [Google Scholar] [CrossRef]
- Lorenzo, P.R.; Nalepa, J.; Ramos, L.S.; Pastor, J.R. Hyper-Parameter Selection in Deep Neural Networks Using Parallel Particle Swarm Optimization. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO), Berlin, Germany, 15–19 July 2017; pp. 1864–1871. [Google Scholar]
- Reinisch, B.W.; Galkin, I.A. Global Ionospheric Radio Observatory (GIRO). Earth Planets Space 2011, 63, 377–381. [Google Scholar] [CrossRef]
- Homam, M.J. Latitudinal Effect on Total Electron Content Variations. In Proceedings of the International Symposium on Antennas and Propagation (ISAP), Kaohsiung, Taiwan, 2–4 December 2014; pp. 127–128. [Google Scholar]
- Zhao, G.C.; Zhang, L.; Wu, F.B. Application of improved median filtering algorithm to image de-noising. J. Appl. Opt. 2011, 32, 678–682. [Google Scholar]
- Tapping, K.F. The 10.7 cm solar radio flux(F10.7). Space Weather-Int. J. Res. Appl. 2013, 11, 394–406. [Google Scholar] [CrossRef]
- Hathaway, D.H. The Solar Cycle. Living Rev. Sol. Phys. 2015, 12, 4. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.X.; Zhang, M.L.; Wan, W.X.; Liu, L.; Ning, B.Q. Modeling M(3000)F2 based on empirical orthogonal function analysis method. Radio Sci. 2008, 43, 1–8. [Google Scholar] [CrossRef]
- Clette, F.; Berghmans, D.; Vanlommel, P.; Van der Linden, R.A.M.; Koeckelenbergh, A.; Wauters, L. From the Wolf number to the International Sunspot Index: 25 years of SIDC. Adv. Space Res. 2007, 40, 919–928. [Google Scholar] [CrossRef]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic Routing Between Capsules. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Bhowmik, P.; Nandy, D. Prediction of the strength and timing of sunspot cycle 25 reveal decadal-scale space environmental conditions. Nat. Commun. 2018, 9, 5209. [Google Scholar] [CrossRef]
- Weerakody, P.B.; Wong, K.W.; Wang, G.J.; Ela, W. A review of irregular time series data handling with gated recurrent neural networks. Neurocomputing 2021, 441, 161–178. [Google Scholar] [CrossRef]
- Shreedevi, P.R.; Choudhary, R.K.; Yadav, S.; Thampi, S.V.; Ajesh, A. Variation of the TEC at a dip equatorial station, Trivandrum and a mid latitude station, Hanle during the descending phase of the solar cycle 24 (2014-2016). J. Atmos. Sol.-Terr. Phys. 2018, 179, 425–434. [Google Scholar] [CrossRef]
- Maruyama, T. Regional reference total electron content model over Japan based on neural network mapping techniques. Ann. Geophys. 2007, 25, 2609–2614. [Google Scholar] [CrossRef]
- Yang, N.; Le, H.J.; Liu, L.B. Statistical analysis of ionospheric mid-latitude trough over the Northern Hemisphere derived from GPS total electron content data. Earth Planets Space 2015, 67, 196. [Google Scholar] [CrossRef]
- Xu, T.; Wu, Z.S.; Wu, J.; Wu, J. Solar cycle variation of the monthly median foF2 at Chongqing station, China. Adv. Space Res. 2008, 42, 213–218. [Google Scholar] [CrossRef]
- Sezen, U.; Gulyaeva, T.L.; Arikan, F. Performance of Solar Proxy Options of IRI-Plas Model for Equinox Seasons. J. Geophys. Res. Space Phys. 2018, 123, 1441–1456. [Google Scholar] [CrossRef]
- Liu, L.; Zou, S.S.; Yao, Y.B.; Wang, Z.H. Forecasting Global Ionospheric TEC Using Deep Learning Approach. Space Weather-Int. J. Res. Appl. 2020, 18, e2020SW002501. [Google Scholar] [CrossRef]
- Zhen, W.M.; Ming, O.; Zhu, Q.L. Review on ionospheric sounding and modeling. Wuhan Univ. J. Nat. Sci. 2023, 38, 625–645. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, Y.; Duan, W. The spring prediction barrier of ENSO in retrospective prediction experiments as shown by the four coupled ocean-atmosphere models. Acta Meteorol. Meteorol. Sinica 2012, 70, 506–519. [Google Scholar]
- Wang, J.; Zhang, T.; Yang, W.; Zhang, X. Measurement and analysis of atmospheric radio noise. J. China Ins. Comm. 2000, 21, 86–90. [Google Scholar]
- Kong, X.; Zheng, W.; Zhang, X.; Wang, M.; Shan, F.; Zhao, Q. Energy-saving control method of air conditioning in mushroom house based on data - physics mixed model. Trans. Chin. Soc. Agric. Eng. 2025, 41, 309–317. [Google Scholar]

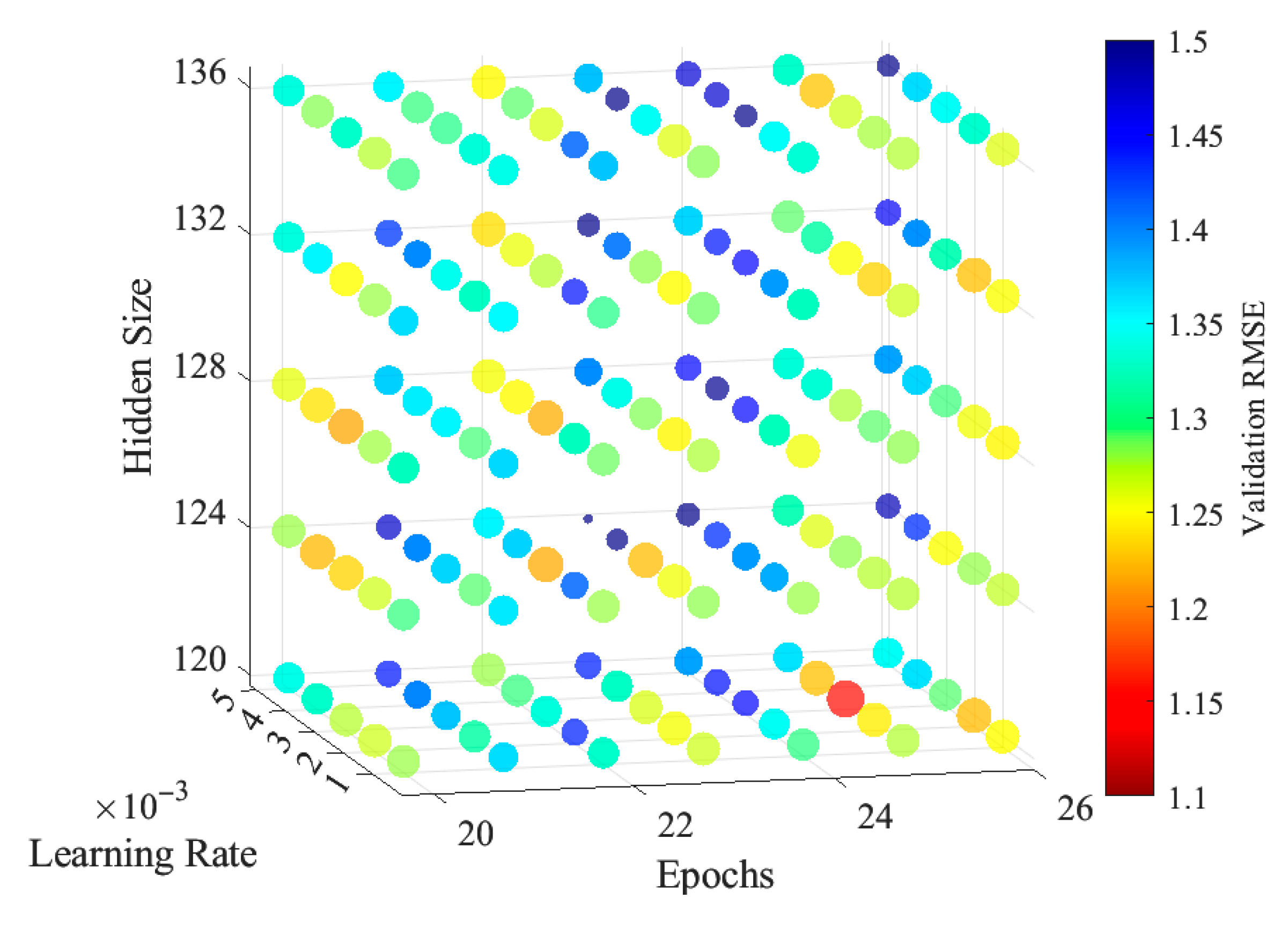
| Model Input | Epoch | Learning Rate | Hidden Size | Timestep | Layer Number | Minimum RMSE (TECU) |
|---|---|---|---|---|---|---|
| OBS | 22 | 0.004 | 128 | 12 | 1 | 1.35 |
| OBS & R12 | 22 | 0.003 | 120 | 12 | 1 | 1.20 |
| OBS & F12 | 22 | 0.003 | 124 | 12 | 1 | 1.16 |
| OBS & R12 & F12 | 25 | 0.003 | 120 | 12 | 1 | 1.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Yang, Z.; Yu, Q.; Wang, J. Grid-Search-Optimized, Gated Recurrent Unit-Based Prediction Model for Ionospheric Total Electron Content. Technologies 2025, 13, 347. https://doi.org/10.3390/technologies13080347
Zhou S, Yang Z, Yu Q, Wang J. Grid-Search-Optimized, Gated Recurrent Unit-Based Prediction Model for Ionospheric Total Electron Content. Technologies. 2025; 13(8):347. https://doi.org/10.3390/technologies13080347
Chicago/Turabian StyleZhou, Shuo, Ziyi Yang, Qiao Yu, and Jian Wang. 2025. "Grid-Search-Optimized, Gated Recurrent Unit-Based Prediction Model for Ionospheric Total Electron Content" Technologies 13, no. 8: 347. https://doi.org/10.3390/technologies13080347
APA StyleZhou, S., Yang, Z., Yu, Q., & Wang, J. (2025). Grid-Search-Optimized, Gated Recurrent Unit-Based Prediction Model for Ionospheric Total Electron Content. Technologies, 13(8), 347. https://doi.org/10.3390/technologies13080347







