Optimal Control Strategy and Evaluation Framework for Frequency Response of Combined Wind–Storage Systems
Abstract
1. Introduction
2. Combined Wind and Storage System Model
2.1. Thermal Power Unit Model
2.2. ESS Model
2.3. WT Model
2.4. System Model
3. Optimization Strategy Based on Model Predictive Control
3.1. Constraint Condition
3.2. Dynamic Weight
3.3. Objective Function
4. Comprehensive Evaluation Index System
5. Case Study
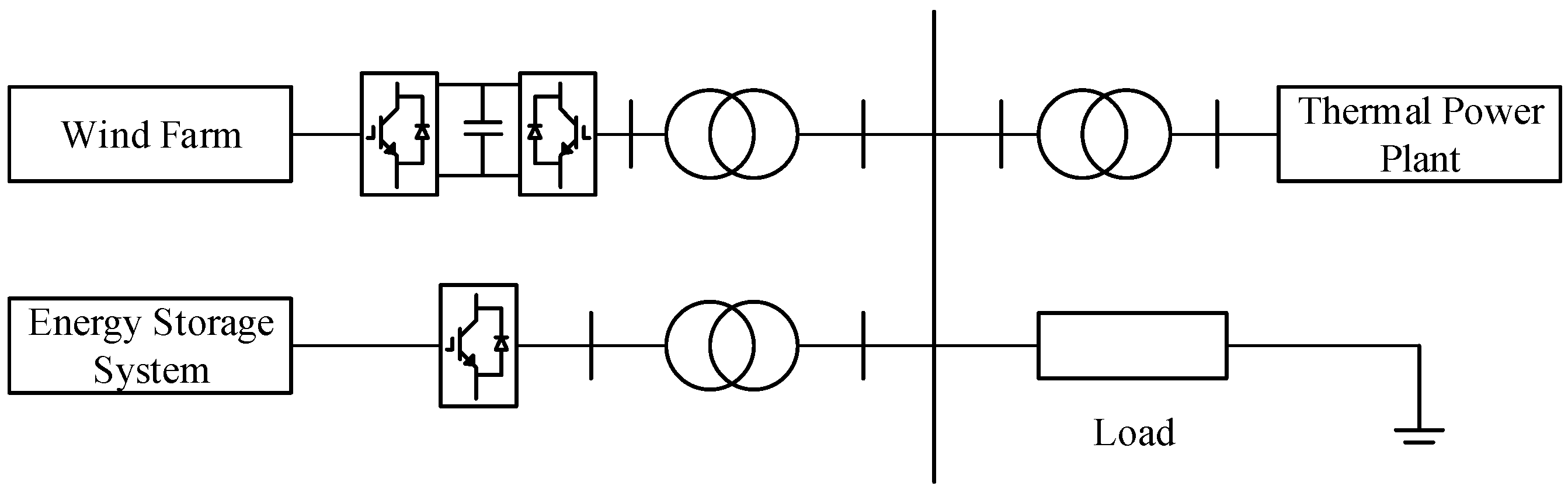
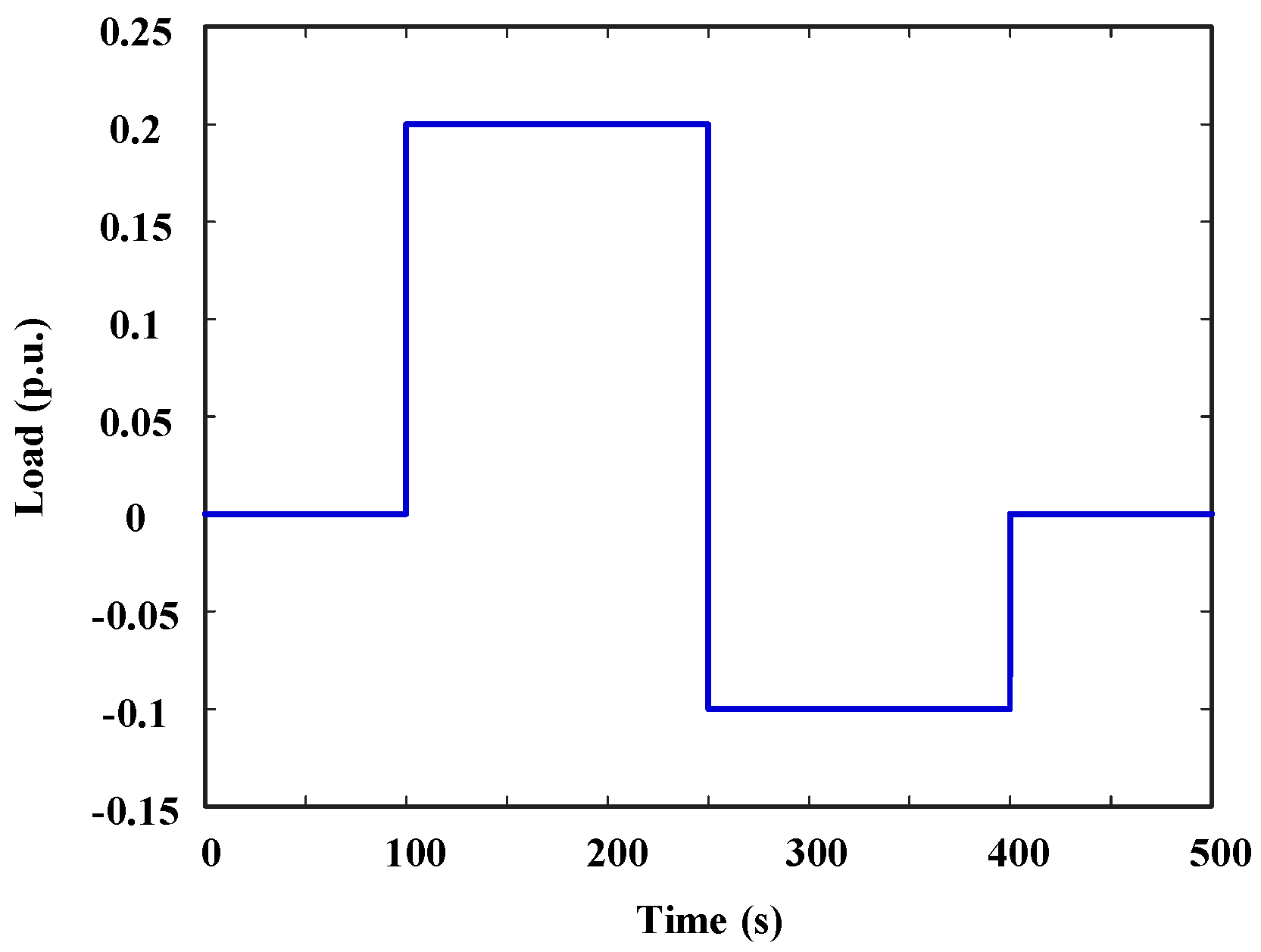
5.1. Test System
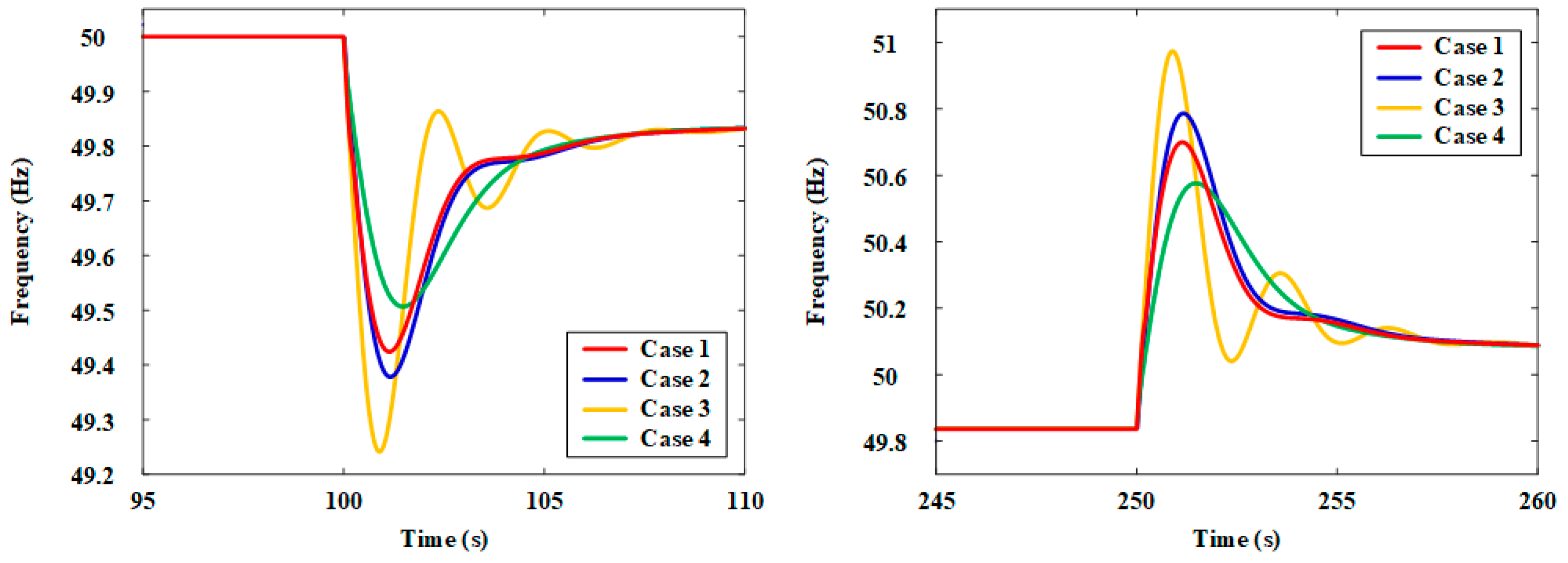
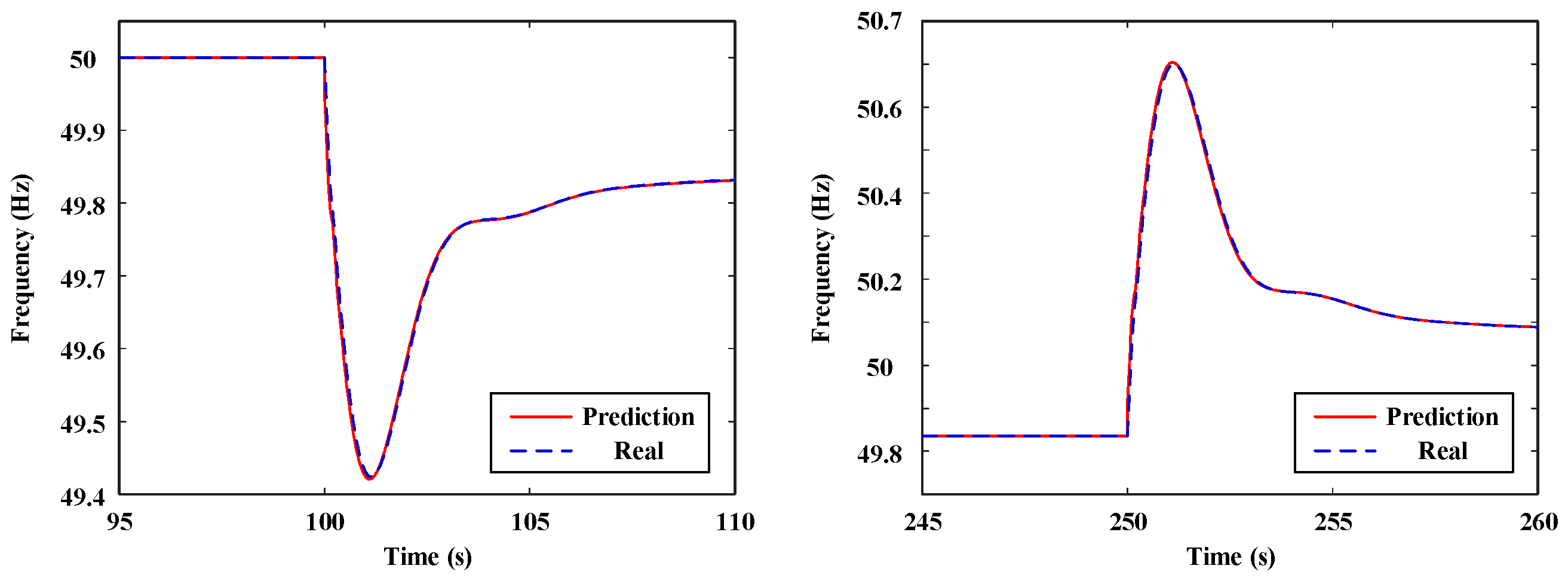
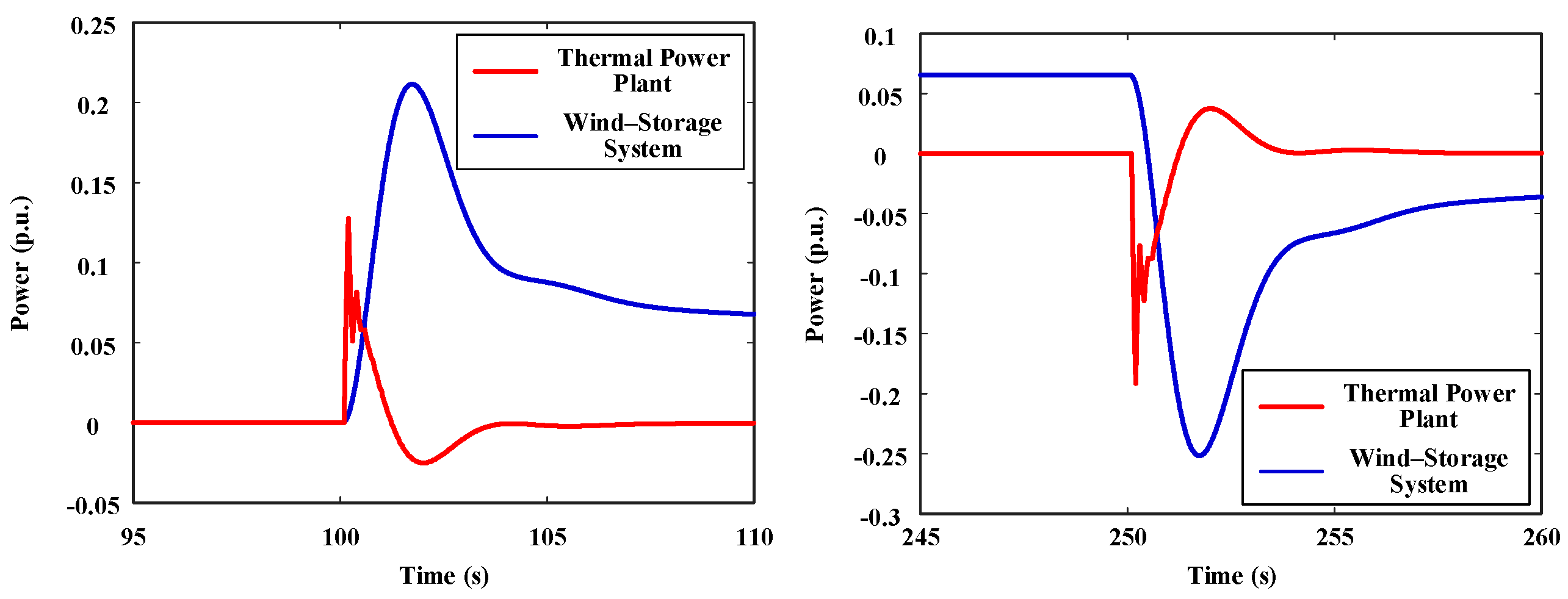
5.2. Control Performance
5.3. Evaluation Result
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WT | Wind Turbine |
| ESS | Energy Storage System |
| FM | Frequency Modulation |
| WT | Wind Farm |
| MPC | Model Predictive Control |
| SOC | State-of-Charge |
References
- Chen, C.; Tang, W.; Xia, Y.; Chen, C. Hybrid-energy storage optimization based on successive variational mode decomposition and wind power frequency modulation power fluctuation. Energies 2024, 17, 4391. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, P.; Gao, W.; Jiang, J.; Chang, J.; Wu, R.; Ai, C. Frequency modulation control of hydraulic wind turbines based on ocean used wind turbines and energy storage. Energies 2022, 15, 4086. [Google Scholar] [CrossRef]
- Qin, R.; Chen, J.; Li, Z.; Teng, W.; Liu, Y. Simulation of secondary frequency modulation process of wind power with the aid of flywheel energy storage. Sustainability 2023, 15, 11832. [Google Scholar] [CrossRef]
- Qing, M.; Tang, F.; Liu, D.; Liang, W.; Du, N.; Liu, F. Calculation of Limit Proportion of Wind Power Considering Primary Frequency Modulation and Frequency Constraints. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020. [Google Scholar]
- Wang, C.; Xu, J.; Wang, L.; Song, D. Research on optimization strategy of grid frequency modulation based on doubly-fed wind turbines. Int. J. Low Carbon Technol. 2021, 16, 229–239. [Google Scholar] [CrossRef]
- Ravanji, M.H.; Cañizares, C.A.; Parniani, M. Modeling and control of variable speed wind turbine generators for frequency regulation. IEEE Trans. Sustain. Energy 2019, 11, 916–927. [Google Scholar] [CrossRef]
- Qi, X.; Madonski, R.; Huang, C.; Ke, Y. Tracking-differentiator-based dynamic virtual inertial control of offshore wind power plant for frequency regulation. Int. J. Electr. Power Energy Syst. 2022, 141, 108150. [Google Scholar] [CrossRef]
- Qi, X.; Lei, L.; Yu, C.; Ma, Z.; Qu, T.; Du, M.; Gu, M. Adaptive distributed MPC based load frequency control with dynamic virtual inertia of offshore wind farms. IET Control Theory Appl. 2024, 18, 2228–2238. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, X.; Hei, Y.; Wang, H. Active participation of variable speed wind turbine in inertial and primary frequency regulations. Electr. Power Syst. Res. 2017, 147, 174–184. [Google Scholar] [CrossRef]
- Shim, J.W.; Verbič, G.; Kim, H.; Hur, K. On droop control of energy-constrained battery energy storage systems for grid frequency regulation. IEEE Access 2019, 7, 166353–166364. [Google Scholar] [CrossRef]
- Zhang, Y. Capacity-Based Adaptive Droop Control for Battery Energy Storage Operation. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar]
- Xu, H.; Pan, Z. An Adaptive Droop Control Strategy of Energy Storage Control for Microgrid with Wind Power and Energy Storage Systems. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017. [Google Scholar]
- Gomez, L.A.; Lourenco, L.F.; Grilo, A.P.; Salles, M.; Meegahapola, L.; Sguarezi Filho, A.J. Primary frequency response of microgrid using doubly fed induction generator with finite control set model predictive control plus droop control and storage system. IEEE Access 2020, 8, 189298–189312. [Google Scholar] [CrossRef]
- Liu, H.; Labonne, J.; Coste, P.; Huchet, E.; Plagnes-Juan, E.; Rives, J.; Veron, V.; Seiliez, I.; Bolliet, V. Looking at the complex relationships between migration behavior and conditional strategy based on energy metabolism in the European glass eel (Anguilla anguilla). Sci. Total Environ. 2019, 696, 134039. [Google Scholar] [CrossRef]
- Zhu, Y.; Shi, Q.; Yao, S.; Wei, Z. Adaptive MPC and power dispersion index based improved hierarchical frequency regulation for wind-storage integrated system. J. Energy Storage 2025, 107, 115006. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, Y.; Liu, X. Distributed MPC Strategy with Application to AGC in the Presence of Variable Speed Wind Turbine. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015. [Google Scholar]
- Hu, Z.; Su, R.; Ling, K.V.; Guo, Y.; Ma, R. Resilient event-triggered MPC for load frequency regulation with wind turbines under false data injection attacks. IEEE Trans. Autom. Sci. Eng. 2023, 21, 7073–7083. [Google Scholar] [CrossRef]
- Liu, X.; Wang, C.; Kong, X.; Zhang, Y.; Wang, W.; Lee, K.Y. Tube-based distributed MPC for load frequency control of power system with high wind power penetration. IEEE Trans. Power Syst. 2023, 39, 3118–3129. [Google Scholar] [CrossRef]
- Sun, S.; Yu, P.; Cheng, Y.; Wang, S.; Wang, Y.; Zhang, Z.; Kou, P. Model Prediction Control Scheme of Wind Farm with Energy Storage for Frequency Support. In Proceedings of the 2021 11th International Conference on Power and Energy Systems (ICPES), Shanghai, China, 18–20 December 2021. [Google Scholar]
- Liu, Q.; He, S.; Lu, W.; Wang, H. Model predictive control method for battery energy storage assisting secondary frequency regulation. Electr. Meas. Instrum. 2020, 57, 119. [Google Scholar] [CrossRef]
- Miao, F.; Tang, X.; Qi, Z. Analysis of frequency characteristics of power system based on wind farm-energy storage combined frequency regulation. Gaodianya Jishu/High Volt. Eng. 2015, 41, 2209. [Google Scholar]


| Category | Reference | Key Features | Methodology | Objective |
|---|---|---|---|---|
| WT-based frequency regulation | [6] | Virtual inertia control, large-disturbance nonlinear model | Optimization of virtual inertia controller tuning based on WT internal dynamics | Enhance the frequency response capabilities of WTs |
| [7] | Dynamic virtual inertia control, linear self-immunity control | Tracking differentiator, real-time control adjustments | Suppress noise amplification, improve robustness against secondary FM disturbances | |
| [8] | Adaptive distributed MPC, dynamic virtual inertia | Dynamic adjustment of control parameters based on operating conditions | Improve the frequency stability of grid-connected offshore WFs | |
| [9] | Integrated wind power frequency regulator, real-time pitch angle adjustment | Predefined load shedding operations, doubly fed WT support | Enhance dynamic frequency stability under high wind power penetration | |
| Storage-assisted frequency regulation | [10] | Sag control with charge state feedback | Theoretical analysis, numerical simulation | Be effective in high renewable penetration scenarios |
| [11] | Decoupled PQ control, adaptive capacity sag control | Autonomous frequency regulation, load sharing in grid-connected and islanded modes | Achieve autonomous frequency regulation and load sharing | |
| [12] | Adaptive sag control, delayed power tracking | Dynamic adjustment of the sag coefficient | Stabilize voltage and frequency during load variations | |
| [13] | Finite control set MPC, sag control | Communication-free frequency regulation, maximum power point tracking | Enable frequency regulation while maintaining power tracking | |
| [14] | Improved sag control strategy | Adjusting energy storage output power based on AC bus voltage and frequency variations | Enhance energy storage function | |
| MPC-based strategies | [15] | Adaptive MPC, hierarchical optimization, power dispersion index | Wind–storage cooperative FM strategy | Enhance FM performance, reduce equipment degradation |
| [16] | Distributed MPC, partitioned optimization, WT impact consideration | Load frequency control for a four-region interconnected grid | Mitigate load disturbances, account for generation rate constraints | |
| [17] | Attack-resilient control, detection mechanisms, event-triggering schemes | Load frequency control for grid-connected wind power systems | Enhance computational efficiency, operational security, and economic performance | |
| [18] | Pipeline-based distributed MPC, virtual inertia control, load shedding | Coordinated multi-regional load frequency control in high wind penetration grids | Suppress frequency deviations induced by load and wind speed fluctuations | |
| [19] | MPC-based cooperative wind–storage FM strategy, adaptive wind speed constraints | Optimize WT and energy storage power commands | Minimize grid frequency deviation and address equipment protection |
| Parameters | Values |
|---|---|
| Differential Coefficients for Primary FM of Thermal Power Units | |
| Thermal Unit Governor Action Time Constant | |
| Main Inlet Chamber Time Constant | |
| Reheater Time Constant | |
| Mechanical Torque of High-Pressure Turbines | |
| Grid Inertia Time Constant | |
| Load Adjustment Factor | |
| Total Installed Capacity of WFs | |
| Pitch Angle Control Response Time Constant | |
| Capacity of ESSs | |
| Rated Power of Energy Storage | |
| Energy Storage Response Time Constant |
| Method | WT | ESS | Grid | System |
|---|---|---|---|---|
| Proposed Method | 0.11 | 0.07 | 0.09 | 0.09 |
| Comparison Method | 0.34 | 0.26 | 0.21 | 0.27 |
| Method | Excellent | Good | Average | Poor | Extremely Poor | Health Level |
|---|---|---|---|---|---|---|
| Proposed Method | 0.58 | 0.42 | 0 | 0 | 0 | Excellent |
| Comparison Method | 0 | 0.87 | 0.13 | 0 | 0 | Good |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, J.; Zheng, H.; Cheng, X.; Li, Y.; Bo, L.; Wei, J. Optimal Control Strategy and Evaluation Framework for Frequency Response of Combined Wind–Storage Systems. Technologies 2025, 13, 259. https://doi.org/10.3390/technologies13060259
Hao J, Zheng H, Cheng X, Li Y, Bo L, Wei J. Optimal Control Strategy and Evaluation Framework for Frequency Response of Combined Wind–Storage Systems. Technologies. 2025; 13(6):259. https://doi.org/10.3390/technologies13060259
Chicago/Turabian StyleHao, Jie, Huiping Zheng, Xueting Cheng, Yuxiang Li, Liming Bo, and Juan Wei. 2025. "Optimal Control Strategy and Evaluation Framework for Frequency Response of Combined Wind–Storage Systems" Technologies 13, no. 6: 259. https://doi.org/10.3390/technologies13060259
APA StyleHao, J., Zheng, H., Cheng, X., Li, Y., Bo, L., & Wei, J. (2025). Optimal Control Strategy and Evaluation Framework for Frequency Response of Combined Wind–Storage Systems. Technologies, 13(6), 259. https://doi.org/10.3390/technologies13060259






