Analysis of Surface Roughness and Machine Learning-Based Modeling in Dry Turning of Super Duplex Stainless Steel Using Textured Tools
Abstract
1. Introduction
- Develop predictive models for surface roughness using advanced ML techniques;
- Improve model robustness through data augmentation strategies tailored for small-scale machining datasets.
2. Overview of Modeling Techniques
2.1. Least-Squares Support Vector Regression
2.2. Multi-Gene Genetic Programming
3. Materials and Method
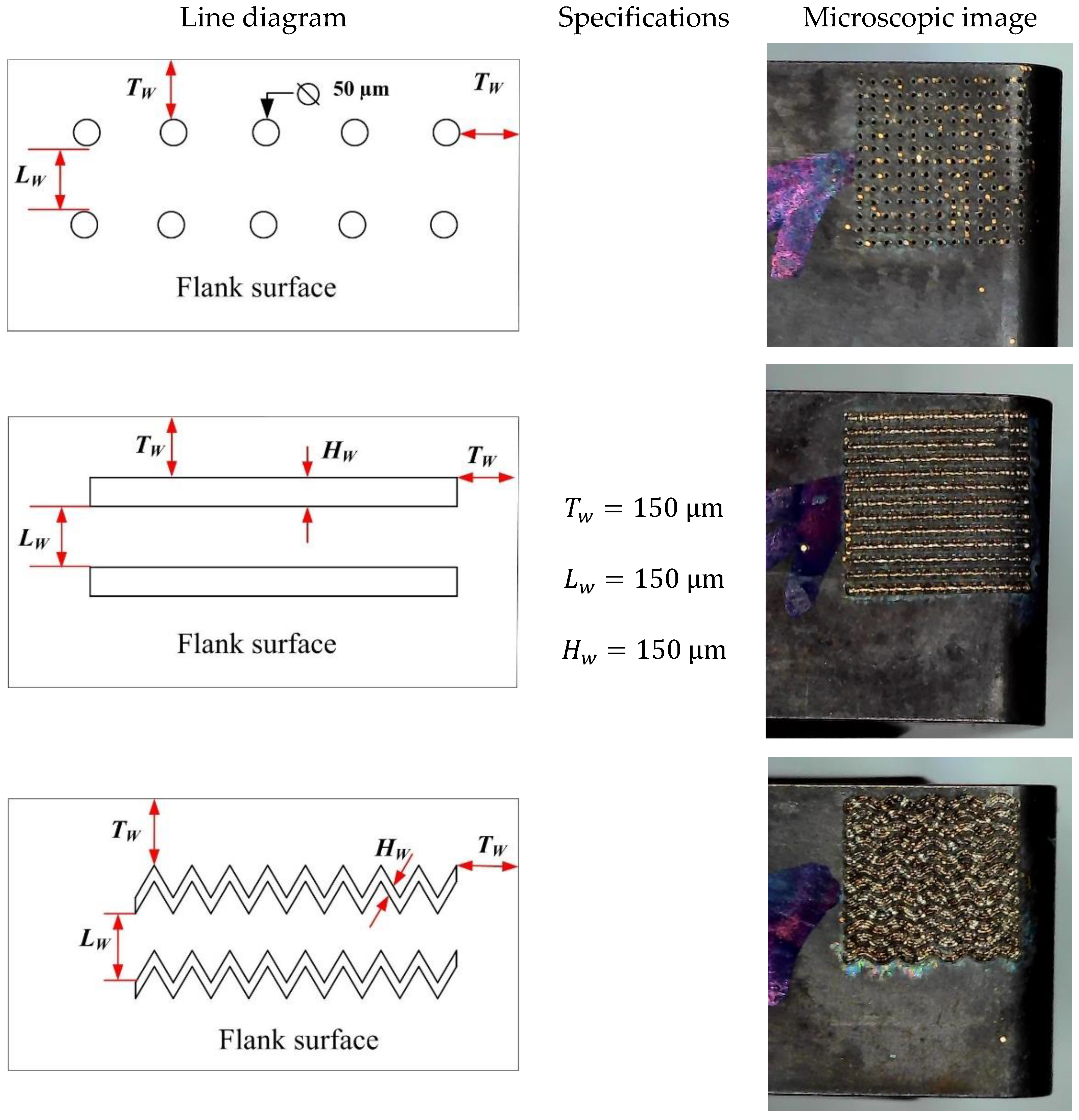
3.1. Experimentation and Measurements
3.2. Data Preprocessing for Machine Learning
4. Implementation of Machine Learning Techniques
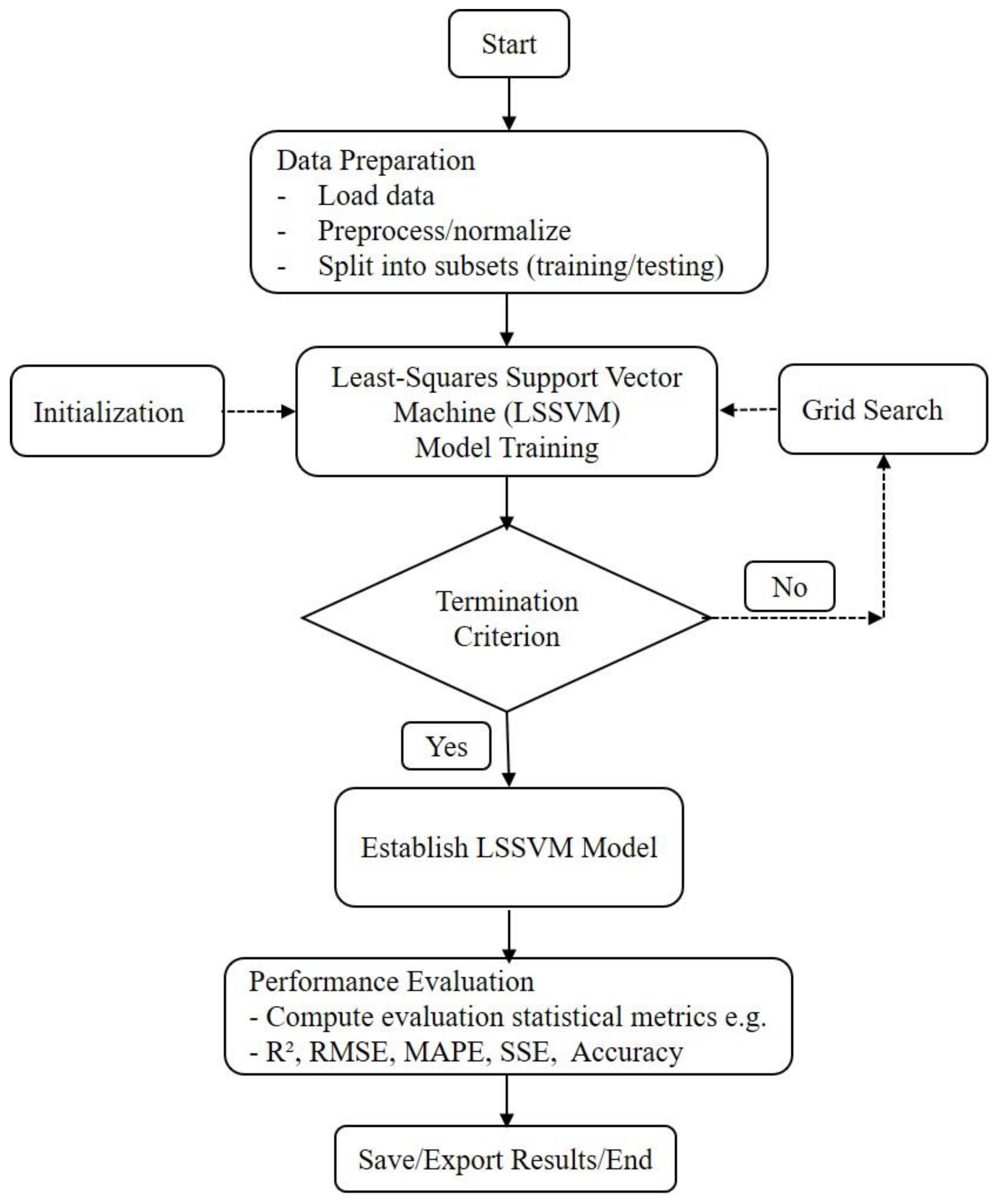
4.1. Least-Squares Support Vector Machine (LSSVM)
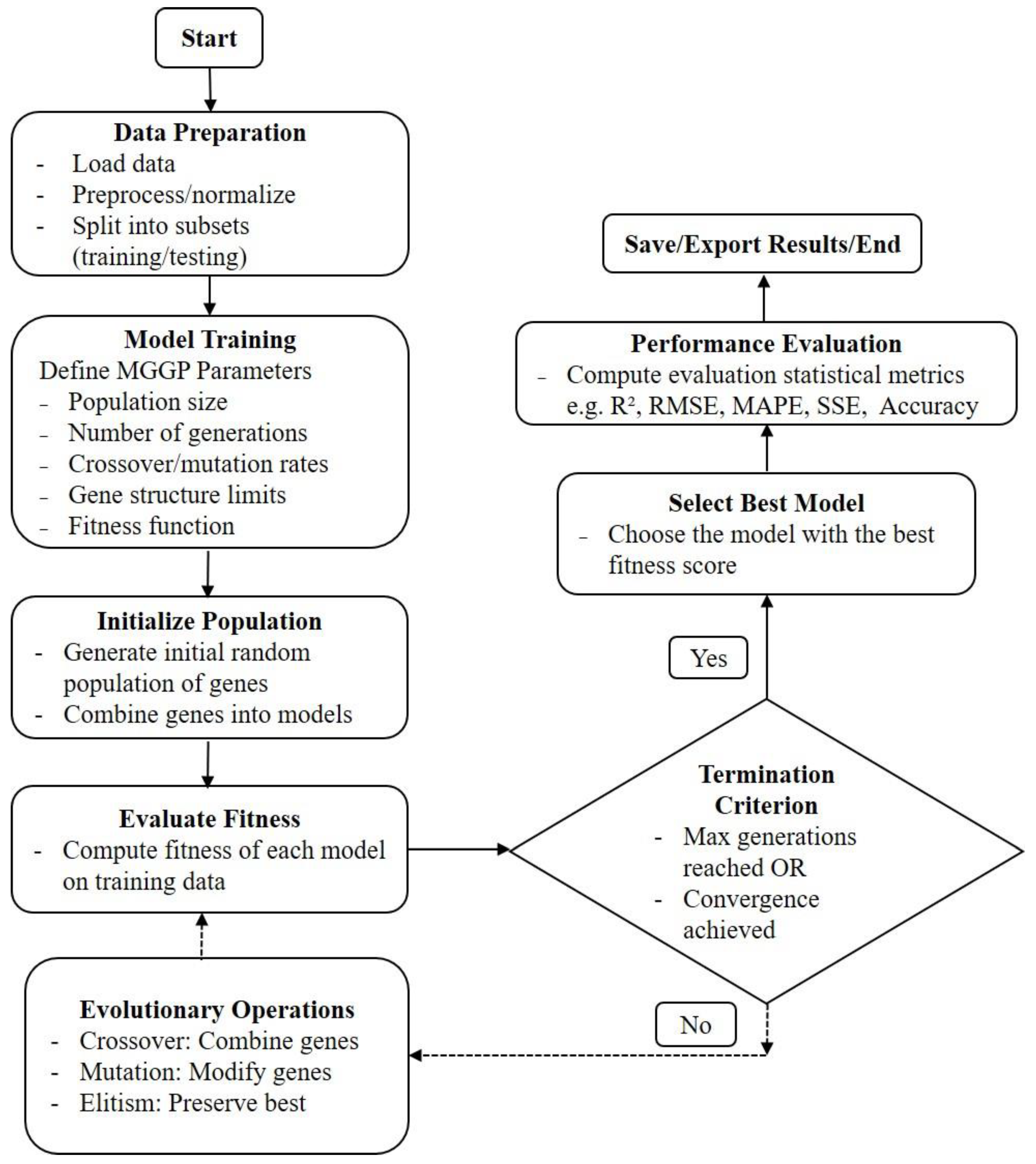
4.2. Multi-Gene Genetic Programming (MGGP)
5. Results and Discussion
5.1. Effect of Machining Parameters on Rz
5.2. Model Evaluation
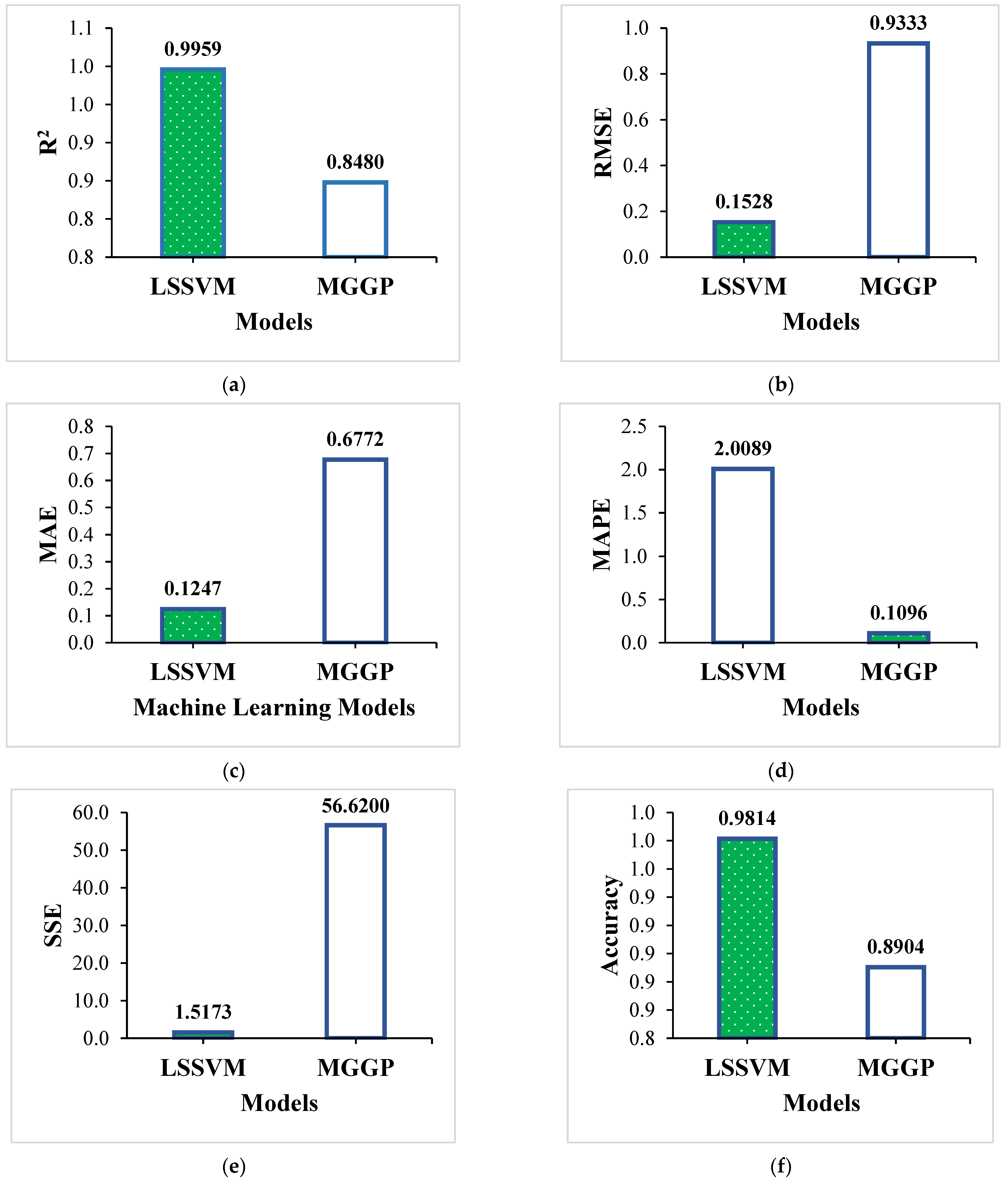
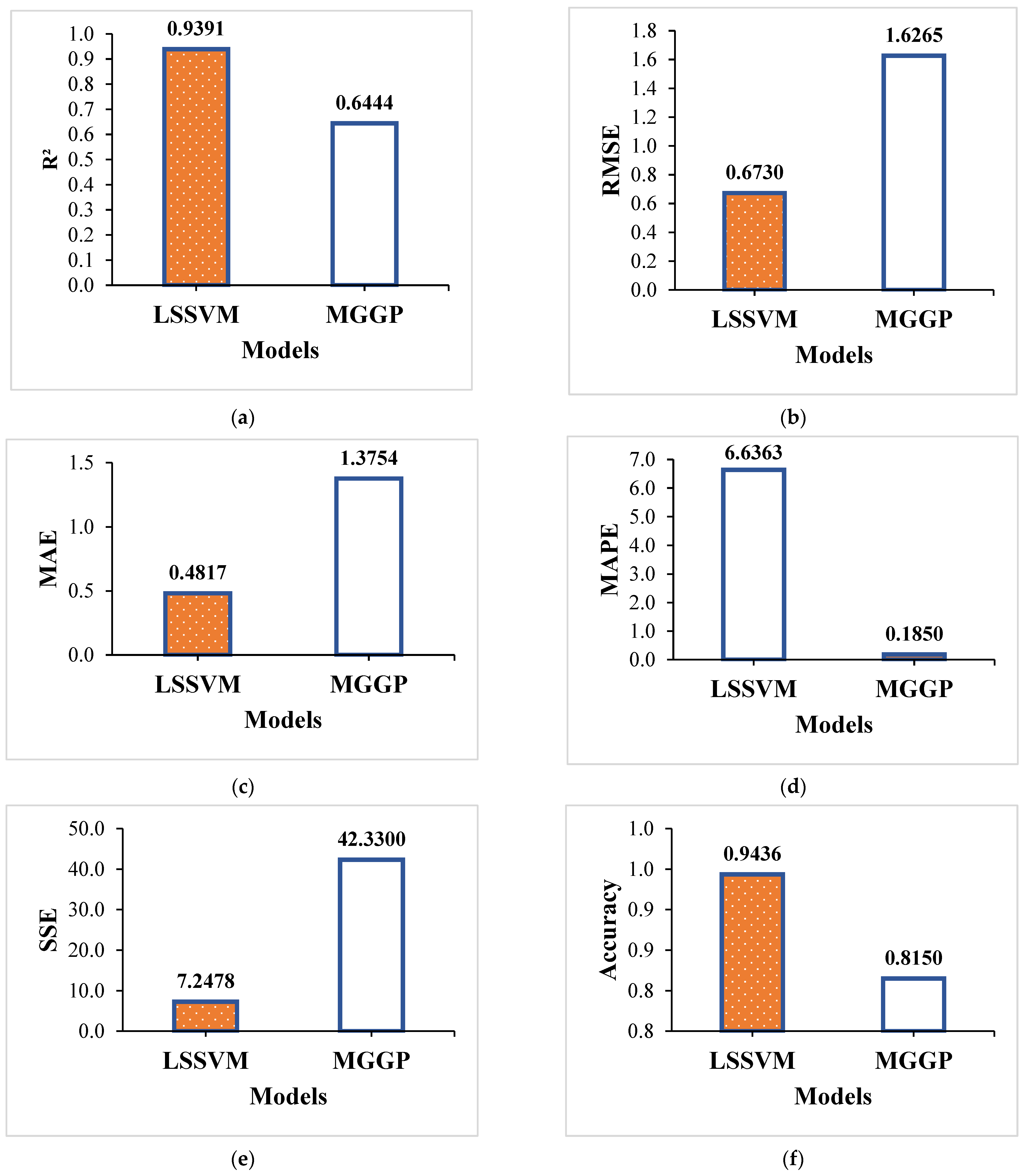
5.3. Comparative Evaluation of Machine Learning Models’ Performances
6. Conclusions
- Feed rate was found to be the most influential parameter affected mean roughness depth.
- To obtain better surface quality, the machining of SDSS 2507 at lower values of machining parameters is recommended.
- The Least-Squares Support Vector Machine (LSSVM) model demonstrated superior predictive performance, achieving an R2 of 0.9959 and 98.14% accuracy on the training dataset, and maintaining strong generalization on unseen data with a testing R2 of 0.9391 and an accuracy of 94.36%, outperforming the Multi-Gene Genetic Programming (MGGP) model.
- The MGGP model also showed reasonable performance with a training R2 of 0.8480 and a testing R2 of 0.6444, though it was less effective than LSSVM in minimizing prediction errors across all evaluated metrics.
- Comprehensive statistical validation using metrics such as RMSE, MAE, MAPE, SSE, and accuracy confirmed the reliability of the LSSVM model for accurate surface roughness prediction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reffas, O.; Boumediri, H.; Karmi, Y.; Kahaleras, M.S.; Bousba, I.; Aissa, L. Statistical Analysis and Predictive Modeling of Cutting Parameters in EN-GJL-250 Cast Iron Turning: Application of Machine Learning and MOALO Optimization. Int. J. Adv. Manuf. Technol. 2025, 137, 1991–2009. [Google Scholar] [CrossRef]
- Kumar, S.T.P.; Prasada, H.P.T.; Nagamadhu, M.; Pattar, N.; Kivade, S.B.; Sachinkumar; Ravichandra, K.R.; Hanumanthlal, S. Experimental Investigation on the Performance of Different Cutting Fluids on Cutting Force During Turning of Duplex Stainless Steel-2205 under MQL Technique. Math. Model. Eng. Probl. 2022, 9, 136–143. [Google Scholar] [CrossRef]
- Khlifi, H.; Abdellaoui, L.; Saï, W.B. Prediction of Cutting Force and Surface Roughness in Turning Using Machine Learning. 2nd International Conference on Innovative Materials, Manufacturing and Advanced Technologies, IMMAT 2022. Mech. Mach. Sci. 2024, 144, 213–222. [Google Scholar]
- Zhang, Y.; Xu, X. Machine Learning Cutting Force, Surface Roughness, and Tool Life in High Speed Turning Processes. Manuf. Lett. 2021, 29, 84–89. [Google Scholar] [CrossRef]
- Abellán-Nebot, J.V.; Vila Pastor, C.; Siller, H.R. A Review of the Factors Influencing Surface Roughness in Machining and Their Impact on Sustainability. Sustainability 2024, 16, 1917. [Google Scholar] [CrossRef]
- Dubey, V.; Sharma, A.K.; Pimenov, D.Y. Prediction of Surface Roughness Using Machine Learning Approach in MQL Turning of AISI 304 Steel by Varying Nanoparticle Size in the Cutting Fluid. Lubricants 2022, 10, 81. [Google Scholar] [CrossRef]
- Jacob, J.; Meurer, M.; Bergs, T. Surface Roughness Prediction in Hard Turning (Finishing) of 16MnCr5 Using a Model Ensemble Approach. Procedia CIRP 2024, 126, 504–507. [Google Scholar] [CrossRef]
- Yeganefar, A.; Niknam, S.A.; Asadi, R. The Use of Support Vector Machine, Neural Network, and Regression Analysis to Predict and Optimize Surface Roughness and Cutting Forces in Milling. Int. J. Adv. Manuf. Technol. 2019, 105, 951–965. [Google Scholar] [CrossRef]
- Pimenov, D.Y.; Bustillo, A.; Mikolajczyk, T. Artificial Intelligence for Automatic Prediction of Required Surface Roughness by Monitoring Wear on Face Mill Teeth. J. Intell. Manuf. 2018, 29, 1045–1061. [Google Scholar] [CrossRef]
- Gupta, M.K.; Mia, M.; Pruncu, C.I.; Khan, A.M.; Rahman, M.A.; Jamil, M.; Sharma, V.S. Modeling and Performance Evaluation of Al2O3, MoS2 and Graphite Nanoparticle-Assisted MQL in Turning Titanium Alloy: An Intelligent Approach. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 207. [Google Scholar] [CrossRef]
- Balonji, S.; Tartibu, L.K.; Okokpujie, I.P. Prediction Analysis of Surface Roughness of Aluminum Al6061 in End Milling CNC Machine Using Soft Computing Techniques. Appl. Sci. 2023, 13, 4147. [Google Scholar] [CrossRef]
- Kosarac, A.; Tabakovic, S.; Mladjenovic, C.; Zeljkovic, M.; Orasanin, G. Next-Gen Manufacturing: Machine Learning for Surface Roughness Prediction in Ti-6Al-4V Biocompatible Alloy Machining. J. Manuf. Mater. Process. 2023, 7, 202. [Google Scholar] [CrossRef]
- Dewangan, A.; Neigapula, V.S.N.; Soni, D.L.; Vaidya, S. Estimation of Surface Quality for Turning Operations Using Machine Learning Approach. Tribol. Mater. Surf. Interfaces 2024, 18, 228–242. [Google Scholar] [CrossRef]
- Adizue, U.L.; Takács, M. Exploring the Correlation between Design of Experiments and Machine Learning Prediction Accuracy in Ultra-Precision Hard Turning of AISI D2 with CBN Insert: A Comparative Study of Taguchi and Full Factorial Designs. Int. J. Adv. Manuf. Technol. 2025, 137, 2061–2090. [Google Scholar] [CrossRef]
- Abbas, A.T.; Sharma, N.; Alqosaibi, K.F.; Abbas, M.A.; Sharma, R.C.; Elkaseer, A. Investigation of Surface Quality and Productivity in Precision Hard Turning of AISI 4340 Steel Using Integrated Approach of ML-MOORA-PSO. Processes 2025, 13, 1156. [Google Scholar] [CrossRef]
- May Tzuc, O.; Hernández-Pérez, I.; Macias-Melo, E.V.; Bassam, A.; Xamán, J.; Cruz, B. Multi-Gene Genetic Programming for Predicting the Heat Gain of Flat Naturally Ventilated Roof Using Data from Outdoor Environmental Monitoring. Measurement 2019, 138, 106–117. [Google Scholar] [CrossRef]
- Garg, A.; Lam, J.S.L. Improving Environmental Sustainability by Formulation of Generalized Power Consumption Models Using an Ensemble Based Multi-Gene Genetic Programming Approach. J. Clean. Prod. 2015, 102, 246–263. [Google Scholar] [CrossRef]
- Pawanr, S.; Garg, G.K.; Routroy, S. Prediction of Energy Efficiency, Power Factor and Associated Carbon Emissions of Machine Tools Using Soft Computing Techniques. Int. J. Interact. Des. Manuf. 2023, 17, 1165–1183. [Google Scholar] [CrossRef]
- Xu, C.; Yao, S.; Wang, G.; Wang, Y.; Xu, J. A Prediction Model of Drilling Force in CFRP Internal Chip Removal Hole Drilling Based on Support Vector Regression. Int. J. Adv. Manuf. Technol. 2021, 117, 1505–1516. [Google Scholar] [CrossRef]
- Wang, T.; Noori, M.; Altabey, W.A.; Wu, Z.; Ghiasi, R.; Kuok, S.C.; Silik, A.; Farhan, N.S.D.; Sarhosis, V.; Farsangi, E.N. From Model-Driven to Data-Driven: A Review of Hysteresis Modeling in Structural and Mechanical Systems. Mech. Syst. Signal Process. 2023, 204, 110785. [Google Scholar] [CrossRef]
- Lin, Y.; Li, L.; Yang, S.; Chen, X.; Li, X.; Zhu, Z. Performance Prediction and Optimization of Hydrogenation Feed Pump Based on Particle Swarm Optimization–Least Squares Support Vector Regression Surrogate Model. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2315985. [Google Scholar] [CrossRef]
- Niazkar, M. Multigene Genetic Programming and Its Various Applications; Elsevier Inc.: Amsterdam, The Netherlands, 2022; ISBN 9780128212851. [Google Scholar]
- Bardhan, A. Probabilistic Assessment of Heavy-Haul Railway Track Using Multi-Gene Genetic Programming. Appl. Math. Model. 2024, 125, 687–720. [Google Scholar] [CrossRef]
- Chaubey, S.K.; Gupta, K.; Madić, M. An Investigation on Mean Roughness Depth and Material Erosion Speed During Manufacturing of Stainless-Steel Miniature Ratchet Gears By Wire-Edm. Facta Univ. Ser. Mech. Eng. 2023, 21, 239–258. [Google Scholar] [CrossRef]
- ISO 4287; Geometrical Product Specifications (GPS)–Surface Texture: Profile Method–Terms, Definitions and Surface Texture Parameters. International Organization for Standardization: Geneva, Switzerland, 1997.
- Balasuadhakar, A.; Thirumalai Kumaran, S.; Uthayakumar, M. Machine Learning Prediction of Surface Roughness in Sustainable Machining of AISI H11 Tool Steel. Smart Mater. Manuf. 2025, 3, 100075. [Google Scholar] [CrossRef]
- Avuçlu, E. A New Data Augmentation Method to Use in Machine Learning Algorithms Using Statistical Measurements. Measurement 2021, 180, 109577. [Google Scholar] [CrossRef]
- Rai, A.; Ahmad, Z.; Hasan, M.J.; Kim, J.M. A Novel Pipeline Leak Detection Technique Based on Acoustic Emission Features and Two-Sample Kolmogorov–Smirnov Test. Sensors 2021, 21, 8247. [Google Scholar] [CrossRef]
- Zhang, G.; Eddy Patuwo, B.; Hu, M.Y. Forecasting with Artificial Neural Networks: The State of the Art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Abbed, K.; Kribes, N.; Yallese, M.A.; Chihaoui, S.; Boutabba, S. Effects of Tool Materials and Cutting Conditions in Turning of Ti-6Al-4V Alloy: Statistical Analysis, Modeling and Optimization Using CoCoSo, MABAC, ARAS and CODAS Methods. Int. J. Adv. Manuf. Technol. 2023, 128, 1535–1557. [Google Scholar] [CrossRef]
- Rathod, N.J.; Chopra, M.K.; Shelke, S.N.; Chaurasiya, P.K.; Kumar, R.; Saxena, K.K.; Prakash, C. Investigations on Hard Turning Using SS304 Sheet Metal Component Grey Based Taguchi and Regression Methodology. Int. J. Interact. Des. Manuf. 2024, 18, 2653–2664. [Google Scholar] [CrossRef]
- Bhardwaj, B.; Kumar, R.; Singh, P.K. Surface Roughness (Ra) Prediction Model for Turning of AISI 1019 Steel Using Response Surface Methodology and Box-Cox Transformation. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2014, 228, 223–232. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, Y.; Geng, D.; Zhang, D.; Ying, E.; Liu, R.; Jiang, X. Cutting Performance and Surface Integrity during Rotary Ultrasonic Elliptical Milling of Cast Ni-Based Superalloy. J. Mater. Res. Technol. 2025, 35, 980–994. [Google Scholar] [CrossRef]





| Study | Material/Process | Modeling Techniques | Optimization Techniques | Key Inputs | Performance/ Outputs | Key Findings |
|---|---|---|---|---|---|---|
| Pimenov et al. [9] | Face milling of carbon steel 45 using coated carbide inserts | RF, MLP, RBF, Regression Trees | None (real-time prediction focus) | Tool wear, main drive power | Surface roughness | RF achieved highest accuracy; practical workshop application suggested |
| Yeganefar et al. [8] | Dry slot milling of 7075-T6 aluminum using coated inserts | ANN, SVM | NSGA-II | vc, fr, dc, tool type | Surface roughness, cutting forces | ANN-NSGA-II provided Pareto-optimal solutions; feed per tooth most influential |
| Gupta et al. [10] | Turning Ti alloy under MQL with nanofluids (NFs) using CBN tool | ANFIS, RSM | Coherence Distance Algorithm | vc, fr, approaching angle nanofluid type | Surface roughness, cutting force, temperature | Graphite NF most effective; ANFIS model superior; cutting speed/feed identified as critical factors |
| Zhang and Xu [4] | High-speed turning | GPR | None (prediction focus) | vc, fr, and dc | Cutting force, surface roughness, tool life | GPR provided high accuracy, stability, and robustness |
| Dubey et al. [6] | MQL turning of AISI 304 steel with nanofluids using carbide inserts | SVM, RF, Linear Regression | None (prediction focus) | vc, fr, and dc, cutting fluid type | Surface roughness | RF achieved best R2; highlighted ML’s potential in surface roughness prediction |
| Balonji et al. [11] | Dry milling of Al6061 using carbide inserts | ANN, ANFIS, ANN–PSO, ANN–GA, ANFIS–PSO, ANFIS–GA | PSO, GA (for hybrid models) | Spindle speed, vc and fr | Surface roughness | Hybrid models (ANFIS–GA) outperformed others; emphasized hyperparameter tuning |
| Kosarac et al. [12] | Milling of Ti-6Al-4V under different cooling conditions | RF, GB, Neural Networks | Taguchi design for initial parameter setting | vc, fr, and dc | Surface roughness | RF achieved highest accuracy; feed rate most influential |
| Dewangan et al. [13] | Dry turning of AISI 316 using carbide inserts | SVR, GPR, GBR | PSO | vc, fr, and dc | Surface roughness, Material Removal Rate (MRR) | GBR–PSO combination optimized efficiently the considered responses |
| Khlifi et al. [3] | Turning of AISI4340 using coated carbide insert | MLR, RFR, GBR, Bagging | None (focus on prediction) | vc, fr, and dc | Surface roughness, cutting force | RFR best for Ra; GBR best for force |
| Adizue and Takács [14] | Ultraprecision turning of AISI D2 steel using CBN insert | BRNN | Taguchi and Full Factorial DOE | vc, fr, and dc | Surface roughness, MRR | Full factorial design improved BRNN performance; Ra and MRR predicted accurately |
| Abbas et al. [15] | Dry precision turning of AISI 4340 steel using conventional and wiper inserts | XGBoost + MOORA | MOORA, PSO | vc, fr, dc and tool insert type | Surface roughness, MRR | Wiper inserts improved Ra; hybrid method highly effective |
| Reffas et al. [1] | Turning of cast iron using silicon nitride ceramic inserts | Dragonfly-optimized DNN, SVM | Ant Lion Optimizer, Desirability Function | vc, fr, dc and tool coating | Surface roughness, cutting force, pressure | hybrid ML and optimization improved efficiency and surface finish |
| May Tzuc et al. [16] | Heat gain prediction in flat naturally ventilated roofs | Multi-Gene Genetic Programming (MGGP) | None (focus on prediction) | Ambient air temperature, solar irradiation, wind speed, relative humidity, ventilated roof channel width | Heat flux | MGGP efficiently modeled the heat flux |
| Garg et al. [17] | Turning of AISI 1045 steel and 7075 Al alloy–15 wt% SiC composites | Ensemble-based (EN)-MGGP, MGGP | None (focus on prediction) | vc, fr, and dc | Surface roughness, tool life, power consumption | EN-MGGP outperformed MGGP in generalization; cutting speed had greatest impact on power consumption |
| Pawanr et al. [18] | Dry machining of Al6061 using carbide inserts | MGGP LSSVM Fuzzy-logic | None (focus on prediction) | vc, fr, dc, and nose radius | Power factor, energy efficiency, carbon emission | All ML methods effectively predicted the responses, with LS-SVM demonstrating the best performance |
| Exp No | Texture Type | vc (m/min) | fr (mm/rev) | dc (mm) | Rz1 (μm) | Rz2 (μm) | Rz3 (μm) | Rz_avg (μm) |
|---|---|---|---|---|---|---|---|---|
| 1 | Dimple | 75 | 0.18 | 1.2 | 11.987 | 8.942 | 10.104 | 10.344 |
| 2 | Dimple | 75 | 0.12 | 0.8 | 5.764 | 6.374 | 5.460 | 5.866 |
| 3 | Dimple | 75 | 0.06 | 0.4 | 4.771 | 4.978 | 4.538 | 4.762 |
| 4 | Dimple | 100 | 0.12 | 1.2 | 8.033 | 10.801 | 10.523 | 9.786 |
| 5 | Dimple | 100 | 0.06 | 0.8 | 5.819 | 6.288 | 5.353 | 5.820 |
| 6 | Dimple | 100 | 0.18 | 0.4 | 10.292 | 8.818 | 8.212 | 9.107 |
| 7 | Dimple | 125 | 0.06 | 1.2 | 5.172 | 5.909 | 4.671 | 5.251 |
| 8 | Dimple | 125 | 0.18 | 0.8 | 6.826 | 6.440 | 6.781 | 6.682 |
| 9 | Dimple | 125 | 0.12 | 0.4 | 5.082 | 5.832 | 5.500 | 5.471 |
| 1 | Groove | 75 | 0.18 | 1.2 | 9.255 | 9.608 | 9.072 | 9.312 |
| 2 | Groove | 75 | 0.12 | 0.8 | 6.511 | 6.331 | 7.593 | 6.812 |
| 3 | Groove | 75 | 0.06 | 0.4 | 2.398 | 2.435 | 2.402 | 2.412 |
| 4 | Groove | 100 | 0.12 | 1.2 | 9.843 | 9.459 | 9.326 | 9.543 |
| 5 | Groove | 100 | 0.06 | 0.8 | 4.437 | 3.839 | 4.961 | 4.412 |
| 6 | Groove | 100 | 0.18 | 0.4 | 11.109 | 7.094 | 6.401 | 8.201 |
| 7 | Groove | 125 | 0.06 | 1.2 | 11.536 | 11.818 | 10.743 | 11.366 |
| 8 | Groove | 125 | 0.18 | 0.8 | 4.772 | 6.512 | 7.096 | 6.127 |
| 9 | Groove | 125 | 0.12 | 0.4 | 4.945 | 5.747 | 4.674 | 5.122 |
| 1 | Wave | 75 | 0.18 | 1.2 | 13.817 | 14.535 | 14.512 | 14.288 |
| 2 | Wave | 75 | 0.12 | 0.8 | 7.991 | 7.598 | 8.091 | 7.893 |
| 3 | Wave | 75 | 0.06 | 0.4 | 3.779 | 3.625 | 3.290 | 3.565 |
| 4 | Wave | 100 | 0.12 | 1.2 | 4.720 | 5.056 | 5.309 | 5.028 |
| 5 | Wave | 100 | 0.06 | 0.8 | 5.044 | 5.062 | 4.041 | 4.716 |
| 6 | Wave | 100 | 0.18 | 0.4 | 7.344 | 6.459 | 6.363 | 6.722 |
| 7 | Wave | 125 | 0.06 | 1.2 | 7.697 | 5.073 | 11.735 | 8.168 |
| 8 | Wave | 125 | 0.18 | 0.8 | 7.313 | 6.529 | 6.655 | 6.832 |
| 9 | Wave | 125 | 0.12 | 0.4 | 8.645 | 9.009 | 8.395 | 8.683 |
| Category | Metric | Value |
|---|---|---|
| Tuning Process | Optimization Method | Grid Search |
| Kernel Function | RBF_kernel | |
| Cost Function | leaveoneoutlssvm | |
| Grain (log scale optimization) | 7 | |
| Initial Parameters | Starting gamma | 0.93614 |
| Starting sig2 | 0.022631 | |
| Cost of Starting Values | 3.2322 | |
| Time per Evaluation (sec) | 0.015625 | |
| Grid Limits [gamma] | 0.9361–2790.6037 | |
| Grid Limits [sig2] | 0.022631–3.3588 | |
| Final Hyperparameters | gamma | 23.1689 |
| sig2 | 0.294524 |
| Parameter | Setting/Value |
|---|---|
| Framework | GPTIPS 2 |
| Population size | 100 individuals per generation |
| Evolution runs | 3 independent runs |
| Timeout limit | 10 s per run |
| Selection method | Tournament selection |
| Tournament size | 6 |
| Pareto tournament probability | 0.7 |
| Elitism | Top 70% of individuals retained per generation |
| Early termination criteria | Target fitness value ≤0.2 |
| Maximum number of genes | 8 per individual |
| Function node set | times, minus, plus, sin, cos, exp, tanh, plog |
| Level | Texture Type | Cutting Speed (vc) | Feed Rate (fr) | Depth of Cut (dc) |
|---|---|---|---|---|
| 1 | −16.58 | −16.11 | −14.19 | −14.89 |
| 2 | −16.17 | −16.57 | −16.79 | −15.62 |
| 3 | −16.65 | −16.71 | −18.41 | −18.89 |
| Delta | 0.48 | 0.6 | 4.23 | 4 |
| Rank | 4 | 3 | 1 | 2 |
| LSSVM | MGGP | |
|---|---|---|
| R2 | 0.9959 * | 0.8480 |
| RMSE | 0.1528 * | 0.9333 |
| MAE | 0.1247 * | 0.6772 |
| MAPE | 2.0089 | 0.1096 * |
| SSE | 1.5173 * | 56.6200 |
| Accuracy | 0.9814 * | 0.8904 |
| LSSVM | MGGP | |
|---|---|---|
| R2 | 0.9391 * | 0.6444 |
| RMSE | 0.6730 * | 1.6265 |
| MAE | 0.4817 * | 1.3754 |
| MAPE | 6.6363 * | 0.1850 |
| SSE | 7.2478 * | 42.3300 |
| Accuracy | 0.9436 * | 0.8150 |
| Model | t-Test | F-Test | Pearson Correlation (r) | ||
|---|---|---|---|---|---|
| t-Statistic | p-Value | F-Statistic | p-Value | ||
| MGGP | −0.425 | 0.672 | 1.08 | 0.367 | 0.90 |
| LSSVM | 0.754 | 0.453 | 1.12 | 0.307 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pawanr, S.; Gupta, K. Analysis of Surface Roughness and Machine Learning-Based Modeling in Dry Turning of Super Duplex Stainless Steel Using Textured Tools. Technologies 2025, 13, 243. https://doi.org/10.3390/technologies13060243
Pawanr S, Gupta K. Analysis of Surface Roughness and Machine Learning-Based Modeling in Dry Turning of Super Duplex Stainless Steel Using Textured Tools. Technologies. 2025; 13(6):243. https://doi.org/10.3390/technologies13060243
Chicago/Turabian StylePawanr, Shailendra, and Kapil Gupta. 2025. "Analysis of Surface Roughness and Machine Learning-Based Modeling in Dry Turning of Super Duplex Stainless Steel Using Textured Tools" Technologies 13, no. 6: 243. https://doi.org/10.3390/technologies13060243
APA StylePawanr, S., & Gupta, K. (2025). Analysis of Surface Roughness and Machine Learning-Based Modeling in Dry Turning of Super Duplex Stainless Steel Using Textured Tools. Technologies, 13(6), 243. https://doi.org/10.3390/technologies13060243






