A Dynamic Mechanical Analysis Device for In Vivo Material Characterization of Plantar Soft Tissue

Abstract

Understanding the viscoelastic properties of plantar soft tissue under dynamic conditions is crucial for assessing foot health and preventing injuries. In this work, we document an in vivo device, employing the principles of dynamic mechanical analysis (DMA), which, for the first time, enables in situ, real-time multidimensional mechanical characterization of plantar soft tissues. This device overcomes the limitations of conventional ex vivo and single-DOF testing methods by integrating three sinusoidal mechanism-based multi-DOF dynamic testing modules, providing measurements of tensile, compressive, shear, and torsional properties in a physiological setting. The innovative modular design integrates advanced sensors for precise force and displacement detection, allowing for comprehensive assessment under cyclic loading conditions. Validation tests on volunteers demonstrate the device’s reliability and highlight the significant viscoelastic characteristics of the plantar soft tissue. The example dataset was analyzed to calculate the storage modulus, loss modulus, loss factor, and energy dissipation. All design files, CAD models, and assembly instructions are made available as open-source resources, facilitating replication and further research. This work paves the way for enhanced diagnostics and personalized treatments in orthopedic and rehabilitative medicine.

1. Introduction

The human plantar region consists of specialized soft tissues, predominantly fatty and connective tissues, positioned anatomically between the skin dermis, fascia, and underlying bony structures [1]. The plantar soft tissue demonstrates rate-dependent stress–strain characteristics under large deformations, known as viscoelastic [2]. This behavior can typically be effectively modeled using the Kelvin–Voigt viscoelastic model [3]. The time-dependent viscous properties of plantar soft tissues, particularly in the heel pad and metatarsal head regions, play a crucial role in stress buffering and energy dissipation [4]. These specialized tissues are evolutionarily adapted to provide effective cushioning, absorbing mechanical shocks during weight-bearing activities and thereby protecting underlying skeletal structures from potential injury [5,6,7]. Changes in the mechanical properties of these tissues may compromise their protective functionality, increasing the risk of injury or pathological conditions due to excessive mechanical loading. Consequently, extensive research efforts, both through in vitro and in vivo approaches, have been dedicated to characterizing and quantifying the mechanical behavior of plantar soft tissues to better understand their functional roles and the implications of their mechanical alterations. In vitro methods for characterizing plantar soft tissues typically involve tests performed on excised specimens, which inherently lack the physiological and biochemical environment present in living tissues [8,9]. To overcome this limitation and capture more realistic mechanical behaviors, several in vivo testing approaches have been explored, including ultrasonic shear wave elastography [10], Shore hardness measurements, indentation testing, and magnetic resonance elastography. Ultrasonic shear wave elastography determines Young’s modulus by measuring shear wave propagation speed, assuming linear elasticity and homogeneous, isotropic tissue properties [11]. Shore hardness testing employs a handheld durometer to correlate the resistance of tissues against indentation with their intrinsic stiffness [12]. Nevertheless, these existing methods primarily assess static or quasi-static responses and do not adequately capture the dynamic, viscoelastic properties of plantar soft tissue. Given the importance of time-dependent behavior in accurately evaluating the tissue’s response to repetitive physiological loading, comprehensive assessment methods capable of measuring both elastic and viscoelastic properties in dynamic conditions are critically needed [13].

Dynamic mechanical analysis (DMA) is a fundamental technique in materials science and biomechanics used to characterize the viscoelastic properties of materials by assessing their periodic stress–strain responses under controlled temperature and frequency conditions [14,15,16]. Recent advances have enabled the development of DMA-inspired devices capable of characterizing viscoelastic properties of living human skin in vivo [17]. However, most traditional DMA techniques have primarily been limited to ex vivo analyses of cadaveric tissue samples, lacking the physiological realism of living tissues and resulting in data with inherent limitations [18]. To overcome some of these constraints, recent studies have introduced indentation-based methods, enabling the in vivo measurement of plantar soft tissue properties through the simple application and release of compressive forces [19]. Nevertheless, such indentation approaches typically assess only a limited portion of the tissue’s dynamic stress–strain behavior, capturing primarily single-direction loading and unloading cycles. Consequently, these methods fall short of replicating the comprehensive, cyclic, and multidirectional viscoelastic responses characteristic of plantar tissue during real-world dynamic loading conditions, thus emphasizing the need for improved techniques capable of fully capturing the dynamic viscoelastic properties in vivo.

Directly inspired by dynamic mechanical analysis (DMA)—a well-established technique from materials science for characterizing periodic stress–strain responses to assess both elastic and viscous properties of various materials—we have developed an innovative in vivo and in situ DMA-based device specifically designed for assessing the mechanical properties of human plantar soft tissue under physiological conditions. While conventional approaches (e.g., ex vivo testing, indentation, or elastography) are restricted to static or unidirectional measurements, our system uniquely enables simultaneous multidirectional (tensile/compressive, shear, and torsional) and dynamic cyclic mechanical characterization of plantar soft tissue under physiological conditions. Key advantages of our device include the following: (1) high-precision, real-time, in situ measurements without invasive procedures and (2) the integration of multiple loading modes (compression, shear, torsion) for viscoelastic analysis [20]. However, a current limitation is that the three detection modes require repositioning of the foot, which may slightly increase testing time. Despite this, this device offers unparalleled insights into plantar tissue mechanics, with potential applications in clinical diagnostics and biomechanical research. The primary goal of this paper is to thoroughly document the design, assembly, and operational aspects of this device, providing sufficient details for other researchers and clinicians to replicate, adapt, and expand upon this technology, facilitating further innovation and collaboration within the research community.

2. Materials and Methods

To address the existing technological limitations and fulfill the demand for comprehensive in vivo testing, we developed an innovative device specifically designed to perform in situ DMA-like measurements on live soft tissues (Figure 1). This advanced system accurately measures tensile/compressive resistance, shear resistance, and rotational torque properties, effectively overcoming the constraints associated with traditional DMA methods, which are typically restricted to cadaveric samples, as well as the shortcomings of simpler indentation-based approaches. Our device integrates four essential modules—foot fixation, sensor detection, lifting, and probe-to-tissue interaction—combined with a sophisticated control system to facilitate precise, multidirectional, and cyclic viscoelastic evaluations of plantar soft tissue under physiological conditions. To ensure the replicability of this paper, all design files, including CAD models and detailed specifications, have been made freely accessible online. The specifications table, design files summary, and source of materials can be referenced in Appendix A.

Although plantar soft tissue comprises heterogeneous structures, each exhibiting distinct mechanical properties, it can be approximated as a uniform, single-layer material for analytical simplicity. Consequently, as an initial approach, it is appropriate to analyze the overall mechanical behavior of plantar soft tissue as homogeneous [21]. Extensive previous studies have primarily focused on evaluating tensile and compressive properties; however, limited attention has been given to the characterization of shear and torsional behaviors of plantar tissues, despite their significance in daily functional activities [22]. Considering that plantar soft tissues are continuously subjected to multidirectional forces—such as compression, shear, and torsion—it becomes essential to comprehensively investigate how these directional forces impact tissue integrity and their potential implications for orthopedic and systemic conditions. To address this gap, we designed our testing device to apply sinusoidal displacement stimuli u(t) (in millimeters) along three orthogonal directions (tensile/compressive, shear, and torsion) directly onto the plantar surface using a vacuum composite suction cup attachment, as illustrated in Figure 2. Correspondingly, the induced force responses, F(t), are accurately measured in real-time by integrated force sensors. We simplified the viscoelastic properties of the plantar soft tissue using the Kelvin–Voigt model [23]. In this model, a spring and a dashpot are connected in parallel. The spring corresponds to the elastic response of the material, storing energy, while the dashpot represents the viscous response, dissipating the energy.

2.1. Build Instruction of Hardware

As shown in Figure 1, the three stress–strain detection units (tension/compression, shear, and torque) are integrated within a welded support frame. An iron cover plate with three cross-shaped obround holes is secured to the top of the support frame to position the foot. The probes can pass through these holes to contact the testing points on the plantar surface for the respective measurements.

Each unit’s detection mechanism is mounted on the sliding table of the lead screw lifting module driven by a stepper motor. This allows the probe head to automatically locate the initial position where it just contacts the plantar surface before testing, thereby avoiding subjective errors caused by the subject actively adjusting foot height to match the probe.

In the tension/compression detection unit, a servo motor is mounted on the slide via a bracket. One end of the connecting rod is eccentrically mounted on a disc at the end of the servo motor, while the other end is connected to the shaft via bearings and a clamping device, with the shaft constrained by linear bearings fixed to the frame. Before each test, the sliding table elevates the servo motor and all components connected to its end as a whole to find the test zero point and then remains stationary throughout the testing process. During detection, the mechanical design of vertical reciprocal motion can be simplified as the crank slider mechanism, as shown in Figure 3a. The servo motor rotates the disc, and through the eccentrically mounted connecting rod, the shaft is driven to perform vertical reciprocating linear motion within the constraints of the linear bearings. The force sensor and probe head are mounted sequentially on the shaft, while the displacement sensor is mounted on a fixed plate.

In the shear detection unit, the entire testing mechanism is mounted on a horizontally positioned rectangular base plate. One side of the base plate is secured to the sliding table via a vertical bracket, while the other side features a vertical bracket with a rail. This rail, in conjunction with a slide block mounted on the frame, provides vertical guidance. The mechanism of shearing motion can also be simplified as the crank slider, only horizontally, as shown in Figure 3b. The force sensor is mounted below the probe, while the displacement sensor is fixed to one side of the horizontal base plate.

In the torsion testing unit, the L-shaped support plate is attached to the sliding table with screws. The support plate sequentially accommodates the force sensor, angle sensor, coupling, splined shaft, and probe head, with these components moving together as the sliding table is raised or lowered. The splined shaft is guided by splined bearings, which incorporate a self-machined synchronizing belt pulley shaft on their exterior, with rotating bearings mounted on the belt pulley shaft’s outer surface and secured to the frame by the bearing block. The motor and the torque sensor housing are also fixed to the frame. The horizontal torsion motion can be realized by the crank rocker mechanism, as shown in Figure 3c. The motor rotates the disk, and a slider eccentrically mounted on the disk via bearings drives a guide rail to oscillate reciprocally about the axis of the torque sensor. The other end of the torque sensor drives a belt pulley via a synchronizing belt, resulting in the reciprocating rotation of the probe.

The mechanical performance and system error of displacement excitation is recorded in

Table 1. Mechanical performance and system error of displacement excitation.

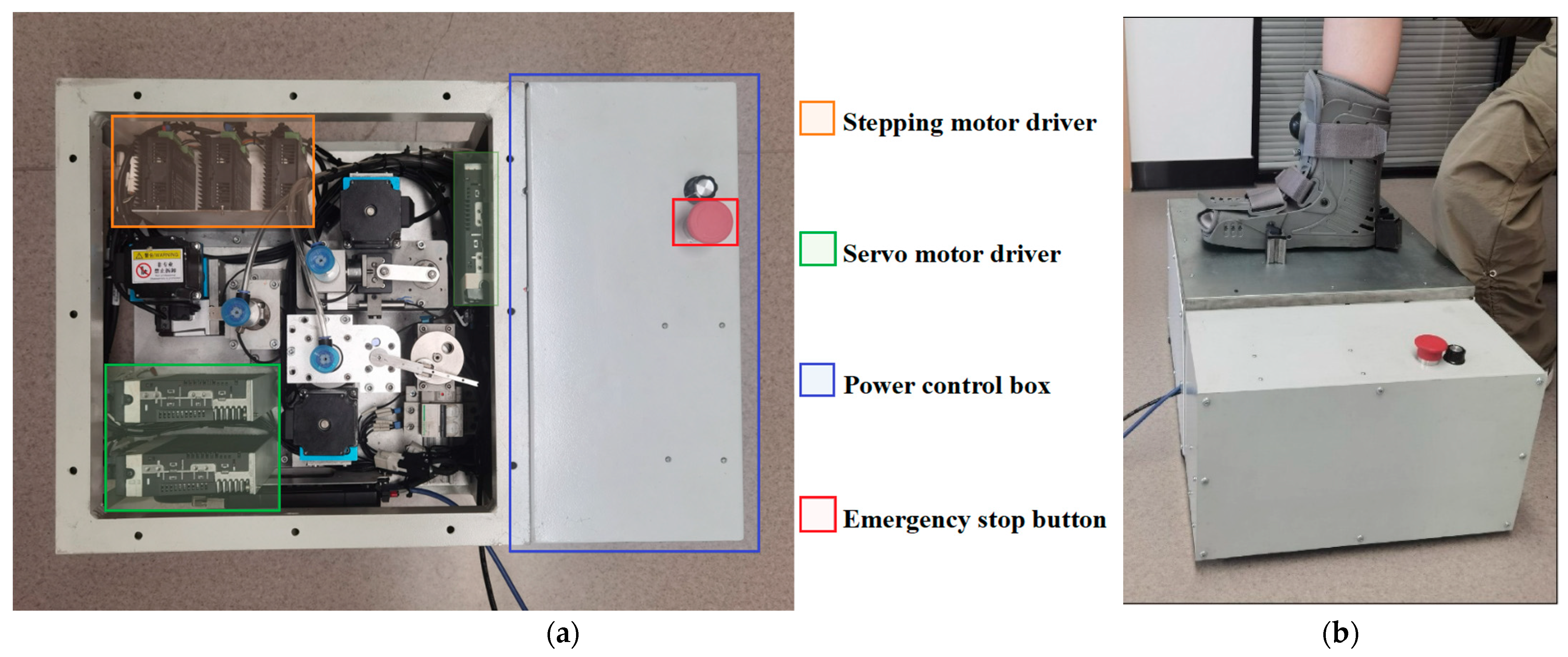
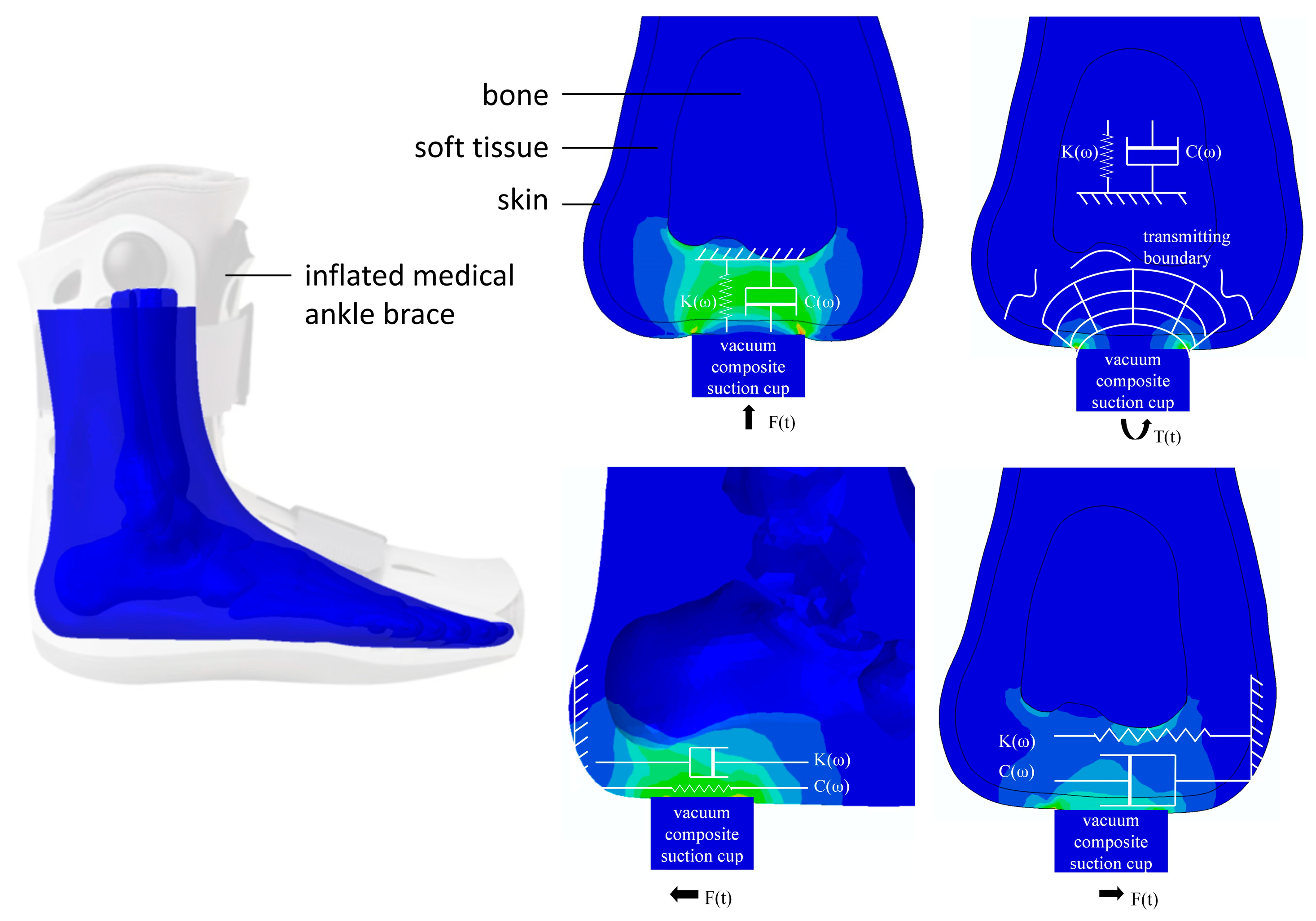
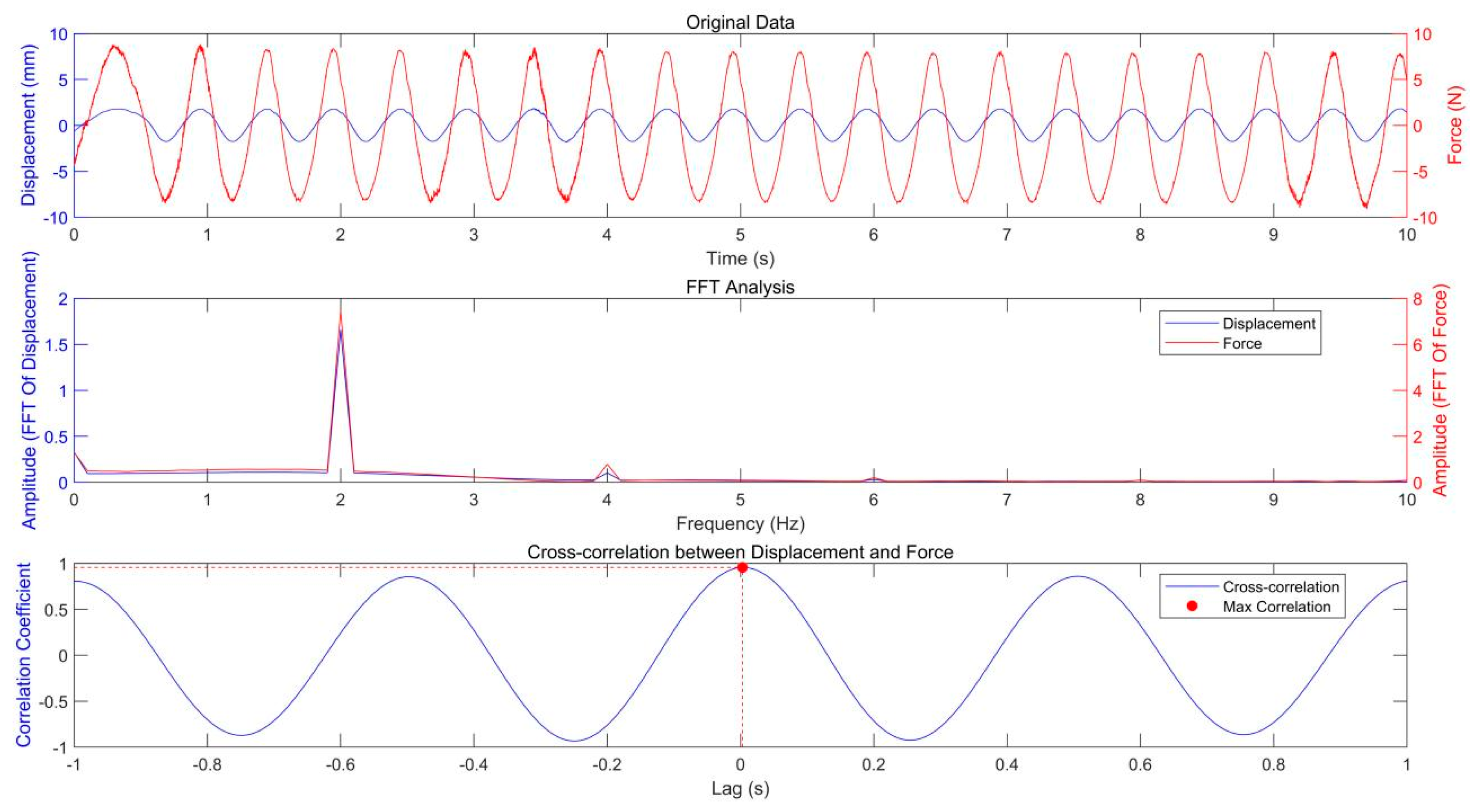
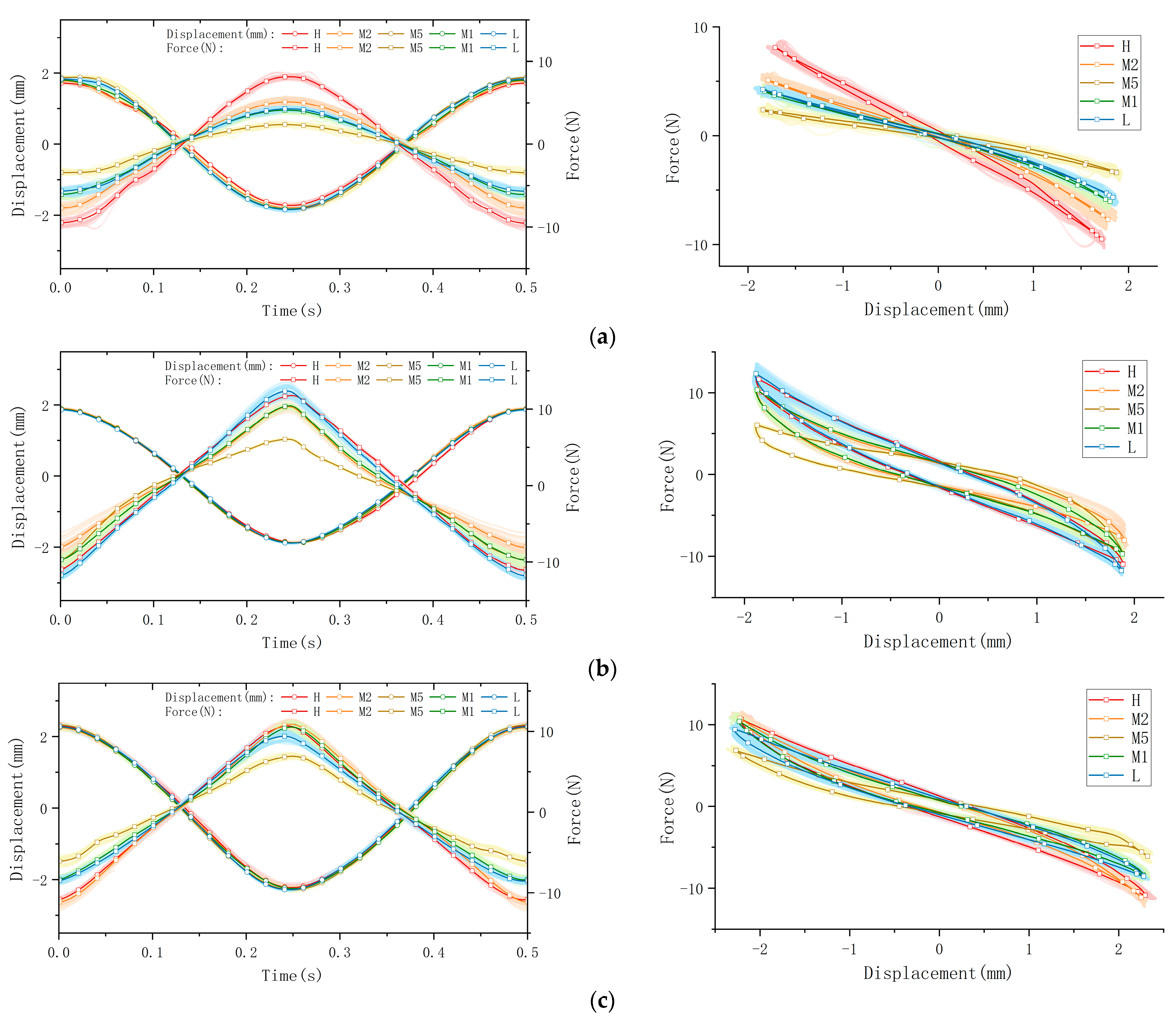
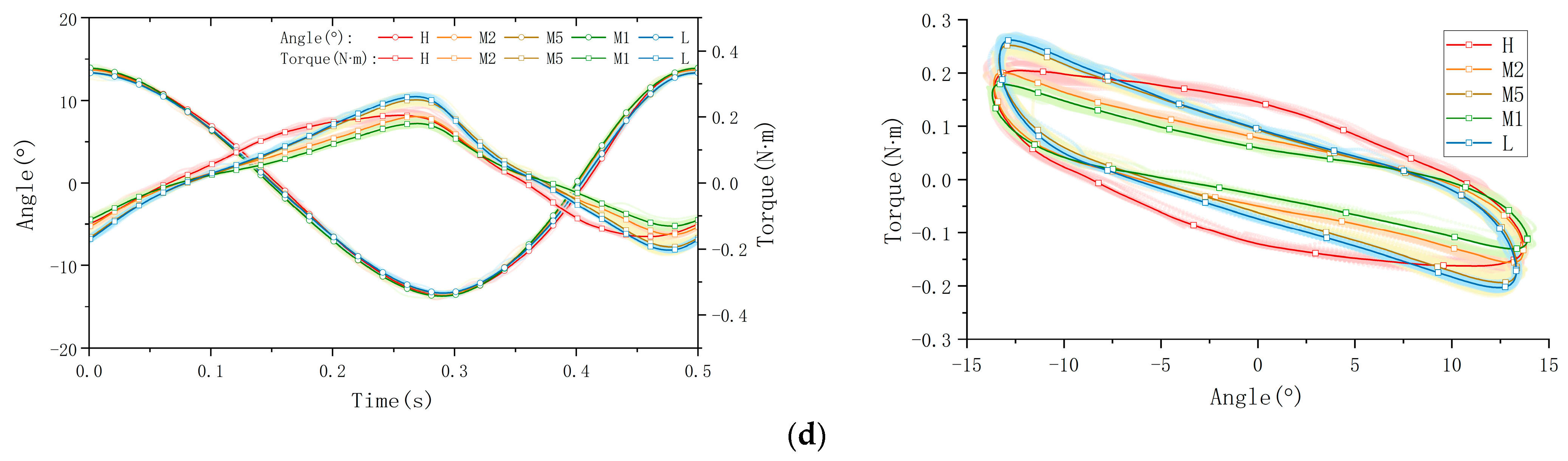
	Tensile/Compress Displacement (mm)	Longitudinal Shear Displacement (mm)	Transverse Shear Displacement (mm)	Torsion Displacement (degree)
Mean Value	3.63506	3.78726	4.57726	27.27410
Standard Deviation	0.08795	0.00477	0.04109	0.40308

. Notably, each test’s standard deviation is remarkably low, indicating the equipment’s stability. The difference between set versus measured value comes from minute redundant spaces between components; therefore, we added displacement sensors to preciously measure the true value. Whether through visual observation or relying on the feelings of the subjects, it could be determined that there is no displacement between the composite vacuum suction cup and the plantar tissue.

Detailed sensor characteristics are provided in

Table 2. Specifics of the sensors.

Sensor	Specifications	Values
Force sensor (DYMH-103)	Capacity	0–5 kg
	Response frequency	10 KHz
	Output sensitivity	1.0–1.5 ± 10% mV/V
	Hysteresis	0.1% F.S.
	Repeatability	0.1% F.S.
	Temperature sensitivity drift	0.1% F.S./10 °C
	Zero temperature drift	0.1% F.S./10 °C
LVDT (GA09)	Capacity	±5 mm
	Response frequency	1–10 KHz
	Nonlinearity error	±0.5% BFSL
Torque sensor (FYAH)	Capacity	0–1 NM
	Response frequency	200 Hz
	Nonlinearity	±0.25% of R.O.
	Hysteresis	±0.25% of R.O.
	Nonrepeatability	±0.1% of R.O.
Angle sensor (GT-D)	Capacity	0–360°
	Resolution	4096, 12 bits
	independent linearity	0.15% F.S.
	Response frequency	5 KHz

. These sensors have been demonstrated to effectively meet our testing requirements, offering satisfactory performance in load capacity, response frequency, output sensitivity, repeatability, resolution, etc.

To ensure accurate and reliable test outcomes, it is essential to immobilize the foot to prevent any internal bone displacement during the testing procedure. This immobilization is achieved using an inflated medical ankle brace featuring a flattened, hollowed base, as depicted in Figure 1b. During testing, the foot is sequentially positioned at five predefined measurement locations directly above the three detection probes. After aligning each test site, the foot is securely stabilized in place by four switchable magnets. Additionally, a vacuum composite suction cup is integrated at the detector joint to provide gentle, non-destructive, and non-invasive contact with the plantar surface throughout the inspection process.

2.2. Operation Instructions

Prior to testing, it is crucial to ensure the plantar surface of each participant is healthy, with no visible injuries, infections, or pain, and that the participant has not experienced foot trauma in the 12 months preceding data collection. A number of clinical specifics, including gender, age, height, weight, foot length, foot width, foot health, shoe-wearing habits, daily average steps, and exercise habits, are requested of the participant for the records. Due to the substantial structural and mechanical heterogeneity of plantar soft tissues, shear properties can differ significantly depending on the loading direction, reflecting the complex functional characteristics of the foot. Accordingly, our testing protocol incorporates two distinct shear testing orientations—longitudinal and transverse—implemented by rotating the foot 90 degrees around the shear probe head as a pivot point. This approach allows detailed characterization of shear properties in multiple directions at each measurement site. In this study, testing is performed at five critical plantar locations known for high load-bearing capacity or increased susceptibility to ulceration [24], as illustrated in Figure 4. Additional anatomical locations can also be selected for testing as required by specific research or clinical objectives.

For each measurement, the participant positions the targeted test site precisely over the appropriate detection hole. After each measurement, the magnetic mounts are manually demagnetized by rotating their switches, allowing repositioning of the foot for subsequent testing modes. Upon correct alignment, the lead screw lifting module elevates the probe until it gently contacts the plantar surface. Once the force sensor detects a predefined threshold indicating sufficient contact, the lifting motion ceases, and a vacuum composite suction cup adheres gently to the plantar surface. This ensures non-invasive, stable engagement, allowing the mechanical linkage to induce controlled cyclic displacement synchronized with tissue deformation. For safety, the procedure includes an emergency stop mechanism accessible via the red button on the power supply unit.

The participant is fully informed and signed the consent before trials. The Ethical Review Committee of Huashan Hospital, Fudan University (HIRB), approves the ethical review (see the Supplemental Materials).

3. Results and Discussion

The reciprocal tension/compression and shearing test amplitude is initially set to be ±2 mm, and the twist range of the torsion test is initially set to be ±14°, with a frequency of 2 Hz for all tests. The amplitude is chosen based on the regular motion of a healthy plantar pad, and the frequency is determined by the practical upper limit of human foot use, as higher frequencies may cause noticeable discomfort to the participant.

The original data of the in vivo test for the volunteer’s plantar soft tissue are shown in Figure 5. To analyze the relationship between load (stimulus) and deformation (response), both FFT and cross-correlation techniques were applied to the corresponding signals. The spectrogram indicates that the peak frequencies of the load and deformation signals are precisely aligned, confirming their frequency synchronization. Cross-correlation analysis produced a maximum coefficient of 0.9559 with a time lag of just 0.003 s, signifying a strong correlation with minimal temporal displacement between the signals. This suggests that the load closely follows the deformation with negligible lag, indicating the soft tissue’s prompt response to applied displacement.

The collected raw data were processed and visualized to clearly illustrate key stress–strain relationships, as shown in Figure 6. The figure is organized into four subplots, each depicting distinct mechanical behaviors: tensile/compression, longitudinal shear, transverse shear, and torsion. Measurements were performed at five anatomical plantar locations (M1, M2, M5, L, and H), chosen for their relevance to load bearing or susceptibility to injury. In the presentation of data and graphs, displacement directions were intentionally reversed relative to applied forces to enhance clarity and highlight peak-to-valley variations. (Note: this is likely a manual phase angle adjustment of 180°, which shall be re-adjusted in following data processing and calculations). To ensure clear representation of viscoelastic behaviors, data from a total of sixty loading cycles—comprising twenty cycles per trial over three repeated trials—are superimposed as cloud plots, with the mean values represented by solid lines. These graphical representations effectively capture the distinctive viscoelastic responses of plantar soft tissue under dynamic cyclic loading.

The processed data are presented through force–time and displacement–time curves, clearly illustrating the mechanical response of plantar soft tissue under dynamic cyclic loading conditions. Since the applied displacement remains constant within each testing mode, variations in force magnitude directly reflect differences in the tissue’s elastic modulus; a higher force magnitude corresponds to increased stiffness. Furthermore, the viscoelastic properties of the plantar soft tissue are distinctly revealed by the characteristic hysteresis loops obtained from the force–displacement curves. The area enclosed by each hysteresis loop, determined by the phase difference between the applied displacement and the resultant force, quantifies the energy dissipated (ΔW) per loading cycle. A larger hysteresis loop area indicates greater energy dissipation and thus higher tissue viscosity, which significantly influences the damping and shock-absorption capabilities of the tissue. Conversely, a smaller hysteresis area indicates lower viscosity and reduced energy loss.

Here, we take the longitudinal shear test on the heel spot as one example calculation of viscoelasticity (the red curve in Figure 6b). The viscoelastic characteristics of the tested material were quantified by analyzing experimental data from synchronized cyclic stress–strain measurements. The phase angle can be directly observed in the graph, which is 11.4° ≈ 0.199 rad. The amplitudes of the stress and strain signals were then determined as ε₀ = 1.891245 mm and σ₀ = 11.738190 N.

The viscoelastic parameters, namely, the storage modulus (E′), loss modulus (E″), and loss factor (tanδ), were computed using the standard definitions as follows:

$$E^{\prime }={\displaystyle \frac{{\sigma }_0}{{\epsilon }_0}}\cos \left(\delta \right)=6.084\mathrm{N}/\mathrm{m}\mathrm{m}$$

$$E″={\displaystyle \frac{{\sigma }_0}{{\epsilon }_0}}\sin \left(\delta \right)=1.227\mathrm{N}/\mathrm{m}\mathrm{m}$$

$$\mathrm{t}\mathrm{a}\mathrm{n} (\delta )={\displaystyle \frac{E^{\prime }}{E^{″}}}=0.202$$

And the dissipated energy (the energy loss per loading–unloading cycle) calculated from the measured stress–strain hysteresis loop is

$$W_d=\oint \sigma d\epsilon =493.16 \mathrm{N}\bullet \mathrm{m}\mathrm{m}(\mathrm{m}\mathrm{J})$$

 i.e., the area surrounded by the red hysteresis loop in Figure 6b.

4. Conclusions

In this work, we introduced a novel in vivo dynamic mechanical analysis (DMA) device specifically designed for comprehensive mechanical characterization of plantar soft tissue under realistic physiological conditions. The device effectively addresses critical gaps in current methodologies by providing precise, multidirectional, and dynamic measurements of tensile, compressive, shear, and torsional responses simultaneously. Through validation tests conducted on human participants, we confirmed its capability to reliably capture significant viscoelastic behaviors and accurately quantify tissue stiffness and viscosity. The device demonstrates strong potential for clinical applications, offering critical insights into the mechanical properties and functional health of plantar tissues. Furthermore, by openly sharing detailed CAD models, specifications, and assembly instructions, we aim to facilitate broader adoption, replication, and further innovation within the biomedical and biomechanics research communities. This technology holds substantial promise for improving diagnostic accuracy, personalized therapeutic interventions, and understanding biomechanical dysfunctions in clinical orthopedics and rehabilitation.

While this study provides decent insights into soft tissue material characterization, some limitations should be noted. We examined the effects of biological factors—including tissue composition, sex, age, body mass index (BMI), and body mass—on tissue characterization; however, the potential influence of disease status was not addressed [25]. Future studies should prioritize comparative analyses of healthy and diseased cohorts to elucidate the impact of pathology on plantar soft tissue. A key challenge lies in recruiting sufficient samples with well-documented disease progression.

5. Patents

China Patent ZL2024101221804: multidimensional and broad-spectrum clinical in situ testing equipment for mechanical properties of plantar soft tissue. Ran Huang; Longyan Wu; Jun Zhu; Xinyi Ning; Xin Ma.

U.S. Patent 18/772,135: MULTIDIMENSIONAL BROAD-SPECTRUM CLINICAL IN SITU TESTING EQUIPMENT FOR EVALUATING MECHANICAL PROPERTIES OF PLANTAR SOFT TISSUE. Ran Huang; Longyan Wu; Jun Zhu; Xin Ma.

Netherlands Patent 2034960: In vivo multidimensional stress–strain testing device for plantar soft tissues. Ran Huang; Longyan Wu; Jun Zhu; Xin Ma.