Integrating Social Sustainability into Supply Chain Design: Optimization of a Capacitated Two-Echelon Location-Routing Problem
Abstract
1. Introduction
2. Literature Review
2.1. Supply Chain Management
2.2. Traditional and Modern Supply Chain Management
- Processes of SCM
- Planning:
- Sourcing:
- Production:
- Delivery:
- Return:
Management Strategies
- Lean Management:
- 2.
- Total Quality Management:
- Quality of Technology:
- Quality of Humans:
- Quality of Economy:
- Quality of Processes:
2.3. Challenges of SCM
2.4. Sustainable Supply Chain Management
2.5. Social Pillar of Sustainability
Challenges Facing the Social Pillar
- Undermining of the Social Pillar
2.6. Problem Definition and Applications
2.6.1. Problem Type
2.6.2. Number of Echelons
2.6.3. Number of Objectives
2.6.4. Type of Input
2.6.5. Solution Methods and Applications
2.7. Literature Findings and Gap
3. Methodology
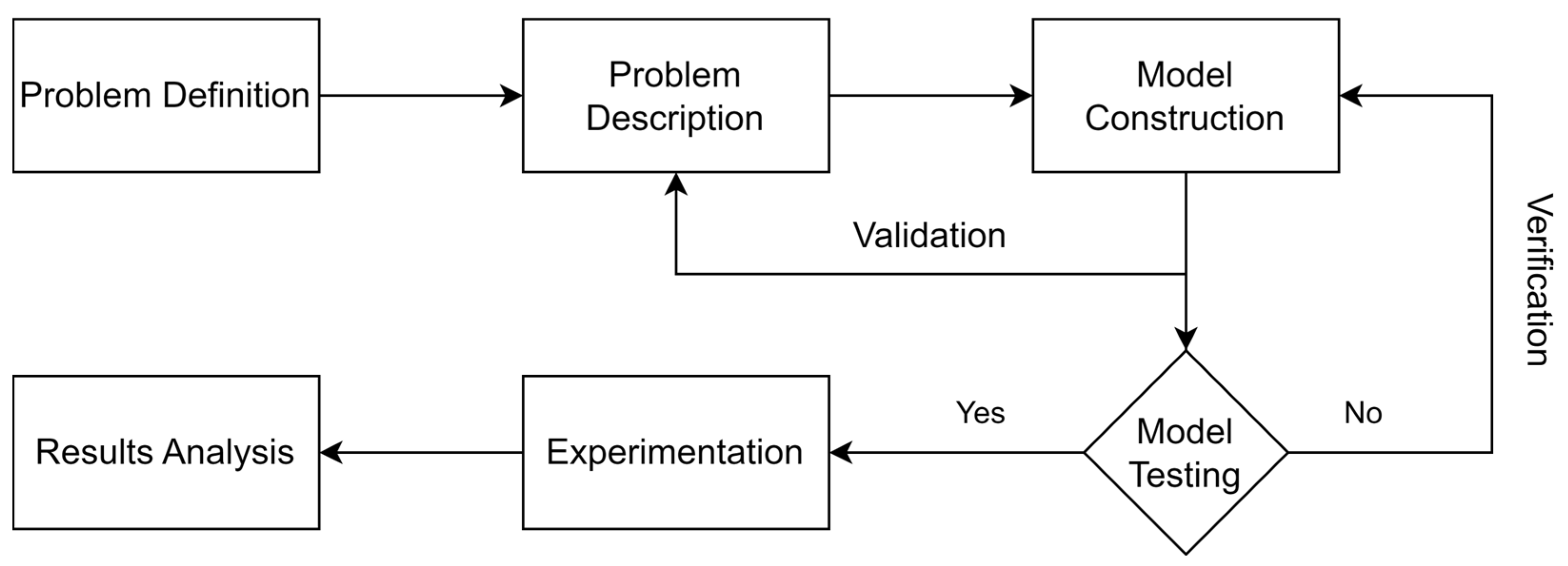
3.1. Research Flow
3.1.1. Problem Definition
3.1.2. Problem Description
3.1.3. Model Construction
3.1.4. Model Testing
3.1.5. Experimentation and Validation
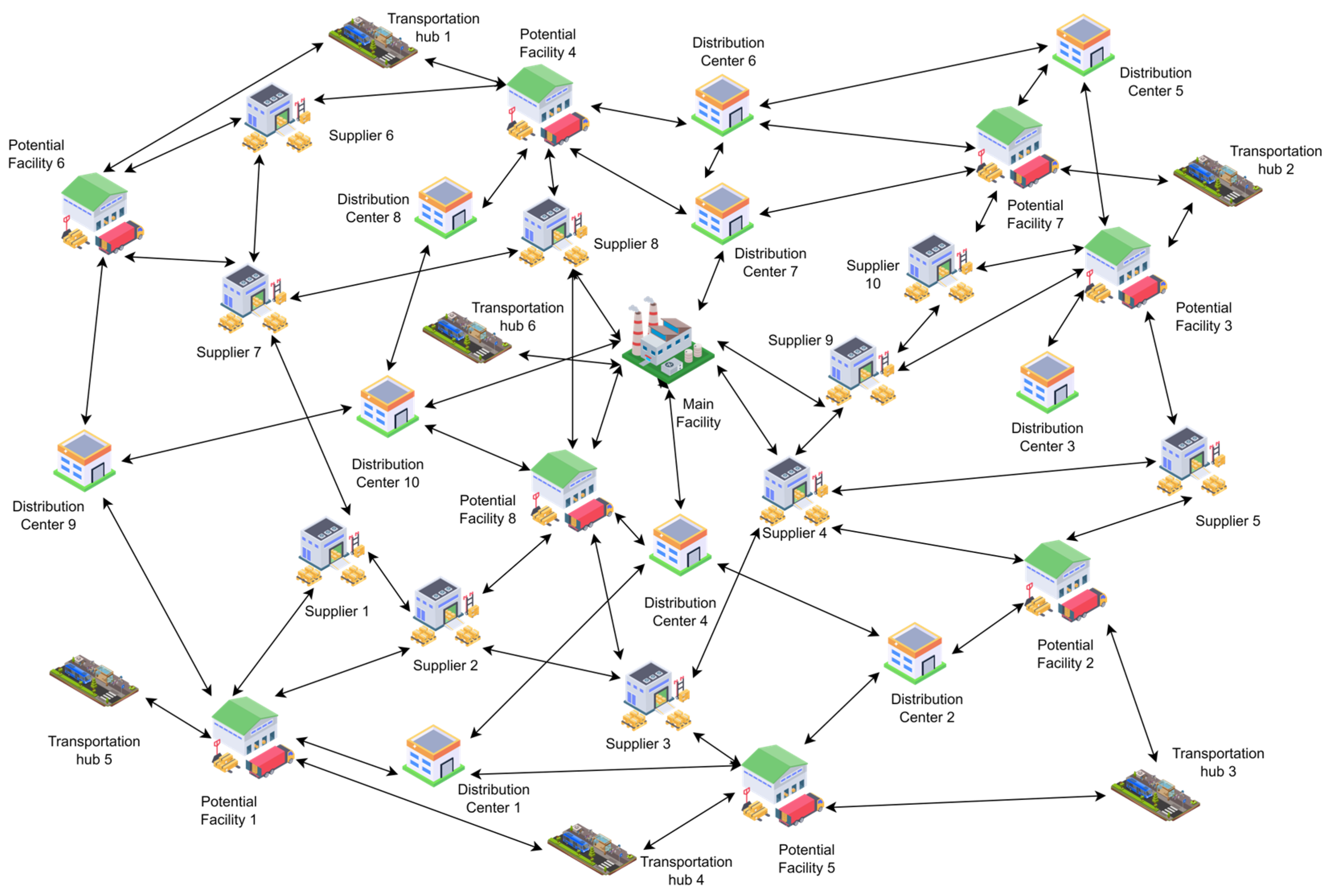
4. Case Study
4.1. Research Flow Application
4.1.1. Problem Description: Normal Case
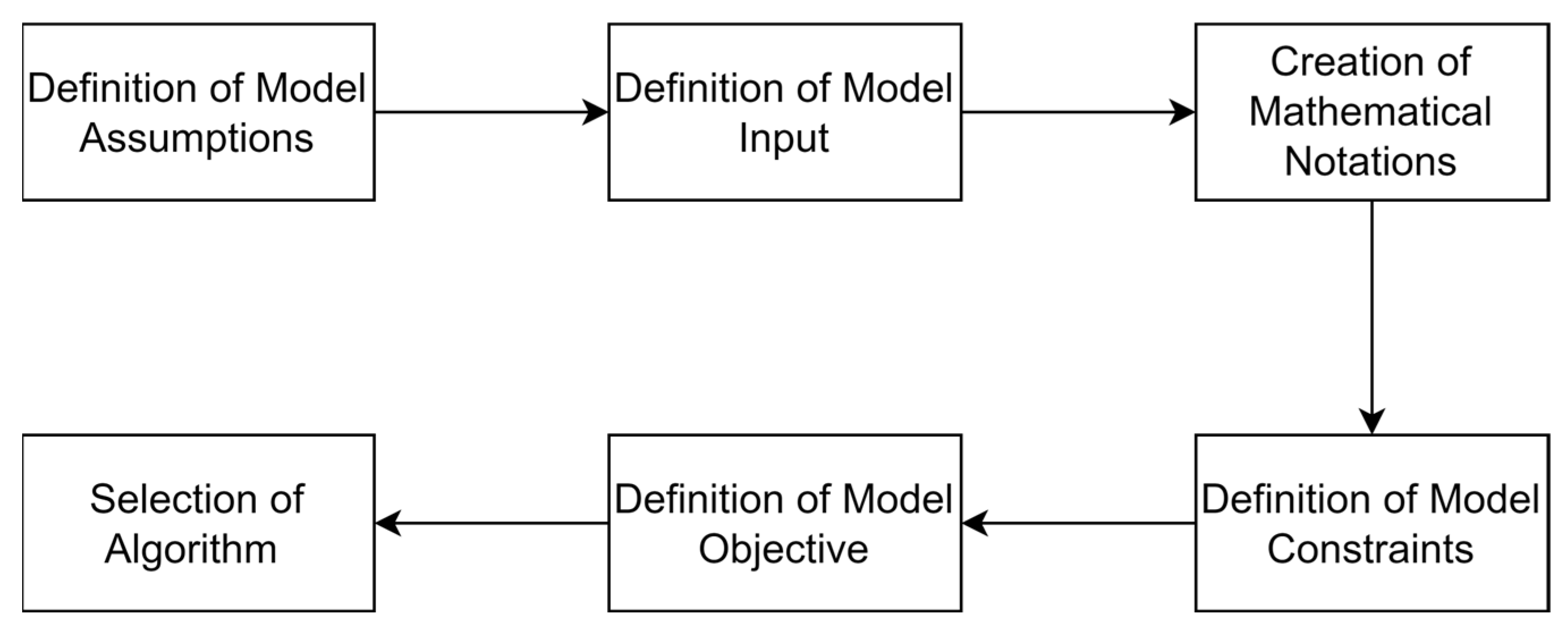
4.1.2. Model Construction: Normal Case
Definition of Model Assumptions
- Assumptions that are used by other authors in the literature:
- Each vehicle can, at most, be at one location at any time.
- The vehicles must start and end at the facility location.
- Each of the two vehicles is assigned to one type of destination (one for suppliers and the other for distribution centers).
- Temporary visits are made to the facility in case the vehicle assigned is fully capacitated for suppliers or empty in case of distribution centers.
- The capacity of both vehicles is equal.
- The cost of leasing/renting both vehicles is equal.
- The number of suppliers required is equal to the number of distribution centers needed.
- Assumptions that are specific to this research article:
- The break time duration for each driver.
- The break rate, in USD, per break.
- The compensation fee for proximity to a transportation hub.
- Number of employees in facility.
Definition of Model Input
- The following information is provided in the model:
- The locations of each possible facility for purchasing, the suppliers, and distribution centers for contracting are given.
- The capacity of each vehicle is given.
- The capacity of each supplier and distribution center is given.
- The distances between each location and the other are given in Euclidean distances.
- The cost of each facility location, each supplier, and distribution center available for contracting are given.
- The cost of fuel liter per kilometer is given.
- The cost of carbon emissions per kilometer is given.
- The leasing/renting cost for each vehicle is given.
- The tank capacity of both vehicles is given.
Creation of Mathematical Notation
Definition of Model Constraints
- No vehicle can be at multiple locations at the same time:
- The trucks should start and finish at the same point:
- A total of three or four suppliers are required (in case of both versions of the model):
- A total of three or four distribution centers are required (in case of both versions of the model):
- The capacity of both vehicles at any time cannot exceed the value of 30:
Definition of Model Objective
4.1.3. Problem Description: Uncertain Case
4.1.4. Model Construction: Uncertain Case
Definition of Model Assumptions
- Temporary visits are made to the main facility and secondary facilities in case the vehicle assigned is fully capacitated for suppliers or empty in case of distribution centers;
- The tank capacity of the new vehicles is the same as the old ones;
- The number of employees in the main facility is equal to the number of employees in the secondary facility;
- The compensation fee given to the employees in the main facility is the same as the one given to the employees in the secondary facility.
Definition of Model Input
- The locations of the secondary facilities to select from are given;
- The purchasing value for each facility is given;
- The fixed cost inflicted as penalties for abandoning the old vehicles’ leases is given;
- The new leasing/renting value of the new vehicles is given.
Creation of Mathematical Notation
Definition of Model Constraints
- No vehicle can be at multiple locations at the same time:
- The trucks should start and finish at the same point:
- A total of four or five suppliers are required (in case of both versions of the model):
- A total of four or five distribution centers are required (in case of both versions of the model):
- The capacity of both vehicles at any time cannot exceed the value of 40:
Definition of Model Objective
4.2. Selection of Algorithm
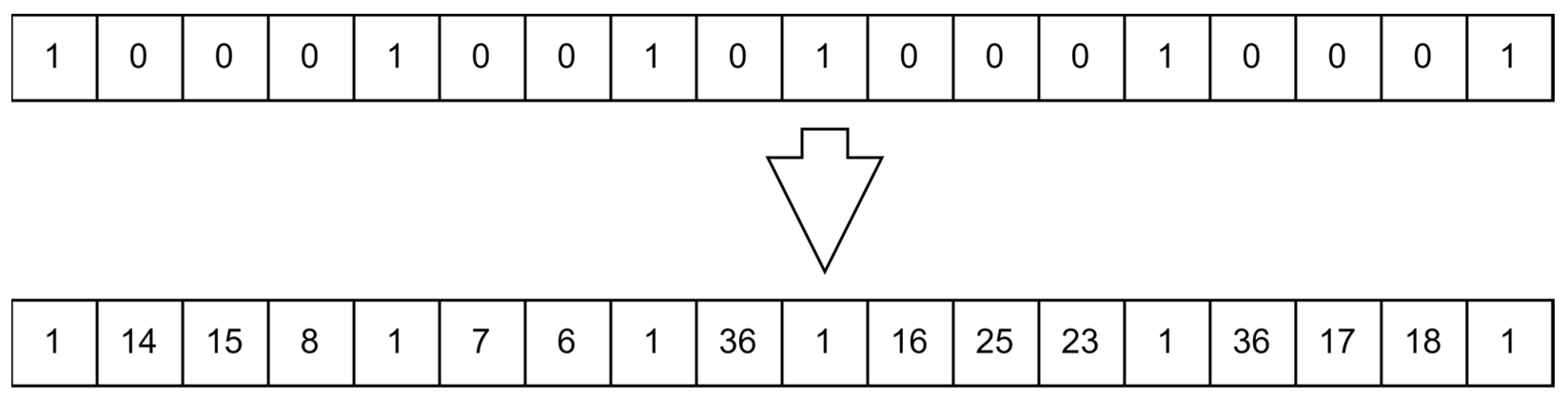
4.2.1. Initial Population Generation
- Normal Case: Initial Population;
- Uncertain Case: Initial Population.
4.2.2. Parents Selection
- Tournament Selection
- 2.
- Stochastic Universal Sampling (SUS) Selection
- 3.
- Elitism Selection
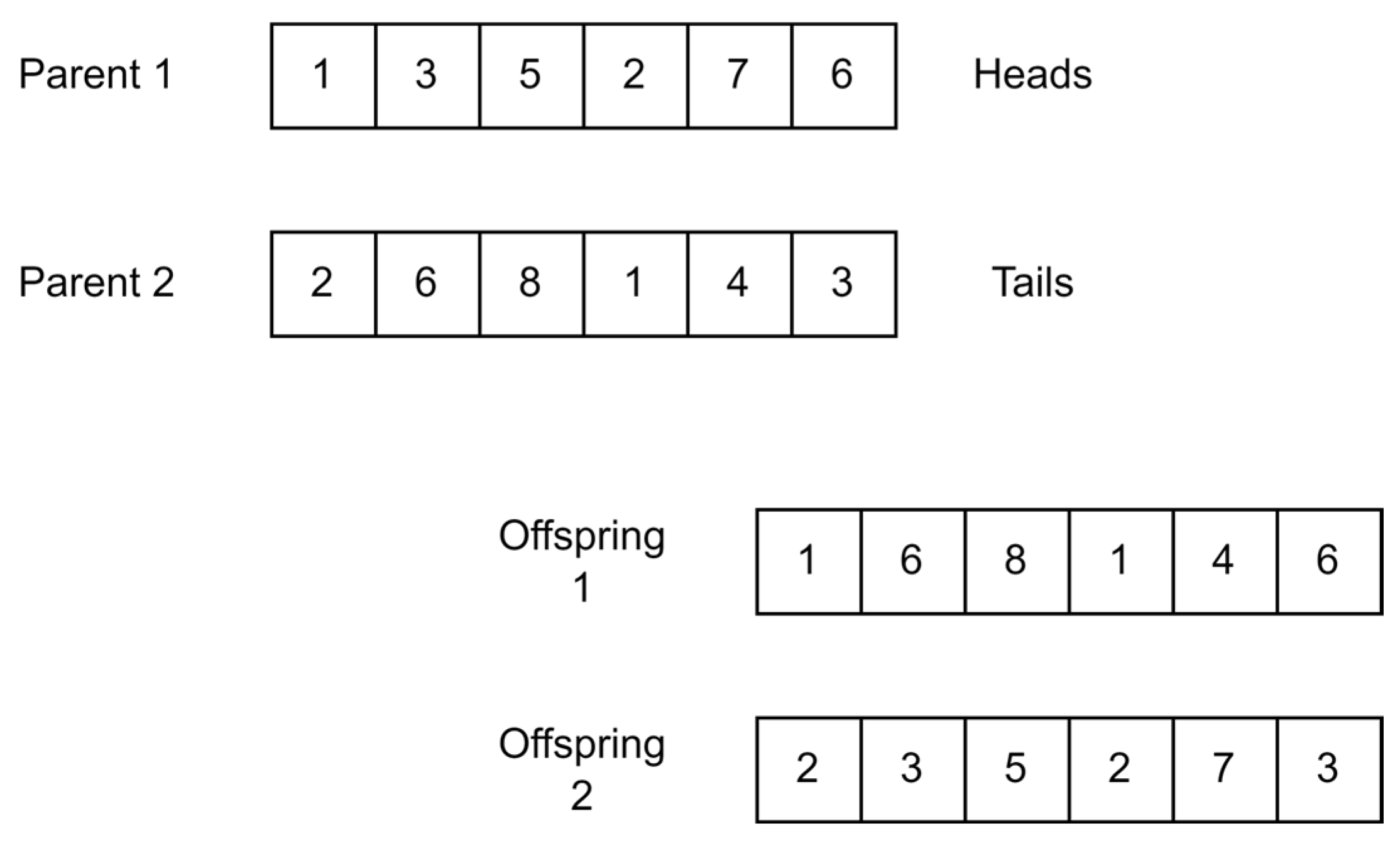
4.2.3. Crossover Agent Selection
- One-Point Crossover
- 2.
- Two-Point Crossover
- 3.
- Uniform Crossover.
4.2.4. Mutation Agent Selection
4.2.5. Algorithm Execution
- Normal Case
- 2.
- Uncertain Case.
4.2.6. Termination Criteria
4.2.7. Model Testing Steps
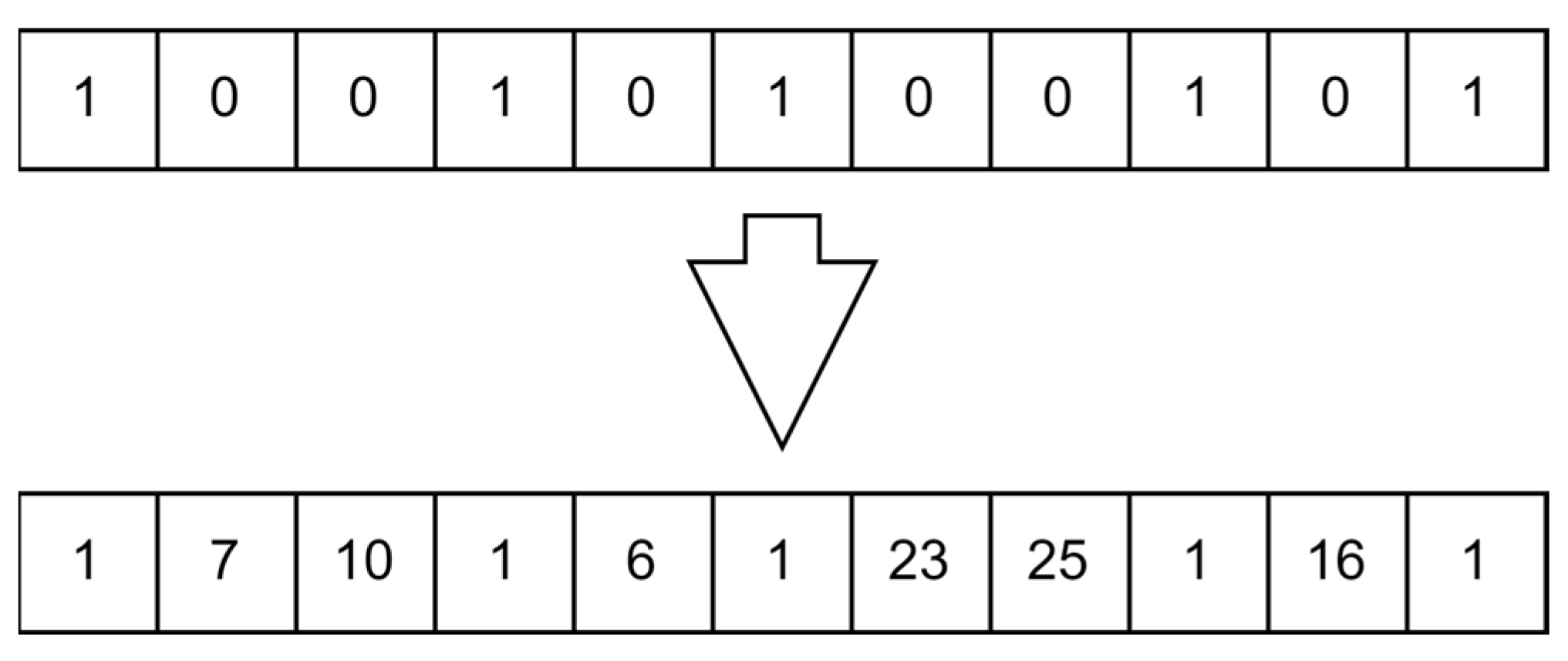
- Verification
- The chromosome is divided into two sections: the first half is for the first echelon and the second half is for the second echelon. This is performed by checking the numbering assigned for each bit, since the suppliers and distribution centers have different numberings.
- No duplication of bits; this means that the numbering of the bits that are assigned to the facilities are different from the other bits.
- The size of the chromosome is the same after crossover and mutation. This ensures that the length of the chromosome is the same after any step.
- The capacity constraint is respected; this is performed by manually calculating the capacities of the bits to make sure that they uphold the capacity constraint.
- 2.
- Validation
5. Experimentation
5.1. Normal Case
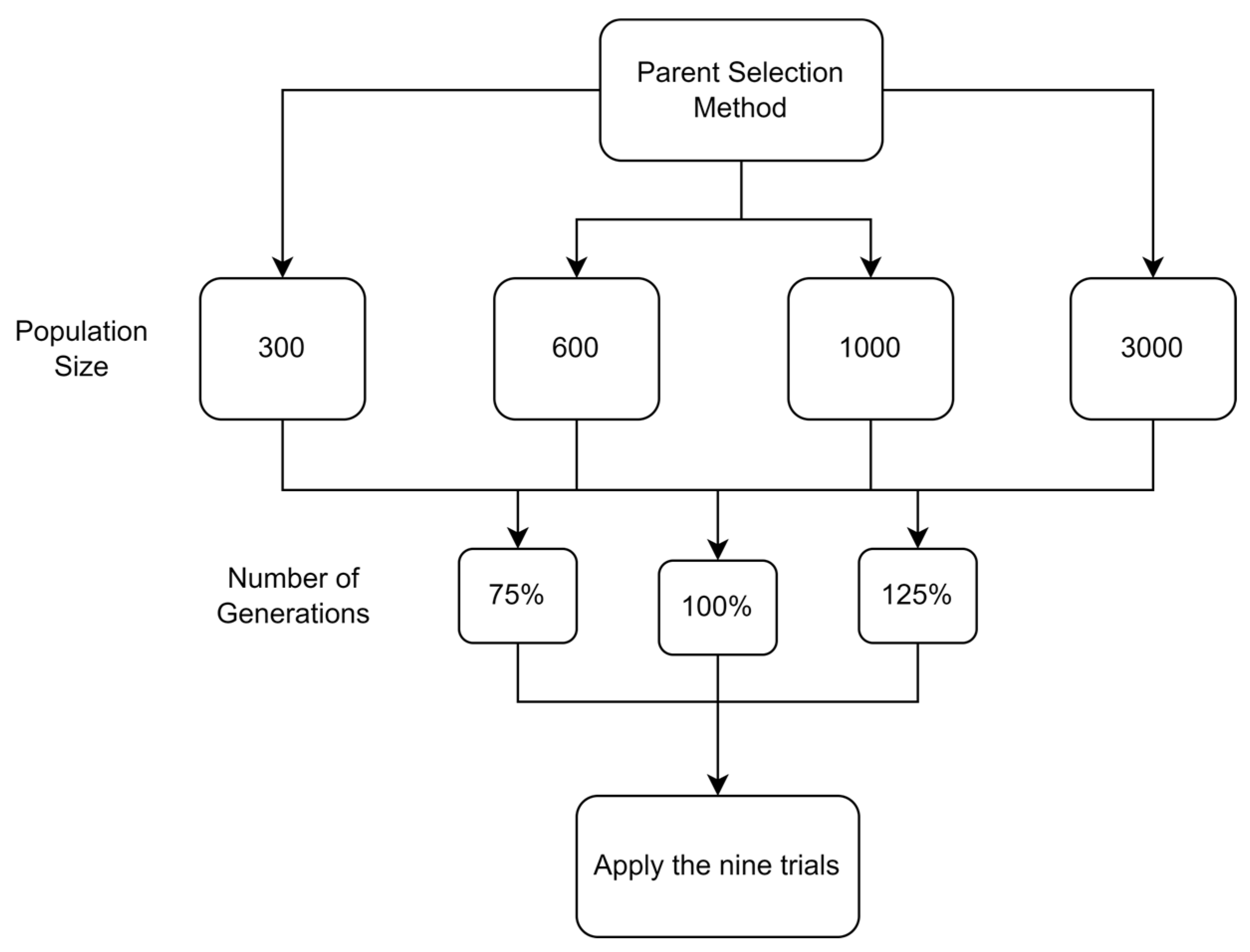
5.1.1. Parameters Setting and Calibration
5.1.2. Experimental Runs
5.2. Uncertain Case
5.2.1. Parameters Setting and Calibration: First Experiment
- Experimental Runs: First Experiment:
- Performance Metrics: First Experiment:
5.2.2. Parameters Setting and Calibration: Second Experiment
- Experimental Runs: Second Experiment:
- Performance Metrics: Second Experiment:
5.2.3. Parameters Setting and Calibration: Third Experiment
- Experimental Runs: Third Experiment:
- Performance Metrics: Third Experiment:
6. Results and Discussion
6.1. Normal Case Results
6.2. Uncertain Case Results
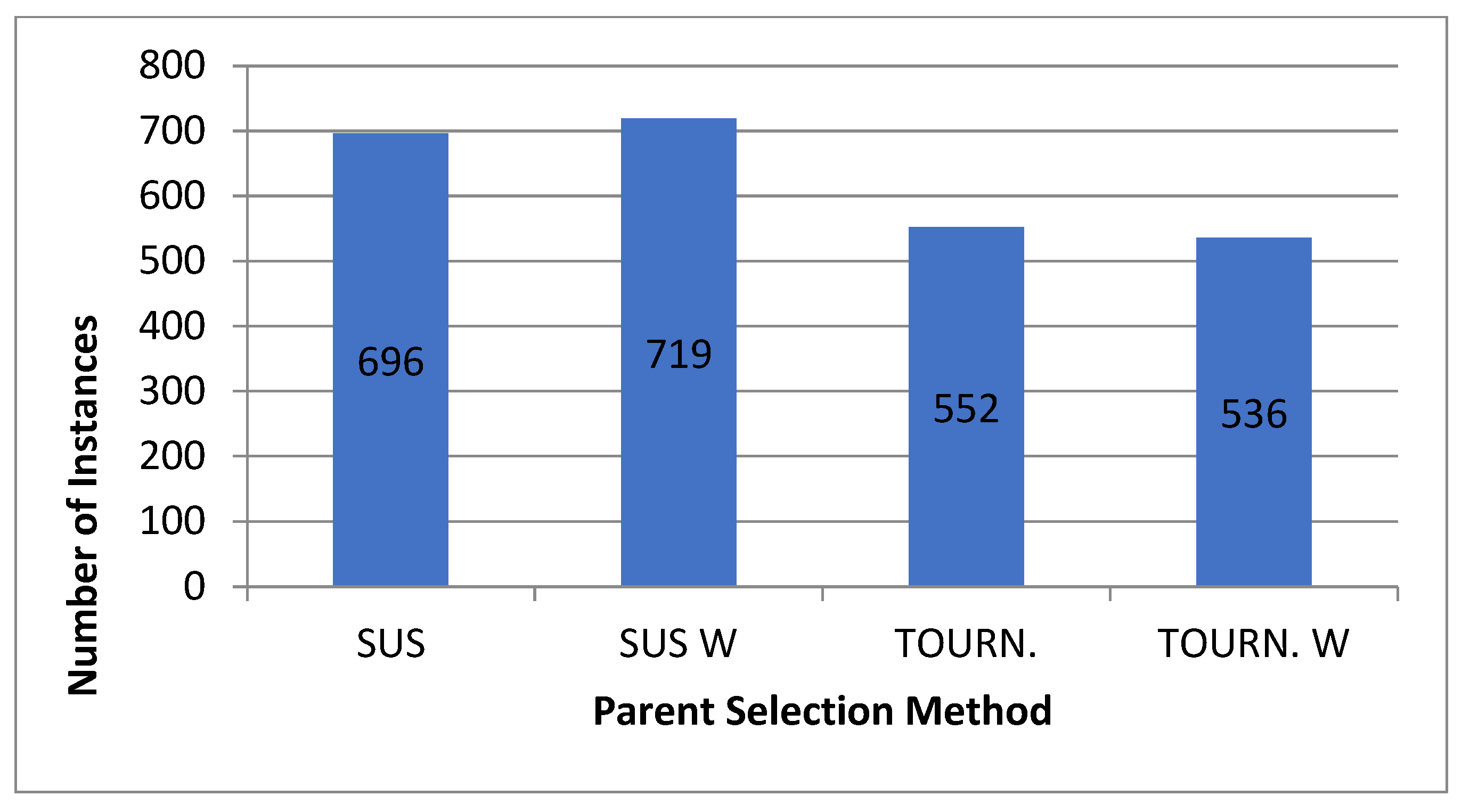
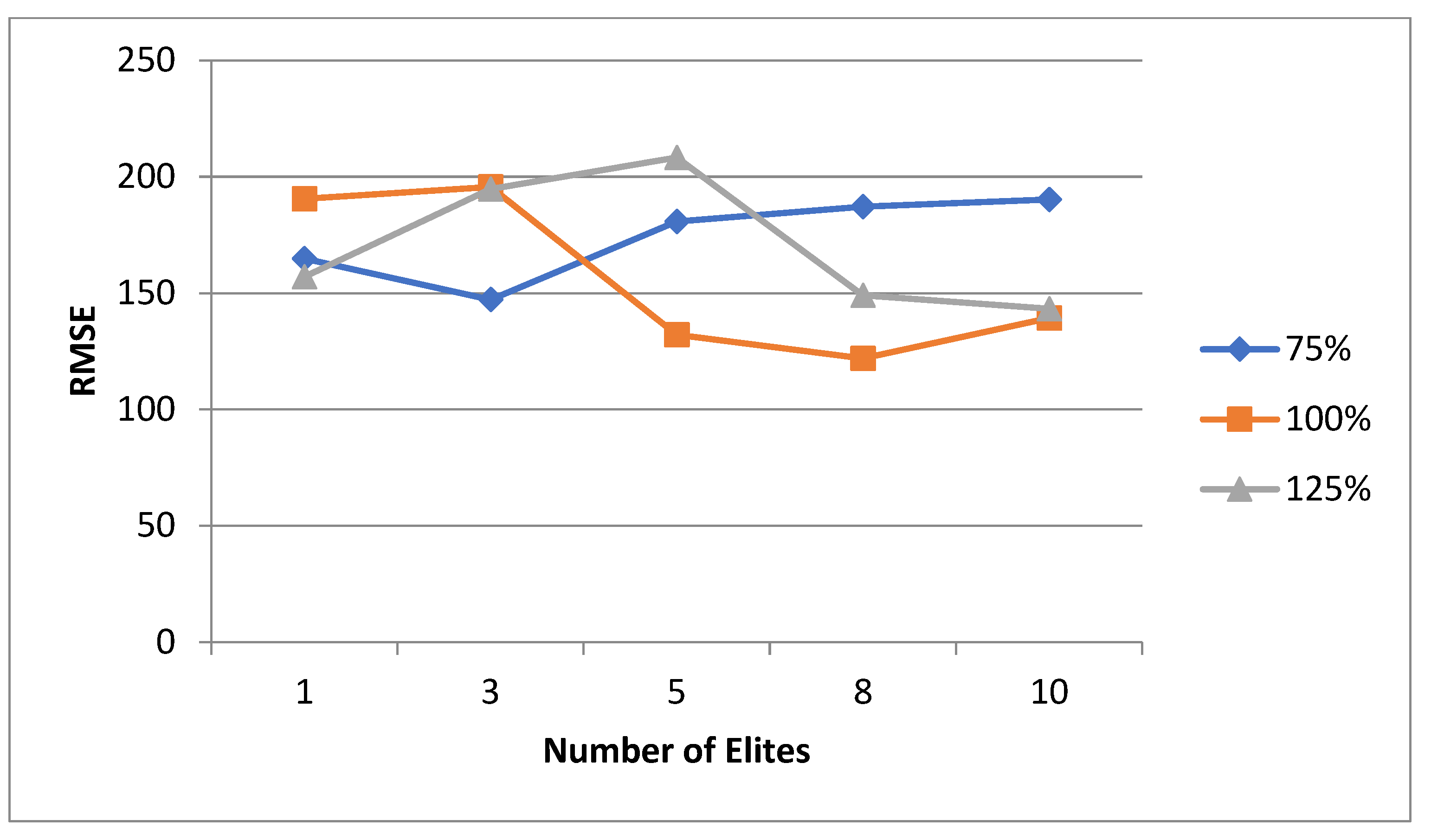
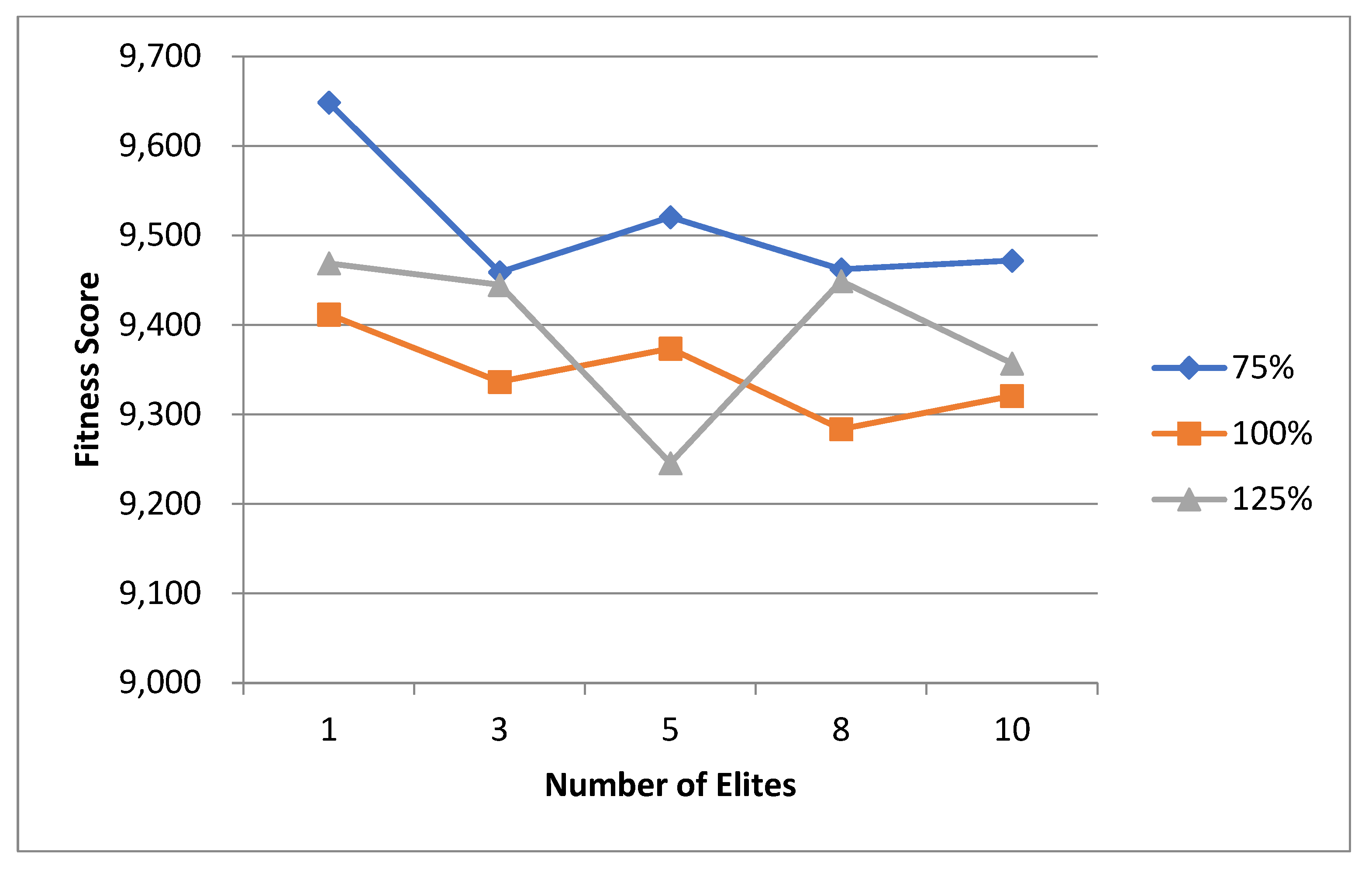
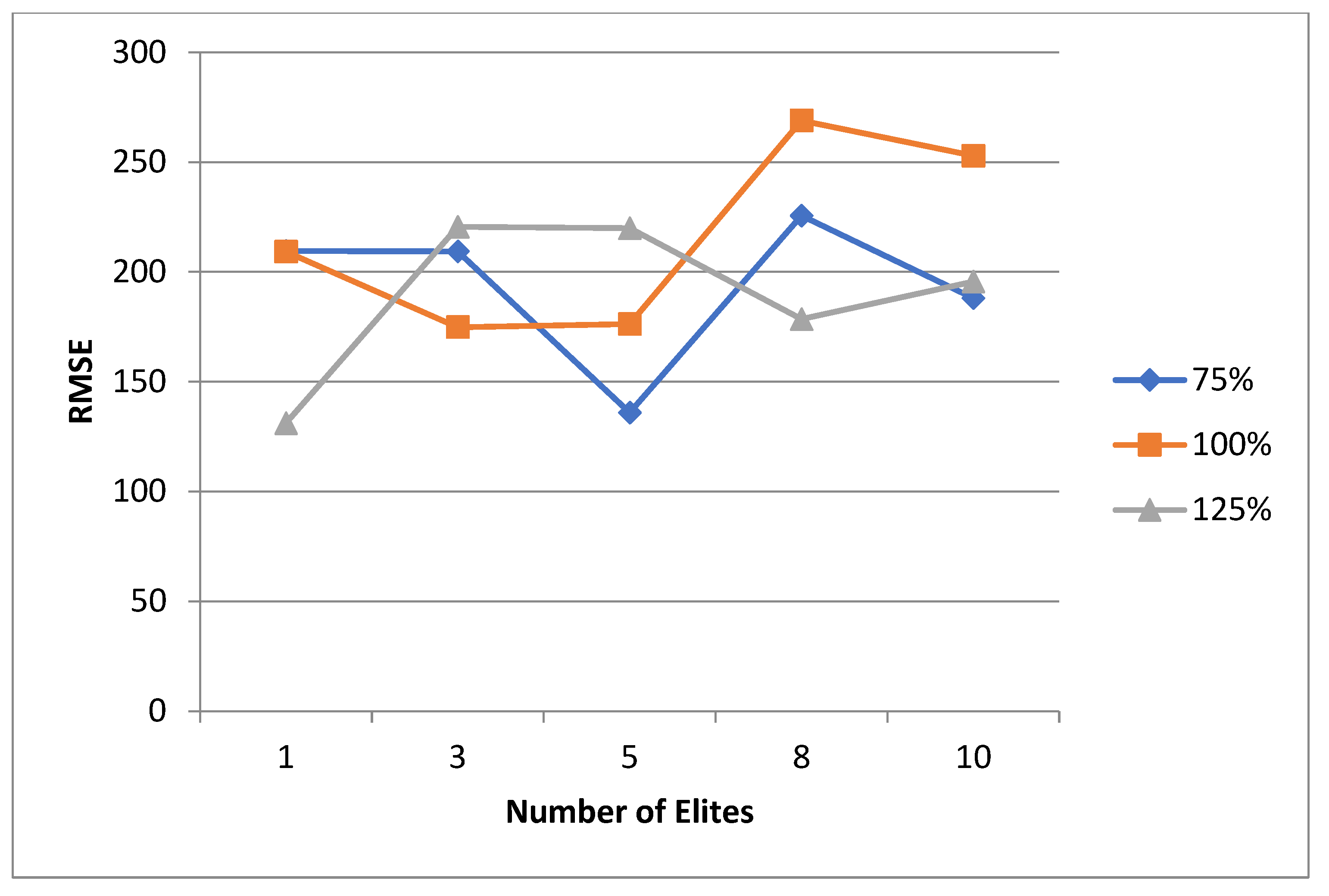
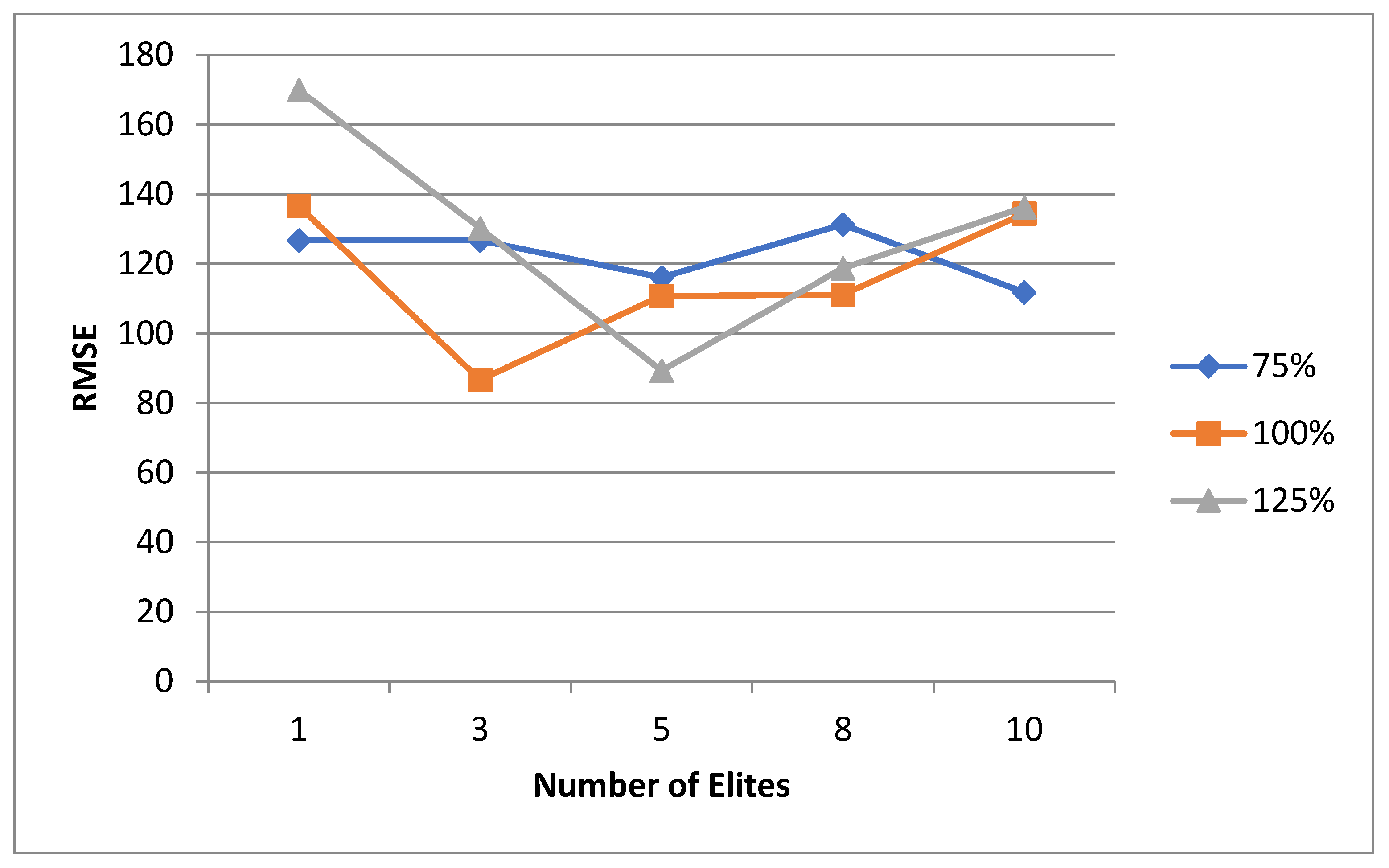
6.2.1. First Experimental Phase
6.2.2. Second Experimental Phase
6.2.3. Third Experimental Phase
6.3. Variable Selection Outlook
6.4. General Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SDGs | Sustainability Development Goals |
| TBL | Triple bottom line |
| LRP | Location-routing problem |
| VRP | Vehicle-routing problem |
| B2B | Business-to-business |
| B2C | Business-to-customer |
| CLRP | Capacitated LRP |
| 2E-CLRP | Two-echelon capacitated LRP |
| GA | Genetic algorithm |
| SCM | Supply chain management |
| TQM | Total quality management |
| WBCSD | World Business Council for Sustainable Development |
| WACOSS | Western Australian Council of Social Services |
| OECD | Organization for Economic Cooperation and Development |
| SSCs | Sustainable supply chains |
| SBD | Sustainable business development |
| SMEs | Small to medium enterprises |
| B&C | Branch and cut algorithm |
| RMSE | Root mean square error |
| SUS | Stochastic universal sampling hybrid with elitism |
| SUS W | Stochastic universal sampling |
| TOURN | Tournament hybrid with elitism |
| TOURN W | Tournament selection |
| PS | Population size |
| NOG | Number of generations |
| NOE | Number of elites |
| CO | Crossover percentage |
| M | Mutation percentage |
References
- Easterly, W. The trouble with the sustainable development goals. Curr. Hist. 2015, 114, 322. [Google Scholar] [CrossRef]
- Hamilton, K. Measuring sustainability in the UN system of environmental-economic accounting. Environ. Resour. Econ. 2016, 64, 25–36. [Google Scholar] [CrossRef]
- Lopes, R.B.; Ferreira, C.; Santos, B.S. A simple and effective evolutionary algorithm for the capacitated location–routing problem. Comput. Oper. Res. 2016, 70, 155–162. [Google Scholar] [CrossRef]
- Pham, Q.D.; Nguyen, T.H.; Bui, Q.T. Modeling and solving a multi-trip multi-distribution center vehicle routing problem with lower-bound capacity constraints. Comput. Ind. Eng. 2022, 172, 108597. [Google Scholar] [CrossRef]
- Kravchenko, M.; Pigosso, D.C.A.; McAloone, T.C. Towards the ex-ante sustain- ability screening of circular economy initiatives in manufacturing companies: Consolidation of leading sustainability-related performance indicators. J. Clean. Prod. 2019, 241, 118318. [Google Scholar] [CrossRef]
- Padilla-Rivera, A.; Russo-Garrido, S.; Merveille, N. Addressing the social as-pects of a circular economy: A systematic literature review. Sustainability 2020, 12, 7912. [Google Scholar] [CrossRef]
- Roos Lindgreen, E.; Salomone, R.; Reyes, T. Measuring circular economy at the micro level: Is the social dimension included? In Proceedings of the Atti XXIX Congresso Nazionale Di Scienze Merceologiche 2020, Milan, Italy, 13–14 February 2020; pp. 396–403. [Google Scholar]
- Toorajipour, R.; Sohrabpour, V.; Nazarpour, A.; Oghazi, P.; Fischl, M. Artificial Intelligence in Supply Chain Management: A systematic literature Review. J. Bus. Res. 2021, 122, 502–517. [Google Scholar]
- Cerqueria-Streit, J.A.; Endo, G.Y.; Guarnieri, P.; Batista, L. Sustainable Supply Chain Management in the Route for a Circular Economy: An Integrative Literature Review. Logistics 2021, 5, 81. [Google Scholar] [CrossRef]
- Putro, P.A.W.; Purwaningsih, E.K.; Sensuse, D.I.; Suryono, R.R. Model and implementation of rice supply chain management: A literature review. Procedia Comput. Sci. 2022, 197, 453–460. [Google Scholar]
- Ugochukwu, P.; Engström, J.; Langstrand, J. Lean in the supply chain: A literature review. Manag. Prod. Eng. Rev. 2012, 3, 87–96. [Google Scholar]
- Baran, E.; Korkusuz Polat, T. Classification of Industry 4.0 for Total Quality Management: A Review. Sustainability 2022, 14, 3329. [Google Scholar] [CrossRef]
- Arora, R.; Haleem, A.; Arora, P.K.; Kumar, H. Impact of Integrating Artificial Intelligence with IOT-Enabled Supply Chain—A Systematic Literature Review. In Advances in Manufacturing and Industrial Engineering; Lecture Notes in Mechanical Engineering; Singari, R., Mathiyazhagan, K., Kumar, H., Eds.; Springer: Singapore, 2021. [Google Scholar]
- Singh, R.K.; Kumar, R. Strategic issues in supply chain management of Indian SMEs due to globalization: An empirical study. Benchmarking Int. J. 2020, 27, 913–932. [Google Scholar] [CrossRef]
- Stroumpoulis, A.; Kopanaki, E. Theoratical Perspectives on Sustainable Supply Chain Managmenet and Digital Transformation: A Literature Review and a Conceptual Framework. Sustainability 2022, 14, 4862. [Google Scholar]
- Ahmad, S.; Wong, K.Y.; Rajoo, S. Sustainability indicators for manufacturing sectors: A literature survey and maturity analysis from the triple-bottom line perspective. J. Manuf. Technol. Manag. 2019, 30, 312–334. [Google Scholar] [CrossRef]
- Correia, M.S. Sustainability: An overview of the Triple Bottom Line and Sustainability Implementation. Int. J. Strateg. Eng. (IJoSE) 2019, 2, 29–38. [Google Scholar] [CrossRef]
- Mani, V.; Delgado, C. Supply Chain Social Sustainability for Manufacturing; India Studies in Business and Economics; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- IUCN; WWF; UNEP. Caring for the Earth, A Strategy for Sustainable Living; WWF: Gland, Switzerland, 1991. [Google Scholar]
- Hill, S.B. Redesigning agro ecosystems for environmental sustainability: A deep systems approach. Syst. Res. Behav. Sci. 1998, 15, 391–402. [Google Scholar] [CrossRef]
- Lafferty, W.M.; Langhelle, O. Towards Sustainable Development: On the Goals of Development-and the Conditions of Sustainability; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Mani, V.; Gunasekaran, A.; Delgado, C. Supply chain social sustainability: Standard adoption practices in Portuguese manufacturing firms. Int. J. Prod. Econ. 2018, 198, 149–164. [Google Scholar] [CrossRef]
- Seuring, S.; Müller, M. From a literature review to a conceptual framework for sustainable supply chain management. J. Clean. Prod. 2008, 16, 1699–1710. [Google Scholar] [CrossRef]
- Ashby, A.; Leat, M.; Hudson-Smith, M. Making connections: A review of supply chain management and sustainability literature. Supply Chain. Manag. Int. J. 2012, 17, 497–516. [Google Scholar] [CrossRef]
- Gunasekaran, A.; Spalanzani, A. Sustainability of manufacturing and services: Investigations for research and applications. Int. J. Prod. Econ. 2012, 140, 35–47. [Google Scholar] [CrossRef]
- Pinar, M.; Cruciani, C.; Giove, S.; Sostero, M. Constructing the FEEM sustainability index: A Choquet integral application. Ecol. Indic. 2014, 39, 189–202. [Google Scholar] [CrossRef]
- Walker, A.M.; Opferkuch, K.; Lindgreen, E.R.; Simboli, A.; Vermeulen, W.J.; Raggi, A. Assessing the social sustainability of circular economy practices: Industry perspectives from Italy and the Netherlands. Sustain. Prod. Consum. 2021, 27, 831–844. [Google Scholar]
- Hervani, A.A.; Nandi, S.; Helms, M.M.; Sarkis, J. A performance measurement framework for socially sustainable and resilient supply chains using environmental goods valuation methods. Sustain. Prod. Consum. 2022, 30, 31–52. [Google Scholar] [CrossRef]
- Nagy, G.; Salhi, S. Location-routing: Issues, models and methods. Eur. J. Oper. Res. 2007, 177, 649–672. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, Y.; Liu, X.F. A novel hybrid genetic algorithm for the location routing problem with tight capacity constraints. Appl. Soft Comput. 2019, 85, 105760. [Google Scholar] [CrossRef]
- Prodhon, C.; Prins, C. A survey of recent research on location-routing problems. Eur. J. Oper. Res. 2014, 238, 1–17. [Google Scholar] [CrossRef]
- Schneider, M.; Drexl, M. A survey of the standard location-routing problem. Ann. Oper. Res. 2017, 259, 389–414. [Google Scholar] [CrossRef]
- Mara, S.T.W.; Kuo, R.J.; Asih, A.M.S. Location-routing problem: A classification of recent research. Int. Trans. Oper. Res. 2021, 28, 2941–2983. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Wei, Y.; Sun, Y.; Fan, J.; Wang, H. Two-echelon multi-depot multi-period location-routing problem with pickup and delivery. Comput. Ind. Eng. 2023, 182, 109385. [Google Scholar] [CrossRef]
- Soto-Mendoza, V.; Ruiz-y-Ruiz, E.; García-Calvillo, I.; Nucamendi-Guillén, S.; Cardona-Valdés, Y. A location-routing problem for local supply chains. Comput. Ind. Eng. 2023, 183, 109528. [Google Scholar] [CrossRef]
- Tian, X.D.; Hu, Z.H. A branch-and-price method for a two-echelon location routing problem with recommended satellites. Comput. Ind. Eng. 2023, 184, 109593. [Google Scholar] [CrossRef]
- Zabihian-Bisheh, A.; Vandchali, H.R.; Kayvanfar, V.; Werner, F. A sustainable multi-objective model for the hazardous waste location-routing problem: A real case study. Sustain. Oper. Comput. 2024, 5, 1–14. [Google Scholar] [CrossRef]
- Du, J.; Wang, X.; Wu, X.; Zhou, F.; Zhou, L. Multi-objective optimization for two-echelon joint delivery location routing problem considering carbon emission under online shopping. Transp. Lett. 2023, 15, 907–925. [Google Scholar] [CrossRef]
- Shi, Y.; Lin, Y.; Wang, S.; Wen, H.; Lim, M.K.; Li, Y. A simultaneous facility location and vehicle routing problem with recyclable express packaging consideration for sustainable city logistics. Sustain. Cities Soc. 2023, 98, 104857. [Google Scholar] [CrossRef]
- Hajghani, M.; Forghani, M.A.; Heidari, A.; Khalilzadeh, M.; Kebriyaii, O. A two-echelon location routing problem considering sustainability and hybrid open and closed routes under uncertainty. Heliyon 2023, 9, e14258. [Google Scholar] [CrossRef]
- Osorio-Mora, A.; Saldanha-da-Gama, F.; Toth, P. A risk-averse latency location-routing problem with stochastic travel times. Eur. J. Oper. Res. 2025, 321, 837–850. [Google Scholar] [CrossRef]
- Eydi, A.; Shirinbayan, P. Multi-modal and multi-product hierarchical hub location problem with fuzzy demands. Eng. Appl. Artif. Intell. 2023, 123, 106282. [Google Scholar] [CrossRef]
- Prodhon, C. A metaheuristic for the periodic location-routing problem. In Proceedings of the Symposium Operations Research 2007, Saarbrücken, Germany, 5–7 September 2007; pp. 159–164. [Google Scholar]
- Mohamed, I.B.; Klibi, W.; Sadykov, R.; Şen, H.; Vanderbeck, F. The two-echelon stochastic multi-period capacitated location-routing problem. Eur. J. Oper. Res. 2023, 306, 645–667. [Google Scholar] [CrossRef]
- Yıldız, E.A.; Karaoğlan, İ.; Altiparmak, F. An exact algorithm for Two-Echelon Location-Routing problem with simultaneous pickup and delivery. Expert Syst. Appl. 2023, 231, 120598. [Google Scholar] [CrossRef]
- Domínguez-Martín, B.; Hernández-Pérez, H.; Riera-Ledesma, J.; Rodríguez-Martín, I. A branch-and-cut algorithm for the one-commodity pickup and delivery location routing problem. Comput. Oper. Res. 2024, 161, 106426. [Google Scholar] [CrossRef]
- Barbati, M.; Corrente, S.; Greco, S. Multiobjective combinatorial optimization with interactive evolutionary algorithms: The case of facility location problems. EURO J. Decis. Process. 2024, 12, 100047. [Google Scholar] [CrossRef]
- Tan, D.; Liu, X.; Zhou, R.; Fu, X.; Li, Z. A novel multi-objective artificial bee colony algorithm for solving the two-echelon load-dependent location-routing problem with pick-up and delivery. Eng. Appl. Artif. Intell. 2025, 139, 109636. [Google Scholar] [CrossRef]
- Mahmoudi, N.; Sadegheih, A.; Hosseini-Nasab, H.; Zare, H.K. Routing and scheduling decisions for a single-hub same-day delivery network. J. Eng. Res. 2023, 11, 198–211. [Google Scholar] [CrossRef]
- Hu, Q.; Hu, Y.; Li, X. Multi-period emergency facility location-routing problems under uncertainty and risk aversion. Socio-Econ. Plan. Sci. 2024, 96, 102093. [Google Scholar] [CrossRef]
- Bootaki, B.; Zhang, G. A location-production-routing problem for distributed manufacturing platforms: A neural genetic algorithm solution methodology. Int. J. Prod. Econ. 2024, 275, 109325. [Google Scholar] [CrossRef]
- Aleksandrov, M. Fairness and Efficiency in Social Vehicle Routing Problems. Transp. Res. Procedia 2025, 82, 1994–2013. [Google Scholar] [CrossRef]
- Azab, E.; Nafea, M.; Shihata, L.A.; Mashaly, M. A Machine-Learning-Assisted Simulation Approach for Incorporating Predictive Maintenance in Dynamic Flow-Shop Scheduling. Appl. Sci. 2021, 11, 11725. [Google Scholar] [CrossRef]
- Fortin, F.-A.; De Rainville, F.-M.; Gardner, M.-A.; Parizeau, M.; Gagné, C. DEAP: Evolutionary Algorithms Made Easy. J. Mach. Learn. Res. 2012, 13, 2171–2175. [Google Scholar]
- Hurbans, R. Grokking Artificial Intelligence Algorithms; Manning: Greenwich, CT, USA, 2020. [Google Scholar]
- Hou, Y.; Wang, H.; Fu, Y.; Gao, K.; Zhang, H. Multi-Objective brain storm optimization for integrated scheduling of distributed flow shop and distribution with maximal processing quality and minimal total weighted earliness and tardiness. Comput. Ind. Eng. 2023, 179, 109217. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, Y.; Gao, K.; Huang, M. Review on ensemble meta-heuristics and reinforcement learning for manufacturing scheduling problems. Comput. Electr. Eng. 2024, 120, 109780. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, H.; Huang, X. A Q-learning-based multi-objective evolutionary algorithm for integrated green production and distribution scheduling problems. Eng. Appl. Artif. Intell. 2024, 127, 107434. [Google Scholar] [CrossRef]
- Zhang, Z.; Fu, Y.; Gao, K.; Pan, Q.; Huang, M. A learning-driven multi-objective cooperative artificial bee colony algorithm for distributed flexible job shop scheduling problems with preventive maintenance and transportation operations. Comput. Ind. Eng. 2024, 196, 110484. [Google Scholar] [CrossRef]























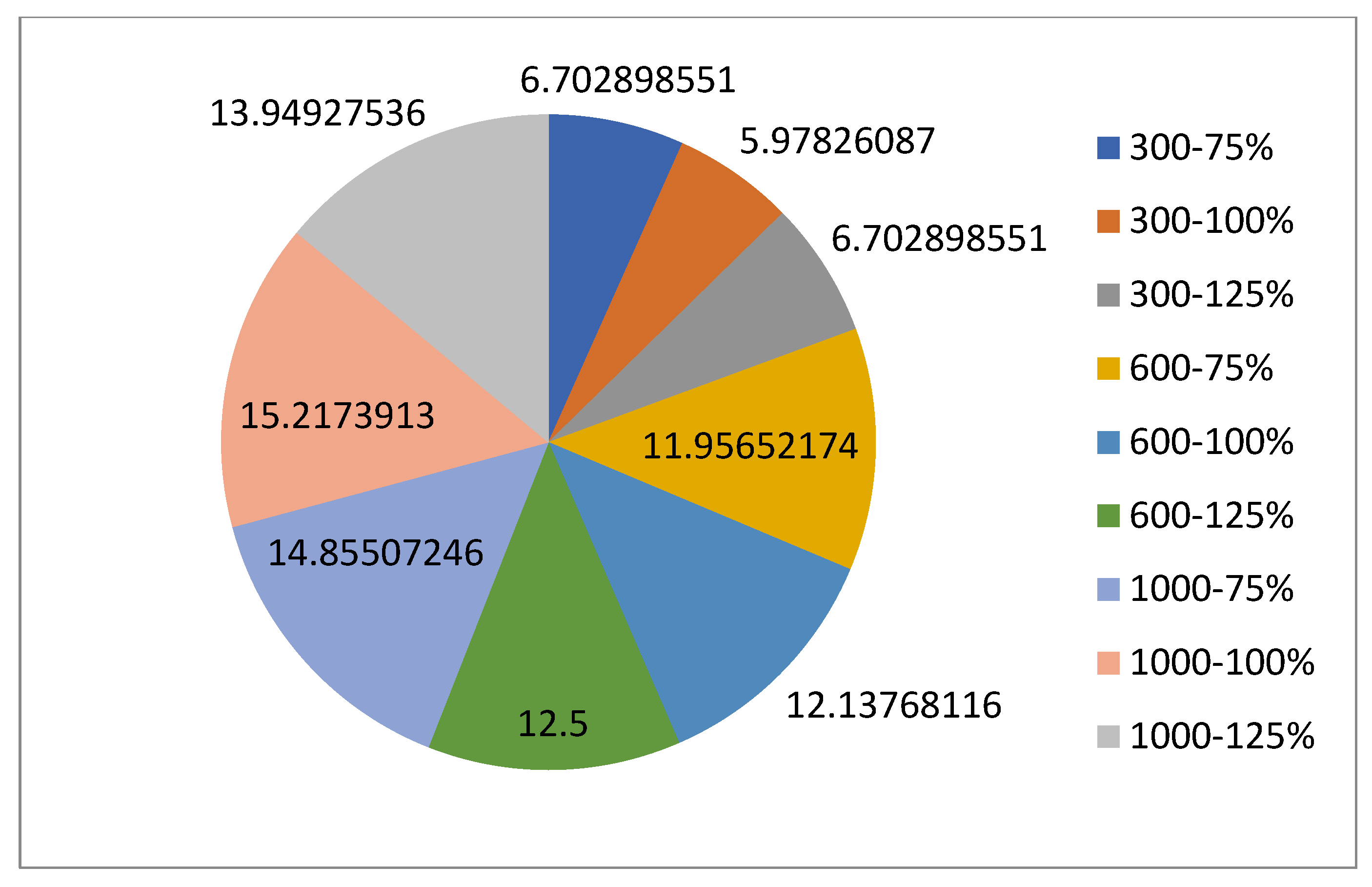
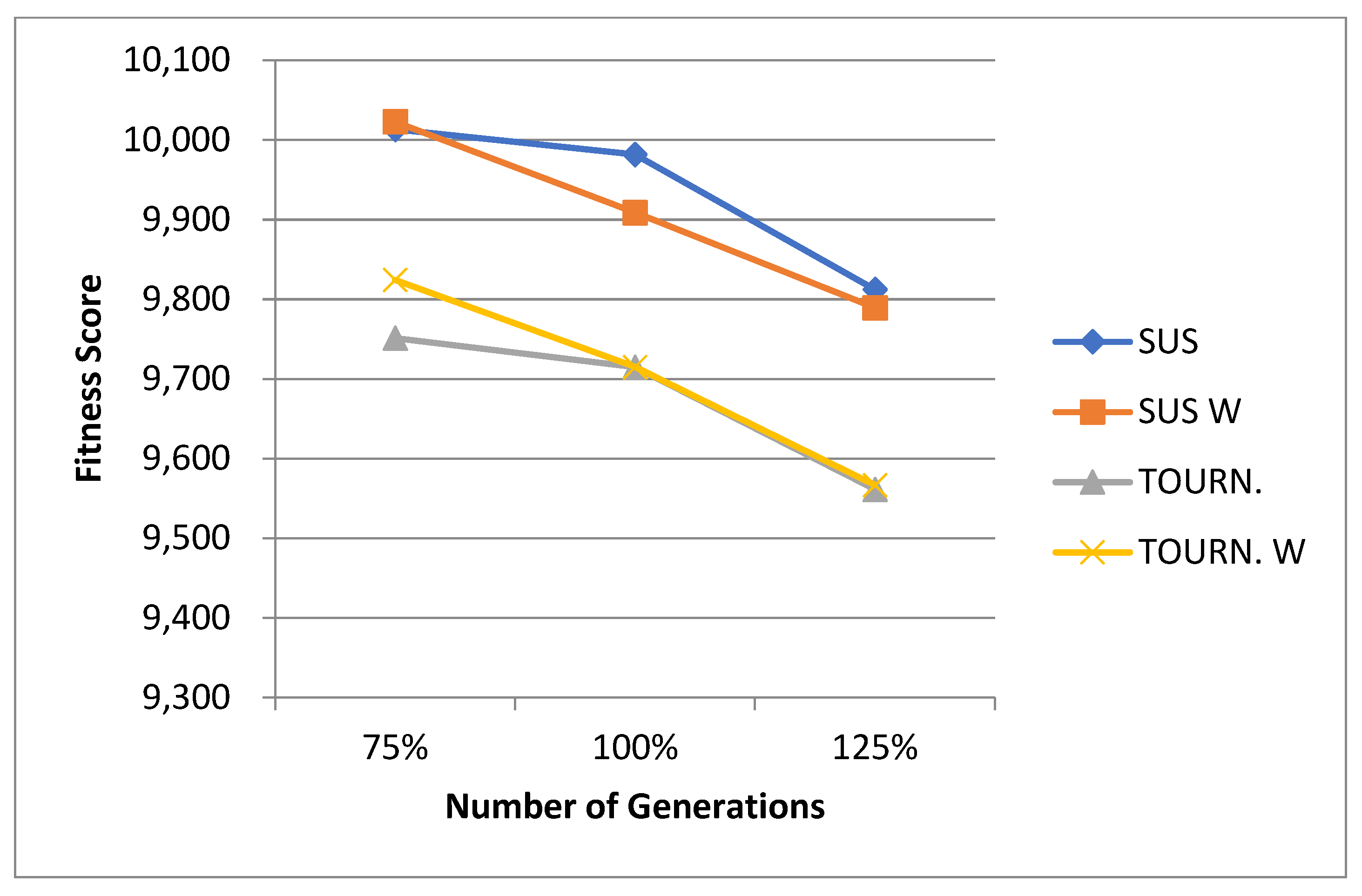
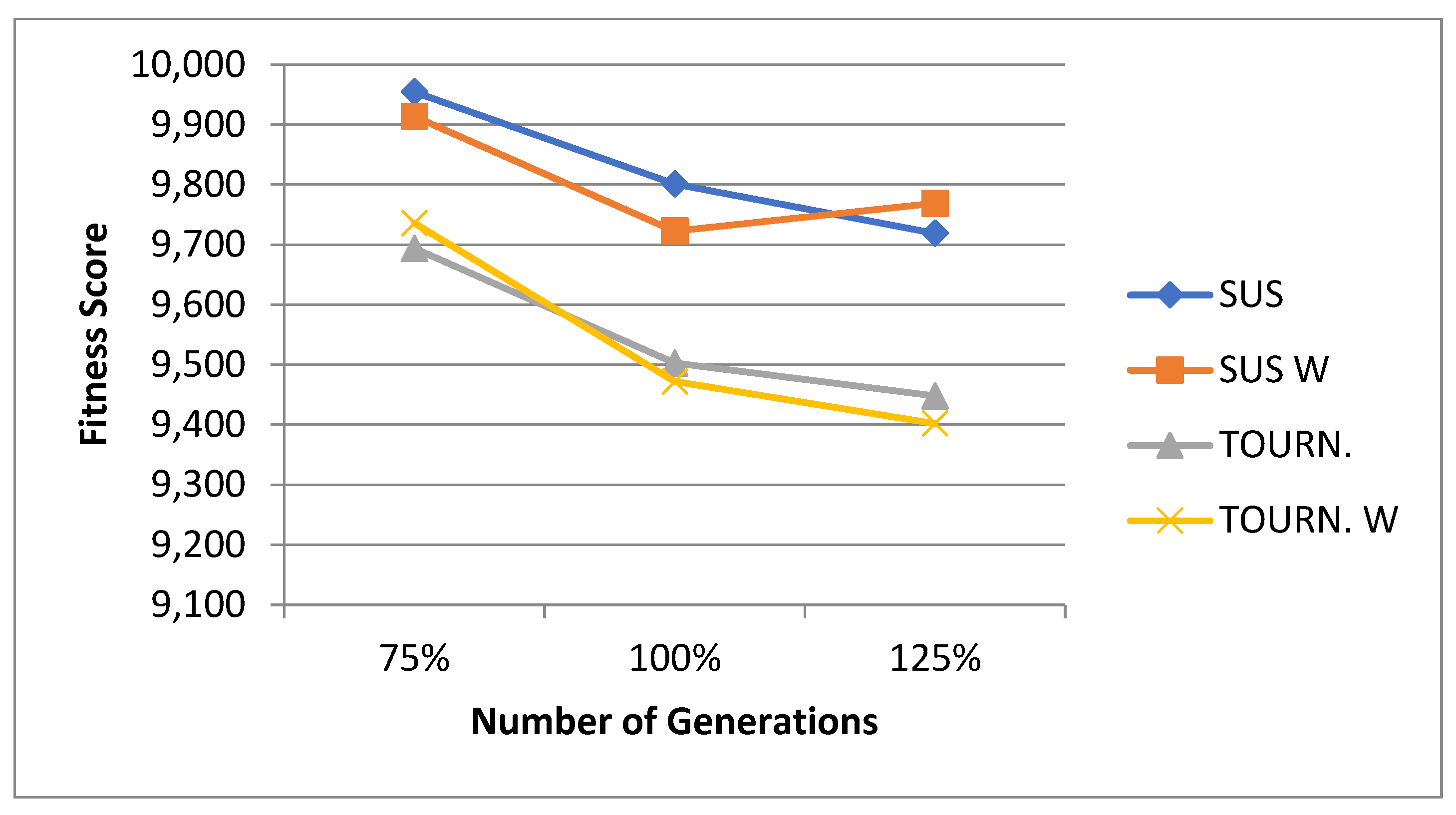
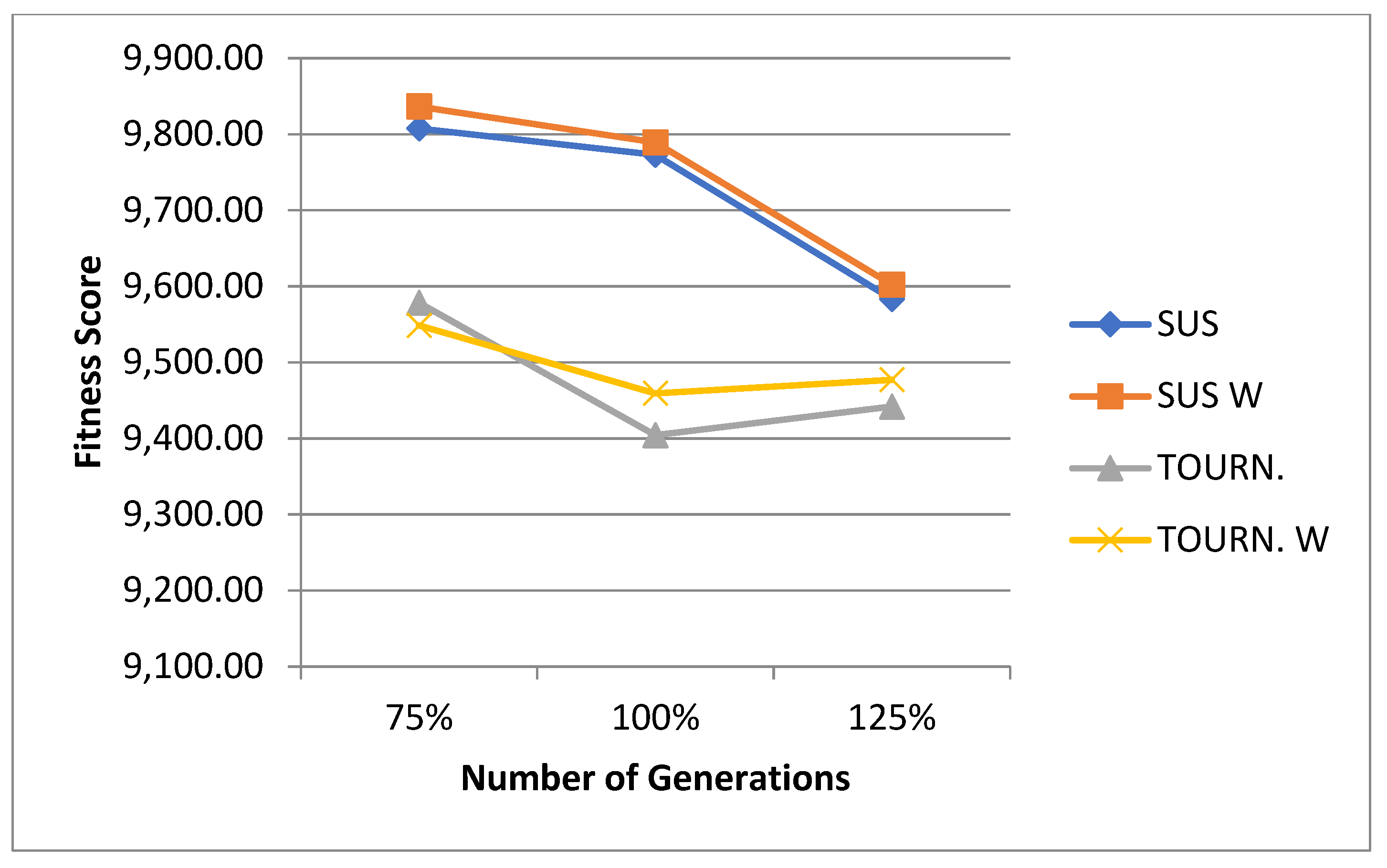
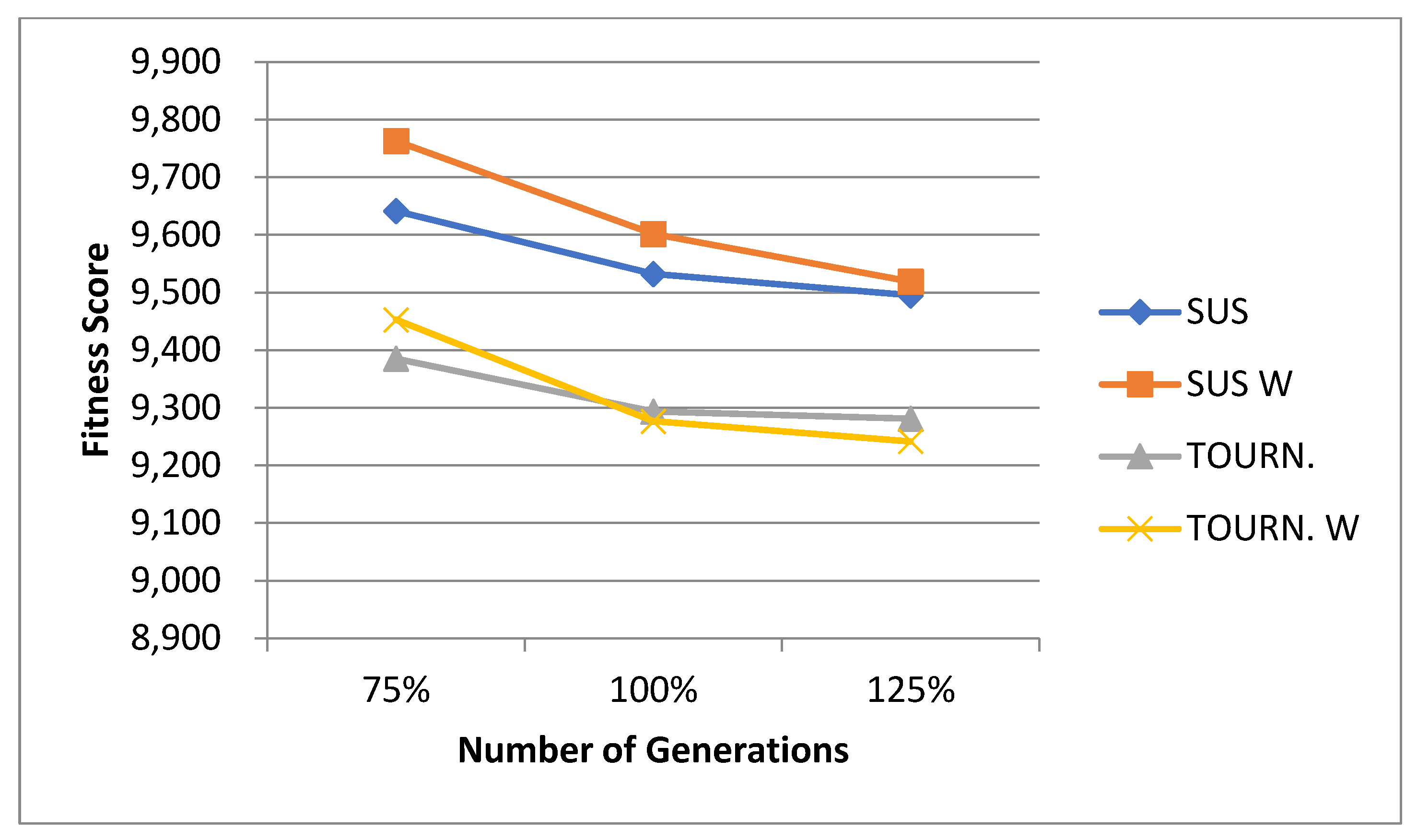





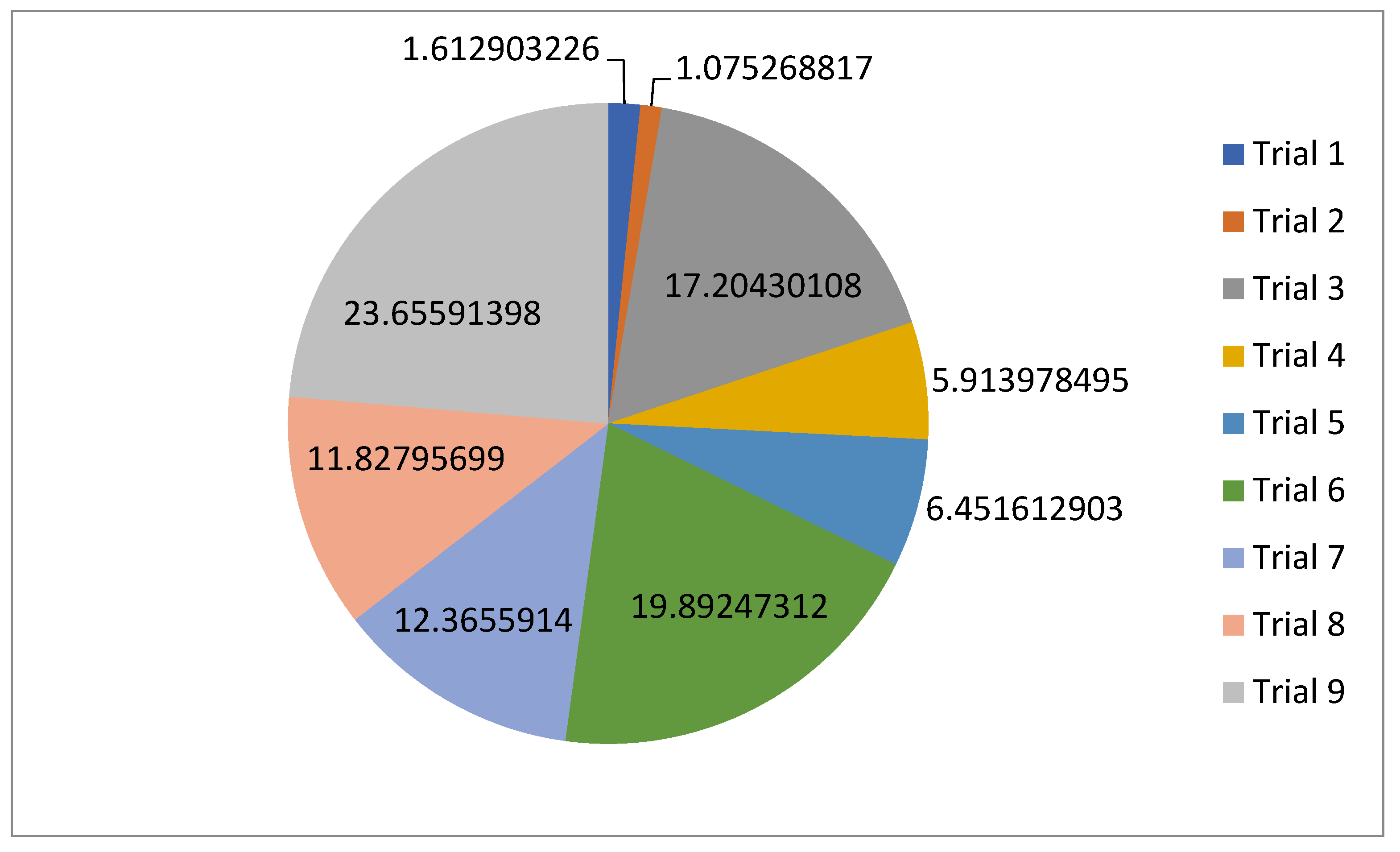

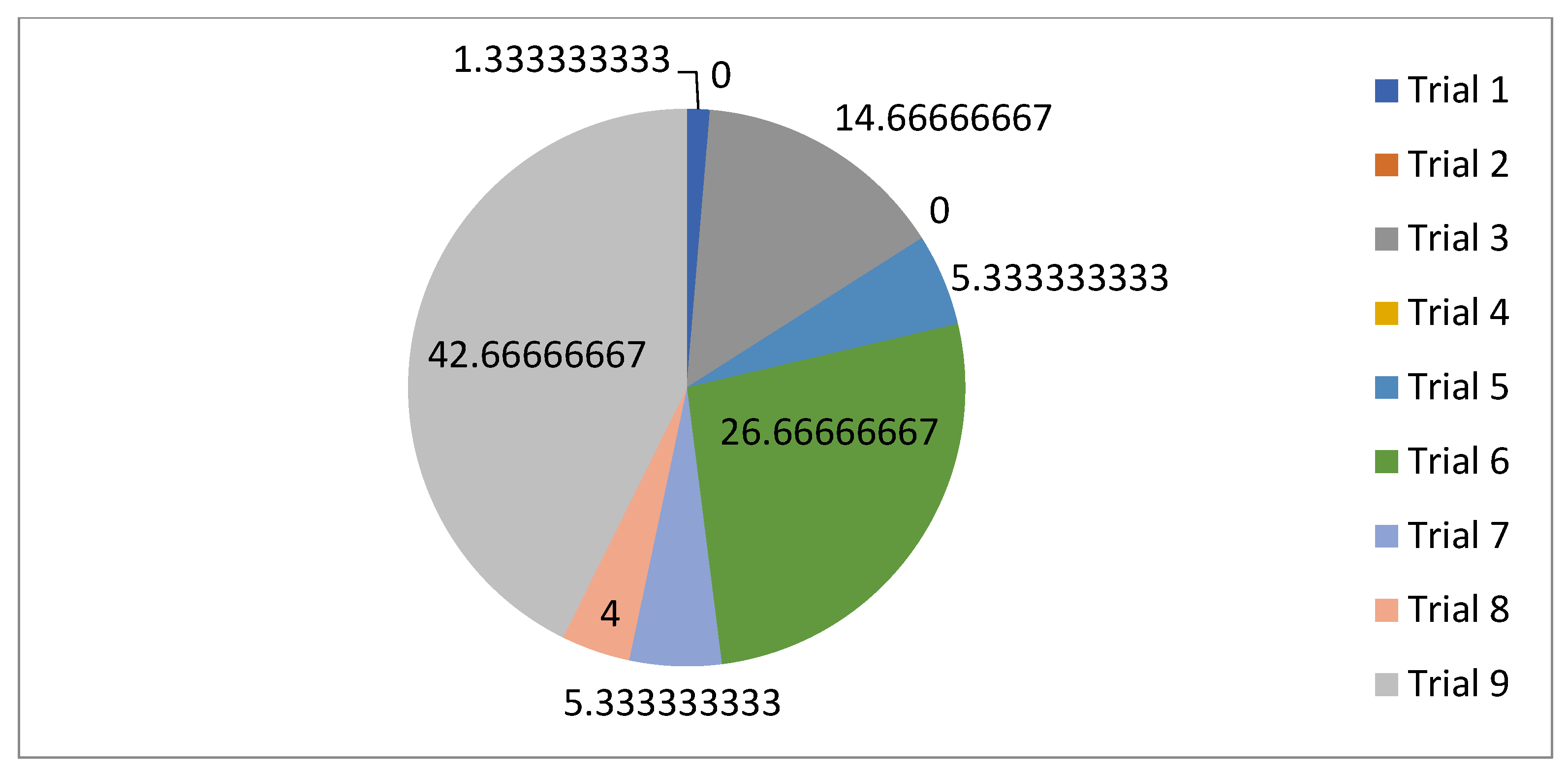
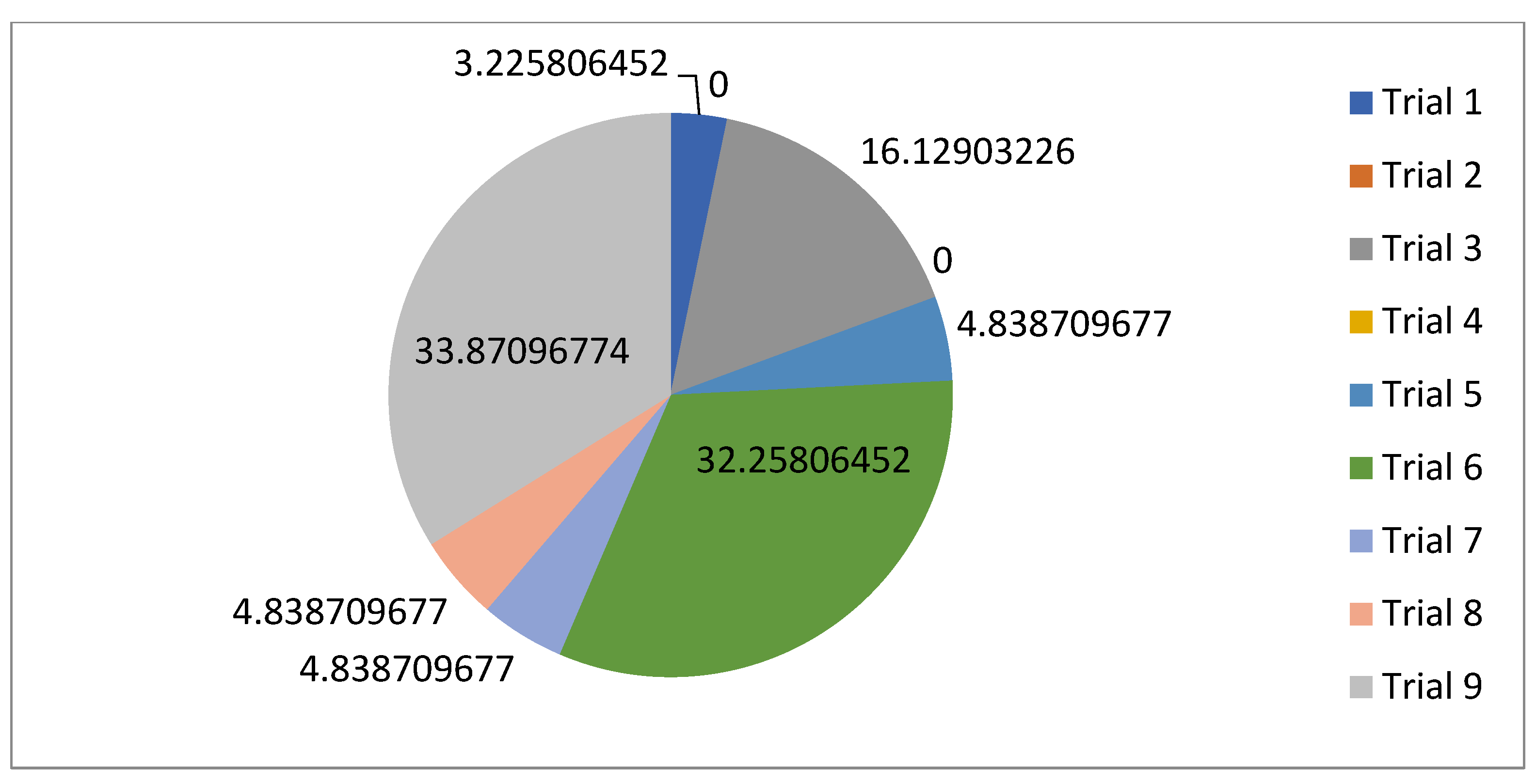
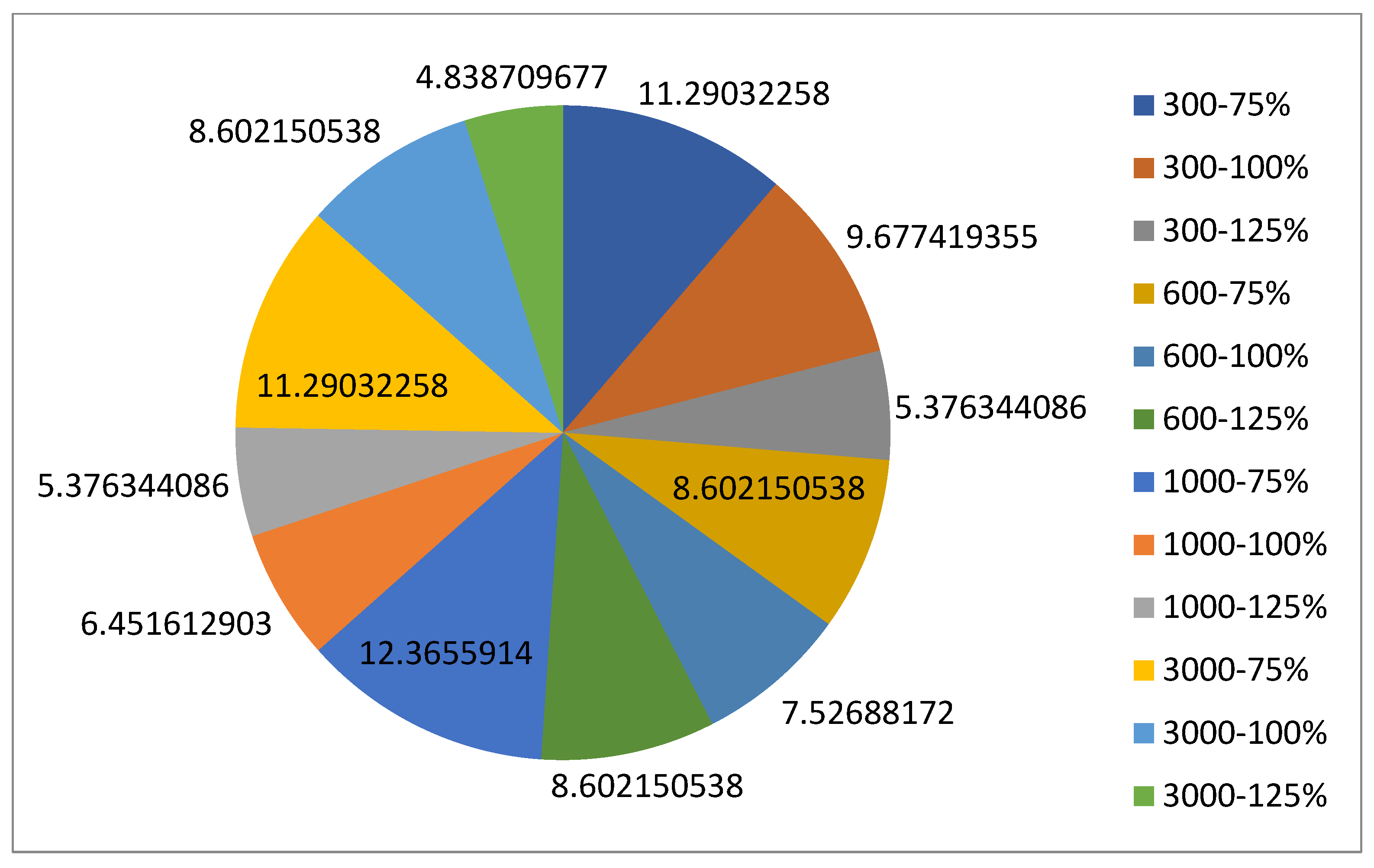

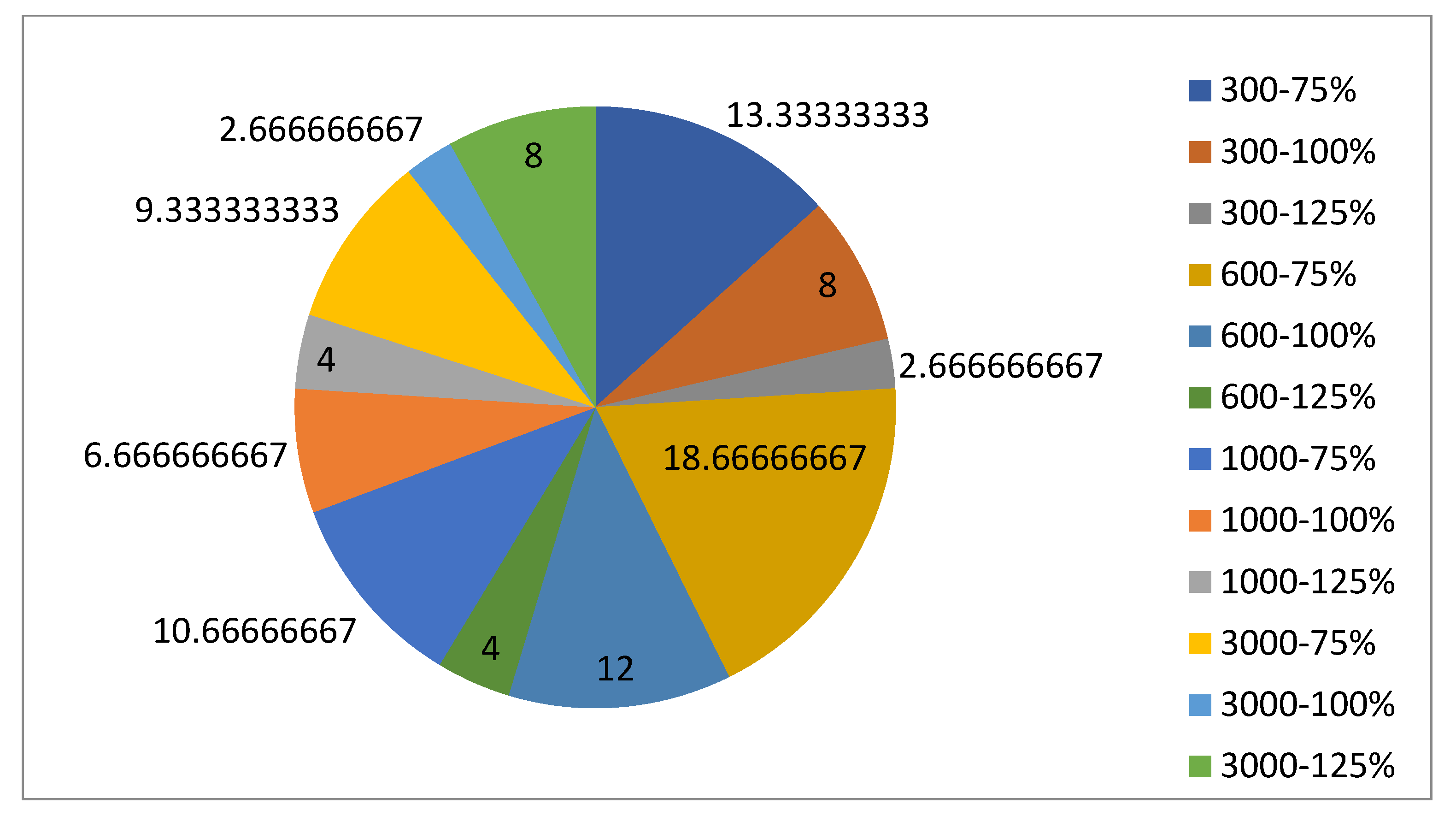
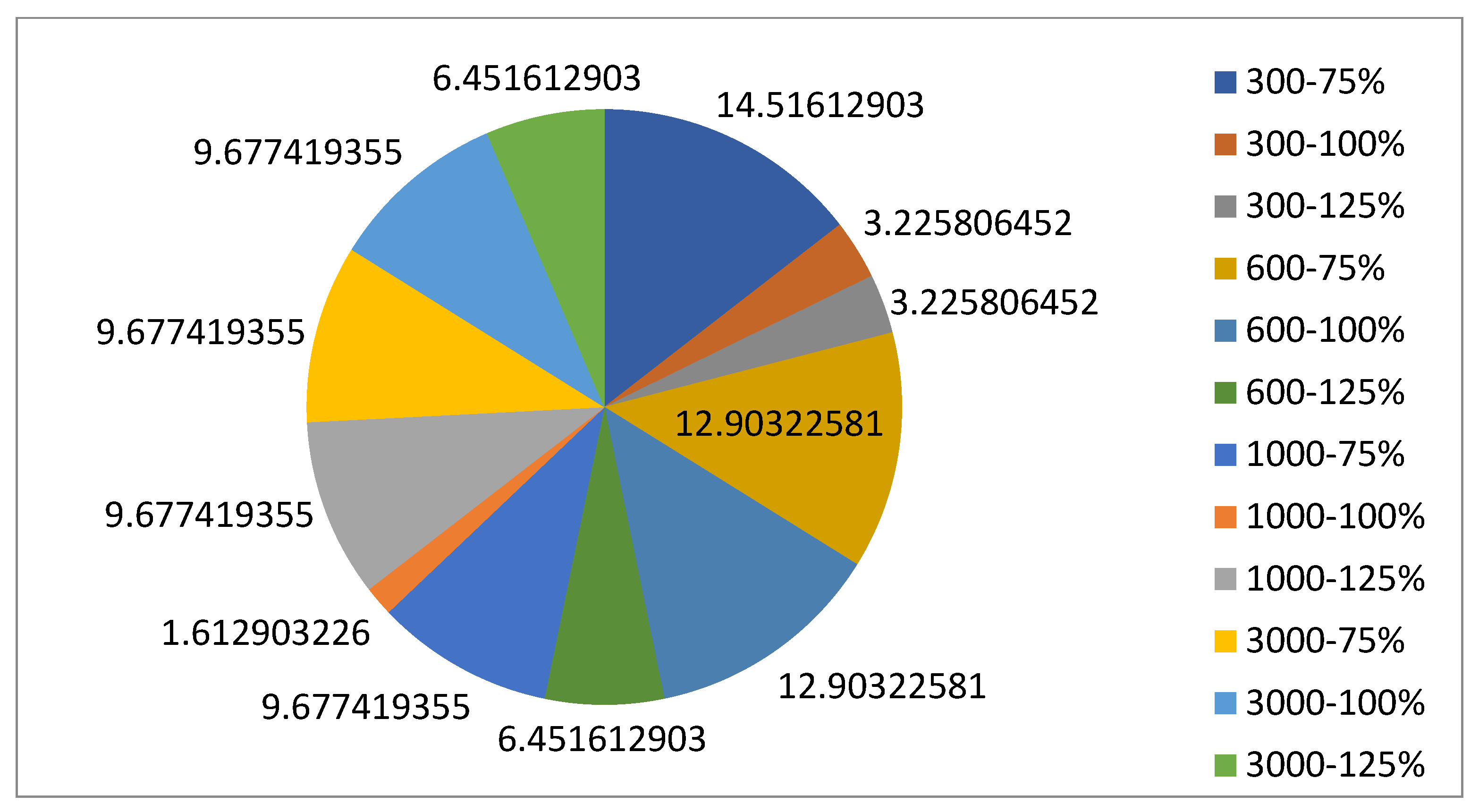


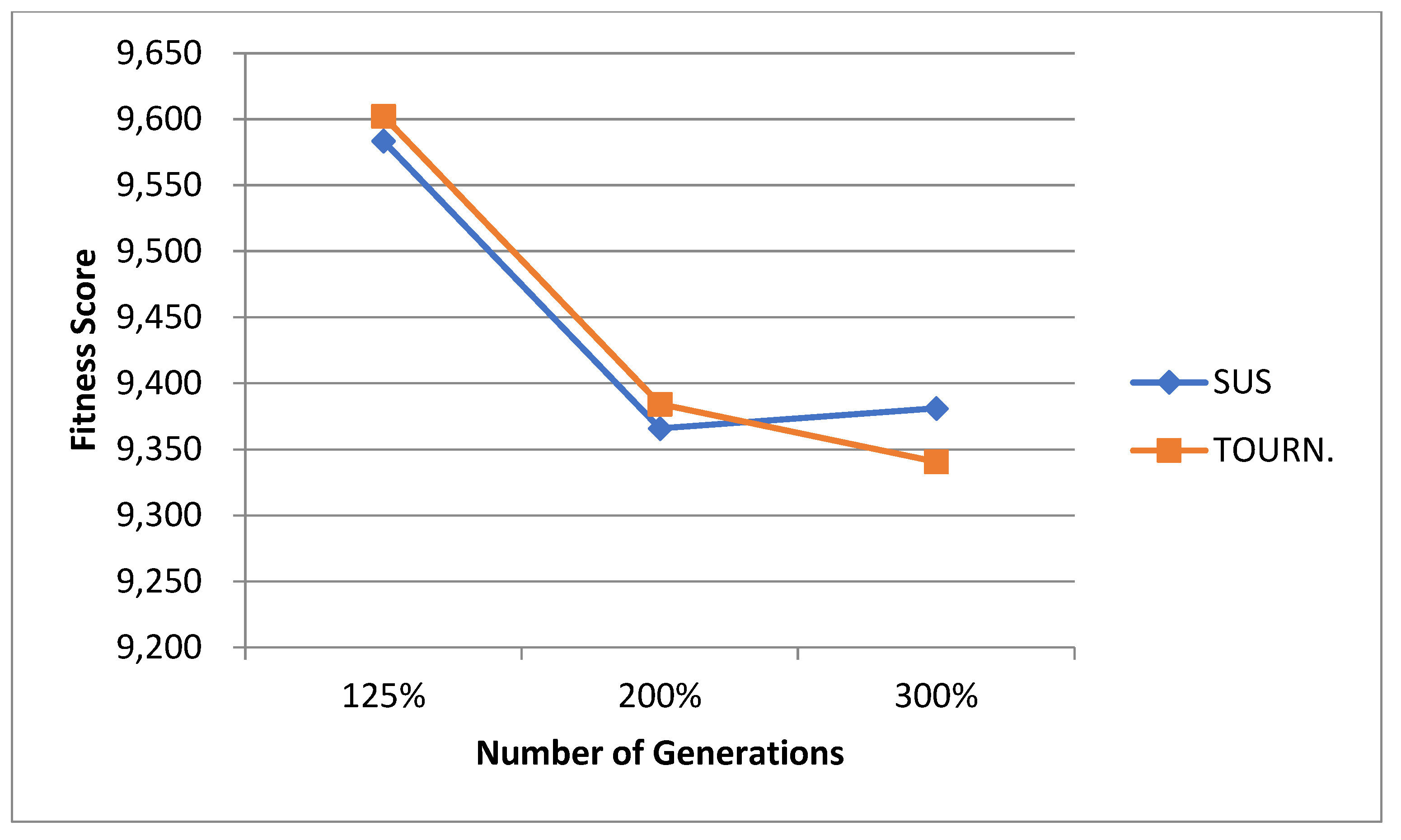





| Mathematical Notation | Explanation |
|---|---|
| T | Time interval |
| D | Distances traveled |
| L | Location of facility |
| S | Social aspects |
| NS | Number of stops |
| PS | Proximity factor |
| NE | Number of employees in main facility |
| SS | Suppliers location |
| DC | Distribution center location |
| TS | Transportation hub |
| K | Vehicle no. 1 |
| M | Vehicle no. 2 |
| TC | Vehicle tank capacity |
| LDC | Distance between facility location and distribution center |
| LSS | Distance between facility location and supplier |
| LTS | Distance between facility location and transportation hub |
| SSS | Distance between one supplier and another |
| DCC | Distance between one distribution center and another |
| CL | Cost of purchasing a facility location |
| CSS | Cost of contracting a supplier |
| CDC | Cost of contracting a distribution center |
| CCE | Cost of carbon emissions per kilometer |
| Cost of vehicle M rental/leasing | |
| Cost of vehicle K rental/leasing | |
| Compensation fee for employee’s proximity to transportation hub | |
| Price of liter per kilometer | |
| Break time for driver | |
| Break rate per USD | |
| Variable is equal to 1 if vehicle M or K is located at the facility at time interval t and 0 otherwise | |
| Variable is equal to 1 if vehicle K is located at the distribution center at time interval t and 0 otherwise | |
| Variable is equal to 1 if vehicle M is located at the supplier at time interval t and 0 otherwise | |
| Vehicle capacity during circulation between suppliers | |
| Vehicle capacity during circulation between distribution centers |
| Mathematical Notation | Explanation |
|---|---|
| LS | Location of secondary facility |
| LLS | Distance between main facility and secondary facility |
| LSDC | Distance between secondary facility and distribution center |
| LSSS | Distance between secondary facility and supplier |
| CLS | Cost of purchasing secondary facility |
| LSTS | Distance between secondary facility and transportation hub |
| New Cost of vehicle M rental/leasing | |
| New Cost of vehicle K rental/leasing | |
| Penalty for abandoning vehicle K rental/leasing | |
| Penalty for abandoning vehicle M rental/leasing | |
| Variable is equal to 1 if vehicle M or K is located at the secondary facility at time interval t and 0 otherwise. |
| Constant Variables | Constant Values |
|---|---|
| Number of parents | 5 |
| Mutation probability | 0.05 |
| Number of elites (hybrid) | 1 |
| Trial Number | Combination of Variables |
|---|---|
| Trial 1 | One-point–90–10% |
| Trial 2 | Two-point–90–10% |
| Trial 3 | Uniform–90–10% |
| Trial 4 | One-point–80–20% |
| Trial 5 | Two-point–80–20% |
| Trial 6 | Uniform–80–20% |
| Trial 7 | One-point–70–30% |
| Trial 8 | Two-point–70–30% |
| Trial 9 | Uniform–70–30% |
| Population Size/Number of Generations | |
|---|---|
| 300 at 300% | 600 at 125% |
| 9663.771 $ | 9719.086 $ |
| 600 at 300% | 1000 at 125% |
| 9412.102 $ | 9583.444 $ |
| 1000 at 300% | 3000 at 125% |
| 9381.037 $ | 9495.474 $ |
| Population Size/Number of Generations | |
|---|---|
| 300 at 300% | 600 at 125% |
| 9530.91 $ | 9768.953 $ |
| 600 at 300% | 1000 at 125% |
| 9405.056 $ | 9602.299 $ |
| 1000 at 300% | 3000 at 125% |
| 9340.663 $ | 9281.44 $ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nafea, M.; Shihata, L.A.; Mashaly, M. Integrating Social Sustainability into Supply Chain Design: Optimization of a Capacitated Two-Echelon Location-Routing Problem. Technologies 2025, 13, 149. https://doi.org/10.3390/technologies13040149
Nafea M, Shihata LA, Mashaly M. Integrating Social Sustainability into Supply Chain Design: Optimization of a Capacitated Two-Echelon Location-Routing Problem. Technologies. 2025; 13(4):149. https://doi.org/10.3390/technologies13040149
Chicago/Turabian StyleNafea, Mohamed, Lamia A. Shihata, and Maggie Mashaly. 2025. "Integrating Social Sustainability into Supply Chain Design: Optimization of a Capacitated Two-Echelon Location-Routing Problem" Technologies 13, no. 4: 149. https://doi.org/10.3390/technologies13040149
APA StyleNafea, M., Shihata, L. A., & Mashaly, M. (2025). Integrating Social Sustainability into Supply Chain Design: Optimization of a Capacitated Two-Echelon Location-Routing Problem. Technologies, 13(4), 149. https://doi.org/10.3390/technologies13040149







