Autonomous Real-Time Mass Center Location and Inertia Identification for Grappling Space Robotics
Abstract
1. Introduction
1.1. Review of the Literature
1.2. State-of-the-Art Benchmarks
- In 2022, Ref. [1] provided an overview survey of the algorithms and test and validation strategies for grappling the robotic free-flying spacecraft, de-emphasizing spacecraft docking and berthing. Core technologies identified includes orientation control (including distributed control systems) and the ability to adapt to unexpected loads. Those core technologies motivate the developments presented in this present study.
- Nonlinear dynamics are highlighted as key, and, therefore, nonlinear approaches are adopted.
- Despite insistence on nonlinear dynamics, linear time-invariant PID control laws are emphasized to be “straightforward to design and relatively easy to tune and provide performance sufficient to meet most operating requirements”.
- Since the dynamics are Hamiltonian, nonlinear adaptive control is also highlighted and adopted in this present study.
- Trajectory planning is highlighted as well, and autonomous trajectory generation is adopted to permit nonlinear control proposals.
- Air-bearing tables are highlighted to aid validation using laboratory experiments, and one such free-floating, highly flexible robotic gripper arm is described.
1.3. Novelties Presented
- Time-varying estimates of mass locations are found with classical adaptive methods compared to optimal learning leveraging nonlinear, projection regression-based methods. Estimates are supported in part by the novel use of nonlinear enhanced Luenberger observers.
- Time-varying estimates of mass locations are used to find time-varying estimates of the location of the system center of mass. Estimates are supported in-part by the novel use of nonlinear enhanced Luenberger observers applying the fundamental relationships between products of inertia and mass center location.
- The requirement to diagonalize the matrix of mass moments of inertia is eliminated.
- The requirement to linearize the governing differential equations is eliminated.
- The requirement to simplify governing equations (e.g., small angle assumption, etc.) is eliminated.
- Analysis precedes modeling and simulation to verify the design, and then, spaceflight experiments are proposed for the sequel to validate the simulation results.
1.4. Conveniences of Presentation
2. Materials and Methods
| 1 | Use the physics-based governing dynamics to embody the control (Section 2.1). |
| a | Do not diagonalize the inertia matrix. |
| b | Do not linearize the governing equations of motion. |
| c | Do not use small-angle assumption to simplify the system equations. |
| d | Establish classical feedback control as a comparative benchmark. |
| 2 | Use nonlinear, enhanced Luenberger observers (Section 2.4, Section 2.5 and Section 2.6) to estimate all motion states and control. |
| 3 | Use projection-based nonlinear regression learning to learn the fully populated mass moments of inertia (masses and mass locations), including principal moments and off-diagonal products of inertia (Section 2.3). |
| 4 | Use off-diagonal products of inertia to estimate the location of the center of mass (Section 2.10). |
2.1. Physics-Based Dynamics
| Variable/Acronym | Definition | Variable/Acronym | Definition |
|---|---|---|---|
| Inertia matrix or tensor | |||
| Angular acceleration | inertia product | ||
| Angular velocity | inertia product | ||
| direction | |||
| direction | inertia product | ||
| direction | |||
| Regression matrix of knowns | Unknown, predicted variables |
A common engineering practice is to simply assume the eigenvector basis is equivalent to the body frame basis vectors, where the engineer is comfortable accepting the accompanying error of such an assumption.
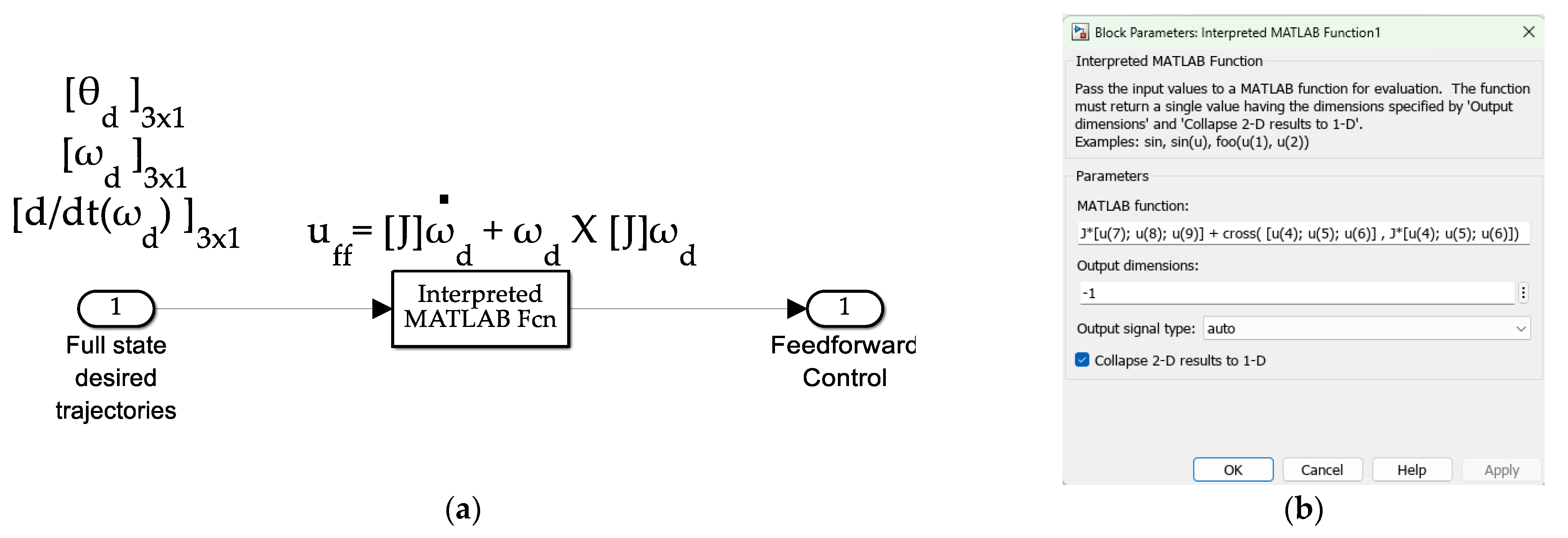
2.2. Feedforward Control Using Physics-Based Dynamic Embodiment
| Variable/Acronym | Definition | Variable/Acronym | Definition |
|---|---|---|---|
| Regression matrix of sensor data | Regression matrix of desired states | ||
| Unknown, predicted variables | Estimated variables | ||
| Total control signal | Feedforward control signal | ||
| Estimated inertia product | |||
| Estimated inertia product | |||
| Estimated inertia product |
2.3. Regression-Based Projection for Learning
2.4. Luenberger Observers
2.5. Enhanced Luenberger Observers
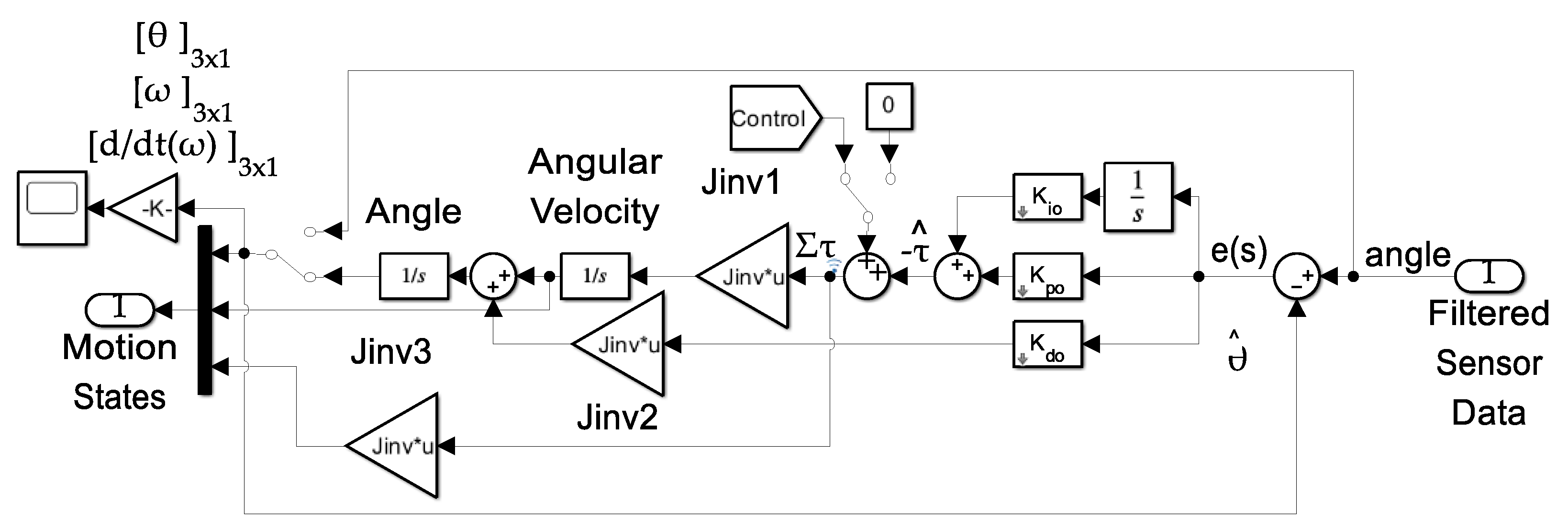
2.6. Nonlinear Enhanced Luenberger Observers
2.7. Classical Feedback Adaption
2.8. Two-Norm Optimal Nonlinear, Projection Regression-Based Learning
2.9. Combined Control
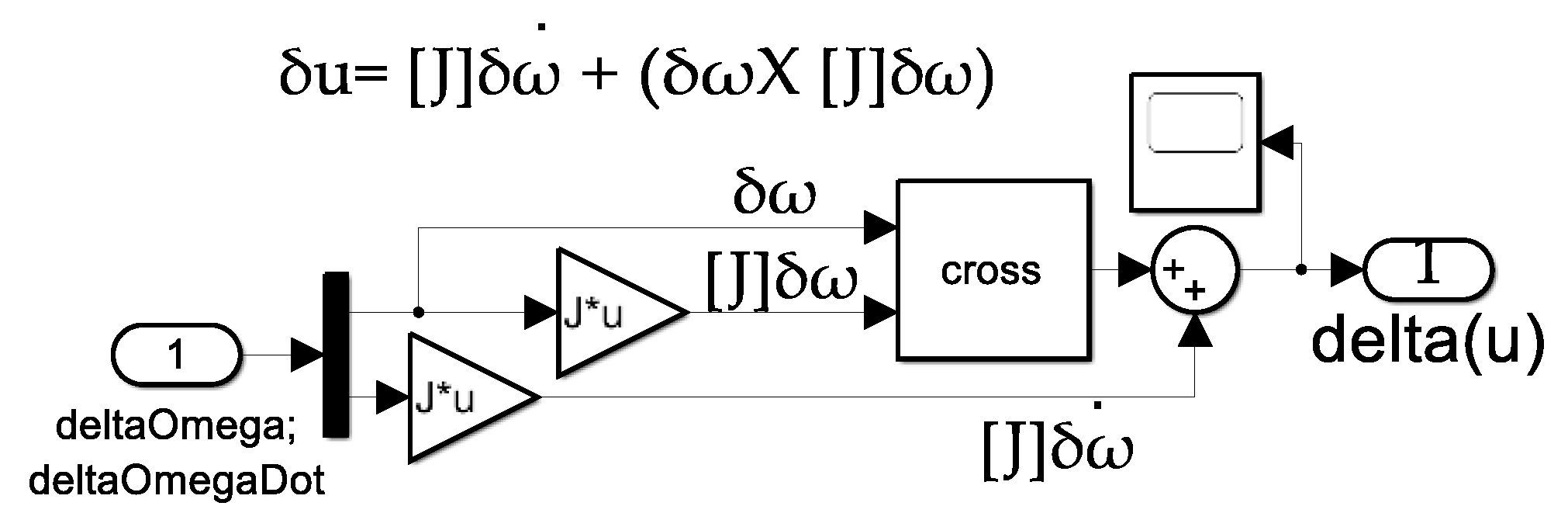
2.10. Estimating Location of the Center of Mass
| Variable/ Acronym | Definition | Variable/Acronym | Definition |
|---|---|---|---|
| Mass index | Defined in Equation (4) | ||
| Moment of inertia index | Defined in Equation (4) | ||
| Moments of inertia | Adaption gain | ||
| Translational displacements | Positive constant reference trajectory gain | ||
| Rotational displacements | Dynamic system matrix | ||
| Control torque | Combined error measure | ||
| Feedforward control | Differential angular velocity | ||
| Control difference | Differential angular acceleration | ||
| Feedback control | Differential time |
| Variable/Acronym | Definition | Variable/ Acronym | Definition |
|---|---|---|---|
| Robot arm base parallel axis | |||
| Inertia moment about mass center | Body center parallel axis | ||
| Total system mass | Radius from parallel axis (not mass center) | ||
| Distance from O to the mass center | Radius vector to the mass center | ||
| Differential mass element | |||
| Center of mass coordinates | |||
2.11. Persistent Excitation of Estimation
| Variable/Acronym | Definition | Variable/Acronym | Definition |
|---|---|---|---|
| Covariance dimension | Control | ||
| Dimension of the control | Indexed time | ||
| System equation | Transposed system equation |
| Input Signal | Order of Persistent Excitation |
|---|---|
| 1 | |
| 2 | |
| commands | n |
2.12. Generic Robotics On-Orbit Trainer (GROOT) and Long-Duration Propulsive EELV Secondary Payload Adapter (LDPE ESPA)
2.13. Implementation Procedures
| Algorithm 1 Pseudocode 1. |
| Input: Desired end state: final velocity and final acceleration |
| Output: Inertia matrix components and three-dimensional coordinates of the center of gravity |
| 1 begin |
| 2 Path planning using sinusoidal trajectories: |
| 3 DesiredVelocity = DesiredFinalVelocity * SineEquation |
| 4 DesiredAcceleration = DesiredFinalAcceleration * CosineEquation |
| 5 Assemble feedforward control |
| 6 Parameterize Euler’s moment equations into standard regression form |
| 7 Control_1 = DesiredStateMatrix * UnknownInertiaRegressionVector |
| 8 OptionalFeedback = DesiredStateMatrixInverse * EstimatedTorque |
| 9 EstimatedInertia = DesiredStateMatrixInverse * AppliedTorque |
| 10 MassCenterCoordinates = Function(InertiaCrossProducts) |
| 11 end |
| 1 Corresponding to Section 2. |
3. Results
3.1. Section Description
3.2. Incremental Development and Presentation of Results
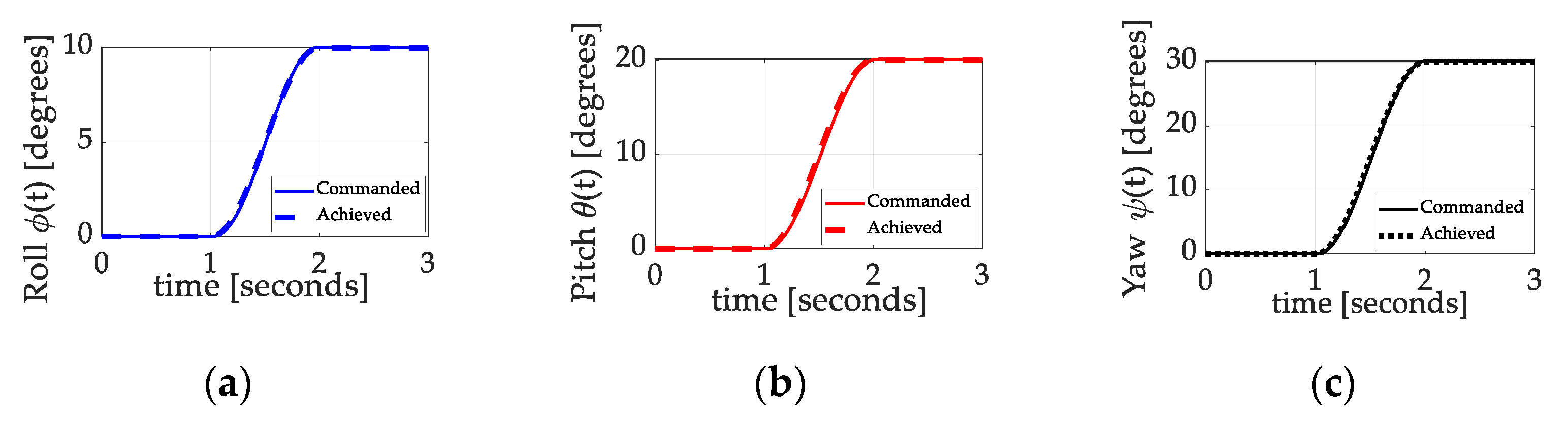
3.2.1. Unperturbed System
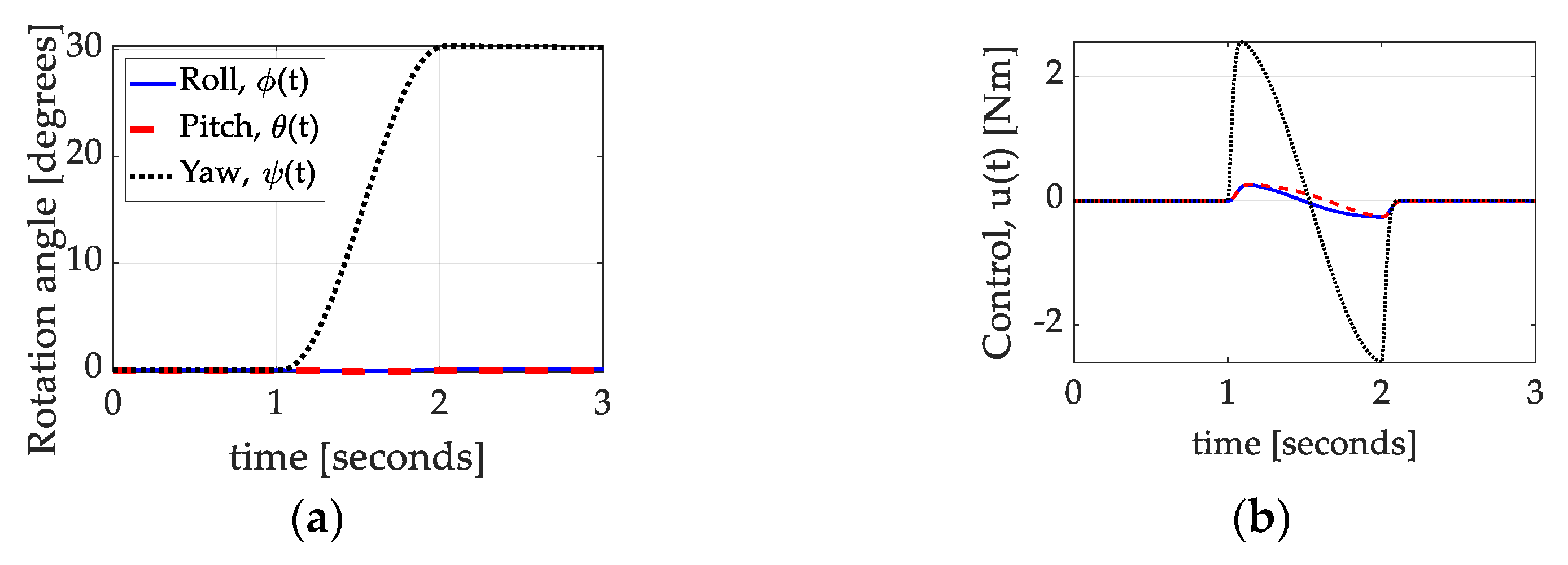

3.2.2. Comparative Benchmark
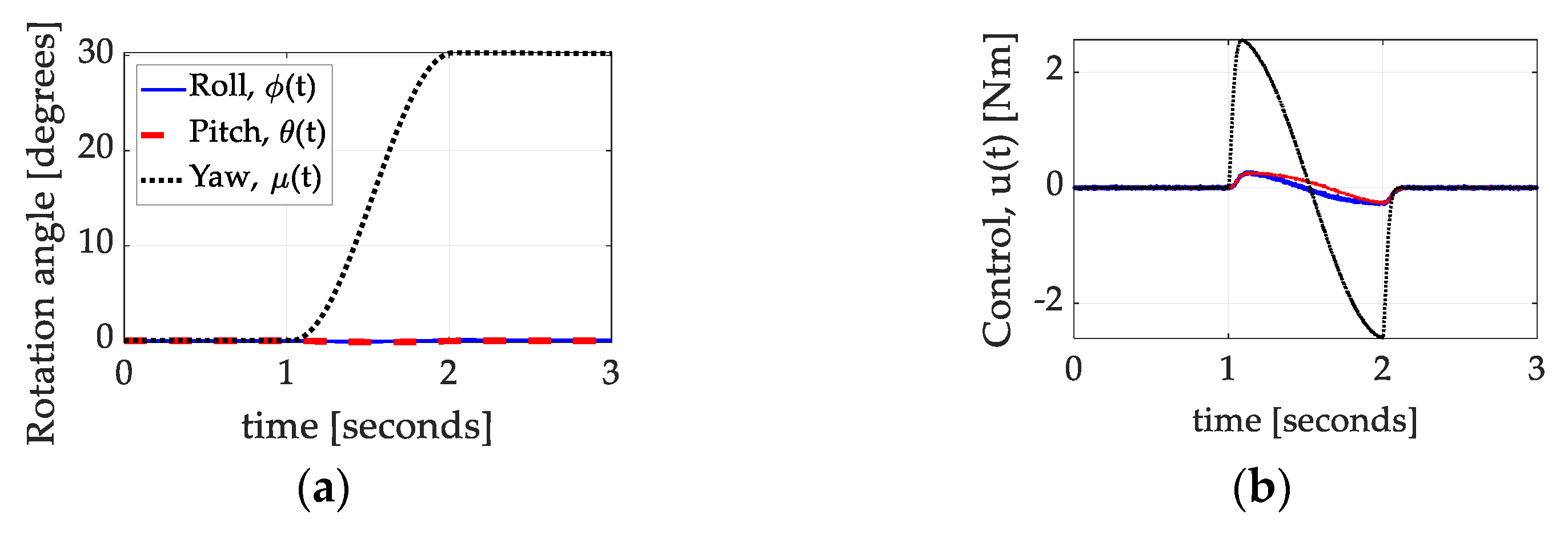
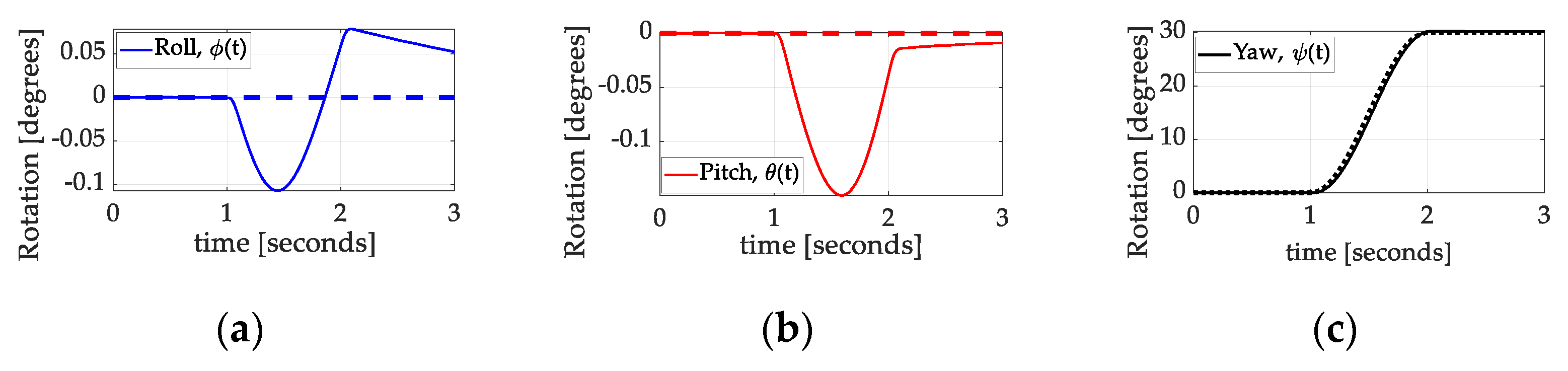
3.2.3. Dynamic Nonlinear Feedforward with PID Feedback and Inertia Adaption
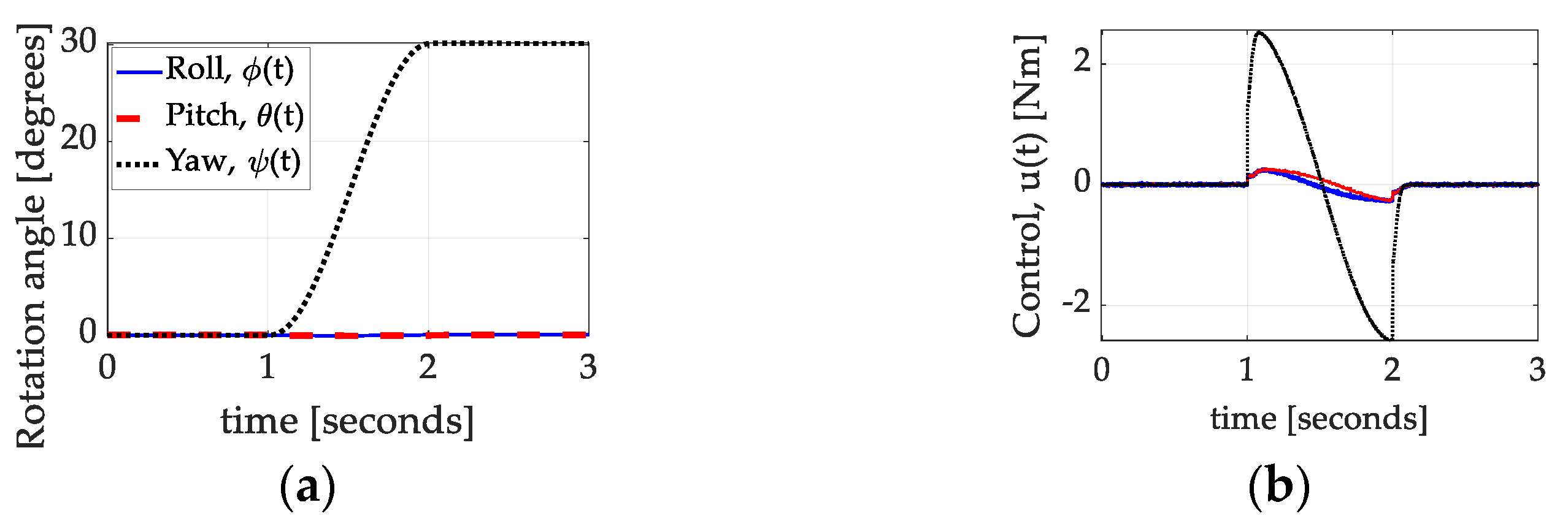

| Roll [Degrees] | Pitch [Degrees] | Yaw [Degrees] | |
|---|---|---|---|
| Mean | |||
| Standard deviation 1 |
3.2.4. Dynamic Nonlinear Feedforward with PID Feedback and Nonlinear Projection-Based Regression Learning
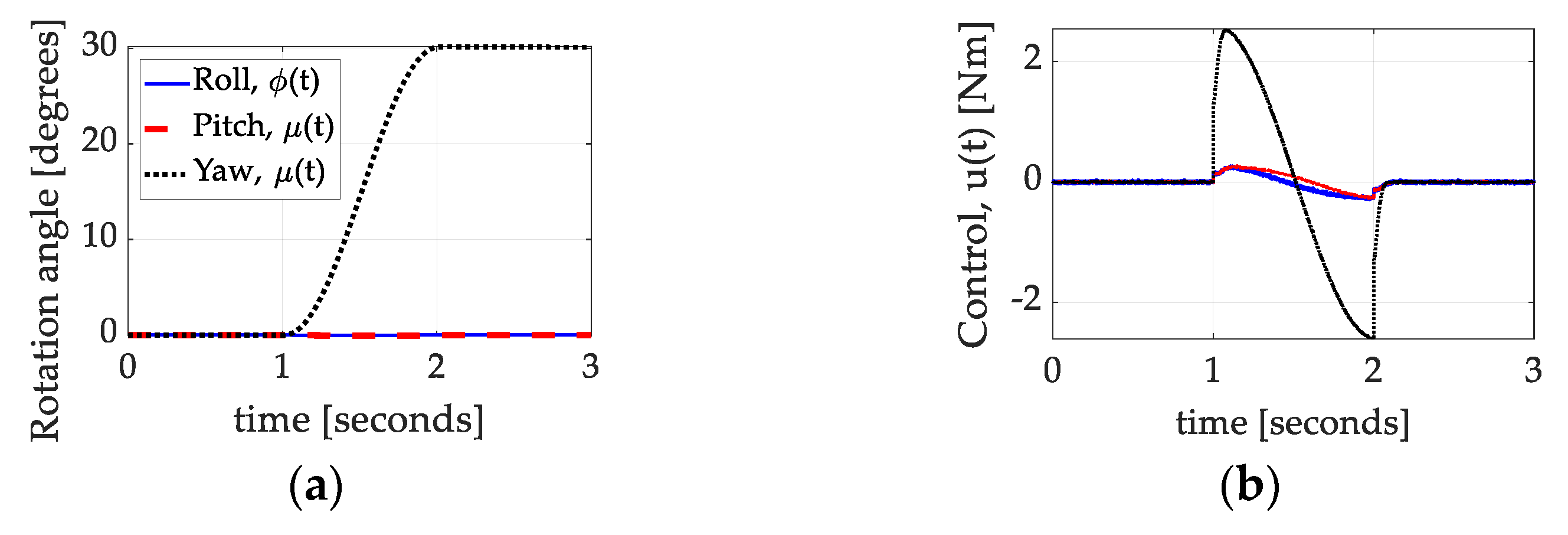

| 0.0075635 | Roll [Degrees] | Pitch [Degrees] | Yaw [Degrees] |
|---|---|---|---|
| Mean | |||
| Standard deviation 1 |
3.2.5. Estimator Performance Comparison
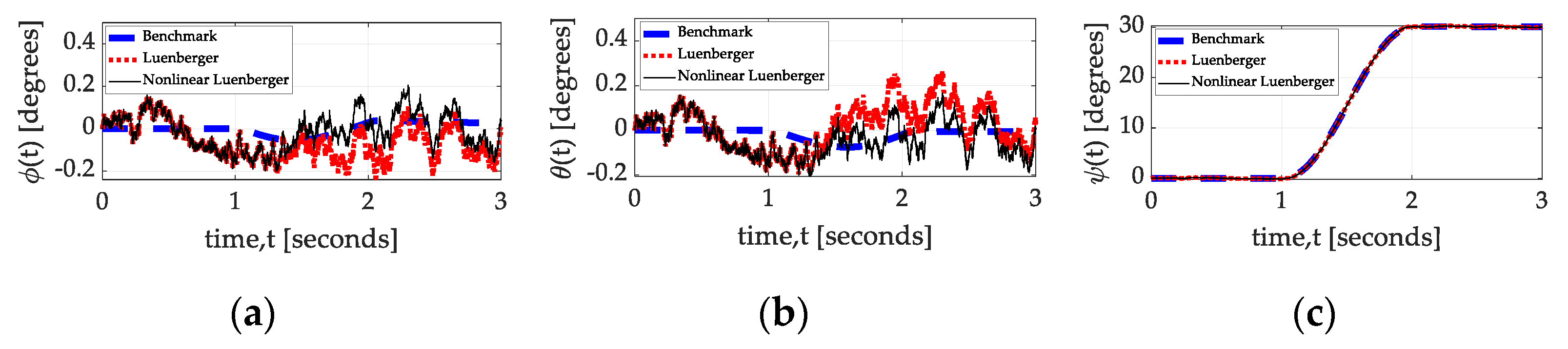
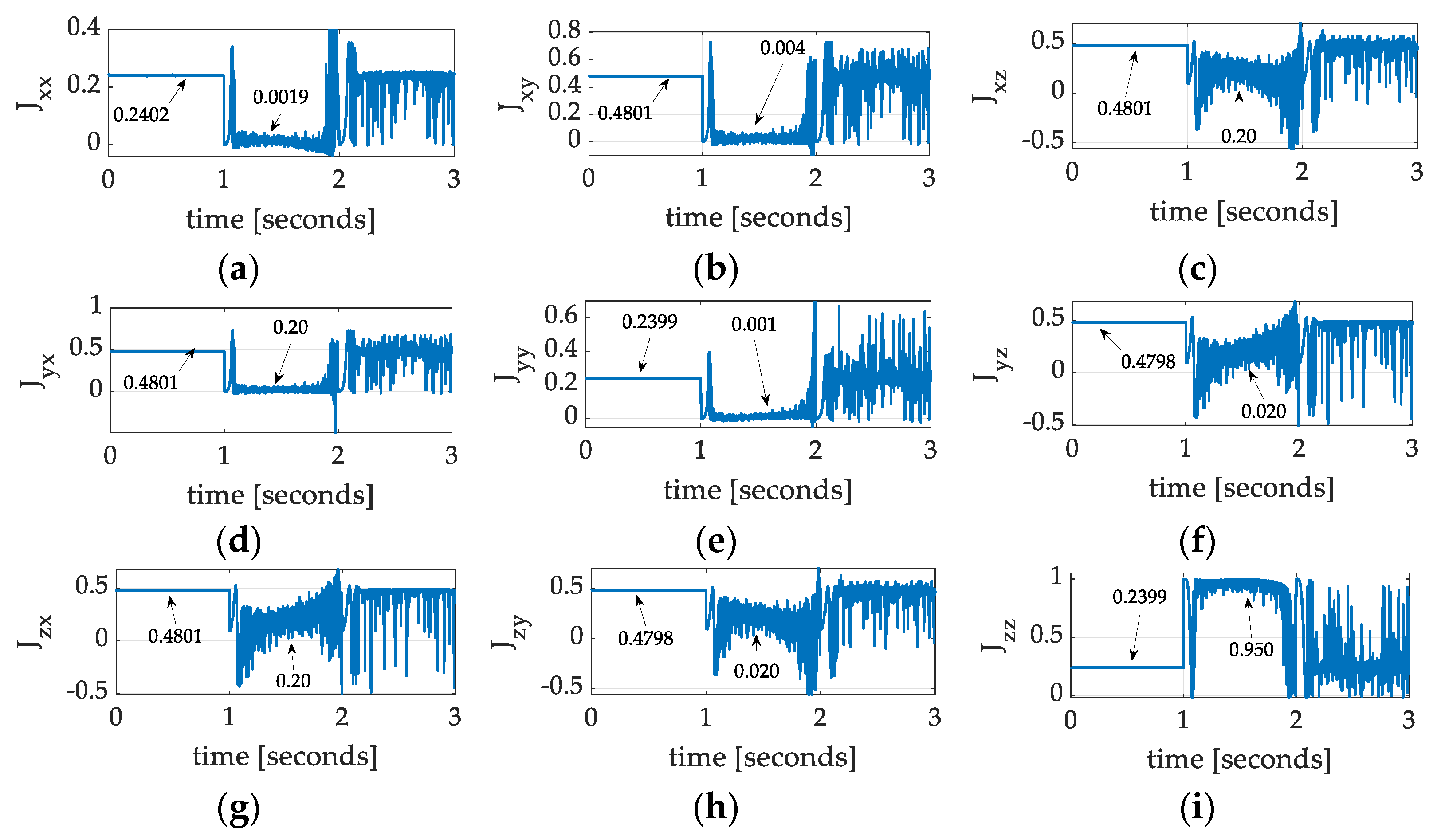
3.3. Identification of Mass Moments and Products
3.3.1. Identification of Mass Moments and Products by Nonlinear Adaption
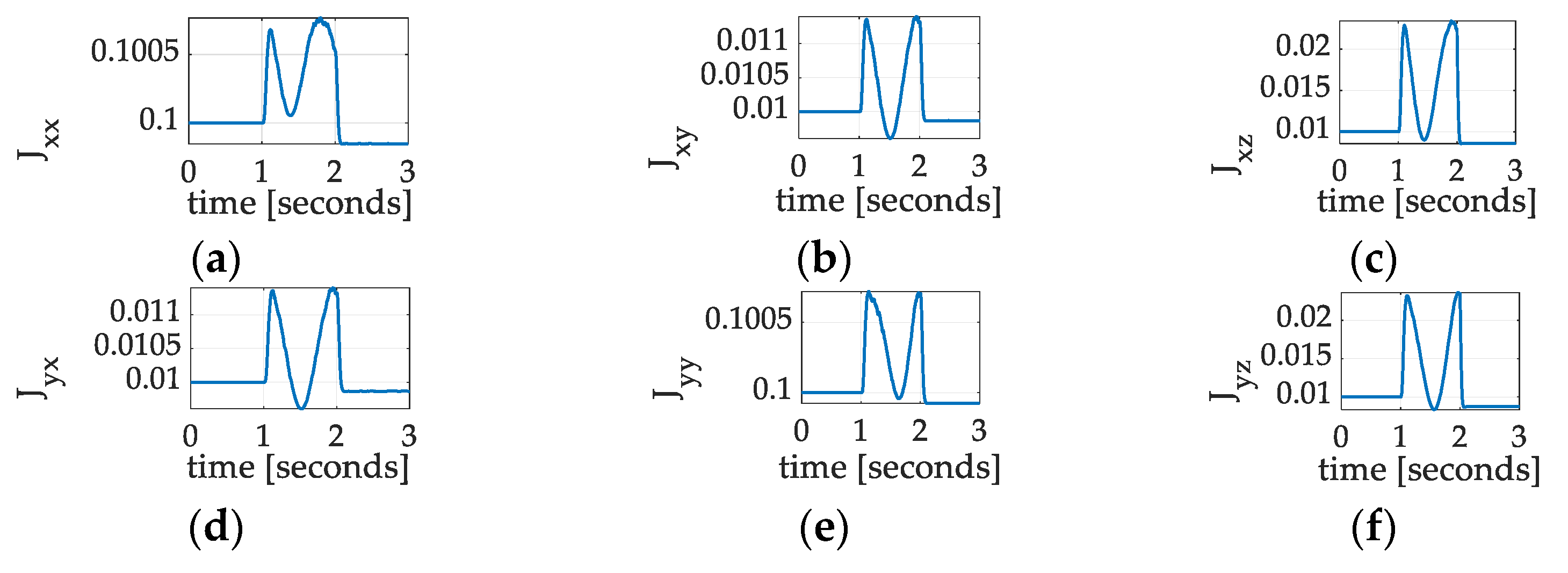
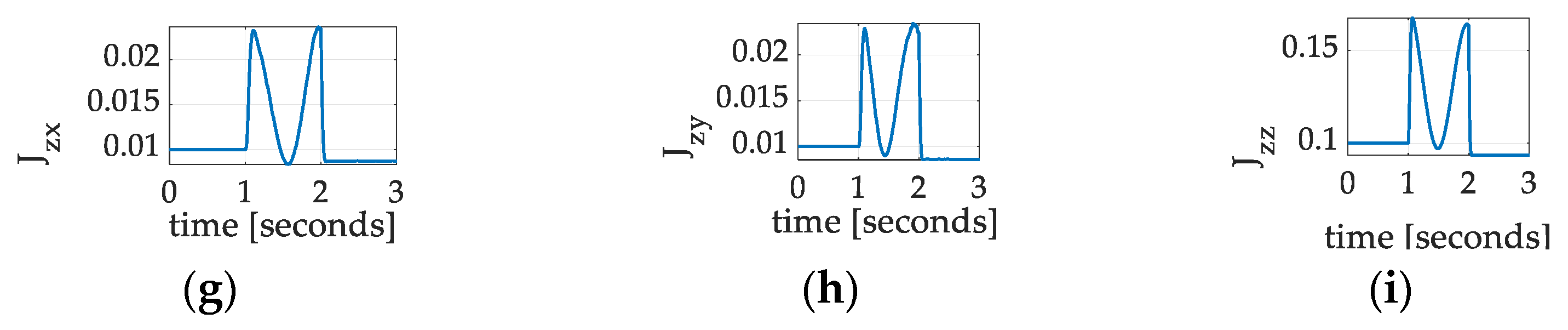
3.3.2. Identification of Mass Moments and Products by Nonlinear Projection-Based Regression Learning
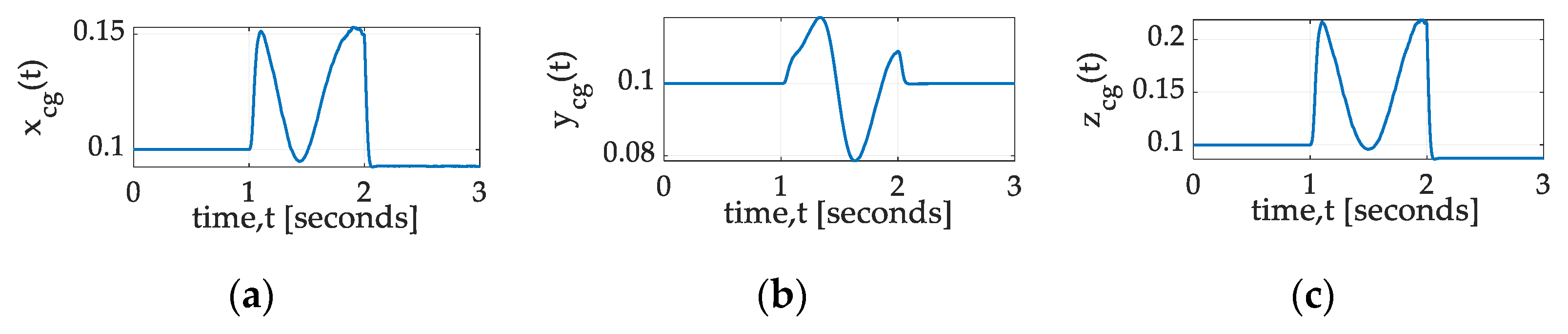
3.4. Location of Mass Center
3.4.1. Identification of Mass Center Coordinates by Nonlinear Adaption
3.4.2. Identification of Mass Center Coordinates by Nonlinear Projection-Based Regression Learning
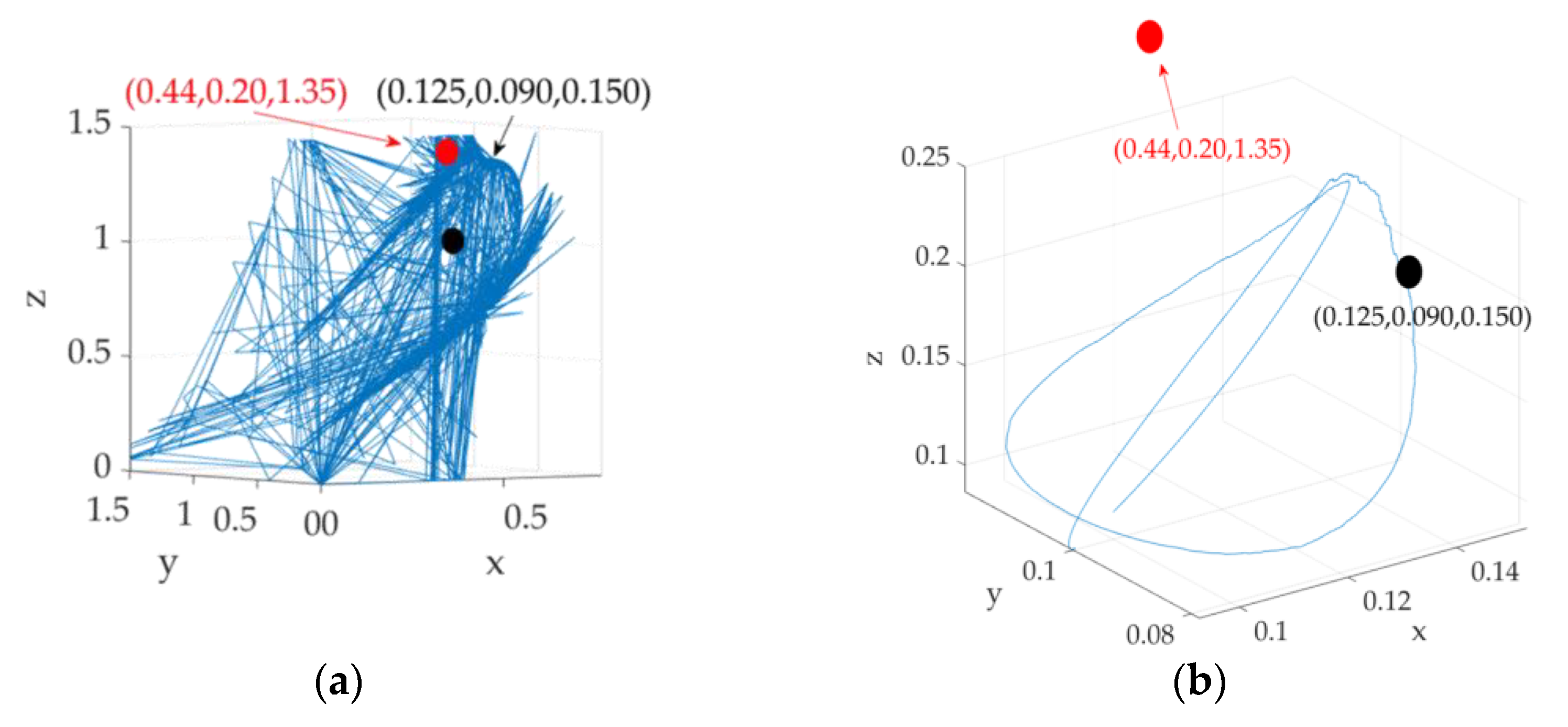
3.4.3. Location of Center of Mass: Three-Dimensional Comparison
3.5. Compound Maneuvers
3.6. Summary of Results
4. Discussion
| 1 | Use the physics-based governing dynamics to embody the control (Section 2.1). |
| 2 | To maximize persistent excitation, autonomous sinusoidal trajectories are recommended with white noise added (Section 2.9). |
| 3 | Simultaneous use of both Luenberger styles is recommended to leverage their relative strengths in the maneuver axis and non-maneuver axis (Section 3.2). |
| 4 | Compared to using nonlinear adaption, the use of nonlinear projection-based regression learning was more sensitive to identical cases of persistent excitation and accordingly produced a better location of mass center (Section 3.4.2). |
| 5 | Compound maneuvers eliminated learning convergence experienced with single-axis maneuvers. Single-axis maneuvers should be sequenced sequentially amongst all three axes (Section 3.4.3). |
Future Research Directions
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
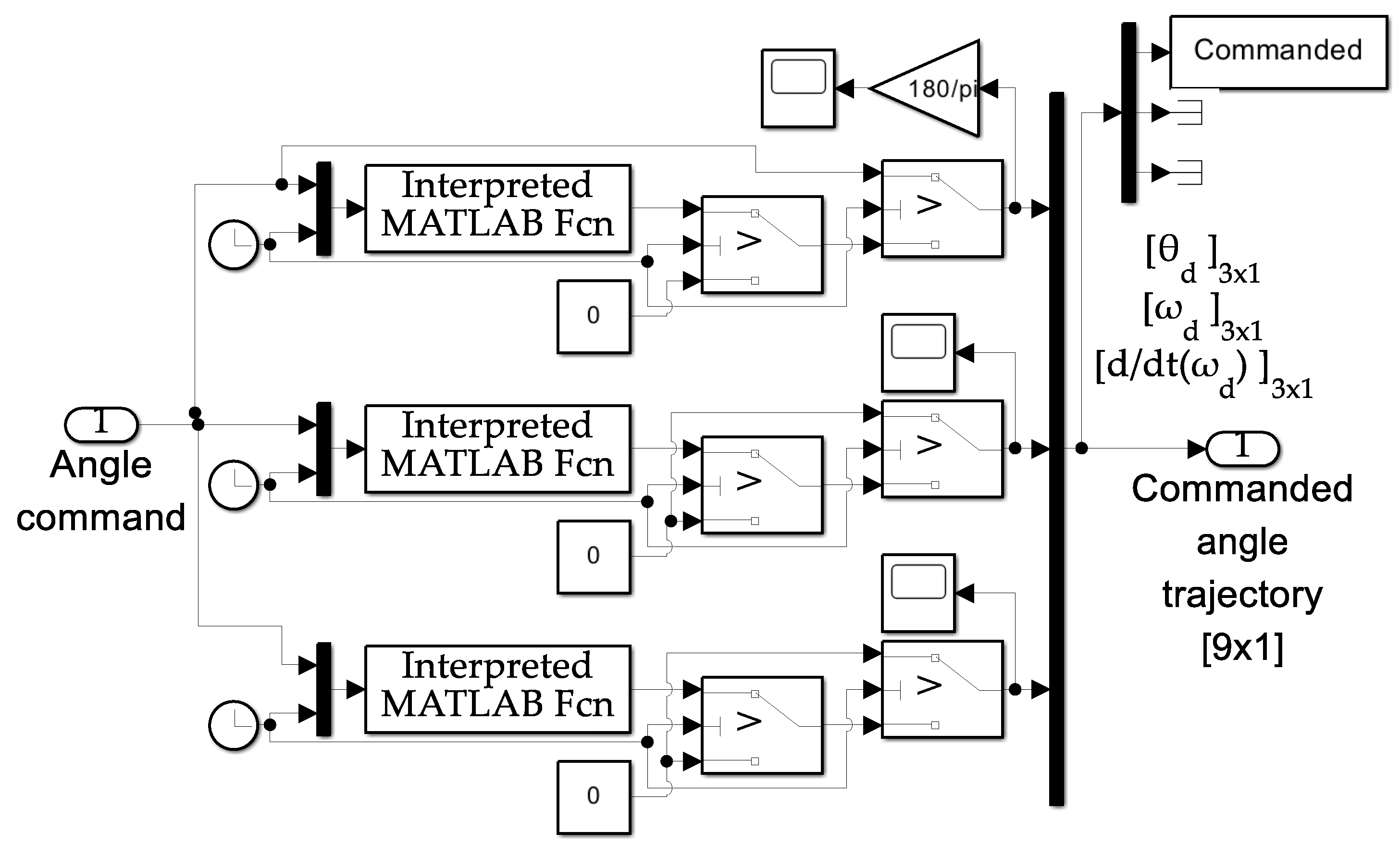
- Create a scheme of command. A sinusoidal scheme is depicted in Figure A1 and may be constructed by dragging and dropping the blocks depicted from the library to the simulation. The switching logic produces smooth sinusoids for angular displacement, velocity, and acceleration. The switch institutes to regulation at the final commanded value, smoothly exiting the sinusoidal curves, respectively. The syntax for the sinusoidal commands is displayed in Figure A2.
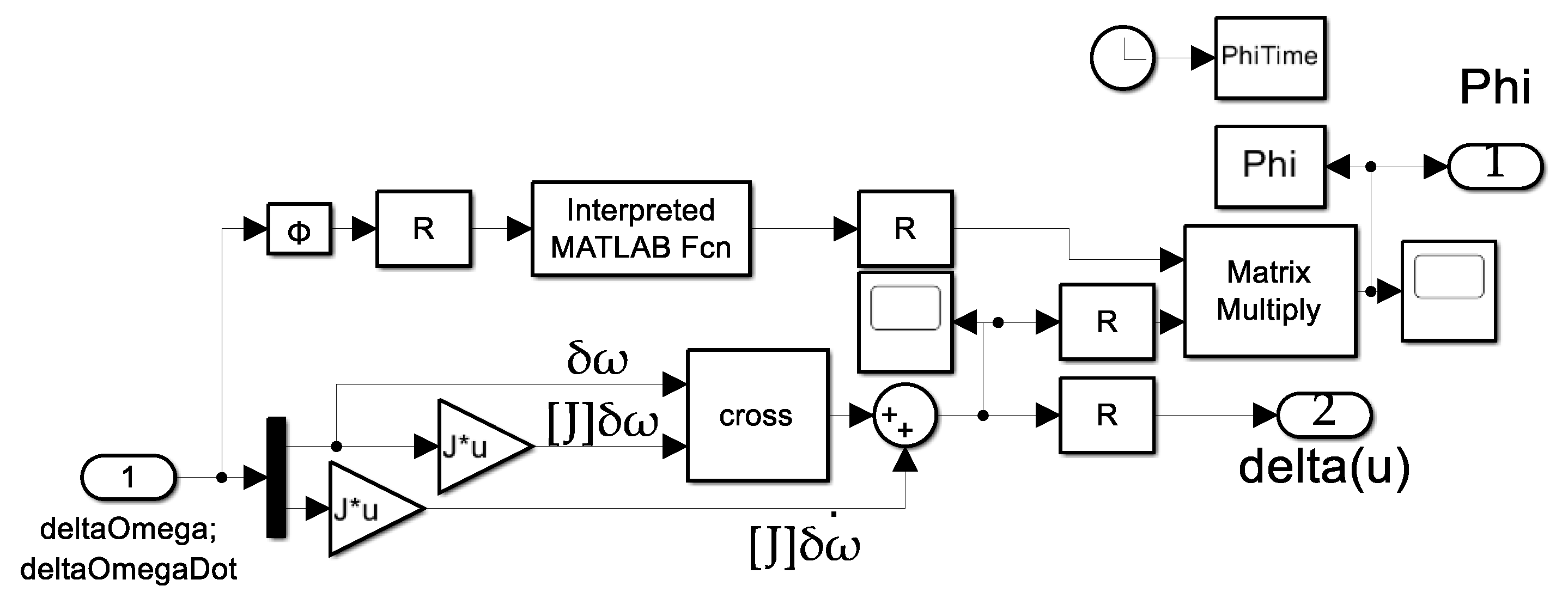
- The attitude controllers are displayed in Figure A3, including both feedforward and feedback controllers. The project-based learning algorithm is also included. Additionally, notice that there is a manual switch away from the input sinusoidal trajectories and optionally towards a simple step command. Lastly, notice that artificially faked inertia values and random perturbations are included as switchable options as well.
- 4.
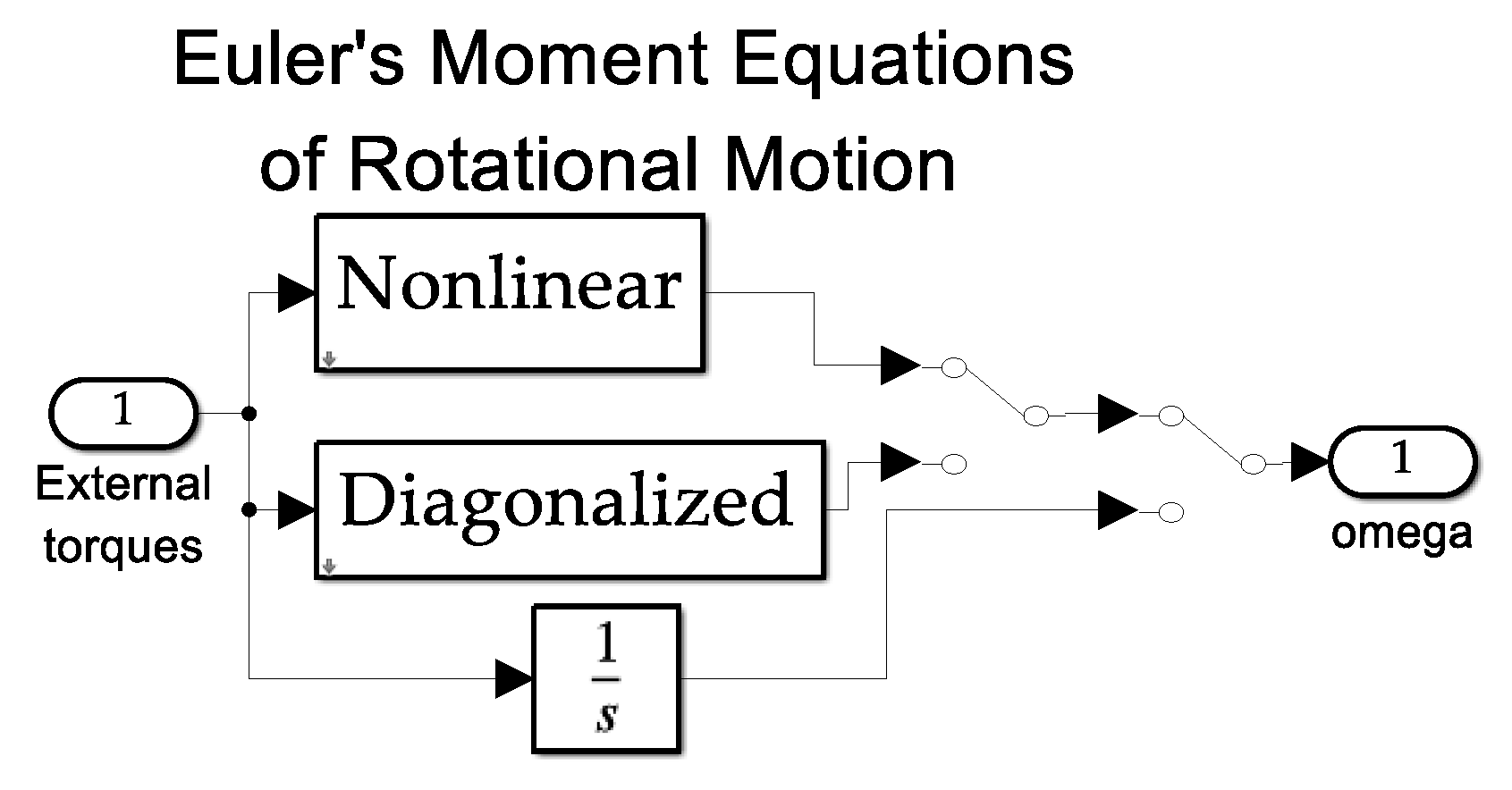
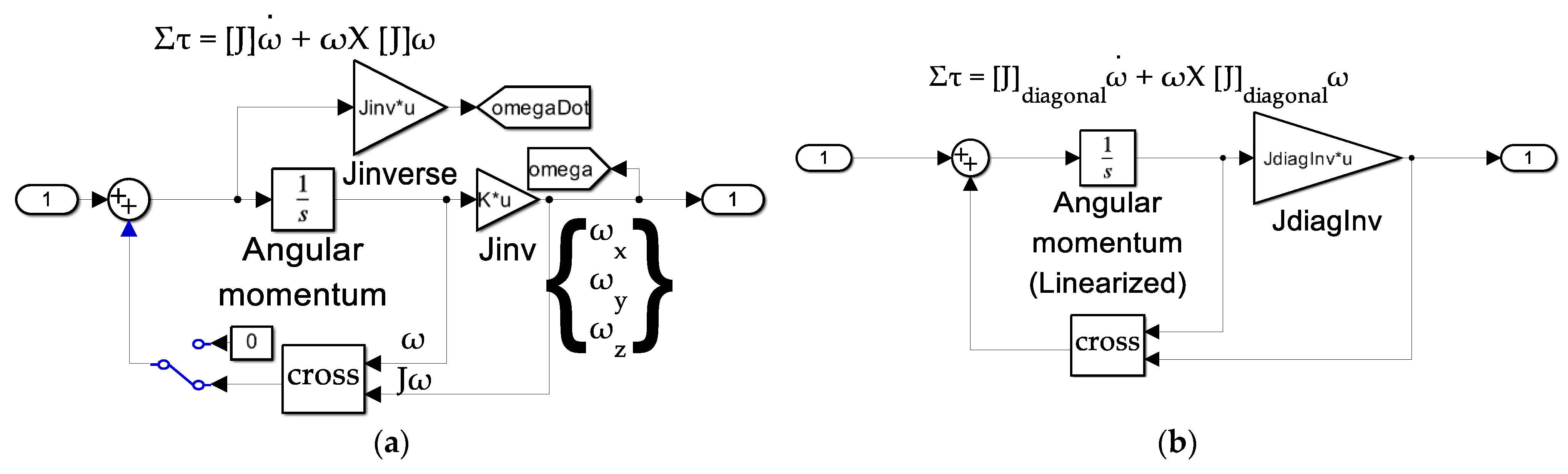
- The reaction wheel actuator is displayed in Figure A9, where the output torque from the actuator is routed to the governing equations of motion depicted in Figure A10 with expanded drilldown elaboration in Figure A11 and Figure A12. The governing equations of motion produce angular velocities relative to the inertial reference frame but need to be expressed in the coordinates of a body frame of interest.
- 5.
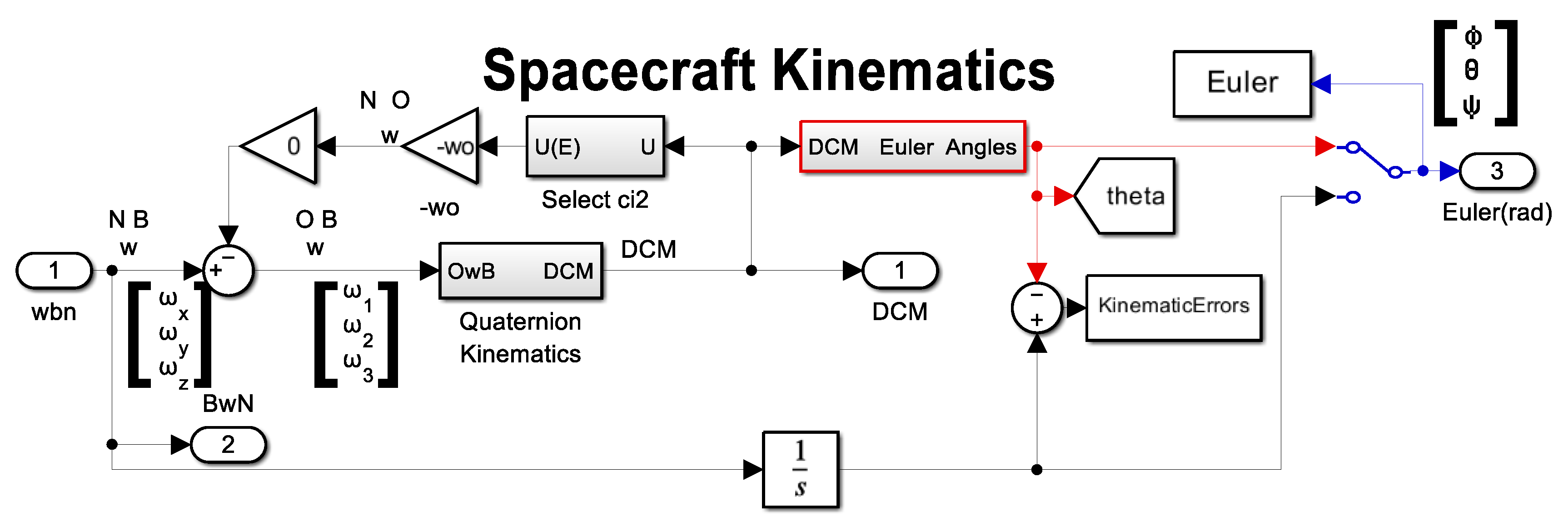
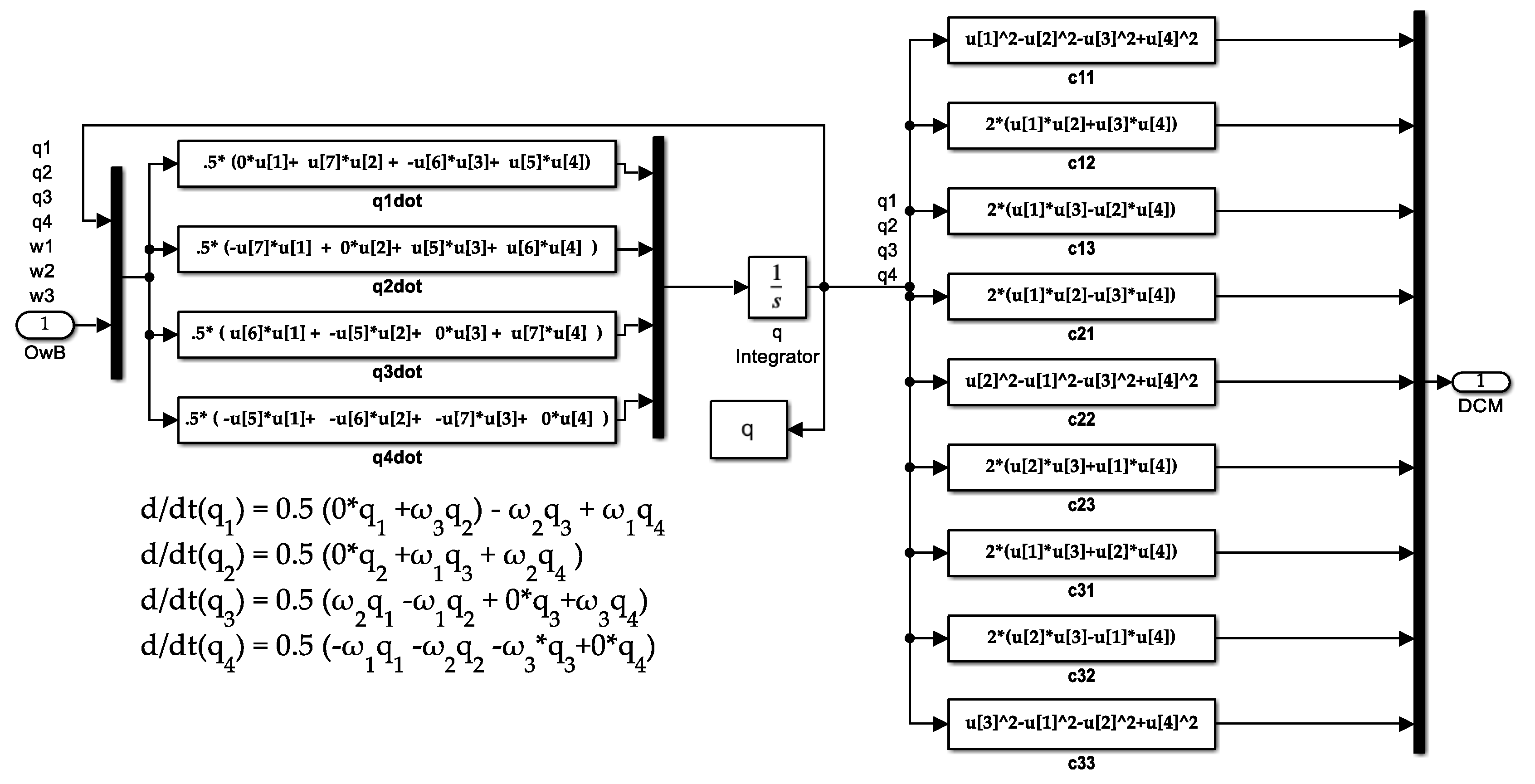
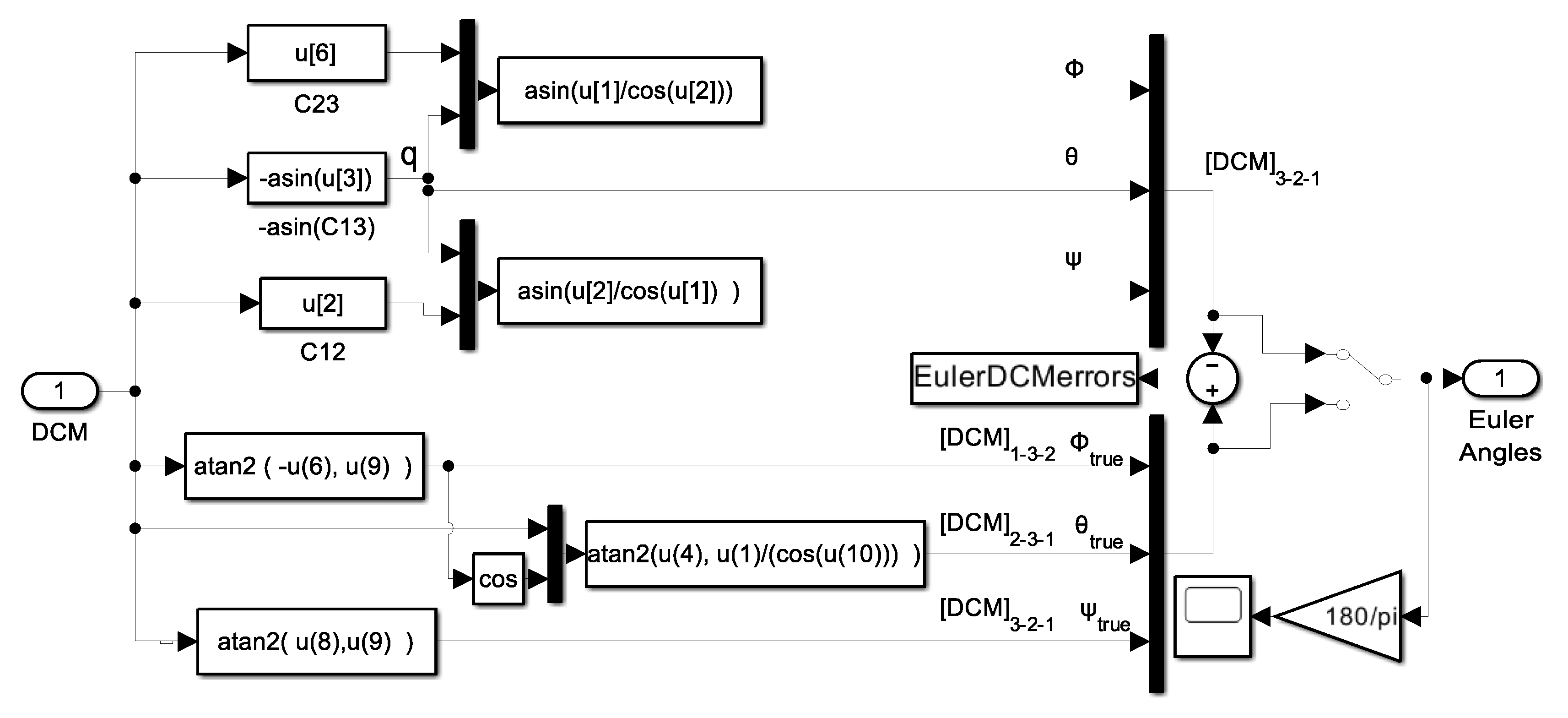
- Figure A12 displays the high-level kinematic topology. Drill downs for quaternions are displayed in Figure A13 where the quaternions are used to construct a nine-element direction cosine matrix transformation between inertial and body coordinates. The direction cosine matrix is used to extract Euler angles where a “321” rotation sequence is assumed, and that code is depicted in Figure A14.
- 6.
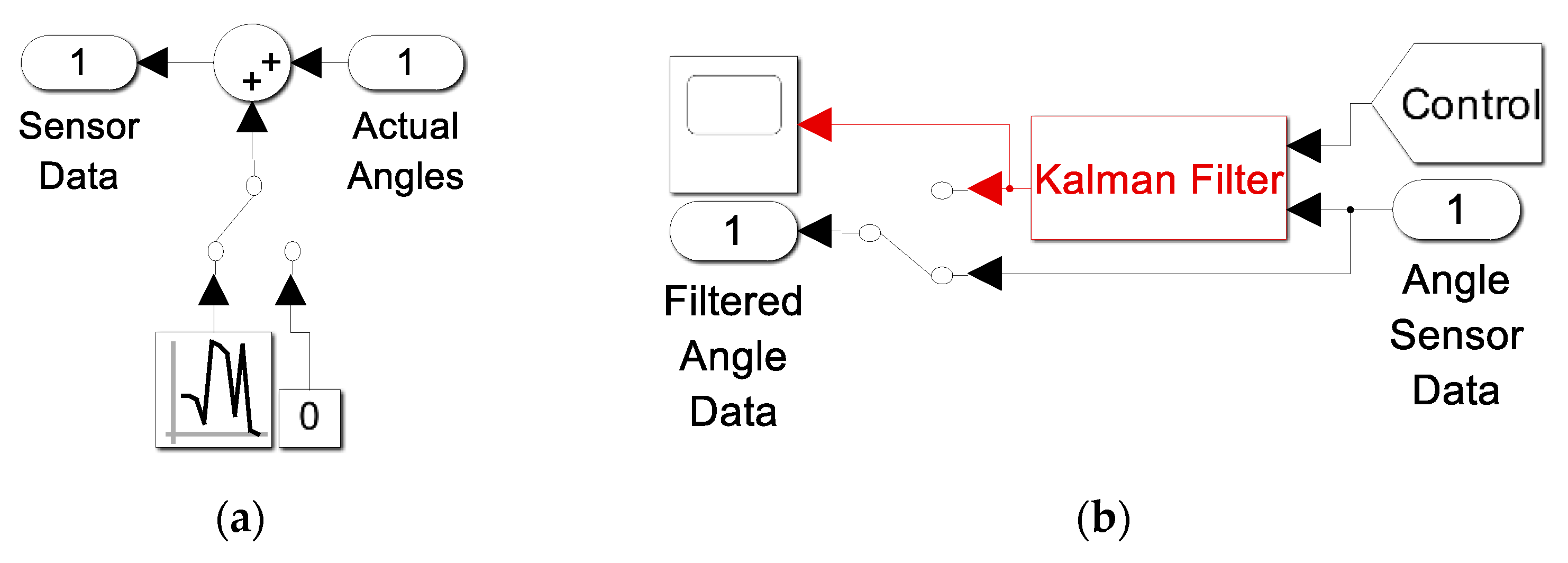
- While the true Euler angles cannot be known by the robot operators, sensors are simulated with additive noise and filters designed to counteract the noise in Figure A15.
- 7.
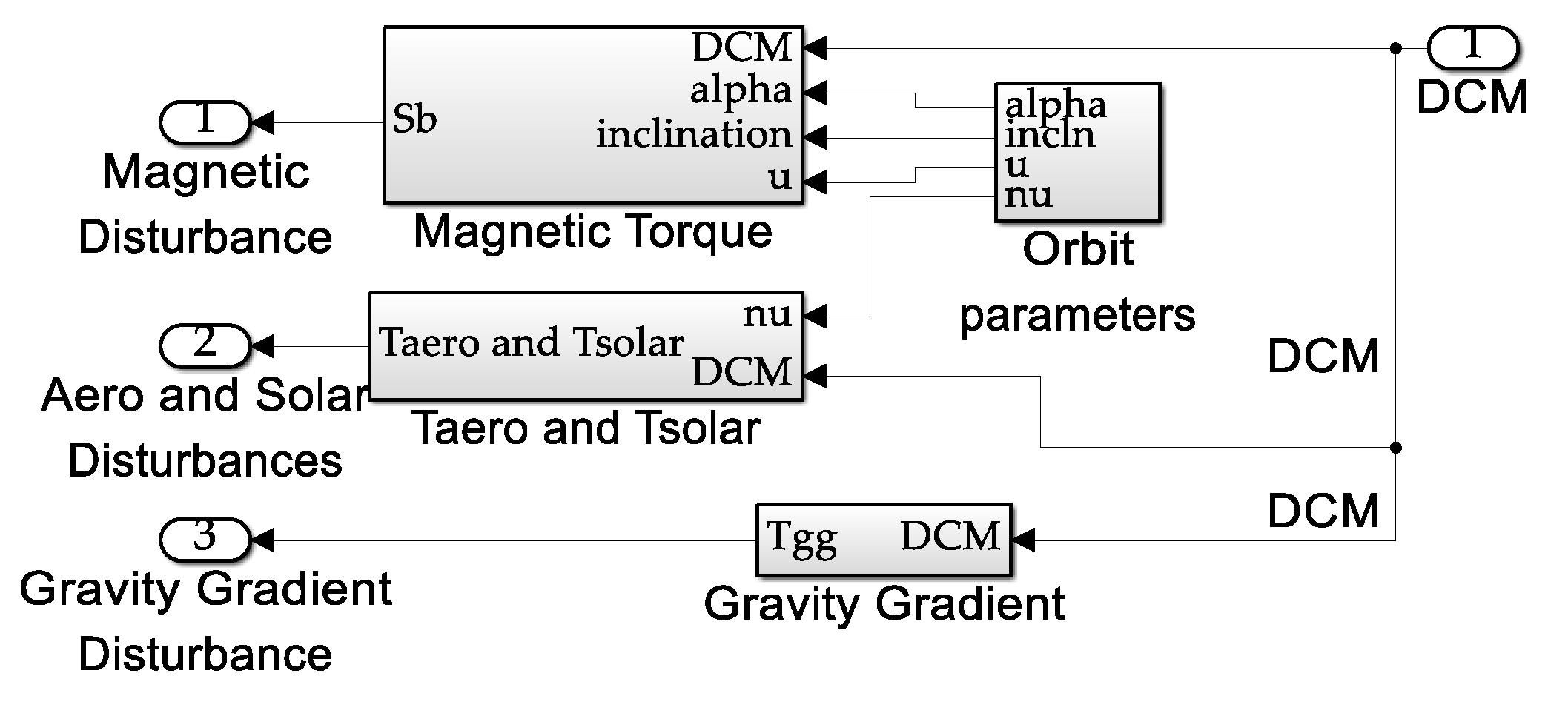
- The direction cosine matrix conveniently reveals the vector locations of the body axes and is used to calculate environmental disturbance torques.
- 8.
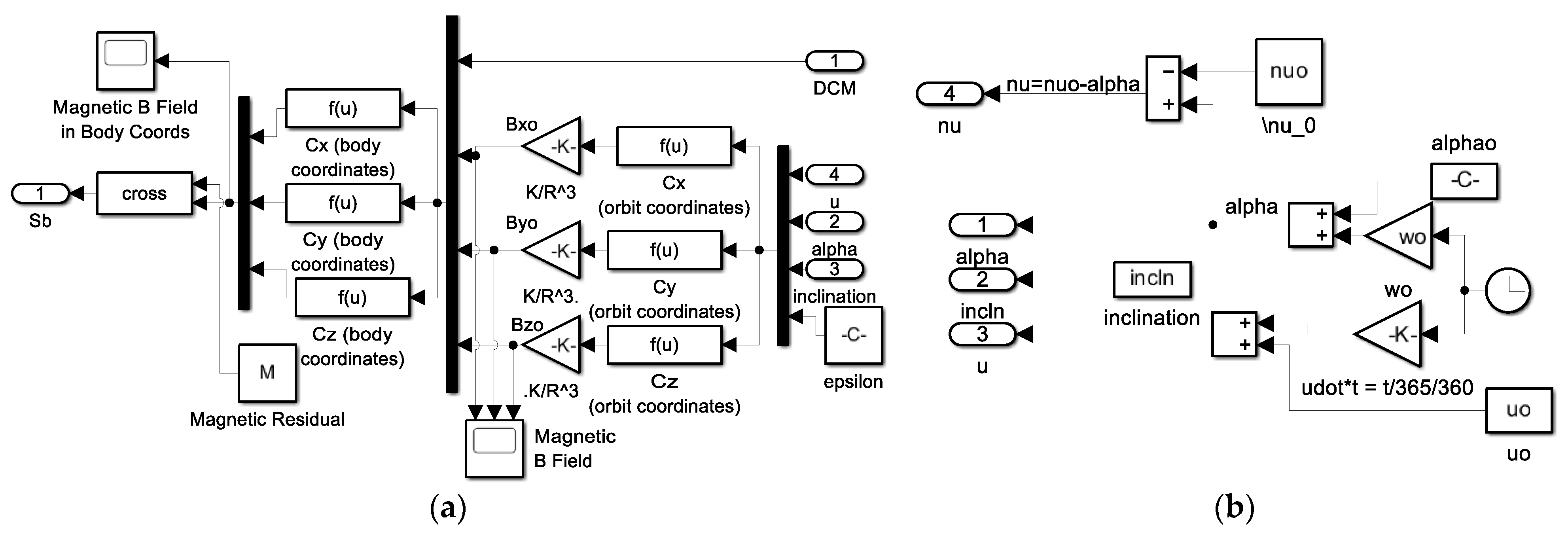
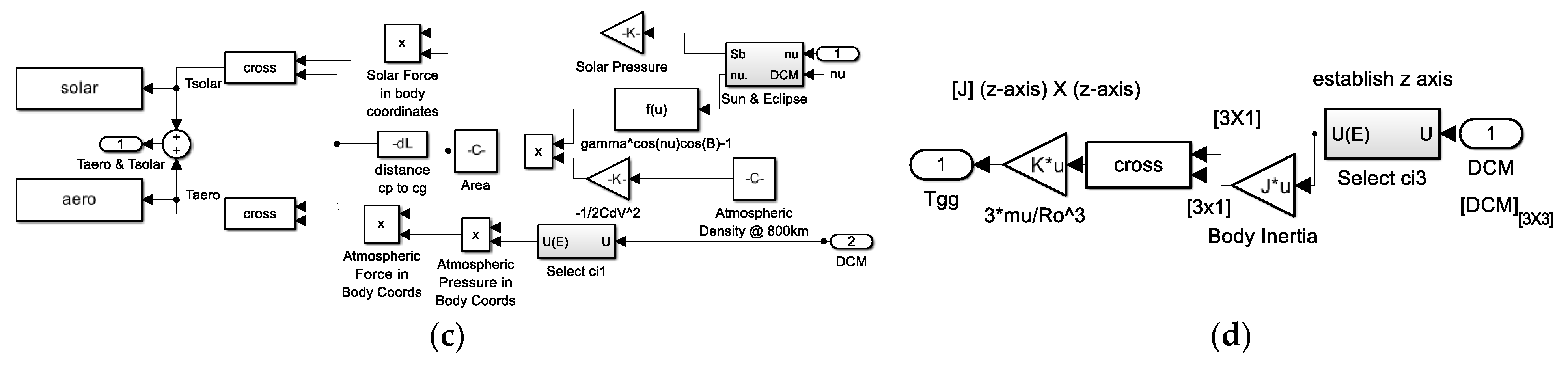
- The top-level topology of environmental disturbances is displayed in Figure A16 where each subsystem is individually displayed in Figure A17 for atmospheric, magnetic, solar radiation, and gravity gradient disturbances.

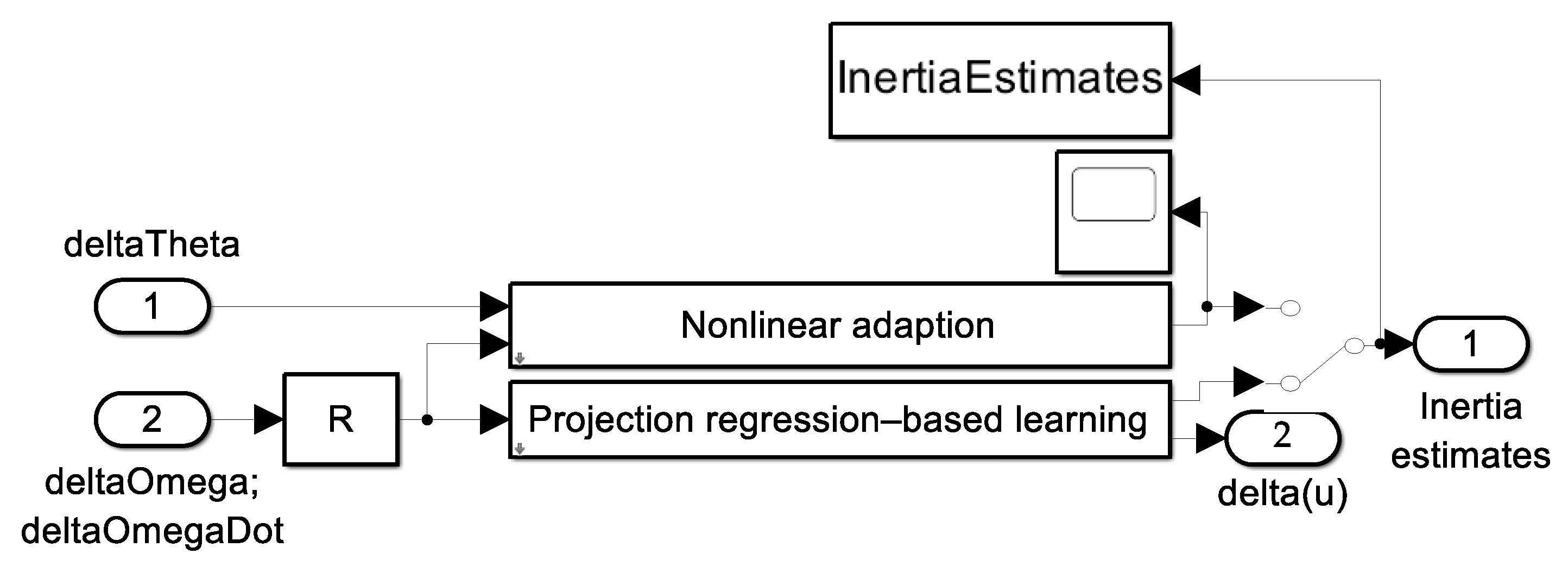


References
- Henshaw, C.; Glassner, S.; Naasz, B.; Roberts, B. Grappling Spacecraft. Annu. Rev. Control Robot. Auton. Syst. 2022, 5, 137–159. [Google Scholar]
- JPL Robotics. Available online: https://www-robotics.jpl.nasa.gov/what-we-do/research-tasks/prototype-grapple-arm-for-space-exploration-vehicle/ (accessed on 13 December 2024).
- PickNik Awarded NASA SBIR Phase 2 for In-Orbit Robot Autonomy. Available online: https://www.aerospacemanufacturinganddesign.com/news/picnik-robotics-awarded-nasa-sbir-phase-2-robot-autonomy/ (accessed on 18 November 2024).
- Robotic Refueling Mission 3 (RRM3). Available online: https://www.nasa.gov/nexis/robotic-refueling-mission-3/ (accessed on 18 November 2024).
- NASA Images and Media Usage Guidelines. NASA Content—Images, Audio, Video, and Media Files Used in the Rendition of 3-Dimensional Models, such as Texture Maps and Polygon Data in Any Format—Generally Are Not Subject to Copyright in the United States. Available online: https://www.nasa.gov/nasa-brand-center/images-and-media/ (accessed on 18 November 2024).
- Maclay, T.; Goff, J.; Sheehan, J.; Han, E. The development of commercially viable ADR services: Introduction of a small-satellite grappling interface. J. Space Saf. Eng. 2020, 3, 364–368. [Google Scholar]
- IEEE Robotics & Automation Society, Technical Committee for Space Robotics. Available online: https://www.ieee-ras.org/space-robotics (accessed on 18 November 2024).
- Hernández-Arias, H.; Prado-Molina, J. On-Orbit Center of Mass Relocation System for A 3U Cubesat. Int. J. Sci. Tech. Res. 2018, 7, 44–51. [Google Scholar]
- Calaon, R.; Kiner, L.; Allard, C.; Schaub, H. Momentum management of a spacecraft equipped with a dual—Gimballed electric thruster. In Proceedings of the AAS Guidance and Control Conference, Breckenridge, CO, USA, 2–8 February 2023. Paper No. AAS-23-178. [Google Scholar]
- Gracey, W. The experimental determination of the moments of inertia of airplanes by a simplified compound-pendulum method. Available online: https://ntrs.nasa.gov/citations/19930082299 (accessed on 25 March 2025).
- Soule, H.; Miller, M. The experimental determination of the moments of inertia of airplanes. Available online: https://ntrs.nasa.gov/citations/19930091541 (accessed on 25 March 2025).
- Genta, G.; Delpreta, C. Some considerations on the experimental determination of moments of inertia. Meccanica 1994, 29, 125–141. [Google Scholar]
- Nocerino, A.; Opromolla, R.; Fasano, G.; Grassi, M.; Balaguer, P.; John, S.; Cho, H.; Bevilacqua, R. Experimental validation of inertia parameters and attitude estimation of uncooperative space targets using solid state LIDAR. Acta Astronaut. 2023, 240, 428–436. [Google Scholar]
- Bourabah, D.; Field, L.; Botta, E. Estimation of uncooperative space debris inertial parameters after tether capture. Acta Astronaut. 2023, 202, 909–926. [Google Scholar] [CrossRef]
- Field, L.; Bourabah, D.; Botta, E. Online Control and Moment of Inertia Estimation of Tethered Debris. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar]
- Sonobe, M.; Inoue, Y. Center of Mass Estimation Using a Force Platform and Inertial Sensors for Balance Evaluation in Quiet Standing. Sensors 2023, 23, 4933. [Google Scholar] [CrossRef]
- Zatsiorsky, V.M.; King, D.L. An algorithm for determining gravity line location from posturographic recordings. J. Biomech. 1997, 31, 161–164. [Google Scholar]
- Caron, O.; Faure, B.; Brenière, Y. Estimating the centre of gravity of the body on the basis of the centre of pressure in standing posture. J. Biomech. 1997, 30, 1169–1171. [Google Scholar]
- Germanotta, M.; Mileti, I.; Conforti, I.; Del Prete, Z.; Aprile, I.; Palermo, E. Estimation of Human Center of Mass Position through the Inertial Sensors-Based Methods in Postural Tasks: An Accuracy Evaluation. Sensors 2021, 21, 601. [Google Scholar] [CrossRef]
- Wang, F.; Bettadpur, S.; Save, H. Determination of the center–of–mass of gravity recovery and climate experimental satellites. J. Spacecr. Rockets 2010, 47, 371. [Google Scholar] [CrossRef]
- Kornfeld, R.; Arnold, B.; Gross, M.; Dahya, N.; Klipstein, W.; Gath, P.; Bettadpur, S. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On Mission. J. Spacecr. Rockets 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Huang, Z.; Li, S.; Cai, L.; Fan, D.; Huang, L. Estimation of the Center of Mass of GRACE-Type Gravity Satellites. Remote Sens. 2022, 14, 4030. [Google Scholar] [CrossRef]
- Pan, Z.; Xiao, Y. Data Quality Assessment of Gravity Recovery and Climate Experiment Follow-On Accelerometer. Sensors 2024, 24, 4286. [Google Scholar] [CrossRef]
- Dou, Y.; Wang, K.; Zhou, Z.; Thomas, P.R.; Shao, Z.; Du, W. Investigation of the Free-Fall Dynamic Behavior of a Rectangular Wing with Variable Center of Mass Location and Variable Moment of Inertia. Aerospace 2023, 10, 458. [Google Scholar] [CrossRef]
- Geng, J.; Langelaan, J.W. Estimation of Inertial Properties for a Multilift Slung Load. J. Guid. Control Dyn. 2021, 2, 220–237. [Google Scholar] [CrossRef]
- Gahramanova, A. Locating Centers of Mass with Image Processing. Undergrad. J. Math. Model 2019, 10, 1. [Google Scholar] [CrossRef]
- Lin, Y.T.; Tian, Y.; Perez, D.; Livescu, D. Regression-Based Projection for Learning Mori–Zwanzig Operators. SIAM J. Appl. Dyn. Sys. 2023, 4, 2890–2926. [Google Scholar] [CrossRef]
- Setterfield, T.; Miller, D.; Leonard, J.; Saenz-Otero, A. Mapping and determining the center of mass of a rotating object using a moving observer. Int. J. Robot. Res. 2018, 37, 83–103. [Google Scholar] [CrossRef]
- Diagonalize the Inertia Tensor. Available online: https://phys.libretexts.org/Bookshelves/Classical_Mechanics/Variational_Principles_in_Classical_Mechanics_(Cline)/13%3A_Rigid-body_Rotation/13.07%3A_Diagonalize_the_Inertia_Tensor (accessed on 26 November 2024).
- Luenberger Observer. Available online: https://www.mathworks.com/help/sps/ref/luenbergerobserver.html (accessed on 19 November 2024).
- Transport Theorem. Available online: https://en.wikipedia.org/wiki/Transport_theorem (accessed on 19 November 2024).
- Fossen, T. Comments on ‘Hamiltonian adaptive control of spacecraft’. IEEE Trans. Autom. Control 1993, 38, 671–672. [Google Scholar] [CrossRef]
- Iven, M.; Mareels, B.; Anderson, R.; Bitmead, R.; Bodson, M.; Sastry, S. Revisiting the MIT rule for adaptive control. In Adaptive Systems in Control and Signal Processing 1986; IFAC Workshop Series; Pergamon Press Ltd.: Oxford, UK, 1987; pp. 161–166. [Google Scholar]
- Kuck, E.; Sands, T. Space Robot Sensor Noise Amelioration Using Trajectory Shaping. Sensors 2024, 24, 666. [Google Scholar] [CrossRef] [PubMed]
- Adams, G. Arizona State University Physics Department Proof of the Parallel Axis Theorem. Available online: https://www.public.asu.edu/~gbadams/sum00/parallelaxisT.pdf (accessed on 19 November 2024).
- Zhu, Y. Identification Test Design and Data Pretreatment. In Multivariable System Identification for Process Control; Zhu, Y., Ed.; Elsevier Science: Maryland Heights, MO, USA, 2001; pp. 31–63. [Google Scholar]
- Persistent Excitation Conditions and Their Implications. Section 8.1 of Study Guide on Adaptive and Self-Tuning Control. Available online: https://library.fiveable.me/adaptive-and-self-tuning-control/unit-8/robustness-issues-adaptive-control/study-guide/yLKsaWxBlamk2I48 (accessed on 22 November 2024).
- Marino, R.; Tomei, P. On exponentially convergent parameter estimation with lack of persistency of excitation. Syst. Control Lett. 2022, 159, 105080. [Google Scholar]
- Korotina, M.; Romero, J.; Aranovskiy, S.; Bobtsov, A.; Ortega, R. A new on-line exponential parameter estimator without persistent excitation. Syst. Control Lett. 2022, 159, 105079. [Google Scholar]
- Software, Robotics, and Simulation Division. Available online: https://www.nasa.gov/software-robotics-and-simulation-division/ (accessed on 21 November 2024).
- Dynamics Operations Training Systems. Available online: https://www.nasa.gov/general/generic-robotics-on-orbit-trainer/ (accessed on 21 November 2024).
- Dai, Q.; Xiao, G.; Zhou, G.; Ye, Q.; Han, S. A novel Gaussian sum quaternion constrained cubature Kalman filter algorithm for GNSS/SINS integrated attitude determination and positioning system. Front. Neurorobotics 2024, 18, 1374531. [Google Scholar]
- Slotine, J.; Di Benedetto, M. Hamiltonian adaptive control of spacecraft. IEEE Trans. Autom. Control 1990, 35, 848–852. [Google Scholar] [CrossRef]
- Sands, T.; Kim, J.; Agrawal, B. Improved Hamiltonian Adaptive Control of spacecraft. In Proceedings of the IEEE Aerospace conference, Big Sky, MT, USA, 7–14 March 2009. [Google Scholar]
- Sands, T.; Kim, J.; Agrawal, B. Spacecraft fine tracking pointing using adaptive control. In Proceedings of the 58th International Astronautical Congress, Hyderabad, India, 24–28 September 2007. [Google Scholar]
- Sands, T.; Kim, J.; Agrawal, B. Spacecraft adaptive control evaluation. In Proceedings of the Infotech@Aerospace, Garden Grove, CA, USA, 19–21 June 2012. [Google Scholar]
- Huang, B.; Sands, T. Novel learning for control of nonlinear spacecraft dynamics. J. AppliedMath 2023, 1, 42. [Google Scholar] [CrossRef]










| Roll [Degrees] | Pitch [Degrees] | Yaw [Degrees] | |
|---|---|---|---|
| Mean | |||
| Standard deviation 1 |
| Roll [Degrees] | Pitch [Degrees] | Yaw [Degrees] | |
|---|---|---|---|
| Mean | |||
| Standard deviation 1 |
| Mean Roll [Degrees] | Mean Pitch [Degrees] | Mean Yaw [Degrees] | |
|---|---|---|---|
| Benchmark Luenberger | |||
| Nonlinear Luenberger 1 | 77% | 144.58% | −1.02% |
| Roll [Degrees] | Pitch [Degrees] | Yaw [Degrees] | |
|---|---|---|---|
| Error mean | 0.00028129 | 0.0027575 | |
| Error standard deviations 1 | 0.0084356 | 0.0054244 | 0.011515 |
| Maneuver Case | Roll Errors | Pitch Errors | Yaw Errors | |||
|---|---|---|---|---|---|---|
| Mean | Deviation | Mean | Deviation | Mean | Deviation | |
| Unperturbed PID unperturbed system * | 3% | 0% | 0% | 0% | 899% | 0% |
| Benchmark case ** | -- | -- | -- | -- | -- | -- |
| Feedforward + feedback + adaption *** or learning **** | −68% | −51% | −50% | −49% | −49% | −50% |
| Case | Cost |
|---|---|
| PID-controlled unperturbed system | −1% |
| Benchmark PID feedback | -- |
| Nonlinear feedforward with inertia adaption and PID feedback | −10% |
| Nonlinear feedforward with regression-based inertia learning | −10% |
| Maneuver Case | x Coordinate | y Coordinate | z Coordinate |
|---|---|---|---|
| Nonlinear adaption | 7% | 0% | 13% |
| Nonlinear projection-based regression learning | 36% | 71% | -95% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sands, T. Autonomous Real-Time Mass Center Location and Inertia Identification for Grappling Space Robotics. Technologies 2025, 13, 148. https://doi.org/10.3390/technologies13040148
Sands T. Autonomous Real-Time Mass Center Location and Inertia Identification for Grappling Space Robotics. Technologies. 2025; 13(4):148. https://doi.org/10.3390/technologies13040148
Chicago/Turabian StyleSands, Timothy. 2025. "Autonomous Real-Time Mass Center Location and Inertia Identification for Grappling Space Robotics" Technologies 13, no. 4: 148. https://doi.org/10.3390/technologies13040148
APA StyleSands, T. (2025). Autonomous Real-Time Mass Center Location and Inertia Identification for Grappling Space Robotics. Technologies, 13(4), 148. https://doi.org/10.3390/technologies13040148








