AI Diffusion Model-Based Technology for Automating the Multi-Class Labeling of Electron Microscopy Datasets of Brain Cell Organelles for Their Augmentation and Synthetic Generation
Abstract
1. Introduction
- ND enables the generation of high-quality images with rich details, realistic textures, and smooth transitions. This approach is capable of eliminating noise and artifacts, resulting in the generation of clean and natural images.
- The ND approach provides control over the image generation process. Through diffusion parameters, one can adjust the level of detail and blur or the degree of preserving the original information. This allows users to customize generated images according to specific requirements.
- ND can be applied to various types of images, including photographs, drawings, textures, and others. This makes it a versatile tool for generating and processing diverse kinds of visual data.
2. Materials and Methods
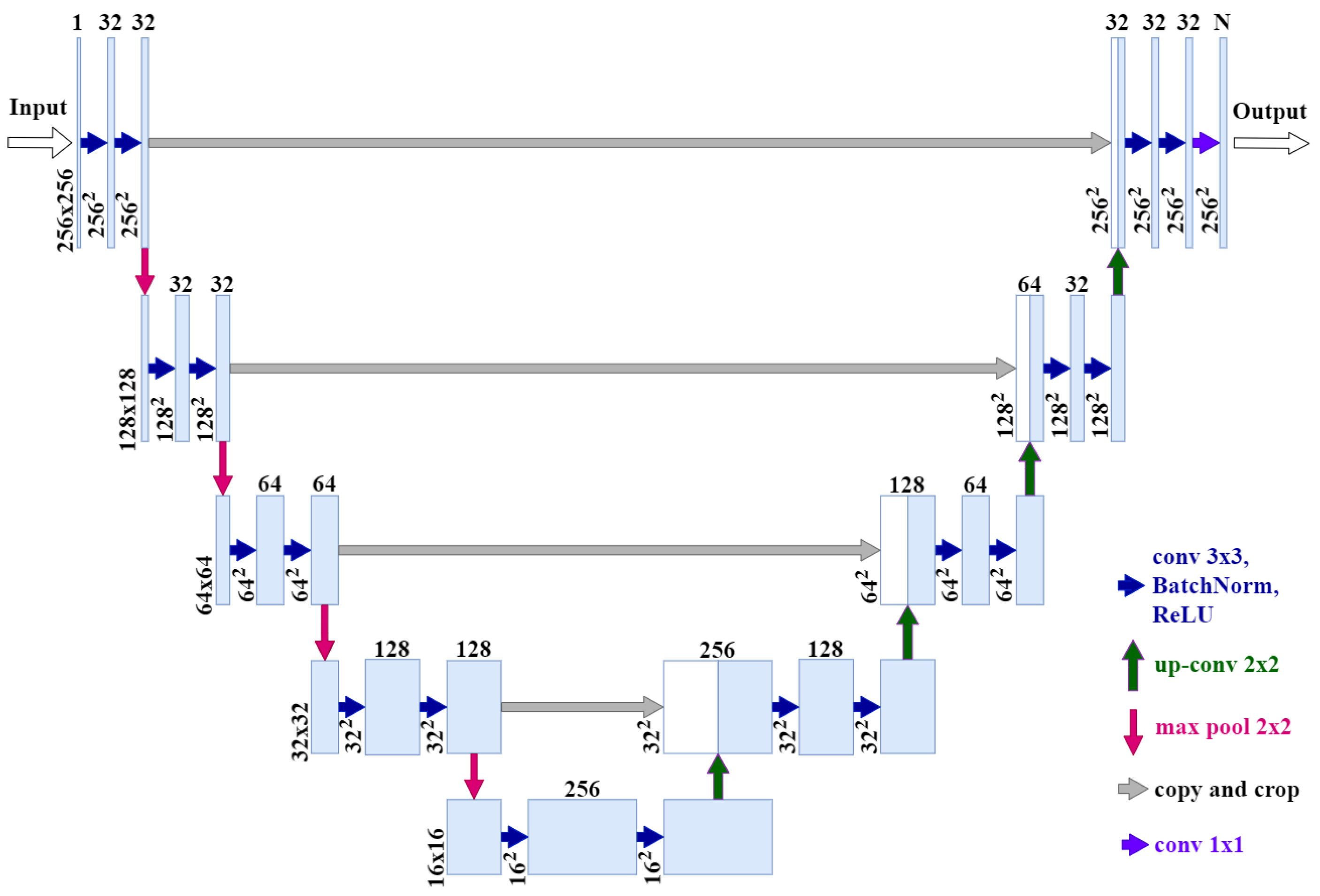
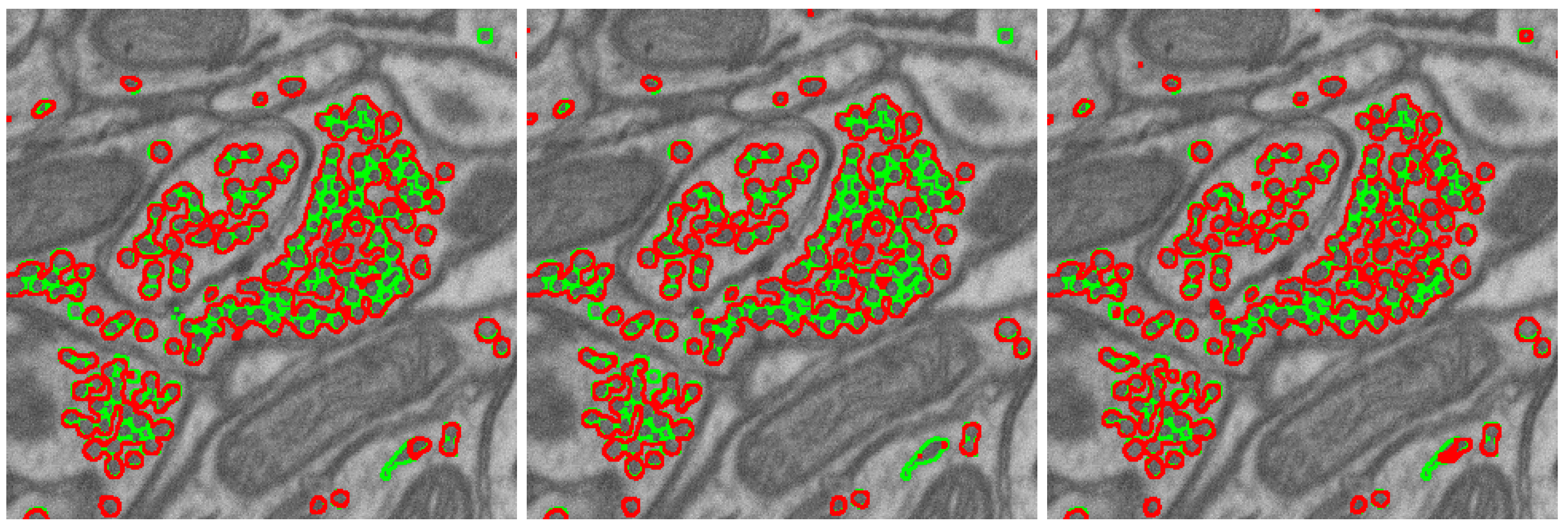
2.1. Segmentation Task, Metric, and Network
Segmentation Network Architecture
- Our network input is an image of size 256 × 256 × 1 instead of 512 × 512 × 1.
- Our network output is 256 × 256 × N instead of 512 × 512 × 1, where N is the number of classes.
- We added batch normalization after each ReLU, convolution, and activation layers.
- Number of channels in the original U-Net convolution blocks: 64 → 128 → 256 → 512 → 1024; number of channels in our architecture: 32 → 32 → 64 → 128 → 256.
- The resulting model contains 15.7 times fewer parameters than the original model and takes up 15.2 times less memory (24 MB instead of 364 MB).
2.2. Datasets and Their Markups
2.3. Segmentation Algorithm Stability
2.4. Technology for the Automatic Labeling of Synthetic Classes Based on the Diffusion Model
- The data with their annotations, layer-by-layer (in order of layer sequence), are combined into one common tensor of size H × W × C, where H and W are the image sizes, and C is the number of channels. The C value determines the number of channels in the original layer image (in our case, the image is grayscale, that is, one channel) plus the number of classes, for each of which a single-channel mask should be generated.
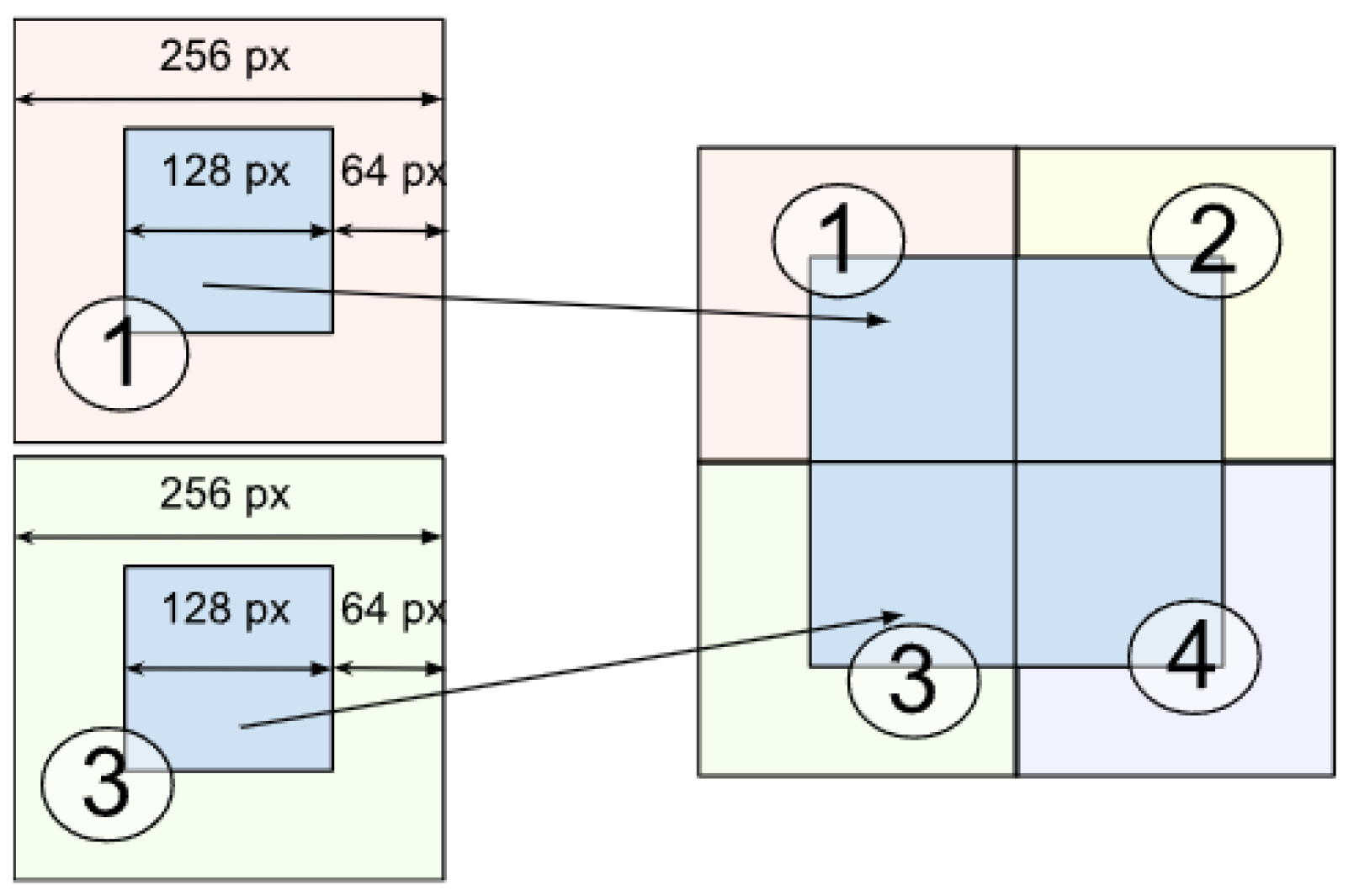
- The layer image is divided into parts of size 256 × 256 pixels. This is performed to avoid scaling the image during the dataset preprocessing before model training, which could lead to loss of information about the original image and its details as well as blurring of images.
- For layers, standardization (or Z-Score normalization) is used, and mask normalization (or Min-Max scaling or division by 255) is used. The raw dataset data are converted using the following formulas:
2.5. Geometric Models for Dataset Synthesis
2.6. Naturalization of Geometric and Other Synthetic Datasets by Diffusion Models
3. Results
3.1. Software and Technologies for Training and Testing
3.2. Generation of Synthetic Multi-Class Datasets by Diffusion Model
- DIFF 6-class 42 layers: 42 layers from the EPFL6 training dataset, all six classes (the example: see Figure 11). The diffusion model was trained on this dataset, and this model synthesized the input datasets DIFF 6 and MIX 6 (with the addition of the EPFL6 dataset images) for the segmentation task in Table 3 and Table 4.
- DIFF 5-class 42 layers: 42 layers from the EPFL6 training dataset, five classes of markup. The diffusion model was trained on this dataset, and this model synthesized the input datasets DIFF 5 and MIX 5 (with the addition of images from the EPFL6 dataset) for the segmentation task in Table 3 and Table 4.
- DIFF 1-class 42 layers: 42 layers from the EPFL6 training dataset, one class of markup. The diffusion model was trained on this dataset, and this model synthesized the input datasets DIFF 1 and MIX 1 (as a fusion with the images from the EPFL6 dataset) for the segmentation task in Table 4.
- DIFF 1-class 165 layers: 165 images from the EPFL one-class training dataset in Lucchi++ labeling. The diffusion model trained on this dataset synthesized the input dataset for the combination: Lucchi++ plus DIFF 1(165), 84 (Table 5).
3.2.1. Training a Segmentation Neural Network on a Dataset Using Synthetic Images Generated by a Diffusion Model
- Input and output image size: 256 × 256 pixels;
- Batch size for the training set: 7;
- Number of epochs: 200;
- Adam optimizer with a variable learning rate from to .
3.2.2. Experiments on Geometric Model for Dataset Synthesis
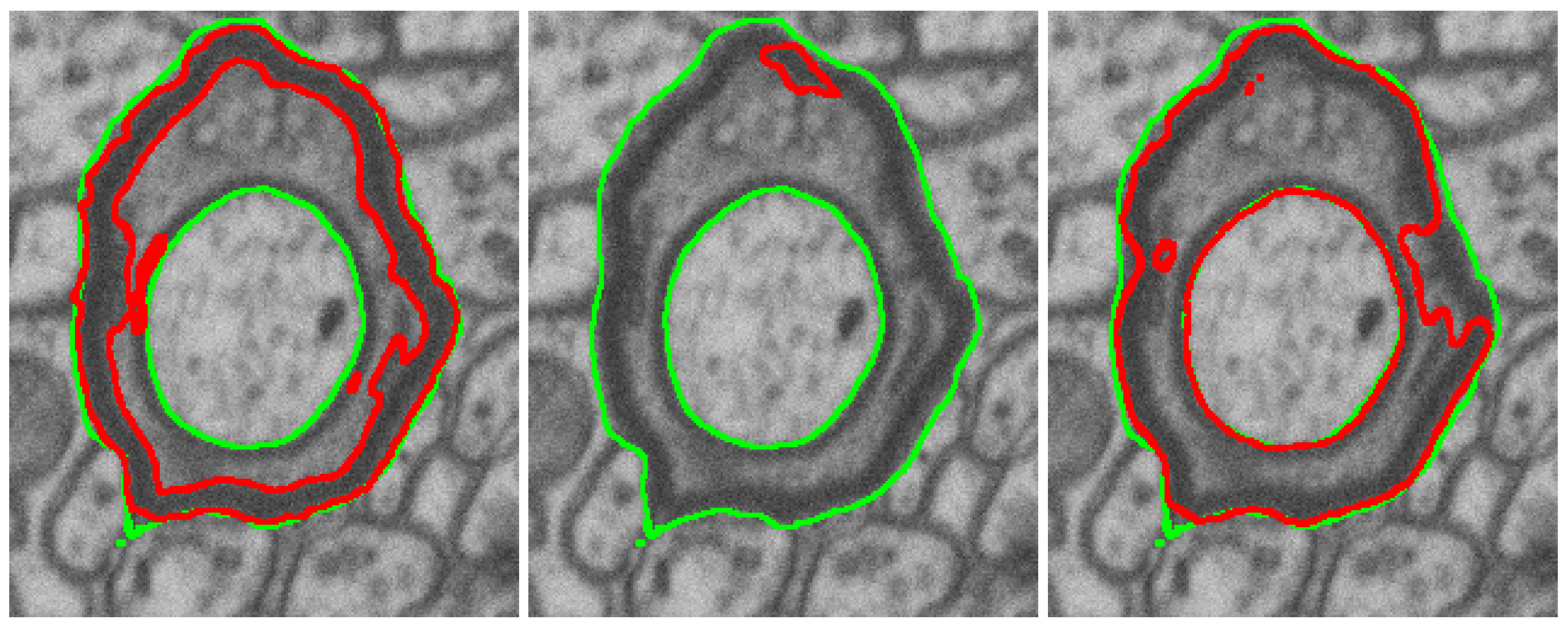
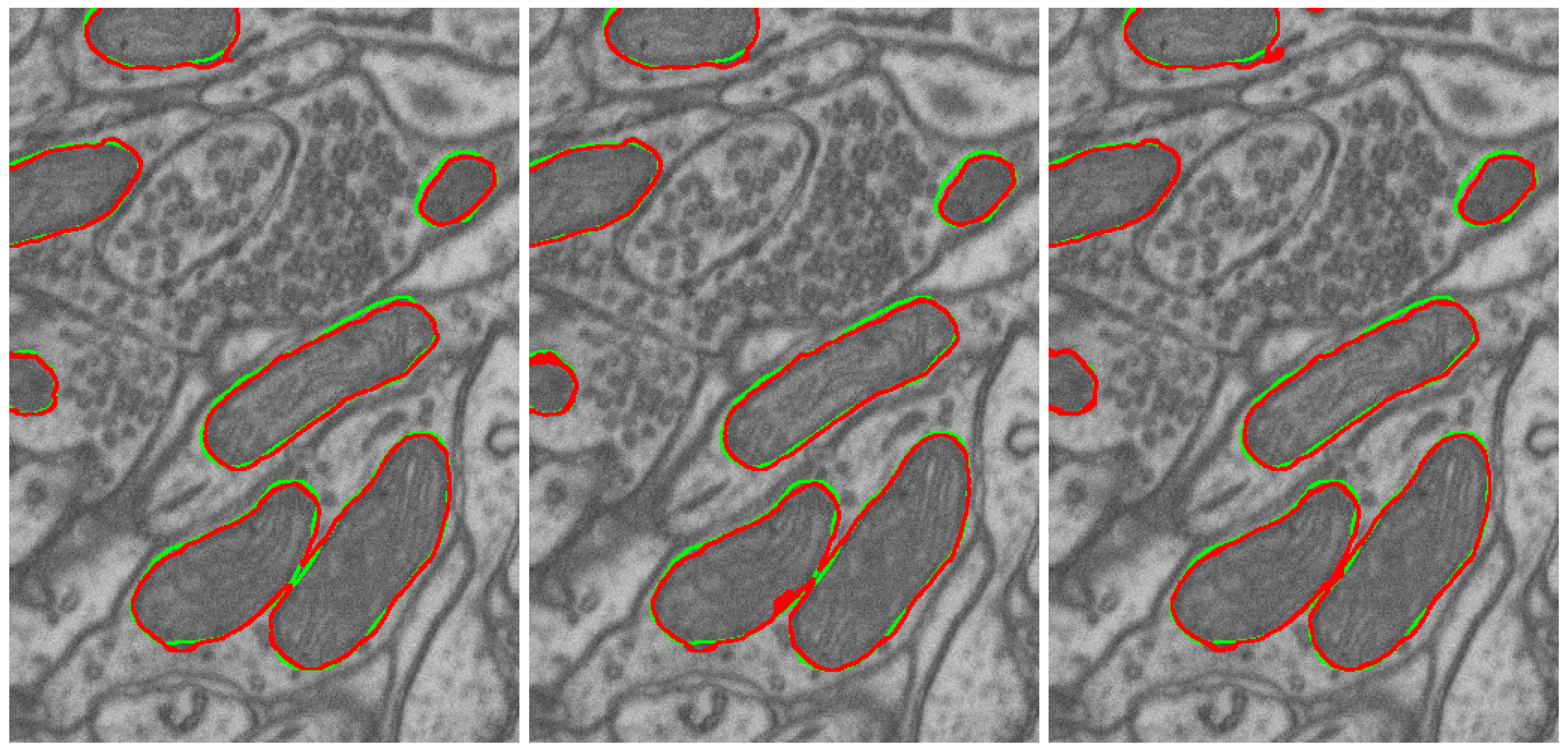
3.2.3. Naturalization Results
3.3. Results’ Comparison
4. Discussion
5. Conclusions
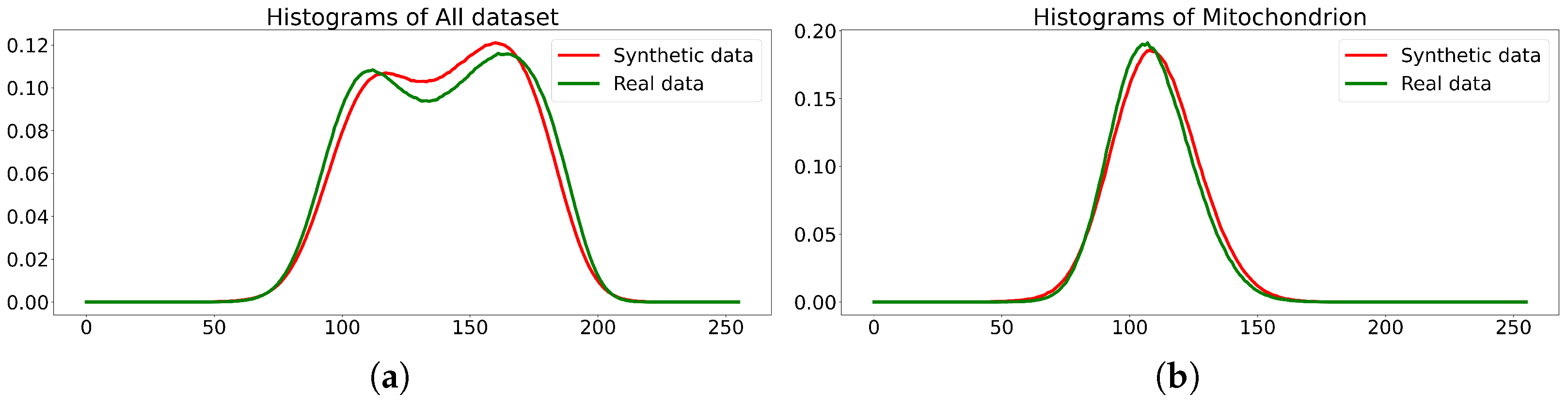
- The quality of multi-class dataset synthesis by the diffusion model, which was trained on the original dataset (EPFL6), can be measured as the accuracy of the synthesized labeling and by the accuracy of class segmentation on the test part of the original dataset, which is achieved by the U-Net-like segmentation model trained on multi-class synthetics.
- The quality (accuracy) of the labeling of the diffusion synthetic multi-class dataset generated via the technology corresponds to the accuracy of the original dataset (EPFL6).
- The synthetic dataset does not replicate the original dataset but closely resembles it. Therefore, the synthetics it suitable for original dataset augmentation or even for use instead of the original data.
- The augmentation of the dataset with adequate geometric synthetics is able to solve the problem of underrepresented classes.
- The naturalization of geometric synthetics by the diffusion model is able to increase the accuracy of synthetic labeling and multi-class segmentation, which is trained on the synthetic dataset.
- The size of the synthetic dataset in tiles (in this case of size 256 × 256) is practically unlimited; the number of classes is limited by the amount of memory and the reasonableness of other necessary computational resources.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EM | Electron microscopy |
| DSC | Dice–Sorencen coefficient |
References
- Chen, M.; Mei, S.; Fan, J.; Wang, M. An Overview of Diffusion Models: Applications, Guided Generation, Statistical Rates and Optimization. arXiv 2024, arXiv:2404.07771. [Google Scholar]
- Bommasani, R.; Hudson, D.A.; Adeli, E.; Altman, R.; Arora, S.; von Arx, S.; Bernstein, M.S.; Bohg, J.; Bosselut, A.; Brunskill, E.; et al. On the Opportunities and Risks of Foundation Models. arXiv 2022, arXiv:2108.07258. [Google Scholar]
- Deerinck, T.; Bushong, E.; Lev-Ram, V.; Shu, X.; Tsien, R.; Ellisman, M. Enhancing Serial Block-Face Scanning Electron Microscopy to Enable High Resolution 3-D Nanohistology of Cells and Tissues. Microsc. Microanal. 2010, 16, 1138–1139. [Google Scholar] [CrossRef]
- Ciresan, D.C.; Gambardella, L.M.; Giusti, A.; Schmidhuber, J. Deep neural networks segment neuronal membranes in electron microscopy images. In Proceedings of the NIPS, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 2852–2860. [Google Scholar]
- Lucchi, A.; Smith, K.; Achanta, R.; Knott, G.; Fua, P. Supervoxel-Based Segmentation of Mitochondria in EM Image Stacks With Learned Shape Features. IEEE Trans. Med Imaging 2012, 31, 474–486. [Google Scholar] [CrossRef] [PubMed]
- Helmstaedter, M.; Mitra, P.P. Computational methods and challenges for large-scale circuit mapping. Curr. Opin. Neurobiol. 2012, 22, 162–169. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Drozdzal, M.; Vorontsov, E.; Chartrand, G.; Kadoury, S.; Pal, C. The Importance of Skip Connections in Biomedical Image Segmentation. arXiv 2016, arXiv:1608.04117. [Google Scholar]
- Fakhry, A.E.; Zeng, T.; Ji, S. Residual Deconvolutional Networks for Brain Electron Microscopy Image Segmentation. IEEE Trans. Med Imaging 2017, 36, 447–456. [Google Scholar]
- Xiao, C.; Liu, J.; Chen, X.; Han, H.; Shu, C.; Xie, Q. Deep contextual residual network for electron microscopy image segmentation in connectomics. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; pp. 378–381. [Google Scholar] [CrossRef]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. arXiv 2016, arXiv:1606.06650. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Kamnitsas, K.; Ledig, C.; Newcombe, V.; Simpson, J.P.; Kane, A.D.; Menon, D.; Rueckert, D.; Glocker, B. Efficient multi-scale 3D CNN with fully connected CRF for accurate brain lesion segmentation. Med. Image Anal. 2017, 36, 61–78. [Google Scholar] [CrossRef]
- Li, W.; Wang, G.; Fidon, L.; Ourselin, S.; Cardoso, M.J.; Vercauteren, T. On the Compactness, Efficiency, and Representation of 3D Convolutional Networks: Brain Parcellation as a Pretext Task. In Proceedings of the Information Processing in Medical Imaging; Niethammer, M., Styner, M., Aylward, S., Zhu, H., Oguz, I., Yap, P.T., Shen, D., Eds.; Springer: Cham, Switzerland, 2017; pp. 348–360. [Google Scholar]
- Zhang, Z.; Wu, C.; Coleman, S.; Kerr, D. DENSE-INception U-net for medical image segmentation. Comput. Methods Prog. Biomed. 2020, 192, 105395. [Google Scholar] [CrossRef] [PubMed]
- Mubashar, M.; Ali, H.; Grönlund, C.; Azmat, S. R2U++: A multiscale recurrent residual U-Net with dense skip connections for medical image segmentation. Neural Comput. Appl. 2022, 34, 17723–17739. [Google Scholar] [CrossRef]
- Chapelle, O.; Weston, J.; Bottou, L.; Vapnik, V. Vicinal Risk Minimization. In Proceedings of the Advances in Neural Information Processing Systems; Leen, T., Dietterich, T., Tresp, V., Eds.; MIT Press: Cambridge, MA, USA, 2000; Volume 13. [Google Scholar]
- Simard, P.Y.; LeCun, Y.A.; Denker, J.S.; Victorri, B. Transformation Invariance in Pattern Recognition—Tangent Distance and Tangent Propagation. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 235–269. [Google Scholar] [CrossRef]
- Gong, X.; Chen, S.; Zhang, B.; Doermann, D. Style Consistent Image Generation for Nuclei Instance Segmentation. In Proceedings of the 2021 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2021; pp. 3993–4002. [Google Scholar] [CrossRef]
- Hou, L.; Agarwal, A.; Samaras, D.; Kurc, T.M.; Gupta, R.R.; Saltz, J.H. Robust Histopathology Image Analysis: To Label or to Synthesize? In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8525–8534. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, Z.; Cheng, K.T.; Chen, H. InsMix: Towards Realistic Generative Data Augmentation for Nuclei Instance Segmentation. arXiv 2022, arXiv:2206.15134. [Google Scholar] [CrossRef]
- Wang, H.; Xian, M.; Vakanski, A.; Shareef, B. SIAN: Style-Guided Instance-Adaptive Normalization for Multi-Organ Histopathology Image Synthesis. arXiv 2022, arXiv:2209.02412. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. arXiv 2014, arXiv:1406.2661. [Google Scholar] [CrossRef]
- Dhariwal, P.; Nichol, A. Diffusion Models Beat GANs on Image Synthesis. arXiv 2021, arXiv:2105.05233. [Google Scholar] [CrossRef]
- Shijie, J.; Ping, W.; Peiyi, J.; Siping, H. Research on data augmentation for image classification based on convolution neural networks. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 4165–4170. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar] [CrossRef]
- Song, Y.; Sohl-Dickstein, J.; Kingma, D.P.; Kumar, A.; Ermon, S.; Poole, B. Score-Based Generative Modeling through Stochastic Differential Equations. arXiv 2020, arXiv:2011.13456. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. arXiv 2020, arXiv:2006.11239. [Google Scholar] [CrossRef]
- Nichol, A.; Dhariwal, P.; Ramesh, A.; Shyam, P.; Mishkin, P.; McGrew, B.; Sutskever, I.; Chen, M. GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models. arXiv 2021, arXiv:2112.10741. [Google Scholar] [CrossRef]
- Wolleb, J.; Bieder, F.; Sandkühler, R.; Cattin, P.C. Diffusion Models for Medical Anomaly Detection. arXiv 2022, arXiv:2203.04306. [Google Scholar] [CrossRef]
- Trabucco, B.; Doherty, K.; Gurinas, M.; Salakhutdinov, R. Effective Data Augmentation With Diffusion Models. arXiv 2023, arXiv:2302.07944. [Google Scholar] [CrossRef]
- Yu, X.; Li, G.; Lou, W.; Liu, S.; Wan, X.; Chen, Y.; Li, H. Diffusion-based Data Augmentation for Nuclei Image Segmentation. arXiv 2024, arXiv:2310.14197. [Google Scholar]
- Kazerouni, A.; Aghdam, E.K.; Heidari, M.; Azad, R.; Fayyaz, M.; Hacihaliloglu, I.; Merhof, D. Diffusion models in medical imaging: A comprehensive survey. Med Image Anal. 2023, 88, 102846. [Google Scholar] [CrossRef] [PubMed]
- Getmanskaya, A.; Sokolov, N.; Turlapov, V. Multiclass U-Net Segmentation of Brain Electron Microscopy Data Using Original and Semi-Synthetic Training Datasets. Program Comput. Soft 2022, 48, 164–171. [Google Scholar] [CrossRef]
- Sokolov, N.; Vasiliev, E.; Getmanskaya, A. Generation and study of the synthetic brain electron microscopy dataset for segmentation purpose. Comput. Opt. 2023, 47, 778–787. [Google Scholar] [CrossRef]
- Sohl-Dickstein, J.; Weiss, E.A.; Maheswaranathan, N.; Ganguli, S. Deep Unsupervised Learning using Nonequilibrium Thermodynamics. arXiv 2015, arXiv:1503.03585. [Google Scholar] [CrossRef]
- Lucchi, A.; Li, Y.; Fua, P. Learning for Structured Prediction Using Approximate Subgradient Descent with Working Sets. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1987–1994. [Google Scholar] [CrossRef]
- Arganda-Carreras, I.; Turaga, S.C.; Berger, D.R.; Cireşan, D.; Giusti, A.; Gambardella, L.M.; Schmidhuber, J.; Laptev, D.; Dwivedi, S.; Buhmann, J.M.; et al. Crowdsourcing the creation of image segmentation algorithms for connectomics. Front. Neuroanat. 2015, 9, 152591. [Google Scholar] [CrossRef]
- Kasthuri, N.; Hayworth, K.; Berger, D.R.; Schalek, R.; Conchello, J.; Knowles-Barley, S.; Lee, D.; Vázquez-Reina, A.; Kaynig, V.; Jones, T.; et al. Saturated Reconstruction of a Volume of Neocortex. Cell 2015, 162, 648–661. [Google Scholar] [CrossRef]
- Žerovnik Mekuč, M.; Bohak, C.; Hudoklin, S.; Kim, B.H.; Romih, R.; Kim, M.Y.; Marolt, M. Automatic segmentation of mitochondria and endolysosomes in volumetric electron microscopy data. Comput. Biol. Med. 2020, 119, 103693. [Google Scholar] [CrossRef]
- Casser, V.; Kang, K.; Pfister, H.; Haehn, D. Fast Mitochondria Detection for Connectomics. arXiv 2020, arXiv:1812.06024. [Google Scholar]
- ITMM. 6-Class Labels for EPFL EM Dataset. 2023. Available online: https://github.com/GraphLabEMproj/unet/tree/master/data (accessed on 2 December 2024).
- Yuan, Z.; Ma, X.; Yi, J.; Luo, Z.; Peng, J. HIVE-Net: Centerline-Aware HIerarchical View-Ensemble Convolutional Network for Mitochondria Segmentation in EM Images. Comput. Methods Programs Biomed. 2021, 200, 105925. [Google Scholar]
- Cheng, H.C.; Varshney, A. Volume segmentation using convolutional neural networks with limited training data. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 590–594. [Google Scholar] [CrossRef]
- Peng, J.; Yuan, Z. Mitochondria Segmentation From EM Images via Hierarchical Structured Contextual Forest. IEEE J. Biomed. Health Inform. 2020, 24, 2251–2259. [Google Scholar] [CrossRef]
- Cetina, K.; Buenaposada, J.M.; Baumela, L. Multi-class segmentation of neuronal structures in electron microscopy images. BMC Bioinform. 2018, 19, 298. [Google Scholar]
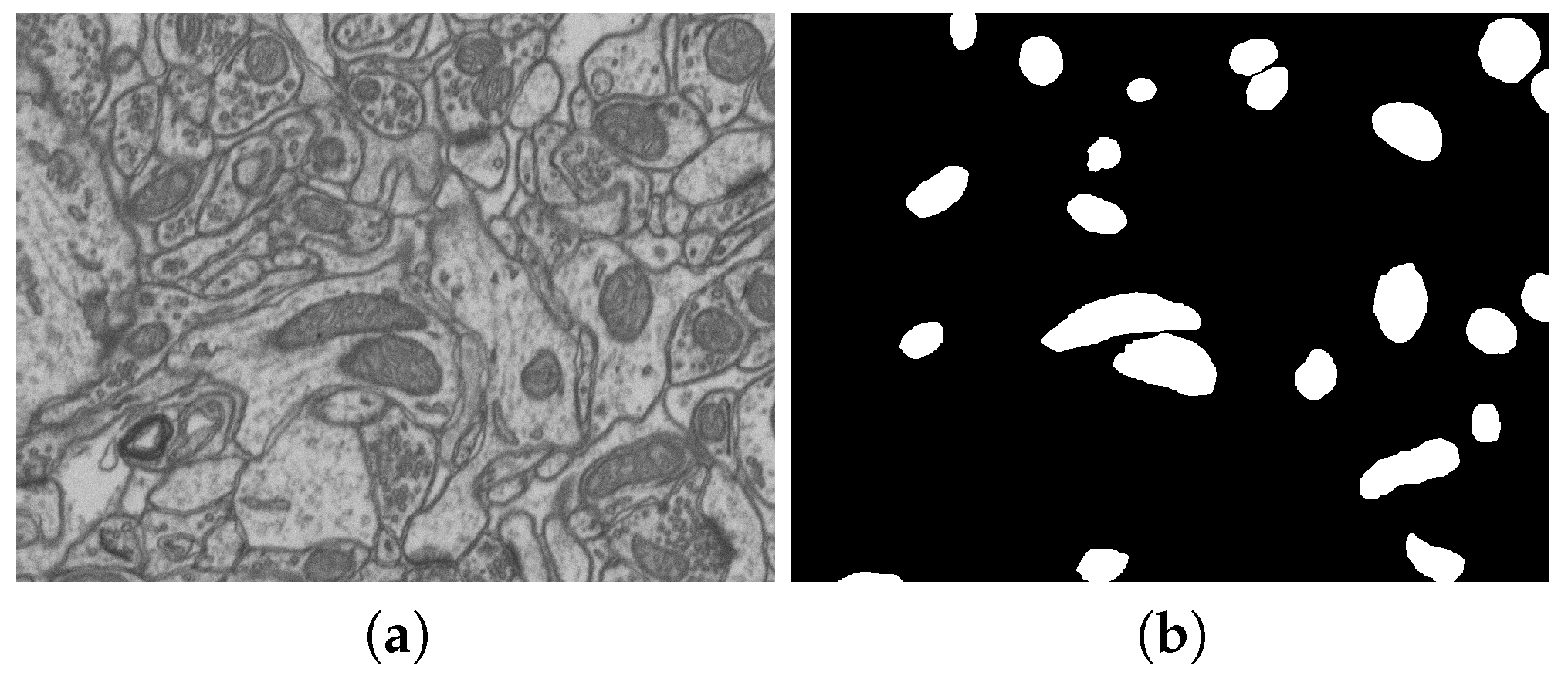
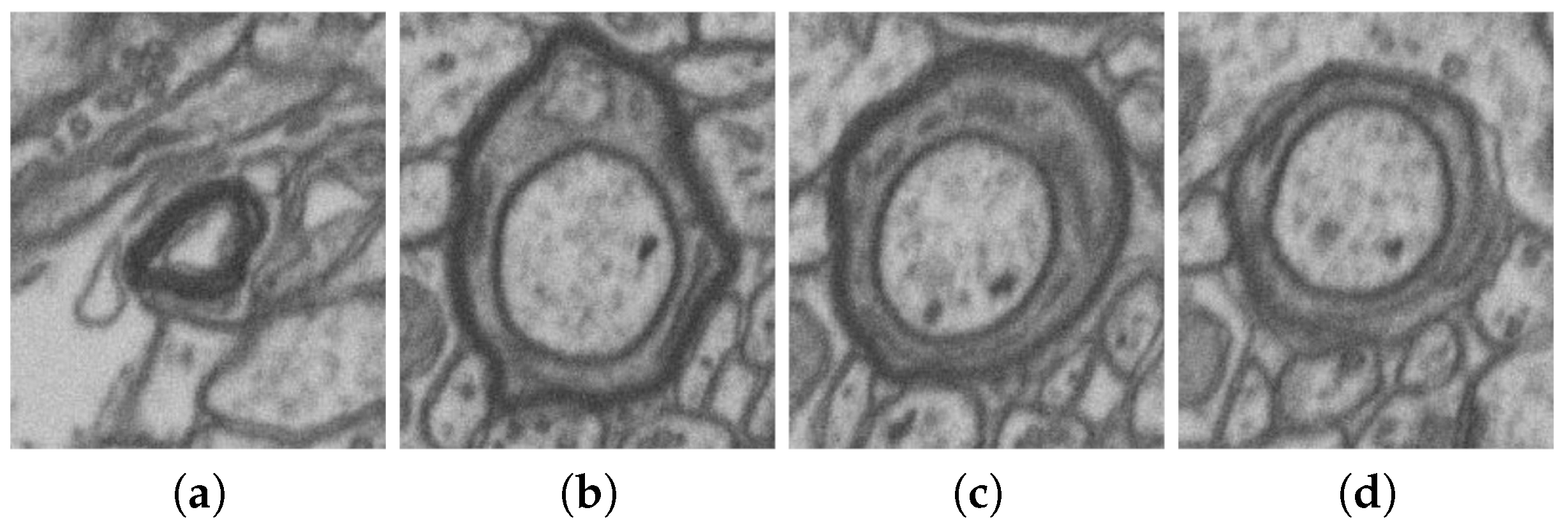




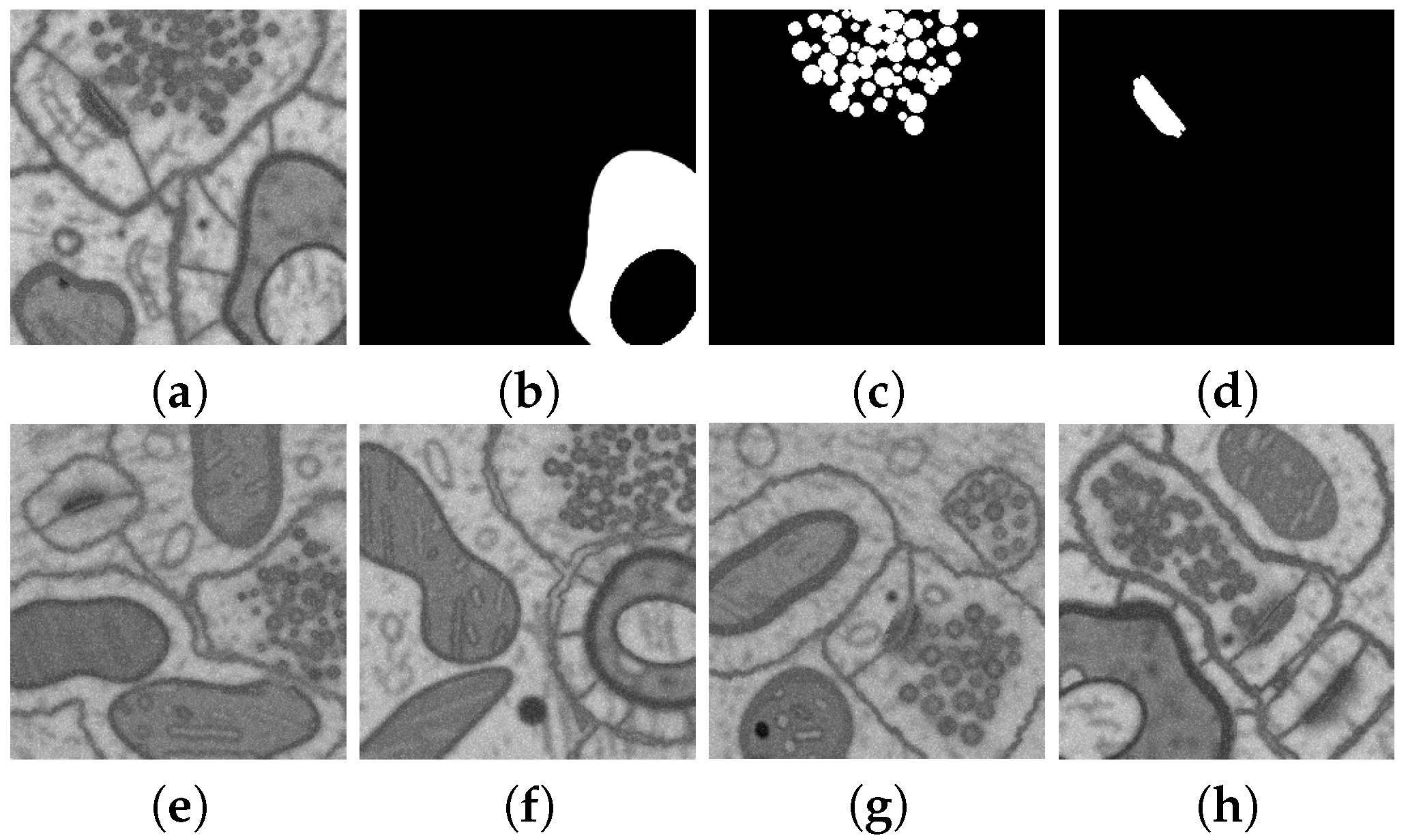


| No. | Name | Data Volumes | Labeled Data Volumes | Labeled Classes | Resolution (nm/voxel) |
|---|---|---|---|---|---|
| 1 | AC4, ISBI 2013 [38] | 4096 × 4096 × 1850 | 1024 × 1024 × 100 | membranes | 6 × 6 × 30 |
| 2 | EPFL b, Lucchi++ c [5] | 1065 × 2048 × 1536 | 2 datasets 1024 × 768 × 165 | mitochondria | 5 × 5 × 5 |
| 3 | Kasthuri et al. [39] | 1334 × 1553 × 75 1463 × 1613 × 85 | mitochondria | 3 × 3 × 30 | |
| 4 | UroCell a [40] | 1366 × 1180 × 1056 | 5 datasets 256 × 256 × 256 | mitochondria, endolysosomes, fusiform vesicles | 16 × 16 × 15 |
| Metric | Mitochondria | PSD | Vesicles | Axon | Membrane | Mit.boundary | Lucchi++ |
|---|---|---|---|---|---|---|---|
| 5 classes, Mean | 0.925 | 0.800 | 0.727 | 0.128 | 0.872 | 0.928 | |
| 5 classes, Std | 0.007 | 0.022 | 0.004 | 0.152 | 0.002 | 0.006 | |
| 6 classes, Mean | 0.927 | 0.775 | 0.725 | 0.125 | 0.872 | 0.798 | 0.934 |
| 6 classes, Std | 0.007 | 0.064 | 0.005 | 0.169 | 0.002 | 0.007 | 0.003 |
| Num | Training Dataset | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MIX | DIFFUSION | ORIGINAL | MIX | DIFFUSION | ORIGINAL | |||||||
| MIX 5 | MIX 6 | DIFF 5 | DIFF 6 | ORIG 5 | ORIG 6 | MIX 1 | MIX 6 | DIFF 1 | DIFF 6 | ORIG 1 | ORIG 6 | |
| Mitochondria | Mitochondria/Mitochondrial boundaries | |||||||||||
| 5 | 0.860 | 0.886 | 0.850 | 0.871 | 0.882 | 0.885 | 0.880 | 0.760 | 0.835 | 0.741 | 0.877 | 0.752 |
| 10 | 0.943 | 0.935 | 0.936 | 0.906 | 0.934 | 0.928 | 0.921 | 0.797 | 0.910 | 0.752 | 0.916 | 0.787 |
| 15 | 0.945 | 0.942 | 0.930 | 0.937 | 0.930 | 0.926 | 0.918 | 0.793 | 0.876 | 0.762 | 0.914 | 0.790 |
| 20 | 0.939 | 0.938 | 0.931 | 0.941 | 0.924 | 0.925 | 0.925 | 0.795 | 0.924 | 0.754 | 0.912 | 0.794 |
| 30 | 0.932 | 0.942 | 0.895 | 0.928 | 0.922 | 0.924 | 0.924 | 0.799 | 0.916 | 0.751 | 0.913 | 0.796 |
| MIX 5 | MIX 6 | DIFF 5 | DIFF 6 | ORIG 5 | ORIG 6 | MIX 5 | MIX 6 | DIFF 5 | DIFF 6 | ORIG 5 | ORIG 6 | |
| PSD | Membranes | |||||||||||
| 5 | 0.672 | 0.654 | 0.513 | 0.582 | 0.556 | 0.566 | 0.868 | 0.868 | 0.849 | 0.852 | 0.861 | 0.862 |
| 10 | 0.820 | 0.783 | 0.735 | 0.532 | 0.755 | 0.754 | 0.869 | 0.872 | 0.854 | 0.847 | 0.872 | 0.873 |
| 15 | 0.723 | 0.755 | 0.621 | 0.643 | 0.685 | 0.697 | 0.869 | 0.864 | 0.844 | 0.814 | 0.871 | 0.872 |
| 20 | 0.821 | 0.773 | 0.748 | 0.731 | 0.755 | 0.726 | 0.865 | 0.864 | 0.831 | 0.813 | 0.871 | 0.873 |
| 30 | 0.816 | 0.810 | 0.472 | 0.783 | 0.723 | 0.766 | 0.872 | 0.864 | 0.849 | 0.791 | 0.872 | 0.873 |
| Vesicles | Axon | |||||||||||
| 5 | 0.692 | 0.697 | 0.687 | 0.693 | 0.689 | 0.686 | 0.094 | 0.043 | 0.023 | 0.036 | 0.144 | 0.282 |
| 10 | 0.734 | 0.719 | 0.727 | 0.704 | 0.720 | 0.714 | 0.009 | 0.062 | 0.013 | 0.178 | 0.304 | 0.265 |
| 15 | 0.730 | 0.728 | 0.735 | 0.725 | 0.716 | 0.714 | 0.030 | 0.007 | 0.013 | 0.024 | 0.122 | 0.274 |
| 20 | 0.734 | 0.728 | 0.736 | 0.729 | 0.714 | 0.713 | 0.000 | 0.000 | 0.022 | 0.097 | 0.243 | 0.181 |
| 30 | 0.725 | 0.735 | 0.731 | 0.730 | 0.720 | 0.720 | 0.274 | 0.010 | 0.376 | 0.007 | 0.192 | 0.312 |
| Metric | Mitochondria | PSD | Vesicles | Axon | Membranes | Mit. Boundaries |
|---|---|---|---|---|---|---|
| MIX NAT 1 | 0.920 | - | - | - | - | - |
| MIX NAT 5 | 0.924 | 0.851 | 0.708 | 0.527 | 0.876 | - |
| MIX NAT 6 | 0.928 | 0.842 | 0.716 | 0.534 | 0.877 | 0.802 |
| MIX DIFF 1 | 0.927 | - | - | - | - | - |
| MIX DIFF 5 | 0.944 | 0.833 | 0.734 | 0.017 | 0.867 | - |
| MIX DIFF 6 | 0.939 | 0.841 | 0.732 | 0.000 | 0.869 | 0.805 |
| MIX GEOM 1 | 0.926 | - | - | - | - | - |
| MIX GEOM 5 | 0.936 | 0.836 | 0.725 | 0.789 | 0.871 | - |
| MIX GEOM 6 | 0.933 | 0.845 | 0.721 | 0.722 | 0.873 | 0.807 |
| SYN NAT 1 | 0.883 | - | - | - | - | - |
| SYN NAT 5 | 0.885 | 0.701 | 0.510 | 0.565 | 0.810 | - |
| SYN NAT 6 | 0.839 | 0.652 | 0.512 | 0.542 | 0.793 | 0.638 |
| SYN DIFF 1 | 0.918 | - | - | - | - | - |
| SYN DIFF 5 | 0.942 | 0.781 | 0.736 | 0.072 | 0.839 | - |
| SYN DIFF 6 | 0.942 | 0.808 | 0.730 | 0.025 | 0.831 | 0.775 |
| SYN GEOM 1 | 0.891 | - | - | - | - | - |
| SYN GEOM 5 | 0.905 | 0.704 | 0.623 | 0.882 | 0.792 | - |
| SYN GEOM 6 | 0.905 | 0.708 | 0.609 | 0.898 | 0.790 | 0.704 |
| ORIGINAL 1 | 0.913 | - | - | - | - | - |
| ORIGINAL 5 | 0.928 | 0.824 | 0.732 | 0.133 | 0.872 | - |
| ORIGINAL 6 | 0.928 | 0.814 | 0.724 | 0.070 | 0.873 | 0.799 |
| Method | Labeling | Dice |
|---|---|---|
| HIVE-net [43] | Lucchi++ | 0.948 |
| tiny-U-Net 2 | Lucchi++ plus DIFF 1 (165), 84 | 0.946 |
| tiny-U-Net 2 | Lucchi++ | 0.934 |
| tiny-U-Net 2 | Lucchi++, 100 (out of 165) | 0.928 |
| tiny-U-Net 2 | DIFF 1 (165), 84 | 0.927 |
| tiny-U-Net 2 | DIFF 6 (42), 84 | 0.917 |
| tiny-U-Net 2 | Lucchi++, 42 (out of 165) | 0.913 |
| 3D Casser et al. [41] 1 | Lucchi++ | 0.942 |
| Cheng et al. (3D) [44] 1 | Lucchi++ | 0.941 |
| 3D U-Net [11] 1 | Lucchi++ | 0.935 |
| Cheng et al. (2D) [44] 1 | Lucchi++ | 0.928 |
| U-Net [7] 1 | Lucchi++ | 0.915 |
| Peng et al. [45] 1 | Lucchi++ | 0.909 |
| 3D Xiao et al. [10] 1 | Lucchi++ | 0.900 |
| Cetina et al. [46] 1 | Lucchi++ | 0.864 |
| Lucchi et al. [5] 1 | Lucchi++ | 0.860 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sokolov, N.; Getmanskaya, A.; Turlapov, V. AI Diffusion Model-Based Technology for Automating the Multi-Class Labeling of Electron Microscopy Datasets of Brain Cell Organelles for Their Augmentation and Synthetic Generation. Technologies 2025, 13, 127. https://doi.org/10.3390/technologies13040127
Sokolov N, Getmanskaya A, Turlapov V. AI Diffusion Model-Based Technology for Automating the Multi-Class Labeling of Electron Microscopy Datasets of Brain Cell Organelles for Their Augmentation and Synthetic Generation. Technologies. 2025; 13(4):127. https://doi.org/10.3390/technologies13040127
Chicago/Turabian StyleSokolov, Nikolay, Alexandra Getmanskaya, and Vadim Turlapov. 2025. "AI Diffusion Model-Based Technology for Automating the Multi-Class Labeling of Electron Microscopy Datasets of Brain Cell Organelles for Their Augmentation and Synthetic Generation" Technologies 13, no. 4: 127. https://doi.org/10.3390/technologies13040127
APA StyleSokolov, N., Getmanskaya, A., & Turlapov, V. (2025). AI Diffusion Model-Based Technology for Automating the Multi-Class Labeling of Electron Microscopy Datasets of Brain Cell Organelles for Their Augmentation and Synthetic Generation. Technologies, 13(4), 127. https://doi.org/10.3390/technologies13040127









