Research on Dynamic Control Strategies for Intermittent Bus Lanes in Mixed Traffic Flow Environments

Abstract

The traditional intermittent bus lane control struggles to achieve an effective balance between bus priority and lane utilization efficiency. To address this limitation, this study proposes a dynamic control strategy that enables the borrowing of intermittent bus lanes in mixed traffic flow environments and constructs a connected vehicle control model encompassing both the target intersection and its upstream segment. First, a dynamic clearance framework is established on the dedicated lane based on the real-time speed of buses. Concurrently, the target connected and automated vehicle (CAV) predicts the traffic signal status upon its arrival at the stop line to determine its traversable zone at the bus lanes. Subsequently, a coordinated control strategy is designed for the dynamic clearance framework and the traversable zone, leading to the development of lane-changing decision models under four distinct scenarios. This approach allows CAVs to dynamically utilize residual lane resources without compromising bus operations. Finally, using average vehicle delay as the evaluation metric, a comparative simulation analysis is conducted against the traditional bus lane utilization method across four dimensions: connected vehicle penetration rate, traffic flow saturation, right-turn proportion, and bus departure frequency. The experimental results demonstrate that the proposed strategy significantly improves both bus priority and overall traffic efficiency.

1. Introduction

The implementation of bus lanes not only aligns with the strategic direction of prioritizing public transportation development, but also reflects a commitment to public interests, shared cultural values, and collective awareness. However, due to the dynamic nature of urban traffic demand, traditional bus lanes often exhibit low efficiency in utilizing temporal and spatial resources, which in turn exacerbates congestion in lanes used by vehicles.

To address this issue, Viegas et al. [1] introduced the concept of the Intermittent Bus Lane (IBL), which allow vehicles to use the dedicated lanes during non-bus operation periods, thereby improving overall road utilization efficiency. Xie Qiu-feng et al. [2] further proposed a control system and method for intermittent bus lane import sections to ensure bus priority. Al Khateeb et al. applied Transit Signal Priority (TSP), and the results show that the impact of actuating traffic signals in the Al Maktoum corridor after extending green time for bus approach (15 s) was a minimum reduction in average travel time for buses by 7.04% and tremendous increase in travel time for cars by 38.68% [3]. Olstam et al. observed that under higher traffic volumes, longer lane reservation durations are necessary to maintain bus operational efficiency. When traffic volume increased by 40%, the dynamic lane closest to the median was reserved for more than 70% of the total time [4]. While these methods have, to some extent, ensured the priority of buses, they also present notable limitations. On the one hand, with the continuous advancement of connected vehicle technology, a new form of mixed traffic flow—comprising both CAVs and human-driven vehicles (HDVs)—is expected to persist for the foreseeable future [5]. Given the fluctuating nature of urban traffic demand, it is essential to systematically review the theoretical foundations of current mixed traffic flow systems and assess their stability and safety. On the other hand, the traditional dynamic control methods for bus lanes cannot simultaneously ensure bus priority and the improvement of lane utilization [6], which limits the overall operational efficiency of the system. Therefore, how to reduce the overall vehicle delay by enhancing the spatio-temporal resource utilization of bus lanes while guaranteeing bus priority has become the key to solving the problem.

Research indicates [7] that the strategic allocation of autonomous vehicles to dedicated rapid bus lanes can significantly enhance road capacity. However, compared to CAVs, HDVs exhibit greater randomness in movement characteristics. Given the prolonged coexistence of this new mixed traffic flow, Jiang et al. [8] proposed the Follower–Stopper–Platoon (FSP) strategy to mitigate traffic oscillation by controlling a platoon of CAVs in a two-lane scenario and demonstrated the efficacy of the FSP strategy by designing simulation experiments. Wang et al. [9] analyzed the controllability of mixed traffic flow systems and developed a system-degree optimal control strategy. Jiang Yangsheng et al. [10] investigated the stability and safety of mixed traffic flow composed of HDVs and intelligent connected vehicles (ICVs), showing that ICVs can significantly improve road traffic safety. Luo Ruifa et al. [11] constructed a fundamental diagram model for mixed traffic flow in an intelligent connected environment, based on vehicle function degradation and fleet strength, and validated the accuracy of the theoretical model. Gong et al. [12] proposed a cooperative platooning control strategy for mixed fleets of CAVs and HDVs, achieving system-degree traffic stability while preserving individual vehicle maneuverability and safety. Chen et al. [13] proposed the notion of “1 + n” mixed platoon, consisting of one leading CAV and n following HDVs, and formulated a platoon-based optimal control framework for CAV control at a signalized intersection. Jiang et al. [14] proposed a platoon-aware cooperative lane-changing (PCLC) strategy inspired by platoon formation; this strategy focused on the formation of CAV platoons in mixed traffic flow, restructured the spatial distribution of CAVs on the road segment, and effectively explored traffic management strategies for mixed traffic flow. Collectively, these studies provide a comprehensive analysis of the emerging mixed traffic flow and demonstrate the safety and stability benefits of intelligent connected vehicles, offering a solid theoretical foundation for further research in this field.

Under the IBL control method, when a bus arrives at the entrance of a road segment, the downstream bus lane is closed to prevent vehicles from entering. However, if the bus lane is excessively long, idle sections may form in front of the bus, leading to inefficient use of road resources. Eichler et al. [15] evaluated strategies for operating buses on signal-controlled arterials using special lanes that are made intermittently available to general traffic; the disadvantage is that they disrupt traffic. To address this issue, Wu et al. [16] introduced a connected vehicle (CV)-based BLIDP strategy to take advantage of the extra capacity of dedicated bus lanes. The general idea of this study is to require non-bus vehicles that are just ahead of the bus to exit the bus lane while allowing vehicles behind or far ahead of the bus use of the extra capacity of the bus lane. Ma et al. [17] proposed dividing the road into multiple static clearance zones of equal length, each with defined sensing mechanisms and operational protocols. However, under mixed traffic conditions, the static clearance zone proposed by Rau et al. [18] is limited by its inherent characteristics and application scope, limiting its effectiveness in optimizing lane space utilization and clearing vehicles ahead of buses. To overcome this limitation, Luo et al. [19] proposed an innovative approach in a CV environment, called dynamic bus lane with moving block (DBLMB). The length of the moving block can be adjusted with the bus speed in real time. Their results indicated a trade-off in clearance distance design: excessive length reduces the utilization of idle bus lane resources, while insufficient length compromises bus priority. Meng Xie et al. [20] proposed a Vehicle-to-Vehicle/Infrastructure (V2X)-based dynamic public transport (PT) priority concept in mixed traffic called Virtual Right of Way (VROW) and evaluated the potential traffic impacts of VROW on both PT and private vehicles. Although the aforementioned studies have addressed bus priority on road segments, they largely overlook the spatio-temporal priority requirements at intersections, which limits the realization of continuous priority for buses throughout the network.

Bus priority is a comprehensive and systematic strategy that must be implemented throughout the entire transportation network. It should not only focus on optimizing bus passage along road segments but also emphasize rational planning and priority guarantees at critical traffic conversion nodes—specifically, intersections. Song Xianmin et al. [21] facilitated efficient bus passage by deploying flashing yellow lights, variable message signs, and clearance distance mechanisms. Chang Yulin et al. [22] improved the control method of intermittent bus lanes by installing signal markers at lane entrances to detect and identify buses. Zhang Wenhui et al. [23] proposed a dynamic sharing mechanism that allows vehicles to use intermittent bus lanes when buses are not present, using pre-signals to regulate vehicle types in real time and achieve temporal sharing of bus lanes. These studies have demonstrated positive outcomes in enhancing bus priority. However, they did not account for CAVs; therefore, there remains potential for further enhancing the efficiency of resource utilization in bus lanes. Pang Mingbao et al. [24] proposed a lane-sharing control strategy for CAVs operating on bus lanes between two signalized intersections. However, their approach neglected the critical aspect of setting clearance distances in front of buses. Li Haoran et al. [25] introduced a novel lane-sharing strategy tailored for a mixed traffic environment comprising HDVs, connected hybrid vehicles (CHVs), and CAVs, offering new insights into improving the dynamic utilization of bus lanes. Nevertheless, their method relied on a centralized control framework, where a central control unit issued commands and CAVs executed them through vehicle-to-vehicle (V2V) coordination, leading to relatively low system response efficiency. In contrast, distributed control leverages the onboard computing capabilities of individual vehicles, reduces the computational burden on the central system, and is better suited for large-scale intelligent vehicle environments in urban settings [26].

In summary, to address the challenge of lane borrowing in mixed traffic flow environments, this paper proposes a dynamically adaptive management method; that is, in a dynamically changing environment, CAVs can perform real-time traffic state recognition and automatically adapt lane-changing decisions according to predefined vehicle priority rules. Furthermore, by leveraging the four distinct traffic scenarios established in this study, they dynamically identify traversable zones within bus lanes. V2X coordination effectively manages the operation of vehicles on bus lanes, thereby enabling coordinated control and dynamic decision-making under diverse traffic conditions. The primary objective of this method is to ensure bus priority by guaranteeing preferential passage both along road sections and at intersections. Based on this principle, the types of vehicles eligible for using the dedicated lanes are defined. Subsequently, through the construction of a traffic simulation environment, the definition of evaluation metrics, and the implementation of comparative simulation experiments on lane borrowing decisions and control strategies, the effectiveness of the proposed approach is systematically validated using the integrated regulation framework of the Simulation of Urban Mobility (SUMO) and Python version 3.9.13.

2. Problem Statement

2.1. Experimental Design

This study investigates a mixed traffic flow environment consisting of HDVs and CAVs. The research scenario involves a road segment with a bus lane located between two consecutive intersections, as well as the downstream signalized intersection. As illustrated in Figure 1, the rightmost lane is designated as a bus lane, which accommodates connected buses, right-turning HDVs, and CAVs that are permitted to borrow the lane under the condition of ensuring bus priority. Adjacent to the left of the bus lane is a regular lane that serves the mixed traffic flow of HDVs and CAVs. CAVs exchange real-time traffic information through vehicle-to-vehicle (V2V) communication, establishing the informational foundation for coordinated control strategies.

The control strategy is illustrated using the scenario depicted in Figure 1. First, the types of vehicles eligible for lane borrowing are specified: straight-moving CAVs and right-turning vehicles are permitted to use the bus lane, whereas straight-moving HDVs are prohibited from entering. At the same time, the priority of vehicle usage of the bus lanes in this control method is determined, as shown in

Table 1. The priority of vehicle usage of the bus lanes.

Vehicle Type	Travel Priority Degree
Bus	Highest priority
Right-turning vehicles	Second priority
Straight-moving CAVs	Third priority

. The highest priority is given to buses. Then, a dynamic clearance framework model is established ahead of the bus, as depicted by the red region in the Figure 1. Entry of lane-changing vehicles into this zone is strictly prohibited, and any vehicles already within the zone are required to perform mandatory lane changes, thereby ensuring the bus’s spatiotemporal priority along the designated roadway segment. Subsequently, without altering the fixed signal timing at the original intersections, signal coordination with connected vehicles is conducted to predict the queue conditions at the downstream intersections along the bus lane, thereby enabling the identification of the “dynamic traversable zone of the intersection”, as illustrated by the green region in the Figure 1. Right-turning vehicles and CAVs may proceed into this zone, while straight-moving CAVs that exceed the boundary of this zone must promptly change lanes to the adjacent regular lane. This approach ensures that bus operations remain unaffected by downstream queues of vehicles while further enhancing lane utilization efficiency. A collaborative control model integrating the dynamic clearance framework on the road segment and the traversable zone at the intersection is developed, which will be elaborated in Section 3.

2.2. Fundamental Assumptions and Lane-Borrowing Regulations for Vehicles

2.2.1. Fundamental Assumptions

• Variations in the size and performance characteristics of conventional vehicles are neglected;
• Pedestrian movements at intersections are excluded from consideration, and right-turning vehicles are not subject to traffic signal control;
• Intelligent connected vehicles maintain a stable operational state without experiencing malfunctions during the control process;
• The impact of bus stopping maneuvers, including dwell time at bus stops, is explicitly considered;
• Only scenarios in which the departure times of the lane-borrowing connected vehicle platoon and the bus departure within the same signal cycle are included in the analysis.

2.2.2. Lane-Borrowing Regulations

• CAVs proceeding straight or turning right fully comply with the lane-borrowing strategy after transitioning to the bus lane and determine whether to continue utilizing the lane or return to their original lane based on control strategies at the road segment and intersection;
• For right-turning HDVs, there are no mandatory constraints regarding the timing or location of lane changes to the bus lane.

3. Dynamic Control Strategy for Intermittent Bus Lane

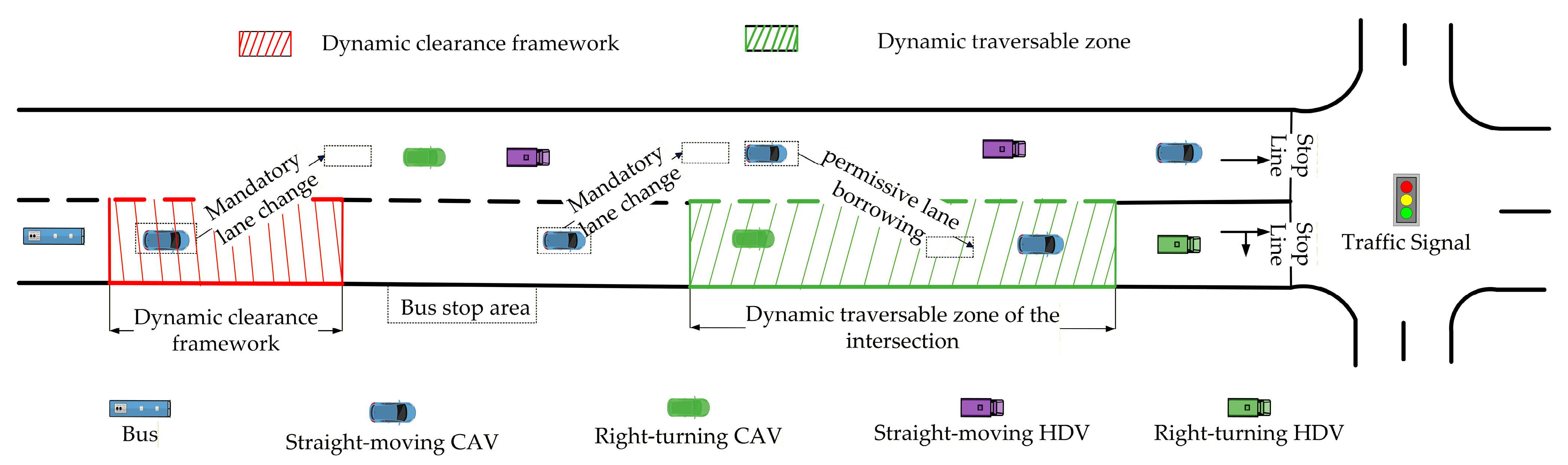
3.1. Dynamic Clearance Framework Model

The clearance distance serves as a critical parameter in lane control strategies, aimed at ensuring priority passage for buses while extending the spatial applicability of the method [27]. Based on the dynamic clearance framework model proposed in reference [6], the calculation formula is expressed as follows:

$$L_{sdb}\left(v,t_{lc}\right)=L_{safe}\left(v\right)+L_{change}\left(v,t_{lc}\right)$$

(1)

$$L_{DCB}(v,t_{lc},S)=\max \{L_{sdb}(v,t_{lc}),L_{utdb}(S)\}$$

(2)

In the formula, $v$ represents the traveling speed of the connected bus; $t_{lc}$ denotes the lane-changing time of the vehicle; $S$ refers to the expected service degree of the lane; and $L_{utdb}(S)$ indicates the clearance framework length required to maintain the service degree of the bus lane. The dynamic clearance framework $L_{sdb}(v,t_{lc})$, which ensures the safety and priority of connected bus operations, comprises two components: the first is the safe braking distance necessary for the connected bus to come to a stop, referred to as the bus braking distance $L_{safe}\left(v\right)$; the second is the lane-changing buffer distance required for connected vehicles to safely exit the dynamic bus lane, known as the vehicle lane-changing distance $L_{change}\left(v,t_c\right)$. Vehicles in adjacent lanes are prohibited from changing lanes into the dynamic clearance framework of the bus.

3.2. Lane Changing Model

Lane changing by vehicles must satisfy general lane-changing conditions as a prerequisite, which include the emergence of lane-changing motivation when traffic conditions in the adjacent lane are superior and the completion of the maneuver while maintaining a predefined safety gap with the following vehicle in the target lane [28].

The MOBIL lane-changing model proposed is governed by two fundamental criteria: lane-changing utility and safety constraints. Lane-changing utility quantifies the improvement in driving conditions for the vehicle after a lane change, while safety constraints evaluate whether the maneuver can be executed without compromising traffic safety. A lane change is executed only when both criteria are satisfied. This model is employed to simulate the lane-changing behavior of right-turning HDVs. Suppose that the driver makes lane-changing decisions in a rational and locally optimal manner. The theoretical basis of this model stems from the longitudinal car-following dynamics model and the utility maximization theory, and a politeness factor is introduced to describe the driver’s consideration of the impact on surrounding vehicles during decision-making.

3.2.1. Lane-Changing Utility

Equation (3) calculates the lateral control variable and determines whether a lane change should be initiated. A lane change is executed when the benefit associated with switching to the target lane surpasses the predefined lane-changing benefit threshold.

$$u_v={\tilde{a}}_V-a_V+\rho \left[{\displaystyle \sum }_{i=1}^n(\tilde{a}{F}_{Fj}-a_{Fj})+{\displaystyle \sum }_{i=1}^n(\tilde{a}{T}_{TFj}-a_{TFj})\right]>\Delta a$$

(3)

In the equation, $u_v$ denotes the lane-changing benefit associated with the target lane; $a_V$ denotes the actual longitudinal acceleration of the target vehicle; ${\tilde{a}}_V$ denotes the desired longitudinal acceleration of the target vehicle after completing the lane change; $a_{Fj}$ denotes the actual acceleration of the j-th following vehicle in the original lane; $\tilde{a}{F}_{Fj}$ denotes the desired acceleration of the j-th following vehicle in the original lane after the lane change; $a_{TFj}$ denotes the actual acceleration of the j-th following vehicle in the target lane; $\tilde{a}{T}_{TFj}$ denotes the desired acceleration of the j-th following vehicle in the bus lane after the lane change; and $\rho$ denotes the politeness factor. The vehicle’s lane-changing benefit is affected by the politeness factor, which represents the degree of altruism. Considering that the traffic flow environment in this paper includes both ordinary vehicles and connected vehicles, different politeness factors are adopted according to their different driving behaviors. When the following vehicle is an ordinary vehicle, the politeness factor is set to 1, and when it is a connected vehicle, it is set to 0.2 [29]. $n$ denotes the number of cooperative vehicles in the ordinary lane; $\Delta a$ denotes the incentive threshold, set to 0.3 [30].

This formula assesses whether the current vehicle needs dynamic adjustment by comparing its politeness factor (‘$\rho$’) with the incentive threshold (‘$\Delta a$’) to ensure the stability of the traffic flow.

3.2.2. Lane Change Safety

Lane change safety requires that during the lane change maneuver, the vehicle must not interfere with the following vehicle in the target lane and must satisfy the required safety distance constraints. This is mathematically formulated in Equations (4) and (5):

$$d\left(t\right)=X_{cav}\left(t\right)-X_{cav}^{adj}\left(t\right)$$

(4)

$$d(t)>d_{safe}$$

(5)

When changing lanes, it is necessary to ensure that the vehicles behind in the target lane will not be forced to brake suddenly due to the lane change, as shown in Equation (6):

$${\tilde{a}}_V,{\tilde{a}}_{TF\mathrm{j}}\ge -b_{safe}$$

(6)

In the equation, $X_{cav}\left(t\right)$ denotes the position of the target vehicle at the current time; $X_{cav}^{adj}\left(t\right)$ denotes the position of the rear vehicle in the adjacent lane at the current time; $d\left(t\right)$ denotes the distance between the target vehicle and the rear vehicle in the adjacent lane at the current time; $d_{safe}$ denotes the minimum safe distance between the leading and following vehicles; and $b_{safe}$ denotes the maximum safe deceleration.

Figure 2 describes the lane-changing decision logic involved in Equations (3)–(6) of the MOBIL model by demonstrating the steps that a vehicle needs to complete in sequence before performing a lane change, including incentive judgment, safety constraint verification, and acceleration impact assessment.

3.3. Dynamic Available Time-Space Computation Model for Intersections

Based on the signal timing and traffic flow characteristics at intersections, a dynamic available passage time model is first developed to predict the time window during which borrowing vehicles can utilize the dedicated lane, while ensuring bus priority. Building upon this, a dynamic available passage zone model is further established to determine the spatial extent of the dedicated lane that borrowing vehicles can access.

3.3.1. Computational Model for Traversable Time

Based on car-following and lane-changing models, the CAV nearest to the stop line on the bus lane and the first bus immediately following it are defined as the “target CAV” and “target bus”, respectively.

Predict the signal status at the moment the target CAV arrives at the stop line and calculate the corresponding available green light duration. The detailed methodology is as follows: First, scan all vehicles on the bus lane and identify the target CAV based on its spatial position—specifically, by solving for $\max \left\{X_{cav1},X_{cav2},\dots ,X_{cavn}\right\}$ and determining the CAV’s current location. Subsequently, using kinematic equations, compute the distance between the target CAV’s current position and the stop line and estimate the time it will take for the vehicle to reach the intersection stop line, along with the associated signal phase. Simultaneously, when predicting the signal status for the target bus arrival at the stop line, the influence of its average dwell time at stops must be incorporated into the calculation.

3.3.2. Computational Model for Traversable Zone

Under the premise of ensuring priority for public transport vehicles, this study proposes a strategy to enhance the utilization efficiency of dedicated lanes by permitting CAVs to remain in the bus lane under specified conditions, without being mandated to return to their original lanes. Two operational conditions are defined to support this strategy:

• When the signal light turns green as the borrowing vehicle fleet arrives at the intersection, the fleet can pass through the intersection without stopping within the seconds of available green light time $\Delta t_1$ prior to the bus’s arrival;
• When the signal light is red at the moment the borrowing vehicle fleet arrives at the intersection, but the nearest bus behind the fleet reaches the intersection during a green phase, the fleet can initiate movement and successfully complete its passage through the intersection within the seconds of available green time $\Delta t_2$ prior to the bus’s arrival.

To fulfill the requirements of both operational conditions, the length of the borrowing vehicle fleet must be constrained, and the traversable zone length at the intersection should be dynamically determined based on the available time window. Following the methodology outlined in the referenced literature [31], the driving behaviors of CAVs and buses are modeled using the Intelligent Driver Model (IDM). The model is based on traffic flow dynamics and driving behavior theory. It assumes that vehicles continuously adjust their acceleration to maintain the desired speed and safe distance, thereby achieving a dynamic balance between safety and comfort.

For condition 1, a dynamic platooning model for CAV fleets is developed based on the IDM to compute the maximum queue length so that the fleet can unimpededly pass through the intersection’s stop line within a specified time window. The acceleration and car-following distance equations for CAVs are formulated as follows:

$$a\left(t\right)=a_{\max }\left(1-{\left({\displaystyle \frac{v\left(t\right)}{v_0}}\right)}^4-{\left({\displaystyle \frac{s^{*}\left(t\right)}{s\left(t\right)}}\right)}^2\right)+K\cdot \Delta a_{\mathrm{lead}}\left(t\right)$$

(7)

$$s^{*}\left(t\right)=s_0+v\left(t\right)T+{\displaystyle \frac{v\left(t\right)\Delta v\left(t\right)}{2\sqrt{a_{\max }b}}}+\gamma \cdot \Delta a_{\mathrm{lead}}\left(t\right)$$

(8)

The acceleration formulation in Equation (7) comprises three components: the free-flow term $a_{\max }\left(1-{\left({\displaystyle \frac{v\left(t\right)}{v_0}}\right)}^4\right)$, which acts to adjust the vehicle’s speed toward the desired speed in the absence of preceding vehicles; the braking term $-a_{\max }{\left({\displaystyle \frac{s^{*}\left(t\right)}{s\left(t\right)}}\right)}^2$, which initiates deceleration when the gap to the leading vehicle falls below the desired spacing to prevent collisions; and the cooperative gain term $K\cdot \Delta a_{\mathrm{lead}}\left(t\right)$, which enables the vehicle to respond cooperatively to changes in the preceding vehicle’s acceleration upon detection, thereby improving coordination within the traffic stream. In Equation (7), $a\left(t\right)$ denotes the current acceleration; $a_{\max }$ denotes the maximum acceleration; $v\left(t\right)$ represents the current speed; $v_0$ indicates the desired speed; $s\left(t\right)$ refers to the actual spacing; $s^{*}\left(t\right)$ corresponds to the desired spacing; $K$ is the cooperative gain coefficient of the CAVs; and $\Delta a_{\mathrm{lead}}\left(t\right)$ denotes the acceleration of the leading vehicle;

Equation (8) provides a dynamic expression for the desired spacing, which includes the minimum safe distance $s_0$, a time headway term $v\left(t\right)T$ that grows linearly with speed, a braking safety term ${\displaystyle \frac{v\left(t\right)\Delta v\left(t\right)}{2\sqrt{a_{\max }b}}}$ based on relative speed, and an acceleration compensation term $\gamma \cdot \Delta a_{\mathrm{lead}}\left(t\right)$ from vehicle-to-vehicle perception. The braking safety term based on relative speed refers to the combined estimation of the braking capabilities of the preceding and following vehicles to ensure no collision occurs when there is a relative speed. $T$ indicates the reaction time; $\Delta v\left(t\right)$ refers to the relative speed; $b$ corresponds to the comfortable deceleration; and $\gamma$ is the dynamic acceleration compensation coefficient. Equation (8) is a specific description of the desired spacing in Equation (7), integrating cooperative sensing information to enhance modeling accuracy in connected driving scenarios.

Given a green light duration of seconds $\Delta t_1$, the length of the region through $L_1$ which the current queue can pass the intersection without interruption can be derived, as mathematically formulated in Equation (9):

$$L_1=v\left(t\right)\cdot \Delta t_1+{\displaystyle \frac{1}{2}}a\left(t\right)\cdot {\left(\Delta t_1\right)}^2$$

(9)

For condition 2, this study develops a dynamic queue prediction model for CAV platoons based on the IDM, which is designed to estimate the maximum queue length achievable when a bus arrives precisely at the moment of queue dissipation during the platoon’s start-up phase. The maximum queue length corresponding to the condition in which all lane-borrowing vehicles can pass the stop line within $\Delta t_2$ seconds is denoted as $L_2$.

First, compute the passage time of the lane-borrowing vehicle through the stop line. The target CAV begins from a stationary state and accelerates to pass through the stop line. Let $t_1$ denote the time required for the target CAV to traverse the stop line, as expressed in the following equation:

$$t_1=\sqrt{{\displaystyle \frac{2L_{\mathrm{v}}}{a_{\max }}}}$$

(10)

In Equation (10), $L_{\mathrm{v}}$ denotes the vehicle length.

Let $t_i$ denote the time at which the last vehicle in the platoon passes the stop line, as expressed in the following equation:

$$t_i=t_1+\left(i-1\right)\cdot T_{\mathrm{gap}}$$

(11)

$$T_{gap}\approx T+{\displaystyle \frac{L}{v_0}}$$

(12)

Here, $T_{gap}$ is the time interval between two adjacent CAVs passing the stop line in the queue; $T$ is the reaction time of the CAV vehicle; and $L$ denotes the average spatial occupancy length of a single CAV in the queue, which includes both the vehicle length $L_{\mathrm{v}}$ and the safe following distance. Within a time period of $\Delta t_2$ seconds, the maximum number of vehicles that pass the stop line is $N\left(t\right)$, and the current maximum queue length is $L_2$, as expressed in the following equation:

$$N\left(t\right)=\max \left\{i| t_i\le \Delta t_2\right\}$$

(13)

$$L_2=N\left(t\right)\cdot L$$

(14)

In the formula, under queuing conditions, the safe following distance is equivalent to the desired spacing $s^{*}\left(t\right)$; $N\left(t\right)$ represents the number of vehicles that successfully pass through the intersection within $\Delta t_2$ seconds.

To verify the accuracy of the dynamic available space-time calculation model for intersections formulated in Equations (7)–(14), this study compares the model’s predictions with queue length and vehicle delay data obtained from SUMO simulations under consistent traffic conditions. The results indicate that the average absolute error in queue length prediction ranges from 0.8 to 1.2 vehicles.

The prediction accuracy of the average delay was evaluated using the relative error (RE), defined as

$$RE={\displaystyle \frac{\left|D_{pred}-D_{sim}\right|}{D_{sim}}}$$

(15)

In Equation (15), $D_{pred}$ denotes the model-predicted average delay and $D_{sim}$ represents the SUMO-simulated value. Across all scenarios, the relative error remained below 5%, demonstrating the reliability of the proposed delay estimation model.

Figure 3 illustrates the dynamic control process for condition 1 at an intersection. Given that the bus arrival status and road traffic conditions are continuously changing, the strategy dynamically updates the borrowable zone in real time. If the queue ahead of the bus is fully dissipated by the time it reaches the downstream intersection, activation of the dynamic clearance framework is unnecessary. Furthermore, traffic resource allocation adheres to the principle of right-turning vehicle priority.

3.4. Dynamic Control Process for Intermittent Bus Lanes

In a mixed traffic flow environment, CAVs are capable of autonomously perceiving and identifying traffic operational conditions [32] and can dynamically adapt to different traffic scenarios, thereby improving system coordination and traffic efficiency. Within the dynamic control strategy proposed in this study, the scenarios are classified into four categories based on the anticipated signal status at the downstream intersection for the target bus and target CAV.

• Scenario 1: When the target CAV arrives at the intersection, the traffic light is green; in contrast, when the target bus arrives, the traffic light is red. As illustrated in Figure 4a, the schematic diagram of the dynamic control strategy for Scenario 1 requires all lane-borrowing CAVs to either pass the stop line smoothly before the current green light phase ends or complete a lane change to the conventional lane prior to that moment. A platoon model is established with the target CAV serving as the lead vehicle, aimed at calculating the maximum platoon length $L_1$ that can fully pass the stop line within a specified time interval of $\Delta t_1$ seconds.
  Assuming the current position of the target CAV is denoted as $(x, 0)$, vehicles located upstream within the range from $(x,0)$ to $(x-L_1,0)$ are capable of passing through the intersection smoothly within $\Delta t_1$ seconds. In contrast, vehicles beyond this range and positioned ahead of the target bus must perform a lane change to the conventional lane.
• Scenario 2: When the target CAV and the target bus arrive at the intersection, both traffic lights are green. Based on the principle of public transport priority, the lane borrowing decision is made by assessing the dynamically traversable zone at the intersection.
• Scenario 3: When the target CAV and the target bus arrive, the traffic light is red. All straight-driving lane-borrowing vehicles, including the target CAV, located in front of the target bus are mandatorily required to change lanes back to the regular lane.
• Scenario 4: When the target CAV arrives, the traffic light is red, whereas when the target bus arrives, the traffic light is green. As illustrated in Figure 4b, the control strategy aims to ensure that the target bus passes through the downstream intersection without stopping during the green phase. To achieve this objective, the available green light duration $\Delta t_2$ before the target bus reaches the stop line is first predicted, followed by the calculation of the maximum queue length $L_2$ that can pass the stop line within this time window.
  Assuming the current position of the target CAV is $(x,0)$, vehicles within the range from $(x,0)$ to $(x-L_2,0)$ are able to pass through the intersection without interruption. In contrast, vehicles that are located beyond this range and ahead of the target bus must be mandated to change lanes back to their original lanes.

In summary, the dynamic clearance framework in front of the bus is activated when it enters the bus lane, but remains inactive when the bus stops at the platform. The control strategy is implemented across four distinct scenarios, based on predictions of the arrival times and signal states of the target CAV and the target bus at the intersection.

4. Simulation Analysis

4.1. Simulation Parameter Configuration

This study establishes a simulation scenario, as illustrated in Figure 5, comprising a main road and its downstream adjacent intersection. The simulation focuses on one-way traffic along the main road. The total length of the modeled road segment is 400 m, with three unidirectional lanes. The lane configuration, from innermost to outermost, consists of a left-turn lane, a through lane, and a bus lane. Buses operate at a departure frequency of 50 vehicles per hour, with an average dwell time of 20 s at each stop.

Based on relevant literature [28,33] and the built-in indicators of SUMO, set the relevant parameters for different types of vehicles: The traffic composition includes CAVs and HDVs, with all buses classified as connected vehicles. The desired speed of buses is set to 11 m/s, while the maximum speed of vehicles is 17 m/s. CAVs employ the SL2015 model for lane-changing behavior. The body lengths of vehicles and buses are 5 m and 10 m, respectively. Then, based on the traffic flow as mentioned in the literature [25] and using the Webster cycle calculation formula, the signal cycle of this intersection is set to 100 s, with the green phase for through traffic lasting 38 s. Right-turning vehicles traveling on regular lanes within 70 m [34] of the stop line are permitted and required to seek lane-changing opportunities into the bus lane. The proportion of right-turning vehicles in the traffic stream is 0.1. The average saturation headway between vehicles is approximately 2.5 s. Vehicles initially travel in the through lane and change lanes to the bus lane based on the defined lane-changing strategy. Each simulation run lasts 3600 s, with a time step resolution of 1 s.

4.2. Simulation Experiment Design

Three schemes are selected for comparative analysis: Scheme One features a dedicated bus lane where only right-turning vehicles are permitted to enter the designated intersection zone, while all other vehicles are prohibited from using the lane [25]. Scheme Two implements the control strategy proposed in this study—an intermittent dedicated bus lane that considers both the clearance model and downstream intersection queue conditions. Scheme Three adopts a fixed clearance distance strategy for the dedicated bus lane [16], strictly forbidding vehicles from entering the clearance zone. The clearance zone in this scheme is set to 200 m, based on findings from prior research.

Vehicle delay is selected as the evaluation metric to assess the effectiveness of each control scheme. The average bus departure interval is set to 50 s, with a variance introduced in the departure times to simulate real-world fluctuations. To mitigate the impact of random arrival times on the experimental outcomes, ten statistically independent sets of departure time series data are generated. Under identical initial conditions, simulation experiments are conducted for all three control schemes, and the results are averaged across the datasets to minimize the influence of random variations on the overall evaluation. A simulation environment is developed using the TraCI (Traffic Control Interface) API of the SUMO software, and the workflow is introduced in Figure 6. Experimental analyses are carried out across four key dimensions—penetration rates of connected vehicles, different traffic saturation degrees, different proportions of right-turning vehicles, and different bus departure frequencies—to investigate how these external factors affect the performance of the control strategies.

Communication delay can introduce a time lag in vehicles’ acquisition of preceding vehicles’ status information. In cooperative acceleration or platooning-based control systems, such delays impair the responsiveness to upstream state changes, leading to inaccuracies in predicted vehicle motion. In this context, the proposed dynamic clearance framework model effectively maintains a safe separation between buses and surrounding traffic. Meanwhile, packet loss may temporarily deprive vehicles of critical perception or signal data—such as remaining phase duration and preceding vehicle acceleration—necessitating conservative operational strategies like bus speed reduction to preserve safety under incomplete information. Despite these challenges, the proposed system continues to ensure bus priority relative to alternative approaches. Simulation results validating these analyses are presented in Section 4.3.

4.3. Analysis of Simulation Results

The analysis was performed under traffic flow saturation degrees of 0.8d, 1.0d, and 1.2d. Specifically, 0.8d represents the normal operating condition where traffic flow remains unsaturated, 1.0d corresponds to the critical state approaching saturation, and 1.2d reflects the oversaturated condition. By establishing these distinct scenarios, the adaptability and effectiveness of the proposed method can be thoroughly evaluated across different traffic intensities.

4.3.1. Parameter Analysis Under Different CAV Penetration Rates

To evaluate the traffic flow performance of each control scheme under different connected vehicle penetration rates, penetration rates of 0.2, 0.4, 0.6, 0.8, and 1.0 were established. Simulation scenarios were developed and compared under two traffic flow saturation degrees—1.0d and 1.2d. The average vehicle delay results for each scheme are presented in Figure 7.

As shown in the Figure 7, vehicle delay for non-right-turn movements increases with higher traffic flow saturation, particularly under low connected vehicle penetration rates. This phenomenon can be attributed to the fact that manually driven vehicles traveling in the through direction are prohibited from entering the bus lane, and the limited number of connected vehicles borrowing the lane leads to a pronounced queuing effect in the through lane.

In Scheme One, the bus lane is restricted to right-turning vehicles only. When the penetration rate of connected vehicles remains at a relatively low degree (20%), non-right-turning vehicles experience the highest delay. In Scheme Three, under low penetration rates, the clearance zone restricts the number of connected vehicles that can borrow the lane, leading to congestion in the through lane and consequently causing significant delays for non-right-turning vehicles. Furthermore, when the traffic flow saturation reaches 1.2d with connected vehicle penetration rates at 40% and 60%, bus operations in Scheme Three are notably impeded. This occurs because more connected vehicles attempt to change lanes into the dedicated bus lane. Upon the arrival of a bus at the intersection, some borrowing vehicles fail to vacate the bus lane in time, thereby obstructing the smooth passage of buses. Right-turning vehicles are also affected, as queuing at the intersection leads to increased delays. In contrast, Scheme Two demonstrates consistent effectiveness in prioritizing bus passage across different traffic flow saturation degrees and connected vehicle penetration rates.

Figure 8 presents the vehicle trajectories within the bus lane under the three schemes, further substantiating the advantages of Scheme Two. Under a traffic flow saturation degree of 1.2d, the superiority of Scheme Two becomes increasingly evident as the connected vehicle penetration rate increases, a trend that is clearly reflected in the corresponding trajectory diagrams. In Scheme One, only right-turning vehicles are permitted to borrow the bus lane, leading to consistently high delays for non-right-turning vehicles. In Scheme Three, when the “non-clearance zone” condition is satisfied, the frequency of connected vehicles borrowing the lane rises significantly with increasing penetration rates. Certain through vehicles enter the bus lane before the bus stop but, due to limited opportunities to return to their original lanes, are forced to stop and wait when the bus dwells at the station. This behavior not only disrupts normal bus operations but also impedes the smooth movement of right-turning vehicles, thereby further increasing overall delays. In contrast, Scheme Two enables right-turning vehicles to complete lane changes earlier when both safety and efficiency criteria are met. This mechanism effectively reduces the delay of right-turning vehicles while better safeguarding bus priority.

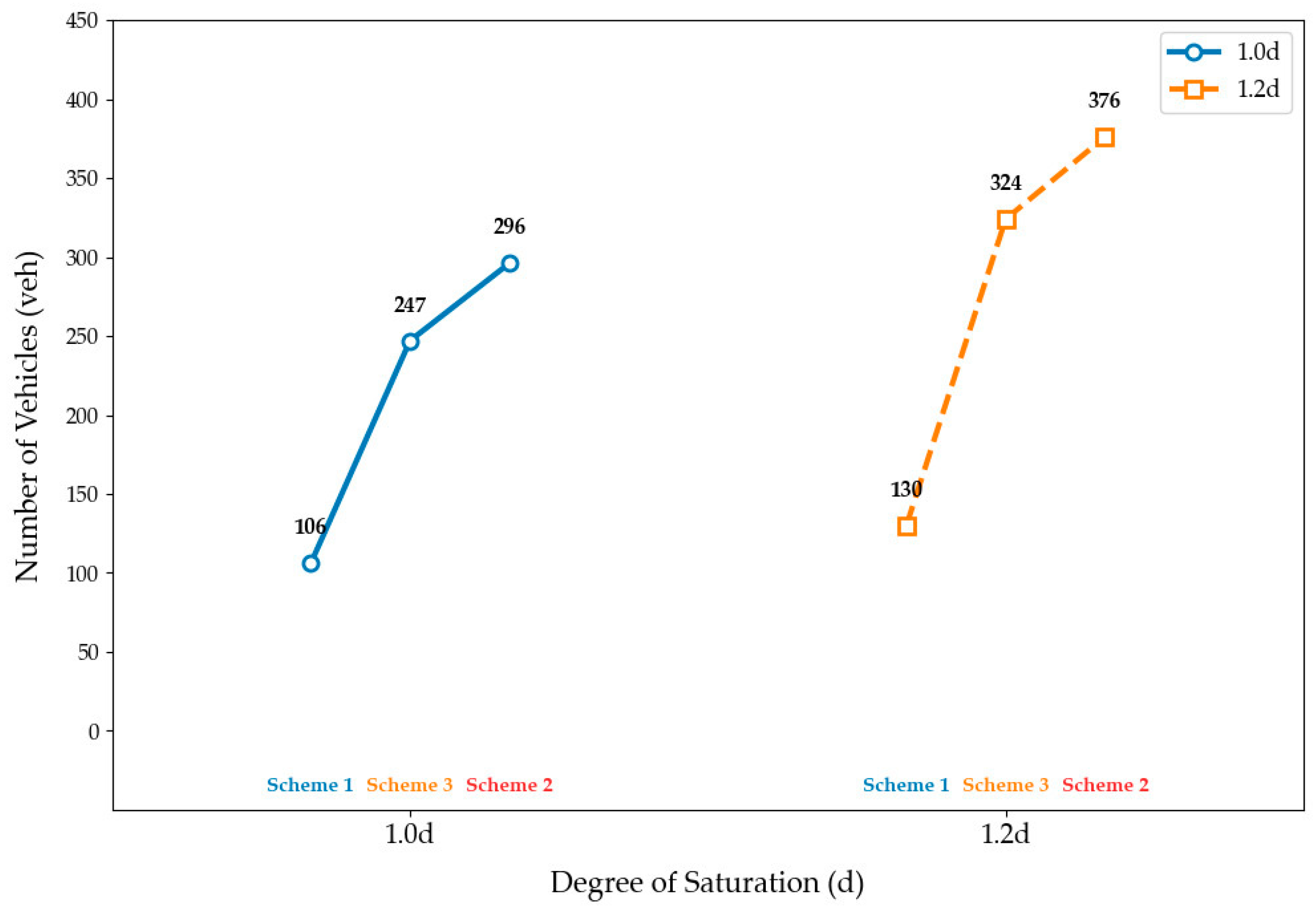
4.3.2. Parameter Analysis Under Different Degrees of Traffic Flow Saturation

Figure 9 shows the vehicle delay of the three schemes under different traffic flow saturation degrees when the penetration rate of connected vehicles is 100%.

Specifically, in Scheme One, the bus lane is exclusively reserved for buses and right-turning vehicles. While this ensures minimal interference from vehicles and maintains a high degree of bus priority, it results in underutilization of time-space resource for the bus lane. Consequently, as traffic flow saturation increases, the delay experienced by non-right-turning vehicles also rises. In Scheme Three, the bus lane is accessible to qualified connected straight-moving vehicles. At a saturation degree of 1.0d, the large clearance distance limits the opportunities for non-right-turning vehicles to utilize the bus lane, leading to inefficient use of the lane. At 1.2d saturation, although some straight-moving vehicles do enter the bus lane, they often fail to return to the adjacent lane in time when a bus approaches from behind. Given that the adjacent lanes are already saturated and lack sufficient space for lane changes, this causes disruptions to bus operations and ultimately leads to the failure of the control strategy in Scheme Three.

In comparison, Scheme Two offers a degree of bus priority comparable to that of Scheme One, while more effectively utilizing the residual capacity of the bus lane. It facilitates the rational borrowing and timely return of passenger vehicles, thereby achieving the best overall performance among the three schemes.

4.3.3. Parametric Analysis Under Different Proportions of Right-Turning Vehicle Flows

Figure 10 presents the delay performance of the three schemes under a traffic flow saturation degree of 1.0d and a 100% penetration rate of connected vehicles across different proportions of right-turning vehicle flows. The tested proportions of right-turning vehicles are 0.1, 0.2, 0.3, and 0.4.

As shown in the Figure 10, under Scheme One, the average bus delay increases progressively with the rising proportion of right-turning vehicles. This indicates that ensuring bus priority becomes increasingly challenging under high right-turning traffic proportions. The primary cause lies in the fact that right-turning vehicles are permitted to enter the bus lane only at designated sections. As the volume of right-turning traffic increases, the frequency of spatial conflicts between buses and right-turning vehicles rises, thereby intensifying bus delays. In contrast, the delays of both non-right-turning and right-turning vehicles remain relatively stable under this scheme, exhibiting no significant fluctuations.

In Scheme Two, the average bus delay consistently remains lower than that of the other two schemes across all tested right-turn proportions, with the performance advantage becoming more pronounced under higher right-turn ratios. For example, when the right-turn proportion reaches 0.4, bus delays are significantly reduced and maintained below 100 s, clearly demonstrating the effectiveness of Scheme Two in safeguarding bus priority. Furthermore, the delay of non-right-turning vehicles is slightly lower compared to Scheme One, indicating a more rational organization of overall traffic flow in Scheme Two. The control strategy enables right-turning vehicles to enter the bus lane in advance when safety conditions permit, thereby reducing weaving conflicts and the frequency of interactions, ultimately leading to improved operational performance. While the delay of right-turning vehicles increases moderately with their proportion, the overall delay degree still outperforms both Scheme One and Scheme Three. These results suggest that Scheme Two not only enhances overall traffic efficiency but also achieves superior coordination and conflict mitigation among different vehicle categories.

In Scheme Three, bus delays increase most markedly as the proportion of right-turning vehicles rises. As the volume of right-turning traffic grows, the system must manage not only the existing straight-through vehicles that temporarily use the bus lane but also an increasing number of right-turning vehicles requiring lane changes, which intensifies conflicts over the use of the bus lane. Additionally, some vehicles stop in front of buses while waiting, obstructing the movement of both buses already in the bus lane and right-turning vehicles attempting to maneuver. Furthermore, the clearance zone requirement restricts the ability of certain right-turning vehicles to perform timely lane changes, this leads to an extended dwell time of the vehicle in the through lane and negatively impacting traffic efficiency in both the through and right-turn movement directions. Overall, Scheme Three is ineffective in ensuring public transportation priority, as right-turning vehicles significantly disrupt bus operations. Concurrently, the average delays of both non-right-turning and right-turning vehicles are consistently higher compared to the other two schemes.

Comprehensive analysis indicates that under Scheme One and Scheme Three, the delay of non-right-turning vehicles slightly decreases as the proportion of right-turning vehicles increases. This occurs because the rising proportion of right-turning vehicles leads to a relative reduction in non-right-turning vehicles, thereby alleviating congestion in general lanes and reducing their queuing and waiting times. Scheme Two demonstrates consistently superior performance across all right-turn proportion scenarios, effectively ensuring public transport priority while maintaining the operational efficiency of non-public transport vehicles. Scheme One performs at a moderate degree—it maintains acceptable delay degrees under low right-turn proportions but experiences a significant increase in public transport delays under high right-turn conditions, thereby compromising the assurance of bus priority. Scheme Three exhibits a decline in overall traffic efficiency as the proportion of right-turning vehicles increases, failing to achieve effective traffic organization and coordinated control.

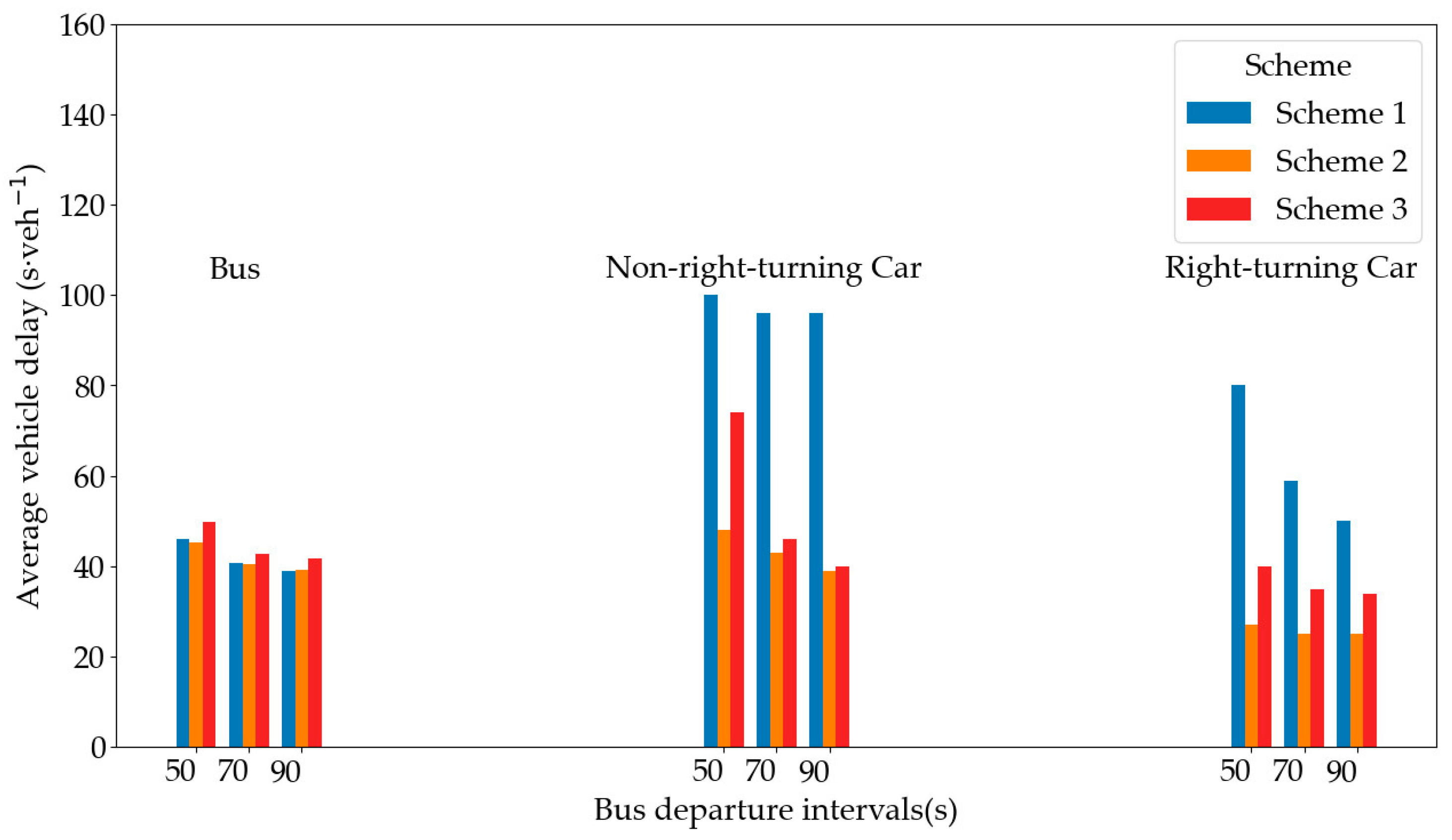
4.3.4. Parameter Analysis Under Different Bus Departure Intervals

Under the conditions of a 100% penetration rate of connected vehicles and a traffic flow saturation degree of 1.2d, bus departure intervals were set at 50, 70, and 90 s. Figure 11 illustrates the delay performance of the three schemes under different departure frequencies.

As shown in the Figure 11, in Scheme One, the delay experienced by non-right-turning vehicles remains largely unaffected by variations in the bus departure time intervals. This is due to the fact that Scheme One permits right-turning vehicles to change lanes and enter the bus lane only at designated locations, a process that is minimally influenced by bus departure frequency. As the bus departure interval increases, the likelihood of interactions between buses and right-turning vehicles diminishes, resulting in a corresponding reduction in the delay of right-turning vehicles.

In Scheme Two, among the vehicles permitted to use the bus lane, right-turning vehicles are granted higher priority in utilizing the dedicated lane. Compared to Scheme One, the overall vehicle delay is significantly reduced. This scheme achieves more effective coordination between bus operations and right-turning movements, thereby minimizing mutual interference between the two.

In Scheme Three, lane-borrowing vehicles must enter the bus lane outside the designated clearance zone, with bus departure frequency directly influencing their entry timing and spatial positioning. When the bus departure interval increases, the idle time of the bus lane expands, permitting a greater number of lane-borrowing vehicles to utilize the lane. However, this may result in delays for certain right-turning vehicles at the intersection, as they can be obstructed by lane-borrowing vehicles proceeding straight. Simultaneously, an increased volume of lane-borrowing vehicles may lead to conflicts when they fail to return to their original lanes promptly upon bus arrival, thereby compromising bus priority.

4.3.5. Number of Vehicles Utilizing the Bus Lane

Under the conditions of a 100% connected vehicle penetration rate and traffic flow saturation levels of 1.0 and 1.2, Figure 12 illustrates the number of vehicles utilizing the bus lane across different scenarios.

This metric can reflect the actual utilization efficiency of the intermittent bus lane. By comparing the number of serviced vehicles across different traffic saturation levels, we are able to examine how many vehicles successfully traverse the bus lane under varying demand and signal conditions.

4.4. Discussion

Based on the descriptions of the different schemes in Section 4.3, the data processing results for each scheme are presented in

Table 2. The average delay of all vehicles under different schemes.

Schemes	Scheme One		Scheme Two		Scheme Three
	1.0d	1.2d	1.0d	1.2d	1.0d	1.2d
Average vehicle delay of buses (s∙veh−1)	46 ± 1	46 ± 1	45 ± 1	45 ± 1	45 ± 2	50 ± 2
Average vehicle delay of non-right-turning cars (s∙veh−1)	48 ± 2	100 ± 4	36 ± 1	48 ± 2	42 ± 2	74 ± 3
Average vehicle delay of right-turning cars (s∙veh−1)	27 ± 1	80 ± 3	18 ± 2	27 ± 1	23 ± 2	40 ± 2

, from which the average delay values of all vehicles under the three schemes are derived. Significant differences in average vehicle delay are observed across the three schemes. At a traffic flow saturation degree of 1.0d, Scheme Two achieves an 18% reduction in average vehicle delay compared to Scheme One and a 10% reduction compared to Scheme Three, while maintaining bus priority and enhancing the utilization efficiency of dedicated lanes. Under the higher saturation degree of 1.2d, these reductions increase to 46% and 27% compared to Scheme One and Scheme Three, respectively. These results indicate that in high-demand scenarios with constrained lane resources, the absence of an effective lane-borrowing guidance mechanism may still lead to disruptions in right-turning traffic flows, resulting in significantly increased delays.

The results demonstrate that the proposed control strategy ensures efficient and rational utilization of spatiotemporal resources within bus-only lanes, offering a viable reference framework for their dynamic management. By leveraging intelligent connected vehicle technology, the approach can enhance bus operational efficiency and reduces overall vehicle delays, all without requiring additional infrastructure investment.

5. Conclusions

The following conclusions are drawn from this study.

Firstly, for road segment control, the dynamic clearance framework ahead of the bus is activated. Regarding intersection control, leveraging the sensing and cooperative capabilities of connected vehicles, four scenarios are defined based on the signal status at the moment when the target CAV and target bus arrive at the intersection, enabling scenario-specific decision-making.

Secondly, simulation results indicate that at a saturation degree of 1.0d, the proposed approach not only ensures public transport priority and enhances the utilization efficiency of dedicated lanes, but also reduces average vehicle delay by 18% compared to Scheme One and by 10% compared to Scheme Three. Under a higher saturation degree of 1.2d, the reductions in average vehicle delay reach 46% and 27%, respectively.

In this study, to further demonstrate the broader applicability of the proposed framework, we discuss its future scalability to multilane arterials, multi-intersection corridors, and real-world urban networks. Advances in connected vehicle infrastructure and adaptive traffic control would enable the clearance distance model and lane-borrowing mechanism to be applied across longer corridors, coordinated among successive intersections, and integrated with real-world network management systems as follows: (1) The clearance distance model and the available lane-borrowing mechanism can be generalized to multilane arterial corridors by applying segment-level control logic to each homogeneous road section. For longer corridors with varying lane configurations or multiple bus-priority lanes, the framework can be adapted by recalibrating the estimation of usable space, adjusting the platoon propagation constraints, and incorporating lane-based priority assignment rules. (2) Extending the model to multi-intersection networks requires coordinated control of successive segments. The clearance distance and dynamic borrowing logic can be harmonized across intersections by integrating signal progression information, synchronizing available space estimation with upstream and downstream signal phases, and introducing corridor-level constraints to avoid spillback or blocking between junctions.

To facilitate the practical deployment of the proposed system, future research can explore implementation strategies within real smart city infrastructures, focusing on the following key aspects:

• Deployment cost assessment and optimization: The deployment of the system must account for a comprehensive range of cost factors, including hardware investment, communication infrastructure development, system integration, and long-term maintenance. Future research should establish a rigorous cost–benefit analysis model to quantitatively assess the operational benefits—such as reduced traffic delays and energy consumption—generated by the system across varying urban scales and traffic flow regimes. Furthermore, adopting a modular design paradigm can enhance the scalability and interoperability of on-board units and roadside equipment, effectively minimizing expenses related to secondary development, upgrades, and ongoing operation and maintenance. For initial implementation, phased deployment in high-priority corridors or representative intersections is recommended to validate system performance under real-world conditions while managing financial risk.
• Data requirements and communication architecture design: The operation of the system relies on diverse multi-source traffic data, including real-time vehicle positions, velocities, signal phases, traffic flow densities, and lane occupancy rates. To ensure efficient and scalable communication, the following three measures can be implemented: (1) At the vehicle level, V2V communication enables real-time acquisition of neighboring vehicles’ states; (2) at the roadside unit (RSU) level, local data preprocessing and decentralized decision-making are performed to reduce upstream data transmission load; and (3) at the central control level, system-wide coordination and strategic optimization are carried out based on aggregated information.
• Optimization of the Configuration and Layout of Roadside Units (RSUs): RSUs serve as critical infrastructure enabling reliable information exchange within intelligent transportation systems. An optimized RSU deployment ensures that vehicles receive essential real-time information—such as traffic signal status, lane-change advisories, and priority access strategies. To achieve optimal spatial distribution, future research should develop and apply layout optimization models grounded in network topology and communication coverage analysis. These models must integrate key factors including the number of deployed units, effective communication range, latency requirements, and economic constraints to systematically determine cost-effective and performance-driven RSU placement.