A Review on Risk-Averse Bidding Strategies for Virtual Power Plants with Uncertainties: Resources, Technologies, and Future Pathways
Abstract
1. Introduction
- (1)
- It establishes a comprehensive, resource-centric taxonomy and an integrated analytical framework for risk-averse VPP bidding. The review categorizes VPPs into four primary archetypes based on their dominant aggregated resource and the primary source of flexibility they provide—DER-driven, demand response-oriented, electric vehicle-integrated, and multi-energy systems. This classification, while acknowledging that real-world VPPs are often hybrids, provides a structured lens to examine how each category’s unique characteristics shape its market participation strategies, dominant risk exposures, and suitable optimization methodologies.
- (2)
- It delivers a detailed and comparative analysis of the risk-averse optimization techniques employed across different VPP archetypes. The review meticulously surveys a spectrum of methods, from established approaches like stochastic programming with Conditional Value at Risk (CVaR) and robust optimization to emerging paradigms such as distributionally robust optimization and AI-driven learning. It critically assesses their application contexts, computational trade-offs, and effectiveness in mitigating specific uncertainties related to price volatility, renewable generation, and prosumer behavior, providing a practical guide for method selection.
- (3)
- It synthesizes cutting-edge research trends, identifies critical unresolved challenges, and outlines a forward-looking research agenda. The review consolidates the latest advancements while highlighting persistent barriers such as computational bottlenecks, data privacy issues, and a lack of interoperability standards. Building upon this diagnosis, it proposes concrete pathways to advance the field, including the development of hybrid AI–physical models, the creation of standardized interfaces and novel market mechanisms, and the promotion of collaborative VPP ecosystems, thereby providing a comprehensive roadmap for future research and development.
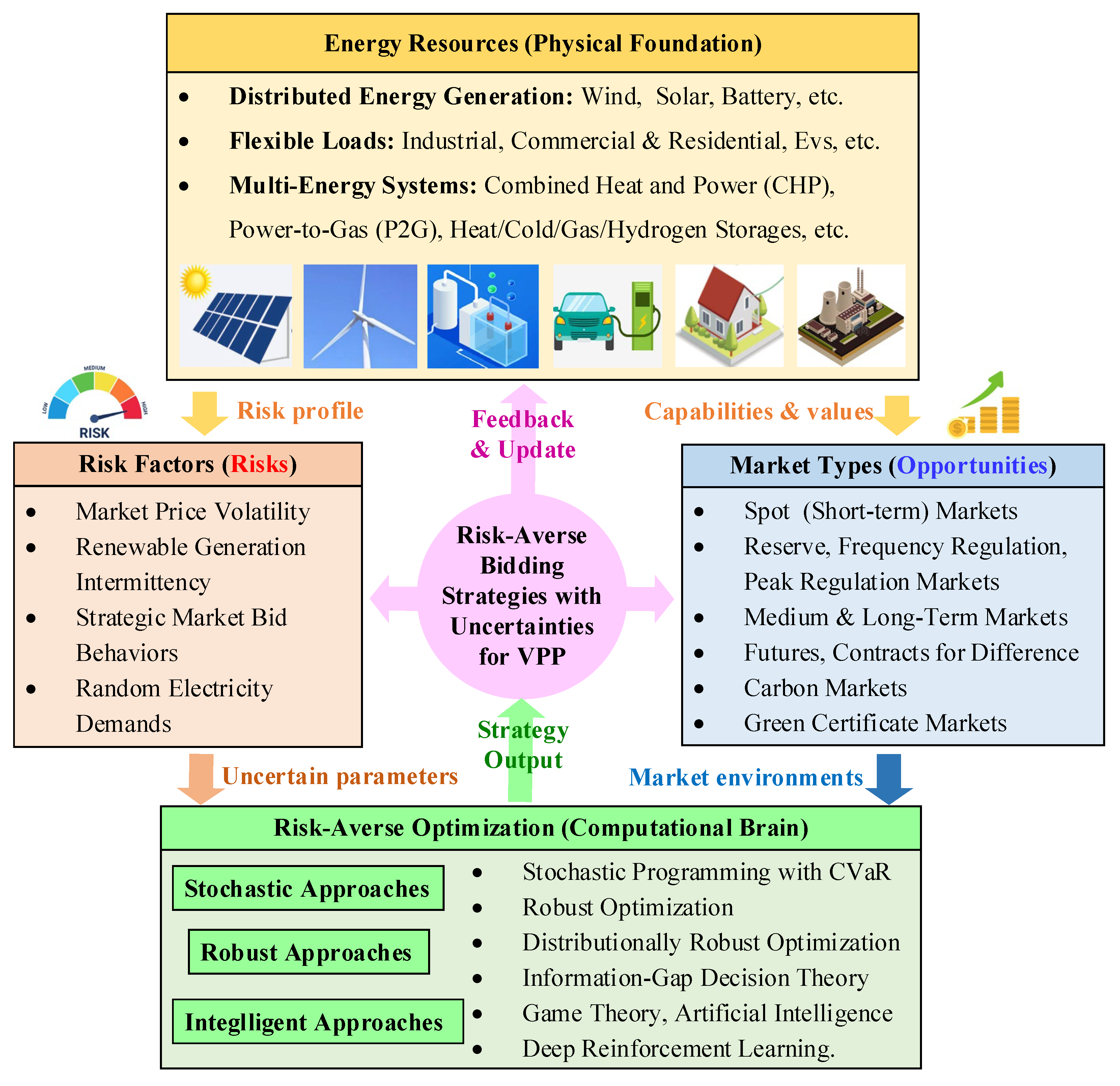
2. Resources and Decision Framework
3. DER-Driven VPP
3.1. Basic Structure
3.2. Market Types and Opportunities
3.3. Risk-Averse Optimization Methods
3.3.1. Stochastic Approaches
3.3.2. Robust Approaches
3.3.3. Game-Theoretic Approaches
4. DR-Oriented VPP
4.1. The Centrality of DR in VPP Resource Aggregation
4.2. Risk-Averse DR Scheduling Optimization
4.3. Integrated Coordination Mechanisms for DR-Oriented VPPs
4.4. Advanced Methodologies and Market Integration
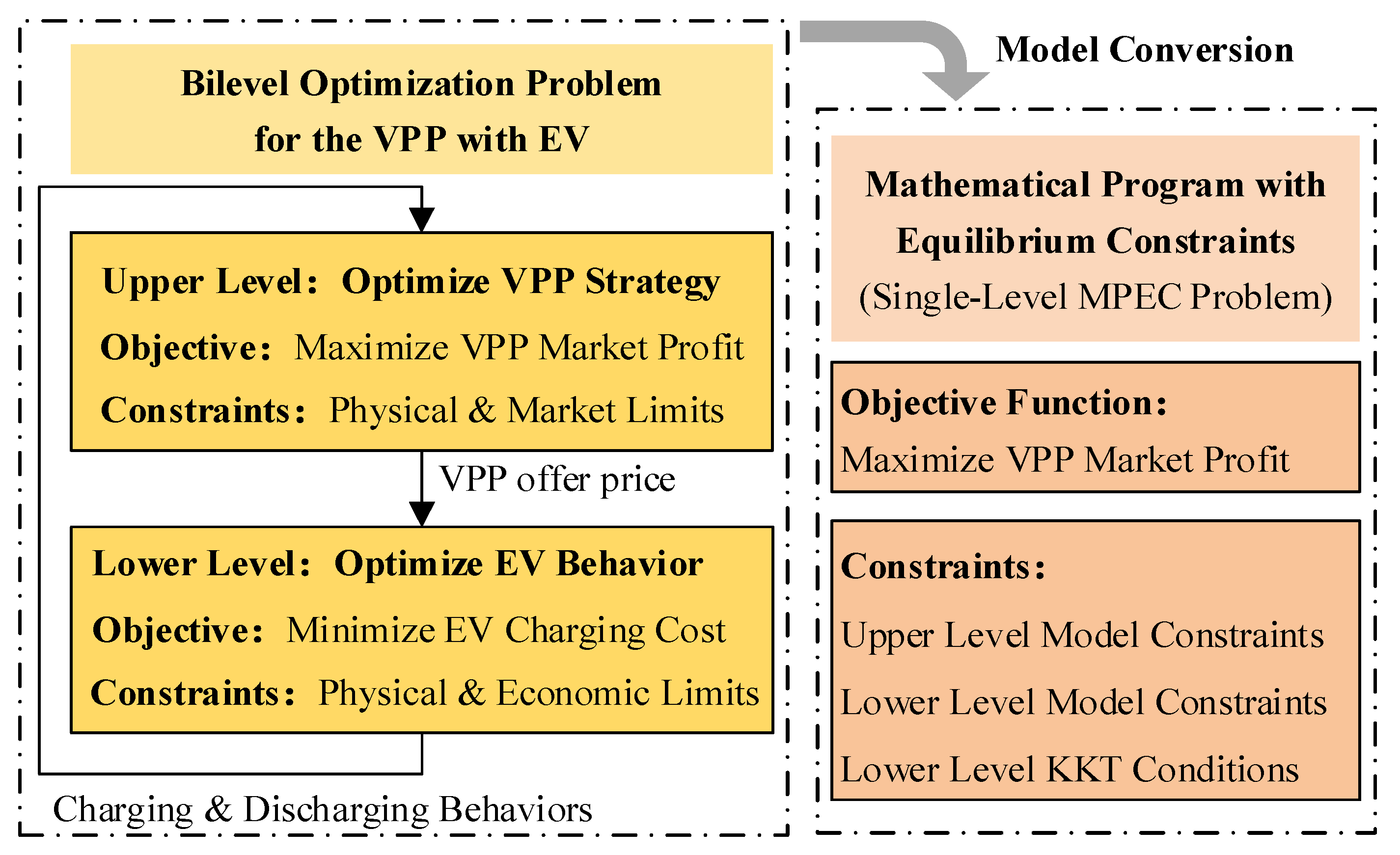
5. Electric Vehicle-Integrated VPP
5.1. Uncertainty Modeling and Risk Quantification
5.2. Risk-Averse Optimization for EV Charging and Discharging
- Upper Level (VPP—Leader): Maximizes its profit, considering the response of EVs.
- Lower Level (EV—Follower): Each EV minimizes its charging cost based on the VPP’s offered price πEV.
5.3. Multi-Market Participation and Risk Management
6. Multi-Energy VPP
6.1. Modeling Multi-Energy Flexibility and Complementarity
6.2. Risk-Aware Multi-Energy Scheduling
6.3. Strategic Participation Considering Multi-Energy Market Environments
7. Conclusions and Discussions
- (1)
- Firstly, a primary challenge lies in the escalating complexity of modeling and computation. As VPPs evolve to encompass multi-energy carriers, numerous distributed assets, and participation in multiple simultaneous markets [127], the resulting optimization problems become high-dimensional, non-convex, and computationally intractable for real-world applications. While techniques like scenario reduction offer partial solutions, efficiently solving large-scale stochastic or distributionally robust models for real-time bidding remains a significant hurdle, a challenge acknowledged in studies dealing with complex multi-objective problems [131].
- (2)
- Secondly, there is a critical gap in standardization and interoperability. The lack of universal communication protocols and market interfaces creates friction for integrating diverse DERs and for seamless participation in different regional markets, which complicates the aggregation process and limits scalability, an issue that decentralized approaches like P2P trading [112] and blockchain [126] aim to address but have not yet solved at scale.
- (3)
- Thirdly, data availability and quality pose a substantial obstacle. Accurate risk assessment and bidding rely heavily on high-resolution data for forecasting prices, renewable output, and consumer behavior. Issues of data privacy, ownership, and the cost of acquiring reliable data can impede the development of robust models, a challenge particularly acute when dealing with unobservable prosumers [90]. Moreover, existing risk-management frameworks often struggle with multi-domain risk correlation. Many models treat uncertainties in isolation, failing to capture the complex tail dependencies between different market commodities [125] and external factors like extreme weather events, which can lead to an underestimation of systemic risk.
- (4)
8. Future Directions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chu, S.; Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, C.; Li, M. Impacts of electricity market reforms: From the perspective of economic-energy-environment system synergies. J. Clean. Prod. 2025, 509, 145603. [Google Scholar] [CrossRef]
- Danielian, A. Regulating electricity spot markets during extreme events: The 2021 Texas case. Util. Policy 2025, 93, 101891. [Google Scholar] [CrossRef]
- Fabra, N. Reforming European electricity markets: Lessons from the energy crisis. Energy Econ. 2023, 126, 106963. [Google Scholar] [CrossRef]
- Holt, C.A.; Laury, S.K. Risk aversion and incentive effects. Am. Econ. Rev. 2002, 92, 1644–1655. [Google Scholar] [CrossRef]
- Huang, J.; Li, H.; Zhang, Z. Review of Virtual Power Plant Response Capability Assessment and Optimization Dispatch. Technologies 2025, 13, 216. [Google Scholar] [CrossRef]
- Esfahani, M.; Alizadeh, A.; Cao, B.; Kamwa, I.; Xu, M. Bridging theory and practice: A comprehensive review of virtual power plant technologiesand their real-world applications. Renew. Sust. Energy Rev. 2025, 222, 115929. [Google Scholar] [CrossRef]
- Alajlan, R.; Rahman, M.H.; Alnaeem, M.; Almaiah, M. A literature review on cybersecurity risks and challenges assessments in virtual power plants: Current landscape and future research directions. IEEE Access 2024, 12, 188813–188827. [Google Scholar] [CrossRef]
- Gao, H.; Jin, T.; Feng, C.; Li, C.; Chen, Q.; Kang, C. Review of virtual power plant operations: Resource coordination and multidimensional interaction. Appl. Energy 2024, 357, 122284. [Google Scholar] [CrossRef]
- Naval, N.; Yusta, J.M. Virtual power plant models and electricity markets—A review. Renew. Sust. Energy Rev. 2021, 149, 111393. [Google Scholar] [CrossRef]
- Rouzbahani, H.M.; Karimipour, H.; Lei, L. A review on virtual power plant for energy management. Sustain. Energy Technol. Assess. 2021, 47, 101370. [Google Scholar] [CrossRef]
- Yu, S.; Fang, F.; Liu, Y.; Liu, J. Uncertainties of virtual power plant: Problems and countermeasures. Appl. Energy 2019, 239, 454–470. [Google Scholar] [CrossRef]
- Ruan, G.; Qiu, D.; Sivaranjani, S.; Awad, A.S.A.; Štrbac, G. Data-driven energy management of virtual power plants: A review. Adv. Appl. Energy 2024, 14, 100170. [Google Scholar] [CrossRef]
- Wang, G.; Lin, Z.; Chen, Y.; Qiu, R.; Zhang, H.; Yan, J. Carbon-billed future for virtual power plants: A comprehensive review. Renew. Sust. Energ. Rev. 2025, 217, 115719. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y. A comprehensive review on electric vehicles integrated in virtual power plants. Sustain. Energy Technol. Assess. 2021, 48, 101678. [Google Scholar] [CrossRef]
- Cheng, L.; Huang, P.; Zou, T.; Zhang, M.; Peng, P.; Lu, W. Evolutionary game-theoretical approaches for long-term strategic bidding among diverse stakeholders in large-scale and local power markets: Basic concept, modelling review, and future vision. Int. J. Electr. Power 2025, 166, 110589. [Google Scholar] [CrossRef]
- Li, G.; Shi, J.; Qu, X. Modeling methods for GenCo bidding strategy optimization in the liberalized electricity spot market-A state-of-the-art review. Energy 2011, 36, 4686–4700. [Google Scholar] [CrossRef]
- Lu, X.; Li, K.; Xu, H.; Wang, F.; Zhou, Z.; Zhang, Y. Fundamentals and business model for resource aggregator of demand response in electricity markets. Energy 2020, 204, 117885. [Google Scholar] [CrossRef]
- Peng, F.; Zhang, W.; Zhou, W.; Tao, J.; Sun, H.; Hu, S.; Lyu, Q.; Wang, Y.; Fan, X. Review on bidding strategies for renewable energy power producers participating in electricity spot markets. Sustain. Energy Technol. 2023, 58, 103329. [Google Scholar] [CrossRef]
- Toufani, P.; Karakoyun, E.C.; Nadar, E.; Fosso, O.B.; Kocaman, A.S. Optimization of pumped hydro energy storage systems under uncertainty: A review. J. Energy Storage 2023, 73, 109306. [Google Scholar] [CrossRef]
- Mei, S.; Tan, Q.; Trivedi, A.; Srinivasan, D. A two-step optimization model for virtual power plant participating in spot market based on energy storage power distribution considering comprehensive forecasting error of renewable energy output. Appl. Energy 2024, 376, 124234. [Google Scholar] [CrossRef]
- Ghanuni, A.; Sharifi, R.; Feshki-Farahani, H. A risk-based multi-objective energy scheduling and bidding strategy for a technical virtual power plant. Electr. Power Syst. Res. 2023, 220, 109344. [Google Scholar] [CrossRef]
- Ghamarypour, S.; Rahimiyan, M. Energy resources investment for industrial virtual power plants under techno-economic uncertainties. Int. J. Electr. Power 2025, 164, 110409. [Google Scholar] [CrossRef]
- Emarati, M.; Keynia, F.; Rashidinejad, M. A two-stage stochastic programming framework for risk-based day-ahead operation of a virtual power plant. Int. Trans. Electr. Energy 2020, 30, 12255. [Google Scholar] [CrossRef]
- Lima, R.M.; Conejo, A.J.; Giraldi, L.; Le Maître, O.; Hoteit, I.; Knio, O.M. Sample average approximation for risk-averse problems: A virtual power plant scheduling application. EURO J. Comput. Optim. 2021, 9, 100005. [Google Scholar] [CrossRef]
- Lima, R.M.; Conejo, A.J.; Giraldi, L.; Le Maître, O.; Hoteit, I.; Knio, O.M. Risk-Averse Stochastic Programming vs. Adaptive Robust Optimization: A Virtual Power Plant Application. INFORMS J. Comput. 2022, 34, 1795–1818. [Google Scholar] [CrossRef]
- Sun, G.; Qian, W.; Huang, W.; Xu, Z.; Fu, Z.; Wei, Z.; Chen, S. Stochastic adaptive robust dispatch for virtual power plants using the binding scenario identification approach. Energies 2019, 12, 1918. [Google Scholar] [CrossRef]
- Liu, H.; Qiu, J.; Zhao, J. A data-driven scheduling model of virtual power plant using Wasserstein distributionally robust optimization. Int. J. Electr. Power 2022, 137, 107801. [Google Scholar] [CrossRef]
- Akkaş, O.P.; Çam, E. Risk-based Optimal Bidding and OperationalScheduling of a Virtual Power Plant Considering Battery Degradation Cost and Emission. Adv. Electr. Comput. Eng. 2023, 23, 19–28. [Google Scholar] [CrossRef]
- Kardakos, E.G.; Simoglou, C.K.; Bakirtzis, A.G. Optimal Offering Strategy of a Virtual Power Plant: A Stochastic Bi-Level Approach. IEEE Trans. Smart Grid 2016, 7, 794–806. [Google Scholar] [CrossRef]
- Shafiekhani, M.; Ahmadi, A.; Homaee, O.; Shafie-Khah, M.; Catalão, J.P.S. Optimal bidding strategy of a renewable-based virtual power plant including wind and solar units and dispatchable loads. Energy 2022, 239, 122379. [Google Scholar] [CrossRef]
- Khandelwal, M.; Mathuria, P.; Bhakar, R. Virtual Power Plant (VPP) scheduling with uncertain multiple Locational Marginal Prices. IET Energy Syst. Integr. 2022, 4, 436–447. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X.; Jiang, C.; Bai, B.; Zhang, K. Day Ahead Bidding Strategy for Virtual Power Plants Considering Sharpe Ratio. Power Syst. Technol. 2023, 47, 1512–1522. [Google Scholar]
- Singh, K.N.; Goswami, A.K.; Chudhury, N.B.D.; Shuaibu, H.A.; Ustun, T.S. Enhancing cybersecurity in virtual power plants by detecting network based cyber attacks using an unsupervised autoencoder approach. Sci. Rep. 2025, 15, 32374. [Google Scholar] [CrossRef] [PubMed]
- Rahmani-Dabbagh, S.R.; Sheikh-El-Eslami, M.K. Risk-based profit allocation to DERs integrated with a virtual power plant using cooperative Game theory. Electr. Power Syst. Res. 2015, 121, 368–378. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, M.; Ao, J.; Wang, Z.; Dong, H.; Zeng, M. Profit Allocation Strategy of Virtual Power Plant Based on Multi-Objective Optimization in Electricity Market. Sustainability 2022, 14, 6229. [Google Scholar] [CrossRef]
- Baringo, A.; Baringo, L.; Arroyo, J.M. Holistic planning of a virtual power plant with a nonconvex operational model: A risk-constrained stochastic approach. Int. J. Electr. Power 2021, 132, 107081. [Google Scholar] [CrossRef]
- Castillo, A.; Flicker, J.; Hansen, C.W.; Watson, J.P.; Johnson, J. Stochastic optimisation with risk aversion for virtual power plant operations: A rolling horizon control. IET Gener. Transm. Dis. 2019, 13, 2182–2189. [Google Scholar] [CrossRef]
- Deng, J.; Guo, Q. Decentralized energy management system of distributed energy resources as virtual power plant: Economic risk analysis via downside risk constraints technique. Comput. Ind. Eng. 2023, 183, 109522. [Google Scholar] [CrossRef]
- Gao, R.; Guo, H.; Zhang, R.; Mao, T.; Xu, Q.; Zhou, B.; Yang, P. A two-stage dispatch mechanism for virtual power plant utilizing the CVaR theory in the electricity spot market. Energies 2019, 12, 3402. [Google Scholar] [CrossRef]
- Huang, M.; Cui, X.; Wang, Y. Distributed differentially private energy management of virtual power plants. Electr. Power Syst. Res. 2024, 234, 110687. [Google Scholar] [CrossRef]
- Li, N.; Tan, C.; Lin, H.; Ma, X.; Zhang, X. Three-level interactive energy management strategy for optimal operation of multiple virtual power plants considering different time scales. Int. J. Energy Res. 2021, 45, 1069–1096. [Google Scholar] [CrossRef]
- Lin, W.M.; Yang, C.Y.; Wu, Z.Y.; Tsay, M.T. Optimal control of a virtual power plant by maximizing conditional value-at-risk. Appl. Sci. 2021, 11, 7752. [Google Scholar] [CrossRef]
- Liu, J.; Song, Y. Research on Risk Assessment of Virtual Power Plant Transaction Based on Text Mining and Cloud Models. Power Syst. Technol. 2025, 49, 1089–1097. [Google Scholar]
- Qi, N.; Cheng, L.; Li, H.; Zhao, Y.; Tian, H. Portfolio optimization of generic energy storage-based virtual power plant under decision-dependent uncertainties. J. Energy Storage 2023, 63, 107000. [Google Scholar] [CrossRef]
- Qiu, J.; Meng, K.; Zheng, Y.; Dong, Z.Y. Optimal scheduling of distributed energy resources as a virtual power plant in a transactive energy framework. IET Gener. Transm. Dis. 2017, 11, 3417–3427. [Google Scholar] [CrossRef]
- Rahmani-Dabbagh, S.R.; Sheikh-El-Eslami, M.K. Risk Assessment of Virtual Power Plants Offering in Energy and Reserve Markets. IEEE Trans. Power Syst. 2016, 31, 3572–3582. [Google Scholar] [CrossRef]
- Sadeghian, O.; Mohammadpour Shotorbani, A.M.; Mohammadi-ivatloo, B. Generation maintenance scheduling in virtual power plants. IET Gener. Transm. Dis. 2019, 13, 2584–2596. [Google Scholar] [CrossRef]
- Sadeghian, O.; Oshnoei, A.; Khezri, R.; Muyeen, S.M. Risk-constrained stochastic optimal allocation of energy storage system in virtual power plants. J. Energy Storage 2020, 31, 101732. [Google Scholar] [CrossRef]
- Shabanzadeh, M.; Sheikh-El-Eslami, M.K.; Haghifam, M.R. Risk-based medium-term trading strategy for a virtual power plant with first-order stochastic dominance constraints. IET Gener. Transm. Dis. 2017, 11, 520–529. [Google Scholar] [CrossRef]
- Sreenivasulu, G.; Sahoo, N.C.; Balakrishna, P. Low economic risk operation of transactive energy markets with renewable sources and virtual power plants using self-adaptive particle swarm optimization. Electr. Eng. 2022, 104, 2729–2755. [Google Scholar] [CrossRef]
- Sučić, S.; Dragičević, T.; Capuder, T.; Delimar, M. Economic dispatch of virtual power plants in an event-driven service-oriented framework using standards-based communications. Electr. Power Syst. Res. 2011, 81, 2108–2119. [Google Scholar] [CrossRef]
- Tajeddini, M.A.; Rahimi-Kian, A.; Soroudi, A. Risk averse optimal operation of a virtual power plant using two stage stochastic programming. Energy 2014, 73, 958–967. [Google Scholar] [CrossRef]
- Wang, S.; Jia, R.; Shi, X.; Luo, C.; An, Y.; Huang, Q.; Guo, P.; Wang, X.; Lei, X. Research on Capacity Allocation Optimization of Commercial Virtual Power Plant (CVPP). Energies 2022, 15, 1303. [Google Scholar] [CrossRef]
- Wozabal, D.; Rameseder, G. Optimal bidding of a virtual power plant on the Spanish day-ahead and intraday market for electricity. Eur. J. Oper. Res. 2020, 280, 639–655. [Google Scholar] [CrossRef]
- Xu, Z.; Guo, Y.; Sun, H. Competitive Pricing Game of Virtual Power Plants: Models, Strategies, and Equilibria. IEEE Trans. Smart Grid 2022, 13, 4583–4595. [Google Scholar] [CrossRef]
- Zamani, A.G.; Zakariazadeh, A.; Jadid, S. Day-ahead resource scheduling of a renewable energy based virtual power plant. Appl. Energy 2016, 169, 324–340. [Google Scholar] [CrossRef]
- Shabanzadeh, M.; Sheikh-El-Eslami, M.K.; Haghifam, M.R. A medium-term coalition-forming model of heterogeneous DERs for a commercial virtual power plant. Appl. Energy 2016, 169, 663–681. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, J.; De, G. Research on Trading Optimization Model of Virtual Power Plant in Medium- and Long-Term Market. Energies 2022, 15, 759. [Google Scholar] [CrossRef]
- Jafari, M.; Akbari Foroud, A. A medium/long-term auction-based coalition-forming model for a virtual power plant based on stochastic programming. Int. J. Electr. Power 2020, 118, 105784. [Google Scholar] [CrossRef]
- Jafari, M.; Akbari Foroud, A. A Medium-Term Virtual Power Plant Optimization Framework Considering the Failure Rate of Its Intermittent Units Using Stochastic Programming. Electr. Power Compon. Syst. 2023, 1–16. [Google Scholar] [CrossRef]
- Shabanzadeh, M.; Sheikh-El-Eslami, M.K.; Haghifam, M.R. The design of a risk-hedging tool for virtual power plants via robust optimization approach. Appl. Energy 2015, 155, 766–777. [Google Scholar] [CrossRef]
- Maiz, S.; Baringo, L.; García-Bertrand, R. Dynamic expansion planning of a commercial virtual power plant through coalition with distributed energy resources considering rival competitors. Appl. Energy 2025, 377, 124665. [Google Scholar] [CrossRef]
- Mashhour, E.; Moghaddas-Tafreshi, S.M. Bidding strategy of virtual power plant for participating in energy and spinning reserve markets-Part I: Problem formulation. IEEE Trans. Power Syst. 2011, 26, 949–956. [Google Scholar] [CrossRef]
- Mashhour, E.; Moghaddas-Tafreshi, S.M. Bidding strategy of virtual power plant for participating in energy and spinning reserve markets-Part II: Numerical analysis. IEEE Trans. Power Syst. 2011, 26, 957–964. [Google Scholar] [CrossRef]
- Rahmani-Dabbagh, S.; Sheikh-El-Eslami, M.K. A profit sharing scheme for distributed energy resources integrated into a virtual power plant. Appl. Energy 2016, 184, 313–328. [Google Scholar] [CrossRef]
- Jadidoleslam, M. Risk-constrained participation of virtual power plants in day-ahead energy and reserve markets based on multi-objective operation of active distribution network. Sci. Rep. 2025, 15, 9145. [Google Scholar] [CrossRef] [PubMed]
- Mujeeb, A.; Hu, Z.; Wang, J.; Diao, R.; Liu, L.; Bao, Z. Optimizing Virtual Power Plant Operations in Energy and Frequency Regulation Reserve Markets: A Risk-Averse Two-Stage Scenario-Oriented Stochastic Approach. Int. Trans. Electr. Energy 2025, 2025, 6640754. [Google Scholar] [CrossRef]
- Yan, X.; Gao, C.; Francois, B. Multi-objective optimization of a virtual power plant with mobile energy storage for a multi-stakeholders energy community. Appl. Energy 2025, 386, 125553. [Google Scholar] [CrossRef]
- Fan, Q.; Liu, D. A Wasserstein-distance-based distributionally robust chance constrained bidding model for virtual power plant considering electricity-carbon trading. IET Renew. Power Gen. 2024, 18, 545–557. [Google Scholar] [CrossRef]
- Singh, K.N.; Goswami, A.K.; Chudhury, N.B.D.; Cali, U.; Ustun, T.S. A risk-aware bidding model for virtual power plants: Integrating renewable energy forecasting and carbon market strategies. Energy Rep. 2025, 14, 1222–1239. [Google Scholar] [CrossRef]
- Wu, C.; Wei, Z.; Cao, Y.; Xu, Y.; Wei, T.; Han, H.; Chen, S.; Zang, H. Low-carbon scheduling model of multi-virtual power plants based on cooperative game considering failure risks. IET Renew. Power Gen. 2024, 18, 3923–3935. [Google Scholar] [CrossRef]
- Li, J.; Ai, Q. Operation mode of virtual power plant considering peak regulation auxiliary service. Electr. Power Autom. Equip. 2021, 41, 1–7. [Google Scholar]
- Olanlari, F.; Moradi-Sepahvand, M.; Amraee, T. Two-stage risk-constrained stochastic optimal bidding strategy of virtual power plant considering distributed generation outage. IET Gener. Transm. Dis. 2023, 17, 1884–1901. [Google Scholar] [CrossRef]
- Shabanzadeh, M.; Sheikh-El-Eslami, M.K.; Haghifam, M.R. An interactive cooperation model for neighboring virtual power plants. Appl. Energy 2017, 200, 273–289. [Google Scholar] [CrossRef]
- Yu, H.; Wang, Y.; Lyu, R.; Jin, L.; Lin, Z.; Li, L. Two-stage Distributionally Robust Optimization Operation Strategy of Virtual Power Plants Considering Flexible Ramping Products. Autom. Electr. Power Syst. 2024, 48, 16–27. [Google Scholar]
- Afzali, S.; Parsa Moghaddam, M.; Sheikh-El-Eslami, M.K.; Zamani, R. A flexibility-oriented bidding strategy for virtual power plants incorporating local energy communities: A bi-level stochastic-robust methodology. Appl. Energy 2025, 399, 126355. [Google Scholar] [CrossRef]
- Cheng, Y.; Gao, H.; Wang, R.; Gao, Y.; Liu, J. Optimal Strategy for Two Stage Customer Directrix Load Based Demand Response and Profit Sharing-Risk Sharing Decision-making Method for Virtual Power Plant. Power Syst. Technol. 2024, 48, 799–808. [Google Scholar]
- Kuang, Y.; Wang, X.; Zhao, H.; Qian, T.; Li, N.; Wang, J.; Wang, X. Model-free Demand Response Scheduling Strategy for Virtual Power Plants Considering Risk Attitude of Consumers. Csee. J. Power Energy 2023, 9, 516–528. [Google Scholar]
- Liang, H.; Ma, J. Data-Driven Resource Planning for Virtual Power Plant Integrating Demand Response Customer Selection and Storage. IEEE Trans. Ind. Inform. 2022, 18, 1833–1844. [Google Scholar] [CrossRef]
- Hooshmand, R.A.; Nosratabadi, S.M.; Gholipour, E. Event-based scheduling of industrial technical virtual power plant considering wind and market prices stochastic behaviors—A case study in Iran. J. Clean. Prod. 2018, 172, 1748–1764. [Google Scholar] [CrossRef]
- Nosratabadi, S.M.; Hooshmand, R.A. Stochastic electrical energy management of industrial Virtual Power Plant considering time-based and incentive-based Demand Response programs option in contingency condition. Int. J. Emerg. Electr. Power Syst. 2020, 21, 20190263. [Google Scholar] [CrossRef]
- Shayegan-Rad, A.; Badri, A.; Zangeneh, A.; Kaltschmitt, M. Risk-based optimal energy management of virtual power plant with uncertainties considering responsive loads. Int. J. Energy Res. 2019, 43, 2135–2150. [Google Scholar] [CrossRef]
- Vahedipour-Dahraie, M.; Rashidizadeh-Kermani, H.; Anvari-Moghaddam, A.; Siano, P. Risk-averse probabilistic framework for scheduling of virtual power plants considering demand response and uncertainties. Int. J. Electr. Power 2020, 121, 106126. [Google Scholar] [CrossRef]
- Vahedipour-Dahraie, M.; Rashidizadeh-Kermani, H.; Shafie-Khah, M.; Catalão, J.P.S. Risk-Averse Optimal Energy and Reserve Scheduling for Virtual Power Plants Incorporating Demand Response Programs. IEEE Trans. Smart Grid 2021, 12, 1405–1415. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, H.; Huang, Y.; Wu, X.; Zhu, Y.; Zhang, J. Robust Optimal Scheduling Strategy for Virtual Power Plant Participation in Electric Energy and Demand Response Markets Under Multiple Uncertainties. Power Gener. Technol. 2024, 45, 1173–1185. [Google Scholar]
- Xiao, D.; Lin, Z.; Chen, H.; Hua, W.; Yan, J. Windfall profit-aware stochastic scheduling strategy for industrial virtual power plant with integrated risk-seeking/averse preferences. Appl. Energ. 2024, 357, 122460. [Google Scholar] [CrossRef]
- Aguilar, J.; Bordons Alba, C.; Arce, A.; Galán, R. Intent Profile Strategy for Virtual Power Plant Participation in Simultaneous Energy Markets with Dynamic Storage Management. IEEE Access 2022, 10, 22599–22609. [Google Scholar] [CrossRef]
- Ruiz, N.; Cobelo, I.; Oyarzabal, J. A direct load control model for virtual power plant management. IEEE Trans. Power Syst. 2009, 24, 959–966. [Google Scholar] [CrossRef]
- Jing, Y.; Tao, Y.; Hong, Z.; Huang, H.; Weihua, W.; Yexiao, L. Trading Incentive Mechanism and Response Model for High-Frequency Interaction Between Virtual Power Plants and Main Grid Under Spot Markets. Int. J. High Speed Electron. Syst. 2025, 2540275. [Google Scholar] [CrossRef]
- Wu, H.; Liu, X.; Ye, B.; Xu, B. Optimal dispatch and bidding strategy of a virtual power plant based on a stackelberg game. IET Gener. Transm. Dis. 2020, 14, 552–563. [Google Scholar] [CrossRef]
- Feng, C.; Zheng, K.; Zhou, Y.; Palensky, P.; Chen, Q. Update Scheduling for ADMM-Based Energy Sharing in Virtual Power Plants Considering Massive Prosumer Access. IEEE Trans. Smart Grid 2023, 14, 3961–3975. [Google Scholar] [CrossRef]
- Lin, W.T.; Chen, G.; Li, C. Risk-averse energy trading among peer-to-peer based virtual power plants: A stochastic game approach. Int. J. Electr. Power 2021, 132, 107145. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, C.; Dou, Z.; Wang, L.; Jiang, C.; Wang, S. Risk Scheduling and Power Sharing Mechanism for Sharing-based Virtual Power Plant. Autom. Electr. Power Syst. 2024, 48, 104–114. [Google Scholar]
- Zhou, K.; Chu, Y.; Yin, H. Peer-to-peer electricity trading model for urban virtual power plants considering prosumer preferences and power demand heterogeneity. Sustain. Cities Soc. 2024, 107, 105465. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, W.; Chen, H.; Yu, Z.; Hu, L.; Huang, Y. Optimal scheduling strategy for virtual power plants with aggregated user-side distributed energy storage and photovoltaics based on CVaR-distributionally robust optimization. J. Energy Storage 2024, 86, 110770. [Google Scholar] [CrossRef]
- Gao, Y.; Gao, L.; Zhang, P.; Wang, Q. Two-Stage Optimization Scheduling of Virtual Power Plants Considering a User-Virtual Power Plant-Equipment Alliance Game. Sustainability 2023, 15, 13960. [Google Scholar] [CrossRef]
- Power, T.; Verbič, G. A Novel Approach for Modeling Spatial and Temporal Correlations of PV Generation Applied to Prosumer Virtual Power Plants. IEEE Trans. Smart Grid 2025, 16, 183–193. [Google Scholar] [CrossRef]
- Papalexopoulos, A.; Oren, S.; Chao, H.P. Integrating Behind-the-Meter Grid Edge Technologies Into Wholesale Electricity Markets: A Novel Methodology Using Virtual Power Plants. IEEE Power Energy Mag. 2024, 22, 91–100. [Google Scholar] [CrossRef]
- Abbasi, M.H.; Taki, M.; Rajabi, A.; Li, L.; Zhang, J. Coordinated operation of electric vehicle charging and wind power generation as a virtual power plant: A multi-stage risk constrained approach. Appl. Energy 2019, 239, 1294–1307. [Google Scholar] [CrossRef]
- Chen, Y.; Niu, Y.; Du, M.; Wang, J. A two-stage robust optimization model for a virtual power plant considering responsiveness-based electric vehicle aggregation. J. Clean. Prod. 2023, 405, 136690. [Google Scholar] [CrossRef]
- Alahyari, A.; Pozo, D. Performance-based virtual power plant offering strategy incorporating hybrid uncertainty modeling and risk viewpoint. Electr. Power Syst. Res. 2022, 203, 107632. [Google Scholar] [CrossRef]
- Al-Gabalawy, M. Reinforcement learning for the optimization of electric vehicle virtual power plants. Int. Trans. Electr. Energy 2021, 31, 12951. [Google Scholar] [CrossRef]
- Chen, Y.; Niu, Y.; Qu, C.; Du, M.; Liu, P. A pricing strategy based on bi-level stochastic optimization for virtual power plant trading in multi-market: Energy, ancillary services and carbon trading market. Electr. Power Syst. Res. 2024, 231, 110371. [Google Scholar] [CrossRef]
- Ma, Q.; Jia, H.; Guo, Y.; Li, P.; Yang, Y.; Liu, D.; Zhao, Z. Stackelberg Game Optimization Strategy of Virtual Power Plants and Electric Vehicles Based on Conditional Value-at-Risk. Electr. Power Constr. 2025, 46, 53–66. [Google Scholar]
- Deng, X.; Chen, Y.; Fan, D.; Liu, Y.; Ma, C. GRU-integrated constrained soft actor-critic learning enabled fully distributed scheduling strategy for residential virtual power plant. Glob. Energy Interconnect. 2024, 7, 117–129. [Google Scholar] [CrossRef]
- Li, X.; Qin, W.; Jing, X.; Zhu, Z.; Lu, R.; Han, X. Joint Optimization for Virtual Power Plant Participating in Main and Auxiliary Markets Considering Uncertain Risks and Multi-agent Coordination. Power Syst. Technol. 2024, 48, 4553–4567. [Google Scholar]
- Qin, W.; Li, X.; Jing, X.; Zhu, Z.; Lu, R.; Han, X. Multi-Temporal Optimization of Virtual Power Plant in Energy-Frequency Regulation Market Under Uncertainties. J. Mod. Power Syst. Clean Energy 2025, 13, 675–687. [Google Scholar] [CrossRef]
- Shan, J.; Hu, J.; Wu, J. Peer-to-peer Market Trading Mechanism and Model for Virtual Power Plant Energy Management. Power Syst. Technol. 2020, 44, 3401–3408. [Google Scholar]
- Feng, Y.; Jia, H.; Wang, X.; Ning, B.; Liu, Z.; Liu, D. Review of operations for multi-energy coupled virtual power plants participating in electricity market. Energy Rep. 2023, 9, 992–999. [Google Scholar] [CrossRef]
- Ju, L.; Zhao, R.; Tan, Q.; Lu, Y.; Tan, Q.; Wei, W. A multi-objective robust scheduling model and solution algorithm for a novel virtual power plant connected with power-to-gas and gas storage tank considering uncertainty and demand response. Appl. Energy 2019, 250, 1336–1355. [Google Scholar] [CrossRef]
- Tan, Z.; Fan, W.; Li, H.; De, G.; Ma, J.; Yang, S.; Ju, L.; Tan, Q. Dispatching optimization model of gas-electricity virtual power plant considering uncertainty based on robust stochastic optimization theory. J. Clean. Prod. 2020, 247, 119106. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, K.; Liu, N.; Xie, Y. Unlock the aggregated flexibility of electricity-hydrogen integrated virtual power plant for peak-regulation. Appl. Energy 2024, 360, 122747. [Google Scholar] [CrossRef]
- Wang, J.; Ilea, V.; Bovo, C.; Wang, Y. Two-stage coordinated scheduling of hydrogen-integrated multi-energy virtual power plant in joint capacity, energy, and ancillary service markets. Renew. Energy 2024, 235, 121282. [Google Scholar] [CrossRef]
- Yin, Z.; Tan, Z.; Zheng, H.; Ju, L.; Tan, C. Two-stage information-gap optimization decision model of electricity-hydrogen integrated virtual power plant with shared energy storage. J. Energy Storage 2024, 100, 113612. [Google Scholar] [CrossRef]
- Akkaş, Ö.P.; Çam, E. Optimal operation of a virtual power plant in a day-ahead market considering uncertainties of renewable generation and risk evaluation. El-Cezeri J. Sci. Eng. 2020, 7, 448–460. [Google Scholar]
- Tan, C.; Wang, J.; Geng, S.; Pu, L.; Tan, Z. Three-level market optimization model of virtual power plant with carbon capture equipment considering copula--CVaR theory. Energy 2021, 237, 121620. [Google Scholar] [CrossRef]
- Meng, F.; Nan, Y.; Zheng, G.; Lu, C.; Mi, Y.; Li, C.; Shen, J. A risk-aware scheduling method of multienergy virtual power plant based on the denoising diffusion probabilistic model. Front. Energy Res. 2024, 12, 1425202. [Google Scholar] [CrossRef]
- Zheng, Y.; Yang, Y.; Jiao, F.; Wen, F.; Zhao, J.; Dong, Z. Bidding strategies for virtual power plants including wind power generation units and power-to-gas facilities. Electr. Power Constr. 2017, 38, 88–95. [Google Scholar]
- Cui, Z.; Chang, X.; Xue, Y.; Yi, Z.; Li, Z.; Sun, H. Distributed peer-to-peer electricity-heat-carbon trading for multi-energy virtual power plants considering copula-CVaR theory and trading preference. Int. J. Electr. Power 2024, 162, 110231. [Google Scholar] [CrossRef]
- Shahkoomahalli, A.; Koochaki, A.; Shayanfar, H. Risk-Based Electrical-Thermal Scheduling of a Large-Scale Virtual Power Plant Using Downside Risk Constraints for Participating in Energy and Reserve Markets. Arab. J. Sci. Eng. 2022, 47, 2663–2683. [Google Scholar] [CrossRef]
- Fan, P.; Xue, Y.; Zhao, H.; Chang, X.; Su, J.; Wang, K.; Sun, H. Enhancing flexibility of virtual power plants considering reconfiguration of district heating network. CSEE J. Power Energy 2024, 40, 394–407. [Google Scholar]
- Rezaee Jordehi, A. A stochastic model for participation of virtual power plants in futures markets, pool markets and contracts with withdrawal penalty. J. Energy Storage 2022, 50, 104334. [Google Scholar] [CrossRef]
- Li, Y.; Liu, F.; Zhang, X.; Zhang, X.; Zhang, J.; Tian, X. A Day-ahead Bidding Strategy of the Energy-auxiliary Service Market Considering the Participation of Photothermal Virtual Power Plants. Mod. Electr. Power 2024, 41, 1156–1166. [Google Scholar]
- Wang, Q.; Qi, H.; Tan, H.; Wang, H.; Zhu, Y.; Wang, P.; Li, Z. Low-carbon scheduling of CHP virtual power plant considering carbon market risk. Electr. Power Autom. Equip. 2024, 44, 8–15. [Google Scholar]
- Zheng, C.; Huang, W.; Zhai, S.; Pan, K.; He, X.; Liu, X.; Su, S.; Shen, C.; Ai, Q. Blockchain-Enabled Cross-Chain Coordinated Trading Strategy for Electricity-Carbon-Green Certificate in Virtual Power Plants: Multi-Market Coupling and Low-Carbon Operation Optimization. Energies 2025, 18, 3443. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, R.; Zeng, Z.; Feng, J.; Cheng, Y.; Fang, S. Internal Optimization Stochastic Model of Virtual Power Plant Participating in Gas and Electricity Market. Electr. Power 2020, 53, 181–188. [Google Scholar]
- Wen, J.; Jia, R.; Cao, G.; Guo, Y.; Jiao, Y.; Li, W.; Li, P. Multi-source shared operation optimization strategy for multi-virtual power plants based on distributionally robust chance constraint. Energy 2025, 322, 135761. [Google Scholar] [CrossRef]
- Gholami, K.; Arif, M.T.; Haque, M.E. Dynamic Boundary Dissemination to Virtual Power Plants for Congestion and Voltage Management in Power Distribution Networks. Energies 2025, 18, 518. [Google Scholar] [CrossRef]
- Gholami, K.; Arif, M.T.; Haque, M.E. IGDT-based participation of hybrid renewable-hydrogen virtual power plants in frequency control ancillary services. Int. J. Hydrogen Energy 2025, 139, 630–645. [Google Scholar] [CrossRef]
- Lin, X.; Lin, X.; Zhong, W.; Zhou, Y. Predictive operation optimization of multi-energy virtual power plant considering behavior uncertainty of diverse stakeholders. Energy 2023, 280, 128130. [Google Scholar] [CrossRef]


| Reference | Spot Market | Medium and Long-Term Markets | Frequency Regulation Market | Reserve Market | Peak Regulation Market | Flexible Ramping Markets | Carbon Market | Futures Market |
|---|---|---|---|---|---|---|---|---|
| [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57] | ✓ | |||||||
| [58,59] | ✓ | |||||||
| [60,61,62,63] | ✓ | ✓ | ||||||
| [64,65,66,67] | ✓ | ✓ | ||||||
| [68,69] | ✓ | ✓ | ||||||
| [70,71,72] | ✓ | ✓ | ||||||
| [73] | ✓ | ✓ | ||||||
| [74,75] | ✓ | ✓ | ✓ | |||||
| [76] | ✓ | ✓ |
| Reference | Application Focus | Methodology | Market Participation |
|---|---|---|---|
| [77] | Local energy communities | Bi-level stochastic-robust optimization | Spot and flexibility |
| [78] | Intent profile strategy for multi-market participation | Hierarchical MPC, storage virtualization | Spot markets |
| [79] | Customer directrix load DR and profit-risk sharing | Two-stage, improved shapley value | Regulation |
| [80] | ADMM-based energy sharing with massive prosumers | Online partial-update ADMM | P2P energy sharing |
| [81] | User-VPP-equipment alliance game | Two-stage, cooperative game | Spot market |
| [82] | Event-based scheduling for industrial VPP | Stochastic scheduling, contingency management | Spot market |
| [83] | High-frequency interaction and incentive mechanism | Data-driven forecasting and optimization | Spot market |
| [84] | Model-free DR scheduling with consumer | DRL, prospect theory | Spot market |
| [85] | Data-driven resource planning with DR customer selection | Multistage stochastic programming | Spot market |
| [86] | Risk-averse P2P energy trading among VPPs | Two-stage stochastic game | Day-ahead, P2P trading |
| [87] | Power sharing and risk scheduling for VPP | Min-max regret method, consensus theory | Power sharing market |
| [88] | Energy management for industrial VPP | Stochastic optimization, contingency planning | Spot market |
| [89] | BTM DER integration via VPPs | Risk-based supply functions | Spot market |
| [90] | Spatial-temporal modeling of PV for VPP | Bayesian vector autoregression | Multi-markets |
| [91] | Direct load control for VPP management | Optimization for thermostatic loads | Electricity market |
| [92] | Risk-based energy and regulation service market participation | Stochastic scheduling, IGDT | energy and regulation |
| [93] | Probabilistic scheduling with DR | Risk-constrained stochastic programming | Spot and reserve markets |
| [94] | Optimal bidding in multiple markets | Two-stage stochastic programming | Spot and spinning reserve |
| [95] | Scheduling under multiple uncertainties | Two-stage robust optimization, CVaR-based polyhedral set | Spot and DR markets |
| [96] | Distributionally robust optimization | Two-stage DRO with CVaR | Spot market |
| [97] | Stackelberg game-based bidding strategy | Stackelberg game model | Spot market |
| [98] | Windfall profit-aware scheduling | Value-at-Best (VaB) and CVaR | Spot market |
| [99] | P2P trading with prosumer preferences and heterogeneity | Game model, market bidding mechanism | P2P trading |
| Ref. | Application Focus | Methodology | Market Participation |
|---|---|---|---|
| [100] | Coordinated EV-wind operation | Multi-stage risk constrained stochastic optimization | Three-settlement spot market |
| [101] | EV aggregation with responsiveness | Two-stage robust optimization, C&CG algorithm | Energy market with carbon trading |
| [102] | EV fleet balancing services | Reinforcement learning, hybrid uncertainty modeling | Multiple electricity markets |
| [103] | VPP optimization with uncertain EVs | Reinforcement learning, risk-averse/profit-seeking strategies | Spot market |
| [104] | Multi-market VPP trading | Bi-level Stackelberg game, stochastic optimization with CVaR | Energy, ancillary services, carbon trading markets |
| [105] | VPP-EV interaction optimization | Bi-level Stackelberg game, CVaR, particle swarm optimization | Energy and ancillary services markets |
| [106] | Residential VPP scheduling | GRU-integrated deep reinforcement learning, constrained soft actor-critic | Spot markets |
| [107] | Energy and auxiliary market participation | Master-slave game, CVaR, dispatchable domain evaluation | Energy and frequency regulation markets |
| [108] | Energy-frequency regulation market | Multi-temporal optimization, Stackelberg game, CVaR | Energy and frequency regulation market |
| [109] | Peer-to-peer energy trading with EVs | P2P trading mechanism, VCG rule, multilateral bidding | Peer-to-peer energy market |
| Ref. | Energy Types | Energy Conversion/Storage | Optimization and Risk Handling | Market Participation |
|---|---|---|---|---|
| [111] | Electricity, gas | P2G and gas storage | Robust optimization with CVaR | Electricity and gas markets |
| [112] | Electricity, gas | P2G and gas storage | Robust stochastic optimization | Multi-energy markets |
| [113] | Electricity, hydrogen | EVs, ACs, hydrogen refueling stations | Polytope flexibility aggregation with CVaR | Peak regulation market |
| [114] | Electricity, hydrogen | Daily and seasonal hydrogen storage | Two-stage stochastic programming with CVaR | Capacity, energy, and ancillary service markets |
| [115] | Electricity, hydrogen | Battery and hydrogen storages | IGDT | Spot markets |
| [116] | Electricity, heat | CHP, thermal buffer tank | Stochastic MINLP with CVaR | Spot market |
| [117] | Electricity, gas | Carbon capture, P2G | Copula-CVaR, three-level optimization | Electricity, gas, carbon markets |
| [118] | Electricity, gas, heat | Waste heat boiler, heat pump, heat storage | Denoising diffusion probabilistic model with CVaR | Electricity, carbon and green certificate markets |
| [119] | Electricity, gas | P2G | IGDT | Day-ahead electricity market |
| [120] | Electricity, heat | CHP, gas boiler | Distributed P2P trading with copula-CVaR | Electricity-heat-carbon markets |
| [121] | Electricity, heat | BESS, thermal buffer tank | Two-stage stochastic programming with Downside risk constraints | Energy and reserve markets |
| [122] | Electricity, heat | District heating network | Adjustable robust optimization | Energy and reserve bilateral markets |
| [123] | Electricity, heat | CHP, thermal storage | Stochastic model with CVaR | Futures, pool, and contracts |
| [124] | Electricity, heat | Concentrating solar power with thermal storage | Stochastic programming with CVaR | Energy and ancillary service markets |
| [125] | Electricity, heat, gas | Ground-source heat pump, P2G | CVaR | Electricity and carbon markets |
| [126] | Electricity, green certificate | Carbon capture, P2G | Blockchain cross-chain trading with LHS and k-means clustering | Electricity, carbon, and green certificate markets |
| [127] | Electricity, heat, gas | P2G, carbon capture | Superquantile Stochastic optimization | Electricity and gas markets |
| [128] | Electricity, heat | EV quotas, P2P Trading | Distributionally robust chance constraint with CVaR | Electricity and heat markets |
| [129] | Electricity, hydrogen | Electrolyzers, hydrogen storage, fuel cells | IGDT | Energy and frequency control ancillary services (FCAS) |
| [130] | Electricity, hydrogen | Electrolyzers, hydrogen storage, fuel cells | Decentralized co-optimization privacy Preservation | Energy and FCAS |
| [131] | Electricity, gas | Carbon capture, P2G, energy storage | Predictive optimization with sliding time windows and uncertain behavior | Electricity and gas markets |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, D. A Review on Risk-Averse Bidding Strategies for Virtual Power Plants with Uncertainties: Resources, Technologies, and Future Pathways. Technologies 2025, 13, 488. https://doi.org/10.3390/technologies13110488
Xiao D. A Review on Risk-Averse Bidding Strategies for Virtual Power Plants with Uncertainties: Resources, Technologies, and Future Pathways. Technologies. 2025; 13(11):488. https://doi.org/10.3390/technologies13110488
Chicago/Turabian StyleXiao, Dongliang. 2025. "A Review on Risk-Averse Bidding Strategies for Virtual Power Plants with Uncertainties: Resources, Technologies, and Future Pathways" Technologies 13, no. 11: 488. https://doi.org/10.3390/technologies13110488
APA StyleXiao, D. (2025). A Review on Risk-Averse Bidding Strategies for Virtual Power Plants with Uncertainties: Resources, Technologies, and Future Pathways. Technologies, 13(11), 488. https://doi.org/10.3390/technologies13110488






