1. Introduction
Nowadays, machine learning applications are becoming more and more pervasive, requiring efficient hardware solutions to perform complex computations. Linear algebra operations, such as matrix multiplication and vector operations, are at the core of these applications. However, while these operations can be efficiently implemented using dedicated hardware, nonlinear functions, mainly used in neural networks and transformers for activation functions, are often computed using software libraries, which can be slow and inefficient. As reported by [
1], the execution of nonlinear functions can take up to 50% of the total execution time of a vision transformer model, which is a significant overhead that can impact the overall performance of the system.
To address this issue, we propose TOXOS, a hardware architecture based on the CORDIC algorithm [
2], with the aim of efficiently computing nonlinear functions in floating-point format. The CORDIC (COordinate Rotation DIgital Computer) algorithm is a well-known iterative algorithm that can compute a wide range of mathematical functions, including trigonometric, hyperbolic, and logarithmic functions, using only addition, subtraction, and bit-shifting operations.
To easily integrate the CORDIC algorithm into a RISC-V processor, we designed a custom instruction set extension that includes dedicated CORDIC operations. This allows for seamless execution of CORDIC-based computations within the RISC-V architecture, enabling efficient hardware acceleration for nonlinear functions. Such an approach demonstrates how using a coprocessor for nonlinear functions can significantly improve the performance of machine learning applications, as it allows for faster execution of these functions compared to software libraries.
The paper introduces TR-HEEP (
Figure 1), a microcontroller based on the X-HEEP [
3] architecture, integrating TOXOS as a coprocessor. In TR-HEEP, TOXOS is tightly coupled to the CV32E40PX core through the CoreV eXtension InterFace (CV-X-IF) by Open Hardware Group [
4]. This interface allows defining ISA extensions without modifying the core internal pipeline.
Moreover, the proposed architecture is designed to be flexible and scalable, allowing for different configurations depending on the application requirements. This flexibility makes TOXOS suitable for a wide range of applications, from edge devices to high-performance computing systems. Supporting a variety of nonlinear functions, TOXOS can be used in a wide range of automotive applications, such as advanced driver assistance systems (ADAS), autonomous driving, and on-board signal processing applications, where efficient computation of nonlinear functions is crucial for real-time decision-making.
This paper is organized as follows:
Section 1 introduces the work and the AI challenges in automotive applications,
Section 2 provides an overview of the state-of-the-art in hardware accelerators for nonlinear functions, amd
Section 3 provides an overview of the CORDIC algorithm.
Section 4 describes the architecture of TOXOS,
Section 5 presents an architectural exploration tuning the available parameters, and
Section 6 introduces TR-HEEP, a microcontroller based on X-HEEP [
3], integrating TOXOS as a coprocessor.
Section 7 presents a comparison of TOXOS in latency and energy with the floating-point unit available in the CV32E40PX (CVFPNEW) and other state-of-the-art accelerators. Finally,
Section 8 concludes the paper and presents some future developments of TOXOS.
AI Challenges in Automotive Applications
Artificial intelligence (AI) is rapidly transforming the automotive industry, driving advancements in safety, efficiency, and user experience. Recent comprehensive reviews highlight that AI has revolutionized multiple facets of the sector, including intelligent manufacturing, diagnostic systems, control mechanisms, supply chain operations, and traffic management [
5]. Deep learning (DL) methods, especially multilayered neural networks, are increasingly deployed for predictive maintenance, driver behavior analysis, demand forecasting, and advanced driver assistance systems, with implementation growing dramatically in recent years [
5,
6]. These techniques have significantly expedited the development of autonomous vehicles, particularly in navigation, decision-making, and safety features [
5,
6]. However, the deployment of AI in vehicles presents unique challenges, especially regarding real-time processing, power consumption, and reliability [
5,
6,
7,
8].
As vehicles become more connected and autonomous, the need for efficient AI algorithms and hardware accelerators becomes paramount [
7]. Hardware accelerators such as GPUs, FPGAs, and ASICs are increasingly used to offload computationally intensive tasks from the main processor, enabling real-time data processing and improved energy efficiency [
7]. Despite these advancements, most research and development efforts focus on optimizing the execution of linear layers (e.g., matrix multiplications) in deep neural networks, as these are well-suited for parallelization and hardware acceleration [
7].
By contrast, nonlinear layers—such as activation functions and pooling operations—are equally critical for model performance and reliability, especially in safety-critical automotive applications. However, these nonlinear operations often receive less attention in terms of dedicated hardware support and algorithmic optimization [
1,
7,
8]. This imbalance can limit the overall efficiency and reliability of AI systems in vehicles, particularly as models become deeper and more complex.
2. Related Works
The literature presents several works that propose hardware accelerators for the computation of nonlinear functions.
Some works focus on the implementation of specific functions, such as the tanh and sigmoid functions [
9], which are widely used in machine learning applications. As reported in [
9], the implementation of these functions can be optimized using CORDIC-based architectures.
Other works propose softmax and exponential function accelerators in the wider context of transformer acceleration [
1]. These works target high performance and low latency, but they do not address the need for a wide range of nonlinear functions, which may be required in applications beyond transformers.
The solution proposed in [
10] implements a DMA-based ISA extension for CORDIC, which can be used to accelerate the computation of various nonlinear functions. However, being DMA-based, it may suffer from the overhead of DMA programming and data transfer, which can limit its performance in case of small data sizes or frequent function calls.
In contrast, our proposed architecture (TOXOS) is designed to be flexible and efficient, supporting a wide range of nonlinear functions with low latency and high throughput. It is tightly integrated with the processor pipeline, minimizing overhead and maximizing performance for various applications.
3. CORDIC Algorithm
The iterative COordinate Rotation Digital Computer (CORDIC) algorithm was first presented by J. E. Volder in 1959, when he proposed a special-purpose digital computing unit [
2] whose aim was to evaluate trigonometric functions by means of plane rotation. Starting from Givens rotation equations, the algorithm decomposed the larger rotation angle
into several smaller ones
, so that the 2D vector rotation by an angle
could be performed by a sequence of micro-rotations implying only additions and right-shift operations. Assuming a precision of
n bits, the algorithm needed
n iterations to achieve that accuracy, and the final values of the coordinates
x and
y were scaled by a factor
K to compensate for the effects of the algorithm itself. In its original form, the CORDIC algorithm could work in two modes, rotation and vectoring, and could use only a circular coordinate system. Then, in 1971, J. S. Walther [
11] modified the original algorithm to propose a unified version capable of computing also other mathematical functions, such as hyperbolic sine, cosine, and arctangent, as well as multiplication and division.
Figure 2 gives a visual comparison between the different coordinate systems. In order to achieve this variety of functions, Walther included a new variable,
m, into the original equations to represent the coordinate system to be used and found specific shift sequences for each of them. As a result, CORDIC equations can be written as:
where
Therefore, as summarized in
Table 1, the number of available operational modes has now become six, given that each of the original working modes can be used with each of the three coordinate systems.
To achieve such variety, some modifications in the computation of the angles
and the scaling factor
were made necessary, as described in Equations (
4) and (
5) and in
Table 2:
However, as shown in
Table 1, this flexibility of the CORDIC algorithm comes at a cost, since the range of values that can produce a valid result (Range Of Convergence, ROC) and then be accepted as inputs is rather restricted.
Floating-Point Extension for CORDIC Algorithm
In order to enlarge the range of representable values, the CORDIC algorithm can be easily extended to floating-point arithmetic [
13]. This can be achieved by adopting two possible strategies:
Local floating-point: each micro-rotation performs floating-point operations, hence adjusting the exponents and normalizing the result at each iteration. It is very costly in terms of hardware and speed, since floating-point adders and shifters are needed for each stage. In addition, it leads to useless operations, because, between two iterations, numbers are unnecessarily denormalized and normalized again.
Global floating-point: the floating-point inputs are converted into specific fixed-point formats that include additional overflow and guard bits to take care of accuracy loss throughout the iterations. With this approach, the CORDIC algorithm remains fixed-point, and floating-point-specific operations are performed only at the beginning and at the end of the unit. This makes global floating-point the most speed-effective solution.
4. Proposed Architecture
TOXOS implements the global floating-point CORDIC algorithm to compute nonlinear functions as follows:
Direct trigonometric functions: ,
Inverse trigonometric functions: , ,
Direct hyperbolic functions: ,
Inverse hyperbolic functions:
The exponential function:
Cartesian to polar coordinates conversion:
Division
We choose the global floating-point approach since this allows us to keep the internal architecture simple and avoid the use of complex floating-point units.
TOXOS is designed to be highly configurable and adaptable to various application requirements. In fact, it allows the user to select which functions to enable, the number of iterations of the CORDIC algorithm, the latency in clock cycles, and the fixed-point representation format. This configurability enables fine-tuning of the area-performance tradeoff according to specific application needs.
Due to the internal implementation of the CORDIC algorithm, it is possible to define a certain level of rolling/unrolling of the algorithm [
14]. In fact, both the number of algorithm iterations and the latency can be set, resulting in the instantiation of a number of CORDIC units equal to:
where
is the number of CORDIC units,
is the input output latency of TOXOS, and
is the number of iterations of the CORDIC algorithm. So the user is free to choose a smaller architecture with a higher latency or a larger architecture with a lower latency without paying any penalty in terms of accuracy.
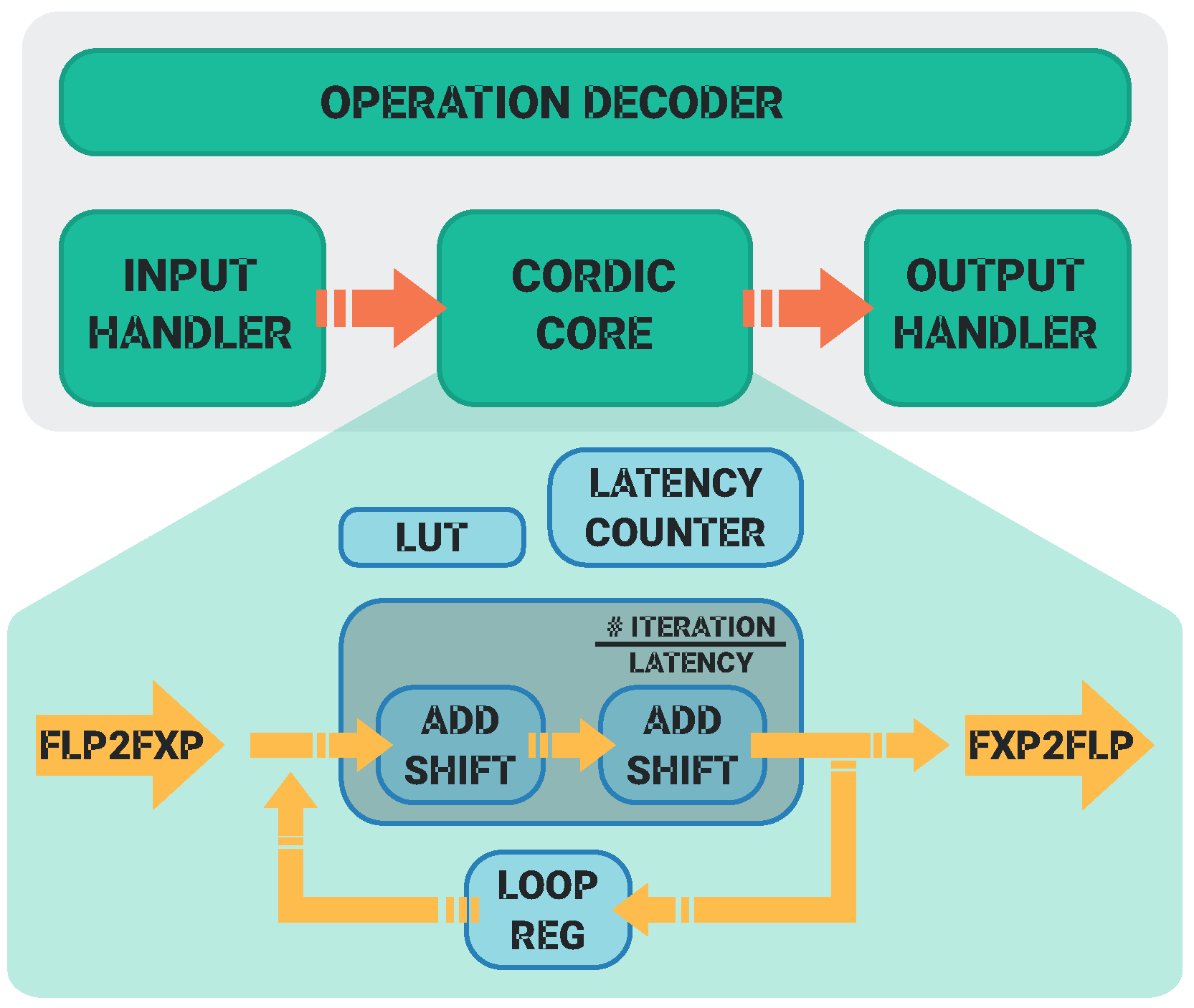
Figure 3 shows the architecture of TOXOS. The
Input Handler dispatches the input data to the right input port of the CORDIC unit and sets the
and
m parameters in (
1), (), and () according to the function to be computed. The
FLP2FXP module converts the input data from floating-point to fixed-point representation. The
Latency Counter keeps track of the number of iterations of the CORDIC algorithm, then
(
6) instances of add and shift units are used for the computation.
iterations are performed, and the result is sent to the
FXP2FLP module, which converts the fixed-point result to the floating-point representation. Then, the result is sent to the
Output Handler, which reads the result and sends it to the output port.
5. Architectural Exploration
The high level of internal parametrization of TOXOS gave us the possibility to perform an exploration of the architecture in the area and on the critical path.
This subsection presents an exploration of the architectural parameters of TOXOS on:
Mean Square Error changing the number of CORDIC iterations and the width of the mantissa in the internal fixed-point representation.
Area overhead partially enables different operations.
Operational frequency for different mantissa widths.
Area for different mantissa widths.
5.1. Error Analysis
To analyze the accuracy of TOXOS, we performed a mean square error (MSE) analysis using the sin function as a benchmark. Reported results are obtained by behavioral simulation of the TOXOS RTL model. This simulation was performed to verify the correctness of the RTL implementation and to obtain a precise measure of the MSE.
Our error characterization reveals two distinct regimes governing TOXOS’s computational accuracy (
Figure 4). For configurations with less than 24 CORDIC iterations, the mean square error (MSE) follows the theoretical CORDIC convergence rate of approximately 1 bit per iteration [
2]. Beyond 24 iterations, the single-precision floating-point format’s 24-bit mantissa becomes the dominant error source [
13].
CORDIC-Limited Regime (Iterations <24): MSE decreases exponentially with additional iterations, following:
where
represents the iteration count. At 8 iterations, MSE plateaus at
due to 8-bit precision limitation.
Mantissa-Limited Regime (Iterations ≥24): MSE plateaus at
regardless of iteration count, matching the theoretical limit for 24-bit significand precision:
This bifurcation has critical design implications:
- 1.
Below 24 iterations: Accuracy improves linearly with both iteration count and mantissa width, until the mantissa width is around the number of iterations of the CORDIC algorithm.
- 2.
Above 24 iterations: Additional iterations provide diminishing returns despite area increase
The analysis identifies 20 iterations and 20-bit mantissa width for the internal fixed-point representation as the optimal configuration, while avoiding unnecessary hardware overhead from excessive iterations or bit-widths. This configuration balances CORDIC’s algorithmic accuracy with the physical constraints of single-precision floating-point representation.
5.2. Area and Timing Analysis
Our implementation leverages the unified CORDIC algorithm [
11] to maximize hardware reuse across trigonometric, hyperbolic, and linear operations.
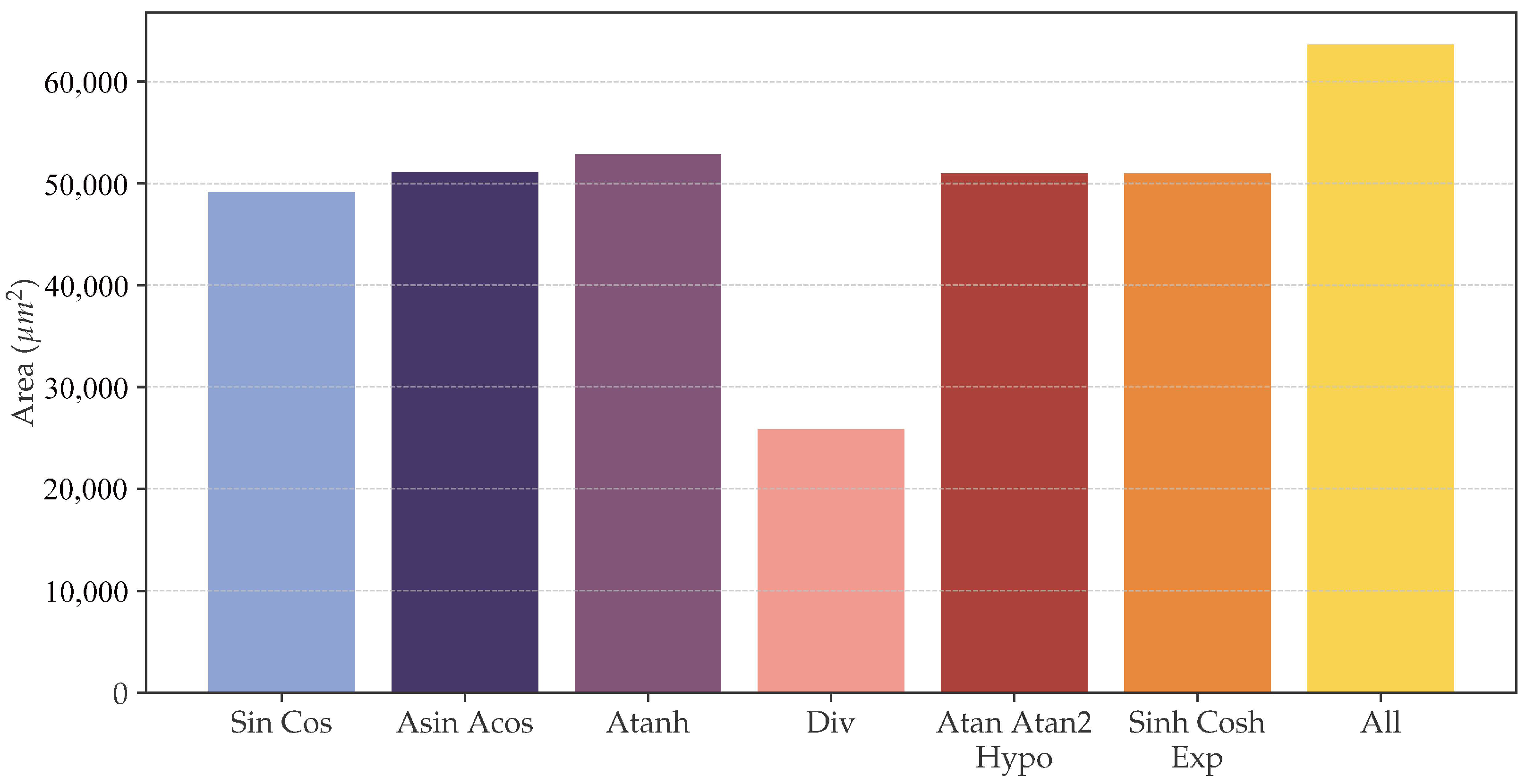
Figure 5 quantifies the area efficiency gained through this architectural approach:
Multi-Operation Overhead: Enabling all supported functions (sin, cos, tanh, exp, log, division) incurs only 12% area overhead compared to individual operations, demonstrating effective resource sharing through shared rotation datapaths.
Division-Specific Optimization: The division-only configuration requires less area than trigonometric functions, primarily due to the fact that angular constant storage becomes unnecessary for linear coordinate transformations.
This unified approach demonstrates superior area scaling compared to discrete CORDIC implementations, particularly when supporting multiple function classes.
Figure 5 groups functions depending on the coordinate system and the mode of the unified CORDIC system. For example, sin and cos share the same hardware, so they are grouped in the figure, but TOXOS can be configured to individually enable single functions.
As expected, the area and critical path length depend almost linearly on the width of the mantissa part of the fixed-point representation. The bar plots in
Figure 6 visually report this correlation for a configuration with 20 iterations and a latency of 4 cycles. In the case of 16 mantissa bits, the critical path is shorter since the synthesizer selected a different architecture for the adders in the internal stage. While the increase in area and latency is justified when the number of bits in the mantissa is lower than 24, since the MSE is reduced (as shown in
Figure 4), when incrementing the number of bits in the mantissa, the error is not reducing, so the increase in area and latency is not justified. In fact, the MSE is bounded by the accuracy of the mantissa of the floating-point representation, which is 24 bits in single precision.
The results reported in this section were obtained by performing synthesis with low-power TSMC 65 CMOS standard cells to evaluate the area and performance trade-offs of different architectural configurations. To obtain the critical path, the clock cycle timing constraint is set to 0 .
6. TOXOS System Integration
To showcase the actual capabilities of TOXOS, it has been integrated into X-HEEP [
3], a RISC-V-based 32-bit microcontroller. In particular, the Core-V eXtension interface (CV-X-IF) [
4] of the CV32E40PX [
15] core has been used. This interface can be used to define custom RISC-V extensions without modifying the core internal pipe [
16].
The presented architectural exploration led to the definition of TOXOS parameters to find a tradeoff between area, latency, and accuracy.
As discussed in
Section 5.2, we decided to use a fixed-point representation with 4 bits for the integer part and 20 bits for the fractional part, which gives a total of 24 bits for the internal representation. The number of iterations of the CORDIC algorithm is set to 20 (
), while the latency is set to 4 clock cycles (
). So the number of CORDIC units is
, as per (
6). This guarantees a good trade-off between MSE and area (see
Section 4). Indeed, increasing the bit-width beyond 24 bits would reduce error, but would lead to high area and long critical path delay. On the contrary, a bit-width lower than 24 bits would reduce cost at the expense of unacceptable accuracy. Similarly, 20 iterations is a good balance between accuracy and latency, as more iterations would improve precision at the expense of extending pipeline depth. Furthermore, instantiating 5 CORDIC units avoids throughput bottlenecks and area scales almost linearly with the area, highlighting how gains in terms of latency come at the expense of area and energy increases.
The obtained system, here identified as TR-HEEP (Trigonometric Rotation X-HEEP), features the CV32E40PX core equipped with the floating-point unit and TOXOS as a tightly coupled coprocessor. The system contains 8 memory banks of 32 KiB each for a total of 256 KiB of memory, for code and data. Among other peripherals, the system features a 1D DMA that can be used to transfer data between an off-chip memory and the on-chip SRAM.
Figure 1 presents a high-level representation of TR-HEEP.
We synthesized TR-HEEP using low-power TSMC 65 nm CMOS standard cells and the memory macros provided by TSMC, targeting a clock frequency of 160 MHz and obtaining a total area of 2.25 mm2. In particular, the area of the floating-point unit is 29,082 μm2, while the area of TOXOS is 41,375 μm2.
As can be observed, the TOXOS area is less than twice the area of the floating-point unit, showing a good speedup compared to software execution of the same functions. Nevertheless, TR-HEEP’s scalability is limited by the target technology node and the available on-chip SRAM.
Figure 7 reports the area breakdown of TR-HEEP. As expected, the largest component is the actual cordic unit, which occupies 85% of the total TOXOS area. The area occupied by the CORDIC unit mainly depends on the selected parameters, such as the number of iterations and the latency. Meanwhile, the converters from floating- to fixed-point and vice versa occupy 4.5% and 6.5% of the total area, respectively. The control and interfacing logic occupy only 4% of the total area, so the overhead of interfacing TOXOS with the CV32E40PX core is minimal.
6.1. Core-V eXtension Interface (CV-X-IF)
The Core-V eXtension Interface (CV-X-IF) enables seamless integration of custom ISA extensions without requiring modifications to the processor’s internal pipeline. When the decode stage encounters an instruction it does not recognize, it automatically forwards the instruction to the extension interface. The coprocessor connected via CV-X-IF then assumes control of the instruction’s execution.
Operands are sourced directly from the core’s register file, and upon completion, the coprocessor writes the result back to the same register file, ensuring transparent operation from the programmer’s perspective. The CV-X-IF employs a lightweight handshake protocol to coordinate data and control transfer between the core and the coprocessor, minimizing both latency and hardware overhead.
This flexible interface design allows for rapid prototyping and deployment of custom accelerators—such as TOXOS—while preserving the modularity and maintainability of the processor architecture.
6.2. ISA Extension
We introduce the
x-cordic ISA extension using the reserved opcode
0b0001011, with specific functions encoded in the
func7 field to select between transcendental operations. Dual-operand functions like polar coordinate conversion (
,
) and division utilize paired
.qq suffixes in their mnemonics. The full operation mapping and corresponding compiler builtins are detailed in
Table 3.
Despite TOXOS’s floating-point capabilities, the CV-X-IF interface requires using general-purpose registers (GPRs) due to the lack of floating-point register forwarding in the CV32E40PX implementation. The operands of the builtins need to be stored in the general-purpose registers, despite being floating-point numbers. This necessitates explicit bitcasting between IEEE-754 and raw binary formats.
7. Results
To analyze the performance of TOXOS, we compared it with the execution of the same functions using C standard library implementations. The results are reported in
Table 4. The code was compiled both using the RISC-V GNU Compiler Collection (GCC) and the fork of LLVM with the x-cordic extension. The performance was measured on the CV32E40PX core, a fork of the CV32E40P core [
17]. The code was compiled passing both the
-march=rv32imc and
-march=rv32imfc flags; the former uses the softfloat library, while the latter uses the floating-point unit (CVFPU) [
18] of the CV32E40PX core.
To compute the number of clock cycles, we used the mcycles status register, which returns the number of clock cycles since the last reset. To obtain an average value, we executed each operation 1000 times and computed the average number of clock cycles. When possible, the overhead of the fetch of the operands from the memory was removed.
The results show that TOXOS is significantly faster than both the softfloat library and the CVFPU for all the operations. The speedup ranges from to compared to softfloat, and from to compared to CVFPU.
The latency of TOXOS is set by the number of pipeline stages. In fact, the number of cycles required to execute an operation is constant for all the operations, as reported in
Table 4. The latency can be adjusted by changing the number of pipeline stages, which is determined by the number of iterations and the number of cycles per iteration. The operations that require two operands, such as the Cartesian to polar coordinates conversion, have a slightly higher latency due to the need to read two operands from memory. In fact, TOXOS is stalled if the operands are not available in the register file, as is the case when the load instruction is not completed before the offloading of the instruction to TOXOS.
While TOXOS has a fixed latency, the latency of the software implementations depends on how the standard library implements the function. For example, the implementation of the sin function in the glibc library uses a combination of polynomial approximations and table lookups to compute the sine of a given angle. The implementation is optimized for accuracy and performance, but it is not designed to be as fast as a dedicated hardware accelerator like TOXOS.
As the number of iterations and the input latency are two independent parameters, one can increase the accuracy of the overall computation while paying little or almost no hardware cost. For example, assuming a fixed fractional representation of the values (24 bits), and the number of internal add and shift units is kept constant (
Figure 3), for example to four, it is sufficient to add two latency cycles to reduce the MSE by 100 times while increasing the number of CORDIC iterations from 16 to 24 (purple to pink line in
Figure 4) at almost no hardware cost. As highlighted in
Table 4, two more clock cycles are not a big issue compared to the software-only execution.
The same methodology was used to measure the performance of some common nonlinear functions used in machine learning, such as the sigmoid, the gelu, the tanh, and the softmax. These functions are often used as activation functions in neural networks and transformers. The analyzed activation functions are not directly supported by TOXOS, so they were implemented using TOXOS as a coprocessor to compute intermediate values. For example, the tanh function is computed as:
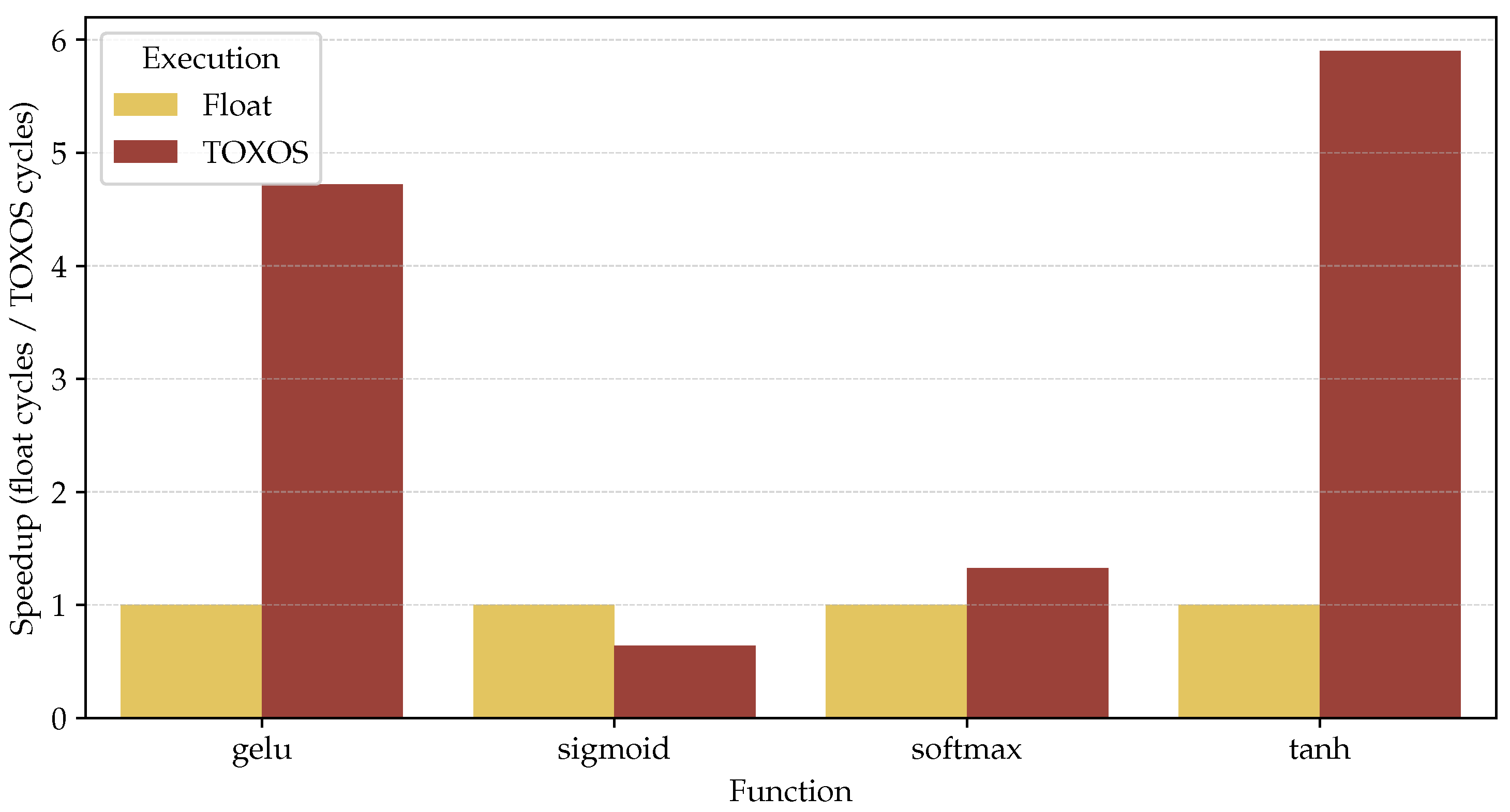
The results are reported in
Figure 8. TOXOS outperforms the CPU in the computation of gelu and tanh, presenting a speedup of
and
, respectively. While the execution of sigmoid is slower than the CPU, as reported in
Section 6.2, it was not possible to use the floating-point registers of the CV32E40PX core to pass the input and output of TOXOS, so the input and output of the function are stored in the general-purpose registers, which requires movement between the floating-point and the general-purpose register file to add the 1 in the denominator. For the softmax function, performance is similar to the CPU, since the main bottleneck is the computation of the elementwise division of the input vector for the sum of the exponentials, which is not supported by TOXOS.
The main outcome of this analysis is that TOXOS can significantly accelerate the computation of nonlinear functions, but it needs to be extended to support more complex functions, such as the sigmoid and the softmax. Moreover, a key limitation of the current implementation of the CORE-V eXtension InterFace is the inability to use floating-point registers in the offloaded instructions. Future work will address this limitation, enabling TOXOS to fully leverage the floating-point capabilities of the CV32E40PX core.
7.1. Energy Consumption
To analyze the energy consumption of TOXOS, we used Synopsys PrimePower to perform power analysis on the synthesized design. In particular, the system was simulated at 100 MHz, computing the activation functions analyzed in
Section 7 on arrays of 64 elements to keep the simulation time manageable. The results are reported in
Figure 9 and
Figure 10.
Figure 9 reports the normalized energy consumption at the system level, including the core, the memory, the floating-point unit, and TOXOS. The results show that TOXOS is more energy efficient than CVFPU for tanh and gelu, while for the softmax, the energy consumption is similar to the case of CVFPU. In fact, TOXOS does not introduce a significant improvement in terms of performance for this function, as stated in
Section 7. For the sigmoid function, TOXOS is less energy efficient than CVFPU, due to the overhead of moving data between the floating-point and the general-purpose register file, as already observed in
Section 7.
Figure 10 reports the energy consumption of TOXOS, CVFPU, and softfloat for the computation of the different CORDIC-supported functions. The results show that TOXOS is significantly more energy efficient than both CVFPU and softfloat for all operations. The energy contribution of the memory is significantly reduced using TOXOS, since the number of instructions executed, and thus fetched from memory, is lower.
7.2. Comparison with Similar Studies
TOXOS can be compared to similar architectures. Some exploit the CORDIC algorithm to implement nonlinear functions [
10], others use piecewise polynomial approximation [
19] or the modified Schraudolph’s method [
1].
As one can expect, TOXOS, not being a special-purpose accelerator, cannot compete in performance with specialized hardware as [
1] and [
19], but the suboptimal performance is balanced by greater flexibility. In fact, TOXOS, paired with the floating-point unit of the core, can implement virtually any new activation function, while specialized hardware cannot without redesign of the hardware itself.
This comparative study highlights the main limitations of TOXOS, which currently resides in the lack of direct activation functions computation without the overhead of data movement between the floating-point register file, the standard register file, and the coprocessor.
Table 5,
Table 6 and
Table 7 reports a short comparison of TOXOS and other architectures.
8. Conclusions
This paper presents TOXOS, a configurable CORDIC-based coprocessor designed to accelerate the computation of nonlinear functions in AI applications for automotive systems. The proposed architecture addresses a critical performance bottleneck in modern machine learning workloads, where nonlinear activation functions can represent an actual bottleneck in inference [
1].
Our experimental results demonstrate significant performance improvements over traditional software implementations. TOXOS achieves speedups ranging from to compared to softfloat library implementations and to compared to hardware floating-point units. The constant latency of 8–10 clock cycles for all supported operations, combined with the configurability of the architecture, makes TOXOS particularly suitable for real-time automotive applications where predictable performance is crucial.
The integration of TOXOS into the X-HEEP system [
3] showcases its practical applicability in microcontroller-based platforms. With an area less than twice that of fpnew [
18], TOXOS provides an efficient solution for edge AI applications in resource-constrained automotive environments.
We plan to further extend and develop TR-HEEP to test the execution of real-world inference to actually test the expected gain in performance and reduction in energy. The half-precision format [
13] is gaining more and more popularity, representing a good tradeoff between accuracy and memory footprint. We plan to implement support for other floating-point formats in the near future. To address the bottleneck introduced by the extension interface, we plan to expand it by adding support to floating-point registers.
The automotive industry’s transition toward software-defined vehicles and autonomous driving systems creates increasing demand for efficient AI acceleration at the edge [
20]. TOXOS represents a significant step forward in providing the computational capabilities needed for these applications while maintaining the power efficiency crucial for electric vehicles and the real-time constraints essential for safety-critical automotive systems.