1. Introduction
Against the backdrop of the advancing global energy transition and carbon neutrality objectives, industrial park energy systems face dual pressures [
1]. On the one hand, the large-scale development of renewable energy sources (RESs) such as wind and solar power presents significant opportunities for emission reduction [
2]. However, their intermittent and unpredictable nature increases operational instability within systems [
3]. On the other hand, the loads within these parks typically exhibit characteristics of rigidity [
4], continuity, and high intensity, creating a significant mismatch with the fluctuating nature of renewable energy [
5]. This limits the level of renewable energy integration and undermines the overall potential for emission reduction [
6].
Electricity–hydrogen integrated energy systems (EH-ESs) are viewed as a potential solution to these contradictions [
7], as their complementary multi-energy and cross-scale regulation capabilities can enhance system flexibility to some extent [
8,
9]. Meanwhile, EH-ESs offer a viable pathway for achieving low-carbon targets in energy-intensive industries and sectors where emission reduction proves challenging, such as chemicals, ceramics, and metallurgy [
10]. However, existing research has primarily focused on capacity optimisation and equipment configuration, with limited exploration of their dynamic response mechanisms and carbon reduction efficacy under complex operational conditions [
11]. Moreover, the intrinsic coupling between energy losses and carbon emissions remains unsystematically characterised, leaving the emission reduction potential of EH-ESs without a verifiable quantitative foundation.
Consequently, in-depth operational research on EH-ESs is imperative to elucidate their operational characteristics, energy loss patterns, and carbon reduction potential under various typical operating conditions. This will provide theoretical underpinnings and methodological support for subsequent low-carbon optimisation of integrated energy systems (IESs).
A significant portion of existing research has focused on the capacity scale and investment allocation of electricity–hydrogen systems and IESs. Employing methods such as multi-objective optimisation and two-level optimisation, scholars have explored optimal combinations of equipment including electrolysers (ELs), fuel cells (FCs), hydrogen storage tanks (HSTs), and battery energy storage (BES) systems, balancing economic viability against emission reduction outcomes. For example, Li K et al. 2024 developed a multi-objective pathway model integrating energy structure, industrial layout, land use, and economic costs [
12]; Mu Y and Guo H employed a bilevel programming approach to achieve the coordinated optimisation of multi-energy and carbon flows, thereby enhancing long-term investment returns and decarbonisation efficiency [
13]; Ref. [
14] synthesised twelve carbon-neutrality pathways for industrial parks, offering strategic guidance for policymakers and park administrators; and Ref. [
15] comprehensively reviewed bioeconomy strategies and synergistic carbon reduction pathways. Wu D et al. designed an IES that integrates photovoltaic (PV), wind turbine (WT), and energy storage components, achieving multi-objective coordination through the joint optimisation of operating conditions and equipment configuration [
16]; additionally, one research group [
17] developed a microgrid integrating hydrogen storage and carbon capture, utilisation, and storage (CCUS) technologies, proposing a two-stage scheduling model. Ref. [
18] developed an industrial park energy system model covering hydrogen production, compression, transportation, and storage; Ref. [
19] proposed a bilevel scheduling strategy for electricity–storage–hydrogen coupling systems; and Ref. [
20] constructed a low-carbon electricity–heat–hydrogen integrated modelling framework based on mixed-integer linear programming (MILP). However, such studies are generally based on static or long-term planning scenarios, lacking characterisation of systems’ operational responses and dynamic adaptability under multi-disturbance conditions.
Another category of research focuses more on the operational processes and low-carbon operation strategies of EH-ESs, encompassing energy conversion modelling, energy storage dispatch mechanisms, and the impact of external market signals such as carbon quotas and electricity pricing mechanisms [
21]. This work demonstrates the significant potential of EH-ESs in enhancing renewable energy integration and reducing carbon emissions. Ref. [
22] constructed IESs for industrial parks, incorporating advanced technologies such as CCUS, hydrogen production via electrolysis, hydrogen storage, and combined cooling, heating, and power (CCHP) load management. Ref. [
23] conducted scenario-based optimisation for synergistic decarbonisation and pollution reduction in energy-intensive parks; Zhu J et al. 2025 employed blockchain technology to ensure data credibility and incorporated a tiered carbon trading mechanism to optimise park-level scheduling [
24]; Gu H et al. 2022 constructed a dual-level ‘city–park’ carbon quota scheduling model to coordinate interactions across different system hierarchies [
25]; and Shi Z et al. 2023 proposed a carbon quota allocation and economic scheduling model spanning annual, monthly, and daily timescales, applicable to systems integrated with CCUS [
26]. However, such studies are often validated solely within a single energy pathway or under idealised institutional conditions [
27], lacking quantitative analysis of the coupling relationship between energy losses and carbon emissions. Furthermore, insufficient attention is paid to systems’ adaptability under typical disturbance conditions.
In summary, existing research has made significant progress in capacity optimisation, operational mechanisms, and low-carbon strategies, yet several shortcomings remain. Firstly, capacity optimisation studies emphasise long-term planning and equipment configuration while neglecting systems’ performance under short-term disturbances and dynamic operating conditions. Secondly, although research on operational optimisation and market mechanisms has partially revealed the potential of EH-ESs, it lacks a quantitative analytical framework linking energy losses to carbon emissions, making it difficult to comprehensively explain emission reduction variations under different operating conditions. Finally, current research generally pays insufficient attention to external grid dynamics and typical disturbance scenarios, limiting the applicability of findings to complex industrial environments. To address these shortcomings, further systematic research at the operational level is necessary to uncover the emission reduction potential and operational mechanisms of EH-ESs under multi-disturbance conditions.
This study proposes an evaluation framework for assessing the low-carbon performance of EH-ESs. Rather than focusing solely on capacity optimisation or isolated operational cases, the framework emphasises a comprehensive integration of modelling, quantitative evaluation, and scenario-based validation. By combining objective functions with system-level constraints and analysing system behaviour under diverse operating conditions, the framework enhances the methodological robustness of EH-ES evaluation and provides insights into these systems’ adaptability to complex energy environments. Through this approach, this study not only quantifies the decarbonisation potential of EH-ESs but also elucidates their operational trade-offs across economic, environmental, and technical dimensions. The key contributions of this study are summarised as follows:
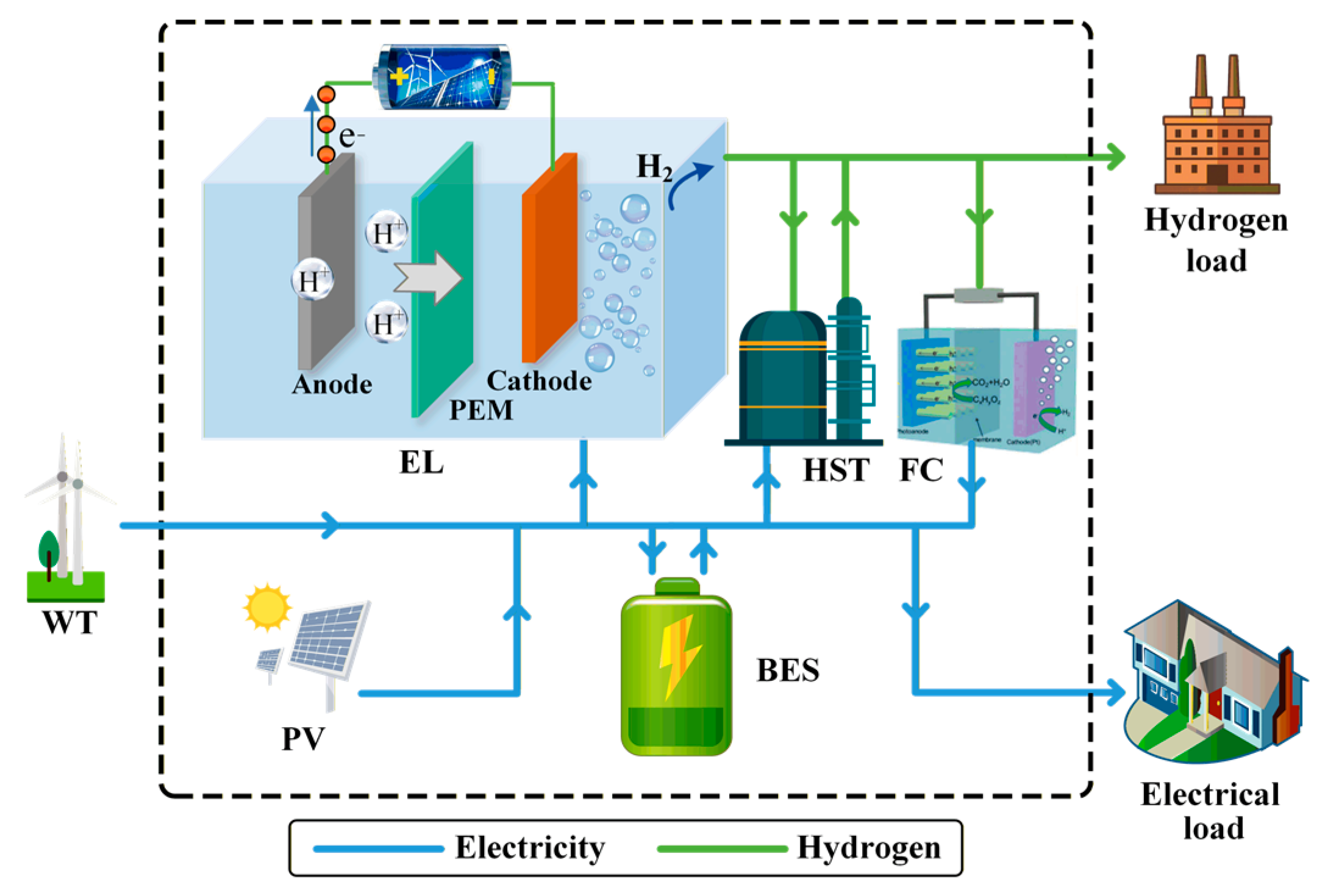
Comprehensive modelling of EH-ES: A detailed system representation was established, covering EL, FC, HST, and BES, thereby capturing the structural and operational characteristics of electricity–hydrogen conversion.
Quantitative evaluation of carbon reduction capability: A systematic method was developed to measure the decarbonisation performance of the EH-ES across different optimisation objectives, enabling consistent comparisons among cost, emissions, and energy loss indicators.
Operational behaviour analysis under multi-disturbance conditions: A series of representative scenarios were designed to evaluate the system’s response and resilience, revealing its adaptability in managing external fluctuations and internal constraints.
The remainder of this study is organised as follows.
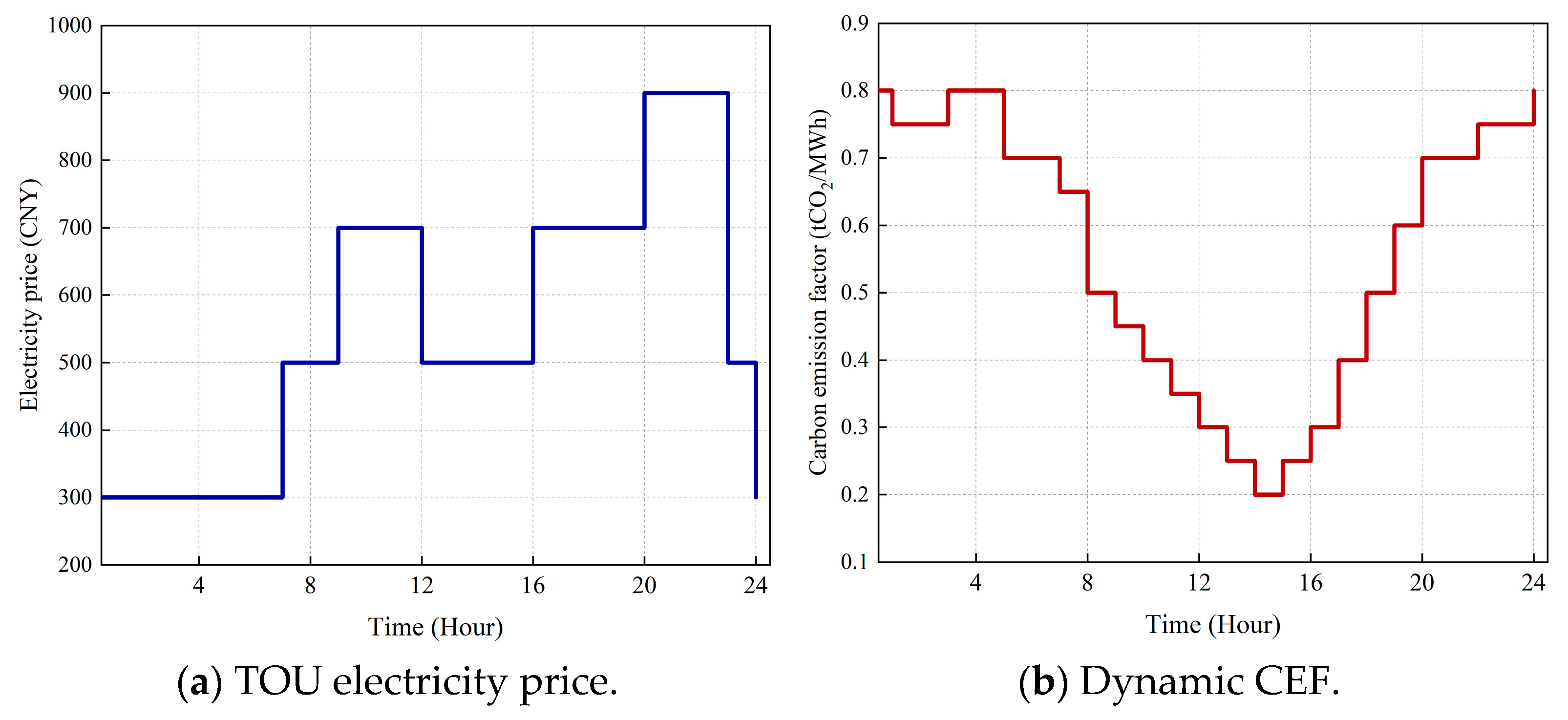
Section 2 introduces the system architecture and the operation mechanism of the EH-ES, and formulates the optimisation model, including the definition of objective functions and the establishment of constraint conditions.
Section 3 presents the design of solution algorithms, including linearisation techniques and multi-objective optimisation approaches.
Section 4 presents a case study based on typical multi-disturbance operating conditions to validate the proposed model and evaluate its performance in terms of cost, carbon emissions, and energy losses.
Section 5 concludes the study by summarising the main findings and highlighting future research directions. Specifically, the list of names for parameters, abbreviations, superscripts and subscripts is provided in
Appendix A,
Table A1.
5. Conclusions
In this study, a comprehensive optimisation framework is developed and validated for an electricity–hydrogen integrated energy system (EH-ES) tailored to ceramic industrial parks. By incorporating multi-objective optimisation with time-of-use (TOU) pricing, the dynamic carbon emission factor (CEF), and detailed equipment models, the study evaluates the system’s configuration and operational responses under multi-disturbance conditions. Through case studies, the proposed framework demonstrates the capability to flexibly coordinate electricity and hydrogen storage, achieve stable operation under diverse scenarios, and quantitatively assess the trade-offs among cost, carbon emissions, and energy losses.
Three important findings emerge from this analysis.
The proposed model is technically feasible and operationally robust, with high adaptability across different load and renewable conditions.
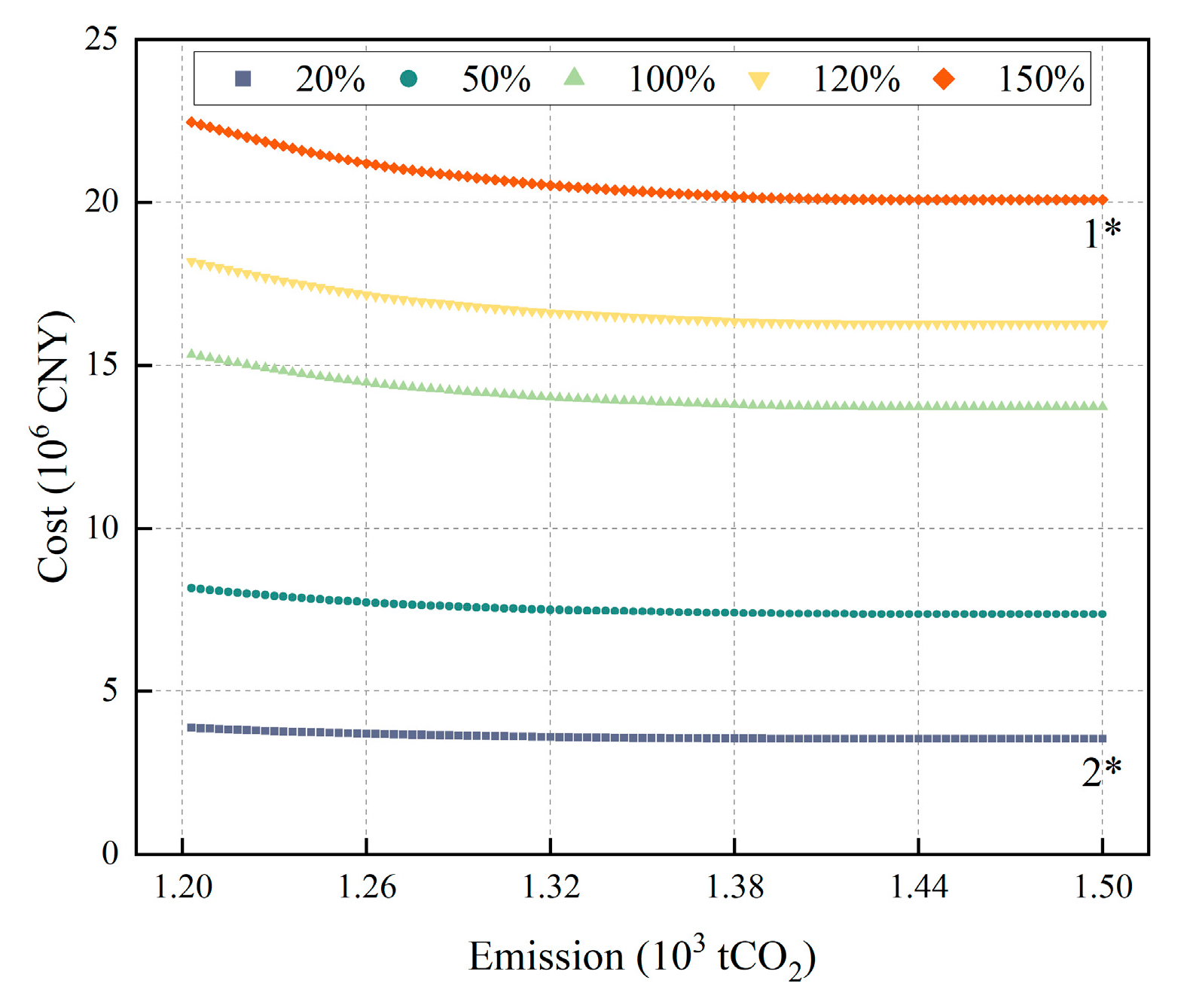
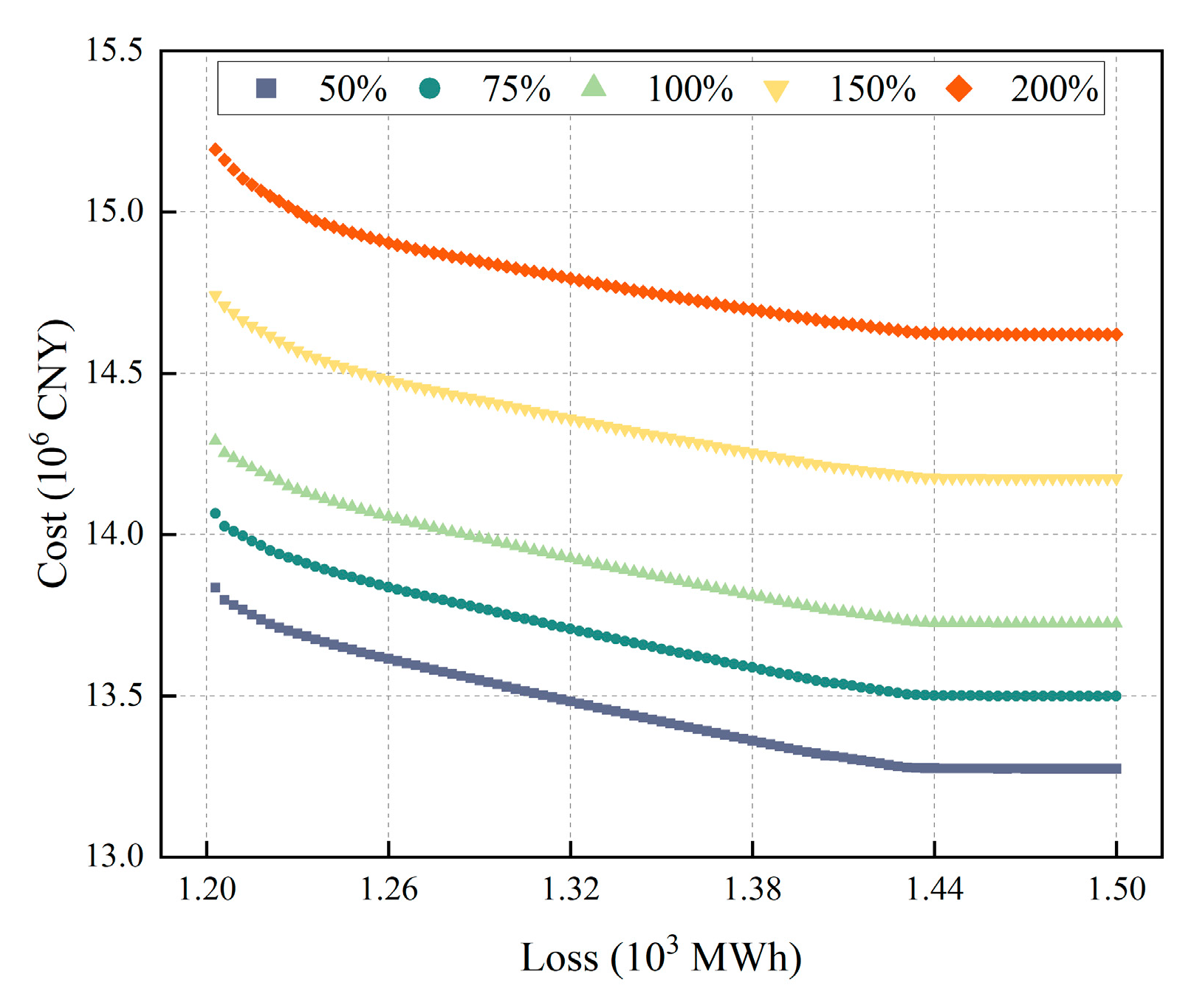
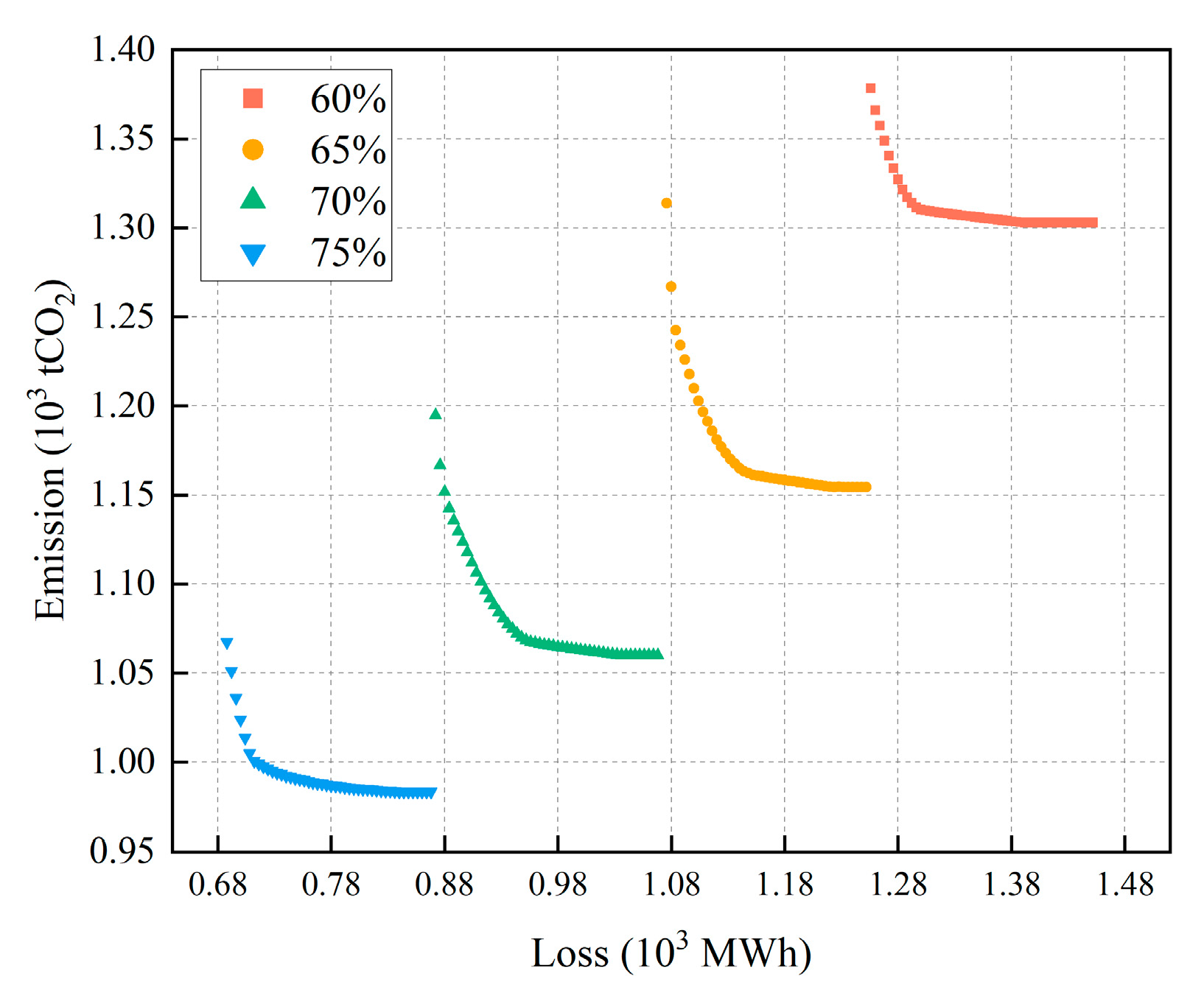
The carbon reduction potential is strongly shaped by equipment efficiency and the electricity trading ratio (self-sufficiency rate), underscoring the importance of external–internal interactions in determining system performance.
The efficiency and cost of the electrolyser (EL) and fuel cell (FC) are the most critical bottlenecks: significant reductions in equipment prices can make emission reduction economically viable, while efficiency improvements both enhance decarbonisation effectiveness and mitigate energy losses.
Looking forward, these results highlight several promising directions. Improving EL and FC efficiency not only strengthens the environmental benefits of hydrogen utilisation but also shifts the system towards higher hydrogen load levels with greater carbon reduction potential, thereby supporting the broader substitution of hydrogen in industrial energy structures. Moreover, only when equipment costs decline to approximately 20% of current levels does emission reduction become economically attractive under existing carbon prices, suggesting that cost breakthroughs are essential for market-driven decarbonisation. Finally, strategies should increasingly move toward more direct carbon mitigation pathways—such as direct hydrogen supply or process substitution—to achieve deeper and more cost-effective reductions in high-emission industries. Nevertheless, this study is limited by the fixed renewable generation profiles and region-specific operational data, which may affect the generalisability of the results. Future work will extend the framework to include stochastic renewable variations, different market and policy scenarios, and multi-regional system interactions to further validate and expand the applicability of the proposed approach.