Design, Simulation, Construction and Experimental Validation of a Dual-Frequency Wireless Power Transfer System Based on Resonant Magnetic Coupling
Abstract
1. Introduction
- development and simulation of a WPT system using two control frequencies to improve power transfer under varying coupling conditions;
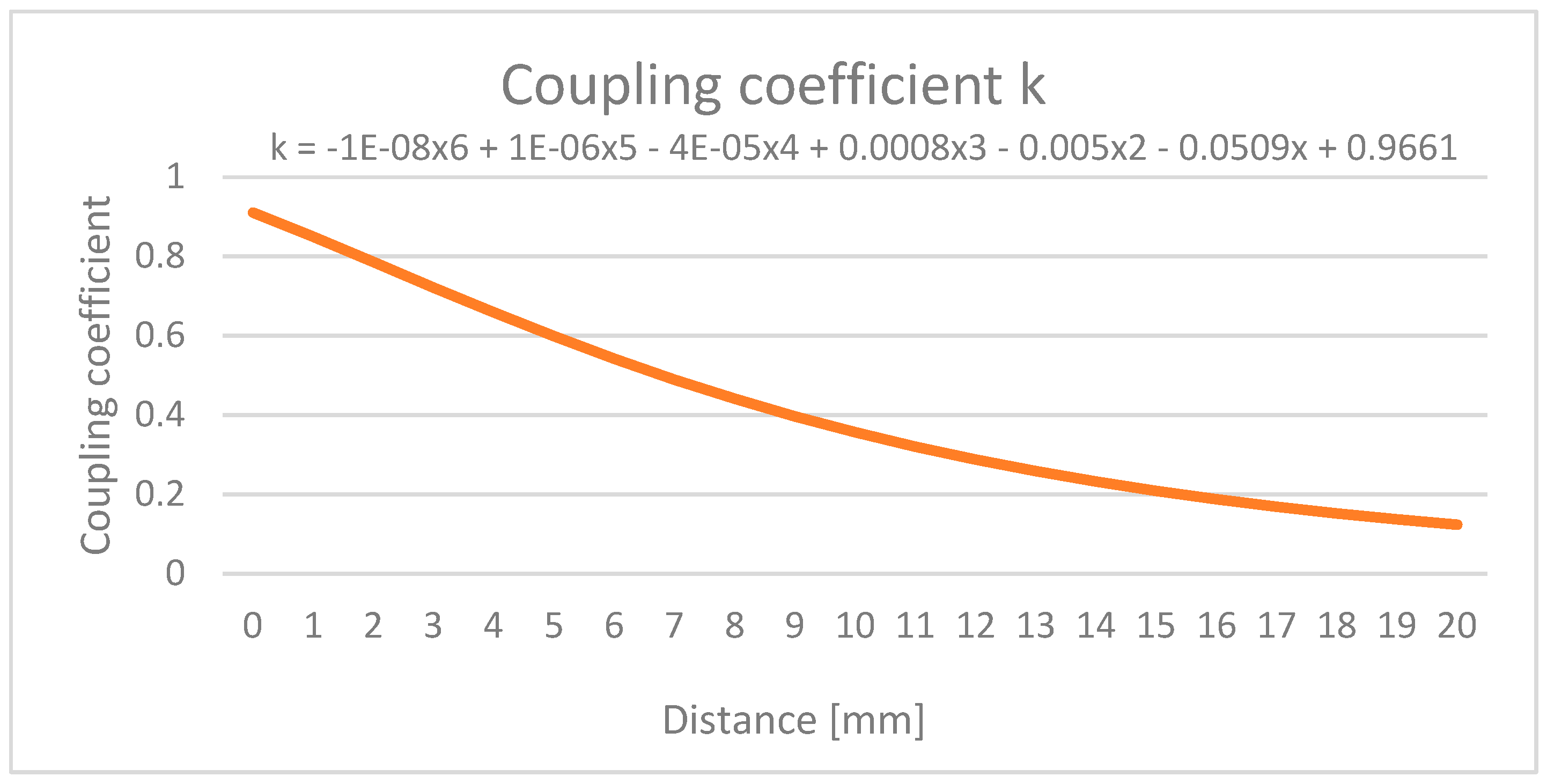
- derivation of a sixth-degree polynomial to model the coupling coefficient as a function of coil distance, enabling predictive tuning;
- experimental construction and validation of the proposed system, demonstrating consistent agreement with simulation results;
- identification of optimal control signal periods that maximize the induced voltage for a given range of coupling coefficients.
- the use of dual-frequency control applied independently on two transistors, which allows the dynamic adaptation of the system to variations in coupling factors and different load conditions;
- the derivation of a sixth-degree polynomial model that describes the variation in the coupling coefficient as a function of the distance between the coils, providing a predictive tool for parameter tuning;
- the experimental validation of the constructed prototype, which confirms the numerical results as well as the advantages of the proposed method. Unlike existing studies, which are mainly based on a single frequency or passive compensation methods, the proposed approach demonstrates greater robustness and flexibility in wireless energy transfer.
2. Materials and Methods
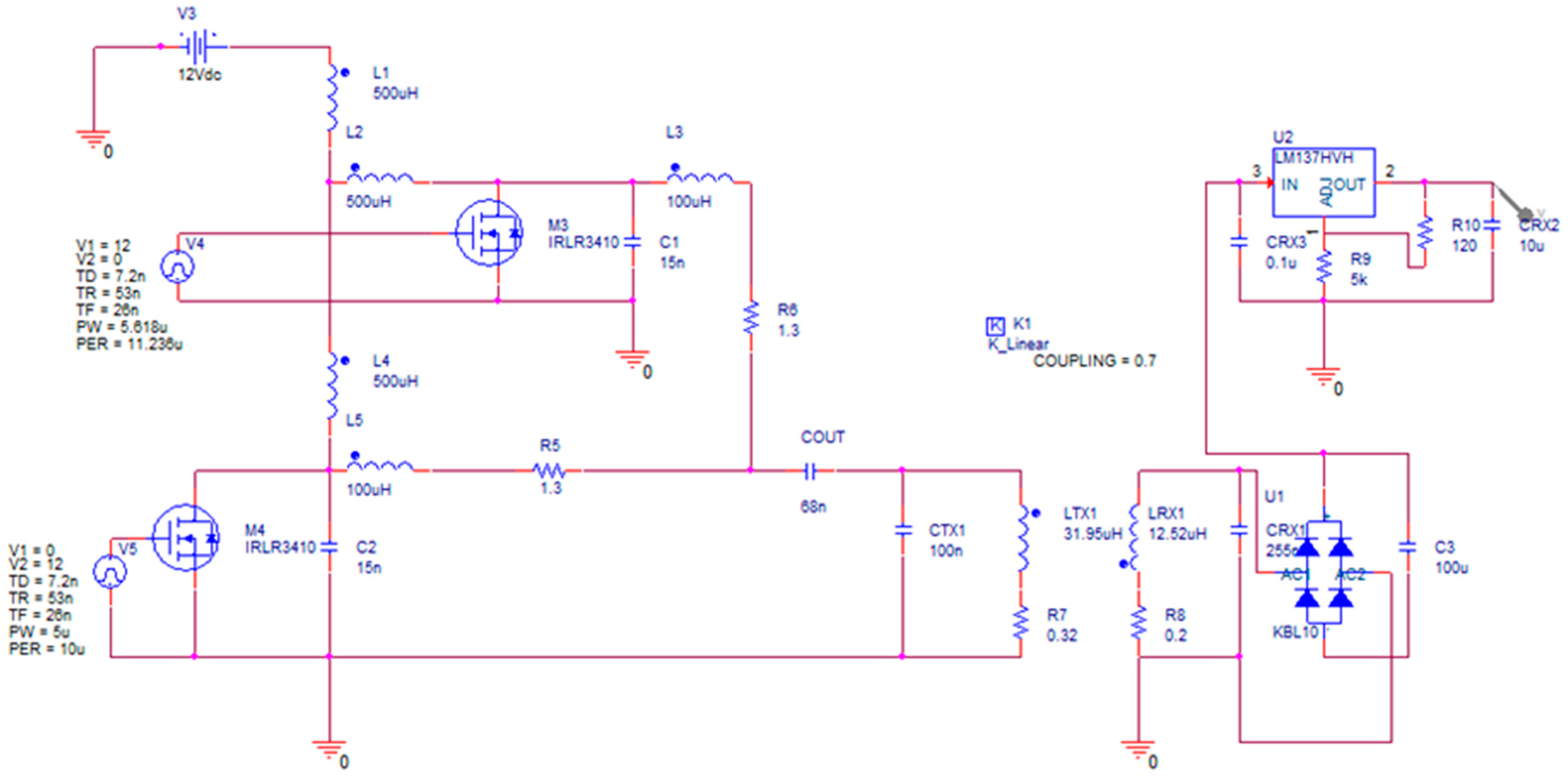
2.1. Numerical Modeling and Circuit Simulations
- dual-frequency excitation applied to both control transistors;
- single-frequency excitation applied to the upper transistor (M3) only;
- single-frequency excitation applied to the lower transistor (M4) only.
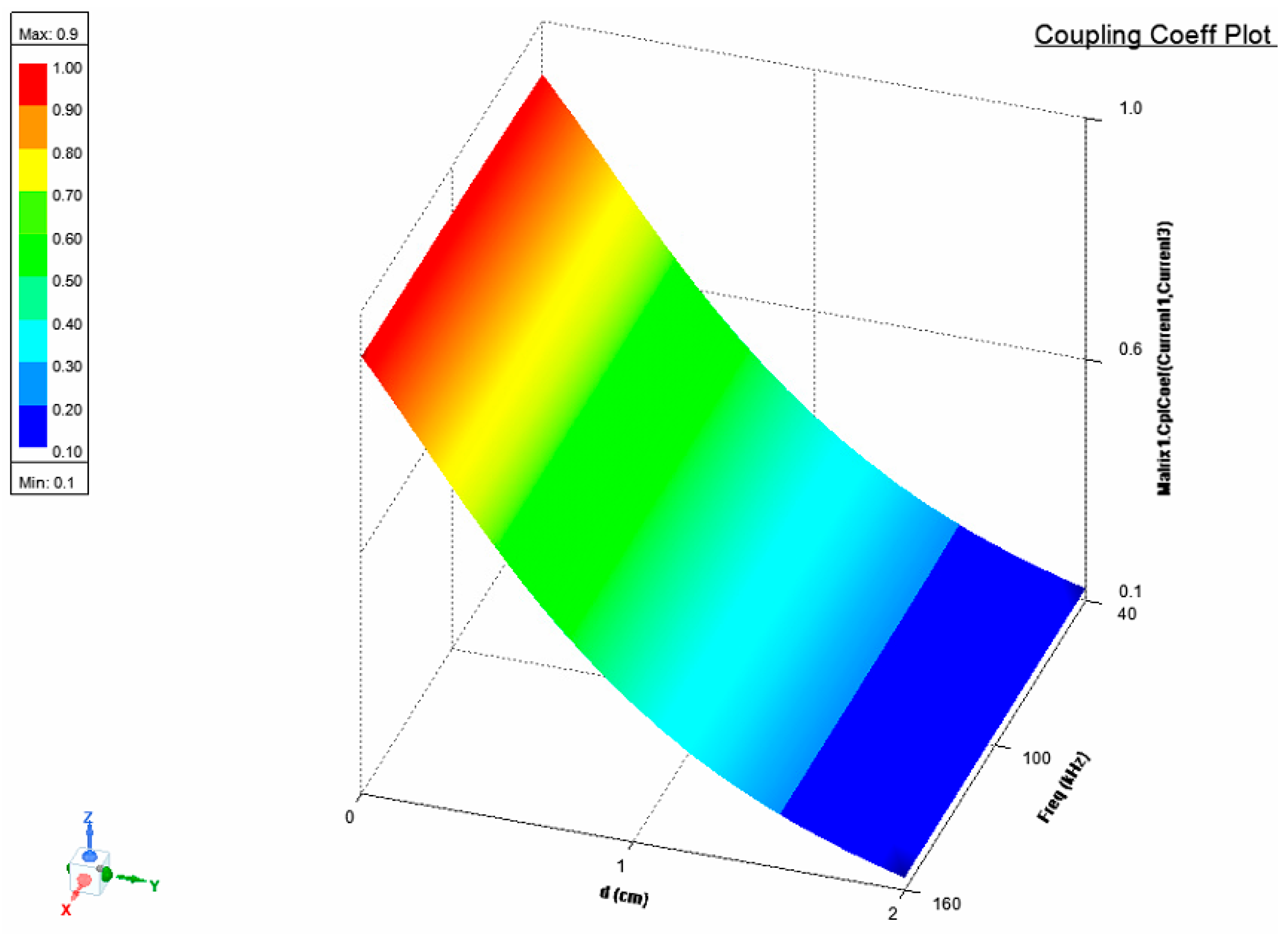
2.2. Electromagnetic Field Simulation
2.3. Construction of the WPT Prototype
2.4. Data Availability
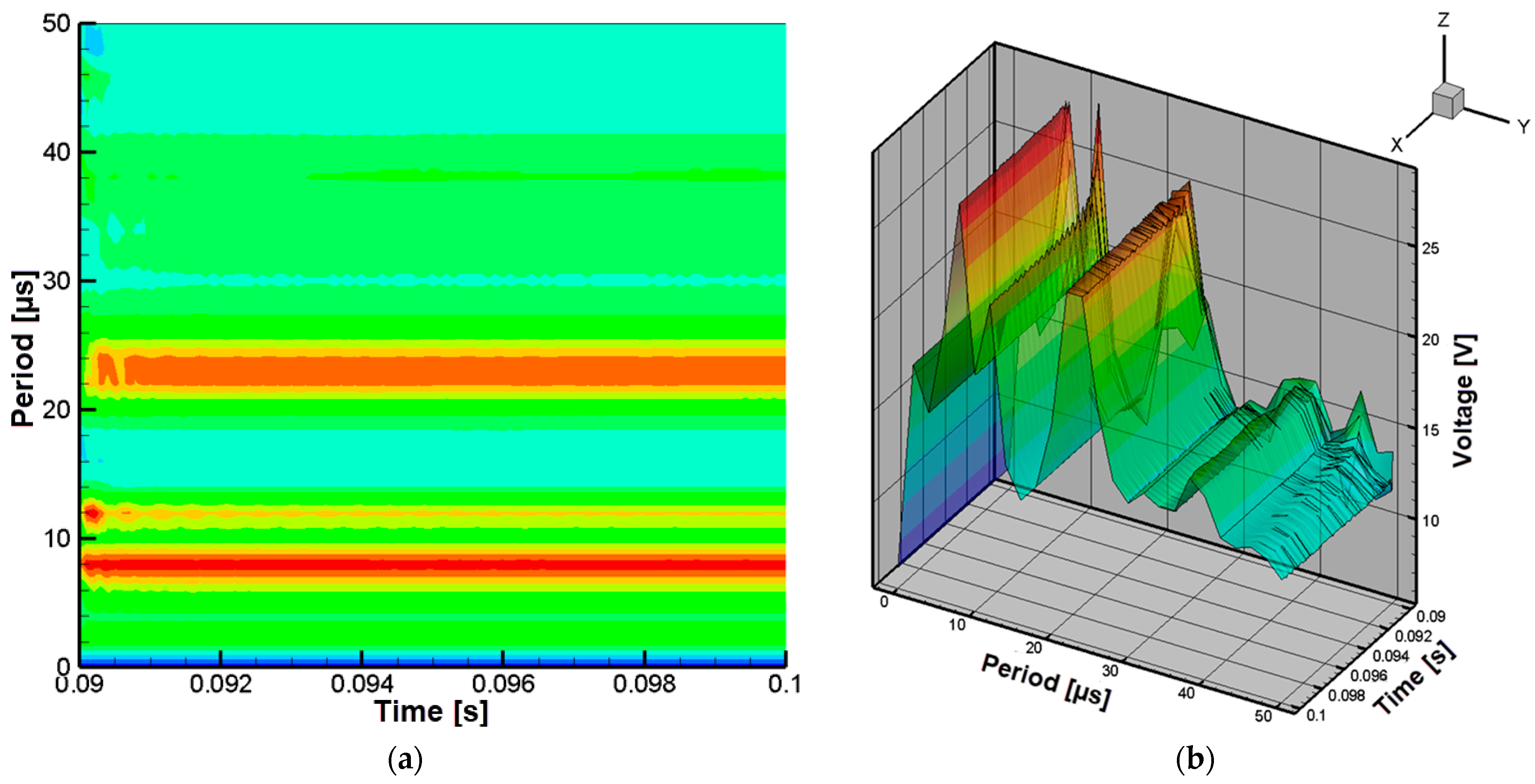
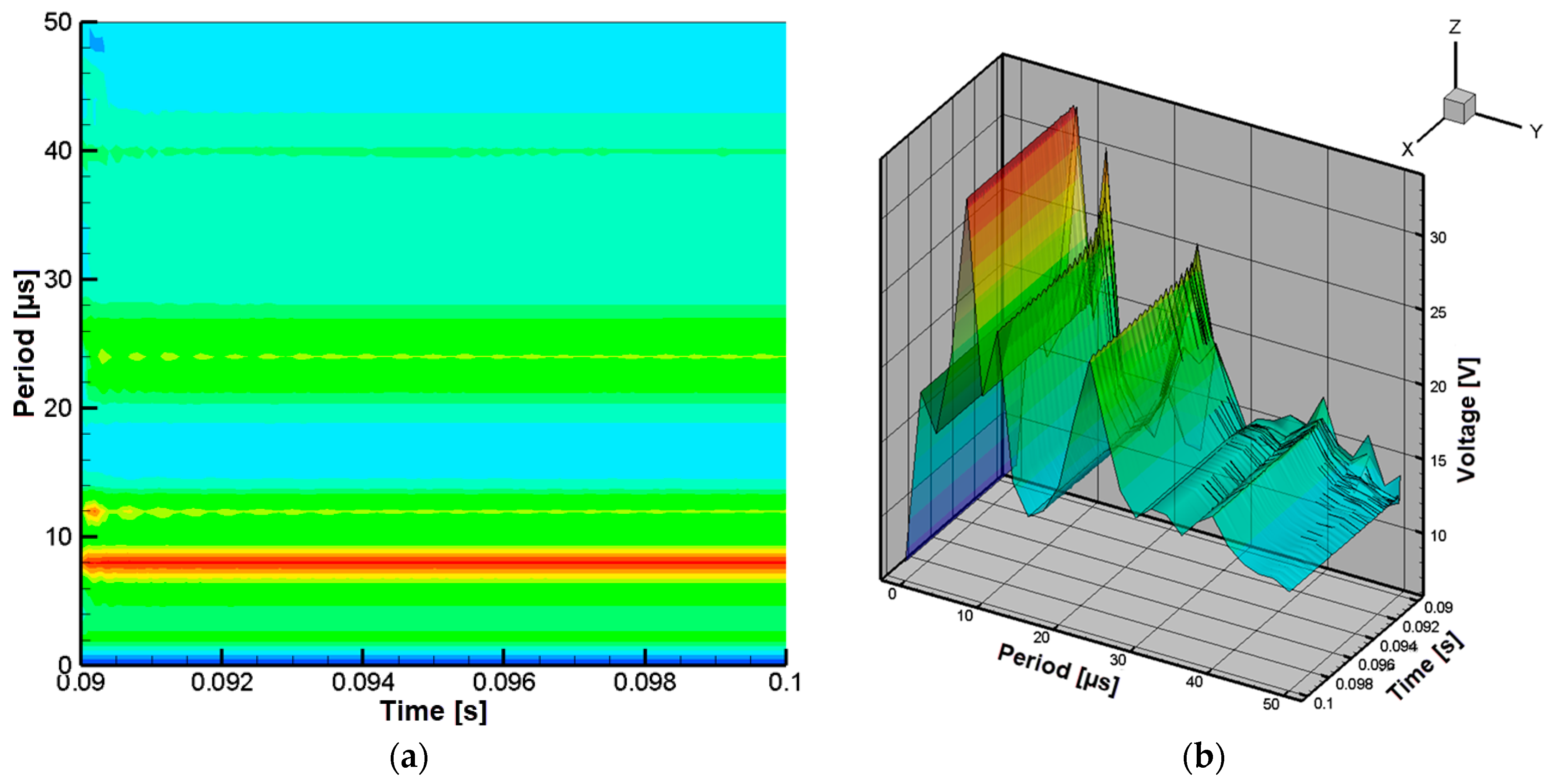
3. Results
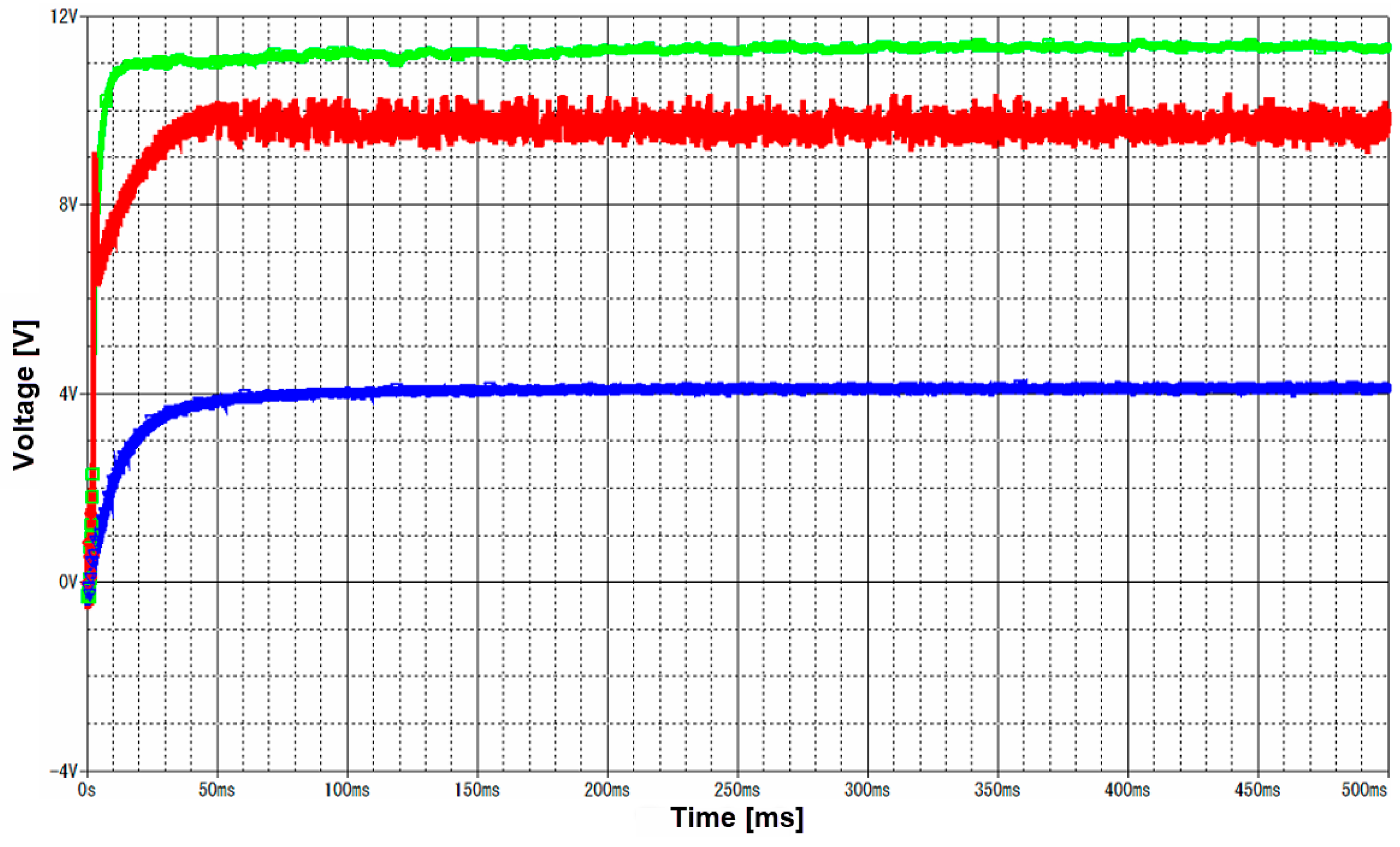
3.1. Numerical Modeling of the Electric Circuit
- (a)
- operation with two control frequencies;
- (b)
- operation with a single control frequency applied to the upper transistor (M3);
- (c)
- operation with a single control frequency applied to the lower transistor (M4).
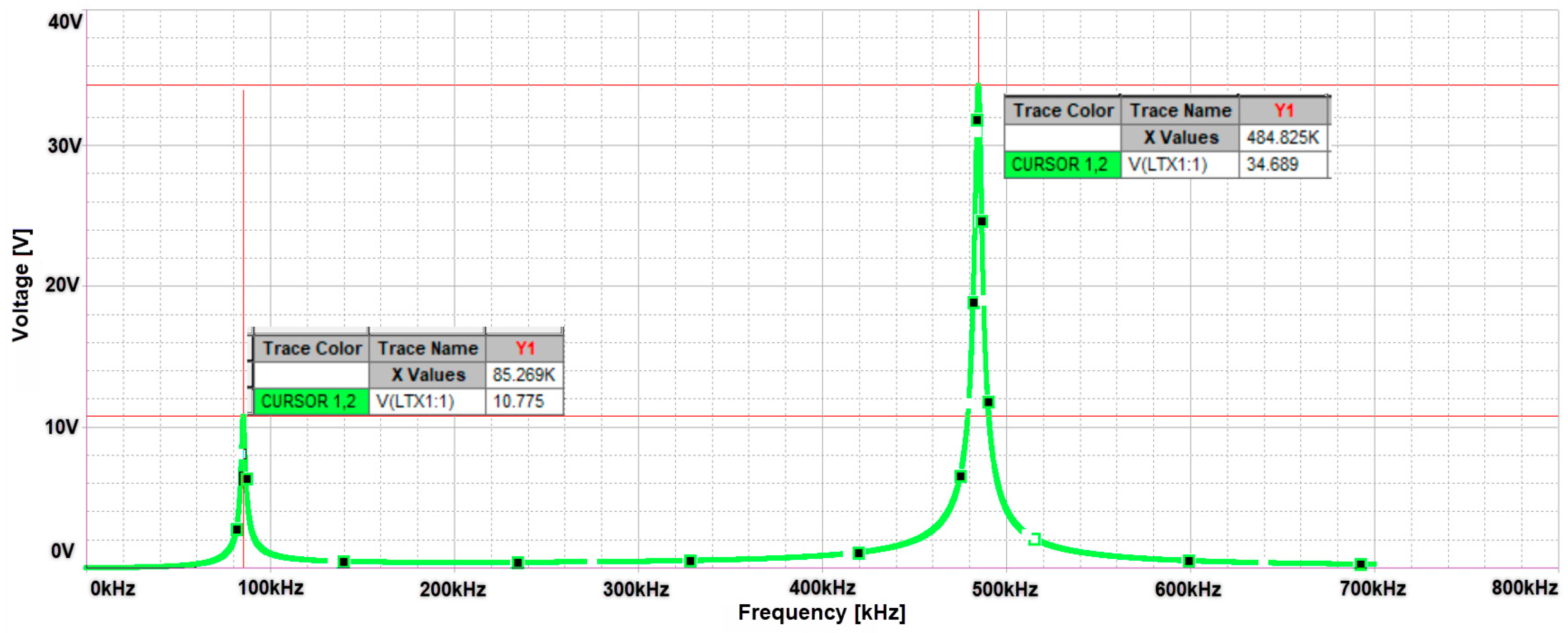
Analysis of the Optimized Wireless Power Transfer System Using Real Coil Parameters
- fr = resonance frequency [Hz];
- L = inductance of the coil [H]; (LTX1, LRX1)
- C = capacitance of the capacitor [F]; (CTX1, CRX1)
- RL = resistance of the coil [Ω]; (R7, R8)
- RC = resistance of the capacitor [Ω];
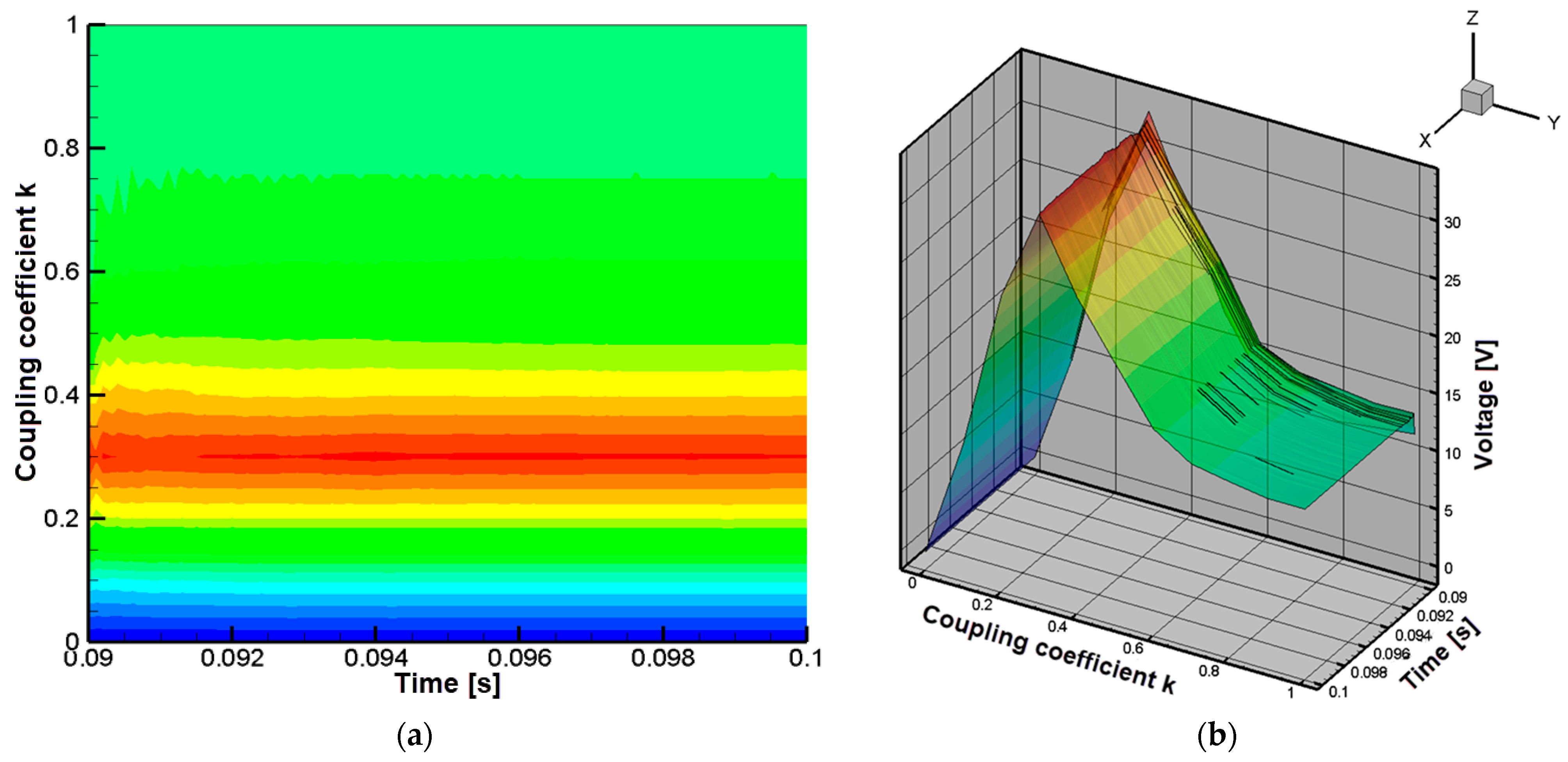
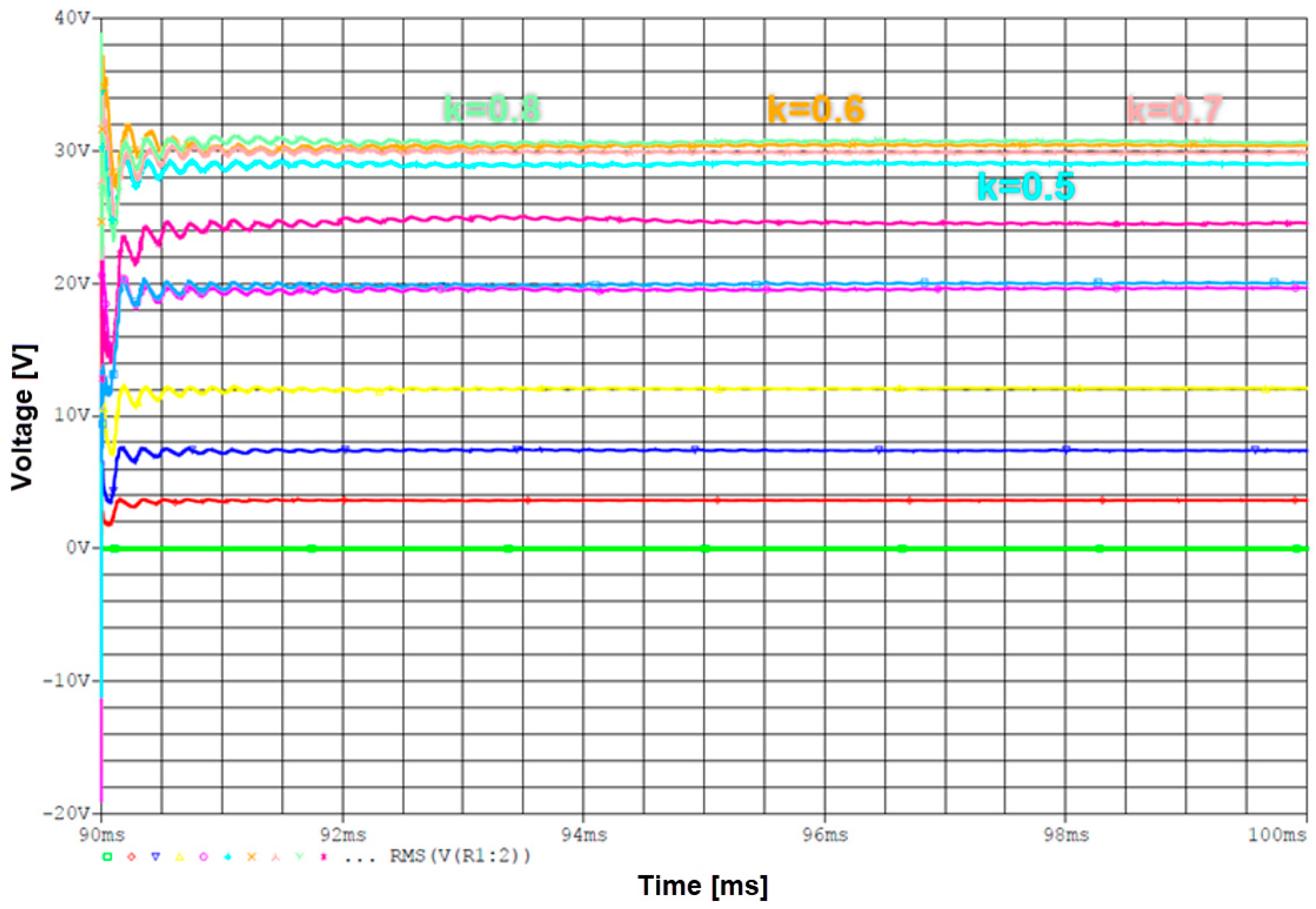
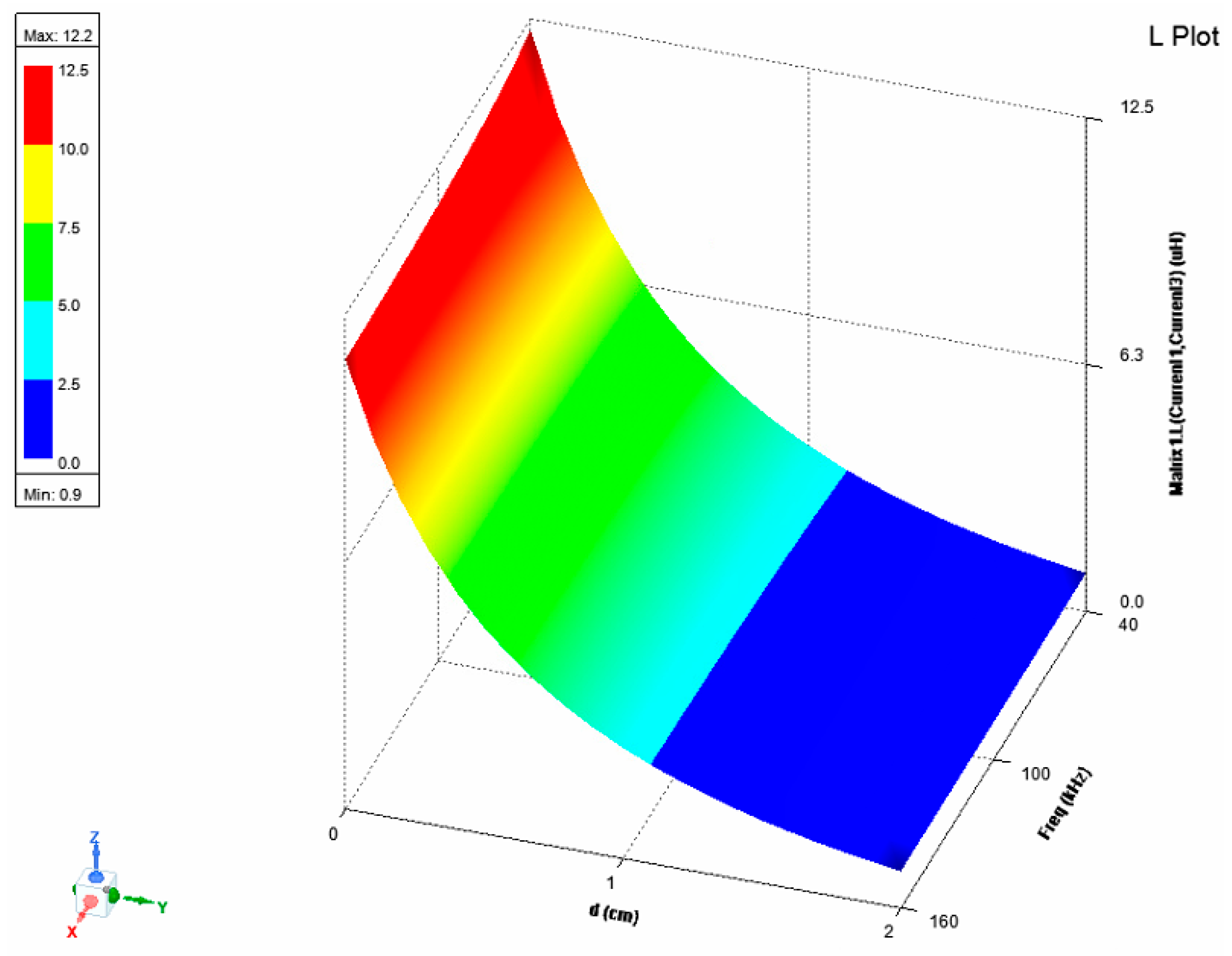
3.2. Impact of the Receiver Coil Position on the Parameters of the Wireless Power Transfer System
- (a)
- Coupling coefficient
- (b)
- Mutual inductance
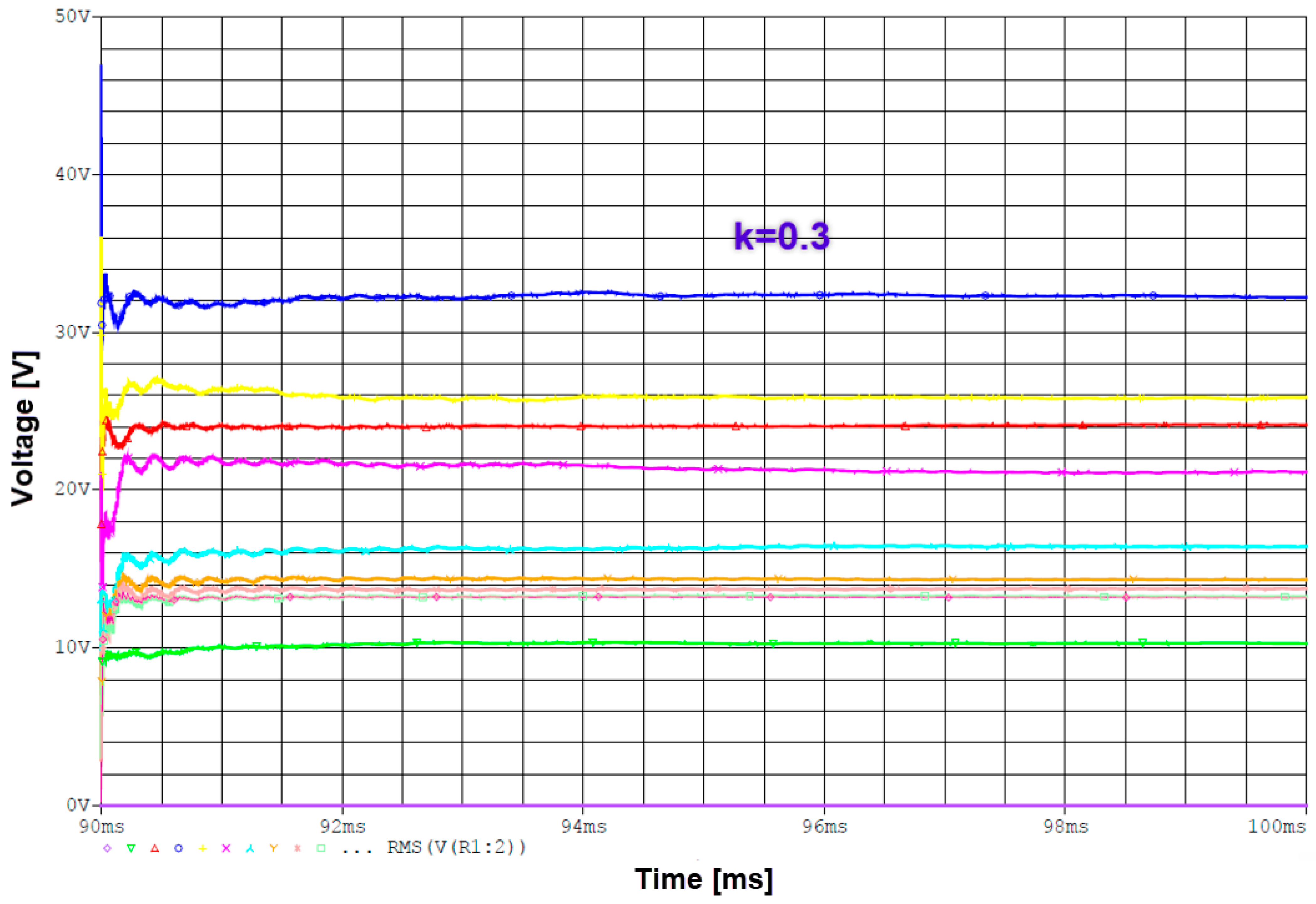
4. Construction and Experimental Testing of the Designed Wireless Power Transfer System
4.1. Experimental Construction of the Wireless Power Transfer System
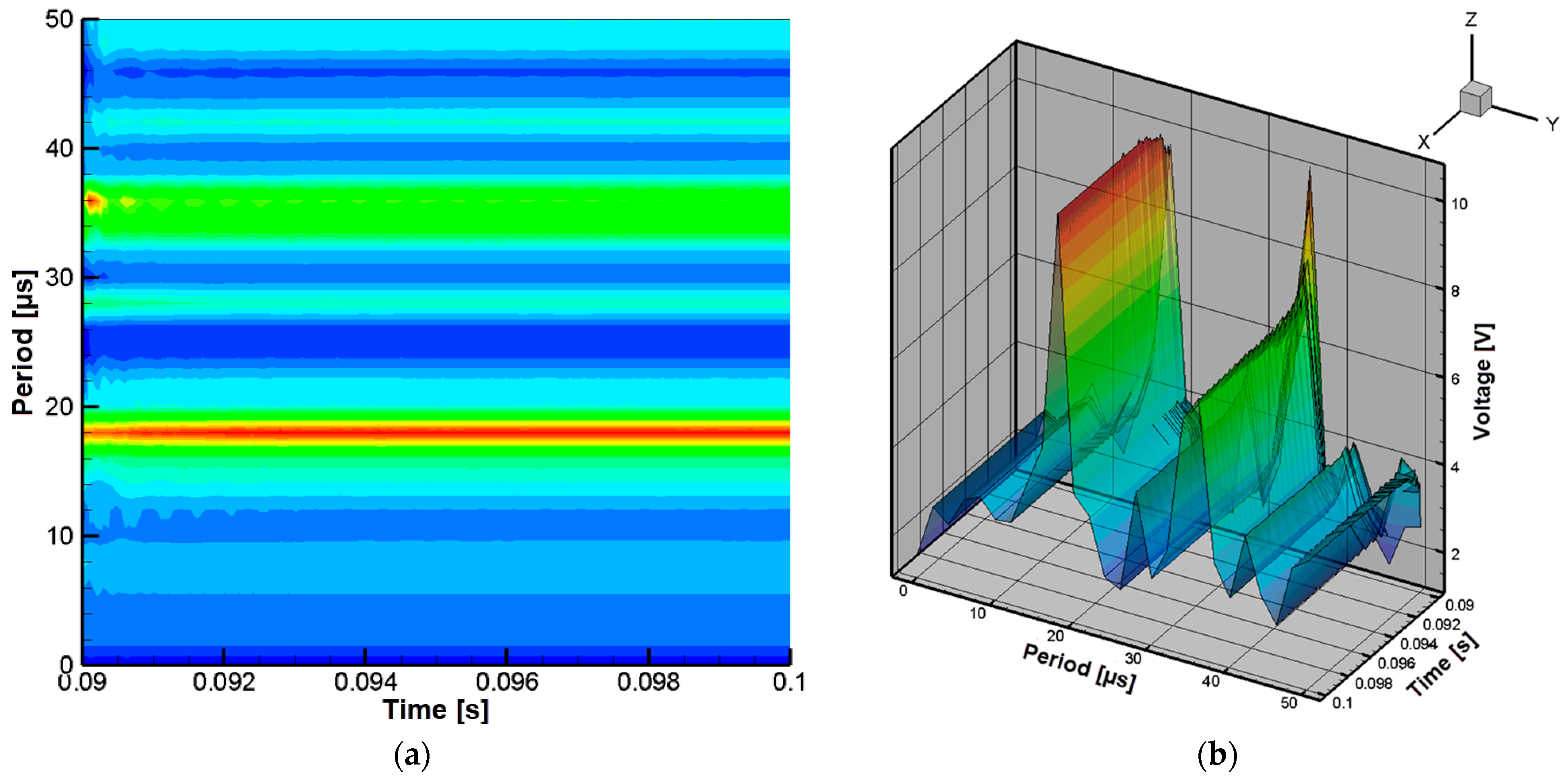
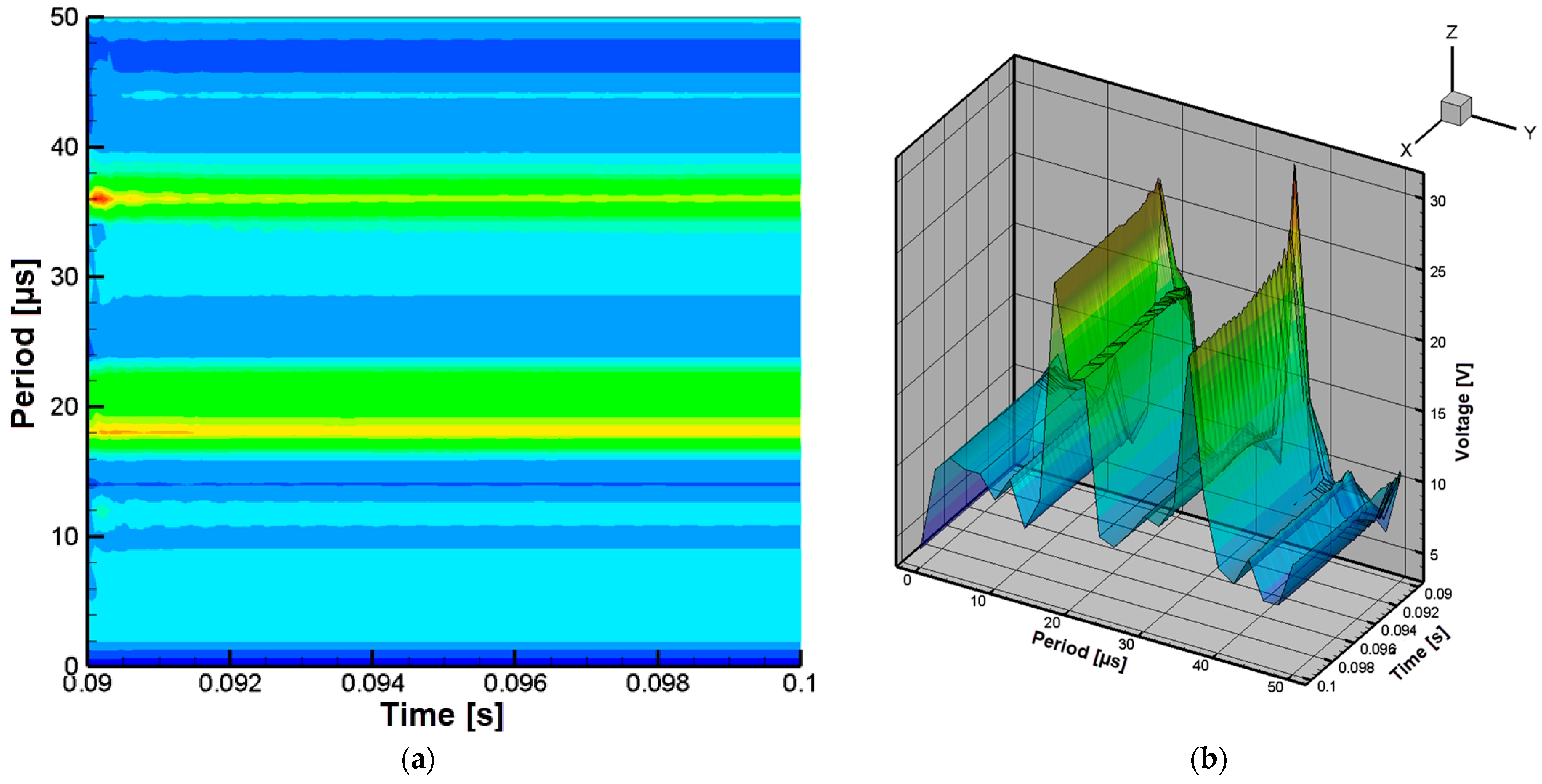
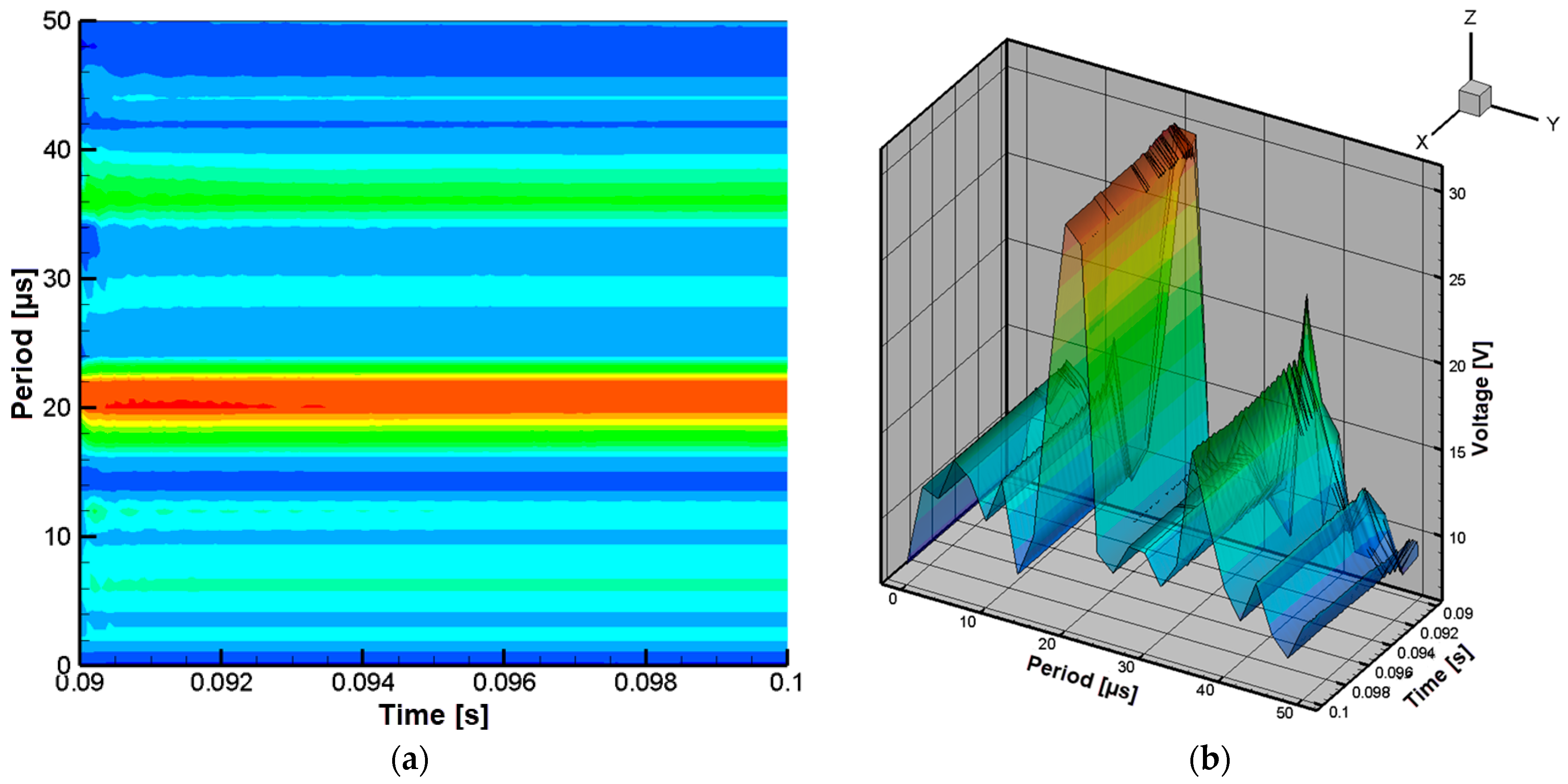
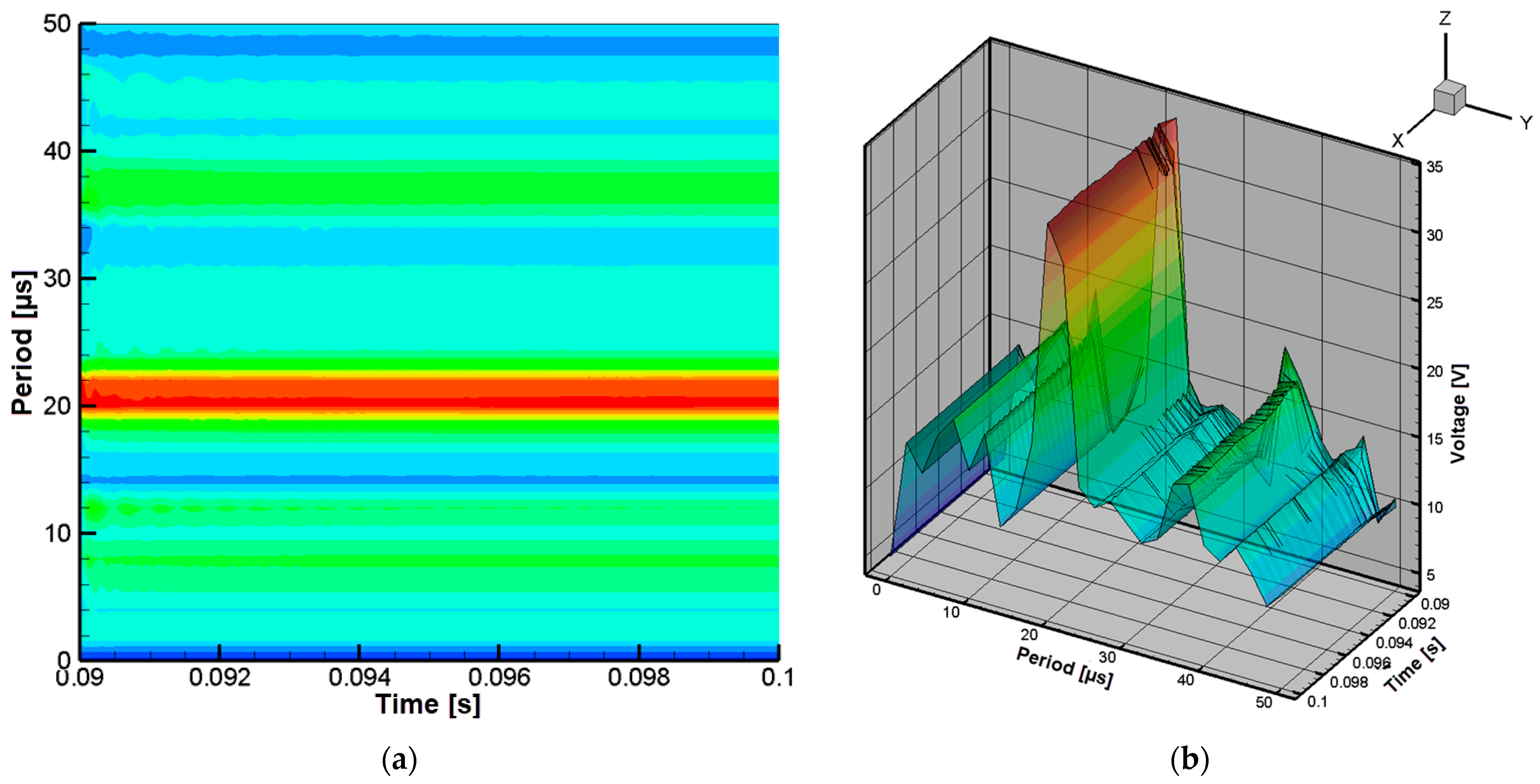
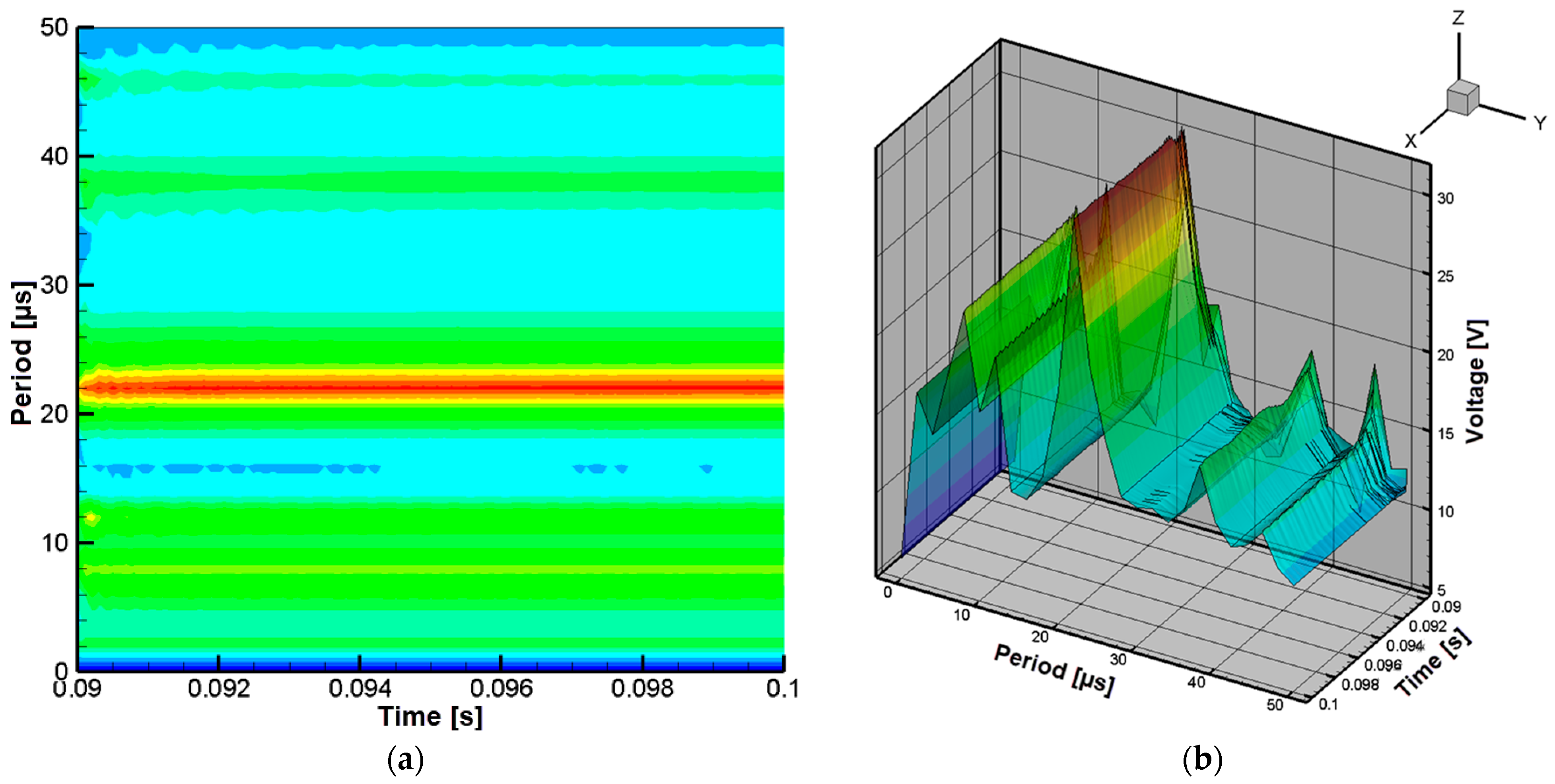
4.2. Experimental Testing of the Constructed Wireless Power Transfer System
5. Discussion
6. Conclusions and Future Work
- The findings from this study open several promising directions for future research:
- Adaptive Control Algorithms: Integration of feedback-based control to dynamically adjust the signal period and frequency based on load and coupling conditions.
- Miniaturization and Integration: Development of compact, PCB-integrated coil designs for applications in biomedical implants or consumer electronics.
- Efficiency Optimization: Exploration of resonant impedance matching techniques and energy harvesting circuits to further improve power transfer efficiency.
- Multi-Coil Architectures: Investigation of multi-coil or array-based systems to extend transmission range or improve spatial flexibility.
- Robustness to Misalignment: Study of alignment-tolerant topologies and compensation techniques for variable receiver positions.
- By combining numerical modeling, real-time tuning, and experimental validation, future work can lead to the development of high-efficiency, self-adaptive WPT systems suitable for a wide range of industrial and consumer applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WPT | Wireless Power Transfer |
| FEM | Finite Element Method |
| PCB | Printed Circuit Board |
| DC | Direct Current |
| AC | Alternating Current |
| MOSFET | Metal–Oxide–Semiconductor Field-Effect Transistor |
| kHz | KiloHertz |
| µs | Microsecond |
| V | Volt |
| CAD | Computer-Aided Design |
| RMS | Root Mean Square |
| L | Inductance |
| C | Capacitance |
| RL | Inductor resistance |
| RC | Capacitor resistance |
| ωr | Resonant Angular |
| M3, M4 | Transistors MOSFET |
| Tx | Transmitter |
| Rx | Receiver |
| k | Coupling Coefficient |
| fr | Resonant Frequency |
| µH | MicroHenry |
| mΩ | MilliOhm |
| ηF | nanoFarad |
Appendix A
| d [mm] | Freq 40 [kHz] | Freq 50 [kHz] | Freq 60 [kHz] | Freq 70 [kHz] | Freq 80 [kHz] | Freq 89 [kHz] | Freq 90 [kHz] | Freq 100 [kHz] | Freq 110 [kHz] | Freq 120 [kHz] | Freq 130 [kHz] | Freq 140 [kHz] | Freq 150 [kHz] | Freq 160 [kHz] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.901 | 0.904 | 0.906 | 0.908 | 0.910 | 0.911 | 0.911 | 0.912 | 0.913 | 0.913 | 0 914 | 0.915 | 0.915 | 0.915 |
| 1 | 0 842 | 0.845 | 0.846 | 0.848 | 0.849 | 0.850 | 0.850 | 0.850 | 0.851 | 0.852 | 0 852 | 0.852 | 0.853 | 0.853 |
| 2 | 0.780 | 0.782 | 0.784 | 0.785 | 0.785 | 0.786 | 0.786 | 0.786 | 0.787 | 0.787 | 0.788 | 0.788 | 0.788 | 0.788 |
| 3 | 0.717 | 0.718 | 0.719 | 0.720 | 0.721 | 0.721 | 0.721 | 0.722 | 0.722 | 0.722 | 0.722 | 0.723 | 0.723 | 0.723 |
| 4 | 0.655 | 0.656 | 0.657 | 0.658 | 0.659 | 0.659 | 0.659 | 0.659 | 0.659 | 0.650 | 0.650 | 0.660 | 0.650 | 0.650 |
| 5 | 0.595 | 0.596 | 0.597 | 0.598 | 0.598 | 0.598 | 0.599 | 0.599 | 0.599 | 0.599 | 0.599 | 0.599 | 0.599 | 0.599 |
| 6 | 0.539 | 0.540 | 0.541 | 0.541 | 0.541 | 0.542 | 0.542 | 0.542 | 0.542 | 0.542 | 0.542 | 0.542 | 0.542 | 0.542 |
| 7 | 0.486 | 0.488 | 0.488 | 0.489 | 0.489 | 0.489 | 0.489 | 0.489 | 0.490 | 0.490 | 0.490 | 0.490 | 0.490 | 0.490 |
| 8 | 0.438 | 0.439 | 0.440 | 0.440 | 0.441 | 0.441 | 0.441 | 0.441 | 0.441 | 0.441 | 0.441 | 0.441 | 0.441 | 0.441 |
| 9 | 0.394 | 0.395 | 0.396 | 0.396 | 0.396 | 0.396 | 0.396 | 0.397 | 0.397 | 0.397 | 0.397 | 0.397 | 0.397 | 0.397 |
| 10 | 0.354 | 0.355 | 0.356 | 0.356 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 |
| 11 | 0.318 | 0.319 | 0.320 | 0.320 | 0.320 | 0.320 | 0.320 | 0.320 | 0.321 | 0.321 | 0.321 | 0.321 | 0.321 | 0.321 |
| 12 | 0.286 | 0.286 | 0.287 | 0.287 | 0.287 | 0.288 | 0.288 | 0.288 | 0.288 | 0.288 | 0.288 | 0.288 | 0.288 | 0.288 |
| 13 | 0.257 | 0.257 | 0.258 | 0.258 | 0.258 | 0.258 | 0.258 | 0.258 | 0.258 | 0.259 | 0.259 | 0.259 | 0.259 | 0.259 |
| 14 | 0.230 | 0.231 | 0.231 | 0.232 | 0.232 | 0.232 | 0.232 | 0.232 | 0.232 | 0.232 | 0.232 | 0.232 | 0.232 | 0.232 |
| 15 | 0.207 | 0.208 | 0.208 | 0.208 | 0.208 | 0.208 | 0.208 | 0. 208 | 0.208 | 0.208 | 0.208 | 0.208 | 0.208 | 0.208 |
| 16 | 0.186 | 0.187 | 0.187 | 0.187 | 0.187 | 0.187 | 0.187 | 0.188 | 0.188 | 0.188 | 0.188 | 0.188 | 0.188 | 0.188 |
| 17 | 0.168 | 0.168 | 0.168 | 0.169 | 0.169 | 0.169 | 0.169 | 0.169 | 0.169 | 0.169 | 0.169 | 0.169 | 0.169 | 0.169 |
| 18 | 0.151 | 0.151 | 0.152 | 0.152 | 0.152 | 0.152 | 0.152 | 0.152 | 0.152 | 0.152 | 0.152 | 0.152 | 0.152 | 0.152 |
| 19 | 0.136 | 0.136 | 0.136 | 0.137 | 0.137 | 0.137 | 0.137 | 0.137 | 0.137 | 0.137 | 0.137 | 0.137 | 0.137 | 0.137 |
| 20 | 0 123 | 0.123 | 0.123 | 0.123 | 0.123 | 0.123 | 0.123 | 0.123 | 0 123 | 0.123 | 0.123 | 0.123 | 0.123 | 0.123 |
| d [mm] | Freq 40 [kHz] | Freq 50 [kHz] | Freq 60 [kHz] | Freq 70 [kHz] | Freq 80 [kHz] | Freq 89 [kHz] | Freq 90 [kHz] | Freq 100 [kHz] | Freq 110 [kHz] | Freq 120 [kHz] | Freq 130 [kHz] | Freq 140 [kHz] | Freq 150 [kHz] | Freq 160 [kHz] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 12.224 | 12.022 | 11.868 | 11.752 | 11.663 | 11.601 | 11.595 | 11.542 | 11.499 | 11.465 | 11.437 | 11.414 | 11.395 | 11.378 |
| 1 | 10.165 | 10.014 | 9.895 | 9.803 | 9.733 | 9.683 | 9 678 | 9.634 | 9.600 | 9.572 | 9.549 | 9.529 | 9.513 | 9.499 |
| 2 | 8.592 | 8.475 | 8.382 | 8.309 | 8.252 | 8.211 | 8.207 | 8.172 | 8.143 | 8.120 | 8.101 | 8.085 | 8.071 | 8.060 |
| 3 | 7.358 | 7.268 | 7.194 | 7.135 | 7.089 | 7.056 | 7.052 | 7.023 | 6.999 | 6.980 | 6.964 | 6.950 | 5.939 | 5.929 |
| 4 | 6.344 | 6.259 | 6.208 | 6.159 | 6.121 | 6.093 | 6.090 | 6.056 | 6.045 | 6.030 | 6.016 | 6.005 | 5.995 | 5.987 |
| 5 | 5.518 | 5.457 | 5.405 | 5.366 | 5.334 | 5.310 | 5.308 | 5.287 | 5.270 | 5.256 | 5.245 | 5.235 | 5.227 | 5.220 |
| 6 | 4.834 | 4.784 | 4.743 | 4.709 | 4.682 | 4.662 | 4.660 | 4.642 | 4.627 | 4.615 | 4.604 | 4.596 | 4.588 | 4.582 |
| 7 | 4.248 | 4.207 | 4.172 | 4.143 | 4.120 | 4.103 | 4.101 | 4.086 | 4.073 | 4.062 | 4.053 | 4.046 | 4.039 | 4.034 |
| 8 | 3.750 | 3.715 | 3.685 | 3.661 | 3.641 | 3.626 | 3.625 | 3.611 | 3.600 | 3.590 | 3.583 | 3.576 | 3.570 | 3.565 |
| 9 | 3.316 | 3.286 | 3.261 | 3.240 | 3.223 | 3.210 | 3.209 | 3.197 | 3.187 | 3.179 | 3.172 | 3.166 | 3.161 | 3.156 |
| 10 | 2.945 | 2.920 | 2.899 | 2.881 | 2.866 | 2.855 | 2.853 | 2.843 | 2.834 | 2.827 | 2.821 | 2.815 | 2.811 | 2.807 |
| 11 | 2.617 | 2.595 | 2.576 | 2.561 | 2.548 | 2.538 | 2.537 | 2.528 | 2.520 | 2.514 | 2.508 | 2.503 | 2.499 | 2.496 |
| 12 | 2.330 | 2.311 | 2.294 | 2.281 | 2.269 | 2.260 | 2.260 | 2.251 | 2.245 | 2.239 | 2.234 | 2.230 | 2.226 | 2.223 |
| 13 | 2.081 | 2.064 | 2.050 | 2.038 | 2.028 | 2.021 | 2.020 | 2.013 | 2.007 | 2.002 | 1.997 | 1.993 | 1.990 | 1.987 |
| 14 | 1.857 | 1.842 | 1.830 | 1.819 | 1.810 | 1.803 | 1.802 | 1.796 | 1.791 | 1.786 | 1.782 | 1.779 | 1.776 | 1.774 |
| 15 | 1.662 | 1.649 | 1.638 | 1.628 | 1.620 | 1.614 | 1.613 | 1.608 | 1.603 | 1.599 | 1.595 | 1.592 | 1.590 | 1.587 |
| 16 | 1.491 | 1.479 | 1.459 | 1.461 | 1.454 | 1.448 | 1.448 | 1.442 | 1.438 | 1.435 | 1.431 | 1.429 | 1.425 | 1.424 |
| 17 | 1.338 | 1.327 | 1.318 | 1.311 | 1.305 | 1.300 | 1.299 | 1.295 | 1.291 | 1.288 | 1.285 | 1.282 | 1.280 | 1.278 |
| 18 | 1.202 | 1.193 | 1.185 | 1.178 | 1.172 | 1.168 | 1.158 | 1.154 | 1.160 | 1.157 | 1.155 | 1.152 | 1.151 | 1.149 |
| 19 | 1.081 | 1.073 | 1.065 | 1.060 | 1.055 | 1.051 | 1.050 | 1.047 | 1.044 | 1.041 | 1.039 | 1.037 | 1.035 | 1.034 |
| 20 | 0.974 | 0.967 | 0.961 | 0.955 | 0.950 | 0.947 | 0.947 | 0.943 | 0.940 | 0.938 | 0.936 | 0.934 | 0.933 | 0.931 |
References
- Pahlavan, S.; Shooshtari, M.; Jafarabadi Ashtiani, S. Star-Shaped Coils in the Transmitter Array for Receiver Rotation Tolerance in Free-Moving Wireless Power Transfer Applications. Energies 2022, 15, 8643. [Google Scholar] [CrossRef]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljačić, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Liu, X.; Chen, T. Electromagnetic power harvesting using hollow cylinders. IEEE Trans. Microw. Theory Tech. 2023, 71, 5055–5065. [Google Scholar]
- Huang, M.; Chen, L.; Wu, Q. Efficient mid-range wireless energy transfer with radiation-loss compensation. Phys. Rev. Appl. 2023, 19, 024011. [Google Scholar]
- Balanis, C.A.; Konstantinou, K. The role of reactive power in the radiation of a dipole antenna. IEEE Trans. Antennas Propag. 2015, 63, 2022–2031. [Google Scholar]
- Chen, K.; Zhang, Z. Rotating-Coordinate-Based Mutual Inductance Estimation for Drone In-Flight Wireless Charging Systems. IEEE Trans. Power Electron. 2023, 38, 11685–11693. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, J.; Liang, Z.; Zhang, Z. Flexible Constant-Power Range Extension of Self-Oscillating System for Wireless In-Flight Charging of Drones. IEEE Trans. Power Electron. 2024, 39, 15342–15355. [Google Scholar] [CrossRef]
- Wu, Z.; Yu, H.; Schreurs, D.; Huangfu, J. Wireless power transfer based on 2D routing. Sci. Rep. 2022, 12, 17345. [Google Scholar] [CrossRef] [PubMed]
- Narayanamoorthi, R.; Ramachandaramurthy, V.K.; Dominic, S.A.; Gono, R.; Bernat, P.; Kacor, P. Design of Dual Frequency Class E Resonant Converters for Simultaneous Wireless Power and Data Transfer in Low Power Applications. Results Eng. 2024, 24, 103558. [Google Scholar] [CrossRef]
- Song, C.-M.; Lim, H.-J.; Trinh-Van, S.; Lee, K.-Y.; Yang, Y.; Hwang, K.-C. Dual-Band RF Wireless Power Transfer System with a Shared-Aperture Dual-Band Tx Array Antenna. Energies 2021, 14, 3803. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, H.; Shi, Z.; Guo, Y.; Sun, H. Research on dual-frequency modulation strategy of wireless power transfer system. Int. J. Circ. Theor. Appl. 2022, 50, 4342–4356. [Google Scholar] [CrossRef]
- Zhang, Z.; Lai, J.; Huang, Y.; Hao, X.; Yin, K.; Jiang, Z.; Wang, C.; Ma, X.; Huang, M.; Dong, T. Communication-free robust wireless power transfer with constant output power and stable frequency. Phys. Rev. Appl. 2025, 23, 014029. [Google Scholar] [CrossRef]
- Liu, Z.; Tao, C.; Wang, L.; Zhang, Y.; Li, F. A Research on Characteristics of Wireless Power Transfer System Based on LCC/N Magnetic Integration Compensation Circuit. In Proceedings of the Emerging Technologies: Wireless Power Transfer (WoW), San Diego, CA, USA, 1–4 June 2021. [Google Scholar]
- Qiao, X.; Niu, S.; Lin, J.; Chen, M.; Wu, Y. A Novel Magnetically Coupled Resonant Wireless Power Transfer Technique Used in Rotary Ultrasonic Machining Process. In Proceedings of the 2021 IEEE Wireless Power Transfer Conference (WPTC), San Diego, CA, USA, 1–4 June 2021. [Google Scholar]
- Stillig, J.; Enssle, A.; Parspour, N. Modular Wireless Power Transfer System for the Supply of Mobile Industrial Production Equipment. In Proceedings of the Emerging Technologies: Wireless Power Transfer (WoW), San Diego, CA, USA, 1–4 June 2021. [Google Scholar]
- Pacurar, C.; Topa, V.; Giurgiuman, A.; Munteanu, C.; Constantinescu, C.; Gliga, M.; Andreica, S. The Construction of a Wireless Power Supply System using Planar Spiral Inductors. In Proceedings of the 2019 8th International Conference on Modern Power Systems (MPS), Cluj-Napoca, Romania, 21–23 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Gliga, M.; Racasan, A.; Munteanu, C.; Pacurar, C.; Constantinescu, C.; Andreica, S. The influence of ferrite on the spiral inductors inductance used for the design of wireless power systems. In Proceedings of the 2017 International Conference on Modern Power Systems (MPS), Cluj-Napoca, Romania, 6–9 June 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Giurgiuman, A.; Pacurar, C.; Constantinescu, C.; Munteanu, M.G.C.; Andreica, S. Analysis and Optimal Design of a Wireless Power Transfer System for Electrical Vehicles. In Proceedings of the Electrical and Power Engineering (EPE), Iasi, Romania, 20–22 October 2022. [Google Scholar]
- Kim, J.; Kim, H.; Kim, D.; Jeong, D.; Ahn, S. Analysis of Efficiency According to the Design of Transmitter Coil for Wireless Power Transfer Implantable Medical Device. In Proceedings of the 2020 IEEE Wireless Power Transfer Conference (WPTC), Seoul, Republic of Korea, 15–19 November 2020. [Google Scholar]
- Mohamed, N.F.A.; Agbinya, J.I.; Okaf, A. Magnetic Field Tuning and Control for Wireless Power Transfer Using Inductive Tuning Plunger and Conical Coils. In Proceedings of the Emerging Technologies: Wireless Power Transfer (Wow), Montreal, QC, Canada, 3–7 June 2018. [Google Scholar]
- Gliga, M.; Munteanu, C.; Andreica, S.; Giurgiuman, A.; Pacurar, C.; Contantinescu, C.; Mociran, B.; Morar, D. The influence of the distance between the transmitter and the receiver of a wireless power system on the coupling factor and the voltage induced. In Proceedings of the Modern Power Systems (MPS), Cluj-Napoca, Romania, 21–23 June 2023. [Google Scholar]
- Pacurar, C.; Topa, V.; Racasan, A.; Munteanu, C.; Hebedean, C. Spiral inductors analysis and modelling. In Proceedings of the 2014 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Bran, Romania, 22–24 May 2014; pp. 210–215. [Google Scholar] [CrossRef]
- Mototani, S.; Yamamoto, R.; Doki, K.; Torii, A. Possibility of the Undersea Wireless Power Transfer Using a Cone Spiral Coil. In Proceedings of the 2020 IEEE Wireless Power Transfer Conference (WPTC), Seoul, Republic of Korea, 15–19 November 2020. [Google Scholar]
- Zhaksylyk, Y.; Hanke, U.; Azadmehr, M. Impedance Matching using Interspiraled Coils for Wireless Power Transfer. In Proceedings of the 2020 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Seoul, Republic of Korea, 15–19 November 2020. [Google Scholar]
- Racasan, A.; Munteanu, C.; Pacurar, C.; Topa, V.; Constantinescu, C.; Pop, F.; Andreica, S.; Cislariu, M. Analysis, identification and minimization the parasitic effects of the multilayer spiral inductors. In Proceedings of the Electrical and Power Engineering (EPE), Iasi, Romania, 20–22 October 2016. [Google Scholar]
- Hwang, K.; Chung, S.; Yoon, U.; Lee, M.; Ahn, S. Thermal analysis for temperature robust wireless power transfer systems. In Proceedings of the 2013 IEEE Wireless Power Transfer (WPT), Perugia, Italy, 15–16 May 2013. [Google Scholar]
- Andreica, S.; Munteanu, C.; Gliga, M.; Pacurar, C.; Giurgiuman, A.; Constantinescu, C. Design of Multilayer Spiral Coils with Different Geometries to Determine the Inductance. In Proceedings of the Electrical and Power Engineering (EPE), Iasi, Romania, 20–23 October 2020. [Google Scholar]
- Gliga, M.; Pacurar, C.; Munteanu, C.; Andreica, S.; Constantinecu, C.; Giurgiuman, A. Analysis of Different Type of Ring Permanent Magnets in Order to Achieve an Uniform Magnetic Field Around Them. In Proceedings of the Electrical and Power Engineering (EPE), Iasi, Romania, 20–23 October 2020. [Google Scholar]
- Utschick, C.; Merz, C.; Som, C. AC Loss Behavior of Wireless Power Transfer Coils. In Proceedings of the Wireless Power Transfer Conference (WPTC), London, UK, 17–21 June 2019. [Google Scholar]
- Lee, S.; Jung, G.; Shin, S.; Kim, Y.; Song, B.; Shin, J.; Cho, D. The optimal design of high-powered power supply modules for wireless power transferred train. In Proceedings of the 2012 Electrical Systems for Aircraft, Railway and Ship Propulsion, Bologna, Italy, 16–18 October 2012. [Google Scholar]
- Mohamed, N.F.A.; Agbinya, J.I. Magnetic Power Tuning Architectures in Wireless Power Transfer System. In Proceedings of the Emerging Technologies: Wireless Power Transfer (Wow), Montreal, QC, Canada, 3–7 June 2018. [Google Scholar]
- Shin, S.; Shin, J.; Song, B.; Lee, S.; Kim, Y.; Jung, G.; Jeon, S. Wireless power transfer system for high power application and a method of segmentation. In Proceedings of the 2013 IEEE Wireless Power Transfer (WPT), Perugia, Italy, 15–16 May 2013. [Google Scholar]
- Song, J.; Liu, M.; Fu, M.; Ma, C. High Power Density Stacked-Coils Based power Receiver for MHz Wireless Power Transfer. In Proceedings of the Emerging Technologies: Wireless Power Transfer (WoW), London, UK, 17–21 June 2019. [Google Scholar]
- Zhang, Z.; Li, X.; Pang, H.; Komurcugil, H.; Liang, Z.; Kennel, R. Multiple-Frequency Resonating Compensation for Multichannel Transmission of Wireless Power Transfer. IEEE Trans. Power Electron. 2021, 36, 5169–5180. [Google Scholar] [CrossRef]
- Koran, A.; Badran, K. Adaptive Frequency Control of a Sensorless-Receiver Inductive Wireless Power Transfer System Based on Mixed-Compensation Topology. IEEE Trans. Power Electron. 2020, 36, 978–990. [Google Scholar] [CrossRef]
- Stielau, O.H.; Covic, G.A. Design of loosely coupled inductive power transfer systems. In Proceedings of the PowerCon 2000. 2000 International Conference on Power System Technology. Proceedings (Cat. No.00EX409), Perth, WA, Australia, 4–7 December 2000; Volume 1, pp. 85–90. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, C.; Zhou, Y.; Xiao, Y.; Liu, S. Power Allocation for Dynamic Dual-Pickup Wireless Charging System of Electric Vehicle. IEEE Trans. Magn. 2019, 1–6. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Y.; Jiang, Z.; Chen, Q.; Yan, Q.; Wu, Z.; Zhang, B.; Huangfu, J.; Chen, H. Demonstration of topological wireless power transfer. Sci. Bull. 2021, 66, 974–980. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Zeng, J.; Yang, Y.; Hui, S.Y.R. A General Maximum Efficiency Tracking Scheme for Domino Wireless Power Transfer Systems with Quasi-Load-Independent Outputs. IEEE Trans. Power Electron. 2024, 39, 1840–1852. [Google Scholar] [CrossRef]
- Wang, K.; Yang, J.; Sun, Z.; Zeng, J.; Yang, Y. Analysis and Design of Domino Inductive Power Transfer System with Enhanced Quasi-Load-Independent Constant Current Output. In Proceedings of the IEEE Wireless Power Technology Conference and Expo (WPTCE), Kyoto, Japan, 8–11 May 2024; pp. 385–389. [Google Scholar]






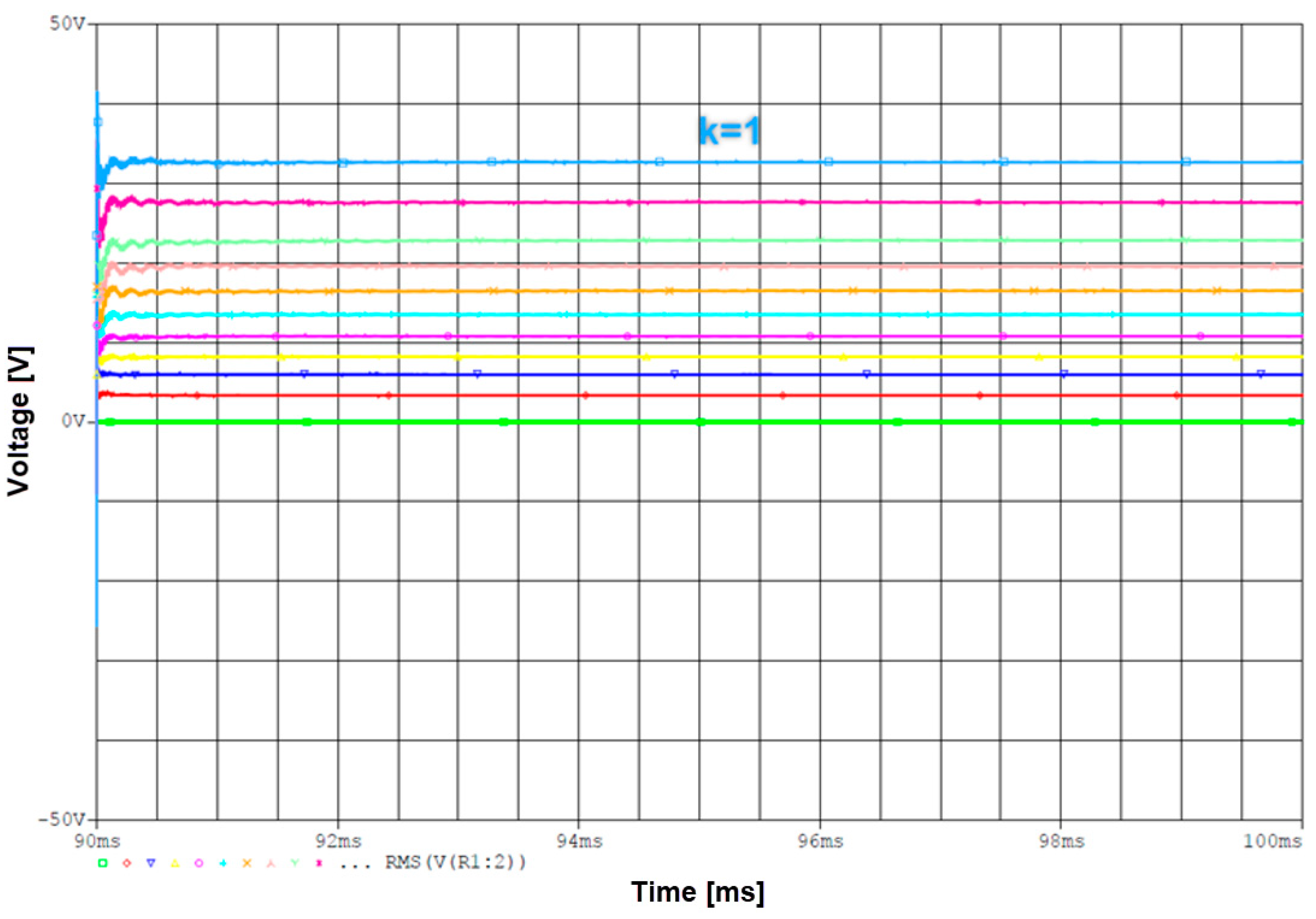
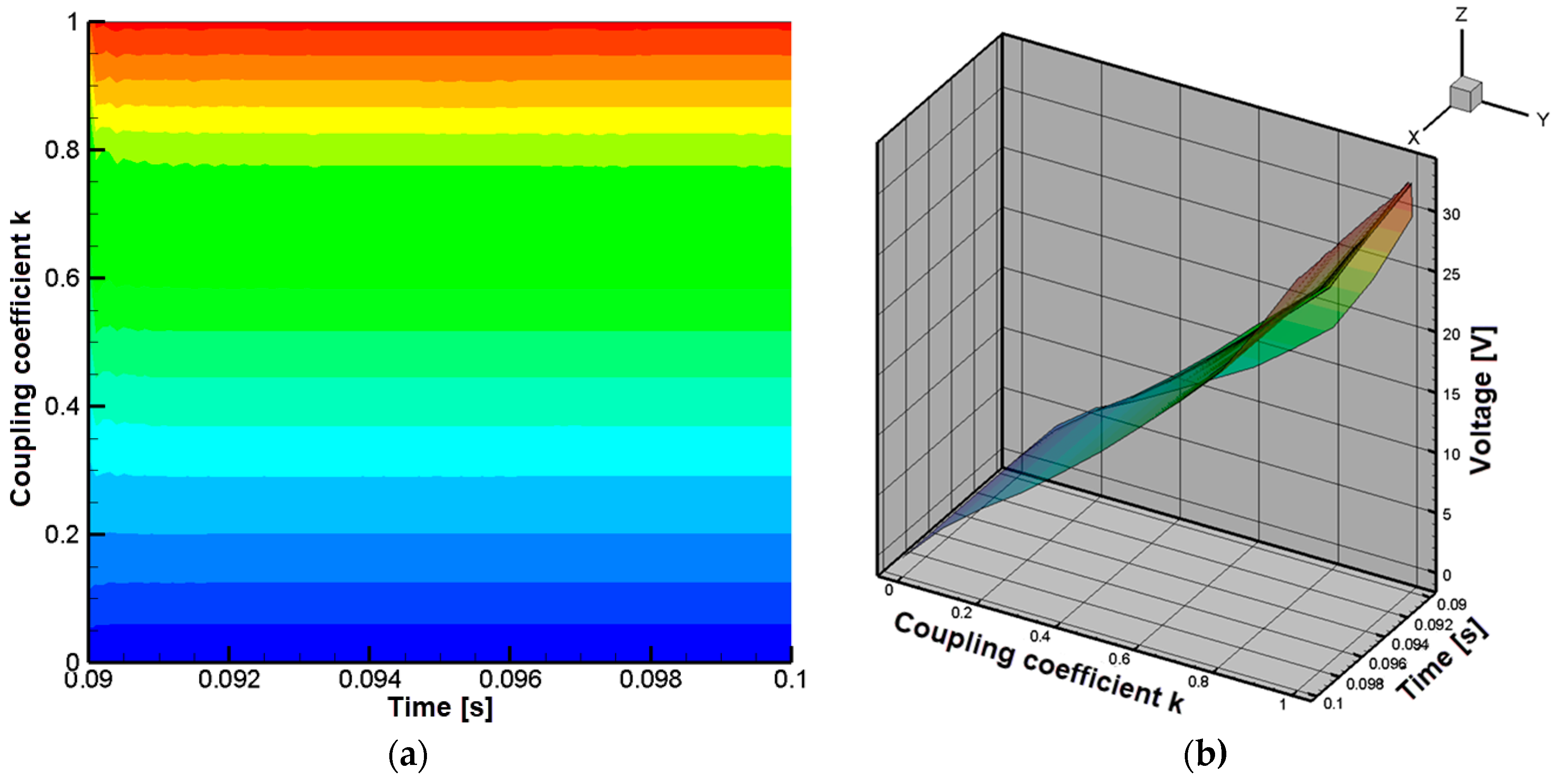
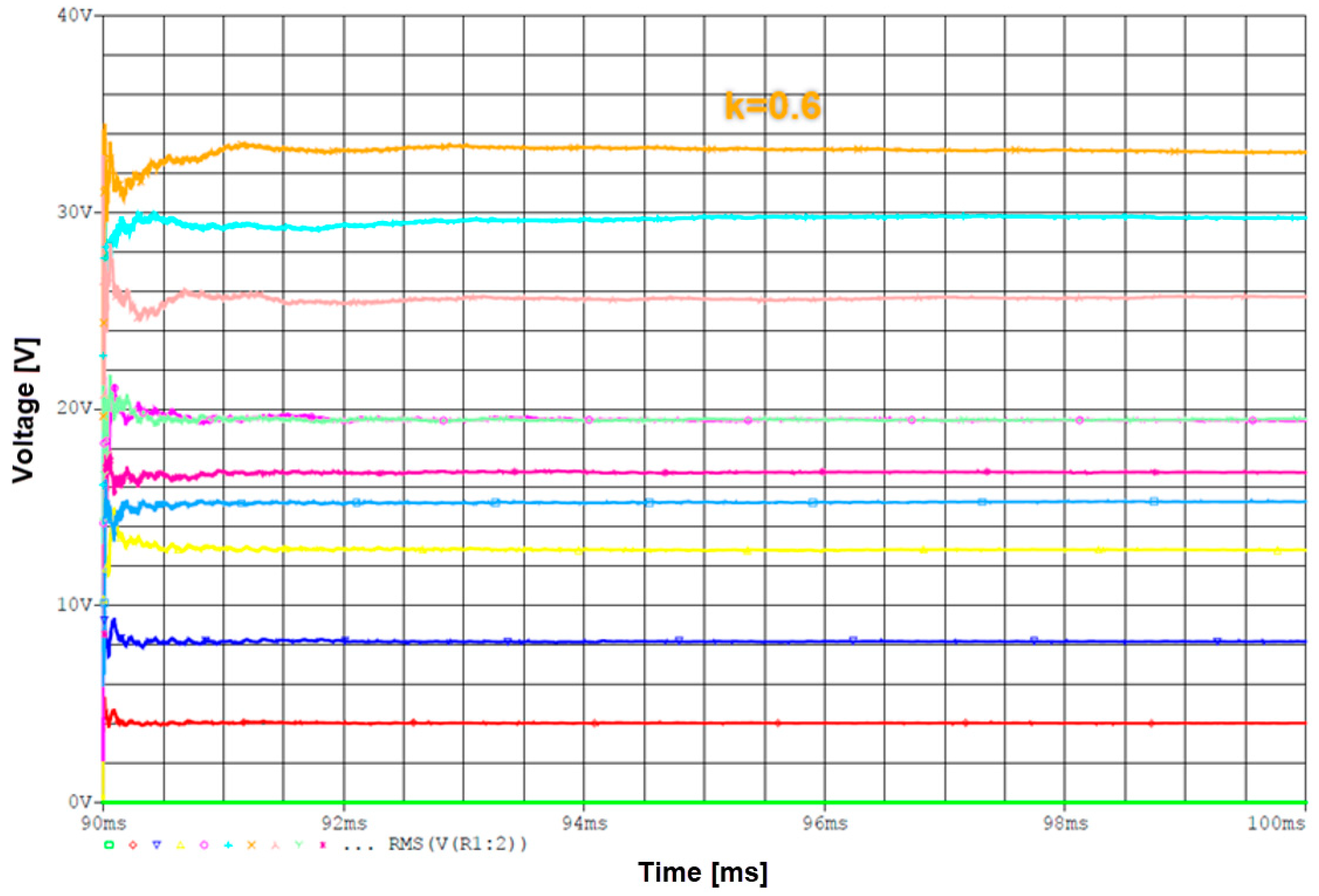
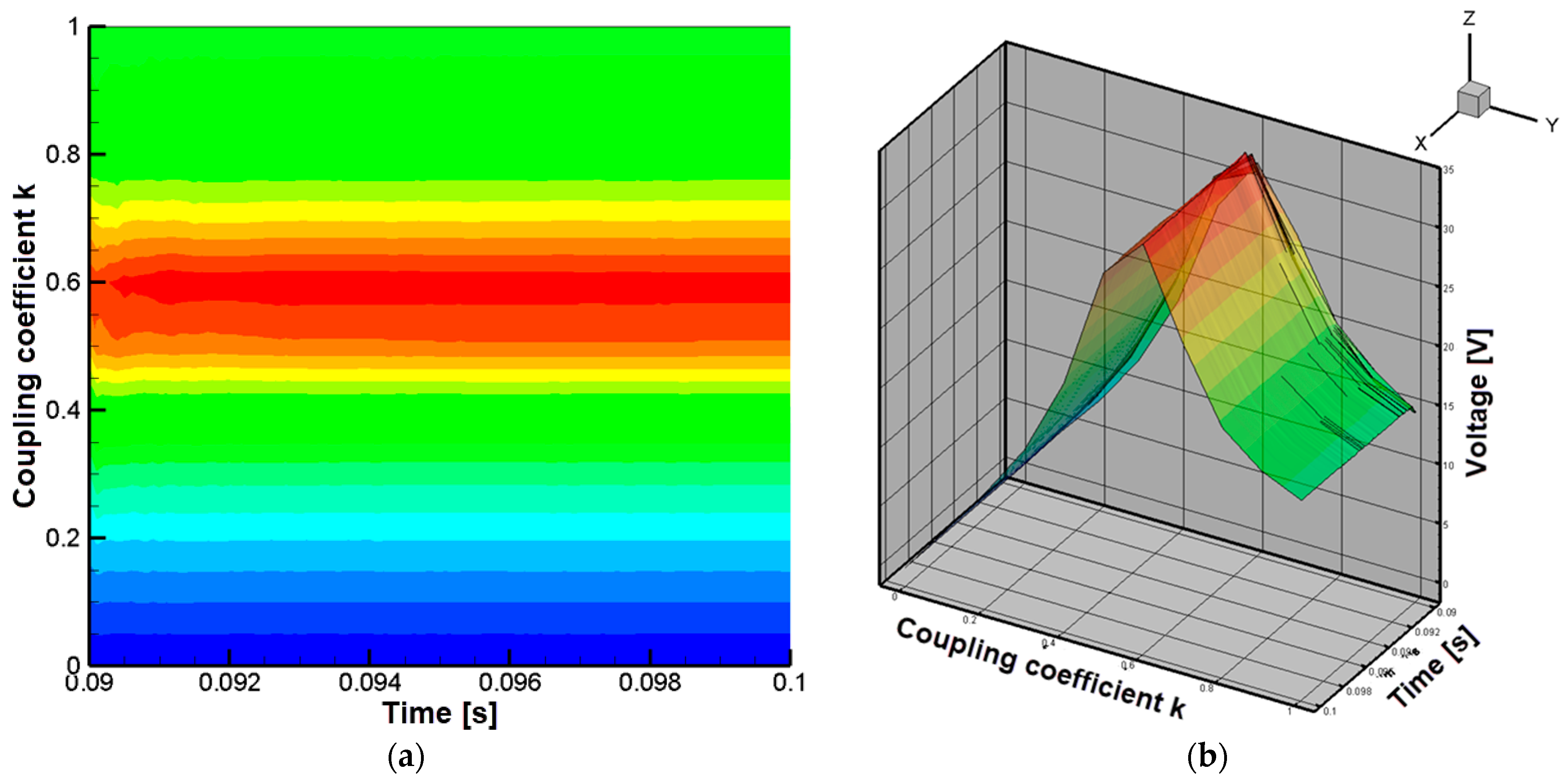

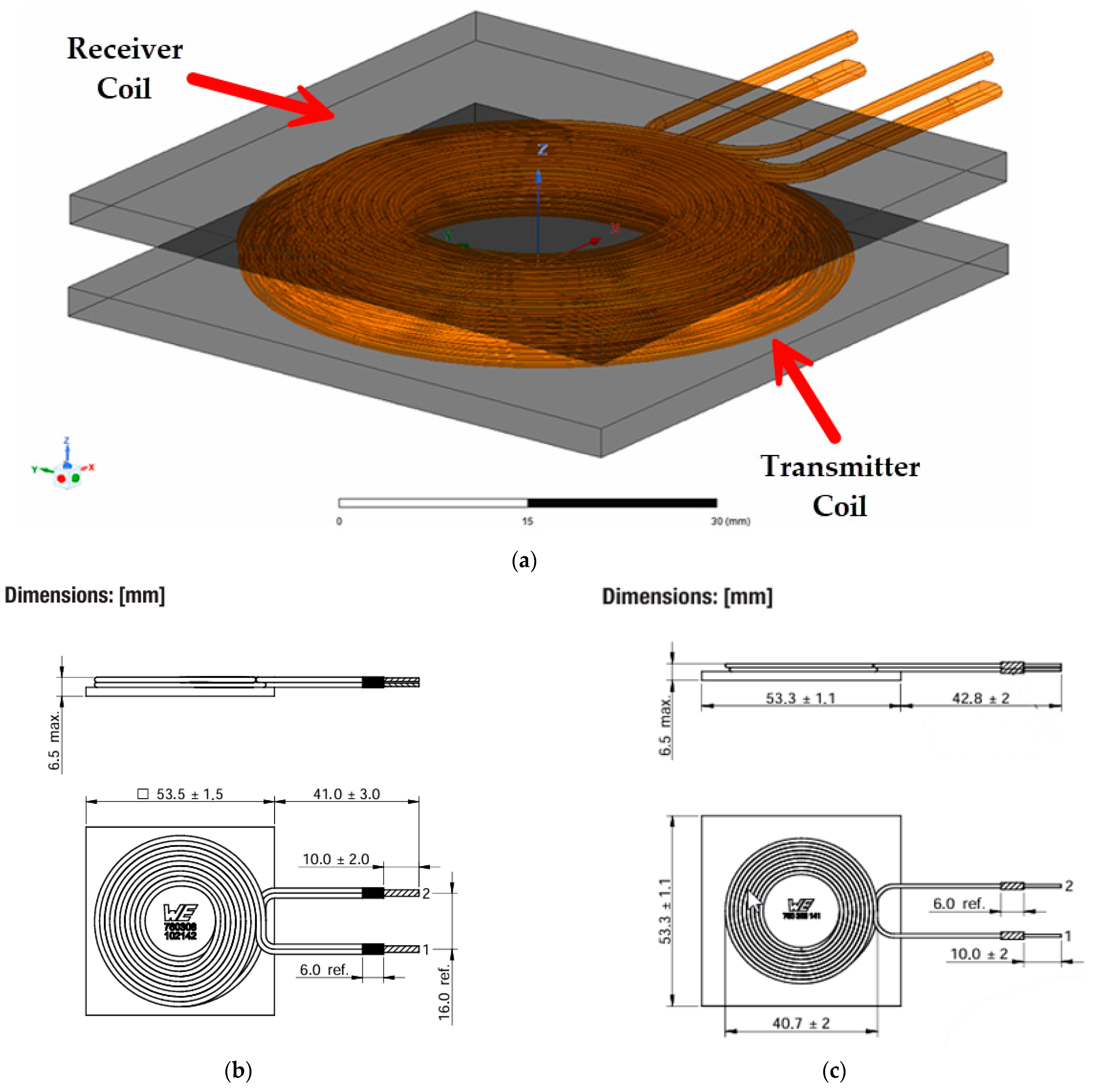







| Coils | Inductance [µH] | Resistance [mΩ] |
|---|---|---|
| Transmitter coil, WE 760308102142 | 5.8 | 12 |
| Receiver coil, WE 760308141 | 10 | 30 |
| Signal Period [µs] | Supply Voltage [V] | Measured Induced Voltage [V] |
|---|---|---|
| 2 | 24 | 1.44 |
| 4 | 24 | 17.65 |
| 6 | 24 | 24 |
| 8 | 24 | 38.3 |
| 10 | 24 | 47.1 |
| 12 | 24 | 43.4 |
| 14 | 24 | 52 |
| 16 | 24 | 36 |
| 18 | 24 | 54.9 |
| 20 | 24 | 36.7 |
| 22 | 24 | 32.9 |
| 24 | 24 | 34.1 |
| 26 | 24 | 45.2 |
| 28 | 24 | 38.1 |
| 30 | 24 | 34.6 |
| 32 | 24 | 35.1 |
| 34 | 24 | 36.5 |
| 36 | 24 | 43.8 |
| 38 | 24 | 43 |
| 40 | 24 | 39.6 |
| 42 | 24 | 36.4 |
| 44 | 24 | 36.9 |
| 46 | 24 | 31.6 |
| 48 | 24 | 31.9 |
| 50 | 24 | 30.8 |
| Signal Period [µs] | Supply Voltage [V] | Measured Induced Voltage [V] |
|---|---|---|
| 2 | 24 | 8.22 |
| 4 | 24 | 6.83 |
| 6 | 24 | 6.11 |
| 8 | 24 | 6.78 |
| 10 | 24 | 6.45 |
| 12 | 24 | 9.28 |
| 14 | 24 | 8.21 |
| 16 | 24 | 10.87 |
| 18 | 24 | 10.97 |
| 20 | 24 | 10.67 |
| 22 | 24 | 10.61 |
| 24 | 24 | 10.8 |
| 26 | 24 | 11.32 |
| 28 | 24 | 11.51 |
| 30 | 24 | 11.71 |
| 32 | 24 | 11.44 |
| 34 | 24 | 11.21 |
| 36 | 24 | 11.89 |
| 38 | 24 | 11.38 |
| 40 | 24 | 11.46 |
| 42 | 24 | 11.04 |
| 44 | 24 | 11.01 |
| 46 | 24 | 10.8 |
| 48 | 24 | 10.52 |
| 50 | 24 | 10.39 |
| Signal Period [µs] | Supply Voltage [V] | Measured Induced Voltage [V] |
|---|---|---|
| 2 | 24 | 3.89 |
| 4 | 24 | 21.8 |
| 6 | 24 | 25.5 |
| 8 | 24 | 38.9 |
| 10 | 24 | 42.5 |
| 12 | 24 | 41.7 |
| 14 | 24 | 41.2 |
| 16 | 24 | 33.7 |
| 18 | 24 | 33.7 |
| 20 | 24 | 31.6 |
| 22 | 24 | 30.6 |
| 24 | 24 | 29.8 |
| 26 | 24 | 38.8 |
| 28 | 24 | 32.4 |
| 30 | 24 | 29.4 |
| 32 | 24 | 29.7 |
| 34 | 24 | 28.3 |
| 36 | 24 | 28.9 |
| 38 | 24 | 30.2 |
| 40 | 24 | 32.8 |
| 42 | 24 | 32 |
| 44 | 24 | 32 |
| 46 | 24 | 31 |
| 48 | 24 | 30.4 |
| 50 | 24 | 30.6 |
| Signal Period [µs] | Supply Voltage [V] | Measured Induced Voltage [V] |
|---|---|---|
| 2 | 24 | 1.485 |
| 4 | 24 | 11.44 |
| 6 | 24 | 13.18 |
| 8 | 24 | 13.72 |
| 10 | 24 | 15.69 |
| 12 | 24 | 15.2 |
| 14 | 24 | 18.58 |
| 16 | 24 | 12.36 |
| 18 | 24 | 13.69 |
| 20 | 24 | 14.03 |
| 22 | 24 | 14.52 |
| 24 | 24 | 13.55 |
| 26 | 24 | 14.76 |
| 28 | 24 | 14.67 |
| 30 | 24 | 13.95 |
| 32 | 24 | 13 |
| 34 | 24 | 12.42 |
| 36 | 24 | 12.07 |
| 38 | 24 | 12.09 |
| 40 | 24 | 12.47 |
| 42 | 24 | 12.24 |
| 44 | 24 | 11.47 |
| 46 | 24 | 10.71 |
| 48 | 24 | 10.15 |
| 50 | 24 | 10.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gliga, M.-R.; Munteanu, C.; Giurgiuman, A.; Constantinescu, C.; Andreica, S.; Pacurar, C. Design, Simulation, Construction and Experimental Validation of a Dual-Frequency Wireless Power Transfer System Based on Resonant Magnetic Coupling. Technologies 2025, 13, 442. https://doi.org/10.3390/technologies13100442
Gliga M-R, Munteanu C, Giurgiuman A, Constantinescu C, Andreica S, Pacurar C. Design, Simulation, Construction and Experimental Validation of a Dual-Frequency Wireless Power Transfer System Based on Resonant Magnetic Coupling. Technologies. 2025; 13(10):442. https://doi.org/10.3390/technologies13100442
Chicago/Turabian StyleGliga, Marian-Razvan, Calin Munteanu, Adina Giurgiuman, Claudia Constantinescu, Sergiu Andreica, and Claudia Pacurar. 2025. "Design, Simulation, Construction and Experimental Validation of a Dual-Frequency Wireless Power Transfer System Based on Resonant Magnetic Coupling" Technologies 13, no. 10: 442. https://doi.org/10.3390/technologies13100442
APA StyleGliga, M.-R., Munteanu, C., Giurgiuman, A., Constantinescu, C., Andreica, S., & Pacurar, C. (2025). Design, Simulation, Construction and Experimental Validation of a Dual-Frequency Wireless Power Transfer System Based on Resonant Magnetic Coupling. Technologies, 13(10), 442. https://doi.org/10.3390/technologies13100442








