Direct Multiple-Step-Ahead Forecasting of Daily Gas Consumption in Non-Residential Buildings Using Wavelet/RNN-Based Models and Data Augmentation— Comparative Evaluation
Abstract
1. Introduction
1.1. Literature Review
1.2. Research Objective
- A regression model will be created to remove the linear dependency on outdoor temperature.
- To improve the model, a wavelet transform will be applied for the decomposition of the time series.
- Two LSTM models will be prepared using different approaches based on actual gas consumption at real temperature values. In the first, the model will be trained with augmented synthetic data generated via the wavelet transform. In the second step, each component of the wavelet decomposition will be trained separately, and the final model will then be constructed.
- The models will be compared with the aim of selecting the most suitable one in terms of prediction error, time requirements, and computational costs.
- The selected model will be used to compare the 7-day gas consumption forecast with the 7-day temperature forecast.
1.3. Introduction of Source Data
2. Materials and Methods
2.1. Wavelet Transform
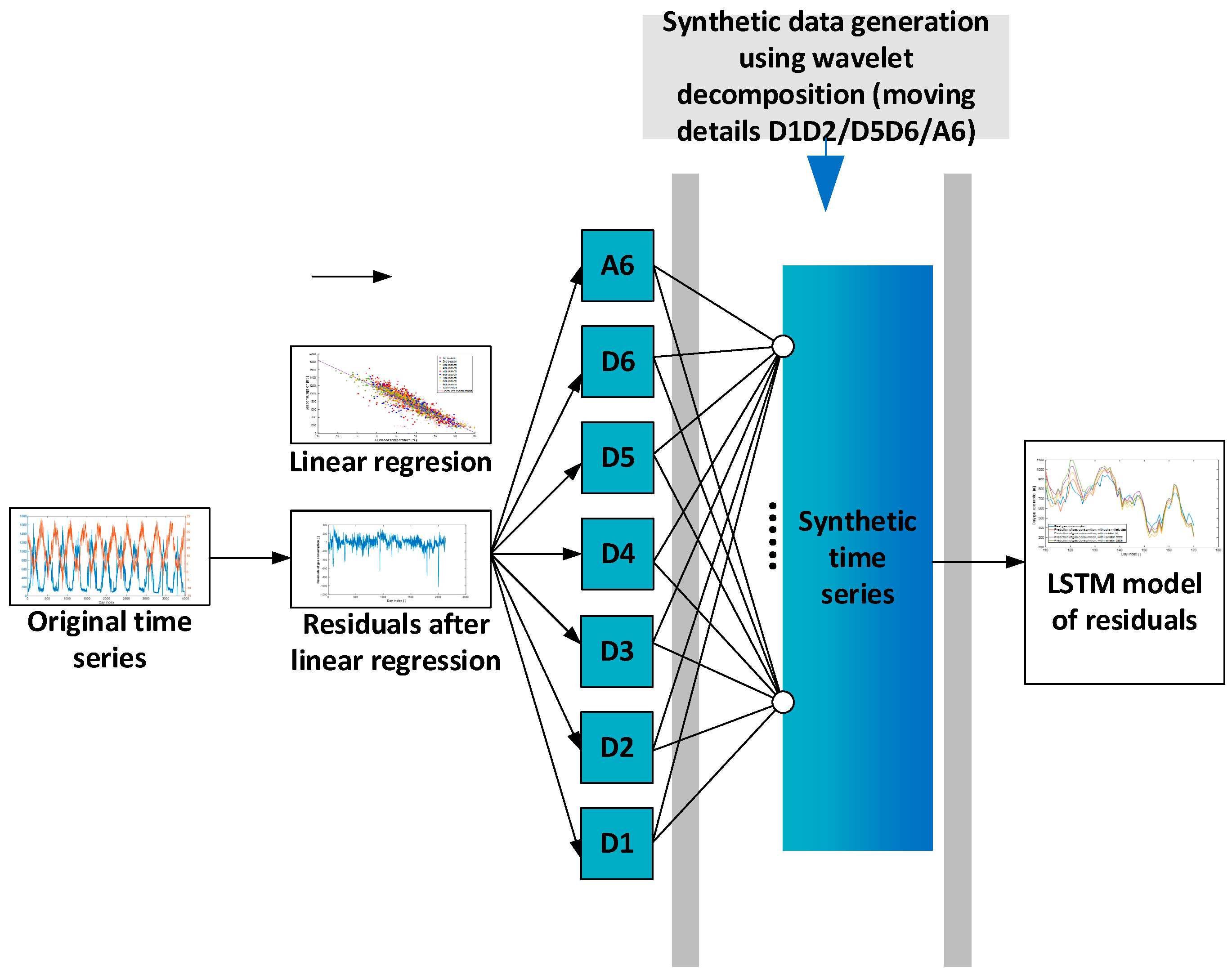
2.2. Data Series Augmentation
2.3. Long Short-Term Memory
3. Results and Discussion
3.1. Wavelet Transform of Data
3.2. Performance of Data Augmentation and Quality Control
3.3. Use of Long Short-Time Method
- The residuals were obtained by subtracting a linear regression model from the original data: .
- These residuals were subsequently normalised using the standard approach: .
- And finally, normalised data were split into training and validation datasets in a 90:10 ratio.
3.3.1. Use of LSTM Methods with Synthetic Data
3.3.2. Use of LSTM for Training of Waves
- Summation of the predicted wavelet components.
- Denormalisation of the resulting signal.
- Addition of the linear regression component.
3.4. Prediction of Daily Gas Consumption Based on the Predicted Temperature
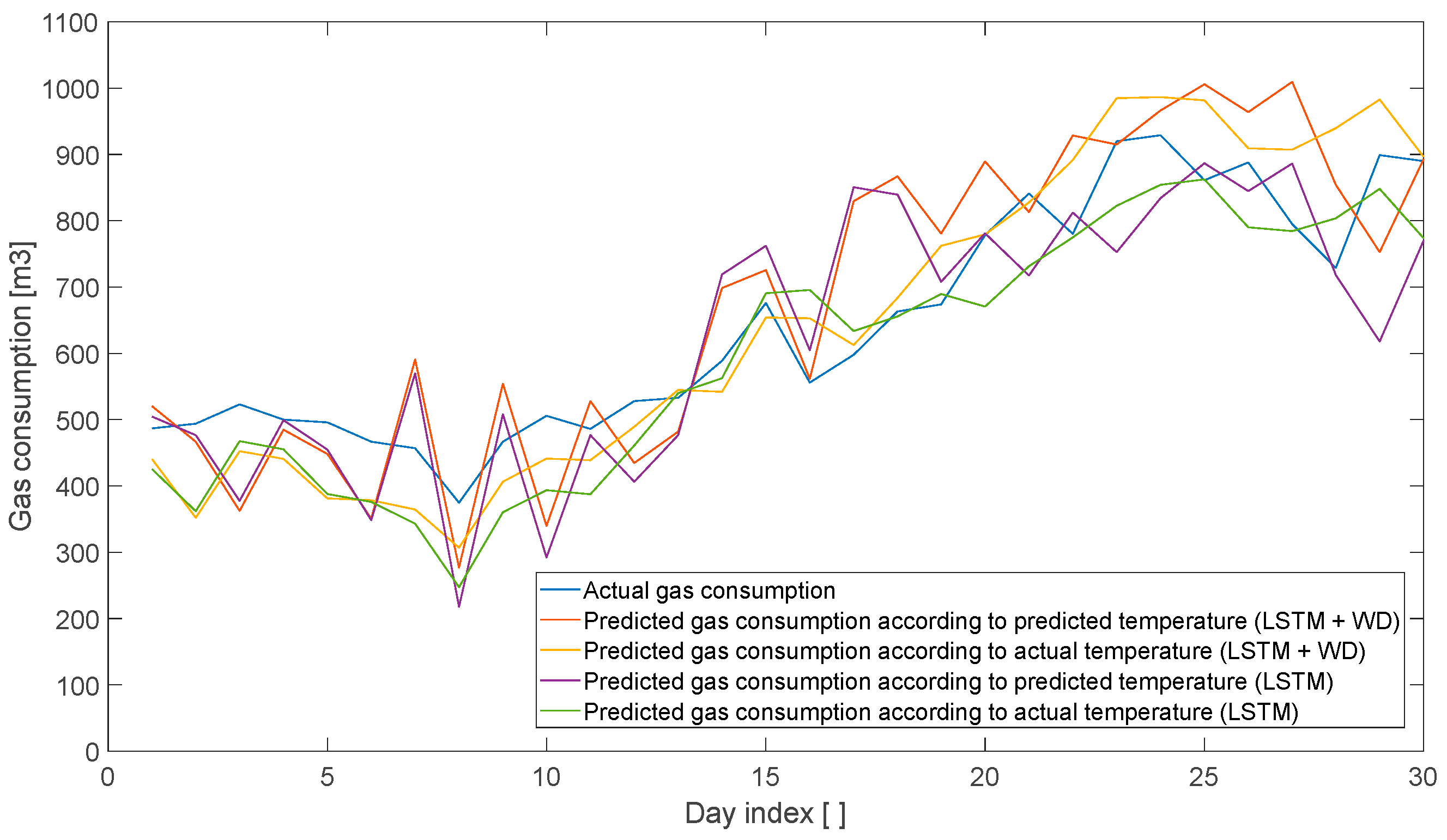
- Actual gas consumption.
- Predicted consumption based on actual temperatures.
- Predicted consumption based on forecasted temperatures.
- ECMWF: European Centre for Medium-Range Weather Forecasts.
- Operates the IFS global weather prediction model.
- Provides forecasts up to 10–15 days in advance, with a 7-day horizon considered its optimal range.
- Updated twice daily (00:00 and 12:00 UTC).
3.5. Summary of Results
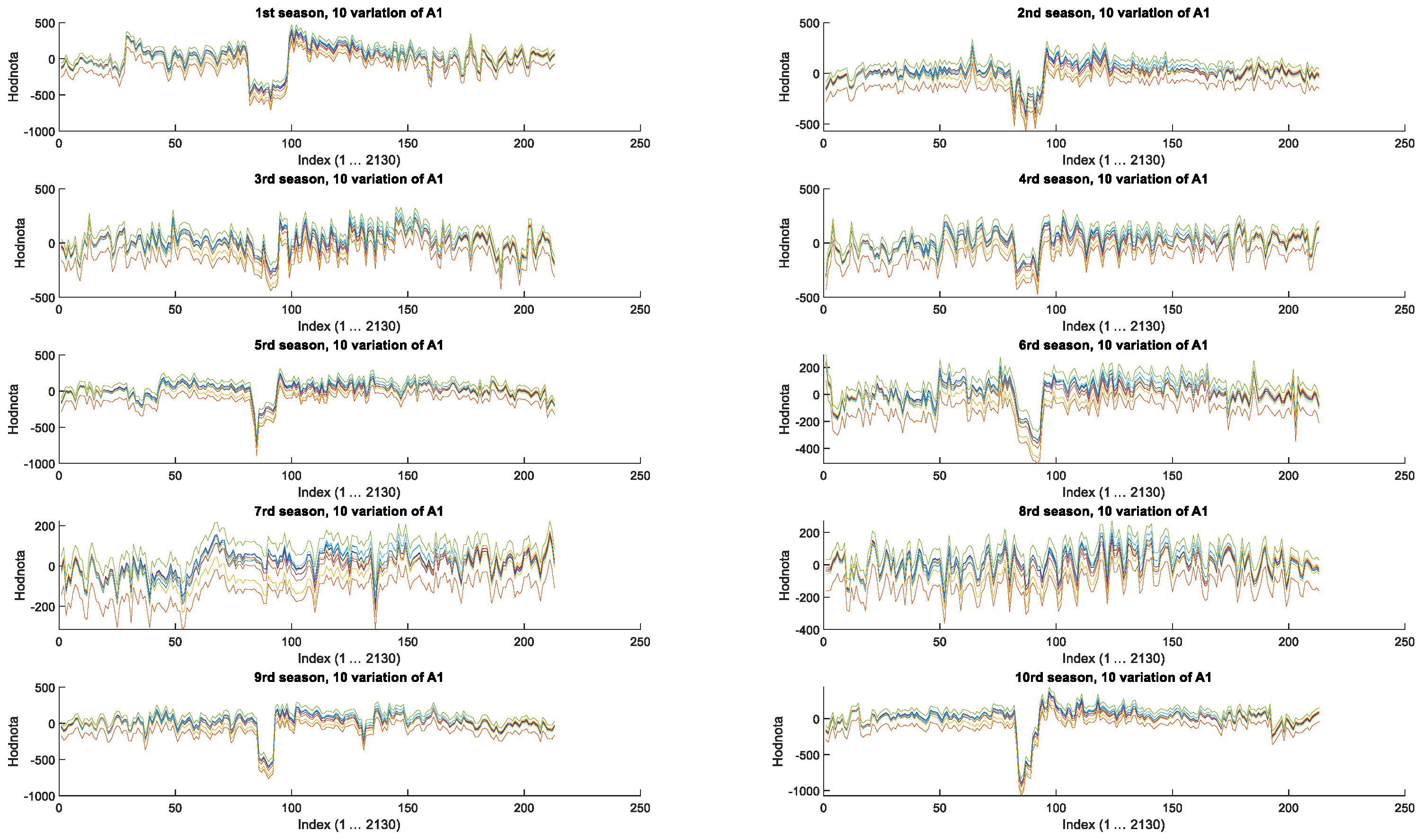
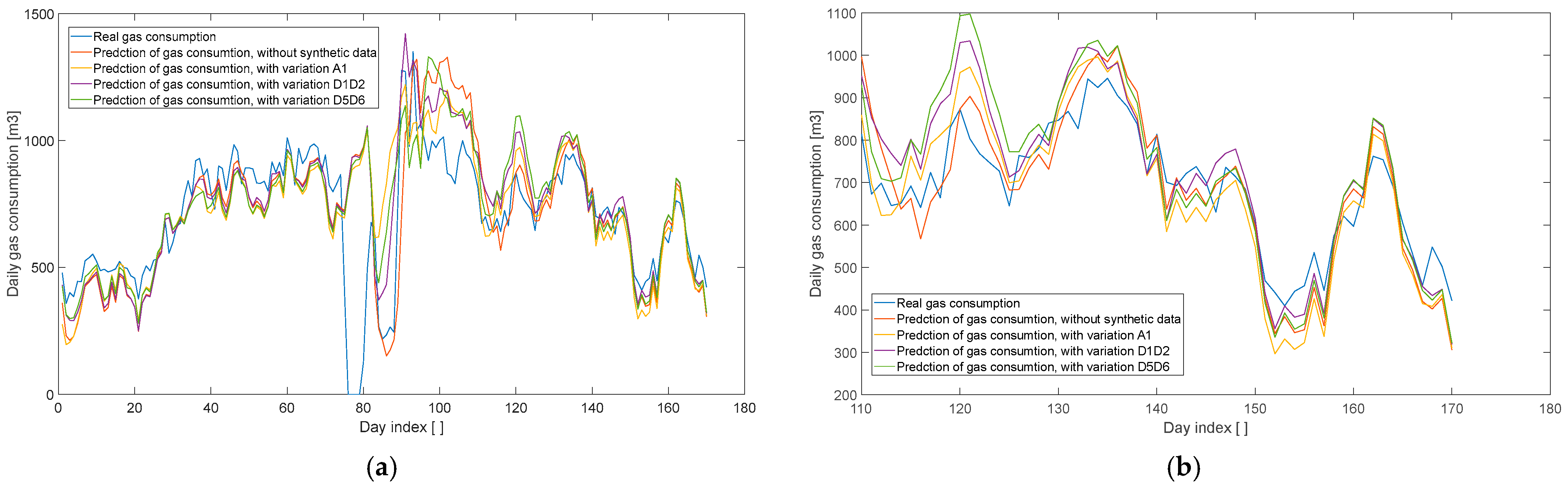
- To enhance the quality of the prediction, we expanded the dataset with synthetic data. These were generated using Wavelet Transform (see Figure 8), by varying approximation components and selected detail components (see Figure 9 and Figure 10). The quality of the augmented dataset was evaluated using normalised Mean Absolute Error (nMAE) and normalised Root Mean Square Error (NRMSE). Training results and comparisons with actual data from the 11th heating season are presented in Figure 14, Figure 15, Figure 16 and Figure 17, with nMAE and NRMSE values summarised in Table 5. However, this approach did not yield the expected improvement. The most promising results were achieved either by models trained on real data alone (computationally less demanding) or by using data with detailed components D1 and D2, varied only within the noise level. As demonstrated in Figure 18, a major limitation of this method is its inability to adequately capture consumption behaviour during operational interruptions caused by holidays.
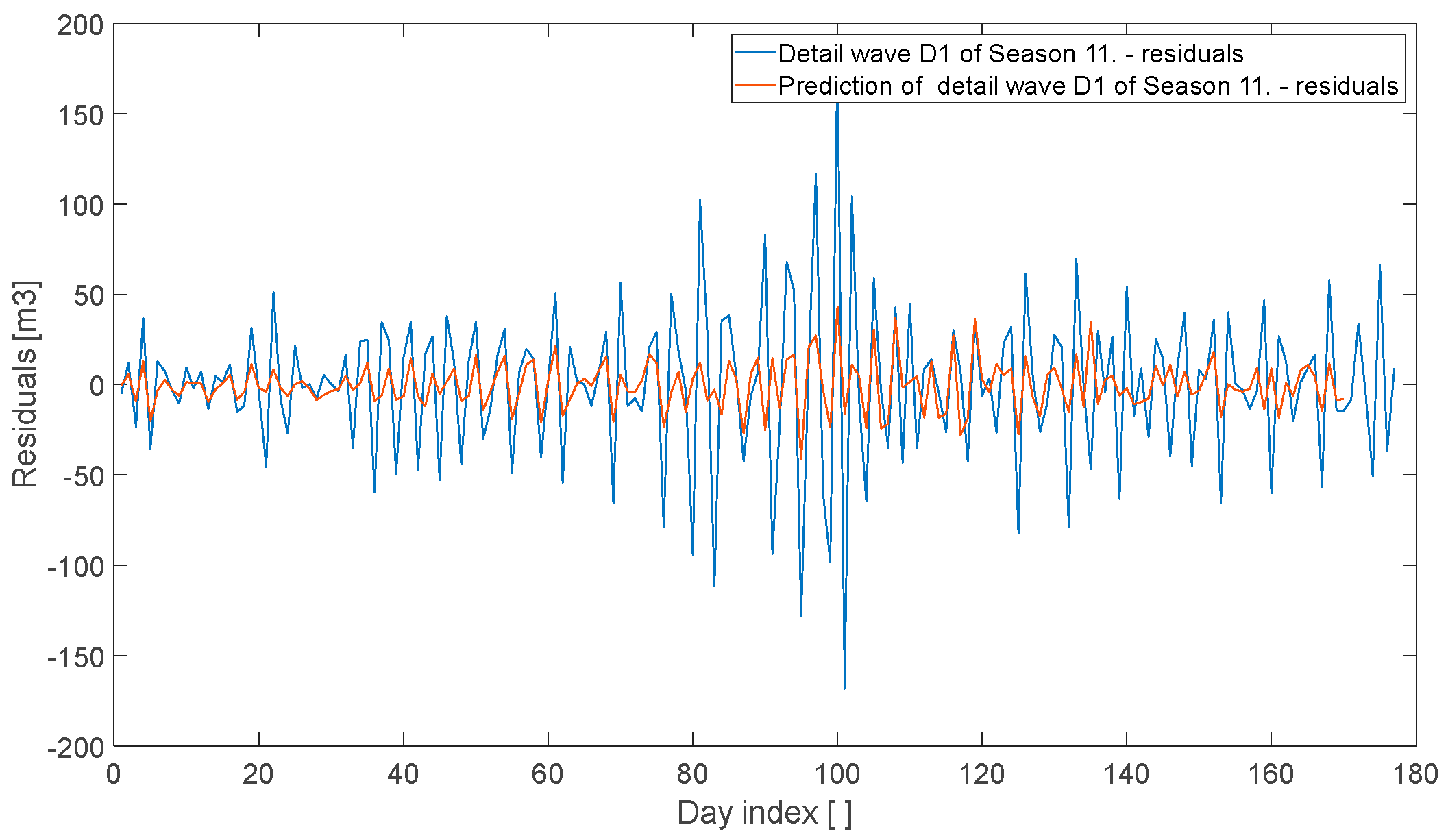
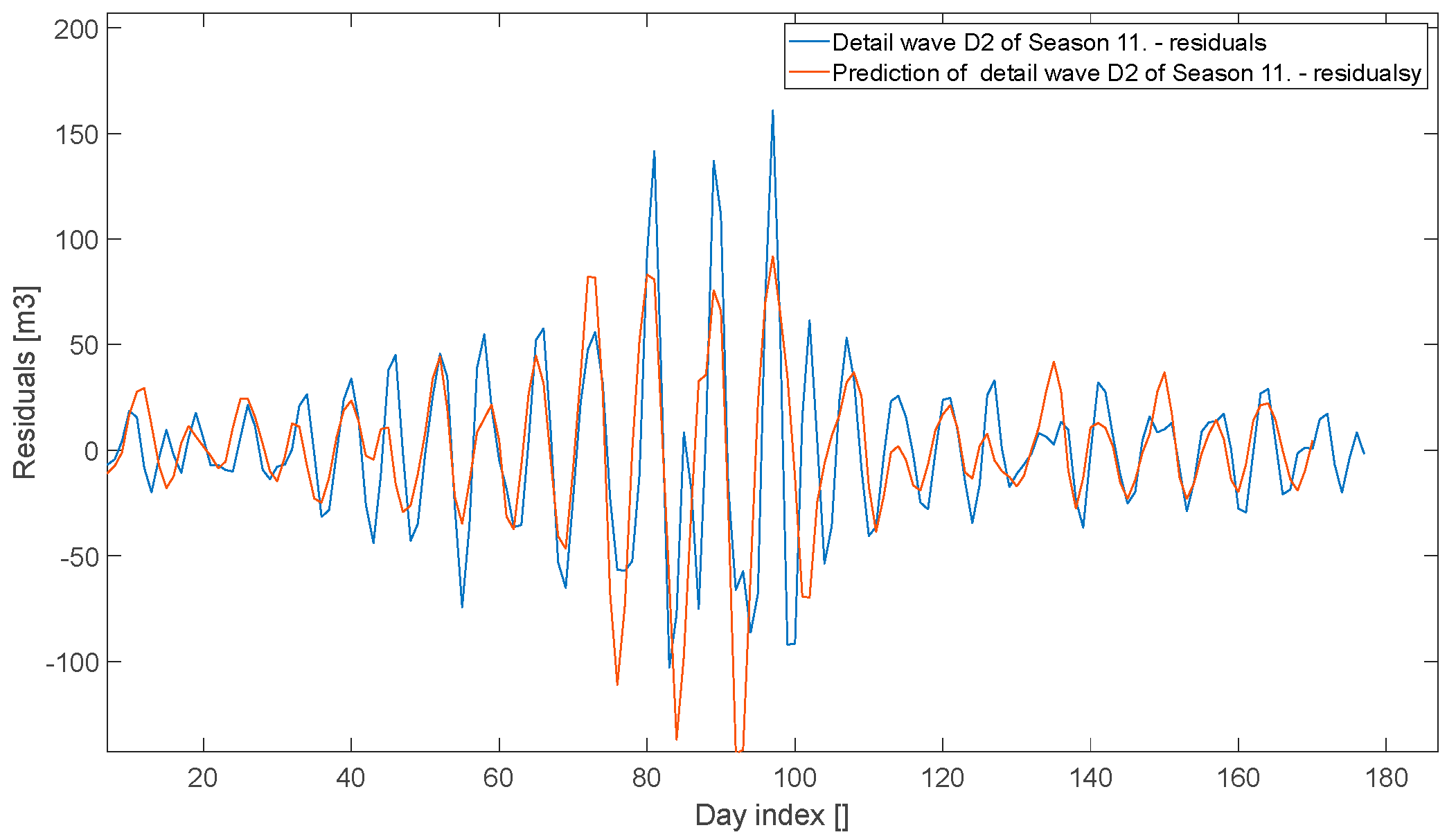
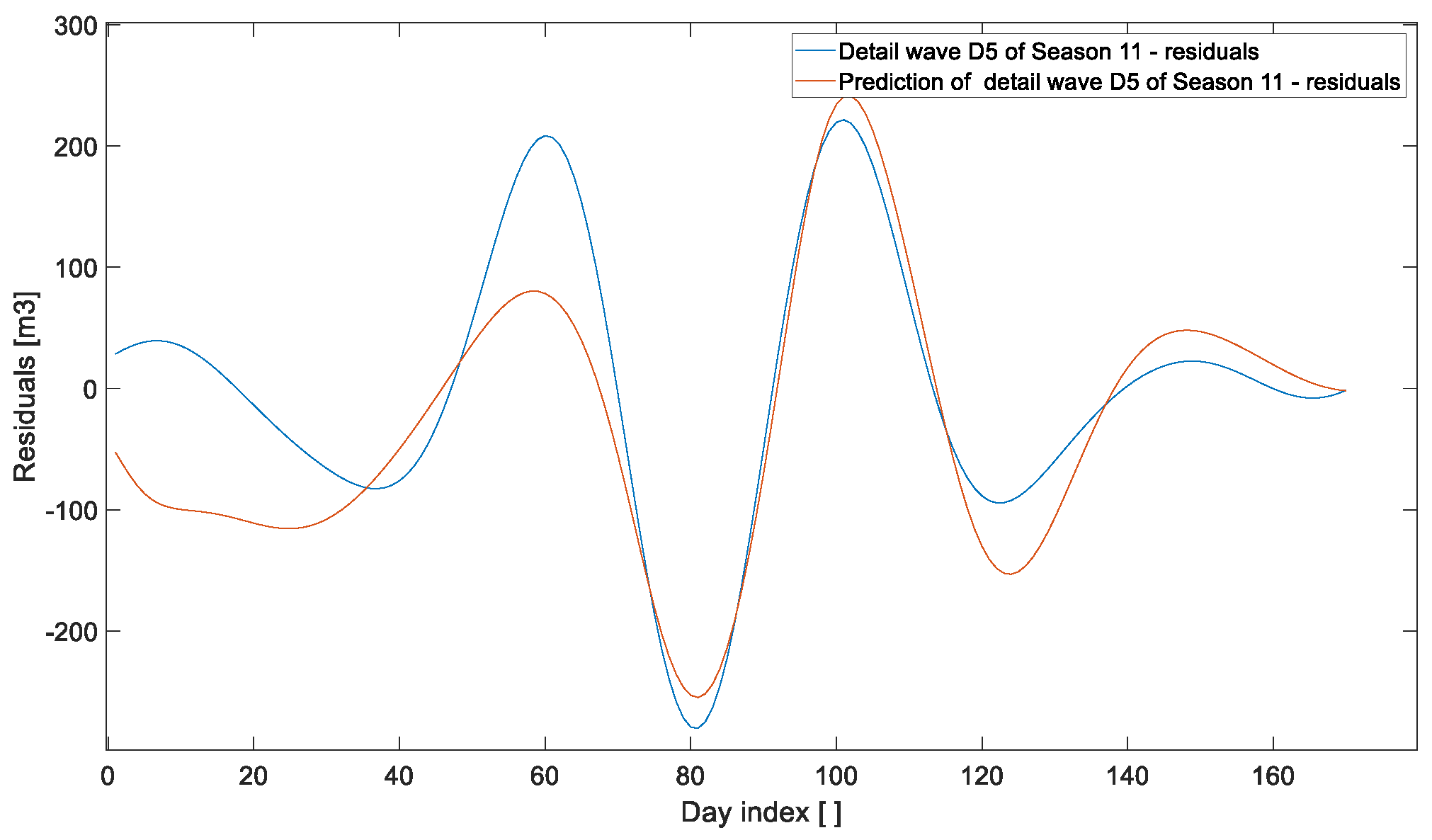
- The second approach excluded synthetic data entirely. The Wavelet Transform was applied and proposed to improve prediction accuracy by forecasting each wavelet component individually (see Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25 and Figure 26). The residual prediction was obtained by summing the predicted wavelet components, and the final gas consumption forecast was reconstructed by adding the previously separated linear component (temperature-dependent). The results, presented in Figure 27, show a 66% improvement in both nMAE and NRMSE compared to the previous approach. This methodology proved significantly more robust in handling operational downtimes during the winter holiday period. Specifically, we achieved nMAE = 5.71% and NRMSE = 7.80%.
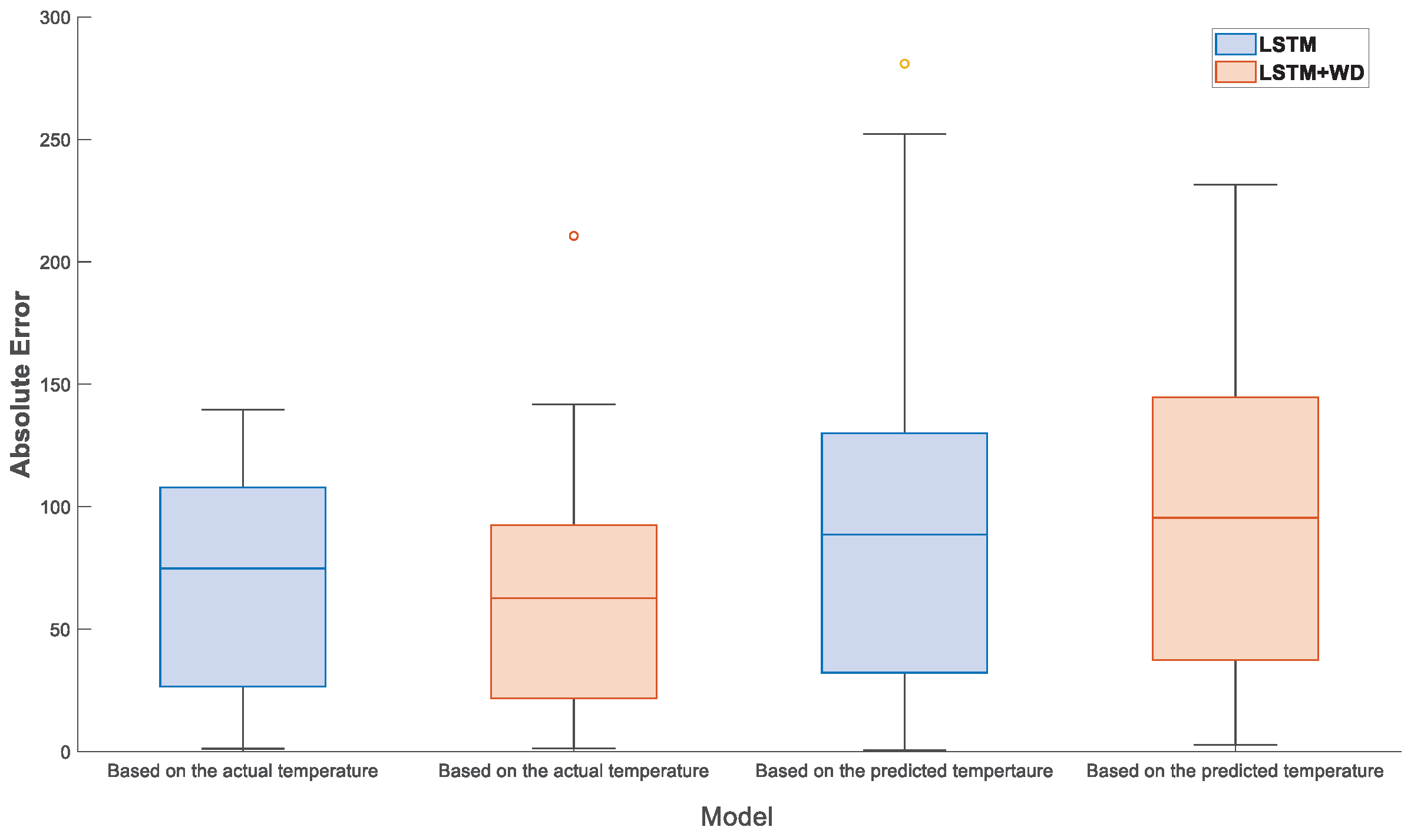
- In the third stage, we employed the best-performing model from Approach 1 and the best-performing model from Approach 2 to generate a 7-day forecast of gas consumption based on 7-day temperature forecasts. The results were then compared to those of models that relied on actual observed temperature and gas consumption data (see Figure 29).
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mahjoub, S.; Chrifi-Alaoui, L.; Marhic, B.; Delahoche, L. Predicting Energy Consumption Using LSTM, Multi-Layer GRU and Drop-GRU Neural Networks. Sensors 2022, 22, 4062. [Google Scholar] [CrossRef] [PubMed]
- Noaman, S.A.; Sahmed Ahmed, A.M.; Salman, A.D. A Prediction Model of Power Consumption in Smart City Using Hybrid Deep Learning Algorithm. Int. J. Inform. Vis. 2023, 7, 2436–2444. [Google Scholar]
- Caicedo-Vivas, J.S.; Alfonso-Morales, W. Short-Term Load Forecasting Using an LSTM Neural Network for a Grid Operator. Energies 2023, 16, 7878. [Google Scholar] [CrossRef]
- Chévez, P.; Martini, I. Applying neural networks for short and long-term hourly electricity consumption forecasting in universities: A simultaneous approach for energy management. J. Build. Eng. 2024, 97, 110612. [Google Scholar] [CrossRef]
- Liu, J.; Wang, S.; Wei, N.; Chen, X.; Xie, H.; Wang, J. Natural gas consumption forecasting: A discussion on forecasting history and future challenges. J. Nat. Gas Sci. Eng. 2021, 90, 103930. [Google Scholar] [CrossRef]
- Tamba, J.G.; Essiane, S.N.; Sapnken, E.F.; Koffi, F.D.; Nsouandélé, J.L.; Soldo, B.; Njomo, D. Forecasting Natural Gas: A Literature Survey. Int. J. Energy Econ. Policy 2018, 8, 216–249. [Google Scholar]
- Liu, J.; Wang, S.; Wei, N.; Yang, Y.; Lv, Y.; Wang, X.; Zeng, F. An Enhancement Method Based on Long Short-Term Memory Neural Network for Short-Term Natural Gas Consumption Forecasting. Energies 2023, 16, 1295. [Google Scholar] [CrossRef]
- Ghasemi, F.; Mehridehnavi, A.; Fassihi, A.; Pérez-Sánchez, H. Deep neural network in QSAR studies using deep belief network. Appl. Soft Comput. 2018, 62, 251–258. [Google Scholar] [CrossRef]
- Šebalj, D.; Mesaric, J.; Davor, D. Analysis of Methods and Techniques for Prediction of Natural Gas Consumption: A Literature Review. J. Inf. Organ Sci 2019, 43, 99–117. [Google Scholar] [CrossRef]
- Paravantis, J.A.; Malefaki, S.; Nikolakopoulos, P.; Romeos, A.; Giannadakis, A.; Giannakopoulos, E.; Mihalakakou, G.; Souliotis, M. Statistical and machine learning approaches for energy efficient buildings. Energ. Build. 2025, 330, 115309. [Google Scholar] [CrossRef]
- Smajla, I.; Vulin, D.; Sedlar, D.K. Short-term forecasting of natural gas consumption by determining the statistical distribution of consumption data. Energy Rep. 2023, 10, 2352–2360. [Google Scholar] [CrossRef]
- Smalja, I.; Sedlar, D.K.; Vulin, D.; Jukić, L. Influence of smart meters on the accuracy of methods for forecasting. Energy Rep. 2021, 7, 8287–8297. [Google Scholar] [CrossRef]
- Deb, C.; Zhang, F.; Yang, J.; Lee, S.E.; Shah, K.W. A review on time series forecasting techniques for building energy consumption. Renew. Sustain. Energy Rev. 2017, 74, 902–924. [Google Scholar] [CrossRef]
- Manigandan, P.; Alam, M.S.; Alharthi, M.; Khan, U.; Alagirisamy, K.; Pachiyappan, D.; Rehman, A. Forecasting Natural Gas Production and Consumption in United States-Evidence from SARIMA and SARIMAX Models. Energies 2021, 14, 6021. [Google Scholar] [CrossRef]
- Rehman, A.; Zhu, J.-J.; Segovia, J.; Anderson, P.R. Assessment of deep learning and classical statistical methods on forecasting hourly natural gas demand at multiple sites in Spain. Energy 2022, 244, 122562. [Google Scholar] [CrossRef]
- Wang, H.; Gao, X.; Zhang, Y.; Yang, Y. Natural Gas Consumption Forecasting Model Based on Feature Optimization and Incremental Long Short-Term Memory. Sensors 2025, 25, 2079. [Google Scholar] [CrossRef]
- Peng, S.; Chen, R.; Yu, B.; Xiang, M.; Lin, X.; Liu, E. Daily natural gas load forecasting based on the combination of long short term memory, local mean decomposition, and wavelet threshold denoising algorithm. J. Nat. Gas Sci. Eng. 2021, 95, 104175. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, X.; Koch, T. Day-ahead high-resolution forecasting of natural gas demand and supply in Germany with a hybrid model. Appl. Energ. 2020, 262, 114486. [Google Scholar] [CrossRef]
- Panek, W.; Wlodek, T. Natural Gas Consumption Forecasting Based on the Variability of External Meteorological Factors Using Machine Learning Algorithms. Energies 2022, 15, 348. [Google Scholar] [CrossRef]
- Qiao, W.; Ma, Q.; Yang, Y.; Xi, H.; Huang, N.; Yang, X.; Zhang, L. Natural gas consumption forecasting using a novel two-stage model based. J. Pipeline Sci. Eng. 2025, 5, 100220. [Google Scholar] [CrossRef]
- Svoboda, R.; Kotik, V.; Platos, J. Data-driven multi-step energy consumption forecasting with complex seasonality patterns and exogenous variables: Model accuracy assessment in change point neighborhoods. Appl. Soft Comput. 2024, 150, 111099. [Google Scholar] [CrossRef]
- Ding, J.; Zhao, Y.; Jin, J. Forecasting natural gas consumption with multiple seasonal patterns. Appl. Energ. 2023, 337, 120911. [Google Scholar] [CrossRef]
- Wei, N.; Li, C.; Peng, X.; Li, Y.; Zeng, F. Daily natural gas consumption forecasting via the application of a novel hybrid model. Appl. Energ. 2019, 250, 358–368. [Google Scholar] [CrossRef]
- Mižáková, J.; Hošovský, A.; Piteľ, J. Design of the One Week-ahead Forecasting of Daily Gas Consumption using ARMA/ARIMA Models. In Proceedings of the 2023 24th International Conference on Process Control, Štrbské Pleso, Slovak Republic, 6–9 June 2023. [Google Scholar]
- Piteľ, J.; Hošovský, A.; Mižáková, J.; Židek, K.; Khovanskyi, S.; Ratnayake, M.; Lazorík, P.; Matisková, D. Monitoring of heat sources using principles of fourth industrial revolution of energy consumption prediction. In Proceedings of the ARTEP 2020, Stará Lesná, Slovak Republic, 5-7 February 2020. [Google Scholar]
- Cheney, W.; Kincaid, D. Numerical Mathematics and Computing; Thomson Brooks/Cole: Belmont, MA, USA, 2013. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing; Elsevier: Burlington, VT, USA, 2009. [Google Scholar]
- Tangirala, A.K. Principles of System Identification; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Soltani, S. On the use of the wavelet decomposition for time series prediction. Neurocomputing 2002, 48, 267–277. [Google Scholar] [CrossRef]
- Alexandridis, A.K.; Zapranis, D.A. Wavelet Neural Networks: With Applications in Financial Engineering, Chaos, and Classification; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Zhou, Y.; Sheremet, A.; Kennedy, J.P.; DiCola, N.M.; Maurer, A.P. High-Order Theta Harmonics Account for the Detection of Slow Gamma. Available online: https://www.biorxiv.org/content/10.1101/428490v2.full.pdf (accessed on 20 February 2025).
- Hošovský, A.; Piteľ, J.; Adámek, M.; Mižáková, J.; Židek, K. Comparative study of week-ahead forecasting of daily gas consumption in buildings using regression ARMA/SARMA and genetic-algorithm-optimized regression wavelet neural network models. J. Build. Eng. 2021, 34, 101955. [Google Scholar] [CrossRef]
- Semenoglou, A.A.; Spiliotis, E.; Assimakopoulos, V. Data augmentation for univariate time series forecasting with neural networks. Pat. Rec. 2023, 134, 109132. [Google Scholar] [CrossRef]
- Bandara, K.; Hewamalage, H.; Liu, Y.-H.; Kang, Y.; Bergmeier, C. Improving the Accuracy of Global Forecasting Models using Time Series Data Augmentation. Pat. Rec. 2021, 120, 108148. [Google Scholar] [CrossRef]
- Bergmeir, C.; Hyndman, R.J.; Benítez, J.M. Bagging exponential smoothing methods using STL decomposition and box–Cox transformation. Int. J. Forecast. 2016, 32, 303–312. [Google Scholar] [CrossRef]
- Forestier, G.; Petitjean, F.; Dau, H.; Webb, G.; Keogh, E. Generating synthetic time series to augment sparse datasets. In Proceedings of the IEEE International Conference on Data Mining (ICDM), Washington, DC, USA, 18–21 November 2017. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Bianchi, F.M.; Maiorino, E.; Kampffmeyer, M.C.; Rizzi, A.; Jenssen, R. Recurent Neural Networks for Short-Term Load Forecasting; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Slovak Act on Thermal Energy No. 657/2004 Coll. Available online: https://www.slov-lex.sk/ezbierky/pravne-predpisy/SK/ZZ/2004/657/ (accessed on 5 July 2025).
- Piras, G.; Muzi, F.; Ziran, Z. A Data-Driven Model for the Energy and Economic Assessment of Building Renovations. Appl. Sci. 2025, 15, 8117. [Google Scholar] [CrossRef]
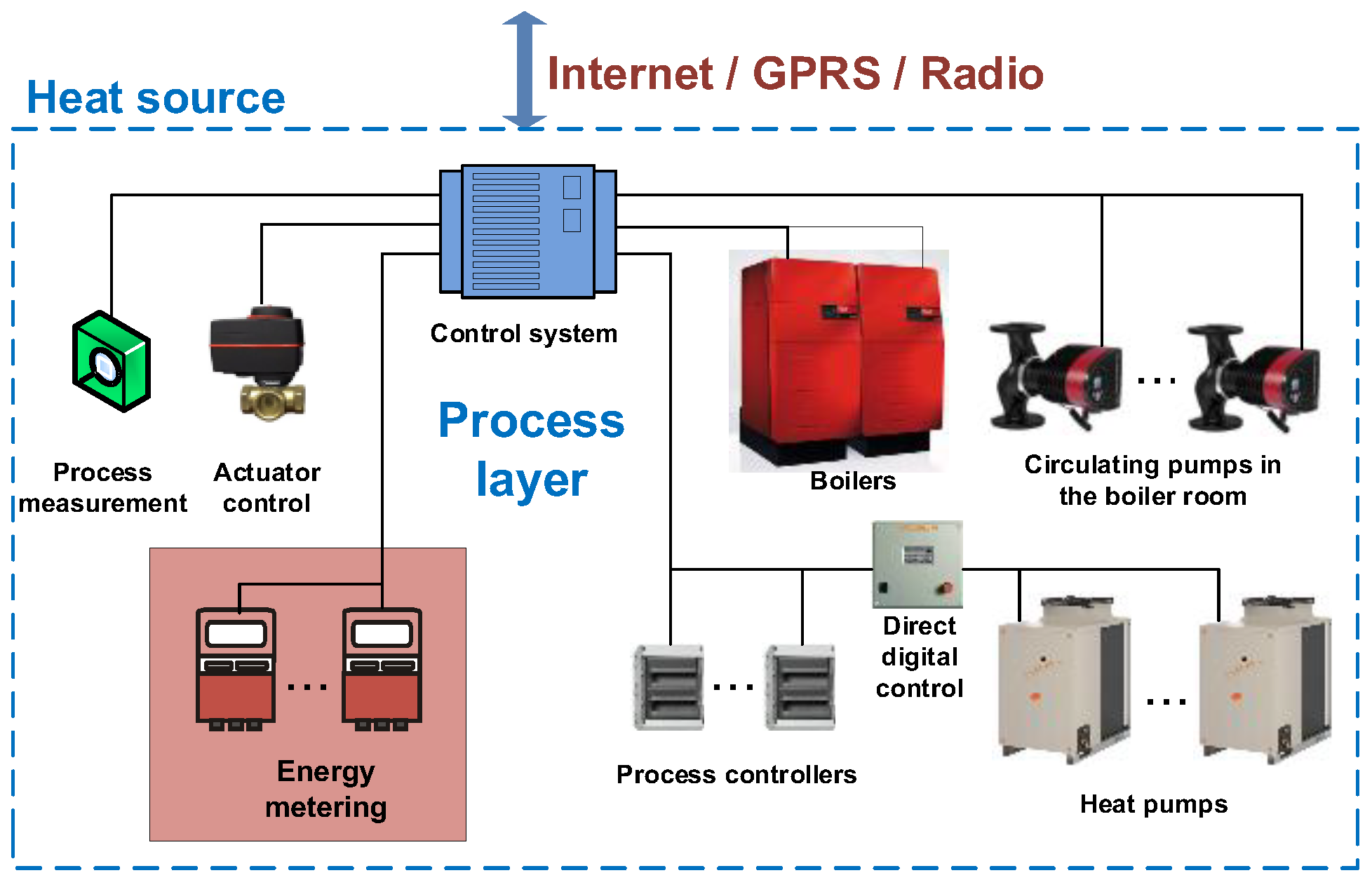
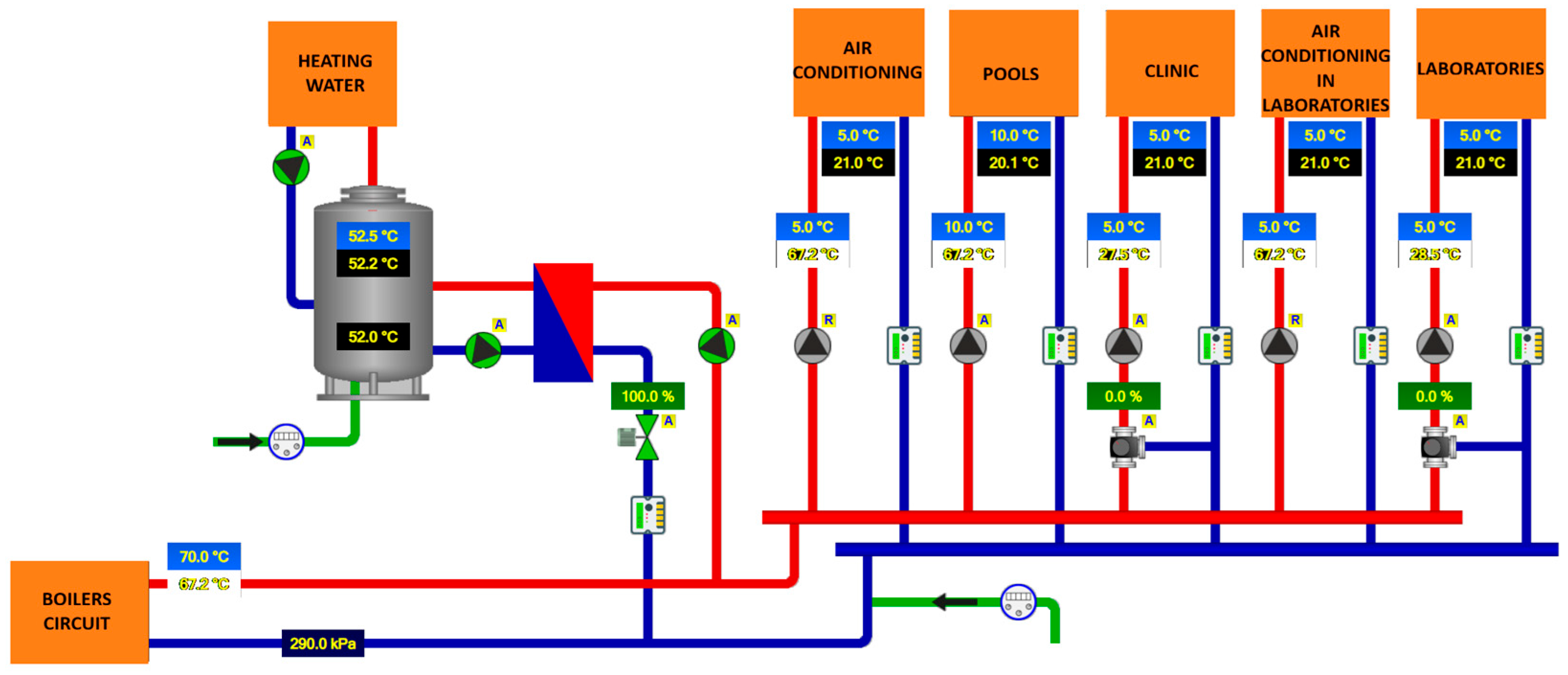
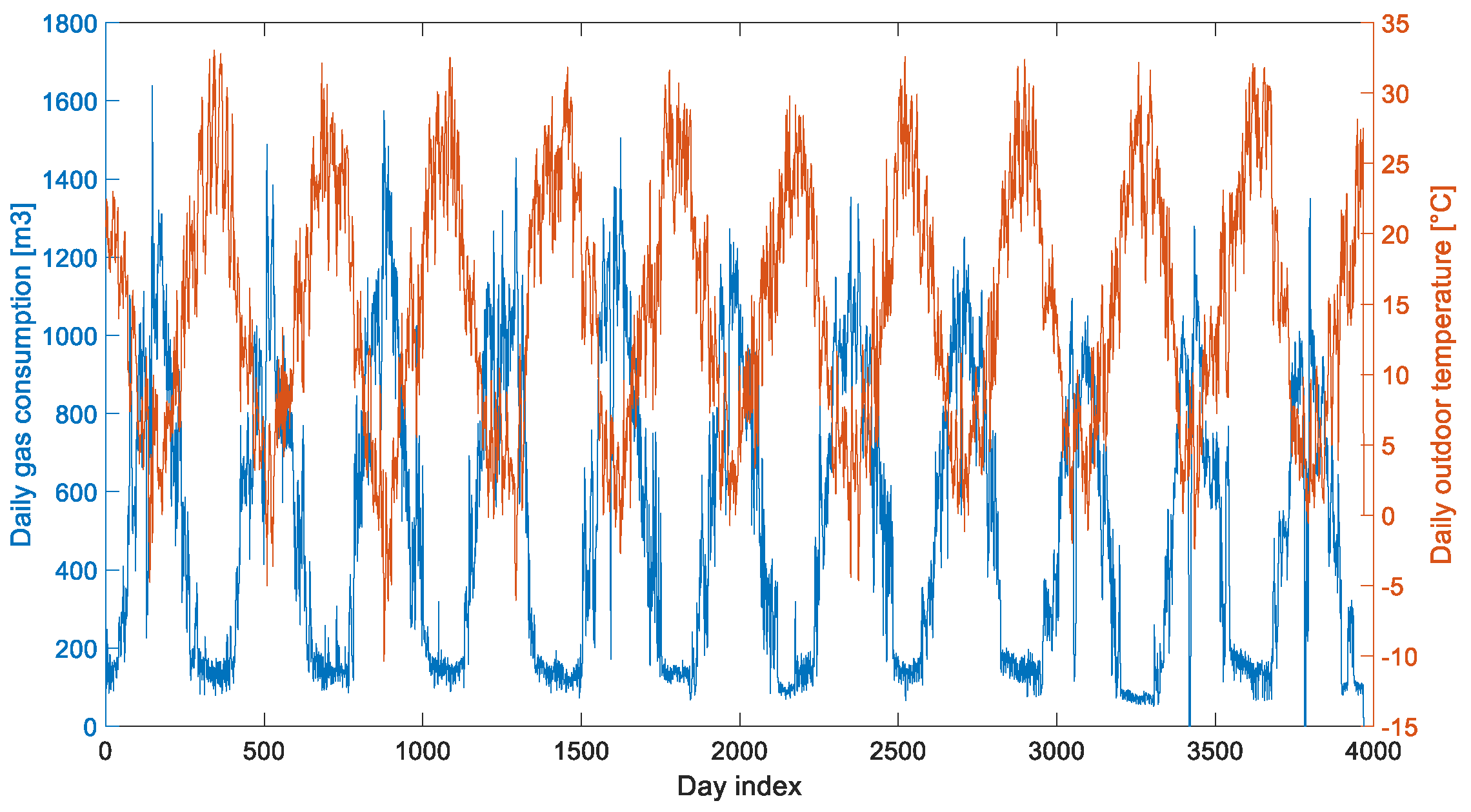

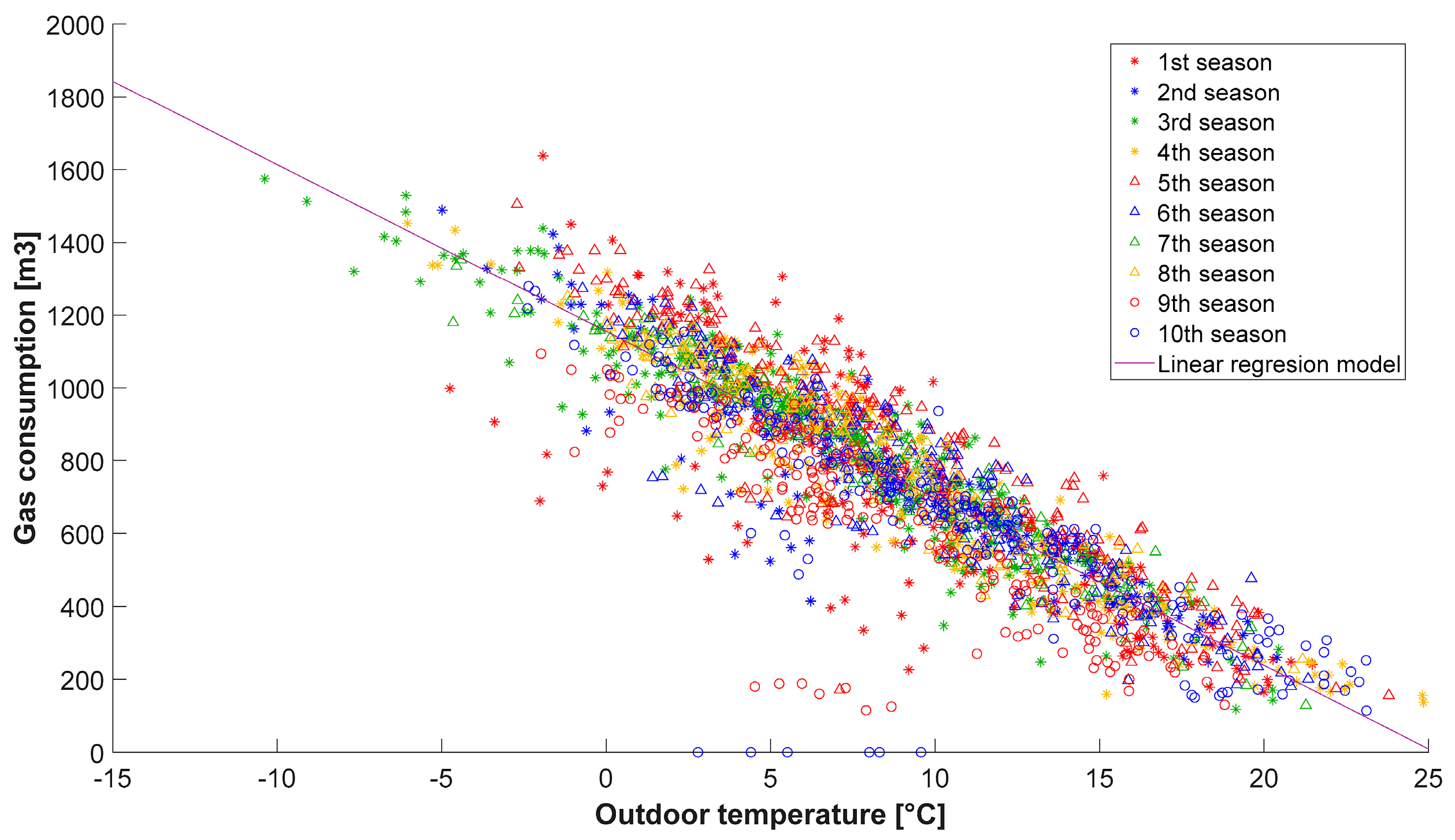


















| Heating Periods | 2014–2015 | 2015–2016 | 2016–2017 | 2017–2018 | 2018–2019 |
|---|---|---|---|---|---|
| Number of days in heating period | 213 | 214 | 213 | 213 | 213 |
| Absolute maximum (gas consumption) | 1638 | 1489 | 1575 | 1453 | 1505 |
| Absolute minimum (gas consumption) | 165 | 247 | 118 | 137 | 156 |
| Mean of gas consumption | 759.4 | 747.8 | 839.3 | 781.3 | 818.2 |
| The standard deviation of gas consumption | 309.4 | 241.2 | 310.6 | 308.1 | 324.1 |
| Total gas consumption | 161,750 | 160,030 | 178,775 | 166,411 | 174,284 |
| Absolute maximum (temperature) | 21.5 | 20.4 | 20.4 | 24.8 | 23.8 |
| Absolute minimum (temperature) | −4.8 | −5.0 | −10.4 | −6.0 | −2.7 |
| Mean of temperature | 9.0 | 8.8 | 6.8 | 8.3 | 9.3 |
| The standard deviation of temperature | 5.4 | 5.0 | 6.3 | 6.4 | 6.1 |
| Heating Periods | 2019–2020 | 2020–2021 | 2021–2022 | 2022–2023 | 2023–2024 |
| Number of days in heating period | 214 | 213 | 213 | 213 | 214 |
| Absolute maximum (gas consumption) | 1273 | 1353 | 1251 | 1094 | 1279 |
| Absolute minimum (gas consumption) | 181 | 129 | 227 | 115 | 0 |
| Mean of gas consumption | 740.9 | 815.0 | 794.0 | 630.4 | 650.4 |
| The standard deviation of gas consumption | 276.0 | 236.0 | 233.3 | 252.6 | 280.0 |
| Total gas consumption | 158,559 | 172,586 | 169,123 | 134,271 | 138,539 |
| Absolute maximum (temperature) | 21.3 | 21.3 | 21.2 | 19.2 | 23.1 |
| Absolute minimum (temperature) | −0.8 | −4.7 | −1.2 | −2.0 | −2.4 |
| Mean of temperature | 9.5 | 7.8 | 8.2 | 8.8 | 10.3 |
| The standard deviation of temperature | 5.3 | 5.0 | 4.7 | 4.8 | 5.9 |
| SSE | 3.52 × 107 |
| R2 | 0.798 |
| RMSE | 126.61 |
| nMAE | OCT | NOV | DEC | JAN | FEB | MAR | APR |
|---|---|---|---|---|---|---|---|
| 1st season, variation of D1D2 | 0.144 | 0.085 | 0.101 | 0.059 | 0.054 | 0.116 | 0.114 |
| 1st season, variation of D5D6 | 0.104 | 0.092 | 0.120 | 0.115 | 0.033 | 0.060 | 0.059 |
| 6th season, variation of D1D2 | 0.152 | 0.078 | 0.066 | 0.047 | 0.051 | 0.066 | 0.130 |
| 6th season, variation of D5D6 | 0.057 | 0.056 | 0.057 | 0.036 | 0.030 | 0.027 | 0.048 |
| 7th season, variation of D1D2 | 0.108 | 0.060 | 0.053 | 0.046 | 0.049 | 0.051 | 0.070 |
| 7th season, variation of D5D6 | 0.0713 | 0.078 | 0.116 | 0.059 | 0.036 | 0.023 | 0.064 |
| 10th season, variation of D1D2 | 0.159 | 0.060 | 0.107 | 0.060 | 0.067 | 0.082 | 0.136 |
| 10th season, variation of D5D6) | 0.080 | 0.053 | 0.103 | 0.061 | 0.039 | 0.037 | 0.081 |
| sMAPE | OCT | NOV | DEC | JAN | FEB | MAR | APR |
|---|---|---|---|---|---|---|---|
| 1st season, variation of D1D2 | 0.080 | 0.120 | 0.117 | 0.080 | 0.135 | 0.211 | 0.117 |
| 1st season, variation of D5D6 | 0.058 | 0.123 | 0.146 | 0.127 | 0.086 | 0.101 | 0.058 |
| 6th season, variation of D1D2 | 0.139 | 0.162 | 0.114 | 0.123 | 0.171 | 0.140 | 0.117 |
| 6th season, variation of D5D6 | 0.053 | 0.116 | 0.096 | 0.096 | 0.101 | 0.058 | 0.039 |
| 7th season, variation of D1D2 | 0.093 | 0.110 | 0.182 | 0.122 | 0.095 | 0.097 | 0.097 |
| 7th season, variation of D5D6 | 0.059 | 0.139 | 0.332 | 0.155 | 0.072 | 0.043 | 0.077 |
| 10th season, variation of D1D2 | 0.177 | 0.101 | 0.102 | 0.148 | 0.146 | 0.137 | 0.113 |
| 10th season, variation of D5D6) | 0.087 | 0.090 | 0.095 | 0.135 | 0.094 | 0.061 | 0.069 |
| Training | nMAE | NRMSE |
|---|---|---|
| Without synthetic data | 0.178 | 0.154 |
| Synthetic data, varying approximation A1 | 0.184 | 0.159 |
| Synthetic data, varying D1 and D2 details | 0.171 | 0.148 |
| Synthetic data, varying D5 and D6 details | 0.189 | 0.156 |
| Step/Operation | Complexity/Estimated Cost of Synthetic Data Training Method | Complexity/Estimated Cost of Wave Training Method |
|---|---|---|
| Data normalisation | ||
| LSTM layer definition | ||
| LSTM training | ||
| Prediction | ||
| Denormalization + linear correction |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mižáková, J.; Piteľ, B.; Pomin, P.; Hošovský, A. Direct Multiple-Step-Ahead Forecasting of Daily Gas Consumption in Non-Residential Buildings Using Wavelet/RNN-Based Models and Data Augmentation— Comparative Evaluation. Technologies 2025, 13, 435. https://doi.org/10.3390/technologies13100435
Mižáková J, Piteľ B, Pomin P, Hošovský A. Direct Multiple-Step-Ahead Forecasting of Daily Gas Consumption in Non-Residential Buildings Using Wavelet/RNN-Based Models and Data Augmentation— Comparative Evaluation. Technologies. 2025; 13(10):435. https://doi.org/10.3390/technologies13100435
Chicago/Turabian StyleMižáková, Jana, Branislav Piteľ, Pavlo Pomin, and Alexander Hošovský. 2025. "Direct Multiple-Step-Ahead Forecasting of Daily Gas Consumption in Non-Residential Buildings Using Wavelet/RNN-Based Models and Data Augmentation— Comparative Evaluation" Technologies 13, no. 10: 435. https://doi.org/10.3390/technologies13100435
APA StyleMižáková, J., Piteľ, B., Pomin, P., & Hošovský, A. (2025). Direct Multiple-Step-Ahead Forecasting of Daily Gas Consumption in Non-Residential Buildings Using Wavelet/RNN-Based Models and Data Augmentation— Comparative Evaluation. Technologies, 13(10), 435. https://doi.org/10.3390/technologies13100435








