Abstract
Semiconductors play a crucial role in a wide range of applications and are integral to essential infrastructures. Manufacturers of these semiconductors must meet specific quality and lifetime targets. To estimate the lifetime of semiconductors, accelerated stress tests are conducted. This paper introduces a novel approach to modeling drift in discrete electrical parameters within stress test devices. It incorporates a machine learning (ML) approach for arbitrary panel data sets of electrical parameters from accelerated stress tests. The proposed model involves an expert-in-the-loop MLOps decision process, allowing experts to choose between an interpretable model and a robust ML algorithm for regularization and fine-tuning. The model addresses the issue of outliers influencing statistical models by employing regularization techniques. This ensures that the model’s accuracy is not compromised by outliers. The model uses interpretable statistically calculated limits for lifetime drift and uncertainty as input data. It then predicts these limits for new lifetime stress test data of electrical parameters from the same technology. The effectiveness of the model is demonstrated using anonymized real data from Infineon technologies. The model’s output can help prioritize parameters by the level of significance for indication of degradation over time, providing valuable insights for the analysis and improvement of electrical devices. The combination of explainable statistical algorithms and ML approaches enables the regularization of quality control limit calculations and the detection of lifetime drift in stress test parameters. This information can be used to enhance production quality by identifying significant parameters that indicate degradation and detecting deviations in production processes.
1. Introduction
1.1. Problem Definition
Semiconductor device reliability is crucial in an industry where strict quality standards are the norm. One standard requirement, especially in automotive applications, is that failure rates should not exceed one in a million, highlighting the importance of precise lifetime quality prediction by the manufacturer. To achieve this, lifetime stress tests are employed to simulate lifetime degradation and generate data on the lifetime drift of electrical parameters. These parameters are deemed to be within specification if they do not exceed certain predefined limits over their lifetime.
To ensure quality for customers, tighter limits than those specified in their product sheets are introduced at the final test step before shipping. These tighter limits, known as test limits, serve to ensure that the devices will remain within specification throughout their lifetime. Deviations or outliers in stress test data that can be quantified via a statistical model may also give indications of deviations in production processes and be utilized to better the quality control feedback loop.
Several challenges come with calculating these test limits. Firstly, the parameters can only be simulated via rapid stress testing, not real-time tests. Additionally, the parts are typically measured at different temperatures. The electrical parameters measured depend on the type of device and the reason for lifetime drift investigation. The types of parameters are typically specified by engineering or quality departments. This leads to potentially thousands of different electrical parameters being measured per device.
The electrical parameters measured depend on the type of device and the reason for lifetime drift investigation. The types of parameters are typically specified by engineering or quality departments. This leads to potentially thousands of different electrical parameters being measured per device. Such parameters may be continuous, for example, threshold voltage, or discrete, such as the results of go/no-go tests, counts of bit-flips occurring in a logic device or data that are only available with a certain measurement granularity. In general, discrete electrical parameters are more difficult to handle mathematically than continuous ones.
Although the behavior of parameters over different electrical parameters and temperatures may be correlated, traditional methods still require fitting a model to each parameter individually to remain suitable. Secondly, the models developed thus far are designed for continuous electrical parameters only. In the case of discrete parameters, some theoretical assumptions no longer hold, leading to numerical instabilities. Moreover, the non-uniqueness of some solutions in standard approaches may result in different test limits for very similar data. An illustration of this instability can be observed in Figure 1. This instability over similar patterns of data may lead to different limit predictions for data that basically look the same when using standard methods.
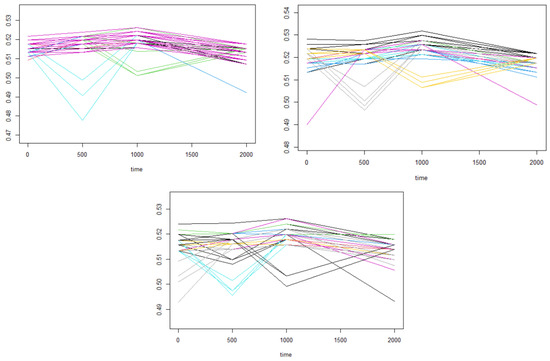
Figure 1.
Three different outcomes emerge from clustering highly similar trajectory data. Different clusters are indicated by different colors. Statistical models may yield divergent results on similar data sets due to the non-deterministic nature of clustering algorithms. In this example, similar data lead to widely different clustering.
A more robust approach for regularizing lifetime drift limits is needed. Inclusion of human supervision of such algorithms is also necessary, especially in the context of quality control. In this paper, we investigate the potential of machine learning methods for regularizing and streamlining statistical calculations of test limits for electrical parameter lifetime drift. We further propose a method of keeping expert-in-the-loop checking of results for plausibility and use the results from the machine learning approach to aid the decision-making process for more optimal results.
1.2. Relevance to the Field
Ensuring safety in automotive semiconductor manufacturing is a critical aspect, particularly in the context of autonomous vehicles. An emerging approach in this regard is prognostics and health management, or predictive maintenance. The goal is to develop statistical degradation models of semiconductor chips that can run online on edge devices within vehicles. These models aim to predict potential part failures and trigger maintenance actions autonomously, thereby converting potential issues into preventive maintenance actions. However, this requires the allocation of resources for such calculations, either on-board in micro-controllers within the vehicle or on cloud-based architectures that necessitate a functional connection and bandwidth. A proposed compromise is to have the models run only when the vehicle is in downtime, such as when parked in a garage overnight. This approach would lead to a more efficient use of resources, as the vehicle could utilize the available calculation power during periods of inactivity. A common assumption for a feasible indication of degradation is that the stress test data obtained in the rapid stress test environment are representative of the lifetime degradation of the parameter in the real-world field. More lightweight models may help in optimizing the resources used in calculation for such applications. Furthermore, the same models used by experts for setting statistical test limits based on lifetime drift data of electrical parameters may be employed for online calculation as well.
1.3. Previous Work
The previous research has been conducted on setting tighter limits to control for lifetime drift in electrical parameters in semiconductor devices. The issue of guard banding parameters is discussed in [1,2,3,4,5]. However, these works only consider the case of a one-time measurement being taken in the presence of measurement granularity. The topic of guard banding longitudinal data for lifetime quality based on a stress test has been expanded upon in [6,7,8,9], where statistical methods are employed to calculate optimal guard bands based on assumptions about the shape of the distributions of the parameters. In [6], the multivariate behavior is modeled using copulae based on skew-normal marginals, while in [9], the multivariate behavior is captured via a mixture of multivariate Gaussian distributions. In both cases, optimization is non-trivial and achieved via numerical calculations. These numerical optimizations and the fitting of non-deterministic multivariate models may lead to the same data being assigned slightly different guard bands with repeat calculations.
1.4. Contribution of the Paper
In this paper, we explore the potential of machine learning methods, specifically random forest regression, for calculating robust estimates for test limits for electrical parameters in semiconductor devices. This approach addresses both the issue of numerical and algorithmic instability in standard statistical methods and can serve as an extension to the classical methods in the case of online-monitoring due to the ability to fit a model once and then use it for prediction, which is computationally faster than recalculating the statistical model for each parameter. Furthermore, we evaluate the performance of random forest regression on lifetime prediction for continuous data and discuss the application of quantile random forest regression to incorporate expert knowledge into the model.
Moreover, the approach of training a random forest model on a data set of all the parameters of a rapid stress test examination of an electrical device addresses the issues of being robust to outliers in stress test data and capturing dependencies between correlated parameter drift patterns. We also incorporate the differences between readout as explicit features, as these are typically used as a basis to determine test limits by experts, and investigate the effect on the performance of the models.
It is important to note that ensuring the accuracy regarding target probabilities in real data is a challenging task. Typically, the sample data do not contain failed devices, and the test limits are only rarely exceeded. Therefore, the results mainly depend on the theoretical assumptions or construction of statistical or physical models. A machine learning approach can serve as an extension to the process of finding the best fit models. However, it should not be used as the sole approach unless verified by further physical simulation.
2. Theoretical Framework
2.1. Electrical Parameter Drift
Rapid stress testing is a standard practice for simulating lifetime aging of semiconductor devices. This involves exposing a sample of electrical devices to higher-than-usual stress conditions, such as high heat (as in HTOL or high-temperature operating life tests) or temperatures well below freezing point, sometimes in combination with high ambient humidity (as in the THB or temperature humidity bias test). These tests are also mentioned in industry standards, such as [10,11,12]. The parts are tested using specialized equipment, and the electrical parameters are first measured as a baseline. Then, the parts are subjected to stress tests, and at certain predetermined times, called readout times, the parameters are measured again, and the device is put back into the stress test. This process is repeated until the desired lifetime simulation length has been reached.
Using these data, product engineers then determine optimal test limits for the parameters. Test limits serve to limit shipped parts to only those parts that are certain to guarantee a specified quality target to the customer. For example, this may be 1 ppm, or one part per million parts. From a semiconductor manufacturer’s standpoint, the area between specified limits and test limits should be wide enough to guarantee quality yet also maximize the shipped good parts. In this area, it is crucial to neither over- nor underestimate the optimal test limit.
2.2. Statistical Discussion of Current Models
State-of-the-art methods for determining optimal quality limits, such as [6,8,9], typically focus on both statistical modeling and optimization of the guard band, or the area between test limits and specified limits. The currently available methods only determine test limits based on separate data-driven statistical models for each electrical parameter separately. While copula-based methods handle the issue of skewed multivariate distributions of data points well, they are not suited to depict the effect of grouping of parameters within a single electrical parameter test. Multivariate mixed methods were developed to deal with both grouped data and outliers but rely on a non-deterministic clustering algorithm and assumptions about the distribution of outliers, which still have a significant effect on the resulting outcome. Both models do not consider correlation effects between separate parameters or regularization effects to smooth the effect of outliers. Noisy data can be considered separately using Gr&R testing and incorporated into the multivariate mixed model. Machine learning models may provide a solution to a more regularized prediction by fitting a single model on the data set using all parameters. This also solves the issues of non-terminating fitting in statistical algorithms and may help smooth out the differences in results that arise due to clustering very similar data in different ways.
3. Materials and Methods
3.1. Data Collection
For this paper, we consider a real-life sample of 1322 electrical parameters from an industrial rapid stress test procedure. Furthermore, for each electrical test, we also consider a smaller sample of m comparison parts (VGTs, from the German “Vergleichsteile”, lit. “comparison parts”) to control for tester offset, as in [6,9]. The data each consist of a set of 110 devices that are measured at 4 readout times. The assumption is that a model should be trained on data from similar device types or ideally data from the same device, if available, in order to achieve the best results. The electrical parameters chosen represent a subset of all the electrical parameters available within the data set. The goal was to obtain as complete as possible a set of parameters to best represent the real data. The test limits were modeled using the algorithm presented in [9].
For a subset of parameters, the clustering algorithm did not terminate in some way (approximately 5% of samples). We removed these parameters from the training and testing data. Additionally, data sets that showed no change at all, i.e., just consisting of the same value being measured at all times, were removed. In total, 1057 electrical parameters containing continuous values, each containing trajectories of 110 devices, were chosen for the training set, and 265 continuous electrical parameters were randomly chosen for the validation set.
An example of trajectories of an anonymized real data set can be seen in Figure 2;
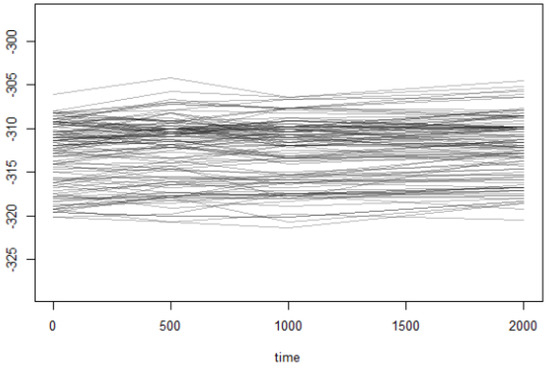
Figure 2.
An anonymized example showing a set of trajectories for an electrical parameter. Electrical parameter values are on the y-axis, with time in hours on the x-axis. In this case, the electrical parameter values remain relatively consistent across the four readings and show low variability.
3.2. Pre-Processing Steps
The data were corrected for tester offset using the method described in [6,9]. This involves subtracting the drift from the unstressed reference devices from the drift of the data points themselves. These data points were then used to fit a model for optimal test limits as described in [9], including measurement error, if available. As the specified limits and standard unit of measurement are different for each type of electrical parameter, the parameters and specified limits were normalized such that the lower specified limit lies at 0 and the upper specified limit lies at 1. In such a way, the test limits naturally fall between 0 and 1 also and, at the same time, give the percentage of area they occupy of the total allowable window for each parameter. This also serves the purpose of making model training easier and to make input data comparable so meaningful learning can be taking place. Otherwise, the model would train on the order of magnitude of the electrical parameter, which we wish to avoid. We want to have the model only consider the data and drift of the parameter itself.
Furthermore, we include the total differences between readout points as an extra feature. This is implemented in order to give the model an easier time to quantify parameter drift.
Finally, the data from all devices for each electrical parameter are flattened to a vector and used for model training. The process is shown in Figure 3.
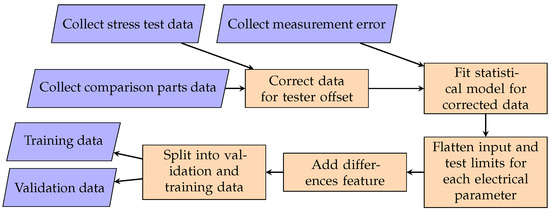
Figure 3.
A flowchart showing the data preparation pipeline used to generate training and validation data. Feature engineering and train/test splitting plus pre-processing are included.
3.3. Comparing Different Models
For optimal model type selection, a set of different candidate models were considered. The parameters for all models were chosen via 10-fold cross validation [13] and the comparison of models between each other was achieved via resampling.
- A generalized linear model [14] approach was fitted using the R function glmnet.
- A gradient-boosting approach [15] was fitted using the R function gbm.
- A support vector machine [16] approach using radial basis functions was performed using the R function svmRadial.
- Finally, a random forest approach [17] was fitted using the fast R implementation ranger.
The target variable for model choice was the lower test limit as calculated by the statistical model in [9]. The models were compared via mean square error, root mean square error and -score.
In all relevant metrics, seen in Figure 4 and Figure 5 and Table 1, Table 2 and Table 3, the random forest implementation performed best. This is somewhat expected due to the unstructured nature of the data. Random forests are well known to perform well on these high-dimensional types of unstructured input data. Note that even in the best model, the inclusion of differences between readout points as extra features provided a significant improvement in RMSE. On a 13th Gen Intel(R) Core(TM) i5-1345U with 16 GB RAM, the training time with hyper-parameter optimization and 10-fold cross validation for the respective models are min for the generalized linear model, min for the gradient boosting model, min for the support vector machine model and min for the random forest model.
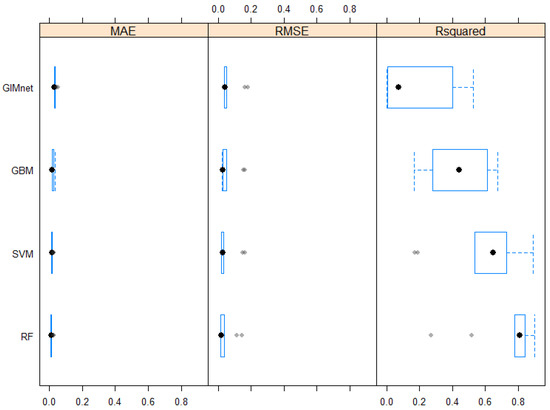
Figure 4.
A comparison of MAE, RMSE and for the different candidate models. Lower is better for MAE and RMSE; higher is better for . The random forest model shows the best results on real data. Standard Boxplot, black dot as Median, blue frame as Box.
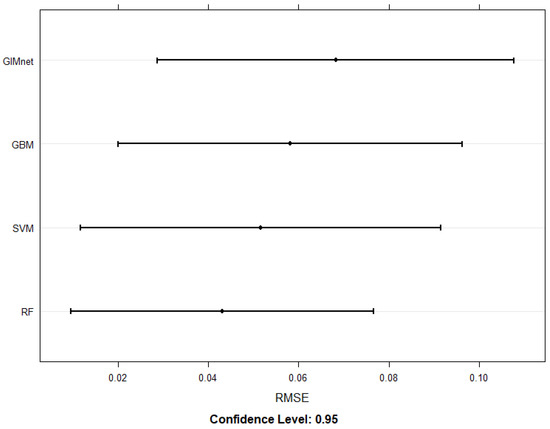
Figure 5.
A comparison of RMSE confidence intervals for the different models. Lower is better. Again, random forest shows the best results.

Table 1.
Mean absolute error resampling confidence quantiles comparison between candidate models. Lower is better. RF has the edge over the other candidate models.

Table 2.
Root mean square error resampling confidence quantiles for different candidate models. Lower is better. Of the chosen models, random forest shows the best results.

Table 3.
R-squared confidence quantiles for different candidate models. Higher is better. Again, random forest shows the best results.
3.4. Model Building
The model choice of a random forest from the options above is clear given the results outlined in Section 3.3. Furthermore, it offers us the opportunity to use the fast implementation [18] of a quantile regression forest approach to even better control the level of conservatism of our final estimation. This is especially important as in quality control applications, experts need to check the results and possibly choose a confidence level that both manufacturer and customer agree on. In other words, quantile regression forests allow for fitting an ensemble model to the data and then allow fine-tuning of the confidence levels to include expert opinions. Fitting a quantile regression forest is implemented in the R package ranger via including the parameters quantreg = TRUE and keep.inbag = TRUE to the model fitting function. The hyper-parameters for the best fitting model were determined individually for both upper and lower test limits using 10-fold cross validation. The results for both limits agree on the optimal hyper-parameters: mtry = 770, min.node.size = 5 and splitrule = extratrees. More information can be found in Figure 6.
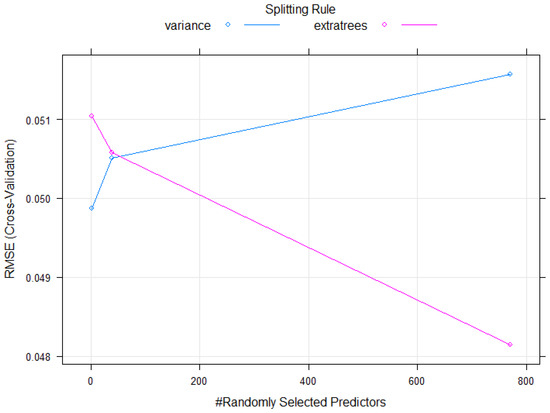
Figure 6.
Plot of cross-validation results with varying parameters. Lower is better. The extratrees splitrule wins out with increasing number of predictors.
3.5. Random Forests
Random forests were first introduced by Breitman [17] based on a previous work by Ho [19]. Rabdin forests work as an ensemble method of decision tree models achieved via bagging or bootstrapping of the results of individual decision trees. This works by repeatedly sampling (B times, with replacement) from the training data, fitting decision trees to the samples (with predictions ) and averaging the results of predictions on unseen data :
Random forests are widely used in a variety of industrial applications. As an extension to the classical regression random forest, quantile regression random forests were developed [20]. They have the additional benefit of allowing for a wider range of desired uncertainty and quantification of that uncertainty in their prediction. The principal difference between classical random forests and quantile regression forests is that instead of only keeping the information of the mean of all observations in each node, the quantile regression forests keep the value of all observations in that node and assess the conditional distribution based on this additional information [20]. For a good account on Random Forest methodology and its use in prediction tasks, we refer to [21].
4. Results
4.1. Model Evaluation
The results of the goodness-of-fit values for the quantile regression forest can be found in Table 4.

Table 4.
Goodness-of-fit measures for best fit of median of quantile regression forest.
All in all, the quantile model with the best chosen hyper-parameters also outperforms the comparison models. Furthermore, the quantile approach gives the engineer expert a further hyper-parameter to tune to make statistically founded decisions about setting optimal limits. The further introduction of the quantile parameter also may help tune the model even better to more closely resemble the statistically calculated limits. This is helpful as the machine learning model typically has a regularizing function, i.e., it does not predict the extreme values with the same extremity as the statistical model. If the expert agrees that the statistical calculation is overestimating the risk, the machine learning model proposal may be chosen. Otherwise, the expert may tune the quantile parameter to obtain a more conservative estimation that remains consistent with the rest of the parameter estimations.
4.2. Statistical Findings
To demonstrate the effect of choice of quantile for the quantile regression forest, we plot the RSME of the model versus the chosen quantile output of the model in Figure 7 and Figure 8. It can be seen that in both cases of upper and lower test limit prediction, the model has a less conservative output than the statistical model. In both cases, choosing to pick a different quantile in the corresponding direction (lower for upper test limits and upwards for lower test limits), leads to the random forest regression.
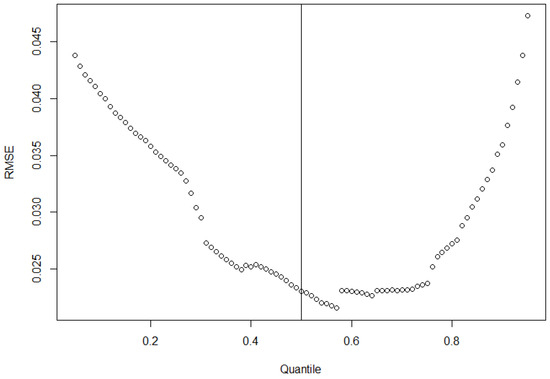
Figure 7.
Quantile forest regression predictions of lower test limit RMSE vs. quantiles. Lower is better. Some improvement with better quantile choice is possible. The black line denotes the 0.5-quantile. Dots are prediction results.
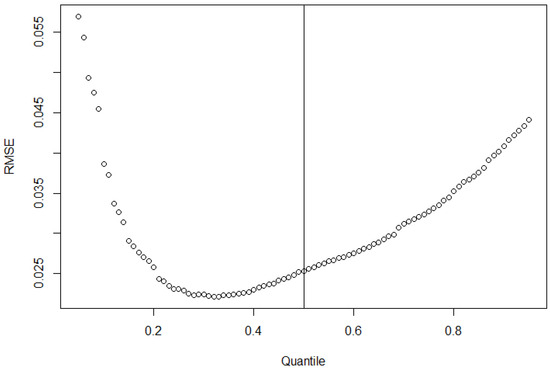
Figure 8.
Quantile forest regression predictions of upper test limit RMSE vs. quantiles. Lower is better. The median prediction can again be improved via smart quantile choice. The black line denotes the 0.5-quantile. Dots are prediction results.
It is apparent that the proposed prediction is not the best fitting to the real data in our case. The optimal value for RSME is only reached at quantile . This means that the ML model has a tendency to perform less conservative as a default than the statistical calculation. To better compare the results of the different quantile predictions, we have plotted the predictions for both the statistical model and quantile regression forest in Figure 9 and Figure 10. We see that the shape of the distribution is similar, with further quantile predictions being more conservative on average and lesser quantiles leading to smaller lower test limits. In the case of our real data, the best fitting results to the statistical test limits are a quantile of for upper test limits and for lower test limits. The predicted 0.05–0.95 quantiles and 0.1–0.9 quantiles, together with the actual values from the validation set in black, can be found in Figure 11 and Figure 12.
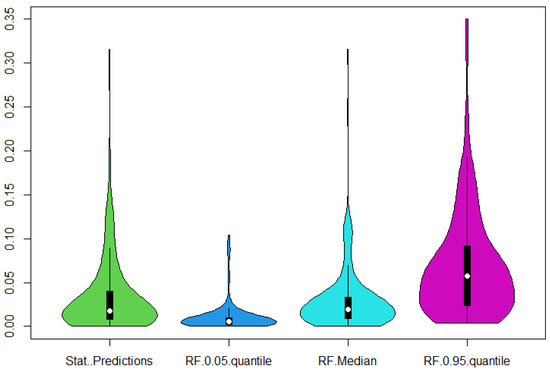
Figure 9.
Violin plots of the calculated statistical lower test limits (Stat. Predictions) and the quantiles of the random forest regression. Higher means more conservative, and closer to the statistical predictions is better. Visually, slightly above the median seems to capture the predictions best.
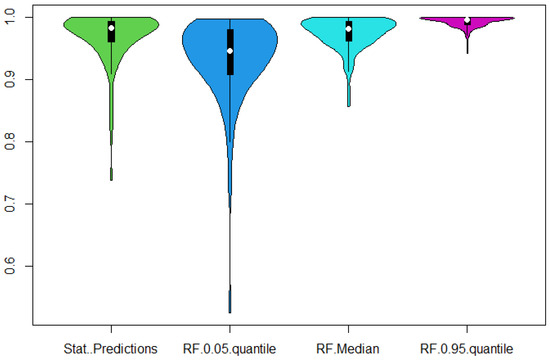
Figure 10.
Violin plots of the calculated statistical upper test limits (Stat. Predictions) and the quantiles of the random forest regression. Lower means more conservative, and closer to the statistical predictions is better. Visually, a quantile slightly below the median should capture the predictions best.
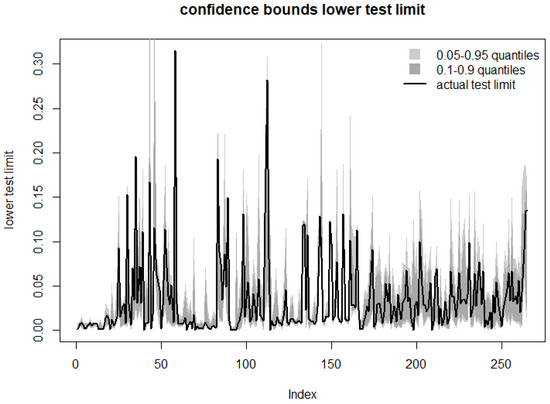
Figure 11.
Visualizing regularization: quantile predictions of lower test limit vs. actual statistical predictions on the validation set. The confidence bound tends to overlap the calculated limit.
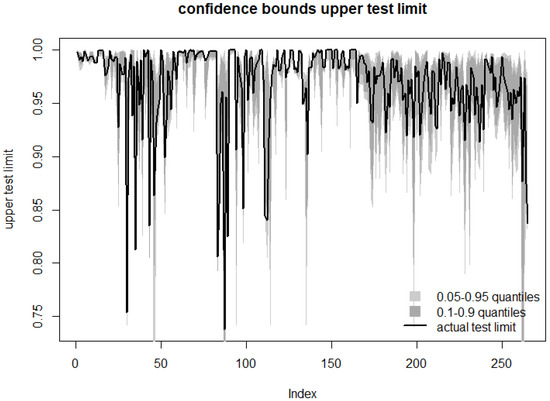
Figure 12.
Visualizing regularization: Quantile predictions of upper test limit vs. actual statistical predictions on validation set. The confidence bound tends to overlap the calculated limit.
The goodness-of-fit measures for the models with the best quantile hyper-parameter, chosen as a minimum of the sum of root mean squared error and mean absolute error, can be found in Table 5. In both cases, making the model deliberately slightly more conservative finds more agreement with the statistical model used as training data. The results of the mean values of the test limits can be found in Table 6. In both the case of upper and lower limits, the results from the random forest suggest a less conservative prediction than the original statistical one. The best result from the quantile regression forest was chosen as the optimal quantile parameter minimizing both MAE and RSME for each model separately.
where is the prediction error with regard to the statistical test limits. For lower limits, in our data set, the optimal quantile to replicate the statistical test limits was . For upper limits, .

Table 5.
Goodness-of-fit measures for best fit of best quantile parameter in quantile regression forest. The results outperform pure median predictions in Table 4.

Table 6.
Mean of predicted standardized test limits and validation set true mean for upper and lower test limits. Closer to the edges of the interval means less conservative. On average, the proposed model errs on the side of conservative predictions.
4.3. Computation Time
On a 13th Gen Intel(R) Core(TM) i5-1345U with 16 GB RAM, the model training of the best random forest model takes s. Hyper-parameter tuning to obtain the best parameters for the model took min. The data-set used was the anonymized data set with 1057 parameters measured in 110 devices each. As a comparison, the calculation of statistical limits for ground truth took min on the same data set
5. Discussion
5.1. Interpretation of Results
It has been shown that quantile random forest regression performs better than other candidate models when trained on statistically calculated limits for lifetime drift in semiconductor devices. On average, the results from the random forest regression are less conservative, i.e., less prone to test limits very far from the original specified limits. This can be interpreted as a kind of regularizing of the original statistical problem away from extreme solutions. Furthermore, the quantile parameter can be chosen in a way that the results are even closer to the statistical test limits on average. This allows experts to have a robust way of proposing or adjusting test limits for cases where the typical statistical calculation leads to unrealistically extreme results. One possible decision process for an expert-in-the-loop system is given in Figure A1.
5.2. Model Limitations and Assumptions
As a purely data-driven model, the proposed model can be used to predict theoretically any type of electrical parameter lifetime drift, e.g., threshold voltage in MOSFETs. However, it is trained on a subset of the results from mathematically calculated limits. This means that it is assumed that training data behavior is representative of the data to be predicted. If the underlying production process changes, or a different type of device is to be investigated, a retraining of the data has to be performed.
For a single product, the training time of a quantile forest regression model, as well as the mathematical calculation of true underlying guard bands, is feasible to use in practice, as shown in Section 4.3.
In quality control applications, the usage of machine learning to obtain results is often a topic of contention. As the models learn only from past data and make generally no assumptions on quality targets or probabilities, the question of how interpretable the results are remains. In this case, the machine learning algorithm is used to train on statistically calculated limits, which may be prone to some instabilities in order to regularize the results and give experts an informed option to adjust test limits if needed. For this to work, the training data have to be representative of the data to predict. Furthermore, if the test data exhibit too many outliers or unrealistic results, the model itself will also learn these results as a baseline. This may lead to a skew in the resulting proposed limits. Furthermore, the model will, on average, predict the electrical parameter data skewed to the average of the results of data in the past. Therefore, real outliers in data that may indicate true degradation may be under-estimated. This is why it is important to use the machine learning approach as an additional tool in the arsenal of an expert but not as the sole crutch in the case of guaranteeing quality.
6. Conclusions
6.1. Summary of Key Findings
In the topic of setting test limits for lifetime drift behavior, often the target of very low probabilities (e.g., 1 ppm) leads to problems in verifying models after building them. This is due to the fact that the samples that are stressed are too few to empirically verify the model. Therefore, all models for lifetime drift have to make assumptions of some kind. The non-deterministic fitting of hyper-parameters in statistical models may lead to instability in solutions for very similar data sets. We propose a method of an expert-in-the loop system where training a quantile regression forest on the statistical results may lead to both a regularization behavior and a possibility of modeling cases where the current methods may become stuck in local optima or have numerical issues. The quantile regression forest allows for fast, robust results that may then be adjusted by the expert by tuning the quantile parameter to be more or less like the statistical original results, depending on the plausibility of the results according to expert opinion and physical properties of the process.
6.2. Future Work
In future work, more refined investigations of the topic are possible. One promising avenue is the comparison of several state-of-the-art quantile regression forest implementations, such as LightGBM 4.3.0 [22] or catboost 1.2.3 [23]. Furthermore, currently, only one sample at one temperature is being considered. In the future, the outcome of adding the temperature parameter of the stress test data and predicting from one to up to three samples that are typically taken may be considered. Last but not least, the performance may be improved by smart feature engineering such as including additional features or structuring the input data in some way that makes it easier for the random forest model to take meaningful decisions. Furthermore, the issue of performance may be investigated separately for different implementations and in comparison to classical statistical methods. Depending on the outcome, a mixture of using the statistical model to generate enough training data and then fitting the random forest model on the rest of the data may be considered to optimize both accuracy and total calculation time.
Author Contributions
Conceptualization, L.S.; methodology, L.S.; validation, L.S.; formal analysis, L.S.; investigation, L.S.; resources, L.S.; data curation, L.S.; writing—original draft preparation, L.S.; writing—review and editing, L.S. and J.P.; visualization, L.S.; supervision, J.P.; project administration, L.S.; funding acquisition, L.S. All authors have read and agreed to the published version of the manuscript.
Funding
The project AIMS5.0 is supported by the Chips Joint Undertaking and its members, including the top-up funding by National Funding Authorities from involved countries under grant agreement no. 101112089.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets presented in this article are not readily available because of confidentiality agreements with the industry partner. Requests to access the datasets should be directed to lukas.sommeregger@infineon.com.
Conflicts of Interest
Lukas Sommeregger has produced this research while employed at Infineon Technologies Austria AG.
Abbreviations
The following abbreviations are used in this manuscript:
| quantile parameter. | |
| optimal quantile parameter. | |
| B | number of bagging iterations. |
| random forest prediction on unseen data. | |
| GB | gradient Boosting. |
| GLM | generalized linear Model. |
| LSL | lower specification limit. |
| LTL | lower test limit. |
| MAE | mean absolute error. |
| ppm | parts per million. |
| RMSE | root mean square error. |
| RF | random forest algorithm. |
| SVM | support vector machine. |
| USL | upper specification limit. |
| UTL | upper test limit. |
| VGT | comparison parts. |
Appendix A. Flowchart Decision Process
A possible expert-in-the-loop decision process using both statistical calculations of limits and the proposed ML results utilizing quantile forest regression can be found in Figure A1.
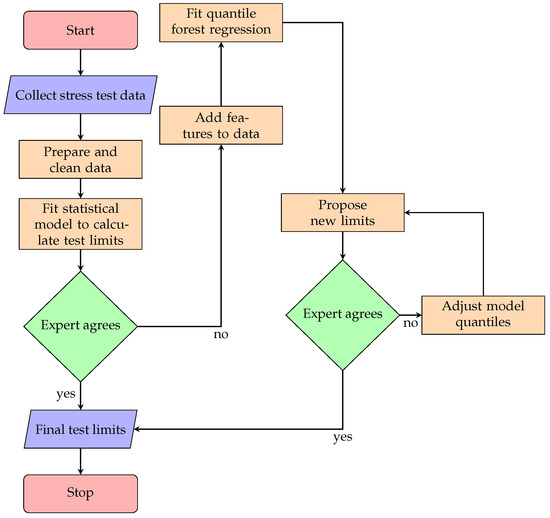
Figure A1.
A flowchart showing a possible expert-in-the-loop decision process for automatically generating and proposing test limits.
Appendix B. Additional Data
Figures for model comparison for the target variable of upper test limits can be found in Figure A2. The results agree with the findings in Figure 4 and are given for completeness’ sake.
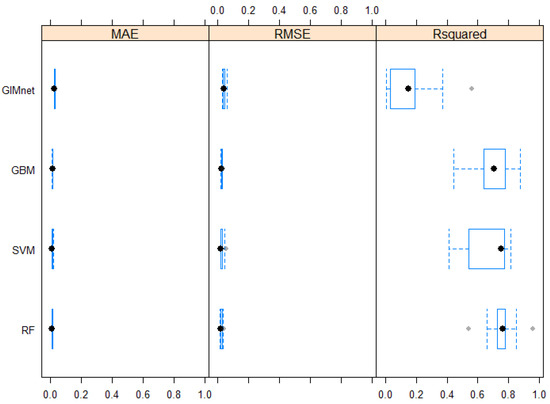
Figure A2.
A comparison of MAE, RMSE and for the different candidate models. Lower is better for MAE and RMSE; higher is better for . Standard boxplot with black dot for median and blue box for quartiles.
References
- Grubbs, F.; Coon, H. On setting test limits relative to specification limits. Ind. Qual. Control 1954, 10, 15–20. [Google Scholar]
- Mottonen, M.; Harkonen, J.; Haapasalo, H.; Kess, P. Manufacturing Process Capability and Specification Limits. Open Ind. Manuf. Eng. J. 2008, 1, 29–36. [Google Scholar] [CrossRef]
- Chou, Y.; Chen, K. Determination of optimal guardbands. Qual. Technol. Quant. Manag. 2005, 2, 65–75. [Google Scholar] [CrossRef]
- Jeong, K.; Kahng, A.; Samadi, K. Impact of guardbanding reduction on design outcomes: A quantitative approach. IEEE Trans. Semicond. Manuf. 2009, 22, 552–565. [Google Scholar] [CrossRef]
- Healy, S.; Wallace, M.; Murphy, E. Mathematical Modelling of Test Limits and Guardbands. Qual. Reliab. Eng. Int. 2009, 25, 717–730. [Google Scholar] [CrossRef]
- Hofer, V.; Leitner, J.; Lewitschnig, H.; Nowak, T. Determination of tolerance limits for the reliability of semiconductor devices using longitudinal data. Qual. Reliab. Eng. Int. 2017, 33, 2673–2683. [Google Scholar] [CrossRef]
- Sommeregger, L. A Piecewise Linear Stochastic Drift Model for Guard Banding of Electrical Parameters in Semiconductor Devices. Master’s Thesis, AAU Klagenfurt, Klagenfurt, Austria, 2019. Unpublished. [Google Scholar]
- Hofer, V.; Lewitschnig, H.; Nowak, T. Spline-Based Drift Analysis for the Reliability of Semiconductor Devices. Adv. Theory Simul. 2021, 4, 2100092. [Google Scholar] [CrossRef]
- Lewitschnig, H.; Sommeregger, L. Quality Control of Lifetime Drift Effects. Microelectron. Reliab. 2022, 139, 114776. [Google Scholar] [CrossRef]
- AEC Council. AEC Failure Mechanism Based Stress Test Qualification for Integrated Circuits—Q100 Rev. H; AEC Council: Brussels, Belgium, 2014. [Google Scholar]
- AEC Council. AEC Failure Mechanism Based Stress Test Qualification for Discrete Semiconductors in Automotive Applications—Q101 Rev. D; AEC Council: Brussels, Belgium, 2013. [Google Scholar]
- JEDEC. JESD22-A108F, Temperature, Bias, and Operating Life; JEDEC: Arlington County, VA, USA, 2017. [Google Scholar]
- Celisse, A. Optimal cross-validation in density estimation with the L²-loss. Ann. Stat. 2014, 42, 1879–1910. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. Available online: https://www.jstatsoft.org/index.php/jss/article/view/v033i01 (accessed on 13 July 2024). [CrossRef] [PubMed]
- Friedman, J. Stochastic Gradient Boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Hearst, M.; Dumais, S.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wright, M.; Ziegler, A. ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. Available online: https://www.jstatsoft.org/index.php/jss/article/view/v077i01 (accessed on 13 July 2024). [CrossRef]
- Ho, T. Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995. [Google Scholar]
- Meinshausen, N. Quantile Regression Forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. Adv. Neural Inf. Process. Syst. 2017, 30. Available online: https://papers.nips.cc/paper_files/paper/2017/hash/6449f44a102fde848669bdd9eb6b76fa-Abstract.html (accessed on 13 July 2024).
- Hancock, J.; Khoshgoftaar, T. CatBoost for big data: An interdisciplinary review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).