Abstract
Driven by the growing interest of the scientific community and the proliferation of research in this field, cranial implants have seen significant advancements in recent years regarding design techniques, structural optimisation, appropriate material selection and fixation system method. Custom implants not only enhance aesthetics and functionality, but are also crucial for achieving proper biological integration and optimal blood irrigation, critical aspects in bone regeneration and tissue health. This research aims to optimize the properties of implants designed from triply periodic minimal surface structures. The gyroid architecture is employed for its balance between mechanical and biological properties. Experimental samples were designed varying three parameters of the surface model: cell size, isovalue and shape factor. Computational simulation tools were used for determining the relationship between those parameters and the response variables: the surface area, permeability, porosity and Young modulus. These tools include computer aided design, finite element method and computational fluid dynamics. With the simulated values, the corresponding regression models were fitted. Using the NSGA-II, a multi-objective optimisation was carried out, finding the Pareto set which includes surface area and permeability as targets, and fulfil the constraints related with the porosity and Young modulus. From these non-dominated solutions, the most convenient for a given application was chosen, and an optimal implant was designed, from a patient computed tomography scan. An implant prototype was additively manufactured for validating the proposed approach.
1. Introduction and Brief Survey of the State of the Art
Cranioplasty is the surgical repair of damaged cranial bone resulting from congenital defects such as complex craniosynostosis, tumours, traumas caused by previous surgeries, infections, or fractures resulting from vehicular, sports, or everyday accidents [1]. Its primary goal is to restore the protective function of the neurocranium, and secondarily, to improve craniofacial aesthetics. A cranial implant or prosthesis is the biomedical device used to mend the protective function of the affected portions of the skull [2].
The ideal material for the creation of cranial implants for cranioplasty should be: radiolucent, resistant to infections and biomechanical processes, malleable to adapt to defects with a complete closure, non-conductive of heat or cold, inexpensive, and easy to apply [3]. Realistically, there is currently no single material that meets all these requirements and is always applicable, it must be chosen taking into account the patient’s age, the complexity of the defect, the specialist’s judgement and the main reason for performing the cranioplasty [4].
Currently, the most commonly used materials for the construction of cranial implants are metals, polymers and ceramics. Particularly popular are the titanium alloy Ti6Al4V, and the polymers Polyether-ether-ketone (PEEK) and Polymethylmethacrylate (PMMA). Ti6Al4V is widely used to make customised cranial prosthesis [5]. However Kim2023 [6] reported that alloy-based cranial implants can provoke an increase in thermal conduction inside the cranial defect zone, because of their higher density, making them less suitable in cases with direct heat exposure. PEEK, a semi-crystalline polymer that is radiotransparent and chemically inert, offers greater strength, rigidity, and durability compared to other alloplastic materials. It has been used more recently in cranioplasty showing several advantages due to its high strength and toughness and its compatibility with the skull [7]. Current trends are directed to optimize the process of fabrication using PEEK, as is the case with the study presented by Smith2023 [8], which presents a series of configurations for improving the robustness and aesthetics, over other conventional approaches.
It has been also reported that compared to titanium alloys, PEEK implants presents lower rates of complications and failures [9]. One of the main disadvantages of using PEEK lies in its high cost of acquisition and manufacturing [10,11]. This has led to the use of PMMA as a cheaper alternative, given that the material cost is significantly less expensive and the process of manufacture much easier [12]. PMMA has less durability, strength and biocompatibility when compared to PEEK [13]. On the other hand, Moncayo2023 [14] compared the mechanical response of cranial implants fabricated with both PEEK and PMMA, and showing that there were no noticeable discrepancies between personalised implants made from PMMA and PEEK, concerning the mechanical response under a load of 8 kN, while the Von Misses stress distribution performs significantly different for both materials, with PEEK implants presenting better results. Furthermore, PMMA implants exhibits higher infection and complications rate compared to PEEK ones [9]. As currently stands, PEEK is closer to being the gold standard material for the construction of personalised cranial implants.
When designing a customised cranial implant adjusted to the specifics requirements of the patients, computer aided design (CAD) techniques and methodologies give optimal results [15]. Common approaches consist in using commercial software such as Mimics, Magics and SolidWorks, with highly specialised features for the task, or employing classic design procedures such as the mirroring technique. While yielding particularly good results, these methods are usually time-consuming and require highly skilled operators, which represents a real disadvantage still to overcome [16]. Directed efforts towards automation have been made. In [17], the authors propose an automated design methodology for the construction of a customised cranial implant using image processing and open-source python libraries to obtain the implant in stereolithographic (STL) format from DICOM image data. Pimentel and co-authors introduce an automated approach for reconstructing damaged regions in the skull using a 3D statistical shape model and a 2D generative adversarial network trained unsupervised on healthy data [18]. With the rise and popularity of artificial intelligence, further advances are expected in this field [19,20,21].
Studies about optimisation and design considerations have also flourished, with focus on enhancing the mechanical features of the prosthesis and the aesthetics of the repaired skull [8,22,23]. Research by [24] explores extensively the optimal configurations for fixation mechanisms and the adequate separation between these points, suggesting four to five fixations, independently to size of the defect, with symmetrical orientation of the fixation screws where feasible. Another important line of development is to redesign implants based on natural analogies. Works such as [25] presented two implant variants for the studied case, based on dissimilar scaffold architecture that showed mechanical response adequate for implantation. Sharma2021 [26] They propose a workflow to design a cranial prosthesis that moulds to the specific characteristics of the patient, with a macrostructure of interconnected struts that mimics trabecular bone based on the Voronoi diagram, resulting in a lightweight titanium prosthesis with a good fit to the skull. Sivakumar2023 [27] suggest a biomimetic cranial prosthesis made of PMMA and optimised by incorporating a square-type porous lattice structure, considered a suitable for the development of cranial implants reducing the weight without compromising quality. Lattice structures are a type of architectural framework composed of repeating units or cells, typically arranged in a periodic or non-periodic pattern, characterised by their lightweight and high strength-to-weight ratios [28]. Furthermore, they can replicate the porous nature of natural bone, which is crucial for facilitating cell attachment, proliferation, and differentiation [29]. It could be considered that further developments can be achieved following this line of research.
Among lattice architectures, the so-called Triply Periodic Minimal Surfaces (TPMS) are intricate structures widely utilised within scaffold design to ensure optimal porosity and interconnectivity [30]. These surfaces, known for their topological complexity, have attracted considerable attention due to their ability to be entirely defined through mathematical expressions. This mathematical foundation enables precise control over design parameters such as porosity and unit cell size, essential for adapting the scaffold properties to the desired medical applications [31,32]. TPMS exhibit exceptionally smooth surfaces devoid of sharp edges or peaks, facilitating fluid flow without causing abrasion or fluid build-up. Moreover, their high degree of interconnectivity enhances their effectiveness as supportive frameworks in tissue engineering and medical implants, highlighting their versatility and importance in modern biomedical research and practice [33].
Additionally, gyroid TPMS have emerged as highly promising architectures for bone tissue engineering because of their unique structural characteristics like surface area and interconnected porosity [34]. When compared against other popular TPMS based structures such as the Diamond and Primitive, gyroid based scaffolds showed the better compromise between higher bone ingrowth and bone-to-implant contact in vivo, and mechanical strength, as shown by [32]. Numerous researches have also been conducting exploring the design parameters and its influences on mechanical properties of gyroid based scaffolds [35,36,37].
Surface area directly influences several key aspects of bone regeneration, being a key property in porous scaffold architectures. A larger surface area enhances cell attachment and proliferation by providing more sites for cell adhesion, which is vital for the initial stages of bone formation [38]. It also enhances protein adsorption, nutrient and waste exchange [39] and enables better mechanical interlocking with native bone tissue, enhancing the scaffold’s stability and integration [40]. The surface topography of a scaffold can influence stem cell differentiation into osteoblasts, with a larger surface area promoting osteogenic differentiation [41]. Highly porous structures, often associated with high surface areas, provide pathways for vascularisation and bone ingrowth [42].
Another critical property of porous scaffolds for bone applications is their permeability, which quantitatively measures a porous medium’s ability to allow fluid flow [43]. Permeability is affected by porosity, pore size, orientation, tortuosity, and interconnectivity [44,45,46]. It is essential for describing tissue growth and the diffusion of nutrients and oxygen through scaffold pores. While highly dependent on the type of bone, generally high permeability values provide more desirable conditions for in vivo bone formation, while inadequate values can lead to the formation of cartilaginous tissue instead of bone [47].
Numerical simulations, including methods such as Finite Element Method (FEM) and Computational Fluid Dynamics (CFD), are critical tools in evaluating and optimizing the properties of scaffolds for bone regeneration. FEM allows researchers to model the mechanical behaviour of scaffolds under various loading conditions, providing insights into stress distribution, deformation, and potential failure points, which are essential for ensuring that the scaffold can withstand physiological loads while promoting proper load transfer to the regenerating bone [48]. FEM is also widely used to predict the mechanical response of the cranial implant [14,49]. CFD, enables the analysis of fluid flow within the scaffold’s porous structure, to assess the permeability of the medium [50].
This study focuses on the optimisation of design of TMPS scaffolds for cranial implants, using computer simulation techniques for modelling the relationship between decision variables (TMPS structure parameters) and optimisation objectives (surface area and permeability) and constraints (porosity and elasticity). The optimal scaffold configuration was used to construct, then, a customised cranial implant prototype.
2. Materials and Methods
2.1. Experimental Design
The design method used for creating the samples was the parametric modelling, given that, of all the existing methodologies to construct TPMS-based structures, this one allows for greater control over the scaffold properties. These parametric equations are obtained from nodal approximations to the Fourier series expansion of minimal surfaces [51]. The following expression shows the modified gyroid equation used for our experimental setup:
where c represents the isovalue, a constant for defining and manipulating specific shape and characteristics of TPMS structures. When , the obtained structure is divided into regions of equal volumes. As the value of c increases or decreases, the thickness of the structure changes, therefore being an important parameter for the control of the porosity of the scaffolds [52].
On the other hand, gives the size of the unit cell and was a size factor, introduced for changing the ratio of the cell size on the z-axis with respect to the other two axes.
Based on this equation, its three parameters (i.e., the isovalue, c; the cell size, ; and the size factor, ) were chosen as decision variables of the considered optimisation. In order to carry out the simulations required for modelling how the scaffold properties depend on these variables, the following experimental levels were considered for each of them (see Table 1).

Table 1.
Experimental levels for the decision variables.
A Box-Behnken experimental design was used for defining the level of each variable, for the simulations. The Box-Bahnken was chosen as it is particularly efficient because it requires fewer experiments than other alternatives (like the full factorial design). Box-Bahnken also avoids extreme conditions, focusing instead on a more central, balanced experimental region. Table 2 shows the values of the decision variables at each of the 15 experimental points.

Table 2.
Box-Behnken experimental design.
The 15 experimental samples were constructed using an in-house MATLAB script and converted to STL format with the STLWRITE function. Figure 1 shows some of the obtained models when changing the magnitude of the decision variables.
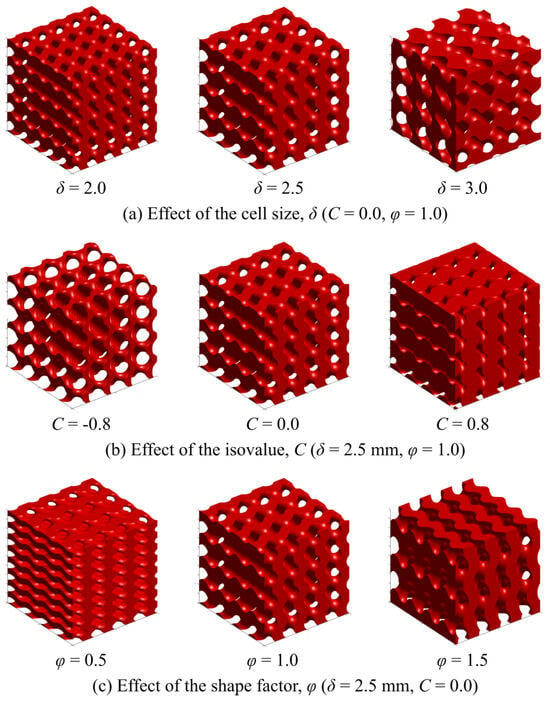
Figure 1.
Constructed scaffolds keeping a constant block size.
2.2. Computing the Porosity
One of the studied scaffold properties is the porosity, which plays an important role when designing cranial implants, because it facilitates bone ingrowth and the formation of new tissues within the scaffold structure. Porosity, also, ensures that the scaffold does not act as a barrier to the infiltration of cells and growth factors, which are crucial for the successful integration of the implant with the host tissue.
In this study, the porosity, P, was computed from the previously obtained geometrical models of the scaffolds, through the expression:
where is the volume of the solid TPMS structure and is the total volume of the prism (i.e., solid volume plus void volume). Both volumes were obtained by using the CAD software Meshmixer v3.5, through its stability analysis tool.
2.3. Computing the Surface Area
The surface area, A, is another important property of the scaffolds used for cranial implants, because it is beneficial for enhancing cell attachment and proliferation. This property provides more sites for osseous cells to attach to, promoting osteointegration and accelerating the healing process, ensuring the stability and functionality of the implant.
The surface area of each scaffold specimen was also determined from its 3d geometric model, by using the stability analysis tool of Meshmixer v3.5.
2.4. Computing the Young Modulus
The elasticity also plays a key role in cranial implants due to the need of ensuring the scaffold mimics the mechanical properties of natural bone. This compatibility minimizes stress shielding and promotes the integration and longevity of the implant within the cranial structure.
For computing the elasticity (Young) modulus, a Finite Element-based simulation was executed. For this purpose, the STL files were transformed into solid models, using FreeCAD v20.2. To carry out the analysis, two plates were modelled at both ends (top and bottom). With this configuration, they were exported in STEP format and imported into the static structural analysis module of ANSYS 2022R1.
The same boundary conditions were applied for all finite element models, as shown in Figure 2. The plates were scoped as rigid bodies, while the TPMS structure was defined as flexible. A force of 100 N was applied on the upper plate downward (i.e., in the negative direction of the z-axis), while the lower plate was constrained to keep it fixed. Frictional contact connections between the plates and the samples were established with a friction coefficient of 0.1. This value was selected because it corresponds to the range reported for the coefficient of friction of PEEK under lubrication, which is done to decrease the effect of the forces in the transverse direction [53,54,55]. The scaffolds were meshed with tetrahedral elements with a minimum element size of 0.2 mm, while the two plates were meshed with hexahedral elements.
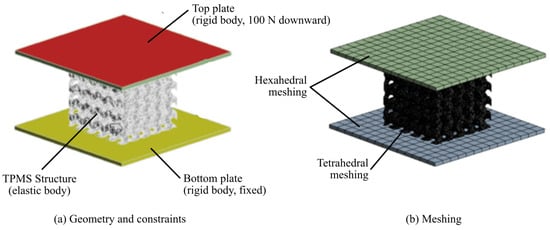
Figure 2.
Finite element analysis setup.
The scaffolds were assigned PEEK as material. As discussed previously, selecting PEEK for a 3D printed cranial implant is ideal due to its biocompatibility and bone-like mechanical properties, ensuring safe and durable integration. The radiolucency of PEEK allows for clear postoperative monitoring without interference in medical imaging. In addition, 3D printing with PEEK enables the creation of customised implants with high precision and detail, perfectly fitting the patient’s anatomy, while fast and economical production optimises time and costs, ensuring an effective and efficient solution for cranial reconstruction [8,56]. The parameters for the material selected are shown in Table 3, which are based on VICTREX PEEK 151G grade filament.

Table 3.
Properties of the TPMS structure material.
With the height deformation, , obtained after the finite element simulation, the Young modulus is computed by using the equation:
where F is applied force (, in this study), and V is the volume of the scaffold specimen, equal to the product of its dimensions: length, L; width, B; and height, H:
2.5. Computing the Permeability
Another important property of the scaffolds is the permeability, which facilitates the transport of nutrients and waste, supporting cell growth and tissue regeneration. High permeability ensures effective vascularisation, which is critical for healing and integrating the implant with surrounding biological tissues.
For the calculation of permeability, a laminar model of computational fluid dynamics (CFD) was designed and solved using the ANSYS Fluent module. The value of residual sensitivity criterion was set at for an easier convergence. Water was chosen as the fluid for the analysis, with density, , and dynamic viscosity, . The proposed model corresponds to an incompressible fluid with constant density and viscosity, and steady flow that obeys the Navier-Stokes equations:
where is the fluid density, is the fluid velocity, t is the time, is the dynamic viscosity, p is the pressure and represents the action of external forces (in this study, ). It should be remarked that this approach is appropriate to mimic the general behaviour of human body fluids [57].
For each design, the fluid domain was obtained by subtracting the 3D scaffold structure from a rectangular prism. A virtual volume was modelled at the top to extend the inlet; previous studies have shown how this helps to improve convergence and allows the fluid to fully develop [58,59]. Velocity at the inlet was set as , while the pressure at the outlet was assumed to be . No slip boundary condition was applied to the walls [60]. Figure 3 shows the final setup.
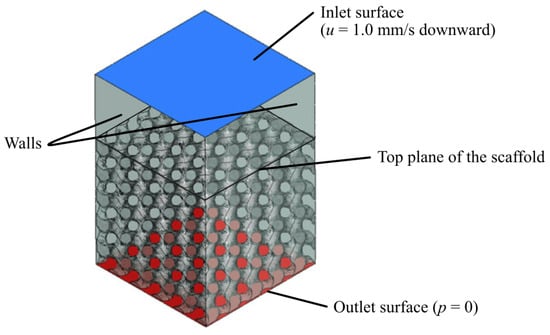
Figure 3.
CFD analysis setup.
Given the height of the scaffold, H, the pressure drop, , required to determine the permeability was calculated by subtracting the pressure at the top plane of the scaffold from the pressure at the outlet. In order to simplify the simulation and the necessary computational requirements, the entire domain of the model was set as the fluid domain. All models were meshed with tetrahedral 0.2 mm-sized elements.
With the values of volumetric flow, Q; and pressure drop, , obtained from the CFD analysis, Darcy’s Law equation was used for the permeability calculation [61]:
where H is the height of the scaffold and A is its cross-section area.
2.6. Modelling
For modelling the relationship between the decision variables (i.e., cell size, isovalue and size factor) and the scaffold properties (i.e., porosity, surface area, Young modulus and permeability), linear regression models were fitted. When proper, some transformations, such as logarithms or linear combinations, were applied to the decision variables.
For all the obtained models, the goodness of fit was evaluated by computing the corresponding coefficient of determination. However, it cannot be assumed that a regression showing a high value of the coefficient of determination is implicitly a reliable model. Issues, such as the distribution of the residuals, the statistical significance of the relationship between the variables and the statistical significance of the model coefficients, should be addresses to ensure the quality and usefulness of the models.
2.7. Optimisation
After the regression models were fitted, a multi-objetive optimisation was carried out for obtaining the best scaffold designs. As it was previously stated, the decision variables were the TPMS parameters: cell size, ; isovalue, c; and size factor, . All of them should be constrained to their respective experimental intervals:
The more relevant properties for the cranial implants were selected as optimisation targets. Maximising the surface area:
was selected as the first objective, in order to enhance the cell attachment and proliferation. The second objective selected was the maximisation of permeability:
for ensuring effective vascularisation.
In addition to the objectives, constraints were considered in the optimisation problem. Firstly, it was established that the porosity had to be in the interval from 60 to 80%:
to ensure bone formation and integration with the scaffold. This is because these conditions allow for better vascularisation and nutrient supply to the cells involved in bone regeneration [52]. Scaffolds with this range of porosity facilitate bone ingrowth. This is critical for the long-term success of cranial implants, ensuring they remain integrated with the host bone and maintain their structural integrity over time [62].
On the other hand, the Young modulus of the scaffold had to be in the range of the replaced bone, i.e., from 0.5 to 5.0 GPa:
In order to homogenise the values of the constraints, Equations (13) and (14) were rewritten as follows:
The total amount of unfeasibility, , is then computed by the expression:
As both optimisation objective are conflictive (i.e., improving one of them worsens the other one.), an a posteriori approach was used, where the non-dominated solutions, which form the so-called Pareto front, are obtained and, then, the most convenient solution is chosen, depending on the user’s preferences.
The Non-Dominated Sorting Genetic Algorithm II (NSGA-II) [63] was chosen as optimisation technique, due to its efficiency in multi-objective optimisation, offering a blend of non-dominated sorting techniques, crowding distance techniques for diversity preservation, and elitist techniques to maintain high-quality solutions across generations. It achieves fast convergence to Pareto-optimal solutions, making it suitable for a wide range of problems.
Table 4 shows the NSGA-II parameters that were set for solving the addressed problem.

Table 4.
NSGA-II parameters.
3. Results
3.1. Simulation Results
Porosity and surface area were numerically computed from the geometric model, as explained in Section 2.2 and Section 2.3. Their respective obtained values are shown in the second and third columns of Table 5. As can be seen, their values range from 22.73 to 79.45%, for the porosity, and from 1003.1 to 2570.0 , for the surface area.

Table 5.
Outcomes of the simulations.
On the other hand, the Young modulus was computed from the outcomes of the finite element-based simulations, as explained in Section 2.4. Figure 4 shows an example of the obtained deformation and stress profiles, for one of the scaffolds specimens. The values of Young modulus, computed from the simulated mechanical behaviour of the scaffold specimens, are shown in the fourth column of Table 5 and range from 0.038 to 2.357 GPa.
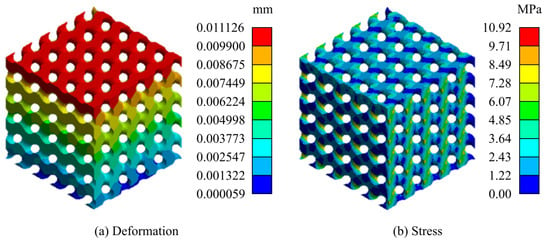
Figure 4.
Example of the deformation and stress profiles obtained by FEM-based simulation.
Finally, the permeability was computed, as explained in Section 2.5, from the pressure profile, obtained by CFD-based simulation (see Figure 5), by using the Darcy’s equation. The obtained values are shown in the fifth column of Table 5 and range from to .
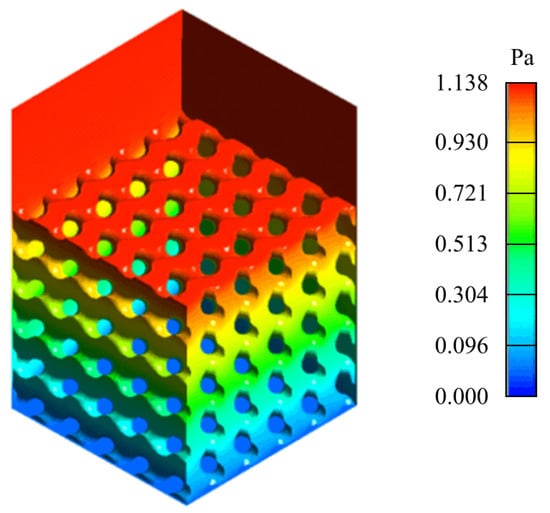
Figure 5.
Example of the pressure profiles obtained by CFD-based simulation.
The permeability values obtained are in the order of to which align with the results reported in the consulted scientific literature [58,60,64]. The scaffolds with the lower values of the isovalue constant were the ones that presented higher permeability values. It can be observed how cell size factor of 0.5 can impact negatively on the permeability results, while the opposite results in an increase of this property.
3.2. Regression Models
After applied the regression technique, as explained in Section 2.6, linear models were obtained for each studied dependent variable.
For the porosity, the model was
This model has a determination coefficient equal to and a standard error of the estimate of 0.6313. It should be remarked that only the C variable remains in the model as all the other independent variables were removed, through a backward stepwise regression, due to, after the t-Student test, they were no statistically significant. Figure 6a shows the graphical representation of the obtained model.
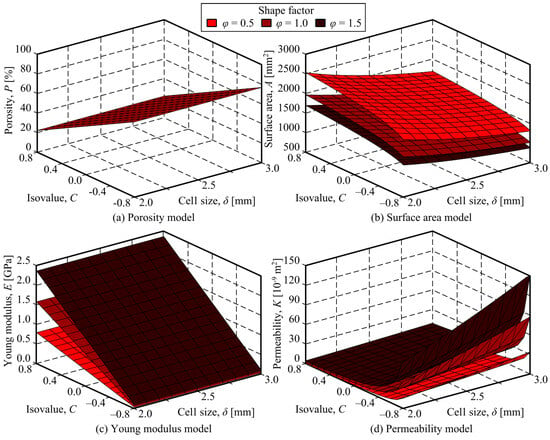
Figure 6.
Graphical representation of the regression models.
For the surface area, the model was obtained after applying a logarithmic transformation was applied to all variables, both independent and dependent. In the case of the isovalue, C, as part of the transformation, was increased by one unit, to make all its values positive. The model is given by the expression:
and has a determination coefficient of 94.6% and a standard error of the estimate equal to 0.06750. In this model, all the independent variables are significant. Consequently, they were kept into the model. Figure 6b shows the graphical representation of the computed model.
On the other hand, the model for the Young modulus was obtained by considering a second order interaction between the variables and applying a backward stepwise regression, for removing the non-significant variables. The obtained model has, then, the expression:
with a determination coefficient of 90.9% and standard error of the estimate 0.3546. Figure 6c shows the model.
Finally, the model of the permeability was fitted after a logarithmic transformation, obtaining the equation:
with a determination coefficient of 84.6% and a standard error of the estimate of 0.6254. All the variables are significant and, consequently, they were kept into the model. The model is depicted in Figure 6d.
In all these models there is a 99% confidence level-significant relationship between the variables, given from the ANOVA table.
Figure 6 shows that porosity mainly depends on the isovalue C, increasing linearly with its decrease, while cell size has a lesser influence. The Young’s modulus is strongly influenced by the isovalue C and the shape factor, which should be investigated further. Additionally, the change in the slope of the permeability curve is noteworthy. These variations should be considered when selecting printing parameters to ensure the highest precision and desired properties.
3.3. Optimisation Results
After the optimisation process, carried out as explained in Section 2.7, the corresponding Pareto front and set were obtained. The Pareto front (i.e., the values of the objective for the non-dominated solutions—see Figure 7a) is composed by two curves: A first segment going from point A to point B, and a second one, going from point C to point D. Nevertheless, for practical purposes, points B and C are close enough to be considered the same point.
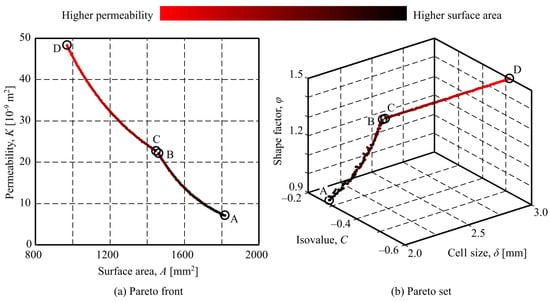
Figure 7.
Outcomes of the optimisation.
It should be noted that the Pareto portfolio values include only a part of the target ranges. In this sense, the optimal surface area ranges from 969 to 1817 , with their respective values as predicted by the model ranging from 875 to 2500 . With respect to the permeability, its optimal values range from to , while the corresponding model gives values from to .
On the other hand, the Pareto set (i.e, the values of the decision variables corresponding to the non-dominated solutions) is also composed by two segments, the first one, from point A to point B, included solutions with a constant cell size, , and isovalues decreasing from to , and values of shape factor increasing from to .
The second segment, from point C to point D, on the other hand, included solutions with constant isovalue, , and shape factor, , while the cell size increases from to . In can be noted that, while the optimal cell sizes ranges over its whole interval, to , the shape factor only ranges from to , and the isovales barely covers a small subinterval, from to .
A brief comparison of the results obtained with others reported in the literature reveals interesting aspects. Firstly, the proposed approach, due to its multi-objective character, presents greater flexibility, although its results present specific coincidences with other works that employ, for example, Taguchi’s method [27] or a biomimetic approach [65]. On the other hand, there are works where the multi-objective approach is also used [66], although considering only two objectives (stiffness and permeability), reaching a significant coincidence in the permeability values achieved (from to ), results that cover the entire range of values measured in the literature for the permeability of human trabecular bone [67].
4. Discussion
The first issue to be remarked when discussing the obtained results is that all the points shown in Figure 7 corresponds to solutions which are optimal in the wide sense that no other solution, in the feasible search space, can improve one of the objective without worsening the other one. Consequently, any of these points can be used for designing the optimal scaffold structure for a cranial implant. The finally chosen solution should depend on which goal (or goal combination) will be preferred by the decision-maker.
Under this point of view, there are three specially interesting points (see Table 6): point A represents the best permeability values and (as they are contradictory) the worst surface area. It should be chosen if enhancing cell attachment and proliferation is the prioritised criterion. On the contrary, if facilitating the transport of nutrients and wastes, and ensuring effective vascularisation is the most important goal, point D should be chosen, as it gives the higher value of permeability. Finally, any other point (including B and C) can be considered as trade-off solutions, that can be chosen if both goals are to be considered together. Values of decision variables, objectives and constraints for the four points discussed are shown in Table 6.

Table 6.
Values of discussed points from the Pareto front.
As an example, it was designed a cranial implant for the skull defect shown in Figure 8a. The optimized custom cranial implant was designed using the optimal parameters corresponding to point B: unit cell size, ; isovalue, ; and shape factor, . Point B was selected as it is the most balanced option for the cranial implant design due to its combination of high permeability, adequate surface area, and favourable porosity, which promotes better biological integration and mechanical stability.
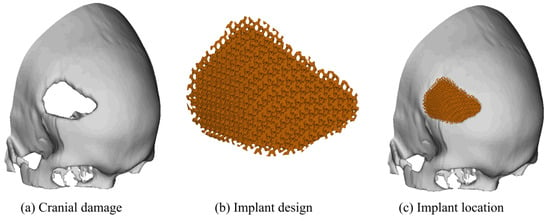
Figure 8.
Cranial implant example.
The optimised custom cranial implant was designed in Ntopology v4.20.2 software using a custom infill volume box, unit cell adjustments and thickness were selected according to the optimal scaffold settings. Figure 8b shows the final results for the designed prosthesis and Figure 8c, the location of the implant, showing the fitting to the skull.
An implant prototype was finally additively manufactured (see Figure 9) for validating the technological feasibility of the processes. However, the practical introduction of these results still requires in vitro and in vivo testing, as regulated by the medical certification agencies, which will be the continuation of this work. In this context, an important aspect to be addressed in the future is the long-term behaviour of the structure, taking into account its integration with the bone tissue [68,69].

Figure 9.
Additively manufactured implant.
5. Conclusions
The main outcome of the work is the methodology to optimise the design of cranial implants based on TPMS scaffolds. These approach considers two optimisation targets: the surface area and the permeability. Both are key issues in cranial implants, as the first one promotes the cellular adhesion and the mechanical stability of the implant, while the second one enhances the cellular adhesion and bone growth. Nevertheless, they are conflictive and cannot be simultaneously optimised.
The proposed a posteriori approach, where a set of non-dominated solutions (also known as Pareto front) are obtained through the NSGA-II, showed to be effective, as it offers a set of solutions that can be considered optimal as they are those for which no other solution can be found, in the feasible search space, that simultaneously improve both objectives. It can be remarked that the proposed optimisation approach guaranties the fulfilment of the considered constraints: the elasticity, which minimises stress shielding, and porosity, which promotes the formation of new bone tissue within the implant structure.
The presented case study allowed not only to demonstrate the presented approach but also its validation through the design of an implant for a given case.
As future development of this work, firstly, the practical validation of the results obtained can be considered, based on experimental measurements of stiffness, porosity, permeability and surface area, in order to verify the accuracy of the simulations carried out. The inclusion of manufacturing parameters as decision variables can also be considered, in order to study their influence on the variables studied and, consequently, on the results of the optimisation process.
Author Contributions
Conceptualisation, M.R., R.Q. and J.P.D.; methodology, B.J.M., M.R. and R.Q.; software, B.J.M.; validation, B.J.M.; formal analysis, M.R. and J.P.D.; writing—original draft preparation, B.J.M. and M.R.; writing—review and editing, R.Q. and J.P.D.; visualisation, B.J.M. and R.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partialfunded by grant “Additive technology for the bioprinting of porous three-dimensional scaffolds for tissue engineering, made of biodegradable composites with programmable properties”, funded by the Matanzas Science and Technology Park.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki and approved by the Scientific Council of the Faculty of Technical Sciences at the University of Matanzas (protocol code 17/2023 and date of approval 6 July 2023).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CAD | Computer Aided Design |
| CFD | Computational Fluid Dynamics |
| FEM | Finite Element Method |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm II |
| PEEK | Polyether-ether-ketone |
| PMMA | Polymethylmethacrylate |
| STL | Stereolithography |
| TPMS | Triply Periodic Minimal Surface |
References
- Alkhaibary, A.; Alharbi, A.; Alnefaie, N.; Oqalaa Almubarak, A.; Aloraidi, A.; Khairy, S. Cranioplasty: A comprehensive review of the history, materials, surgical aspects, and complications. World Neurosurg. 2020, 139, 445–452. [Google Scholar] [CrossRef] [PubMed]
- Joseph, T.M.; Ravichandran, R.; Harshakumar, K.; Lylajam, S. Prosthetic rehabilitation in neurosurgical cranioplasty. J. Indian Prosthodont. Soc. 2018, 18, 76–81. [Google Scholar] [CrossRef] [PubMed]
- Siracusa, V.; Maimone, G.; Antonelli, V. State-of-Art of standard and innovative materials used in cranioplasty. Polymers 2021, 13, 1452. [Google Scholar] [CrossRef] [PubMed]
- Still, M.E.; Samant, S.; Alvarado, A.; Neal, D.; Governale, L.S.; Ching, J.A. Considerations for choice of cranioplasty material for pediatric patients. Pediatr. Neurosurg. 2022, 58, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Selvaraj, S.; Dorairaj, J.; Shivasankar, N. 3d cranial reconstruction using titanium implant—A case report. Afr. Health Sci. 2022, 22, 383–390. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.N.T.; Binh, C.X.; Dung, V.T.; Toan, T.V. Design and mechanical evaluation of a large cranial implant and fixation parts. Interdiscip. Neurosurg. 2023, 31, 101676. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, W.; Chen, J.; Yu, J.; Zhang, J.; Chen, J. The application of polyetheretherketone (PEEK) implants in cranioplasty. Brain Res. Bull. 2019, 153, 143–149. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.A.; Petersmann, S.; Arbeiter, F.; Schäfer, U. Optimization and manufacture of polyetheretherketone patient specific cranial implants by material extrusion—A clinical perspective. J. Mech. Behav. Biomed. Mater. 2023, 144, 105965. [Google Scholar] [CrossRef]
- Koller, M.; Rafter, D.; Shok, G.; Murphy, S.; Kiaei, S.; Samadani, U. A retrospective descriptive study of cranioplasty failure rates and contributing factors in novel 3D printed calcium phosphate implants compared to traditional materials. 3D Print. Med. 2020, 6, 14. [Google Scholar] [CrossRef]
- Kinsman, M.; Aljuboori, Z.; Ball, T.; Nauta, H.; Boakye, M. Rapid high-fidelity contour shaping of titanium mesh implants for cranioplasty defects using patient-specific molds created with low-cost 3D printing: A case series. Surg. Neurol. Int. 2020, 11, 288. [Google Scholar] [CrossRef]
- Moiduddin, K.; Mian, S.H.; Elseufy, S.M.; Alkhalefah, H.; Ramalingam, S.; Sayeed, A. Polyether-Ether-Ketone (PEEK) and its 3D-printed quantitate assessment in cranial reconstruction. J. Funct. Biomater. 2023, 14, 429. [Google Scholar] [CrossRef] [PubMed]
- Binhammer, A.; Jakubowski, J.; Antonyshyn, O.; Binhammer, P. Comparative cost-effectiveness of cranioplasty implants. Plast. Surg. 2020, 28, 29–39. [Google Scholar] [CrossRef] [PubMed]
- Shrivastava, S.P.; Dable, R.; Raj, A.P.N.; Mutneja, P.; Srivastava, S.B.; Haque, M. Comparison of mechanical properties of PEEK and PMMA: An in vitro study. J. Contemp. Dent. Pract. 2021, 22, 179–183. [Google Scholar] [PubMed]
- Moncayo-Matute, F.P.; Vázquez-Silva, E.; Peña-Tapia, P.G.; Torres-Jara, P.B.; Moya-Loaiza, D.P.; Viloria-Ávila, T.J. Finite Element Analysis of patient-specific 3D-printed cranial implant manufactured with PMMA and PEEK: A mechanical comparative study. Polymers 2023, 15, 3620. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Xu, L.; Li, X.; Egger, J. Computer-aided implant design for the restoration of cranial defects. Sci. Rep. 2017, 7, 4199. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; von Campe, G.; Pepe, A.; Gsaxner, C.; Wang, E.; Chen, X.; Zefferer, U.; Tödtling, M.; Krall, M.; Deutschmann, H.; et al. Automatic skull defect restoration and cranial implant generation for cranioplasty. Med. Image Anal. 2021, 73, 2102171. [Google Scholar] [CrossRef] [PubMed]
- Venugopal, V.; Ghalsasi, O.; McConaha, M.; Xu, A.; Forbes, J.; Anand, S. Image processing-based method for automatic design of patient-specific cranial implant for additive manufacturing. Procedia Manuf. 2021, 53, 375–386. [Google Scholar] [CrossRef]
- Pimentel, P.; Szengel, A.; Ehlke, M.; Lamecker, H.; Zachow, S.; Estacio, L.; Doenitz, C.; Ramm, H. Automated virtual reconstruction of large skull defects using statistical shape models and generative adversarial networks. In Proceedings of the towards the Automatization of Cranial Implant Design in Cranioplasty, Lima, Peru, 8 October 2020; Lecture Notes in Computer Science. Li, J., Egger, J., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 16–27. [Google Scholar] [CrossRef]
- Saranya, A.; Subhashini, R. A systematic review of explainable artificial intelligence models and applications: Recent developments and future trends. Decis. Anal. J. 2023, 7, 100230. [Google Scholar] [CrossRef]
- Rasteau, S.; Ernenwein, D.; Savoldelli, C.; Bouletreau, P. Artificial intelligence for oral and maxillo-facial surgery: A narrative review. J. Stomatol. Oral Maxillofac. Surg. 2022, 123, 276–282. [Google Scholar] [CrossRef]
- Rong, G.; Mendez, A.; Bou Assi, E.; Zhao, B.; Sawan, M. Artificial intelligence in healthcare: Review and prediction case studies. Engineering 2020, 6, 291–301. [Google Scholar] [CrossRef]
- Moiduddin, K.; Darwish, S.; Al-Ahmari, A.; ElWatidy, S.; Mohammad, A.; Ameen, W. Structural and mechanical characterization of custom design cranial implant created using additive manufacturing. Electron. J. Biotechnol. 2017, 29, 22–31. [Google Scholar] [CrossRef]
- Santos, P.O.; Carmo, G.P.; Sousa, R.J.A.d.; Fernandes, F.A.O.; Ptak, M. Mechanical strength study of a cranial implant using computational tools. Appl. Sci. 2022, 12, 878. [Google Scholar] [CrossRef]
- Haque, F.; Luscher, A.F.; Mitchell, K.A.S.; Sutradhar, A. Optimization of fixations for additively manufactured cranial implants: Insights from Finite Element Analysis. Biomimetics 2023, 8, 498. [Google Scholar] [CrossRef] [PubMed]
- El Halabi, F.; Rodriguez, J.F.; Rebolledo, L.; Hurtós, E.; Doblaré, M. Mechanical characterization and numerical simulation of polyether–ether–ketone (PEEK) cranial implants. J. Mech. Behav. Biomed. Mater. 2011, 4, 2135–2152. [Google Scholar] [CrossRef] [PubMed]
- Sharma, N.; Ostas, D.; Rotar, H.; Brantner, P.; Thieringer, F.M. Design and additive manufacturing of a biomimetic customized cranial implant based on Voronoi diagram. Front. Physiol. 2021, 12, 647923. [Google Scholar] [CrossRef]
- Sivakumar, N.K.; Palaniyappan, S.; Sekar, V.; Alodhayb, A.; Braim, M. An optimization approach for studying the effect of lattice unit cell’s design-based factors on additively manufactured poly methyl methacrylate cranio-implant. J. Mech. Behav. Biomed. Mater. 2023, 141, 105791. [Google Scholar] [CrossRef] [PubMed]
- Egan, P.; Gonella, V.; Engensperger, M.; Ferguson, S.; Shea, K. Computationally designed lattices with tuned properties for tissue engineering using 3D printing. PLoS ONE 2017, 12, e0182902. [Google Scholar] [CrossRef] [PubMed]
- Ataollahi, S. A review on additive manufacturing of lattice structures in tissue engineering. Bioprinting 2023, 35, e00304. [Google Scholar] [CrossRef]
- Dong, Z.; Zhao, X. Application of TPMS structure in bone regeneration. Eng. Regen. 2021, 2, 154–162. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, D.; Yu, X.; Ren, Z.; Mao, S.; Zheng, X. A novel design method for TPMS lattice structures with complex contour based on moving elements method. Int. J. Adv. Manuf. Technol. 2022, 123, 21–33. [Google Scholar] [CrossRef]
- Maevskaia, E.; Guerrero, J.; Ghayor, C.; Bhattacharya, I.; Weber, F.E. Triply periodic minimal surface-based scaffolds for bone tissue engineering: A mechanical, in vitro and in vivo study. Tissue Eng. Part A 2023, 29, 507–517. [Google Scholar] [CrossRef] [PubMed]
- González González, A.; Rivas Santana, M.; Zambrano Robledo, P.; Quiza, R. Thermal and morphological characterization of 3D-printed PLA scaffolds for biomedical applications. MRS Adv. 2022, 7, 1206–1211. [Google Scholar] [CrossRef]
- Alemayehu, D.; Todoh, M. Enhanced energy absorption in bioinspired combined TPMS-gyroid and walled TPMS-gyroid lattice structure manufactured via Fused Filament Fabrication (FFF). J. Manuf. Mater. Process. 2024, 8, 86. [Google Scholar] [CrossRef]
- Khrapov, D.; Kozadayeva, M.; Koptyug, A.; Mishurova, T.; Meinel, D.; Surmenev, R.; Surmeneva, M. Geometrical features and mechanical properties of the sheet-based gyroid scaffolds with functionally graded porosity manufactured by electron beam melting. Mater. Today Commun. 2023, 35, 106410. [Google Scholar] [CrossRef]
- N. Musthafa, H.S.; Walker, J.; Rahman, T.; Bjørkum, A.; Mustafa, K.; Velauthapillai, D. In-silico prediction of mechanical behaviour of uniform gyroid scaffolds affected by its design parameters for bone tissue engineering applications. Computation 2023, 11, 181. [Google Scholar] [CrossRef]
- Ziaie, B.; Velay, X.; Saleem, W. Exploring the mechanical properties of the gyroid sheet network for the additive manufacturing of biomedical structures: A numerical analysis approach. Eng. Proc. 2024, 65, 7. [Google Scholar] [CrossRef]
- Hayashi, K.; Yanagisawa, T.; Kishida, R.; Ishikawa, K. Effects of scaffold shape on bone regeneration: Tiny shape differences affect the entire system. ACS Nano 2022, 16, 11755–11768. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.D.; Kadri, O.E.; Sikavitsas, V.I.; Voronov, R.S. Scaffolds with a high surface area-to-volume ratio and cultured under fast flow perfusion result in optimal O2 delivery to the cells in artificial bone tissues. Appl. Sci. 2019, 9, 2381. [Google Scholar] [CrossRef]
- Teimouri, R.; Abnous, K.; Taghdisi, S.M.; Ramezani, M.; Alibolandi, M. Surface modifications of scaffolds for bone regeneration. J. Mater. Res. Technol. 2023, 24, 7938–7973. [Google Scholar] [CrossRef]
- Zhou, J.; Xiong, S.; Liu, M.; Yang, H.; Wei, P.; Yi, F.; Ouyang, M.; Xi, H.; Long, Z.; Liu, Y.; et al. Study on the influence of scaffold morphology and structure on osteogenic performance. Front. Bioeng. Biotechnol. 2023, 11, 1127162. [Google Scholar] [CrossRef]
- Lv, N.; Zhou, Z.; Hou, M.; Hong, L.; Li, H.; Qian, Z.; Gao, X.; Liu, M. Research progress of vascularization strategies of tissue-engineered bone. Front. Bioeng. Biotechnol. 2024, 11, 1291969. [Google Scholar] [CrossRef]
- Dias, M.R.; Fernandes, P.R.; Guedes, J.M.; Hollister, S.J. Permeability analysis of scaffolds for bone tissue engineering. J. Biomech. 2012, 45, 938–944. [Google Scholar] [CrossRef]
- Prakoso, A.T.; Basri, H.; Adanta, D.; Yani, I.; Ammarullah, M.I.; Akbar, I.; Ghazali, F.A.; Syahrom, A.; Kamarul, T. The effect of tortuosity on permeability of porous scaffold. Biomedicines 2023, 11, 427. [Google Scholar] [CrossRef]
- Truscello, S.; Kerckhofs, G.; Van Bael, S.; Pyka, G.; Schrooten, J.; Van Oosterwyck, H. Prediction of permeability of regular scaffolds for skeletal tissue engineering: A combined computational and experimental study. Acta Biomater. 2012, 8, 1648–1658. [Google Scholar] [CrossRef]
- Yeranee, K.; Rao, Y. A review of recent investigations on flow and heat transfer enhancement in cooling channels embedded with Triply Periodic Minimal Surfaces (TPMS). Energies 2022, 15, 8994. [Google Scholar] [CrossRef]
- Basri, H.; Nasution, J.; Syahrom, A.; Sulong, M.A.; Putra, A.; Prakoso, A.; Aminin, F. The effect of flow rate characteristic on biodegradation of bone scaffold. Malays. J. Fundam. Appl. Sci. 2017, 13, 546–552. [Google Scholar] [CrossRef]
- Yang, Z. Finite Element Analysis for Biomedical Engineering Applications; CRC Press: Boca Raton, FL, USA; Taylor and Francis Group: Abingdon, UK, 2019. [Google Scholar] [CrossRef]
- Popp, M.; Rusu, G.; Racz, S.G.; Popp, I.O. Force and thickness prediction with FEA of the cranial implants manufactured through SPIF. Matec Web Conf. 2019, 290, 04008. [Google Scholar] [CrossRef]
- Kumar, J.; Nirala, N.s.; Singh, N.K.; Gupta, N.; Dwivedi, Y.D.; Verma, R.; Rai, S.K.; Gupta, M. Design, development and fluidic behavior analysis of triply periodic minimal surface (TPMS) based scaffolds for bone-applications. Int. J. Interact. Des. Manuf. 2023, 18, 3077–3087. [Google Scholar] [CrossRef]
- Jones, A.; Leary, M.; Bateman, S.; Easton, M. Parametric design and evaluation of TPMS-like cellular solids. SSRN Electron. J. 2022, 221, 110908. [Google Scholar] [CrossRef]
- Verma, R.; Kumar, J.; Singh, N.K.; Rai, S.K.; Saxena, K.K.; Xu, J. Design and analysis of biomedical scaffolds using TPMS-based porous structures inspired from additive manufacturing. Coatings 2022, 12, 839. [Google Scholar] [CrossRef]
- Tatsumi, G.; Ratoi, M.; Shitara, Y.; Hasegawa, S.; Sakamoto, K.; Mellor, B.G. Mechanism of oil-lubrication of PEEK and its composites with steel counterparts. Wear 2021, 486–487, 204085. [Google Scholar] [CrossRef]
- Pedroso, J.M.; Enger, M.; Bandeira, P.; Magalhães, F.D. Comparative study of friction and wear performance of PEK, PEEK and PEKK Binders in tribological coatings. Polymers 2022, 14, 4008. [Google Scholar] [CrossRef] [PubMed]
- Unal, H.; Mimaroglu, A. Friction and wear characteristics of PEEK and its composite under water Lubrication. J. Reinf. Plast. Compos. 2006, 25, 1659–1667. [Google Scholar] [CrossRef]
- Moharil, S.; Reche, A.; Durge, K. Polyetheretherketone (PEEK) as a biomaterial: An overview. Cureus 2023, 15, e44307. [Google Scholar] [CrossRef] [PubMed]
- Matienzo, D.; Bordoni, B. Anatomy, Blood Flow; StatPearls Publishing: Treasure Island, FL, USA, 2023. [Google Scholar]
- Asbai-Ghoudan, R.; Ruiz de Galarreta, S.; Rodriguez-Florez, N. Analytical model for the prediction of permeability of triply periodic minimal surfaces. J. Mech. Behav. Biomed. Mater. 2021, 124, 104804. [Google Scholar] [CrossRef] [PubMed]
- Shi, C.; Lu, N.; Qin, Y.; Mingdi, L.; Li, H.; Li, H. Study on mechanical properties and permeability of elliptical porous scaffold based on the SLM manufactured medical Ti6Al4V. PLoS ONE 2021, 16, e0247764. [Google Scholar] [CrossRef]
- Ali, D.; Ozalp, M.; Blanquer, S.B.G.; Onel, S. Permeability and fluid flow-induced wall shear stress in bone scaffolds with TPMS and lattice architectures: A CFD analysis. Eur. J. Mech.-B/Fluids 2020, 79, 376–385. [Google Scholar] [CrossRef]
- Zimmerman, R. The Imperial College Lectures in Petroleum Engineering; World Scientific Publishing Europe: London, UK, 2018; p. 205. [Google Scholar] [CrossRef]
- Chao, L.; He, Y.; Gu, J.; Xie, D.; Yang, Y.; Shen, L.; Wu, G.; Wang, L.; Tian, Z. Evaluation of compressive and permeability behaviors of trabecular-like porous structure with mixed porosity based on mechanical topology. J. Funct. Biomater. 2023, 14, 28. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Karaman, D.; Ghahramanzadeh Asl, H. The effects of sheet and network solid structures of similar TPMS scaffold architectures on permeability, wall shear stress, and velocity: A CFD analysis. Med. Eng. Phys. 2023, 118, 104024. [Google Scholar] [CrossRef]
- Nowak, M.; Sokołowski, J.; Żochowski, A. Biomimetic approach to compliance optimization and multiple load cases. J. Optim. Theory Appl. 2020, 184, 210–225. [Google Scholar] [CrossRef]
- Foroughi, A.H.; Razavi, M.J. Multi-objective shape optimization of bone scaffolds: Enhancement of mechanical properties and permeability. Acta Biomater. 2022, 146, 317–340. [Google Scholar] [CrossRef] [PubMed]
- Adams, G.; Cook, R.; Hutchinson, J.; Zioupos, P. Bone surface distribution across a wide porosity range in mammalian bone tissue. In Proceedings of the 7th World Congress Biomechanics, Boston, MA, USA, 6–11 July 2014. [Google Scholar]
- Giorgio, I.; dell’Isola, F.; Andreaus, U.; Misra, A. An orthotropic continuum model with substructure evolution for describing bone remodeling: An interpretation of the primary mechanism behind Wolff’s law. Biomech. Model. Mechanobiol. 2023, 22, 1206–1211. [Google Scholar] [CrossRef]
- Grillo, A.; Stefano, S.D. An a posteriori approach to the mechanics of volumetric growth. Math. Mech. Complex Syst. 2023, 11, 57–86. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).