Abstract
Modern agriculture faces the dual challenge of ensuring sustainability while meeting the growing global demand for food. Smart agriculture, which uses data from the environment and plants to deliver water exactly when and how it is needed, has attracted significant attention. This approach requires precise water management and highly accurate real-time monitoring of crop water stress. Existing monitoring methods pose challenges such as the risk of plant damage, costly sensors, and the need for expert adjustments. Therefore, a low-cost, highly accurate water stress estimation model was developed that uses deep learning and commercially available sensors. The model uses the relative stem diameter as a water stress index and incorporates data from environmental sensors and an RGB camera, which are processed by the proposed daily normalization. In addition, domain adaptation in our Transformer model was implemented to enable robust learning in different areas. The accuracy of the model was evaluated using real cultivation data from tomato crops, achieving a coefficient of determination (R2) of 0.79 in water stress estimation. Furthermore, the model maintained a high level of accuracy when applied to different areas, with an R2 of 0.76, demonstrating its high adaptability under different conditions.
1. Introduction
In today’s era of agriculture, there is an increasing need to use new technologies, such as the Internet of Things (IoT) and artificial intelligence (AI), to meet the growing global demand for food quality and quantity. This new era of smart agriculture is characterized by remote sensing through the IoT and automatic control by edge computers, which enable the collection of diverse data on the spatial and temporal variability of production [1,2,3]. In smart agriculture, the development of high-precision irrigation management systems is an important research topic. Monitoring the environmental conditions and plant health in fields not only prevents over- or under-irrigation and promotes optimal plant growth but also conserves water resources and reduces labor costs associated with irrigation [4,5]. In addition, studies on tomatoes have shown that finely controlled irrigation to maintain mild water stress can increase the soluble solids content (Brix, which indicates sweetness) and improve the quality of tomato fruits [6,7]. As tomatoes are one of the most widely cultivated vegetables globally [8], research into the development of precision irrigation systems for tomatoes could significantly contribute to water conservation and improved crop quality.
The realization of high-precision irrigation monitoring systems requires technologies that are able to accurately measure the indicators of water stress in plants. Water stress-monitoring methods can be broadly categorized into direct and indirect measurement techniques. Direct methods include sap flow sensors, bioristor sensors, dendrometers, strain gauges, and laser displacement sensors [9,10,11,12,13,14,15,16,17]. These methods have the advantage of accurately measuring the water content within plants. However, there are risks of damaging the plants through invasive procedures such as inserting electrodes, or the high cost of the devices can become an economic burden. Indirect measurement methods include the use of soil moisture sensors, which indirectly assess plant water stress by measuring volumetric soil water content. These methods have the advantage that the sensor devices are inexpensive. However, the accuracy of soil moisture sensors is highly dependent on the physical and electrical properties of the soil, which means that they may not accurately reflect plant water stress [18,19].
As a method that encompasses both advantages, techniques using RGB camera devices are also being explored [20,21,22,23,24]. Leaf wilting is one of the most commonly observed plant responses to water stress. Under water stress, the turgor pressure in the leaves decreases, causing them to move downwards, thereby reducing their leaf area [25]. This movement, known as “leaf wilting”, is captured by a camera and quantified using computer vision techniques. Takayama et al. [20] quantified changes in the projected leaf area using image-processing software (Adobe Photoshop 6.0, Adobe Systems, San Jose, CA, USA) to isolate only the leaf areas in images taken vertically from above the plant. Wakamori et al. [21] used optical flow on images captured horizontally from the plant to quantify the vertical movement of leaves at one-minute intervals. This method is non-destructive and can be performed with inexpensive cameras, providing a cost-effective alternative to other techniques. However, detection by optical flow also identifies movements other than those of the leaves, such as the movement of clouds in the background or people at work. Consequently, mask processing using the excess green (ExG) index was considered [26]; however, this issue has not yet been fully resolved. Furthermore, the degree of leaf movement is a relative indicator of water stress that depends on the specific object being observed, as it varies greatly with the cameras’ field of view and the size of the leaf. Therefore, it is impossible to consistently scale data gathered from various sites.
When considering the installation of irrigation systems in multiple fields or expansive greenhouses, it is necessary to adjust the irrigation control parameters for each specific site. For example, if the irrigation system adjusted for greenhouse A is extended to greenhouse B, it may need to be adapted to local conditions in terms of sunlight hours, air circulation, irrigation frequency, and ventilation methods. These differences are likely to lead to variations in data distribution and are recognized as domain shift problems in the context of machine learning. Currently, skilled farmers manually adapt the system to the respective location. However, an automatic adjustment mechanism is desirable for easier handling and more accurate control.
Although there are different methods for measuring plant water stress indicators, each has its own advantages and disadvantages. Therefore, a water stress measurement method that can directly reflect plant water stress, is easy to implement, and can be monitored with low-cost equipment is desired. In this study, a deep learning-based model that estimates the stem diameter as an indicator of water stress was developed using the leaf wilting index and environmental data. Using an inexpensive camera and common environmental sensors to estimate changes in stem diameter, which is a direct response to water stress, a cost-effective and easy-to-use model for estimating water stress is proposed. Figure 1 provides an overview of this study.
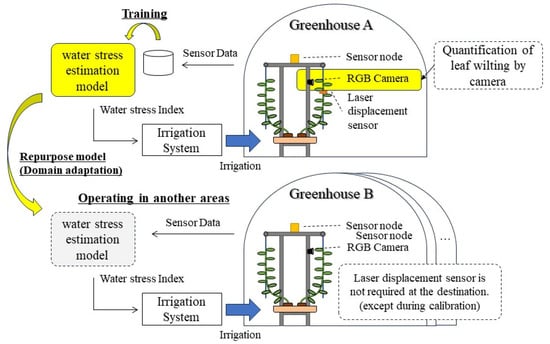
Figure 1.
Overview of the model for estimating water stress using leaf wilting index and adaptation in different areas.
Our contributions are threefold. First, a method to accurately quantify leaf wilting is proposed that uses a combination of the Segment Anything Model (SAM) [27], which is a foundation model for segmentation, and CoTracker [28], which is a foundation model for tracking arbitrary points. To realize an accurate irrigation control system, leaf wilting should be detected in real time. This approach is expected to reduce the effects of disturbances such as background elements and enable highly accurate quantification of leaf wilting. Second, a model for estimating water stress is proposed based on the Transformer architecture that takes into account the correlation between multivariate data from quantified leaf wilting and environmental data. Third, local normalization and unsupervised domain adaptation were incorporated when training the model using data obtained from environmental sensors [29,30,31,32]. Experiments have shown that this model can be easily adapted for use in multiple fields or large greenhouses, even with multiple installations.
2. Related Works
2.1. Deep Learning in Agriculture
In recent years, advances in machine learning have led to a new movement toward data-intensive approaches in the agricultural sector [33,34]. In particular, deep learning, proposed by Hinton et al. [35] in 2006, has rapidly evolved and is now used for various classification and estimation tasks in a wide range of fields, including the agricultural field. Sladojevic et al. [36] developed a model using convolutional neural networks that can recognize 13 types of plant diseases from healthy leaves with an average accuracy of 96.3%. Peng et al. [37] developed a weed detection model for rice crop images using RetinaNet, achieving accurate real-time detection and low machine costs. Rahnemoonfar et al. [38] developed an Inception-ResNet-based model for counting flowers and fruits, demonstrating an average accuracy of 91% in experiments using images of tomato fruits. Nan et al. [39] developed HyperYOLO, which is capable of real-time lightweight object detection for remote sensing, achieving a 76.72% mean average precision (mAP) in experiments. Liu et al. [40] developed RemoteCLIP, the first vision–language foundation model for remote sensing. It learns robust visual features with rich semantics and aligned text embeddings, which can be transferred to various tasks such as zero-shot image classification, image-text retrieval, and object counting in remote-sensing images.
In the research on water stress estimation, which is the scope of this study, Cai et al. [41] proposed a deep neural network regression model trained on meteorological data and soil moisture sensor data from Beijing, China, from 2012 to 2016 and showed that it could predict soil moisture with a coefficient of determination (R2) = 0.98. Song et al. [42] proposed a model combining a deep belief network and a macroscopic cellular automaton based on deep learning and showed a method for estimating the soil moisture content from the meteorological data, leaf area index, and soil surface temperature data of a corn field. In addition, in their research on stem diameter estimation, Wakamori et al. [14] showed that it is possible to estimate stem diameter with an R2 = 0.43 by using a long short-term memory (LSTM) model that learns from features extracted from leaf images, environmental data, and data related to circadian rhythms.
The Transformer architecture [43] is a deep learning-based framework that has been shown to be highly effective in various tasks such as natural language processing [44], image recognition [45], and time series forecasting [46]. In this study, the Transformer architecture was used to adapt the model configuration proposed in Vision Transformer (ViT) for multivariate time series estimation tasks.
2.2. Domain Adaptation
In general machine learning theory, it is assumed that the data used for training and testing come from the same distribution. However, in reality, the two distributions are not identical. Tasks that involve learning models assuming a shift between training and testing distributions are known as domain adaptation, which is a well-known research theme in the field of machine learning [31]. The goal of unsupervised domain adaptation (UDA) is to develop models that function effectively in the target domain by using labeled data from the source domain and unlabeled data from the target domain during training [29,32]. One approach to domain adaptation involves the incorporation of adversarial training to improve the robustness of a domain [30,47,48]. Ganin et al. [30] added a domain classifier to the feature extraction network for classification for domain adaptation. This was achieved by introducing a gradient inversion layer that multiplies the gradient by a certain negative constant during training. This process adjusts the feature distribution between the source and target domains extracted by the network so that they are similar (indistinguishable by the domain classifier), resulting in domain-independent features. Another method is domain adaptation based on moment matching [49,50]. Zellinger et al. [50] proposed Central Moment Discrepancy, which is a new distance metric for the distribution of hidden layer outputs of a feature extraction network. They achieved domain adaptation by adding a regularization term to minimize the discrepancies in feature distributions between the source and target domains.
Inspired by the moment-matching approach, a domain adaptation method is proposed that incorporates a regularization term to minimize the discrepancy in the distribution of estimates at different times of the day, taking into account the circadian rhythms of plants.
3. Materials and Methods
3.1. Relative Stem Diameter (RSD) as Water Stress
Ohishi [13] analyzed the relationship between water stress and changes in stem diameter in tomatoes grown in rockwool-based hydroponic systems and demonstrated a non-destructive evaluation method for water stress based on stem diameter changes. They measured the typical changes in stem diameter (SD (mm)) during the stem enlargement phase of tomatoes grown under water stress on sunny days. They found that transpiration increased from sunrise to noon, the relative stem water content decreased, leaf wilting began, and the SD decreased. After this period, as transpiration decreased from the afternoon to night, the RSW increased, leaf wilting recovered, and the maximum SD increased owing to plant growth. Based on these results, the relative stem diameter (RSD (%)) was defined, which represents the changes in SD due to water stress, adjusted for growth-related enlargement. The RSD at a time follows the following formula:
where represents the stem diameter at a specific time , and denotes the maximum stem diameter observed from the start of the measurement up to time . The RSD was used as an indicator of water stress. The start of the measurement is defined as time , which corresponds to the sunrise of each day (when ambient light exceeds 20 lux), and the RSD is calculated every 5 min, increasing the time accordingly.
3.2. Dataset
The data used in this paper were collected in a greenhouse located in Fukuroi City, Shizuoka Prefecture, Japan, where tomatoes (Solanum lycopersicum L. “Frutica”) are grown using a hydroponic system. As shown in Figure 2, data were obtained from four cultivation areas, each area having a different irrigation control. Each area was equipped with environmental sensor nodes placed above the plants, a laser displacement meter (HL-T1010A, Panasonic Corp., Osaka, Japan) placed between the 9th and 10th nodes of the plants, and an RGB camera (GoPro HERO5 Session, GoPro Inc., San Mateo, CA, USA) placed near the leaves. These devices collected data at five-minute intervals on temperature, relative humidity, scattered light illumination, CO2 concentration, SD, and images of the plant canopy. The data also contained time information, such as the elapsed time since sunrise and the time of irrigation. The vapor pressure deficit (VPD) was calculated from the temperature and relative humidity, and the RSD was calculated from the SD and scattered light illumination. The images of the plant canopy captured by the RGB camera were resized from full HD to a 342 × 456 resolution and saved in JPG format. The data collection period was from the pinching stage to the end of the tomato harvest and covered the period from October 23, 2018, to January 16, 2019, excluding rainy days when no leaf wilting occurred. The distribution of key data for each cultivation area is shown in Figure 3.
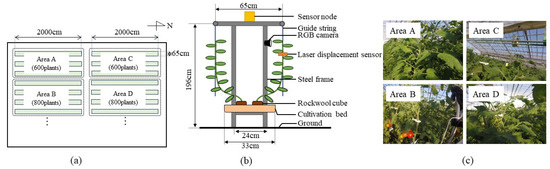
Figure 2.
Data collection environment. (a) Cultivation areas (b) Sensor position (c) Camera angles of view.
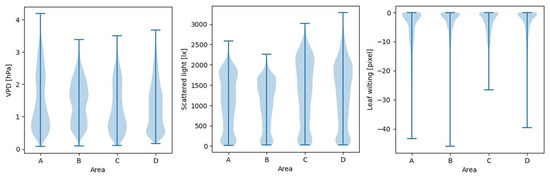
Figure 3.
Distribution of collected data by area.
The dataset was divided into four areas designated as {“A”, “B”, “C”, “D”}, with the number of data points in each area as 4620 (44 days), 4410 (42 days), 4935 (47 days), and 3885 (37 days), respectively. Each day’s data included 105 data points measured at five-minute intervals from sunrise to sunset, ensuring that each day was temporally independent. For each area, 14 days of data were used as test data, while the remaining data were used as training data, and cross-validation was performed. The split for cross-validation was performed daily; therefore, data points from the same day were not included in both the training and test datasets simultaneously. Additionally, when using datasets from different areas for training and testing, the model was trained with the training dataset of area A and tested with the test data from area C (A–C). Similarly, B–D, C–A, and D–B were performed.
3.3. Quantification of Leaf Wilting
A method is proposed to quantify leaf wilting from images of the canopy taken with a camera. To do so, SAM, a foundation model for segmentation, and CoTracker, a foundation model, were combined for arbitrary point tracking. In tomato cultivation, leaves are removed at an appropriate frequency to improve sunlight exposure and ventilation to in-crease yield. Therefore, it must be assumed that the monitored leaves can be removed on a given day. To solve this problem, an algorithm was developed that automatically selects leaves for wilting monitoring every morning. By selecting multiple leaves as monitoring targets each morning, the continuity of monitoring is ensured, even if some leaves are removed during the process.
First, the method for selecting multiple leaves to monitor from a canopy image is explained. As depicted in Figure 4, an ExG mask was applied to the canopy image, and SAM was used to create segmentation masks for potential leaf areas. As the segmentation created by SAM also contained non-leaf elements, such as stems, fruits, and sensor devices, the criteria were set to exclude non-leaf elements. Specifically, segmentation masks with an area between 400 px2 and less than 10,000 px2 and aspect ratios between 0.3 and less than 3.0 were retained. Masks that did not meet these standards were discarded. The central coordinates of the remaining segmentation masks were designated as tracking points for CoTracker.
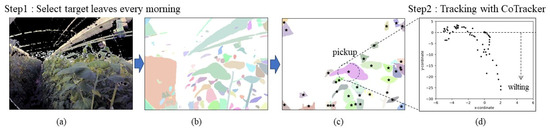
Figure 4.
Processing steps for the quantification of leaf wilting. (a) ExG mask (b) Segmentation mask using SAM (c) Calculate tracking points (d) Tracking trajectory.
Subsequently, the tracking point was tracked using CoTracker. Let be the number of tracking points and be the elapsed processing time. The tracking process is performed at five-minute intervals, starting at and incrementing with each subsequent tracking process. Next, let be the index of the tracking point and be the Y-coordinate of the -th tracking point at time . Therefore, the relative amount of leaf wilting at time can be calculated as follows:
where time is the time of sunrise, similar to the RSD.
3.4. Daily Normalization
Normalization of the environmental data and the RLW was performed as part of the data preprocessing. Normalization is an important preprocessing step in machine learning. Data series such as temperature (approximately 22–33 °C) and illuminance (approximately 30–26,000 lux) often greatly vary in their range of maximum and minimum values. Normalization equalizes the scale between variables with different magnitudes, which is known to improve the performance of machine learning models, stabilize learning, and reduce the time required for training. However, when data collected from multiple cultivation areas contain “dataset shift”, such as differences in scale and distribution, a simple normalization that amalgamates data might inadvertently distort the overall distribution of the dataset [51].
Data from greenhouse environments and plant physiology in agriculture are likely to be affected by various disturbances during data collection. In this case, the four areas from which data were collected showed biases in the distribution of environmental data even within the same greenhouse, owing to differences in location, orientation (sunlight exposure), air circulation, and irrigation frequency. In addition, the RLW calculated from image data can significantly vary in scale owing to variations in camera placement and field of view. Furthermore, agricultural practitioners know that a plant’s response to water stress in the form of stem contraction can diminish owing to individual differences, age, and growth stages. This can be interpreted as a “concept shift”, where the distribution of independent and dependent variables changes over time. In this case, in addition to normalization for each domain, it is also necessary to consider normalization along the temporal axis.
Therefore, we propose daily normalization. A day was defined from sunrise () to sunset (), and after calculating the difference from sunrise for each dataset collected during this time, it was divided by the standard deviation within each area. The normalized RLW at time () was calculated as follows:
where is a function that calculates the standard deviation, and represents the RLW observed in a given area up to the previous day. Assuming that other data series were normalized in the same way, the standard deviation of each data series was summarized, and the normalization parameter was used in normalizing each series data.
By applying this normalization, the differences in scale between areas for daytime environmental data and RLW became uniform. In addition, by accounting for differences based on sunrise, the application of a daily time window and canceling shifts in the time-series data caused by plant age and growth could be taken into account. This approach is based on the assumption that although the scale and trend of data from each area and plant may vary, the response of plants to water stress is consistent over the daytime period.
3.5. Water Stress Estimation Model
The architecture of the model for estimating RSD as an indicator of water stress is shown in Figure 5. The RSD estimation process involves a pipeline of sequential operations: input data from environmental sensors and the RLW computed from images. Daily normalization is performed, which is processed by a Transformer-based model , and then denormalization is performed.
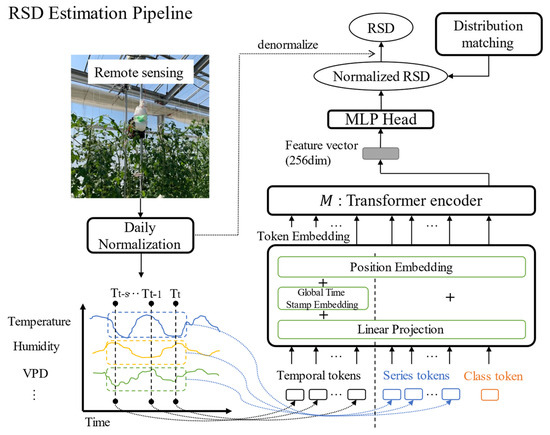
Figure 5.
Model pipeline for estimating water stress.
Model , which estimated the normalized RSD, was constructed using a transformer encoder similar to that used for ViT [45]. However, it was modified with variable-token embeddings (Section 3.6) and an MLP head to perform estimation tasks with time series data instead of classification tasks. The MLP head of model consists of a single linear layer that estimates the normalized RSD from the feature vector output of the Transformer. Let represent the data obtained from environmental sensors and RLW at a given time , where is the number of series, and in this case, (temperature, relative humidity, VPD, scattered illumination, CO2 concentration, irrigation status, and RLW). The estimation of the normalized RSD uses data from the past time points. Therefore, the input for model is , and the output of model is the normalized RSD.
Finally, the scale of the normalized RSD was returned to the original RSD. The estimated RSD at time : using this pipeline is expressed as follows:
Here, is the daily normalization mentioned above. is a learning parameter of the model, which was trained only with data obtained from a certain area . The used for denormalization is the standard deviation of the RSD obtained in the past in the area where the operation is performed, which must be determined in advance. The final term of the equation is .
3.6. Embedding Variable Tokens
In Transformer-based time series prediction models [46,52], it is common to sequentially embed data into variable tokens for autoregressive learning. Conversely, a study on an inverted Transformer model aimed at predicting multivariate time series has shown that embedding each series independently into variable tokens to capture correlations between multiple variables can improve prediction accuracy [53]. Both approaches were used. Let represent the time series tokens at a given time before embedding. The series tokens are represented by , which is the transpose of the time series tokens . In addition, similar to ViT, a class token (CLS) was added for use in the MLP-based estimation. The embedding of the variable tokens used linear projection (LP) and position embedding (PE) as employed in the ViT. In addition, for time series tokens, global time stamp embedding (GTSE), which was proposed in the informer model, was incorporated for time series predictions [46]. The PE adds information about the position within the token (local time stamp), and GTSE adds more global timestamp information, such as the day of the week or holiday information. Drawing on the concept of GTSE, the time elapsed since sunrise and since the last irrigation was used as global time stamps—and embedded into the time series tokens. Therefore, with the embedding vector dimension the tokens after embedding , can be expressed as follows:
3.7. Domain Adaptation Considering the Circadian Rhythm
It is well-known that most organisms, including plants, have circadian rhythms. Tomatoes exhibit a circadian rhythm in which stem diameter begins to decrease in the early morning, as transpiration and photosynthesis become more active at sunrise, recover in the evening, and increase during the night [13,54]. Although the absolute changes in stem diameter based on this circadian rhythm may vary due to local field conditions and irrigation status, the distribution of relative daily changes is thought to be largely consistent. Figure 6 shows the distribution of the RSD for areas A and C and the normalized RSD distribution for each area. The time intervals were divided into four segments from sunrise to sunset, the period when data collection began. In Figure 6, it is evident that the distribution of normalized RSD for each time interval in the areas is largely consistent, even though the areas are different.
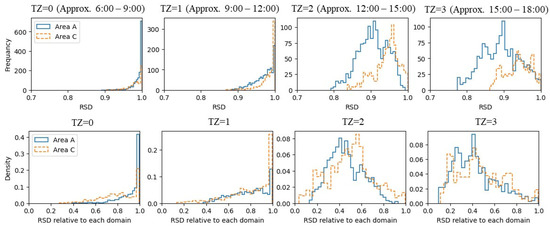
Figure 6.
Distribution of RSD by area and time period. (Top) Without normalization. (Bottom) With normalization per time period.
Therefore, it is assumed that the distribution of normalized RSD by time period roughly coincides in different areas treated as domains, and a domain adaptation approach is proposed based on matching the distribution for different time periods. Using the timestamp information attached to the data collected by each sensor, the time zone is defined as , which indicates the time zone in which each data point was collected. Let the dataset of the particular area be the source domain dataset , and let the label data for each time period contained in the dataset be . Similarly, let the dataset in the area different from the source domain be the target domain dataset , and let the training data for each time period contained in the dataset be By defining the water stress estimation model , the loss function for domain adaptation can be expressed as follows:
Here, represents the transformation to a normalized distribution that enables backpropagation, and represents the KL divergence. Therefore, the loss function L during model training can be expressed as follows:
Here, is the mean squared error loss for RSD estimation, and is a hyperparameter and takes a value between 0.0 and 1.0.
3.8. Evaluation Methods
The experiments were conducted on a desktop PC equipped with an Nvidia RTX3090 GPU and an Intel i9-10900 K CPU at 3.7 GHz with 64 GB of memory. The parameters for the Transformer model used in the experiments were as follows: the feature dimension was set to 256, the number of heads in the multi-head self-attention task was eight, the number of layers was three, and the dropout rate was 0.05. These parameters were derived from the Informer model referenced in the token embedding and were used in all folds of cross-validation without hyperparameter tuning. The model was implemented in Python using the PyTorch ver.2.2.2 library. The Adam optimizer with a learning rate of 1 × 10−4 and 100 epochs was used to train the model to ensure that the loss converged in all training sessions.
In the leaf wilting quantification experiment, we used images of tomato canopies taken with an RGB camera. For comparison, the experiment was conducted using the existing optical flow method and the proposed method. In addition, two different methods for selecting tracking points were compared in the proposed method: random selection and selection with SAM. In the random selection, the tracking point coordinates were randomly selected from within the image. This comparison aimed to verify the effect of the choice of leaves to be tracked on the quantification accuracy. The metric used for the quantification accuracy was the correlation coefficient with the RSD, an index of water stress. Leaf wilting and RSD exhibit a positive correlation; therefore, a higher correlation with the RSD indicates a more accurate quantification of leaf wilting.
In the investigations on daily normalization and token embedding, comparative experiments were conducted using the following three normalization methods to evaluate the estimation accuracy due to differences in the normalization methods.
- Global normalization:The data were normalized to the statistical values of the entire dataset. Standardization was performed using the average and standard deviation of all data.
- Domain-specific normalization:The data were normalized based on the statistical values for specific groups or domains. In this experiment, standardization was performed for each area using the average and standard deviation.
- Daily normalization:The method described in Section 3.4 was used for normalization. Normalization was performed for each day using the difference between sunrise and the standard deviation for each area.
The normalization parameter was calculated from the data of the last 20 days in the target area. The number of time points of the explanatory variables input entered into the model was set to , and the task of estimating the RSD from the environmental data of the last 30 min (every 5 min 6 time points) and the extent of leaf wilting was learned. After performing normalization and model learning using the dataset for each area, there were cases where an accuracy evaluation was performed using test data from the same area and test data from different areas. The metrics used for the estimation accuracy were the mean absolute error (MAE), mean squared error (MSE), and R2.
In the experiments on normalization parameter adaptation and domain adaptation, the focus was on evaluating a model trained in one area when applied to another area. To obtain the normalization parameter , it is necessary to measure the RSD with a laser displacement meter in the target area over a certain period. However, it is desirable that the model adjusts within the shortest possible time period. Therefore, the model’s estimation accuracy was calculated based on the number of days needed to calculate the normalization parameter. In the domain adaptation experiment, a comparative study was conducted between the existing method, unsupervised domain adaptation by backpropagation [30] (UDAB), the proposed method, i.e., domain adaptation considering the circadian rhythm (DAC), and a combination of UDAB and DAC. The time zone parameter was set by dividing the day into four segments, and the loss function was adjusted to ensure that the distribution of estimates matched each time segment. The hyperparameter of the loss function for domain adaptation was set to 0.8.
4. Results
4.1. Experiment on Leaf Wilting Quantification
Table 1 shows the experimental results with the correlation coefficients between the wilting indices calculated by each method and the RSD. The results showed that CoTracker + SAM had the highest correlation between the images from all areas. Figure 7 depicts some characteristic examples of the daily changes in RSD together with the daily variations in the wilting index calculated using optical flow and CoTracker + SAM. A typical change in the RSD on a sunny day was characterized by a rapid decrease around noon, followed by a slight increase in the evening (Figure 7, left). On days with significant humidity fluctuations, the RSD exhibited more pronounced oscillations (Figure 7, upper right). Conversely, on cloudy days with minimal wilting, the RSD decreased at around noon but reverted to its original state by evening (Figure 7, lower right). Although the CoTracker + SAM generally followed the RSD trend, significant deviations were observed in optical flow. When reviewing these instances in the images, it was found that changes in shadows were detected due to moving clouds and movements in the background that were not adequately masked by the ExG. Moreover, only CoTracker + Random showed lower accuracy compared with the baseline optical flow method. With the random method, tracking points may stochastically select coordinates outside of leaf areas, and in some cases, all tracking points may fall outside the leaf area that moves in response to water stress, thereby reducing the accuracy. These results confirm that leaf selection for tracking is a critical factor in methods using CoTracker.

Table 1.
Correlation coefficient by area for each leaf wilting method.
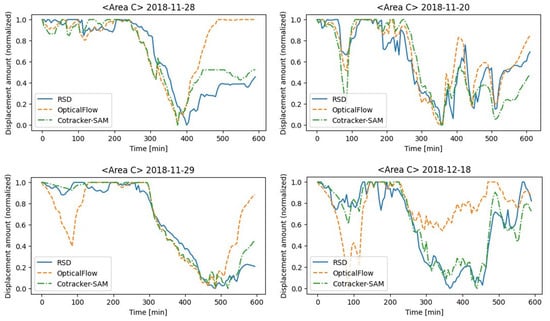
Figure 7.
Daily trends in RSD and leaf wilting index.
4.2. Daily Normalization Experiment
Table 2 shows the results for the same areas, and Table 3 shows the results for different areas. Table 4 shows the aggregated results for all areas. It was confirmed that daily normalization and domain-specific normalization had better accuracy compared with global normalization. When comparing daily normalization and domain-specific normalization, the estimation accuracy was approximately the same when training and testing took place in the same area. However, when training and testing took place in different areas, the R2 improved by approximately 0.03. Daily normalization had an accuracy of more than R2 , both when the test areas were the same and different. This confirms that the estimated value of the proposed model can explain approximately 71.9% of the variation in the RSD in the test area.

Table 2.
RSD estimation results by normalization in the same areas (MAE and MSE).

Table 3.
RSD estimation results by normalization in different areas (MAE and MSE).

Table 4.
RSD estimation results by normalization in the same/different areas (MAE, MSE, and R2).
4.3. Experiment on the Adaptation of Normalization Parameters
Table 5 lists the experimental results obtained. The 0 days scenario refers to the case where the normalization parameter , calculated from the area used to train the model, was applied directly to the target area. The results indicate that using data from the target area for more than 10 days made it possible to achieve an accuracy with an R2 above 0.7. Furthermore, it was found that even with only one day of data, the accuracy reached an R2 of approximately 0.6.

Table 5.
RSD estimation accuracy for each number of calculation days in the target area.
4.4. Experiment on Variable Token Embedding
Table 6 lists the experimental results obtained. Regardless of whether the normalization method was global or daily, the proposed method generally showed the highest estimation accuracy. In particular, when global normalization was applied, significant improvements were observed in different areas. Considering that R2 dropped by 0.283 when only temporal tokens were used, compared with a decrease of 0.163 when only series tokens were used, it can be concluded that the characteristics of the correlations between series contributed to the improved estimation accuracy in cases where the scale differed between different areas. Conversely, in daily normalization, where the scale was adjected between areas, a greater improvement in accuracy was observed within the same area than in different areas.

Table 6.
RSD estimation accuracy using the variable token-embedding method.
4.5. Experiment on Domain Adaptation
Table 7 lists the experimental results. The results show that both UDAB and DAC improved the estimation accuracy compared with scenarios without domain adaptation. The highest accuracy was achieved when both UDAB and DAC were applied. Compared with the non-adaptation scenario, there was an improvement of 0.105 in the R2 with global normalization and 0.037 with daily normalization. Figure 8 shows a histogram of the normalized estimated RSD values compared with the true values of the target domain. When looking at the distribution of the estimates for the target domain, it was found that using the DAC reduced the KL divergence from 0.225 to 0.198, bringing it closer to the true value distribution. In addition, the reduction in KL divergence was correlated with improved estimation accuracy.

Table 7.
RSD estimation accuracy by the domain adaptation method in different areas.
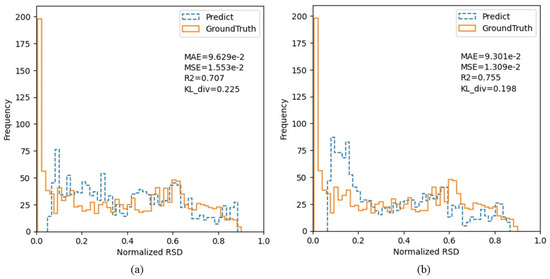
Figure 8.
Histogram of RSD estimation and ground truth data with and without domain adaptation. (a) Without domain adaptation (b) DAC.
Next, Table 8 shows the estimation accuracy when the time zone parameter was varied from one to six. Of the results obtained, the case showed the highest accuracy, with an R2 of 0.75. The lowest accuracy was observed in the case without division into time zones based on circadian rhythms, , where considering the circadian rhythms led to an improvement of 0.027 in the R2.

Table 8.
RSD estimation accuracy by time zone parameter TZ.
5. Discussion
A new method was developed for estimating water stress in tomatoes that considers the transferability of the model. Experiments confirmed the effectiveness of (1) a new technique to quantify leaf wilting from images of tomato canopies and (2) an RSD estimation model based on daily normalization and a Transformer architecture. In addition, (3) it was shown that a model trained in one area can be adapted to another area without compromising accuracy by using domain adaptation that considers circadian rhythms.
When quantifying leaf wilting using images, the combination of CoTracker and SAM successfully produced an indicator that had a high correlation coefficient of approximately 0.82 with the RSD, which indicates water stress. This is an improvement compared with the previous study using optical flow in which the average correlation between the SD and leaf wilting index was 0.6. Optical flow is designed to detect motion at the pixel level and may inadvertently detect unrelated motion such as the movement of cloud shadows and objects in the background that ExG cannot adequately mask. In contrast, the method using CoTracker, similar to object detection, uses the image features of the tracked object, allowing accurate detection of only the movements of leaves, which are the intended targets for wilt detection. However, even when using CoTracker, the random selection of tracking points resulted in a lower correlation than with optical flow. When reviewing images of cases where accuracy decreased, it was found that the problems arose from the tracked leaves either moving out of the camera’s field of view or overlapping with other leaves, causing CoTracker to lose track. Therefore, the selection of leaves to be tracked is crucial for quantifying leaf wilting with CoTracker. This result supports the effectiveness of using SAM for segmentation and selecting tracking targets based on the area and aspect ratio. In this study, simple criteria based on the area and aspect ratio were used to select leaf-like objects. Furthermore, improvements, such as using the foundational model for depth estimation to select leaves closer to the foreground, or selecting leaves closer to the center of the image to prevent them from moving out of the camera’s field of view, could potentially increase the accuracy of quantification.
For the RSD estimation model applying daily normalization, it was shown that the model could estimate the RSD with high accuracy, achieving an R2 of approximately 0.79 when training and testing were performed within the same area. Although a direct comparison is difficult owing to differences in the datasets, this represents a significant improvement over a previous study that used an LSTM model to estimate the stem diameter (R2 ). Moreover, this study proposed the normalization and token embedding methods and reused existing model architectures. Therefore, detailed comparative experiments of water stress estimation algorithms, including model architectures, were not conducted. However, it is considered beneficial for future research to compare the accuracy with existing water stress estimation algorithms and to verify the effect of applying daily normalization as a preprocessing step to existing algorithms. From the perspective of model transferability, daily normalization enabled the transformation of data offsets and distributional differences caused by the physical location of the fields, environmental conditions, and individual plant differences into normalized residuals relative to sunrise. This transformation allows the Transformer model to effectively learn variations in RSD from changes in environmental conditions and leaf wilting, regardless of the source of data collection. In addition, the model can be adapted to different areas without the need for expert adjustments by simply collecting data for approximately 10 days from the target area, with less loss of accuracy. Furthermore, considering that the diurnal response of plants under water stress is common, our method may be applicable to various crops by applying daily normalization.
In domain adaptation considering circadian rhythms, when adapting a water stress estimation model with an R2 of approximately 0.79 to different areas, the accuracy, which would drop to approximately 0.72 without domain adaptation, was maintained at approximately 0.75 by the proposed domain adaptation. This improvement can be attributed to the effective combination of daily normalization and DAC. This allows the incorporation of knowledge of the basic diurnal changes in plants, known as circadian rhythms, into the estimation process. This regularization of the estimates ensures that the distribution of estimates remains reliably within the range of circadian rhythms, thereby reducing the decline in estimation accuracy. Additionally, it was confirmed that the effect of domain adaptation is further enhanced when both DAC and UDAB are used. Because UDAB and DAC are independent domain adaptation methods, both can be used simultaneously. Using both methods together leverages the strong regularization achieved by DAC’s matching of output distributions and UDAB’s matching of distributions in the latent feature space, thereby improving the estimation accuracy in the target domain compared with using either method alone. Regarding the question of how finely the time zone parameter is subdivided, the results in Table 8 show that provides the best accuracy, and further subdivisions tend to reduce accuracy. These results suggest that the granularity at which circadian rhythms are applied is a hyperparameter and that the use of strong regularization at a finer granularity may be counterproductive. Additionally, they suggest that adopting more detailed and flexible time zone parameters aligned with the circadian rhythm of tomatoes could potentially improve the estimation accuracy.
6. Conclusions
A highly accurate water stress estimation model was proposed that supports the automation of precision irrigation control and can be adapted to different domains. A laser displacement sensor is temporarily required for calibration for normalization, but after calibration, the water stress estimation model can be operated with only affordable environmental sensors and an RGB camera. First, to quantify leaf wilting, which represents water stress, two foundational models were used, the CoTracker model for any point tracking and the SAM model for object segmentation, from tomato canopy images captured by an RGB camera. As a result, we succeeded in quantifying leaf wilting with a correlation coefficient of 0.82 with the RSD. Second, daily normalization was suggested as a means to cope with data domain shifts, and environmental and leaf wilting data were used to estimate the RSD as a water stress index. An experiment was conducted to evaluate the estimation accuracy of the model using actual environmental and canopy image data collected from tomato fields, and we demonstrated that it could be estimated with an R2 value of 0.79. Third, to enable the application of the developed model across multiple fields, domain adaptation was proposed, which considered the circadian rhythms of tomatoes, and we combined it with unsupervised domain adaptation by backpropagation. This approach was tested with data from different areas and proved to be adaptable, with an R2 of 0.76.
However, this study has several limitations. The data used in the evaluation experiments were limited to cultivation data from October 2018 to January 2019. Therefore, it is necessary to collect cultivation data from other years and seasons to conduct a comprehensive evaluation. In addition, detailed accuracy comparisons between the developed water stress estimation model and existing water stress estimation algorithms should be performed. Further research will involve connecting the developed water stress estimation model to an automatic irrigation system, conducting field trials in tomato cultivation, and evaluating the subsequent impact on fruit quality.
Author Contributions
Conceptualization, methodology, software, validation, investigation, data curation, formal analysis, and writing—original draft preparation, M.K.; writing—review and editing, R.O. and R.A.; supervision, writing—review and editing, and project administration, H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Japan Science and Technology Agency (JST) FOREST Program (grant number JPMJFR201B).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author because of a contract with a joint research destination.
Acknowledgments
We greatly appreciate Makoto Miyachi, Yuki Furuta (Happy Quality Co., Ltd., Hamamatsu, Japan), and Daigo Tamai (Sun Farm Nakayama Co., Inc., Fukuroi, Japan) for providing the environment for data collection and experimentation.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, N.; Wang, M.; Wang, N. Precision agriculture—A worldwide overview. Comput. Electron. Agric. 2002, 36, 113–132. [Google Scholar] [CrossRef]
- Sinha, B.B.; Dhanalakshmi, R. Recent advancements and challenges of Internet of Things in smart agriculture: A survey. Future Gener. Comput. Syst. 2022, 126, 169–184. [Google Scholar] [CrossRef]
- Obaideen, K.; Yousef, A.A.; AlMallahi, M.; Tan, Y.; Mahmoud, M.; Jaber, H.; Ramadan, M. An overview of smart irrigation systems using IoT. Energy Nexus 2022, 7, 100124. [Google Scholar] [CrossRef]
- Abioye, E.A.; Hensel, O.; Esau, T.J.; Elijah, O.; Abidin, M.S.; Ayobami, A.S.; Yerima, O.; Nasirahmadi, A. Precision Irrigation Management Using Machine Learning and Digital Farming Solutions. AgriEngineering 2022, 4, 70–103. [Google Scholar] [CrossRef]
- Togneri, R.; Kamienski, C.; Dantas, R.; Prati, R.; Toscano, A.; Soininen, J.P.; Cinotti, T.S. Advancing IoT-Based Smart Irrigation. IEEE Internet Things Mag. 2019, 2, 20–25. [Google Scholar] [CrossRef]
- Buttaro, D.; Santamaria, P.; Signore, A.; Cantore, V.; Boari, F.; Montesano, F.F.; Parent, A. Irrigation Management of Greenhouse Tomato and Cucumber Using Tensiometer: Effects on Yield, Quality and Water Use. Agric. Agric. Sci. Procedia 2015, 4, 440–444. [Google Scholar] [CrossRef]
- Nemeskéri, E.; Neményi, A.; Bőcs, A.; Pék, Z.; Helyes, L. Physiological factors and their relationship with the productivity of processing tomato under different water supplies. Water 2019, 11, 586. [Google Scholar] [CrossRef]
- Favati, F.; Lovelli, S.; Galgano, F.; Miccolis, V.; Di Tommaso, T.; Candido, V. processing tomato quality as affected by irrigation scheduling. Sci. Hortic. 2009, 122, 562–571. [Google Scholar] [CrossRef]
- Burgess, S.S.; Dawson, T.E. Using branch and basal trunk sap flow measurements to estimate whole-plant water capacitance: A caution. Plant Soil 2008, 305, 5–13. [Google Scholar] [CrossRef]
- Bettelli, M.; Vurro, F.; Pecori, R.; Janni, M.; Coppede, N.; Zappettini, A. Classification and Forecasting of Water Stress in Tomato Plants Using Bioristor Data. IEEE Access 2023, 11, 34795–34807. [Google Scholar] [CrossRef]
- Gallardo, M.; Thompson, R.B.; Valdez, L.C.; Fernández, M.D. Use of stem diameter variations to detect plant water stress in tomato. Irrig. Sci. 2006, 24, 241–255. [Google Scholar] [CrossRef]
- Meng, Z.; Duan, A.; Chen, D.; Dassanayake, K.B.; Wang, X.; Liu, Z.; Gao, S. Suitable indicators using stem diameter variation-derived indices to monitor the water status of greenhouse tomato plants. PLoS ONE 2017, 12, e0171423. [Google Scholar] [CrossRef] [PubMed]
- Oishi, N. Development of Irrigation Control System in Response to Plant Water Stress in Tomato Hydroponics (2). Environ. Control. Biol. 2002, 40, 91–98. [Google Scholar] [CrossRef][Green Version]
- Wakamori, K.; Mizuno, R.; Nakanishi, G.; Mineno, H. Multimodal neural network with clustering-based drop for estimating plant water stress. Comput. Electron. Agric. 2020, 168, 105118. [Google Scholar] [CrossRef]
- Fernández, J.E.; Cuevas, M.V. Irrigation scheduling from stem diameter variations: A review. Agric. For. Meteorol. 2010, 150, 135–151. [Google Scholar] [CrossRef]
- Ohashi, Y.; Nakayama, N.; Saneoka, H.; Fujita, K. Effects of drought stress on photosynthetic gas exchange, chlorophyll fluorescence and stem diameter of soybean plants. Biol. Plant. 2006, 50, 138–141. [Google Scholar] [CrossRef]
- De Swaef, T.; De Schepper, V.; Vandegehuchte, M.W.; Steppe, K. Stem diameter variations as a versatile research tool in ecophysiology. Tree Physiol. 2015, 35, 1047–1061. [Google Scholar] [CrossRef]
- Thompson, R.B.; Gallardo, M.; Valdez, L.C.; Fernández, M.D. Using plant water status to define threshold values for irrigation management of vegetable crop using soil moisture sensors. Agric. Water Manag. 2007, 88, 147–158. [Google Scholar] [CrossRef]
- SU, S.L.; Singh, D.N.; Baghini, M.S. A critical review of soil moisture measurement. Measurement 2014, 54, 92–105. [Google Scholar] [CrossRef]
- Takayama, K.; Nishina, H. Early Detection of Water Stress in Tomato Plants Based on Projected Plant Area. Environ. Control Biol. 2007, 45, 241–249. [Google Scholar] [CrossRef]
- Wakamori, K.; Mineno, H. Optical Flow-Based Analysis of the Relationships between Leaf Wilting and Stem Diameter Variations in Tomato Plants. Plant Phenomics 2019, 2019, 9136298. [Google Scholar] [CrossRef]
- Zhao, F.; Yoshida, H.; Goto, E.; Hikosaka, S. Development of an Irrigation Method with a Cycle of Wilting-Partial Recovery Using an Image-Based Irrigation System for High-Quality Tomato Production. Agronomy 2022, 12, 1410. [Google Scholar] [CrossRef]
- Shibata, S.; Kaneda, Y.; Mineno, H. Motion-specialized deep convolutional descriptor for plant water stress estimation. In Proceedings of the Engineering Applications of Neural Networks: 18th International Conference, EANN 2017, Athens, Greece, 25–27 August 2017; pp. 3–14. [Google Scholar]
- Kaneda, Y.; Shibata, S.; Mineno, H. Multi-modal sliding window-based support vector regression for predicting plant water stress. Knowl.-Based Syst. 2017, 134, 135–148. [Google Scholar] [CrossRef]
- Yang, X.; Lu, M.; Wang, Y.; Wang, Y.; Liu, Z.; Chen, S. Response Mechanism of Plants to Drought Stress. Horticulturae 2021, 7, 50. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, C.; Robertson, J.S.; Sun, S.; Xu, R.; Paterson, A.H. GPhenoVision: A ground mobile system with multi-modal imaging for field-based high throughput phenotyping of cotton. Sci. Rep. 2018, 8, 1213. [Google Scholar] [CrossRef]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.Y.; et al. Segment Anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–3 October 2023; pp. 4015–4026. [Google Scholar]
- Karaev, N.; Rocco, I.; Graham, B.; Neverova, N.; Vedaldi, A.; Rupprecht, C. Cotracker: It is better to track together. arXiv 2023, arXiv:2307.07635. [Google Scholar]
- Wilson, G.; Cook, D.J. A survey of Unsupervised Deep Domain-Adaptation. ACM Trans. Intell. Syst. Technol. 2020, 11, 1–46. [Google Scholar] [CrossRef]
- Ganin, Y.; Lempitsky, V. Unsupervised Domain Adaptation by Backpropagation. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1180–1189. [Google Scholar]
- Mansour, Y.; Mohri, M.; Rostamizadeh, A. Domain Adaptation: Learning Bounds and Algorithms. arXiv 2009, arXiv:0902.3430. [Google Scholar]
- Redko, I.; Morvant, E.; Habrard, A.; Sebban, M.; Bennani, Y. A survey on domain adaptation theory: Learning bounds and theoretical guarantees. arXiv 2020, arXiv:2004.11829. [Google Scholar]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine Learning in Agriculture: A Review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [PubMed]
- Samuel, O.I.; Chandra, A.M. Recent advances in crop water detection. Comput. Electron. Agric. 2017, 141, 267–275. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Sladojevic, S.; Arsenovic, M.; Anderla, A.; Culibrk, D.; Stefanovic, D. Deep neural networks based recognition of plant diseases by leaf image classification. Comput. Intell. Neurosci. 2016, 2016, 3289801. [Google Scholar] [CrossRef]
- Peng, H.; Li, Z.; Zhou, Z.; Shao, Y. Weed detection in paddy field using an improved RetinaNet network. Comput. Electron. Agric. 2022, 199, 107179. [Google Scholar] [CrossRef]
- Rahnemoonfar, M.; Sheppard, C. Deep count: Fruit counting based on deep simulated learning. Sensors 2017, 17, 905. [Google Scholar] [CrossRef] [PubMed]
- Nan, G.; Zhao, Y.; Fu, L.; Ye, Q. Object Detection by Channel and Spatial Exchange for Multimodal Remote Sensing imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 8581–8593. [Google Scholar] [CrossRef]
- Liu, F.; Chen, D.; Guan, Z.; Zhou, X.; Zhu, J.; Ye, Q.; Fu, L.; Zhou, J. Remoteclip: A vision language foundation model for remote sensing. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5622216. [Google Scholar] [CrossRef]
- Cai, Y.; Zheng, W.; Zhang, X.; Zhangzhong, L.; Xue, X. Research on soil moisture prediction model based on deep learning. PLoS ONE 2019, 14, e0214508. [Google Scholar] [CrossRef]
- Song, X.; Zhang, G.; Liu, F.; Li, D.; Zhao, Y.; Yang, J. Modelling spatio-temporal distribution of soil moisture by deep learning-based cellular automata model. J. Arid Land 2016, 8, 734–748. [Google Scholar] [CrossRef]
- Vaswani, A. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Floridi, L.; Chiriatti, M. GPT-3: Its nature, scope, limits, and consequences. Minds Mach. 2020, 30, 681–694. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Benaim, S.; Wolf, L. One-Sided Unsupervised Domain Mapping. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Bousmalis, K.; Silberman, N.; Dohan, D.; Erhan, D.; Krishnan, D. Unsupervised Pixel-Level Domain Adaptation with Generative Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3722–3731. [Google Scholar]
- Peng, X.; Bai, Q.; Xia, X.; Huang, Z.; Saenko, K.; Wang, B. Moment Matching for Multi-Source Domain Adaptation. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1406–1415. [Google Scholar]
- Zellinger, W.; Grubinger, T.; Lughofer, E.; Natschläger, T.; Saminger-Platz, S. Central Moment Discrepancy (CMD) for Domain-invariant representation learning. arXiv 2017, arXiv:1702.08811. [Google Scholar]
- Moreno-Torres, J.G.; Raeder, T.; Alaiz-Rodríguez, R.; Chawla, N.V.; Herrera, F. A unifying view on dataset shift in classification. Pattern Recognit. 2012, 45, 521–530. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers are Effective for Time Series Forecasting. arXiv 2023, arXiv:2310.06625. [Google Scholar]
- Kanai, S.; Adu-Gymfi, J.; Lei, K.; Ito, J.; Ohkura, K.; Moghaieb, R.E.A.; El-Shemy, H.; Mohapatra, R.; Mohapatra, P.K.; Saneoka, H.; et al. N-deficiency damps out circadian rhythmic changes of stem diameter dynamics in tomato plant. Plant Sci. 2008, 174, 183–191. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).