Multi-Objective Optimisation of the Battery Box in a Racing Car

Abstract

The optimisation of electric vehicle battery boxes while preserving their structural performance presents a formidable challenge. Many studies typically involve fewer than 10 design variables in their optimisation processes, a deviation from the reality of battery box design scenarios. The present study, for the first time, attempts to use sensitivity analysis to screen the design variables and achieve an efficient optimisation design with a large number of original design variables. Specifically, the sensitivity analysis method was proposed to screen a certain number of optimisation variables, reducing the computational complexity while ensuring the efficiency of the optimisation process. A combination of the Generalised Regression Neural Network (GRNN) and the Non-Dominated Sorting Genetic Algorithm II (NSGA-II) was employed to construct surrogate models and solve the optimisation problem. The optimisation model integrates these techniques to balance structural performance and weight reduction. The optimisation results demonstrate a significant reduction in battery box weight while maintaining structural integrity. Therefore, the proposed approach in this study provides important insights for achieving high-efficiency multi-objective optimisation of battery box structures.

1. Introduction

Electric vehicles (EVs) are increasingly popular due to their environmental benefits. Lightweight designs enhance EV efficiency by extending driving range and battery lifespan [1,2]. Over the past few decades, with the rapid development of the automotive industry, researchers have achieved significant progress in the lightweight design of traditional fuel-powered vehicle structures. Examples include advancements in lightweight designs for the vehicle bodies [3], suspension control arms [4], bumpers [5,6], and vehicle doors [7]. Topology optimisation, size optimisation, and topography optimisation are often used in lightweight automotive designs because of their powerful optimisation effects [8,9]. Unlike traditional fuel-powered vehicles, EVs feature unique battery systems. This presents unique challenges for the lightweight design of EV components and parts. For example, an electric vehicle’s battery box must be stronger to protect the battery pack from impacts that could result in accidents and injure passengers [10]. However, a higher-strength battery box will inevitably affect the progress of the vehicle’s weight. Therefore, it becomes a focal point to realize the lightweight design of EVs to ensure that the battery box has sufficiently high strength.

In recent years, considerable efforts have been made in the structural optimisation of battery boxes for EVs. For example, Dong et al. [11] proposed a design concept for a two-level protection scheme, optimising the battery box’s sheet metal structure into a frame-type structure. Zhao et al. [12] conducted shape optimisation on the upper enclosure of the battery box to obtain the distribution of free-reinforcing ribs. Pan et al. [13] proposed a lightweight design method for battery enclosure based on size optimisation. Overall, size optimisation methods are the most popular and widely used in battery box structural design [13,14,15], primarily because batteries are composed of sheet metal.

Improving the mechanical performance of the battery box is also a hot research issue [16,17,18,19,20]. In the process of lightweight design while reducing the weight of the design object, it is essential to ensure that the stiffness, vibration characteristics, and other performance parameters of the battery box are minimally affected [13,21]. This makes the study become a multi-objective optimisation problem (MOOP). When tackling a MOOP, the most common approach currently used is to employ a combination of surrogate models and optimisation algorithms [22,23,24]. The surrogate model methods and optimisation algorithms utilised in the open literature are presented in

Table 1. Overview of surrogate models and optimisation algorithms applied to lightweight design.

Number	Sampling Method	Surrogate Model Methods	Optimisation Algorithms	Number of Design Variables	Reference
1	OED	Response surface models	NSGA II	6	[25]
2	CCD	Artificial neural network	NSGA-II	6	[2]
3	LHS	Genetic programming	NSGA-II	4	[26]
4	LHS	The kriging model	MOGA	5	[27]
5	NA	RBF neural network structure	NSGA-II	3	[15]
6	LHS	Response surface models	NSGA-II	7	[21]

.

However, the research objects in the above studies have relatively few design variables, which means that the optimisation methods may not be suitable for practical battery boxes with a large number of design variables. When it comes to optimising battery box structures with a significant number of original design variables, it is crucial to consider how to choose the appropriate optimisation algorithm and how to establish suitable selection criteria for a certain number of design variables so as to reduce computational complexity. The current literature has not yet discussed these important considerations in detail. Hence, the present study attempts to incorporate sensitivity analysis into the optimisation process to improve the efficiency of optimisation methods for battery boxes with numerous optimisation variables. Specifically, sensitivity analysis is introduced to determine the influence of each optimisation variable on the overall optimisation objective. Based on the sensitivity analysis results, an appropriate number of variables are selected for optimisation, significantly reducing computational costs while ensuring the reliability of the optimisation results. This study will use the battery box of a Formula Student car as a case study to highlight the superiority of the optimisation method proposed in this study.

2. Research Methodology

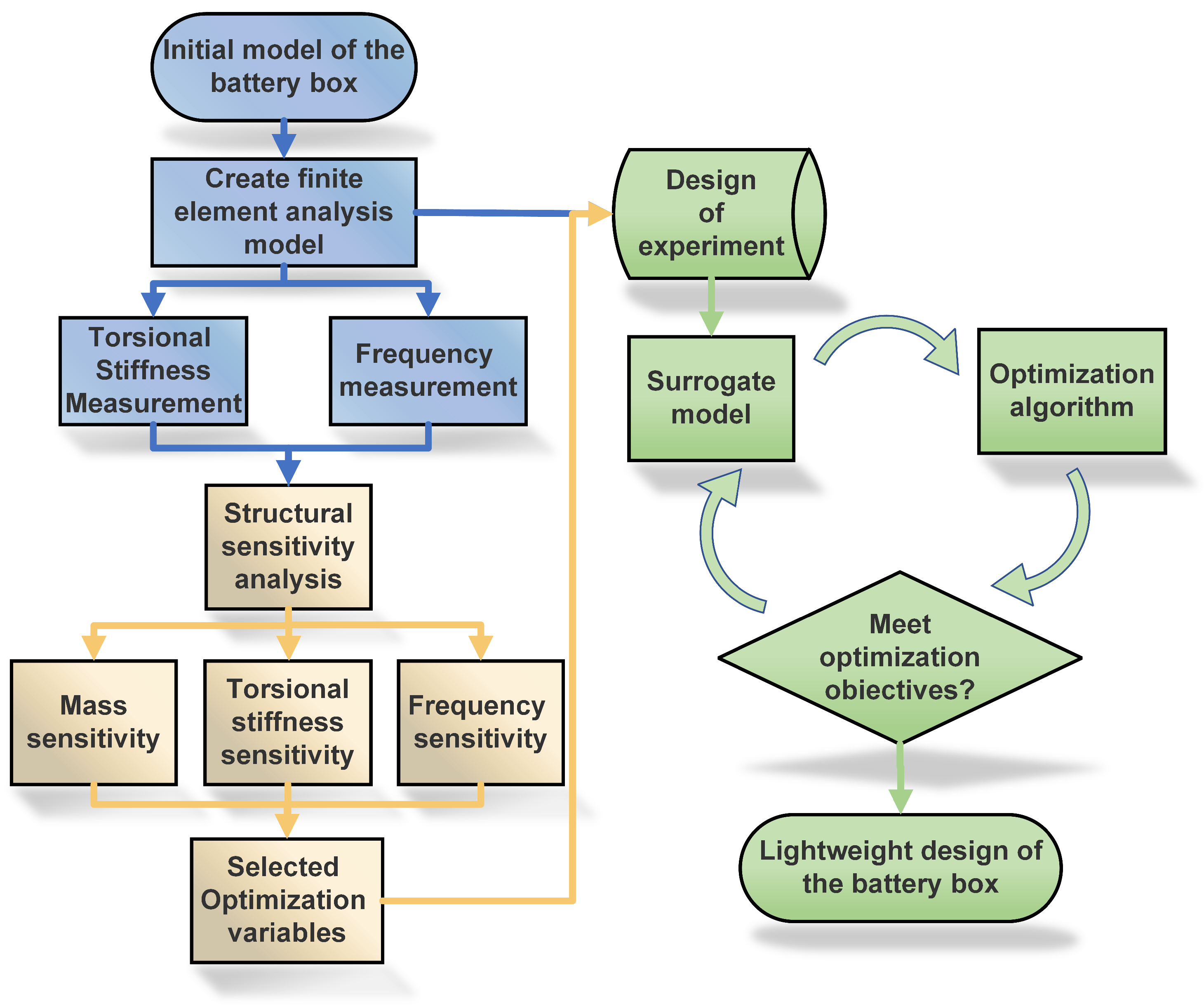
Figure 1 illustrates the overall workflow of the present study. For the first part, the 3D model of the battery box was created using Catia. On this basis, the finite element model of the battery box was developed using Abaqus. Subsequently, the torsional stiffness and frequency of the initial model were evaluated.

For the second part, sensitivity analysis was introduced to select key panels for optimisation to reduce computational effort. First, three sensitivity analysis evaluation metrics from modal analysis were defined: mass, torsional stiffness, and first-order natural frequency. Mass evaluates the weight reduction, which is crucial for the racing car’s performance. Torsional stiffness ensures structural integrity under dynamic loads. First-order natural frequency prevents resonance issues, maintaining safety and performance [3,28].

The sensitivity test results show variations in these three parameters as panel thickness changed from the original 3.00 mm to 1.50 mm. Subsequently, based on the established panel selection principles, certain panels were chosen from all panels as the optimisation variables going forward.

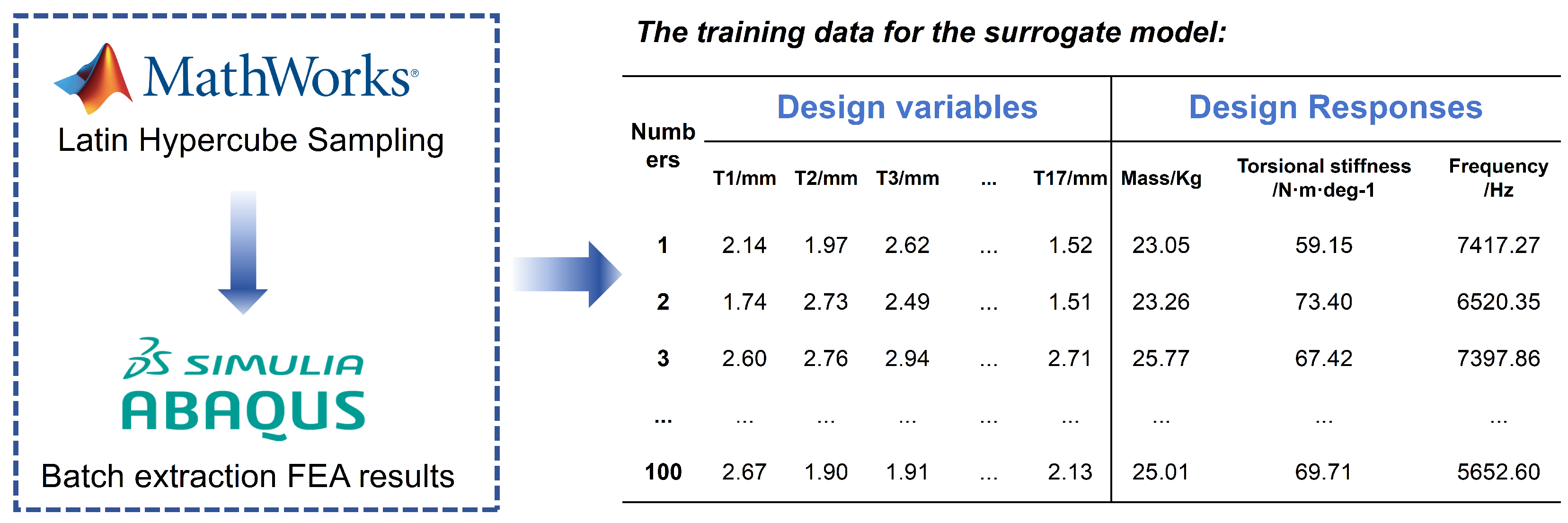
For the third part, the design of experiments based on the Optimal Latin Hypercube Sampling (OLHS) method was performed to select appropriate samples and provide reliable training data for the surrogate model. Matlab R2023a was used to modify the Abaqus input file (.inp), which defines the geometry, material properties, boundary conditions, and loads for batch analysis of various design scenarios. After Abaqus completed the simulations, the resulting displacement and stress data were extracted from the result files to obtain accurate and reliable training samples, the Generalised Regression Neural Network (GRNN) method was utilised to develop the surrogate model, enabling the prediction of output design responses based on input thickness variables. Subsequently, by defining suitable design objectives, constraints, and responses, a mathematical optimisation model was formulated. Finally, a Non-Dominated Sorting Genetic Algorithm II (NSGA-II) was implemented to find the optimal structural design solution based on the established optimisation model.

3. FE Modelling and Sensitivity Test

This section will provide a detailed explanation of the process and basis for developing the finite element model. After that, the methods and the results of the sensitivity analysis testing will be thoroughly introduced.

3.1. FE Modelling

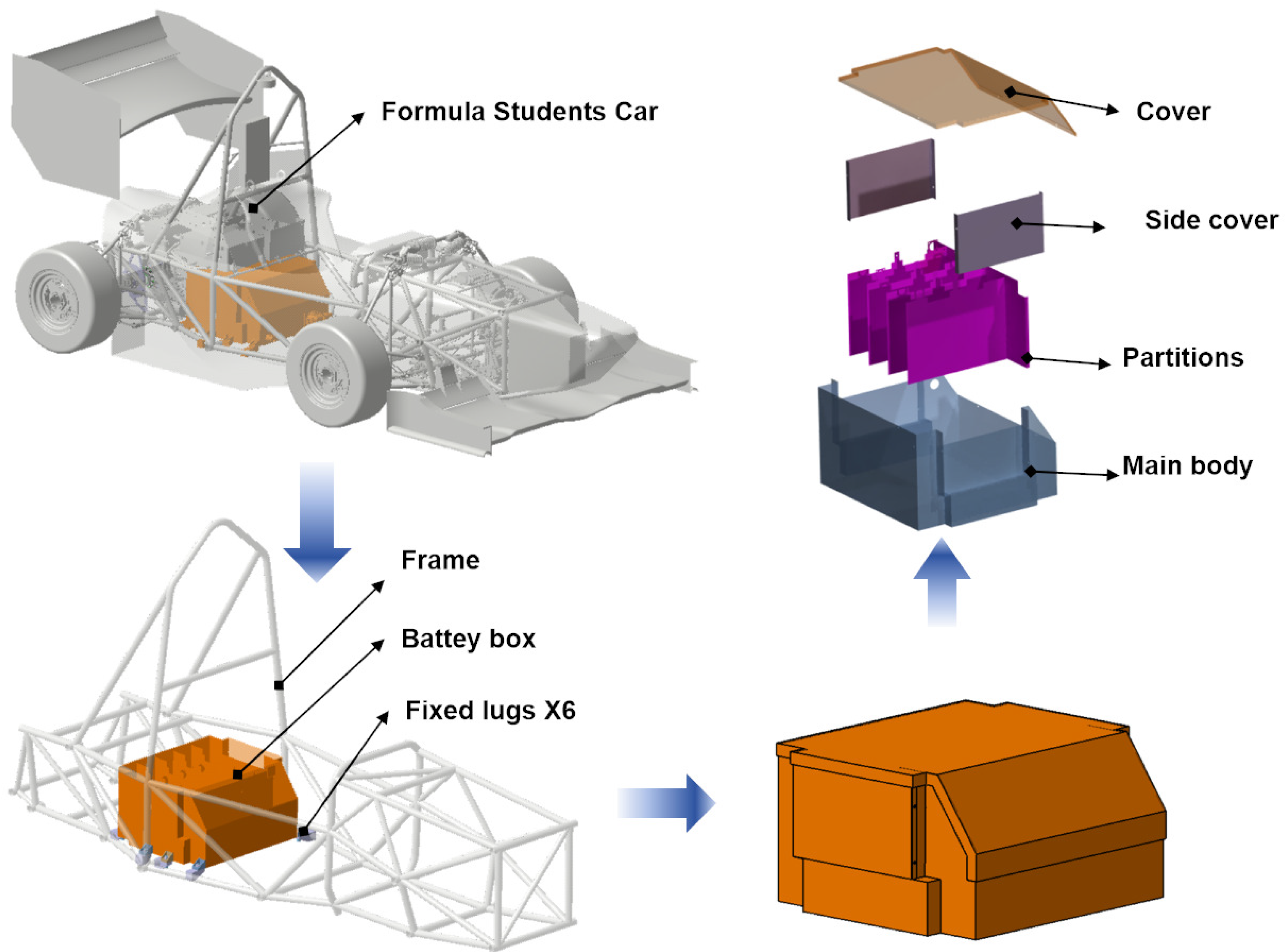
The 3D model of the battery box comprises four components: cover, side cover, partitions, and main body. It is attached to the vehicle’s frame via eight lugs. The dimensional details, design parameters of the battery box model, and mounting locations are presented in

Table 2. Dimensional details and design parameters for the battery box.

Parameter	Value	Unit
Length	420	mm
Width	450	mm
Height	260	mm
Number of battery cells	105	NA
Weight of battery cell	0.305	kg
Number of fixed lugs	8	NA

and Figure 2.

Currently, the materials used for battery boxes include three types: high-strength steel [13], carbon fibre composites [29], and aluminium alloys [14]. To reduce material costs, DC01 (a European standard cold-rolled quality low-carbon steel flat product for cold forming) was selected as the material for the battery box. The material properties of DC01 are shown in

Table 3. Material properties of DC01 [30].

Parameter	Value	Unit
Young’s Modulus	$2.1\times {10}^5$	MPa
Poisson’s Ratio	0.3	NA
Density	8000	${\mathrm{kg}/\mathrm{m}}^3$
Yield Strength	210	MPa
Ultimate Tensile Strength	270	MPa

.

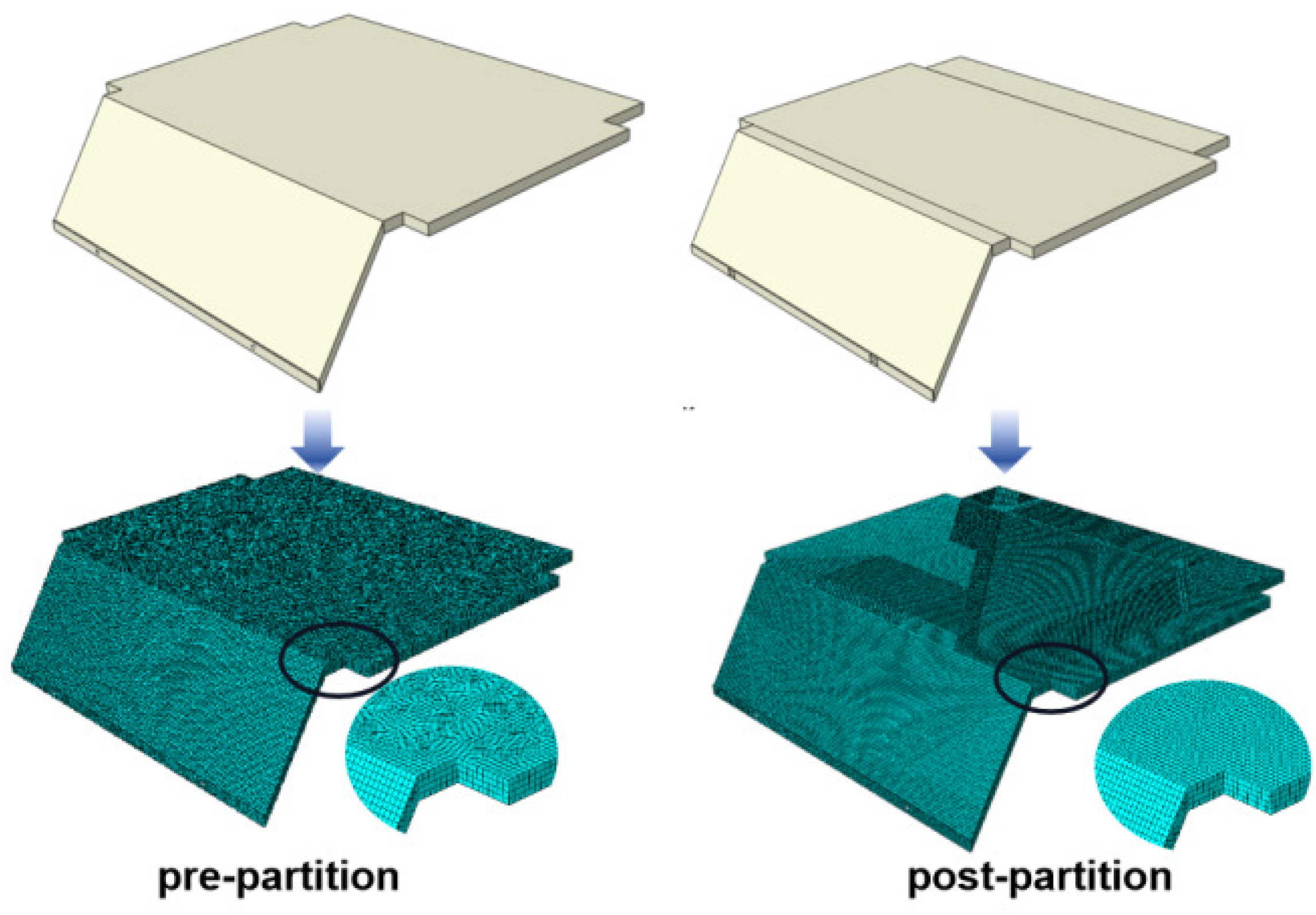
Based on the original design of the battery box model, the initial thickness of each battery box panel was set to 3 mm. Shell elements with an edge length of 4 mm were utilised for meshing in Abaqus. Before partitioning the mesh, it is necessary to create rectangular surfaces from the ones with polygons to improve mesh quality. It should be noted that the surface partitioning process should be performed before establishing the connection relationships to avoid any interference with the connections and prevent them from being invalidated. Figure 3 presents a comparison of the mesh division. The final finite element analysis model consists of 91,209 mesh elements.

3.2. Mesh Convergence Test

Along with the torsional stiffness analysis of the battery box, a mesh independence analysis was conducted to validate the accuracy of the selected mesh size, with the results shown in Figure 4. Five finite element models with varying mesh sizes, ranging from large to small, were created initially. The stress values in the same region were then extracted from the results of these five models and plotted in Figure 4. The mesh convergence testing involved varying only the mesh size as the sole variable to ensure result accuracy. From Figure 4, it can be observed that as the mesh size decreases, the rate of stress variation also decreases. When the mesh size is reduced to 4mm, the stress variation rate is already below 5%. Therefore, it can be considered that the influence of mesh size on the stress results has been minimised and falls within an acceptable range. Considering that further reducing the mesh size would increase computational time and decrease computational efficiency, a final decision was made to choose a mesh size of 4mm. This result verifies the accuracy of the mesh size.

3.3. Boundary and Load Condition

In real-world conditions, the load on the battery box is primarily due to the weight of the five battery modules installed inside—other components, like wires, controllers, resistors, etc., have negligible weights and are ignored. The load acts at the two bolt fixation points and the bottom contact surface. To simulate this, the centre of gravity of the five modules was created and coupled to the two bolt points and bottom surface using the couple command. This ensured loads at the centroids were transmitted to the entire box. Schematics of the centre of gravity and connections are shown in Figure 5a.

Due to its connection with the vehicle frame, the battery box experiences the torsional force exerted on the frame. As a result, the battery box undergoes certain deformation due to the applied torsional force, posing a threat to the safety of the battery modules inside. Therefore, ensuring that the battery box possesses good torsional stiffness is essential to minimise deformation under torsional loads. Torsional stiffness conditions were established as a basis for subsequent sensitivity analysis. The schematic diagram of the torsional load applied to the battery box is shown in Figure 5b. To determine if resonance could structurally damage the battery box, the natural frequencies of the battery box also need to be evaluated. Figure 5c shows the loading condition for measuring natural frequencies.

3.4. Sensitivity Test

This project utilises a commonly employed size optimisation method for the battery box to achieve the lightweight design objective. Figure 6 shows that the battery box consists of 50 panels. Optimising all of the panels would increase computational workload and make finding the optimal solution difficult, due to the excessive number of variables. To address this, a sensitivity test approach is adopted, which involves selecting a certain number of battery box panels based on their impact on three evaluation criteria of the battery box for further optimisation. The mass, torsional stiffness, and first natural frequency obtained from the constrained modal analysis of the battery box were introduced as the three evaluation metrics for the sensitivity analysis.

Sensitivity analysis is an essential tool in design optimisation that helps identify the influence of each design variable on the performance metrics. It provides a quantitative measure of how changes in design variables affect the objectives and constraints of the optimisation problem. To be specific, the sensitivity test measures the extent to which a change in the independent variable of panel thickness affects a dependent variable (battery box overall mass, torsional stiffness, and frequency). In general, the sensitivity of the battery box panel thickness to a specific evaluation metric for the battery box can be defined as Equation (1):

$$S_i=\frac{𝜕e}{𝜕t_i}$$

(1)

where e is the specific evaluation indicator, and $t_i$ is the thickness of the ith panel. In this study, the variation range of the thickness variable is from 50% to 100% [28]. Since the initial thickness is 3 mm, the variation range of the thickness variable is 1.5 mm to 3 mm.

(1)

Mass sensitivity

The mass sensitivity is calculated by taking the derivative of the total mass with respect to the thickness of each panel. The detailed calculation method is as follows. The total mass of the battery box is given as the following equation:

$$M=\sum _{i=1}^{n_i}{m}_i=\sum _{i=1}^{n_i}{\rho }_i{V}_i=\sum _{i=1}^{n_i}{\rho }_i{A}_i{t}_i$$

(2)

where ${\rho }_i$ is the density of the ith panel, $V_i$ is the volume of the ith panel, and $A_i$ is the surface area of the ith panel. The sensitivity of the panel thickness to the mass of the whole battery box becomes:

$$S_M\left(t_i\right)=\frac{𝜕M}{𝜕t_i}=\rho A_i$$

(3)

Since all panels use the same material, they share the same density. Based on Equation (3), the mass sensitivity of each panel is a constant value equal to the product of the panel’s surface area and density.

(2)

Torsional stiffness sensitivity

The torsional stiffness sensitivity involves more complex calculations that consider the structural geometry. It is derived from the torsional moment equation and the strain energy due to the applied torque. The equation to calculate the torsional stiffness of the battery box is as follows [28].

$$R_T=\frac{T}{\varphi }=\frac{F·L}{arctan\left(\frac{u}{L}\right)}$$

(4)

in which T is the torque due to the force applied to the battery box, $\varphi$ is the torsional angle, F is the lumped force, L is the length of the battery box (y-direction), and u is the strain caused by F. The sensitivity of the panel thickness to the torsional stiffness of the whole battery box is shown in Equation (5):

$$\begin{array}{cc}\hfill S_{R_T}\left(t_i\right)=& \frac{𝜕R_T}{𝜕t_i}\hfill \\ \hfill =& \frac{-F}{arctan\left(\frac{u}{L}\right)·\left[1+{\left(uL\right)}^2\right]}·\frac{𝜕u}{𝜕t_i}\hfill \end{array}$$

(5)

(3)

Frequency sensitivity

The sensitivity of the natural frequency to panel thickness is related to the structural dynamics of the battery box. It is calculated using the eigenvalue problem of the system and considering the mass and stiffness matrices. As for the model analysis, the eigenvalue equation is given in Equation (6).

$$(\left[K\right]-{\omega }_n\left[M\right]){\phi }_n=0$$

(6)

where ${\omega }_n$ is the nth eigenvalue, ${\varphi }_n$ is the eigenvector, $\left[K\right]$ and $\left[M\right]$ is the structure stiffness and structure mass, respectively. The sensitivity of the panel thickness to the natural frequency obtained from the constrained modal analysis of the battery box becomes

$$\begin{array}{cc}\hfill S_f\left(t_i\right)=& \frac{𝜕{\omega }_n}{𝜕t_i}\hfill \\ \hfill =& \frac{{\left\{{\varphi }_n\right\}}^T\left(\frac{𝜕\left[K\right]}{𝜕t_i}-{\omega }_n\frac{𝜕\left[M\right]}{𝜕t_i}\right)\left\{{\varphi }_n\right\}}{{\left\{{\varphi }_n\right\}}^T\left[M\right]\left\{{\varphi }_n\right\}}\hfill \end{array}$$

(7)

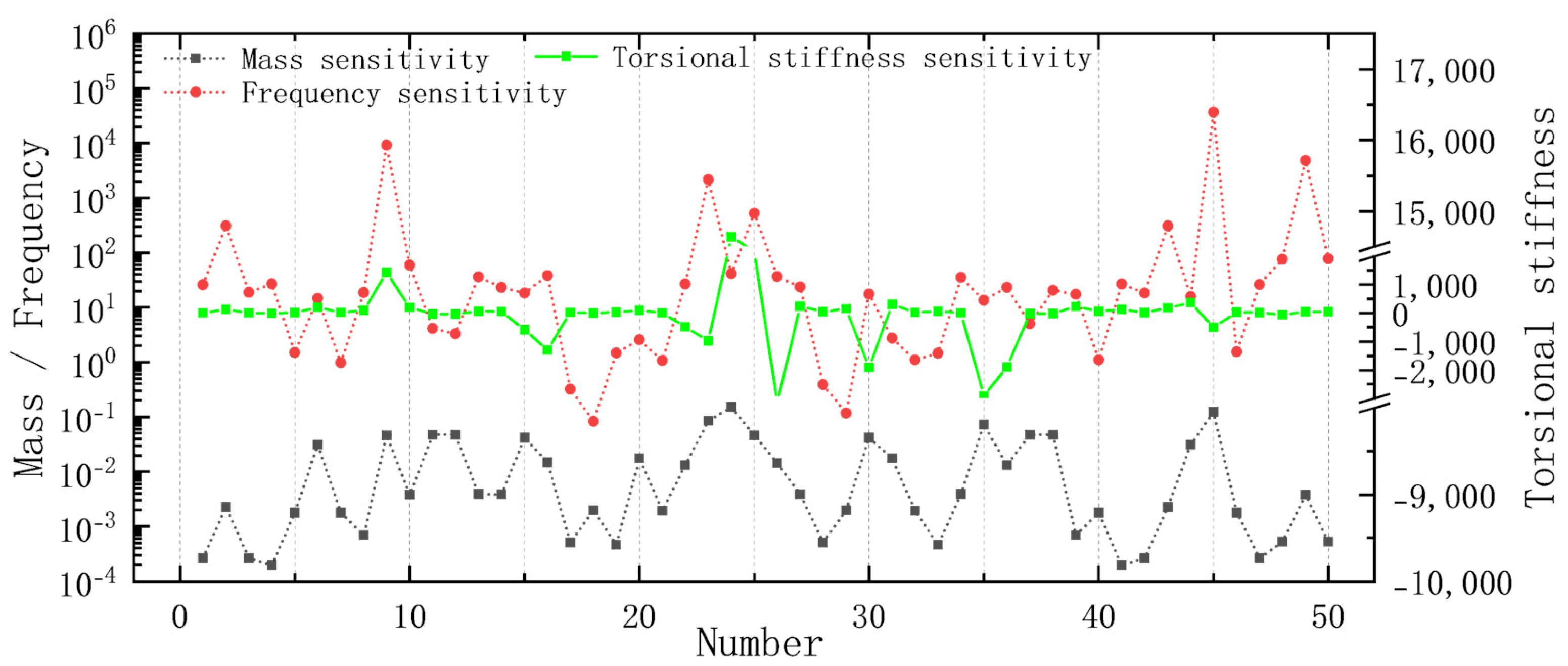
Based on the established finite element model, the sensitivity analysis results were solved in Abaqus. This involved determining the variation in the three evaluation indicators, i.e., the battery box’s overall mass, torsional stiffness, and the first natural frequency from the constrained modal analysis, for each panel’s thickness in the range of 1.5 mm to 3 mm. The results are depicted in Figure 7. Positive sensitivity indicates a positive correlation, e.g., battery box overall mass increases with panel thickness, and negative sensitivity represents a negative correlation. It can be observed that, for the same panel, there are differences in the magnitude and sign of the sensitivity results for the three evaluation indicators.

To address this issue, this project proposes two selection principles for identifying suitable panels for subsequent optimisation design. The mathematical expressions for the two selection principles are shown in Equation (8).

$$\left\{\begin{array}{c}{S}_M>4.8\%\hfill \\ S_{R_T}<0and{S}_f<60\hfill \end{array}\right.$$

(8)

The first principle is that the mass sensitivity should be greater than 4.8%. The rationale for this principle is that selected panels with high mass sensitivity cannot be ignored during optimisation; otherwise, significant lightweighting effects would be hindered. The selection of 4.8% as the lower threshold for mass sensitivity is grounded in rigorous data analysis and optimisation strategies. To adhere to the first principle and identify approximately half of the panels (totalling 50), an initial screening revealed a sensitivity range starting at 4.95%. However, closer examination highlighted a concentrated distribution of data points within the 4.8% to 4.95% mass sensitivity interval, suggesting these panels possess greater potential impact and influence on lightweight design efforts. Therefore, 4.8% was established as a prudent lower limit for mass sensitivity to ensure the optimisation process effectively leverages panels with higher sensitivity.

The second principle is that torsional stiffness sensitivity should be less than 0, and frequency sensitivity should be less than 60. The selection of 60 as a threshold for frequency sensitivity is based on data analysis showing that the 0–60 range contains a dense concentration of data points. Panels with a frequency sensitivity greater than 60 have an average frequency sensitivity greater than 600, indicating significant influence. Optimising these panels can increase the battery box’s torsional stiffness while ensuring a controlled frequency reduction. Based on the above selection principles, a total of 17 panels have been chosen as the subsequent optimisation variables (highlighted in red in Figure 6).

4. Optimisation Process

In this section, the generation process of initial samples for training the surrogate model will first be presented. Next, the selection process, principles, and development of the surrogate modelling method will be explained, along with the evaluation process for the predictive accuracy of the surrogate model. Finally, the principles of the chosen optimisation algorithm and the results will be presented.

4.1. Design of Experiment

Different sampling methods can impact the fitting accuracy of surrogate models [2,31,32]. It has been proven that the Optimal Latin Hypercube Sampling (OLHS) method has significant advantages in fully exploring the design space [33]. Optimal Latin Hypercube Sampling (OLHS) is a sampling technique that stratifies the entire design space prior to sampling. As a result, it has advantages in achieving uniform sampling in multidimensional space. Therefore, the OLHS method was selected for sampling in the present study. In the present study, the total sample consisted of the thicknesses of 17 panels, with each panel’s thickness ranging from 1.5 mm to 3 mm. In order to save costs and ensure the manufacturing accuracy of the raw material for the battery box panels, the panel thickness accuracy was determined to be 0.01 mm. Therefore, the sampling interval was set at 0.01 mm. The number of sampling points was set to 100. After completing the sampling process, Abaqus was utilised to calculate the response values (battery box weight, torsional stiffness, and the first natural frequency from the constrained modal analysis) for the 100 samples. The above process is depicted in Figure 8.

4.2. Surrogate Modelling

Different surrogate models exhibit varying levels of accuracy when fitting different engineering problems. As a result, it is common practice to employ multiple methods to construct surrogate models and then select the one with the highest accuracy as the final surrogate model [2,3,26]. Three methods, namely Kriging, Generalised Regression Neural Network, and Response Surface Method were utilised to develop surrogate models for predicting the relationship between the thickness of 17 panels and the torsional stiffness and the natural frequency of the battery box. To determine the surrogate model with the highest predictive accuracy among the three methods, the following four statistical evaluation criteria are introduced:

(1)

Coefficient of determination ($R^2$)

The coefficient of determination measures the model’s goodness of fit to the dependent variable (the target variable) and ranges between 0 and 1. A higher $R^2$ value indicates a better fit, with 1 representing a perfect fit and 0 indicating a poor fit. The equation for the coefficient of determination is shown in Equation (9).

$$R^2=1-\frac{{\sum }_{i=1}^N{(y_i-\widehat{y_i})}^2}{{\sum }_{i=1}^N(y_i-{\overline{y_i})}^2},$$

(9)

where N is the number of the samples, $y_i$ is the actual values, and $\widehat{y_i}$ is the predicted values from the surrogate model.

(2)

Root Mean Squared Error (RMSE)

The Root Mean Squared Error (RMSE) measures the average error between the model’s predicted and actual values. A smaller RMSE indicates a better predictive performance of the model. The equation for the RMSE is shown in Equation (10).

$$RMSE=\sqrt{\frac{1}{N}\sum _{i=1}^N{(y_i-\widehat{y_i})}^2}$$

(10)

(3)

Average Relative Deviation (ARD)

The Average Relative Deviation (ARD) measures the average relative error between the model’s predicted values and the actual values. A smaller ARD indicates better predictive performance. The expression for the ARD is shown in Equation (11).

$$ARD=\frac{1}{N}\sum _{i=1}^N|\frac{y_i-\widehat{y_i}}{y_i}|$$

(11)

(4)

The Maximum Relative Error Rate

The Maximum Relative Error Rate measures the maximum relative error between the model’s predicted values and the actual values. The equation for the maximum relative error is shown in Equation (12).

$$\mathrm{The}\mathrm{Maximum}\mathrm{Relative}\mathrm{Error}\mathrm{Rate}=max|\frac{y_i-\widehat{y_i}}{y_i}|$$

(12)

Figure 9 presents the comparative results of the three surrogate models across the four statistical evaluation metrics. Ultimately, since the Generalised Regression Neural Network (GRNN) outperformed the other two methods across the four metrics, it was selected as the approach for building the surrogate model.

4.3. Optimisation Result

In the research process of structural optimisation, there are various algorithms applied. In this project, the Elitist Non-dominated Sorting Genetic Algorithm (NSGA-II) was selected from among various algorithms used for structural optimisation problems due to its low computational complexity and its ability to find the optimal set of solutions through the most robust and direct approach [34,35]. NSGA-II was first proposed by Deb et al. [34] in 2002 as a fast nondominated sorting method based on the original Nondominated Sorting Genetic Algorithm (NSGA), significantly improving the algorithm’s convergence and simplicity. The mathematical model for optimisation study in this paper is represented as Equation (13).

$$\left\{\begin{array}{c}\mathrm{find}T=(T_1,T_2,\dots ,T_{17})\hfill \\ \mathrm{Obj}.\mathrm{Min}f\left(x\right)\hfill \\ \mathrm{Max}{S}_T\left(x\right)\hfill \\ \mathrm{Max}{f}_T\left(x\right)\hfill \\ \mathrm{S}.\mathrm{t}.f_T^{\left(min\right)}<f_T\hfill \\ S_T^{\left(min\right)}<S_T\hfill \\ \mathrm{d}.\mathrm{v}.T_i^{\left(min\right)}\le T_i\le T_i^{\left(max\right)}\hfill \end{array}\right.$$

(13)

where M is the total mass of the battery box, $S_T$ is the torsional stiffness, $f_T$ is the first natural frequency of the battery box from the constraint modal analysis, and $T_i$ is the panel thickness of the ith panel. The definitions of the other symbols are summarised in

Table 4. The definition of the other symbols for the mathematical model in Equation (13).

Symbol	Meaning	Value
$f_T^{\left(min\right)}$	The lower limits of the natural frequency	60 Hz
$S_T^{\left(min\right)}$	The lower limits of the torsional stiffness	7000 N· m/deg
$T_i^{\left(min\right)}$	The lower limits of the panel thickness	1.5 mm
$T_i^{\left(max\right)}$	The upper limits of the panel thickness	3 mm

. The model aims to find the battery box structure with the lowest mass within a certain range of panel thicknesses while ensuring that the torsional stiffness and natural frequency are within a predetermined range.

The NSGA-II algorithm was employed to solve the aforementioned multi-objective deterministic optimisation design model in MATLAB, with the algorithm’s parameters given in

Table 5. The NSGA-II algorithm’s parameters.

Parameter	Value
Population Size	1000
Generations	100
Pareto fraction	0.4
Tolerance level	$1\times {10}^{-10}$

.

In MOOP, the objectives often exhibit conflicting or competing natures, leading to no single design point being superior in all the optimisation objectives. Therefore, the optimisation result consists of a set of solutions rather than a single optimal solution, known as the Pareto solution. Based on the results obtained from NSGA-II, the Pareto solutions are shown in Figure 10. According to Equation (13), within this Pareto solution, the solution with the lowest mass while meeting specific ranges for torsional stiffness and natural frequency was selected as the final optimisation result for this study. This selected point is also marked in Figure 10. Torsional stiffness and frequency are shown in the graphs as the negative of the actual values to accommodate the optimisation results.

After selecting the appropriate optimisation result, the corresponding thicknesses of the 17 panels are extracted and validated using Abaqus. The optimisation results and original data of the battery box are given in

Table 6. Comparison of optimised and original results.

Type	Mass (kg)	Frequency (Hz)	Torsional Stiffness (N· m/deg)
Original	25.91	143.58	8309.35
NSGA-II solution	21.99	63.55	7050.73
Change rate	−15.13%	−55.74%	−15.15%

. It shows that the final chosen optimisation result achieves the initial lightweight design target (10%), maintaining the structural performance to meet the design requirements. Although the natural frequency has decreased significantly, its value is still sufficiently high to avoid resonance.

5. Superiority of the Optimisation Approach

To highlight the advantages of the proposed approach, it is compared with the optimisation method involving all variables. By comparing the calculation time and optimisation results of the two methods, the superiority of the proposed method is highlighted, which is summarised in

Table 7. Summary of surrogate models and optimisation algorithms.

Type	Solution Duration (h)	Mass (kg)	Frequency (Hz)	Torsional Stiffness (N· m/deg)
optimised results for 17 panels	0.21	22.09	70.17	7175.45
optimised results for 50 panels	0.89	21.85	108.49	5599.8
Relative change	323.81%	−0.63%	54.61%	21.96%

. The solution duration for the optimisation with 17 panels was significantly shorter (0.21 h) compared to 50 panels (0.89 h). This demonstrates a considerable reduction in computation time by 323.81% when using variable screening. The method proposed in this paper maintained the effectiveness of the optimisation process. For instance, the mass and torsional stiffness were comparable in both scenarios, with the mass slightly decreasing by 0.63% and torsional stiffness increasing by 21.96% for the 17 panels scenario. The frequency saw a notable increase of 54.61%, indicating enhanced performance. Therefore, using sensitivity analysis to select an appropriate number of design variables has been proven to be a relatively superior multi-objective optimisation approach for battery boxes.

To demonstrate the reliability of the optimisation results, the final results were validated through the finite element analysis model, with the validation results presented in

Table 8. Comparison of predicted and actual data.

Type	Mass (Kg)	Frequency (Hz)	Torsional Stiffness (N·m/deg)
Actual(Abaqus)	22.09	70.17	7175.45
Predicted	21.99	63.55	7050.73
Relative error	0.45%	9.43%	1.74%

. From the table, it can be seen that all the errors are less than 10%, which proves that the optimisation process ensures better accuracy while maintaining efficiency.

6. Concluding Remarks

This study introduced an efficient approach applicable to multi-objective lightweight design optimisation of battery boxes, including FE modelling, sensitivity analysis, and multi-objective optimisation based on GRNN method and NSGA-II. The main conclusions of this study are as follows:

• Applying sensitivity analysis in the lightweight design process to select a certain number of panels as variables effectively reduced computational complexity while ensuring sufficient optimisation potential during the process.
• The relative error assessment between predicted and actual values indicated that the surrogate model based on the GRNN method has high accuracy.
• Leveraging the precise finite element model and high-fidelity surrogate model, the optimisation algorithm successfully achieved a lightweight design of the battery box.

Section 2 discussed the thought process behind establishing the research flowchart. This exploration provided valuable insights into the coherent progression of the study, elucidating the intricate interconnections among its diverse components. In Section 3, the relationship between the FEA model and the real-world scenario was considered, as well as the data processing of sensitivity analysis results. These discussions highlighted the importance of ensuring the accuracy of the finite element analysis model and the significance of effectively handling sensitivity analysis results. The two-panel selection principles proposed in this section lay the foundation for a subsequent, efficient optimisation process. In Section 4, the thought process behind selecting the sampling method, surrogate model construction method, and optimisation algorithm was discussed. These discussions were crucial as they determined the rigour and reliability of the analytical results obtained throughout the study.

In the context of multi-objective optimisation problems, the various objectives often exhibit conflicting or competing characteristics, leading to the absence of a single data point that is optimal for all optimisation goals. As a result, optimisation outcomes consist of a set of solutions, rather than a singular optimal solution. Therefore, the process of selecting the most suitable results from the entire set of optimised solutions is crucial for multi-objective optimisation problems.

The present study effectively addressed the multi-objective optimisation problem for battery boxes with numerous variables. The presented approach in this paper offers valuable insights for performing efficient multi-objective optimisation of battery box structures containing numerous original design variables. The optimisation approach incorporating sensitivity analysis can also be applied to other areas of automotive structures, to aid in designing safe and reliable mechanical structures. Future research in these areas can be pursued in the following three aspects:

• Experimental verification: conduct structural testing on the battery box to validate the accuracy of the finite element analysis results, thereby ensuring the reliability of the optimisation outcomes.
• Reduce optimisation algorithm complexity: There might be combinations of surrogate model methods and optimisation algorithms with higher precision to optimise the structure of the battery box. Thus, this becomes a focal point for future research.