Numerical Simulation and Design of a Mechanical Structure of an Ankle Exoskeleton for Elderly People

Abstract

This article presents the numerical simulation and design of an ankle exoskeleton oriented to elderly users. For the design, anatomical measurements were taken from a user of this age group to obtain an ergonomic, resistant, and exceptionally reliable mechanical structure. In addition, the design was validated to support a “weight range” of users between 50 and 80 kg in order to evaluate the reaction of the mechanism within the range of loads generated in relation to the first principal stress, the safety coefficient, the Von Mises stress, and principal deformations, for which the 3D CAD software Autodesk Inventor and theoretical correlations were used to calculate the displacement and rotation angles of the ankle in the structure. Likewise, two types of materials were evaluated: ABS (acrylonitrile butadiene styrene) and a polymer reinforced with carbon fiber. Finally, the designed pieces were assembled with the guarantee that the mobility of the system had been validated through the numerical simulation environment, highlighting that by being generated through 3D printing, manufacturing costs are reduced, allowing them to be accessible and ensuring that more people can benefit from this ankle exoskeleton.

1. Introduction

Walking is one of the most common actions performed on a daily basis; in this context, the legs play a very important role since they are the main engine of movement in human beings [1]. Among the parts that make up the leg is the ankle, one of the most injury-prone joints, and elderly people are more prone to suffer injuries in this joint (approximately 80% of patients with a history of ankle sprain undergo surgery for post-traumatic ankle osteoarthritis [2]).

The past ten years have seen the development of several prototypes of exoskeletons, although not all of them have been designed for the same purpose. The authors Hong, M. B., Kim, G. T., and Yoon, Y. H. [3] offer an example of such mechanisms. They describe an ankle exoskeleton that is designed for military applications and eliminates the hazards that may be encountered while walking. This enables users to boost their physical capacity and performance significantly. Another study is the one that was designed by Cho, Y. K., Kim, K., Ma, S., and Ueda, J. [4]. This research effort was aimed at the construction industry, with the authors designing an exoskeleton to improve workers’ posture while also reducing tiredness in their muscles and joints. Additional applications for exoskeletons include those used in agriculture [5], those used in physical rehabilitation clinics [6], and those created for medical purposes [7].

As a result of the fact that the human body poses a wide variety of challenges, the applications of exoskeletons in the field of medicine are virtually limitless. For example, lower-limb exoskeletons have been developed that use finite-time extended-state observers to compensate for uncertainties and improve assistance in people’s daily activities by dynamically adjusting assistance strategies according to human motor intentions and probabilistic models of knee motion [8]. Another investigation matched geometric lengths to simplify the designed model. Their focus was on the dynamics of swing during walking, and they used a spring-damper system to analyze human–exoskeleton interaction forces. They also took into consideration existing deviations between the design and people’s legs [9]. One of the most common types of injuries is a joint injury, which can cause discomfort, a reduction in movement, or a weakening of the muscles’ resistance. Thus, exoskeletons offer a possible answer to these issues, which may explain why they are presently available for purchase in the medical field; however, not everyone can afford them, as they are quite expensive [10]. Because of its high injury risk, this article will use the ankle as its focus joint in its numerical simulation of an exoskeleton with the goal of reducing joint problems. It is more practical to focus on a single joint at a time to achieve an anatomically appropriate mechanical design [11]. As a result of the fact that it is common knowledge that people’s physical limitations vary depending on their age [12], it is essential to direct the research towards a particular group, specifically the elderly, due to the fact that they are more likely to experience ankle complaints. Also, since it is desired that this mechatronic device be low-cost, it is imperative to create a simple but effective mechanical design that can be fabricated using techniques that do not significantly increase the total cost of the prototype. These reasons led us to consider research on ankle exoskeletons carried out by other authors.

Using an ankle exoskeleton, Van Dijk, W., Meijneke, C., and Van Der Kooij, H. [13] presented a device designed to deliver a force impulse to the ankle joint. For the purpose of providing the user with a comfortable and ergonomic experience, the mechanical design is sturdy, and there is a separate one for each leg. Despite this, it is a very pricey design that is out of reach for the majority of people because it is constructed out of carbon fiber and comprises high-end components.

Through the use of an untethered device, Lerner, Z. F. et al. [14] suggested an ankle exoskeleton as a means of lowering the amount of metabolic energy that is consumed. Their mechanical design is composed of steel cables, pulleys, tensioners, and other components attached to the ankle weighing 0.55 kg in addition to other control and actuation components, which are located on the back of the hip and weigh 1.30 kg. Although it is a lightweight mechanism, they showed that this weight increased the metabolic consumption of some users significantly.

Jacobs, D. A., Koller, J. R., Steele, K. M., and Ferris, D. P. [15] developed an exoskeleton to investigate muscle recruitment patterns during walking. Their mechanical design was composed of hard plastic sections placed under the user’s foot, an ankle joint made of stainless steel, and a padded plastic brace to hold the shin, among other components. Techniques such as welding and riveting were used for the assembly. Although the exoskeleton was tested under two conditions, with assisted force and without assisted force, the results were shown to be similar, which does not guarantee that the use of this device will be of great help in understanding muscle recruitment.

2. Materials and Methods

2.1. Anatomy and Biomechanics of the Foot

For the completion of this research work, concepts of anatomy and biomechanics of the ankle were needed to define the travel distances and rotation angles of some of the pieces of the exoskeleton and thus emulate the natural movement of people during walking. The most important concepts are defined below: among the most important parts of the musculoskeletal system are the foot and the ankle, which perform important functions in walking and running, supporting and distributing body weight.

The foot is divided into different zones: plantar [16], dorsal, medial, and lateral borders. Balance and gait depend on the proper functioning of the feet [17]. When analyzing its skeletal structure, the foot has 28 bones divided into three parts: the tarsus [18], metatarsus [19], and phalanges [20].

Likewise, the muscles of the foot are divided into two categories: extrinsic muscles, which originate from the external part of the foot and act on the foot, and intrinsic muscles, which arise from the bones of the foot and attach to them [21]. Regarding the ankle, it should be noted that it is a hinge-type synovial joint formed by three bones [22]: the tibia, the fibula, and the talus. Within this joint group, there are the tibioastragaline, peroneoastragaline, and tibioperoneal ligaments. Because it is a synovial joint, the joint capsule covers the articular surfaces of the three bones that make up the ankle [23]. This joint is one of the most complicated joints in terms of mobility since it has a shape that is half spherical, and this is the primary reason why it features movements in all three planes that intersect it [24].

The ankle has six movements, two for each plane that crosses it:

• Dorsiflexion and plantar flexion in the sagittal plane [25];
• Abduction and adduction in the transverse plane [26];
• Inversion and eversion in the frontal plane [27].

This joint has an angular sweep of 40° of dorsiflexion and 30° of plantar flexion. The abduction and adduction movements are performed by moving the toe toward or away from the medial axis of the body so the plane of support is not modified. The arc of motion for inversion–eversion is 20° and 30°, respectively.

Walking is the process by which the human body stands upright, moves forward, and supports its weight on the legs during the gait cycle [28]. As the body moves on one supporting leg, the other leg swings forward in preparation for the next step. One foot is always in contact with the ground, and both feet remain on the ground for some time, transferring the weight from the rear leg to the front leg. A summary of the phases involved and the leg muscles that are activated are listed in

Table 1. Summary of the phases involved in human walking and their muscles of activation.

Phase	Activated Muscle
Initial foot contact	Dorsal flexors, hamstrings, gluteus maximus, and medius
Initial of support	Dorsal flexors, hamstrings, gluteus maximus, and medius
Middle of support	Soleus, posterior tibialis, and peroneals
End of support	Triceps suralis
Pre-oscillation	Hip flexors and calf muscles
Initial of oscillation	Flexor of the first finger
Middle of swing	Dorsi flexors
End of Swing	Quadriceps and dorsal extensor flexors

[29].

This muscle action allows the synchronization of joint movements and allows the individual to adjust the speed of the movement through the action of each muscle [30]. If a kinematic approach is performed on the ankle during human walking, three main stages and cyclic intervals are described as follows.

The first phase involves the outer back of the heel, which contacts the ground. The ankle leaves the neutral position to approximately 15° of plantar flexion.

The second phase involves a fluctuation from the back to the front of the second leg, which is about to receive support during the movement. The dorsiflexion movement in this phase increases from the previous position to approximately 5°.

The third phase allows the ankle to extend progressively. At the beginning, the ankle is positioned at approximately 15° of dorsiflexion to end the movement at about 25° of dorsiflexion [31].

Indeed, it is essential to analyze some materials, as well as their physical characteristics, in order to have a better idea of what each one offers. First, we have acrylonitrile butadiene styrene (ABS), which is a resistant material with good performance [32]. This material is characterized as being one of the most resistant within the family of synthesized polymers, which is why it is one of the most used in different industries, such as automobile and manufacturing, among others [33].

Likewise, a carbon fiber-reinforced polymer is a tentative option. Carbon fiber is a material composed of thousands of carbon fibers approximately 5 to 10 micrometers in diameter [34], and due to its geometry, it is one of the most used materials in the aeronautical industry, aerospace, military applications, etc. [35].

Following an examination of prior research, the research team evaluated the idea of developing a mechanical system for an ankle exoskeleton that would be geared toward older adults with the goal of boosting motor abilities and reducing joint difficulties.

2.2. Proposed Method

Four distinct steps make up the methodology that has been proposed for the mechanical design of the ankle exoskeleton. It was proposed during the first stage (A) to acquire anatomical measurements of the leg of an old user in order to produce pieces that were ergonomic and easy to modify. This would ensure that the device would not be a burden to the user when they were wearing it. As part of the second step (B), a kinematic analysis of the ankle was carried out, and some physical calculations of the forces and stresses that are associated with this device were also carried out. On the basis of these findings, it proceeded to the third stage (C), which consisted of the design of each individual component of the exoskeleton as well as the assembly of the entire structure. In the last step, which was designated as (D), the emphasis was placed on numerical simulations in order to determine the most suitable composite material for 3D printing the mechanism. An illustration of the block diagram of this process can be found in Figure 1.

2.2.1. Taking Anatomical Measurements

Using a tape measure, it was required to record the main anatomical measurements of the user’s leg in order to build biomedical equipment that is user-friendly and ergonomic. In this particular instance, the user was a 66-year-old male who weighed 70 kg and stood at 172 cm tall. It should be noted that the user had no pathological conditions that altered the way he walked or stepped and no supination or pronation movements; that is, he was ideal for the use of the device. This user was chosen for his standard anatomical measurements (mainly his size and calf circumference) since, as explained in some studies [36,37], the measurements of elderly people do not fluctuate significantly. That is, by having average measurements, it is guaranteed that the designed device can be easily used by different elderly users without compromising its ergonomics and comfort.

Table 2. Anatomical measurements of the user.

Zone	Measurements (mm)
1/2 of calf length	170.00
Calf circumference	361.85
3/4 of foot length	170.00
Foot width	69.15
Vertical distance between the heel and fibula	50.00

contains the results of the measurements that were taken. These measurements were utilized during the third stage (C).

2.2.2. Kinematic Analysis and Physical Calculations

Analyses were performed on the kinematics of the ankle as well as the many motions that it can perform. Because this joint appears to be in the shape of an uneven sphere [38], it exhibits movement in all three planes that intersect it. Particular attention was devoted, for the objective of design, to the axial plane of the ankle, which is the plane in which plantar flexion and dorsiflexion movements are accomplished.

Since the magnitude of the Von Mises stress is comparable to that of the elastic strain energy, it is a physical quantity that is utilized extensively in the field of structural engineering. It is also used as an indicator when designing pieces with ductile materials in the analysis of structures on elastic failure theories [39].

In mathematical terms, the Von Mises stress at a point must not exceed the yield stress for elastic failure not to occur [40]. This interpretation is depicted in Equation (1):

$${\sigma }_{VM}=\sqrt{\frac{1}{2}\left({({\sigma }_1-{\sigma }_2)}^2+{({\sigma }_1-{\sigma }_3)}^2+{({\sigma }_2-{\sigma }_3)}^2\right)}<S_y,$$

(1)

where ${\sigma }_{VM}$ is the Von Mises stress, ${\sigma }_1$, ${\sigma }_2$, and ${\sigma }_3$ are the principal stresses of a ductile object at a specific point, and $S_y$ is the tensile yield stress.

One way to calculate the safety coefficient is to divide the maximum capacity of a system by the value of the real expected requirement [41]. In this sense, in Equation (2), the parameters involved are the following:

$$FS=\frac{{\sigma }_{MAX}}{{\sigma }_{RE}},$$

(2)

where FS is the safety factor (safety coefficient), ${\sigma }_{MAX}$ is the maximum stress, and ${\sigma }_{RE}$ is the real expected calculated stress. Likewise, the safety coefficient can be expressed in terms of the Von Mises stress. Taking Equation (1) and defining an analysis point, Equation (3) is obtained as follows:

$$n=\frac{S_y}{\sqrt{\frac{1}{2}\left({({\sigma }_1-{\sigma }_2)}^2+{({\sigma }_1-{\sigma }_3)}^2+{({\sigma }_2-{\sigma }_3)}^2\right)}},$$

(3)

where n is the safety coefficient, S_y is the tensile yield stress, and ${\sigma }_1$, ${\sigma }_2$, and ${\sigma }_3$ are principal stresses of an object.

In this sense, such an operation may be greater or less than one. On the one hand, the first case means that the loads assigned to the piece can be resisted by the manufacturing material. On the contrary, if the result is less than one, it is very likely that the piece will break at some point in its geometry. Thus, this implies resizing the part or simply changing the material [42].

When a kinematic analysis was taken into consideration, Erdogan et al. [43] stated that the dorsiflexion movement spreads approximately 30 degrees, while the plantar flexion motion spreads a 40-degree sexagesimal. Therefore, we may utilize these factors and raise a proportion (displayed in Equation (4)), which will be significant for establishing the rotation restrictions when developing exoskeleton components.

$$\frac{{\theta }_{\mathrm{dorsiflexi}ó\mathrm{n}}}{{\theta }_{\mathrm{plantar}\mathrm{flexi}ó\mathrm{n}}}=\frac{{30}^{\circ }}{{40}^{\circ }}=\frac{3}{4},$$

(4)

where ${\theta }_{\mathrm{dorsiflexi}ó\mathrm{n}}$ is the angular sweep of the dorsiflexion movement, and ${\theta }_{\mathrm{plantar}\mathrm{flexi}ó\mathrm{n}}$ is the angular sweep of the plantar flexion movement.

Conversely, as numerical simulations will be conducted later using software, it is crucial to analyze the Von Mises stress and safety coefficient parameters provided by Autodesk Inventor 2021 software (Version 2021, Autodesk Inc., San Rafael, CA, USA).

The first physical parameter is the Von Mises stress expressed in Equation (5):

$${\sigma }_{\mathrm{VM}}=\sqrt{{\sigma }_{xx}^2+{\sigma }_{yy}^2+{\sigma }_{zz}^2-({\sigma }_{xx}{\sigma }_{yy}+{\sigma }_{yy}{\sigma }_{zz}+{\sigma }_{zz}{\sigma }_{xx})+3({\tau }_{xx}^2+{\tau }_{yy}^2+{\tau }_{zz}^2)},$$

(5)

where ${\sigma }_{xx}$, ${\sigma }_{yy}$, and ${\sigma }_{zz}$ indicate the stresses on the x, y, and z axes, and ${\tau }_{xx}$, ${\tau }_{yz}$, and ${\tau }_{zx}$ are the principal stresses. Finally, the expression can be simplified if three principal stresses are used, as can be seen in Equation (6):

$${\sigma }_{\mathrm{VM}}=\sqrt{\frac{{({\sigma }_1-{\sigma }_2)}^2+{({\sigma }_1-{\sigma }_3)}^2+{({\sigma }_2-{\sigma }_3)}^2}{2}},$$

(6)

where ${\sigma }_{\mathrm{VM}}$ is the Von Mises stress, which is expressed in terms of the principal stresses ${\sigma }_1$, ${\sigma }_2$, and ${\sigma }_3$. On the other hand, two terms (the design stress of a material and its permissible stress) are divided to arrive at the second term, which is the safety coefficient. This coefficient is the result of the division of both terms (Equation (7)).

$$n=\frac{{\sigma }_Y}{{\sigma }_P},$$

(7)

where n is the safety coefficient, ${\sigma }_Y$ is the design stress of a material, and ${\sigma }_P$ is the allowable stress of the material. The final consideration is the load that will be supported by the heel of the exoskeleton, which is the component that will be responsible for carrying the entire weight of the user. In accordance with Newton’s second law, the load can be defined [44] (Equation (8)).

$$F=m·a,$$

(8)

where F is the load that will support the heel of the exoskeleton [N], m is the mass of the user (kg), and a is the acceleration of gravity (m/s²). Equation (9) is obtained by substituting the values in Equation (8) with $m=70\mathrm{kg}$ and $a=9.81{\mathrm{m}/\mathrm{s}}^2$, which gives us the following:

$$F=70\mathrm{kg}·9.81{\mathrm{m}/\mathrm{s}}^2=686.7\mathrm{N}.$$

(9)

It should be noted that the force or load analyzed in Equation (9) is not the only one present in the ankle during walking. There is also a torque on the ankle produced mainly by the action of the tibialis anterior and gastrocnemius muscles [45], which generate a rotational movement. This torque has a value of approximately 14 N.m [46,47], and in comparison with the torques of the hip and knee (joints present during walking), this value is the lowest of the three [48]. On the other hand, when comparing the magnitude of the ankle torque with the load applied to the exoskeleton, it can be observed that it represents only 2.04% of the total. The two previous supports serve to determine that the ankle torque will not be of great importance at the time of performing the analysis in the exoskeleton since the ankle is not the joint that exerts the greatest torque during walking, and its nominal value is very small compared to the vertical load, which will produce greater deformations in the design.

2.2.3. Three-Dimensional Design of Pieces and General Assembly

The ankle exoskeleton was designed using the patient’s data and computational methods.

The design of the piece called the support was made to wrap the user’s leg and keep it fixed. This piece will also be used to assemble the other components that will be detailed later and was designed based on the figure of a real leg, taking the silhouette of each of its shapes in the sagittal and frontal planes, resulting in a piece that easily adapts to the user and does not represent a nuisance at the time of use.

The heel was designed after the support, based on the shape of the sole of the foot, for better ergonomics. Each foot had a different heel according to their natural anatomical orientation, and the heel was attached to the support.

Afterwards, it was necessary to elaborate a bar that keeps the support and the heel together, and this ensures the natural movement of the leg. For this reason, the design of the piece called the axis was made with a length of 300 mm and a width of 10 mm, according to the user’s measurements.

The next piece, named the support, had two sections with a total extension of 90 mm. The first section was 35 mm long, and the second one was 55 mm long to allow foot mobility when walking. The user’s leg measurements determined the dimensions of this piece.

The design of a piece necessary for the rear coupling of the frame was made; this piece was called the grip and was designed with a triangular shape, which simulates a crosshead to obtain a better proportion of weight in the pieces. This piece is 39.3 mm in length and 42.13 mm in width.

The mechatronic architecture of this exoskeleton necessitated the creation of a cylinder to house the many control and motor mechanisms.

These are all the pieces that were developed for the ankle exoskeleton; however, some holes of 6 mm and 10 mm diameter were observed in the pieces, which correspond to the space where couplings will be placed to join the pieces. In general, they were designed as solid cylinders with the specified diameters of variable extensions depending on the geometry of the pieces at the time of assembly. Next, Figure 2 illustrates the general detailed plan of the exoskeleton pieces: (1) coupling of 6 mm × 10 mm, (2) grips, (3) shaft, (4) support, (5) coupling of 10 mm × 30 mm, (6) heel, (7) cylinder, (8) support, (9) coupling of 6 mm × 40 mm, and (10) coupling 6 mm × 30 mm.

3. Results

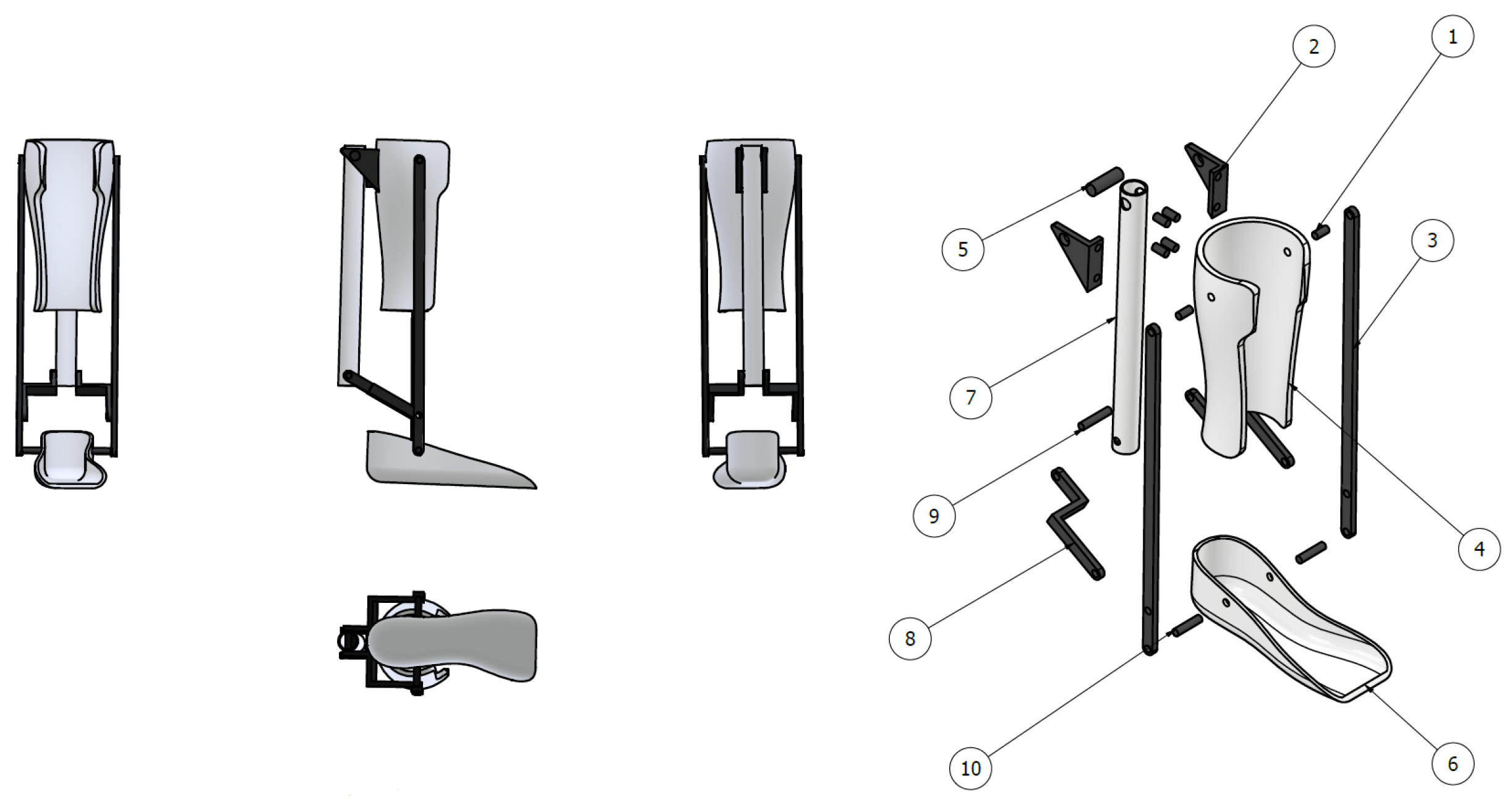
3.1. Results of Main Parameters for the 70 kg User

All of the aforementioned procedures were carried out in order to create an exoskeleton that was a perfect fit for the leg of the 66-year-old user. Using the anatomical dimensions of his leg, an ergonomic exoskeleton was created, which included the following:

The device’s viability in the market necessitated the decision to 3D-print the whole mechanical design, and choosing a composite with high hardness and reasonable pricing was a key component in this process. For this reason, a numerical simulation was carried out in the environment of Autodesk Inventor 2021 in order to evaluate two composites. The first composite was ABS, which is a material that is frequently used in applications that include 3D printing [49]. Furthermore, a carbon fiber-reinforced polymer (with a percentage of 20% of carbon fiber) of the brand Bambu Lab was also used due to its great performance in the prototyping of trans-medium vehicles [50].

The materials library in Autodesk Inventor 2021 was used to conduct numerical simulations of all the composites used in the piece design. While ABS is already available at this gallery, carbon fiber-reinforced polymer is not. So, with the goal of incorporating the physical features that this material delivers per the manufacturer’s standards, a new material named “Carbon Fiber-Reinforced Polymer” was added to the program gallery.

Performing the numerical simulations on the exoskeleton was the following step, followed by a numerical comparison of both materials’ physical quantities. We simulated ABS and “Carbon Fiber-Reinforced Polymer” in Autodesk Inventor 2021 to determine their Von Mises stress, first principal stress, and safety coefficient.

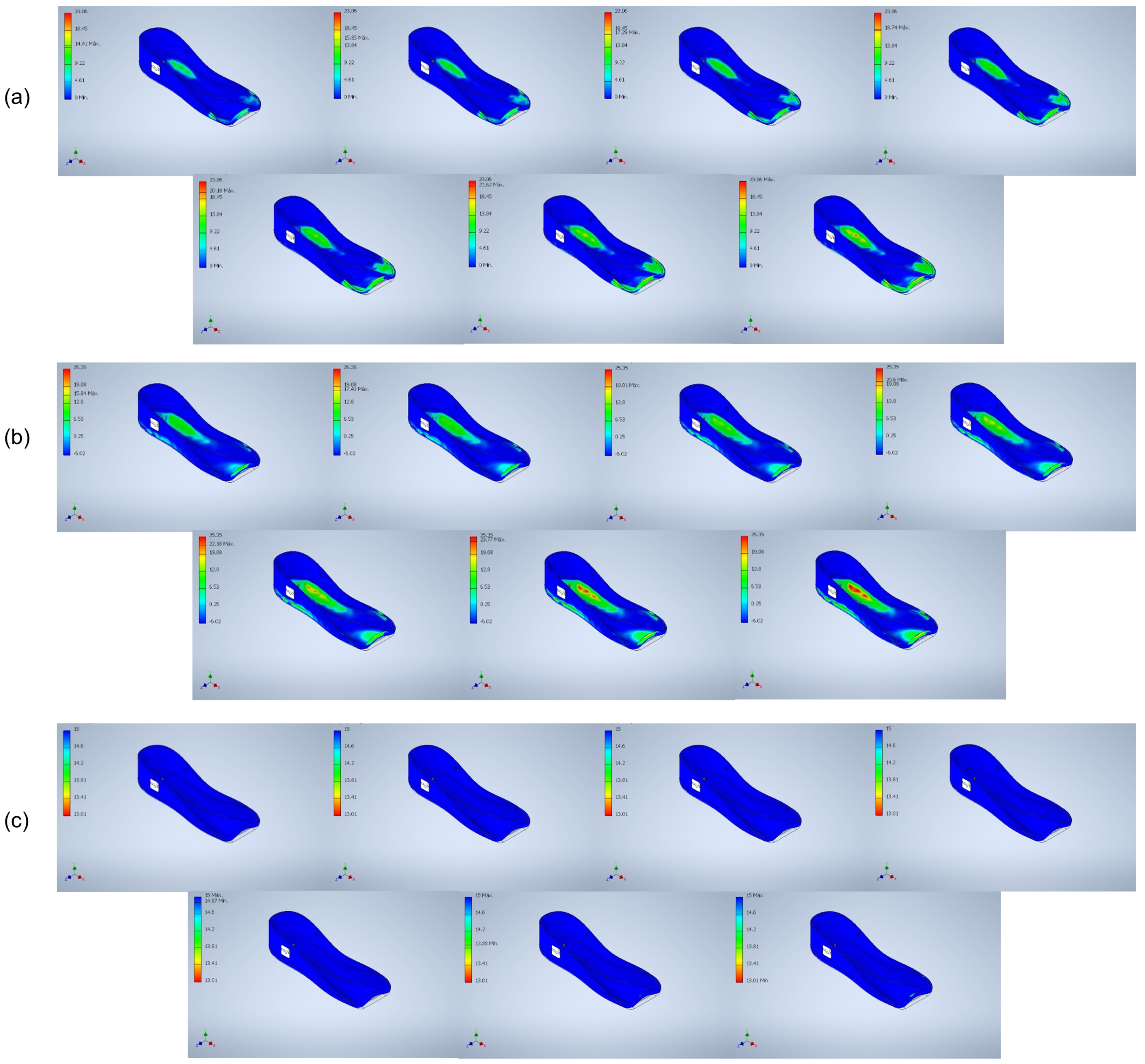
ABS was the first composite material to be simulated. Figure 3a shows its Von Mises stress, Figure 3b shows the first principal stress, and Figure 3c shows the safety coefficient results, respectively.

As may be seen from the figures, numerical data pertaining to the magnitudes were gathered and are displayed in

Table 3. Numerical data obtained from ABS.

Physical Magnitude	Minimum	Maximum
Von Mises stress	0.000 MPa	20.26 MPa
First principal stress	−7.960 MPa	22.11 MPa
Safety coefficient	0.994 μL	15.00 μL

.

Figure 4 shows the outcomes of applying the same simulations to the carbon fiber-reinforced polymer.

Next,

Table 4. Numerical data obtained from carbon fiber-reinforced polymer.

Physical Magnitude	Minimum	Maximum
Von Mises stress	0.000 MPa	20.176 MPa
First principal stress	−8.440 MPa	22.183 MPa
Safety coefficient	14.869 μL	15.00 μL

contains the numerical values for this composite.

The following conclusions can be drawn once the lowest and highest values for the two composites have been recorded in Table 3 and Table 4, respectively:

• Since the average Von Mises stress value for ABS is 10.13 MPa and for carbon fiber-reinforced polymer, it is 10.09 MPa, there is not much difference between the two composites. The results of the simulations (shown in Figure 3a and Figure 4a) demonstrate this.
• Based on the first principal stress data, it is evident that the ABS (Figure 3b) has closer minimum and maximum values compared to the carbon fiber-reinforced polymer (Figure 4b). As a result, the average first principal stress for ABS is 7.075 MPa, while for the polymer, it is 6.87 MPa.
• The safety coefficient values obtained from the ABS and polymer simulations are drastically different. The ABS simulation shows numerous red-colored zones in its structure with values ranging from 0.994 μL to 15 μL (Figure 3c), while the polymer simulation shows substantially higher values ranging from 14.869 μL to 15.00 μL (Figure 4c).

Following a comparison of the numerical values for the required physical magnitudes, it is possible to conclude that the Von Mises stress and first principal stress parameters do not determine which simulated material is better for the ankle exoskeleton. This is due to the reason that both of these parameters exhibit optimal structural values.

On the other hand, when the safety coefficient is analyzed, the values of ABS are found to be lower than 1 μL in some regions. Instead, values that are lower than 14.869 μL along the structure do not appear in the simulations that were carried out with the carbon fiber-reinforced polymer.

In order to choose which of the two materials is the best for the manufacture of this exoskeleton, it is important to take into account design criteria for plastic components, in which it is explained that the safety coefficient for this kind of component, according to the behavior of the mechanism designed in this research, must be at least 10 μL [51]. This makes it possible to specify that the carbon fiber-reinforced polymer (14.869 μL) offers better performance for the development of the ankle exoskeleton of the research since it offers optimum hardness and the necessary reliability for the application of the device in comparison with ABS (0.994 μL).

3.2. Results of Main Parameters Varying the User’s Weight

After comparing the breaking capacity of both materials for a 70 kg user, it was necessary to study the behavior of the mechanical design in different scenarios. To carry out the analysis, the simulation environment carried out with the software was entered, and new numerical simulations were performed by varying the user’s weight, which caused Equation (9) to be modified for each of them; based on this, new load values were entered in the software.

On the other hand, as shown in Figure 3 and Figure 4, most of the pieces of the exoskeleton did not suffer considerable deformations or stress with the applied load since, along their geometries, they presented blue zones or optimum design zones. However, it was observed that the piece called the heel of the exoskeleton suffered considerable deformations and stress since it presented zones where a greater analysis should be carried out (red-colored zones). For this reason, and to improve the analysis of the mechanical design, subsequent simulations will focus only on this part and not on the entire exoskeleton since doing so would incur an unnecessary computational cost for the other parts that are not in a risky condition and do not need to be analyzed in greater detail.

Also, since it was determined that carbon fiber-reinforced polymer is better than ABS, a graphical approach was taken for this material, but the numerical approach for both materials is presented later.

Table 5. New weights and their respective generated loads.

Weight (kg)	Generated Load (N)
50	490.50
55	539.55
60	588.60
65	637.65
70	686.70
75	735.75
80	784.80

shows a summary of the weights entered and their respective loads generated.

The loads described in the table above were entered into the software, and with them, new plots were obtained for the carbon fiber-reinforced polymer. First, seven Von Mises stress plots were obtained, which are shown as a set in Figure 5a. Then, under the same data entry process with the new loads generated in the software, the new seven first principal stresses applied to the mechanical design for users between 50 and 80 kg were obtained. They are shown grouped in Figure 5b. Finally, the safety coefficient plots validated in the research ankle exoskeleton design were simulated with the same weights, and the results obtained were grouped into one, as shown in Figure 5c.

The graphical results show slight visual variations. Contrasting each group of simulations in which the minimum and maximum peaks of each study are presented, the following is observed:

• Blue areas predominate in the seven Von Mises stress plots. In the last image of this group, there is more green coloration, but it does not represent a significant area of the total, indicating that there is no considerable deformation in the exoskeleton heel structure.
• In the first principal stress graphs, it is observed that there are no critical areas (red-colored zones) until the last image of the group is reached. However, this is not enough to consider that the piece may suffer some kind of volumetric deformation when used.
• If attention is paid to the last graph of the safety coefficient study, slight green coloration is observed at the heel end of the exoskeleton, but it does not represent a risk factor for breakage of the piece since more than 99% of the area presents blue zones (optimum design zones).

The above graphs are useful for observing the piece in real conditions, but to understand the behavior of the exoskeleton it is necessary to analyze the numerical values for each of the studies.

Table 6. Weights and values of Von Mises stress, first principal stress, and safety coefficient of carbon fiber-reinforced polymer.

Weight (Kg)	Von Mises Stress		First Principal Stress		Safety Coefficient
	Minimum	Maximum	Minimum	Maximum	Minimum	Maximum
50	0.0001319	14.4116	−6.0286	15.8447	15.0000	15.0
55	0.0001451	15.8528	−6.6314	17.4292	15.0000	15.0
60	0.0001582	17.2939	−7.2343	19.0137	15.0000	15.0
65	0.0001714	18.7350	−7.8372	20.5982	15.0000	15.0
70	0.0001846	20.1763	−8.4400	22.1827	14.8689	15.0
75	0.0001978	21.6174	−9.0429	23.7671	13.8777	15.0
80	0.0002110	23.0586	−9.6457	25.3516	13.0104	15.0

shows the weights used as input data to the software and then the corresponding minimum and maximum values of Von Mises stress, the first principal stress, and safety coefficient for the carbon fiber-reinforced polymer.

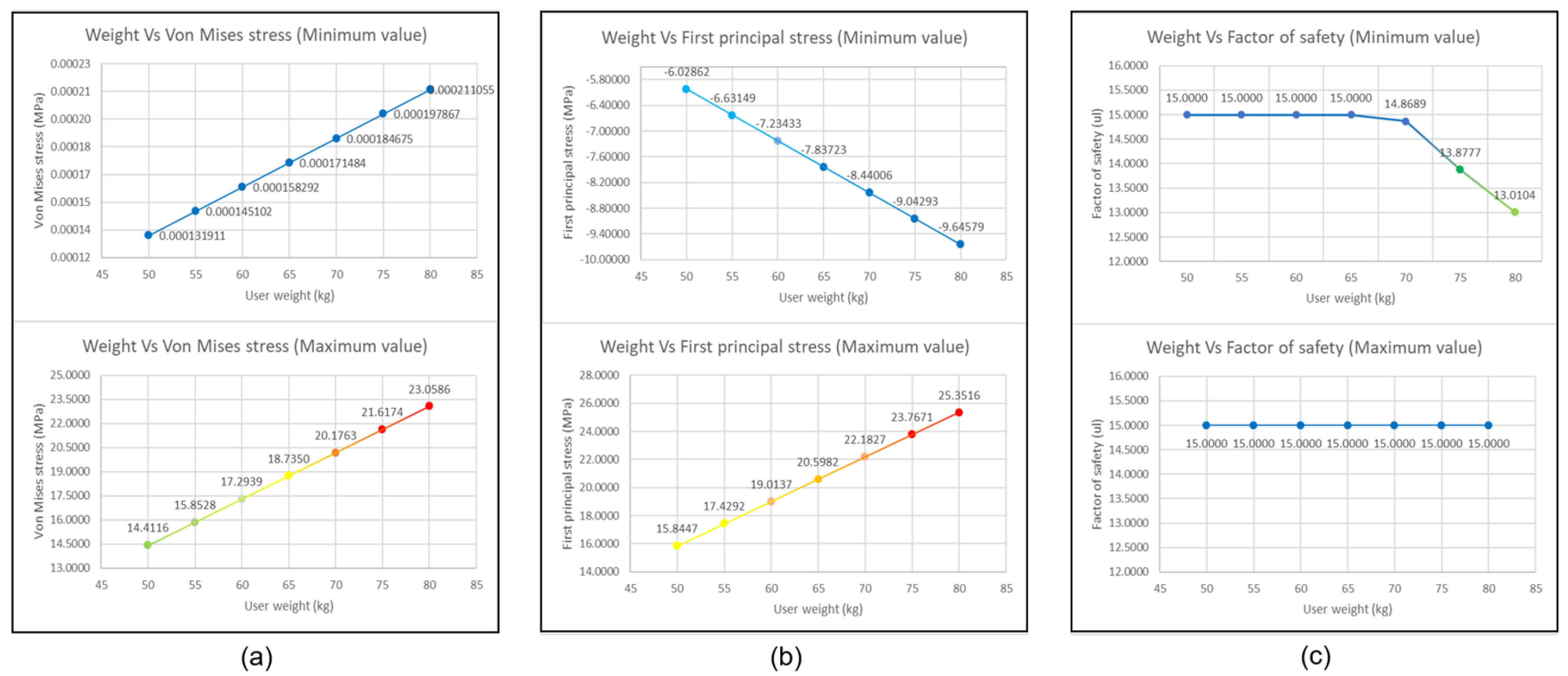
It is clear from looking at this table that, as the user’s weight increases (from 50 kg to 80 kg), the minimum and maximum values of Von Mises stress also increase: the minimum values range from 0.0001319 MPa to 0.0002110 MPa, and the maximum values range from 14.4116 MPa to 23.0586 MPa. For the case of the first principal stress, the same thing happens: the maximum values increase from 15.8447 MPa to 25.3516 MPa, and the minimum values change on a negative scale, starting at −6.0286 MPa and ending at −9.6457 MPa.

Finally, when looking at the safety coefficient, the maximum values remain at 15 μL, but the minimum values decay as the weight increases, going from 15 μL to 13.0104 μL for the heaviest user. These values make sense because, as the weight of the user increases, so does the Von Mises and first principal stresses in a direct proportion; in addition, as for the safety coefficient, an inverse proportion is observed.

With the numerical data obtained, scatter plots were generated, which were used to draw trend lines and to predict the behavior of the piece at more specific values that can be placed in the range of 50–80 kg. Figure 6a, which represents the trend lines for the Von Mises stress, is shown below. Likewise, the graphs for the first principal stress are shown in Figure 6b. Finally, Figure 6c shows the trend lines of the piece for the safety coefficient.

Looking at Figure 6a, concerning Von Mises tension, it can be determined that the trend line of minimum values and that of maximum values behaves linearly with increasing projection. In Figure 6b, regarding first principal stress, we can see that the trend line of minimum values has a linearity with a tendency to increase on a negative scale, and the trend line of maximum values also shares linearity but with projection to grow in positive scale. In the case of Figure 6c, regarding the safety coefficient, the trend line of the minimum values is a constant with a value of 15 μL until reaching a value of 65 Kg; from there, we can see how the trend line behaves in a decreasing and linear way, and finally, the trend line of maximum values is a constant with a value of 15 μL.

Parallel to this,

Table 7. Weights and values of Von Mises stress, first principal stress, and safety coefficient of ABS.

Weight (Kg)	Von Mises Stress		First Principal Stress		Safety Coefficient
	Minimum	Maximum	Minimum	Maximum	Minimum	Maximum
50	0.0001279	14.4707	−5.6852	15.7933	1.3821	15.0
55	0.0001407	15.9177	−6.2537	17.3726	1.2565	15.0
60	0.0001535	17.3648	−6.8222	18.9519	1.1518	15.0
65	0.0001661	18.8119	−7.3907	20.5313	1.0632	15.0
70	0.0001790	20.2590	−7.9593	22.1106	0.9872	15.0
75	0.0001916	21.7060	−8.5278	23.6899	0.9214	15.0
80	0.0002283	23.1543	−9.0971	25.2703	0.8638	15.0

presents the numerical values of the simulations performed on the exoskeleton heel, but with ABS as the manufacturing material, only to compare both materials. When analyzing this table, the behavior of the user’s weight with respect to the Von Mises stress and first principal stress is directly proportional to the safety coefficient, inversely proportional in the same way as observed in Table 6.

On the other hand, the values of the first two parameters are very similar to those in Table 6; however, the safety coefficient does present a notable difference in the minimum values, which range from 1.3821 μL to values below zero, such as 0.8638 μL, and this shows, once again, that the carbon fiber-reinforced polymer offers better performance than ABS.

Finally, plots were made to compare the deviation between simulated and theoretical values. For this, and for practical purposes, the exact point where the load is assigned to the heel of the exoskeleton was taken as a reference. At this point, the values of Von Mises stress, the first principal stress, and safety coefficient simulated with the help of the software were calculated, and the theoretical values were also found for each weight of the previous study (users between 50 and 80 kg). The results obtained are presented in Figure 7. Analysis of these graphs shows that the theoretical values of Von Mises stress are higher compared to the simulated values according to Figure 7a, and considering that Von Mises stress translates into the deformation of an object, it can be stated that the simulated figures offer a better scenario for the piece in which the piece is guaranteed to be rigid and firm. For the first principal stress, it was obtained, according to Figure 7b, that the simulated values are higher than the theoretical values, and because they are on the negative scale, both values are optimal for the exoskeleton design. Finally, based on Figure 7c, it is observed that the simulated values are higher than the theoretical values, and as it is already known, the higher the values of this parameter, the more durable and resistant to fracture or cracking the analyzed body will be. In other words, within the simulation framework, this piece offers better performance.

As can be seen in the previous figures, the theoretical values are not equal to those of the simulations obtained, and this is mainly because we focused on only one point of the entire geometry of the exoskeleton heel to calculate the theoretical values. In contrast, in the simulation environment, all the values for the infinite points of the piece geometry are mapped, and based on these, an average is performed to show the value at a specific point.

As the values of the three parameters were focused on the same point, the calculation criteria were different, and these caused the theoretical and simulated figures not to be the same. The deviation between theoretical and simulated values is seen in

Table 8. New weights and their respective generated loads.

Weight (kg)	Von Mises Stress Deviation (%)	First Principal Stress Deviation (%)	Safety Coefficient Deviation (%)
50	19.2910374	16.70287647	19.29103741
55	19.20381308	21.813275	19.20381308
60	19.30388656	26.74666721	19.30388656
65	19.22907816	29.2646197	19.22907816
70	19.31306799	32.99317465	19.31306799
75	19.24761232	36.57184605	19.24761232
80	19.31995596	35.98199506	19.3199559

.

After analyzing both criteria and the three measured parameters, it should be noticed that the simulated environment presents the piece with a better performance for the range of users of the study case compared to the theoretical environment and, as the simulation generates its result based on many more values than the theoretical calculation, it can be concluded that this criterion will be more accurate and reliable when validating the geometry of the heel of the exoskeleton.

In contrast, to determine whether the contacts designed for the exoskeleton were optimal, an interference check was performed. For this application it was necessary to use other software specialized in this type of analysis, and in this case, Ansys tools were used. First, the design made in Autodesk Inventor 2021 was imported to Ansys SpaceClaim 2024, and then Ansys Mechanical 2024 was used to configure a mesh with 47,934 elements and perform the necessary analysis. 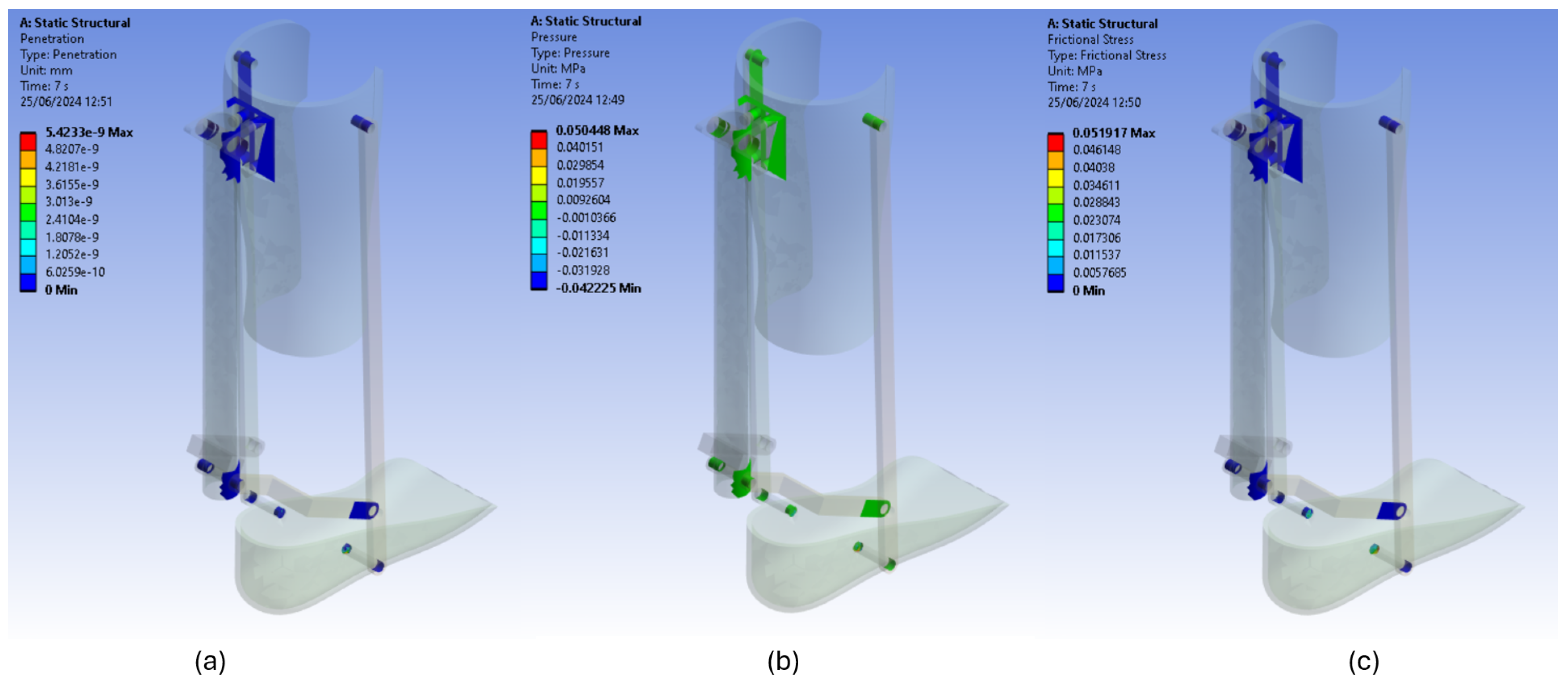Figure 8 shows three graphs in which the exoskeleton contacts were analyzed.

After analyzing the previous graph, the following was determined:

• Figure 8a shows the penetration that exists between the contacts of the exoskeleton, and as can be seen in the numerical scale, the values range from 0 mm to $5.4233\times {10}^{-9}$ mm. The second value shows that there is practically no penetration in the contacts of the design since this value is very low and reaches almost zero. This allows for the definition that the design of the contacts is optimal since no considerable penetration is observed, and although it is true that there are values different from zero, it may be due to the configuration of the mesh and not to the geometry of the components.
• On the other hand, Figure 8b shows the pressure between the exoskeleton contacts. The range of values for this analysis fluctuates between −0.042225 MPa and 0.050448 MPa, which shows that the contacts are not subjected to considerable pressure after applying the load since, if we analyze these values, it can be defined that the magnitude of pressure in the contacts is very low with respect to other values present in the analysis, such as the Von Mises stress that reaches up to 23.0586 MPa (Table 6). This remarkable difference allows us to define that the pressure in the contacts will not be a risk factor for the design of the exoskeleton.
• Finally, Figure 8c shows the frictional stress in the exoskeleton contacts, and its numerical values range from 0 MPa to 0.051917 MPa. As can be observed in the graph, red zones (zones of maximum value) are not very present in the contacts, and this is mainly due to the fact that, at the time of designing the exoskeleton parts, some necessary distances were taken into consideration so that each of them is not exposed to a frictional force. This is reflected in the values of the graph and allows us to determine that the contacts are well-designed and will support the load that the user will produce during its use.

Likewise, tests were carried out to determine the ergonomics of the designed device and establish whether the mechanism could be used by the user of the study. In this sense, as analyzed in previous sections, the dorsiflexion movement sweeps an angle of 30°, whereas the plantar flexion movement has 40° of angular travel.

This is the reason why a schematic of the human´s lower extremity was designed in the Autodesk Inventor environment with its approximate measurements.

This model was then configured with that of the ankle exoskeleton to simulate the attachment of the device and to determine whether the mechanism developed complies with the normal anatomical rotation function of the human body. Planes were deployed in the vertical and horizontal axes around what would become the user’s ankle.

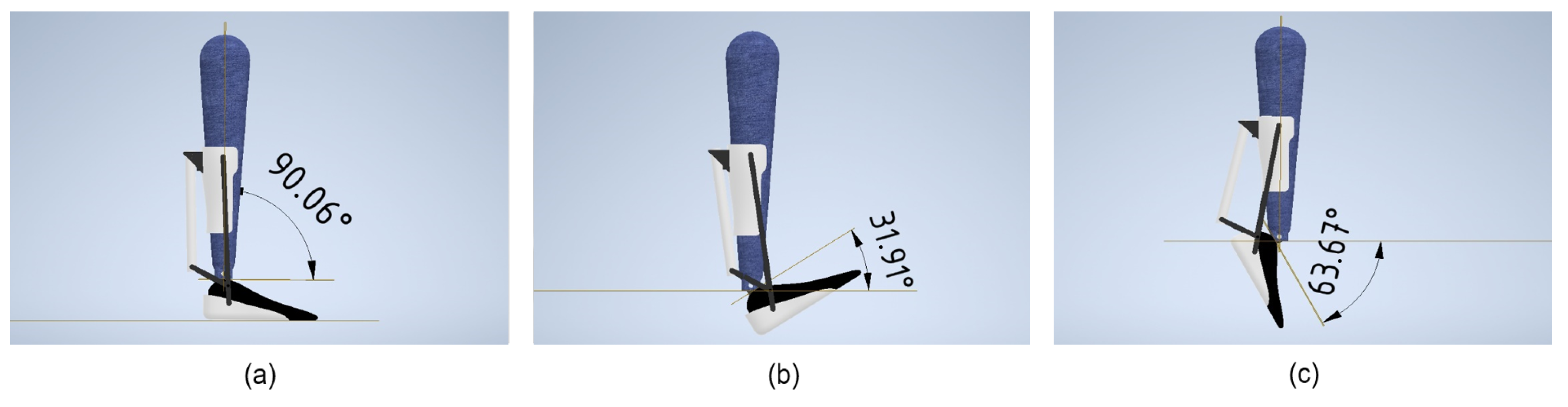
Then the device was placed together with the leg in a neutral position in which they would form an approximate angle of 90°. For this simulation, an angle of 90.06° was achieved, as can be seen in Figure 9a. Afterwards, a maximum dorsiflexion movement was simulated so that the device did not suffer alterations in its structure; that is, the maximum movement allowed by the design was carried out. In this sense, as can be seen in Figure 9b, the angle obtained between the initial axial plane and the axial plane during movement was 31.91°. In contrast, for the plantar flexion movement, the maximum movement was performed without altering the structure of the mechanism in the Autodesk Inventor 2021 environment, as presented in Figure 9c.

The angle formed between the initial axial plane of the ankle and the axial plane during movement was 63.67°.

Table 9. Numerical data obtained from simulated vs. theoretical angular motions.

Angular Motion	Obtained	Theoretical
Dorsiflexion movement	31.91°	30°
Plantar flexion movement	63.67°	40°

shows the data obtained and the theoretical data studied in the previous sections.

Likewise, to observe the behavior of the ankle exoskeleton together with the model of the leg of the user of this study during walking, a simulation was performed, as shown in Figure 10. This graph presents the main moments of walking: the initial contact, support phase, and propulsive phase, where the movements of dorsiflexion and plantar flexion of the ankle are involved. The graph demonstrates that the design correctly fulfils its mobility in conjunction with the user’s leg and its anatomical principle.

Finally, because the mass of the designed exoskeleton is important in order not to generate a greater weight on the user, a data export was performed from the Autodesk Inventor software, and a report was obtained, as shown in Figure 11, where it is observed that the mass of the device is 0.361456 kg. This value confirms once again that the design is optimal because it has a very light mass and will not affect the user during testing.

4. Conclusions and Discussions

The tests and simulations carried out throughout this research were important to reach three conclusions.

On the one hand, based on the data in Table 3 and Table 4, it can be observed that the values of Von Mises stress and first principal stress are close for both materials (about 0.4096% for Von Mises stress and 1.8424% for first principal stress); however, when analyzing the numbers obtained for the safety coefficient, an important variation (about 99.06515%) is observed since the structure developed with ABS reaches values below 0, which implies that the piece can suffer cracks along its geometry. Therefore, it is concluded that the carbon fiber-reinforced polymer is much more resistant, and considering the characteristics of the use of the mechanism, this is the best material to use for 3D printing if a reliable, robust, and durable design is required for the application of this exoskeleton.

In contrast, additional simulations were conducted by inputting new weights (in the range of 50 to 80 kg, as shown in Table 5) and load data to forecast the device’s performance based on its trend lines (as seen in Figure 6). In accordance with these trend lines, it can be defined that users of the ankle exoskeleton within the weight range of 50 to 80 kg will be able to use the device without any issues. This conclusion is supported by the lower and upper bounds of the minimum and maximum values of the Von Mises stress, first principal stress, and safety coefficient demonstrated that the mechanical design carried out in the present research does not present critical numbers that could generate deformations or breakages at the moment of using the ankle exoskeleton (values greater than 23.0586 MPa and 25.3516 MPa for Von Mises stress and first principal stress, respectively, and values less than 13.0104 for safety coefficient).

Finally, with regard to the ergonomics of the mechanical design, the analysis of Table 9 reveals that the range of motion angles in the mechanical design of this project (31.91° for dorsiflexion and 63.67° for plantar flexion) surpass the natural anatomical angles of movement in the human leg (30° for dorsiflexion and 40° for plantar flexion). Therefore, it can be affirmed that the mechanism is ergonomic, effectively accommodating the user’s leg in accordance with the principles of biomechanics and anatomy.

In summary, this work demonstrates the feasibility of designing an ankle exoskeleton tailored to elderly people utilizing the mechanical design presented herein. Furthermore, it is expected to be a durable and sturdy device, owing to its construction with carbon fiber-reinforced polymer (by a percentage of 20%) and ergonomic material, as it does not impede the user’s natural leg movements during use.