Abstract
In the dynamic landscape of autonomous transport, the integration of intelligent transport systems and embedded control technology is pivotal. While strides have been made in the development of autonomous agents and multi-agent systems, the unique challenges posed by two-wheeled vehicles remain largely unaddressed. Dedicated control strategies for these vehicles have yet to be developed. The vertical balance of an autonomous two-wheeled single-track vehicle is a challenge for engineering. This type of vehicle is unstable and its dynamic behaviour changes with the forward velocity. We designed a scheduled-gain proportional–integral controller that adapts its gains to the forward velocity, maintaining the vertical balance of the vehicle by means of the steering front-wheel angle. The control law was tested with a prototype designed by the authors under different scenarios, smooth and uneven floors, maintaining the vertical balance in all cases.
1. Introduction
In the rapidly evolving landscape of intelligent transport systems, where the main objective is to upgrade existing traffic systems, autonomous driving vehicles and the implementation of proper control strategies are increasingly gaining significance (e.g., [1,2,3]). As we witness the advent of autonomous agents and multi-agent systems reshaping the future of transport, ensuring the stability of vehicles, particularly those with only two wheels, emerges as a critical enabling technology [4]. Specially, the control strategy for the lateral stability of two-wheeled vehicles holds paramount significance, as well as facing greater difficulty [5,6].
Two-wheeled vehicles, such as motorcycles and scooters, pose unique challenges in terms of lateral stability due to their inherent design and dynamics [7]. Unlike their four-wheeled counterparts, these vehicles are more susceptible to lateral disturbances, making precise control strategies essential for safe and efficient operation [8]. The integration of intelligent control systems within the framework of these vehicles becomes a pivotal aspect in guaranteeing both rider safety and overall system performance.
In the context of autonomous agents, where vehicles navigate complex environments without direct human intervention, lateral stability control becomes even more vital. The embedded control system plays a crucial role in real-time decision-making, ensuring that the vehicle responds appropriately to varying road conditions [9], unexpected obstacles [10], and dynamic environmental factors [11]. A well-designed control strategy contributes to the vehicle’s ability to maintain stability during cornering, abrupt manoeuvres, and adverse weather conditions.
The coordination and communication between autonomous agents require a robust control strategy to harmonize the movement of vehicles, preventing potential conflicts and enhancing overall traffic flow efficiency [12]. Such is its relevance that significant public investments are being made with the aim of providing solutions to the problem. An example can be seen in the Cooperative Vehicle-Infrastructure Systems (CVIS) project, with 75 European participants, and whose main topic is eSafety Cooperative Systems for Road Transport [13]. In this sense, as the transport ecosystem transitions towards a more interconnected and collaborative model with multi-agent systems, two-wheeled vehicles become a key element in the seamless integration of different vehicles and traffic participants, thanks to their great mobility and compact size. However, the integration of this type of vehicle requires a robust lateral stability control system.
In conclusion, the control strategy for the lateral stability of two-wheeled vehicles stands at the forefront of intelligent transport systems, serving as a linchpin in the realization of autonomous agents and multi-agent systems. By embracing advanced control technologies, we pave the way for safer, more efficient, and interconnected transport, ushering in a new era of mobility that prioritizes both innovation and user well-being.
The first two-wheeled single-track gadget can be attributed to Jean Théson in 1645. Some later inventors, such as Jhon Kemp Starly [14], added new elements, such as the transmission chain, wire spokes, and a handlebar, until evolving to the current bikes and motorbikes.
Although nowadays, there is a wide variety of studies that deal with mathematical models of two-wheeled single-track vehicles [15], the first contributions were made by Whipple [16] and Carvallo [17]. Both authors defined a mechanism composed of three parts: a rear frame, a steering drive system, and wheels. All parts were hinged together. In this case, as well as in [18]’s analysis, the model assumed a front wheel with zero radius, without lateral displacement of the tires, and took into account non-holonomic constraints in the longitudinal and lateral directions.
These simplified models do not take into account certain complex dynamics such as tire contact [19], which is highly non-lineal, or the driver’s position influence [20], which would cause displacements on the centre of mass. Additionally, these dynamics vary depending on external conditions while the vehicle is moving, such as the ratio between the temperature of the road and the vehicle tires, the geometry and design of the tires, and the driver’s posture [21]. Since these parameters are difficult to model, and in many of these cases, consistent models are lacking, some studies rely on online estimations [22].
However, the use of simplified models allows authors to use ad hoc methods, i.e., obtaining a particular solution of a more complex problem. An example of this is the study of the vehicle stability through its handlebar rotation [23].
Vertical balance of autonomous two-wheeled single-track vehicles is a challenge because these types of systems are unstable and their dynamic behaviour changes with the forward velocity. Control techniques used for an inverted pendulum are also used for these types of vehicles because of its similar dynamics. Some examples of these control techniques are the following: classical PID controllers [24], adaptive fuzzy logic control [25], and neural networks [26]. But these techniques are useless when the forward velocity of the vehicle changes. Two control strategies are commonly used to solve this problem: (1) By adding mechanical systems that change the centre of mass of the vehicle [27], the most commonly used technique in stabilization involves using gyroscopes [28]. This strategy is the most used because the vertical balance of the vehicle can be achieved at low velocities, even when the vehicle is stationary [29]. Some studies were reported by the Department of Systems and Control Engineering, Tokyo Institute of Technology [30,31,32,33]. (2) By using the steering front-wheel angle [34]. This strategy is useless under certain forward velocity because it uses the acceleration of the vehicle to achieve the vertical balance [35]. Most studies about this strategy are theoretical, as reported in [36,37,38]. Some experimental results are obtained from prototypes based on commercial bikes [39,40] and roller test platforms [41,42,43,44]. Nevertheless, the dynamic behaviour of the vehicle on a roller test platform is different from moving freely and therefore, the required control system is different.
This study was proposed as a continuation of the authors’ previous works (see [7,45]), where a two-wheeled single-track vehicle was modelled following Limebeer and Sharp’s work [35]. In [45], the model of the bicycle was presented, establishing the range of variation in the main system parameters at which the model could be considered as linear and proposing a technique to find the optimal parameters of the adaptive PI controller in terms of energy consumption but guaranteeing the stability of the controlled system. The performance of the adaptive PI controller was obtained by means of simulation, checking the trajectory tracking and the energy consumption for all forward velocities inside the allowed range. In [7], the adaptive PI controller was tested to determine the energy consumption of each degree of freedom and to determine the robustness of the system in rejecting lateral disturbances. As continuation of these works, an adaptive control strategy was then developed, taking into account the worst possible conditions for the vehicle’s movement. In this novel work, the prototype presented uses the steering front-wheel angle to maintain the vertical balance of the vehicle. The designed adaptive proportional–integral controller, which adapts its gains to the forward velocity wasting the minimum energy consumption, is experimentally tested. This control strategy is tested on both smooth and uneven floors. It should be noted that the aim of this study was not to track a desired trajectory of the vehicle but maintain its vertical balance.
Two-wheeled vehicles have certain advantages over other types of vehicles such as their size, weight, and turning radius. In order to use this type of vehicle autonomously, it is necessary to address its main issue, lateral stability. Additional elements such as gyroscopes or balanced masses can be used for this purpose, which add complexity to the mechanism and increase the weight of the vehicle, thus reducing the payload capacity. The ability to control the vehicle through the roll angle allows us to maintain the lateral stability without any additional element in the vehicle.
Nevertheless, only a few works about the lateral stability control of two wheels vehicles can be found. Some of the most important ones during the last years are [46,47,48,49,50,51,52,53,54,55]. For comparison purposes, Table 1 describes the control approach, the tuning method (if possible), and evaluate if any energy optimisation is or can be included during the tune process.

Table 1.
Comparison of lateral stability method for two-wheel vehicles.
Note that while some of the works presented in Table 1 may incorporate energy optimisation into their controller tuning process, none of them directly address this issue. This aspect should be considered a fundamental prerequisite for all vehicles, particularly for electric vehicles.
The rest of the paper is structured as follows: Section 2 presents the dynamic model of the proposed two-wheeled single-track vehicle and proposes a control law accordingly to the vehicle dynamics; Section 3 presents the prototype, from the mechanics to the electric/electronics details, used for the experiments carried out in Section 4. Finally, Section 5 summarizes the conclusions of this work and proposes future ones.
2. Mathematical Modelling
This section develops the dynamic model used for the two-wheeled single-track vehicle. Once the dynamics are defined, the control law governing the control strategy is presented.
2.1. Dynamic Model
In order to model the dynamic behaviour of the two-wheeled single-track vehicle, the point-mass model proposed by Limebeer and Sharp in [35], inspired by the Boussinesq bicycle model [18], was used. The Boussinesq model assumes a front tire of zero radius, presupposes that the movement of the vehicle is limited, i.e., it does not take into account the lateral displacement of the tires, and considers non-holonomic limitations in the longitudinal and lateral directions. Moreover, the obtained model is not self-stable and can be classified according to the models that use a simplified analysis.
Figure 1 shows a scheme of the vehicle (front-wheel steering) where all the mass is concentrated at the centre of mass (CM) and the steering axis angle is 90º (zero trail).
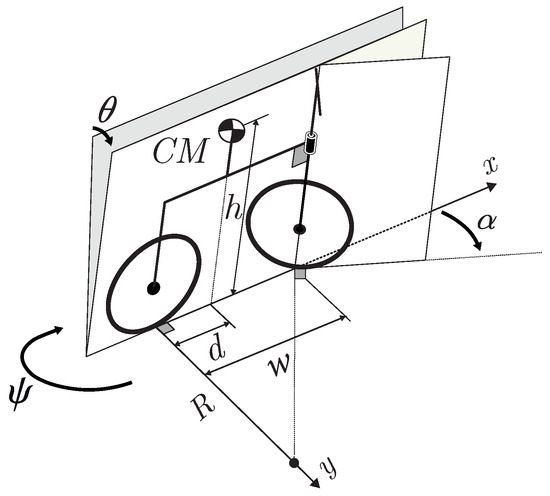
Figure 1.
Scheme of a two-wheeled single-track vehicle for mathematical modelling.
The vehicle moves according to the following cinematic equations:
where are the Cartesian coordinates of the vehicle motion, v is the forward velocity of the vehicle, , , and are, respectively, the yaw, steering, and roll angle, and w is the wheelbase.
On the other hand, the dynamics of the vehicle is defined as [35]
where h is the height of the CM, d is the distance between the CM and the rear-wheel axis, g is the gravity acceleration, and is the trajectory curvature (inverse of the radius of curvature R), defined as
The control input is and the output is . In order to simplify the design of the control law, the previous nonlinear equation is linearized around the equilibrium point () assuming a constant forward velocity.
Notice that the coefficients of depend on the forward velocity, and therefore, they are different for each forward velocity. By using the Laplace transform, the following transfer function is defined
where a, b y c are
All assumptions necessary to derive the dynamic model described in Equation (8) and evaluate its effectiveness are outlined in [45].
2.2. Control Law
Because the dynamics of the vehicle changes with the forward velocity as shown in (7), we propose a real-time adaptive controller that depends on it. A gain-scheduled proportional–integral controller is designed where the forward velocity is the scheduling variable (Figure 2), where and are the proportional and integral gains of the controller, respectively. The control law in Figure 2 is with , being the error signal and and the physical limit of the steering angle (see Section 3.1).
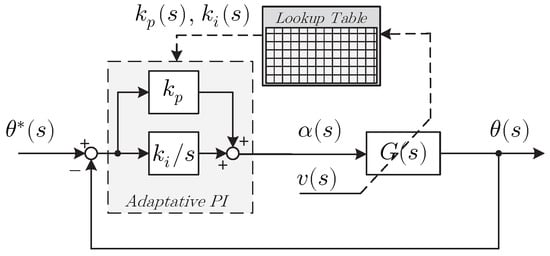
Figure 2.
Scheme of the control law: adaptive PI controller with lookup table for parameter selection.
A lookup table is used to choose the controller gains as a function of the velocity (Figure 3). The lookup table, which contains the optimal controller parameters, was developed in [7]. The chosen design specifications for this optimisation were: (a) the bicycle lateral stability must be achieved even in cases of disturbances such as uneven floor or wind gusts; (b) the steady-state error of the output signal must be as close to zero as possible; (c) the settling time of the output signal must be less than 3 s; (d) the system energy consumption must be minimal. More details can be found in [7]. The absolute value of the gains decreases as the velocity increases. The vertical balance of the vehicle cannot be achieved below 1.21 m/s with the proposed method. The design of the controller can be consulted in previous studies of the authors [7,45]. The resulting and values, shown in Figure 3, results at any time in a stable controlled system. In [45] the stability of the system was checked using the Routh–Hurwitz criterium.
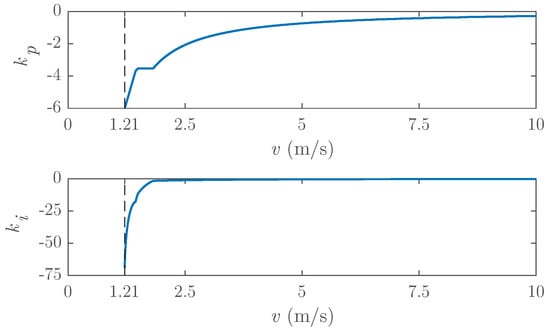
Figure 3.
Lookup table values: controller gains y as a function of the forward velocity, v.
It is important to mention that the plant to be controlled, , is a non-minimum-phase system with poles in the positive region of the plane; thus, the parameters of the controller and are negative. The resulting controller could also be expressed in an equivalent way in “zeros–poles–gain” form with a negative gain and minimum phase zeros/poles.
3. Description of the Experimental Prototype
Figure 4a,b show, respectively, the 3D SolidWorks design and an image of the manufactured prototype. First, we describe the mechanical structure. Second, we describe the electric/electronic system.
3.1. Mechanical Structure
The main characteristics of the prototype structure are the following: the chassis is robust to avoid structural vibrations; the height of the CM is small to facilitate the vertical balance of the vehicle; the wheels have a small radius to reduce the gyroscopic effect; and the steering axis angle is 90º (zero trail) so that the only cause that controls the roll angle is the steering angle . Table 2 shows the dimensions and mass of the vehicle as well as some constraints on and , as shown in Figure 5. The steering angle is controlled by means of a rack and pinion drive (ratio 15.7:1) as shown in the scheme of Figure 6a. On the other hand, the forward velocity of the vehicle is controlled by means of a pulley drive (ratio 4:1) as shown in the scheme of Figure 6b.

Table 2.
Mechanical parameters of the prototype.
Table 2.
Mechanical parameters of the prototype.
| Parameter | Value [unit] |
|---|---|
| h | [m] |
| w | [m] |
| d | [m] |
| r | [m] |
| m | [kg] |
| [rad] | |
| [rad] |

Figure 4.
Mechanical details of the design and prototype: (a) 3D SolidWorks design; (b) image of the prototype; (c) vehicle supported on the wheels of the roll-over protection system.
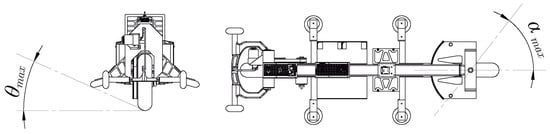
Figure 5.
Mechanical constraints: the steering angle is in the range rad, and the rolling angle rad.
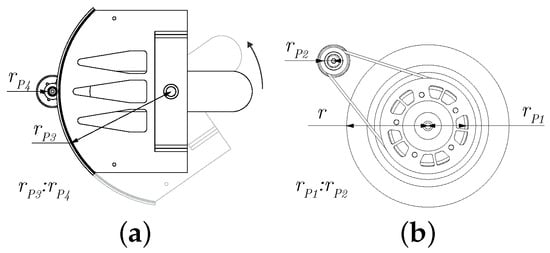
Figure 6.
Mechanical transmission of the steering and forward systems: (a) steering drive: pinion drive transmission; (b) forward drive system: belt–pulley transmission.
Two security devices were added to the vehicle: (1) a roll-over protection system with four small wheels, two on either side of the vehicle (Figure 4); (2) an automatic system that move up and down two small stabilizer wheels, one on either side of the rear wheel of the vehicle (Figure 7). This system keeps the stabilizer wheels down as long as a threshold velocity is not exceeded (1.21 m/s).
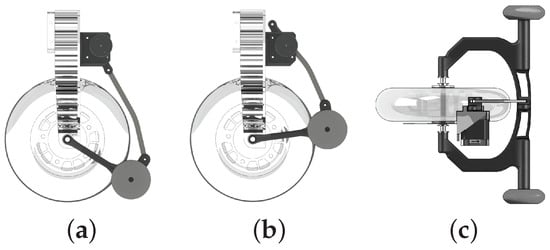
Figure 7.
Mechanical scheme of the stabilizer system for security purpose: (a) Stabilizer wheel down. (b) Stabilizer wheel up. (c) Top view of the stabilizer wheel system.
3.2. Electric/Electronic System
Figure 8 shows a scheme of the electric/electronic system. It is composed of four decentralized subsystems: a power system; actuation systems; a control system; and a stabilizer wheel system. The decentralized systems allowed us to reduce the computational cost. Figure 9 shows the distribution of the electronic devices in the vehicle. All subsystems are described in detail below.
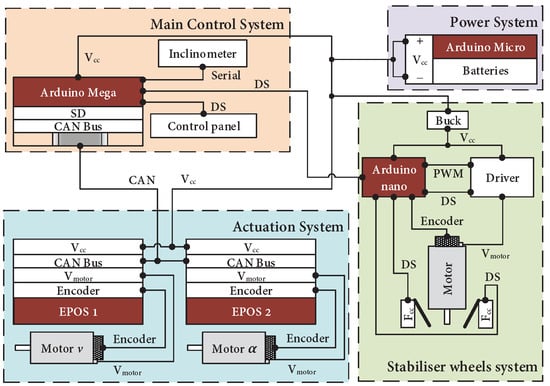
Figure 8.
Scheme of the electric/electronic system. is the voltage power supply; is the voltage power supply of the motor; is a limit switch; PWM is a pulse-width modulation signal; DS is a digital signal; Serial is a standard serial communication signal; CAN is a CAN bus communication signal; and Encoder is a quadrature encoder signal.
3.2.1. Power Supply
3.2.2. Actuation Systems
The steering angle and the forward velocity of the vehicle were commanded by electric DC current motors, model maxon RE 40, without a gearbox (images 3 and 8 in Figure 9), controlled by a modular digital controller, model maxon EPOS2 70/10 (image 7 in Figure 9).
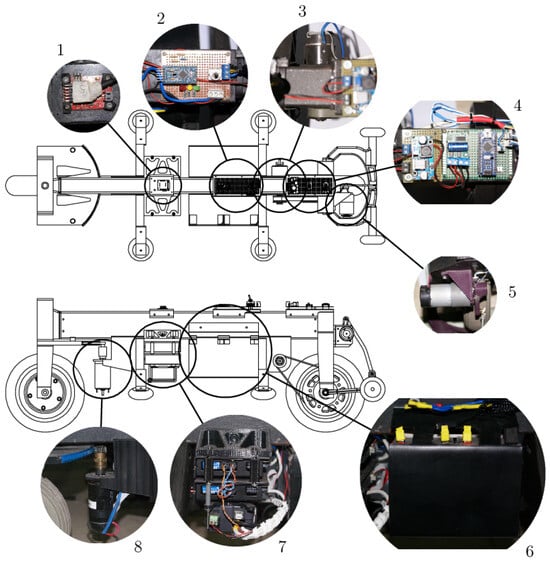
Figure 9.
Distribution of the electronic devices: 1. inclinometer sensor; 2. battery monitor; 3. forward wheels’ control; 4. stabilizer wheels’ control; 5. stabilizer wheels’ actuators; 6. batteries; 7. main control board; 8. steering angle actuator.
3.2.3. Control System
A microcontroller board, model Arduino Mega, controlled all electric/electronic systems of the vehicle. It communicated with the two EPOS through a CAN-BUS shield, with the stabilizer wheel system through a microcontroller board, model Arduino Nano, and with an inclination sensor that measured the roll angle , located at the top of the vehicle (image 1 in Figure 9).
The implementation of the adaptive PI controller was carried out on the Arduino Mega board. A control loop was implemented and at each iteration, the forward velocity was acquired. With the instant velocity value, the and values were extracted from the lookup table and used to update every sample time the control signal, which was sent to the EPOS servocontroller. The sample time of this control loop was 1 ms, and no sample was lost during the experiments. In this sense, the computational requirement to implement the control strategy was very low, since a low-cost ATmega2560 can execute the control loop, measure the forward velocity, look for and values from the lookup table, compute these proportional and integral actions and send the control signal, , to the servocontrollers via the CAN-bus with a sample frequency of 1 kHz.
3.2.4. Stabilizer Wheel System
4. Performance Analysis
Vertical balance control of the vehicle was tested in two different scenarios: a smooth floor (pallet wood) and an uneven floor (paving stones). All tests were performed by using the following sequence: (1) the vehicle started moving with the stabilizer wheel system down until the desired forward velocity was reached; (2) At that instant, the stabilizer wheel system was up, and the control system maintained the vertical balance of the vehicle during 12 s; (3) Finally, the stabilizer wheel system moved down, and the control system was deactivated.
4.1. Tests Performed on Smooth Floor
Figure 10a shows the sport hall of the university campus of Toledo, Universidad de Castilla-La Mancha, where some tests were performed. The floor is made from pallet wood as shown in Figure 10b. Figure 11 shows the results of one test with a forward velocity of 1.5 m/s. We chose that value because it was close to the threshold below which the prototype could not maintain vertical balance by means of the steering front-wheel angle, which was 1.2 m/s, and therefore, it was the worst-case scenario. Vertical balance control was easier as the forward velocity increased. A dotted line marks the instant at which the stabilizer wheel system finished going up (2 s). We see the vehicle maintaining its vertical balance (roll angle approximately zero) without the steering angle exceeding its maximum value (0.61 rad). We also see the forward velocity control system maintaining a value close to 1.5 m/s.

Figure 10.
Place used for control testing on smooth floor: (a) sport hall of the university campus of Toledo, Universidad de Castilla-La Mancha; (b) pallet wood floor.
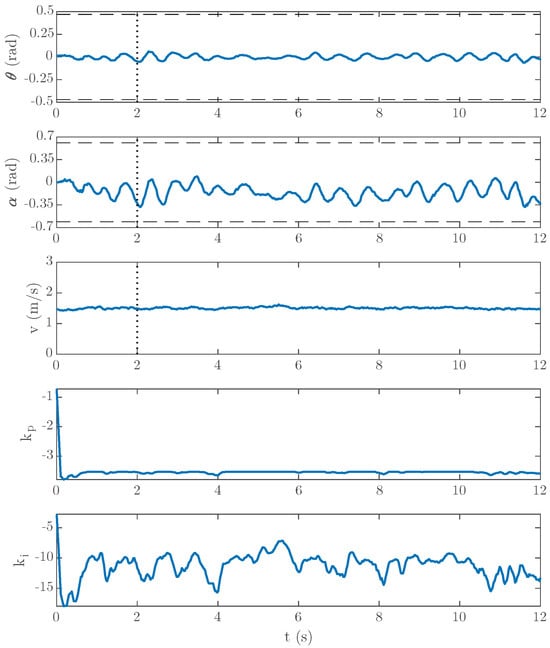
Figure 11.
Experimental results (forward velocity reference: 1.5 m/s2 over the smooth surface). The roll angle, , changes to maintain the steering angle, , close to 0, ensuring the lateral stability. The real velocity, v, is maintained around its reference value. The last two figures show the online variation in the controller parameters, and , during the experiment.
A new test was performed to demonstrate that the vertical balance control also worked from an unfavourable roll angle, that is, when the vehicle was supported on the wheels of the roll-over protection system () as shown in Figure 4c. This test was performed by using the following sequence: (1) the vehicle started moving supported on the wheels of the roll-over protection system with the stabilizer wheel system up until the desired forward velocity was reached (2.2 m/s); (2) at that instant, the vertical balance control was activated trying to maintain the vertical balance of the vehicle for 12 s; (3) finally, the stabilizer wheel system moved down, and the control system was deactivated. Figure 12 shows the results of this test. After 1 s, the roll angle was below 0.47 rad (maximum value), that is, the wheels of the roll-over protection system did not touch the floor meaning that the vertical balance control worked in a proper way. We see that the steering angle reached its maximum value (0.61 rad) for most of the test to maintain the vertical balance of the vehicle. We also see that the forward velocity control system did not maintain the desired velocity during the first second after starting the vertical balance control.
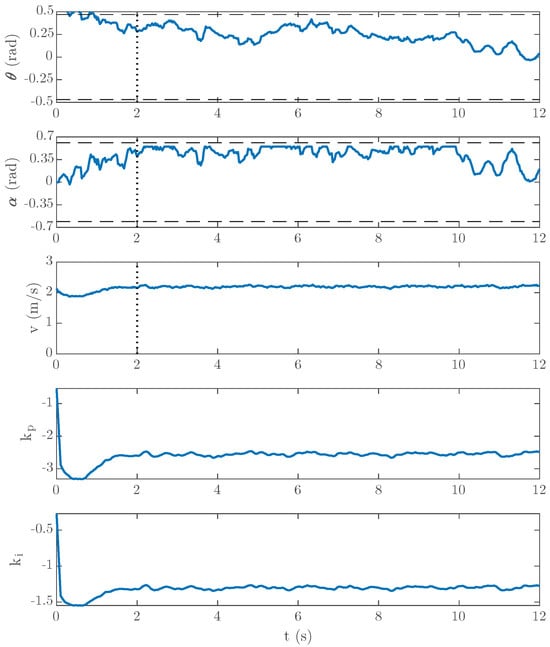
Figure 12.
Experimental results (forward velocity reference: 2.2 m/s2 over a smooth surface). The roll angle, , changes to maintain the steering angle, , close to 0, ensuring the lateral stability. The real velocity, v, is maintained around its reference value. The steering angle is now closer to the mechanical limits. The online variations in the controller parameters, and , during the experiment are shown in the last two figures.
4.2. Tests Performed on Uneven Floor
After testing the vertical balance control on a smooth floor, we decided to test it on an uneven floor to see how it affected the vertical balance. Figure 13a shows the place where some tests were performed (a square of the university campus of Toledo, Universidad de Castilla-La Mancha). The floor was made of rough paving stones as shown in Figure 13b. All tests were performed by following the same procedure used in the tests on the smooth floor. Figure 14 shows the results of one of the tests with a forward velocity of 1.5 m/s. We see that the control system maintained the vertical balance of the vehicle but with more effort, that is, the vehicle required larger oscillations of the steering angle than on a smooth floor. We also see that the forward velocity control system did not maintain the desired velocity during the first second after starting the vertical balance control.

Figure 13.
Place used for control testing on an uneven floor: (a) square of the university campus of Toledo, Universidad de Castilla-La Mancha; (b) rough paving-stone floor.
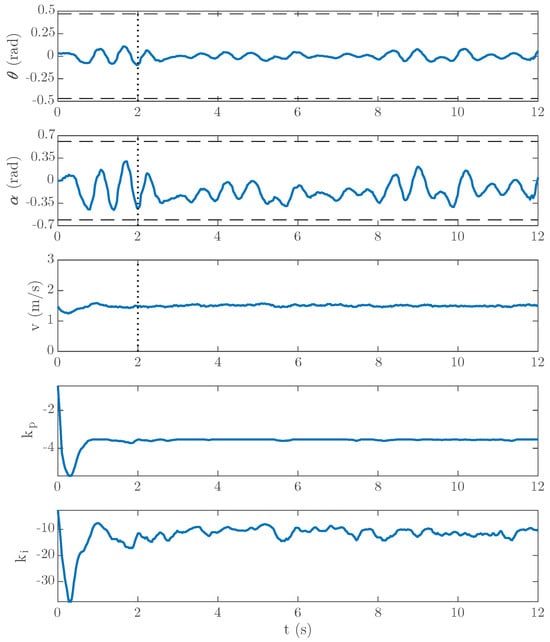
Figure 14.
Experimental results (forward velocity reference: 1.5 m/s2 over rough pavement). A similar behaviour to the first experiment is observed. The roll angle, , changes to maintain the steering angle, , close to 0, ensuring the lateral stability. The real velocity, v, is maintained around its reference value. The steering angle is now closer to the mechanical limits. The online variation in the controller parameters, and , during the experiment are shown in the last two figures.
In order to continue testing the robustness of the vertical balance control, we decided to hit the vehicle on one of its sides during a test with a forward velocity of 2 m/s, obtaining the results shown in Figure 15. The dotted red line indicates the moment of the impact on the vehicle. We see that large oscillations appeared in the roll angle as well as in the steering angle when we hit the vehicle, but the control maintained the vertical balance. We see again that the forward velocity control system did not maintain the desired velocity during the first second after starting the vertical balance control.
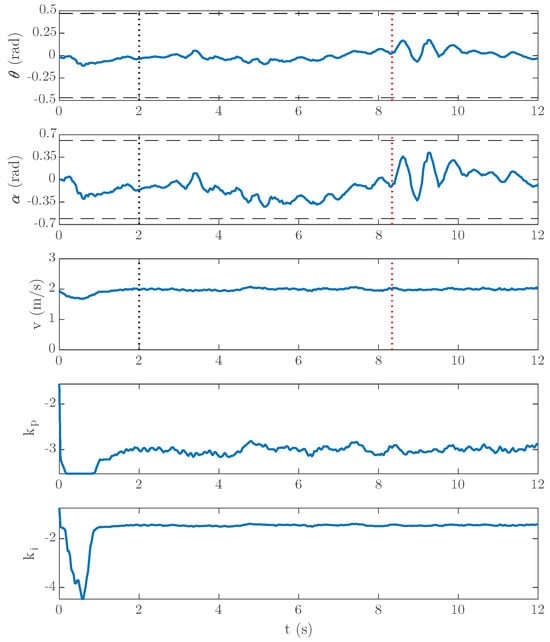
Figure 15.
Experimental results (forward velocity reference: 2 m/s2 over rough pavement). A similar behaviour to the second experiment is observed. The roll angle, , changes to maintain the steering angle, , close to 0, ensuring the lateral stability. The real velocity, v, is maintained around its reference value. The steering angle is now closer to the mechanical limits. The online variation in the controller parameters, and , during the experiment are shown in the last two figures. The proportional gain of the controller reaches the minimum allowed value during the first part of the experiment. Red dotted line represents the time of a lateral impact.
4.3. Robustness Analysis
Although the previous section showed the controller’s performance at different forward velocities, on various surfaces, and in the presence of lateral disturbances, this section presents, through simulations, a robustness/sensitivity analysis of the proposed adaptive PI controller.
For this purpose, following the procedure described in [56], a variation in the parameter of model (8) was assumed for different values of the forward velocity. Taking as reference the nominal parameters shown in Table 2, their variations were simulated inside of the allowed range shown in Table 3.

Table 3.
Parameters’ variation for the robustness analysis.
To illustrate the robust behaviour of the controlled system, Figure 16 represents the roll angle for a forward speed of 1.5 and 2.0 m/s2, when h, w, and d parameters changed within the range presented in Table 3. Note that the adaptive PI controller had a low sensitivity to parameter changes. The parameters of the controller for the 1.5 m/s2 reference forward velocity were and , and the ones for 2.0 m/s2 reference velocity were and (see Figure 3).
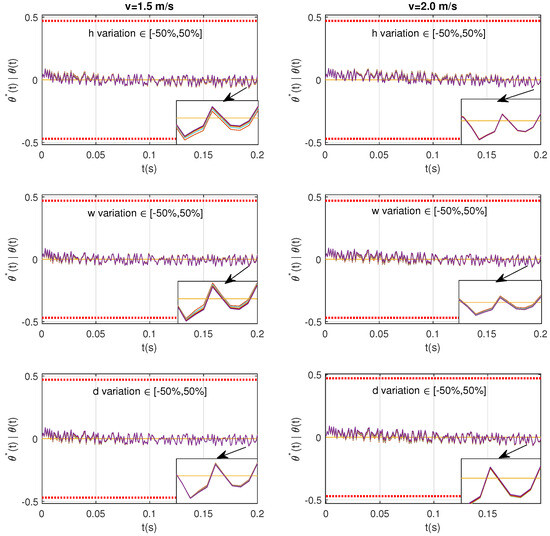
Figure 16.
Simulated results for the robustness analysis: inclination of the bike when h, w, and d changed .
Finally, we assumed the worst scenario, where all parameters could change simultaneously. To quantify the robustness of the controller, the integral absolute error of the roll angle, in Equation (12), was computed when h, w, and d simultaneously changed from −50% to 50% of their nominal values. Table 4 presents the obtained results, showing that the performance of the roll angle was not affected by the parameters’ variation.

Table 4.
Performance of the roll angle when all parameters changed within the [−50%,50%] range.
4.4. Discussion
This section summarizes the obtained results and discusses them. The steering and roll angles, and , the forward velocity, and the instant gain values of the controller, and , were recorded for the four experiments carried out ( m/s and m/s vs. smooth and rough surfaces).
As the main target of the control proposal was to ensure the lateral stability, a tracking functional was proposed for the roll angle, , by considering a reference of rad. In this way, the integral absolute error between and could quantify the goodness of the stability control approach:
In the same way, the integral absolute error between the steering angle and rad indicated the efforts of the controller to ensure the lateral stability:
being the experimental time.
Additionally, each experiment was characterised by a reference forward velocity, and in an analogous way, the following integral absolute error could be defined to quantify the capability of the controlled system to follow the desired forward velocity:
being the velocity reference.
Finally, to quantify the variation in the controller parameters, and , the mean value, , and its standard deviation, , were determined in each experiment.
All these results are summarized in Table 5.

Table 5.
Comparison of lateral stability method for two-wheel vehicles.
Attending to the results in Table 5, some overall conclusions about the controller performance can be stated:
- The stability performance, , is better at low speed.
- When the forward velocity increases, the required steering angle is smaller.
- The integral action of the controller is more required to maintain the lateral stability at low velocity and over rough terrain.
- The proportional action of the controller presents a similar behaviour at any speed.
- Based on the robustness analysis presented, the adaptive PI controller presents a robust behaviour when plant parameters vary within a reasonable range of .
5. Conclusions and Future Work
In recent years, the academic community has directed significant effort toward intelligent transport. However, this focus has predominantly centred on four-wheeled vehicles, whose autonomous driving technology is more advanced, while two-wheeled vehicles are often overlooked in this context.
Only a few studies addressing the lateral stability or autonomous navigation of two-wheeled vehicles can be found, and most of them do not consider the energy consumption in the control design process.
This paper experimentally validated an adaptive PI controller for the lateral stability of an autonomous two-wheel vehicle. The primary objective was not only to enhance the bike’s lateral stability but also to minimize energy consumption.
The proposed adaptive PI controller was tested across various forward velocities and two types of terrain: smooth and rough. The experimental results demonstrated that the proposed controller effectively maintained the vehicle’s lateral stability under all tested conditions.
Future work will expand upon this research by incorporating a trajectory tracking layer into the control system. This will enhance the system’s autonomy and demonstrate the proposed prototype’s ability to track a desired trajectory while maintaining vertical balance before integration into an intelligent transport network.
Author Contributions
Conceptualization, D.R.-R., F.J.C.-G. and I.P.-G.; methodology, D.R.-R., A.M.-P. and A.G.-V.; software, D.R.-R., F.M.-F. and A.M.-P.; validation, A.M.-P. and D.R.-R.; investigation, D.R.-R., I.P.-G. and A.G.-V.; writing—original draft preparation, A.M.-P. and D.R.-R.; supervision, F.M.-F. and I.P.-G.; project administration, F.J.C.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by University of Castilla-La Mancha pre-doctoral grant 2020-PREDUCLM-16080 and by Junta de Comunidades de Castilla-La Mancha and European Regional Development Fund grant SBPLY/21/180501/000238.
Data Availability Statement
Data are available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xiong, R.; Kim, J.; Shen, W.; Lv, C.; Li, H.; Zhu, X.; Zhao, W.; Gao, B.; Guo, H.; Zhang, C.; et al. Key technologies for electric vehicles. Green Energy Intell. Transp. 2022, l1, 100041. [Google Scholar] [CrossRef]
- Chen, C.; Xiong, R.; Yang, R.; Li, H. A novel data-driven method for mining battery open-circuit voltage characterization. Green Energy Intell. Transp. 2022, 1, 100001. [Google Scholar] [CrossRef]
- Shao, L.; Karci, A.E.H.; Tavernini, D.; Sorniotti, A.; Cheng, M. Design approaches and control strategies for energy-efficient electric machines for electric vehicles—A review. IEEE Access 2020, 8, 116900–116913. [Google Scholar] [CrossRef]
- Medaglia, A.; Wilches-Mogollon, M.; Sarmiento, O.; Montes, F.; Guzman, L.; Sanchez-Silva, M.; Menezes, R.; Hidalgo, D.; Parra, K.; Useche, A.; et al. Towards Intelligent Dynamics of an Active Transport System for Biking. R. Acad. Eng. 2022. [Google Scholar]
- Stilo, L.; Segura-Velandia, D.; Lugo, H.; Conway, P.P.; West, A.A. Electric bicycles, next generation low carbon transport systems: A survey. Transp. Res. Interdiscip. Perspect. 2021, 10, 100347. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, J.; Zhu, X.; Xu, Y. Lateral stability integrated with energy efficiency control for electric vehicles. Mech. Syst. Signal Process. 2019, 127, 1–15. [Google Scholar] [CrossRef]
- Rodriguez-Rosa, D.; Payo-Gutierrez, I.; Castillo-Garcia, F.J.; Gonzalez-Rodriguez, A.; Perez-Juarez, S. Improving Energy Efficiency of an Autonomous Bicycle with Adaptive Controller Design. Sustainability 2017, 9, 866. [Google Scholar] [CrossRef]
- Manrique-Escobar, C.A.; Pappalardo, C.M.; Guida, D. On the analytical and computational methodologies for modelling two-wheeled vehicles within the multibody dynamics framework: A systematic literature review. J. Appl. Comput. Mech. 2022, 8, 153–181. [Google Scholar]
- Ni, T.; Li, W.; Zhao, D.; Kong, Z. Road profile estimation using a 3D sensor and intelligent vehicle. Sensors 2020, 20, 3676. [Google Scholar] [CrossRef]
- Wang, D.; Tahmasebi, K.N.; Chen, D. Integrated Control of Steering and Braking for Effective Collision Avoidance with Autonomous Emergency Braking in Automated Driving. In Proceedings of the 2022 30th Mediterranean Conference on Control and Automation (MED), Vouliagmeni, Greece, 28 June–1 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 945–950. [Google Scholar]
- Tahir, M.N.; Mäenpää, K.; Sukuvaara, T.; Leviäkangas, P. Deployment and analysis of cooperative intelligent transport system pilot service alerts in real environment. IEEE Open J. Intell. Transp. Syst. 2021, 2, 140–148. [Google Scholar] [CrossRef]
- Vu, V.; Warg, F.; Thorsén, A.; Ursing, S.; Sunnerstam, F.; Holler, J.; Bergenhem, C.; Cosmin, I. Minimal Risk Manoeuvre Strategies for Cooperative and Collaborative Automated Vehicles. In Proceedings of the 2023 53rd Annual IEEE/IFIP International Conference on Dependable Systems and Networks Workshops (DSN-W), Porto, Portugal, 27–30 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 116–123. [Google Scholar]
- Koenders, E.; Vreeswijk, J. Cooperative infrastructure. In Proceedings of the 2008 IEEE Intelligent Vehicles Symposium, Eindhoven, The Netherlands, 4–6 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 721–726. [Google Scholar]
- Malizia, F.; Blocken, B. Bicycle aerodynamics: History, state-of-the-art and future perspectives. J. Wind. Eng. Ind. Aerodyn. 2020, 200, 104134. [Google Scholar] [CrossRef]
- Meijaard, J.; Papadopoulos, J.M.; Ruina, A.; Schwab, A. Supplementary appendices. Linearized dynamics equations for the balance and steer of a bicycle: A benchmark and review. Proc. R. Soc. Ser. 2007. [Google Scholar] [CrossRef]
- Whipple, F.J. The stability of the motion of a bicycle. Q. J. Pure Appl. Math. 1899, 30, 312–384. [Google Scholar]
- Carvallo, E. Théorie du mouvement du monocycle et de la bicyclette. L’Ecole Polytech. 1900. [Google Scholar]
- Boussinesq, J. Aperçu sur la théorie de la bicyclette. J. MathÉMatiques Pures AppliquÉEs 1899, 5, 117–136. [Google Scholar]
- Rill, G. Sophisticated but quite simple contact calculation for handling tire models. Multibody Syst. Dyn. 2019, 45, 131–153. [Google Scholar] [CrossRef]
- Schwab, A.L.; Meijaard, J.P. A review on bicycle dynamics and rider control. Veh. Syst. Dyn. 2013, 51, 1059–1090. [Google Scholar] [CrossRef]
- Carputo, F.; D’Andrea, D.; Risitano, G.; Sakhnevych, A.; Santonocito, D.; Farroni, F. A neural-network-based methodology for the evaluation of the center of gravity of a motorcycle rider. Vehicles 2021, 3, 377–389. [Google Scholar] [CrossRef]
- Hu, J.; Rakheja, S.; Zhang, Y. Real-time estimation of tire–road friction coefficient based on lateral vehicle dynamics. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2020, 234, 2444–2457. [Google Scholar] [CrossRef]
- Manrique-Escobar, C.A.; Pappalardo, C.M.; Guida, D. A multibody system approach for the systematic development of a closed-chain kinematic model for two-wheeled vehicles. Machines 2021, 9, 245. [Google Scholar] [CrossRef]
- Wang, J.J. Simulation studies of inverted pendulum based on PID controllers. Simul. Model. Pract. Theory 2011, 19, 440–449. [Google Scholar] [CrossRef]
- Dang, Q.V.; Allouche, B.; Vermeiren, L.; Dequidt, A.; Dambrine, M. Design and implementation of a robust fuzzy controller for a rotary inverted pendulum using the Takagi-Sugeno descriptor representation. In Proceedings of the 2014 IEEE Symposium on Computational Intelligence in Control and Automation (CICA), Orlando, FL, USA, 9–12 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Wei, E.; Li, T.; Li, J.; Hu, Y.; Li, Q. Neural network-based adaptive dynamic surface control for inverted pendulum system. In Foundations and Practical Applications of Cognitive Systems and Information Processing; Springer: Berlin/Heidelberg, Germany, 2014; pp. 695–704. [Google Scholar]
- Gupta, N.K.; Ambikapathy, A. Self-Balancing Bicycle using Reaction Wheel. Int. J. Eng. Sci. 2019, 21405, 21402–21407. [Google Scholar]
- Zheng, X.; Zhu, X.; Chen, Z.; Sun, Y.; Liang, B.; Wang, T. Dynamic modeling of an unmanned motorcycle and combined balance control with both steering and double CMGs. Mech. Mach. Theory 2022, 169, 104643. [Google Scholar] [CrossRef]
- Yang, C.; Murakami, T. Full-speed range self-balancing electric motorcycles without the handlebar. IEEE Trans. Ind. Electron. 2015, 63, 1911–1922. [Google Scholar] [CrossRef]
- Yamakita, M.; Utano, A.; Sekiguchi, K. Experimental study of automatic control of bicycle with balancer. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 5606–5611. [Google Scholar]
- Keo, L.; Yamakita, M. Controlling balancer and steering for bicycle stabilization. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 4541–4546. [Google Scholar]
- Keo, L.; Yoshino, K.; Kawaguchi, M.; Yamakita, M. Experimental results for stabilizing of a bicycle with a flywheel balancer. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 6150–6155. [Google Scholar]
- Kawaguchi, M.; Yamakita, M. Stabilizing of bike robot with variable configured balancer. In Proceedings of the SICE Annual Conference 2011, Tokyo, Japan, 13–18 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1057–1062. [Google Scholar]
- Yeh, T.J.; Lu, H.; Tseng, P. Balancing Control of a Self-driving Bicycle. In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics, Prague, Czech Republic, 29–31 July 2019; Volume 2, pp. 34–41. [Google Scholar] [CrossRef]
- Limebeer, D.J.; Sharp, R.S. Bicycles, motorcycles, and models. IEEE Control. Syst. 2006, 26, 34–61. [Google Scholar]
- Anjumol, M.; Jisha, V. Optimal stabilization and straight line tracking of an electric bicycle. In Proceedings of the 2014 International Conference on Power Signals Control and Computations (EPSCICON), Thrissur, India, 6–11 January 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Yuan, J.; Chen, H.; Sun, F.; Huang, Y. Trajectory planning and tracking control for autonomous bicycle robot. Nonlinear Dyn. 2014, 78, 421–431. [Google Scholar] [CrossRef]
- Yuan, J.; Zhang, J.; Ding, S. Pseudospectral motion planning for autonomous bicycles. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Republic of Korea, 7–11 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 482–487. [Google Scholar]
- Zhuang, W.; Zhang, R.; Su, X.; Huang, Y. Research on the Lateral Balance Control of a Bicycle Robot. In Proceedings of the 2019 International Conference on Robotics, Intelligent Control and Artificial Intelligence, Beijing, China, 19–22 April 2019; pp. 744–750. [Google Scholar]
- Hatano, R.; Tani, T.; Iwase, M. Stability analysis and autonomous stabilization control of a bicycle based on a three-dimensional detailed physical model. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 324–329. [Google Scholar]
- Tanaka, Y.; Murakami, T. A study on straight-line tracking and posture control in electric bicycle. IEEE Trans. Ind. Electron. 2008, 56, 159–168. [Google Scholar] [CrossRef]
- Defoort, M.; Murakami, T. Sliding-mode control scheme for an intelligent bicycle. IEEE Trans. Ind. Electron. 2009, 56, 3357–3368. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Shibata, T.; Murakami, T. Self-sustaining approach of electric bicycle by acceleration control based backstepping. In Proceedings of the IECON 2007-33rd Annual Conference of the IEEE Industrial Electronics Society, Taipei, Taiwan, 5–8 November 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 2610–2614. [Google Scholar]
- Defoort, M.; Murakami, T. Second order sliding mode control with disturbance observer for bicycle stabilization. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 2822–2827. [Google Scholar]
- Rodriguez-Rosa, D.; Payo-Gutierrez, I.; Gonzalez-Lucena, I.; Gonzalez-Rodriguez, A.; Castillo-Garcia, F.J.; Gonzalez-Rodriguez, A. Controlador proporcional-integral adaptativo para el ahorro energético en bicicletas autónomas. DYNA 2014, 89, 656–664. [Google Scholar] [CrossRef]
- Hashemnia, S.; Shariat Panahi, M.; Mahjoob, M.J. Unmanned bicycle balancing via Lyapunov rule-based fuzzy control. Multibody Syst. Dyn. 2014, 31, 147–168. [Google Scholar] [CrossRef]
- Dao, T.K.; Chen, C.K. Sliding-mode control for the roll-angle tracking of an unmanned bicycle. Veh. Syst. Dyn. 2011, 49, 915–930. [Google Scholar] [CrossRef]
- Keo, L.; Masaki, Y. Trajectory control for an autonomous bicycle with balancer. In Proceedings of the 2008 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Xi’an, China, 2–5 July 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 676–681. [Google Scholar]
- Getz, N.H.; Marsden, J.E. Control for an autonomous bicycle. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Aichi, Japan, 21–27 May 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 2, pp. 1397–1402. [Google Scholar]
- Baquero-Suárez, M.; Cortés-Romero, J.; Arcos-Legarda, J.; Coral-Enriquez, H. A robust two-stage active disturbance rejection control for the stabilization of a riderless bicycle. Multibody Syst. Dyn. 2019, 45, 7–35. [Google Scholar] [CrossRef]
- Xiong, C.; Huang, Z.; Gu, W.; Pan, Q.; Liu, Y.; Li, X.; Wang, E. Static balancing of robotic bicycle through nonlinear modeling and control. In Proceedings of the 2018 3rd International Conference on Robotics and Automation Engineering (ICRAE), Guangzhou, China, 17–19 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 24–28. [Google Scholar]
- Tanaka, Y.; Murakami, T. Self sustaining bicycle robot with steering controller. In Proceedings of the 8th IEEE International Workshop on Advanced Motion Control, 2004. AMC’04, Kawasaki, Japan, 25–28 March 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 193–197. [Google Scholar]
- Li, C.; Xie, Y.F.; Wang, G.; Zeng, X.F.; Jing, H. Lateral stability regulation of intelligent electric vehicle based on model predictive control. J. Intell. Connect. Veh. 2021, 4, 104–114. [Google Scholar] [CrossRef]
- Wen, G.; Sjöberg, J. Lateral control of a self-driving bike. In Proceedings of the 2022 IEEE International Conference on Vehicular Electronics and Safety (ICVES), Bogota, Colombia, 14–16 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Chu, T.; Chen, C. Modelling and model predictive control for a bicycle-rider system. Veh. Syst. Dyn. 2018, 56, 128–149. [Google Scholar] [CrossRef]
- Coppola, A.; Lui, D.G.; Petrillo, A.; Santini, S. Eco-driving control architecture for platoons of uncertain heterogeneous nonlinear connected autonomous electric vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24220–24234. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).