Effect of Oscillating Area on Generating Microbubbles from Hollow Ultrasonic Horn
Abstract
1. Introduction
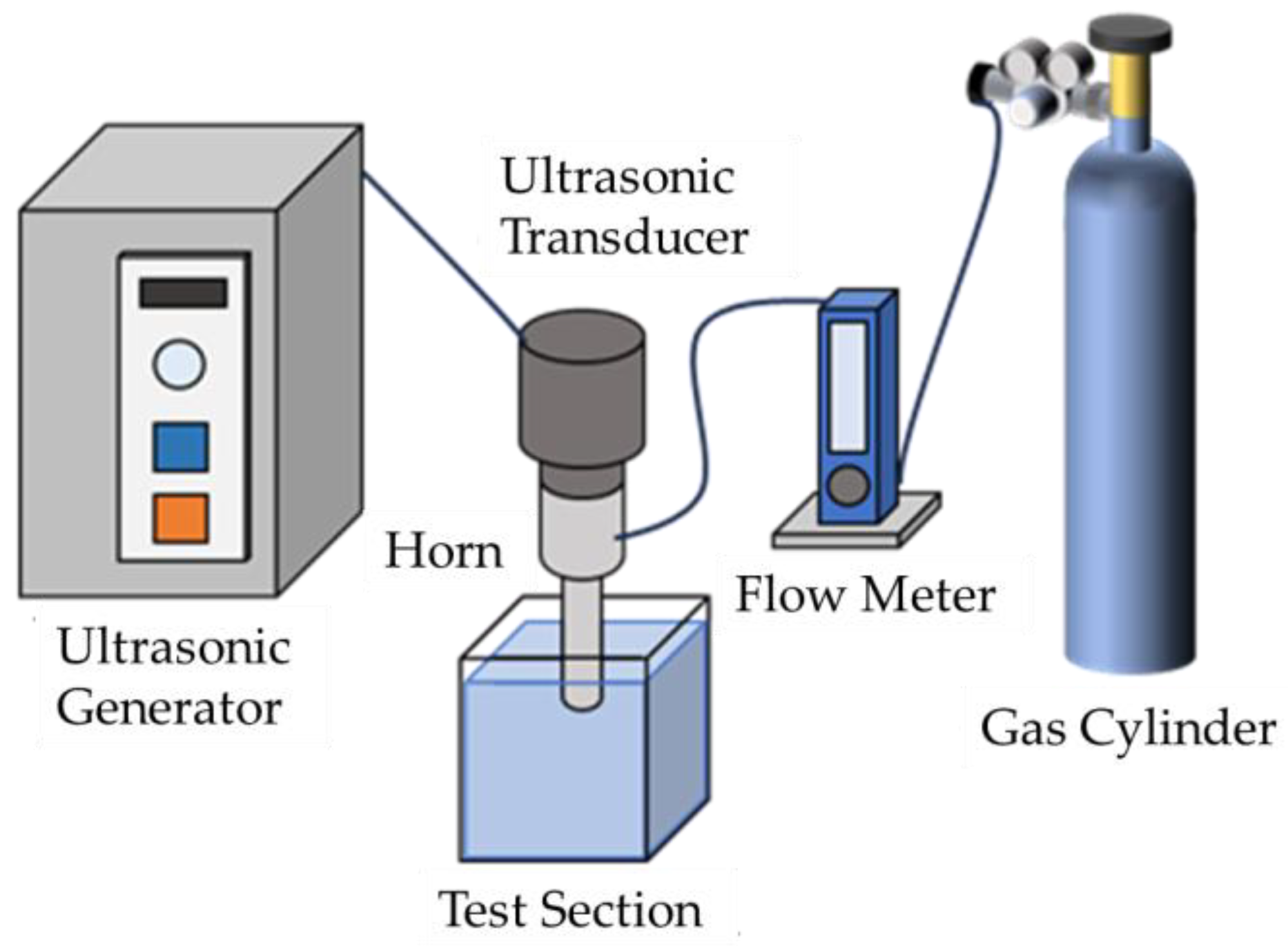
2. Experimental Apparatus and Evaluation Methods
2.1. Experimental Apparatus
- (1)
- Insert the tip of the hollow ultrasonic horn into the liquid.
- (2)
- Supply gas to the gas supply port to form a gas–liquid interface at the tip of the horn.
- (3)
- By ultrasonic oscillation of the horn tip, the surface waves formed at the gas–liquid interface are separated and miniaturized to generate microbubbles.
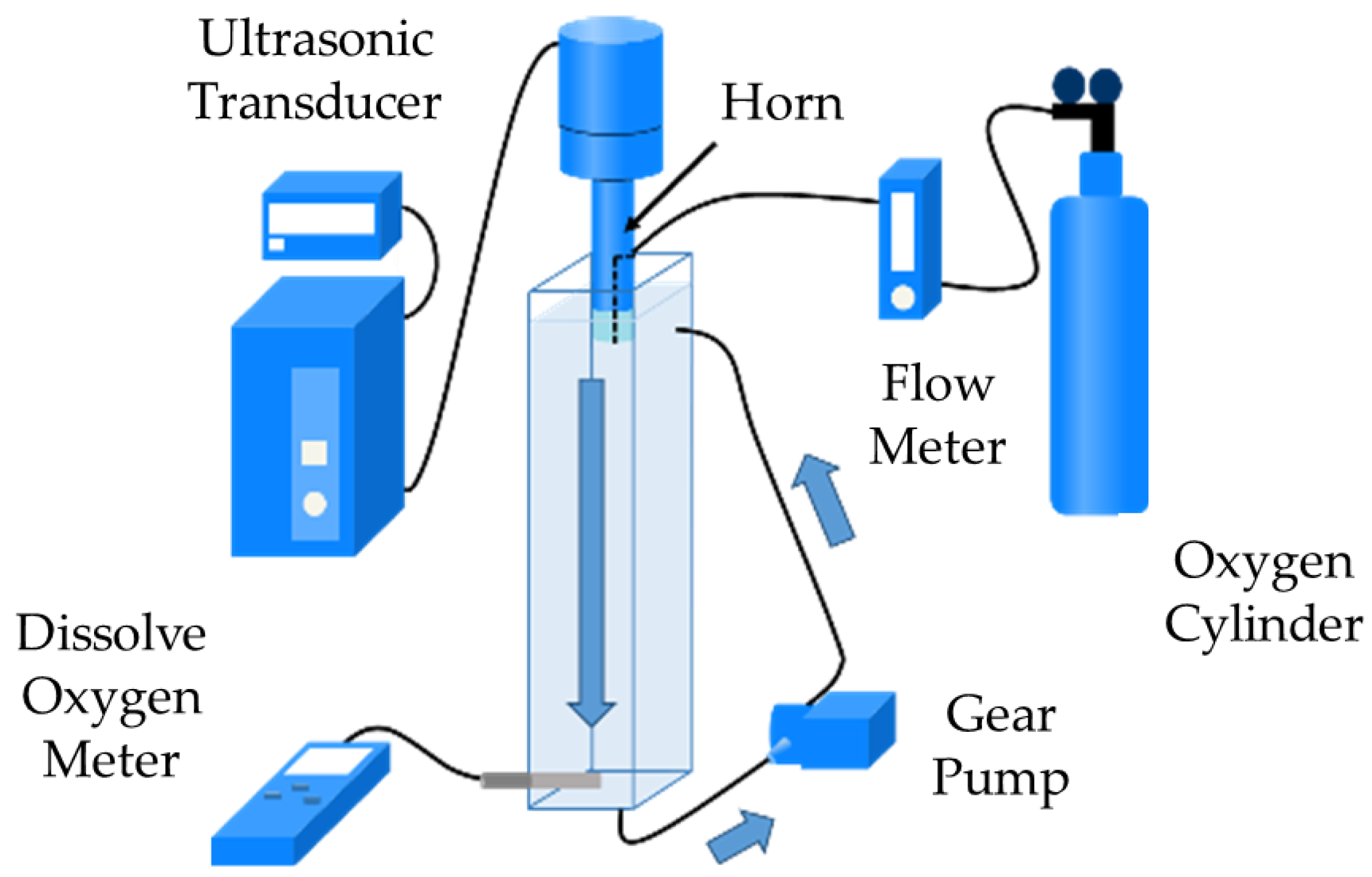
2.2. Evaluation Methods
3. Experimental Results and Discussion
3.1. Generation Behavior of Microbubbles in Water
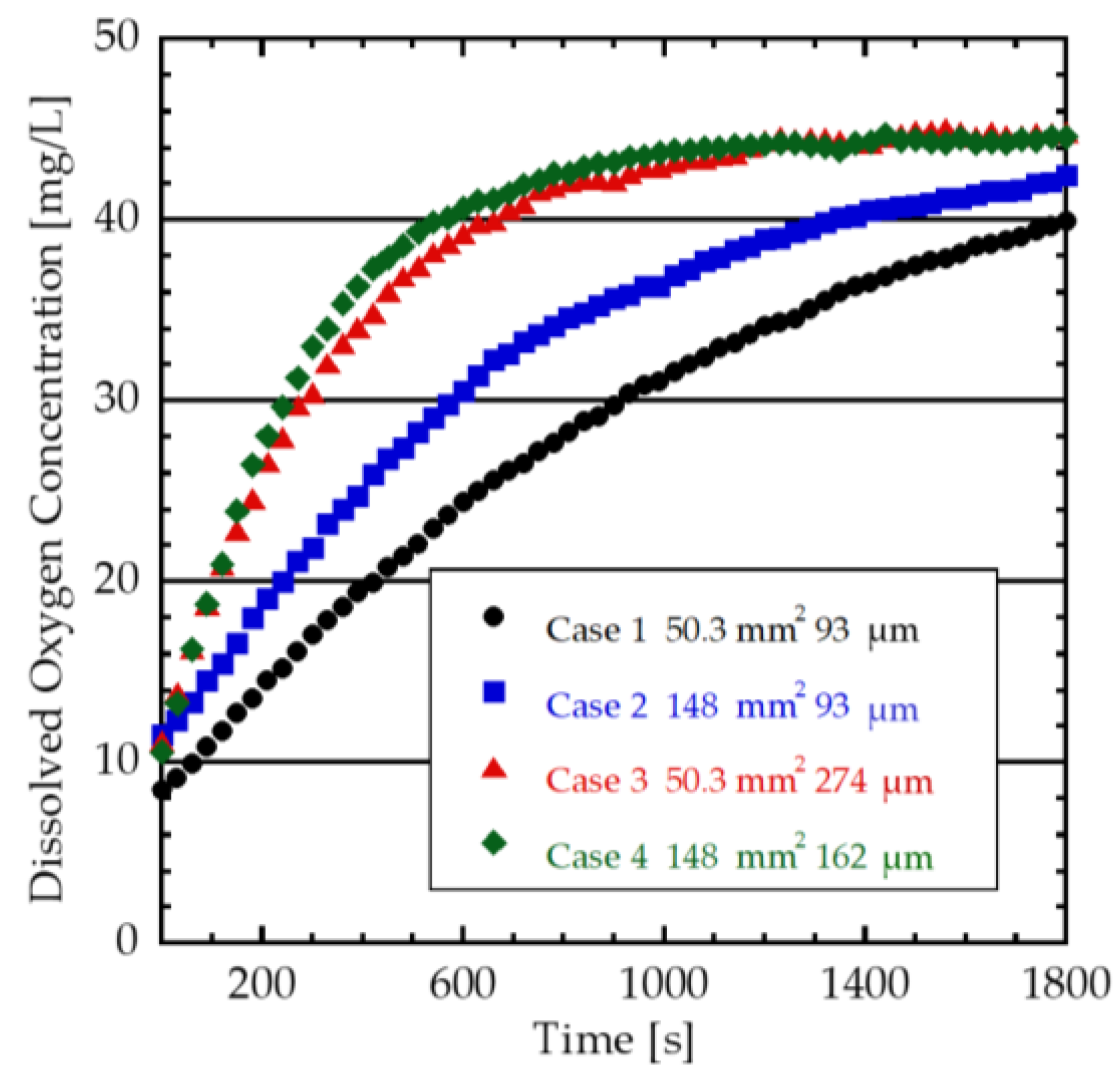
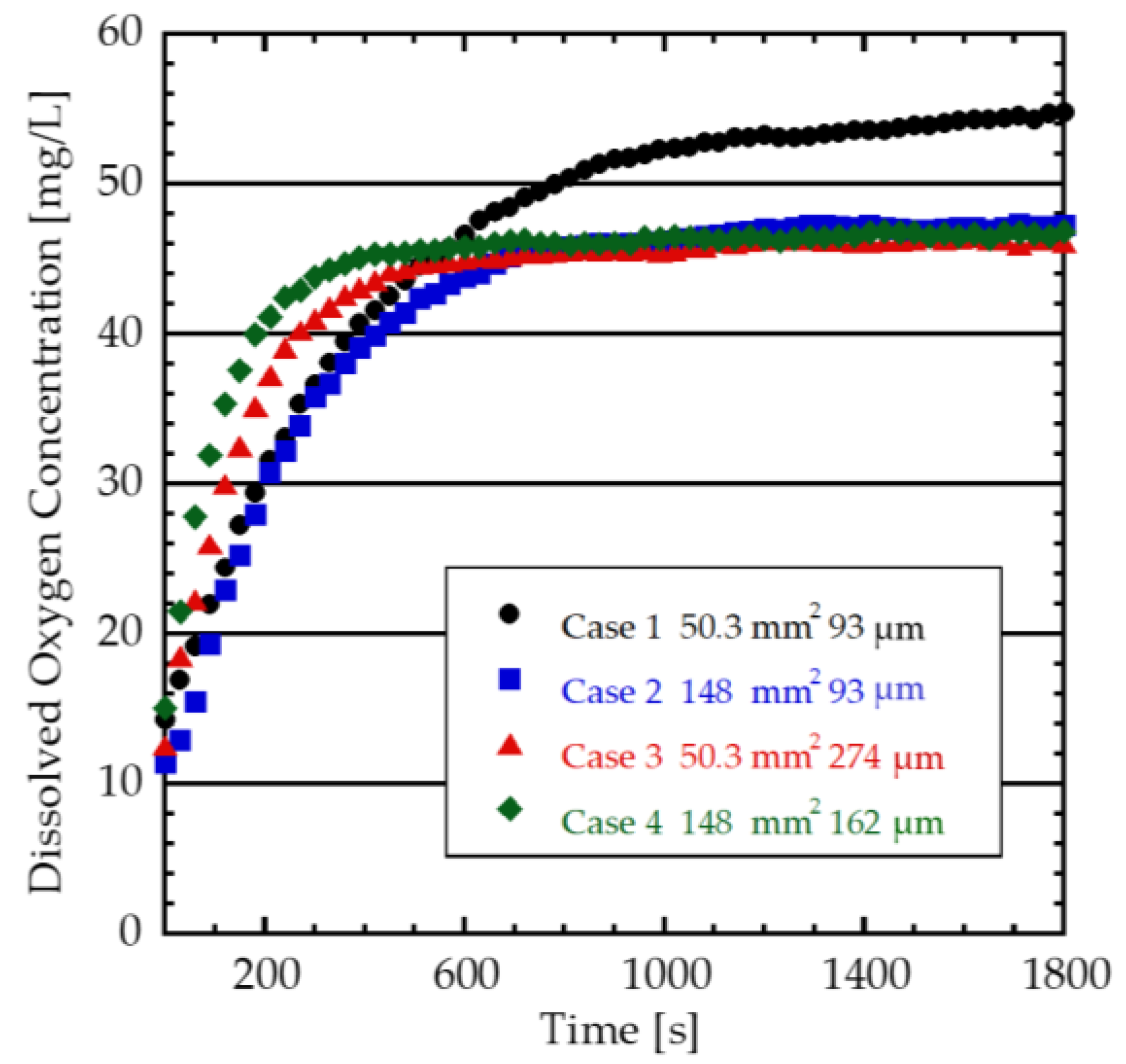
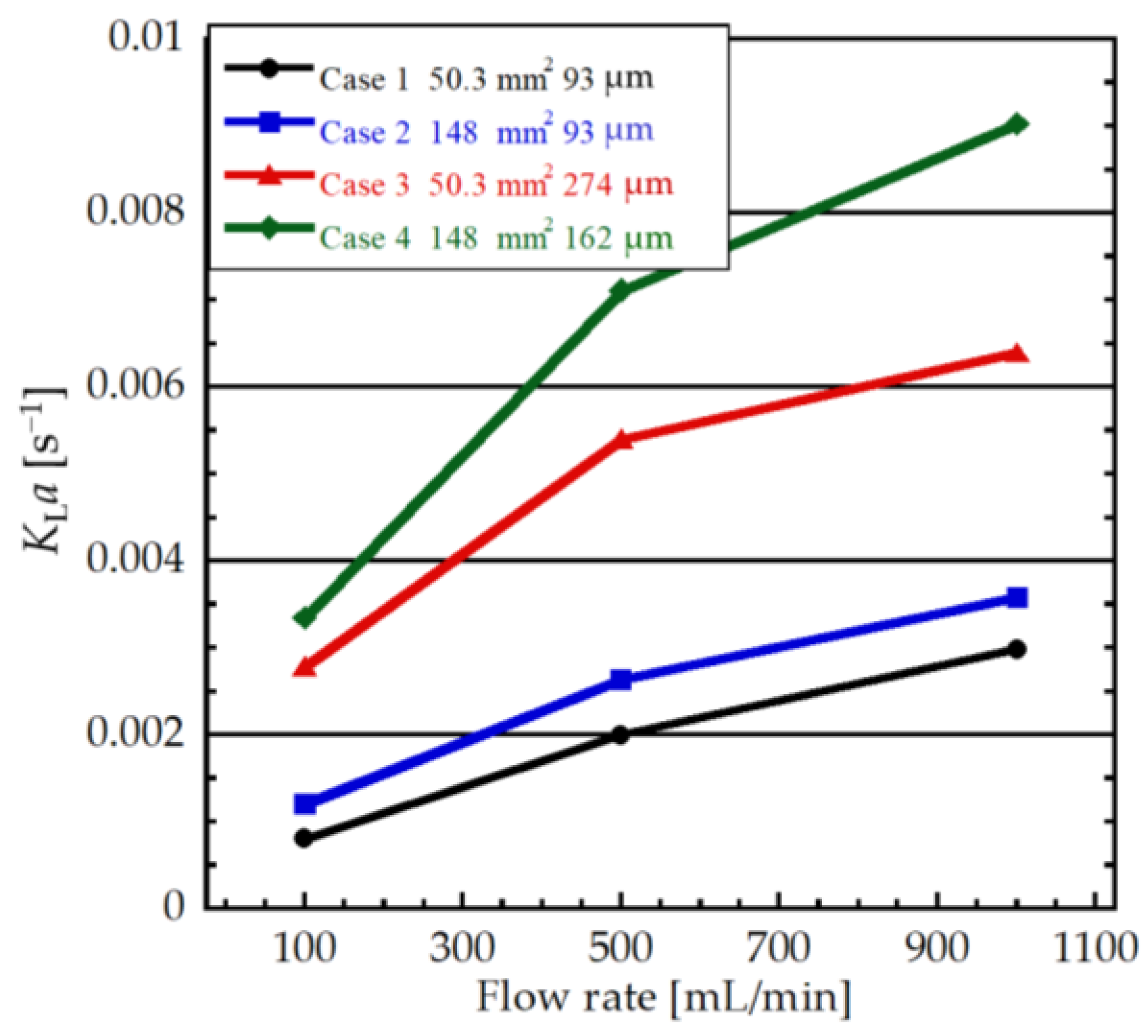
3.2. Evaluation of Microbubble Generation Yield by Dissolved Oxygen Concentration
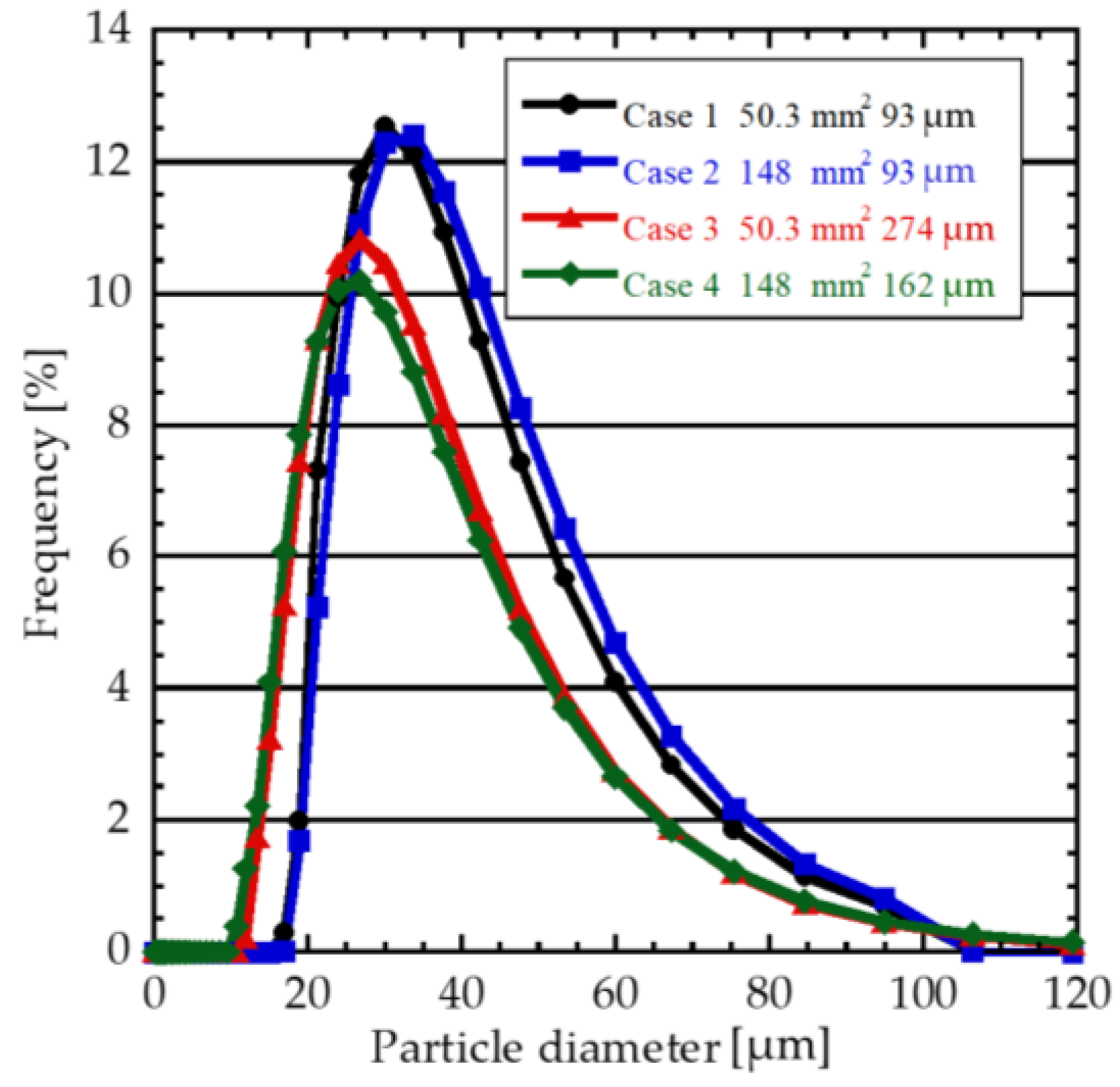
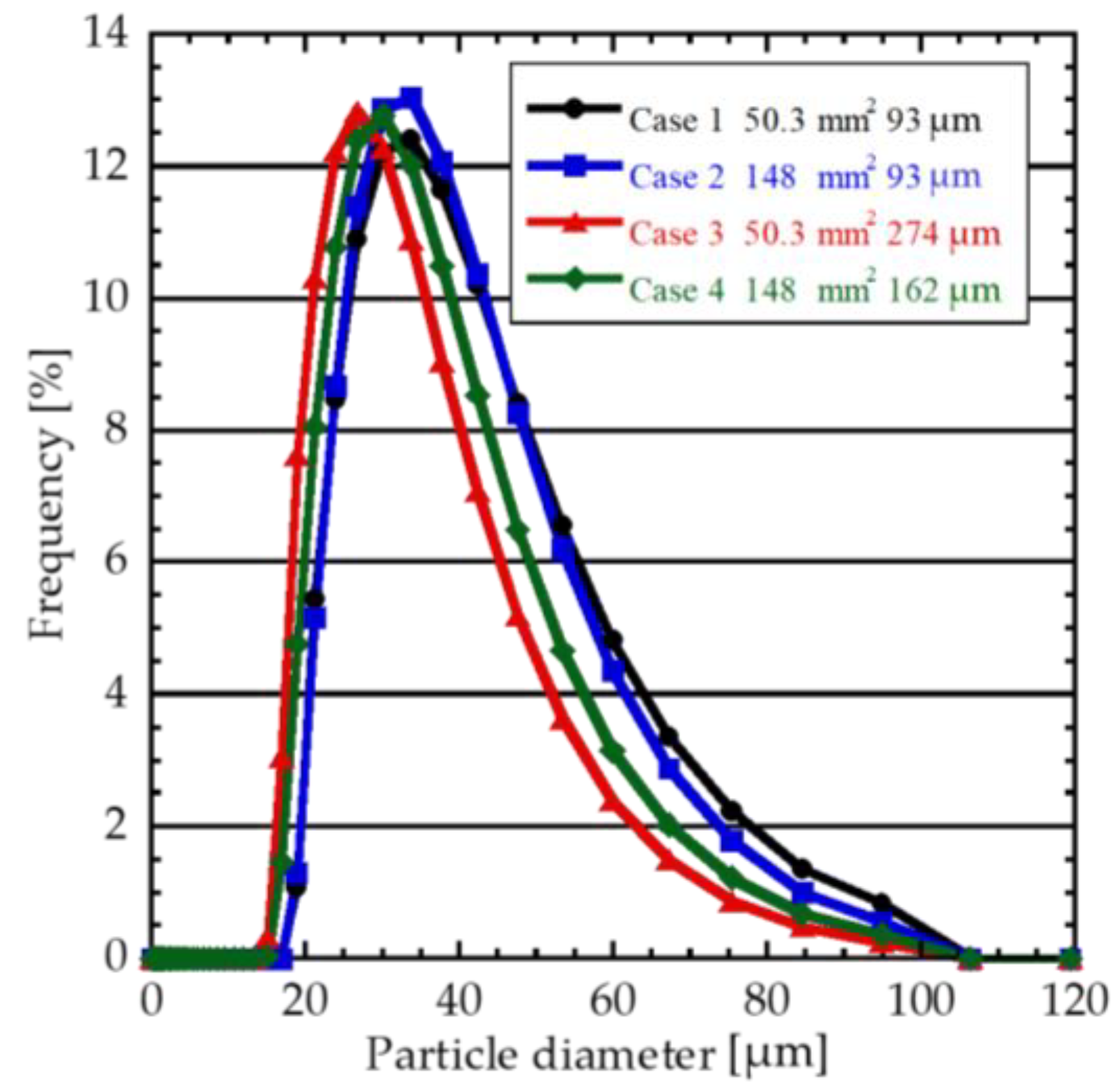
3.3. Diameter Distribution of Microbubble
4. Practical Application and Future Trends
5. Conclusions
- Increasing the oscillation amplitude is necessary for stable microbubble generation, and increasing the tip area at an oscillation amplitude slightly above the threshold for microbubble generation has little effect.
- For microbubble generation at high gas flow rates, the amount of microbubbles generated can be significantly increased by increasing the tip area while keeping the oscillation amplitude sufficiently larger than the threshold value.
- Both oscillation amplitude and tip area have little effect on the bubble diameter distribution.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tsuge, H. The Latest Technology on Microbubbles and Nanobubbles; CMC Publishing Co., Ltd.: Tokyo, Japan, 2007; pp. 1–296. [Google Scholar]
- Zimmerman, W.B.; Hewakandamby, B.N.; Tesar, V.; Bandulasena, H.C.H.; Omotowa, O.A. On the design and simulation of an airlift loop bioreactor with microbubble generation by fluidic oscillation. Food Bioprod. Process. 2009, 87, 215–227. [Google Scholar] [CrossRef]
- Tsuge, H. Fundamentals of microbubbles and nanobubbles. Bull. Soc. Sea Water Sci. 2010, 64, 4–10. [Google Scholar]
- Kukizaki, M.; Goto, M. Spontaneous formation behavior of uniform-sized microbubbles from Shirasu porous glass (SPG) membranes in the absence of water-phase flow. Colloids Surf. A Physicochem. Eng. Asp. 2007, 296, 174–181. [Google Scholar] [CrossRef]
- Ohnari, H. The Characteristics and possibilities of micro bubble technology. Min. Mater. Process. Inst. Jpn. 2007, 123, 89–96. [Google Scholar]
- Makuta, T.; Suzuki, R.; Nakao, T. Generation of microbubbles from hollow cylindrical ultrasonic horn. Ultrasonics 2013, 53, 196–202. [Google Scholar] [CrossRef]
- Kataoka, H.; Kameda, R.; Makuta, T. Optimization of orifice shape and oscillatory displacement of an ultrasonic microbubble generator to increase microbubble yield. Adv. Exp. Mech. 2020, 5, 31–37. [Google Scholar]
- Neppiras, E.A. Very high energy ultrasonics. Br. J. Appl. Phys. 1960, 11, 143. [Google Scholar] [CrossRef]
- Electronic Industries Association of Japan. Ultrasonic Engineering, 3rd ed.; CORONA Publishing Co., Ltd.: Tokyo, Japan, 1999; pp. 77–79. [Google Scholar]
- Chiba, C. Ultrasonic Spray; SANKAIDO Publishing Co., Ltd.: Tokyo, Japan, 1990; pp. 42–171. [Google Scholar]
- Lewis, W.K.; Whitman, W.G. Principles of Gas Absorption. Ind. Eng. Chem. 1924, 16, 1215–1220. [Google Scholar] [CrossRef]
- Leighton, T.G.; Walton, A.J.; Pickworth, M.J.W. Primary Bjerknes forces. Eur. J. Phys. 1990, 11, 47–50. [Google Scholar] [CrossRef]
- Hatanaka, S.; Yasui, K.; Kozuka, T.; Tuziuti, T.; Mitome, H. Influence of bubble clustering on multibubble sonoluminescence. Ultrasonics 2002, 40, 655–660. [Google Scholar] [CrossRef] [PubMed]
- Weiss, R.F. The solubility of nitrogen, oxygen, and argon in water and seawater. Deep. Sea Res. Oceanogr. Abstr. 1970, 17, 721–735. [Google Scholar] [CrossRef]
- Davidson, G.R. Use of SF6 to label drilling air in unsaturated, fractured rock studies: Risk of over-purging. Appl. Geochem. 2002, 17, 1361–1370. [Google Scholar] [CrossRef]
- Jiao, J.; He, Y.; Kentish, S.E.; Ashokkumar, M.; Manasseh, R.; Lee, J. Experimental and theoretical analysis of secondary Bjerknes forces between two bubbles in a standing wave. Ultrasonics 2015, 58, 35–42. [Google Scholar] [CrossRef] [PubMed]
- Syukuya, N.; Makuta, T. An Experimental Study on Disinfection System using Ozone Microbubbles Generated by the Hollow Ultrasonic Horn. J. Jpn. Soc. Exp. Mech. 2011, 11, 116–121. [Google Scholar]
- Saito, Y.; Nozawa, H.; Xing, W.; Makuta, T. Porous Fabrication of White Metal Using Ultrasonically Generated Microbubbles. Metals 2023, 13, 1648. [Google Scholar] [CrossRef]
- Dias, F.; Dutykh, D.; Ghidaglia, J.M. A two-fluid model for violent aerated flows. Comput. Fluids 2010, 39, 283–293. [Google Scholar] [CrossRef]
- Meyapin, Y.; Dutykh, D.; Gisclon, M. Velocity and Energy Relaxation in Two-Phase Flows. Stud. Appl. Math. 2010, 125, 179–212. [Google Scholar] [CrossRef][Green Version]
- Makuta, T.; Takemura, F. Simulation of micro gas bubble generation of uniform diameter in an ultrasonic field by a boundary element method. Phys. Fluids 2006, 18, 108102. [Google Scholar] [CrossRef]


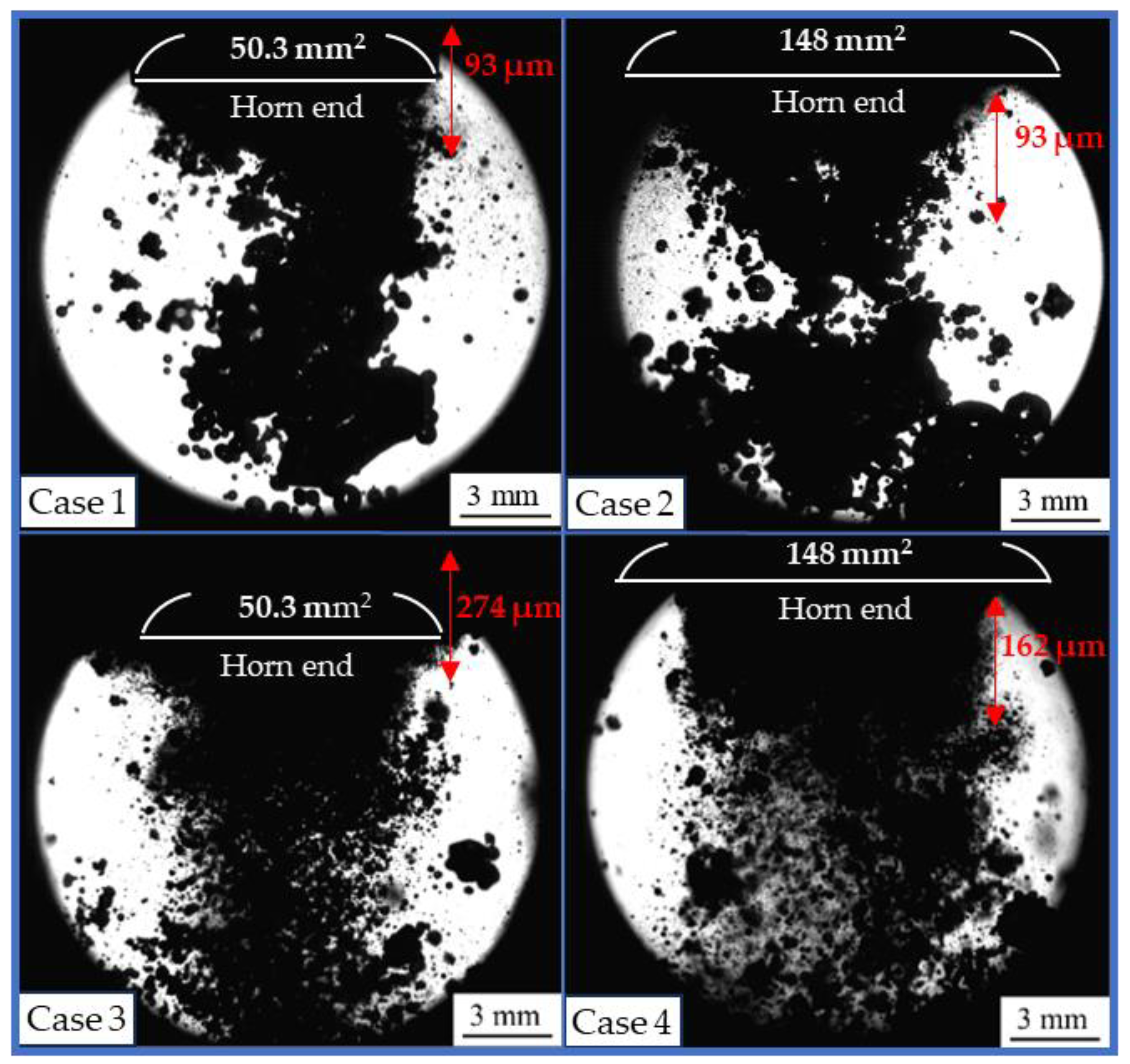


| Case | Horn Type | Oscillating Area | Amplitude |
|---|---|---|---|
| 1 (Default) | (a) | 50.3 mm2 | 93 µm |
| 2 (Large Area) | (b) | 148 mm2 | 93 µm |
| 3 (High Amplitude) | (a) | 50.3 mm2 | 274 µm |
| 4 (Large area, High Amplitude) | (b) | 148 mm2 | 162 µm |
| End Temperature [°C] | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| 100 mL/min | 11.6 | 13.0 | 14.7 | 14.8 |
| 500 mL/min | 11.6 | 13.2 | 17.7 | 15.6 |
| 1000 mL/min | 11.0 | 13.2 | 14.6 | 15.0 |
| Case | 100 mL/Min | 500 mL/Min | 1000 mL/Min |
|---|---|---|---|
| 1 (Default) | 39.7 [µm] | 41.6 [µm] | 42.9 [µm] |
| 2 (Large Area) | 41.2 [µm] | 40.7 [µm] | 41.9 [µm] |
| 3 (High Amplitude) | 34.7 [µm] | 34.6 [µm] | 33.4 [µm] |
| 4 (Large Area, High Amplitude) | 34.0 [µm] | 37.3 [µm] | 36.4 [µm] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasegawa, K.; Yabuki, N.; Makuta, T. Effect of Oscillating Area on Generating Microbubbles from Hollow Ultrasonic Horn. Technologies 2024, 12, 74. https://doi.org/10.3390/technologies12060074
Hasegawa K, Yabuki N, Makuta T. Effect of Oscillating Area on Generating Microbubbles from Hollow Ultrasonic Horn. Technologies. 2024; 12(6):74. https://doi.org/10.3390/technologies12060074
Chicago/Turabian StyleHasegawa, Kodai, Nobuhiro Yabuki, and Toshinori Makuta. 2024. "Effect of Oscillating Area on Generating Microbubbles from Hollow Ultrasonic Horn" Technologies 12, no. 6: 74. https://doi.org/10.3390/technologies12060074
APA StyleHasegawa, K., Yabuki, N., & Makuta, T. (2024). Effect of Oscillating Area on Generating Microbubbles from Hollow Ultrasonic Horn. Technologies, 12(6), 74. https://doi.org/10.3390/technologies12060074





