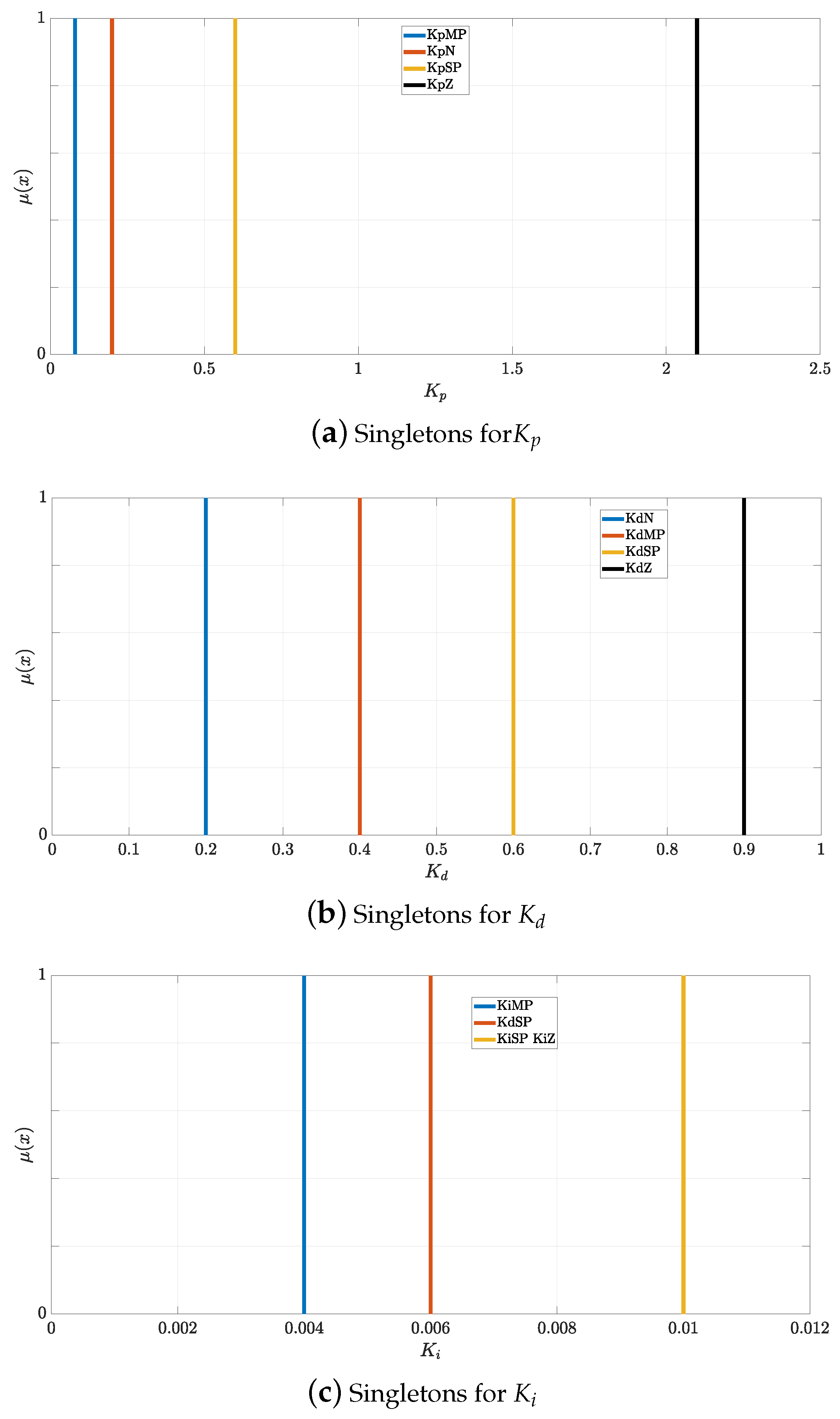Hunting Search Algorithm-Based Adaptive Fuzzy Tracking Controller for an Aero-Pendulum

Abstract

The aero-pendulum is a non-linear system used broadly to develop and test new controller strategies. This paper presents a new methodology for an adaptive PID fuzzy-based tracking controller using a Hunting Search (HuS) algorithm. The HuS algorithm computes the parameters of the membership functions of the fuzzification stage. As a novelty, the algorithm guarantees the overlap of the membership functions to ensure that all the functions are interconnected, generating new hunters to search for better solutions in the overlapping area. For the defuzzification stage, the HuS algorithm sets the singletons in optimal positions to evaluate the controller response using the centroid method. To probe the robustness of the methodology, the PID fuzzy controller algorithm is implemented in an embedded system to track the angular position of an aero-pendulum test bench. The results show that the adaptive PID fuzzy controller proposed presents root mean square error values of 0.42, 0.40, and 0.49 for 80, 90, and 100 degrees, respectively.

1. Introduction

The aero-pendulum is a widely used case study to design classical and robust control strategies for linear and non-linear systems. It comprises an arm that can rotate around its pivot, driven by the thrust produced by a coaxial contra-rotating motorized propeller affixed at its free end [1,2]. It is considered to be a non-linear system, which can be linearized once all the parameters and functionality are known. Among the classic control systems are Proportional–Integral–Derivative (PID) controllers that work efficiently in linear systems [3,4]. For non-linear systems, adjustments must be made to the control algorithms to suppress the inherent non-linearities of the system [5]. Over time, engineers have proposed solutions for the PID controllers using auto-tune strategies to correct the steady-state error. These strategies have shown promising results in changing systems, even in the control of non-linear systems [6].

On the other hand, different techniques have been applied for advanced control strategies like state-space controllers, optimal controllers, artificial neural networks, sliding mode controllers, and fuzzy logic [7,8]. Fuzzy controllers have been developing exponentially in increasingly complex applications. However, the structure of this type of controller has been adapted to the needs of the current systems, making fuzzy controllers more robust and more efficient, combining methodologies so that the controllers are appropriately adapted to the systems to be controlled [9,10,11]. For instance, fuzzy logic and artificial neural network controllers are used when the mathematical model of the system under observation is impossible to obtain and even when the system is inherently non-linear [12]. All these techniques have been combined with metaheuristic algorithms to improve their performance and identify unknown system parameters. Metaheuristic algorithms are optimization techniques to solve complex computational problems when the classical methods tend to fail. Regarding control engineering problems, metaheuristics algorithms obtain specific system parameters, such as identification [13,14]. Another aspect could be that, in the case of the PID controller, it is necessary to know the model to optimize the controller gains carried out with the proposed design brief [15,16]. The convergence of metaheuristic algorithms with control methodologies has experienced notable expansion, primarily propelled by advancements in computational power. Numerous examples illustrate the fusion of control methodologies with optimization algorithms, underscoring the synergistic potential of integrating these domains to address intricate engineering challenges with enhanced efficiency. For example, an identification method was developed by [17] to obtain local linear models and enable the design of automatic controllers using linear matrix inequalities. For modern control combined with fuzzy logic strategies applied to an aero-pendulum, the authors of [18] proposed an observer-based fuzzy regulator for stabilization and tracking control. The observer is designed for operating points using linear matrix inequality. Also, the equilibrium states of a reduced-order non-linear plant model are shifted to the origin. Subsequently, the model is converted into a Takagi–Sugeno fuzzy model utilizing the sector non-linearity method. The research detailed in [19] proposes an advancement strategy for an aero-pendulum control system, offering a comprehensive approach to addressing position control and disturbance compensation. Integrating a multi-loop feedback control mechanism with PID and PI controllers demonstrates a refined capability to maintain precise arm positioning, crucial for various applications ranging from experimental research to industrial automation. Additionally, utilizing the particle swarm optimization (PSO) algorithm to determine optimal PID controller gains underscores the innovative nature of the proposed strategy, offering a systematic and efficient means to enhance the system performance. Furthermore, the authors in [20] reported the performance of classical and adaptive backstepping control schemes for the angular position control of an aero-pendulum where a PSO algorithm is utilized to tune the design parameters of the controllers. The Classical and Adaptive Back-Stepping Controllers have been developed based on Lyapunov stability analysis to establish the convergence of the system’s error over time. They report only the simulation results in Matlab.

This work combines the Hunting Search (HuS) algorithm with fuzzy logic to control an aero-pendulum. Several works have used the HuS algorithm to solve problems related to control engineering [21]. For instance, the authors in [22] validate through simulations the effectiveness of a Multi-Input Fuzzy PID (MIFPID) controller for Automatic Generation Control (AGC) in a two-area interconnected power system, comparing it with two single-input FPID (SIFPID-1 and SIFPID-2) controllers. The objective function incorporates frequency undershoot, overshoot, and settling time, with each controller implemented separately in both areas. They propose the Modified Group Hunting Search optimization (MGHS) algorithm to optimize the controller gain parameters, addressing a multi-objective problem with constraints. Performance evaluations are conducted with a $1\%$ load disturbance in area-1, showing that the MIFPID controller optimized by the MGHS algorithm outperforms the others in the system studied. On the other hand, [23] presents an approach of utilizing the HuS algorithm to fine-tune a Takagi–Sugeno–Kang-type neuro-fuzzy model. It encodes the fuzzy model’s structure and parameters into particles, enabling simultaneous optimization.

In this paper, we introduce a novel approach to adaptive fuzzy control. Our methodology involves optimizing the membership functions utilized in both the fuzzification and defuzzification stages using the HuS algorithm. The aim is to employ this optimized fuzzy controller to effectively regulate an aero-pendulum, which tracks a parabolic motion profile as its set point. This innovative technique promises to enhance the control precision and adaptability, offering potential applications in various domains requiring robust and flexible control systems.

This paper is organized as follows: Section 2 presents the background on the dynamics of an aero-pendulum, fuzzy systems, motion profiles, and the HUS algorithm. Section 3 describes the materials used in the experimentation and outlines the methodology followed during the experimentation. Section 4 and Section 5 contain the results and discussion, respectively. Section 6 contains the conclusion and references.

2. Background

2.1. System Dynamics of Aero-Pendulum

An aero-pendulum system is commonly described as a pendulum driven by a motorized propeller assembly attached to the free end of a rod of negligible mass, the fixed end of which is pivoted about a rotating shaft encoder. A rotary axis encoder measures the angular position of the rod concerning the downward vertical axis [24,25].

The control of the angular position of the driven pendulum is achieved by manipulating the propeller’s thrust force using different control strategies. These strategies may include techniques to adjust the orientation of the propeller direction or speed control systems for position adjustment depending on its inclination. Figure 1 shows the proposed plant, which consists of a suspended mass, but, instead of a negligible mass, it uses a counterweight of 0.34 kg at the end of the arm. This arm is joined to a brushless direct current motor (BLDC), A2012 1000 KV, with propellers at the other end for oscillatory motion driven by a 30A ESC (Electronic Speed Controller), which is an electronic circuit board that enables the control over the BLDC motors. An angular displacement sensor is adapted to the test bench to measure the angular position. The structure is built with an aluminum profile of 20 mm, corner brackets, and Allen screws.

The dynamic model of the aero-pendulum is shown in Equation (1) according to [26,27,28]. Figure 2 shows a cross-section of the test bench used and the model parameters. Where I inertia of the pendulum, B viscous damping coefficient M is weight of pendulum, m mass of the counterweight, g gravity, P thrust from dc motor, $\alpha$ angle of the pendulum, L total distance of the pendulum, h distance from the counterweight to the fulcrum, and l distance from the center of mass of the pendulum to the fulcrum.

Table 1. Numerical parameters of the aero-pendulum.

Mechanical Parameters			Electrical Parameters
Parameter	Symbol	Value	Parameter	Symbol	Value
Counterweight mass	m	0.34 kg	Maximum efficiency current	$\eta$	6–12 A
Counterweight to fulcrum distance	h	0.108 m	Maximum efficiency	$\eta$max	78%
Pendulum length	L	0.45 m	No load current	IO	0.7 A
Center of mass to fulcrum distance	l	0.04 m	Maximum current	Imax	16 A
Pendulum weight	M	0.166 kg	Maximum output	Pmax	180 W
Gravity	g	9.81 $\mathrm{m}/{\mathrm{s}}^2$	Internal resistance	r	65 mΩ
DC motor throttle	P	0.35 kg

shows the mechanical and electrical parameters of the test bench used in experimentation. The parameters from the BLDC motor are $\eta$ maximum efficiency current, $\eta$$max$ maximum efficiency, $IO$ no-load current, $Imax$ maximum current, $Pmax$ maximum output, and r internal resistance.

The equation governing the system in Figure 2 is obtained using Newton’s laws. This equation is as follows.

$$I\ddot{\alpha }+B\dot{\alpha }+Mglsin\alpha +mghsin\alpha =P$$

(1)

The Equation (1) can be linearized for small values of the angle $\alpha$ to obtain the transfer function from Equation (2); in this function, it takes the relation between the angle of the pendulum and the throttle from the motor [19,25].

$$\frac{\alpha \left(s\right)}{P\left(s\right)}=\frac{\frac{1}{I}}{I{s}^2+Bs+(Ml+mh)g}$$

(2)

The MATLAB System Identification Toolbox was utilized to identify the model parameters. Two-step inputs were proposed, each with amplitudes equivalent to 8% and 14% of throttle power. Subsequently, the response of the system, denoted by the ordered pairs ($v,\alpha$), was plotted. In Figure 3, the response of the system graphs depicts estimates of the transfer functions ${\alpha }_{e1}$ and ${\alpha }_{e2}$ corresponding to the 8% and 14% throttle power inputs, respectively. These graphs include the measured system data, and the plotted data points ${\alpha }_{m1}$ and ${\alpha }_{m2}$ corresponding to the 8% and 14% power inputs, respectively. The tool’s approximation accuracy was evaluated to be 93%. Equation (3) presents the resulting transfer function.

$$\frac{\alpha \left(s\right)}{V\left(s\right)}=\frac{54.82}{s^2+4.368s+16.88}$$

(3)

2.2. Fuzzy Systems

A wide variety of controllers serve to execute control in different cases. The PID controller is more often used thanks to its practicality and efficiency in controlling labor [29]. For this case, a fuzzy controller based on PID is the central part of the controller. On the other hand, fuzzy logic is a particular area of artificial intelligence in which there is not a true or false response but a set of values that provide more weight to each decision, providing a more flexible means to make decisions [30]. So, a fuzzy logic controller takes advantage of being flexible by using rules proposed by the user to make the controller more suitable for different situations. Using the fuzzy logic and also the properties of the PID enables the creation of different sets of controllers that would provide an efficient and adequate response regarding the system [31,32].

In the first place, to create a fuzzy controller, certain steps are required to elaborate a fuzzy system. The structure comprises four primary blocks: fuzzification, the establishment of rules, logic inference, and defuzzification.

• The fuzzification or fuzzifier is in charge of making and proposing the inputs of the fuzzy systems, considering the properties of the system to be modeled.
• The rule base is the step of setting up rules. In this phase, the designer establishes the range in which each decision from the inputs/outputs is being taken.
• Then comes the inference logic phase in which the rules from the inputs are related to the rules of the outputs. Various techniques can be completed in this phase; for this project, the technique max-product is used to create relations between the inputs and outputs.
• Finally comes the ending block from the fuzzy system called defuzzification. As the name suggests, it is the contrary part of the first step in which the fuzzy rules established before are now going into the system to create the crisp signal.

2.3. Trajectory Definition

In motion control, trajectory planning consists of obtaining a function of time to describe the cinematic magnitudes of a movement, such as position, velocity, or acceleration. The model obtained is also known as the motion profile. One of the most used due to its simplicity is the parabolic motion profile, which models a movement with continuous speed and constant acceleration [33,34]. As shown in Figure 4, this type of trajectory, a third-degree polynomial, describes the position, whereas velocity takes on a parabolic shape.

Equation (4) describes the position of the movement at each instant in time.

$$\begin{array}{cc}\hfill \theta \left(t\right)={\theta }_0+\frac{2{\dot{\theta }}_{max}}{T}{(t-t_0)}^2-\frac{4{\dot{\theta }}_{max}}{3T^2}{(t-t_0)}^3,& 0<t\le T\end{array}$$

(4)

Equations (5)–(7) relate the speed, acceleration, and execution time of the movement, respectively.

$${\dot{\theta }}_{max}=\frac{3h}{2T}$$

(5)

$${\ddot{\theta }}_{max}=\frac{6h}{T^2}=\frac{4{\dot{\theta }}_{max}}{T}$$

(6)

$$T=\frac{3h}{2{\dot{\theta }}_{max}}$$

(7)

2.4. HuS Algorithm

The HuS algorithm conceptualized the hunting process of catching prey in group hunting [21]. The collaboration among group members, referred to as hunters, is essential for encircling and capturing prey, mirroring the optimization process aimed at attaining a global solution based on an objective function. Just as hunters coordinate their efforts to corner and seize their target effectively, optimization techniques leverage collective strategies to converge towards the most optimal outcome, driven by the pursuit of maximizing or minimizing a defined objective. The likelihood of a hunter catching its prey is contingent upon its positional relationship to the prey. Likewise, the value of the objective function is contingent upon the collective assignment of values to each decision variable. The HuS algorithm is formulated upon a model of group hunting observed in animals seeking food, resembling the cooperative hunting strategies employed by wolves, for instance. The following steps display the procedure of the HuS:

1.

Define the optimization problem and the design parameters: The HuS algorithm sets out crucial parameters for tackling the optimization task. These parameters encompass the hunting group size (HGS), indicating the number of solution vectors within the hunting group, as well as the maximum movement towards the leader (MML) and the hunting group consideration rate (HGCR), which varies between 0 and 1. MML and HGCR play pivotal roles in fine-tuning the positions of hunters (solution vectors), as elaborated in subsequent Steps 3 and 4.

2.

Initialize the hunting group (HG): The hunting group matrix is populated with feasible randomly generated solution vectors contingent upon the number of hunters (HGS). Subsequently, the objective function values are computed, and the leader is determined based on these values across the objective functions of the hunters.

3.

Move toward the leader: The updated positions of the hunters (new solution vectors) ${\displaystyle h\prime }$ are generated by advancing toward the leader, the hunter possessing the best position within the group. Equation (8) is used to correct the positions.

$$\begin{array}{c}\hfill {h\prime }_i=h_i+rand\times MML\times ({h\prime }_i-h_i)\end{array}$$

(8)

The $MML$ represents the maximum movement towards the leader, where $rand$ denotes a uniformly distributed random number ranging from 0 to 1, and $h_i^L$ is the position value of the leader for the i-th variable.

4.

Correct the positions (cooperation between members): This step simulates the collaborative behavior among the hunters to enhance the efficiency of the hunt. Following their movement toward the leader, the hunters select new positions, guided by the positions of other hunters, and incorporate random factors to discover improved solutions. Updating the variable value is thus carried out as presented in Equation (9).

$$\begin{array}{c}\hfill h_i^{j^{\prime }}=\left\{\begin{array}{ccc}{h}_i^{j^{\prime }}\in \{h_i^1,h_i^2,\dots ,h_i^{HGS}\}\hfill & & \mathrm{with}\mathrm{probability}HGCR\\ h_i^{j^{\prime }}=h_i^j\pm Ra\hfill & & \mathrm{with}\mathrm{probability}(1-HGCR)\end{array}\right.\end{array}$$

(9)

where $i=1,\dots ,N$ and $j=1,\dots ,HGS$. The $HGCR$ parameter determines the likelihood of selecting a value from the hunting group stored in HG, while $(1-HGCR)$ represents the probability of performing a position correction. The $Ra$ only begins to contract after a certain number of iterations. An exponential function is used for $Ra$ reduction as expressed in Equation (10).

$$\begin{array}{c}\hfill Ra\left(k\right)=R{a}_{min}(max\left(h_i\right)-min\left(h_i\right))e^{\frac{ln(\frac{R{a}_{min}}{R{a}_{max}})\times k}{itm}}\end{array}$$

(10)

where k is the iteration number, $max\left(h_i\right)$ and $min\left(h_i\right)$ denote the maximum or minimum possible value of vector $h_i$, respectively. $R{a}_{max}$ and $R{a}_{min}$ indicate the maximum and minimum of the relative search radius of the hunter, respectively, and $itm$ is the maximum number of iterations in the optimization process.

5.

Reorganize the hunting group: As the search progresses, the hunters can become ensnared in a local minimum (or a local maximum if the objective is to find the maximum). In such instances, the hunters must regroup and recalibrate their strategies to afford themselves another opportunity to pinpoint the optimal solution. The algorithm executes this process under two distinct conditions. Firstly, if the discrepancy between the objective function values for the leader and the poorest-performing hunter within the group diminishes to a level below a predetermined threshold and the termination criterion remains unmet, the algorithm restores the hunting group for every hunter. Alternatively, once a designated number of search iterations has transpired, the hunters undertake a self-reorganization process autonomously. The series of search iterations leading to the entrapment of the group in a local minimum, or the completion of a predetermined number of searches, constitutes one epoch. During the reorganization, the leader maintains its position, while the remaining hunters randomly select new positions within the design space by Equation (11).

$$\begin{array}{c}\hfill {h\prime }_i=h_i^L\pm rand\times (max\left(h_i\right)-min\left(h_i\right))\times \alpha e^{-\beta \times Tr}\end{array}$$

(11)

In this reorganization phase, $h_i^L$ represents the position value of the leader for the i-th variable. Including the uniform random number $rand$, fluctuating between 0 and 1, facilitates the selection process. Furthermore, $max\left(h_i\right)$ and $min\left(h_i\right)$ denote the maximum or minimum possible value of vector $h_i$, respectively. In the meantime, $Tr$ records the occurrences of the group being trapped up to this point. The parameters $\alpha$ and $\beta$ are positive real numbers that establish the algorithm’s overall convergence rate.

6.

Repeat Steps 3, 4, and 5 until the termination criterion is satisfied.

The convergence of the HuS algorithm is achieved quickly since, at each stage of the algorithm, the hunters move significantly, with only those that are moving closer to the solution prevailing. If observed from the point of view that the hunters must move according to the position of the prey, as mentioned above, the algorithm is executed depending on the size of the group of hunters, where the grouping of the hunters changes within a matrix of HGS hunters, leaving only the best; that is, the hunters who present the best results go to the next cyclical stage. These movements are undertaken three times in a single epoch since they have to move towards the leader, correct their positions, and reorganize the group of hunters, searching for a more dynamic solution in each iteration since each step evaluates the objective function, enabling the hunters to obtain better results. For example, in related work, the convergence of the HuS algorithm is found quickly, as documented in [22], where the algorithm showed a convergence of ten generations with eight parameters to be optimized in a fuzzy PID controller.

3. Materials and Methods

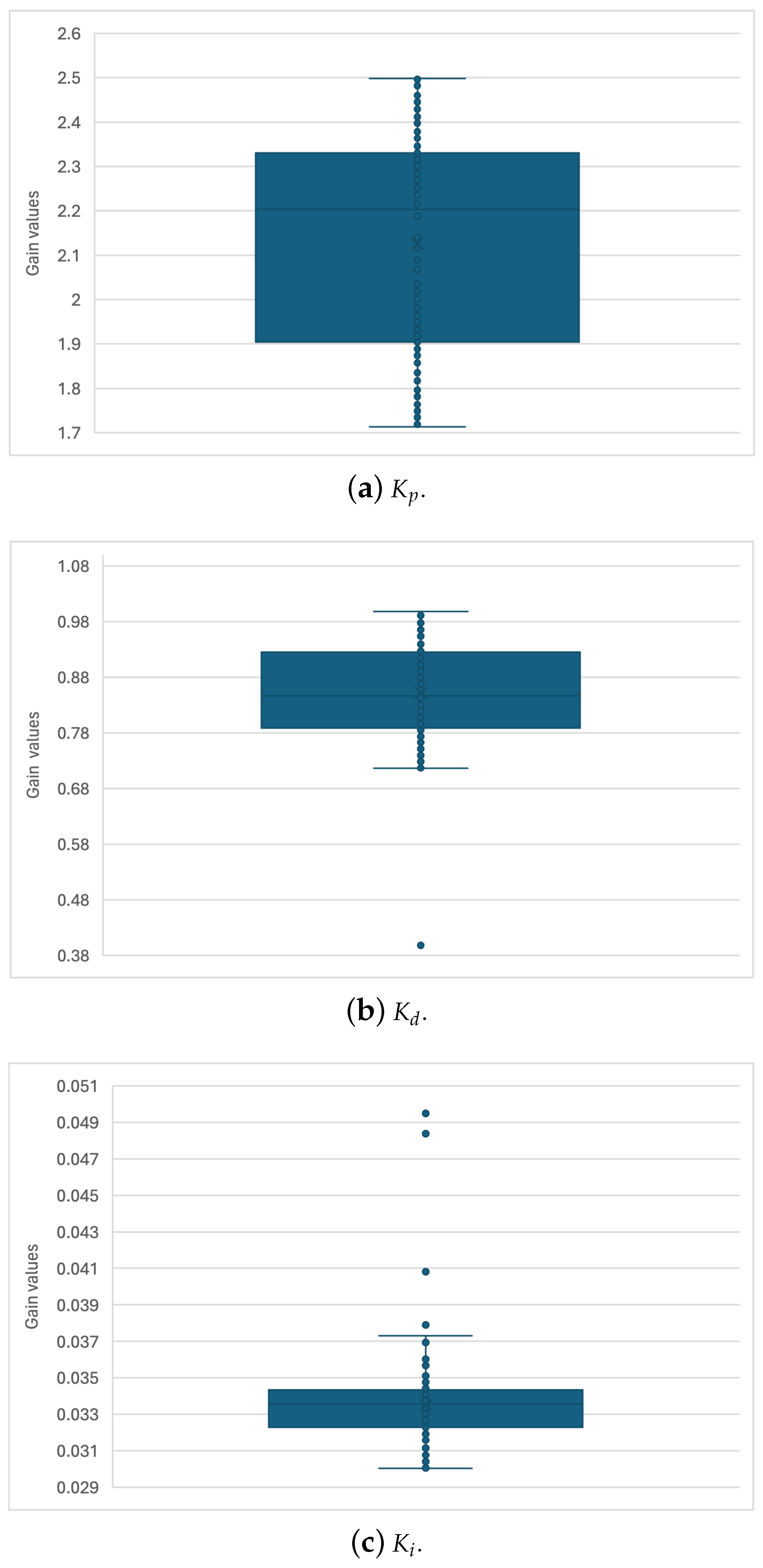
The fuzzy controller developed in this paper is a PID fuzzy controller, a compound of three separate parts: the proportional, derivative, and integral. Each part has its separate fuzzy system with three different sub-systems; each will calculate the correspondent gain: the $K_p$, $K_d$, and $K_i$. These values are calculated depending on the values of the derivative and integral errors. Once each part has been calculated, the following procedure is to add them together to create the controller response that will go directly to the system. In this PID fuzzy controller, the HuS algorithm will focus on fuzzy systems in charge of obtaining the proper gains, as shown in Figure 5, where the main goal is to obtain more suitable values. This controller references Equation (12), the classical PID controller. The parameters modified within the controller are proportional, derivative, and integral gains ($K_p$, $K_d$, $K_i$), which change in real time, meaning that these gains do not stay static. The consequential values of these gains are determined by the input error present in the system, meaning that, in different error situations, the gains will behave differently; on the contrary, in classical controllers, the gains stay permanently static.

$$u\left(t\right)=K_p\ast e\left(t\right)+K_d\ast \frac{de\left(t\right)}{dt}+K_i\ast \int e\left(t\right)dt$$

(12)

Because the applied controller is a PID, the closed-loop poles of the system are found in Equation (13).

$$s^3+(54.82K_d+4.368)s^2+(54.82K_p+16.88)s+54.82K_i=0$$

(13)

To ensure the stability of the system, it is considered that $K_i>0$, $K_d>0$, $(54.82K_d+4.368)\times (54.82K_p+16.88)>54.82K_i$ are taken into account based on an analysis by Routh Hourwitz.

The PID fuzzy controller proposed is fixed by 12 rules, as shown in

Table 2. Fuzzy rules for the aero-pendulum fuzzy tracking controller.

${\mathit{K}}_{\mathit{p}}$	${\mathit{K}}_{\mathit{d}}$	${\mathit{K}}_{\mathit{i}}$
If e(t) is NP, then $K_p$ is KpN	If de(t) is ND, then $K_d$ is KdN	If ie(t) is NI, then $K_i$ is KiN
If e(t) is ZP, then $K_p$ is KpZ	If de(t) is ZD, then $K_d$ is KdZ	If ie(t) is ZI, then $K_i$ is KiZ
If e(t) is SPP, then $K_p$ is KpSP	If de(t) is SPD, then $K_d$ is KdSP	If ie(t) is SPI, then $K_i$ is KiSP
If e(t) is MPP, then $K_p$ is KpMP	If de(t) is MPD, then $K_d$ is KdMP	If ie(t) is MPI, then $K_i$ is KiMP

. These rules describe the control of the aero-pendulum test bench.

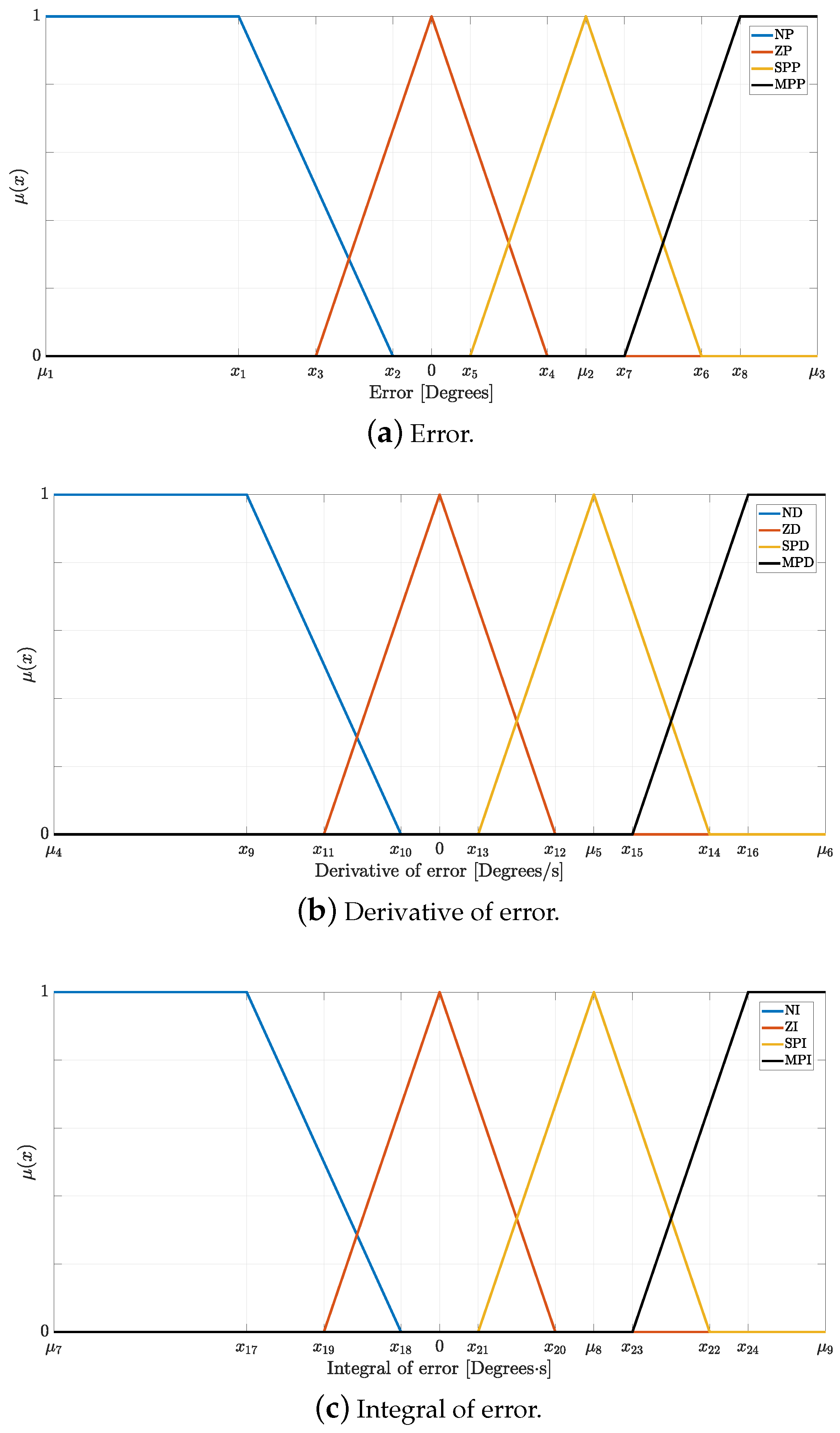
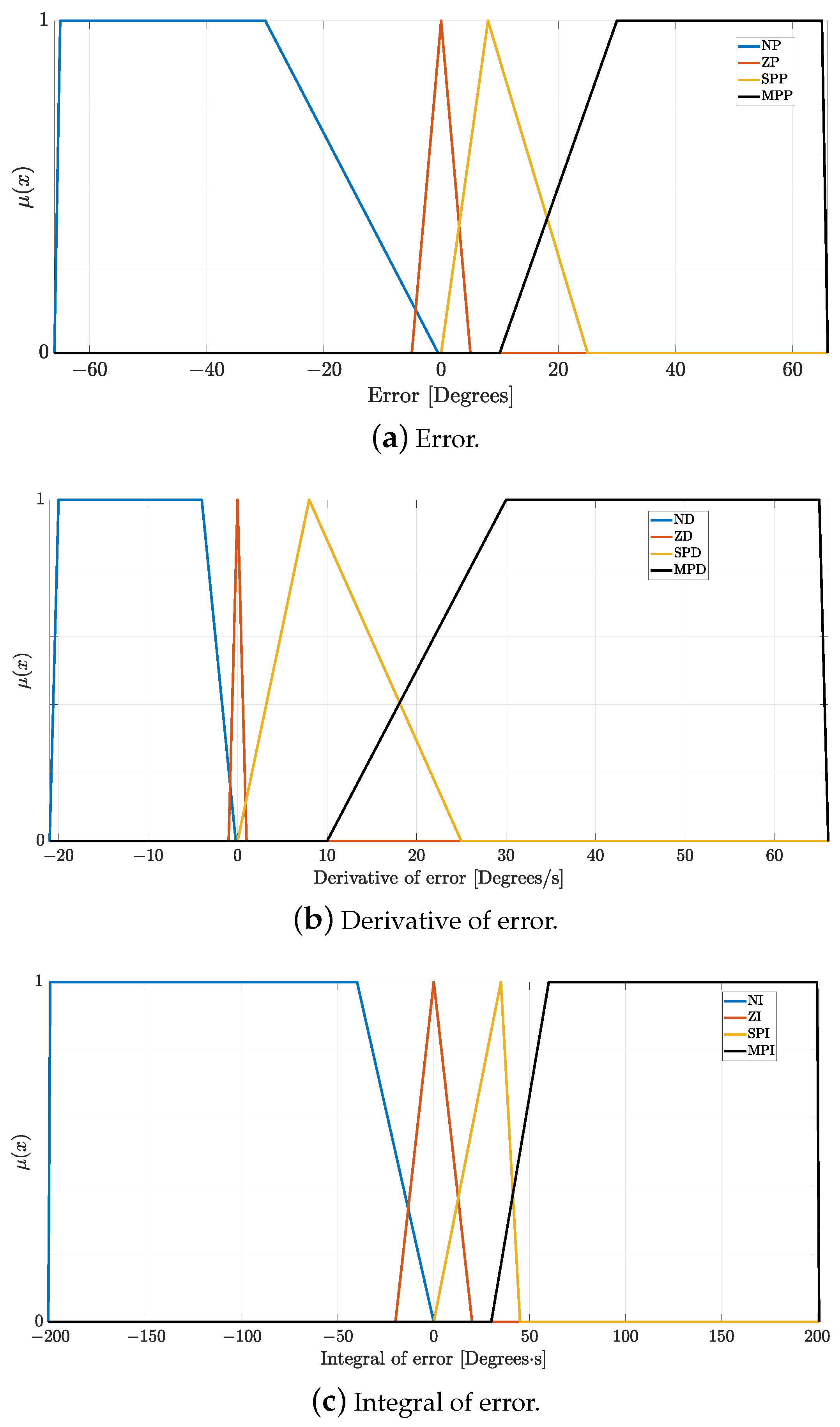
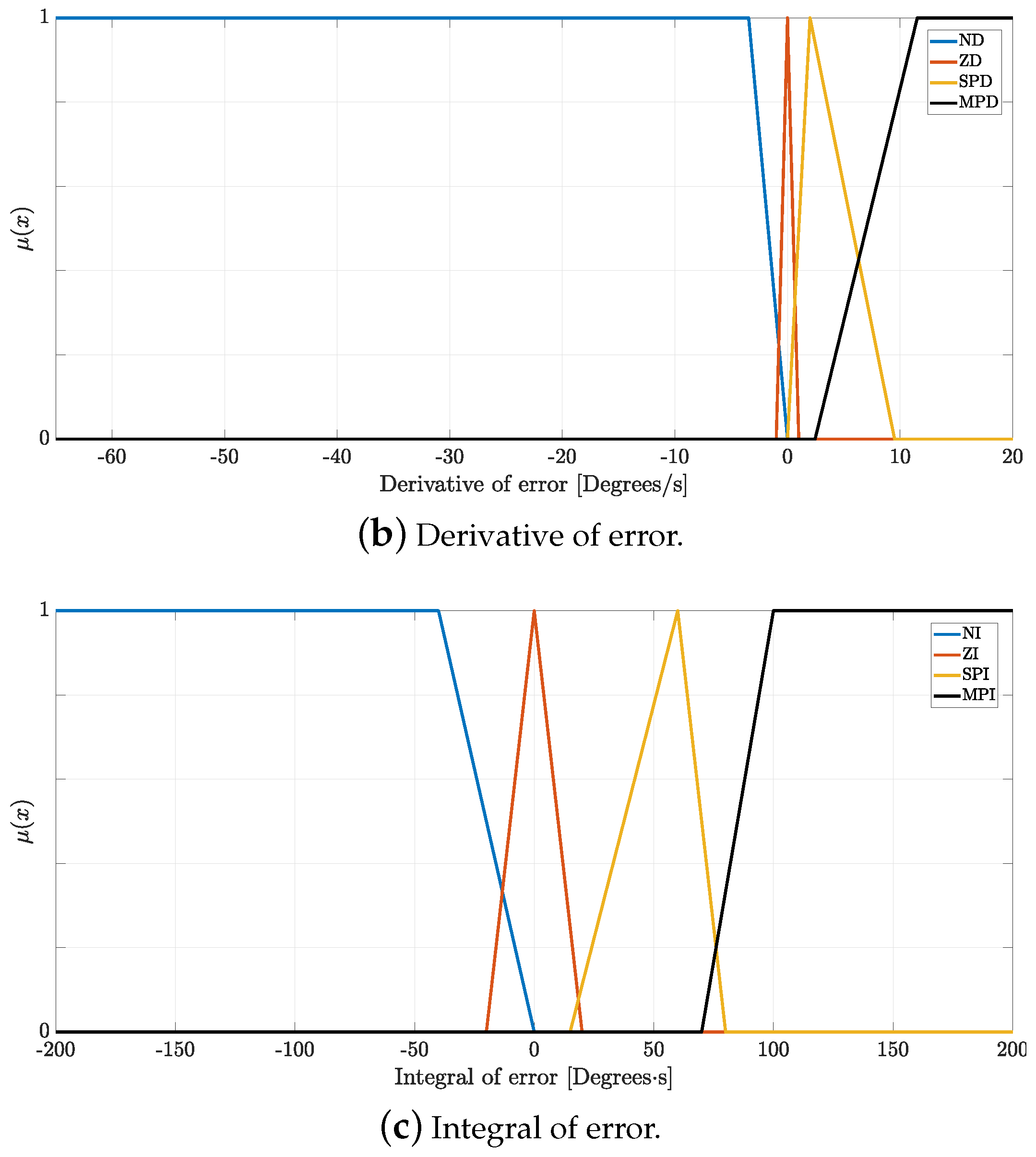
The fuzzification stage is developed using three linguistic variables: the error measured in degrees, the error derivative measured in degrees per second, and the integral error measurement. Each linguistic variable is expressed by two triangular and two trapezoidal linguistic values: the trapezoidal would indicate the larger positive and negative values of error (MP and N). One triangular value is positioned in zero to demonstrate the absence of zero (Z), and the last triangle indicates the minor presence of error (P). The triangular membership function is presented in Equation (14), and the trapezoidal membership function is displayed in Equation (15).

$${\mu }_{triangular}\left(x\right)=\left\{\begin{array}{ccc}0,\hfill & if\hfill & x\le x_i^L\hfill \\ \frac{x-x_i^L}{{\mu }_i-x_i^L},\hfill & if\hfill & x\in (x_i^L,{\mu }_i]\hfill \\ \frac{x_{i+1}^R-x}{x_i^R-{\mu }_i},\hfill & if\hfill & x\in ({\mu }_i,x_i^R)\hfill \\ 0,\hfill & if\hfill & x\ge x_i^R\hfill \end{array}\right.$$

(14)

$${\mu }_{trapezoidal}\left(x\right)=\left\{\begin{array}{ccc}0,\hfill & if\hfill & x\le x_i^L\hfill \\ \frac{x-x_i^L}{{\mu }_i^L-x_i^L},\hfill & if\hfill & x\in (x_i^L,{\mu }_i^L]\hfill \\ 1\hfill & if\hfill & x\in ({\mu }_i^L,{\mu }_i^R]\hfill \\ \frac{x_{i+1}^R-x}{x_i^R-{\mu }_i^R},\hfill & if\hfill & x\in ({\mu }_i^R,x_i^R)\hfill \\ 0,\hfill & if\hfill & x\ge x_i^R\hfill \end{array}\right.$$

(15)

where $x_i^L$ and $x_i^R$ represent the start (left slope) and end (right slope), respectively, of the i-th triangular and trapezoidal membership functions and the ${\mu }_i$ is the core point of the membership function, x is the input of the fuzzy system. The HuS algorithm has to find the best position for the parameters of the triangular membership functions. For the case of the error linguistic variable, the algorithm has to find ten optimized parameters related to the slopes and three optimized parameters for the centers, as presented in Figure 6a. The same process occurs for the error derivative linguistic variable, shown in Figure 6b.

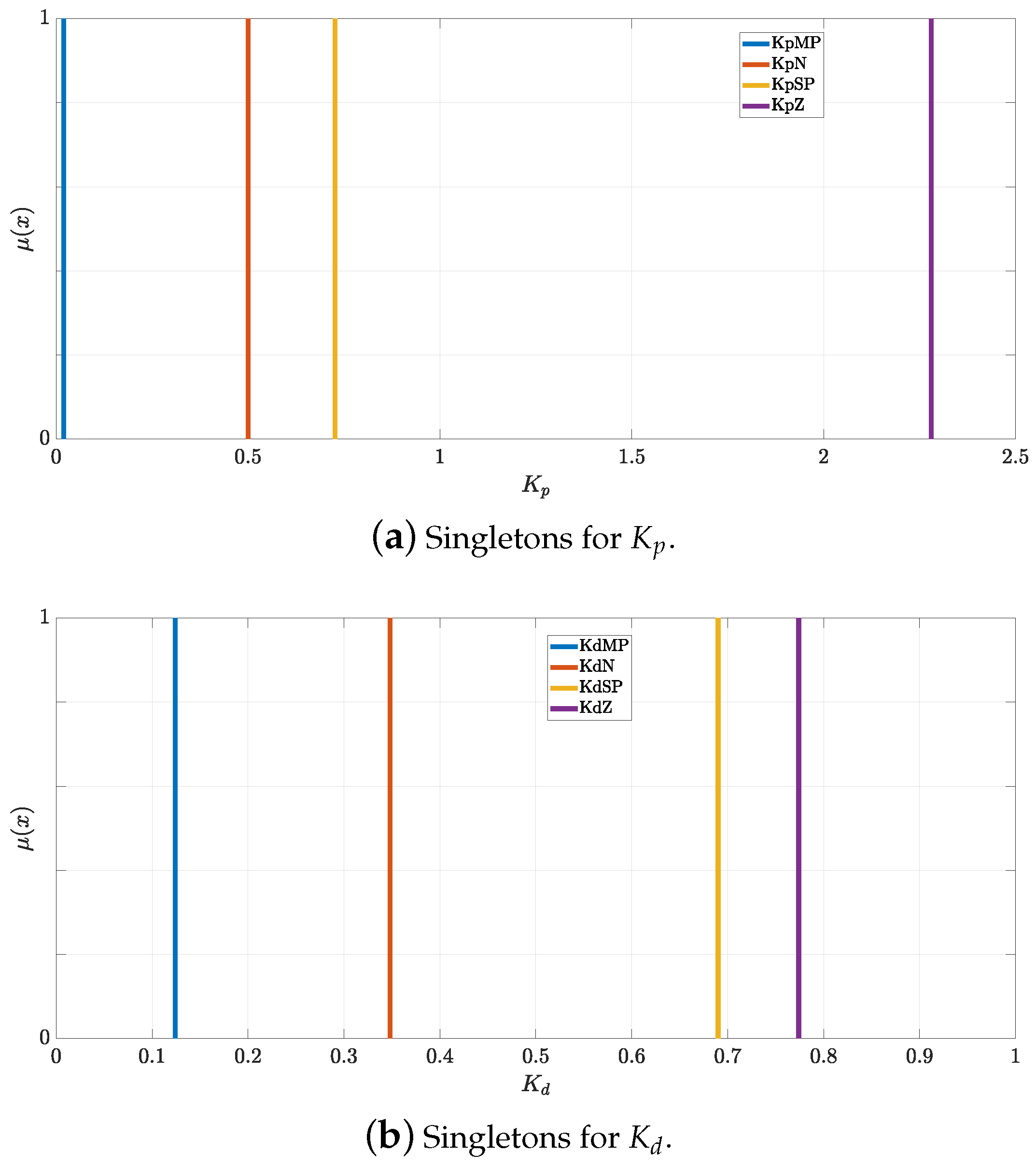
There is a set of gains for each fuzzy system, with the controller having three different total, illustrated in Figure 7. There are four different singletons located in a range used as a restriction of the gains; the names of these singletons are N (negative), Z (zero), SP (small positive), and MP (much positive). These values are related to their corresponding linguistic variables from Figure 6 that have similar names. It is important to note that the proposed values of the gains are greater than zero since the gains of a classical PID controller must be greater than zero to ensure stability.

To compute the gains of controllers $K_p$, $K_i$, and $K_d$, the centroid method displayed in Equation (16) is used.

$$uK\left(t\right)=\frac{\sum \mu \left(x_n\right)·x_n}{\sum \mu \left(x_n\right)}=\frac{x_n\left(N\right)+x_{n+1}\left(Z\right)+x_{n+2}\left(SP\right)+x_{n+3}\left(MP\right)}{N+Z+SP+MP}$$

(16)

Once all the parameters (hunters) are identified, the HuS algorithm is implemented to find these parameters of the PID fuzzy controller based on the mathematical model of the aero-pendulum and the motion profile as the reference. The flowchart, Figure 8, presents the overall process to find the best solution for the gains of the controller. In the first step, the initialization of the HuS algorithm parameters is proposed according to Section 2.4. The random initialization of the hunters is carried out in step 2. Equation (17) represents the first group of hunters. The hunters are uniformly distributed in the search area.

$$h=\{x_1,x_2,x_3,\dots ,x_{24},x_{25}\}$$

(17)

The fitness function for evaluating the hunters’ position is the root mean square error (RMSE) detailed in Equation (18). The HuS algorithm finds membership function parameters to minimize the Euclidean distance between the reference and the computed response.

$$f{\left(h\right)}_{RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^n{(r\left(i\right)-\widehat{\theta }\left(i\right))}^2}$$

(18)

where $r\left(i\right)$ and $\widehat{\theta }\left(i\right)$ are the desired value and the computed measured in the i-th iteration, respectively, and n is the total number of iterations. Once the fitness function is evaluated, the hunters with the best position are preserved to accommodate their position into the loop. Steps 3 to 5 reorganize the hunters, evaluate Equation (18), and save the best hunters for step 6. Step 6 is the enhancement proposed. This phase evaluates the hunters to ensure the overlapping of the membership functions.

In this work, the concept of overlapping holds significant importance as it enables the inclusion of an appropriate control surface. It is widely acknowledged that, when the membership functions of a linguistic variable fail to interact, dead zones may arise, leading to situations where the actuator receives no signal from the controller or experiences instability. Therefore, adequate overlapping can mitigate the risk of such dead zones and ensure smooth and stable control system operation. This emphasizes the critical role of overlapping in achieving effective and reliable control in various applications. Step seven guarantees that all membership functions interact properly by randomly moving the hunters in the range of the overlapping. For instance, using $x_2$ and $x_3$ from Figure 6a, some hunters of column $x_2$ are smaller than $x_3$, when $x_3$ is supposed to be smaller than each hunter in $x_2$; the algorithm provides a chance to the hunters that do not carry out this assertion to pass to the successive movements since they present a linguistic value interaction. Still, if this assertion is the opposite, the hunters in $x_3$ reorganize in the interval $[x_1,x_2]$ using Equation (19).

$$x_{i+1}=abs(\gamma \times rand({\mu }_i,x_i))\pm x_i$$

(19)

where $x_{i+1}$ is the hunter that moves between the core membership function ${\mu }_i$ and the left/right slope if the membership function $x_i$ is triangular or trapezoidal. $rand({\mu }_i,x_i)$ finds a uniformly random number among ${\mu }_i$ and $x_i$. The parameter $\gamma$ plays a critical role in determining the movement behavior of hunters within the defined overlap area. Representing a real number within the $[0.2, 0.7]$ range, $\gamma$ is the hunter movement factor, dictating the magnitude of steps taken during the hunting process. When $\gamma$ approaches the lower bound of $0.2$, hunters are inclined to proceed cautiously with smaller steps, exhibiting a more conservative approach to navigation. Conversely, as $\gamma$ approaches the upper bound of $0.7$, hunters adopt a more assertive stance, traversing the terrain with larger strides. This distinction in movement strategy, dictated by the value of $\gamma$, underscores its significance in optimizing hunting behaviors within the specified overlap region.

4. Results

4.1. General Controller Programming

An embedded system board based on a microcontroller ESP32 with two 32-bit Xtensa LX6 processing cores can run at speeds up to 240 MHz. A variety of peripherals, including GPIO, UART, SPI, I2C, 10-bit PWM, and ADC with 12 bits of resolution, make it a good choice for real-time implementation. C++ was used to test the control algorithms on the aero-pendulum test bench using a sample time of $0.02$ s. The code structure initiates by declaring the variables and constants of the system, including the specific fuzzy parameters; some functions are subsequently declared that are needed within a main function, and, finally, it initiates the primary function. The main function undertakes various actions, such as generating the motion profile, receiving the degrees sensor reading, processing the fuzzy controller, generating the response from the controller, creating an offset (the relation from the angle and the throttle), and sending the response to the BLDC. The Algorithm 1 presents the structure of the motion controller algorithm.

Algorithm 1: Motion controller algorithm
Declare the inputs and outputs;
Declare the constants and variables;
Indicate the fuzzy gain of $K_p$, $K_d$, and $K_i$ from Figure 7 and the fuzzy variables;
Function LinguisticValues(error, anchoring points):
	Create the figures of the functions;
	Calculate the membership degree;
Function SetUp ():
	Configure the BLDC frequency, PWM, and channel;
	Create the interruption of 0.02s;
while True do
	Generate the parabolic profile in Figure 4;
	Measure the position from the angular displacement sensor;
	Filter the readings obtained from the sensor;
	Calculate error $e\left(t\right)$;
	Calculate the derivative error $de\left(t\right)$;
	Calculate the integral error $ie\left(t\right)$;
	Evaluate the linguistic variable of error $e\left(t\right)$ presented in Figure 6a;
	Evaluate the linguistic variable of derivative error $de\left(t\right)$ presented in Figure 6b;
	Evaluate the linguistic variable of integral error $ie\left(t\right)$ presented in Figure 6c;
	Calculate the controller response;
	Calculate the offset from the system;
	Adjust the output signal by adding the controller response and the offset together;
	Send the output signal to the BLDC;
end

4.2. Non-Optimized PID Fuzzy Logic Controller

The design and implementation of control systems for complex mechanical systems like the aero-pendulum present numerous challenges, particularly when employing fuzzy logic controllers that require more precise tuning.

Understanding the behavior of an aero-pendulum system poses the initial challenge of designing effective control strategies. The dynamic interactions of the system between the pendulum, motor, and counterweight offer a more complex way to analyze the system. For example, stabilizing the aero-pendulum in a particular position requires a specific amount of throttle from the propeller; another example would be the inability to control how the pendulum lowers and leaves primarily due to gravity because there is only one propeller aiming upwards. The examples mentioned are some conditions one must consider when proposing the controller.

It is important to mention that the aero-pendulum used in this paper has a counterweight situated at one end of the pendulum. Adding a counterweight can adjust the center of mass, minimizing the erratic behavior and uneven weight distributions in the system. This counterweight directly impacts stabilizing the pendulum, so every test regarding this system starts at a position of 63 degrees.

Another problem when controlling the system includes the inconsistencies in the sensor and actuator. For the input, an angular displacement sensor is used to measure the position of the pendulum; the problem with this sensor is that it usually causes a great deal of noise regarding the signal, making it difficult to obtain a proper reading. To fix this, a filter was added, making this sensor more suitable. Then, for the output, a BLDC uses a duty cycle with little resolution, which causes problems when correcting a minimum quantity of errors. These two devices provide certain inconsistencies when trying to control the pendulum because they do not have an accurate way of eliminating the error. The fuzzy controller is based on the set of rules in Table 2. The first test of this controller uses the parameters established by the user considering his knowledge of the system. Figure 9 shows the aero-pendulum maintaining the position of a 90-degree angle, which is also demonstrated by the plotter observed over the screen.

On the other hand, certain points should be considered when proposing the gain values. The controller response is evaluated as the product of the gains and the current error. It is very important to consider the magnitude of the error when proposing the gain values because the error could be large or small, meaning that, if the gains are wrongly established, there could be an aggressive or weak response. Also, the gains are not allowed to take negative values.

For this controller, the gains were established as inversely proportional to the error, meaning that, if the error increases its value, the gain will tend to reduce. The reason for this is to avoid the aggressiveness issue mentioned previously. For that reason, the gains related to the absence of zero are larger; this can be seen in Figure 7.

The linguistic values depicted in Figure 10 were proposed by experimentation. Initially, the process involved defining linguistic values based on Figure 10a and Figure 11a, which served as the foundation for this controller. The error values from Figure 10a were determined by analyzing the error presence across various positions of the aero-pendulum. The $K_p$ values were established through experimentation with the system, identifying those values that yielded superior responses. After establishing these initial parameters, the subsequent step involved incorporating the derivative values from Figure 10b, which would be settled by analyzing the error of just the P fuzzy controller. The $K_d$ values from Figure 11b were assigned heuristically and maintained at the best values to provide the best results. Once the PD fuzzy controller is designed, the final part is to adjust the integral linguistic values and $K_i$ as shown in Figure 10c and Figure 11c, respectively. The integral linguistic variable universe was set to work in a range of two degrees of error because it would correct the final portions of error. The values of $K_i$ are the smallest because it does not require much power to eliminate the remaining error.

Figure 12a illustrates the trajectory followed by the aero-pendulum, reaching its final position of 90 degrees within a time of 7 s. Upon examining the error depicted in Figure 12b, it is evident that the error fluctuates between 0 and 1.5 degrees. However, the most significant error peaks lie within 1.5 to 1.8 degrees along the trajectory, rendering it not quite precise for a PID fuzzy controller with an RMSE magnitude of 0.54. Analyzing Figure 12c reveals the controller’s response in the presence of error, which is deemed sub-optimal based on the obtained results. Consequently, adjustments to this controller response are necessary. The throttle signal is the direct value from the fuzzy controller, which serves as a way to correct the error by accelerating or decelerating the system. The positive values are the ones in charge of providing more throttle, and the negative values provide less to the system.

4.3. Optimized PID Fuzzy Logic Controller with HuS Algorithm

For the computing of the PID fuzzy controller using the HuS algorithm, Equation (3) was employed. The HuS algorithm was implemented in Python 3 programming on a Macbook Pro M2 Pro computer, and it calculates 36 parameters in the optimization process. These parameters correspond to the triangular membership functions, using Equations (14)–(16), in the fuzzification phase and the position of the singletons in the defuzzification stage, respectively.

Table 3. Descriptions of the parameters.

Parameter	Description	Value
MML	Maximum movement towards the leader	0.4
HGCR	Hunting group consideration rate	0.3
$R_{a_{max}}$	Maximum relative search radius of the hunter	$1.00\times {10}^2$
$R_{a_{min}}$	Minimum relative search radius of the hunter	$1.00\times {10}^{-7}$
$\alpha$	Positive real numbers that establish convergence	0.01
$\beta$	Positive real numbers that establish convergence	−1
$\gamma$	Hunter movement factor in the overlapping	0.2
HGS	Hunting group size	50
m	Number of variables	36
$K_p$	Proportional gain restriction	$(0,3]$
$K_d$	Derivative gain restriction	$(0,1]$
$K_i$	Integral gain restriction	$(0,0.8]$
N	Number of generations	20

displays the parameters used by the HuS algorithm to compute the fuzzy controller. On the other hand, in Figure 13, the depiction of the parabolic motion profile trajectory, Equation (4), can be observed. The response derived from Equation (3) represents the mathematical model of the test bench and the optimized fuzzy controller. The HuS algorithm, guided by the parameters outlined in Table 3, successfully generates a well-suited PID fuzzy controller through simulation. As a restriction of the HuS algorithm to search the range of the gains, Equation (13) is used.

The number of rules used to build this controller is set to over 12, and this magnitude is chosen over the necessities of the system. The error linguistic values were determined to be four for each fuzzy system. Two are set to eradicate positives that act on small or large presences of error. One is set to eliminate the negative error; there is only one rule here because the deceleration of the system does not require many more specifics; this is presumed by conducting tests over the system. Finally, one variable is placed on zero to represent the absence of error.

The error linguistic variable ranges from $-65$ to 65 degrees.

Table 4. Optimized parameters of the error linguistic variables.

Linguistic Value	${\mathit{x}}_{\mathit{i}}^{\mathit{L}}$	${\mathit{\mu }}_{\mathit{i}}$	${\mathit{x}}_{\mathit{i}}^{\mathit{R}}$
NP	−65	−24.89	−4.9
ZP	−5	0	1
MPP	0.6	8	15.61
SPP	9.33	33	65

displays the optimized parameters of the triangular (ZP and MPP) and trapezoidal (NP and SPP) linguistic values. There are three variables for the trapezoid, displaying a half-trapezoid shape. The form of each linguistic value is presented in Figure 14a.

The error derivative linguistic variable uses a similar approach as the proportional variable. The derivative rules permit the system to comprehend and predict more suitable behavior.

Table 5. Optimized parameters of the error derivative linguistic variables.

Linguistic Value	${\mathit{x}}_{\mathit{i}}^{\mathit{L}}$	${\mathit{\mu }}_{\mathit{i}}$	${\mathit{x}}_{\mathit{i}}^{\mathit{R}}$
ND	−65	−3.45	0
ZD	−1	0	1
SPD	0	2	9.31
MPD	2.45	11.53	20

displays the optimized parameters of the triangular (ZD and SPD) and trapezoidal (ND and MPD) derivative error linguistic values. The derivative error linguistic variable ranges from $-65$ to 20 degrees; these values are obtained by analyzing the response of the error measured and are used as a restriction of the HuS algorithm. The shape of each linguistic value is presented in Figure 14b.

The error integral linguistic variable is observed in

Table 6. Optimized parameters of the error integral linguistic variables.

Linguistic Value	${\mathit{x}}_{\mathit{i}}^{\mathit{L}}$	${\mathit{\mu }}_{\mathit{i}}$	${\mathit{x}}_{\mathit{i}}^{\mathit{R}}$
NI	−200	−40	0
ZI	−20	0	20
SPI	15	60	80
MPI	70	100	200

; the integral controller has as its main aim to correct the last amounts of error present within the system. As a result, it would only work in a range of 2 degrees of error. For this reason, the universe of the linguistic variable goes from $-200$ to 200. The system comprehends four different variables: two triangular (ZI and SPI) and two trapezoids (NI and MPI). The shape of each linguistic value is presented in Figure 14c.

Table 7. Optimized parameters for the output linguistic variables.

Linguistic Value	${\mathit{K}}_{\mathit{p}}$	${\mathit{K}}_{\mathit{d}}$	${\mathit{K}}_{\mathit{i}}$
N	0.5	0.348	0.03
Z	2.28	0.774	0.025
SP	0.727	0.69	0.022
MP	0.02	0.124	0.02

shows the corresponding optimized values of $K_p$, $K_d$, and $K_i$. The values of $K_p$ end up being the largest because the proportional controller is in charge of providing the aggressive response; the following value, $K_d$, is smaller because it is only in charge of the erratic behavior of the proportional controller. Finally, the values of $K_i$ are the smallest because the integral controller focuses on eliminating the small magnitude of error.

Figure 14 and Figure 15 provide a visual representation of the linguistic variables utilized in the fuzzy controller, as detailed in Table 4, Table 5, and Table 7. According to the stability analysis from Routh Hourwitz, regarding the values obtained from the controller by the proposed algorithm when the controller accomplishes the permanent regimen, it accomplishes the condition $(54.82K_d+4.368)(54.82K_p+16.88)>54.82K_i$ so that the system could maintain stability. The gain values displayed by the controller from the HuS algorithm are $kp=1.963, kd=0.7234, ki=0.023$. Substituting the values in the condition previously mentioned, $3067.3>1.2609$ demonstrates the system stability in a closed loop.

Moving on to Figure 16, it displays the performance of the PID fuzzy controller optimized using the HuS algorithm. This evaluation shares identical experimental parameters with the un-optimized PID fuzzy controller from Figure 12. Figure 16a illustrates the response of the optimized adaptive PID fuzzy controller designed by the HuS algorithm, tracing the same trajectory over 7 s and stabilizing at 90 degrees. Figure 16b shows that the error provided from the error oscillates over 0.5 error degrees and oscillates around an error of 0.3 degrees when settling at 90 degrees; the response makes it an acceptable and notably improved controller over the initially proposed one by having an RMSE of 0.4. Finally, Figure 16c provides insight into the controller’s response to the error.

Figure 17 shows that the proposed algorithm converges to the optimized parameters in the fifth iteration. This is fast since the modified HuS algorithm develops four search stages, enabling the hunters to move considerably toward the prey (solution) per generation. As mentioned in Section 2.4, the unmodified HuS algorithm has three stages where the hunters have to move towards the leader, correct their positions based on the target values, and reorganize to improve the position of each hunter. In this proposal, as mentioned in Section 3, the hunters will be reorganized based on the overlaps of the membership functions of each controller stage to enable the hunters to work better with the uncertainty of the measurements. The HuS algorithm has to find 36 parameters for the fuzzy PID controller.

Table 8. Statistical values of the gain triplets.

Linguistic Value	${\mathit{K}}_{\mathit{p}}$	${\mathit{K}}_{\mathit{i}}$	${\mathit{K}}_{\mathit{d}}$
Min	1.7132	0.0200	0.3987
Max	2.4988	0.0495	0.9987
Mean	2.1266	0.0335	0.8528
St.Dev.	0.2444	0.0022	0.0874

displays the statistical values of the gain triplets, including the mean, standard deviation, minimum value, and maximum value. The consistency of the gains can be verified by the minimums and maximums, which show the complete range of possible values for each gain, all of which fall within the constraints considered in the HUS algorithm. However, the standard deviation for $K_p$ and $K_i$ is relatively low compared to the mean values of these parameters. Although the standard deviation for $K_p$ is higher than its mean value, the parameters do not reflect significant variability among the individual values. For all the gains, it can be observed that the values are more clustered around the mean, as shown in the box and whisker plot displayed in Figure 18. The diagram in Figure 18a shows the absence of outliers. The data distribution does not contain extreme values significantly beyond the limits established by the HUS algorithm constraints, and they fall within quartiles Q1 and Q3.

By conducting 400 experiments to obtain the profit tuples for $K_p$ and $K_i$, these exhibit only one and four values outside the interquartile range, as can be seen in Figure 18b,c, respectively. This indicates a uniform distribution without a notable presence of outliers that could significantly affect the central tendency and dispersion measures.

5. Discussion

In this section, two cases will be discussed: the comparison of the PID fuzzy controller with a step input, compared with a Mamdani controller that was designed with 36 rules for the aero-pendulum, and, second, the response of the PID fuzzy controller with the trajectory will be discussed, including a third-degree polynomial with a duration of 7 s, varying the set point to show that the system responds to any target position.

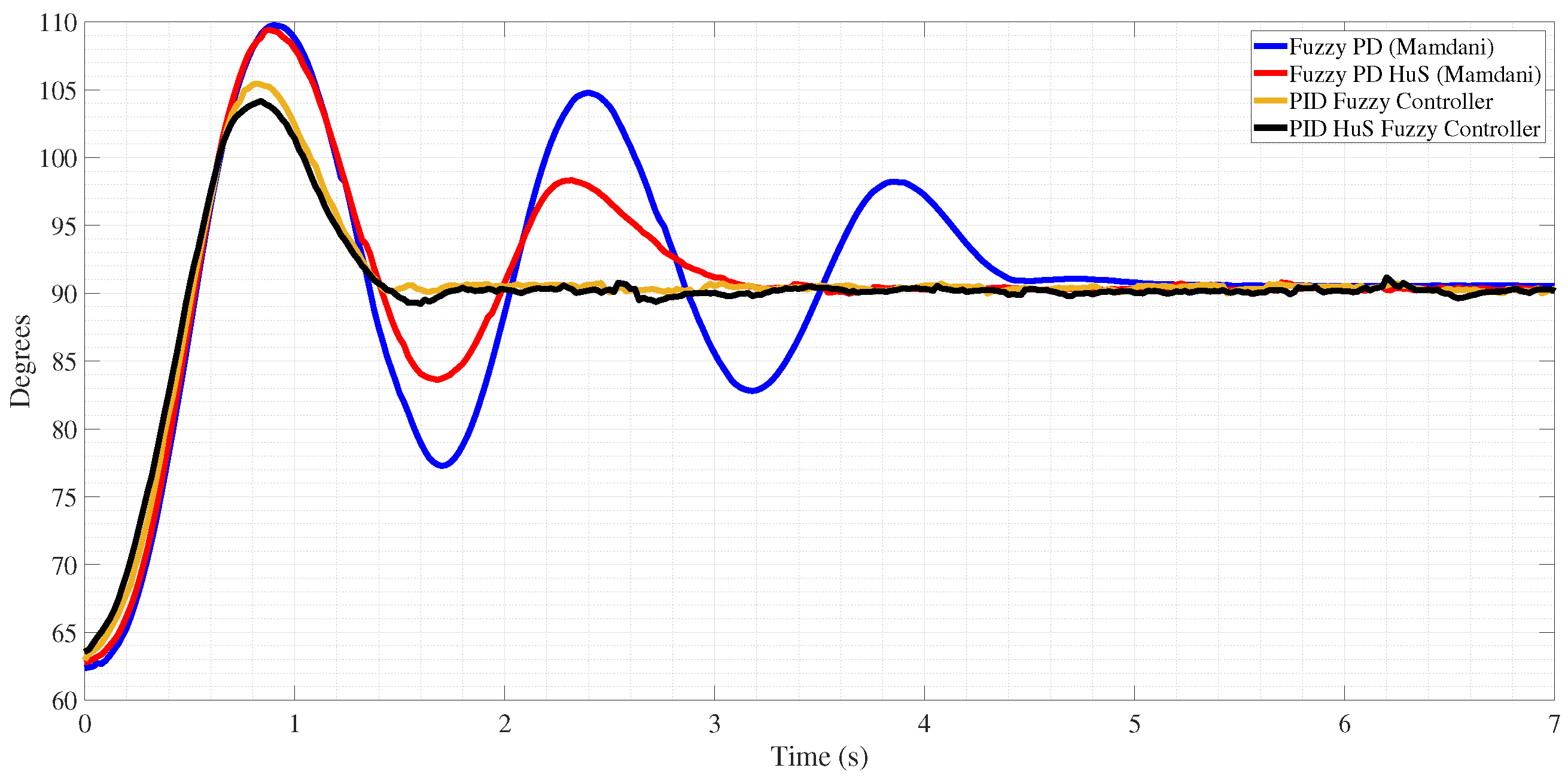
In Figure 19, a comparative examination between the adaptive and non-adaptive fuzzy controllers, implemented using the HuS algorithm, is presented. The PID fuzzy controller was compared with a Mamdani controller that was provided a step input. The fuzzy controller using the Mamdani inference method was designed from 36 rules; this controller tends to consume too many computational resources because all 36 rules must be evaluated to calculate the control signal. This controller presents aggressive oscillations when it has not been optimized. The optimization carried out as a test of the operation of the HuS algorithm has to find 29 optimization parameters. These parameters correspond to the membership functions of the fuzzification stage and the positions of the singletons of the defuzzification stage. When optimized, the Mamdani fuzzy controller considerably reduces the oscillations and settling time. However, the PID fuzzy controller presents a better response, with a considerable overshoot and a significant improvement in the steady-state error with a settling time of 1.45 s, less than either version of the Mamdani fuzzy controller with 5 s for the non-optimized one and 3.2 s for the optimized one. The PID fuzzy controller was designed with a total of 12 rules to calculate the gains $K_p$, $K_i$, and $K_d$, using one-to-one fuzzy relationships, which means that the calculation of the gains is computed directly using Equation (16), which entails a lower computational cost when compared to the Mamdani controller.

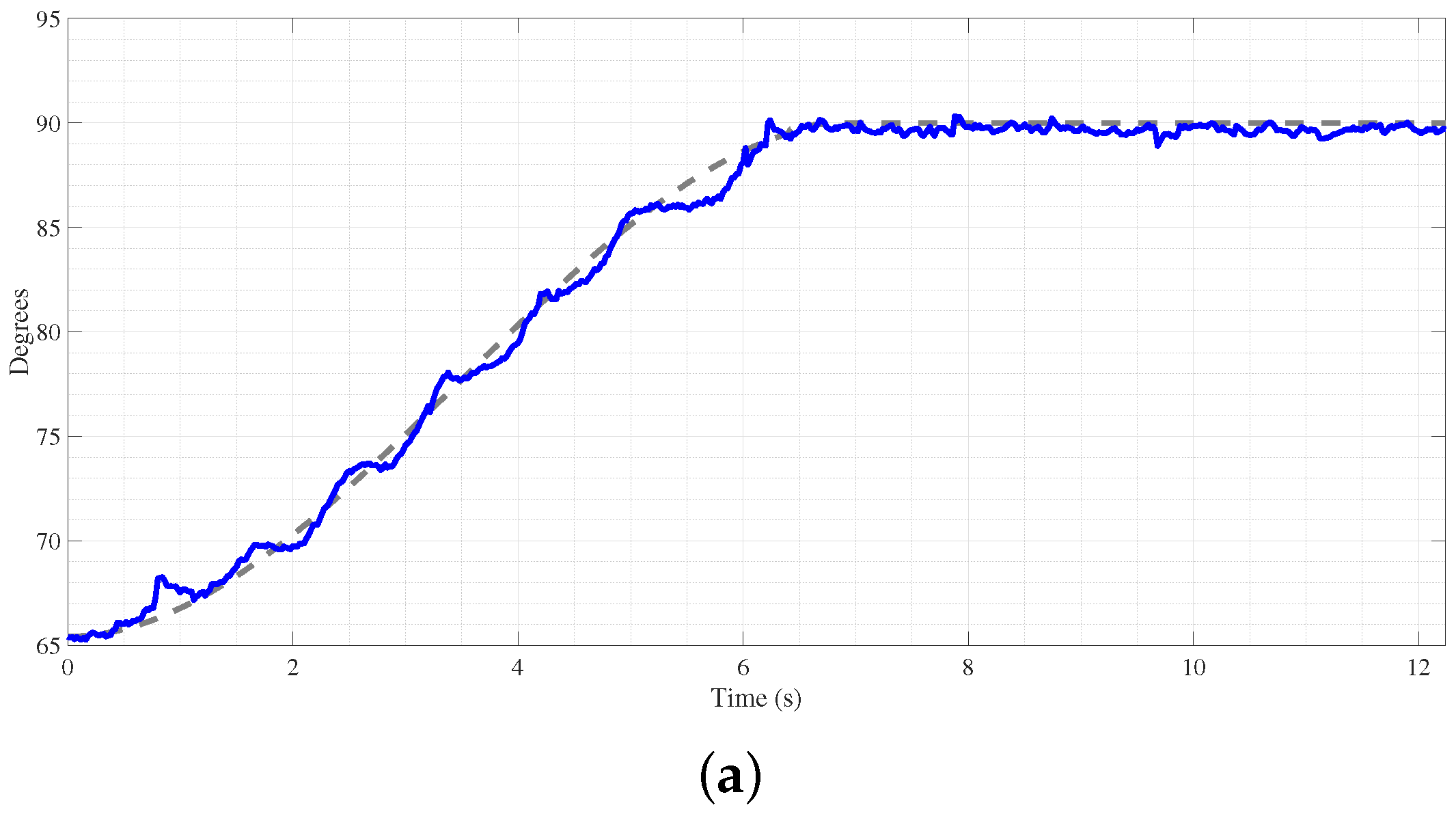
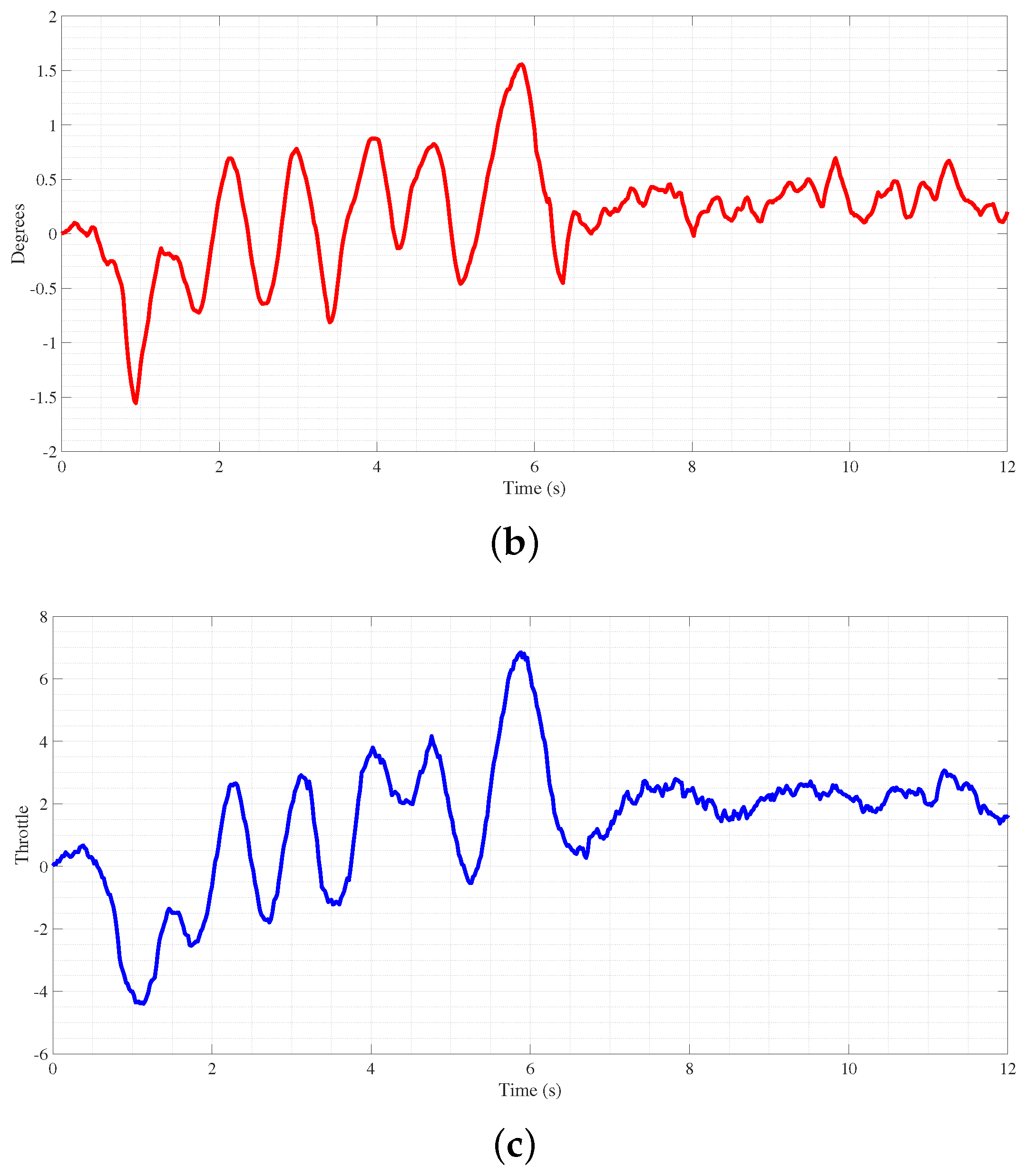
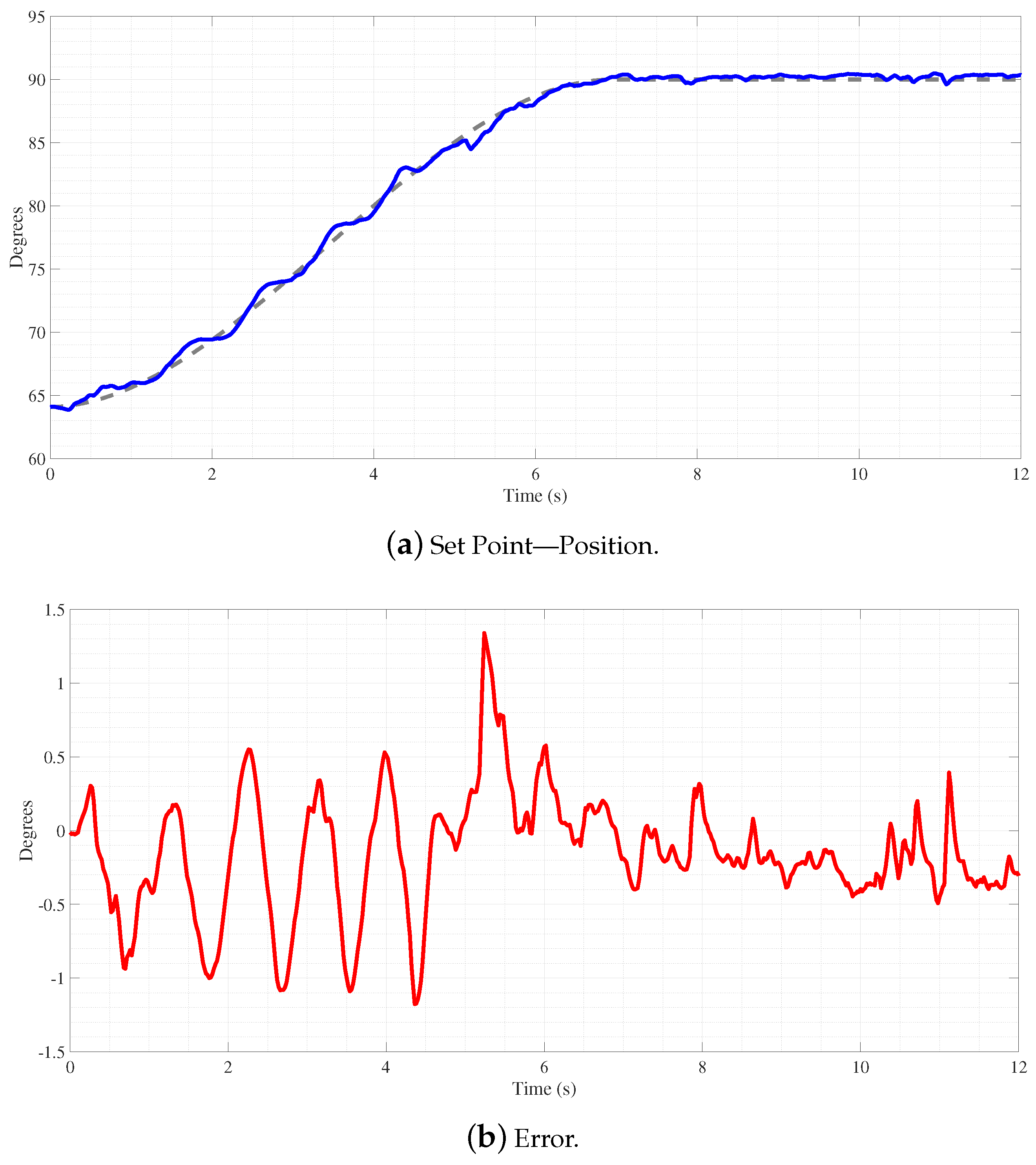
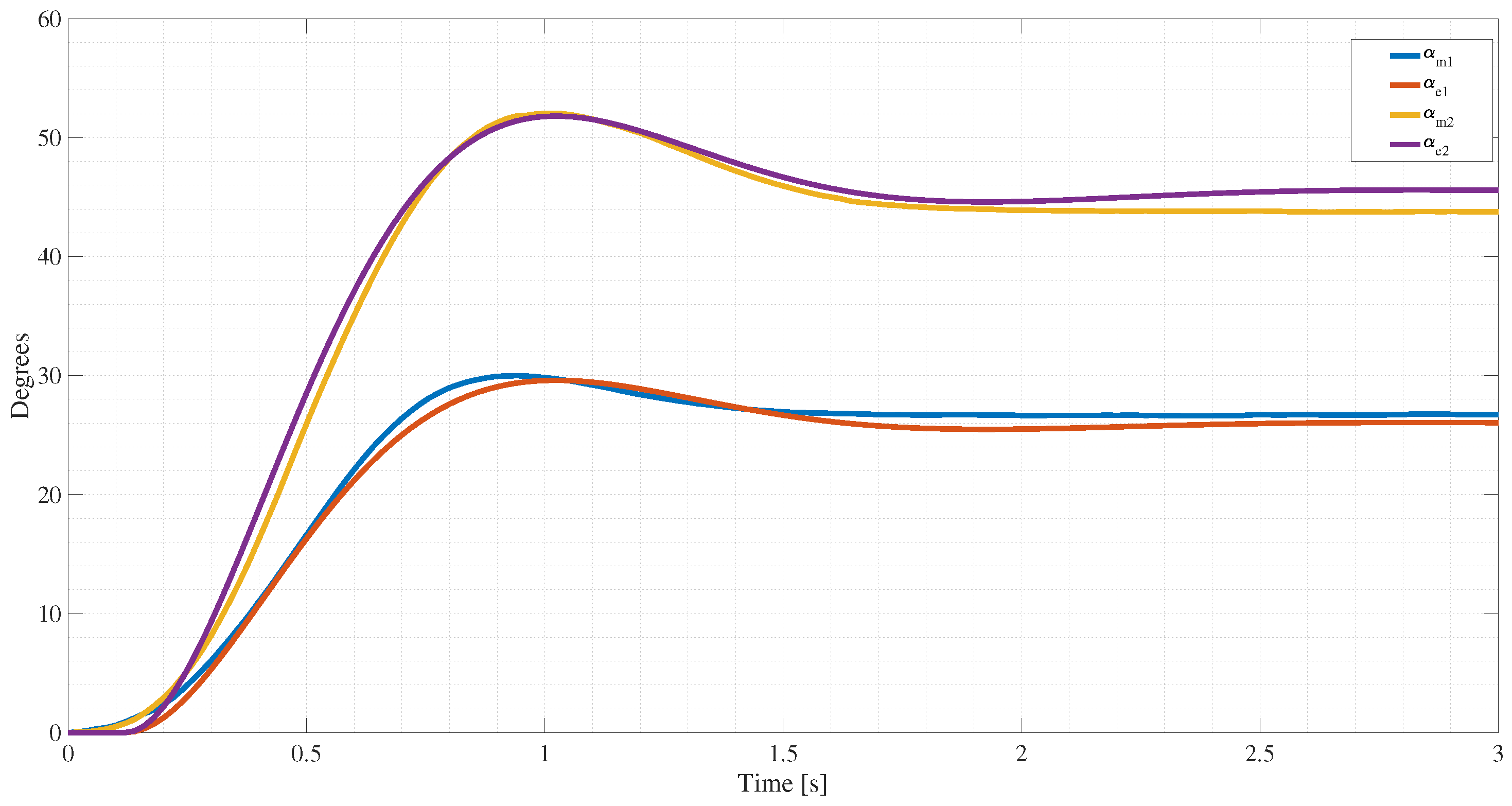
With the third-degree polynomial trajectory, regarding the parabolic motion profile, Figure 20a shows three adaptive PID fuzzy controller signals. In each signal, the controller follows different trajectories, one for a settlement at 80 degrees, the second at 90 degrees, and the third at 100 degrees; every trajectory settles at 7 s. A higher settlement position makes the trajectory change faster, meaning each signal faces different magnitudes of change. For the 80-degree trajectory, the magnitude of change is lower than the other two; meanwhile, the 100-degree trajectory faces a major quantity of change, making it more difficult to track.

Examining the error patterns illustrated in Figure 20b, it provides valuable insights into the efficacy of the response of the controller across different trajectories. Notably, when comparing the trajectories reaching 80 and 90 degrees, a striking similarity in error presence is observed, characterized by an acceptable level of deviation and commendable settlement behavior. This consistency suggests the robust performance of the controller in maintaining the desired positions within these ranges. However, upon closer inspection of the trajectory aimed at 100 degrees, a slightly heightened error level becomes apparent, surpassing that observed in the other trajectories. Despite this, the controller exhibits adaptive and responsive behavior, compensating for the increased error magnitude, particularly in the rapid trajectory changes and beyond the analysis of the error behavior.

Figure 20c provides a more comprehensive view of the controller’s dynamic response across the entire error spectrum. By visualizing the controller’s actions concerning varying degrees of error, these supplementary data enhance the understanding of its adaptive capabilities and ability to navigate diverse operating conditions effectively. Overall, the combination of error analysis and controller behavior visualization offers a comprehensive assessment of the controllers’ performance, showing their robustness and adaptability in achieving precise trajectory tracking in dynamic environments.

Table 9. RMSE comparison.

Controller	PID Fuzzy Controller	PID Fuzzy Controller HuS—80	PID Fuzzy Controller HuS—90	PID Fuzzy Controller HuS—100
RMSE	0.54	0.42	0.4	0.49

presents the RMSE values obtained from the tests conducted with the optimized and non-optimized controllers, as depicted in Figure 12 and Figure 20, respectively. The RMSE is used to conduct a more general comparison between the response of the controller and, in that way, obtain a better conclusion. The non-optimized controller ended up with an RMSE of 0.54; meanwhile, the optimized controller, submitted to different tests, ended up with a lower RMSE than the non-optimized one. The comparison in the table unequivocally demonstrates that the optimized controller exhibits a superior performance compared to its non-optimized counterpart. This outcome validates the efficacy of the optimization methodology proposed in this paper, underscoring its success in enhancing the controller’s responsiveness and accuracy in trajectory-tracking tasks.

The HuS algorithm presents a good response in the optimization process of the fuzzy controller, as shown in

Table 10. Controller performance comparison.

Work	[19]	[20]	Proposed
Controller	PID	Backstepping	Fuzzy Controller
Application	Experimental	Simulation	Experimental
Number of Iterations	32	18	5
Number of Parameters to Optimize	12	2	36
Settling Time (s)	10.24	0.5	7
Steady Error (degrees)	0.4	0	0.28

. The methodology proposed in this paper shows better results than those presented in Refs. [19,20], where a PSO algorithm is utilized. The analysis of an aero-pendulum is presented in [20]. The methodology is well-described, with two parameters to optimize being proposed for a backstepping controller. The paper demonstrates good results; for instance, the number of iterations is 18, the settling time is 0.5 s, and the steady error is 0 degrees. This methodology only includes the simulated results, creating a large panorama if the implementation is carried out since, in many cases, some inherent characteristics of the system are not considered.

In contrast, the study referenced in [19] introduces a comprehensive control scheme featuring a PID position controller, feed-forward mechanism, and a PI current component. Specifically tailored for an aero-pendulum system equipped with two propellers, the PID controller undergoes optimization through a PSO algorithm. Notably, developing a rigorous mathematical model facilitates a deeper understanding of the system dynamics, particularly treating the two propellers as single entities to streamline the analysis and design. Remarkably, the study yields promising outcomes, with the authors optimizing their proposal using 12 parameters. Despite the inherent complexity of the control scheme and the system dynamics, the convergence process is reported to require a manageable 32 iterations in the best-case scenario, showcasing the efficiency of the optimization approach. Furthermore, the experimental validation of the proposed control scheme corroborates its effectiveness, with a settling time of $10.24$ s and a steady-state error of $0.4$ degrees reported. These findings underscore the practical viability of the control scheme in real-world applications, providing tangible evidence of its ability to achieve the desired performance metrics under experimental conditions.

The methodology proposed in this paper focuses on optimizing a fuzzy controller, achieving remarkable results with efficiency. By employing only five iterations and targeting thirty-six parameters for optimization, the approach demonstrates an excellent process that minimizes the computational overhead while maximizing the effectiveness. Central to the methodology is using a parabolic motion profile to define the settling time. Specifically, a settling time of 7 s is adopted as a default value within this framework, providing a balance between a rapid response and stability. Notably, the flexibility of the methodology allows the users to adjust the settling time according to the specific application requirements, offering adaptability to diverse scenarios and preferences. The experimental validation of the proposed method underscores its efficacy, as evidenced by the achieved steady-state error of only 0.28 degrees. This impressive degree of precision highlights the robustness and reliability of the optimized fuzzy controller, showcasing its potential for real-world implementation and practical impacts.

6. Conclusions

The implementation of fuzzy control systems may be considered confusing at times because of the lack of specific parameters for correctly proposing the fuzzy rules and the ignorance of the system’s dynamics. Consequently, this normally results in erratic fuzzy systems that create inadequate behaviors that must be controlled.

The proposed solution is a method that helps to optimize unstable fuzzy systems by formulating more suitable fuzzy parameters. The technique used was an HuS algorithm that analyzes the parameters provided by the membership functions for multiple iterations until it finds the best generation or results for the fuzzy system. The HuS algorithm ensures that the membership functions overlap so the controller does not present discontinuities. This process enables the creation of new parameters from those calculated in moving toward the leader, cooperation between the members, and reorganizing the hunting group processes, causing the search to be carried out using the values that do not meet the present conditions and generating the new ones in a heuristic way. In this way, it is assured that the testing will succeed.

In this paper, an aero-pendulum system is used, and a PID fuzzy controller is designed by experimentation so that the system can follow a trajectory; following this, the HuS optimizer will be used to improve this controller. The results detailed in the articles demonstrate that this method is reliable and functional thanks to the improvements obtained by a decrease of 26 percent in the error in the new and improved controller. The use of heuristic algorithms to generate fuzzy systems and improve them may be useful not only due to the enhancement of the response from the controller but also to facilitate the creation of these systems by making them more accurate, reducing the time in the design process according to the tuning specification.