Abstract
In 3D segmentation, point-based models excel but face difficulties in precise class delineation at class intersections, an inherent challenge in segmentation models. This is particularly critical in medical applications, influencing patient care and surgical planning, where accurate 3D boundary identification is essential for assisting surgery and enhancing medical training through advanced simulations. This study introduces the Nested Contrastive Boundary Learning Point Transformer (NCBL-PT), specially designed for 3D point cloud segmentation. NCBL-PT employs contrastive learning to improve boundary point representation by enhancing feature similarity within the same class. NCBL-PT incorporates a border-aware distinction within the same class points, allowing the model to distinctly learn from both points in proximity to the class intersection and from those beyond. This reduces semantic confusion among the points of different classes in the ambiguous class intersection zone, where similarity in features due to proximity could lead to incorrect associations. The model operates within subsampled point clouds at each encoder block stage of the point transformer architecture. It applies self-attention with k = 16 nearest neighbors to local neighborhoods, aligning with NCBL calculations for consistent self-attention regularization in local contexts. NCBL-PT improves 3D segmentation at class intersections, as evidenced by a 3.31% increase in Intersection over Union (IOU) for aneurysm segmentation compared to the base point transformer model.
1. Introduction
Intracranial aneurysms are a relatively common occurrence within the brain. When unruptured, they may remain unnoticed. However, the true peril lies in the event of an aneurysm rupture, which can lead to a subarachnoid hemorrhage (SAH), a scenario that frequently unfolds. Aneurysms are often serendipitously discovered during unrelated medical investigations, primarily because they tend to remain asymptomatic until rupture. Furthermore, the growth of these aneurysms is unpredictable, and even small ones carry the risk of rupture, transforming SAH into a catastrophic event with a mortality rate ranging from 25% to 50%. A staggering 50% of survivors grapple with permanent disability, resulting in a positive outcome for only about one-third of SAH patients [1,2].
Fortunately, significant strides have been made in the field of computer vision, driven by artificial intelligence algorithms and deep learning techniques. These advancements have sought to provide detection and segmentation tools for anomalies like intracranial aneurysms.
However, these efforts have predominantly concentrated on 2D data, relying on conventional convolutional models. Although these applications have shown promise in aneurysm detection [3,4,5,6], the segmentation of aneurysms remains a relatively unexplored domain, with numerous approximations primarily revolving around and being evaluated within a detection framework, even though the process of segmentation may also be addressed and carried out [7,8].
In recent years, the field of 3D model segmentation, particularly in the context of aneurysms, has witnessed a resurgence of interest after a period of relative neglect [9,10,11]. The dimensional depth provided by 3D models facilitates a more nuanced representation of an aneurysm’s shape, size, and relationship to surrounding tissues, in contrast with 2D models. This depth is crucial for understanding the characteristics of the aneurysm, leading to more precise and targeted treatment strategies. This revival of interest has led to the development of innovative approaches. Notably, there has been a growing exploration of novel techniques, such as point cloud segmentations.
The introduction of advanced methods like PointNet [12] and PointNet++ [13] marked a significant shift in this field. PointNet, known for its direct processing of point clouds and global feature recognition, set the stage for PointNet++, which further enhanced the technique by focusing on local structures through a hierarchical network. This era of innovation was further enriched by PointCNN [14], which introduced a unique X-Conv operation for the structured processing of point clouds, and RandLA-Net [15], which is acclaimed for its efficiency in handling large-scale point cloud data through random sampling and local feature aggregation.
These technological advancements have inspired more recent researchers to develop and propose advanced methods in point cloud segmentation. A notable example is the work of Shao et al. [16], and their Dual Branch learning method. Their approach, focused on aneurysm segmentation, achieved an overall average Intersection over Union (IoU) of 67.05%, considering two distinct classes: aneurysm and vessel. In the vessel class segmentation, it achieved an impressive 82.65% IoU. However, it encountered challenges in aneurysm class segmentation, achieving a 51.45% IoU in this specific aspect.
On a separate note, a proposal by Yifan Liu et al. [17] introduces a combination of two innovative models: the point transformer, which integrates the concept of attention, and a more extensive modularization process able to refine segmentation results around the class intersection. This innovative approach achieved an impressive average IoU of 91.52%, signifying substantial progress in both vessel class segmentation, where it excelled with a remarkable 95.46% IoU, and, perhaps more notably, in aneurysm class segmentation, where it displayed an impressive 87.58% IoU. While these results are promising, they also suggest the potential for developing lighter frameworks that can address the evident need for good aneurysm segmentation performance while maintaining a streamlined framework suitable for implementation across various domains and models.
These advancements offer extensive potential, not only in computer-assisted surgical techniques, which aid medical professionals in guiding their interventions through AR-imposed anatomical segmentations, but also in significantly improving patient outcomes. By enabling real-time anatomical visualization, these technologies facilitate surgical manipulation and flow interpretation during complex surgical procedures, thereby enhancing surgical precision and reducing the risk of complications [18]. Furthermore, the integration of augmented reality technologies has shown remarkable promise in the domain of medical education and training through sophisticated simulation systems. These systems not only enhance the learning experience for aspiring surgeons, but also serve as a powerful tool for improving operative preparedness. Trainees gain hands-on experience in a safe and controlled environment, honing their surgical skills and deepening their understanding of intricate anatomical structures. This comprehensive training approach is vital for preparing surgeons to handle real-life scenarios, ultimately promising improved patient outcomes and contributing to the development of better-trained medical professionals [19].
In this context, our study endeavors to enhance the segmentation of intracranial aneurysms within 3D models, with the overarching goal of advancing the understanding and application of this critical domain. This effort is particularly vital considering the unpredictable growth and rupture risk of aneurysms, often leading to subarachnoid hemorrhage (SAH) and its associated high mortality and disability rates. Therefore, tools that can speed up diagnoses, interventions, and prevent such ruptures are of great importance for clinical care. In this scenario, pertaining to situations in which each moment gained holds significant value, an exemplary instance is the proposed pipeline by Fernando Navarro et al. [20], which is used to create a unified 3D framework for Organs at Risk Localization and Segmentation for Radiation Therapy Planning. This aims to introduce a unified pipeline rather than a novel localization or segmentation method, which, despite not being new, marks a significant advancement in medical processes. Such approaches are vital for enhancing the speed and efficiency of medical treatments in sensitive cases like aneurysms, highlighting the potential for new methodologies that streamline critical healthcare procedures. This underscores the importance of various research efforts that advance this endpoint, whether through pipeline propositions or methods that could potentially be adopted by researchers to develop them. Collectively, these endeavors underscore the intricate and nuanced nature of challenges pertaining to human health.
By addressing the inherent geometric and spatial variability in medical imaging, we aim to contribute to the refinement of models by utilizing an attentional mechanism model regularized via intuitive nested contrastive learning. This approach aims to simplify and streamline the development and research of lighter solutions, eliminating the necessity for extensive additional modularization and thereby enabling its extension across multiple fields of application.
2. Materials and Methods
This section introduces our Nested Contrastive Boundary Learning Point Transformer (NCBL-PT) tailored for 3D point cloud segmentations, as depicted in Figure 1 This framework utilizes contrastive learning to enhance learned representations, maximizing the discrimination of class features across boundary points. This enhancement enables a more precise prediction of points’ class in proximity to the class intersection, a critical area in which class definitions may become ambiguous.
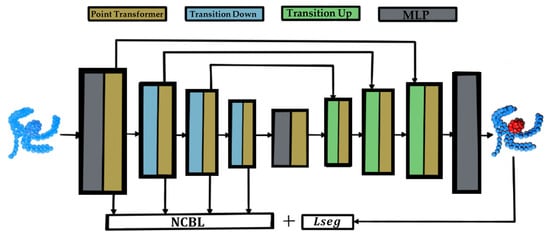
Figure 1.
Nested Contrastive Boundary Learning Point Transformer (NCBL-PT).
While contrastive learning typically assesses class similarity to establish positive or negative pairs of relationships, our approach exceeds this by not only distinguishing class differences, but also identifying membership within or outside the boundary, adding an enhanced level of edge-aware learning. Consequently, to significantly improve the model’s performance in handling this challenge, we activate the framework within every subsampled point cloud generated in each stage of the encoder blocks, refining the learning process across the architecture in terms of feature extraction.
2.1. Dataset
In our research, we harnessed the publicly accessible IntrA dataset curated by Xi Yang et al. [21]. This dataset comprises 1909 blood vessel point clouds generated from the reconstructed 3D models of patients, meticulously capturing the nuances of vascular structures. Within this dataset, we find 1694 distinct healthy vessel segments, providing a foundational basis for comparative analyses and diagnostic assessments; this is alongside 215 aneurysm segments, facilitating an in-depth study of pathological vascular conditions.
A noteworthy aspect is that 116 out of the 215 aneurysm segments have undergone thorough subdivision and meticulous annotation by medical experts, significantly enhancing the dataset’s suitability for segmentation and diagnostic investigations, which are used in this research. Furthermore, they use MeshLab to generate the normal vector for each point. In each aneurysm/vessel subdivision, every point is characterized by its coordinates, the corresponding normal vector, and a binary label indicating whether it is an aneurysm point or not. Additionally, geodesic distance matrices are thoughtfully included for each of these annotated 3D segments. This enhancement is particularly valuable, as the geodesic distance offers a more precise measurement than the Euclidean distance, adapting to the intricate shapes of vascular structures. These matrices are formatted as N × N, optimizing computational efficiency for point-based models.
2.2. Nested Contrastive Boundary Learning Point Transformer (NCBL-PT)
2.2.1. Contrastive Learning
With the IntrA dataset forming the cornerstone of our research, our focus now turns to the methodology that underlies our investigative approach. Central to our strategy is the concept of the regularization of categorical classification, which plays a pivotal role in discerning semantic features among labeled data. This, in turn, enhances our capability to achieve precise categorization and notably leads to improved segmentation results.
At the heart of this approach lies the contrastive learning technique, which empowers us to unearth deeper insights from our dataset. By leveraging the intrinsic relationships embedded within the data, we delve into the widely employed InfoNCE loss [22]. Alongside its generalization [23] and the contrastive boundary learning (CBL) proposed by Liyao Tang et al. [24], in this context, contrastive learning is oriented toward nurturing the development of feature representations, thus motivating these learned representations to exhibit greater similarity to neighboring points within the same class while simultaneously being more distinguishable from those belonging to a different class.
This intricate balance is encapsulated by Equation (1), which serves as a fundamental framework encapsulating the discussed concept as a form of the mean probability that point neighbors, based on learned features, will exhibit similarity within their respective class. It is important to highlight that this concept is applied within the equation not to average the probabilities across the entire point cloud, but applied specifically to the points associated with class intersections. These points can also be described as the boundary between the classes.
where:
- |Bl| denotes the number of points in the border Bl;
- fk denotes the learned feature of neighbor χk that is within the neighborhood Ni;
- fi denotes the learned feature of central point xi;
- −d is the negative Euclidean distance.
2.2.2. Edge Definition
Having established the foundation for the concept of contrastive learning with feature points along the border, the subsequent imperative is to precisely locate and identify these crucial boundary points to enable their incorporation into our calculations. Our methodology defines these boundaries as the distinct points that delineate the transitions between classes within the point cloud. To achieve this, we employ a k-nearest neighbors (KNN) method, with k set to 8, representing the eight closest neighbors to each point. Notably, we incorporate geodesic distances to determine these nearest neighbors. Geodesic distances are employed to capture the paths along the surface of the point cloud, providing a more accurate representation of the actual proximity and connectivity between points.
Including geodesic distances is a deliberate choice and is performed to address the potential directional bias concerns inherent in irregular 3D point clouds. Unlike the Euclidean distance, which may introduce biases in a particular direction, geodesic distances account for the shortest paths along the point cloud’s surface. This consideration ensures that the selected neighbors truly reflect the spatial relationships in the irregular 3D space. For every point xi in the point cloud X, we evaluate whether any of its eight nearest neighbors Ni exhibit a different class label from the point in question. If this condition is met, we classify the point as belonging to the edge Bl. This classification can be expressed mathematically as follows:
where:
- li denotes the ground truth label of point xi in the point cloud X;
- lk denotes the ground truth label of neighbor xk that is within the neighborhood Ni;
- xi is the central point under consideration;
- xk is a neighbor point of xi within the neighborhood Ni;
- Ni is the neighborhood set containing k nearest neighbors of xi in the point cloud X.
This labeling mechanism effectively identifies points associated with class transitions, which can be better visualized, as shown in Figure 2 forming the foundational basis for subsequent boundary analyses.

Figure 2.
Edge definition.
2.2.3. Partitioning the edge Neighboring Points
Segmentation can pose a challenging task when attempting to discern the various parts of a single object, particularly in proximity to class intersections. Objects with well-defined geometries may have more easily discernible parts to be learned. However, in the case of variable anatomies, such as aneurysms within vascular structures, which often exhibit irregular and difficult-to-generalize shapes and patterns, defining the parts constituting the aneurysm class versus the blood vessel class becomes a complex endeavor. Once the presence of an aneurysm is identified, distinguishing its parts from the blood vessel becomes relatively straightforward, at least up to the point of their intersection. As one approaches this intersection, defining classes becomes more challenging due to the semantic ambiguity generated in that region.
Therefore, once a reference framework—in this case, the edge definition ground truth—is established, one can argue, even from a human learning perspective, that the points defined as part of the edge could exhibit a more ambiguous semantic relationship to the spatially neighboring points within the edge compared to those outside the edge and their neighbors, around which are not in this class intersection. The latter generally display a lower degree of semantic ambiguity as they move away from the edge.
To study the proposed learning framework, it is imperative to delve into the spatial relationships between points within the same class neighborhood of the proposed edge points. This exploration can be partitioned into two distinct groups, a conceptual division that aligns with the methodology introduced by Lixia He et al. [25], where four discrete groupings are employed for analytical purposes; this is primarily contingent on whether a point resides within the edge or outside of it. Our framework adopts this fundamental division of neighboring concepts within the same class neighborhood. This division empowers the model’s ability to discern whether each neighboring edge point falls within a zone characterized by greater semantic ambiguity. This distinction allows the model to focus on learning not only from close point features within this class intersection but also from points that exist beyond this intersection. The objective is to avoid entangling the model in making feature relationships between different class points in an area that may exhibit ambiguity. This scenario is where points from different classes within the intersection may become erroneously associated due to their feature similarities and proximity.
As dictated by ground truth annotations, points situated along the edge necessitate a heightened degree of semantic relevance, particularly concerning shared features with other points from the same class. As a result, we use the concept of two distinct groups to categorize the same class neighborhood of each edge point: those that comprise the edge itself and those that lie outside of it, as illustrated in Figure 3. This categorization enables us to foster similarity learning through two distinct approaches.
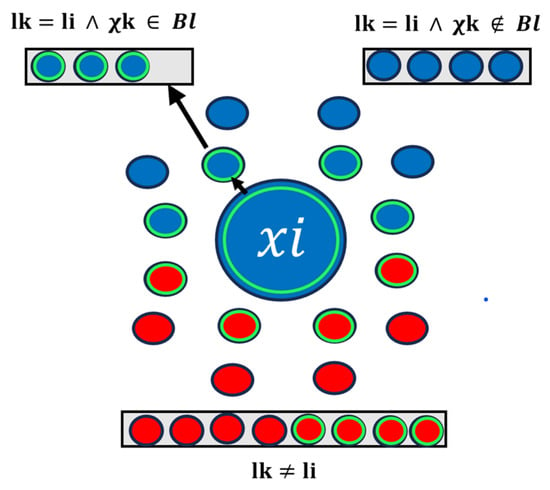
Figure 3.
Partitioning the edge Neighboring Points.
Hence, it is imperative that the model not only learns to establish similarities with nearby points of the same class within this intersection but also prioritizes learning from more distant points of the same class that reside outside the boundary. These distant points offer a greater degree of semantic certainty regarding their class affiliation, as they are not situated within the ambiguous region of class intersection. Consequently, the model gains a more reliable basis for identifying them as members of the same class.
This grouping can be expressed mathematically as follows:
2.2.4. Nested Contrastive Boundary Learning (NCBL)
In this context, we apply the principles of contrastive learning to mitigate the semantic ambiguity that can arise with learned features at class intersections. This is accomplished by partitioning the neighborhood of edge points that belong to the same class into the two distinct groups established. We define the neighborhood as the 16 neighbors. We capitalize on the generalization of contrastive learning from the two distinct perspectives. We strive to enhance the feature similarity for each edge point with pairs of classes both inside and outside the edge. This approach allows us to achieve a form of nested contrastive learning, as depicted in Equation (3). In this equation, the logarithm is applied directly to the summation of the calculations of both conditional probabilities.
As previously mentioned, these probabilities signify the likelihood that the neighborhood defined by the proximity of learned features for each edge point belongs to the same class. Now, we refine this concept by distinguishing the probability of feature-based neighbors outside the border from those inside the border. This approach enriches the characterization of class similarity, providing a more layered and multifaceted understanding based on proximity.
This adaptation grants the algorithm the ability to learn in a specific manner through contrastive learning, providing supplementary insights from the edge-aware information.
2.2.5. Nested Contrastive Boundary Learning Point Transformer (NCBL-PT)
The learning approach of Nested Contrastive Boundary Learning (NCBL) seamlessly integrates into the architecture proposed by Hengshuang Zhao et al. [26], known as the Point Transformer, as illustrated in Figure 1. To adapt the learning within the architecture, modifications were made to the logic of the architecture’s transition-down block. As mentioned before, NCBL necessitates the utilization of features learned by the model. Specifically, the feature extractions defined by the Point Transformer attention modules are employed in this case. Additionally, the ground truth class labels for each point and the points belonging to the edge are necessary.
The Point Transformer architecture follows a U-net style encoder–decoder design. Its core components include the Point Transformer module, which replaces conventional convolutions by employing vector self-attention. For each subset X(i) ⊆ X, which represents a set of points within a local neighborhood of xi, we apply self-attention. Specifically, we utilize k = 16 nearest neighbors, maintaining consistency with the same neighborhood defined in NCBL calculations for each xi point. This ensures local neighborhood self-attention context regularization, as the NCBL value can also be thought of as the degree of attention between point xi and the neighboring points within the same class that were established in groupings. This effectively reduces feature ambiguity among points of the same class at the border, describing the class intersection, and introducing this additional regularization level.
The architecture further encompasses transition-down and transition-up modules alongside a multi-layer perceptron (MLP). As mentioned, we adapted the transition-down module to meet the NCBL framework’s requirements. This module operates through farthest point sampling (FPS) and k-nearest neighbors (kNN) to transform high-dimensional point cloud space C1 features into a lower-dimensional space C2.
The FPS algorithm plays a crucial role in the transformation process from space C1 to C2. Initially, it creates an empty set for selected points and picks a random point from C1 as the starting point of the subset. The algorithm then calculates the distances between this point and the others in C1. The point farthest from the current selection is added to the subset. This procedure repeats iteratively, each time expanding the subset with the point most distant from those already selected. This method aims to preserve the overall structure and dispersion of the data, which is crucial for maintaining the fidelity of the data in the reduced dimensional space C2. The FPS algorithm effectively maintains the relative distances and spatial relationships, which are essential for the integrity of the transformed data. This iterative process continues until the subset reaches a predefined number of points, which, in this context, corresponds to a downsampling rate of 0.5 at each encoder block of the architecture. This approach is efficient in reducing dimensionality while capturing the essence of the original data structure.
This downsampling results in a cardinality reduction in the point set at each stage. During this process, in accordance with the NCBL framework, we also transfer the ground truth class and edge labels to this lower-dimensional space, as illustrated in Figure 4 and Figure 5.

Figure 4.
Ground truth class label propagation through encoder space dimensionality reduction.

Figure 5.
Ground of Truth edge label propagation through Encoder Space Dimensionality Reduction.
To achieve this, after obtaining the lower-dimensional space C2 from C1, we calculate the three nearest neighbors for each point in C2 from C1. This is facilitated because C2⊂C1. For class labels, we assign the majority class among these three neighbors to the corresponding point in C2, as shown in Figure 6. Similarly, we consider only the closest neighbor of each point for edge labels. If this neighbor in C1 was part of the edge, then in space C2, that point also belongs to the edge.
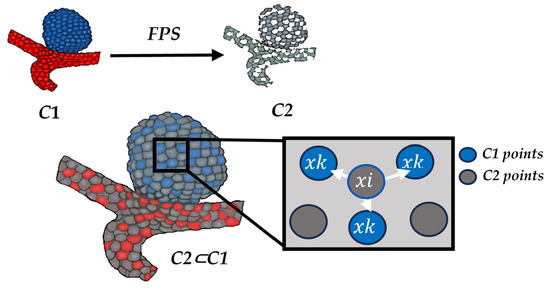
Figure 6.
Transition down label propagation through Farthest Point Sampling (FPS) and KNN.
This process ensures that within each feature extraction and dimensionality reduction step, we meet the prerequisites for calculating the NCBL for every encoder module, effectively applying learning regularization to prevent semantic ambiguities among the edge point features.
As a result of this comprehensive approach, we introduce the Nested Contrastive Boundary Learning Point Transformer (NCBL-PT). Our nested contrastive learning spans various levels of the architecture, ranging from low-level feature extractions in high-dimensional spaces to the final encoder block, which handles high-level features in lower-dimensional spaces.
To effectively navigate the NCBL integration, Figure 7 includes a flow chart that elucidates the integral workflow for integrating NCBL. It highlights the specific processes within each encoder block necessary for NCBL integration. Importantly, the chart distinctly separates the needed standard operations of the point transformer architecture from the newly needed integrations required for NCBL. This separation demonstrates how the native modules of the point transformer are adapted and utilized within the NCBL framework. Such integration is crucial, as it allows the NCBL modules to operate within the point transformer’s native environment. This enables the use of specific parts of the point transformer processes to gather the data needed for ultimately obtaining the data required to ultimately finish with each encoder block by calculating the NCBL.

Figure 7.
Nested Contrastive Boundary Learning Point Transformer (NCBL-PT) flow chart showcasing what is happening in each block to obtain to the NCBL calculations.
2.2.6. Global Loss
The optimization of the model transformer’s weights is achieved through our global loss function. This comprehensive loss function integrates a traditional component aimed at overall semantic segmentation performance, along with the previously explained contrastive learning methodology, which seeks to maximize feature similarities and reduce the semantic ambiguity around the class intersection. Equation (4) visually represents this loss function, combining a supervised cross-entropy loss based on semantic labels (Lseg) with the contrastive learning-inspired NCBL loss. Here, represents the NCBL loss at stage n, aggregating the results from each encoder block. This dual-loss configuration aimed to enrich the learning process, capitalizing on the strengths of both the labeled border-aware data and contrastive learning principles.
2.2.7. Training
During the training phase, we utilized Google Colab Pro+ with its A100 GPU resources to efficiently handle the demanding computational tasks. A batch size of 8 was employed, and the training proceeded over 200 epochs with a consistent learning rate of 0.001. To mitigate overfitting, a dropout rate of 0.5 was applied during training, ensuring that the model’s performance extended well to unseen data. Furthermore, the point cloud density was set at 2048 points, providing a suitable representation for the 3D structures. The training split adhered to a recurrent distribution, with proportions of 60% for training, 20% for validation, and 20% for testing.
2.3. GPT 3.5
To avoid any language barriers, the use of GPT3.5 was employed to prevent any orthographic or redaction misunderstanding in the writing of this Editorial Article.
3. Results
In this study, we rigorously evaluated the performance of our proposed segmentation method by comparing it against our trained base method, utilizing Intersection over Union (IoU) as the principal assessment metric.
Our study’s quantitative analysis, detailed in Table 1, highlights the advancements of our proposed method. It shows a notable 3.31% increase in Intersection over Union (IoU) for aneurysm segmentation compared to the base model. This improvement demonstrates enhanced segmentation detail without compromising the overall performance. In vessel segmentation, the IoU maintains consistent performance, with a slight 0.32% improvement, balancing enhancements in one area without causing deterioration in another. Figure 8 visually illustrates these enhancements, focusing on the comparison with the base model. This targeted depiction aids in understanding our method’s improvements.

Table 1.
Performance comparison using a 2048 sampling scheme.
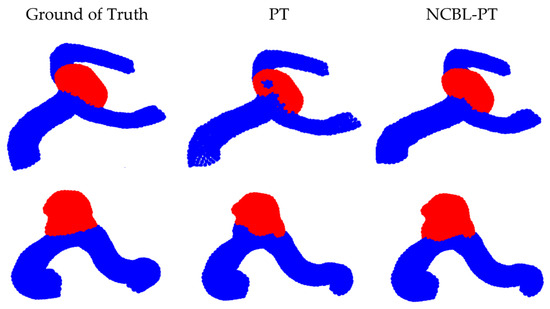
Figure 8.
Exploring segmentation results: A comparative analysis between ground of truth, point transformer base model, and the proposed NCBL-PT.
Table 1 also includes a broader comparative analysis with other state-of-the-art methods using the same dataset and point density scheme. This comparison underscores the superiority of our approach over several leading models, including Point Net++ [13], PointCNN [14], RandLA-Net [15], and the recently proposed Dual Branch Learning model [16]. Our method shows improvements in the mean IoU of 5.04%, 6.19%, 9.13%, and 22.72% over these models, respectively. Furthermore, in aneurysm IoU, our method achieves even more significant gains of 8.21%, 10.84%, 15.21%, and 32.97%, respectively.
It is important to note the performance of EPT-Net [17], which achieves a 3.63% overall mean IoU improvement over the same base model. While the EPT-Net employs a multiple modularization strategy using two models in the same pipeline, our method’s strength lies in its simplicity and efficiency. We utilize a single model with one additional module within the main architecture, offering significant advantages in its ease of implementation and potential scalability.
4. Discussion
In this study, we employed contrastive learning to augment the feature similarity for each edge point, considering pairs of classes inside and outside the edge. By partitioning the neighborhood of edge points within the same class into two distinct groups, we achieved a nested form of contrastive learning. This approach allowed us to investigate and visualize the level of semantic ambiguity present in these regions, providing an overall understanding of discernable features between classes. This was prominently visible in the scatter plot depicting the probabilities sought by the algorithm for maximization, as exemplified in Figure 9. In this figure, we utilized the feature extraction from the first encoder Point Transformer block to plot the probabilities of the model trained with the base method as well as with the implementation of contrastive learning, showing a clear semantic feature improvement.
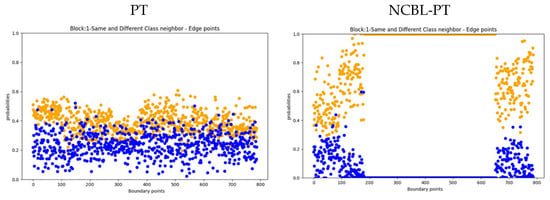
Figure 9.
Analyzing feature similarities in the output of trained encoder’s first block: probability distributions of same-class neighbors (orange points) vs. different-class neighbors (blue points).
5. Conclusions
In this study, we introduced the Nested Contrastive Boundary Learning Point Transformer (NCBL-PT) framework, tailored for point-based 3D aneurysm segmentation. We emphasized the importance of achieving better semantic feature similarity without needing complex and intricate modules that could potentially hinder the learning process. Addressing two significant challenges, our framework simplifies the inherent difficulty in segmenting around edges, a problem often made worse by the model’s potential to generate semantically ambiguous features when different classes are in proximity. This issue is particularly pronounced given the variable and complex anatomies in aneurysms. Additionally, our approach reduces the reliance on extensive modularization to handle this, which often complicates the learning process and results in solutions that are more difficult to adapt to other applications. We achieved this by employing a nested contrastive boundary learning framework (NCBL). Our approach is fully integrated at each spatial and feature generation stage of the encoder block, which strives to comprehensively extract the characterization of our target affliction. This methodology not only addresses the previously mentioned challenges effectively, but also enhances the framework’s versatility. It facilitates integration into various models for medical applications and beyond, while also being potentially adaptable to different types of images beyond just point clouds. Furthermore, our strategy recognizes the issue of feature ambiguity caused by the proximity of different classes. We address this by dividing the learning process into two distinct approaches: one to learn from sections with closely situated classes that might pose semantic ambiguity, and another to understand sections with clearer semantic related features. This approach results in a multi-stage, border-aware, and semantic ambiguity-aware learning process within a single flexible algorithm.
Our results strongly indicate that the integration of NCBL, built on contrastive learning principles, significantly reduces the semantic ambiguity of learned features in the context of border-aware learning. This is evident in the 3.31% improvement in the Intersection over Union (IoU) for aneurysm segmentation compared to the base Point Transformer model. This implementation of learning opens up exciting possibilities for improving semantic segmentation in various medical analyses, refining the delineation of class intersections and potentially advancing toward applications in computer-assisted surgeries.
Author Contributions
Conceptualization, L.F.E.-I.; Methodology, L.F.E.-I.; Software, A.d.L.-C. and L.F.E.-I.; Validation, A.d.L.-C. and S.T.-A.; Formal analysis, L.F.E.-I.; Investigation, L.F.E.-I.; Resources, A.d.L.-C. and S.T.-A.; Writing original draft preparation, L.F.E.-I.; Writing review and editing, A.d.L.-C. and S.T.-A.; Visualization, L.F.E.-I. and A.d.L.-C.; Supervision, A.d.L.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The dataset used in this work are publicly accessible. For more information, see the respective article of the dataset. Available online: https://github.com/intra3d2019/IntrA (accessed on 12 December 2023).
Acknowledgments
We extend our gratitude for the support from Luis Aguilar, Alejandro Ávalos, Jair García from LAVIS, and Erick Pasaye, as well as Domínguez Frausto from LANIREM at INB UNAM Juriquilla. We also extend our appreciation to CONAHCYT for providing the necessary scholarship to conduct this research. ChatGPT 3.5 has been used for orthographic corrections and improved composition of some sentences in this Editorial Article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Keedy, A. An overview of intracranial aneurysms. McGill J. Med. 2020, 9, 141–146. [Google Scholar] [CrossRef]
- Nieuwkamp, D.J.; Setz, L.E.; Algra, A.; Linn, F.H.; De Rooij, N.K.; Rinkel, G.J. Changes in case fatality of aneurysmal subarachnoid haemorrhage over time, according to age, sex, and region: A meta-analysis. Lancet Neurol. 2009, 8, 635–642. [Google Scholar] [CrossRef] [PubMed]
- Hou, W.; Mei, S.; Gui, Q.; Zou, Y.; Wang, Y.; Deng, X.; Cheng, Q. 1D CNN-Based Intracranial Aneurysms Detection in 3D TOF-MRA. Complexity 2020, 2020, 7023754. [Google Scholar] [CrossRef]
- Rahmany, I.; Guetari, R.; Khlifa, N. A Fully Automatic based Deep Learning Approach for Aneurysm Detection in DSA Images. In Proceedings of the IEEE International Conference on Image Processing, Applications and Systems (IPAS), Sophia Antipolis, France, 12–14 December 2018; pp. 303–307. [Google Scholar]
- Ueda, D.; Yamamoto, A.; Nishimori, M.; Shimono, T.; Doishita, S.; Shimazaki, A.; Katayama, Y.; Fukumoto, S.; Choppin, A.; Shimahara, Y.; et al. Deep Learning for MR Angiography: Automated Detection of Cerebral Aneurysms. Radiology 2019, 290, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Nakao, T.; Hanaoka, S.; Nomura, Y.; Sato, I.; Nemoto, M.; Miki, S.; Maeda, E.; Yoshikawa, T.; Hayashi, N.; Abe, O. Deep neural network-based computer-assisted detection of cerebral aneurysms in MR angiography. J. Magn. Reson. Imaging 2018, 47, 948–953. [Google Scholar] [CrossRef] [PubMed]
- Stember, J.N.; Chang, P.; Stember, D.M.; Liu, M.; Grinband, J.; Filippi, C.G.; Meyers, P.; Jambawalikar, S. Convolutional Neural Networks for the Detection and Measurement of Cerebral Aneurysms on Magnetic Resonance Angiography. J. Digit. Imaging 2019, 32, 808–815. [Google Scholar] [CrossRef] [PubMed]
- Park, A.; Chute, C.; Rajpurkar, P.; Lou, J.; Ball, R.L.; Shpanskaya, K.; Jabarkheel, R.; Kim, L.H.; McKenna, E.; Tseng, J.; et al. Deep Learning–Assisted Diagnosis of Cerebral Aneurysms Using the HeadXNet Model. JAMA Netw. Open 2019, 2, e195600. [Google Scholar] [CrossRef] [PubMed]
- Sichtermann, T.; Faron, A.; Sijben, R.; Teichert, N.; Freiherr, J.; Wiesmann, M. Deep Learning–Based Detection of Intracranial Aneurysms in 3D TOF-MRA. Am. J. Neuroradiol. 2019, 40, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Shahzad, R.; Penning, L.; Goertz, L.; Thiele, F.; Kabbasch, C.; Schlamann, M.; Krischek, B.; Maintz, D.; Perkuhn, M.; Borggrefe, J. Fully automated detection and segmentation of intracranial aneurysms in subarachnoid hemorrhage on CTA using deep learning. Sci. Rep. 2020, 10, 21799. [Google Scholar] [CrossRef] [PubMed]
- Claux, F.; Baudouin, M.; Bogey, C.; Rouchaud, A. Dense, deep learning-based intracranial aneurysm detection on TOF MRI using two-stage regularized U-Net. J. Neuroradiol. 2023, 50, 9–15. [Google Scholar] [CrossRef] [PubMed]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 2–8 December 2017. [Google Scholar]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. PointCNN: Convolution On X-Transformed Points. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–14 December 2018; pp. 828–838. [Google Scholar]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. RandLA-Net: Efficient Semantic Segmentation of Large-Scale Point Clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, Washington, DC, USA, 14–19 June 2020; pp. 11108–11117. [Google Scholar]
- Shao, D.; Lu, X.; Liu, X. 3D Intracranial Aneurysm Classification and Segmentation via Unsupervised Dual-Branch Learning. IEEE J. Biomed. Health Inform. 2023, 27, 1770–1779. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Liu, J.; Yuan, Y. Edge-Oriented Point-Cloud Transformer for 3D Intracranial Aneurysm Segmentation; Lecture Notes in Computer Science; Springer Nature: Basel, Switzerland, 2022; Volume 13435, pp. 97–106. [Google Scholar]
- Carl, B.; Bopp, M.; Benescu, A.; Saß, B.; Nimsky, C. Indocyanine Green Angiography Visualized by Augmented Reality in Aneurysm Surgery. World Neurosurg. 2020, 142, 307–315. [Google Scholar] [CrossRef] [PubMed]
- Alaraj, A.; Luciano, C.J.; Bailey, D.P.; Elsenousi, A.; Roitberg, B.C.; Bernardo, A.; Banerjee, P.P.; Charbel, F.T. Virtual Reality Cerebral Aneurysm Clipping Simulation With Real-Time Haptic Feedback. Oper. Neurosurg. 2015, 11, 52–58. [Google Scholar] [CrossRef] [PubMed]
- Navarro, F.; Sasahara, G.; Shit, S.; Ezhov, I.; Peeken, J.C.; Combs, S.E.; Menze, B.H. A unified 3D framework for Organs at Risk Localization and Segmentation for Radiation Therapy Planning. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Glasgow, Scotland, UK, 11-15 July 2022; pp. 1544–1547. [Google Scholar]
- Yang, X.; Xia, D.; Kin, T.; Igarashi, T. IntrA: 3D Intracranial Aneurysm Dataset for Deep Learning. April 2020. Available online: https://github.com/intra3d2019/IntrA (accessed on 7 July 2022).
- Oord, A.; Li, Y.; Vinyals, O. Representation Learning with Contrastive Predictive Coding. arXiv 2019, arXiv:1807.03748. [Google Scholar] [CrossRef]
- Frosst, N.; Papernot, N.; Hinton, G. Analyzing and Improving Representations with the Soft Nearest Neighbor Loss. arXiv 2019, arXiv:1902.01889. [Google Scholar] [CrossRef]
- Tang, L.; Zhan, Y.; Chen, Z.; Yu, B.; Tao, D. Contrastive Boundary Learning for Point Cloud Segmentation. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; IEEE: New Orleans, LA, USA, 2022; pp. 8479–8489. [Google Scholar]
- He, L.; She, J.; Zhao, Q.; Wen, X.; Guan, Y. Boundary–Inner Disentanglement Enhanced Learning for Point Cloud Semantic Segmentation. Appl. Sci. 2023, 13, 4053. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.; Koltun, V. Point Transformer. In Proceedings of the International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).