Assessment of Slow Feature Analysis and Its Variants for Fault Diagnosis in Process Industries
Abstract
1. Introduction
2. Slow Feature Analysis
- Data Augmentation with Lag FeaturesGiven a dataset X, the first step is to augment it by incorporating historical data (lags) to capture temporal dependencies. If X has shape , where N is the number of samples and M is the number of features, the augmented matrix is formed as follows in Equation (1):Here, d is the number of lags. This results in a new data matrix of shape
- NormalizationNormalization standardizes the features of the dataset to have zero mean and unit variance. Given a dataset X, the normalized version is computed by Equation (2):where is the mean and is the standard deviation of the dataset X. Both and are calculated across each feature.
- Slow Feature Analysis (SFA)Whitening Transformation Compute the covariance matrix B of the normalized training data as mentioned in Equation (3):where is defined in Equation (2). Perform Singular Value Decomposition (SVD) on B:where U is the matrix of eigenvectors and is the diagonal matrix of eigenvalues. The whitened data Z is then given by:Calculate the covariance matrix of :where is defined in Equation (6). Perform SVD on C:where P is a matrix of eigenvectors, and is a diagonal matrix containing the eigenvalues of C The transformation matrix W is:Select a subset of slow features based on the eigenvalues in .
- Statistical MonitoringWith W defining a projection to a space emphasizing slow variations, compute the monitoring statistics for new test data after similar preprocessing and projection:where is the derivative of the test data and W is defined in Equation (9).
- Thresholds for Fault DetectionThresholds are computed based on the desired confidence levels and the distributions of and under the assumption of normal operation:
- threshold from the Chi-squared distribution.
- threshold from the F-distribution.
- Visualization and EvaluationFinally, visualize and evaluate the model performance using the computed statistics and thresholds to monitor system status and detect potential faults.These mathematical operations and transformations enable the SFA-based fault diagnosis system to effectively use temporal features, reduce dimensionality, emphasize slowly varying features, and monitor system health via statistical control limits.
3. Kernel Slow Feature Analysis
- Data Preparation and Lag Feature AdditionAdd d lag features to a dataset X of dimensions , where N represents the number of samples and M is the number of features. An augmented matrix is the outcome of this:where is the data at time t, and is the data at time for each lag k from 1 to d.
- Data NormalizationNormalize the dataset X by subtracting the mean and dividing by the standard deviation for each feature:where is the mean and is the standard deviation calculated across each feature of X.
- Kernel Matrix Computation and CentralizationCompute the kernel matrix K using the Gaussian radial basis function (RBF)where and are the normalized training data points defined in Equation (12), and is the kernel width parameter. Centralize the kernel matrix K using:where is an matrix of ones.
- Eigen Decomposition and Feature ExtractionPerform eigen decomposition on the centralized kernel matrix :Extract the principal components (slow features) Z and their derivatives:where is defined in Equation (15) andwhere is the matrix of inverse square roots of the eigenvalues, ensuring whitening of the data.
- Statistical Monitoring and Threshold EstimationFor control and fault detection, compute the monitoring statistics D for each test sample using a norm-based measure between the training set features y and the test set featuresEstimate control limits (UCL and LCL) using kernel density estimation (KDE) on the distribution of D values from a setting training set.
- Fault DetectionEvaluate the statistical monitoring metrics D against the control limits for fault detection. If or , a potential fault or anomaly is indicated.
- Visualization and Performance EvaluationPlot the monitoring statistics over time with the thresholds to visualize the system behavior and evaluate the performance using metrics such as the false alarm rate (FAR) and missed alarm rate (MAR).
4. Dynamic Slow Feature Analysis DSFA
5. Assessment and Results
5.1. Case Study 1
TE Dataset Details
5.2. Discussion
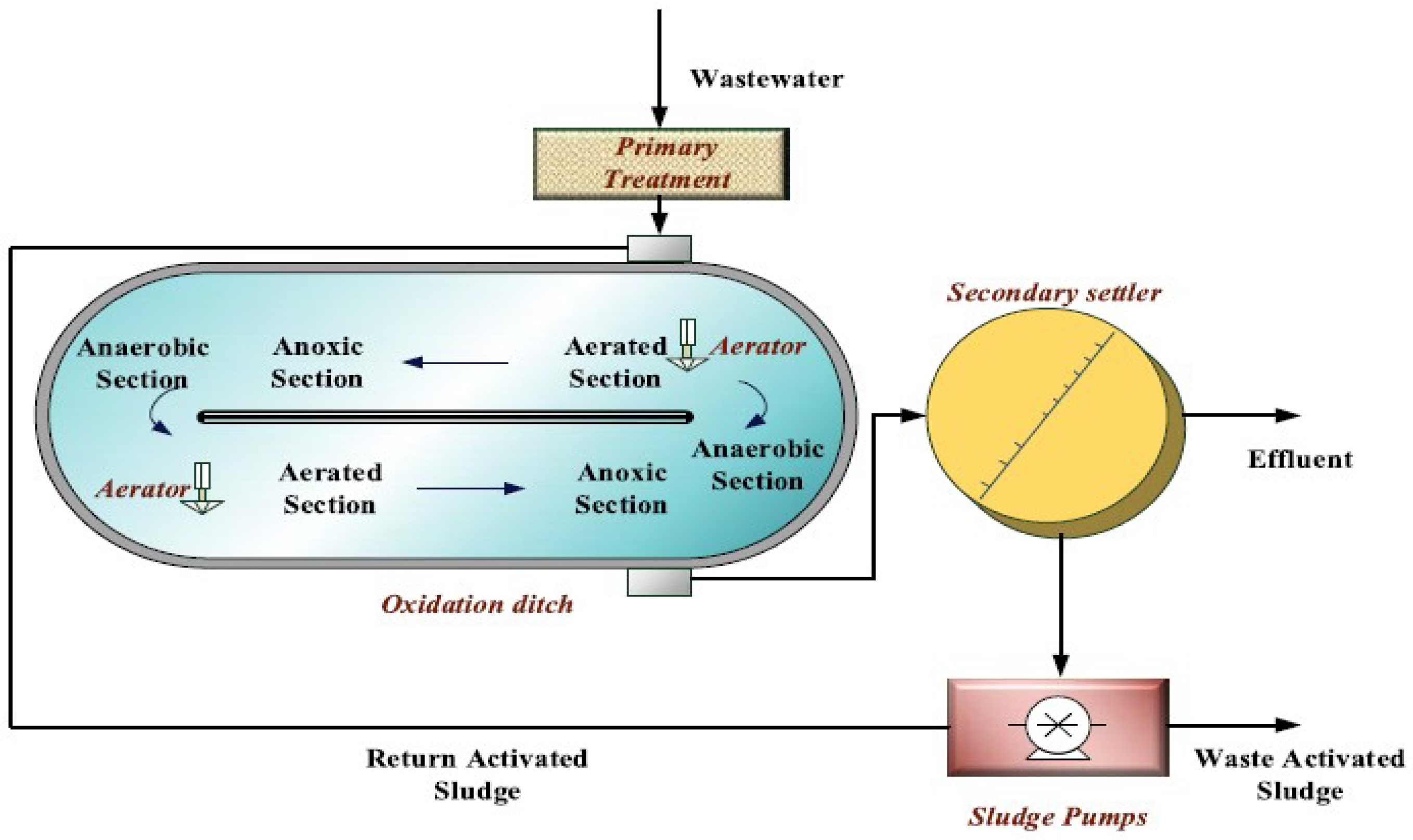
5.3. Case Study 2: Benchmark Simulation 1 (BSM 1)
6. Discussion
Performance Evaluation of Monitoring Methods
7. Real World Wastewater Treatment Plant
8. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Huang, R.; Li, J.; Liao, Y.; Chen, Z.; He, G.; Yan, R.; Gryllias, K. A perspective survey on deep transfer learning for fault diagnosis in industrial scenarios: Theories, applications and challenges. Mech. Syst. Signal Process. 2022, 167, 108487. [Google Scholar] [CrossRef]
- Wang, J.; Ye, L.; Gao, R.X.; Li, C.; Zhang, L. Digital Twin for rotating machinery fault diagnosis in smart manufacturing. Int. J. Prod. Res. 2019, 57, 3920–3934. [Google Scholar] [CrossRef]
- Wan, J.; Li, X.; Dai, H.N.; Kusiak, A.; Martinez-Garcia, M.; Li, D. Artificial-intelligence-driven customized manufacturing factory: Key technologies, applications, and challenges. Proc. IEEE 2020, 109, 377–398. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Wang, R.; Zhan, X.; Bai, H.; Dong, E.; Cheng, Z.; Jia, X. A Review of Fault Diagnosis Methods for Rotating Machinery Using Infrared Thermography. Micromachines 2022, 13, 1644. [Google Scholar] [CrossRef] [PubMed]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Huang, R.; Li, J.; Wang, S.; Li, G.; Li, W. A robust weight-shared capsule network for intelligent machinery fault diagnosis. IEEE Trans. Ind. Inform. 2020, 16, 6466–6475. [Google Scholar] [CrossRef]
- Liu, D.; Song, Y.; Li, L.; Liao, H.; Peng, Y. On-line life cycle health assessment for lithium-ion battery in electric vehicles. J. Clean. Prod. 2018, 199, 1050–1065. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, W.; Mo, Y.; Yuan, X.; Wang, Y.; Yang, C. New mode cold start monitoring in industrial processes: A solution of spatial–temporal feature transfer. Knowl.-Based Syst. 2022, 248, 108851. [Google Scholar] [CrossRef]
- Fang, R.; Wang, K.; Li, J.; Yuan, X.; Wang, Y. Unsupervised domain adversarial network for few-sample fault detection in industrial processes. Adv. Eng. Inform. 2024, 61, 102684. [Google Scholar] [CrossRef]
- Peres, F.A.P.; Peres, T.N.; Fogliatto, F.S.; Anzanello, M.J. Fault detection in batch processes through variable selection integrated to multiway principal component analysis. J. Process Control 2019, 80, 223–234. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, M.; Hong, X. Nonlinear process monitoring using a mixture of probabilistic PCA with clusterings. Neurocomputing 2021, 458, 319–326. [Google Scholar] [CrossRef]
- Huang, J.; Yang, X.; Shardt, Y.A.; Yan, X. Sparse modeling and monitoring for industrial processes using sparse, distributed principal component analysis. J. Taiwan Inst. Chem. Eng. 2021, 122, 14–22. [Google Scholar] [CrossRef]
- Liu, Y.; Pan, Y.; Sun, Z.; Huang, D. Statistical monitoring of wastewater treatment plants using variational Bayesian PCA. Ind. Eng. Chem. Res. 2014, 53, 3272–3282. [Google Scholar] [CrossRef]
- Yang, Y.H.; Chen, Y.L.; Chen, X.B.; Qin, S.K. Multivariate statistical process monitoring and fault diagnosis based on an integration method of PCA-ICA and CSM. Appl. Mech. Mater. 2011, 84, 110–114. [Google Scholar] [CrossRef]
- Kini, K.R.; Madakyaru, M. Improved process monitoring scheme using multi-scale independent component analysis. Arab. J. Sci. Eng. 2022, 47, 5985–6000. [Google Scholar] [CrossRef]
- Harkat, M.F.; Mansouri, M.; Nounou, M.N.; Nounou, H.N. Fault detection of uncertain chemical processes using interval partial least squares-based generalized likelihood ratio test. Inf. Sci. 2019, 490, 265–284. [Google Scholar]
- Zhang, K.; Hao, H.; Chen, Z.; Ding, S.X.; Peng, K. A comparison and evaluation of key performance indicator-based multivariate statistics process monitoring approaches. J. Process Control 2015, 33, 112–126. [Google Scholar] [CrossRef]
- Liu, H.; Yang, J.; Zhang, Y.; Yang, C. Monitoring of wastewater treatment processes using dynamic concurrent kernel partial least squares. Process Saf. Environ. Prot. 2021, 147, 274–282. [Google Scholar] [CrossRef]
- Yao, L.; Shao, W.; Ge, Z. Hierarchical quality monitoring for large-scale industrial plants with big process data. IEEE Trans. Neural Netw. Learn. Syst. 2019, 32, 3330–3341. [Google Scholar] [CrossRef]
- Zou, W.; Xia, Y.; Li, H. Fault diagnosis of Tennessee—Eastman process using orthogonal incremental extreme learning machine based on driving amount. IEEE Trans. Cybern. 2018, 48, 3403–3410. [Google Scholar] [CrossRef] [PubMed]
- Qian, Q.; Qin, Y.; Wang, Y.; Liu, F. A new deep transfer learning network based on convolutional auto-encoder for mechanical fault diagnosis. Measurement 2021, 178, 109352. [Google Scholar] [CrossRef]
- Cai, L.; Tian, X.; Chen, S. Monitoring nonlinear and non-Gaussian processes using Gaussian mixture model-based weighted kernel independent component analysis. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 122–135. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-M.; Yoo, C.K.; Choi, S.W.; Vanrolleghem, P.A.; Lee, I.-B. Nonlinear process monitoring using kernel principal component analysis. Chem. Eng. Sci. 2004, 59, 223–234. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, P.; Lang, X.; Miao, A. Improved dynamic kernel principal component analysis for fault detection. Measurement 2020, 158, 107738. [Google Scholar] [CrossRef]
- Dong, Q. Implementing deep learning for comprehensive aircraft icing and actuator/sensor fault detection/identification. Eng. Appl. Artif. Intell. 2019, 83, 28–44. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, C. Robust monitoring and fault isolation of nonlinear industrial processes using denoising autoencoder and elastic net. IEEE Trans. Control Syst. Technol. 2020, 28, 1083–1091. [Google Scholar] [CrossRef]
- Xiao, Y.C.; Wang, H.G.; Zhang, L.; Xu, W.L. Two methods of selecting Gaussian kernel parameters for one-class SVM and their application to fault detection. Knowl.-Based Syst. 2014, 59, 75–84. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, C. Slow-feature-analysis-based batch process monitoring with comprehensive interpretation of operation condition deviation and dynamic anomaly. IEEE Trans. Ind. Electron. 2018, 66, 3773–3783. [Google Scholar] [CrossRef]
- Guo, F.; Shang, C.; Huang, B.; Wang, K.; Yang, F.; Huang, D. Monitoring of operating point and process dynamics via probabilistic slow feature analysis. Chemom. Intell. Lab. Syst. 2016, 151, 115–125. [Google Scholar] [CrossRef]
- Shang, C.; Huang, B.; Yang, F.; Huang, D. Slow feature analysis for monitoring and diagnosis of control performance. J. Process Control 2016, 39, 21–34. [Google Scholar] [CrossRef]
- Pilario, K.E.; Shafiee, M.; Cao, Y.; Lao, L.; Yang, S.H. A review of kernel methods for feature extraction in nonlinear process monitoring. Processes 2019, 8, 24. [Google Scholar] [CrossRef]
- Song, P.; Zhao, C. Slow down to go better: A survey on slow feature analysis. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 3416–3436. [Google Scholar] [CrossRef] [PubMed]
- Melo, A.; Câmara, M.M.; Pinto, J.C. Data-Driven Process Monitoring and Fault Diagnosis: A Comprehensive Survey. Processes 2024, 12, 251. [Google Scholar] [CrossRef]
- Zhang, N.; Tian, X.; Cai, L.; Deng, X. Process fault detection based on dynamic kernel slow feature analysis. Comput. Electr. Eng. 2015, 41, 9–17. [Google Scholar] [CrossRef]
- Fang, M. Hierarchical Monitoring and Probabilistic Graphical Model Based Fault Detection and Diagnosis. Ph.D Thesis, Department of Chemical and Materials Engineering, University of Alberta, Edmond, AB, USA, 2020. [Google Scholar]
- Bounoua, W.; Aftab, M.F. Improved extended empirical wavelet transform for accurate multivariate oscillation detection and characterisation in plant-wide industrial control loops. J. Process Control. 2024, 138, 103226. [Google Scholar] [CrossRef]
- Liu, S.; Lei, F.; Zhao, D.; Liu, Q. Abnormal Situation Management in Chemical Processes: Recent Research Progress and Future Prospects. Processes 2023, 11, 1608. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, D.; Lian, P.; Wan, Z.; Yang, Y. Will structure-environment-fit result in better port performance? An empirical test on the validity of Matching Framework Theory. Transp. Policy 2020, 86, 23–33. [Google Scholar] [CrossRef]
- Downs, J.J.; Vogel, E.F. A plant-wide industrial process control problem. Comput. Chem. Eng. 1993, 17, 245–255. [Google Scholar] [CrossRef]
- Chiang, L.H.; Russell, E.L.; Braatz, R.D. Fault Detection and Diagnosis in Industrial Systems; Springer Science Business Media: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Cheng, H.; Wu, J.; Huang, D.; Liu, Y.; Wang, Q. Robust adaptive boosted canonical correlation analysis for quality-relevant process monitoring of wastewater treatment. ISA Trans. 2021, 117, 210–220. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, Y.; Huang, D.; Liu, B. Optimized forecast components-SVM-based fault diagnosis with applications for wastewater treatment. IEEE Access 2019, 7, 128534–128543. [Google Scholar] [CrossRef]
- Qiu, Y.; Liu, Y.; Huang, D. Date-driven soft-sensor design for biological wastewater treatment using deep neural networks and genetic algorithms. J. Chem. Eng. Jpn. 2016, 49, 925–936. [Google Scholar] [CrossRef]
- Wu, J.; Cheng, H.; Liu, Y.; Huang, D.; Yuan, L.; Yao, L. Learning soft sensors using time difference–based multi-kernel relevance vector machine with applications for quality-relevant monitoring in wastewater treatment. Environ. Sci. Pollut. Res. 2020, 27, 28986–28999. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Huang, D.; Cai, B.; Chen, H.; Liu, Y. A complex-valued slow independent component analysis based incipient fault detection and diagnosis method with applications to wastewater treatment processes. ISA Trans. 2023, 135, 213–232. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Guo, J.; Wang, Q.; Huang, D. Prediction of filamentous sludge bulking using a state-based Gaussian processes regression model. Sci. Rep. 2016, 6, 31303. [Google Scholar] [CrossRef]
- Reifsnyder, S. Dynamic Process Modeling of Wastewater-Energy Systems. Ph.D Thesis, University of California, Irvine, CA, USA, 2020. [Google Scholar]
- Xu, C.; Huang, D.; Li, D.; Liu, Y. Novel process monitoring approach enhanced by a complex independent component analysis algorithm with applications for wastewater treatment. Ind. Eng. Chem. Res. 2021, 60, 13914–13926. [Google Scholar] [CrossRef]
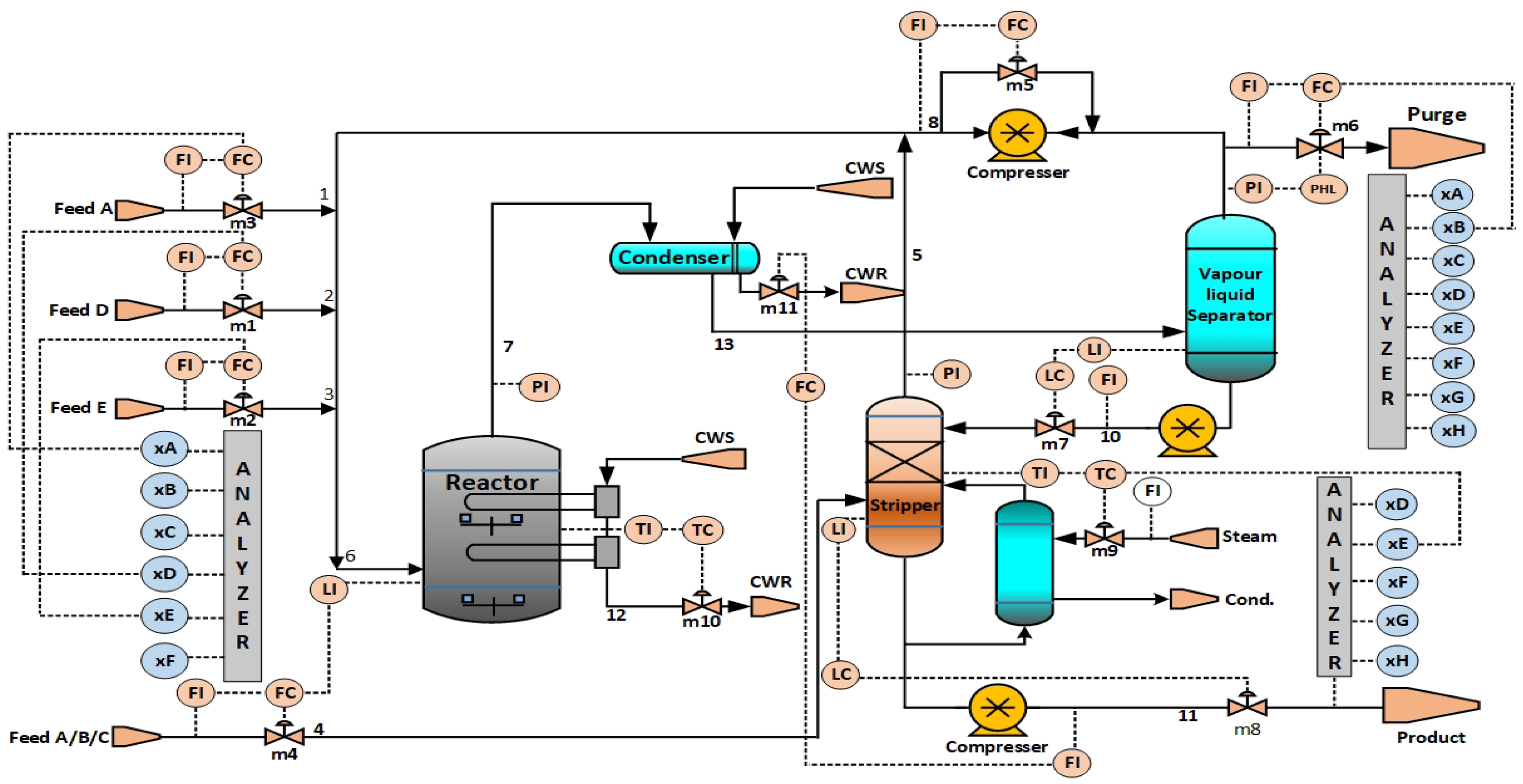




| Fault ID | Description |
|---|---|
| IDV0 | Normal operation |
| IDV1 | Variations in A/C feed ratio with constant B composition |
| IDV2 | Changes in B composition with a constant A/C ratio |
| IDV4 | Fluctuations in reactor cooling water inlet temperature |
| IDV5 | Variations in condenser cooling water inlet temperature |
| IDV6 | Loss of A feed (stream 1) |
| IDV7 | Pressure drop in C header, leading to reduced availability (stream 4) |
| IDV8 | Variations in feed composition of A, B, and C (stream 4) |
| IDV10 | Changes in C feed temperature (stream 4) |
| IDV11 | Reactor cooling water inlet temperature variations |
| IDV12 | Condenser cooling water inlet temperature variations |
| IDV13 | Changes in reaction kinetics |
| IDV14 | Issues with the reactor cooling water valve |
| IDV16 | Unknown fault type |
| IDV17 | Unknown fault type |
| IDV18 | Unknown fault type |
| IDV19 | Unknown fault type |
| IDV20 | Unknown fault type |
| Metric | SFA | KSFA | DSFA | PCA |
|---|---|---|---|---|
| 0 | - | - | 0 | |
| 18.125 | - | - | 100 | |
| 62.907 | 1.961 | - | 0 | |
| 10 | 1.389 | - | 99.375 | |
| 0 | - | - | - | |
| 10.625 | - | - | - | |
| 93.484 | - | - | - | |
| 3.75 | - | - | - | |
| - | 1.961 | - | - | |
| - | 2.778 | - | - | |
| - | - | 76.441 | - | |
| - | - | 0 | - |
| Metric | SFA | KSFA | DSFA | PCA |
|---|---|---|---|---|
| MAR_T2 | 92.07082 | NA | NA | 27.30769 |
| FAR_T2 | 0 | NA | NA | 70.45455 |
| MAR_S2 | 26.097 | 54.92308 | NA | 99.61538 |
| FAR_S2 | 65.90909 | 2.272727 | NA | 0 |
| MAR_T2e | 86.98999 | NA | NA | NA |
| FAR_T2e | 2.272727 | NA | NA | NA |
| MAR_S2e | 97.5366 | NA | NA | NA |
| FAR_S2e | 2.272727 | NA | NA | NA |
| MAR_SPE | NA | 80 | NA | NA |
| FAR_SPE | NA | 0 | NA | NA |
| MAR_D | NA | NA | 61.89376 | NA |
| FAR_D | NA | NA | 0 | NA |
| SFA | KSFA | DSFA | PCA | ||||||
|---|---|---|---|---|---|---|---|---|---|
| SPE | SPE | ||||||||
| MAR | 5.421 | 38.55 | 0 | 0 | 27.54 | 2 | 53.01 | 3.5 | 16.7 |
| FAR | 0 | 0 | 0 | 0 | 2 | 6 | 0 | 28.8 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aman, A.; Chen, Y.; Yiqi, L. Assessment of Slow Feature Analysis and Its Variants for Fault Diagnosis in Process Industries. Technologies 2024, 12, 237. https://doi.org/10.3390/technologies12120237
Aman A, Chen Y, Yiqi L. Assessment of Slow Feature Analysis and Its Variants for Fault Diagnosis in Process Industries. Technologies. 2024; 12(12):237. https://doi.org/10.3390/technologies12120237
Chicago/Turabian StyleAman, Abid, Yan Chen, and Liu Yiqi. 2024. "Assessment of Slow Feature Analysis and Its Variants for Fault Diagnosis in Process Industries" Technologies 12, no. 12: 237. https://doi.org/10.3390/technologies12120237
APA StyleAman, A., Chen, Y., & Yiqi, L. (2024). Assessment of Slow Feature Analysis and Its Variants for Fault Diagnosis in Process Industries. Technologies, 12(12), 237. https://doi.org/10.3390/technologies12120237







