On the Integration of Standard Deviation and Clustering to Promote Scalable and Precise Wi-Fi Round-Trip Time Positioning
Abstract
1. Introduction
- The use of the STD of RTT measurements is proposed. The impact of coupling the STD with the average RTT delivered by the Wi-Fi RTT procedure is assessed and compared with the coupling of the RTT and RSSI proposed in [18]. To the best of our knowledge, this approach has been poorly investigated in the literature so far.
- A novel solution is proposed, that enables the selection of the best APs on which the Wi-Fi RTT procedure must be initiated based on the highest RSSI, thus enhancing scalability.
- The ability of obtaining a precise location estimate with COTS devices by coupling the measurements provided by a single AP is studied for the first time in the literature.
- Finally, the use of clustering is assessed as a measure to not only enhance the position estimate but also to foster sectorization, so that UE in different clusters is less likely to exchange FTM traffic with the same APs. In this way, the localization overhead is expected to better distribute among several APs, thus improving scalability in the whole network.
2. Wi-Fi RTT Positioning: Overview and Related Work
2.1. Overview of the IEEE 802.11mc Standard
2.2. Advances in Wi-Fi RTT-Based Location Solutions: Trends and Challenges
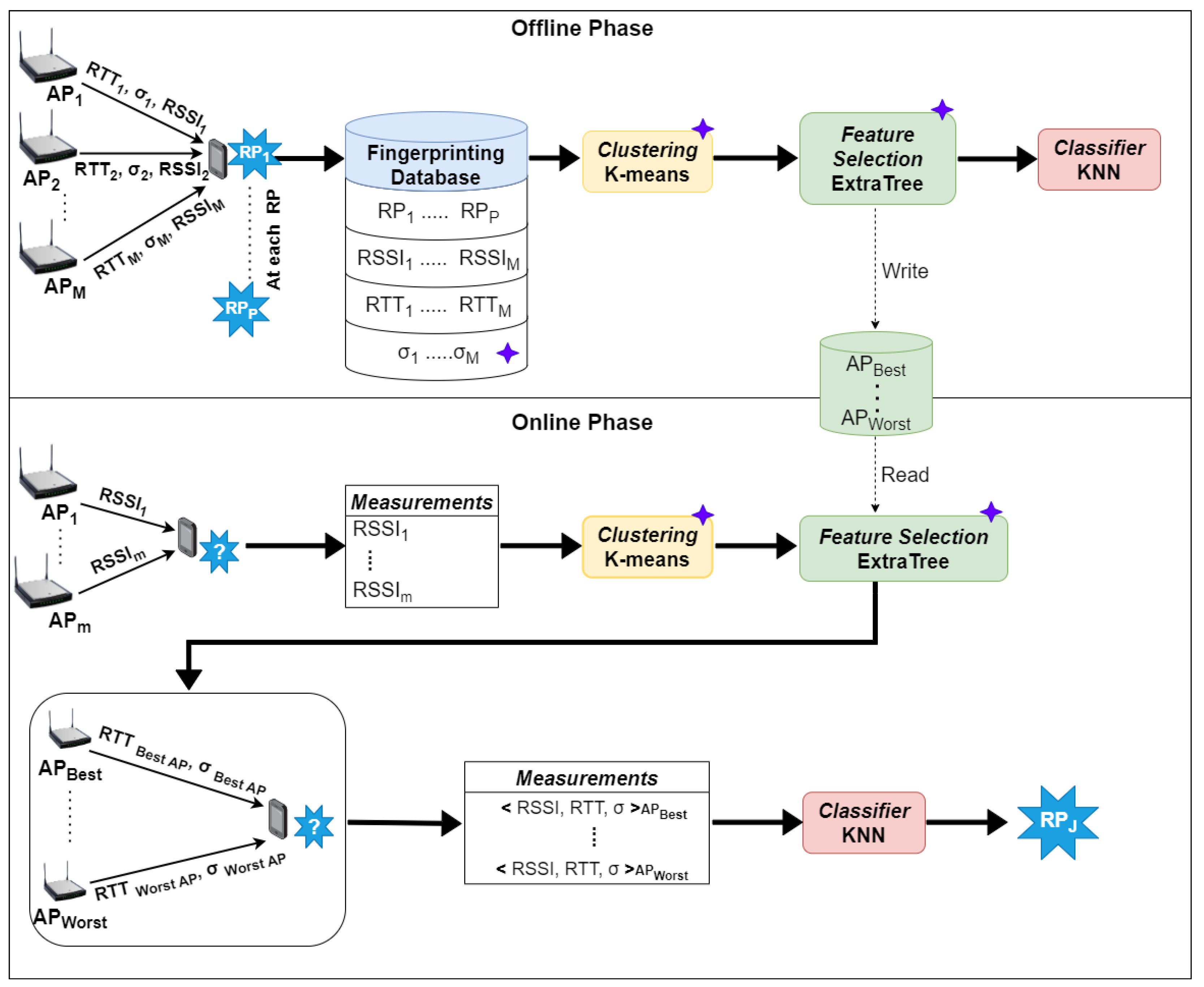
3. Proposed Wi-Fi RTT Fingerprinting Positioning System
3.1. General Description
3.2. Data Models
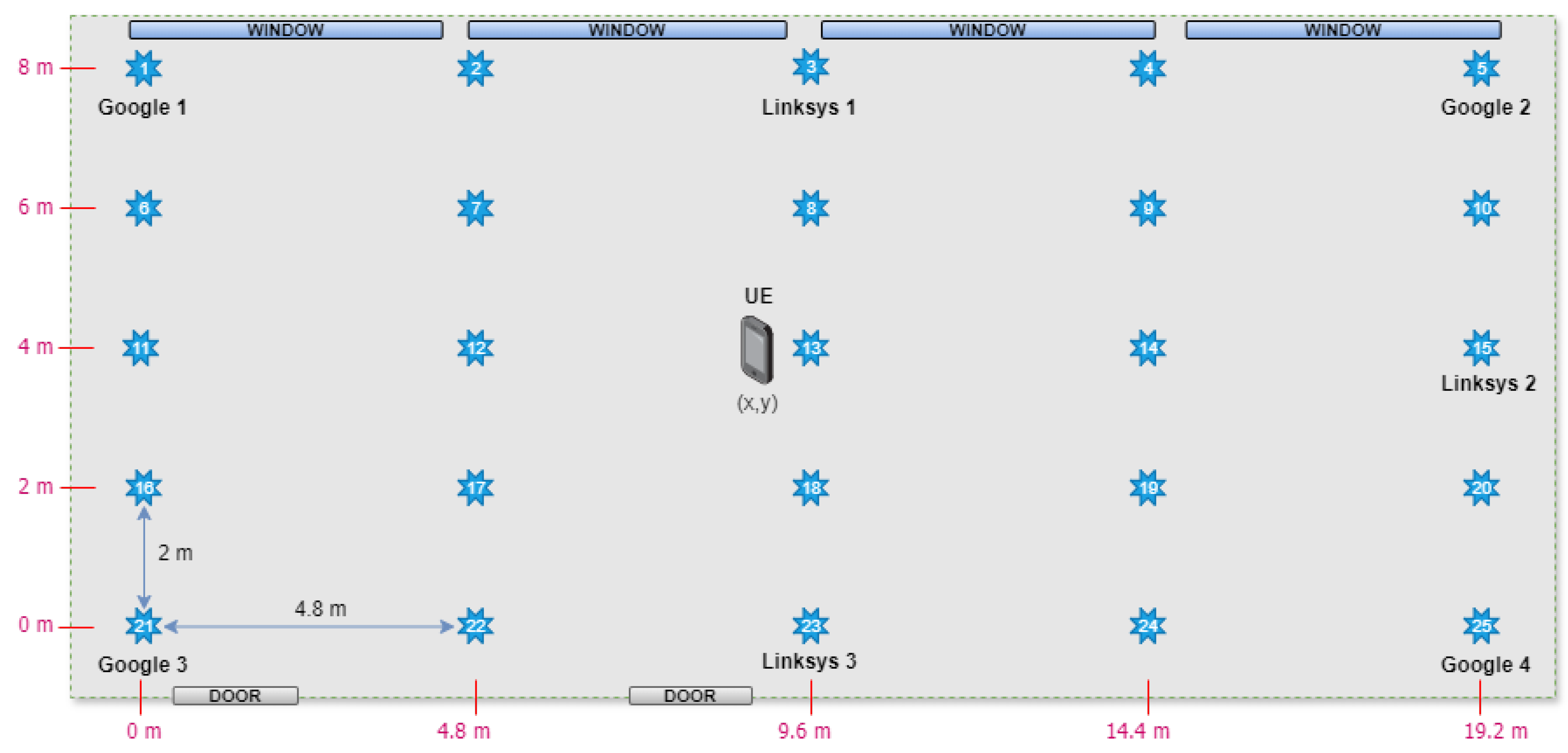
4. Evaluation Scenario and Metrics
5. Assessing Performance of Wi-Fi RTT Measurements
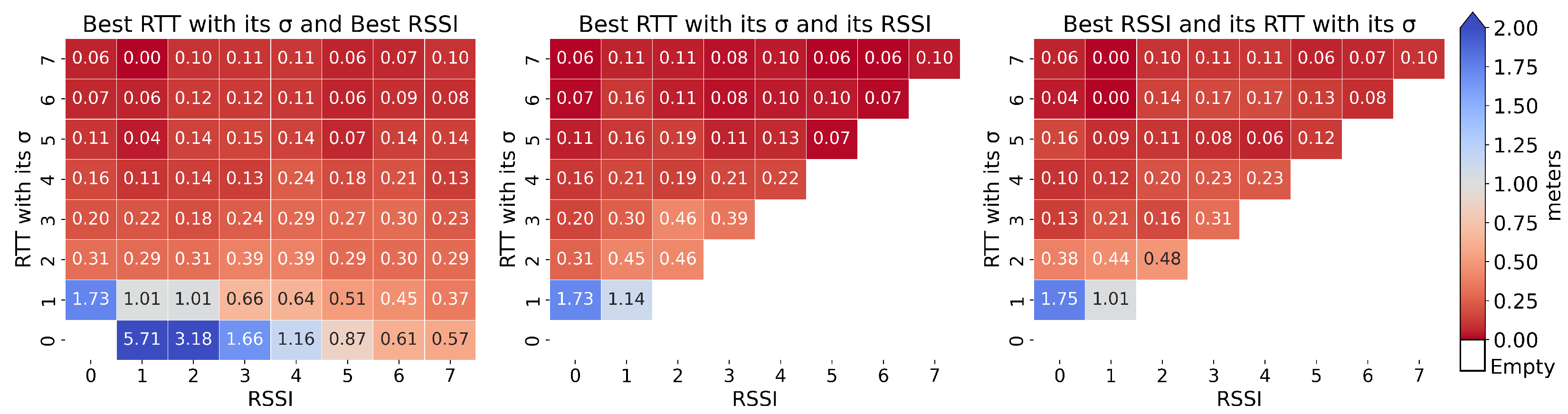
5.1. Coupling RTT and RSSI Measurements
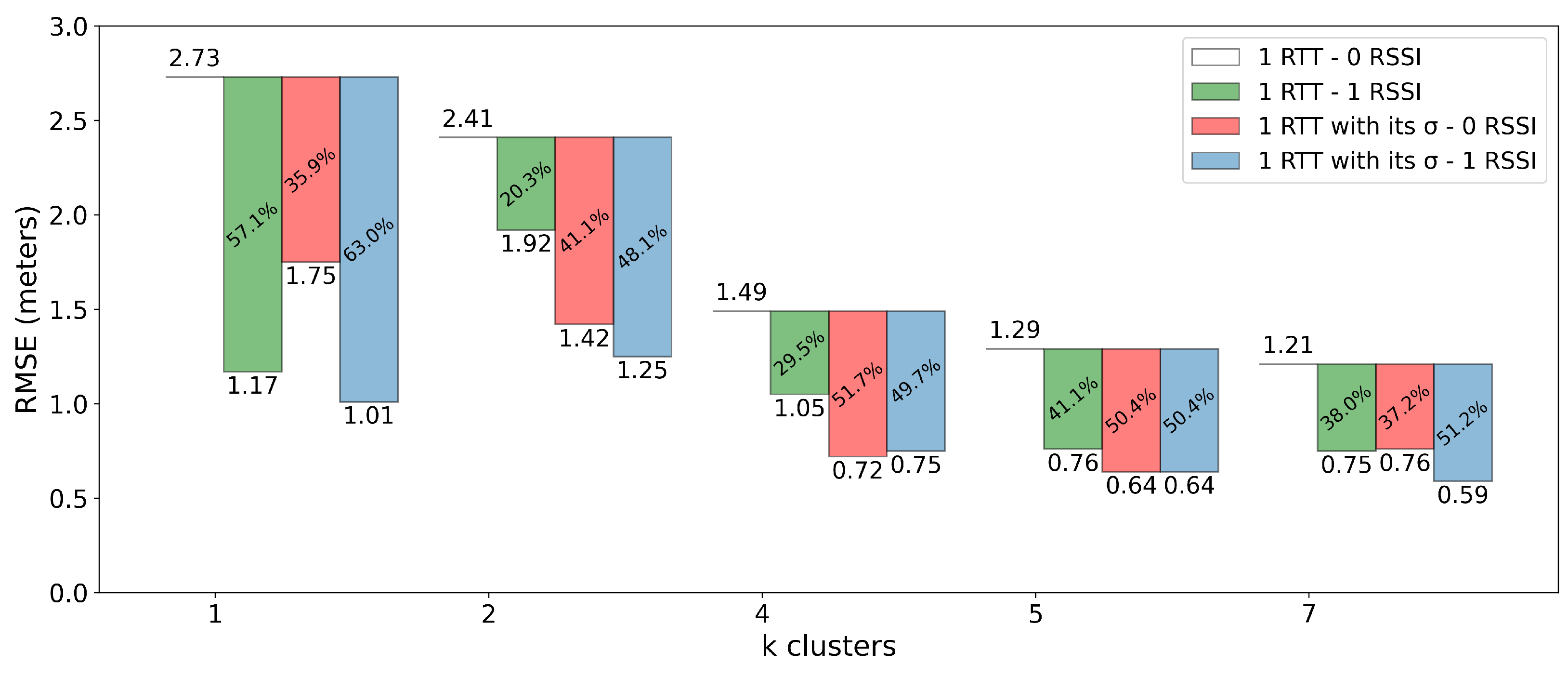
5.2. Integrating the Standard Deviation
6. Clustering for a Precise and Scalable Positioning System
6.1. Impact of Applying Clustering
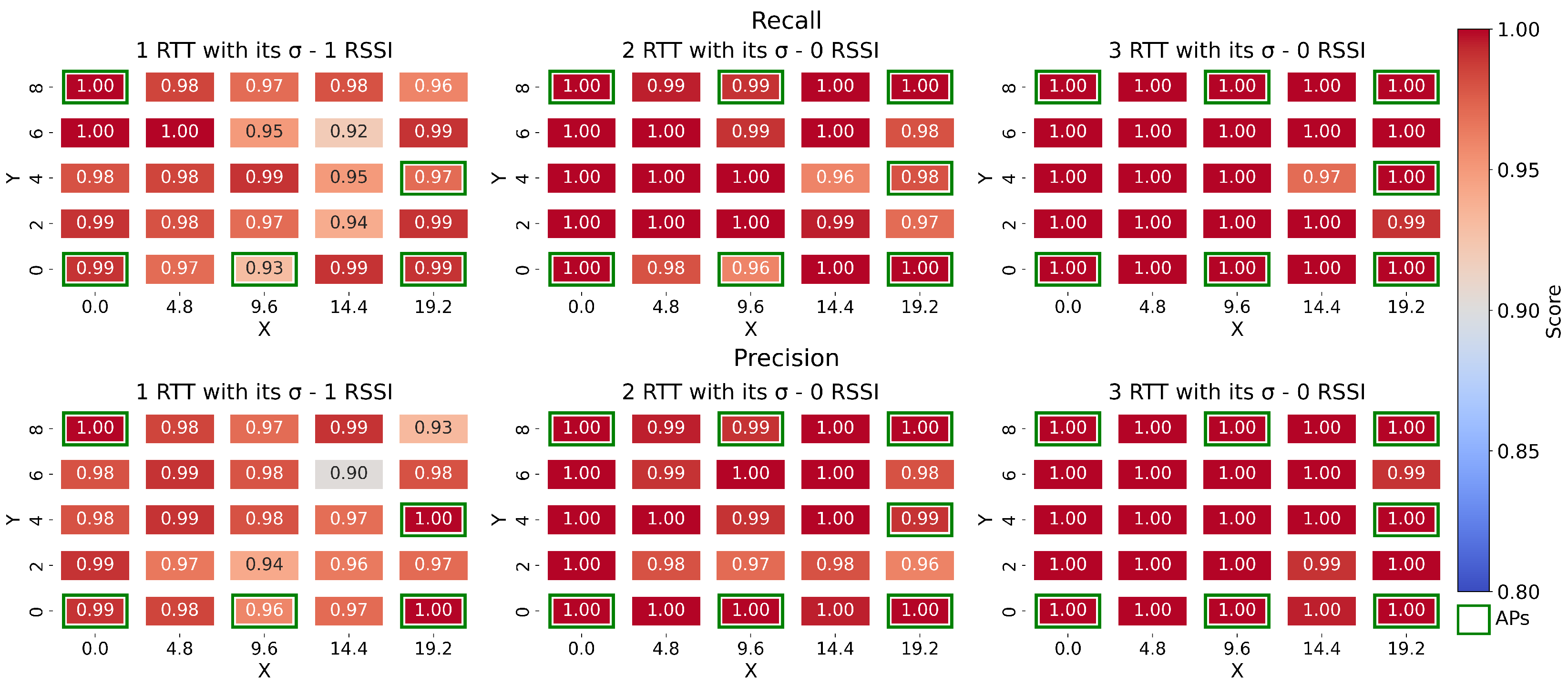
6.2. Distribution of the Overhead Among the Available APs
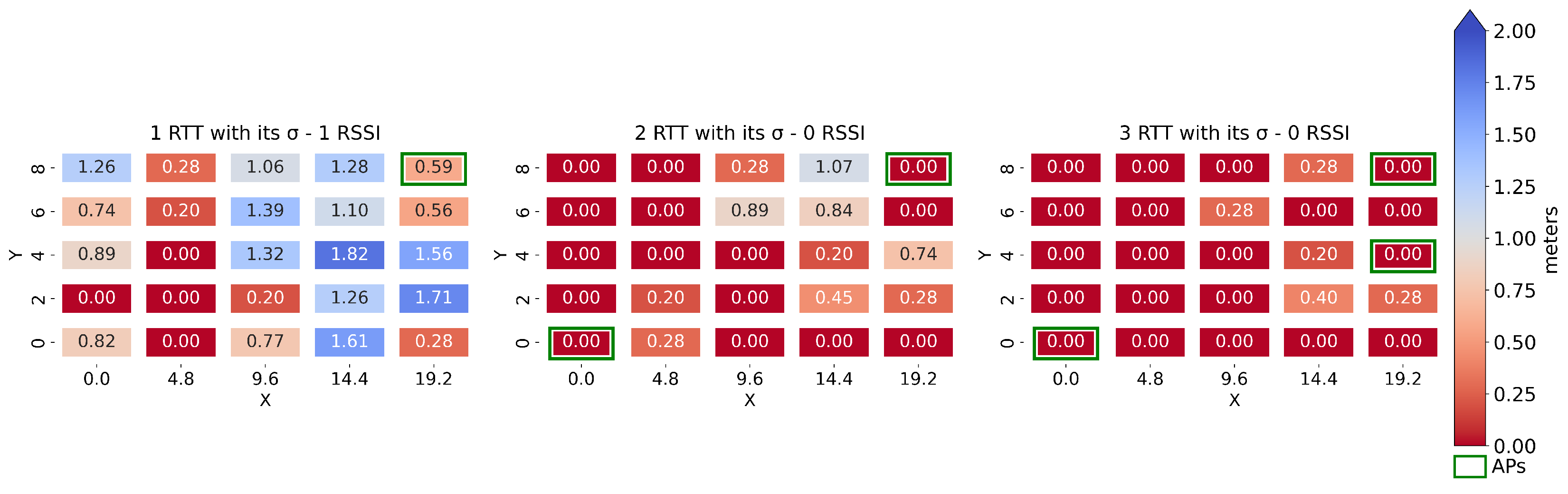
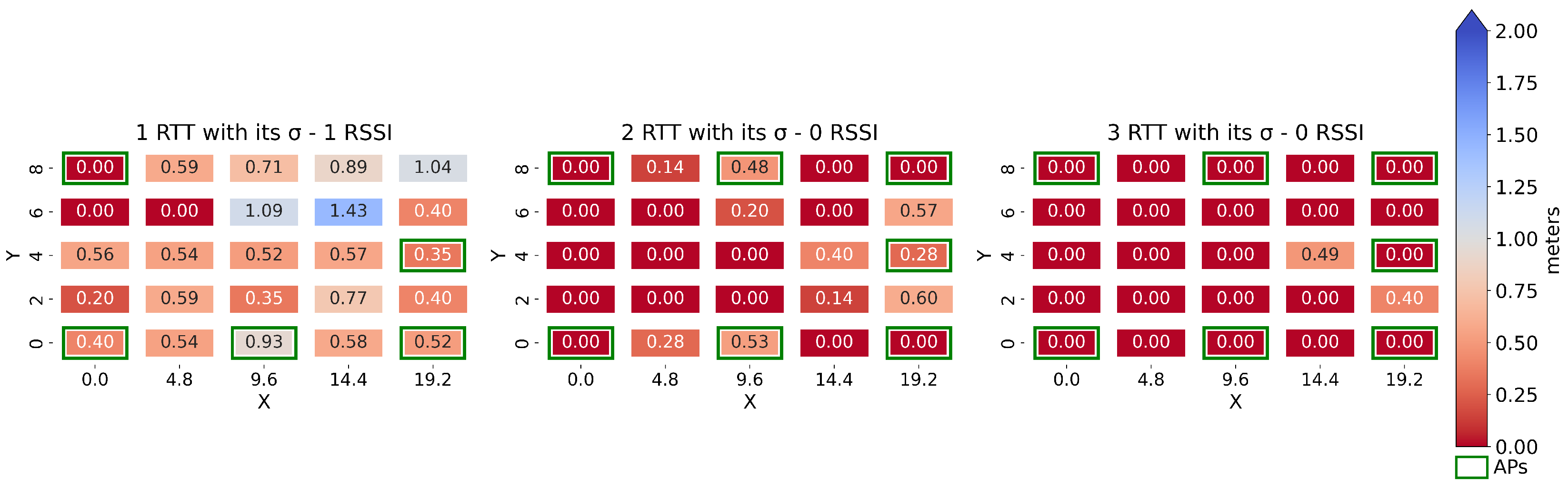
6.3. Spatial Distribution of the RMSE
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACK | Acknowledgement |
| AP | Access Point |
| BLE | Bluetooth Low Energy |
| COTS | Common Off-The-Shelf |
| CSI | Channel State Information |
| DNN | Deep Neural Network |
| DoA | Direction of Arrival |
| FP | fingerprinting |
| FTM | Fine Timing Measurement |
| GPS | Global Positioning System |
| IPS | Indoor Positioning System |
| ISTA | Initiating Station |
| KNN | K-Nearest Neighbors |
| LBS | Location-Based Service |
| LoS | Line of Sight |
| ML | Machine Learning |
| NLoS | Non-Line-of-Sight |
| OS | Operating System |
| P2P | Peer-to-Peer |
| RF | Random Forest |
| RMSE | Root-Mean-Square Error |
| RP | Reference Point |
| RSSI | Received Signal Strength Indicator |
| RSTA | Responding Station |
| RTT | Round-Trip Time |
| SoA | State of the Art |
| STD | standard deviation |
| ToF | Time-of-Flight |
| UE | User Equipment |
| UWB | Ultra-Wide Band |
| Wi-Fi | Wireless Fidelity |
References
- Qi, L.; Liu, Y.; Yu, Y.; Chen, L.; Chen, R. Current Status and Future Trends of Meter-Level Indoor Positioning Technology: A Review. Remote Sens. 2024, 16, 398. [Google Scholar] [CrossRef]
- Retscher, G. Fundamental Concepts and Evolution of Wi-Fi User Localization: An Overview Based on Different Case Studies. Sensors 2020, 20, 5121. [Google Scholar] [CrossRef]
- Yin, H.; Xu, X.; Lu, S.; Chen, X.; Xiong, R.; Shen, S. A Survey on Global LiDAR Localization: Challenges, Advances and Open Problems. Int. J. Comput. Vis. 2024, 132, 3139–3171. [Google Scholar] [CrossRef]
- Khan, D.; Cheng, Z.; Uchiyama, H.; Ali, S.; Asshad, M.; Kiyokawa, K. Recent advances in vision-based indoor navigation: A systematic literature review. Comput. Graph. 2022, 104, 24–45. [Google Scholar] [CrossRef]
- Hanssens, B.; Plets, D.; Tanghe, E.; Oestges, C.; Gaillot, D.P.; Liénard, M.; Li, T.; Steendam, H.; Martens, L.; Joseph, W. An Indoor Variance-Based Localization Technique Utilizing the UWB Estimation of Geometrical Propagation parameters. IEEE Trans. Antennas Propag. 2018, 66, 2522–2533. [Google Scholar] [CrossRef]
- Ma, W.; Fang, X.; Liang, L.; Du, J. Research on indoor positioning system algorithm based on UWB technology. Meas. Sens. 2024, 33, 101121. [Google Scholar] [CrossRef]
- Zafari, F.; Gkelias, A.; Leung, K.K. A Survey of Indoor Localization Systems and Technologies. IEEE Commun. Surv. Tutor. 2019, 21, 2568–2599. [Google Scholar] [CrossRef]
- Suryavanshi, N.B.; Viswavardhan Reddy, K.; Chandrika, V.R. Direction Finding Capability in Bluetooth 5.1 standard. In Proceedings of the Ubiquitous Communications and Network Computing: Second EAI International Conference, Bangalore, India, 8–10 February 2019; Proceedings 2. Springer: Berlin/Heidelberg, Germany, 2019; pp. 53–65. [Google Scholar]
- Jin, Z.; Li, Y.; Yang, Z.; Zhang, Y.; Cheng, Z. Real-Time Indoor Positioning Based on BLE Beacons and Pedestrian Dead Reckoning for Smartphones. Appl. Sci. 2023, 13, 4415. [Google Scholar] [CrossRef]
- Yaro, A.S.; Maly, F.; Prazak, P. A Survey of the Performance-Limiting Factors of a 2-Dimensional RSS Fingerprinting-Based Indoor Wireless Localization System. Sensors 2023, 23, 2545. [Google Scholar] [CrossRef]
- Martin-Escalona, I.; Zola, E. Improving Fingerprint-Based Positioning by Using IEEE 802.11 mc FTM/RTT Observables. Sensors 2022, 23, 267. [Google Scholar] [CrossRef]
- IEEE Std 802.11-2016 (Revision of IEEE Std 802.11-2012); IEEE Standard for Information Technology—Telecommunications and Information Exchange between Systems Local and Metropolitan Area Networks—Specific Requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications. IEEE: New York, NY, USA, 2016; pp. 1–3534. [CrossRef]
- Martin-Escalona, I.; Zola, E. Ranging Estimation Error in WiFi Devices Running IEEE 802.11mc. In Proceedings of the GLOBECOM 2020-2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–7. [Google Scholar]
- Horn, B.K. Doubling the Accuracy of Indoor Positioning: Frequency Diversity. Sensors 2020, 20, 1489. [Google Scholar] [CrossRef]
- Hashem, O.; Harras, K.A.; Youssef, M. Accurate Indoor Positioning Using IEEE 802.11mc Round Trip Time. Pervasive Mob. Comput. 2021, 75, 101416. [Google Scholar] [CrossRef]
- Feng, X.; Nguyen, K.A.; Luo, Z. Wifi Access Points Line-of-Sight Detection for Indoor Positioning Using the Signal Round Trip Time. Remote Sens. 2022, 14, 6052. [Google Scholar] [CrossRef]
- Banin, L.; Bar-Shalom, O.; Dvorecki, N.; Amizur, Y. Scalable Wi-Fi Client Self-Positioning Using Cooperative FTM-Sensors. IEEE Trans. Instrum. Meas. 2019, 68, 3686–3698. [Google Scholar] [CrossRef]
- Gonzalez Díaz, N.; Zola, E.; Martin-Escalona, I. Assessing the Impact of Coupling RTT and RSSI Measurements in Fingerprinting Wi-Fi Indoor Positioning. In Proceedings of the Int’l ACM Conference on Modeling Analysis and Simulation of Wireless and Mobile Systems, Montreal, QC, Canada, 29 October–2 November 2023; pp. 19–26. [Google Scholar]
- Corrêa Oliveira, D.; Zola, E.; Martin-Escalona, I. Impact of the Burst Size on the FTM Procedure in Android Phones. In Proceedings of the Int’l ACM Conference on Modeling Analysis and Simulation of Wireless and Mobile Systems, Montreal, QC, Canada, 29 October–2 November 2023; pp. 205–208. [Google Scholar]
- Wi-Fi Location: Ranging with RTT. Available online: https://developer.android.com/develop/connectivity/wifi/wifi-rtt#supported-phones (accessed on 1 July 2024).
- Horn, B.K. Indoor Localization Using Uncooperative Wi-Fi Access Points. Sensors 2022, 22, 3091. [Google Scholar] [CrossRef]
- Truong, H.; Justin, L.X.K.; Anish, G.A.; Balan, R.K. Applicability and Challenges of Indoor Localization Using One-Sided Round Trip Time Measurements. In Proceedings of the Workshop on Body-Centric Computing Systems, Tokyo, Japan, 3–7 June 2024; pp. 1–6. [Google Scholar]
- Dong, Y.; Shi, D.; Arslan, T.; Yang, Y. Error Investigation on Wi-Fi RTT in Commercial Consumer Devices. Algorithms 2022, 15, 464. [Google Scholar] [CrossRef]
- Google LLC. Wi-Fi RTT (IEEE 802.11mc). Available online: https://source.android.com/docs/core/connect/wifi-rtt (accessed on 1 July 2024).
- Guo, G.; Chen, R.; Ye, F.; Peng, X.; Liu, Z.; Pan, Y. Indoor Smartphone Localization: A Hybrid WiFi RTT-RSS Ranging Approach. IEEE Access 2019, 7, 176767–176781. [Google Scholar] [CrossRef]
- Dong, J.; Rana, L.; Cui, S.; Li, J.; Hwang, J.; Park, J. Investigation on Indoor Positioning by Improved RTT-RSS Fusion Ranging Method. In Proceedings of the 2023 IEEE 6th International Conference on Electronics and Communication Engineering (ICECE), IEEE, Xi’an, China, 15–17 December 2023; pp. 49–53. [Google Scholar]
- Ma, C.; Wu, B.; Poslad, S.; Selviah, D.R. Wi-Fi RTT Ranging Performance Characterization and Positioning System Design. IEEE Trans. Mob. Comput. 2022, 21, 740–756. [Google Scholar] [CrossRef]
- Choi, J.; Choi, Y.S.; Talwar, S. Unsupervised Learning Techniques for Trilateration: From Theory to Android APP Implementation. IEEE Access 2019, 7, 134525–134538. [Google Scholar] [CrossRef]
- Rizk, H.; Elmogy, A.; Yamaguchi, H. A Robust and Accurate Indoor Localization Using Learning-Based Fusion of Wi-Fi RTT and RSSI. Sensors 2022, 22, 2700. [Google Scholar] [CrossRef]
- Wang, J.; Park, J.G. A Novel Indoor Ranging Algorithm Based on a Received Signal Strength Indicator and Channel State Information Using an Extended Kalman Filter. Appl. Sci. 2020, 10, 3687. [Google Scholar] [CrossRef]
- López-Pastor, J.A.; Poveda-García, M.; Gil-Martínez, A.; Cañete-Rebenaque, D.; Gómez-Tornero, J.L. 2-D Localization System for Mobile IoT Devices Using a Single Wi-Fi Access Point With a Passive Frequency-Scanned Antenna. IEEE Internet Things J. 2023, 10, 14995–15011. [Google Scholar] [CrossRef]
- Numan, P.E.; Park, H.; Laoudias, C.; Horsmanheimo, S.; Kim, S. DNN-based Indoor Fingerprinting Localization with WiFi FTM. In Proceedings of the 2022 23rd IEEE International Conference on Mobile Data Management (MDM), Paphos, Cyprus, 6–9 June 2022; pp. 367–371. [Google Scholar] [CrossRef]
- Rana, L.; Dong, J.; Cui, S.; Li, J.; Hwang, J.; Park, J. Indoor Positioning using DNN and RF Method Fingerprinting-based on Calibrated Wi-Fi RTT. In Proceedings of the 2023 13th International Conference on Indoor Positioning and Indoor Navigation (IPIN), Nuremberg, Germany, 25–28 September 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, T.; Cabani, A.; Chafouk, H. A Survey of Recent Indoor Localization Scenarios and Methodologies. Sensors 2021, 21, 8086. [Google Scholar] [CrossRef]
- Ibrahim, M.; Liu, H.; Jawahar, M.; Nguyen, V.; Gruteser, M.; Howard, R.; Yu, B.; Bai, F. Verification: Accuracy Evaluation of WiFi Fine Time Measurements on an Open Platform. In Proceedings of the 24th Annual International Conference on Mobile Computing and Networking, New Delhi, India, 29 October–2 November 2018; pp. 417–427. [Google Scholar]
- Roy, P.; Chowdhury, C. A survey of Machine Learning Techniques for Indoor Localization and Navigation Systems. J. Intell. Robot. Syst. 2021, 101, 63. [Google Scholar] [CrossRef]
- AlHajri, M.I.; Ali, N.T.; Shubair, R.M. Indoor Localization for IoT Using Adaptive Feature Selection: A Cascaded Machine Learning Approach. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2306–2310. [Google Scholar] [CrossRef]
- Soper, D.S. Greed is good: Rapid Hyperparameter Optimization and Model Selection Using Greedy K-Fold Cross Validation. Electronics 2021, 10, 1973. [Google Scholar] [CrossRef]
- Szeghalmy, S.; Fazekas, A. A Comparative Study of the Use of Stratified Cross-Validation and Distribution-Balanced Stratified Cross-Validation in Imbalanced Learning. Sensors 2023, 23, 2333. [Google Scholar] [CrossRef] [PubMed]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Sonny, A.; Kumar, A.; Cenkeramaddi, L.R. Carry Objects Detection utilizing mmWave Radar Sensor and Ensemble Based Extra Tree Classifier on the Edge Computing Systems. IEEE Sens. J. 2023, 23, 20137–20149. [Google Scholar] [CrossRef]
- Shang, S.; Wang, L. Overview of WiFi fingerprinting-based indoor positioning. IET Commun. 2022, 16, 725–733. [Google Scholar] [CrossRef]
- Liu, S.; De Lacerda, R.; Fiorina, J. WKNN Indoor Wi-Fi Localization Method Using K-means Clustering Based Radio Mapping. In Proceedings of the 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), Virtual, 25 April–19 May 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, C.; Qin, N.; Xue, Y.; Yang, L. Received Signal Strength-Based Indoor Localization Using Hierarchical Classification. Sensors 2020, 20, 1067. [Google Scholar] [CrossRef] [PubMed]
- Sabanci, K.; Yigit, E.; Ustun, D.; Toktas, A.; Aslan, M.F. WiFi Based Indoor Localization: Application and Comparison of Machine Learning Algorithms. In Proceedings of the 2018 XXIIIrd International Seminar/Workshop on Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED), Tbilisi, Georgia, 24–27 September 2018; pp. 246–251. [Google Scholar] [CrossRef]
- Mahida, P.; Shahrestani, S.; Cheung, H. Deep Learning-Based Positioning of Visually Impaired People in Indoor Environments. Sensors 2020, 20, 6238. [Google Scholar] [CrossRef] [PubMed]
- Google LLC. Google WiFi AP. Available online: https://store.google.com/product/google_wifi (accessed on 1 July 2024).
- Linksys Velop Intelligent Mesh WiFi System, Tri-Band. Available online: https://www.linksys.com/whw0303---tri-band-intelligent-mesh-wifi-5-system-3-pack/WHW0303.html (accessed on 1 July 2024).





| RTT List | RSSI List | ||||
|---|---|---|---|---|---|
| AP Name | Score | Position (x, y) | AP Name | Score | Position (x, y) |
| Linksys 2 | 0.1780 | (19.2, 4) | Google 2 | 0.1638 | (19.2, 8) |
| Google 4 | 0.1653 | (19.2, 0) | Google 3 | 0.1541 | (0, 0) |
| Google 2 | 0.1509 | (19.2, 8) | Linksys 2 | 0.1491 | (19.2, 4) |
| Google 3 | 0.1422 | (0, 0) | Google 4 | 0.1454 | (19.2, 0) |
| Linksys 1 | 0.1276 | (9.6, 8) | Google 1 | 0.1384 | (0, 8) |
| Linksys 3 | 0.1210 | (9.6, 0) | Linksys 1 | 0.1277 | (9.6, 8) |
| Google 1 | 0.1150 | (0, 8) | Linksys 3 | 0.1214 | (9.6, 0) |
| k | Google 3 | Google 4 | Linksys 2 | Linksys 3 | Google 1 | Google 2 | Linksys 1 | |
|---|---|---|---|---|---|---|---|---|
| 2 | 57.80% | 42.20% | - | - | - | - | - | 100% |
| 4 | 25.88% | 15.96% | 24.12% | 34.04% | - | - | - | 100% |
| 5 | 16.16% | 15.96% | 24.12% | 27.92% | 15.84% | - | - | 100% |
| 7 | 15.96% | 25.96% | 12.08% | 24.00% | - | 22.00% | - | 100% |
| k | Simultaneous User Devices | Maximum | Difference (%) |
|---|---|---|---|
| 2 | 52 | 60 | 13.33% |
| 4 | 88 | 120 | 26.66% |
| 5 | 107 | 150 | 28.66% |
| 7 | 116 | 210 | 44.76% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez Diaz, N.; Zola, E.; Martin-Escalona, I. On the Integration of Standard Deviation and Clustering to Promote Scalable and Precise Wi-Fi Round-Trip Time Positioning. Technologies 2024, 12, 172. https://doi.org/10.3390/technologies12100172
Gonzalez Diaz N, Zola E, Martin-Escalona I. On the Integration of Standard Deviation and Clustering to Promote Scalable and Precise Wi-Fi Round-Trip Time Positioning. Technologies. 2024; 12(10):172. https://doi.org/10.3390/technologies12100172
Chicago/Turabian StyleGonzalez Diaz, Nestor, Enrica Zola, and Israel Martin-Escalona. 2024. "On the Integration of Standard Deviation and Clustering to Promote Scalable and Precise Wi-Fi Round-Trip Time Positioning" Technologies 12, no. 10: 172. https://doi.org/10.3390/technologies12100172
APA StyleGonzalez Diaz, N., Zola, E., & Martin-Escalona, I. (2024). On the Integration of Standard Deviation and Clustering to Promote Scalable and Precise Wi-Fi Round-Trip Time Positioning. Technologies, 12(10), 172. https://doi.org/10.3390/technologies12100172






