Revisiting Probabilistic Latent Semantic Analysis: Extensions, Challenges and Insights
Abstract
1. Introduction
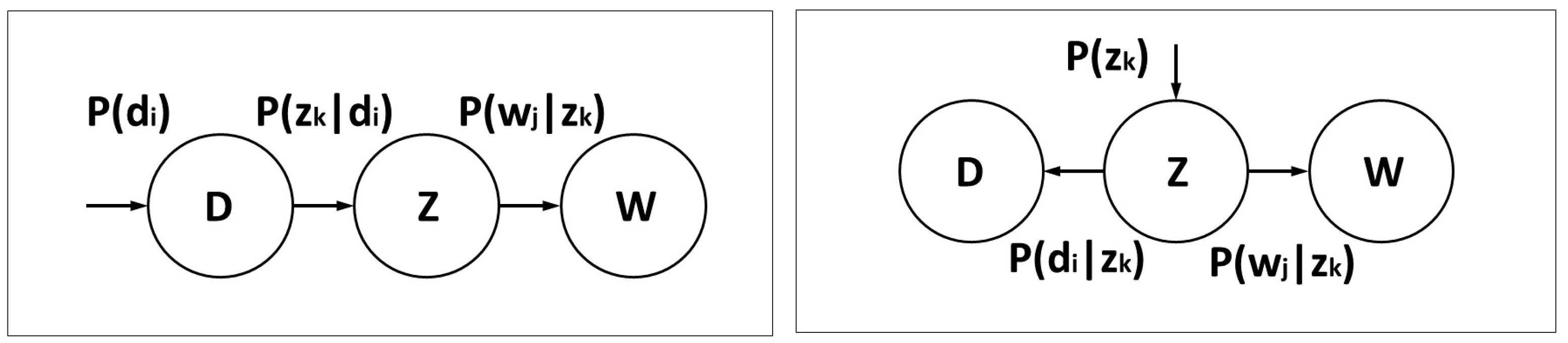
2. The Method: PLSA Formulas
| Aspect 1 | Aspect 2 | Aspect 3 | Aspect 4 |
| imag | video | region | speaker |
| SEGMENT | sequenc | contour | speech |
| color | motion | boundari | recogni |
| tissu | frame | descript | signal |
| Aspect1 | scene | imag | train |
| brain | SEGMENT | SEGMENT | hmm |
| slice | shot | precis | sourc |
| cluster | imag | estim | speakerindepend |
| mri | cluster | pixel | SEGMENT |
| algorithm | visual | paramet | sound |
3. Criticism: LDA and Reformulations
3.1. Latent Dirichlet Allocation
3.2. Other Formulations
3.2.1. Probabilities for Unseen Documents
3.2.2. Extension to Continuous Data
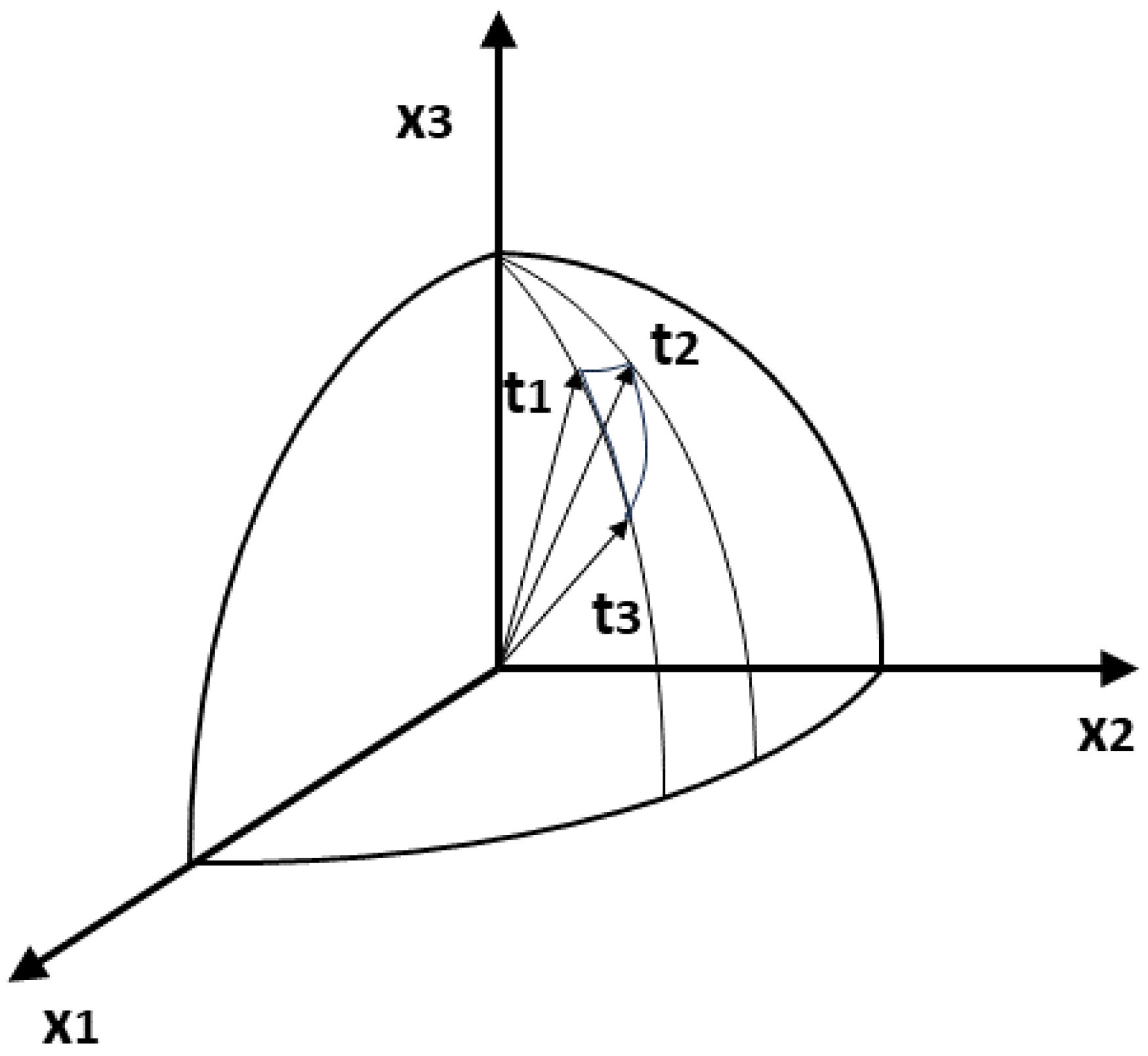
3.2.3. Tensorial Approach
3.2.4. Overfitting
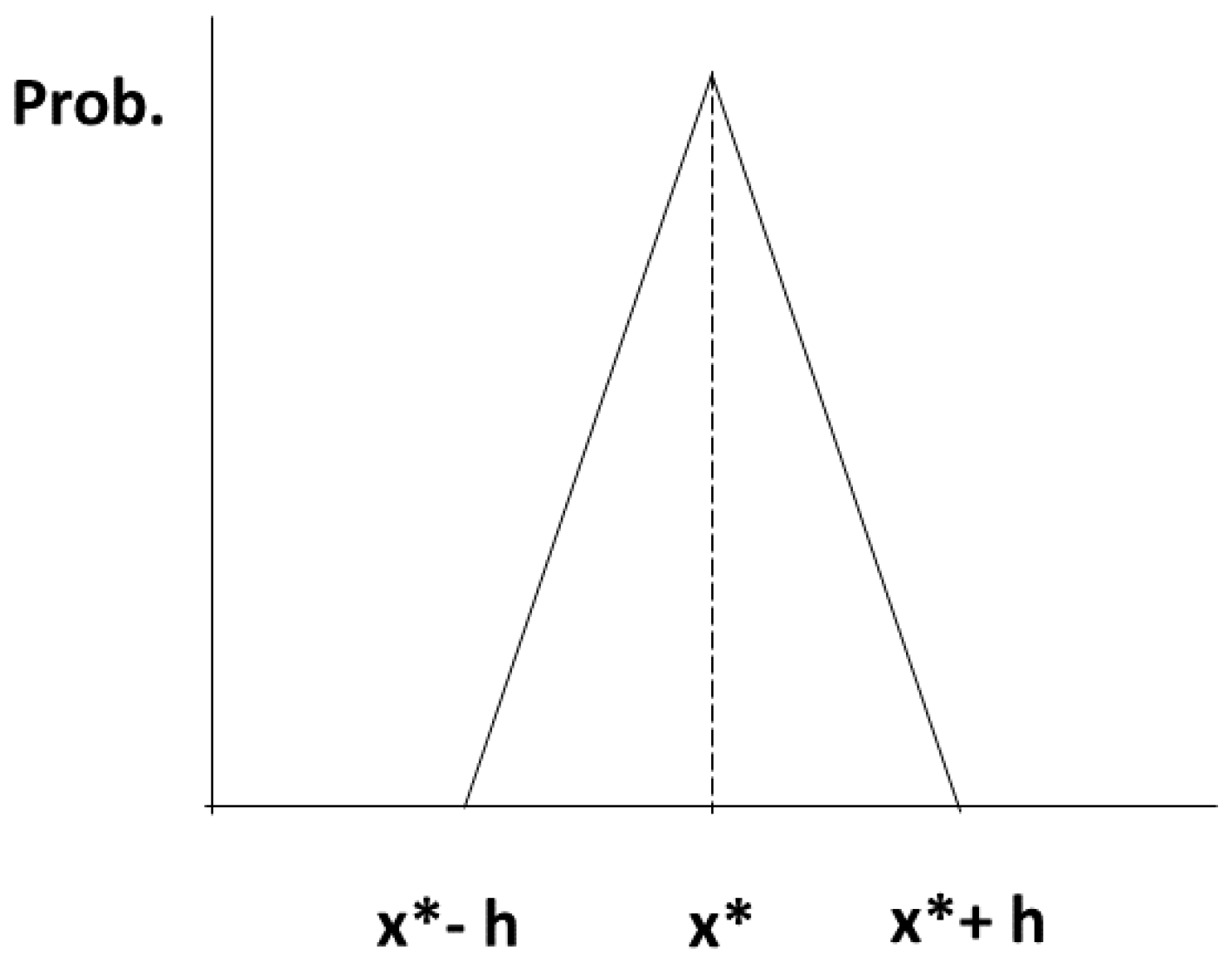
3.2.5. Discrete and Continuous Variables Case Equivalence
3.2.6. Inference
3.3. Extensions Significance
4. The Landscape of Applications
4.1. Engineering
4.2. Computer Science
4.3. Semantic Image Analysis
4.4. Life Sciences
4.5. Fundamental Sciences
4.6. Other Applications
5. NMF Point of View
6. Extensions
6.1. Kernelization
6.2. Principal Component Analysis
6.3. Clustering
6.4. Information Theory Interpretation
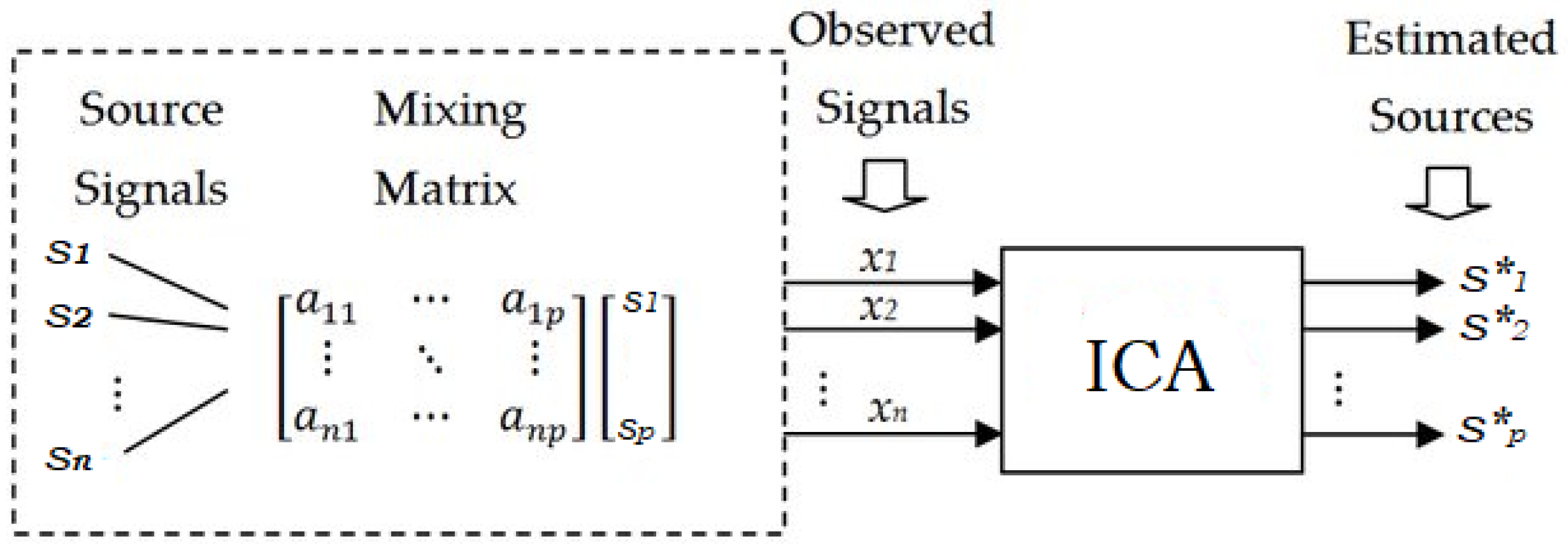
6.5. Independent Component Analysis and Blind Source Separation
6.6. Transfer Learning
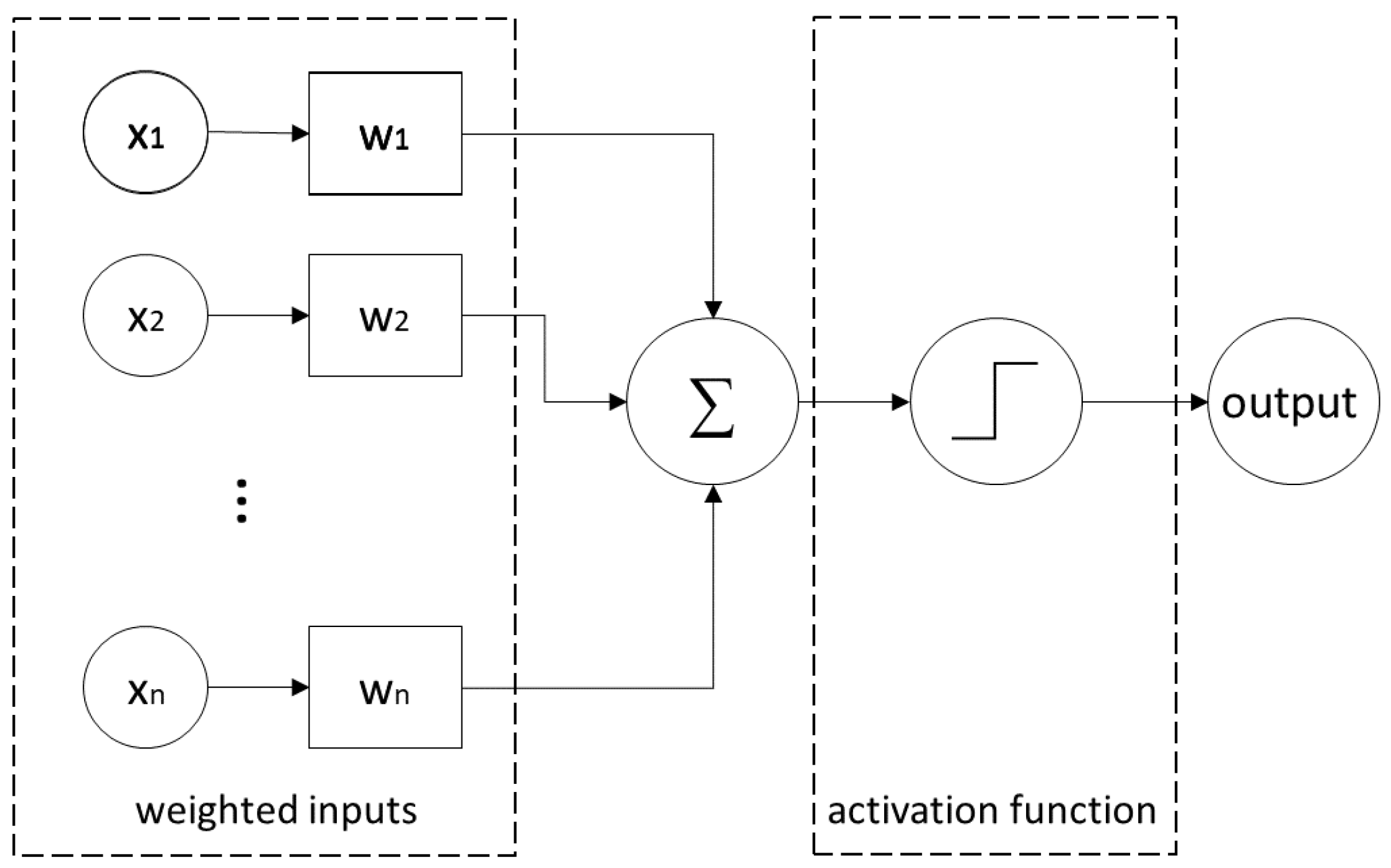
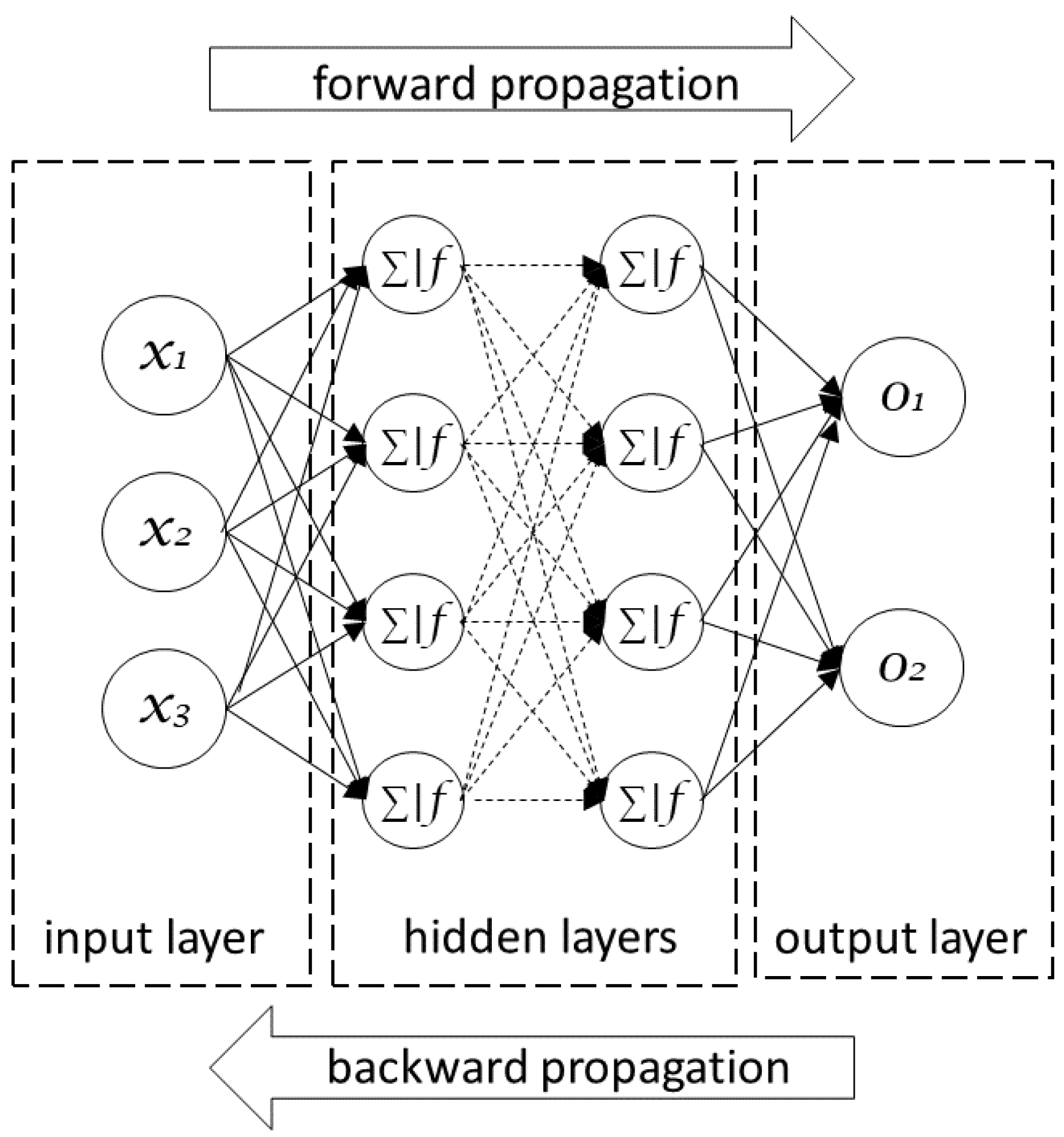
6.7. Neuronal Networks
6.8. Open Questions
7. PLSA Processing Steps and State-of-the-Art Solutions
7.1. Algorithm Initialization
7.2. Algorithms Based on Expectation–Maximization Improvement
7.2.1. Tempered EM
7.2.2. Sparse PLSA
7.2.3. Incremental PLSA
7.3. Use of Computational Techniques
7.4. Open Questions
8. Future Work
9. Discussion
10. Conclusions
Funding
Conflicts of Interest
References
- Hofmann, T. Probabilistic latent semantic indexing. In Proceedings of the 22nd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Berkeley, CA, USA, 15–19 August 1999. [Google Scholar]
- Hofmann, T. Probabilistic latent semantic analysis. In Proceedings of the Uncertainty in Artificial Intelligence, Eindhoven, The Netherlands, 1–5 August 1999. [Google Scholar]
- Hofmann, T. Unsupervised learning by probabilistic latent semantic analysis. In Machine Learning; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Deerwester, S.; Dumais, S.T.; Furnas, G.W.; Landauer, T.K.; Harshman, R. Indexing by latent semantic analysis. J. Am. Soc. Inf. Sci. 1990, 41, 391–407. [Google Scholar] [CrossRef]
- Saul, L.; Pereira, F. Aggregate and mixed-order Markov models for statistical language processing. arXiv 1997, arXiv:cmp-lg/9706007. [Google Scholar]
- Barde, B.V.; Bainwad, A.M. An overview of topic modeling methods and tools. In Proceedings of the 2017 International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 15–16 June 2017; pp. 745–750. [Google Scholar]
- Ibrahim, R.; Elbagoury, A.; Kamel, M.S.; Karray, F. Tools and approaches for topic detection from Twitter streams: Survey. Knowl. Inf. Syst. 2018, 54, 511–539. [Google Scholar] [CrossRef]
- Tian, D. Research on PLSA model based semantic image analysis: A systematic review. J. Inf. Hiding Multimed. Signal Process. 2018, 9, 1099–1113. [Google Scholar]
- Brants, T. Test data likelihood for PLSA models. Inf. Retr. 2005, 8, 181–196. [Google Scholar] [CrossRef]
- Masseroli, M.; Chicco, D.; Pinoli, P. Probabilistic latent semantic analysis for prediction of gene ontology annotations. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Hofmann, T. Collaborative filtering via gaussian probabilistic latent semantic analysis. In Proceedings of the 26th Annual International ACM SIGIR Conference on Research and Development in Informaion Retrieval, Toronto, ON, USA, 28 July–1 August 2003; pp. 259–266. [Google Scholar]
- Figuera, P.; García Bringas, P. Non-Parametric Nonnegative Matrix Factorization Fisher Kernel. SSRN 2023, 4585853. [Google Scholar] [CrossRef]
- Tar, P.D.; Thacker, N.A.; Deepaisarn, S.; O’Connor, J.; McMahon, A. A reformulation of pLSA for uncertainty estimation and hypothesis testing in bio-imaging. Bioinformatics 2020, 36, 4080–4087. [Google Scholar] [CrossRef]
- Gaussier, E.; Goutte, C. Relation between PLSA and NMF and implications. In Proceedings of the 28th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR’05), Virtual, 11–15 July 2005. [Google Scholar]
- Ding, C.; He, X.; Simon, H.D. On the equivalence of nonnegative matrix factorization and spectral clustering. In Proceedings of the 2005 SIAM international conference on data mining (SIAM), Newport Beach, CA, USA, 21–23 April 2005; pp. 606–610. [Google Scholar]
- Figuera, P.; García Bringas, P. On the Probabilistic Latent Semantic Analysis Generalization as the Singular Value Decomposition Probabilistic Image. J. Stat. Theory Appl. 2020, 19, 286–296. [Google Scholar]
- Hofmann, T. Learning the similarity of documents: An information-geometric approach to document retrieval and categorization. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 2000; pp. 914–920. [Google Scholar]
- Chappelier, J.C.; Eckard, E. Plsi: The true fisher kernel and beyond. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Bled, Slovenia, 7–11 September 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 195–210. [Google Scholar]
- Klingenberg, B.; Curry, J.; Dougherty, A. Non-negative matrix factorization: Ill-posedness and a geometric algorithm. Pattern Recognit. 2009, 42, 918–928. [Google Scholar] [CrossRef]
- Chaudhuri, A.R.; Murty, M.N. On the Relation Between K-means and PLSA. In Proceedings of the 2012 21st International Conference on Pattern Recognition, Tsukuba, Japan, 11–15 November 2012. [Google Scholar]
- Krithara, A.; Paliouras, G. TL-PLSA: Transfer learning between domains with different classes. In Proceedings of the 2013 IEEE 13th International Conference on Data Mining, Dallas, TX, USA, 7–10 December 2013; pp. 419–427. [Google Scholar]
- Ba, S. Discovering topics with neural topic models built from PLSA assumptions. arXiv 2019, arXiv:1911.10924. [Google Scholar]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent Dirichlet Allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Ding, C.H.; Li, T.; Jordan, M.I. Convex and semi-nonnegative matrix factorizations. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 32, 45–55. [Google Scholar] [CrossRef] [PubMed]
- Devarajan, K.; Wang, G.; Ebrahimi, N. A unified statistical approach to non-negative matrix factorization and probabilistic latent semantic indexing. In Machine Learning; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Vangara, R.; Bhattarai, M.; Skau, E.; Chennupati, G.; Djidjev, H.; Tierney, T.; Smith, J.P.; Stanev, V.G.; Alexandrov, B.S. Finding the number of latent topics with semantic non-negative matrix factorization. IEEE Access 2021, 9, 117217–117231. [Google Scholar] [CrossRef]
- Hong, L. A tutorial on probabilistic latent semantic analysis. arXiv 2012, arXiv:1212.3900. [Google Scholar]
- Dempster, A.; Laird, N.; Rubin, D. Maximum Likelihood from Incomplete Data via the EM Agorithm. J. R. Stat. Soc. Ser. Methodol. 1977, 39, 1–22. [Google Scholar]
- Jebara, T.; Pentland, A. On reversing Jensen’s inequality. In Proceedings of the Advances in Neural Information Processing Systems, San Francisco, CA, USA, 30 November–3 December 2001; pp. 231–237. [Google Scholar]
- Wu, C.J. On the convergence properties of the EM algorithm. Ann. Stat. 1983, 11, 95–103. [Google Scholar] [CrossRef]
- Boyles, R.A. On the convergence of the EM algorithm. J. R. Stat. Soc. Ser. (Methodol.) 1983, 45, 47–50. [Google Scholar] [CrossRef]
- Gupta, M.D. Additive non-negative matrix factorization for missing data. arXiv 2010, arXiv:1007.0380. [Google Scholar]
- Archambeau, C.; Lee, J.A.; Verleysen, M. On Convergence Problems of the EM Algorithm for Finite Gaussian Mixtures. In Proceedings of the European Symposium on Artificial Neural Networks (ESANN), Bruges, Belgium, 23–25 April 2003; Volume 3, pp. 99–106. [Google Scholar]
- Blei, D.M.; Lafferty, J.D. Dynamic topic models. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 113–120. [Google Scholar]
- Girolami, M.; Kabǿn, A. On an equivalence between PLSI and LDA. In Proceedings of the 26th Annual International ACM SIGIR Conference on Research and Development In Informaion Retrieval, Toronto, ON, Canada, 28 July–1 August 2003. [Google Scholar]
- Teh, Y.W.; Jordan, M.I.; Beal, M.J.; Blei, D.M. Hierarchical Dirichlet Processes. J. Am. Stat. Assoc. 2006, 101, 1566–1581. [Google Scholar] [CrossRef]
- Mimno, D.; Li, W.; McCallum, A. Mixtures of hierarchical topics with pachinko allocation. In Proceedings of the 24th International Conference on Machine Learning, Corvalis, OR, USA, 20–24 June 2007; pp. 633–640. [Google Scholar]
- Koltcov, S.; Ignatenko, V.; Terpilovskii, M.; Rosso, P. Analysis and tuning of hierarchical topic models based on Renyi entropy approach. arXiv 2021, arXiv:2101.07598. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Clustering, C.R.D. Algorithms and Applications; CRC Press Taylor and Francis Group: Boca Raton, FL, USA, 2014. [Google Scholar]
- Brants, T.; Chen, F.; Tsochantaridis, I. Topic-based document segmentation with probabilistic latent semantic analysis. In Proceedings of the Eleventh International Conference on Information and Knowledge Management, McLean, VA, USA, 4–9 November 2002; pp. 211–218. [Google Scholar]
- Brants, T.; Tsochantaridis, I.; Hofmann, T.; Chen, F. Computer Controlled Method for Performing Incremental Probabilistic Latent Semantic Analysis of Documents, Involves Performing Incremental Addition of New Term to Trained Probabilistic Latent Semantic Analysis Model. U.S. Patent Number US2006112128-A1, 14 April 2006. [Google Scholar]
- Zhuang, L.; She, L.; Jiang, Y.; Tang, K.; Yu, N. Image classification via semi-supervised pLSA. In Proceedings of the 2009 Fifth International Conference on Image and Graphics, Xi’an, China, 20–23 September 2009; pp. 205–208. [Google Scholar]
- Niu, L.; Shi, Y. Semi-supervised plsa for document clustering. In Proceedings of the 2010 IEEE International Conference on Data Mining Workshops, Sydney, Australia, 13 December 2010; pp. 1196–1203. [Google Scholar]
- Bosch, A.; Zisserman, A.; Muñoz, X. Scene classification via pLSA. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 517–530. [Google Scholar]
- Hörster, E.; Lienhart, R.; Slaney, M. Continuous visual vocabulary modelsfor plsa-based scene recognition. In Proceedings of the 2008 International Conference on Content-Based Image and Video Retrieval, Niagara Falls, ON, Canada, 7–9 July 2008; pp. 319–328. [Google Scholar]
- Li, Z.; Shi, Z.; Liu, X.; Shi, Z. Modeling continuous visual features for semantic image annotation and retrieval. Pattern Recognit. Lett. 2011, 32, 516–523. [Google Scholar] [CrossRef]
- Ma, H.; King, I.; Lyu, M.R. Effective missing data prediction for collaborative filtering. In Proceedings of the 30th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Amsterdam, The Netherlands, 23–27 July 2007; pp. 39–46. [Google Scholar]
- Tian, D. Extended Probabilistic Latent Semantic Analysis for Automatic Image Annotation. J. Inf. Hiding Multim. Signal Process. 2017, 8, 903–915. [Google Scholar]
- Shashua, A.; Hazan, T. Non-negative tensor factorization with applications to statistics and computer vision. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 792–799. [Google Scholar]
- Peng, W.; Li, T. On the equivalence between nonnegative tensor factorization and tensorial probabilistic latent semantic analysis. Appl. Intell. 2011, 35, 285–295. [Google Scholar] [CrossRef]
- Harshman, R.A. Foundations of the PARAFAC Procedure: Models and Conditions for an Explanatory Multimodal Factor Analysis; University of California: Los Angeles, CA, USA, 1970. [Google Scholar]
- Balažević, I.; Allen, C.; Hospedales, T.M. Tucker: Tensor factorization for knowledge graph completion. arXiv 2019, arXiv:1901.09590. [Google Scholar]
- Yoo, J.; Choi, S. Probabilistic matrix tri-factorization. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 1553–1556. [Google Scholar]
- Sun, L.; Axhausen, K.W. Understanding urban mobility patterns with a probabilistic tensor factorization framework. Transp. Res. Part B Methodol. 2016, 91, 511–524. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, S.; Sun, L.; Du, W.; Cao, X. Characterizing flight delay profiles with a tensor factorization framework. Engineering 2021, 7, 465–472. [Google Scholar] [CrossRef]
- Anisimov, A.; Marchenko, O.; Taranukha, V.; Vozniuk, T. Development of a semantic and syntactic model of natural language by means of non-negative matrix and tensor factorization. In Proceedings of the Text, Speech and Dialogue: 17th International Conference (TSD 2014), Brno, Czech Republic, 8–12 September 2014; Proceedings 17. Springer: Berlin/Heidelberg, Germany, 2014; pp. 324–335. [Google Scholar]
- Cichocki, A.; Zdunek, R.; Amari, S.I. Nonnegative Matrix and Tensor Factorizations; John Willey and Sons Ltd.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Rodner, E.; Denzler, J. Randomized probabilistic latent semantic analysis for scene recognition. In Proceedings of the Iberoamerican Congress on Pattern Recognition, Guadalajara, Mexico, 15–18 November 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 945–953. [Google Scholar]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Kokonendji, C.C.; Senga Kiesse, T.; Zocchi, S.S. Discrete triangular distributions and non-parametric estimation for probability mass function. J. Nonparametric Stat. 2007, 19, 241–254. [Google Scholar] [CrossRef]
- Senga Kiesse, T.; Cuny, H.E. Discrete triangular associated kernel and bandwidth choices in semiparametric estimation for count data. J. Stat. Comput. Simul. 2014, 84, 1813–1829. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Nevzorov, V.B. A Primer on Statistical Distributions; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Bowman, A.W.; Azzalini, A. Applied Smoothing Techniques for Data Analysis: The Kernel Approach with S-Plus Illustrations; Oxford University Press: Oxford, UK, 1997; Volume 18. [Google Scholar]
- Tao, Z.; Qi, Z.; Dequn, L. A Novel Probabilistic Latent Semantic Analysis Based Image Blur Metric. In Proceedings of the 2014 IEEE 12th International Conference on Dependable, Autonomic and Secure Computing, Dalian, China, 24–27 August 2014; pp. 310–315. [Google Scholar]
- Murphy, L.; Sibley, G. Incremental unsupervised topological place discovery. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 1312–1318. [Google Scholar]
- Wang, X.; Geng, T.; Elsayed, Y.; Ranzani, T.; Saaj, C.; Lekakou, C. A new coefficient-adaptive orthonormal basis function model structure for identifying a class of pneumatic soft actuators. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 530–535. [Google Scholar] [CrossRef]
- Barbu, C.; Simina, M. A probabilistic information filtering using the profile dynamics. In Proceedings of the SMC’03 Conference Proceedings. 2003 IEEE International Conference on Systems, Man and Cybernetics. Conference Theme-System Security and Assurance (Cat. No. 03CH37483), Washington, DC, USA, 8 October 2003; Volume 5, pp. 4595–4600. [Google Scholar]
- Gangatharan, N.; Reddy, P. The PLSI method of stabilizing two-dimensional nonsymmetric half-plane recursive digital filters. EURASIP J. Adv. Signal Process. 2003, 2003, 381073. [Google Scholar] [CrossRef]
- Bai, S.; Huang, C.L.; Tan, Y.K.; Ma, B. Language models learning for domain-specific natural language user interaction. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guilin, China, 19–23 December 2009; pp. 2480–2485. [Google Scholar] [CrossRef]
- Kim, S.; Georgiou, P.; Narayanan, S. Latent acoustic topic models for unstructured audio classification. APSIPA Trans. Signal Inf. Process. 2012, 1, e6. [Google Scholar] [CrossRef]
- Nakano, T.; Yoshii, K.; Goto, M. Vocal timbre analysis using latent Dirichlet allocation and cross-gender vocal timbre similarity. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 5202–5206. [Google Scholar]
- Leng, Y.; Zhou, N.; Sun, C.; Xu, X.; Yuan, Q.; Cheng, C.; Liu, Y.; Li, D. Audio scene recognition based on audio events and topic model. Knowl.-Based Syst. 2017, 125, 1–12. [Google Scholar] [CrossRef]
- Rani, S.; Kumar, M. Topic modeling and its applications in materials science and engineering. Mater. Today Proc. 2021, 45, 5591–5596. [Google Scholar] [CrossRef]
- Eichel, A.; Schlipf, H.; Walde, H.; Schulte, S. Made of Steel? Learning Plausible Materials for Components in the Vehicle Repair Domain. arXiv 2023, arXiv:2304.14745. [Google Scholar]
- Alqasir, A.; Kamal, A.E. Power Management in HetNets with Mobility Prediction and Harvested Energy. In Proceedings of the ICC 2020-2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Ke, X.; Luo, H. Using LSA and PLSA for text quality analysis. In Proceedings of the 2015 International Conference on Electronic Science and Automation Control, Zhengzhou, China, 15–16 August 2015; Atlantis Press: Amsterdam, The Netherlands, 2015; pp. 289–291. [Google Scholar]
- Wang, S.; Schuurmans, D.; Peng, F.; Zhao, Y. Combining statistical language models via the latent maximum entropy principle. Mach. Learn. 2005, 60, 229–250. [Google Scholar] [CrossRef]
- Monay, F.; Gatica-Perez, D. PLSA-based image auto-annotation: Constraining the latent space. In Proceedings of the 12th Annual ACM International Conference on Multimedia, New York, NY, USA, 10–16 October 2004; pp. 348–351. [Google Scholar]
- Shen, C.; Li, T.; Ding, C. Integrating clustering and multi-document summarization by bi-mixture probabilistic latent semantic analysis (plsa) with sentence bases. In Proceedings of the AAAI Conference on Artificial Intelligence, Menlo Park, CA, USA, 12–17 February 2011; Volume 25, pp. 914–920. [Google Scholar]
- Zhang, X.; Li, H.; Liang, W.; Luo, J. Multi-type co-clustering of general heterogeneous information networks via nonnegative matrix tri-factorization. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016; pp. 1353–1358. [Google Scholar]
- Hsieh, C.H.; Huang, C.L.; Wu, C.H. Spoken document summarization using topic-related corpus and semantic dependency grammar. In Proceedings of the 2004 International Symposium on Chinese Spoken Language Processing, Hong Kong, China, 15–18 December 2004; pp. 333–336. [Google Scholar]
- Madsen, R.E.; Larsen, J.; Hansen, L.K. Part-of-speech enhanced context recognition. In Proceedings of the 2004 14th IEEE Signal Processing Society Workshop Machine Learning for Signal Processing, Sao Luis, Brazil, 29 September–1 October 2004; pp. 635–643. [Google Scholar]
- Tsai, F.S.; Chan, K.L. Detecting cyber security threats in weblogs using probabilistic models. In Proceedings of the Pacific-Asia Workshop on Intelligence and Security Informatics, Chengdu, China, 11–12 April 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 46–57. [Google Scholar]
- Kagie, M.; Van Der Loos, M.; Van Wezel, M. Including item characteristics in the probabilistic latent semantic analysis model for collaborative filtering. Ai Commun. 2009, 22, 249–265. [Google Scholar] [CrossRef]
- Farhadloo, M.; Rolland, E. Fundamentals of sentiment analysis and its applications. In Sentiment Analysis and Ontology Engineering; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–24. [Google Scholar]
- Xie, X.; Ge, S.; Hu, F.; Xie, M.; Jiang, N. An improved algorithm for sentiment analysis based on maximum entropy. Soft Comput. 2019, 23, 599–611. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, Y.; Wang, Y.; Wang, G. A novel multimodal retrieval model based on ELM. Neurocomputing 2018, 277, 65–77. [Google Scholar] [CrossRef]
- Sun, Y.; Yu, Y.; Han, J. Ranking-based clustering of heterogeneous information networks with star network schema. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 797–806. [Google Scholar]
- Deng, H.; Han, J.; Zhao, B.; Yu, Y.; Lin, C.X. Probabilistic topic models with biased propagation on heterogeneous information networks. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011; pp. 1271–1279. [Google Scholar]
- Yan, M.; Fu, Y.; Zhang, X.; Yang, D.; Xu, L.; Kymer, J.D. Automatically classifying software changes via discriminative topic model: Supporting multi-category and cross-project. J. Syst. Softw. 2016, 113, 296–308. [Google Scholar] [CrossRef]
- Sandhu, P.S.; Singh, H. Software reusability model for procedure based domain-specific software components. Int. J. Softw. Eng. Knowl. Eng. 2008, 18, 1063–1081. [Google Scholar] [CrossRef]
- Mehta, B.; Hofmann, T. A Survey of Attack-Resistant Collaborative Filtering Algorithms. IEEE Data Eng. Bull. 2008, 31, 14–22. [Google Scholar]
- Burke, R.; O’Mahony, M.P.; Hurley, N.J. Robust collaborative recommendation. In Recommender Systems Handbook; Springer: Berlin/Heidelberg, Germany, 2015; pp. 961–995. [Google Scholar]
- Hu, R.; Pan, S.; Jiang, J.; Long, G. Graph ladder networks for network classification. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 2103–2106. [Google Scholar]
- Monay, F.; Gatica-Perez, D. On image auto-annotation with latent space models. In Proceedings of the Eleventh ACM International Conference on Multimedia, Berkeley, CA, USA, 2–8 November 2003; pp. 275–278. [Google Scholar]
- Lienhart, R.; Hauke, R. Filtering adult image content with topic models. In Proceedings of the 2009 IEEE International Conference on Multimedia and Expo, New York, NY, USA, 28 June–3 July 2009; pp. 1472–1475. [Google Scholar]
- Jacob, G.M.; Das, S. Moving object segmentation for jittery videos, by clustering of stabilized latent trajectories. Image Vis. Comput. 2017, 64, 10–22. [Google Scholar] [CrossRef]
- Shah-Hosseini, A.; Knapp, G.M. Semantic image retrieval based on probabilistic latent semantic analysis. In Proceedings of the 14th ACM International Conference on Multimedia, Santa Barbara, CA, USA, 23–27 October 2006; pp. 703–706. [Google Scholar]
- Foncubierta-Rodríguez, A.; García Seco de Herrera, A.; Müller, H. Medical image retrieval using bag of meaningful visual words: Unsupervised visual vocabulary pruning with PLSA. In Proceedings of the 1st ACM International Workshop on Multimedia Indexing and Information Retrieval for Healthcare, Barcelona, Spain, 22 October 2023; pp. 75–82. [Google Scholar]
- Cao, Y.; Steffey, S.; He, J.; Xiao, D.; Tao, C.; Chen, P.; Müller, H. Medical image retrieval: A multimodal approach. Cancer Inform. 2014, 13, CIN–S14053. [Google Scholar] [CrossRef] [PubMed]
- Fasel, B.; Monay, F.; Gatica-Perez, D. Latent semantic analysis of facial action codes for automatic facial expression recognition. In Proceedings of the 6th ACM SIGMM International Workshop on Multimedia Information Retrieval, New York, NY, USA, 15–16 October 2004; pp. 181–188. [Google Scholar]
- Jiang, Y.; Liu, J.; Li, Z.; Li, P.; Lu, H. Co-regularized plsa for multi-view clustering. In Proceedings of the Asian Conference on Computer Vision, Daejeon, Republic of Korea, 5–9 November 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 202–213. [Google Scholar]
- Quelhas, P.; Monay, F.; Odobez, J.M.; Gatica-Perez, D.; Tuytelaars, T.; Van Gool, L. Modeling scenes with local descriptors and latent aspects. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; Volume 1, pp. 883–890. [Google Scholar]
- Zhu, S. Pain expression recognition based on pLSA model. Sci. World J. 2014, 2014, 736106. [Google Scholar] [CrossRef] [PubMed]
- Haloi, M. A novel plsa based traffic signs classification system. arXiv 2015, arXiv:1503.06643. [Google Scholar]
- Chang, J.M.; Su, E.C.Y.; Lo, A.; Chiu, H.S.; Sung, T.Y.; Hsu, W.L. PSLDoc: Protein subcellular localization prediction based on gapped-dipeptides and probabilistic latent semantic analysis. Proteins Struct. Funct. Bioinform. 2008, 72, 693–710. [Google Scholar] [CrossRef] [PubMed]
- Su, E.C.Y.; Chang, J.M.; Cheng, C.W.; Sung, T.Y.; Hsu, W.L. Prediction of nuclear proteins using nuclear translocation signals proposed by probabilistic latent semantic indexing. In BMC Bioinformatics; BioMed Central: London, UK, 2012; Volume 13, pp. 1–10. [Google Scholar]
- Cheng, X.; Shuai, C.; Liu, J.; Wang, J.; Liu, Y.; Li, W.; Shuai, J. Topic modelling of ecology, environment and poverty nexus: An integrated framework. Agric. Ecosyst. Environ. 2018, 267, 1–14. [Google Scholar] [CrossRef]
- Pulido, A.; Rueda, A.; Romero, E. Extracting regional brain patterns for classification of neurodegenerative diseases. In Proceedings of the IX International Seminar on Medical Information Processing and Analysis, Mexico City, Mexico, 11 November 2013; Brieva, J., Escalante-Ramírez, B., Eds.; International Society for Optics and Photonics SPIE: Bellingham, WA, USA, 2013; Volume 8922, p. 892208. [Google Scholar] [CrossRef]
- Du, X.; Qian, F.; Ou, X. 3D seismic waveform classification study based on high-level semantic feature. In Proceedings of the 2015 1st International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM), Barcelona, Spain, 28–30 April 2015; pp. 1–5. [Google Scholar]
- Wang, X.; Geng, T.; Elsayed, Y.; Saaj, C.; Lekakou, C. A unified system identification approach for a class of pneumatically-driven soft actuators. Robot. Auton. Syst. 2015, 63, 136–149. [Google Scholar] [CrossRef]
- Kumar, K. Probabilistic latent semantic analysis of composite excitation-emission matrix fluorescence spectra of multicomponent system. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 239, 118518. [Google Scholar] [CrossRef]
- Nijs, M.; Smets, T.; Waelkens, E.; De Moor, B. A Mathematical Comparison of Non-negative Matrix Factorization-Related Methods with Practical Implications for the Analysis of Mass Spectrometry Imaging Data. Rapid Commun. Mass Spectrom. 2021, 35, e9181. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Y.; Wang, J.; Cambria, E.; Li, X. Real-time video emotion recognition based on reinforcement learning and domain knowledge. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 1034–1047. [Google Scholar] [CrossRef]
- Shashanka, M.; Raj, B.; Smaragdis, P. Probabilistic latent variable models as nonnegative factorizations. Comput. Intell. Neurosci. 2008, 2008, 947438. [Google Scholar] [CrossRef] [PubMed]
- Cajori, F. A History of Mathematical Notations; Courier Corporation: North Chelmsford, MA, USA, 1993; Volume 1. [Google Scholar]
- Biletch, B.D.; Yu, H.; Kay, K.R. An Analysis of Mathematical Notations: For Better or for Worse; Worcester Polytechnic Institute: Worcester, MA, USA, 2015. [Google Scholar]
- Cayley, A. Remarques sur la Notation des Fonctions Algébriques; Worcester Polytechnic Institute: Worcester, MA, USA, 1855. [Google Scholar]
- Paatero, P.; Tapper, U. Positive matrix factorization: A non-negative factor model with optimal utilization of error estimates of data values. Environmetrics 1994, 5, 111–126. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Chen, J. The nonnegative rank factorizations of nonnegative matrices. Linear Algebra Its Appl. 1984, 62, 207–217. [Google Scholar] [CrossRef]
- Zhang, X.D. Matrix Analysis and Applications; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Beltrami, E. Sulle funzioni bilineari. G. Mat. Uso Degli Stud. Delle Univ. 1873, 11, 98–106. [Google Scholar]
- Martin, C.D.; Porter, M.A. The extraordinary SVD. Am. Math. Mon. 2012, 119, 838–851. [Google Scholar] [CrossRef]
- Lin, B.L. Every waking moment Ky Fan (1914–2010). In Notices of the AMS; American Mathematical Society: Providence, RI, USA, 2010; Volume 57. [Google Scholar]
- Moslehian, M.S. Ky fan inequalities. Linear Multilinear Algebra 2012, 60, 1313–1325. [Google Scholar] [CrossRef]
- Higham, N.J.; Lin, L. Matrix functions: A short course. Matrix Funct. Matrix Equ. 2013, 19, 1–27. [Google Scholar]
- Eckart, C.; Young, G. A principal axis transformation for non-Hermitian matrices. Bull. Am. Math. Soc. 1939, 45, 118–121. [Google Scholar] [CrossRef]
- Zhang, Z. The Singular Value Decomposition, Applications and Beyond. arXiv 2015, arXiv:1510.08532. [Google Scholar]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Ding, C.; Li, T.; Peng, W. On the equivalence between non-negative matrix factorization and probabilistic latent semantic indexing. Comput. Stat. Data Anal. 2008, 52, 3913–3927. [Google Scholar] [CrossRef]
- Mnih, A.; Salakhutdinov, R.R. Probabilistic matrix factorization. Adv. Neural Inf. Process. Syst. 2007, 20, 1257–1264. [Google Scholar]
- Khuri, A.I. Advanced Calculus with Applications in Statistics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 486. [Google Scholar]
- Amari, S.I. Information geometry of the EM and em algorithms for neural networks. Neural Netw. 1995, 8, 1379–1408. [Google Scholar] [CrossRef]
- Zhang, L.; Xia, Y. Text Study of Reader Magazine in the Context of Big Data. Appl. Math. Nonlinear Sci. 2023. [Google Scholar] [CrossRef]
- Hofmann, T.; Schölkopf, B.; Smola, A.J. Kernel methods in machine learning. Ann. Stat. 2008, 36, 1171–1220. [Google Scholar] [CrossRef]
- Tsuda, K.; Akaho, S.; Kawanabe, M.; Müller, K.R. Asymptotic properties of the Fisher kernel. Neural Comput. 2004, 16, 115–137. [Google Scholar] [CrossRef]
- Wang, X.; Chang, M.C.; Wang, L.; Lyu, S. Efficient algorithms for graph regularized PLSA for probabilistic topic modeling. Pattern Recognit. 2019, 86, 236–247. [Google Scholar] [CrossRef]
- Shamna, P.; Govindan, V.; Abdul Nazeer, K. Content based medical image retrieval using topic and location model. J. Biomed. Inform. 2019, 91, 103112. [Google Scholar] [CrossRef]
- Bishop, C.M. Bayesian pca. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 8–14 December 1999; pp. 382–388. [Google Scholar]
- Kim, D.; Lee, I.B. Process monitoring based on probabilistic PCA. Chemom. Intell. Lab. Syst. 2003, 67, 109–123. [Google Scholar] [CrossRef]
- Casalino, G.; Del Buono, N.; Mencar, C. Nonnegative matrix factorizations for intelligent data analysis. In Non-Negative Matrix Factorization Techniques; Springer: Berlin/Heidelberg, Germany, 2016; pp. 49–74. [Google Scholar]
- Schachtner, R.; Pöppel, G.; Tomé, A.; Lang, E. From binary NMF to variational bayes NMF: A probabilistic approach. In Non-Negative Matrix Factorization Techniques; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–48. [Google Scholar]
- Tayalı, H.A.; Tolun, S. Dimension reduction in mean-variance portfolio optimization. Expert Syst. Appl. 2018, 92, 161–169. [Google Scholar] [CrossRef]
- Dougherty, E.R.; Brun, M. A probabilistic theory of clustering. Pattern Recognit. 2004, 37, 917–925. [Google Scholar] [CrossRef]
- Bailey, J. Alternative clustering analysis: A review. In Data Clustering; Taylor and Francis: Abingdon, UK, 2018; pp. 535–550. [Google Scholar]
- Shashanka, M. Simplex decompositions for real-valued datasets. In Proceedings of the 2009 IEEE International Workshop on Machine Learning for Signal Processing, Grenoble, France, 1–4 September 2009; pp. 1–6. [Google Scholar]
- Rao, C.R. Diversity and dissimilarity coefficients: A unified approach. Theor. Popul. Biol. 1982, 21, 24–43. [Google Scholar] [CrossRef]
- Rao, C.R. Diversity: Its measurement, decomposition, apportionment and analysis. Sankhyā Indian J. Stat. Ser. A 1982, 44, 1–22. [Google Scholar]
- Rao, C.R. Differential metrics in probability spaces. Differ. Geom. Stat. Inference 1987, 10, 217–240. [Google Scholar]
- Atkinson, C.; Mitchell, A.F. Rao’s distance measure. Sankhyā Indian J. Stat. Ser. A 1981, 43, 345–365. [Google Scholar]
- Sejdinovic, D.; Sriperumbudur, B.; Gretton, A.; Fukumizu, K. Equivalence of distance-based and RKHS-based statistics in hypothesis testing. Ann. Stat. 2013, 41, 2263–2291. [Google Scholar] [CrossRef]
- Uhler, C. Geometry of Maximum Likelihood Estimation in Gaussian Graphical Models; University of California: Berkeley, CA, USA, 2011. [Google Scholar]
- Amari, S.I. Information Geometry and Its Applications; Springer: Berlin/Heidelberg, Germany, 2016; Volume 194. [Google Scholar]
- Mika, D.; Budzik, G.; Jozwik, J. Single channel source separation with ICA-based time-frequency decomposition. Sensors 2020, 20, 2019. [Google Scholar] [CrossRef]
- Oja, E. Principal components, minor components, and linear neural networks. Neural Netw. 1992, 5, 927–935. [Google Scholar] [CrossRef]
- Chen, T.; Amari, S.I.; Lin, Q. A unified algorithm for principal and minor components extraction. Neural Netw. 1998, 11, 385–390. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.K.; Lv, J.C.; Yi, Z.; Huang, S. Adaptive multiple minor directions extraction in parallel using a PCA neural network. Theor. Comput. Sci. 2010, 411, 4200–4215. [Google Scholar] [CrossRef][Green Version]
- Cichocki, A.; Georgiev, P. Blind source separation algorithms with matrix constraints. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2003, 86, 522–531. [Google Scholar]
- Hanselmann, M.; Kirchner, M.; Renard, B.Y.; Amstalden, E.R.; Glunde, K.; Heeren, R.M.; Hamprecht, F.A. Concise representation of mass spectrometry images by probabilistic latent semantic analysis. Anal. Chem. 2008, 80, 9649–9658. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Vardhan, M. Aspect-Based Sentiment Analysis of Tweets Using Independent Component Analysis (ICA) and Probabilistic Latent Semantic Analysis (pLSA). In Advances in Data and Information Sciences: Proceedings of ICDIS 2017; Springer: Singapore, 2019; Volume 2, pp. 3–13. [Google Scholar]
- Chuanqi, T.; Sun, F.; Kong, T.; Zhang, W.; Yang, C.; Liu, C. A Survey on Deep Transfer Learning. arXiv 2018, arXiv:cs.LG/1808.01974. [Google Scholar]
- Bozinovski, S. Reminder of the first paper on transfer learning in neural networks, 1976. Informatica 2020, 44. [Google Scholar] [CrossRef]
- Zhao, R.; Mao, K. Supervised adaptive-transfer PLSA for cross-domain text classification. In Proceedings of the 2014 IEEE International Conference on Data Mining Workshop, Shenzhen, China, 14 December 2014; pp. 259–266. [Google Scholar]
- Carrera, D. Learning and adaptation to detect changes and anomalies in high-dimensional data. Special Topics in Information Technology; Springer: Berlin/Heidelberg, Germany, 2020; pp. 63–75. [Google Scholar]
- Yang, T.; Kumoi, G.; Yamashita, H.; Goto, M. Transfer learning based on probabilistic latent semantic analysis for analyzing purchase behavior considering customers’ membership stages. J. Jpn. Ind. Manag. Assoc. 2022, 73, 160–175. [Google Scholar]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef]
- Manly, B.F. Exponential data transformations. J. R. Stat. Soc. Ser. Stat. 1976, 25, 37–42. [Google Scholar] [CrossRef]
- Kyurkchiev, N.; Markov, S. Sigmoid Functions: Some Approximation and Modelling Aspects; LAP LAMBERT Academic Publishing: Saarbrucken, Germany, 2015; Volume 4. [Google Scholar]
- Widrow, B.; Hoff, M.E. Adaptive switching circuits. In Proceedings of the IRE WESCON Convention Record, New York, NY, USA, 19–26 August 1960; Volume 4, pp. 96–104. [Google Scholar]
- Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Graupe, D. Principles of Artificial Neural Networks; World Scientific: Singapore, 2013; Volume 7. [Google Scholar]
- Mirsky, L. An Introduction to Linear Algebra; Dover Publications Inc.: Mineola, NY, USA, 1990. [Google Scholar]
- Huang, K.; Sidiropoulos, N.D.; Swami, A. Non-Negative Matrix Factorization Revisited: Uniqueness and Algorithm for Symmetric Decomposition. IEEE Trans. Signal Process. 2014, 62, 211. [Google Scholar] [CrossRef]
- Wan, R.; Anh, V.N.; Mamitsuka, H. Efficient probabilistic latent semantic analysis through parallelization. In Proceedings of the Asia Information Retrieval Symposium, Sapporo, Japan, 21–23 October 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 432–443. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations. Johns Hopkins Studies in the Mathematical Sciences; Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, L.S.; Demmel, J.; Dongarra, J.; Du Croz, J.; Greenbaum, A.; Hammarling, S.; McKenney, A.; et al. LAPACK Users’ Guide; SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]
- Farahat, A.; Chen, F. Improving probabilistic latent semantic analysis with principal component analysis. In Proceedings of the 11th Conference of the European Chapter of the Association for Computational Linguistics, Trento, Italy, 3 April 2006. [Google Scholar]
- Zhang, Y.F.; Zhu, J.; Xiong, Z.Y. Improved text clustering algorithm of probabilistic latent with semantic analysis. J. Comput. Appl. 2011, 3, 674. [Google Scholar] [CrossRef]
- Ye, Y.; Gong, S.; Liu, C.; Zeng, J.; Jia, N.; Zhang, Y. Online belief propagation algorithm for probabilistic latent semantic analysis. Front. Comput. Sci. 2013, 7, 526–535. [Google Scholar] [CrossRef]
- Bottou, L. Online learning and stochastic approximations. On-Line Learn. Neural Netw. 1998, 17, 142. [Google Scholar]
- Zeng, J.; Liu, Z.Q.; Cao, X.Q. Fast online EM for big topic modeling. IEEE Trans. Knowl. Data Eng. 2015, 28, 675–688. [Google Scholar] [CrossRef]
- Shen, Y.; Guo, H. Research on high-performance English translation based on topic model. Digit. Commun. Netw. 2023, 9, 505–511. [Google Scholar] [CrossRef]
- Watanabe, M.; Yamaguchi, K. The EM Algorithm and Related Statistical Models; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Meng, X.L.; Van Dyk, D. The EM algorithm—An old folk-song sung to a fast new tune. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1997, 59, 511–567. [Google Scholar] [CrossRef]
- Roche, A. EM algorithm and variants: An informal tutorial. arXiv 2011, arXiv:1105.1476. [Google Scholar]
- Hinton, G.E.; Zemel, R.S. Autoencoders, minimum description length, and Helmholtz free energy. Adv. Neural Inf. Process. Syst. 1994, 6, 3–10. [Google Scholar]
- Neal, R.M.; Hinton, G.E. A view of the EM algorithm that justifies incremental, sparse, and other variants. In Learning in Graphical Models; Springer: Berlin/Heidelberg, Germany, 1998; pp. 355–368. [Google Scholar]
- Hazan, T.; Hardoon, R.; Shashua, A. Plsa for sparse arrays with Tsallis pseudo-additive divergence: Noise robustness and algorithm. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Kanzawa, Y. On Tsallis Entropy-Based and Bezdek-Type Fuzzy Latent Semantics Analysis. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 3685–3689. [Google Scholar]
- Xu, J.; Ye, G.; Wang, Y.; Herman, G.; Zhang, B.; Yang, J. Incremental EM for Probabilistic Latent Semantic Analysis on Human Action Recognition. In Proceedings of the 6th IEEE International Conference on Advanced Video and Signal Based Surveillance, Genoa, Italy, 2–4 September 2009. [Google Scholar] [CrossRef]
- Wu, H.; Wang, Y.; Cheng, X. Incremental probabilistic latent semantic analysis for automatic question recommendation. In Proceedings of the 2008 ACM Conference on Recommender Systems, Lausanne, Switzerland, 23–25 October 2008; pp. 99–106. [Google Scholar]
- Li, N.; Luo, W.; Yang, K.; Zhuang, F.; He, Q.; Shi, Z. Self-organizing weighted incremental probabilistic latent semantic analysis. Int. J. Mach. Learn. Cybern. 2018, 9, 1987–1998. [Google Scholar] [CrossRef]
- Bassiou, N.; Kotropoulos, C. Rplsa: A novel updating scheme for probabilistic latent semantic analysis. Comput. Speech Lang. 2011, 25, 741–760. [Google Scholar] [CrossRef]
- Asanovic, K.; Bodik, R.; Catanzaro, B.C.; Gebis, J.J.; Husbands, P.; Keutzer, K.; Patterson, D.A.; Plishker, W.L.; Shalf, J.; Williams, S.W.; et al. The Landscape of Parallel Computing Research: A View from Berkeley; University of California: Berkeley, CA, USA, 2006. [Google Scholar]
- Hong, C.; Chen, W.; Zheng, W.; Shan, J.; Chen, Y.; Zhang, Y. Parallelization and characterization of probabilistic latent semantic analysis. In Proceedings of the 2008 37th International Conference on Parallel Processing, Portland, OR, USA, 9–12 September 2008; pp. 628–635. [Google Scholar]
- Dean, J.; Ghemawat, S. MapReduce: Simplified data processing on large clusters. Commun. ACM 2008, 51, 107–113. [Google Scholar] [CrossRef]
- Jin, Y.; Gao, Y.; Shi, Y.; Shang, L.; Wang, R.; Yang, Y. P 2 LSA and P 2 LSA+: Two paralleled probabilistic latent semantic analysis algorithms based on the MapReduce model. In Proceedings of the International Conference on Intelligent Data Engineering and Automated Learning, Norwich, UK, 7–9 September 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 385–393. [Google Scholar]
- Grigoriev, D.V.; Chumichkin, A.A.; Khalyutin, S.P. Methodology for Scientific Publications Search Results Automated Structuring to Analyze the Level of Elaboration of Scientific and Technical Problems in the Aviation Industry. In Proceedings of the 2021 XVIII Technical Scientific Conference on Aviation Dedicated to the Memory of N.E. Zhukovsky (TSCZh), Moscow, Russia, 14–15 April 2021; pp. 24–29. [Google Scholar] [CrossRef]
- Kouassi, E.K.; Amagasa, T.; Kitagawa, H. Efficient probabilistic latent semantic indexing using graphics processing unit. Procedia Comput. Sci. 2011, 4, 382–391. [Google Scholar] [CrossRef][Green Version]
- Jaramago, J.A.G.; Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, A.; Plaza, J. GPU parallel implementation of dual-depth sparse probabilistic latent semantic analysis for hyperspectral unmixing. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2019, 12, 3156–3167. [Google Scholar] [CrossRef]
- Saâdaoui, F. Randomized extrapolation for accelerating EM-type fixed-point algorithms. J. Multivar. Anal. 2023, 196, 105188. [Google Scholar] [CrossRef]
- Figuera, P.; Cuzzocrea, A.; García Bringas, P. Probability Density Function for Clustering Validation. In Proceedings of the Hybrid Artificial Intelligent Systems, Salamanca, Spain, 5–7 September 2023; Springer: Cham, Switzerland, 2023; pp. 133–144. [Google Scholar]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J.; Lafferty, J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Schmidt, E. Zur Theorie der linearen und nichtlinearen Integralgleichungen. In Integralgleichungen und Gleichungen mit unendlich vielen Unbekannten; Springer: Berlin/Heidelberg, Germany, 1989; pp. 190–233. [Google Scholar]
- Valiant, L.G. A theory of the learnable. Commun. ACM 1984, 27, 1134–1142. [Google Scholar] [CrossRef]
- Wall, J.D.; Stahl, B.C.; Salam, A. Critical discourse analysis as a review methodology: An empirical example. Commun. Assoc. Inf. Syst. 2015, 37, 11. [Google Scholar] [CrossRef]

| Year | Contribution | Remarks |
|---|---|---|
| 2000 | PLSA | PLSA formulation in conference proceedings [1,2,3] comments on the connections among NMF, SVD, and information geometry. |
| 2001 | Kernelization | Fisher kernel derivation from PLSA [17]. |
| 2003 | LDA | Criticism of PLSA: LDA formulation [23]. |
| 2003 | Gaussian PLSA | Assumption of Gaussian mixtures [11]. |
| 2005 | NMF | PLSA solves the NMF problem [14]. Introduction to stochastic matrices [15]. |
| 2008 | k-means | Equivalence between k-means and NMF [24]. |
| 2009 | PCA | Comparison of NMF, PLSA, and PCA [19]. |
| 2012 | Information Geometry | Relationship between Fisher information matrix and variance from the PLSA context [20]. |
| 2013 | Transfer Learning | Use of latent variables weight for classifying most relevant variables [21]. |
| 2015 | Unified framework for PLSA and NMF. | Algorithm for NMF and PLSI based on Poisson likelihood [25]. |
| 2019 | Neural Networks | Neural networks training with PLSA [22]. |
| 2020 | SVD | Establishment of conditions for equivalence of NMF, PLSA, and SVD [16]. |
| 2020 | Inference | Construction of hypothesis tests [13] |
| 2021 | Number of topics | NMF and Silhouette index to determine the number of latent variables [26]. |
| 2023 | Discrete and continuous case equivalence. | Relation between co-occurrences and continuous variables [12]. |
| Asymmetric Formulation | Symmetric Formulation | |
|---|---|---|
| E-step | ||
| M-step | ||
| Discipline | Research Area | % |
|---|---|---|
| Engineering (43%) | Mechanics & Robotics | 35 |
| Acoustics | 4 | |
| Telecommunications & Control Theory | 3 | |
| Materials Science | 1 | |
| Computer Science (34%) | Clustering | 18 |
| Information retrieval | 9 | |
| Networks | 4 | |
| Machine learning applications | 3 | |
| Semantic image analysis (10%) | Image annotation | 4 |
| Image retrieval | 3 | |
| Image classification | 3 | |
| Life Sciences (5%) | Computational Biology | 2 |
| Biochemistry & Molecular Biology | 2 | |
| Environmental Sciences Ecology | 1 | |
| Methodological (4%) | Statistics & Computational Techniques | 4 |
| Fundamental Sciences (2%) | Geochemistry & Geophysics | 1 |
| Instrumentation | 1 | |
| Other Applications (2%) | Pain Detection | 1 |
| Sentiment Analysis | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Figuera, P.; García Bringas, P. Revisiting Probabilistic Latent Semantic Analysis: Extensions, Challenges and Insights. Technologies 2024, 12, 5. https://doi.org/10.3390/technologies12010005
Figuera P, García Bringas P. Revisiting Probabilistic Latent Semantic Analysis: Extensions, Challenges and Insights. Technologies. 2024; 12(1):5. https://doi.org/10.3390/technologies12010005
Chicago/Turabian StyleFiguera, Pau, and Pablo García Bringas. 2024. "Revisiting Probabilistic Latent Semantic Analysis: Extensions, Challenges and Insights" Technologies 12, no. 1: 5. https://doi.org/10.3390/technologies12010005
APA StyleFiguera, P., & García Bringas, P. (2024). Revisiting Probabilistic Latent Semantic Analysis: Extensions, Challenges and Insights. Technologies, 12(1), 5. https://doi.org/10.3390/technologies12010005







