The Holby–Morgan Model of Platinum Catalyst Degradation in PEM Fuel Cells: Range of Feasible Parameters Achieved Using Voltage Cycling
Abstract
:1. Introduction
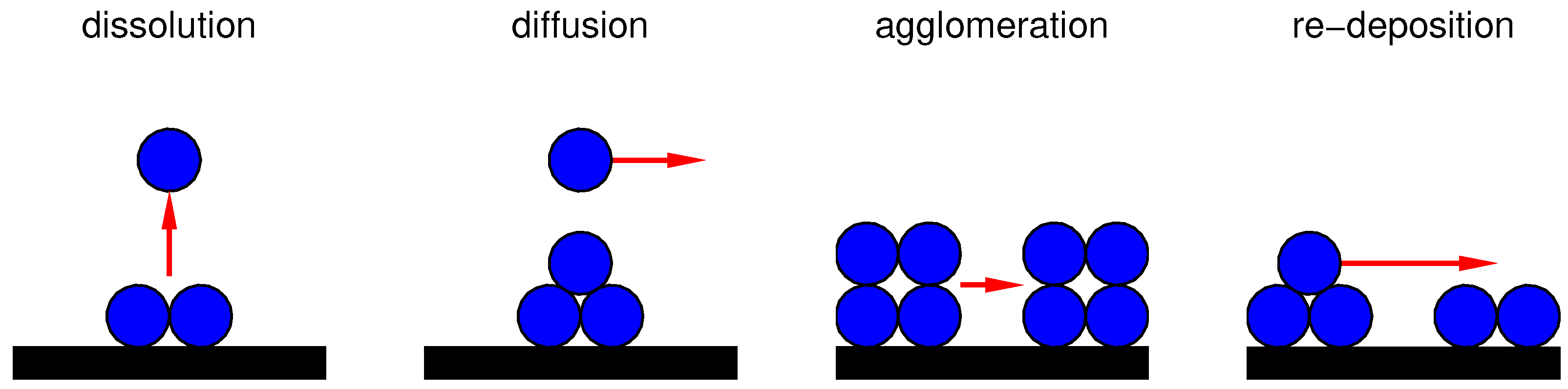
- Platinum is fully dissolved from catalyst;
- Platinum surface is fully covered by oxide;
- Platinum nano-particles, which were initially uniformly distributed, agglomerate in a single band in the middle of the catalyst layer.
2. Materials
3. Methods
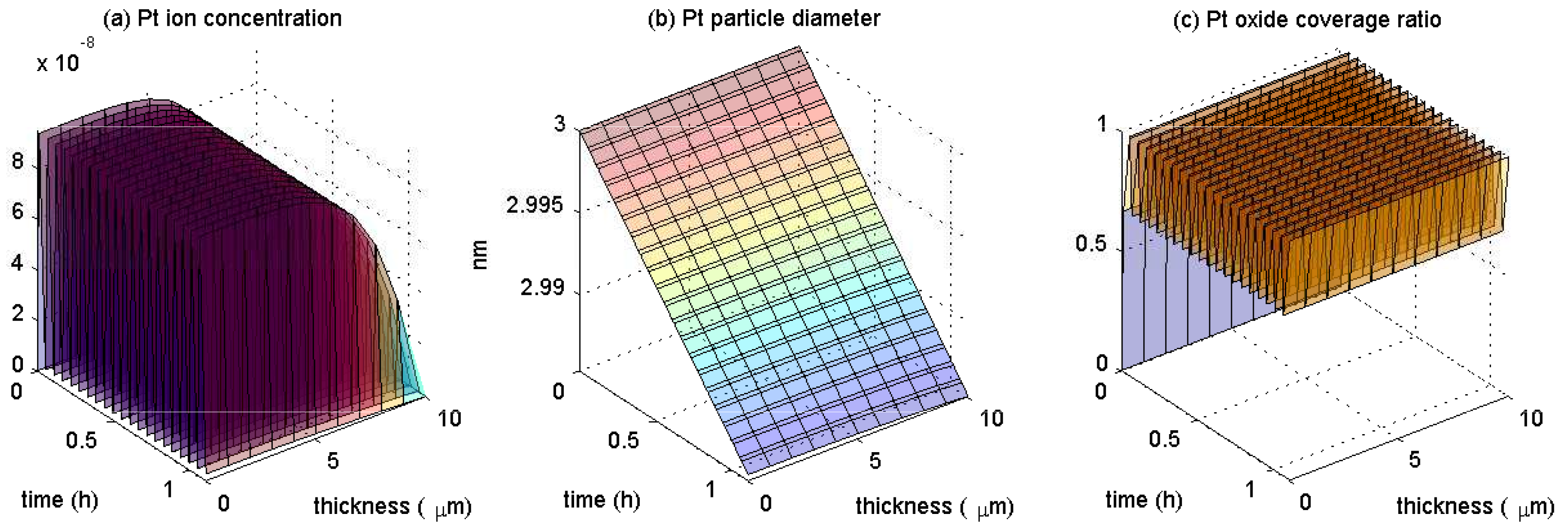
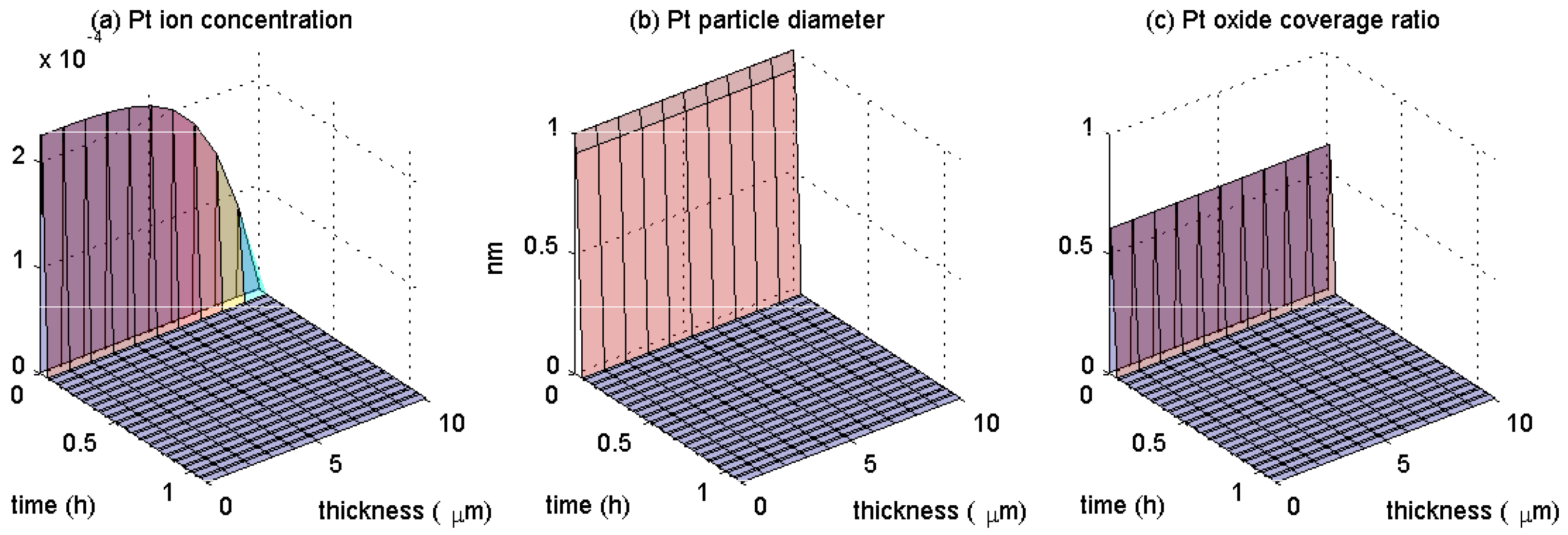
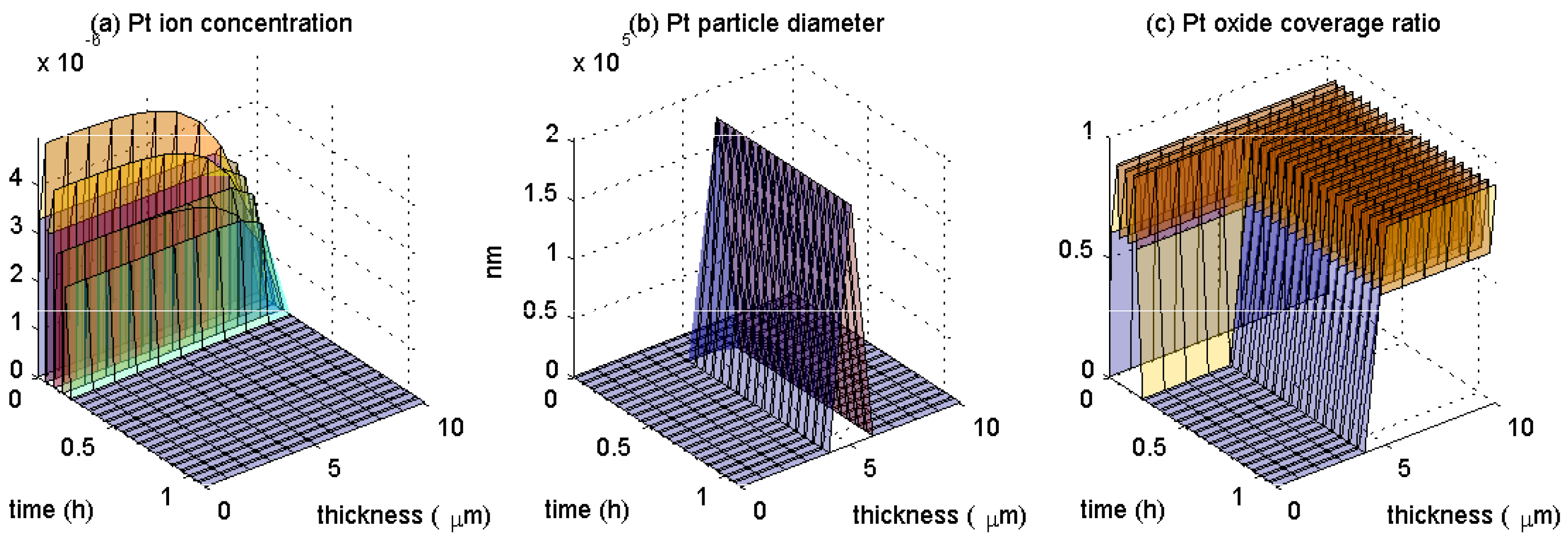
4. Results
5. Discussion
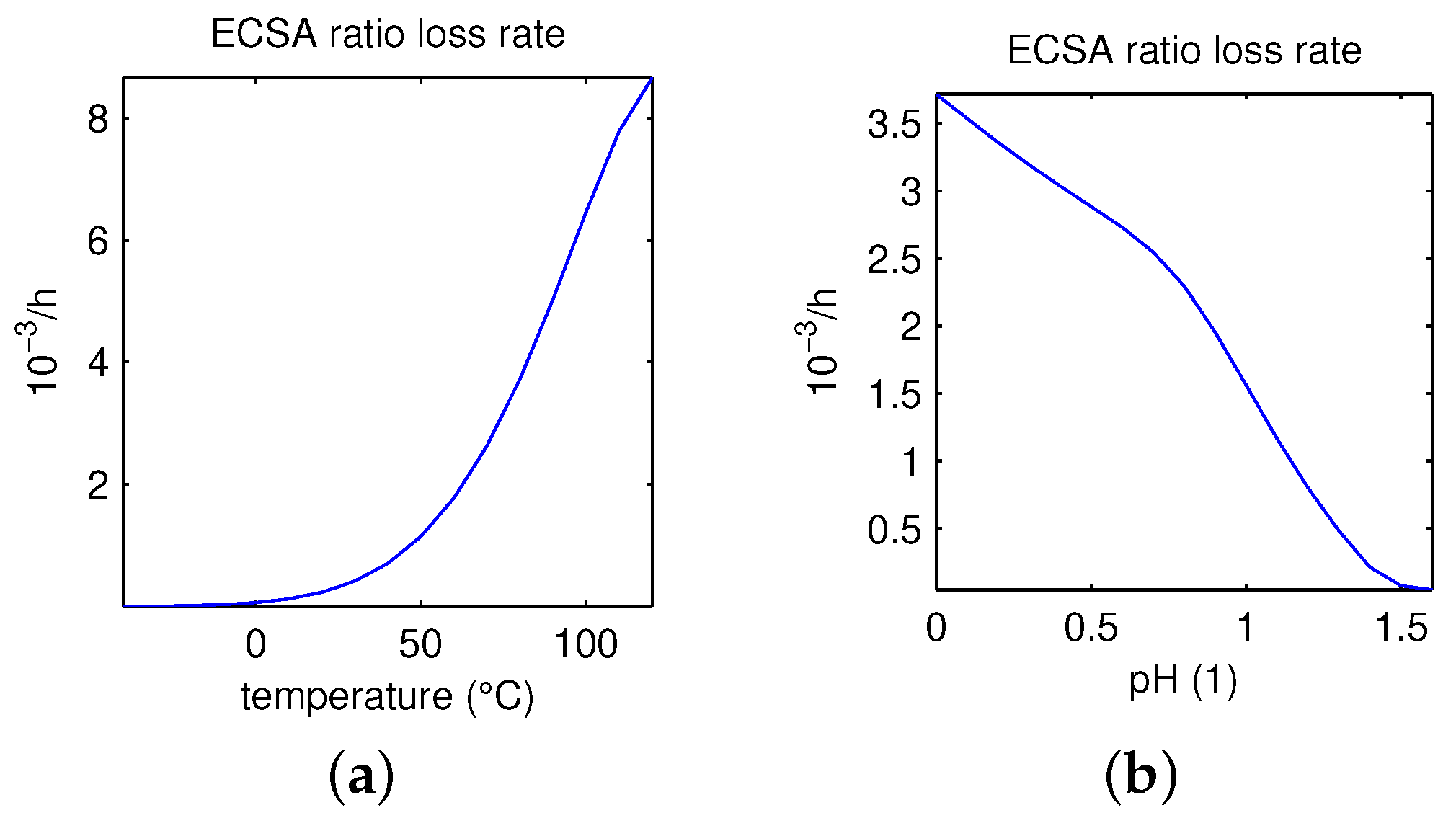
- For basis values of the model parameters, the critical value of maximum feasible temperatures is about 110 °C.
- ECSA ratio loss rate in (14) increases monotonically with the increase in the temperature in the feasible range.
- For the temperature fixed at °C, the maximum value for feasible pH is around 1.4.
- Active area RLR decreases monotonically with the increase in pH within the feasible range 0–1.4.
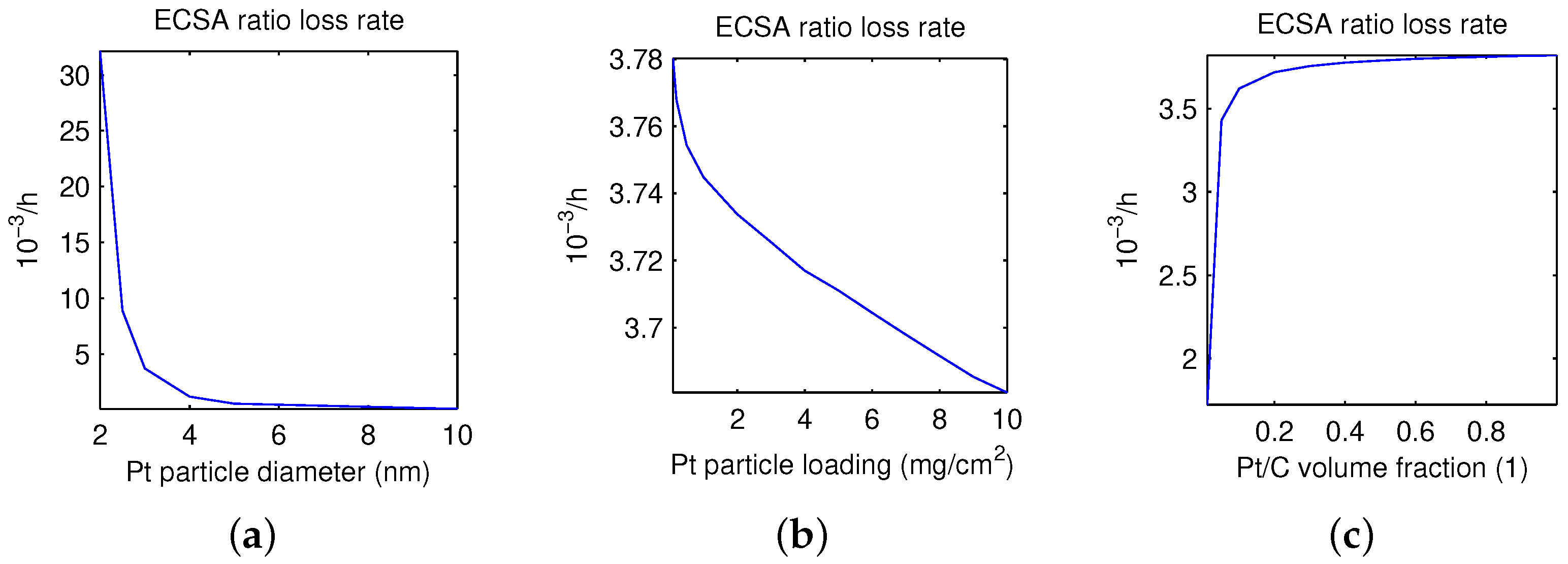
- For pH = 0 fixed, tested diameters of platinum particles are feasible when larger than the minimum of 2 nm.
- ECSA RLR decreases monotonically when increasing the Pt diameter in the range of 2–10 nm.
- drops significantly for less than 2.5 nm, and shows few changes for larger than 5 nm.
- For nm fixed, ECSA RLR decreases monotonically when increasing the Pt particle loading within all tested ranges of 0–10 mg/cm.
- shows a larger drop for 0–1 mg/cm than for 1–10 mg/cm, where it is close to a linear relationship.
- For mg/cm fixed, the platinum to carbon volume fraction has the minimum of 0.002 for feasible values.
- ECSA RLR raises monotonically with the increase in the Pt/C volume fraction within the feasible range of 0.002–1.
- lifts significantly for , and changes very little for .
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D/3D | Two/three dimensions |
| AST | Accelerated stress test |
| BoL/EoL | Beginning/end of life |
| C | Carbon |
| CL | Catalyst layer |
| CV | Cyclic voltammetry |
| ECSA | Electrochemical surface area |
| FC | Fuel cell |
| FCH JU | Fuel cell and hydrogen joint undertaking |
| GDL | Gas diffusion layer |
| HOR | Hydrogen oxidation reaction |
| LPL/UPL | Lower/upper potential level |
| MEA | Membrane electrode assembly |
| OAT | One parameter at a time |
| ORR | Oxygen reduction reaction |
| PEM | Polymer electrolyte membrane/proton exchange membrane |
| PEMFC | Polymer electrolyte fuel cell |
| pH | Potential of hydrogen |
| PSD | Particle size distribution |
| Pt/PtO/Pt | Platinum/platinum oxide/platinum ion |
| Pt/C | Platinum on carbon |
| RLR | Ratio loss rate |
| RH | Relative humidity |
| SW/TW | Square/triangle wave |
References
- Basile, A.; Gupta, R.; Veziroǧlu, T.N. Compendium of Hydrogen Energy: Hydrogen Storage, Distribution and Infrastructure; Woodhead Publishing: Sawston, UK, 2016. [Google Scholar]
- Ferrara, A.; Jakubek, S.; Hametner, C. Energy management of heavy-duty fuel cell vehicles in real-world driving scenarios: Robust design of strategies to maximize the hydrogen economy and system lifetime. Energy Convers. Manag. 2021, 232, 113795. [Google Scholar] [CrossRef]
- Saravanan, R.; Sobhana, O.; Lakshmanan, M.; Arulkumar, P. Fuel cell electric vehicles equipped with energy storage system for energy management: A hybrid JS-RSA approach. J. Energy Storage 2023, 72, 108646. [Google Scholar] [CrossRef]
- Gallo, M.; Marinelli, M. The impact of fuel cell electric freight vehicles on fuel consumption and CO2 emissions: The case of Italy. Sustainability 2022, 14, 13455. [Google Scholar] [CrossRef]
- Meier, J.C.; Galeano, C.; Katsounaros, I.; Witte, J.; Bongard, H.J.; Topalov, A.A.; Baldizzone, C.; Mezzavilla, S.; Schüth, F.; Mayrhofer, K.J.J. Design criteria for stable Pt/C fuel cell catalysts. Beilstein J. Nanotechnol. 2014, 5, 44–67. [Google Scholar] [CrossRef]
- Eikerling, M.; Kulikovsky, A. Polymer Electrolyte Fuel Cells: Physical Principles of Materials and Operation; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Hacker, V.; Mitsushima, S. (Eds.) Fuel Cells and Hydrogen: From Fundamentals to Applied Research; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Kulikovsky, A. Analytical Modeling of Fuel Cells; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Mench, M.; Kumbur, E.C.; Veziroǧlu, T.N. (Eds.) Polymer Electrolyte Fuel Cell Degradation; Academic Press: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Fellner, K.; Kovtunenko, V.A. A singularly perturbed nonlinear Poisson–Boltzmann equation: Uniform and super-asymptotic expansions. Math. Meth. Appl. Sci. 2015, 38, 3575–3586. [Google Scholar] [CrossRef]
- Fellner, K.; Kovtunenko, V.A. A discontinuous Poisson–Boltzmann equation with interfacial transfer: Homogenisation and residual error estimate. Appl. Anal. 2016, 95, 2661–2682. [Google Scholar] [CrossRef] [PubMed]
- González Granada, J.R.; Kovtunenko, V.A. Entropy method for generalized Poisson–Nernst–Planck equations. Anal. Math. Phys. 2018, 8, 603–619. [Google Scholar] [CrossRef]
- Kovtunenko, V.A.; Zubkova, A.V. On generalized Poisson–Nernst–Planck equations with inhomogeneous boundary conditions: A-priori estimates and stability. Math. Meth. Appl. Sci. 2017, 40, 2284–2299. [Google Scholar] [CrossRef]
- Kovtunenko, V.A.; Zubkova, A.V. Mathematical modeling of a discontinuous solution of the generalized Poisson–Nernst–Planck problem in a two-phase medium. Kinet. Relat. Mod. 2018, 11, 119–135. [Google Scholar] [CrossRef]
- Khludnev, A.M.; Kovtunenko, V.A. Analysis of Cracks in Solids; WIT-Press: Southampton, UK; Boston, UK, 2000. [Google Scholar]
- Theiler, A.; Karpenko-Jereb, L. Modelling of the mechanical durability of constrained Nafion membrane under humidity cycling. Int. J. Hydrogen Energy 2015, 40, 9773–9782. [Google Scholar] [CrossRef]
- Kneer, A.; Jankovic, J.; Susac, D.; Putz, A.; Wagner, N.; Sabharwal, M.; Secanell, M. Correlation of changes in electrochemical and structural parameters due to voltage cycling induced degradation in PEM fuel cells. J. Electrochem. Soc. 2018, 165, F3241–F3250. [Google Scholar] [CrossRef]
- Marcu, A.; Toth, G.; Pietrasz, P.; Waldecker, J. Cathode catalysts degradation mechanism from liquid electrolyte to membrane electrode assembly. Comptes Rendus Chim. 2014, 17, 752–759. [Google Scholar] [CrossRef]
- Medvedev, D.A. Current drawbacks of proton-conducting ceramic materials: How to overcome them for real electrochemical purposes. Curr. Opin. Green Sustain. Chem. 2021, 32, 00549. [Google Scholar] [CrossRef]
- Cherevko, S.; Kulyk, N.; Mayrhofer, K.J.J. Durability of platinum-based fuel cell electrocatalysts: Dissolution of bulk and nanoscale platinum. Nano Energy 2016, 29, 275–298. [Google Scholar] [CrossRef]
- Nondudule, Z.; Chamier, J.; Chowdhury, M. Effect of stratification of cathode catalyst layers on durability of proton exchange membrane fuel cells. Energies 2021, 14, 2975. [Google Scholar] [CrossRef]
- Kravos, A.; Kregar, A.; Mayer, K.; Hacker, V.; Katrašnik, T. Identifiability analysis of degradation model parameters from transient CO2 release in low-temperature PEM fuel cell under various AST protocols. Energies 2021, 14, 4380. [Google Scholar] [CrossRef]
- Mayur, M.; Gerard, M.; Schott, P.; Bessler, W.G. Lifetime prediction of a polymer electrolyte membrane fuel cell under automotive load cycling using a physically-based catalyst degradation model. Energies 2018, 11, 2054. [Google Scholar] [CrossRef]
- Schneider, P.; Sadeler, C.; Scherzer, A.-C.; Zamel, N.; Gerteisen, D. Fast and reliable state-of-health model of a PEM cathode catalyst layer. J. Electrochem. Soc. 2019, 166, F322–F333. [Google Scholar] [CrossRef]
- Darling, R.M.; Meyers, J.P. Kinetic model of platinum dissolution in PEMFCs. J. Electrochem. Soc. 2003, 150, A1523–A1527. [Google Scholar] [CrossRef]
- Holby, E.F.; Morgan, D. Application of Pt nanoparticle dissolution and oxidation modeling to understanding degradation in PEM fuel cells. J. Electrochem. Soc. 2012, 159, B578–B591. [Google Scholar] [CrossRef]
- Holby, E.F.; Sheng, W.; Shao-Horn, Y.; Morgan, D. Pt nanoparticle stability in PEM fuel cells: Influence of particle size distribution and crossover hydrogen. Energy Environ. Sci. 2009, 2, 865–871. [Google Scholar] [CrossRef]
- Li, Y.; Moriyama, K.; Gu, W.; Arisetty, S.; Wang, C.Y. A one-dimensional Pt degradation model for polymer electrolyte fuel cells. J. Electrochem. Soc. 2015, 162, F834–F842. [Google Scholar] [CrossRef]
- Kovtunenko, V.A.; Karpenko-Jereb, L. Study of voltage cycling conditions on Pt oxidation and dissolution in polymer electrolyte fuel cells. J. Power Sources 2021, 493, 229693. [Google Scholar] [CrossRef]
- Kovtunenko, V.A.; Karpenko-Jereb, L. Lifetime of catalyst under voltage cycling in polymer electrolyte fuel cell due to platinum oxidation and dissolution. Technologies 2021, 9, 80. [Google Scholar] [CrossRef]
- Karpenko-Jereb, L.; Kovtunenko, V.A. Modeling of the impact of cycling operating conditions on durability of polymer electrolyte fuel cells and its sensitivity analysis. Int. J. Hydrogen Energy 2023, 48, 15646–15656. [Google Scholar] [CrossRef]
- Kovtunenko, V.A. Variance-based sensitivity analysis of fitting parameters to impact on cycling durability of polymer electrolyte fuel cells. Technologies 2022, 9, 111. [Google Scholar] [CrossRef]
- Pivac, I.; Barbir, F. Impact of shutdown procedures on recovery phenomena of proton exchange membrane fuel cells. Fuel Cells 2020, 160, 185–195. [Google Scholar] [CrossRef]
- Goshtasbi, A.; Chen, J.; Waldecker, J.R.; Hirano, S.; Ersal, T. Effective parameterization of PEM fuel cell models—Part I: Sensitivity analysis and parameter identifiability. J. Electrochem. Soc. 2020, 167, 044504. [Google Scholar] [CrossRef]
- Kravos, A.; Ritzberger, D.; Tavčar, G.; Hametner, C.; Jakubek, S.; Katrašnik, T. Thermodynamically consistent reduced dimensionality electrochemical model for proton exchange membrane fuel cell performance modelling and control. J. Power Sources 2020, 454, 227930. [Google Scholar] [CrossRef]
- Kregar, A.; Frühwirt, P.; Ritzberger, D.; Jakubek, S.; Katrašnik, T.; Gescheidt, G. Sensitivity based order reduction of a chemical membrane degradation model for low-temperature proton exchange membrane fuel cells. Energies 2020, 31, 5611. [Google Scholar] [CrossRef]
- Blanco-Cocom, L.; Botello-Rionda, S.; Ordoñez, L.C.; Ivvan Valdez, S. Design optimization and parameter estimation of a PEMFC using nature-inspired algorithms. Soft Comput. 2023, 27, 3765–3784. [Google Scholar] [CrossRef]
- Priya, K.; Sathishkumar, K.; Rajasekar, N. A comprehensive review on parameter estimation techniques for Proton Exchange Membrane fuel cell modelling. Renew. Sust. Energ. Rev. 2018, 93, 121–144. [Google Scholar] [CrossRef]
- Soomro, I.A.; Memon, F.H.; Mughal, W.; Khan, M.A.; Ali, W.; Liu, Y.; Choi, K.H.; Thebo, K.H. Influence of operating and electrochemical parameters on PEMFC performance: A simulation study. Membranes 2023, 13, 259. [Google Scholar] [CrossRef] [PubMed]
- Stropnik, R.; Mlakar, N.; Lotrič, A.; Sekavčnik, M.; Mori, M. The influence of degradation effects in proton exchange membrane fuel cells on life cycle assessment modelling and environmental impact indicators. Int. J. Hydrogen Energy 2022, 47, 24223–24241. [Google Scholar] [CrossRef]
- Tochigi, S.; Dowaki, K. Environmental impact assessment of PEM fuel cell combined heat and power generation system for residential application considering cathode catalyst layer degradation. Energies 2023, 16, 1985. [Google Scholar] [CrossRef]
- Pandy, A.; Yang, Z.; Gummalla, M.; Atrazhev, V.V.; Kuzminyh, N.Y.; Sultanov, V.I.; Burlatsky, S. A carbon corrosion model to evaluate the effect of steady state and transient operation of a polymer electrolyte membrane fuel cell. J. Electrochem. Soc. 2013, 160, F972–F979. [Google Scholar] [CrossRef]
- Burlatsky, S.F.; Gummalla, M.; Atrazhev, V.V.; Dmitriev, D.V.; Kuzminyh, N.Y.; Erikhman, N.S. The dynamics of platinum precipitation in an ion exchange membrane. J. Electrochem. Soc. 2011, 158, B322–B330. [Google Scholar] [CrossRef]
- Bi, W.; Gray, G.E.; Fuller, T.F. PEM fuel cell Pt/C dissolution and deposition in Nafion electrolyte. Electrochem. Solid-State Lett. 2007, 10, B101–B104. [Google Scholar] [CrossRef]
- Jahnke, T.; Futter, G.A.; Baricci, A.; Rabissi, C.; Casalegno, A. Physical modeling of catalyst degradation in low temperature fuel cells: Platinum oxidation, dissolution, particle growth and platinum band formation. J. Electrochem. Soc. 2020, 167, 013523. [Google Scholar] [CrossRef]
- Sethuraman, V.A.; Weidner, J.W.; Haug, A.T.; Motupally, S.; Protsailo, L.V. Hydrogen peroxide formation rates in a PEMFC anode and cathode: Effect of humidity and temperature. J. Electrochem. Soc. 2007, 155, B50–B57. [Google Scholar] [CrossRef]
- Yu, K.; Groom, D.J.; Wang, X.; Yang, Z.; Gummalla, M.; Ball, S.C.; Myers, D.J.; Ferreira, P.J. Degradation mechanisms of platinum nanoparticle catalysts in proton exchange membrane fuel cells: The role of particle size. Chem. Mater. 2014, 26, 5540–5548. [Google Scholar] [CrossRef]


| Symbol | Value | Units | Description |
|---|---|---|---|
| Hz | Dissolution attempt frequency | ||
| Hz | Backward dissolution rate factor | ||
| 0.5 | Butler transfer coefficient for Pt dissolution | ||
| n | 2 | Electrons transferred during Pt dissolution | |
| 1.118 | V | Pt dissolution bulk equilibrium voltage | |
| 9.09 | cm/mol | Molar volume of Pt | |
| J/cm | Pt [1 1 1] surface tension | ||
| 1 | mol/cm | Reference Pt ion concentration | |
| J/mol | partial molar Pt dissolution activation enthalpy | ||
| cm/s | Diffusion coefficient of Pt ion in the membrane | ||
| Hz | Forward Pt oxide formation rate constant | ||
| Hz | Backward Pt oxide formation rate constant | ||
| mol/cm | Pt surface site density | ||
| 0.5 | Butler transfer coefficient for PtO formation | ||
| 2 | Electrons transferred during Pt oxide formation | ||
| 0.8 | V | Pt oxide formation bulk equilibrium voltage | |
| J/mol | Pt oxide dependent kinetic barrier constant | ||
| J/mol | Pt oxide-oxide interaction energy | ||
| J/mol | Partial molar oxide formation activation enthalpy |
| Symbol | Value | Units | Description |
|---|---|---|---|
| T | 353.15 | K | Temperature |
| 0 | Potential of hydrogen | ||
| cm | Pt particle diameter | ||
| g/cm | Pt particles loading | ||
| 0.02 | Pt/C volume fraction | ||
| 21.45 | g/cm | Pt particles density |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovtunenko, V.A. The Holby–Morgan Model of Platinum Catalyst Degradation in PEM Fuel Cells: Range of Feasible Parameters Achieved Using Voltage Cycling. Technologies 2023, 11, 184. https://doi.org/10.3390/technologies11060184
Kovtunenko VA. The Holby–Morgan Model of Platinum Catalyst Degradation in PEM Fuel Cells: Range of Feasible Parameters Achieved Using Voltage Cycling. Technologies. 2023; 11(6):184. https://doi.org/10.3390/technologies11060184
Chicago/Turabian StyleKovtunenko, Victor A. 2023. "The Holby–Morgan Model of Platinum Catalyst Degradation in PEM Fuel Cells: Range of Feasible Parameters Achieved Using Voltage Cycling" Technologies 11, no. 6: 184. https://doi.org/10.3390/technologies11060184
APA StyleKovtunenko, V. A. (2023). The Holby–Morgan Model of Platinum Catalyst Degradation in PEM Fuel Cells: Range of Feasible Parameters Achieved Using Voltage Cycling. Technologies, 11(6), 184. https://doi.org/10.3390/technologies11060184







