A Monotonic Early Output Asynchronous Full Adder

Abstract

This article introduces a novel asynchronous full adder that operates in an input–output mode (IOM), displaying both monotonicity and an early output characteristic. In a monotonic asynchronous circuit, the intermediate and primary outputs exhibit similar signal transitions as the primary inputs during data and spacer application. The proposed asynchronous full adder ensures monotonicity for processing data and spacer, utilizing dual-rail encoding for inputs and outputs, and corresponds to return-to-zero (RtZ) and return-to-one (RtO) handshaking. The early output feature of the proposed full adder allows the production of sum and carry outputs based on the adder inputs regardless of the carry input when the spacer is supplied. When utilized in a ripple carry adder (RCA) architecture, the proposed full adder achieves significant reductions in design metrics, such as cycle time, area, and power, compared to existing IOM asynchronous full adders. For a 32-bit RCA implementation using a 28 nm CMOS technology, the proposed full adder outperforms an existing state-of-the-art high-speed asynchronous full adder by reducing the cycle time by 10.4% and the area by 15.8% for RtZ handshaking and reduces the cycle time by 9.8% and the area by 15.8% for RtO handshaking without incurring any power penalty. Further, in terms of the power-cycle time product, which serves as a representative measure of energy, the proposed full adder yields an 11.8% reduction for RtZ handshaking and an 11.2% reduction for RtO handshaking.

1. Introduction

Input–output mode (IOM) asynchronous circuits use delay-insensitive codes for data encoding and rely on a four-phase handshake protocol for data communication. Unlike synchronous circuits that depend on a clock signal, IOM asynchronous circuits operate based on events, making them inherently more robust. This event-driven nature of IOM asynchronous circuits provides them with increased resistance to process, voltage, and temperature variations, making them more adaptable [1]. Moreover, IOM asynchronous circuits offer modularity and reduced vulnerability to electromagnetic interference compared to synchronous circuits, which makes them suitable for security applications [2].

IOM asynchronous circuits can be categorized as quasi-delay-insensitive (QDI) and non-QDI. QDI circuits rely on isochronic forks [3], which are electrical nodes from which multiple wires may emerge, and the signal transitions on those wires are assumed to occur simultaneously. This assumption has been found to hold good in the realm of microelectronics and nanoelectronics [4]. Quasi-delay-insensitivity requires that all the outputs of a circuit be generated only after all inputs have been received, and the internal processing is fully completed. While this feature enhances the robustness of QDI circuits, it also increases their implementation costs, such as area, delay, and power dissipation, compared to non-QDI circuits.

There are different types of QDI circuits, namely strong indication and weak indication [5], as well as early output QDI circuits [6]. In strong indication circuits, all primary inputs must be processed to produce all primary outputs. In contrast, weak indication circuits can process a subset of primary inputs to produce some primary outputs, but the final primary output is produced only after processing the last primary input. Early output circuits can process a subset of primary inputs to produce all primary outputs, particularly when the spacer is applied. It is worth noting that early output circuits may or may not be QDI. The assumption of isochronic forks applied to the primary inputs handles the acknowledgment of delayed primary inputs in early output QDI circuits.

IOM asynchronous circuits that do not fall into the QDI category encompass relative-timed circuits [7] and monotonous/monotonic circuits [8]. Relative-timed circuits operate based on internal timing to sequence the inputs and generate the outputs, whereas monotonic circuits only ensure the monotonicity of signal transitions within a circuit. Monotonicity guarantees that rising signal transitions (say, from binary 0 to 1) on inputs result in rising signal transitions on outputs, and falling signal transitions (say, from binary 1 to 0) on inputs result in falling signal transitions on outputs. A circuit may be monotonically increasing, monotonically decreasing, monotonically increasing and decreasing, or non-monotonic. Synchronous circuits typically exhibit non-monotonic behavior, while IOM asynchronous circuits generally display monotonic behavior. In this article, the term ‘monotonic circuits’ shall henceforth refer to asynchronous circuit implementations that are monotonically increasing and decreasing, unless stated otherwise.

Monotonic circuits typically function as early output circuits but do not fall into the QDI category, and they do not require the completion of internal processing to produce all the primary outputs [9]. Compared to QDI asynchronous circuits, non-QDI asynchronous circuits offer more flexibility, allowing for a reduction in circuit complexity and implementation costs in the design of asynchronous circuits. As a result, they could achieve superior performance metrics. The proposed asynchronous full adder is a monotonic circuit that enables significant optimizations to design metrics compared to existing asynchronous full adders. An abridged version of this work has been accepted for presentation at the IEEE MIEL 2023 conference [10], and this article is an extension that includes (100%) extra results for RtO handshaking, in addition to the results for RtZ handshaking given in [10]. Further, a comparison between the calculated theoretical cycle time and the estimated actual cycle time of asynchronous adders is given in this article. Towards this, the delay expressions governing the forward latency and reverse latency of various N-bit asynchronous carry-ripple adders are also given as an Appendix in this article.

The subsequent sections of this article cover the following: Section 2 discusses the fundamentals of IOM asynchronous circuit design. Section 3 provides an overview of the existing literature on IOM asynchronous full adders. The design of the proposed IOM asynchronous full adder is described in Section 4. In Section 5, the design metrics of asynchronous adders implemented using different asynchronous full adders, including the proposed design, are presented. Finally, Section 6 concludes this article.

2. IOM Asynchronous Circuit Design—Fundamentals

Figure 1a showcases the block diagram of a single stage of an IOM asynchronous pipeline [1]. A pipeline stage comprises an asynchronous circuit that is positioned between banks of input and output registers. The input registers may act as the output registers for a preceding circuit in the pipeline, and the output registers may act as the input registers for a subsequent circuit in the pipeline. The input registers are responsible for providing inputs to the asynchronous circuit, which then processes the input and produces the output that is subsequently directed to the output registers. A completion detector is used to indicate the completion of production of all outputs by an asynchronous circuit. Example completion detectors corresponding to RtZ handshaking and RtO handshaking are shown in Figure 1b,c, respectively—the handshaking schemes shall be discussed later in this section. The completion detector associated with the output registers sends an acknowledgment output (AckO) signal, which, after inversion, becomes the acknowledgment input (AckI) signal that is used to enable the input registers to supply new inputs (data or spacer) to the asynchronous circuit for processing. The communication process between input and output registers is called ‘handshaking’ in IOM asynchronous circuits.

The Muller C-element [11] is used as a register in an IOM asynchronous circuit. The Muller C-element produces a binary 1 when all its inputs are binary 1 and a binary 0 when all its inputs are binary 0. If the inputs to a C-element are different, it would maintain its current steady state. Assuming A and B are the inputs of a C-element, the output of the C-element, say M, is expressed as M = AB + (A + B) M. The transistor-level implementation of a 2-input Muller C-element is shown in Figure 1d, which can be obtained by incorporating feedback in an AO222 complex gate realization [12]. Full-custom transistor-level realizations of the C-element have been presented and analyzed in [13,14], but these were not used as we have utilized a semi-custom realization of the C-element shown in Figure 1d to implement IOM asynchronous RCAs comprising different asynchronous full adders in a semi-custom design fashion at the gate-level.

The encoding of an IOM asynchronous circuit involves the utilization of a delay-insensitive code [15], with the dual-rail code widely used to encode inputs and outputs. We first explain the process of encoding an input/output using dual-rail encoding according to RtZ handshaking and RtO handshaking before describing the handshaking schemes. According to dual-rail encoding and RtZ handshaking [1], an input signal, S, is represented by two wires or rails, namely S1 and S0. If the value of S is 1, it is encoded as S1 = 1 and S0 = 0, whereas if S is 0, it is encoded as S0 = 1 and S1 = 0. These assignments are referred to as ‘data.’ S1 = S0 = 0 represents the ‘ (zeroes) spacer’ that is inserted between two consecutive data. In the context of RtZ handshaking, S1 = S0 = 1 is invalid and illegal since the coding scheme should be unordered [16]. According to dual-rail encoding and RtO handshaking [17], an input signal, S, is represented by two wires or rails, say S1 and S0. If the value of S is 1, it is encoded as S1 = 0 and S0 = 1, whereas if S is 0, it is encoded as S0 = 0 and S1 = 1. These two assignments are referred to as ‘data.’ S1 = S0 = 1 represents the ‘ (ones) spacer’ that is inserted between two consecutive data. In the context of RtO handshaking, S1 = S0 = 0 is invalid and illegal since the coding scheme should be unordered [16].

Figure 1b,c highlights example dual-rail encoded inputs (X1, X0) and (Y1, Y0). In the bank of input registers shown in Figure 1b,c, each C-element has one of its inputs tied to the AckI signal, while its other input is connected to an encoded input rail. Figure 1b shows an example completion detector that relates to RtZ handshaking. Here, the completion detector consists of a series of 2-input OR gates in the initial level, where each OR gate combines the respective dual rails of each encoded input. The outputs from these OR gates are then fed into a C-element or a tree of C-elements to generate the AckO signal. Figure 1c shows an example completion detector that relates to RtO handshaking. Here, the completion detector consists of a series of 2-input AND gates in the initial level, where each AND gate combines the respective dual rails of each encoded input. The outputs from these AND gates are then fed into a C-element or a tree of C-elements to generate the AckO signal.

We shall now explain the RtZ and RtO handshaking schemes. Concerning RtZ handshaking, the initial step is setting AckI to 1 while AckO is at 0. This action triggers the input registers to transmit the data to the asynchronous circuit for processing. During this phase, one of the encoded input rails of the entire data bus will be set to 1, indicating that data is being sent for processing by the asynchronous circuit. In the second phase, the output registers will receive all the outputs generated by the asynchronous circuit and then send an AckO signal of 1. In the third phase, the input registers will wait for AckI to become 0 and then supply the asynchronous circuit with the (zeroes) spacer for processing. Lastly, in the fourth and final phase, the output registers will receive the spacer output from the asynchronous circuit, and an AckO signal of 0 will be issued. This signifies the completion of one data transaction and the readiness to initiate the next data transaction when AckI subsequently becomes 1.

Concerning RtO handshaking, the initial step is setting AckI to 1 while AckO is at 0. This action triggers the input registers to transmit the (ones) spacer to the asynchronous circuit for processing. During this phase, all the encoded input rails of the entire data bus will be set to 1, indicating that the spacer is being sent for processing by the asynchronous circuit. In the second phase, the output registers will receive all the outputs generated by the asynchronous circuit and then send an AckO signal of 1. In the third phase, the input registers will wait for AckI to become 0 and then supply the asynchronous circuit with the data for processing, which implies one of the encoded input rails of the entire data bus will be driven to 0. Lastly, in the fourth and final phase, the output registers will receive the data output from the asynchronous circuit, and an AckO signal of 0 will be issued. This signifies the completion of one data transaction and the readiness to initiate the next data transaction when AckI subsequently becomes 1.

To ensure delay insensitivity in QDI circuits, a spacer is inserted between two input data. On the other hand, by introducing a spacer between two input data for a monotonic circuit, delay insensitivity can be achieved externally for handshaking purposes so that data and spacer do not collide. Figure 1a shows an IOM asynchronous pipeline stage where the primary timing parameter is the ‘cycle time,’ representing the duration required to complete a single data transaction. The processing time for data (worst-case scenario) is known as forward latency, while the processing time for the spacer (worst-case scenario) is referred to as reverse latency. The forward latency may or may not be equal to the reverse latency in an IOM asynchronous circuit, depending on the logic composition of the asynchronous circuit. In an IOM asynchronous circuit, the cycle time is determined by the sum of forward and reverse latencies. The critical data path governing the latency in an IOM asynchronous circuit involves an input register bank and an asynchronous circuit, which is emphasized by the pink dashed line in Figure 1a.

3. IOM Asynchronous Full Adders—A Survey

By cascading N full adders, it is possible to create an N-bit ripple carry adder (RCA). Although the RCA demonstrates advantages, such as less area and low power compared to other high-speed adders, it leads to relatively slower performance for synchronous design. However, in the context of IOM asynchronous design, the RCA architecture becomes valuable, especially due to some RCAs exhibiting a small reverse latency that is challenging to attain with alternative adder architectures. Further, the RCA has the smallest area among other adders, contributing to low power dissipation. We consider the RCA architecture here as a platform to comparatively evaluate the performance of various IOM asynchronous full adders.

A binary full adder takes two input bits and a carry input, producing a sum output and any carry overflow. The output expressions of a dual-rail full adder, which corresponds to RtZ handshaking, are presented in Equations (1) through (4). In the equations, the inputs of the dual-rail full adder are represented by (X1, X0) and (Y1, Y0), along with the dual-rail carry input represented by (C1, C0). The dual-rail sum output is denoted by (Sum1, Sum0), while the dual-rail carry overflow, also called carry output resulting from the addition, is denoted by (Carry1, Carry0).

Sum1 = X0Y0C1 + X0Y1C0 + X1Y0C0 + X1Y1C1

(1)

Sum0 = X0Y0C0 + X0Y1C1 + X1Y0C1 + X1Y1C0

(2)

Carry1 = X0Y1C1 + X1Y0C1 + X1Y1C0 + X1Y1C1

(3)

Carry0 = X0Y0C0 + X0Y0C1 + X0Y1C0 + X1Y0C0

(4)

We will now survey the existing IOM asynchronous full adders. By employing different types of full adders, we provide a theoretical analysis of latency and cycle time for various asynchronous RCAs. However, it is important to note that the theoretical modeling of latency and cycle time for different asynchronous RCAs is only an approximation. This is because the modeling only considers the delays of the building blocks (i.e., full adders) for simplicity, while disregarding gate, interconnect, or parasitic delays. Also, the small delay caused by the input register is not considered in the theoretical modeling for simplicity.

The full adders of [18,19] demonstrate a strong indication property, and it is possible to realize a strong indication full adder using the delay-insensitive minterm synthesis method [20]. When these full adders are individually replicated and interconnected to form N-bit RCAs, where N represents the adder size, such RCAs would exhibit the same forward and reverse latency of O[N × D_FA], where D_FA represents the propagation delay of a full adder. It should be noted that RCAs employing strong indication full adders experience higher forward and reverse latencies due to maximum-length carry propagation while processing both data and spacer. Consequently, the cycle time of these RCAs is O[2 × N × D_FA], resulting in significantly slower performance.

Reference [21] introduced a full-custom weak indication full adder design based on static CMOS implementation, using 42 transistors. However, it is worth noting that the pull-up network in this design involves a series stack of four PMOS transistors, which is not considered optimal for modern CMOS technologies. Moreover, optimum transistor sizing should be performed to make the full adder suitable for driving different loads. In contrast, several existing asynchronous full adders are semi-custom gate-level designs that can be quite conveniently realized using a standard cell library. Nonetheless, the C-element, which is not part of a typical standard cell library, may be designed in a full-custom fashion [13,14] or in a semi-custom fashion (as shown in Figure 1d) and used for implementation.

The full adders discussed in [22,23,24] demonstrate weak indication behavior. Also, it is possible to realize a weak indication full adder using the delay-insensitive minterm synthesis method [20]. The weak indication full adders presented in [20,22] exhibit a cycle time of O[2 × N × D_FA], with equal forward and reverse latencies of O[N × D_FA]. This is a result of the maximum carry propagation involved during the processing of both data and the spacer. On the other hand, the weak indication full adders described in [23,24] have a cycle time of O[(N + 2) × D_FA], with a forward latency of O[N × D_FA] and a reverse latency of O[2 × D_FA]. The reduction in reverse latency is achieved through biased weak indication, where the responsibility of indicating all the adder inputs is assigned to the sum output of the full adders, while the carry output is exempted from the indication.

A recent work [25] introduced three weak indication full adders, leveraging the concept of binary sorting networks (SN). These full adders are labeled as the SN full adder, SNFC full adder, and SNX full adder. However, it is worth noting that none of these full adders were physically implemented in [25]. An N-bit RCA realized using SN full adder would have a cycle time of O[2 × N × D_FA], which indicates that its forward and reverse latencies are equal. In contrast, N-bit RCAs realized using SNFC and SNX full adders would have a cycle time given by O[(N + 2) × D_FA], suggesting that their reverse latency is significantly lower than their forward latency. This reduction in reverse latency is attributed to the phenomenon of biased weak indication incorporated in SNFC and SNX full adders.

Reference [26] presented an early output QDI full adder. When this full adder is replicated and interconnected to form an N-bit RCA, it will exhibit a forward latency of O[N × D_FA] and a reverse latency of O[2 × D_FA]. Accordingly, the cycle time of the RCA would be given by O[(N + 2) × D_FA].

The early output QDI full adders discussed in [27] can be utilized to construct relative-timed RCAs. Among these full adders, one is optimized for area, while the other is optimized for latency. Consequently, the resulting RCAs exhibit a forward latency of O[N × D_FA] while achieving a minimized reverse latency of O[D_FA]. The reduction in reverse latency is made possible because all the full adders within the RCA can simultaneously produce the sum output without waiting for the carry input during the application of the spacer, thus allowing for more efficient processing. The cycle time of the relative-timed RCAs is calculated to be O[(N + 1) × D_FA], which is theoretically the least among the cycle times of existing IOM asynchronous RCAs.

4. Proposed Monotonic Asynchronous Full Adder

Figure 2 portrays the gate-level diagram of the monotonic asynchronous full adder proposed corresponding to RtZ handshaking. The adder inputs are dual-rail encoded and represented by (X1, X0), (Y1, Y0), and (C1, C0), and the adder outputs are also dual-rail encoded and denoted by (Sum1, Sum0) and (Carry1, Carry0). There are four intermediate nodes, namely J1, J2, J3, and J4, which are highlighted in red. The proposed full adder using dual-rail encoding comprises a total of eight gates, specifically four AO22 complex gates, two AO21 complex gates, and two 2-input AND gates. The logic expressions governing the proposed full adder are given by Equations (5) to (8), where J1 = X0Y0 + X1Y1, J2 = X0Y1 + X1Y0, J3 = X1Y1, and J4 = X0Y0.

Sum1 = J1C1 + J2C0

(5)

Sum0 = J1C0 + J2C1

(6)

Carry1 = J2C1 + J3

(7)

Carry0 = J2C0 + J4

(8)

The two comprehensive example scenarios below demonstrate and explain the proposed full adder’s monotonicity and early output characteristics corresponding to RtZ handshaking.

4.1. Scenario 1

When data is supplied, if either X0 and Y0 or X1 and Y1 are set to binary 1, J1 will assume 1. Depending on whether C1 or C0 is 1, either Sum1 or Sum0 will assume 1, respectively. Also, if X1 and Y1 or X0 and Y0 are both 1, Carry1 or Carry0 will assume 1, respectively. As a result, all signal transitions in the full adder during data processing increase monotonically. Subsequently, when the (zeroes) spacer is supplied, even if X0 or Y0 (or X1 or Y1) assumes binary 0, J1 will assume 0. Consequently, either Sum1 or Sum0 (whichever assumed 1 earlier) will assume 0 without waiting for C1 or C0 (whichever became 1 earlier) to assume 0. Further, if X1 or Y1 (or X0 or Y0) assumes 0, J3 or J4 (whichever became 1 earlier) will assume 0, and either Carry1 or Carry0 (whichever became 1 earlier) will assume 0 without both X1 and Y1 or X0 and Y0 assuming 0. This demonstrates the early output nature and the monotonically decreasing property of the proposed full adder during spacer processing.

4.2. Scenario 2

When data is supplied, if either X0 and Y1 or X1 and Y0 assume 1, J2 will assume 1. Depending on whether C0 or C1 is 1, either Sum1 or Sum0 will assume 1, respectively. Also, if C1 or C0 assumes 1, either Carry1 or Carry0 will assume 1. Hence, all signal transitions within the full adder during data processing increase monotonically. Subsequently, when the (zeroes) spacer is supplied, even if X0 or Y1 (or X1 or Y0) assumes binary 0, J2 will assume 0. Consequently, either Sum1 or Sum0 (whichever became 1 earlier) will assume 0 without waiting for C0 or C1 (whichever became 1 earlier) to assume 0. Additionally, Carry1 or Carry0 (whichever became 1 earlier) will assume 0 without waiting for C1 or C0 to assume 0. This further demonstrates the early output nature and the monotonically decreasing property of the proposed full adder during spacer processing.

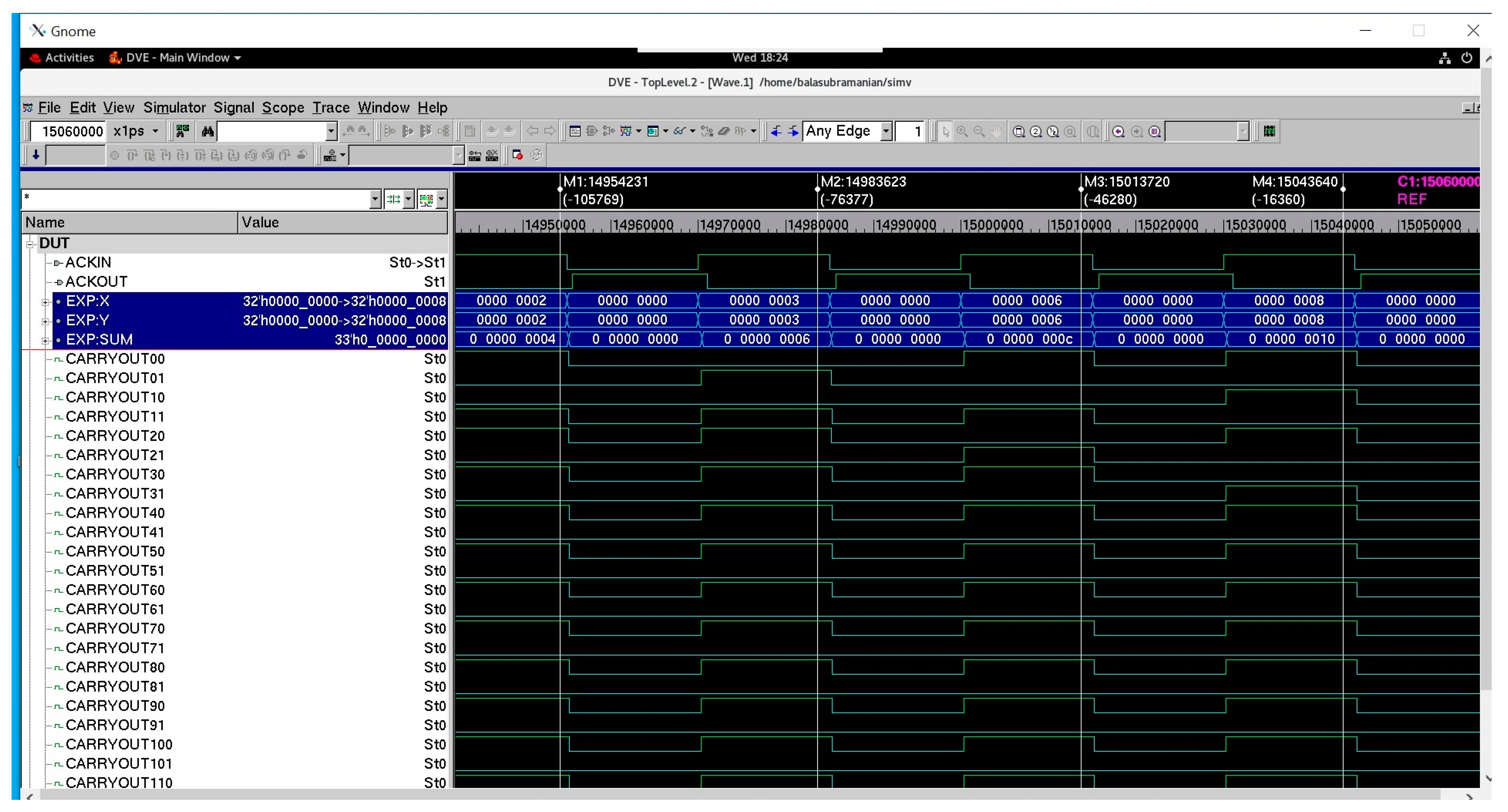
Figure 3 shows a screenshot of a portion of waveforms of a 32-bit asynchronous RCA constructed using the proposed full adder that corresponds to RtZ handshaking. The dual-rail 32-bit adder inputs are represented by (X311, X310), (X301, X300), …, (X01, X00) and (Y311, Y310), (Y301, Y300), …, (Y01, Y00). The dual-rail 33-bit adder output is represented by (SUM311, SUM310), (SUM301, SUM300), …, (SUM01, SUM00), and (CARRYOUT311, CARRYOUT310), with the last output bit representing the carry overflow from the addition. In Figure 3, data buses X and Y represent the adder inputs, and the data bus SUM represents the adder output. X comprises X311, X301, X291, …, X01, and Y comprises Y311, Y301, Y291, …, Y01, and SUM comprises CARRYOUT311, SUM311, SUM301, …, SUM01. Example addition of two hexadecimal numbers is captured in Figure 3, which is highlighted by the markers in the waveforms. The binary zeroes spacer separates two input data in the case of RtZ handshaking, and hence, the spacer is produced between two valid sum outputs in Figure 3.

The logical equivalent of the proposed full adder that corresponds to RtO handshaking is shown in Figure 4. Figure 4 is obtained by replacing all the gates in Figure 2 with their respective duals, as suggested in [17,28]. Reference [28] details, along with proofs, of how an IOM asynchronous circuit that corresponds to RtZ handshaking can be converted into an equivalent circuit that corresponds to RtO handshaking and vice versa by using the duals of logic gates (excepting for the C-element). Figure 4 uses the same number of gates as in Figure 2. However, the AO22 complex gates, 2-input AND gates, and the AO21 complex gates of Figure 2 are replaced by their corresponding duals viz. OA22 complex gates, 2-input OR gates, and OA21 complex gates, respectively, in Figure 4. The internal nodes K1, K2, K3, and K4 are highlighted in red in Figure 4.

The two comprehensive example scenarios below demonstrate and explain the proposed full adder’s monotonicity and early output characteristics corresponding to RtO handshaking.

4.3. Scenario 3

When data is supplied, if either X0 and Y0 or X1 and Y1 are set to binary 0, K1 will assume 0. Depending on whether C1 or C0 is 0, either Sum1 or Sum0 will assume 0, respectively. If X1 and Y1 or X0 and Y0 are both 0, either Carry1 or Carry0 will assume 0, respectively. As a result, all signal transitions in the proposed full adder during data processing are observed to be monotonically decreasing. Subsequently, when the (ones) spacer is supplied, even if X0 or Y0 (or X1 or Y1) assumes binary 1, K1 will assume 1. Consequently, either Sum1 or Sum0 (whichever assumed 0 earlier) will now assume 1 without waiting for C1 or C0 (whichever became 0 earlier) to assume 1. Further, if X1 or Y1 (or X0 or Y0) assumes 1, K3 or K4 (whichever became 0 earlier) will now assume 1. Also, if X0 or Y0 and X1 or Y1 assumes 1, K2 will assume 1. With K2 and K3 or K2 and K4 assuming 1, Carry1 or Carry0 (whichever became 0 earlier) will now assume 1 regardless of C1 or C0 assuming 1, and without both X0 and Y0 or X1 and Y1 assuming 1. This demonstrates the early output nature and the monotonically increasing property of the proposed full adder during spacer processing.

4.4. Scenario 4

When data is supplied, if either X0 and Y1 or X1 and Y0 assume 0, K2 will assume 0. Depending on whether C0 or C1 is 0, either Sum1 or Sum0 will assume 0, respectively. If C1 or C0 assumes 0, either Carry1 or Carry0 will assume 0, respectively. Hence, all signal transitions in the proposed full adder during data processing are observed to be monotonically decreasing. Subsequently, when the (ones) spacer is supplied, even if X0 or Y1 (or X1 or Y0) assumes binary 1, K2 will assume 1. Consequently, either Sum1 or Sum0 (whichever became 0 earlier) will now assume 1 without waiting for C0 or C1 (whichever became 0 earlier) to assume 1. Further, if X1 or Y0 (or X0 or Y1) assumes 1, K3 or K4 will assume 1. Thus, Carry1 or Carry0 (whichever became 0 earlier) will assume 1 without waiting for C1 or C0 to assume 1. This also demonstrates the early output nature and the monotonically increasing property of the proposed full adder during spacer processing.

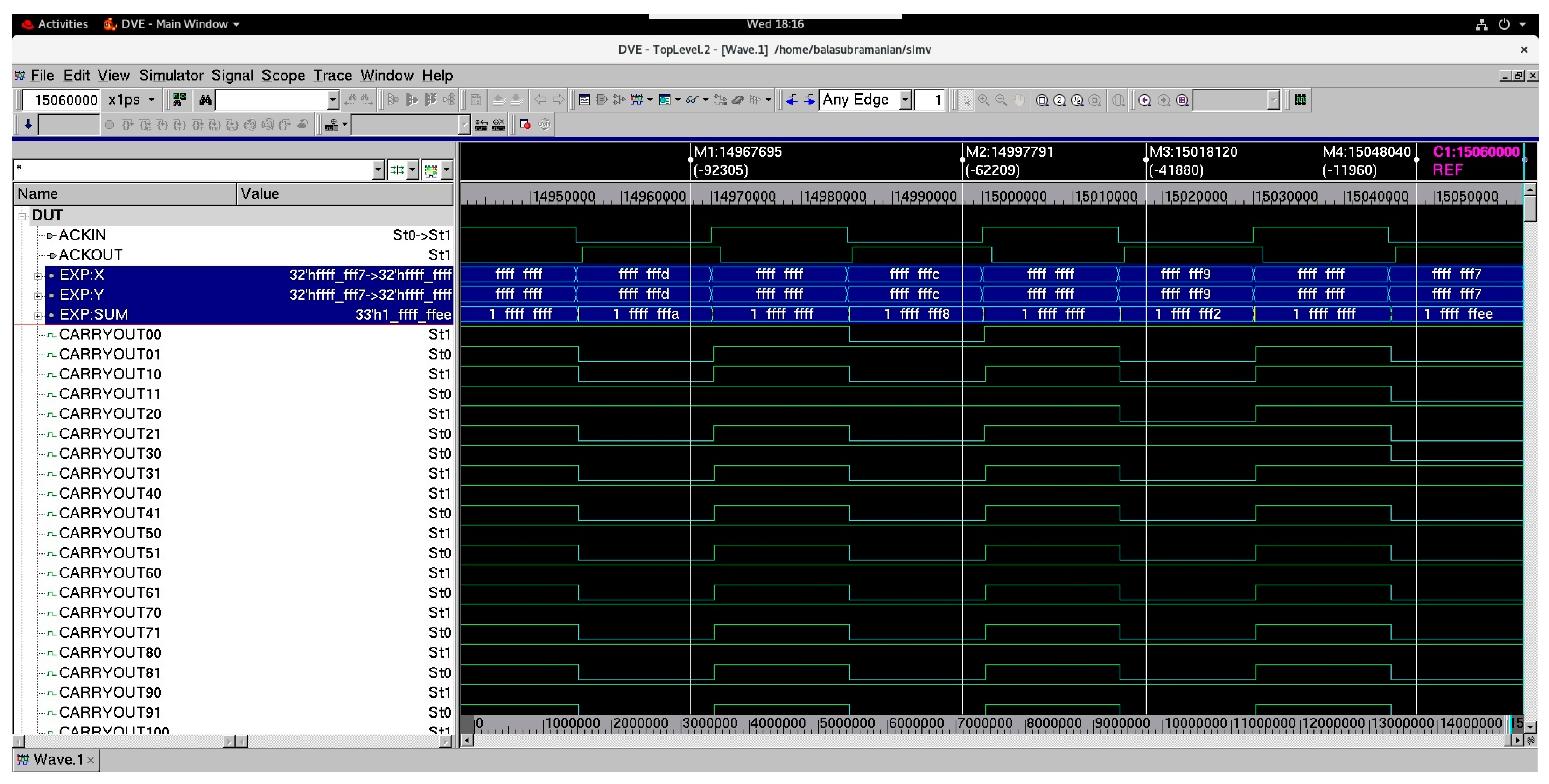
Figure 5 shows a screenshot of a portion of waveforms of a 32-bit asynchronous RCA constructed using the proposed asynchronous full adder that corresponds to RtO handshaking. As mentioned earlier, the dual-rail 32-bit adder inputs are represented by (X311, X310), (X301, X300), …, (X01, X00), and (Y311, Y310), (Y301, Y300), …, (Y01, Y00). The dual-rail 33-bit adder output is represented by (SUM311, SUM310), (SUM301, SUM300), …, (SUM01, SUM00), and (CARRYOUT311, CARRYOUT310), with the last output bit representing the carry overflow from the addition. In Figure 5, data buses X and Y represent the adder inputs, and the data bus SUM represents the adder output. X comprises X310, X300, X290, …, X00, and Y comprises Y310, Y300, Y290, …, Y00, and SUM comprises CARRYOUT310, SUM310, SUM300, …, SUM00. Example addition of two hexadecimal numbers is captured in Figure 5, which are highlighted by the markers in the waveforms. The binary ones spacer separates two input data in the case of RtO handshaking, and hence, the ones spacer is produced between two valid sum outputs in Figure 5.

From Section 4.1 to Section 4.4, it may be observed that the proposed asynchronous full adder, when incorporated in an N-bit RCA, would give rise to a forward latency of O[N × D_FA] and an optimal reverse latency of O[D_FA], thus resulting in an optimized cycle time of O[(N + 1) × D_FA]. Although the early output full adders of [27] also result in a similar cycle time magnitude when used to realize an N-bit RCA, nevertheless, compared to the proposed full adder, the full adders of [27] incorporate more gates, including C-elements and thus tend to occupy more area and dissipate more power. Further, the proposed full adder has a reduced number of logic levels compared to the full adders of [27], and this helps in a better optimization of forward and reverse latencies and the cycle time in comparison.

5. Implementation and Design Metrics

For physical realization, an IOM asynchronous circuit stage was implemented, consisting of an input register bank and an asynchronous circuit (here, an RCA), as depicted in Figure 1. A 32-bit addition was considered. It was assumed that AckI is supplied by the environment. The RCA is used as a platform for evaluating the performance of various full adders. Hence, many RCAs were realized by individually replicating and cascading different full adders, corresponding to RtZ and RtO handshaking separately.

In the RCAs, the carry input to the first (least significant) full adder is set to 0. For RtZ handshaking, this was achieved by connecting encoded rail C1 of the carry input to a tie-to-low standard cell and connecting encoded rail C0 to the AckI signal. Hence, when AckI = 1, C1 = 0, and C0 = 1 implies a carry input of 0 is given to the first full adder in the RCA. On the other hand, when AckI = 0, C1 = C0 = 0 signifies the provision of the (zeroes) spacer as the carry input to the first full adder in the RCA. For RtO handshaking, rail C1 of the carry input was connected to a tie-to-high standard cell, and rail C0 was connected to the AckI signal. Consequently, when AckI = 1, C1 = C0 = 1 signifies the provision of the (ones) spacer as the carry input to the first full adder in the RCA. When AckI = 0, C1 = 1, and C0 = 0 implies a carry input of 0 is given to the first full adder in the RCA. To realize the full adders and RCAs, a semi-custom design approach was adopted by utilizing the gates available in a 28 nm CMOS standard digital cell library [29]. The different asynchronous RCAs were structurally described in Verilog HDL and then simulated, and their design metrics were estimated. Since the standard cell library does not include a native C-element, a semi-custom realization of the 2-input C-element involving the provision of feedback in an AO222 complex gate (as shown in Figure 1d) was used to implement different full adders, RCAs, registers, and completion detectors. However, the proposed full adder does not require any C-element for its implementation, evident from Figure 2 and Figure 4.

To estimate the design characteristics of different asynchronous RCAs consisting of various full adders, we utilized a typical case high V_th (low leakage) standard cell library specification [29], which features a supply voltage of 1.05V and an operating temperature of 25 °C. To conduct simulations and estimate the design metrics, we used Synopsys EDA tools. To perform functional simulations using VCS, we used a test bench containing approximately a thousand random data inputs (plus an equal number of spacer inputs), which were supplied at a latency of 15 ns to accommodate the slowest RCA. Two test benches were used, one corresponding to RtZ handshaking and an equivalent one corresponding to RtO handshaking. The test benches included both data and spacer. The total power dissipation was estimated based on the switching activity captured during the functional simulations. Default wire loads were assumed, and a fanout-of-4 drive strength was assigned to all the sum bits of the adders during the design metrics estimation. An advanced timing analysis was performed using PrimeTime by employing a virtual clock to constrain the input and output ports of the adders, although the clock itself was not physically implemented. Thus, the clock being virtual did not contribute to the design metrics estimated. The forward latency of the adders (which is equivalent to the standard critical path delay) was directly estimated, while the reverse latency was estimated based on the path delays specified in the timing reports. The cycle time, which represents the duration to complete a data transaction, was determined as the sum of the forward and reverse latencies. The total (average) power dissipation was estimated using PrimePower.

Table 1. Design metrics of 32-bit asynchronous RCAs corresponding to RtZ and RtO handshaking, implemented using a 28 nm CMOS technology.

Reference; RCA Legend	Timing Parameters (ns)			Area (µm2)	Power (µW)
	Forward Latency	Reverse Latency	Cycle Time
RtZ Handshaking
[18]; RZ1 *	14.70	14.70	29.40	2518.32	1446
[20]; RZ2 *	9.34	9.34	18.68	2493.93	1449
[20]; RZ3 #	8.31	8.31	16.62	2412.60	1445
[19]; RZ4 *	9.12	9.12	18.24	2282.47	1429
[22]; RZ5 #	7.07	7.07	14.14	2005.96	1415
[23]; RZ6 #	4.52	0.74	5.26	2087.28	1431
[24]; RZ7 #	3.40	0.82	4.22	2038.49	1421
[26]; RZ8 $	3.19	0.70	3.89	1648.12	1405
[27]; RZ9 $%	3.14	0.73	3.87	1534.27	1396
[27]; RZ10 $^	3.02	0.72	3.74	1648.12	1403
[25]; RZ11 #α	8.97	8.97	17.94	2103.55	1424
[25]; RZ12 #β	6.64	1.42	8.06	2282.47	1451
[25]; RZ13 #γ	6.20	1.04	7.24	2339.40	1437
RZ14 (Proposed)	2.87	0.48	3.35	1387.88	1381
RtO Handshaking
[18]; RO1 *	14.24	14.24	28.48	2518.32	1445
[20]; RO2 *	8.84	8.84	17.68	2363.80	1443
[20]; RO3 #	8.12	8.12	16.24	2347.53	1442
[19]; RO4 *	8.97	8.97	17.94	2282.47	1429
[22]; RO5 #	7.04	7.04	14.08	2005.96	1415
[23]; RO6 #	3.88	0.73	4.61	2087.28	1431
[24]; RO7 #	3.39	0.81	4.20	2038.49	1421
[26]; RO8 $	3.02	0.70	3.72	1648.12	1404
[27]; RO9 $%	3.16	0.72	3.88	1534.27	1395
[27]; RO10 $^	2.99	0.70	3.69	1648.12	1402
[25]; RO11 #α	9.05	9.05	18.10	2103.55	1424
[25]; RO12 #β	6.75	1.19	7.94	2282.47	1456
[25]; RO13 #γ	6.31	1.03	7.34	2339.40	1437
RO14 (Proposed)	2.85	0.48	3.33	1387.88	1380

* Uses strong indication full adder; ^# uses weak indication full adder. ^$ Uses early output full adder (^% AOPT_EO_FA, ^{^} LOPT_EO_FA of [27]). ^α Uses SN full adder, ^β SNX full adder, and ^γ SNFC full adder of [25].

displays the estimated design metrics for the IOM asynchronous RCAs realized using different asynchronous full adders, including the proposed full adder. The design metrics include forward latency, reverse latency, cycle time, area, and total power dissipation. The input registers and the completion detector remain the same for all the RCAs for RtZ/RtO handshaking, with the only variation being the underlying adder logic. Therefore, the variations in the design metrics of the RCAs can be attributed to the differences in the full adder logic. For reference purposes and to discuss the results, adder legends RZ1 to RZ14 (for RtZ handshaking) and RO1 to RO14 (for RtO handshaking) are used, as given in Table 1. The adder legends represent various asynchronous RCAs comprising different asynchronous full adders, including the proposed full adder, which were discussed in Section 3 and Section 4.

The forward latency and reverse latency of RZ14 are approximately represented by Equations (9) and (10), and the forward latency and reverse latency of RO14 are approximately represented by Equations (11) and (12) for an N-bit addition. Equations (9) to (12) represent approximate delay models since interconnect and parasitic delays are not accounted for in the theoretical delay modeling. In the equations, D_Register, D_AO22, D_AO21, D_OA22, and D_OA21 denote the typical propagation delay of the register (which is a 2-input C-element), an AO22 complex gate, an AO21 complex gate, an OA22 complex gate, and an OA21 complex gate, respectively.

RZ14_{Forward_Latency} = D_Register + (D_AO22 + D_AO21) + (N − 2) × D_AO21 + D_AO22

(9)

RZ14_{Reverse_Latency} = D_Register + 2 × D_AO22

(10)

RO14_{Forward_Latency} = D_Register + (D_OA22 + D_OA21) + (N − 2) × D_OA21 + D_OA22

(11)

RO14_{Reverse_Latency} = D_Register + 2 × D_OA22

(12)

In Equations (9) and (11), the first term on the right side denotes the delay associated with an input register, which corresponds to the delay of a 2-input C-element. The second term signifies the delay encountered in the first full adder to generate the carry output. The third term represents the delay involved in carry propagation through (N − 2) full adders. Finally, the fourth term accounts for the delay in the last full adder to generate the most significant sum bit of the addition. In Equations (10) and (12), the first term on the right side represents the delay of an input register, while the second term signifies the delay incurred to produce the spacer sum output, which is produced simultaneously by all the N full adders.

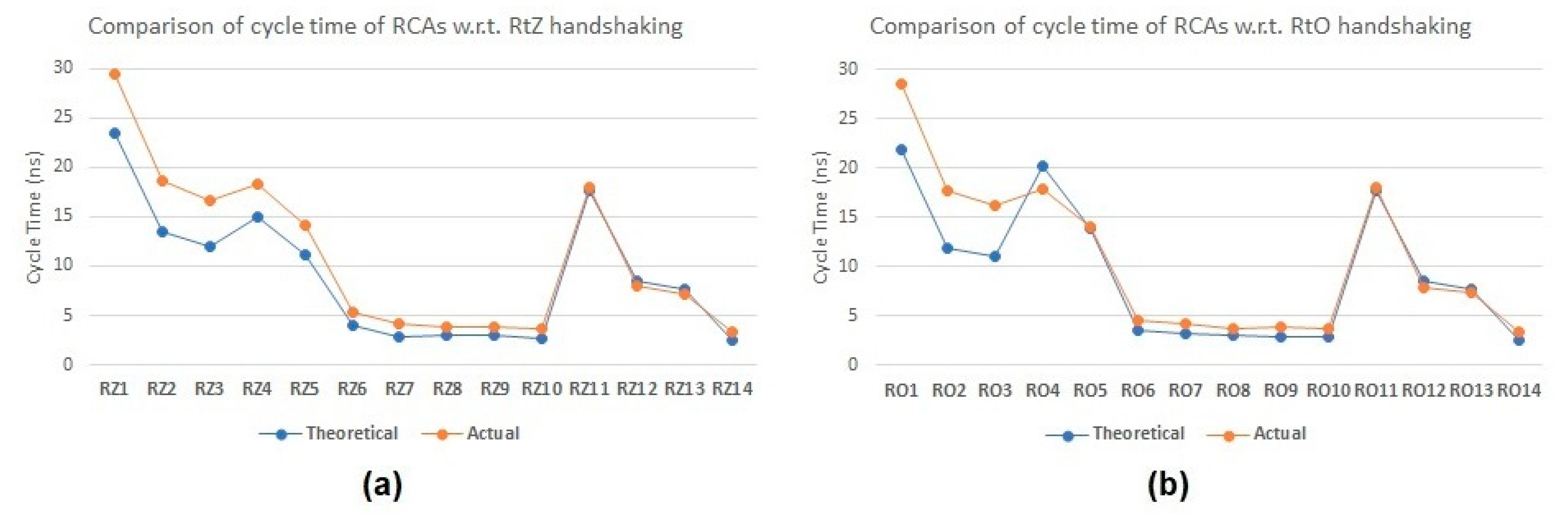
From Table 1, it is evident that the RCAs implemented using the proposed full adder viz. RZ14 and RO14 exhibit the lowest forward latency and reverse latency, resulting in the shortest cycle time compared to RCAs comprising other full adders for RtZ and RtO handshaking, respectively. This is mainly because the proposed full adder does not contain any C-element and, thus, has a relatively reduced logic complexity and fewer elements in the critical data path. Furthermore, it may be recalled from the previous section that the proposed asynchronous full adder is both monotonic and of the early output type. Consequently, irrespective of the receipt of the carry input, the sum and carry outputs of the proposed full adder can assume the spacer during the RtZ/RtO phase. Therefore, the reverse latency of the RCA incorporating the proposed full adder is governed by the delay of just one full adder, thus resulting in an optimal configuration. To affirm this reasoning, we theoretically calculated the cycle time of RCAs comprising different full adders and compared those with the actual (estimated) cycle time of RCAs for RtZ and RtO handshaking; this comparison is illustrated in Figure 6a,b. For a theoretical calculation of the cycle time, we used only the typical propagation delays given in the datasheet [29], and interconnect delays and parasitics were not accounted for. Thus, a variation between the theoretical and actual cycle times can be expected, as seen in Figure 6. However, Figure 6a,b shows a good correlation and/or reflects a similar trend between the theoretical and actual cycle time of almost all asynchronous RCAs comprising different asynchronous full adders for RtZ and RtO handshaking, respectively. Equations underpinning the theoretical calculation of cycle time for various asynchronous RCAs, which govern their forward latency and reverse latency, are given in Appendix A.

The areas of the full adders utilized in RCAs RZ1 to RZ14 and RO1 to RO14 are graphically represented in Figure 7a,b, with the red bar indicating the (optimized) area occupancy of the proposed full adder. RZ14 and RO14 utilize the smallest area for RtZ and RtO handshaking among their counterparts. This is attributed to the fact that the proposed full adder employed in RZ14 and RO14 occupies less silicon in comparison to other asynchronous full adders, as depicted in Figure 7a,b. Unlike the other full adders, the proposed full adder does not include the C-element in its logic implementation. This is the reason for its reduced area occupancy. Consequently, due to its smaller area, RZ14 and RO14 incorporating the proposed full adder dissipate less power in comparison to other RCAs that employ different full adders, as seen in Table 1. It may be noted from Table 1 that there is no big difference between the power dissipation of various RCAs. This is because all the IOM asynchronous RCAs incorporate the monotonic cover constraint [1], which results in the activation of one signal path from a primary input to a primary output.

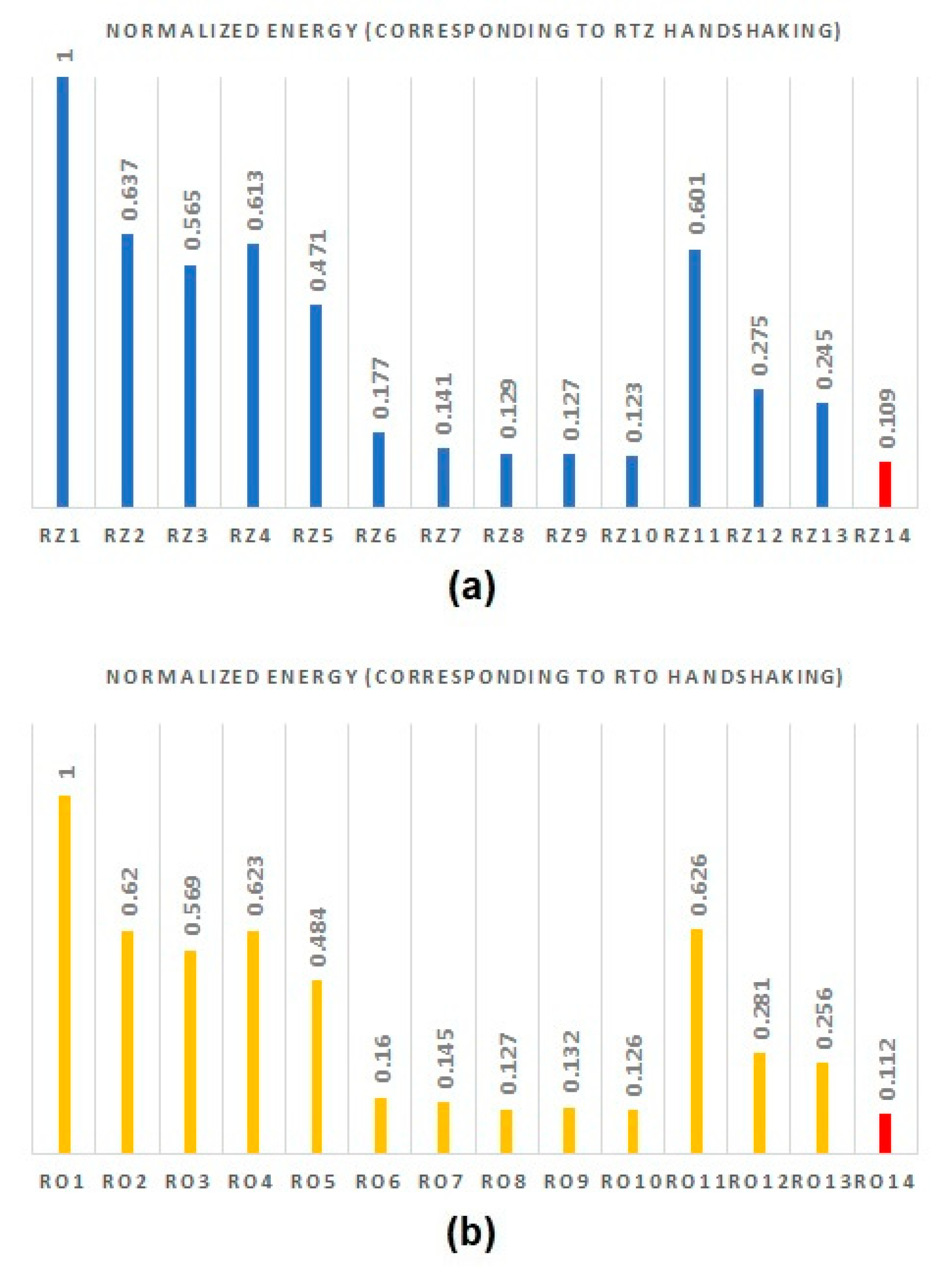
In IOM asynchronous circuits, the energy metric, which is an important figure of merit for low-power design [30], is obtained by multiplying power dissipation and cycle time. Since power and cycle time are desirable to be minimized, the power–cycle time product is also desirable to be minimum. The power and cycle time given in Table 1 are multiplied and then normalized. The normalized power–cycle time product of the asynchronous RCAs is plotted in Figure 8a,b, which corresponds to RtZ and RtO handshaking. To achieve normalization, the actual product of power and cycle time for each RCA is divided by the highest value of the power–cycle time product for RtZ and RtO handshaking separately, which corresponds to RZ1 and RO1, respectively. In Figure 7a,b, the highest value of 1 for the normalized power–cycle time product indicates an inferior design in terms of energy efficiency. Thus, the smallest value of the normalized power–cycle time product represents the most energy-efficient design, which corresponds to RZ14 and RO14 comprising the proposed full adder with respect to RtZ and RtO handshaking. The least values of normalized power–cycle time product are highlighted by the red bar in Figure 8a,b.

According to Table 1, among the existing designs, RZ10 and RO10 utilizing the latency-optimized early output full adder from [24], known as LOPT_EO_FA, demonstrate a shorter cycle time for RtZ handshaking and RtO handshaking, respectively. In comparison with RZ10, RZ14, incorporating the proposed full adder, achieves a 10.4% reduction in cycle time, a 15.8% reduction in area, and an 11.8% reduction in the power–cycle time product for RtZ handshaking with no power penalty. Likewise, in comparison with RO10, RO14, incorporating the proposed full adder, achieves a 9.8% reduction in cycle time, a 15.8% reduction in area, and an 11.2% reduction in the power–cycle time product for RtO handshaking with no power penalty. Between RZ14 and RO14 (which is the proposed full adder corresponding to RtZ and RtO handshaking), there is no notable difference in terms of the design metrics, and both are competitive designs.

6. Conclusions

The full adder serves as a fundamental component, i.e., a building block in arithmetic circuits. This article introduced a novel IOM asynchronous full adder, which is both monotonic and of the early output type. The RCA was considered as a platform to evaluate the performance of various asynchronous full adders, and it was found that the proposed full adder performs better than existing gate-level asynchronous full adders across all the design metrics. In future studies, it would be worthwhile to explore the usefulness of the proposed full adder in efficiently implementing other computer arithmetic operations, such as, say, multiplication, to enhance the performance of IOM asynchronous multipliers.