Fuzzy Logic System for Classifying Multiple Sclerosis Patients as High, Medium, or Low Responders to Interferon-Beta

Abstract

Interferon-beta is one of the most widely prescribed disease-modifying therapies for multiple sclerosis patients. However, this treatment is only partially effective, and a significant proportion of patients do not respond to this drug. This paper proposes an alternative fuzzy logic system, based on the opinion of a neurology expert, to classify relapsing–remitting multiple sclerosis patients as high, medium, or low responders to interferon-beta. Also, a pipeline prediction model trained with biomarkers associated with interferon-beta responses is proposed, for predicting whether patients are potential candidates to be treated with this drug, in order to avoid ineffective therapies. The classification results showed that the fuzzy system presented 100% efficiency, compared to an unsupervised hierarchical clustering method (52%). So, the performance of the prediction model was evaluated, and 0.8 testing accuracy was achieved. Hence, a pipeline model, including data standardization, data compression, and a learning algorithm, could be a useful tool for getting reliable predictions about responses to interferon-beta.

1. Introduction

Multiple sclerosis (MS) is a chronic inflammatory disease of the central nervous system (CNS) [1]. Although MS can take several different forms, the most common type is relapsing–remitting MS (RRMS), characterized by alternating periods of remission and intensification of symptoms [2]. The etiology of MS can include several factors, such as genetic susceptibility and viral infections [3,4,5], which activate the immune system, generating immune dysregulation, and producing an immune attack against the myelin covering of the CNS [6]. Studies have shown that susceptibility to MS is genetically dependent, but the specific gene factors remain largely unknown. It is known that peripheral self-antigen-specific immune cells are activated during the antigen presentation process, and that they enter the CNS through the disrupted blood-–brain barrier (BBB) [7]. The route of entry depends on the phenotype and activation state of the T cells. T cells play important roles in cellular immunity [8]. T cells are divided into helper T cells (Th) and regulatory T cells (Treg).

The autoimmune etiology of MS has been the target of the therapeutic approach to patients. Treatment of MS can be divided into treatment of MS symptoms, treatment of MS relapse, and treatment modifying disease progression. The main target of MS treatment is delaying the disease progression [9]. Interferon-beta (IFN-$\beta$) is one of the most widely prescribed disease-modifying therapies for RRMS patients. IFN-$\beta$ has multiple pathways of action on the immune system. IFN-$\beta$ inhibits the activated proliferation of T cells, and prevents the migration of activated immune cells through the BBB. Also, this drug inhibits the production of pro-inflammatory cytokines (e.g., IL-2, IL-12, IFN-$\gamma$), induces an increase in anti-inflammatory cytokines (e.g., IL-4, IL-5, IL-10 and TGF-$\beta$), and promotes re-myelination in CNS [10,11]. IFN-$\beta$ can also prevent the differentiation of inflammatory Th1/Th17 cells, and it can change the phenotype of Th cells from inflammatory Th1 to anti-inflammatory Th2 cells. Studies have shown that IFN-$\beta$ can significantly improve the clinical symptoms of patients, reduce the annual recurrence rate, and delay the progress of the disease [12]. However, IFN-$\beta$ is only partially efficient, and a significant proportion of MS patients do not respond to this treatment, with the proportion of non-responders ranging from 20 to 50% [13]. Hence, in this paper, a pipeline model based on potential biomarkers associated with the response to IFN-$\beta$ is proposed, to predict whether MS patients are potential candidates to be treated with this drug. Studies have researched the effect of gene polymorphisms on therapeutic responses to IFN-$\beta$, which can affect the efficacy of this therapy. Bustamante et al. [14] analyzed the relationship between single-nucleotide polymorphisms (SNPs) disposed in type I IFN-induced genes, genes becoming the toll-like receptor (TLR) pathway, and genes encoding neurotransmitter receptors, and the response to IFN-$\beta$ treatment in MS patients. Martinez et al. [15] evaluated the effect of polymorphisms in some genes (CD46, CD58, FHIT, IRF5, GAPVD1, GPC5, GRBRB3, MxA, PELI3, and ZNF697) on responses to IFN-$\beta$ treatment among RRMS patients. From seven selected SNPs, PELI3 and GABRR3 polymorphisms were exposed, to be related to IFN-$\beta$ responses.

Genome-wide research is generated in large numbers of data, and there is a need for soft computing methods (SCMs)—such as artificial neural networks, fuzzy systems, evolutionary algorithms, or metaheuristic and swarm intelligence algorithms—that can deal with this amount of data [16]. Studies of fuzzy systems have only focused on MS diagnosis. Ayangbekun & Jimoh [17] designed a fuzzy inference system for diagnosing five brain diseases: Alzheimer’s, Creutzfeldt–Jakob, Huntington’s, MS, and Parkinson’s. Hosseini et al. [18] developed a clinical decision support system (CDSS), to help specialists diagnose MS with a relapsing–remitting phenotype. Matinfar et al. [19] proposed an expert system for MS diagnosis, based on clinical symptoms and demographic characteristics. However, it is necessary to design new expert systems that can classify the possible responses to treatments in MS patients. Other studies have applied machine learning (ML) techniques to diagnose early MS. Goyal et al. [20] trained a random forest (RF) model with the serum level of eight cytokines (IL-1$\beta$, IL-2, IL-4, IL-8, IL-10, IL-13, IFN-$\gamma$, and TNF-$\alpha$) in MS patients, to detect predictors for disease. Chen et al. [21] implemented a support vector machine (SVM) model, using gene expression profiles to identify potential biomarkers for MS diagnosis. CXCR4, ITGAM, ACTB, RHOA, RPS27A, UBA52, and RPL8 genes were detected. Among the studies that suggest genetics can predict the pharmacological response to a treatment, Fagone et al. [22] trained an uncorrelated reduced centroid (UCRC) algorithm to identify a subset of genes that could predict the responses to natalizumab in RRMS patients. A specific gene expression profile of CD4+ T cells could characterize the responsiveness.

Although the studies presented above have shown the efficiency of IFN-$\beta$ at improving the clinical symptoms of MS patients, a proportion of patients did not respond to this treatment. Genome-wide analytical studies have been conducted, in order to identify genetic factors associated with the responses to IFN-$\beta$ treatment. Gurevich et al. [23] identified a subgroup of secondary progressive MS (SPMS) patients presenting a gene expression signature similar to that of RRMS patients who are clinical responders to IFN-$\beta$ treatment. SPMS patients were classified using unsupervised hierarchical clustering, according to IFN-inducible gene expression profiling identified in RRMS clinical responders to treatment. Although, the hierarchical clustering method is easy to implement, it rarely provides the best solution, due to lots of arbitrary decisions. Clarelli et al. [24] detected genetic factors that affect the long-term response to IFN-$\beta$. The found pathways associated with inflammatory processes and presynaptic membrane, i.e., the genes related to the glutamatergic system (GRM3 and GRIK2), play a potential role in the response to IFN-$\beta$. Jin et al. [25] implemented a feature selection method based on differentially correlated edges (DCE), to identify the most relevant genes associated with the response to IFN-$\beta$ treatment in RRMS patients. Of the 23 identified genes, 7 had a confidence score > 2: CXCL9, IL2RA, CXCR3, AKT1, CSF2, IL2RB, and GCA. Because the analyzed data were unlabeled, the responder category was restricted to patients whose first relapse time was more than five years (60 months), resulting in nine responders and nine non-responders. So, seven patients were excluded from the analysis. Hence, we attempt to address some of the issues above in this research. The main contributions of this paper are as follows:

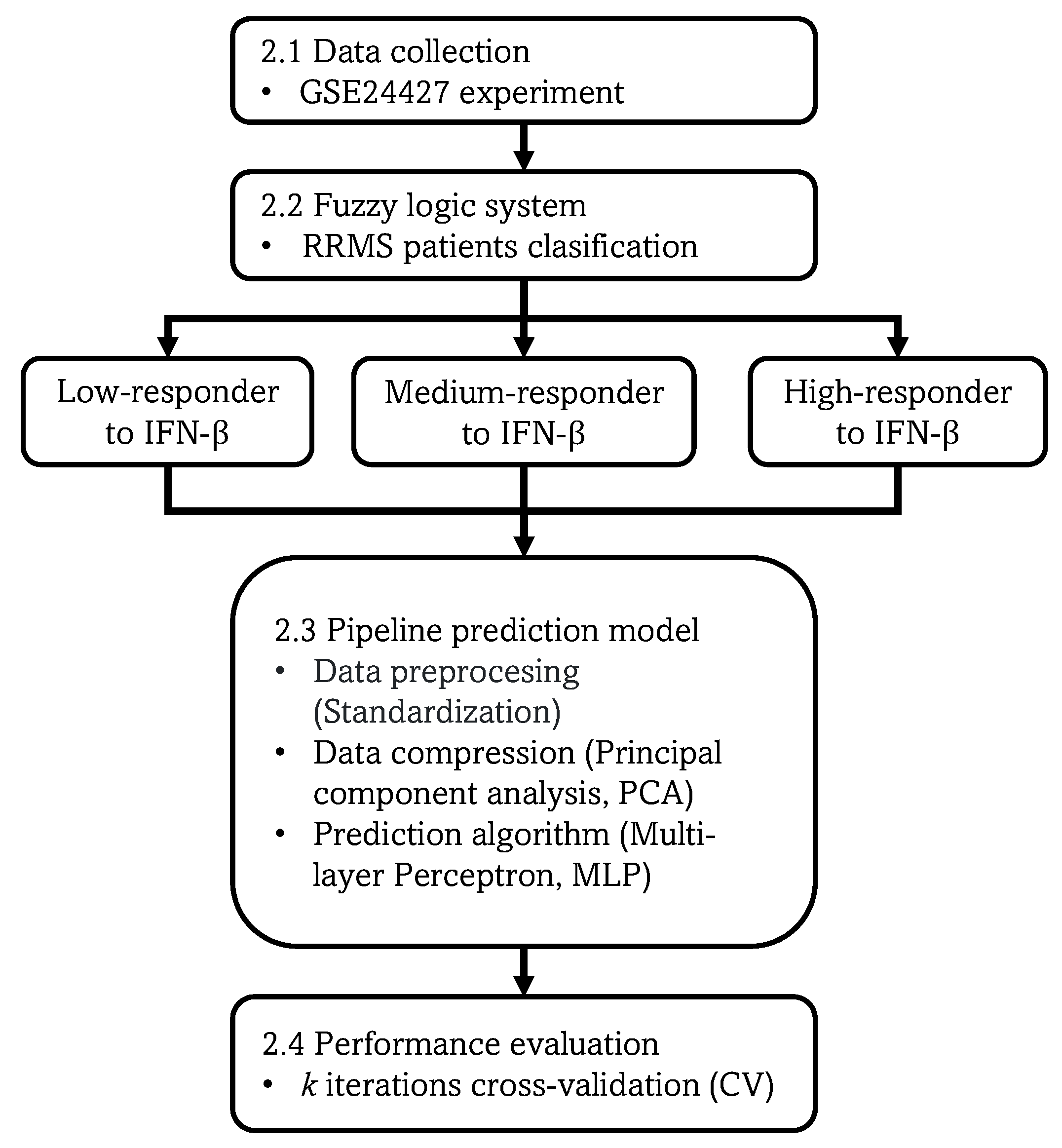
• An alternative fuzzy system based on expert knowledge, with linguistic rules to classify RRMS patients as high, medium, or low responders to IFN-$\beta$ treatment.
• A pipeline prediction model, including a data preprocessing technique, a transformation technique for data compression, and a learning algorithm for making predictions on new data. The prediction model is trained with biomarkers associated with the IFN-$\beta$ response for predicting whether MS patients are potential candidates to be treated with this drug, in order to avoid ineffective therapies.

2. Materials and Methods

The strategy followed in this research is described in the flowchart of Figure 1, which divides the proposal into four stages.

Figure 1. Proposed methodology. The gene data, demographic, and clinical characteristics are collected. Then, the RRMS patients are classified by the fuzzy logic system. A pipeline prediction model is implemented, including data standardization, PCA for data compression, and an MLP algorithm for making predictions. Finally, the k-iterations CV is implemented, for evaluating the model prediction performance.

2.1. Data Collection

The dataset was collected from the GSE24427 expression profiling by array experiment, available in the public repository of genomic data GEO [26]. Through the GPL96 [HG-U133A] platform (Affymetrix Human Genome U133A Array), the genome-wide expression profiles of peripheral blood mononuclear cells from 25 RRMS patients were obtained. Patients were treated with subcutaneous IFN-beta-1b (Betaferon, Bayer Healthcare) at the standard dose (250 µg every other day). Patient blood samples were drawn before first-dose, second-dose, 1st-month, 12th-month, and 24th-month IFN-$\beta$ injection. The expression summary values were analyzed by GEO2R, an interactive web tool that allows viewing of a specific gene expression through the profile graph tab. On the one hand, the GPL96 platform enabled us to see demographic and clinical characteristics of RRMS patients, which were used as input variables for the proposed fuzzy system, and these are presented in Table 1.

Table 1. Demographic and clinical characteristics.

Sample	Gender	Age	EDSS 1 1st Month	EDSS 1 24th Month
1	Female	63	4	5.5
2	Male	45	1	1
3	Female	25	1	1
4	Female	27	4	3.5
5	Female	51	3	2.5
6	Female	41	2	4.5
7	Female	44	4	3
8	Male	30	1.5	2
9	Female	26	4	3.5
10	Male	42	1	1
11	Male	29	2	2.5
12	Female	28	1.5	2.5
13	Female	48	1	1
14	Female	47	3.5	3
15	Female	42	2	3
16	Female	50	3.5	3.5
17	Male	37	1.5	4.5
18	Female	43	2	2
19	Male	54	3	2
20	Male	40	1	1
21	Female	48	2	2
22	Female	38	2	3
23	Male	18	1.5	2
24	Female	24	1	1
25	Male	38	1	1

¹ Expanded disability status scale.

On the other hand, through the GPL96 platform, the expression values of 15 biomarkers associated with the response to IFN-$\beta$—IL-2, IL-12, IFN-$\gamma$, TNF-$\alpha$, IL-4, IL-10, TGF-$\beta$, CD46, CD58, FHIT, IRF5, GAPVD1, GPC5, GRM3, and GRIK2—were collected and integrated into an Excel spreadsheet, for training the proposed pipeline prediction model. For example, the IL-2 and IL-4 cytokines expression values are displayed in Figure 2 and Figure 3. The database is the same as the one used by Jin et al. [25]. However, the biomarkers are a little different.

Figure 2. IL-2 cytokine. The expression values of 25 RRMS patients corresponding to five doses: before first-dose, second-dose, 1st-month, 12th-month, and 24th-month IFN-$\beta$ injection.

Figure 3. IL-4 cytokine. The expression values seem more scattered than IL-2 cytokine.

2.2. Fuzzy Logic System

Fuzzy systems are structures based on fuzzy sets and fuzzy logic theories for processing inaccurate information [27]. Their main property includes symbolic knowledge representation in a form of fuzzy conditional (if-then) rules. The typical structure of a fuzzy system is described in Figure 4.

Figure 4. Fuzzy system structure. The fuzzyfier transforms the values of input variables into an N-dimensional fuzzy set A (linguistic values of the output variable) defined on the universe $\mathbb{X}$, by means of approximate reasoning (inference engine) using expert knowledge, which is represented as a set of fuzzy conditional rules (knowledge base). The result of the approximate reasoning is a fuzzy set $B\left(y\right)$. The defuzzyfier computes a representative numerical output $y_0$ from the result of fuzzy set $B\left(y\right)$ defined on the universe $\mathbb{Y}$.

The fuzzyfier can be defined as the membership function ${\mu }_A\left(x\right)$ of the fuzzy set A. Demographic and clinical characteristics of RRMS patients are used as input variables for the fuzzyfier. The numerical output $y_0$ is computed using the center of gravity (COG) method [28], as in Equation (1):

$$y_0=\frac{{\sum }_{i=1}^n{y}_i{\mu }_B\left(y_i\right)}{{\sum }_{i=1}^n{\mu }_B\left(y_i\right),}$$

(1)

where ${\mu }_B\left(y\right)$ represents the membership function of fuzzy set $B\left(y\right)$. The proposed fuzzy system is designed through the Fuzzy Logic Designer App of MATLAB R2023a software. The structure of the proposed fuzzy system is based on the Mamdani-–Assilan fuzzy system (MAFS) [29], which includes a set of conditional fuzzy rules, in the form of Equation (2), that can be determined by a human expert:

$$\mathcal{R}={\left\{R^i\right\}}_{i=1}^N={\{ifan{d}_{n=1}^N\left(X_{n}is{L}_{A_n}^{\left(i\right)}\right),thenYis{L}_B^{\left(i\right)}\}}_{i=1}^I,$$

(2)

where I is the number of rules, $X_n$ represents the input linguistic variables, Y is the output linguistic variable, and $L_{A_n}$ and $L_B$ are the linguistic values, defined by fuzzy sets $A_N$, and B on universes ${\mathbb{X}}_N$ and $\mathbb{Y}$, respectively. In this paper, the input linguistic variables describing the demographic characteristics—including gender and age—and the clinical characteristics—including expanded disability status scale (EDSS) 1st month and 24th month—are defined: ${\mathcal{N}}_1=$ “mean gender”; ${\mathcal{N}}_2$ = “mean age”; ${\mathcal{N}}_3$ = “mean EDSS 1st month”; ${\mathcal{N}}_4$ = “mean EDSS 24th month”. The sets of possible linguistic values are collections of different labels describing the gender, age, EDSS 1st month, and EDSS 24th month: $L_{A_1}$ = {“female”, “male”}; $L_{A_2}$ = {“pediatric”, “adult”, “elderly”}; $L_{A_3}$ = {“low”, “medium”, “high”}; $L_{A_4}$ = {“low”, “medium”, “high”}, and response to IFN-$\beta$: $L_B$ = {“low”, “medium”, “high”}. To each one of the labels, the fuzzy sets $A_N^{\left(i\right)}$ are assigned, defined on the universe ${\mathbb{X}}_N$, which represents the range of possible values. The whole description of the defined linguistic variables is presented in Table 2.

Table 2. Linguistic variables description.

Membership Function	Fuzzy Set	Universe of Discourse	Parameters and Type
${\mu }_{A_1^{\left(1\right)}}\left(gender\right)$	$A_1^{\left(1\right)}$	${\mathbb{X}}_1$: [0 a 1]	Female: [−0.75; −0.083; 0.083; 0.75] Trapezoidal
			Male: [0.25; 0.916; 1.083; 1.75] Trapezoidal
${\mu }_{A_2^{\left(1\right)}}\left(age\right)$	$A_2^{\left(1\right)}$	${\mathbb{X}}_2$: [0 a 100] years	Pediatric: [−37.5; −4.167; 4.167; 37.5] Trapezoidal
			Adult: [8.333; 50; 91.666] Triangular
			Elderly: [62.5; 95.83; 104.2; 137.5] Trapezoidal
${\mu }_{A_3^{\left(1\right)}}\left(EDSS{}^{1}1stmonth\right)$	$A_3^{\left(1\right)}$	${\mathbb{X}}_3$: [0 a 10] units	Low: [−3.75; −0.416; 1.0; 5.0] Trapezoidal
			Medium: [1.0; 5.0; 9.0] Triangular
			High: [5.0; 9.0; 10.42; 13.75] Trapezoidal
${\mu }_{A_4^{\left(1\right)}}\left(EDSS{}^{1}24thmonth\right)$	$A_4^{\left(1\right)}$	${\mathbb{X}}_4$: [0 a 10] units	Low: [−3.75; −0.416; 1.0; 5.0] Trapezoidal
			Medium: [1.0; 5.0; 9.0] Triangular
			High: [5.0; 9.0; 10.42; 13.75] Trapezoidal
${\mu }_B\left(ResponsetoIFNb\right)$	$B\left(y\right)$	$\mathbb{Y}$: [0 a 1] units	Low: [−0.375; −0.04167; 0.1, 0.5] Trapezoidal
			Medium: [0.1; 0.5; 0.9] Triangular
			High: [0.5; 0.9; 1.042; 1.375] Trapezoidal

¹ Expanded disability status scale.

For example, the graphics of the membership functions ${\mu }_{A_2^{\left(1\right)}}\left(age\right)$, ${\mu }_{A_4^{\left(1\right)}}$$\left(EDSS24thmonth\right)$, and ${\mu }_B(ResponsetoIFN-\beta )$ of the fuzzy sets $A_2^{\left(1\right)}$, $A_4^{\left(1\right)}$, and $B\left(y\right)$ are displayed in Figure 5, Figure 6 and Figure 7, respectively.

Figure 5. Set of linguistic values, which are three labels describing the “age” input variable, corresponding to fuzzy set $A_2^{\left(1\right)}$.

Figure 6. Set of linguistic values, which are three labels describing the “EDSS 24th month” input variable, corresponding to fuzzy set $A_4^{\left(1\right)}$.

Figure 7. Set of linguistic values, which are three labels describing the “Response to IFN-$\beta$” output variable, corresponding to fuzzy set $B\left(y\right)$.

The fuzzy conditional rules (knowledge base) are meant to decide the influence of the input variables on responses to IFN-$\beta$ treatment. Table 3 and Table 4 display the 36 defined rules, according to the opinion of a neurology expert:

Table 3. Fuzzy rules definition (first part).

#	Rule
1	If gender is female and age is adult, and if EDSS 1st month is low and EDSS 24th month is low, then response to IFNb is medium.
2	If gender is female and age is adult, and if EDSS 1st month is medium and EDSS 24th month is medium, then response to IFNb is medium.
3	If gender is female and age is adult, and if EDSS 1st month is high and EDSS 24th month is high, then response to IFNb is medium.
4	If gender is female and age is elderly, and if EDSS 1st month is low and EDSS after 24th month is low, then response to IFNb is medium.
5	If gender is female and age is elderly, and if EDSS 1st month is medium and EDSS 24th month is medium, then response to IFNb is medium.
6	If gender is female and age is elderly, and if EDSS 1st month is high and EDSS 24th month is high, then response to IFNb is medium.
7	If gender is male and age is adult, and if EDSS 1st month is low and EDSS 24th month is low, then response to IFNb is medium.
8	If gender is male and age is adult, and if EDSS 1st month is medium and EDSS 24th month is medium, then response to IFNb is medium.
9	If gender is male and age is adult, and if EDSS 1st month is high and EDSS 24th month is high, then response to IFNb is medium.
10	If gender is male and age is elderly, and if EDSS 1st month is low and EDSS 24th month is low, then response to IFNb is medium.
11	If gender is male and age is elderly, and if EDSS 1st month is medium and EDSS 24th month is medium, then response to IFNb is medium.
12	If gender is male and age is elderly, and if EDSS 1st month is high and EDSS 24th month is high, then response to IFNb is medium.
13	If gender is female and age is adult, and if EDSS 1st month is low and EDSS 24th month is medium, then response to IFNb is low.
14	If gender is female and age is adult, and if EDSS 1st month is low and EDSS 24th month is high, then response to IFNb is low.
15	If gender is female and age is adult, and if EDSS 1st month is medium and EDSS 24th month is high, then response to IFNb is low.
16	If gender is female and age is elderly, and if EDSS 1st month is low and EDSS 24th month is medium, then response to IFNb is low.
17	If gender is female and age is elderly, and if EDSS 1st month is low and EDSS 24th month is high, then response to IFNb is low.
18	If gender is female and age is elderly, and if EDSS 1st month is medium and EDSS 24th month is high, then response to IFNb is low.

Table 4. Fuzzy rules definition (second part).

#	Rule
19	If gender is male and age is adult, and if EDSS 1st month is low and EDSS 24th month is medium, then response to IFNb is low.
20	If gender is male and age is adult, and if EDSS 1st month is low and EDSS 24th month is high, then response to IFNb is low.
21	If gender is male and age is adult, and if EDSS 1st month is medium and EDSS 24th month is high, then response to IFNb is low.
22	If gender is male and age is elderly, and if EDSS 1st month is low and EDSS 24th month is medium, then response to IFNb is low.
23	If gender is male and age is elderly, and if EDSS 1st month is low and EDSS 24th month is high, then response to IFNb is low.
24	If gender is male and age is elderly, and if EDSS 1st month is medium and EDSS 24th month is high, then response to IFNb is low.
25	If gender is female and age is adult, and if EDSS 1st month is high and EDSS 24th month is medium, then response to IFNb is high.
26	If gender is female and age is adult, and if EDSS 1st month is high and EDSS 24th month is low, then response to IFNb is high.
27	If gender is female and age is adult, and if EDSS 1st month is medium and EDSS 24th month is low, then response to IFNb is high.
28	If gender is female and age is elderly, and if EDSS 1st month is high and EDSS 24th month is medium, then response to IFNb is high.
29	If gender is female and age is elderly, and if EDSS 1st month is high and EDSS 24th month is low, then response to IFNb is high.
30	If gender is female and age is elderly, and if EDSS 1st month is medium and EDSS 24th month is low, then response to IFNb is high.
31	If gender is male and age is adult, and if EDSS 1st month is high and EDSS 24th month is medium, then response to IFNb is high.
32	If gender is male and age is adult, and if EDSS 1st month is high and EDSS 24th month is low, then response to IFNb is high.
33	If gender is male and age is adult, and if EDSS 1st month is medium and EDSS 24th month is low, then response to IFNb is high.
34	If gender is male and age is elderly, and if EDSS 1st month is high and EDSS 24th month is medium, then response to IFNb is high.
35	If gender is male and age is elderly, and if EDSS 1st month is high and EDSS 24th month is low, then response to IFNb is high.
36	If gender is male and age is elderly, and if EDSS 1st month is medium and EDSS 24th month is low, then response to IFNb is high.

2.3. Pipeline Prediction Model

A pipeline is a tool for setting a learning model, including a data preprocessing technique (for instance standardization for feature scaling), a transformation technique (such as PCA for data compression), and a learning algorithm (like MLP) for making predictions on new data. The structure of the proposed pipeline is shown in Figure 8.

Figure 8. Structure of proposed pipeline model, including feature scaling, data compression, and prediction algorithm.

PCA is a technique of dimensionality reduction, which transforms data from a high-dimensional space to a space of lower dimensions. The dimension reduction is achieved by selecting the principal components (directions of maximum variance) as a basis set for the new space [30]. Applications of PCA include analysis of genome data and gene expression levels. For extracting the principal components, the data are standardized; then, the covariance matrix is built, to store the pairwise covariances between features. For example, the covariance between two features $x_j$ and $x_k$ can be computed by Equation (3):

$${\sigma }_{jk}=\frac{1}{n}\sum _{i=1}^n(x_j^{\left(i\right)}-{\mu }_j)(x_k^{\left(i\right)}-{\mu }_k),$$

(3)

where ${\mu }_j$ and ${\mu }_k$ are the representative samples of the j and k features, respectively (${\mu }_k$, ${\mu }_j=0$, because of the standardization). The eigenvectors of the covariance matrix represent the principal components, and the eigenvalues define the magnitude of the eigenvectors, so the eigenvalues have to be ordered by decreasing the magnitude [31]. The ratio of an explained variance of an eigenvalue ${\lambda }_j$ is the fraction of the eigenvalue and the total sum of the eigenvalues, as shown by Equation (4):

$$\frac{{\lambda }_j}{{\sum }_{j=1}^d{\lambda }_j}$$

(4)

MLP is a supervised learning algorithm that uses the backpropagation technique for learning. The structure of MLP consists of an input layer of neurons that receive the $X=x_1,x_2,\dots ,x_m$ sample inputs, one or more hidden layers of neurons that convert the values from the previous layer to a weighted linear summation, $w_1{x}_1+w_2{x}_2+\dots +w_m{x}_m$, followed by a non-linear activation function that is used to learn the weights, and then the output layer that predicts the class label of the samples [32]. During the learning stage, MLP compares the true class labels to the continuous output values of the non-linear activation function, to compute the prediction error and update the weights. The hyperparameters of MLP are arbitrarily set as follows: solver = ’sgd’, activation = ’tanh’, and learning_rate_init = 0.01.

2.4. Performance Evaluation

One of the key steps in building an ML or deep learning (DL) model is estimating its performance with new data. A model can suffer underfitting (high bias) if the model is too simple, or can suffer overfitting (high variance) if the model is too complex for the subjacent training data [31]. In order to get an acceptable bias–variance rate, the k-iterations cross-validation (CV) technique is implemented, which can obtain reliable estimates of the model’s generalization performance.

In the k-iterations CV, the training dataset is randomly split into k iterations without replacement, where $k-1$ iterations are used for model training, and 1 iteration is used for performance evaluation. This process is repeated k times, to obtain k models and performance estimates. Then, the average performance of the models is computed by Equation (5), based on the independent iterations, to obtain a performance estimate:

$$E=\frac{1}{k}\sum _{i=1}^k{E}_i$$

(5)

Typically, the k-iterations CV is used for model fitting, to find the optimal values of the hyperparameters that produce satisfactory generalization performance. Also, the confusion matrix (CM) is computed, which reports the count of the predictions of a classifier [33]: true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN).

3. Results

For this paper, a fuzzy logic system based on MAFS was implemented, to classify RRMS patients as high, medium, or low responders to IFN-$\beta$ treatment. Also, for comparison purposes, a hierarchical clustering technique was implemented, to classify the same patients. After the dataset outputs were labeled, the gene features were used as training inputs for the proposed pipeline prediction model.

3.1. Fuzzy Logic System

At fuzzification stage, the membership values were computed for each one of the input variables. Table 5 and Table 6 display the computed values of each membership function for all the samples.

Table 5. Fuzzification results (gender and age).

Sample	${\mathit{\mu }}_{\mathit{Female}}\left(\mathit{Gender}\right)$	${\mathit{\mu }}_{\mathit{Male}}\left(\mathit{Gender}\right)$	${\mathit{\mu }}_{\mathit{Pediatric}}\left(\mathit{Age}\right)$	${\mathit{\mu }}_{\mathit{Adult}}\left(\mathit{Age}\right)$	${\mathit{\mu }}_{\mathit{Elderly}}\left(\mathit{Age}\right)$
1	1	0	0	0.687	0.015
2	0	1	0	0.88	0
3	1	0	0.375	0.4	0
4	1	0	0.315	0.448	0
5	1	0	0	0.975	0
6	1	0	0	0.784	0
7	1	0	0	0.856	0
8	0	1	0.225	0.479	0
9	1	0	0.345	0.424	0
10	0	1	0	0.808	0
11	0	1	0.255	0.496	0
12	1	0	0.258	0.472	0
13	1	0	0	0.952	0
14	1	0	0	0.928	0
15	1	0	0	0.808	0
16	1	0	0	1	0
17	0	1	0.015	0.688	0
18	1	0	0	0.832	0
19	0	1	0	0.903	0
20	0	1	0	0.76	0
21	1	0	0	0.952	0
22	1	0	0	0.712	0
23	0	1	0.585	0.232	0
24	1	0	0.405	0.376	0
25	0	1	0	0.712	0

Table 6. Fuzzification results (EDSS 1st month and EDSS 24th month).

Sample	${\mathit{\mu }}_{\mathit{Low}}\left(\mathit{EDSS}{}^1\right)$	${\mathit{\mu }}_{\mathit{Med}}\left(\mathit{EDSS}{}^1\right)$	${\mathit{\mu }}_{\mathit{High}}\left(\mathit{EDSS}{}^1\right)$	${\mathit{\mu }}_{\mathit{Low}}\left(\mathit{EDSS}{}^2\right)$	${\mathit{\mu }}_{\mathit{Med}}\left(\mathit{EDSS}{}^2\right)$	${\mathit{\mu }}_{\mathit{High}}\left(\mathit{EDSS}{}^2\right)$
1	0.25	0.75	0.0	0.0	0.875	0.125
2	1.0	0.0	0.0	1.0	0.0	0.0
3	1.0	0.0	0.0	1.0	0.0	0.0
4	0.25	0.75	0.0	0.375	0.625	0.0
5	0.5	0.5	0.0	0.625	0.375	0.0
6	0.75	0.25	0.0	0.125	0.875	0.0
7	0.25	0.75	0.0	0.5	0.5	0.0
8	0.875	0.125	0.0	0.75	0.25	0.0
9	0.25	0.75	0.0	0.25	0.75	0.0
10	1.0	0.0	0.0	1.0	0.0	0.0
11	0.75	0.25	0.0	0.625	0.375	0.0
12	0.875	0.125	0.0	0.625	0.375	0
13	1.0	0.0	0.0	1.0	0.0	0.0
14	0.375	0.625	0.0	0.5	0.5	0.0
15	0.75	0.25	0.0	0.5	0.5	0.0
16	0.375	0.625	0.0	0.375	0.625	0.0
17	0.875	0.125	0.0	0.125	0.875	0.0
18	0.75	0.25	0.0	0.75	0.25	0.0
19	0.5	0.5	0.0	0.75	0.25	0.0
20	1.0	0.0	0.0	1.0	0.0	0.0
21	0.75	0.25	0.0	0.75	0.25	0.0
22	0.75	0.25	0.0	0.5	0.5	0.0
23	0.875	0.125	0	0.75	0.25	0.0
24	1.0	0.0	0.0	1.0	0.0	0.0
25	1.0	0.0	0.0	1.0	0.0	0.0

¹ 1st month. ² 24th month.

At the approximate reasoning stage, each one of the 36 inference rules from the knowledge base were evaluated with the obtained membership values from Table 5 and Table 6. For example, considering the input values of #7 sample (gender: “female”, age: “44”, EDSS 1st month: “4”, and EDSS 24th month: “3”), the inference engine results are shown in Table 7. In this case, only four rules—1, 2, 13, and 27—had an inference result different to zero. Figure 9 displays the evaluation graph of previous inference rules.

Table 7. Inference results for #7 sample.

#	Rule	Inference Engine
1	If gender is “female” and age is “adult”, and if EDSS 1st month is “low” and EDSS 24th month is “low”, then the response to IFNb is “medium”.	min(1.0, 0.856, 0.25, 0.5) = 0.25
2	If gender is “female” and age is “adult”, and if EDSS 1st month is “medium” and EDSS 24th month is “medium”, then the response to IFNb is “medium”.	min(1.0, 0.856, 0.75, 0.5) = 0.5
13	If gender is “female” and age is “adult”, and if EDSS 1st month is “low” and EDSS 24th month is “medium”, then the response to IFNb is “low”.	min(1.0, 0.856, 0.25, 0.5) = 0.25
27	If gender is “female” and age is “adult”, and if EDSS 1st month is “medium” and EDSS 24th month is “low”, then the response to IFNb is “high”.	min(1.0, 0.856, 0.75, 0.5) = 0.5

Figure 9. Evaluation graph of the 1, 2, 13, and 27 inference rules. The result graph consists of the combination of the four rules’ inference values.

At defuzzification stage, the numerical outputs were computed, substituting the inference engine results into Equation (1), based on the inference result graphs. For example, for the inference results of #7 sample according to the result graph of Figure 10, the numerical output was computed as follows:

$$y_0=\frac{0\ast 0.25+0.1\ast 0.25+0.2\ast 0.25+0.3\ast 0.5+0.4\ast 0.5+\cdots +0.9\ast 0.5+1\ast 0.5}{0.25+0.25+0.25+0.5+0.5+\cdots +0.5+0.5}$$

(6)

$$y_0=\frac{2.675}{4.75}=0.563\approx 0.554$$

(7)

Figure 10. Inference result graph of #7 sample, which includes the values of the “Low”, “Medium”, and “High” linguistic labels.

The small difference in calculation was due to the fuzzy system implementation in Matlab software providing more accurate results than by hand.

Finally, a classification of high, medium, and low responders to the IFN-$\beta$ drug was carried out, by three different methods: (1) opinion of a neurology expert, (2) proposed fuzzy system, and (3) agglomerative clustering model. The results are displayed in Table 8.

Table 8. Classification of response to IFN-$\beta$. The resulting numerical values of defuzzification less than 0.5 are considered as low responder (LR), those equal to 0.5 as medium responder (MR), and those greater than 0.5 as high responder (HR). For comparison purposes, the input data of Table 1 were preprocessed by the StandardScaler technique, and they were used to train a prediction model of agglomerative clustering (n_clusters = 3).

Sample	Expert Opinion	Fuzzy System (Deffuzification)	Agglomerative Clustering
1	LR	0.459 ⇒ LR	HR
2	MR	0.5 ⇒ MR	LR
3	MR	0.5 ⇒ MR	MR
4	HR	0.529 ⇒ HR	HR
5	HR	0.527 ⇒ HR	HR
6	LR	0.337 ⇒ LR	HR
7	HR	0.554 ⇒ HR	HR
8	LR	0.474 ⇒ LR	LR
9	HR	0.53 ⇒ HR	HR
10	MR	0.5 ⇒ MR	LR
11	LR	0.472 ⇒ LR	LR
12	LR	0.445 ⇒ LR	MR
13	MR	0.5 ⇒ MR	MR
14	HR	0.527 ⇒ HR	HR
15	LR	0.446 ⇒ LR	MR
16	MR	0.5 ⇒ MR	HR
17	LR	0.302 ⇒ LR	HR
18	MR	0.5 ⇒ MR	MR
19	HR	0.554 ⇒ HR	LR
20	MR	0.5 ⇒ MR	LR
21	MR	0.5 ⇒ MR	MR
22	LR	0.446 ⇒ LR	MR
23	LR	0.463 ⇒ LR	LR
24	MR	0.5 ⇒ MR	MR
25	MR	0.5 ⇒ MR	LR

As Table 6 shows, 100% of the outputs were correctly labeled by the proposed fuzzy system, while 52% were correctly labeled by agglomerative clustering according to an expert opinion.

3.2. Pipeline Prediction Model

Once the dataset output labels had been classified, the pipeline prediction model was implemented, for making predictions on new data. First, the gene expression values were scaled by the StandardScaler technique. Then, the PCA technique was used, to reduce the dimensionality of the gene dataset by compressing it into a new subspace, so that only the subset of the eigenvectors (principal components) that contained more information (maximum variance) were selected. Figure 11 shows the results of the explained variance ratio of the eigenvalues.

Figure 11. Explained variance ratio. The first principal component by itself accounts for almost 20% of the total variance. Furthermore, the first two combined principal components represent approximately 40% of the variance.

Figure 12 shows the graph used to determine the optimal value of the number of principal components (n_components) for the PCA technique to achieve the high testing accuracy of the MLP prediction algorithm.

Figure 12. Optimal value of n_components. The value of the n_components is arbitrarily set to 13, for attaining a 0.8 average testing accuracy.

3.3. Performance Evaluation

In this paper, the $k=8$-iterations CV technique was implemented for evaluating the prediction model performance. Table 9 presents the CV accuracy results for each fold. The maximun CV accuracy was achieved at the 7th and 8th folds, and the average estimate performance was 0.521 +/− 0.327.

Table 9. K-iterations cross-validation results.

Fold	CV Accuracy
1	0.333
2	0.667
3	0.333
4	0.333
5	0.500
6	0.000
7	1.000
8	1.000

The input data (1875 samples) were divided into 80% $X\_train$ (1500 samples) and 20% $X\_test$ (375 samples), according to Pareto analysis [34], in order to avoid overfitting. In addition, the output labels (25 samples) were divided into 80% $y\_train$ (20 samples) and 20% $y\_test$ (5 samples), for validation. The CM was computed with test and predicted data, and the results are shown in Figure 13.

Figure 13. Confusion matrix results: (0) high responder to IFN-$\beta$, (1) low responder to IFN-$\beta$, and (2) medium responder to IFN-$\beta$.

The CM results represents one high-responder patient who was correctly predicted as a high responder, one low-responder patient who was correctly predicted as a low responder, one low-responder patient who was wrongly predicted as a medium responder, and two medium-responder patients who were correctly predicted as medium responders. Based on previous results, the prediction model achieved 0.8 testing accuracy.

4. Discussion

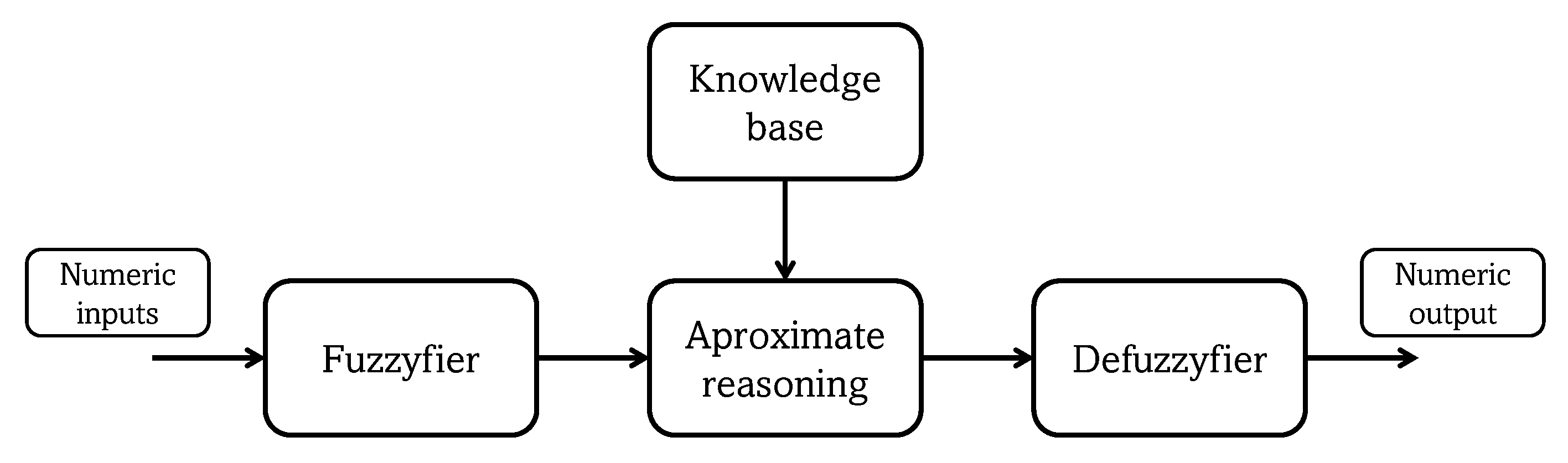
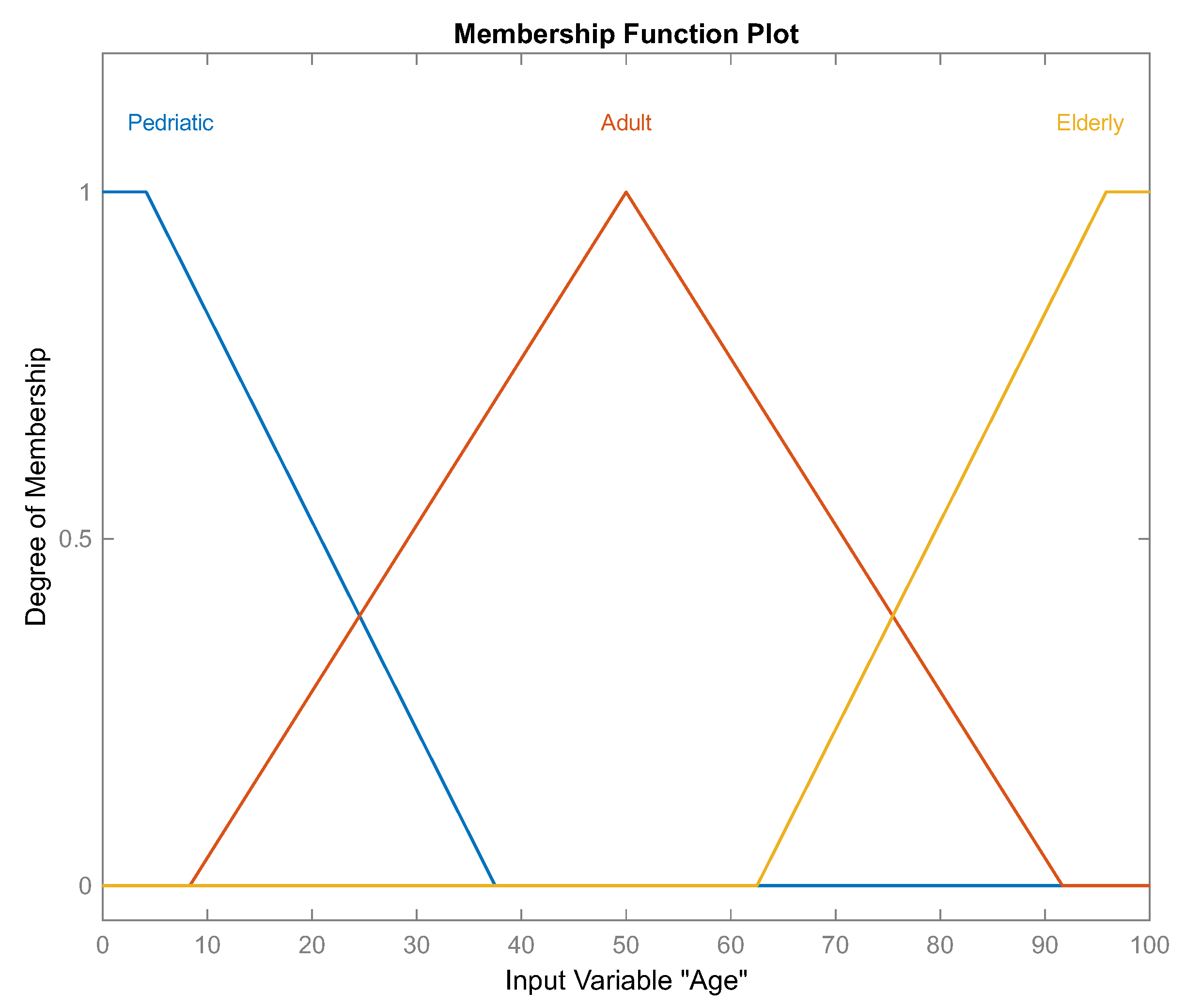
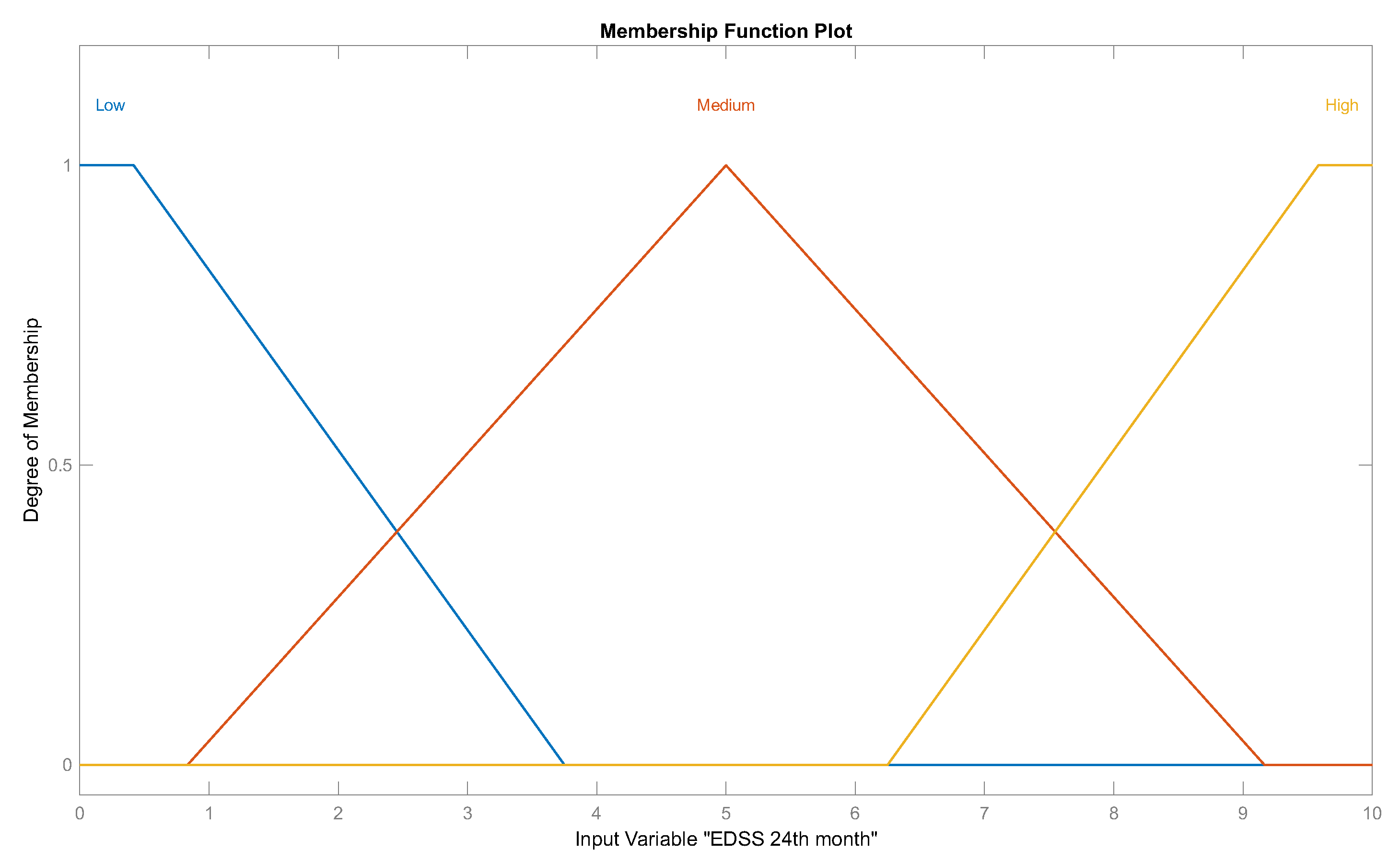
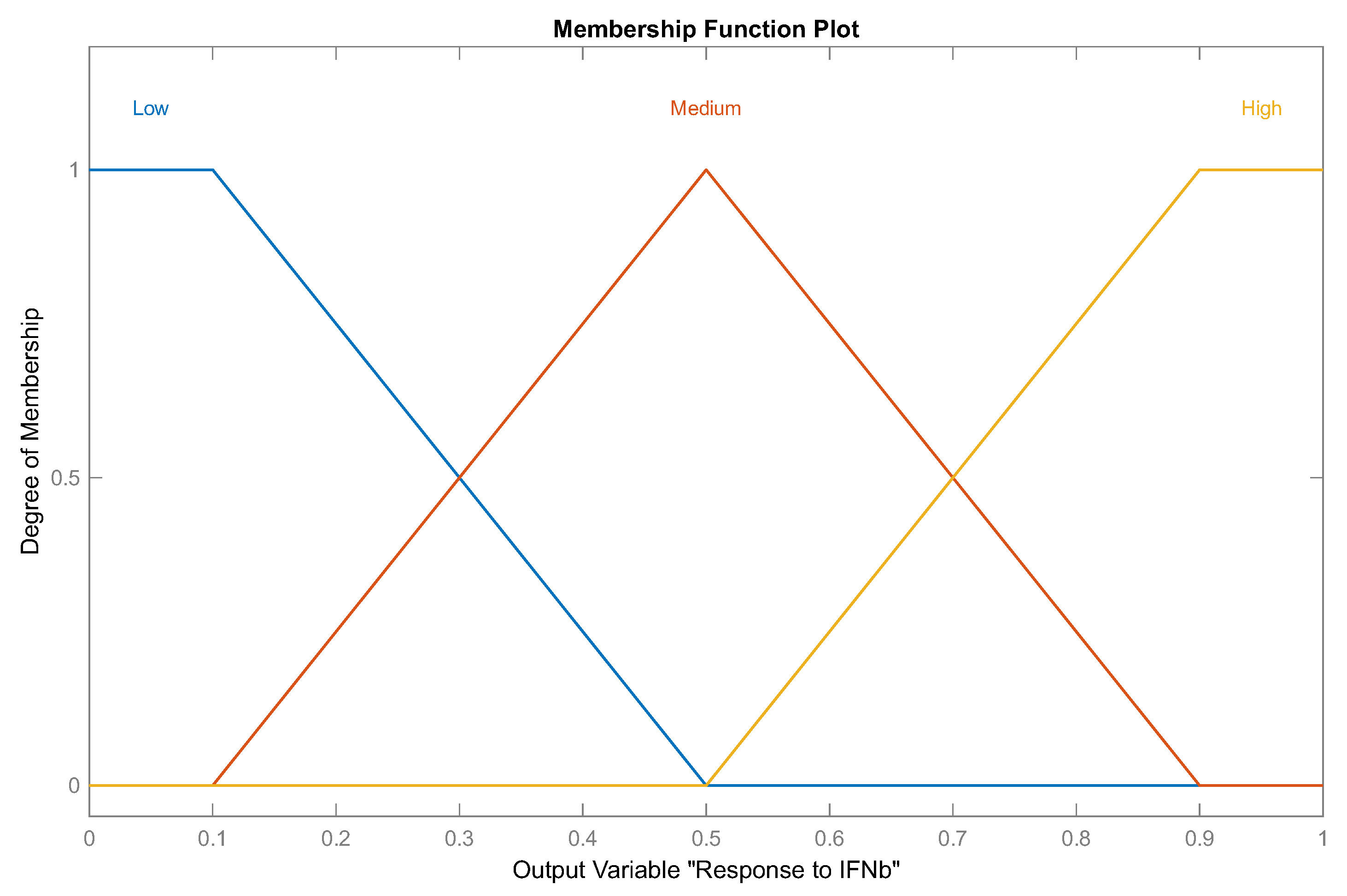
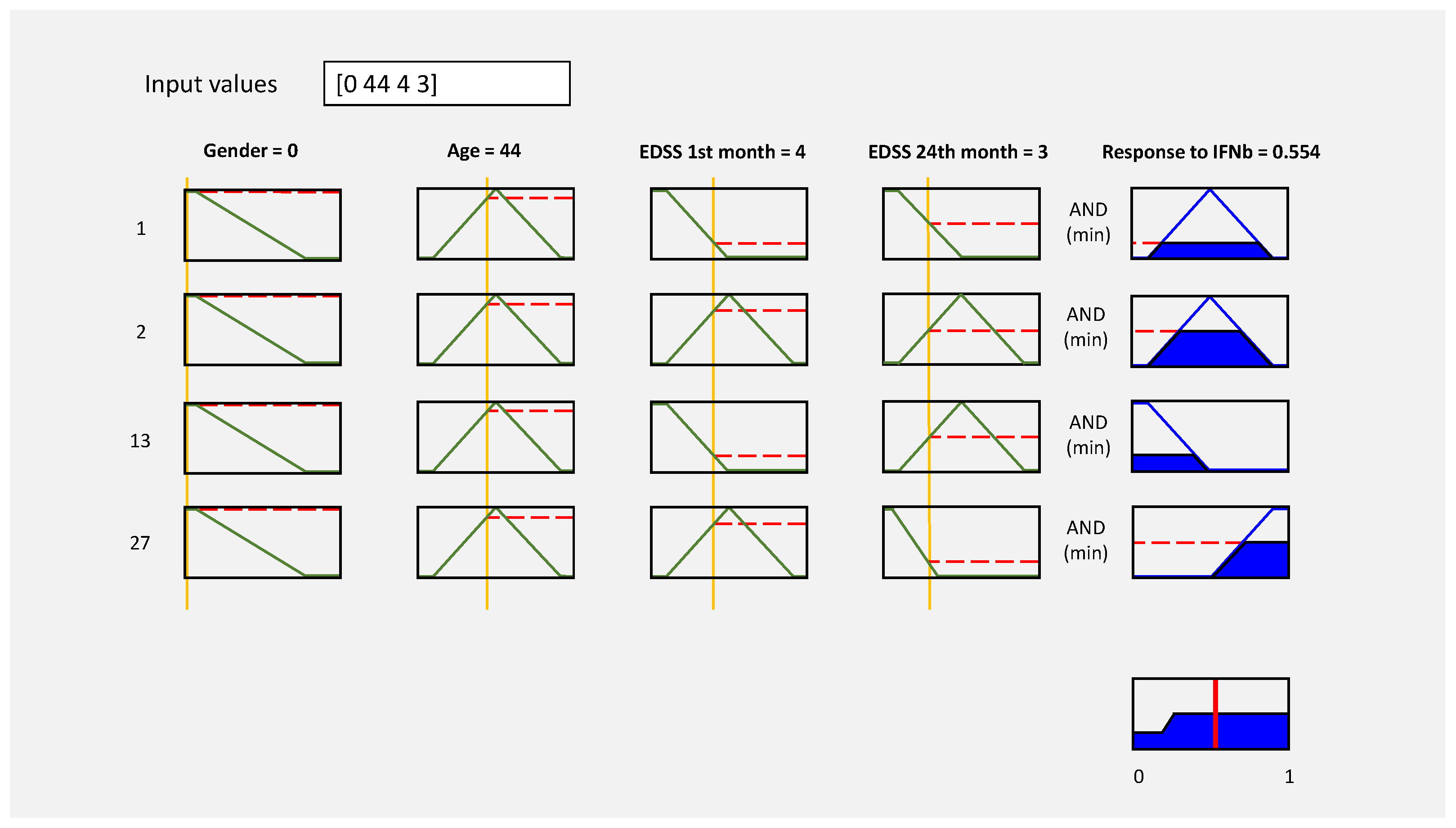
While binary logic generates only two output types—[0, 1]—fuzzy inference engines use approximate reasoning based on generalized rules of inference. Hence, fuzzy systems are convenient methods for decision support, due to their ability to process inaccurate information. For this paper, an alternative fuzzy system based on expert knowledge was implemented, for decision support in classification of the response to IFN-$\beta$ treatment of RRMS patients. Demographic and clinical characteristics were used as input variables to the fuzzy system. As shown in Table 8, the classification of the proposed fuzzy system achieved better results than the agglomerative clustering, because the latter did not consider the intrinsic properties of the data, it simply used the distance between the data points to group them into clusters. A software issue in the fuzzy system design was to set a small number of input variables: the greater the number of variables, the greater the data processing time.

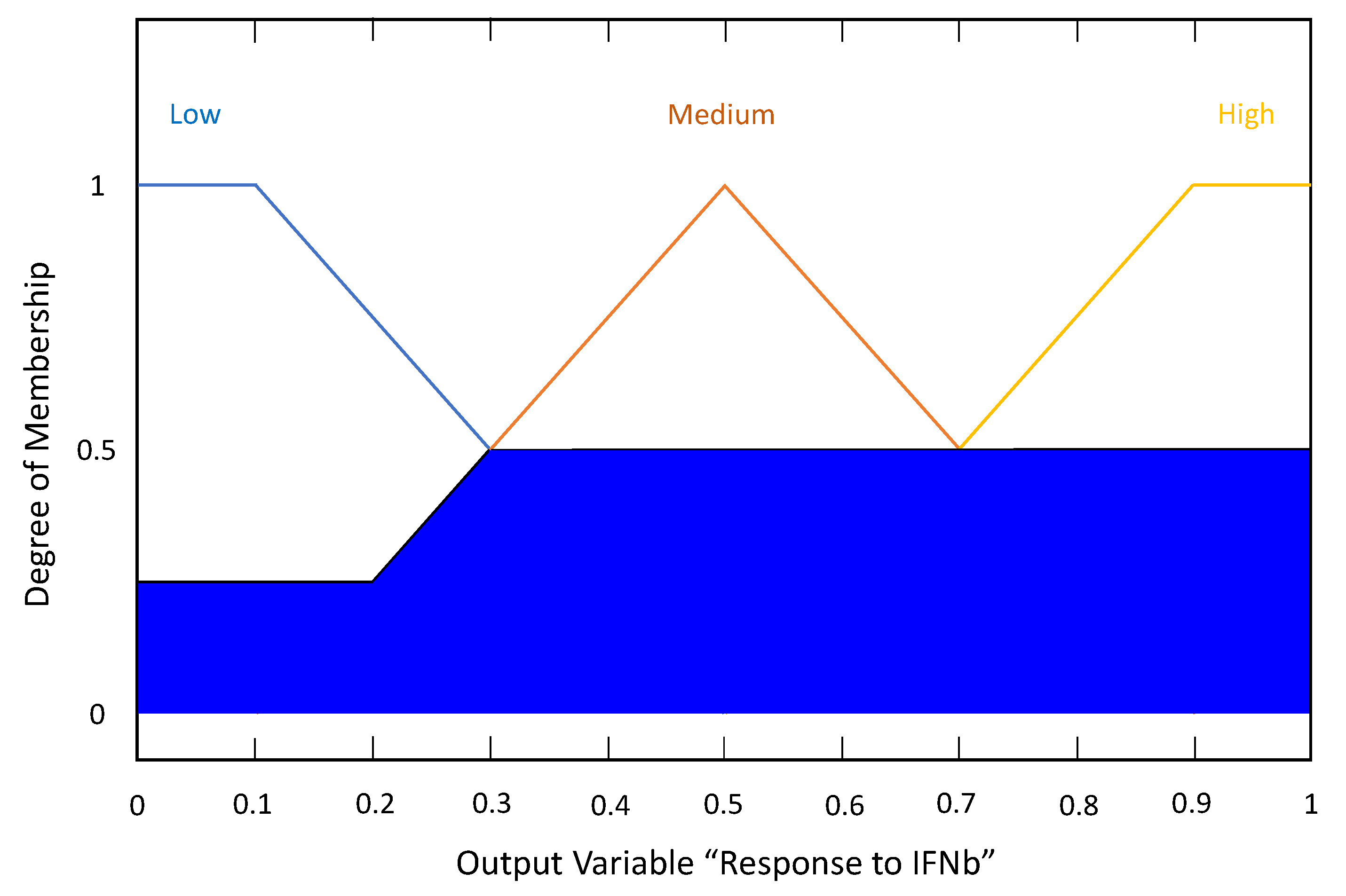
It is important to mention that at the beginning of the fuzzy system design, a proposal of fuzzy rules definition was reviewed by the expert neurologist, who considered only two output linguistic labels: “low” and “high” responder to IFN-$\beta$. Under these conditions, 88% efficiency was obtained in the results. After validating the results, the expert recommended adding an extra label—“medium”—to classify MS patients who had the same EDSS level at the beginning as at the end of treatment. After redefining the fuzzy rules, 100% efficiency was achieved.

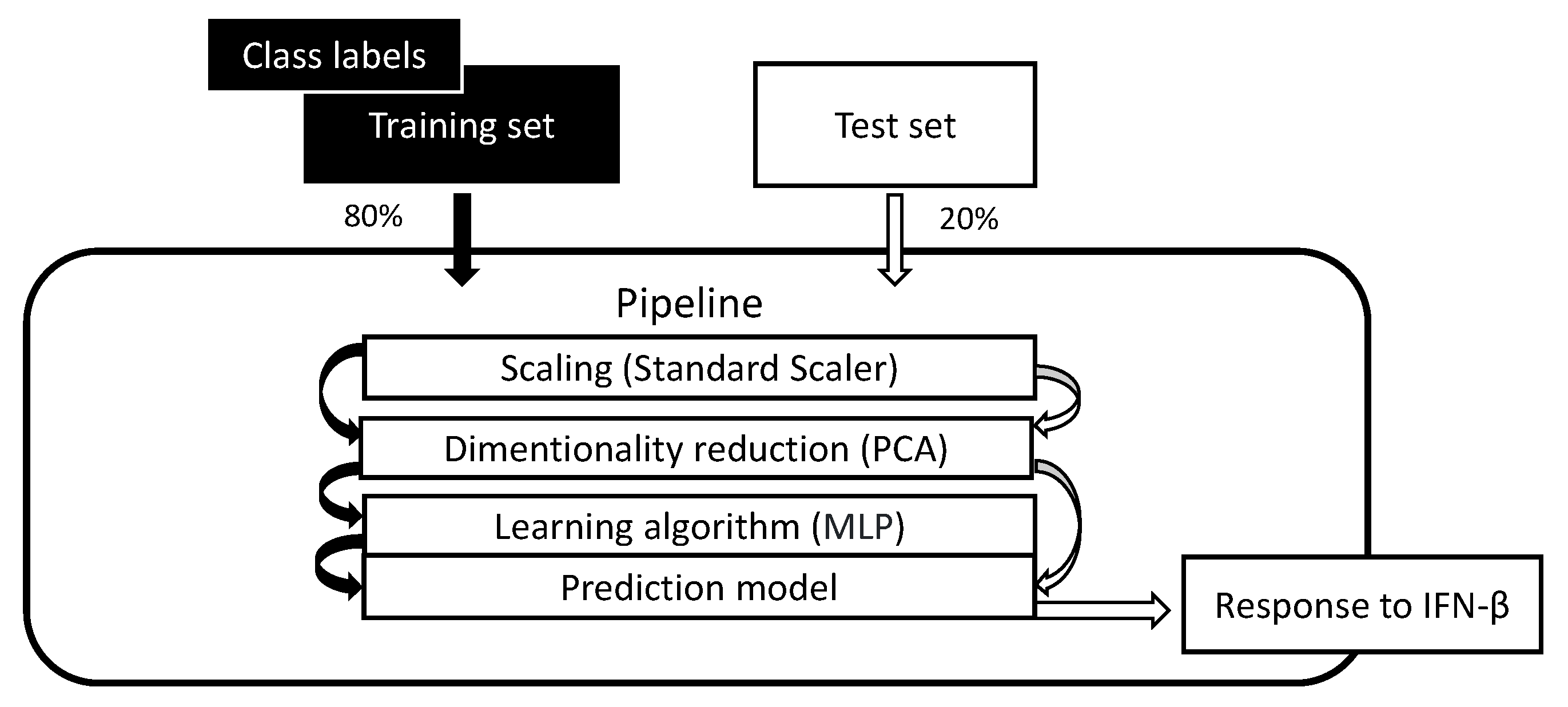
Once the dataset output labels were classified by the fuzzy system, a pipeline prediction model was implemented, including data standardization, data compression through the PCA technique, and an MLP learning algorithm. The pipeline model was trained with 15 biomarkers associated with the response to IFN-$\beta$ for predicting whether RRMS patients were potential candidates to be treated with this drug. 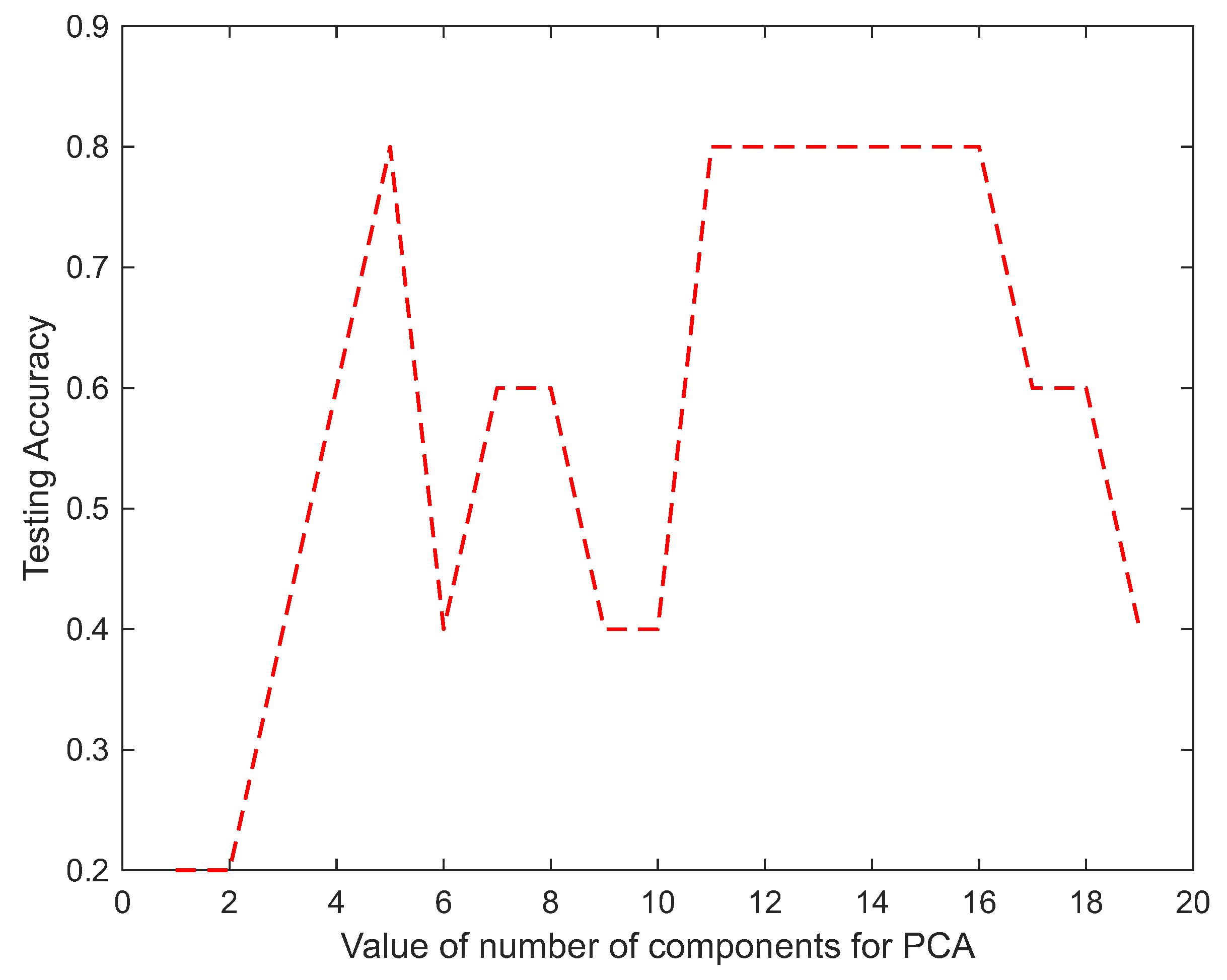As shown in Figure 12, by setting 13 principal components for PCA, 0.8 testing accuracy was achieved. The use of the PCA technique for data compression provides some advantages: (1) the reduced dimension has the property of keeping most of the useful information, while reducing noise and other undesirable data, (2) the time and memory used in the data processing are smaller, (3) it provides a way to understand and visualize the structure of complex datasets. 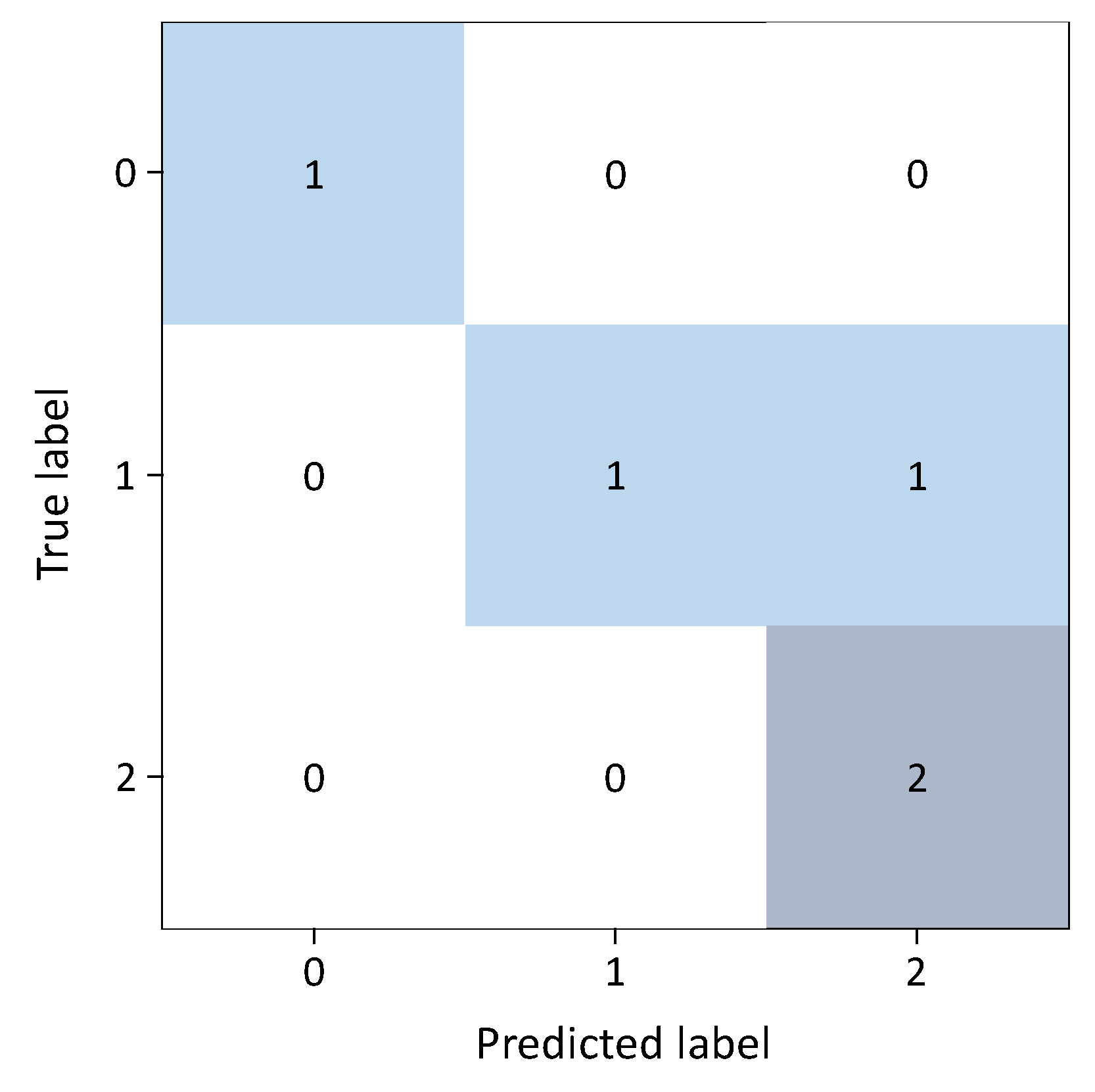The use of the k-iterations CV technique helps to obtain a good bias–variance rate. The highest CV accuracy was achieved at the 7th and 8th folds, as shown in Table 9. One disadvantage in evaluating the prediction model performance was that the test samples size was too small. Therefore, the number of iterations for the CV technique was limited to eight.

ML algorithms can find natural patterns in the data, and they are a useful alternative in the field of bio-informatics. These algorithms have been implemented to improve the MS diagnosis [20,21] and to help specialists to predict the response to drug treatments in MS patients [22,25]. Table 10 presents a comparison of the performance results of some ML applications in MS study.

Table 10. Performance results comparison of ML applications in MS study.

Author	Prediction	ML Technique	Accuracy
Fagone et al. [22]	Response to Natalizumab	UCRC	0.892
Goyal et al. [20]	MS diagnostic	RF	0.909
Jin et al. [25]	Response to IFN-$\beta$	SVM	0.809
Chen et al. [21]	MS diagnostic	SVM	0.930
Actual Paper	Response to IFN-$\beta$	MLP	0.521 +/− 0.327 1

¹ Average estimate performance achieved by k=8-iterations cross-validation.

The results obtained in this paper could be a reference for future works, using other genes related to the response to IFN-$\beta$ treatment, as training data. Also, new prediction models, such as evolutionary or DL algorithms, could be designed, to improve model performance.

5. Conclusions

In general, IFN-$\beta$ treatment effectively reduces the rate of relapse and delays the progression of neurological disability in MS patients. However, a percentage of patients do not respond, or partially respond to this drug. In this paper, the proposed fuzzy system, based on the opinion of an expert, demonstrated high efficiency in decision support, and it could be a useful tool in labeling classes, such as classification of the response to IFN-$\beta$ therapy.

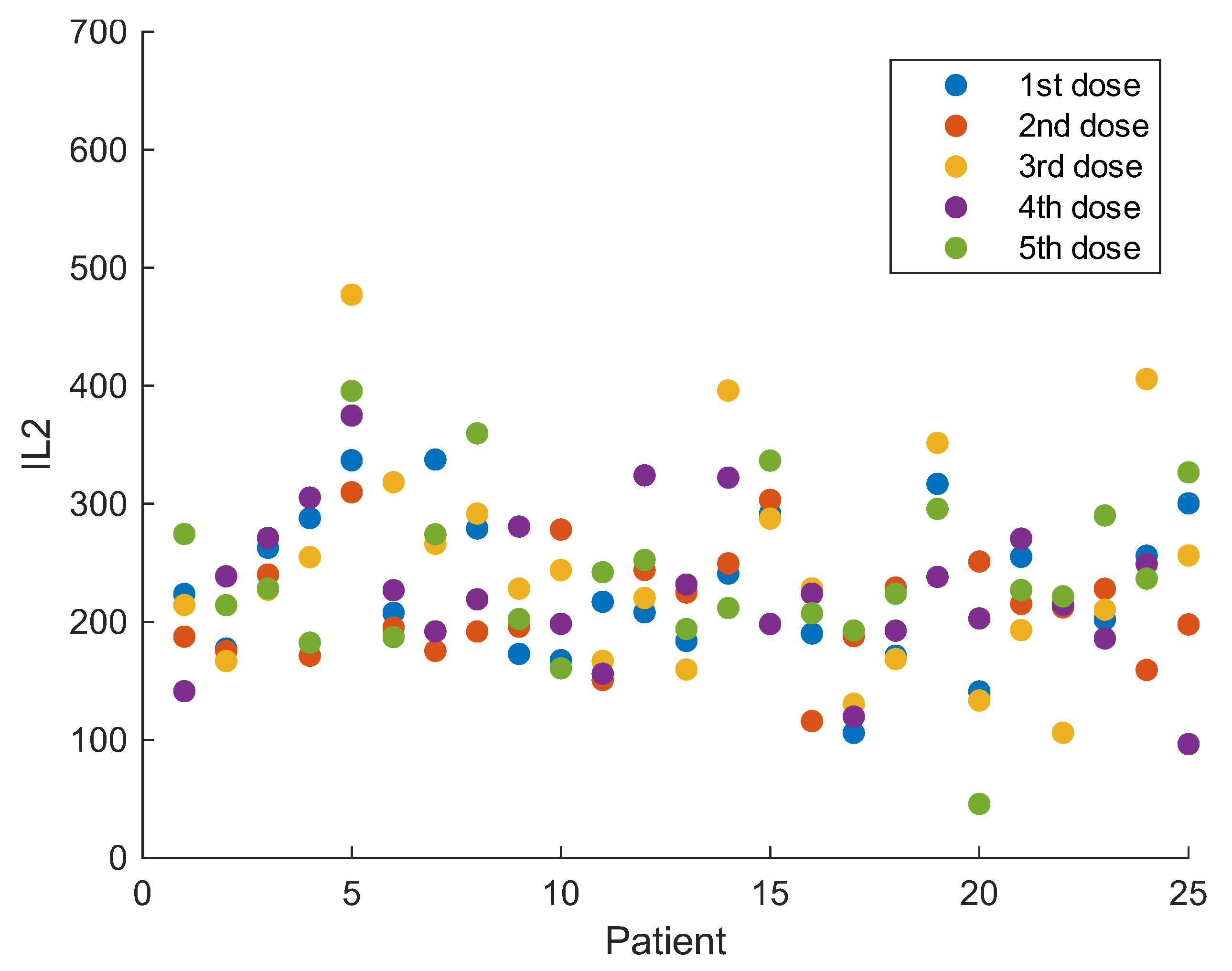
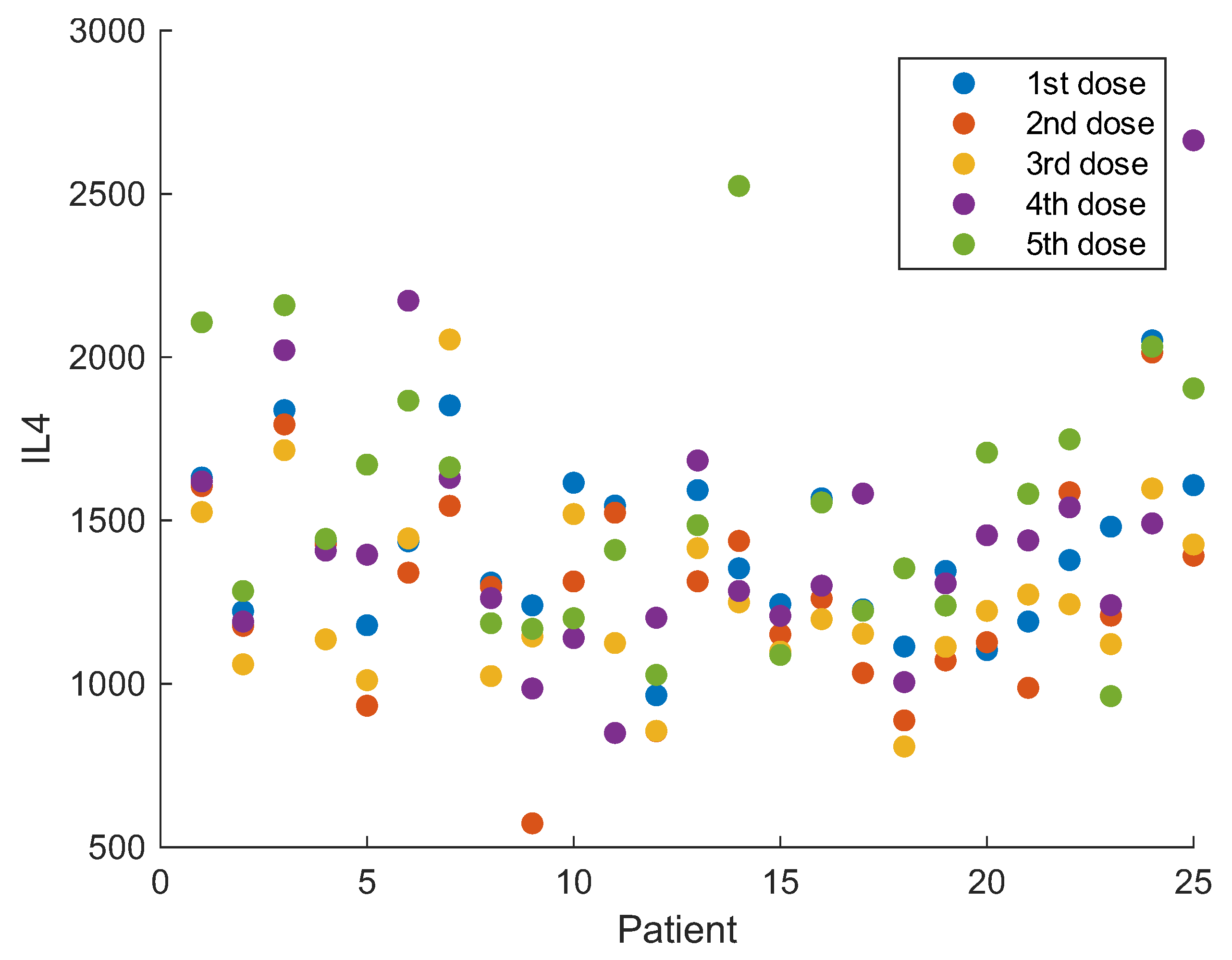
Although genome research is complex, there are ML methods—for instance, the proposed pipeline model—that can effectively deal the gene data for obtaining reliable predictions, to guide specialists in the selection of MS patients who may obtain the greatest benefit from IFN-$\beta$ treatment. Biomarkers—in particular IL-2, IL-12, IFN-$\gamma$, TNF-$\alpha$, IL-4, IL-10, TGF-$\beta$, CD46, CD58, FHIT, IRF5, GAPVD1, GPC5, GRM3, and GRIK2—can be convenient predictive variables for improving the comprehension of the influence of IFN-$\beta$ therapy in MS patients.